Functional connectome reorganization relates to post-stroke motor recovery and structural and functional disconnection

Abstract

Motor recovery following ischemic stroke is contingent on the ability of surviving brain networks to compensate for damaged tissue. In rodent models, sensory and motor cortical representations have been shown to remap onto intact tissue around the lesion site, but remapping to more distal sites (e.g. in the contralesional hemisphere) has also been observed. Resting state functional connectivity (FC) analysis has been employed to study compensatory network adaptations in humans, but mechanisms and time course of motor recovery are not well understood. Here, we examine longitudinal FC in 23 first-episode ischemic pontine stroke patients and utilize a graph matching approach to identify patterns of functional connectivity reorganization during recovery. We quantified functional reorganization between several intervals ranging from 1 week to 6 months following stroke, and demonstrated that the areas that undergo functional reorganization most frequently are in cerebellar/subcortical networks. Brain regions with more structural and functional connectome disruption due to the stroke also had more remapping over time. Finally, we show that functional reorganization is correlated with the extent of motor recovery in the early to late subacute phases, and furthermore, individuals with greater baseline motor impairment demonstrate more extensive early subacute functional reorganization (from one to two weeks post-stroke) and this reorganization correlates with better motor recovery at 6 months. Taken together, these results suggest that our graph matching approach can quantify recovery-relevant, whole-brain functional connectivity network reorganization after stroke.

1. Introduction

Motor deficits are among the most common and disruptive symptoms of ischemic stroke. Spontaneous recovery of motor function occurs for most patients (Duncan et al., 2000), and largely depends on the ability of brain networks to functionally reorganize and compensate for lost function (Grefkes et al., 2008; Rehme and Grefkes, 2013). As demonstrated by animal models, the functionality of damaged motor regions may be remapped to surviving tissue around the lesion (Winship and Murphy, 2009). However, brain areas distant to the lesion that have similar function and/or connectivity as the damaged area have also been shown to compensate for lost function (Adam et al., 2020; Brown et al., 2009; Murata et al., 2015; Winship and Murphy, 2009).

In humans, functional reorganization has been studied with functional magnetic resonance imaging (fMRI). Task fMRI studies have demonstrated that cortical reorganization related to motor recovery can be characterized by task-based activation of surviving ipsilesional cortex, contralesional areas, and even regions not classically activated by motor tasks in healthy subjects (Ward et al., 2003). Recently, resting-state fMRI has emerged as a means to study connectivity changes after stroke in subjects who are severely impaired and cannot perform motor tasks. Resting-state fMRI has been used to identify recovery-related changes in functional connectivity between specific brain regions, reflecting network-level changes (Park et al., 2011). However, few studies to date have attempted to capture longitudinal network-level reorganization after stroke using resting-state fMRI.

Prior studies investigating neural correlates of motor recovery have also focused almost exclusively on supratentorial strokes that impact the internal capsule and surrounding areas. Infratentorial pontine strokes may impact the corticospinal tract directly or the connections between motor cortex and the cerebellum (Lu et al., 2011). These strokes account for roughly 7 percent of all ischemic strokes (Saia and Pantoni, 2009), and may have different mechanisms of recovery-related reorganization from those of more well-studied supratentorial strokes.

Remote brain areas anatomically connected to the lesion undergo structural and functional changes through a process known as diaschisis (Carrera and Tononi, 2014). Functional remapping of areas structurally disconnected by the lesion may be an important component of the recovery process that has not been deeply explored. Recent studies have also demonstrated that functional connectivity (FC) changes occur following structural connectivity disruption after stroke (Griffis et al., 2020; Lu et al., 2011). We hypothesize that functional reorganization may also occur in areas whose FC is reduced due to the stroke. In this study, we propose a novel measure to capture adaptive functional network reorganization after pontine stroke, outlined below, and relate it to patterns of regional stroke-related structural connectome disruption and measures of upper-arm motor recovery.

Connectivity to the rest of the brain is one aspect of a brain region’s functional role in the network. We propose that instances of functional reorganization over time may be captured by identifying brain regions whose pattern of FC with the rest of the brain is more closely matched by a different brain region at a later date. Considering functional connectomes as a graph, the task of identifying similar nodes (gray matter regions, in this case) between two functional connectomes can be considered a graph matching problem (Conte et al., 2004). Conceptually, the process of graph matching exchanges the labels of regions in a network when doing so results in increased similarity of the two networks. When two regions exchange FC profiles, the regions are said to have been “remapped”. We hypothesize that graph matching, applied recently to brain networks for the first time to assess the relationship between functional and structural connectivity networks (Osmanlıoğlu et al., 2019), will allow accurate quantification of whole brain, network-level, recovery-relevant functional reorganization after stroke.

As far as we know, no work has attempted to detect connectivity network-level functional reorganization in post-stroke recovery with longitudinal MRI, much less correlate it with measures of recovery or patterns of structural connectome damage. We hypothesize that (1) brain regions with more structural and functional damage due to the stroke will more frequently functionally reorganize, (2) more impaired subjects will have more early functional reorganization in the sub-acute stages, (3) the amount or early reorganization will be correlated with long-term recovery, and (4) the amount of functional reorganization over time will correlate with the change in motor impairment between subsequent sessions.

2. Materials and methods

2.1. Data description

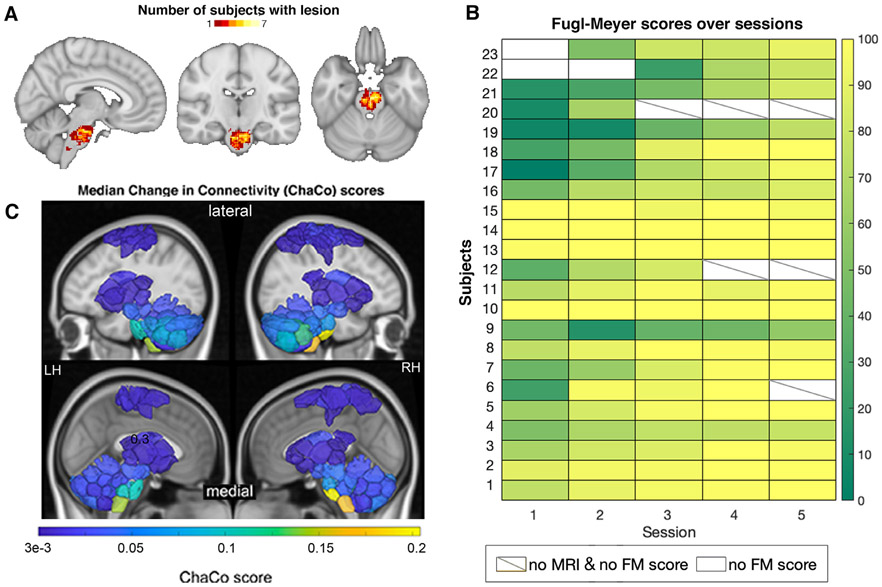
The data consist of 23 first-episode stroke patients (34–74 years old; mean age 57 years; 8 female) with isolated pontine infarcts and 24 healthy age- and sex-matched controls (33–65 years old; mean age 52 years; 10 female). A subset of the data (11 stroke subjects and 11 healthy control subjects) used here has been previously described in Lu et al., 2011; this study includes an additional 12 stroke subjects and 13 control subjects. Of the twenty-three stroke subjects, fourteen had right brainstem infarcts and nine had left brainstem infarcts (Fig. 1A). Patients were scanned five times over a period of 6 months. Specifically, MRIs were obtained at 7, 14, 30, 90 and 180 days after stroke onset on a 3T TimTrio Siemens using a 12-channel phase-array head coil. Fugl-Meyer motor scores were obtained twice at each session, and later averaged and normalized to a range of 0–100 (Fig. 1B). Anatomical images were acquired using a sagittal MP-RAGE three-dimensional T1-weighed sequence (TR, 1600ms; TE 2.15ms; flip angle, 9, 1.0 mm isotropic voxels, FOV 256 x 256). Each MRI session involved between two and four runs of resting-state fMRI at 6 minutes each. Subjects were instructed to stay awake with their eyes open; no other task instruction was provided. Images were acquired using the gradient-echo echo-planar pulse sequence (TR, 3000ms; TE, 30ms; flip angle, 90, 3 mm isotropic voxels).

Fig. 1.

Overview of individuals’ stroke lesions, resulting structural disconnection and Fugl-Meyer score trajectories. A. Distribution of lesions across the brain. Colors indicate the number of subjects with a lesion in that voxel. B. Normalized Fugl-Meyer scores for all subjects over the five post-stroke sessions. Boxes colored white indicate missing motor scores and diagonal lines within the box indicate missing MRI data for the corresponding time point. C. Group median structural disconnection scores for each brain region calculated as the number of streamlines connected to each region that intersect with the lesion, normalized by the total number of streamlines connecting to that region (only displaying regions with disconnection scores > 0.0003). Cortical areas with non-zero median ChaCo scores reflect motor regions at the end of disrupted corticospinal tracts. Top row of each subject inset shows a lateral view of the brain, bottom row of each inset shows a medial view.

2.2. Structural data processing

Preprocessing of the longitudinal structural data included affine registration of each subject’s T1 scans to the baseline T1 scan, collapsing co-registered files to an average T1 and creation of a skull-stripped brain mask followed by manual editing and binarization of the hand-edited mask. The brain mask was then transformed back to each of the follow-up T1s in native space using the inverse registration acquired from the first step. This was followed by bias field correction of all the T1 scans, transformation of native-space bias field-corrected data back to baseline space, and the creation of an average bias field-corrected scan for each subject. Stroke lesion masks were hand-drawn on these transformed T1 scans by ADB and JEB. Structural normalization was performed with the CONN toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012).

2.3. Functional data processing

Preprocessing of the longitudinal functional data was performed using the CONN toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012), including functional realignment of volumes to the baseline volume, slice timing correction for alternating acquisition, segmentation and normalization, and smoothing with a 4 mm FWHM kernel. The WM and CSF probability maps used to derive WM and CSF BOLD signal were first thresholded above 50% for each subject, and a one-voxel binary erosion step was applied to these thresholded maps (Whitfield-Gabrieli and Nieto-Castanon, 2012). This was followed by a denoising protocol (CompCor) (Behzadi et al., 2007) which regressed out the cerebrospinal fluid and white matter signal, as well as 24 realignment parameters (added first-order derivatives and quadratic effects). Temporal band pass filtering (0.008–0.09Hz), despiking and global signal removal regression were also performed. The first four frames of each BOLD run were removed. Frame censoring was applied to scans with a framewise displacement threshold of 0.5 mm along with its preceding scan (Power et al., 2012). Regional time series were acquired by parcellating the scans into 268 non-overlapping brain regions using a functional atlas derived from healthy controls (Shen et al., 2013) and averaging the time course of all voxels within a given region. Voxels identified as lesioned were excluded from regional timeseries calculations. Regions were assigned to one of 8 functional networks (Fig. S1), identified by (Finn et al., 2015) using spectral clustering in healthy subjects.

2.4. Functional connectivity calculation

Functional connectivity (FC) matrices were calculated as the regularized inverse of precision matrices. Calculating FC using precision minimizes the effect of indirect connections and has been shown to result in connectomes that are more similar to structural connectivity (Liégeois et al., 2020; Wodeyar et al., 2020). To compute the precision FC, we first calculated the full Pearson correlation-based FC (Σ_i) for each individual i by correlating region-pair time series. We then took the unregularized inverse of Σ_i, denoted P_i, and averaged them over the i subjects to obtain the population-level precision FC matrix P_avg. We then calculated the individual precision FC matrices using Tikhonov regularization, which adds a full-rank regularization term (scaled identity) to the correlation matrix before inversion (Liégeois et al., 2020).

$$P_i^{reg}=({\Sigma }_i+\lambda \cdot I{)}^{-1}$$ (1)

where I is the identity matrix and λ ∈ [0, 1] is the regularization parameter. The regularization parameter λ was chosen via a grid search to be the value that minimized the root mean squared error of the Frobenius norm of the difference in regularized subject precision matrices ${\mathit{P}}_i^{reg}$ and the population-level unregularized precision matrix P_avg, which was found to be λ = 0.71 (Fig. S2). Partial correlation (precision) involves the inversion of the correlation matrix, and to stably invert this matrix, regularization is needed. Tikhonov regularization (a.k.a. L2 ridge regression), employed here, involves addition of an identity term scaled by a constant λ. The group average unregularized precision matrix is only used for the optimization of this λ term, not in the matrix inversion, and is performed as previously described (Golub et al., 1999; Liégeois et al., 2020). The unregularized group average precision matrix is used as a benchmark for tuning this hyperparameter, as some of the inversion noise has been smoothed out in the calculation of the average. The values along the diagonal were set to 0 prior to graph matching; this is a form of regularization that penalizes off-diagonal swaps, which we employ to control the effect of regions with low SNR; a noisy region will be more likely to be assigned to itself because the zeroes are aligned. For completeness, the main analyses have been replicated with Pearson correlation-based FC, and results are provided in the supplementary material (Figs. S13, S14, S15), with few differences to the overall findings with the precision FC.

Estimated structural disconnection

Deficits from subcortical stroke may be related to functional alterations at distant sites via metabolic diaschisis (Corbetta et al., 2015; Hillis et al., 2002) or remote degeneration that spreads along the white matter connectivity network (Cheng et al., 2015; Duering et al., 2015). In order to account for the impact of lesions on the structural connectome, the extent of regional structural connectivity (SC) disruption due to the lesion was assessed for each stroke subject with the Network Modification (NeMo) Tool (Kuceyeski et al., 2013). The NeMo Tool v2 requires only an individual’s lesion mask in MNI space, which was obtained as described above, to produce an estimate of structural disconnection to each brain voxel, or to each region in a user-defined atlas. The newest version of the NeMo Tool, originally published in 2013, includes a reference database of SC from 420 unrelated individuals from the Human Connectome Project’s (HCP) 1200 release (50 percent female, aged 25–35). The NeMo Tool begins by mapping the lesion mask into this healthy database’s collection of tractography streamlines that quantify likely white matter pathways. It then identifies streamlines that pass through the lesion mask and records the gray matter voxels/regions that are at the ends of that streamline. The NeMo Tool produces the regional structural disconnection vector (ChaCo score, Change in Connectivity) that is an estimate of the percent of damaged streamlines at each voxel or region in the atlas. ChaCo scores were calculated for each stroke subject and the median was taken across the sample to create a group-level structural disconnection map (Fig. 1C).

Estimated functional disconnection

For each subject, we use FC matrices derived as described above to calculate the node strength, which quantifies the overall strength of all connections to and from a node, calculated the sum of all FC connection to the node (excluding a node’s connection weight to itself). Then, for each time point, we performed an unpaired t-test at each node to determine whether its node strength was significantly different between stroke subjects and controls. The 268 p-values were corrected for multiple comparisons using Benjamini-Hochberg FDR correction at a corrected alpha of 0.05. We observed node strength disruptions in the stroke subjects at 1 week, 2 weeks, and 6 months post stroke, where stroke subjects had lower node strength in the brainstem, cerebellum, and temporal lobes compared to controls, and increased node strength in the lateral and medial frontal cortex (Fig. S3).

2.5. Graph matching

We used a graph matching algorithm to capture FC network reorganization over time (Fig. 2). Graph matching is an algorithmic process that maximizes the similarity between two networks by identifying an optimal mapping between nodes in the networks. One approach to identifying this optimal mapping is with a combinatorial optimization problem known as linear assignment.

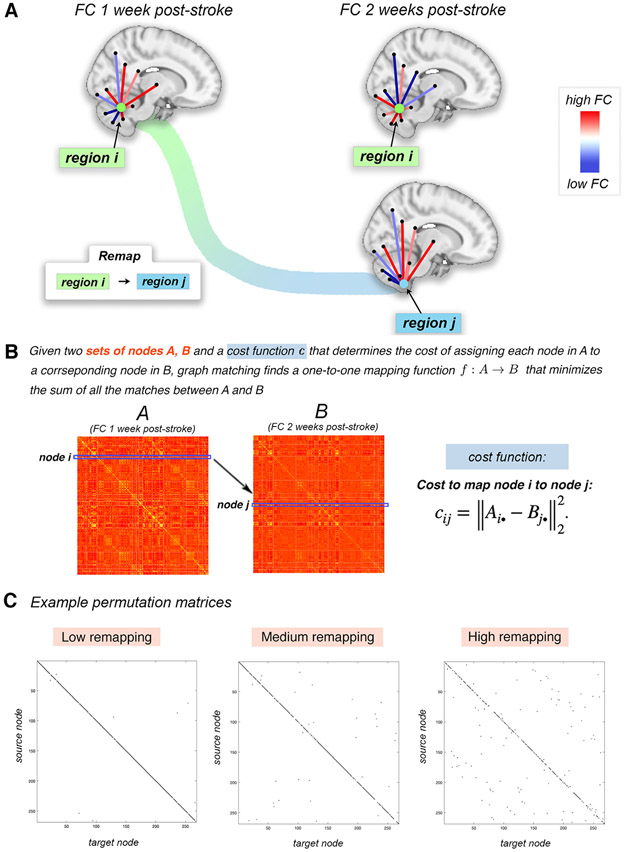
Fig. 2.

Overview of the graph matching procedure used to identify brain regions whose FC is more similar to a different region’s FC in the subsequent imaging session, i.e. regions that “remap” functional profiles. A. Example of a pair of regions that remap. Region i at 1 week post-stroke and region j at 2 weeks post-stroke have highly similar FC with the rest of the brain (moreso than region i at 1 week to region i at 2 weeks). The cost to remap i to j is low, and these regions would likely be remapped in the graph matching algorithm. B. The cost of remapping each region pair is used as input to the graph matching algorithm; the output of graph matching is the assignment of each region in one imaging session to a single corresponding region in the subsequent imaging session. If this assignment is to a different region, then it said to have “remapped”. C. Three examples of permutation matrices of three subjects with varying amounts of remapping; black entries represent the assignment of a source node (y-axis) to its target node (x-axis).

Take two n × n networks A and B and a cost function $c:A\times B\to \mathbb{R}$ that determines the cost of assigning each node in A to each node in B. Entries in the cost matrix C = (c_ij) are defined by the Euclidean distance between row i in A and row j in B, i.e. $c_{ij}(A,B)=\Vert A_{i•}-B_{j•}{\Vert }_2^2$. In our application, the rows A_i•, and B_j• represent region i and region j’s FC to the rest of the brain, or FC profile, respectively. The linear assignment problem aims to construct the permutation matrix P = (p_ij) that minimizes the sum of the elements in cost matrix, i.e. $mi{n}_P{\sum }_{i=1}^n{\sum }_{j=1}^n{c}_{ij}{p}_{ij}$. The matrix P is a permutation matrix with exactly one entry equal to 1 in each row and column, the rest being zero. Ones in the diagonal of P indicate the same node in the two networks were mapped to one another, while ones in the off-diagonal indicate a node was “remapped” to another node.

Here, we use the Hungarian algorithm to solve this minimization problem and find the corresponding optimal permutation matrix P. Fig. 2 illustrates how the graph matching is applied to subsequent longitudinal FC networks in the same individual (either post-stroke or control) and depicts an instance of remapping in a single subject. In Fig. 2A, the FC profile of brain region i (green region) at 1 week post-stroke is more closely matched by the FC profile of region j (blue region) at 2 weeks post-stroke than it is to itself at 2 weeks post-stroke. Example permutation matrices for three stroke subjects (one with high amount of remapping, one with an average amount of remapping and one with a low amount of remapping) are also provided.

2.6. Quantification of functional reorganization

We make assumption that remapping in the healthy controls is due to noise. Then, to remove this noise, we observed the set of nodes to which node x got assigned in the healthy control population along with their frequency. If node x was assigned to node y in more than 5 control subjects (across all time point intervals, i.e., > 5% of the time), we remove this entry from the permutation matrices of all stroke subjects. All remaining entries after this removal procedure are considered as significant remappings. The rationale for this thresholding approach is that there may be remapping that happens longitudinally in controls that is either due to noise in the fMRI data or some other physiological noise that is unrelated to stroke recovery. Removal of these normative effects will allow better isolation of remapping likely to be related to the post-stroke reorganization process. Because using the cutoff of 5 control subjects is an arbitrary choice, we have replicated the main analyses using a cutoff of 1 (i.e., remove remap of node x to node y from stroke subjects if node x was assigned to node y in 1 or more control subjects (across all time point intervals, i.e., > 1% of the time). The results with this more conservative threshold are provided in the supplementary material, and are very similar to the main results (Figs. S16, S17, S18).

The permutation matrices, calculated for each pair of time points, were then used to quantify functional reorganization. We defined functional remapping at three levels:

• Subject level: To assess the amount of functional reorganization in an individual, the number nodes that were remapped (sum of the off-diagonal in P) between each time point interval was calculated. This referred to as the ‘number of remaps’ between subsequent imaging sessions for a single subject.

• Node level: To assess the spatial pattern of reorganization across the brain, we calculated each node’s ‘remap frequency’, i.e. the proportion of individuals that had that brain region remap between two subsequent time points.

• Network level: To assess the network-level pattern of reorganization, we calculated the sum of remaps within and between 8 functional brain networks across all subjects. Since there are 8 networks, there are 64 possible source network/target network combinations (including the phenomenon of a node in a network remapping to a different node within the same network). We normalized each sum by the number of subjects, and then by the number of nodes in the source network. This value therefore expresses the proportion of remaps between networks, per subject, adjusted for the total number of possible remaps in each network.

2.7. Statistical analyses

To test the hypothesis that brain regions more structurally disconnected by the stroke lesion would have more frequent remapping, we calculated the correlation between the node remapping frequency and the sample median log-transformed ChaCo scores that quantify the regional amount of white matter connectivity disruption due to the stroke lesion. We removed nodes which had non-zero overlap with each subject’s lesion in the calculation of the median ChaCo score to exclude the effect of direct damage from the lesion. To test the hypothesis that brain regions more functionally disconnected by the stroke lesion would have more frequent remapping, we calculated the correlation between the node remapping frequency and the t-statistic of the node strength. The statistical significance of the correlations described above were assessed with permutation testing.

There are four subject-level remapping values for each subject, representing 4 time point comparisons post-stroke: 1 week - 2 weeks, 2 weeks - 1 month, 1 month - 3 months and 3 months - 6 months. Because there was a statistically significant correlation between scan length and remapping for the time point from 1 week - 2 weeks post-stroke (Fig. S4), the fMRI scan lengths of both time points were included as covariates in analyses concerning remapping over time.

To test the hypothesis that individuals with more baseline remapping would have greater initial motor impairment, we calculated the Pearson correlation between Fugl-Meyer motor scores at 1 week post-stroke and subject-level remapping from 1 week to 2 weeks post-stroke. To test the hypothesis that individuals with more baseline remapping would have greater motor recovery at 6 months, we calculated the Pearson correlation between the change in Fugl-Meyer motor scores from 1 week to 6 months post-stroke and subject-level remapping from 1 week to 2 weeks post-stroke.

To test the hypothesis that individuals with more remapping from one time point to another have better motor improvement, we calculated the Pearson correlation between change in Fugl-Meyer motor scores and subject-level remapping from one time point to the next for all four pairs of subsequent time points. This analysis enables us to identify whether remapping within a particular time point interval is more or less associated with motor improvement. In order to leverage the repeated subject measurements, a linear mixed effects regression model was employed to determine the relationship between the amount of remapping between sessions and the change Fugl-Meyer score between sessions, including age, sex, and scan length as covariates. Let i index a subject, t_ab index a time point interval (t_a = first time point, t_b = second time point, and t_ab = the time point interval). Our model is then:

$$\begin{gathered} changeF{M}_{i{t}_{ab}}={\beta }_0+{\beta }_{1}remappin{g}_{i{t}_{ab}}+{\beta }_{2}scanlengt{h}_{i{t}_a}+{\beta }_{3}scanlengt{h}_{i{t}_b} \\ +{\beta }_{4}ag{e}_i+{\beta }_{5}se{x}_i+b_i+{ϵ}_{i{t}_{ab}} \end{gathered}$$ (2)

where $b_i\sim N(0,{\sigma }_1^2)$ and ${ϵ}_{i{t}_{ab}}\sim N(0,{\sigma }_2^2)$. We include the random effect b_i to account for correlation within a subject at different time points.

2.7.1. Code availability

The code for to replicate this analysis is available on GitHub: https://github.com/emilyolafson/stroke-graph-matching

3. Results

3.1. Functional reorganization is primarily observed in the brainstem and cerebellum

At the node level, remapping occurred most often in the brainstem and cerebellum (Fig. 3A,B), similar to the spatial distribution of median ChaCo scores (amount of structural disconnection) across the stroke sample, which were also highest in the brainstem and cerebellum (Fig. 1C). We also calculated group-level structural connectivity disruption in an approach more analogous to node remapping, by binarizing ChaCo scores into ‘disrupted’ and ‘nondisrupted’ nodes and calculating frequency of disrupted nodes over the population, with similar results (Fig. S5). For this paper, regional ChaCo scores were chosen over disconnection frequencies in order to preserve information about the magnitude of the disconnection. We hypothesize that the magnitude of disconnection influences whether a region is remapped or not.

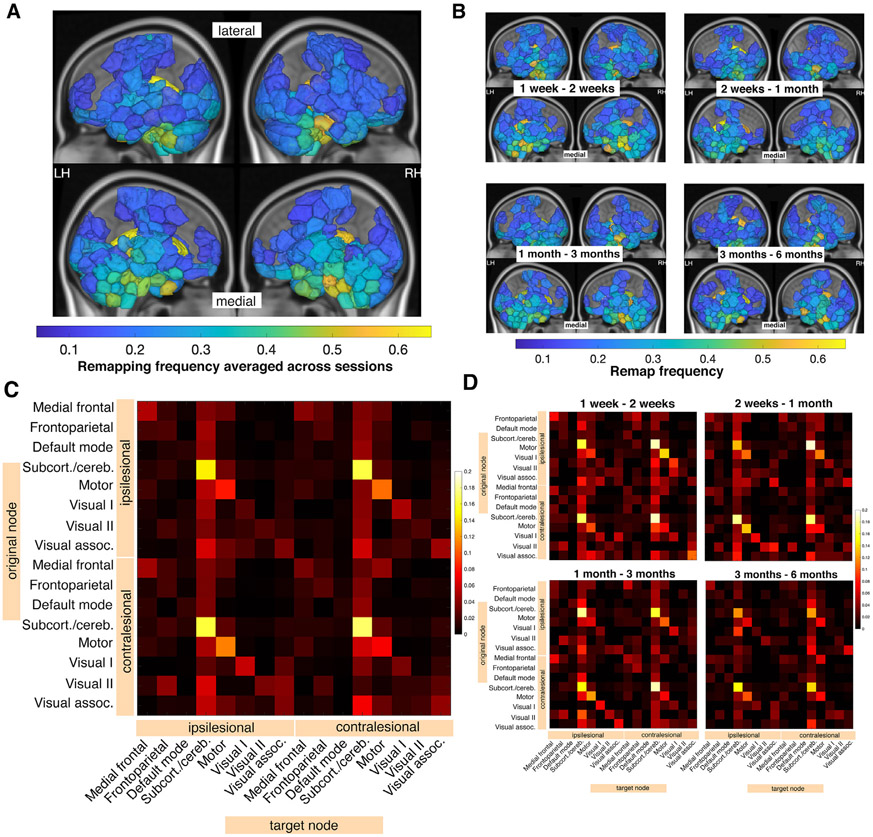
Fig. 3.

Node-level remapping frequencies are related to group-level structural connectivity disruptions due to the lesion. A. Node remap frequencies are plotted on a glass brain averaged across 4 time point comparisons (only displaying values above 0.1, for clarity). Inset figures display a lateral view (top row) and medial view (bottom row). B. Node remap frequencies > 0.1 plotted on a glass brain, displayed separately for each time point comparison. C. Network-level sum of remaps. Remaps are separated based on their position relative to the lesion (contralesional vs. ipsilesional). D. Network-level sum of remaps, displayed separately for each time point comparison. Ipsilesional = same hemisphere as the lesion, contralesional = opposite hemisphere as the lesion.

Next, we assessed network-level remapping within 8 functional networks. The most remaps were observed in the subcortical-cerebellum network (Fig. 3C,D) and in particular between contralesional nodes in the subcortical/cerebellum network (Fig. S6).

3.2. Regions with greater structural and functional disconnection have more functional reorganization over time

There was a significant, positive correlation between node remapping frequency and median regional ChaCo scores from 1 to 2 weeks post-stroke (r = 0.22, p = 3.05e-4), such that those regions with more structural connectivity disruption across the stroke subjects also had more remapping over time (Fig. 4A). This relationship was observed across all time points (Fig. S7A), and furthermore, across subjects, the brain regions that remap have significantly higher ChaCo scores compared to those that do not remap (assessed with permutation testing with 10,000 permutations) (Fig. S7B).

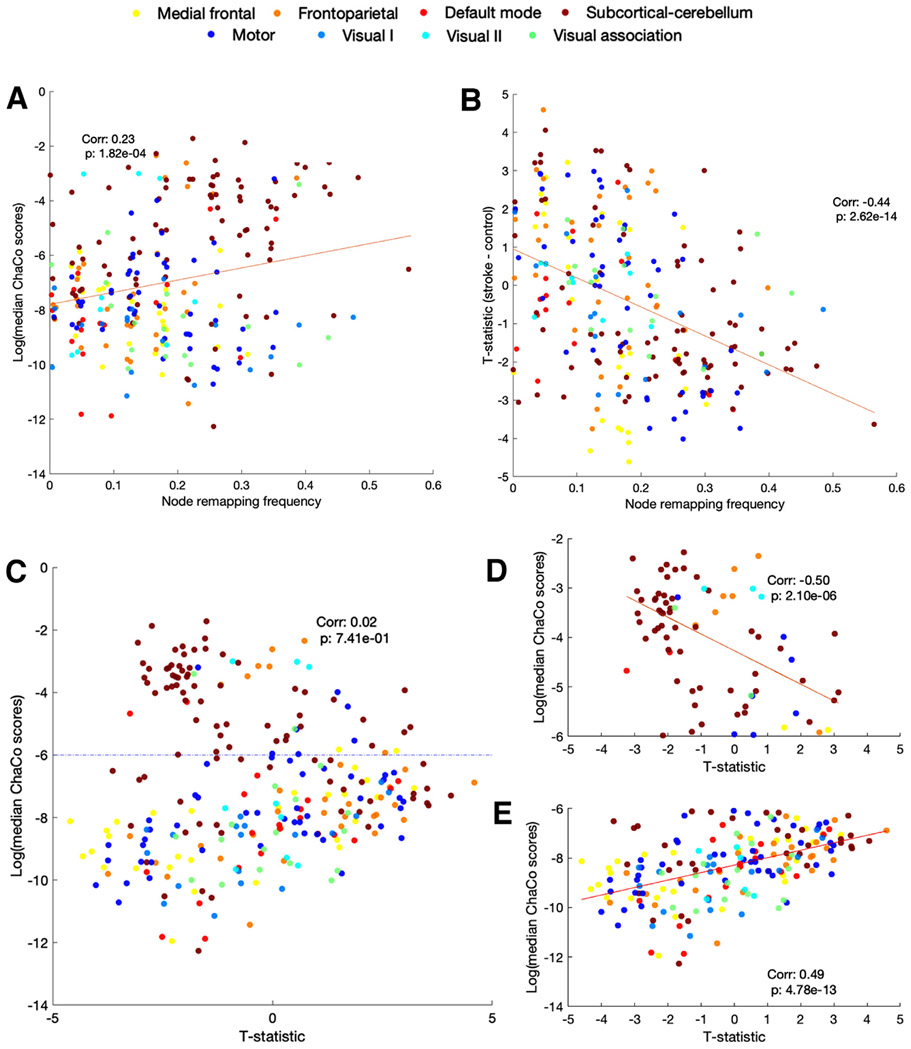
Fig. 4.

Relationships between FC disruption (t-statistic of node strength), SC disruption (ChaCo scores), and remapping over the 1 week - 2 week time interval post-stroke. Nodes are colored by network assignment (legend on top). A. Correlation between node remapping frequency and t-statistic of node strength. A jitter of 0.01 was added to data points along the x-axis to increase visibility. B. Correlation between node remapping frequency and ChaCo scores. A jitter of 0.01 was added to data points along the x-axis to increase visibility. C. Correlation between t-statistic of node strength and ChaCo scores. Dashed horizontal line at y = −6 represents the cut off point of log(ChaCo) −6, representing more SC disruption shown in D, below −6 representing minimal SC disruption is shown in E.

On the other hand, node remapping frequency at 1–2 weeks post stroke was negatively correlated with node strength relative to healthy controls at 1 week post-stroke (r = −0.44, p = 2.62e-14) (Fig. 4B), where regions with lower node strength relative to controls at 1 week underwent the most remapping between 1 and 2 weeks post-stroke. This relationship was present across all time points (Figs. S10, S11, S12) and the correlation is very similar when using the first or second node strength measurement (Fig. S9).

The nodes that underwent the most remapping were the most structurally and functionally disconnected, but the relationship between structural and functional disconnection is non-linear (Fig. 4C). Instead, the relationship between SC and FC disruption is impacted by the magnitude of the structural disruption. As seen in Fig. S8, there is a clear cutoff for regions consistently structurally disrupted across subjects, corresponding to a ChaCo score of 0.0003 (log(ChaCo) of −6). For regions exceeding a ChaCo score of 0.0003 (i.e., with high structural connectivity disruption), there was a significant negative correlation between relative node strength and ChaCo scores (r = −0.50, p = 2.1e-6)(Fig. 4D) and for regions below a ChaCo score of 0.0003 (i.e., with little/no structural connectivity disruption), there was a significant positive correlation between relative node strength and ChaCo scores (r = 0.49, p = 4.78e-13) (Fig. 4E).

3.3. Functional reorganization is related to impairment and recovery

We observed a significant positive correlation between subject-level early post-stroke remaps (between 1 weeks and 2 weeks post-stroke) and the 6 month improvement in motor scores, as measured by the difference in Fugl-Meyer scores at 6 months and 1 week post stroke (controlling for scan lengths). This result indicates that individuals with more early functional remapping had better long-term recovery (Fig. 5A). There was also a significant negative relationship between the number of early post-stroke remaps (between 1 week and 2 weeks) and baseline Fugl-Meyer scores, such that more impaired subjects had more remapping at baseline (Fig. 5B). The linear mixed effects model demonstrated a statistically significant relationship between ‘remapping’ and change in Fugl-Meyer score. For every one unit increase in ‘remapping’, there is an average increase of 0.15 units in the change in Fugl-Meyer scores, holding all other factors constant (p = 0.006) (Fig. 5C). The amount of recovery between subsequent sessions was positively associated with the number of remaps between sessions for the two comparisons between 1 week and 2 weeks post-stroke (Fig. 5D), but only a trend for significance existed at the 2 weeks to 1 month time points and there was no significant correlation for the 3 and 6 months comparison.

Fig. 5.

Subject-level remapping is related to baseline motor impairment and eventual motor recovery. A. Pearson correlation between subject-level remaps between 1 week and 2 weeks post stroke and change in Fugl-Meyer scores between 1 week and 6 months post-stroke. B. Pearson correlation between subject-level remaps between 1 week FC and 2 week FC and 1 week Fugl-Meyer scores, controlling for scan lengths at 1 week post-stroke at 2 weeks post stroke. C. Results from linear mixed effects analysis; each color indicates a different individuals’ longitudinal time point. D. Pearson correlation subject-level remaps for each pair of time points and the change in Fugl-Meyer scores between time points, controlling for the scan length of the 2 scans in the remapping calculation.

Robustness of results

The maximum overlap of lesions with each ROI is no more than 30 percent (Fig. S19) and, importantly, lesioned voxels were excluded from FC calculations. We also found that the number of remaps was not related to differences in in-scanner motion between scans, as measured by framewise displacement (Fig. S20).

4. Discussion

In this paper we proposed a measure of functional connectome reorganization based on graph matching and evaluated its relationship to structural & functional disconnection and motor impairment/recovery in a set of 23 individuals with pontine stroke. We observed instances of functional reorganization over the 1 week to 6 months post-stroke period and demonstrated that the areas that undergo functional reorganization most frequently are in cerebellar/subcortical and motor networks. Furthermore, regions more impacted by stroke via disruption to their structural and functional connections had more functional remapping over time. Finally, we show that functional reorganization one week post-stroke is highly related to both baseline impairment and the extent of motor recovery at 6 months, and, finally, that the extent of functional reorganization between 1 week and 2 weeks post-stroke is correlated with the extent of motor recovery observed in this same subacute time period.

We first note that remaps, defined in this paper as instances where a node is assigned to a different node longitudinally in the linear assignment algorithm, were observed in the control population. This ‘noise’ may be related to inherent variability in subject-level functional connectivity, acquisition-related noise, or a combination of both. Graph matching has recently been used to develop a measure of connectome similarity within healthy controls (Osmanlıoğlu et al., 2020). Consistent with our findings, Osmanlıoğlu et al. (2020) observe that graph matching using the same subject’s functional connectomes acquired during different scans is imperfect, i.e., on average there are several remaps in a single subject’s functional connectomes, suggesting that functional network structure in the same individual over time is variable. To discern the difference between natural individual variability in functional connectivity and signal, we removed all remaps that were observed in more than 5 control subjects. Almost certainly, we have not completely isolated the influence of natural individual variability; this methodology can likely be improved with future studies investigating graph matching patterns within larger populations of healthy individuals. Scan duration also influences functional connectome similarity in healthy controls, driven by the lower SNR of shorter scans. Accordingly, we observed a relationship between subject-level remaps and scan length, such that subjects with shorter scans had more remaps. To account for this influence, we included scan duration - first and second scan length - as covariates in all longitudinal analyses, but future studies should attempt to obtain consistent scan durations for all subjects.

Motor recovery following stroke is supported by active functional and structural remodelling in the area bordering the stroke, including increases in excitability, increases in dendritic spine turnover, and the formation of new axonal projections (Murphy and Corbett, 2009). This remodelling can entail surviving cortical areas remapping functionally to compensate for post-stroke impairment (Brown et al., 2009). The dynamic reorganization of resting-state functional connectivity, observed in this stroke cohort in subcortical and cerebellar areas, may reflect longitudinal compensatory changes in representations of motor functions. Interestingly, we showed correlations between amount of functional remapping and amount of motor improvement but only in the period of time in which most post-stroke recovery occurs (within 3 months after stroke) (Lee et al., 2015). However, resting-state functional connectivity may not be fully representative of brain activation patterns underlying specific behaviors (i.e. during a task), and has shown to be constrained by the structural connectome (Honey et al., 2009; Kuceyeski et al., 2019). Thus, it is possible that the remapping observed is not a functional remapping per se (in the sense of remapping a region’s role in a specific task), but a shift in balance of a brain area’s functional connectivity profile at rest, which could reflect task-based functional compensations, changes in network topology, and/or underlying structural remodelling.

We now understand that deficits arising from stroke are not only related to the damage inflicted at the stroke core, but also to remote cortical areas structurally connected to the lesion, due to retro- and anterograde degeneration (Guggisberg et al., 2019). For instance, several studies have shown that there are local reductions in cortical thickness in areas directly connected to subcortical lesions (Cheng et al., 2015; Duering et al., 2015). These degenerative changes are long-term effects of a stroke. We showed that structural disconnection from a stroke lesion is associated with remapping even at 6 months post-stroke, suggesting that late-stage impacts of the stroke may trigger functional reorganization.

However, as stated earlier, recovery-related reorganization usually occurs within the first three months post-stroke. We observed recovery-related remapping primarily in the acute period (1–2 weeks after stroke), where there was also a significant correlation between structural connectome disruption and remapping as well as functional connectome disruption and remapping. Structural connectivity disruption between nodes has been linked to perturbations of functional connectivity (FC) within the first 2–4 weeks after stroke (Griffis et al., 2019; Griffis et al., 2020; Wodeyar et al., 2020), including by Lu and colleagues (2011), who demonstrated that pontine strokes disrupt FC between the cortex and the cerebellum. These papers generally show that damage to structural connections between nodes, direct or indirect, is associated with reductions in FC between those nodes. We observed that remapping more frequently occurs in nodes with greater structural and functional connectivity disruption due to the stroke. We observed that functional connectivity changes were related to structural connectivity disruption magnitude; nodes with more structural connectivity disruption had a negative relationship with changes in node strength, where more SC disruption was related to weaker FC. These nodes, overwhelmingly a part of the subcortical/cerebellum network, also have the highest levels of remapping. On the other hand, regions with lower structural connectivity disruption have a positive relationship with changes in node strength, where less SC disruption is associated with higher node strength. This result suggests that remapping after pontine stroke may be a mechanism that occurs to only the most severely disrupted brain regions, whose structural connections have been damaged to the point of weakened FC, whereas regions with less structural disruption can compensate for the damage in the form of upregulated FC.

Pontine strokes primarily affect large-diameter projection fibers, which tend to produce more severe functional connectivity deficits when damaged (Griffis et al., 2020). Brain regions that were once structurally and functionally connected via. these fibers may remap more often as their role in the network is taken over by other nodes with more preserved structural connections. For instance, Lu et al. (2011) demonstrated reduced FC between the motor cortex and cerebellum in subjects whose cortico-ponto-cerebellar fibers were damaged from pontine stroke. Regions in the cerebellum and motor cortex that can no longer communicate via. these fibers may remap to other nodes with preserved cortical/cerebellum connectivity.

Other factors may make regions more or less amenable to remapping; perhaps a region is better positioned within the network to assume lost functionality, such as in the cerebellum where there is considerable redundancy in the somatotopic layout (Mottolese et al., 2013) which may enable it to compensate more easily for lost functionality.

We also show that more remapping between sessions is associated with better motor recovery between those same sessions, and that more remapping in the early phase of stroke is related to both amount of baseline impairment and the degree of motor recovery at 6 months. Functional reorganization measured with this remapping technique may be interpreted as reflecting a compensatory, beneficial process that is proportional to the extent of motor recovery. On the other hand, this approach may also be capturing phenomena that occurs during the first 6 months after stroke that are unrelated to recovered functionality, but that correlate with measures of recovery nonetheless. For instance, stroke-related increases in noise in the subcortical/cerebellum network may result in more remapping which could be the result of a random or pathological process concomitant with a recovery mechanism. Thus, more densely-sampled fMRI studies should be performed to identify other elements of this reorganization process.

The most remaps were observed in the subcortical/cerebellum network, suggesting that remapping is likely reflecting a process of functional reorganization that is spatially constrained (Fig. 3). This network-level reorganization is consistent with prior task-based studies showing remapping of motor-based activations to premotor and homologous areas, and with studies of resting-state FC that demonstrate specific spatial patterns of FC changes after stroke, like changes in resting state FC within motor networks (Zhang et al., 2016), and contralesional functional connectivity changes that are concentrated in a small set of brain regions (Yourganov et al., 2021).

4.1. Limitations

There are several limitations to this study. The first is sample size, which is partially mediated by the frequency of the longitudinal sampling and the homogeneity of the population. The second is that the impact of fMRI noise in the remapping procedure cannot be completely accounted for. We do see that some nodes with high frequency remapping are also those that have lower SNR in the fMRI data; generally, the SNR of fMRI is lowest in medial structures such as the thalamus, cortical midsurface, and most consequentially to this study, the cerebellum. Thus, it is possible that noise contamination was captured in the graph matching procedure and has leaked into the results. Our approach of using the arguably more noisy control data to filter this potential source of noise helped mitigate this drawback. Second, structural disconnection metrics were obtained for each individual using indirect methods (i.e. the Network Modification Tool), instead of directly from diffusion MRI in the individuals with stroke. Third, the correlation between baseline and long-term recovery in stroke subjects is generally high (Krakauer and Marshall, 2015); because of the small sample size in this study, it is not possible to discern whether the relationship between early remapping and 6 month recovery holds while controlling for initial impairment. Fourth, we did not have data available regarding the rehabilitation program, as it was not collected at the time of fMRI scanning and motor assessments, so the effect of rehabilitation could not be accounted for.

4.2. Conclusions

In this study we proposed a measure of functional connectome reorganization, called remapping, and applied it to longitudinal resting-state fMRI data in a cohort of pontine stroke patients. Remapping was observed in all stroke subjects and was correlated with recovery over the early to late subacute phases. Areas impacted by the lesion through structural disconnection were more likely to remap than those areas not impacted by the lesion. This work expands our understanding of functional processes related to recovery after stroke, and future studies should examine remapping in other populations beyond pontine stroke subjects, such as those with cortical stroke. If we can identify subjects who have more potential for functional reorganization, or can devise therapeutics to boost this remapping mechanism, we may be able to improve patient outcomes after stroke.