A Guide to ComBat Harmonization of Imaging Biomarkers in Multicenter Studies

Abstract

The impact of PET image acquisition and reconstruction parameters on SUV measurements or radiomic feature values is widely documented. This scanner effect is detrimental to the design and validation of predictive or prognostic models and limits the use of large multicenter cohorts. To reduce the impact of this scanner effect, the ComBat method has been proposed and is now used in various contexts. The purpose of this article is to explain and illustrate the use of ComBat based on practical examples. We also give examples in which the ComBat assumptions are not met and, thus, in which ComBat should not be used.

The emergence of radiomics in mid-2010 renewed interest in quantitative image analysis for prediction and classification tasks. Because radiomics requires large image datasets for designing and validating models, it would largely benefit from pooling images from different sites or from different scanners. However, many quantitative biomarkers and radiomic features are sensitive to a scanner or protocol effect (1–5), referred to here as the site effect, underlining the importance of harmonizing image acquisition and reconstruction procedures to reduce multicenter variability before pooling data from different sites. Similarly, when a new radiomic or quantitative image analysis method is developed at one site, its application to images from another site requires prior verification that the images from the 2 sites are comparable.

Much effort has been deployed in recent years to propose procedures to harmonize image quality (6), including the successful European Association of Nuclear Medicine Research Ltd. (EARL) accreditation program (7,8). However, in retrospective studies, many images have been reconstructed using protocols that did not follow these harmonization guidelines, for which it is impossible to retrieve or perform phantom acquisitions that would be needed to harmonize them a posteriori. Often, the raw data are not stored, hampering any novel reconstruction to target a given image quality. The variability between scans resulting from different acquisition and reconstruction protocols can be reduced using image resampling or filtering (9,10), but these techniques require image postprocessing and most often yield a decrease in spatial resolution in the images acquired using the most recent devices, yielding suboptimal image quality for subsequent quantitative and radiomic studies.

To address these site effects, the ComBat harmonization method has been proposed (11–15) and has produced satisfactory results in various contexts. Since 2017, at least 51 papers have reported the use of ComBat in radiomic analysis of MRI (36%), CT (34%), or PET images (28%). Of these articles, 41% reported higher performance metrics after ComBat than before, and 41% presented only the results with harmonization. Only 18% of the articles did not report a benefit in using ComBat, without any detrimental effect.

ComBat directly applies to features already extracted from the images without the need to retrieve the images. However, as with any harmonization method, it is based on assumptions that have to be met for the method to generate valid results. The objective of this paper is to explain and demonstrate under which conditions ComBat can be used to harmonize image-derived biomarkers measured in different conditions and when it should be used with caution. We first summarize the theory behind ComBat and then illustrate several use cases to demonstrate its ability to compensate for site effects when properly used and to answer practical questions a ComBat user might have. We also give examples of situations in which the ComBat assumptions are not met and, thus, in which ComBat should not be used. Finally, we discuss the assets and limitations of ComBat.

All patient data used in the examples were obtained from previous retrospective studies approved by an institutional review board, and the requirement to obtain informed consent was waived.

THEORY OF COMBAT

ComBat was initially introduced in the field of genomics (16) and has been widely used in this field (17). ComBat assumes that

$$y_{ij}=\text{α}+{\text{γ}}_i+{\text{δ}}_i{\text{ε}}_{ij}$$ Eq. 1

where $j$ denotes the specific measurement of feature y, $i$ denotes the setting, α corresponds to the average value of the feature of interest $y$, ${\text{γ}}_i$ is an additive batch effect affecting the measurement, ${\text{δ}}_i$ is a multiplicative batch effect and, ${\text{ε}}_{ij}$ is an error term. Batch $i$ corresponds to the experimental settings used for making the y measurement, including the possible observer effect, scanner effect, or even sample effect.

In medical imaging, y is an image feature (e.g., SUV); $i$ denotes the scanner, protocol effect, or even observer effect (called the site effect); and $j$ denotes the specific measurement, typically the volume of interest in which the measurement is made.

The model therefore assumes that the value of measurement $i$ of a given feature y in volume of interest $j$ is possibly affected by additive and multiplicative effects that depend on the scanner, protocol, or even observer who made the measurement. These effects are common to all measurements $j$ of that same quantity y made using the same scanner, protocol, or observer. On the basis of multiple measurements $y_{ij}$ of the same feature y made in volume of interest j in different images coming from different scanners $i$, the site effects ${\text{γ}}_i$ and ${\text{δ}}_i$ can be estimated using conditional posterior means (16) and subsequently corrected using

$$y_{ij}^{\text{ComBat}}=\frac{y_{ij}-\widehat{\alpha }-\widehat{{\text{γ}}_i}}{\widehat{{\text{δ}}_i}}+\widehat{\alpha }$$ Eq. 2

where $\widehat{\alpha }$, $\widehat{{\text{γ}}_i}$ and $\widehat{{\text{δ}}_i}$ are estimators of $\text{α}$, ${\text{γ}}_i$ and ${\text{δ}}_i$ and $y_{ij}^{\text{ComBat}}$ is the transformed $y_{ij}$ measurement devoid of the site i effect.

ComBat is a data-driven method that does not require any phantom acquisition to estimate the site effect but requires data from the different sites with sufficient sample size. The site effect can be estimated and corrected directly from the available image feature values measured at different sites without having to perform any image processing or any new measurements in the images. ComBat always theoretically improves the alignment of the mean and SD of the distributions given the criterion optimized by the method. A Kolmogorov–Smirnov test can be used to determine whether the statistical distributions of 2 sets of feature values are significantly different, in which case ComBat is needed, and to check the effectiveness of the applied transformation. A nonsignificant Kolmogorov–Smirnov test suggests that there is no evidence of differences in the 2 distributions, implying that any subsequent analysis should not be affected by a detectable difference between the distributions.

NOTEWORTHY

• •Guidelines are proposed for using the ComBat harmonization method on SUVs, metabolic tumor volume, or any radiomic features illustrated with simulated and real data.
• •Recommendations are made on the use of covariates within ComBat.
• •The ComBat, EARL, and z score harmonization strategies are compared.

EXAMPLE

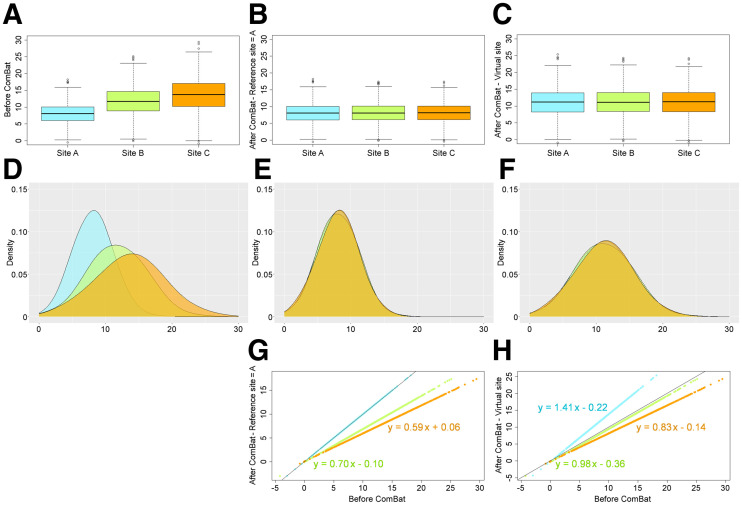
We numerically generated 3,000 values drawn from 3 gaussian distributions with different means (8, 12, or 14) and SDs (3, 4, or 5) (Table 1), mimicking, for example, SUV_max measured in 3 sets of highly metabolic tumors but with 3 scanners of different generations, of which one had a much higher spatial resolution than the others (hence higher SUV_max due to reduced partial-volume effect (18)). As shown in Figure 1, ComBat can be used in 2 ways: either to realign the distributions of the 3 sites to a virtual site (11), which is neither site A nor site B nor site C, or to realign the data from sites B and C to site A chosen as the reference site (or vice versa) (19). Contrary to what has been reported (20), both approaches lead to the same ranking of the patients and, hence, identical receiver-operating-characteristic curves for classification tasks, and only the absolute value of the feature changes. Aligning the data to a reference site may be preferable for feature value interpretation, but the reference site selection has no impact on the quality of the realignment. In the following, harmonization will always be performed with respect to a reference site.

TABLE 1.

Description of Simulations

	Site A		Site B		Site C
Experiment	Limited stage	Advanced stage	Limited stage	Advanced stage	Limited stage
Experiment 1 (virtual site), reference site = A	N = 1,000, μ = 8, SD = 3	ø	N = 1,000, μ = 12, SD = 4	ø	N = 1,000, μ = 14, SD = 5
Experiment 2, reference site = A	N = 1,000, μ = 8, SD = 3	N = 1,000, μ = 10, SD = 3	N = 1,000, μ = 12, SD = 4	N = 1,000, μ = 14, SD = 4	ø
Experiment 3, reference site = A, without and with covariate (=stage)	N = 1,000, μ = 8, SD = 3	N = 1,000, μ = 10, SD = 3	N = 1,000, μ = 12, SD = 4	ø	ø
Experiment 4, reference site = A, without and with covariate (=stage)	N = 1,000, μ = 8, SD = 3	N = 1,000, μ = 10, SD = 3	N = 200, μ = 12, SD = 4	N = 1,800, μ = 14, SD = 4	ø
Experiment 5, reference site = A, without and with covariate (=stage)	N = 1,000, μ = 8, SD = 3	N = 1,000, μ = 10, SD = 3	N = 1,000, μ = 12, SD = 4	N = 1,000, μ = 12, SD = 4	ø
Experiment 6, reference site = A, without and with covariate (=stage)	N = 1,000, μ = 8, SD = 3	N = 1,000, μ = 10, SD = 3	N = 1,000, μ = 12, SD = 4	N = 1,000, μ = 20, SD = 4	ø

N = number of simulated samples; μ = mean of gaussian distribution; ø = no simulation for this category.

FIGURE 1.

Box plot and feature value distributions for experiment 1 (Table 1). (A and D) Plots before ComBat. (B, E, and G) Plots after ComBat by aligning data from sites B and C to site A. (C, F, and H) Plots after ComBat by aligning data on virtual site (intermediate between 3 sites). Bottom graphs show equations of transformations.

COMBAT TO COMPENSATE FOR PROTOCOL DIFFERENCES

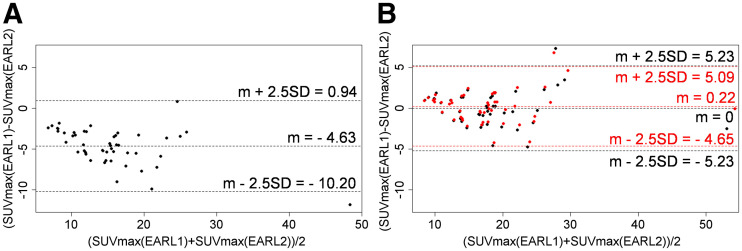
The straightforward application of ComBat in medical imaging is to compensate for differences in radiomic feature values obtained from images acquired using different protocols. To illustrate, we performed an EARL experiment using PET images of 49 lesions from 15 lymphoma patients reconstructed according to the EARL1 and EARL2 standards (8). Without harmonization, we observed a systematic deviation in SUV_max between the 2 reconstructions (Kolmogorov–Smirnov, P = 0.0002; Fig. 2). After applying ComBat considering the EARL2 reconstruction as a reference site, we observed a better concordance of SUV_max (P = 0.6994).

FIGURE 2.

Bland–Altman plots for SUV_max obtained using EARL1 and EARL2 reconstructions before ComBat (A) and after ComBat (B). Black = without covariate; red = with metabolic volume (cm³) as continuous covariate; m = mean.

NEED FOR TISSUE-SPECIFIC AND TUMOR-SPECIFIC TRANSFORMATIONS

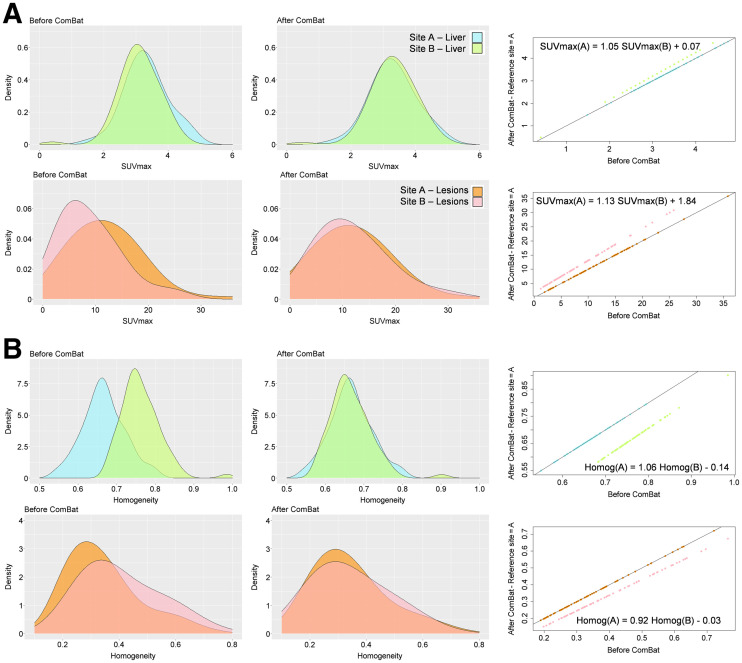
Since ComBat is a data-driven method, the realignment transformation (Eq. 2) is specific to the input data. It is therefore specific to the tissue or tumor type or patient population from which it is estimated. For example, in a previous publication (12), the ComBat transformation appropriate for SUV_max was different for liver tissue and breast tumors when pooling 63 patients from site A and 74 patients from site B (Fig. 3). In that example, values from site B were realigned to values measured at site A, and the resulting transformations were ${\text{SUV}}_{\max }\left(A\right)=1.05\times {\text{SUV}}_{\max }(B)+0.07$ for liver tissue and ${\text{SUV}}_{\max }(A)=1.13\times {\text{SUV}}_{\max }(B)+1.84$ for tumor tissue. This effect of the imaging protocols is different as a function of the structure of interest. SUV_max in the liver is not much impacted by the partial-volume effect, as the liver is a large region; hence, it is relatively robust to the difference in spatial resolution in the images produced by the 2 sites. Therefore, the slope of the transformation was close to 1, and the intercept was close to 0. In contrast, the SUV_max in breast tumors is affected by the partial-volume effect. This translates into a slope farther from 1 and an intercept farther from 0. Therefore, unlike what is stated in a previous publication (21), phantom measurements cannot be used to determine the transformations to be applied to feature values measured at one site to convert them to values that would have been obtained at the other site a priori. Given the ComBat assumptions, Equation 2 can be applied only to data affected by the site effect in the same way as the data used to estimate the α, γ, and δ parameters of the model. This implies that, for example, a transformation derived for lung tumors should not be applied to lymphoma tumors unless the biomarker of interest is affected by the site effect in the same way in the 2 tumor types.

FIGURE 3.

Application of ComBat in liver and tumor tissues for SUV_max (A) and homogeneity (B). (Left) Distributions at 2 sites before ComBat. (Center) Distributions after ComBat (site A = reference site). (Right) Values after ComBat plotted against value for same index and tissue before ComBat. Equation is transformation identified by ComBat to align data from site B to site A.

NEED FOR A FEATURE-SPECIFIC TRANSFORMATION

Just as transformations are specific to each tissue, they are also specific to each index. For example, using the same data as in Figure 3, the equations differ for SUV_max (${\text{SUV}}_{\max }(A)=1.05\times {\text{SUV}}_{\max }(B)+0.07$ for liver tissue) and for the homogeneity feature ($\text{homog}(A)=1.06\times \text{homog}(B)-0.14$). The transformation has to be estimated for each feature independently because not all features are affected in the same way by the site effect. Some features are relatively immune to the site effect (e.g., shape features), unlike others (e.g., SUV_max or metabolic tumor volume).

USE OF COMBAT TO ADJUST CUTOFFS BETWEEN DIFFERENT SITES

Aligning data from different sites might be extremely useful to adjust the cutoff used to distinguish between groups. Let us take the example of lymphoma patients, for whom it is well known that the total metabolic tumor volume (TMTV) calculated from ¹⁸F-FDG PET images is a valuable prognostic factor of progression-free and overall survival (22). However, the cutoff to identify patients with a poor prognosis depends on the segmentation method used for TMTV calculation, and there is no consensus on the optimal segmentation method (23). ComBat can thus be used to automatically determine how the cutoff appropriate for a segmentation method should be shifted to be applicable to TMTV measured using a different segmentation method. To illustrate, we studied a cohort of 280 patients with diffuse large B-cell lymphoma from the REMARC trial (NCT01122472), for whom TMTV was calculated from ¹⁸F-FDG PET images using 2 segmentation methods (24). Method 1 (M1) used a threshold of 41% of SUV_max to segment lesions previously identified by a nuclear medicine physician. Method 2 (M2) used a convolutional neural network model (25). Using M1, the optimal TMTV cutoff was 242 cm³ to best distinguish between patients with short and long progression-free survival. Applying that cutoff to TMTVs measured with M2, the Youden index (sensitivity + specificity − 1) was 0.18 (sensitivity, 41%; specificity, 77%; Table 2). From the TMTV distributions obtained by the 2 methods (Supplemental Figs. 1A–1C; supplemental materials are available at http://jnm.snmjournals.org), ComBat identified the transformation needed to convert M1 TMTVs to TMTVs that would have been obtained if M2 segmentation had been used: ${\text{TMTV}}_{\text{M2}}=0.61\times {\text{TMTV}}_{\text{M1}}-28.64$. This formula can be used to determine how the cutoff appropriate for M1 TMTV should be shifted to be applicable to TMTV measured with M2, which was 119 cm³ (=0.61 × 242 − 28.64). With that cutoff, the Youden index was 0.22 (sensitivity, 64%; specificity, 58%), close to the performance obtained when optimizing the cutoff directly on the M2 TMTV (Youden index, 0.23). These results demonstrate the ability of ComBat to determine how a cutoff should be shifted to account for differences in the segmentation method.

TABLE 2.

Summary of Results Obtained with ComBat to Adjust TMTV Cutoffs Between Different Sites

Parameter	Cutoff	Youden	Sensitivity	Specificity
Cutoff optimized for M1	242 cm3	0.18	41%	77%
Based on M1 cutoff, estimated cutoff for M2 (ComBat without log transformation)	119 cm3	0.22	64%	58%
Optimal cutoff for M2	112 cm3	0.23	66%	57%

CIRCUMSTANCES IN WHICH A COVARIATE IS NEEDED

Equation 1 corresponds to the simplest version of ComBat, which is applicable when the 2 distributions of features to be realigned are drawn from the same population and differ only because of a site effect. However, in many examples, each of these distributions is itself composed of 2 or more distributions. For example, a feature value distribution might be different in patients with different tumor stages. If the subcategories (patients with different stages) are not present with the same frequencies at the 2 sites, then the feature distributions observed at the 2 sites will differ in 2 respects: because of the site effect and because of the different frequencies of subcategories. Equation 1 will not apply unless the subcategory covariate is introduced. Equation 1 then becomes

$$y_{ij}=\text{α}+X_{ij}\text{β}+{\text{γ}}_i+{\text{δ}}_i{\text{ε}}_{ij}$$ Eq. 3

where $X$ is the design matrix for the covariates of interest, and $\text{β}$ is the vector of regression coefficients corresponding to each covariate. The values after realignment are obtained using

$$y_{ij}^{\text{ComBat}}=\frac{y_{ij}-\widehat{\alpha }-X_{ij}\widehat{\beta }-\widehat{{\text{γ}}_i}}{\widehat{{\text{δ}}_i}}+\widehat{\alpha }$$ Eq. 4

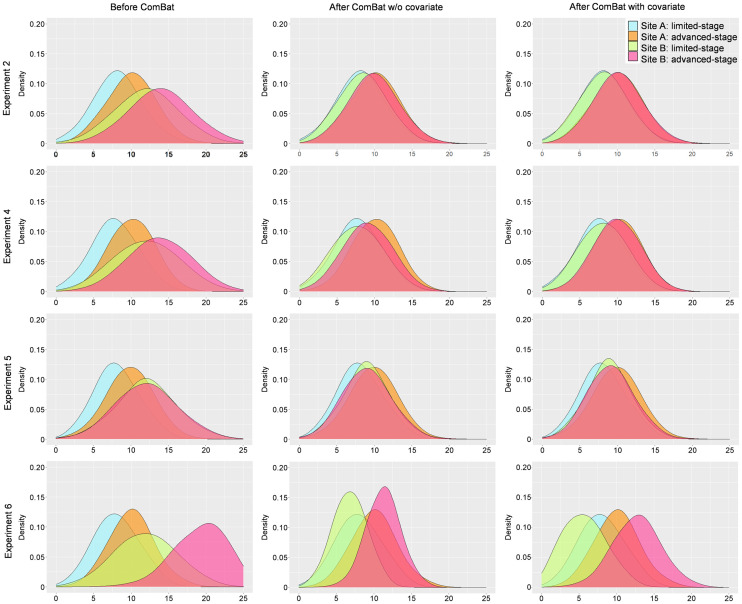
To illustrate the impact of using a covariate, we performed 5 experiments, as listed in Table 1 (experiments 2–6). In all experiments, we assumed we had data from 2 different sites and that at each site there were patients with limited-stage or advanced-stage disease.

In experiment 2, the numbers of patients with limited-stage and advanced-stage disease were identical at both sites. Using ComBat with or without the stage covariate yields almost identical results (Fig. 4). The differences are because only 1 transformation is estimated without a covariate, compared with 2 transformations corresponding to each of the 2 stages in the version including a covariate. Because the proportion of patients in each stage is exactly the same, the stage covariate does not introduce confounding factors. The covariate is thus not necessary, but using it does not influence the ComBat results.

FIGURE 4.

Value distributions for experiments 2, 4, 5, and 6 (Table 1). (Left) Distributions before ComBat. (Center) Distributions after ComBat (without covariates). (Right) Distributions after ComBat and specifying stage as covariate.

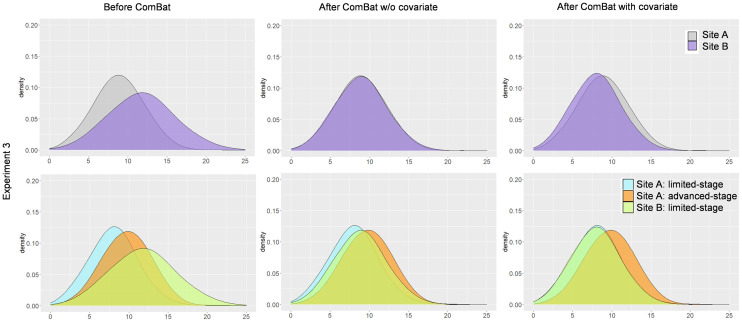
In experiment 3, the samples were the same as in experiment 2, but there were no advanced-stage patients at site B. Without the covariate stage, ComBat realigns patients at site A (limited and advanced stages) with patients at site B (limited stage only), as shown in Figure 5. Although the realignment of the 2 distributions seems to be satisfactory, a closer analysis shows that limited-stage patients are not well aligned between sites A and B because ComBat assumed that all site A patients were drawn from a single distribution, identical to that of the site B patients. When stage information is provided as a covariate, the distributions of limited-stage patients from site B are properly realigned with those of limited-stage patients from site A.

FIGURE 5.

Distributions for experiment 3 (Table 1). (Left) Distributions before ComBat. (Center) Distributions after ComBat (without covariate). (Right) Distributions after ComBat and specifying stage as covariate. (Top) Pooling of data at each site. (Bottom) Data represented per site and stage.

The frequency of the covariate may also differ between the 2 sites, such as in experiment 4 (Table 1). Similar to what was observed for experiment 3, the stage covariate must be introduced in the model to obtain a correct realignment for each stage (Fig. 4).

Applying ComBat with a covariate is different from performing ComBat for each subcategory separately. Using a covariate assumes that the site effect is identical for the 2 (or more) subcategories composing the sample and that only the proportion of individuals in the subcategories differs between the sites. The transformations associated with each subcategory are then constrained to have the same slope and will differ in their intercept only, as the intercept expression includes the design matrix X (Supplemental Fig. 2). If that assumption can be made, using ComBat with a covariate should be preferred to performing ComBat independently for each subcategory, as ComBat parameter estimates will benefit from a larger sample. If the site effect is expected to be different for the subcategories (e.g., for different tissue types), then ComBat should be performed for each subcategory independently. However, introducing covariates implies that the transformation will be determined from a smaller number of patients, which may lead to a less reliable estimate. The need for a covariate must therefore be carefully considered.

NO INTRODUCTION OF SPURIOUS INFORMATION FROM COMBAT COVARIATES

Introducing covariates does not artificially add information to the data, as demonstrated by experiment 5 (Fig. 4). In that setting, the data were the same as in experiment 4, except that at site B, limited- and advanced-stage patients yielded features with the exact same distribution. When ComBat is used with the stage covariate, limited-stage patients from both sites are realigned, advanced-stage patients from both sites are realigned, and the differences in limited- and advanced-stage patient feature distributions are reduced after pooling of the data from both sites, given that there was a real difference between the 2 stages at site A but not at site B. The stage covariate did not introduce any illegitimate differences between the 2 stages in patients scanned at site B (Fig. 4).

Similarly, when the difference between 2 categories (here, stages) is more detectable on feature values measured at one site (here, site B) than at the other (site A), applying ComBat using a covariate will not corrupt the results (Fig. 4). In experiment 6, the gap between the limited and advanced stages is 4 times larger at site B than at site A. After realignment of the distributions with ComBat and the stage covariate, the gap between the 2 stages remains larger at site B (interquartile range of feature values from site B after ComBat with covariate, 7.5) than at site A (interquartile range, 4.2), thus preserving the original properties of the site B distributions (interquartile range, 8.4) compared with without covariate (interquartile range, 4.7).

The fact that ComBat does not introduce false-positives even with the addition of a covariate has been previously demonstrated using sham experiments (15).

The covariate can also take continuous values. In the EARL experiment, the addition of the metabolic tumor volume of the volume of interest in cubic centimeters as a covariate also slightly improved agreement in SUV_max between with the EARL1 and EARL2 reconstructions (Fig. 2), with a reduction in the SD of the Bland–Altman plot from 2.1 SUV to 1.9 SUV.

COMBAT VERSUS Z SCORE

Another frequent harmonization method that can be applied a posteriori to feature values is the calculation of z scores at each site independently (26). The feature values at site A are converted into z scores using the average feature value and associated SD observed over all patients at site A. The same procedure is used for data from site B, using the mean and SD of all measurements made at site B. In doing so, values measured at the 2 sites become comparable. Supplemental Figure 3 shows the result after calculating a z score from the SUV_max in the lesions for centers A and B in comparison with Figure 3. Yet, this does not preserve the original range of values, since SUVs vary between −1.5 and 3.6 when expressed in z scores, against 1.2 SUV and 35.8 SUV on the original data. A second limitation is that it is not possible to account for a covariate. Supplemental Figure 4 shows that the absence of the advanced stage at site B for experiment 3 did not allow the distributions of the limited stages in the 2 sites to be aligned correctly when using a z score, in comparison to Figure 5.

REQUIREMENTS TO PREVENT FAILURE OF COMBAT

For ComBat to be useful, some basic assumptions must be fulfilled. The first assumption is that the distributions of the features to be realigned must be similar except for shift (additive factor) and spread (multiplicative factor) effects. This assumption can be checked by plotting the distributions of the feature values from the 2 sites. ComBat can be used even for nongaussian distributions. A log transformation before applying ComBat (followed by exponentiation after ComBat) can further improve the effectiveness of ComBat for heavy-tailed distributions, as shown in Supplemental Figure 1D.

The second assumption is that covariates (if any) that might explain different distributions at the 2 sites (see the first assumption) have to be identified and considered using the design matrix of Equation 3.

Third, the different sets of feature values to be realigned have to be independent. If not, it is unlikely that the first assumption will be met; hence, ComBat will not provide any sound result. A practical example is the realignment of TMTVs as described in this paper but between 2 segmentation methods, M1 and M2, where M2 produces the same result as M1 in some examples and produces a different result in others. Unless the cases for which the 2 methods produce the same segmentation can be predicted and coded as a covariate (e.g., in small lesions), ComBat should not be used. To illustrate, we analyzed TMTV from 140 lymphoma patients. M1 corresponds to a threshold set to an SUV of 4, and M2 corresponds to a majority vote between 3 segmentation approaches, including M1. In 60 of 140 cases, M2 led to exactly the same TMTV as M1, and the TMTV was different for all other cases. The TMTVs to be aligned are not independent, thus resulting in a misalignment with ComBat (Supplemental Fig. 5), which should realign the cases in which the TMTVs are identical and different separately.

Fourth, determining a single transformation with ComBat from data with different tissue or tumor types does not always lead to satisfactory data realignments, because different texture patterns are not necessarily affected identically by the image acquisition and reconstruction protocols. It is therefore not appropriate to realign them all using a single ComBat transformation. This consideration fully explains why Ibrahim et al. (27) did not realign the data correctly with ComBat: the 10 patterns in the investigated phantom were affected differently by the pixel spacing. When ComBat was applied separately for each of the textural patterns, the realignments were correct (28).

AMOUNT OF DATA NEEDED TO USE COMBAT

The success of ComBat when only small datasets are available depends on the magnitude of the site effect and on the representativeness of the samples available for each site. In previous studies (13), ComBat was successful when the number of patients per site was as low as 20. To illustrate the impact of the number of patients, we reanalyzed previously published data (12) by aligning the feature distribution from site B (74 patients) to site A (63 patients) after estimating the ComBat transformation using only a subset of site B data (74 to 5 patients, 100 repeated random selections). Before ComBat, the distributions from the 2 sites were different (Kolmogorov–Smirnov, P < 5%) for SUV_max or homogeneity measured in the lesions (Supplemental Table 1). After ComBat, the distributions were not significantly different in at least 95 of 100 tests when the transformation was estimated using 25 patients or more from site B for SUV_max (20 patients for homogeneity). Supplemental Figure 6 shows the increase in variability in estimating the intercept and slope of the ComBat transformation when the estimation is based on fewer and fewer patients. These results support the recommendation of using ComBat when at least 20–30 patients per batch are available. Use of a small sample size to estimate the transformations can also lead to a nonsignificant Kolmogorov–Smirnov test because the scanner effect becomes undetectable. In case a covariate is used, a minimum of 20–30 patients per covariate in each batch is also recommended.

A variant of ComBat named B-ComBat, which uses a bootstrap approach to determine the parameters of the transformation, has been proposed (20). However, the use of B-ComBat and the potential benefit of this more computationally demanding approach compared with ComBat have not yet been reported by independent groups.

USE OF COMBAT IN PRACTICE

Different implementations of ComBat are publicly available (R, Python, MATLAB [MathWorks]) and are summarized in Table 3. ComBat can also be used without any third-party software or programming skills using a free online application (https://forlhac.shinyapps.io/Shiny_ComBat/).

TABLE 3.

Implementations of ComBat

Name	Details
neuroComBat (script)	https://github.com/Jfortin1/ComBatHarmonization; language: R, Python, or MATLAB
M-ComBat (script)	https://github.com/SteinCK/M-ComBat; language: R
ComBaTool (standalone web application)	https://forlhac.shinyapps.io/Shiny_ComBat/; language: R

DISCUSSION

In this article, we provide a guide to understanding and using the ComBat harmonization method correctly. The main advantage of ComBat is that it can be used retrospectively and directly on image features that are already calculated without the need to perform phantom experiments. However, given that ComBat is a data-driven method, a highly recommended practice is to scrutinize the distributions of the feature values from the sites to be pooled before using ComBat. This practice usually makes it possible to quickly determine whether the assumptions underlying ComBat are fulfilled, especially whether the distributions observed at the different sites are similar except for shift and spread effects. When this is the case, ComBat can be used; otherwise, the reason should first be identified. Often, the reason is the presence of one or more covariates, such as patient age, disease stage, treatment, molecular subtype, or metabolic volume. When covariates can be identified, it is easy to check whether ComBat assumptions are met for each dataset corresponding to a covariate value and whether the site effect impacts the sample corresponding to each covariate identically. If so, ComBat can be used by including that covariate. If the site effect impacts samples corresponding to each covariate differently, then a specific ComBat transformation should be estimated for each sample independently. Examination of feature distributions in tumors can sometimes be challenging, as the variability in the biologic signal associated with tumor heterogeneity can hide other sources of variability associated with the site effect. An easy check is to segment a reference region of fixed size in a nonpathologic tissue (e.g., healthy liver) and observe feature values within that region in images from different sites. This check is not sufficient, as it will not give precise information about site effects related to the spatial resolution in the images because the liver usually displays a low-frequency signal. However, we still find it useful to characterize how image quality differs between sites.

ComBat users should keep in mind that data can be grouped in the same batch if they were extracted from images obtained using the same setting on the same scanner. If the image acquisition and reconstruction protocols vary on a scanner, a careful check is needed to ensure that this variance does not affect the image properties. Otherwise, different batches should be used for the same scanner corresponding to different settings.

In prospective studies, the transformation to be applied with ComBat can be deduced from data acquired previously for the same patient population. The ComBat method is complementary to the EARL standardization approach. We have summarized the pros and cons of both approaches in Table 4. EARL and ComBat can be used together if differences in feature distributions remain even with an EARL-standardized imaging protocol.

TABLE 4.

Opportunities and Limitations of Harmonization Using EARL and ComBat

Parameter	Upfront harmonization (like EARL)	ComBat
Opportunities	Applicable without restriction on number of patients; valid for any pathology and feature	Applicable directly to calculated radiomic feature values (no need to access images); no need for phantom acquisition; applicable retrospectively; applicable prospectively if data have already been acquired for same pathology with same acquisition and analysis protocols and settings; ability to realign data to particular site
Limitations	Not applicable retrospectively; requires acquisition of phantom images, optimization of reconstruction settings, and access to machine	Requirement for minimum number of patients (∼20–30 per batch); specific transformation for each type of tissue, each type of tumor, each scanner, each material in phantom, each analysis method (e.g., segmentation approach) and each feature; not applicable prospectively if little or no previously acquired data

Harmonization in medical imaging can also be seen as domain adaptation, where the goal would be to produce images belonging to a single domain (here, corresponding to the image quality or accuracy obtained with a specific scanner and protocol) from images recorded in different domains. Promising approaches for domain adaptation using, for example, generative adversarial networks have been developed in recent years (29–31). The role of such approaches in harmonizing PET and SPECT images remains to be studied. Unlike ComBat, generative adversarial networks act on the images and not on the already computed features; this requires access to the images, which could be a limitation.

CONCLUSION

In this article, we provide a guide to using the ComBat method to compensate for multicenter effects affecting quantitative biomarkers extracted from nuclear medicine images and beyond. This harmonization method is largely used in medical imaging and should facilitate large-scale multicenter studies needed to translate radiomics to the clinics.

DISCLOSURE

This work is partially supported by the Dutch Cancer Society (VU 2018-11648). The HOVON-84 study was supported by the Dutch Cancer Society (CKTO-2006-14) and by Roche Nederland. Michel Meignan has received funds from ROCHE for an educational program. Ronald Boellaard is an (unpaid) scientific advisor for the EARL PET/CT accreditation program. No other potential conflict of interest relevant to this article was reported.