Abstract
Mild cognitive impairment (MCI) is often considered the precursor of Alzheimer’s disease. However, MCI is associated with substantially variable progression rates, which are not well understood. Attempts to identify the mechanisms that underlie MCI progression have often focused on the hippocampus but have mostly overlooked its intricate structure and subdivisions. Here, we utilized deep learning to delineate the contribution of hippocampal subfields to MCI progression. We propose a dense convolutional neural network architecture that differentiates stable and progressive MCI based on hippocampal morphometry with an accuracy of 75.85%. A novel implementation of occlusion analysis revealed marked differences in the contribution of hippocampal subfields to the performance of the model, with presubiculum, CA1, subiculum, and molecular layer showing the most central role. Moreover, the analysis reveals that 10.5% of the volume of the hippocampus was redundant in the differentiation between stable and progressive MCI.
Keywords: Alzheimer’s disease, cognitive decline, deep learning, hippocampus, mild cognitive impairment
Introduction
A certain degree of cognitive decline is common and considered a part of the normal aging process. Mild cognitive impairment (MCI) occurs when cognitive decline exceeds what is expected given an individual’s age and education level (Gauthier et al. 2006). MCI can be considered a transitional phase in between age-related cognitive decline and Alzheimer’s disease (AD) or other dementias (Gauthier et al. 2006). However, MCI is associated with marked etiological heterogeneity (DeCarli 2003) and variable progression rates (Roberts and Knopman 2013). Namely, up to 33% of individuals with MCI convert to AD over 5 years (Ward et al. 2013), with annual conversion rates of about 7% (Mitchell and Shiri-Feshki 2009), but others may remain stable or even revert to normal or near-normal cognition levels (Koepsell and Monsell 2012). Identifying prognostic markers that can predict eventual conversion from MCI to AD is of profound clinical interest (Karakaya et al. 2013). However, such markers are not available to date. Fundamentally, despite increased interest in recent years (Thung et al. 2016; Liu et al. 2018; Cheng et al. 2019), a mechanistic framework for understanding progression and stability in MCI remains missing.
The neuropathological profile of MCI is complex and multifaceted (Stephan et al. 2012). As MCI is commonly seen as a precursor to AD, many studies have focused on alterations in structures known to be affected by this disease. The most widely studied target in AD is the hippocampus (Jack et al. 1992; Fox et al. 1996), and indeed, multiple studies have reported hippocampal volume loss in MCI relative to controls (Jack et al. 1999). Studies have also implicated the hippocampus in the progression of MCI (Douaud et al. 2013). Of particular interest, a series of recent studies have utilized deep learning to differentiate progressive and stable MCI (Huang et al. 2019; Li and Liu 2019) or predict individual subjects’ progression from MCI to AD (Li et al. 2019) based on whole hippocampus structural features. However, rather than being a homogeneous structure, the hippocampus is complex and heterogeneous (Duvernoy et al. 2013). The hippocampus is composed of several histologically distinct subfields (Duvernoy et al. 2013), which are characterized by differential connectivity profiles (Dalton et al. 2019) and subserve different memory processes (Bartsch et al. 2011). Thus, a better understanding of MCI progression and stability necessitates a mechanistic framework that takes the structural complexity of the hippocampus into account (Maruszak and Thuret 2014). Whether the different hippocampal subfields contribute differentially to the progression from MCI to AD remains unclear, with mixed and inconsistent findings reported in the literature. Namely, while several studies reported that the CA1 and subiculum are the most central subfields in the progression of MCI (Apostolova et al. 2006; Carlesimo et al. 2015), other studies suggested that the CA2/3, fimbria, and GC-DG were most central (Li et al. 2013; Khan et al. 2015).
In the current study, we investigated the contribution of hippocampal subfields to the progression and stability of MCI. To that end, we utilized a deep learning framework, and a large neuroimaging dataset, to account for the expected complexity in the contribution of the different subfields to the progression of MCI. We propose a deep convolutional neural network trained to classify stable and progressive MCI based on hippocampal structural features derived from magnetic resonance imaging (MRI). We then introduce a novel implementation of occlusion analysis to evaluate the relative contribution of each hippocampal subfield to the performance of the predictive model, thus estimating their role in AD progression. Moreover, the same analysis allowed us to estimate the cumulative contribution of subfields to MCI stability and the possible existence of redundancy within the associated hippocampal features.
Materials and Methods
Experimental Data
Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI). The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial MRI, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. For up-to-date information, see www.adni-info.org. All subjects provided written informed consent and the study protocol was approved by the local Institutional Review Boards. The subjects included in the study were diagnosed as cognitively normal (CN), AD, and MCI. Inclusion criteria for CN subjects were as follows: 1) free of memory complaints. 2) Mini-Mental State Examination (MMSE) scores between 24 and 30. 3) Clinical dementia rating (CDR) score of 0. 4) Normal scores in the Logical Memory II subscale of the Wechsler Memory Scale-Revised, using education-adjusted cutoffs (Wechsler 1987). Inclusion criteria for AD were: 1) subjective memory concerns. 2) MMSE scores between 20 and 26. 3) CDR score of 0.5 or 1. and 4) abnormal scores in the Logical Memory II subscale of the Wechsler Memory Scale-Revised, using education-adjusted cutoffs. Finally, inclusion criteria for MCI subjects were: 1) subjective memory concerns. 2) MMSE scores between 24 and 30. 3). CDR score of 0.5. and 4) abnormal scores in the Logical Memory II subscale of the Wechsler Memory Scale-Revised, using education-adjusted cutoffs. We used baseline MRI data from 349 subjects from ADNI-2/GO to train the deep learning model, with 10-fold cross validation used to optimize the model’s performance. We validated the model with an independent cohort of 427 subjects from ADNI-1 (Supplementary Fig. 1). An additional sample of 381 subjects with MCI at baseline, obtained from ADNI-2/GO, was used to test the model. This dataset was labeled as either stable MCI (sMCI) or progressive MCI (pMCI) based on longitudinal diagnostic evaluations obtained at least 18 months apart. Subjects who were classified as pMCI were those who were diagnosed with MCI at baseline and progressed to a diagnosis of probable AD by the time of the follow-up visit (Supplementary Fig. 1). Subjects in the sMCI group were those who were diagnosed with MCI at baseline and maintained their MCI status at the follow-up visit. We excluded 65 subjects who were diagnosed with MCI at baseline but reverted to CN status during follow-up. Based on these criteria, a total of 118 pMCI and 263 sMCI subjects were included in this study. The demographic characteristics of each cohort analyzed in this study are summarized in Table 1.
Table 1.
Demographics
| ADNI-1 | ADNI-2 and GO | |||||
|---|---|---|---|---|---|---|
| AD | CN | AD | CN | pMCI | sMCI | |
| N | 197 | 230 | 159 | 190 | 118 | 263 |
| Age | 75.6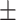 7.7 7.7 |
76.0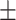 5.0 5.0 |
74.8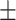 8.1 8.1 |
73.4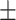 6.4 6.4 |
73.6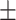 7.1 7.1 |
71.7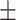 7.3 7.3 |
| Gender (% female) | 95 (48.2%) | 112 (48.7%) | 68 (42.8%) | 100 (52.6%) | 52 (44.1%) | 112 (42.6%) |
| Education | 14.7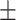 3.1 3.1 |
16.0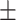 2.8 2.8 |
15.8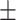 2.7 2.7 |
16.5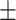 2.6 2.6 |
16.0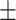 2.7 2.7 |
16.2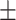 2.7 2.7 |
| MMSE | 23.3 2.0 2.0 |
29.1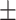 1.0 1.0 |
23.1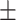 2.1 2.1 |
29.0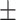 1.3 1.3 |
27.3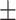 1.8 1.8 |
28.3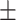 1.7 1.7 |
Notes: Continuous variables are presented as mean 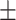 SD and categorical variable is presented as %. Abbreviations: AD = Alzheimer’s disease, CN=cognitively normal, pMCI = progressive mild cognitive impairment, sMCI = stable mild cognitive impairment, N = number of subjects, MMSE = Mini-Mental State Examination.
SD and categorical variable is presented as %. Abbreviations: AD = Alzheimer’s disease, CN=cognitively normal, pMCI = progressive mild cognitive impairment, sMCI = stable mild cognitive impairment, N = number of subjects, MMSE = Mini-Mental State Examination.
Imaging Data
Input data for the deep learning model were acquired at ADNI sites using 1.5T (ADNI-1) and 3T (ADNI-2/GO) scanners and were based on either an inversion recovery-fast spoiled gradient recalled or a magnetization-prepared rapid gradient-echo sequences (Jack et al. 2010). Full details of the image acquisition parameters are listed on the ADNI website (http://adni.loni.usc.edu/methods/documents/mri-protocols/).
Image Processing
All images were corrected for intensity nonuniformity artifacts (Sled et al. 1998) and were registered into the MNI152 template using FMRIB Software Library v6.0 (Jenkinson et al. 2002). Input data from the left and right hippocampus were extracted from the T1-weighted MRI images. We first defined a 3D bounding box of size 44 × 52 × 52 voxels around the hippocampal region. The bounding box’s size was sufficient in covering the hippocampal region in all our target subjects, with its size corresponding to that used in previous studies (Li and Liu 2019; Liu et al. 2020). The voxel intensities within the bounding box were normalized into a range between 0 and 1. Intensity values from each voxel within the bounding box were then extracted and used as inputs in the deep learning model described below.
Data Augmentation
To artificially increase the size of the model’s training dataset and improve its performance and generalizability, we used an image data augmentation technique with Scikit-learn 0.22.1 (Pedregosa et al. 2011). The augmented image data were generated through the addition of noise with mean 0 and standard deviation 1, contrast enhancement by effectively spreading out the most frequent intensity values (stretching out the intensity range) and flipping left and right. In total, 954 AD images and 1140 CN images were generated from the original dataset (AD: N = 159, CN: N = 190) through augmentation and used in the training dataset to improve the performance of the model.
Hippocampal subfield segmentation: Subfields in the hippocampus were segmented with an automated segmentation tool available in FreeSurfer v6.0 (Iglesias et al. 2015), which is based on a new statistical atlas built primarily upon ultra–high-resolution (~0.1 mm isotropic) ex vivo MRI data. This approach uses Bayesian inference that relied on image intensities and a tetrahedral mesh-based probabilistic atlas of the hippocampal formation, constructed from a library of in vivo data and ex vivo–labeled data (Van Leemput et al. 2009; Iglesias et al. 2015). This widely used method was validated with ADNI-based MCI and AD data (Iglesias et al. 2015), with its test–retest reliability established in both AD and CN subjects (Worker et al. 2018). It was used in large multicenter studies (Whelan et al. 2016) and was found as reliable across repeated scans (Quattrini et al. 2020) and between scanners (Brown et al. 2020). Moreover, hippocampal subfield segmentation has been widely applied using 3T MRI data, for example in studies of schizophrenia (Alnæs et al. 2019), psychotic symptoms (Mancini et al. 2020), and visual episodic recollection (Norman et al. 2019) and in genome-wide association studies (Hibar et al. 2017; van der Meer et al. 2020). Thus, automated hippocampal subfield segmentation from in vivo MRI at 3T is a reliable, validated, and widely used approach. In the current study, the left and right hippocampus were segmented into 12 subfields: CA1, CA2/3, CA4, hippocampal–amygdala transition area (HATA), granule cell layer of the dentate gyrus (GC-DG), fimbria, molecular layer, hippocampal fissure, hippocampal tail, subiculum, parasubiculum, and presubiculum.
Deep Learning Model Architecture
A deep learning model based on the DenseNet architecture (Huang et al. 2017) was trained to learn relevant maps for classifying pMCI versus sMCI. This state-of-the-art convolutional neural network architecture was chosen as it shows excellent classification performance with a range of datasets while diminishing the vanishing gradient problem and reducing the number of parameters (Huang et al. 2017). We used deep learning, rather than traditional machine learning models, such as random forest, or support vector machine, primarily since similar models have achieved the best performance in previous studies (Li et al. 2019; Li and Liu 2019; Liu et al. 2020), when based on complex features directly extracted from the raw data (i.e., whole hippocampal intensity values). Moreover, we assumed complex, possibly nonlinear relationships between hippocampal subfields and the progression from MCI to AD, further motivating the use of deep learning.
The deep learning model (see Fig. 1C) comprised of two streams for the left and right hippocampus. Each stream consisted of a convolutional layer, four dense blocks, three transition layers, and a global average pooling layer. The outputs of the two streams were then concatenated as input to a fully connected layer. First, the image was passed through a stack of convolutional layers, where the filters were of size 5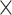 5 × 5. The convolution stride was fixed to one voxel. The max pooling layer had a stride of size 2 × 2 × 2 and a kernel size of 2 × 2 × 2. The dense block implements a dense connection from the lth layer to all its subsequent layers:
5 × 5. The convolution stride was fixed to one voxel. The max pooling layer had a stride of size 2 × 2 × 2 and a kernel size of 2 × 2 × 2. The dense block implements a dense connection from the lth layer to all its subsequent layers:
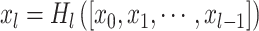 |
(1) |
where 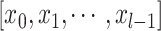 indicates the concatenation operation of the feature maps produced in preceding layers, and
indicates the concatenation operation of the feature maps produced in preceding layers, and 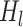 denotes a composite function of four consecutive operations: batch normalization layer, leaky rectified linear unit, 3 × 3 × 3 convolutional layer, and dropout layer. The dense block consisted of multiple convolution units, which were equipped with a 1
denotes a composite function of four consecutive operations: batch normalization layer, leaky rectified linear unit, 3 × 3 × 3 convolutional layer, and dropout layer. The dense block consisted of multiple convolution units, which were equipped with a 1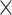 1 × 1 convolutional layer, a 3 × 3 × 3 convolutional layer, batch normalization layer, leaky rectified linear unit, and a dropout layer. Every convolutional unit was connected to all previous layers by shortcut connections. A transition layer allowed for dimensionality reduction of feature maps in between dense blocks. It was composed of a batch normalization layer, leaky rectified linear unit, a 1
1 × 1 convolutional layer, a 3 × 3 × 3 convolutional layer, batch normalization layer, leaky rectified linear unit, and a dropout layer. Every convolutional unit was connected to all previous layers by shortcut connections. A transition layer allowed for dimensionality reduction of feature maps in between dense blocks. It was composed of a batch normalization layer, leaky rectified linear unit, a 1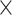 1 × 1 convolutional layer, a 3
1 × 1 convolutional layer, a 3 3 × 3 convolutional layer, a dropout layer, and an averaging pooling layer. The stacks of global averaging pooling layers were concatenated and connected by a fully connected layer. The output value was processed by the fully connected layer with a sigmoid activation function.
3 × 3 convolutional layer, a dropout layer, and an averaging pooling layer. The stacks of global averaging pooling layers were concatenated and connected by a fully connected layer. The output value was processed by the fully connected layer with a sigmoid activation function.
Figure 2 .
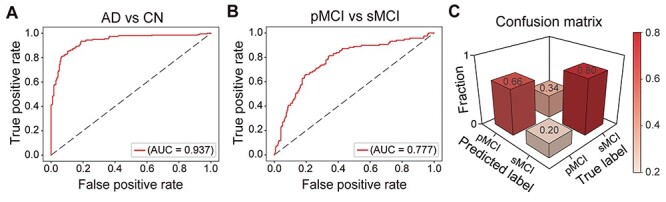
The predictive performance of the proposed deep learning model. (A) ROC curve for the task of classifying AD versus CN. (B) ROC curve for the pMCI versus sMCI task. (C) Confusion matrix, with results from the model showing the best performance, evaluating the sensitivity and specificity obtained in the task of classifying pMCI versus sMCI. The matrix values were rescaled to the range of [0,1]. Abbreviations: AD = Alzheimer’s disease, CN = cognitively normal, pMCI = progressive mild cognitive impairment, sMCI = stable mild cognitive impairment, ROC = receiver operating characteristic, AUC = area under the curve.
Figure 1 .
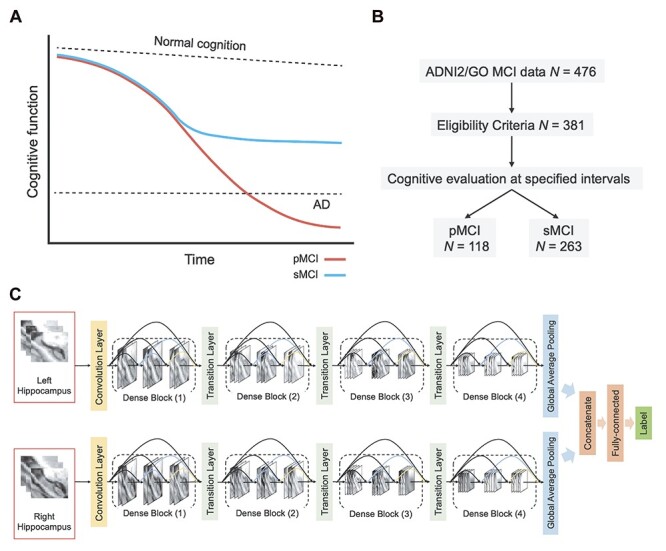
Study design and methods. (A) Hypothetical models of MCI progression. In pMCI, gradual cognitive decline continues until individuals meet the diagnostic criteria of AD. In sMCI, cognitive performance remains relatively stable over time. (B) Group allocation criteria. Cognitive evaluations at baseline and follow-up visits were used to classify subjects in the pMCI and sMCI groups. (C) Illustration of proposed deep learning model. Abbreviations: AD = Alzheimer’s disease, MCI = mild cognitive impairment, pMCI = progressive mild cognitive impairment, sMCI = stable mild cognitive impairment.
Implementation
The deep learning model was built with the Keras application programming interface in TensorFlow 2.0. Training and testing of the model were carried out with an Ubuntu 18.04.3 operating system and two Nvidia Tesla V100 graphic cards with 16GB memory each. The model was parallelized across graphic cards. We trained the model with a mini batch size of 64 and 200 epochs. The deep learning model was optimized using stochastic gradient descent (Kingma and Ba 2014) with momentums and an exponentially decaying learning rate. The initial learning rate was 0.0001 and it was decayed by 0.9 after every 10 000 steps. We added a dropout layer in the dense block and set the dropout rate to 0.2. In the batch normalization, beta and gamma weight were initialized with L2 regularization set at 1 × 10−4 and epsilon set to 1.1 × 10−5. The L2 regularization penalty coefficient was set at 0.01 for the fully connected layer. The deep learning model was stable after an iteration of 150 epochs. During training, a binary cross-entropy loss of predicted output value is calculated as follows:
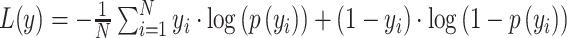 |
(2) |
where y is the true label (1 for AD and 0 for CN), 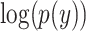 is the log predicted probability of the sample being AD class,
is the log predicted probability of the sample being AD class, 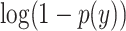 is the log probability for the CN class, and N is the number of samples in a batch. A focal loss function based on cross-entropy loss for imbalanced data was also used, but it had no differential effect on the performance of the model.
is the log probability for the CN class, and N is the number of samples in a batch. A focal loss function based on cross-entropy loss for imbalanced data was also used, but it had no differential effect on the performance of the model.
Validation Framework
We evaluated the performance of the proposed deep learning model both within the training dataset and using an independent validation dataset. First, k-fold cross-validation with k = 10 was applied during the training of the model, which allowed for the optimization of hyperparameters in the training set. The model that yielded the best performance was then validated using an independent dataset from ADNI-1, in the task of differentiating AD versus CN. Subsequently, the model was applied to the main independent testing dataset (based on ADNI-2/GO data), in the task of differentiating pMCI versus sMCI (Supplementary Fig. 1). Thus, similar to previous studies (e.g., Suk et al. 2014; Huang et al. 2019; Li et al. 2019), we used a classification framework in which MCI progression is predicted based on a model that trains to differentiate AD versus CN data. This was based on the assumption that structural features required to differentiate the pMCI and sMCI groups are well within the distribution of features the model learns from.
We additionally evaluated whether the class imbalance in the testing dataset (Table 1) affected the performance of the model, through a random permutation test. We extracted an equally sized randomly selected set of subjects from each group/class, repeating this procedure 10 000 times, while retesting the model at each iteration. This procedure resulted in a distribution of accuracy values for testing sets composed of balanced classes, which were then compared with the accuracy obtained in the original imbalanced testing set. The procedure was repeated for two balanced sample sizes: n = 60 and n = 80.
We also tested whether the performance of the proposed model differed from that of a purely random classifier, through a random permutation test. We generated a null distribution of accuracy, sensitivity, and specificity for the random classifier by randomly assigning subjects to two different classes 10 000 times and retesting the model at each iteration. Differences between the original performance of the model and the resulting null distributions were then computed.
Model Comparison
The performance of the proposed deep learning model was compared with that obtained in three common machine learning models, available from the Scikit-learn library (0.23.2): support vector machine (Platt 1999), random forest (Liaw and Wiener 2002), and logistic regression (Cox 1958). Similar to the training of the deep learning model, voxel intensities from a 3D bounding box surrounding the entire hippocampal region were used as features. The model was trained to first differentiate AD and CN and was then tested on the task of differentiating pMCI versus sMCI. In the classification experiment, support vector machine was set up based on a soft margin with a linear kernel. Logistic regression was initiated with a penalty set to “L2” for regularization, and with other hyperparameters set at default settings. Default settings were also used for random forest classification.
Implementation of Occlusion Analysis
Occlusion analysis was used for investigating the contribution of each hippocampal subfield to the performance of the prediction model. Masks for each hippocampal subfield were generated based on the subfield segmentation procedure described above (see Image Processing). We then masked out each hippocampal subfield (setting voxels of each hippocampal subfield to zero) from the input data of the test phase and retested the trained deep learning model. For any voxel j and corresponding inputs 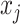 :
:
 |
(3) |
where 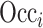 represents the occlusion of hippocampal subfield i. If the value of j is an element of subfield i, the intensity of
represents the occlusion of hippocampal subfield i. If the value of j is an element of subfield i, the intensity of 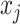 is set to zero. We occluded left and right subfields simultaneously. Each occluded hippocampal subfield was then ranked based on the performance (accuracy) of the model, relative to the original model, where input data from the entire hippocampus was used.
is set to zero. We occluded left and right subfields simultaneously. Each occluded hippocampal subfield was then ranked based on the performance (accuracy) of the model, relative to the original model, where input data from the entire hippocampus was used.
In a second implementation of occlusion analysis, we evaluated the performance of the prediction model under gradually accumulating occlusion of hippocampal subfields. This was achieved by retesting the prediction model, each time masking out an additional subfield (i.e., starting from one masked out subfield, then two, etc.). Let 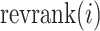 denote the reverse ranking of the i-th hippocampal subfield’s contribution to accuracy in comparison to that of all other subfields (N = 12), as identified in the initial occlusion analysis. Then, the i-th accumulating occlusion is here defined as:
denote the reverse ranking of the i-th hippocampal subfield’s contribution to accuracy in comparison to that of all other subfields (N = 12), as identified in the initial occlusion analysis. Then, the i-th accumulating occlusion is here defined as:
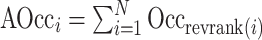 |
(4) |
where 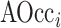 denotes the accumulating occlusion of hippocampal subfields, which were masked out sequentially, in descending order i, according to their contribution to accuracy (as identified in the initial occlusion analysis). This step also allowed us to evaluate the stability of the occlusion analysis, ensuring that it did not result in abrupt changes in classification performance. We additionally estimated the points in which the accumulated occlusion analysis showed large changes in accuracy. First, the results of the analysis (i.e., changes in accuracy observed in each of its 12 steps) were fitted with a nonlinear log-sigmoid curve (Ritz et al. 2015):
denotes the accumulating occlusion of hippocampal subfields, which were masked out sequentially, in descending order i, according to their contribution to accuracy (as identified in the initial occlusion analysis). This step also allowed us to evaluate the stability of the occlusion analysis, ensuring that it did not result in abrupt changes in classification performance. We additionally estimated the points in which the accumulated occlusion analysis showed large changes in accuracy. First, the results of the analysis (i.e., changes in accuracy observed in each of its 12 steps) were fitted with a nonlinear log-sigmoid curve (Ritz et al. 2015):
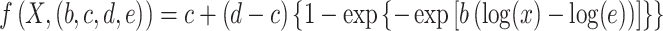 |
(5) |
where X is the set of estimated points. Note that b, c, d, and e are used to indicate that model parameters have to be estimated from the data points. The fitted curve was generated using the drm function in the R drc package with a Weibull distribution. We then sampled 1000 points from the fitted curve to estimate the location of change points in the curve, using the mcp function in the R mcp package (Lindeløv 2020). In this procedure, which relied on default parameters, the location of change points between regression models is inferred using a Bayesian inference approach, with user-defined segments. The predefined segments we considered were based on the assumption of two change points in the curve. In this approach, change points correspond to the points in the curve where the data’s best predictive model changes from one model to another.
Lastly, we evaluated the potential confounding effect that the size of the occluded subfields had on the accuracy of classification through random occlusion analysis. This post hoc analysis focused on the four major subfields that showed the most prominent effects in the original occlusion analysis (presubiculum, subiculum, CA1, and molecular layer). The average size (volume) of each of these four subfields was first calculated. We then generated, for each subfield, random parcels with identical size, but at random spatial locations based on a region growing algorithm (Mary Synthuja Jain Preetha et al. 2012). A total of 1000 random parcels were generated for each subfield. We then repeated the occlusion analysis 1000 times, occluding the random parcels at each permutation. This allowed us to generate a null distribution of accuracy values calculated based on the randomly placed masks. Differences between the original accuracy values and the values obtained via random occlusion were then assessed with a two-sided permutation test.
Results
To delineate the contribution of hippocampal subfields to MCI progression, we analyzed neuroimaging data from the ADNI database. Our analysis focused on individuals with MCI who exhibit progressive deterioration in cognitive performance, evaluated at baseline and follow-up visits, in comparison to those who remain stable over time (Fig. 1A). We thus considered baseline neuroimaging data from two groups (Fig. 1B). First, subjects in the sMCI group had a baseline diagnosis of MCI that was retained at follow-up, with at least 18 months between diagnoses. Secondly, subjects in the pMCI group were subjects who over the course of a similar duration progressed from a diagnosis of MCI to probable AD. To train our deep learning model (see below), we additionally analyzed data from CN subjects along with subjects with a diagnosis of AD. Two independent cohorts were analyzed for the two latter groups (data from ADNI-1 and ADNI-2/GO), used for the training and validation of the deep learning model.
Participant Characteristics
The demographic characteristics of subjects in the AD, CN, pMCI, and sMCI groups are shown in Table 1. Comparing the pMCI and sMCI groups, there were significant differences in age (t379 = 2.449, P = 0.015) and MMSE score (Wilcoxon Rank-sum, Z = 4.938, P = 7.89 10−7). No significant difference was observed for gender distribution (χ2 = 0.072, P = 0.787) or education (t379 = 0.756, P = 0.450). In the comparisons between the AD and CN groups, in both cohorts, there were significant differences in education (ADNI-1: t425 = 4.483, P = 9.47
10−7). No significant difference was observed for gender distribution (χ2 = 0.072, P = 0.787) or education (t379 = 0.756, P = 0.450). In the comparisons between the AD and CN groups, in both cohorts, there were significant differences in education (ADNI-1: t425 = 4.483, P = 9.47 10−6; ADNI-2/GO: t347 = 2.614, P = 0.009) and MMSE score (ADNI-1: Z = 17.900, P = 1.19
10−6; ADNI-2/GO: t347 = 2.614, P = 0.009) and MMSE score (ADNI-1: Z = 17.900, P = 1.19 10−71; ADNI-2/GO: Z = 15.953, P = 2.70 × 10−57). Age differed marginally in the ADNI-2/GO (t347 = 1.901, P = 0.058) cohort, but not in ADNI-1(t425 = 0.562, P = 0.575). Gender distributions were not significantly different in both cohorts (ADNI-1: χ2 = 0.022 P = 0.882; ADNI-2/GO: χ2 = 3.374, P = 0.066).
10−71; ADNI-2/GO: Z = 15.953, P = 2.70 × 10−57). Age differed marginally in the ADNI-2/GO (t347 = 1.901, P = 0.058) cohort, but not in ADNI-1(t425 = 0.562, P = 0.575). Gender distributions were not significantly different in both cohorts (ADNI-1: χ2 = 0.022 P = 0.882; ADNI-2/GO: χ2 = 3.374, P = 0.066).
A Deep Learning Model for Classifying Stable and Progressive MCI
We next developed a deep learning model, based on the DenseNet architecture (Huang et al. 2017) (Fig. 1C), for classification of pMCI versus sMCI, as an initial step prior to delineating the role of hippocampal subfields in MCI progression. As input data, the model utilizes voxel intensity values from a 3D bounding box surrounding the entire hippocampal region. As in previous studies (Huang et al. 2019; Li et al. 2019), the model was trained to first differentiate AD and CN (data source: ADNI-2/GO), with the assumption that these two extreme classes would allow the model to learn the necessary representations for classifying MCI subjects as well. The model was then tested on the task of differentiating pMCI versus sMCI (data source: ADNI-2/GO). We also validated the model’s performance by retesting it on the task of differentiating AD versus CN (data source: ADNI-1). Data augmentation (see Materials and Methods) was applied within the training dataset to improve the performance of the model and its generalizability. We used 10-fold cross-validation within the training dataset to optimize and fine-tune the model’s performance, finding similar performance across the different folds (Supplementary Fig. 2). We fine-tuned the parameter of iteration number in the training step, to obtain optimized performance. The model with the best performance achieved maximal accuracy of 94.07% in one of the folds, with an area under the curve (AUC) of the receiver operating characteristic (ROC) of 0.993. The model was further validated with AD and CN data from ADNI-1, achieving an accuracy of 86.20%, with an AUC of 0.937 (Fig. 2A). Of note, data from ADNI-1, which were acquired with 1.5T MRI scanners, were only used for the validation of the deep learning model. Thus, despite a decrease in accuracy, which may be expected given that ADNI-1 is based on lower MRI field strength (1.5T, relative to ADNI 2/GO’s 3T), the model was overall stable and robust. This model was thus used next for differentiating the pMCI and sMCI groups based on data from ADNI-2/GO. In this task, the model achieved an accuracy of 75.85% and an AUC of 0.777 (Fig. 2B), with a sensitivity of 0.66 and a specificity of 0.8 (Fig. 2C). When retesting the model with equally sized groups/classes in the testing dataset, there were no significant differences relative to the original results (n = 60: P = 0.335, n = 80: P = 0.345, Supplementary Fig. 3). This confirms that the performance of the proposed model was not affected by the class imbalance of the testing set. We additionally evaluated the performance of the model relative to that of a random classifier via a random permutation test, finding significant differences between the two across all performance metrics (all P < 0.001, Supplementary Fig. 4).
Figure 4 .
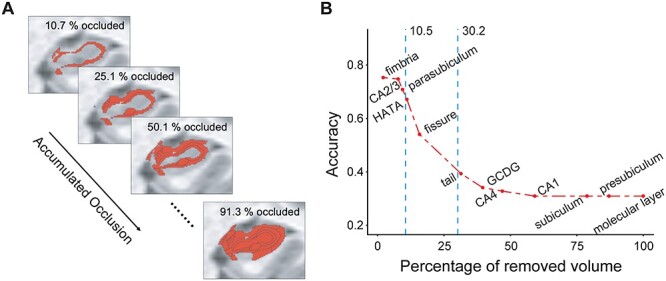
Accumulated occlusion analysis of hippocampal subfields. (A) An illustration of gradually accumulating occlusion. On each step, additional hippocampal volume is masked out of the analysis. (B) The model’s accuracy is shown as a function of accumulated occlusion, with subfields masked out in descending order according to their contribution to the model’s accuracy (as shown in Fig. 3C). The accuracy started decreasing strongly (i.e., relative to the accuracy of the full model) upon removal of 10.5% of the volume of the hippocampus, as identified with change-point analysis. Abbreviations: CA = cornu ammonis, HATA = hippocampus–amygdala–transition area, GC-DG = granule cell layer of the dentate gyrus.
We also compared the performance of the deep learning model with that obtained with standard machine learning algorithms, including support vector machine, random forest, and logistic regression. The deep learning model achieved better classification performance than all other algorithms (Supplementary Fig. 5). Additionally, repeating the analysis with an age- and MMSE-matched test cohort had minimal effects on the accuracy of the model (Supplementary Fig. 6).
Overall our proposed deep learning–based classification framework corroborates earlier results, by demonstrating comparable accuracy performance to those reported previously for the classification of pMCI versus sMCI (Huang et al. 2019; Li et al. 2019; Li and Liu 2019). It establishes that whole hippocampus structural features can be used to differentiate pMCI from sMCI.
Contribution of Hippocampal Subfields to MCI Progression: Occlusion Analysis
We next sought to test if differentiation of pMCI from sMCI can be achieved with data derived from single hippocampal subfields, assessing the relative contribution of each subfield to classification performance. Only data from ADNI-2/GO (all at 3T) were used in this analysis. We first segmented the hippocampal subfields in each of the subjects using a validated automated method (Iglesias et al. 2015) (Fig. 3A). The contribution of each subfield was then assessed using an adaptation of occlusion analysis, a common approach in computer vision (e.g., Sadr et al. 2003). Briefly, in this analysis, we retested the deep learning model, each time occluding a bilateral binary mask of each of the hippocampal subfields from the model’s test data (i.e., from the 3D bounding box). The occlusion of the subfields, which were segmented separately for each individual subject, was achieved by setting the intensity values of each hippocampal subfield to zero in the input data. The performance (accuracy) of the models was then ranked and compared with each other as well as to the model based on an intact hippocampus (Fig. 3B). Accuracy levels for each of the models differed considerably (Fig. 3C). The occlusion of subfields led to a decrease in accuracy. In particular, occlusion of the subiculum, CA1, presubiculum, and molecular layer led to dramatic decreases in accuracy, relative to other subfields, including CA2/3 and CA4 for example. Thus, the presubiculum, subiculum, CA1, and the molecular layer had the largest impact on the performance of the model (Fig. 3D).
Figure 3 .
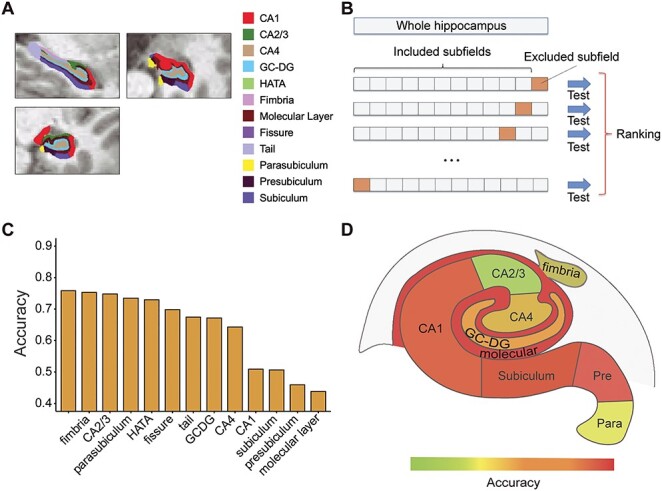
Occlusion analysis of hippocampal subfields. (A) Hippocampal subfield segmentation. The segmentation results of hippocampal subfields are illustrated on a single representative subject. (B) Schematic framework of the occlusion analysis. In each model, one of the hippocampal subfields was occluded (masked out) in the testing data and the performance of the model (its accuracy) was ranked relative to the occlusion of other subfields and to the performance of the original intact model. (C) The results of the occlusion analysis are shown for each model, along with the results of the original intact model (D) Accuracy performance of each model, superimposed on top of an illustration of the major hippocampal subfields (note: not all subfields are shown). Abbreviations: CA = cornu ammonis, HATA = hippocampus–amygdala–transition area, GC-DG = granule cell layer of the dentate gyrus.
We also assessed the effect of laterality on the accuracy of classification by repeating the occlusion analysis with left versus right hippocampal subfield masks tested separately. For the most impacted subfields (subiculum, CA1, presubiculum, and molecular layer), occlusion of the left hemisphere had a more pronounced effect on accuracy relative to occlusion of the right hemisphere (Supplementary Fig. 7).
The occlusion analysis revealed that many of the subfields had little to no contribution to the performance of the model. Namely, occlusion of CA2/3 and parasubiculum, for example, resulted in an accuracy loss of less than 4%. This suggests that in the classification of pMCI and sMCI some of the subfields may be redundant. That is, these results may reflect the existence of a certain degree of duplication or repetition (i.e., redundancy; Tononi et al. 1999) in the hippocampus. We evaluated this possibility by performing a sequential version of the occlusion analysis, where occlusion is accumulated from step to step (Fig. 4A), in descending order with respect to each subfield’s contribution to the model’s performance (as reported in Fig. 3C). The subfields were occluded in descending order, under the assumption that the least central subfields could be more redundant, contributing less to the differentiation of between pMCI and sMCI. Accuracy was evaluated as a function of the ratio of the total occluded volume to the volume of the entire hippocampus.
In comparison to the model with no occlusion, the accuracy started decreasing strongly when 10.5% of the volume of the hippocampus was removed (with occlusion of the fimbria, parasubiculum, and CA2/3), estimated by fitting the data with a log-sigmoid function, and extracting the resulting curve’s change points using a Bayesian inference approach (see Materials and Methods; Supplementary Fig. 8). In other words, we found that around 10.5% of the volume of the hippocampus was redundant in classifying pMCI versus sMCI. Upon removal of more than 30.2% of the volume of the hippocampus, accuracy levels started saturating (Supplementary Fig. 8). Finally, repeating the occlusion analysis with age- and MMSE-matched data had little effect on the results (Supplementary Fig. 9). Of note, since the 3D bounding box surrounding the hippocampal region, where model features were extracted from, contained a small set of nonhippocampal voxels (from regions such as the parahippocampal gyrus and entorhinal cortex), classification of MCI progression with very low accuracy (~30%) was evident even when 100% of the volume of the hippocampus was occluded.
The occlusion of the presubiculum, subiculum, CA1, and molecular layer had the largest impact on the performance of the model. These four subfields are among the largest in the hippocampus, raising the possibility that their occlusion resulted in large losses in accuracy merely because of their large size. To test the possible confounding role of subfield size in our proposed framework, we repeated the occlusion analysis, with random occluded masks, which are of the same size as the presubiculum, subiculum, CA1, and molecular layer (Fig. 5A). We generated a null distribution for each of the four major subfields, based on 1000 random permutations, each of which consisting of random parcels, with the same size as the tested subfields but at random spatial locations (Supplementary Fig. 10). The occlusion of the random parcels resulted in markedly lower loss of accuracy, relative to that observed in the original analysis (all P < 0.001, Fig. 5B). This suggests that the loss of accuracy observed when the presubiculum, subiculum, CA1, and molecular layer were occluded was not merely a reflection of their size.
Figure 5 .
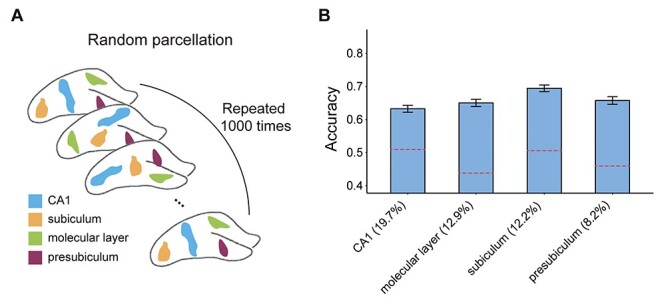
Random occlusion analysis for the major hippocampal subfields. (A) The potential confounding effect of subfield size was assessed by repeating the occlusion analysis 1000 times, each time occluding random parcels, which are of the same size as the presubiculum, subiculum, CA1, and molecular layer but are placed at random spatial locations. (B) The results of the random occlusion analysis are shown with reference to each of the four hippocampal subfields (the relative size of each mask is indicated as % of total hippocampal volume). Dashed red lines denote the original accuracy loss observed (same as Fig. 3C). Error bars denote standard deviation.
Discussion
Individuals with MCI show strongly variable symptomatic trajectories, with some progressing eventually to a probable diagnosis of AD, while others showing a more stable pattern of cognitive performance over time. In this paper, we propose a novel framework for the analysis of the progression and stability of MCI based on deep learning and occlusion analysis. First, we introduced a deep convolutional neural network model based on the DenseNet architecture (Huang et al. 2017) for classifying pMCI versus sMCI. Second, we proposed a novel analytical framework based on occlusion analysis to evaluate the contribution of hippocampal subfields to the performance of the proposed deep learning model, thus assessing the role of the different subfields in the stability and progression of MCI. Finally, as a secondary step, we applied a gradually accumulating occlusion analysis that allowed us to assess the degree of redundancy in the hippocampal features in relation to the classification of pMCI and sMCI.
As an initial step prior to the evaluation of the role of hippocampal subfields, we trained a deep convolutional neural network to classify the pMCI and sMCI groups based on all structural hippocampus features. This model achieved an accuracy of 75.85% (and an AUC of 0.777). This classification performance is on par with earlier deep learning models developed to classify pMCI versus sMCI based on whole hippocampus structural features or multimodel features (e.g., Li et al. 2014; Suk et al. 2014), which ranged from 72% to 76%. For example, a 3D-convolutional neural network based on multimodal data, integrating structural MRI and positron emission tomography (PET), classified pMCI versus sMCI with an accuracy of 72.22% (Huang et al. 2019), while another recently described hybrid convolutional and recurrent neural network based on internal and external hippocampal patches yielded classification accuracy of 72.50% for the same task (Li and Liu 2019). Another recent study utilized deep learning and hippocampal features predicting progression time from MCI to AD with a concordance index of 0.762 (Li et al. 2019). Our model corroborates these earlier reports by demonstrating that prediction of MCI stability and progression can be achieved with good accuracy rates based solely on hippocampal features.
Our findings extend earlier reports by delineating the contribution of single hippocampal subfields to the progression and stability of MCI. Our implementation of occlusion analysis revealed marked differences between the subfields in differentiating the pMCI and sMCI groups. In particular, the results suggest that the subiculum, presubiculum, CA1, and molecular layer were more central to this classification task than any other subfield. While these are among the largest subfields in the hippocampus, our results also demonstrate that their contribution to MCI progression was not merely a reflection of their size. The findings are consistent with earlier reports on the involvement of CA1, the subiculum (Apostolova et al. 2006; Carlesimo et al. 2015), and the molecular layer (Scheff et al. 2006; Zhao et al. 2019) in the progression of MCI. While several other studies implicated CA2/3, fimbria, and GC-DG in MCI progression (Li et al. 2013; Khan et al. 2015), our model suggests that these subfields play a more minor role. Our findings may reflect the neuropathological cascade characteristic of AD. Namely, neurofibrillary tangles in AD neurodegeneration progress from CA1 to the subiculum, before reaching CA2/3 (Braak and Braak 1991). Neuronal loss in CA1 and subiculum is prominent as AD neurodegeneration progresses, while being milder and slower in the CA2/3 and CA4 (Rössler et al. 2002). The results also reveal a more pronounced contribution of subfields in the left hemisphere to the performance of the model, consistent with earlier results (Shi et al. 2009; Sarica et al. 2018). Altogether, although our findings highlight the contribution of subiculum, presubiculum, CA1, and molecular layer in the progression of MCI, further examination into the possible involvement of other subfields is warranted.
As a secondary step to the occlusion analysis, which helped us assess the contribution of single subfields to MCI progression and stability, we also evaluated how accumulated occlusion of hippocampal features affected the results. This analysis revealed that 10.5% of the volume of the hippocampus was redundant in the differentiation between pMCI and sMCI. These results may reflect the progressive nature of neurodegeneration in AD, wherein the redundant subfields have yet to have been affected, and thus do not yet differentiate among individuals with stable and progressive disease trajectories. Another speculative possibility, which remains to be tested in future research, is that the redundancy reflects neuroprotective mechanisms that allow individuals with MCI to compensate for the earlier phases of neurodegeneration (Langella et al. 2021; Sadiq et al. 2021). In both biological and engineered systems, redundancy refers to duplication or repetition of elements within the system that ensure functionality in case of failure (Tononi et al. 1999). Compensatory and reserve mechanisms have been widely postulated to operate in response to aging and neurodegeneration (Cabeza et al. 2018; Montine et al. 2019), and the existence of redundancy in brain networks may counter the earlier phases of neurodegeneration and allow normal function to be retained (Arkadir et al. 2014; Cole et al. 2018). Future research could test if redundancy at the level of hippocampal structure is functionally advantageous, offering patients with a coping mechanism for early-phase neurodegeneration.
Several limitations should be noted. First, while our study considered longitudinal clinical evaluations, we did not examine longitudinal changes in imaging metrics. Our focus here was on evaluations of prognostic markers of conversion from MCI to AD. Future research could use similar methods to examine longitudinal imaging data. Second, we considered a single imaging modality in our models (structural MRI). Studies have consistently revealed the superiority of multimodal features in diagnostic and prognostic models (e.g., Suk et al. 2014). Since our focus here was on hippocampal subfields, integration of data with lower spatial resolution like that obtained from PET amyloid imaging would have been challenging. Yet, we acknowledge that basing our models on a single modality may have reduced its performance in the classification task. Third, the occlusion analysis was performed by setting the intensities of voxels to zero, a step that can potentially introduce noise in the deep learning model in the regions surrounding the occluded voxels. Alternative methods of occlusion should be developed and tested in future work. Finally, it would be beneficial to replicate the results with data obtained with higher-resolution neuroimaging.
In conclusion, the current study delineates the contribution of hippocampal subfields to the progression and stability of MCI, highlighting the central role of the subiculum, presubiculum, CA1, and molecular layer in differentiation between pMCI and sMCI. The results further reveal that around 10.5% of the volume of the hippocampus is redundant in the differentiation between these two groups. These results highlight the need to consider the intricate structure of the hippocampus in studies of AD neurodegeneration.
Supplementary Material
Author contribution
K.K. and E.D. conceived research; K.K. analyzed data; K.K., M.N., K.S.G., M.S., and E.D. interpreted results. K.K. and E.D. wrote the paper.
Funding
National Institute on Aging of the National Institutes of Health (R01AG062590). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org).
Notes
The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California. Competing interest: The authors declare that they have no competing interests.
References
- Alnæs D, Kaufmann T, Van Der Meer D, Córdova-Palomera A, Rokicki J, Moberget T, Bettella F, Agartz I, Barch DM, Bertolino A, et al. 2019. Brain heterogeneity in schizophrenia and its association with polygenic risk. JAMA Psychiat. 76:739–748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apostolova LG, Dutton RA, Dinov ID, Hayashi KM, Toga AW, Cummings JL, Thompson PM. 2006. Conversion of mild cognitive impairment to alzheimer disease predicted by hippocampal atrophy maps. Arch Neurol. 63:693–699. [DOI] [PubMed] [Google Scholar]
- Arkadir D, Bergman H, Fahn S. 2014. Redundant dopaminergic activity may enable compensatory axonal sprouting in Parkinson disease. Neurology. 82:1093–1098. [DOI] [PubMed] [Google Scholar]
- Bartsch T, Döhring J, Rohr A, Jansen O, Deuschl G. 2011. CA1 neurons in the human hippocampus are critical for autobiographical memory, mental time travel, and autonoetic consciousness. Proc Natl Acad Sci USA. 108:17562–17567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braak H, Braak E. 1991. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol. 82:239–259. [DOI] [PubMed] [Google Scholar]
- Brown EM, Pierce ME, Clark DC, Fischl BR, Iglesias JE, Milberg WP, McGlinchey RE, Salat DH. 2020. Test-retest reliability of FreeSurfer automated hippocampal subfield segmentation within and across scanners. Neuroimage. 210:116563. [DOI] [PubMed] [Google Scholar]
- Cabeza R, Albert M, Belleville S, Craik FIM, Duarte A, Grady CL, Lindenberger U, Nyberg L, Park DC, Reuter-Lorenz PA, et al. 2018. Maintenance, reserve and compensation: the cognitive neuroscience of healthy ageing. Nat Rev Neurosci. 19:701–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlesimo GA, Piras F, Orfei MD, Iorio M, Caltagirone C, Spalletta G. 2015. Atrophy of presubiculum and subiculum is the earliest hippocampal anatomical marker of Alzheimer’s disease. Alzheimer’s Dement Diagnosis Assess Dis Monit. 1:24–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng B, Liu M, Zhang D, Shen D. 2019. Robust multi-label transfer feature learning for early diagnosis of Alzheimer’s disease. Brain Imaging Behav. 13:138–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole JH, Jolly A, De Simoni S, Bourke N, Patel MC, Scott G, Sharp DJ. 2018. Spatial patterns of progressive brain volume loss after moderate-severe traumatic brain injury. Brain. 141:822–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DR. 1958. The regression analysis of binary sequences. J R Stat Soc Ser B. 20:215–242. [Google Scholar]
- Dalton MA, McCormick C, Maguire EA. 2019. Differences in functional connectivity along the anterior-posterior axis of human hippocampal subfields. Neuroimage. 192:38–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeCarli C. 2003. Mild cognitive impairment: prevalence, prognosis, aetiology, and treatment. Lancet Neurol. 2:15–21. [DOI] [PubMed] [Google Scholar]
- Douaud G, Menke RAL, Gass A, Monsch AU, Rao A, Whitcher B, Zamboni G, Matthews PM, Sollberger M, Smith S. 2013. Brain microstructure reveals early abnormalities more than two years prior to clinical progression from mild cognitive impairment to Alzheimer’s disease. J Neurosci. 33:2147–2155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duvernoy HM, Cattin F, Risold PY, Vannson JL, Gaudron M. 2013. The human hippocampus: functional anatomy, vascularization and serial sections with MRI. 4th ed. Springer-Verlag Berlin Heidelberg.
- Fox NC, Warrington EK, Freeborough PA, Hartikainen P, Kennedy AM, Stevens JM, Rossor MN. 1996. Presymptomatic hippocampal atrophy in Alzheimer’s disease. Brain. 119:2001–2007. [DOI] [PubMed] [Google Scholar]
- Gauthier S, Reisberg B, Zaudig M, Petersen RC, Ritchie K, Broich K, Belleville S, Brodaty H, Bennett D, Chertkow H, et al. 2006. Mild cognitive impairment. Lancet. 367:1262–1270. [DOI] [PubMed] [Google Scholar]
- Hibar DP, Adams HHH, Jahanshad N, Chauhan G, Stein JL, Hofer E, Renteria ME, Bis JC, Arias-Vasquez A, Ikram MK, et al. 2017. Novel genetic loci associated with hippocampal volume. Nat Commun. 8:13624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang G, Liu Z, Van der Maaten L, Weinberger KQ. 2017. Densely connected convolutional networks. In: CVPR.
- Huang Y, Xu J, Zhou Y, Tong T, Zhuang X. 2019. Diagnosis of Alzheimer’s disease via multi-modality 3D convolutional neural network. Front Neurosci. 13:509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iglesias JE, Augustinack JC, Nguyen K, Player CM, Player A, Wright M, Roy N, Frosch MP, McKee AC, Wald LL, et al. 2015. A computational atlas of the hippocampal formation using ex vivo, ultra-high resolution MRI: application to adaptive segmentation of in vivo MRI. Neuroimage. 115:117–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Bernstein MA, Borowski BJ, Gunter JL, Fox NC, Thompson PM, Schuff N, Krueger G, Killiany RJ, DeCarli CS, et al. 2010. Update on the magnetic resonance imaging core of the Alzheimer’s disease neuroimaging initiative. Alzheimers Dement. 6:212–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Petersen RC, O’Brien PC, Tangalos EG. 1992. MR-based hippocampal volumetry in the diagnosis of Alzheimer’s disease. Neurology. 42:183–183. [DOI] [PubMed] [Google Scholar]
- Jack CR, Petersen RC, Xu YC, O’Brien PC, Smith GE, Ivnik RJ, Boeve BF, Waring SC, Tangalos EG, Kokmen E. 1999. Prediction of AD with MRI-based hippocampal volume in mild cognitive impairment. Neurology. 52:1397–1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. 2002. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 17:825–841. [DOI] [PubMed] [Google Scholar]
- Karakaya T, Fußer F, Schröder J, Pantel J. 2013. Pharmacological treatment of mild cognitive impairment as a prodromal syndrome of Alzheimer’s disease. Curr Neuropharmacol. 11:102–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan W, Westman E, Jones N, Wahlund LO, Mecocci P, Vellas B, Tsolaki M, Kłoszewska I, Soininen H, Spenger C, et al. 2015. Automated hippocampal subfield measures as predictors of conversion from mild cognitive impairment to Alzheimer’s disease in two independent cohorts. Brain Topogr. 28:746–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma DP, Ba J. 2014. Adam: a method for stochastic optimization. arXiv preprint arXiv:14126980.
- Koepsell TD, Monsell SE. 2012. Reversion from mild cognitive impairment to normal or near-normal cognition; risk factors and prognosis. Neurology. 79:1591–1598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langella S, Sadiq MU, Mucha PJ, Giovanello KS, Dayan E. 2021. Lower functional hippocampal redundancy in mild cognitive impairment. Transl Psychiatry. 11:61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F, Liu M. 2019. A hybrid convolutional and recurrent neural network for hippocampus analysis in Alzheimer’s disease. J Neurosci Methods. 323:108–118. [DOI] [PubMed] [Google Scholar]
- Li H, Habes M, Wolk DA, Fan Y. 2019. A deep learning model for early prediction of Alzheimer’s disease dementia based on hippocampal magnetic resonance imaging data. Alzheimers Dement. 15:1059–1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Zhang W, Suk H-I, Wang L, Li J, Shen D, Ji S. 2014. Deep learning based imaging data completion for improved brain disease diagnosis. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2014. Lecture Notes in Computer Science. Springer. 8675:305–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y-D, Dong H-B, Xie G-M, Zhang L. 2013. Discriminative analysis of mild Alzheimer’s disease and normal aging using volume of hippocampal subfields and hippocampal mean diffusivity. Am J Alzheimer’s Dis Other Dementiasr. 28:627–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liaw A, Wiener M. 2002. Classification and regression by randomForest. R News. 2:18–22. [Google Scholar]
- Lindeløv JK. 2020. Mcp: an R package for regression with multiple change points. OSF Preprint at: doi: 10.31219/osf.io/fzqxv. [DOI] [Google Scholar]
- Liu M, Li F, Yan H, Wang K, Ma Y, Shen L, Xu M. 2020. A multi-model deep convolutional neural network for automatic hippocampus segmentation and classification in Alzheimer’s disease. Neuroimage. 208:116459. [DOI] [PubMed] [Google Scholar]
- Liu M, Zhang J, Adeli E, Shen D. 2018. Landmark-based deep multi-instance learning for brain disease diagnosis. Med Image Anal. 43:157–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mancini V, Sandini C, Padula MC, Zöller D, Schneider M, Schaer M, Eliez S. 2020. Positive psychotic symptoms are associated with divergent developmental trajectories of hippocampal volume during late adolescence in patients with 22q11DS. Mol Psychiatry. 25:2844–2859. [DOI] [PubMed] [Google Scholar]
- Maruszak A, Thuret S. 2014. Why looking at the whole hippocampus is not enough-a critical role for anteroposterior axis, subfield and activation analyses to enhance predictive value of hippocampal changes for Alzheimer’s disease diagnosis. Front Cell Neurosci. 8:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mary Synthuja Jain Preetha M, Padma Suresh L, John Bosco M. 2012. Image segmentation using seeded region growing. In: 2012 Int Conf Comput Electron Electr Technol ICCEET. IEEE. 576–583.
- Mitchell AJ, Shiri-Feshki M. 2009. Rate of progression of mild cognitive impairment to dementia - meta-analysis of 41 robust inception cohort studies. Acta Psychiatr Scand. 119:252–265. [DOI] [PubMed] [Google Scholar]
- Montine TJ, Cholerton BA, Corrada MM, Edland SD, Flanagan ME, Hemmy LS, Kawas CH, White LR. 2019. Concepts for brain aging: resistance, resilience, reserve, and compensation. Alzheimer’s Res Ther. 11:10–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman Y, Yeagle EM, Khuvis S, Harel M, Mehta AD, Malach R. 2019. Hippocampal sharp-wave ripples linked to visual episodic recollection in humans. Science (80-). 365:eaax1030. [DOI] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B. 2011. Scikit-learn: machine learning in python. J Mach Learn Res. 12:2825–2830. [Google Scholar]
- Platt J. 1999. Fast training of support vector machines using sequential minimal optimization. In: Advances in Kernel Methods-Support Vector Learning. ed. MIT Press.
- Quattrini G, Pievani M, Jovicich J, Aiello M, Bargalló N, Barkhof F, Bartres-Faz D, Beltramello A, Pizzini FB, Blin O, et al. 2020. Amygdalar nuclei and hippocampal subfields on MRI: test-retest reliability of automated volumetry across different MRI sites and vendors. Neuroimage. 218:116932. [DOI] [PubMed] [Google Scholar]
- Ritz C, Baty F, Streibig JC, Gerhard D. 2015. Dose-response analysis using R. PLoS One. 10:1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts R, Knopman DS. 2013. Classification and epidemiology of MCI. Clin Geriatr Med. 29:753–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rössler M, Zarski R, Bohl J, Ohm TG. 2002. Stage-dependent and sector-specific neuronal loss in hippocampus during Alzheimer’s disease. Acta Neuropathol. 103:363–369. [DOI] [PubMed] [Google Scholar]
- Sadiq MU, Langella S, Giovanello KS, Mucha PJ, Dayan E. 2021. Accrual of functional redundancy along the lifespan and its effects on cognition. Neuroimage. 229:117737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadr J, Jarudi I, Sinha P. 2003. The role of eyebrows in face recognition. Perception. 32:285–293. [DOI] [PubMed] [Google Scholar]
- Sarica A, Vasta R, Novellino F, Vaccaro MG, Cerasa A, Quattrone A. 2018. MRI asymmetry index of hippocampal subfields increases through the continuum from the mild cognitive impairment to the Alzheimer’s disease. Front Neurosci. 12:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheff SW, Price DA, Schmitt FA, Mufson EJ. 2006. Hippocampal synaptic loss in early Alzheimer’s disease and mild cognitive impairment. Neurobiol Aging. 27:1372–1384. [DOI] [PubMed] [Google Scholar]
- Shi F, Liu B, Zhou Y, Yu C, Jiang T. 2009. Hippocampal volume and asymmetry in mild cognitive impairment and Alzheimer’s disease: meta-analyses of MRI studies. Hippocampus. 19:1055–1064. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. 1998. A nonparametric method for automatic correction of intensity nonuniformity in mri data. IEEE Trans Med Imaging. 17:87–97. [DOI] [PubMed] [Google Scholar]
- Stephan BCM, Hunter S, Harris D, Llewellyn DJ, Siervo M, Matthews FE, Brayne C. 2012. The neuropathological profile of mild cognitive impairment (MCI): a systematic review. Mol Psychiatry. 17:1056–1076. [DOI] [PubMed] [Google Scholar]
- Suk H-I, Lee S-W, Shen D. 2014. Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. Neuroimage. 101:569–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thung KH, Wee CY, Yap PT, Shen D. 2016. Identification of progressive mild cognitive impairment patients using incomplete longitudinal MRI scans. Brain Struct Funct. 221:3979–3995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi G, Sporns O, Edelman GM. 1999. Measures of degeneracy and redundancy in biological networks. Proc Natl Acad Sci USA. 96:3257–3262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Meer D, Rokicki J, Kaufmann T, Córdova-Palomera A, Moberget T, Alnæs D, Bettella F, Frei O, Doan NT, Sønderby IE, et al. 2020. Brain scans from 21,297 individuals reveal the genetic architecture of hippocampal subfield volumes. Mol Psychiatry. 25:3053–3065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Leemput K, Bakkour A, Benner T, Wiggins G, Wald LL, Augustinack J, Dickerson BC, Golland P, Fischl B. 2009. Automated segmentation of hippocampal subfields from ultra-high resolution in vivo MRI. Hippocampus. 19:549–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward A, Tardiff S, Dye C, Arrighi HM. 2013. Rate of conversion from prodromal Alzheimer’s disease to Alzheimer’s dementia: a systematic review of the literature. Dement Geriatr Cogn Dis Extra. 3:320–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wechsler D. 1987. Wechsler memory scale-revised. San Antonio, TX: The Psychological Corporation. [Google Scholar]
- Whelan CD, Hibar DP, Van Velzen LS, Zannas AS, Carrillo-Roa T, McMahon KZ, Prasad G, Kelly S, Faskowitz J, De Zubiracay G, et al. 2016. Heritability and reliability of automatically segmented human hippocampal formation subregions. Neuroimage. 128:125–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worker A, Dima D, Combes A, Crum WR, Streffer J, Einstein S, Mehta MA, Barker GJ, Williams SCR, O’daly O. 2018. Test–retest reliability and longitudinal analysis of automated hippocampal subregion volumes in healthy ageing and Alzheimer’s disease populations. Hum Brain Mapp. 39:1743–1754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao W, Wang X, Yin C, He M, Li S, Han Y. 2019. Trajectories of the hippocampal subfields atrophy in the alzheimer’s disease: a structural imaging study. Front Neuroinform. 13:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


