Prediction and Interpretation of Cancer Survival Using Graph Convolution Neural Networks

Abstract

The survival rate of cancer has increased significantly during the past two decades for breast, prostate, testicular, and colon cancer, while the brain and pancreatic cancers have a much lower median survival rate that has not improved much over the last forty years. This has imposed the challenge of finding gene markers for early cancer detection and treatment strategies. Different methods including regression-based Cox-PH, artificial neural networks, and recently deep learning algorithms have been proposed to predict the survival rate for cancers. We established in this work a novel graph convolution neural network (GCNN) approach called Surv_GCNN to predict the survival rate for 13 different cancer types using the TCGA dataset. For each cancer type, 6 Surv_GCNN models with graphs generated by correlation analysis, GeneMania database, and correlation + GeneMania were trained with and without clinical data to predict the prognostic index. The performance of the 6 Surv_GCNN models was compared with two other existing models, Cox-PH and Cox-nnet. The results showed that Cox-PH has the worst performance among 8 tested models across the 13 cancer types while Surv_GCNN models with clinical data reported the best overall performance, outperforming other competing models in 7 out of 13 cancer types including BLCA, BRCA, COAD, LUSC, SARC, STAD, and UCEC. A novel network-based interpretation of Surv_GCNN was also proposed to identify potential gene markers for breast cancer. The signatures learned by the nodes in the hidden layer of Surv_GCNN were identified and were linked to potential gene markers by network modularization. The identified gene markers for breast cancer have been compared to a total of 213 gene markers from three widely cited lists for breast cancer survival analysis. About 57% of gene markers obtained by Surv_GCNN with correlation + GeneMania graph either overlap or directly interact with the 213 genes, confirming the effectiveness of the identified markers by Surv_GCNN.

1. INTRODUCTION

Extensive research has been conducted for cancer prognosis, diagnosis, and treatment since the War on Cancer in 1971. With hundreds of billions of spending on research and clinical care, survival rates of cancers have been improved in general. The mortality rate of cancer has been on the decline by 29% since its peak in 1991, saving an estimated 2.9 million lives. Some cancers are associated with high survival rates, including breast, prostate, testicular, and colon cancer while the brain and pancreatic cancers have a much lower median survival rate that has not improved much over the last forty years, imposing the challenge of finding early detection for cancer and alternative treatment strategies [1, 2]. Research has been conducted to show that early-stage cancer diagnoses can improve cancer treatment outcomes and survival [3–6]. Thus, continuously screening for early-stage cancer not only can improve the chances of survival but also can have a large socioeconomic impact.

Survival analysis has been used to determine the most important features in the survival of a patient to gather more information for early diagnosis and potential treatments [7–11]. The most commonly used method for survival analysis is Cox-Proportional Hazard (Cox-PH) regression [12]. The Cox-PH method employs both quantitative variables such as molecular expression levels, age, and weight and categorical variables including sex and different treatment methods. Furthermore, the Cox regression model extends survival analysis methods to assess the effect of several risk factors on survival time simultaneously. However, the Cox-PH method tends to suffer in high-dimensional data, and regression cannot learn any complex non-linear functions. A previous remedy to this downside is the application of support vector machines in survival analysis[13, 14]. Other machine learning methods have also been applied for survival analysis to extract significant molecular predictors for early diagnosis and optimal treatment outcomes [11, 15]

Recently, deep learning has been used to predict survival outcomes with the loss function from the Cox regression model [16–20]. Ching et al. created a 1-layer artificial neural network (ANN) to predict survival outcomes for 10 cancer types using TCGA (The Cancer Genome Atlas) data [16]. Katzman et al. developed a multilayer ANN to recommend personalized treatments by determining the patients’ risk score (RS) and see which treatment gives this patient the best-predicted outcome [17]. Hoa et al. also created a multilayer integrating biological pathways and clinical data to predict the Prognostic Index (PI) of each patient [18]. Chaudhary et al. developed an autoencoder for liver cancer, where they gathered the features of their bottleneck layer to gather a prediction [19]. Lastly, Huang et al have compared several survival analysis models across 12 cancer types using the TCGA dataset and reported better performance of the Cox-nnet model, providing a rationale to use Cox-nnet as a reference for this study [20]. All these methods used one-dimensional gene expression data in their networks. For most cancer types, all models perform better than the typical Cox-PH model and learn more complex features in the high-dimension dataset.

Other types of data and networks have also been used for survival analysis. Convolutional Neural Networks (CNNs) have been used to predict the survival of patients with pancreatic cancer from CT scans [21] while Recurrent Neural Networks were used for time-series datasets to predict survival outcomes [22, 23]. The challenge of using the CNN method to analyze gene expressions lies in two facts. Gene expression data is 1-dimensional while CNN needs 2-dimensional (2D) input. Different embedding methods have been applied to transform the 1D data into 2D. Further, the convolutional approach works well on the Euclidean manifold. However, molecular expression data, in essence, represents the outcome of molecular interactions, which are in non-Euclidian manifold represented by interaction networks [24]. On the other hand, the one-dimensional gene expression data is easily mappable onto a graph and graph convolutional neural networks (GCNN) is a promising approach for the non-Euclidean manifold, suggesting the effectiveness of using GCNN to analyze molecular expressions. The GCNN algorithm found great success in the drug discovery field and predicting metastatic breast cancer classes [25–28]. Our group used the GCNN model with a protein-protein interaction database (STRING) and a correlation graph to classify the TCGA cancer types along with normal tissues and to identify significant genes associated with each cancer type [29]. The success of applying GCNN in these studies motivates the investigation of applying GCNN to determine the survival rate with the TCGA gene expression data in this work.

We performed survival analysis on 13 TCGA cancer types spanning 5,963 samples with 3 different graphs: a statistical relationship graph using correlation, a database-driven graph from GeneMania including gene-gene and protein-protein interactions, and a merged graph including both correlation and GeneMania to examine which graph can generate the best outcome. We also incorporated clinical data into our model to increase prediction accuracy and compared our survival analysis with and without clinical data to other established models including Cox-PH and Cox-nnet, a one-layer ANN model, to evaluate the performance of GCNN. We then interpreted the best performing GCNN models to identify the most significant genes and biological processes in breast cancer.

2. MATERIAL AND METHODS

2.1. Dataset Preparation

RNA-seq data were downloaded from TCGA using the R/Bioconductor package TCGA bio links [30]. The dataset includes a collection of 10,340 samples from 33 cancer types as of December 2018. The cancer types were filtered into their respective class keeping only the primary tumors and removing any replicate samples from the same patient or incomplete data that were missing follow-up times or day of death. Only the cancer types with more than 250 samples and more than 80 events (deaths) were kept ensuring data balance for GCNN training, resulting in 13 cancer types shown in Supplement Figure 1. The number of samples (250) was determined to keep as many cancer types as possible while keeping sufficient data to train the GCNN model properly. Having enough events in the data is essential for training and survival prediction.

Each sample has the same 56,716 genes represented as expression levels in the log₂(FPKM+1) unit where FPKM is the number of fragments per kilobase per million mapped reads. To lower the computational complexity, the number of genes was reduced by looking at the distribution of the mean and standard deviation of the gene expressions for the entire pan-cancer TCGA dataset to gather the most informative genes. The histogram of the distribution of the mean and standard deviations of all 56,716 genes’ expression levels is shown in Supplement Figure 2. A valley centered at 0.4 is shown in the standard deviation histogram plot in Supplement Figure 2B suggesting that values below 0.4 represent background and noise related to genes with low expression levels around 0. Supplement Figure 2A shows the histogram plot of mean expression levels for all genes. A threshold (0.7) was considered appropriate for two reasons: 1) The histogram in Supplement Figure 2A shows many genes below this point representing low expressing genes, and 2) A mean of 0.7 with a standard deviation of 0.4 allows the gene to be fully expressed through the span of the gene’s distribution without reaching 0. Many cancer types have similar histogram distributions showing that most cancer types have a similar number of genes with the same mean expressions and standard deviation, and thus a total of 15,496 genes were selected for survival analysis for 13 cancer types. The 13 cancer types used in this study, the number of samples, and events are shown in Table 1.

Table 1.

Model parameters and datasets of each cancer type

	BLCA	BRCA	COAD	HNSC	KIRC	LGG	LIHC	LUAD	LUSC	OV	SARC	STAD	UCEC
Number of Total Samples	408	1,080	451	498	532	506	365	511	494	372	259	350	545
Censored Samples- Events	180	152	99	217	173	125	130	185	212	229	98	141	92
Time Range (Median)	13–5050 (527)	1–8605 (866)	6–4502 (700)	2–6417 (640)	2–4537 (1,182)	1– 6423 (678)	1–3675 (596)	4–7248 (664)	1–5287 (663)	8– 5481 (1024)	15– 5723 (947)	3–7437 (476)	1–6859 (915)
Clinical Data	Age Weight Smoking Family Clinical T stage N stage M stage	Age Clinical T stage N stage M stage	Age Weight Clinical T stage N stage M stage	Age Smoking Clinical T stage N stage M stage	Age Clinical T stage N stage M stage	Age Family	Age Weight Smoking Clinical T stage N stage M stage	Age Smoking Clinical T stage N stage M stage	Age Smoking Clinical T stage N stage M stage	Age Clinical	Age	Age Clinical T stage N stage M stage	Age Clinical Weight
Correlation Graph Interactions (Graph Density)	1,223,346 (78.95)	1,183,560 (76.38)	2,086,718 (134.66)	1,683,960 (108.67)	4,016,716 (259.21)	3,379,034 (218.06)	4,849,854 (312.97)	900,192 (58.09)	916,958 (59.17)	586,384 (37.84)	1,378,742 (88.97)	1,389,548 (89.67)	1,944,344 (125.47)
Correlation + GeneMania Interactions (Graph Density)	2,135,982 (137.84)	2,098,548 (135.43)	2,988,902 (192.88)	2,592,694 (167.31)	4,905,018 (316.53)	4,265,568 (275.27)	5,710,822 (368.54)	1,820,950 (117.51)	1,838,704 (118.66)	1,510,576 (97.48)	2,291,796 (147.90)	2,300,554 (148.46)	2,839,154 (183.21)
Batch Size	165	216	181	100	213	203	100	205	100	149	104	140	436
L2 Regularization	0.005	0.005	0.01	0.01	0.005	0.005	0.005	0.001	0.01	0.01	0.005	0.01	.005
Hidden Layer Dropout	0.75	0.75	.75	0.9	0.75	0.75	0.95	0.9	0.9	0.9	0.9	0.85	0.9
Number of Nodes in Hidden Layer	512	256	365	365	512	512	365	256	365	256	256	512	256

The table shows all the parameters of the model, a description of the data, and a description of the graphs. Other parameters stay consistent throughout all models. Including GCNN and Cox layer, learning rate, and regularization in the Cox-PH model and Cox-nnet. The time range represents the minimum and maximum sample follow up time or event time in days with the median time in parenthesis. The clinical data used in each model are shown in the table with the determining factor on what was used being what was available. The number of interactions of the correlation graph and the Correlation + GeneMania graph is shown with the density of the network in parenthesis. The following are the tunable parameters of our GCNN.

To integrate more informative data into the network for training and prediction clinical data was added to the last hidden layer [31, 32]. Extensive research results have shown that smoking history, family history of cancer, weight, age, pathological cancer stage, and TNM staging (T describes the size of the tumor and any spread of cancer into nearby tissue, N describes spread of cancer to nearby lymph nodes, and M describes metastasis) are closely related to survival rate for cancer diseases [7, 33–35]. Therefore, such clinical data were also fed into the GCNN model as shown in Table 1. A family history of cancer and smoking are given as 0s if they have no blood relative with cancer or have not smoked more than 100 cigarettes and 1s otherwise. The mean of the data for each category in the clinical data is substituted for any missing data. We standardized the gene expression and clinical data between 0–1 using min-max normalization in this study using equation (1) to ensure the convergence of the model where v is the covariate variable for patient i,

$$X_i^v=\frac{X_i^v-\text{min}\left(X^v\right)}{\text{max}\left(X^v\right)-\text{min}\left(X^v\right)}.$$ (1)

2.2. GCNN Model for Survival Analysis

The GCNN model in this study includes an input graph represented by an adjacency matrix, graph convolutional layers (coarsening and pooling), and a hidden layer connected to a cox-regression layer with a single output node resulting in a patient’s risk score (RS), η, as shown in Figure 1. The risk score can be considered as a predictor for a patient’s survival. While an RS less than 1 suggests that the inputs are associated with improved survival, an RS greater than 1 is associated with a decreased survival. On the other hand, an RS close to 1 suggests that the inputs have little effect on survival. In some literature, RS is also denoted as a prognostic index (PI) or hazard ratio (HR). The RS can be calculated by the linear combination of the weights and covariates, which will be further explained in section 2.5.

Figure 1.

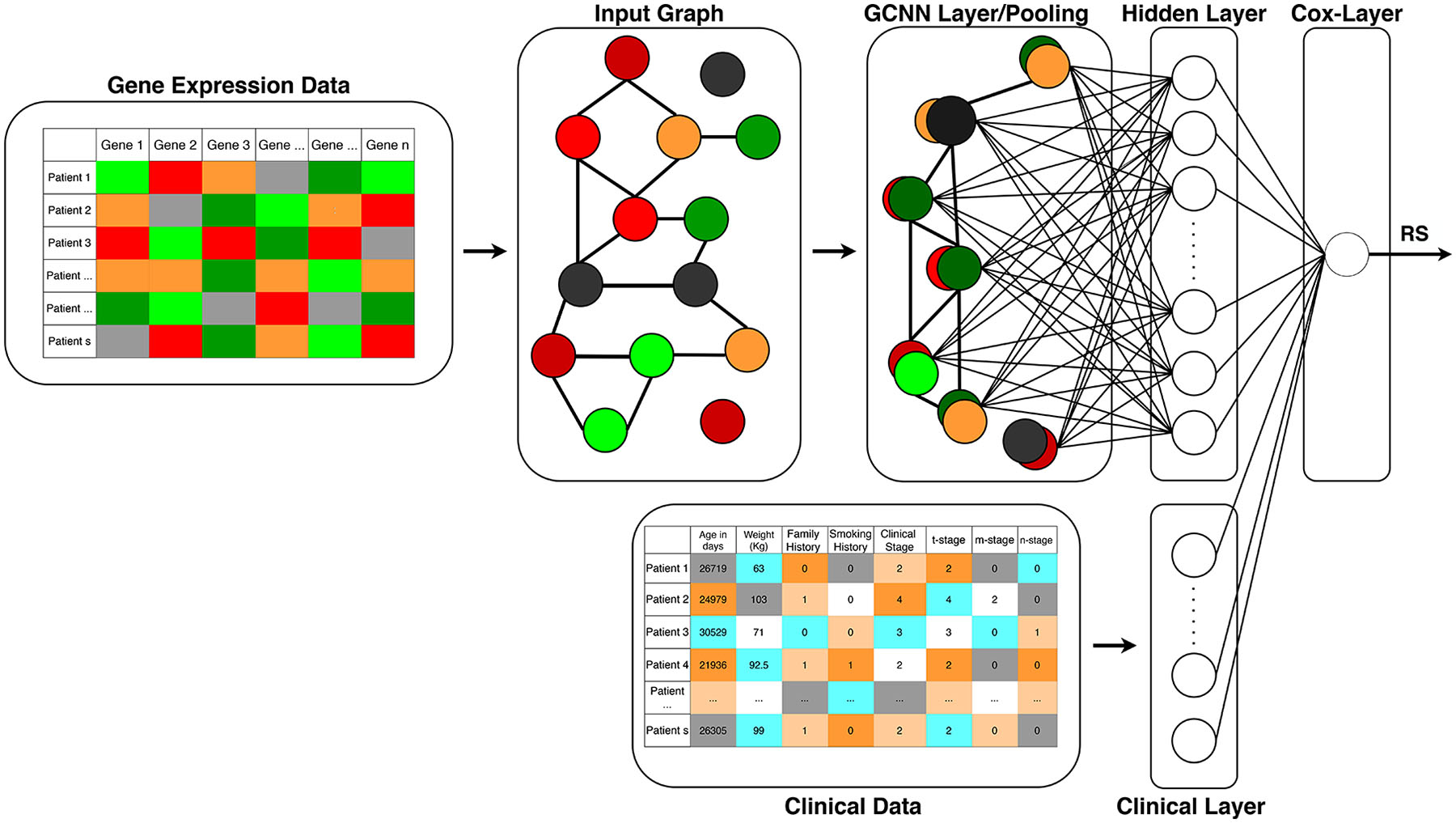
Structure of the proposed Surv_GCNN model. The Surv_GCNN model includes a graph convolution layer and a hidden layer fully connected to the Cox layer that gives the risk score as the output of the Surv_GCNN model. The input to the Surv_GCNN model is a 1D gene expression level of TCGA samples and graphs of the Surv_GCNN can be generated by statistical correlation analysis, existing molecular interaction databases, or a combination of these graphs. The clinical data can also be integrated with the hidden layer to form the Cox layer if needed.

2.3. Three Graphs for GCNN

Three graphs were used in this study: a correlation graph, a database-driven graph generated by the GeneMania interaction database, and a combination of correlation+ GeneMania interactions. The correlation graph was created by taking the Spearman correlation between the 15,496 filtered genes from the TCGA pan-cancer dataset. To make sure only informative relationships are given to the model, the correlations greater than 0.55 are kept into the graph and replaced with a constant value of 1 as a bidirectional connection to create an adjacency matrix. The value 0.55 was chosen as a threshold that gave a sufficient amount of connections without over saturating the number of connections. A second objective in choosing the threshold of 0.55 was to find a balance between the connections and minimizing the number of singleton nodes, which are nodes not connected to any other nodes in the network. Since the singleton nodes do not contribute to the graph filter, the number of singleton nodes needed to be minimized.

The database-driven network graph is taken from the GeneMania database (https://GeneMania.org/) [36]. GeneMania has a large number of interactions and incorporates both gene-to-gene and protein-to-protein interactions. Since the genes remain consistent throughout all models, the GeneMania graph does not change and is established for all models. A p-value threshold was also established for the GeneMania graph to keep only interactions with the confidence of (p < 3×10⁻⁵) from the filtered 15,496 genes. This threshold was chosen for the same reason described above for the correlation graph to get a sufficient number of connections while minimizing the number of singleton nodes.

The combination graph, Correlation + GeneMania, is composed of two portions: correlation and database driven network graph from GeneMania database, including the union of connections determined by both the correlation graph and the GeneMania graph.

2.4. Graph Convolutional Neural Network

The graph convolutional network proposed was created by Deffand et al and later optimized by Kipf et al by reducing the Chebyshev expansion to an order of 1 [37, 38]. A detailed description of the proposed GCNN algorithm was presented in our previous publication [29]. A representation of the GCNN model in this study was shown in Figure 1.

The GCNN performs a similar operation to the traditional convolutional neural networks but it learns features from neighboring nodes in a graph. In this paper, we focus on the Spectral GCNs, which make use of the Eigen-decomposition of graph Laplacian. Given W = (w_ij) ∈ R ^{n × n} denotes the adjacency matrix with edge weights as its elements, the graph Laplacian of W is denoted as

$$L=I_n-D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}},L\in R^{nxn},$$ (2)

where D is the diagonal matrix with D_ii = ∑_jw_ij , and I_n is an n × n identity matrix. The eigendecomposition of L then becomes L = UΛU ^T, where U=[u₁, u₂, …, u_n] represents n eigenvectors of L and the diagonal matrix, Λ = diag[λ₁, λ₂, …, λ_n],with λ_i defined as the eigenvalues of L [37]. The Graph, G, represented by the adjacency matrix, becomes a filter to the input signal x and the output of the filter is calculated by the convolution of G and x shown as

$$y=g\left(L\right)x=g\left(U\Lambda U^T\right)x=Ug\left(\Lambda \right)U^{T}x,$$ (3)

where g_θ is the spectral representation of the filter g(Λ) with learnable parameters θ. The complexity of g_θ grows exponentially as the inputs and the number of neighboring nodes increases.

A polynomial expansion can be used to solve for g_θ since this operation is computationally exhaustive after the eigendecomposition. The Chebyshev approximation was used to estimate the polynomial expansion and is represented by

$$T_m\left(x\right)=2x{T}_{m-1}\left(x\right)-T_{m-2}\left(x\right),$$ (4)

where T₀ (x) = 1 and T₁(x) = x [37, 38.] The local filter can be expressed as

$$g_{\theta }\left(\Lambda \right)={\sum }_{f=0}^F{\theta }_f{T}_f\left(\widehat{\Lambda }\right),$$ (5)

where $\widehat{\Lambda }$ is the scaled eigenvalues between [−1,1], which is defined as, $\widehat{\Lambda }=2\Lambda /{\lambda }_{\mathit{\text{max}}}-I_n$. The Chebyshev expansion uses ${\widehat{x}}_0=x$ and ${\widehat{x}}_1=\widehat{L}x$, which greatly decreases the computational cost. $\widehat{L}$ becomes the renormalized graph Laplacian as introduced by Kipf et al [38]. The filter, f, is set to an order of 1 by letting θ = θ₀ –θ₁, which prevents overfitting and makes $y=\theta \left(I_n+D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}\right)x$. The normalization of the adjacency matrices becomes $\widehat{W}=W+1$ and ${\widehat{D}}_{ii}={\sum }_j{\widehat{W}}_{ij}$ and then the final filter expression is expressed as

$$y=\theta \left({\widehat{D}}^{-\frac{1}{2}}\widehat{W}{\widehat{D}}^{-\frac{1}{2}}\right)x.$$ (6)

Equation (6) describes the graph convolution in this study. To reduce the complexity of graph convolution, a greedy algorithm is used to reduce the number of nodes by around half. Each node will be paired with a neighboring node that has a similar set of edges [39, 40]. Any node without a similar counterpart will be paired with a generated empty singleton node. Max pooling will then coarsen these pairs into one single node, thus reducing the graph by half its size. This final graph will be flattened and connected to a hidden layer with a Relu activation function. The hidden layer then is a part of the Cox-PH layer which is explained in detail in section 2.5.

2.5. Cox-Layer

The output of the graph convolutional network coarsening layers connects to a hidden layer with the number of nodes treated as a hyperparameter. The hidden layer is then connected to a cox-regression layer with a single output node resulting in the patient’s risk score (hazard ratio).

The final layer of our Surv_GCNN, the Cox regression layer is based on the Cox_PH model. The Cox_PH model creates an individual, i, hazard function that defines the likelihood to an event rate as time, t, given K number of hidden nodes, x_i (w) = [x_i,1(w), …, x_i,k(w)]^⊤ [12] as

$$h\left(t\text{|}{\mathit{\text{x}}}_i\left(\mathit{\text{w}}\right)\right)=h_0\left(t\right)\mathit{\text{exp}}\left(\sum _{k=1}^K{ß}_k{x}_{i,k}\left(\mathit{\text{w}}\right)\right),$$ (7)

where w denotes the collection of weight parameters of the graph convolutional network coarsening layers, h₀(t) is the baseline hazard function, and ß_k ∀k = 1, …, K are the coefficients of the Cox model. The partial likelihood for patient i, ${\mathcal{L}}_i$, for an event occurring at the time Y_i, or time-to-event is defined as

$${\mathcal{L}}_i=\frac{h\left(Y_i|x_i\left(\mathit{\text{w}}\right)\right)}{{\sum }_{j:Y_j>Y_i}h\left(Y_i|x_j\left(\mathit{\text{w}}\right)\right)}=\frac{h_0\left(Y_i\right){\phi }_i}{{\sum }_{j:Y_j>Y_i}{h}_0\left(Y_i\right){\phi }_j}=\frac{{\phi }_i}{{\sum }_{j:Y_j>Y_i}{\phi }_j},$$ (8)

where ${\phi }_i=\mathit{\text{exp}}\left({\sum }_{k=1}^K{ß}_k{x}_{i,k}\left(\mathit{\text{w}}\right)\right)$ and the summation is over all the subjects j that has not had an event occur before time Y_i. The partial likelihood for all patients is the multiplicative of all patients with an event occurring defined as

$$\mathcal{L}\left(\varphi \right)={\prod }_{i:C_i=1}{\mathcal{L}}_i,$$ (9)

where ϕ = {w, ß_k∀k} is the collection of Surv_GCNN parameters, C_i = 1 for an occurrence of death for patient i and C_i = 0 for censored data where an event has not occurred. This then makes the log partial likelihood to be

$$\mathbf{\ell }\left(\varphi \right)={\sum }_{i:C_i=1}\left({\sum }_{k=1}^K{\phi }_i-\mathit{\text{log}}\left({\sum }_{j:Y_j>Y_i}{\phi }_j\right)\right).$$ (10)

The parameters ϕ can be learned from the maximum likelihood estimation as

$$\widehat{\varphi }=\mathit{\text{argma}}{x}_{\varphi }\left(\mathbf{\ell }\left(\varphi \right)\right).$$ (11)

2.6. Training the GCNN Model

Gene expression levels from TCGA data is embedded into a graph that goes through a single graph convolutional layer and a single hidden layer first. Both the hidden layer and the clinical data are connected to the output giving the patient’s risk score. To ensure the best possible results, many hyperparameters were tuned using a random search to maximize the concordance index (C-index) that was used to evaluate the model. Some parameters were meant to be tunable hyperparameters but ended up working for all models such as a single GCN layer, a single hidden layer, Relu activation function for all nodes besides the output, and the learning rate of 0.005. Parameters such as batch size, dropout, the number of nodes in the hidden layer, and L₂ regularization were tuned using λ for individual models as shown in equation (12) and added to the loss function in equation (10) to give us the loss function in equation (12) as follows,

$$\mathit{\text{loss}}(ß)=-{\sum }_{i:C_i=1}\left({\sum }_{k=1}^K{\phi }_i-\text{log}\left({\sum }_{j:Y_j>Y_i}{\phi }_j\right)\right)+\lambda \Vert {ß}^2\Vert .$$ (12)

The training was done in Tensorflow 1.14 using the Tensorcox package in python by minimizing the negative log-likelihood function with L₂ regularization shown in (12) with the code found at https://github.com/RicardoRamirez2020/GCN_SURV. The tuned model parameters are also shown in Table 1.

2.7. Evaluation of GCNN-based Survival Prediction

Evaluation of survival analysis using the GCNN approach was conducted for 8 models including Cox-PH, Cox-nnet, 3 GCNN models based on correlation graph, GaneMania graph, and correlation + GeneMania graph without clinical data, and three GCNN models based on the three graphs with clinical data. The performance of these GCNN models was compared with existing methods for survival analysis including Cox-PH and Cox-nnet [12, 16]. We decided on using the Cox-PH since it is the standard of most survival analysis and is then used as an output layer in our GCNN model. The Cox-PH model is a regression-based method where the output is determined based on the input features directly. We used the same equation as (10) with each gene connected directly to the output RS prediction. The Cox-PH model was also performed with Tensorflow using expressions of all 15,496 genes as the inputs.

Comparing against ANN-based Cox-nnet results allows us to evaluate the effect of GCNN and ANN approaches. The Cox-nnet model also implemented equation (10) with an ANN. The Cox-nnet had 15,496 input nodes, a single hidden layer with 143 nodes with a drop out of .08, and the output is the risk score. Comparing with the Cox-PH method, the Cox-nnet has a new feature map since the features to the output come from the hidden layer while Cox-PH extract features from gene expressions directly. In the implementation of the Cox-nnet, we retained the original procedure and parameters described in the publication [9]. The same loss function is shown in equation (8) and optimizer was used as the GCNN with a learning rate of 1e-4 for the same 15,496 genes. Since we incorporated high dimensional data, L2 regularization was added to tune the λ parameter for each model [41]. A universal L2 regularization parameter of 0.01 was used for both the Cox-PH and Cox-nnet models. The Cox-nnet model showed improved results with L2 regularization in the original findings [16].

The performance of the GCNN models obtained from three graphs including correlation, GeneMania, and Correlation + GeneMania, was examined concerning prediction performance and the complexity of the graphs. Since clinical data is one of the most significant indicators of survival times and increase prediction in survival analysis when incorporated with gene expression [42, 43], the effect of clinical data was evaluated by our Surv_GCNN.

Harell’s C-index was calculated based on the RS from the GCNN models and used to evaluate model performance [44, 45]. The C-index was used rather than a traditional mean square error because of the censored data. Since we do not know the true end time, we cannot train the model using a traditional regression approach unless we train with only the non-censored data. Rather than predicting the survival time of each patient, the risk score is the prediction for each patient from the model. The C-index is calculated by gathering every pair of patients and examining their risk score and their times-to-events. If a patient j has a higher RS, η_j, with a shorter time-to-event, Y_j , compared to the RS and time-to-event of patient i, η_i and Y_i, this is called a concordant pair. Since patient, i and j can be interchanged we only focus on the case when Y_i > Y_j to ensure no duplicate pairs. If a patient j has a lower η_j with a shorter Y_j, or higher η_j with a longer Y_j compared to η_i and Y_i of patient i, this is called a dis-concordant pair. This is done for every pair of patients except if both patients are censored or if the censored patient has a longer time-to-event (Y_censored > Y_non-censored). The final C-index is calculated by taking the concordant pairs divided by the sum of the concordant pair and discordant pairs.

$$C–\mathit{\text{index}}=\frac{{\sum }_{i\ne j}1\{{\eta }_i<{\eta }_j\}1\{Y_i>Y_j\}}{{\sum }_{i\ne j}1\{Y_i>Y_j\}}$$ (13)

A C-index value will always be between 0–1. A C-index of 0.5 indicates that the model predicts random RS values, a C-index value less than 0.5 suggests a worse-than-random prediction and a C-index greater than 0.5 implies an improved RS prediction for each patient.

All the models were trained using Tensorflow using Adam optimizer to increase the speed of the PH model and to keep the software consistent. The models were run 10 times while randomly dividing the data into 80%−20% partitions for training and testing, respectively. This was done for each model but made sure that the median values of the time-to-event from both the training and testing groups were within 15% of the larger median value among the two groups. A similar rule was applied to check the number of censored data in the training and testing groups. With these procedures, the data used for each run may have different partitions, but the properties of each partition should remain similar. A paired t-test was used to test for significance between models. There are four specific tests done. The first test is to see how Cox-PH compared to the other models considering that regression cannot learn any complex functions. The second was to compare cox-nnet versus the GCN models to compare the neural network model to the GCNN model without clinical data. The third test was to examine the three graphs to see if any graph filter outperforms the others. Lastly, we investigated if clinical data significantly increased model performance by looking at the model with and without clinical data.

2.8. Interpretation of the GCNN Model

We interpreted the GCNN model using breast cancer samples since it is one of the well-studied cancer types and has the largest sample size in the TCGA dataset. The proposed GCNN model has the input of gene expressions and output of RS which are connected by the GCNN and 256 nodes in the hidden layer. Correspondingly, interpreting the model was separated into two parts: finding the significant nodes in the hidden layer contributing to the RS and dissect the relationship between gene expression levels to the hidden layer nodes.

2.9. Identify Prognostic Nodes in the Hidden Layer

We gathered model parameters from a single run resulting in the median C-index (0.7775) for the correlation + GeneMania graph of breast cancer shown in the box and whisker plot in Figure 2. All 1,080 samples in the breast cancer study were tested using this parameter set. We collected the values of the hidden layer for each patient along with the weights from the hidden layer to the output RS. The contribution of each hidden layer node to determine the RS was calculated by multiplying the value of the node and the weight of the nodes to the RS for each sample in the breast cancer study. All 1,080 samples had the same top contributing nodes from the hidden layer to the RS and were separated into two groups by the median contribution values, group 1 representing a node with contribution larger than the median, and group 2 if the contribution was below. To verify the statistical significance of the features learned in the hidden layer we tested both groups through a Kaplan-Meier (KM) plot using a log-rank p-value [46]. The KM plot requires only 3 labels for each sample, last follow up/ death time, censoring, and which group the sample belongs to.

Figure 2.

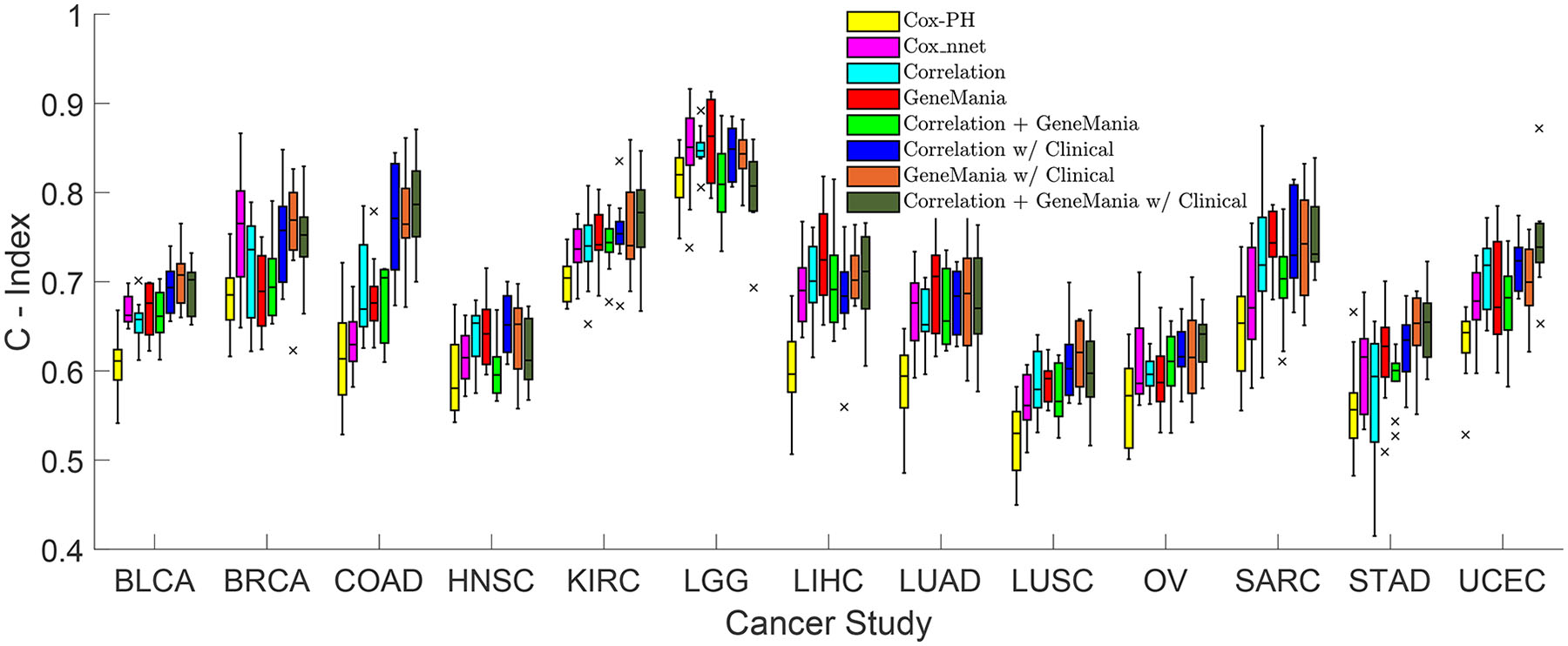
Concordance Index boxplots between 8 models across 13 cancer types from the TCGA dataset. The 8 models include Cox-PH in yellow, Cox-nnet in purple, Correlation in light blue, GeneManiain red, Correlation + GeneMania in light green, Correlation with Clinical in dark blue, GeneMania with Clinical in orange, and Correlation + GeneMania with Clinical in dark green. Each model has 10 runs for each cancer type. The middle line of the box represents the median of the 10 runs while the top and bottom of the box are the 75 and 25 percentiles, respectively. The top and bottom whiskers of the plot represent the 1.5 interquartile range outside the 75 and 25 percentiles, respectively. Each ‘x’ represents the outliers outside the whiskers.

2.10. Dissect the Relationship Between Genes and Hidden Layer Nodes.

Two approaches were used to examine the relationship between genes and hidden layer nodes. A Spearman correlation analysis between the gene expressions and the values of the top contributing nodes in the hidden layer was performed first to see the contribution of each gene on those significant nodes. We took the top correlated genes with an absolute correlation greater than 0.5.

Since the GCNN model is graph-based, we further mine gene modules in the correlation + GeneMania graph for breast cancer with the HotNet2 algorithm [47]. Two different network modules were mined based on mean values and variances of gene expressions in BRCA. We assigned means and variances of expression levels of genes from all BRCA samples as the input heat vector, integrated the correlation + GeneMania networks as the reference functional network, and identified gene modules that have relatively higher expression levels and modules whose expression levels changed more dramatically in all BRCA samples, respectively.

HotNet2 has two parameters β and δ; β is the fraction of the heat that a node in the network retains for itself at each time step and δ is the threshold, which determines whether there is an edge between 2 nodes in the final subnetwork. β can influence the amount of heat that a gene shares with its neighbors and is determined by the topology of the network. We downloaded the HotNet2 tool from https://github.com/raphael-group/hotnet2 and applied it with default parameters. In this study, β was set as 0.5, and δ was automatically determined as 0.0231 for the mean expression level heat input and 0.00673 for the variance heat input.

All potential gene markers identified by Spearman correlation analysis and top modules from the HotNet2 modularization were further examined. The top modules from the HotNet2 were determined by taking a simple linear regression of the gene expressions in each module with an R² value greater than 0.5. Three highly cited gene marker lists for breast cancer from previous studies: Gene Expression Profiling Interactive Analysis (GEPIA), PAM50, and Parker’s results were used as a reference [48–50]. There are 100 genes in the GEPIA list, 55 in PAM50, and 62 in Parker’s results, resulting in a total of 213 unique genes after removing the overlaps as listed in Supplement Table 1.

3. RESULTS

3.1. Selection of Cancer Types and Clinical data

A total of 13 cancer types were selected from the TCGA dataset based on the number of censored samples and events for each cancer type as shown in Table 1. Among these cancer types, breast cancer has the most enriched samples (1,080 samples). The averaged censored samples and events of the 13 cancer types are 504 and 156, respectively. Breast cancer has the least event to censored sample ratio as of 13.7%, while ovarian cancer has the highest ratio of 60.4%.

3.2. Graphs Established

Three graphs were generated based on correlation, molecular interactions from GeneMania, and the combination of Correlation + GeneMania. Table 1 also shows network properties including the number of connections and network density for correlation and correlation + GeneMania for each cancer type. The GeneMania network is the same for all 13 cancer types resulting in 948,742 interactions with 3,041 singleton nodes with a density of 61.22.

3.3. Input, Output, and Parameters in the GCNN

The input of the GCNN survival analysis model includes 15,496 gene expression and clinical data from the TCGA dataset. Clinical data for each cancer type was shown in Table 1 with the determining factor on what was used is what was available in that study. The output of the GCNN model is the risk score (RS). The batch size, L₂ regularization, hidden layer dropout, and the number of nodes in the hidden layer in the GCNN model were also listed in Table 1. A total of 104 models were trained and tested in this study: 6 GCNN models, a Cox PH model, and a Cox-nnet model for each cancer type selected.

3.4. Evaluation of Cox-PH, Cox-nnet, and GCNN Based on Three Graphs

C-Indices predicted by the 104 models (8 models/cancer for 13 cancer types) are shown in Figure 2. We performed t-tests (p-value < 0.05) on the C-Indices between models for each cancer type to test the statistical significance of the model performance (Supplement Table 2). The Cox-PH model generated the worst results for all 13 cancer types. Almost all GCNN models without or with clinical data performed better than Cox-nnet, and Cox-nnet outperformed GCNN based on GeneMania only in BRCA. Among GCNN with three graphs, the GCNN model based on correlation without clinical data performed the worst compared with the other two graphs for HNSC prediction, while all GCNN models without clinical data performed similarly. Comparing GCNN with or without clinical data, clinical data improved the performance of the GCNN model with at least one of the graphs in most cancer types: BLCA, BRCA, COAD, LUSC, SARC, STAD, UCEC.

A value of 1 to 8 was assigned to each GCNN model for a cancer type with 1 and 8 denoting the best and worst performer, respectively, assessed by the mean C-Index. Ranks of 8 models for each cancer type and the overall ranking for a model (the summation of ranks across 13 cancer types) were shown in Figure 3A. Similarly, we also ranked the models based on the standard deviation of C-Index (1 for lease standard deviation) shown in Figure 3B. The reason the mean C-index was used rather than the median, as shown in the box plot, is that the standard deviation of the model is calculated based on the mean values, so mean C-index was adapted because these two values complement each other. In general, GCNN models based on the GeneMania graph or correlation + GeneMania graph with clinical data achieved better performance over other models.

Figure 3.

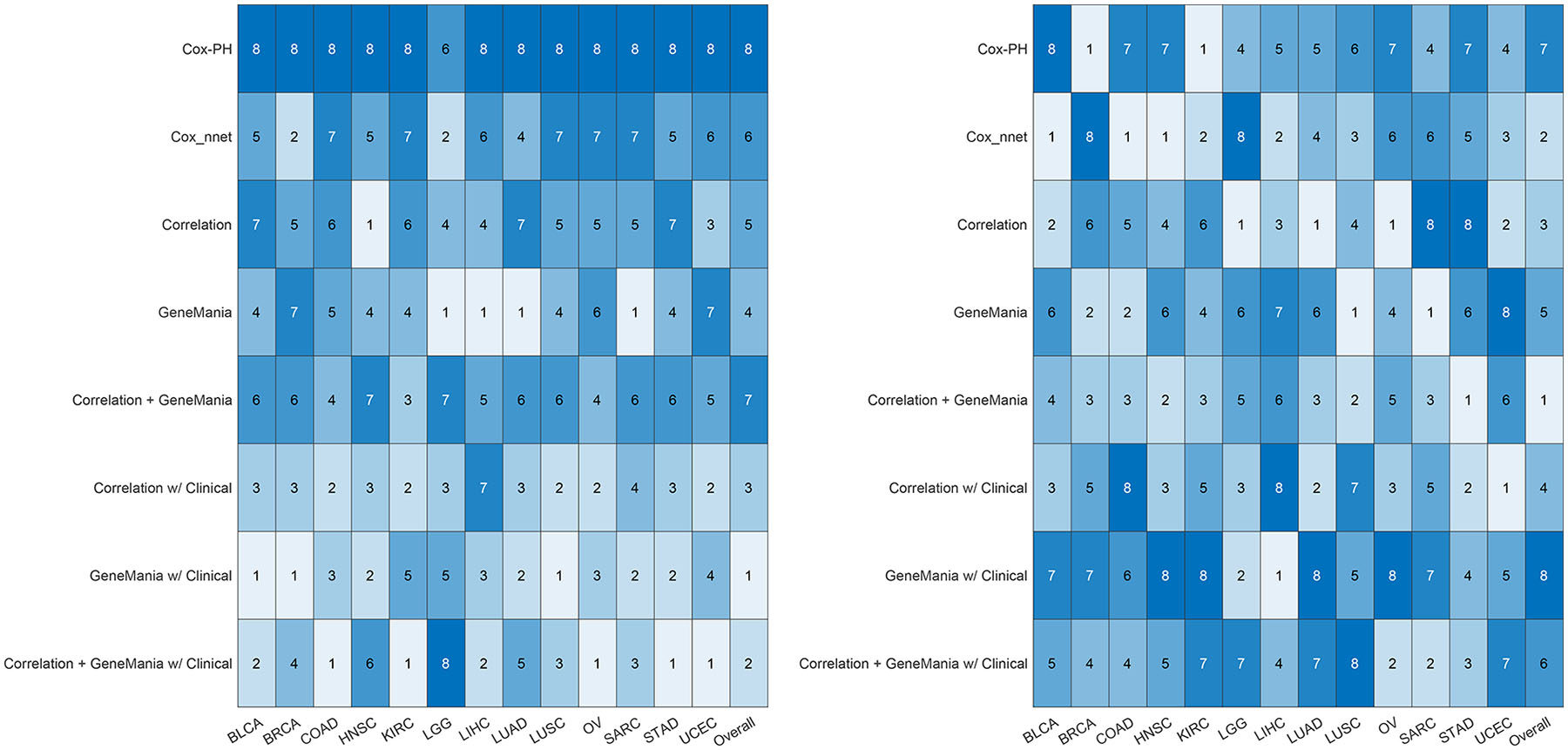
The ranking of the performance of 8 models for every cancer type is shown. (A) Ranked 8 models based on their median from the 10 runs. The value of 1 represents the highest median C-Index and 8 being the lowest. (B) Ranked 8 models based on their standard deviation of the 10 runs. The value of 1 represents the lowest standard deviation and 8 denotes the highest. The overall evaluation of a model is determined by summing the scores for each cancer type first and ranking them from the lowest overall as 1, to the highest value as 8.

3.5. Significant Prognostic Nodes for Breast Cancer

We took BRCA as an example to interpret the constructed GCNN models. We evaluated the survival significance of each node at the hidden layer by comparing the Kaplan-Meier curves of patients with high and low scores of the node (see Methods). Interestingly, all BRCA samples showed the same top 4 prognostic nodes (Figure 4). Along with all the nodes in the hidden layer, the clinical data were significant except for the metastatic status since there was not sufficient data.

Figure 4.

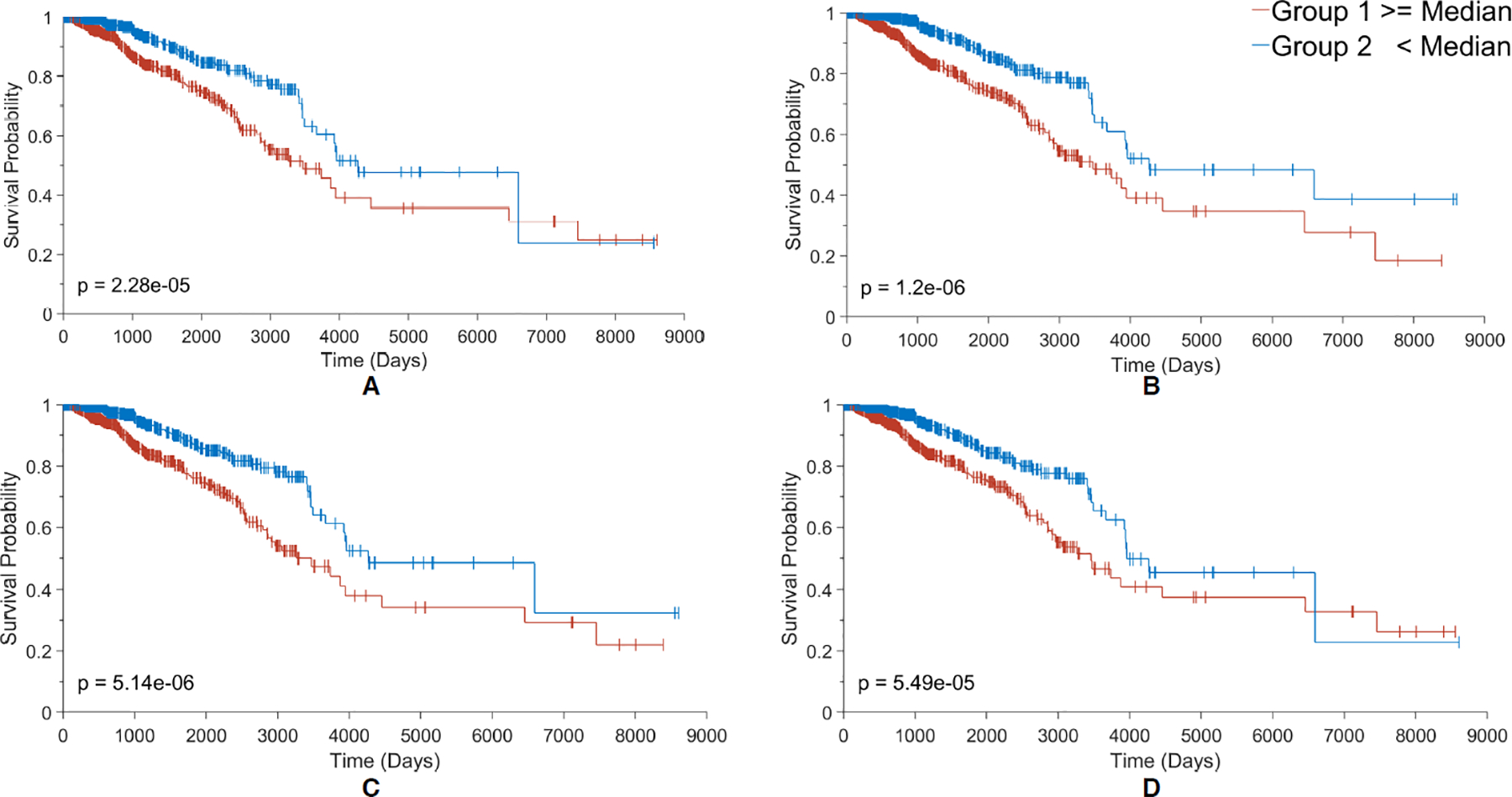
Kaplan Meier plots for the 4 most contributing nodes (A-D) to the RS score in the Surv_GCNN model. (A) KM plot based on node 136, the biggest contributing node; (B) KM plot based on node 131 the second-biggest contributor; (C) KM plot based on node 134 which is the third-biggest; and (D) KM plot for the 4^th-biggest contributor node 58. The groups in each KM plot were divided by their median node value from all 1080 patients. Larger than the median is shown in the red group and less than the median in the blue group. The log-rank p-value was also shown in the bottom corner of the graph.

3.6. Find Potential Gene Markers for Breast Cancer

Three analysis approaches including correlation-based analysis and two network-based analyses were performed to find the potential gene markers for breast cancer prognosis. A total of 318 unique genes were correlated to the top 4 prognostic nodes in the hidden layer. CCDC24 was the only gene shared between the 318 genes and the top 100 genes identified from a reanalysis of TCGA data by GEPIA [48]. Among the 318 genes, 38 genes had a log-rank p-value less than 0.05 between the patients with high or low expression in the gene. There were no overlap genes among the 318 genes and the PAM50 and Parker’s lists of genes that were representative of BRCA subtyping and prognosis [47, 49]. This result implies that a simple linear correlation analysis might not fully capture meaningful prognostic patterns since GCNN models are dependent on higher-order graph features.

3.7. Network Modules Generated by HotNet2 with Mean Expression as Heat Input

To dissect to critical modules of the graphs, we used HotNet2 with the mean or variance of gene expressions in BRCA samples as heat sources. HotNet2 generated 2 groups of gene modules for the integrated correlation + GeneMania network which contained 15,496 gene nodes and 1,041,526 edges after removing self-connections. A total of 275 gene modules were generated with mean expression heat input. The largest module contains 563 genes and the smallest module contains 2 genes.

A total of 4 out of 275 modules were found with an R² value greater than 0.5. The 4 modules contained 696 unique genes. Seven genes were also reported by GEPIA, CHCHD7, CYB561, GTF2H5, LMAN2, PRR13P5, SEC61G, and VDAC1. Three (AP2B1, GSTM3, and MUC1) and two genes (CXXC5 and GRB7) were common with Parker’s and the PAM50 lists. Seventy of these 696 unique genes, including all the 12 genes listed above, had a significant log-rank p-value.

3.8. Network Modules Generated by HotNet2 with Expression Variance as Heat Input

We also tested the possibility to identify network modules with highly variable, thus potentially informative genes in BRCA. With the variance in the gene expression data as heat input, 178 gene modules were generated with the largest module contains 576 genes and the smallest module contains 2 genes. Only one of the modules was found to hold an R² value greater than 0.5 that comprised 576 genes. Four genes, CD24, CYB561, FABP7, and TCN1, overlapped with top genes from GEPIA, seven genes, ERBB2, GSTM3, IGFBP5, MS4A7, MUC1, PLAT, and SCUBE2, overlapped with genes in Parker’s list, and 10 genes, CXXC5, ERBB2, GRB7, KRT14, KRT17, KRT5, MAPT, NAT1, PHGDH, and SFRP1 overlapped with the PAM50 list. A total of 64 out of 576 genes have a log-rank test p-value less than 0.05. Based on the 213 marker genes we identified by different approaches, the network module generated by the HotNet2 with variance as heat input contained the greatest number of known gene markers. The pathways enriched by the 576 genes given by the HotNet2 with variance heat input include pathways in cancer, cell cycles, inflammatory responses, and immune responses.

Among these marker genes, overexpression of human epidermal growth factor 2 (ERBB2) is a key BRCA-subtyping gene and known to enhance metastasis-related properties of cancer cells, and thus a prognostic factor for breast cancer [51, 52]. Another prognostic factor, CXXC5, has been identified as associated with a poor clinical outcome for estrogen receptor-positive (ER+) breast cancer [53, 54]. As suggested by many studies [55–57], many of these marker genes, especially those included in the PAM50 panel [58], are widely used as a genomic test to guide treatments. The results demonstrate the capability of GCNN to capture the well-studied genes and further illuminate novel prognostic markers of BRCA.

3.9. Interpreting Gene Modules with Network Connectivity

To further examine the genes chosen by the gene modules from the GCNN model, we examined the genes directly interacting with the three sets of genes: 318 genes from correlation analysis, 696 genes from HotNet2 modules with the mean expression as input, and 576 genes from HotNet2 modules with variances as input.

From the correlation + GeneMania graph, 58 out of 318 genes were directly linked to the genes in GEPIA, while 34 genes were linked to genes in Parker’s list and 32 genes were linked to genes in the PAM50 list. In the modules identified by HotNet2 with the mean expression as input, there were 80 unique genes that directly interact with the genes in the GEPIA list, while 61 genes interacting with genes in Parker’s list, and 92 interacting with genes in the PAM50 list out of 696 total genes. Lastly, from the HotNet2 analysis with gene variance, 164, 120, and 197 out of 576 genes directly interacted with genes in the GEPIA, Parker’s list, and the PAM50 list, respectively.

In summary, 83 of the 318 (26.1%) selected genes either overlapped or were directly interacted with a gene from the three gene lists, 185 of the 696 (27.4%) for the HotNet2 results with mean gene expression as inputs. Specifically, a total of 329 of the 576 (57.1%) identified by the HotNet2 with gene expression variance overlapped or directly interacted with 136 genes from the GEPIA, Parker’s results, and PAM50 list. The distribution of the 136 genes among the three gene lists is shown in Figure 5B while the Venn diagram for the three gene lists shown in Figure 5A.

Figure 5.

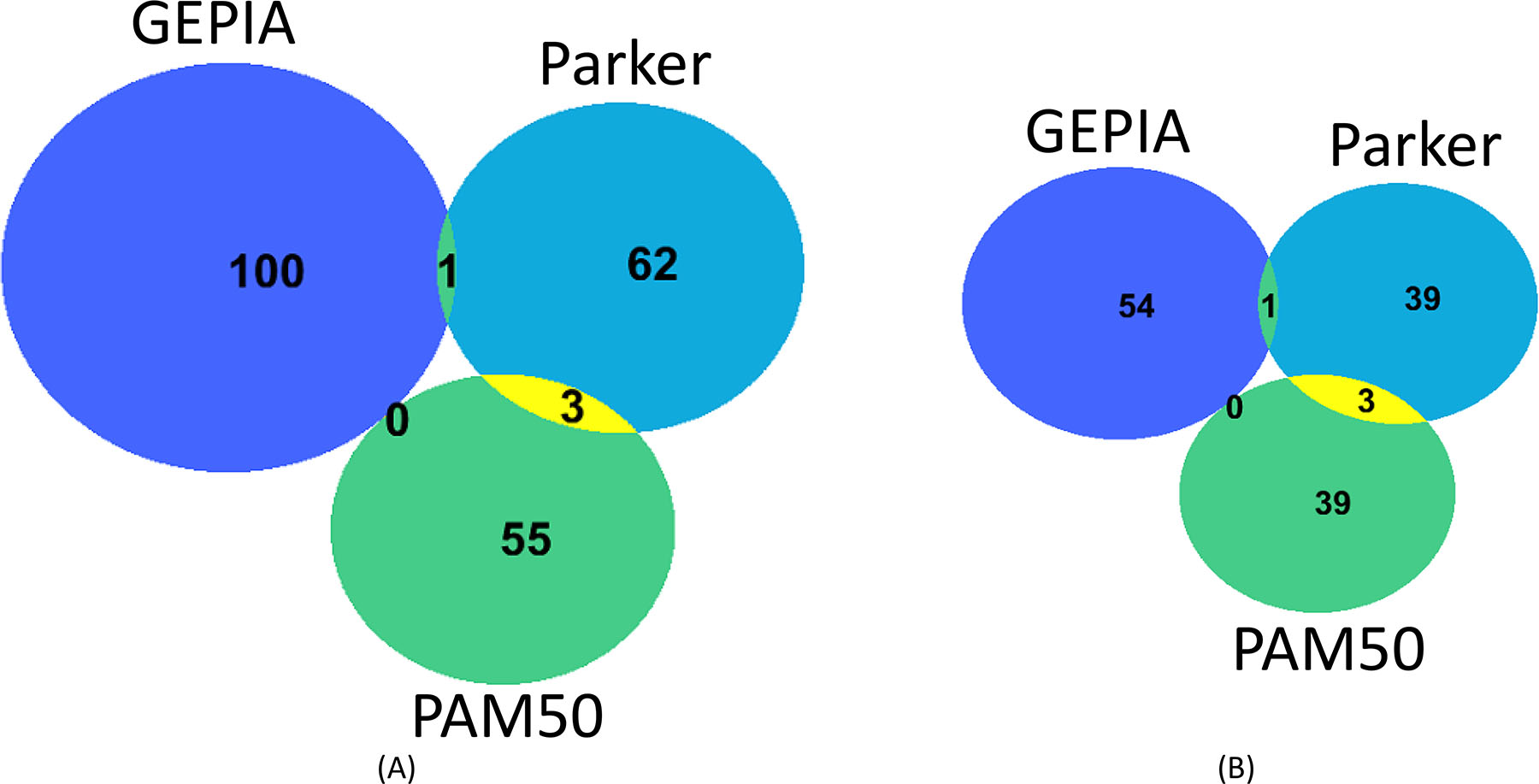
(A) The Venn Diagram of the three sets of highly cited gene markers from GEPIA, PAM 50, and Parker’s lists. (B) A total of 329 out of 576 genes in the variance HotNet2 set directly interact or overlap with 136 genes in the GEPIA, PAM50, and Parker’s list. Venn Diagram of the 136 gens was shown in (B).

4. DISCUSSION

This work is the first attempt to predict and interpret the survival rate for different cancer types using the GCNN approach. Our results suggested that clinical data improves the prediction of 7 cancer types including BLCA, BRCA, COAD, LUSC, SARC, STAD, UCEC, which agrees with existing results [7, 32–34]. The proposed 1-layer GCNN already generated better performance comparing to the regression-based Cox-PH method and neural network-based Cox-nnet method. This confirmed the idea that GCNN is capable of handling data in a non-Euclidean manifold. This property is very helpful in establishing GCNN models with molecular expression data since no embedding is requested comparing to the CNN models. The top two models evaluated by mean C-Index were GCNN based on GeneMania and Correlation +GeneMania with clinical data. Interestingly, the t-test showed there was very little significant difference among the GCNN models generated by three different graphs.

The GCNN model in essence includes convolution on the graph based on the network structure. To investigate whether the structure of the graph was significant, we examined a random graph structure for three cancer types including BRCA, COAD, and LGG as shown in Supplement Table 3. Since the GeneMania graph provided the best results among the three graphs as shown in Figure 3, the features such as the number of nodes, network density, and the number of connections of the GeneMania graph were kept in the generation of the random graphs. To keep these features, we randomly shuffled the genes within the GeneMania graph at each independent run to generate a new random network. The structure of the random network bears no biological meaning embedded from the GenaMania graph structure. To examine the effect of the different embeddings, we constructed a chromosomal embedding and a randomly shuffled embedding convolutional neural network (CNN). The random embedding was created with the same 15,496 genes but placed randomly into a 125×125 image to fit all the genes in a square image with each pixel intensity denoting a gene expression value. There are 129 extra empty pixels (15,496 + 129 = 125²) with value zero due to the square-format 2D embedding. The chromosomal embedding was also a 125×125 image but now ordered based on the Ensembl100 annotation (GRCh38 human genome build) with only 28 genes not found which were placed at the end with the additional 129 empty pixels. The genes filled each row based on the chromosomal ordering (Chromosome 1 to X and Y, and smaller genomic position first) and continued onto the next row until all the genes were filled. Both CNN models used a 5×5 convolutional kernel followed by a 2 × 2 max-pooling to reduce the image by half similar to our GCNN graph. The software implementation remained consistent by using TensorFlow 1.14.

We considered the 3 embedding approaches (random CNN, chromosomal CNN, and random GCNN) on 3 cancer studies, BRCA, COAD, and LGG. Each cancer study was selected for a specific reason. BRCA is well studied and therefore we used it for the interpretation. COAD is tested because our GCNN reported the highest improvement compared to the other models. LGG achieved the highest C-indexes with our GCNN models. Results obtained from random CNN, chromosomal CNN, and random GCNN models were shown in Supplement Table 3 along with our GeneMania, Correlation, and Correlation + GeneMania GCNN models without clinical data. The six models in Supplement Table 3 were all trained on the same 25 partitions to reduce any variation between models. The partitions kept the same data distribution as described in section 2.7.

To further validate the results, a paired one-sided t-test was conducted to test the performance improvement between each model for the 3 selected cancer types with a mean C-index of 25 runs and a p-value for the t-test. For BRCA, the Correlation GCNN model performed better than the random CNN and random GCNN models with a p-value less than .01. The Correlation + GeneMania GCNN model also outperformed the random GCNN and random CNN models with a p-value less than 0.01 and 0.05, respectively. For COAD cancer type, both the Correlation and the GeneMania GCNN models performed better than the random GCNN with a p-value of 0.01. All three GCNN models performed better than the chromosomal CNN with a p-value less than 0.05. While the GeneMania GCNN model outperformed random CNN with a p-value less than 0.05. The LGG cancer type had the highest C-index scores for all GCNN models suggesting that LGG might have the simplest regulations to distinguish important features to determine risk score compared to the other cancer types. The Correlation GCNN model performed significantly better compared to the random CNN, the chromosomal CNN, and the random GCNN giving a p-value less than 0.01. However, the GeneMania GCNN performed worse than the chromosomal GCNN with a p-value of 0.0455, and the Correlation + GeneMania GCNN did perform worst among all 6 models with a p-value less than 0.01. The bad performance of the Correlation + GeneMania GCNN model might be caused by the high density of the network structure from the GeneMania graph. The chromosomal CNN’s specific embedding was expected to improve the performance, but there was no significant performance difference between the random CNN and the chromosomal CNN models for BRCA, COAD, and LGG. Interestingly, our previous study on cancer type classification using the TCGA dataset also showed similar prediction accuracy when genes are ordered randomly, comparing similar studies where input genes are in chromosomal order [59, 60]. By comparing with different embeddings, GCNN models outperformed CNN models and random networks

Interpretation of the GCNN model concerning biological meaning is very hard since the evolution of the data was not assigned any biological meaning from the beginning. A novel network module-based analysis was presented for breast cancer in this study. The proposed method retrieved significant gene markers for breast cancer survival. A total of 329 out 576 genes selected by HotNet2 Modules with variance as heat input either overlapped or directly interacted with the 213 well know gene markers for breast cancer survival. The investigation of graph connectivity shows that a possible reason that the other genes appear in the modules is due to the structure of the graph and its close neighbors. Further interpretation for other cancer types and other GCNN models should be performed in future research to establish a more complete view of significant gene markers for cancer survival.

It is worth noting that the GeneMania graph for GCNN models is the same for all cancer types, while the correlation graphs are different for each cancer type. A correlation graph across 13 cancer types will also be established and refined for each cancer type in our future study to further investigate the effects of graphs on the performance of GCNN models.

Abbreviations

ANN

artificial neural network

ACC

adrenocortical cancer

BLCA

bladder urothelial carcinoma

BRCA

breast invasive carcinoma

C-index

Concordance Inde

CESC

cervical and endocervical cancer

CHOL

cholangiocarcinoma

CNN

convolutional neural network

COAD

colon adenocarcinoma

Cox-PH

Cox-Proportional Hazard

DLBC

diffuse large B-cell lymphoma

ESCA

esophageal carcinoma

GBM

glioblastoma multiforme

GCNN

graph convolutional neural networ

HNSC

head and neck squamous cell carcinoma

KICH

kidney chromophobe

KIRC

kidney clear cell carcinoma

KIRP

kidney papillary cell carcinoma

KM

Kaplan Mierer

LAML

acute myeloid leukemia

LGG

lower grade glioma

LIHC

liver hepatocellular carcinoma

LUAD

lung adenocarcinoma

LUSC

lung squamous cell carcinoma

MESO

mesothelioma

OV

ovarian serous cystadenocarcinoma

PAAD

pancreatic adenocarcinoma

PCPG

pheochromocytoma and paraganglioma

PI

Prognostic Index

PRAD

prostate adenocarcinoma

READ

rectum adenocarcinoma

RS

risk score

SARC

sarcoma

SKCM

skin cutaneous melanoma

STAD

stomach adenocarcinoma

std

standard deviation

TCGA

The Cancer Genome Atlas

TGCT

testicular germ cell tumor

THCA

thyroid carcinoma

THYM

thymoma

UCEC

uterine corpus endometrioid carcinoma

UCS

uterine carcinosarcoma

UVM

uveal melanom