Abstract
Humans spend a lifetime learning, storing and refining a repertoire of motor memories. For example, through experience, we become proficient at manipulating a large range of objects with distinct dynamical properties. However, it is unknown what principle underlies how our continuous stream of sensorimotor experience is segmented into separate memories and how we adapt and use this growing repertoire. Here we develop a theory of motor learning based on the key principle that memory creation, updating and expression are all controlled by a single computation – contextual inference. Our theory reveals that adaptation can arise both by creating and updating memories (proper learning) and by changing how existing memories are differentially expressed (apparent learning). This insight allows us to account for key features of motor learning that had no unified explanation: spontaneous recovery1, savings2, anterograde interference3, how environmental consistency affects learning rate4,5 and the distinction between explicit and implicit learning6. Critically, our theory also predicts novel phenomena – evoked recovery and context-dependent single-trial learning – which we confirm experimentally. These results suggest that contextual inference, rather than classical single-context mechanisms1,4,7–9, is the key principle underlying how a diverse set of experiences is reflected in our motor behaviour.
Throughout our lives, we experience different contexts, in which the environment exhibits distinct dynamical properties, such as when manipulating different objects or walking on different surfaces. Although it has been recognised that the brain maintains multiple motor memories appropriate for these contexts10,11, classical theories of motor learning have focused on how the brain adapts to a single type of environmental dynamics1,7,8. However, with multiple memories come new computational challenges: the brain must decide when to create new memories12 and how much to express and update them for each movement we make. These operations, their governing principles and consequences on motor learning, remain poorly understood. Here, we propose a unifying principle – contextual inference – that specifies how sensory cues and state feedback affect memory creation, expression and updating. We show that contextual inference is the core feature that underlies a range of fundamental aspects of motor learning that were previously explained by a number of distinct and often heuristic processes.
COIN: a model of contextual inference
In order to formalise the role of contextual inference in motor learning, we developed the COIN (COntextual INference) model, a principled nonparametric Bayesian model of motor learning (see Methods). The COIN model is based on an internal model that specifies the learner’s assumptions about how the environment generates their sensory observations (Fig. 1a, Extended Data Fig. 1a). Motor learning corresponds to online Bayesian inference under this generative model (Fig. 1b, Extended Data Fig. 1b). For this, the COIN model jointly infers contexts, their transitions, their dynamical and sensory properties, and the current state of each context, such that each motor memory stores the learner’s inferences about a different context (for validation, see Extended Data Fig. 2a–b). The major challenge in motor learning is that neither contexts nor their transitions come labelled, and thus the learner needs to continually infer which context they are in based on a continuous stream of experience.
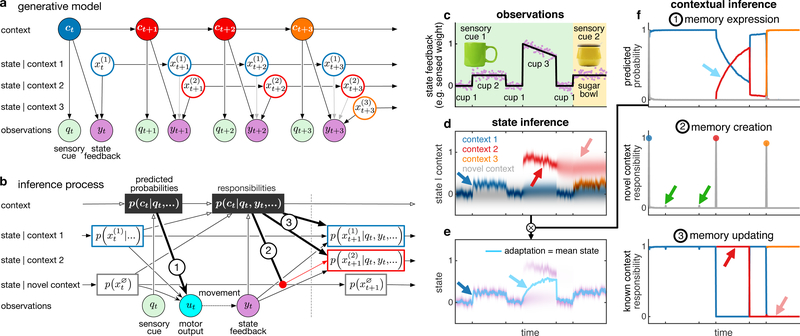
Fig. 1 |. Contributions of contextual inference to motor learning in the COIN model.
a, Generative model. A (potentially) infinite number of discrete contexts ct (colours) exist that transition as a Markov process. Each context j is associated with a time-varying state . The active context can generate a sensory cue qt independent of movement (e.g. the visual appearance of an object) and also determines which state is observed (with noise) as state feedback yt as a consequence of movement (e.g. object weight, black vs. grey arrows). b, Inference process. The learner infers contexts and states (and parameters, not shown) based on observed sensory cues and state feedback. Before movement, predicted context probabilities p(ct | qt,…) are computed by fusing prior expectations from the previous time point (where … refers to all observations before time t) with the likelihood of the current sensory cue qt. For each known context, a predicted distribution over its current state is represented. A potential novel context is always represented, with a stationary state distribution . Motor output ut is the average of the states of the known and novel contexts, weighted by their predicted probabilities (arrow 1). Movement results in state feedback yt, which updates the predicted context probabilities to context responsibilities p(ct | qt, yt,…). A new memory is instantiated with a probability that is the responsibility of the novel context (arrow 2, showing the creation of a red context, initialised as a copy of the state distribution of the novel context). Responsibilities also determine the degree to which state feedback is used to update the predicted state distribution of each context (arrows 3). c, Simulated time series of sensory cues (background colour for object appearance) and state feedback observations (noisy weight, purple) when handling visually-identical cups and a sugar bowl of varying weights (black line, arbitrary scale). The weight of cup 3 decreases as liquid is poured from it, other objects have constant weights. (d-f) The COIN model applied to the observations in c. d, Predicted state distributions for the three contexts inferred by the model and a novel context. e, The predicted state distribution (purple) is a mixture of the individual contexts’ predicted state distributions (d) weighted by their predicted probabilities (f1). The motor output (adaptation, cyan line) is the mean of the predicted state distribution. Intensity of colours in d and purple in e indicates probability density, linearly scaled between 0 and the maximum of the corresponding density. f, Contextual inferences (colours as in d). 1. Predicted probability (before state feedback) of each known context and a novel context. 2. Responsibility (context probability after state feedback) of a novel context. Coloured circles show memory creation events. The novel context responsibility is insufficient to generate a new memory when transitioning to and from cup 2 (green arrows). 3. Responsibility of each known context. See text for arrow explanations in d-f.
The result of contextual inference is a posterior distribution expressing the probability with which each known context, or a yet-unknown novel context, is currently active (Fig. 1b, top row). In turn, contextual inference determines memory creation, expression and updating (Fig. 1b, numbered arrows). Fig. 1c–f (and Extended Data Fig. 1c–e) illustrates this in a simulation of the COIN model (parameters in Extended Data Fig. 3) when handling objects of varying weights. For determining the current motor command (Fig. 1e), rather than selecting a single memory to be expressed11,12, the state associated with each memory (Fig. 1d) is expressed commensurate with the probability of the corresponding context under the posterior, computed after observing the sensory cue but before movement (‘predicted probability’; Fig. 1b, arrow 1; Fig. 1f1). After movement, the ‘responsibility’ of each known context as well as of a novel, yet-unknown context is computed as their posterior probability given both the cue and the resultant state feedback. A new memory is created flexibly, whenever the responsibility of a novel context becomes high (Fig. 1b, arrow 2; Fig. 1f2). Critically, context responsibilities also scale the updating of the previously existing memories and any newly created memory (Fig. 1b, arrows 3; Fig. 1f3, red and pink arrows respectively showing how high and low responsibility for the red context speeds up and slows down the updating of its state, Fig. 1d). Finally, these responsibilities are used to compute the predicted context probabilities on the next time step (Fig. 1f1).
In summary, the COIN model proposes that contextual inference is core to motor learning. In particular, unlike in traditional models of learning, adaptation to a change in the environment (e.g. Fig. 1e, blue and cyan arrows) can arise from two distinct and interacting mechanisms. First, in line with classical notions of learning, proper learning constitutes the creation and updating of memories (the inferred states of known contexts; Fig. 1d, blue arrow). Second, apparent learning occurs due to the updating of the predicted context probabilities (Fig. 1f1, cyan arrow), thereby altering the extent to which existing memories are ultimately expressed in behaviour.
Apparent learning underlies memory recovery
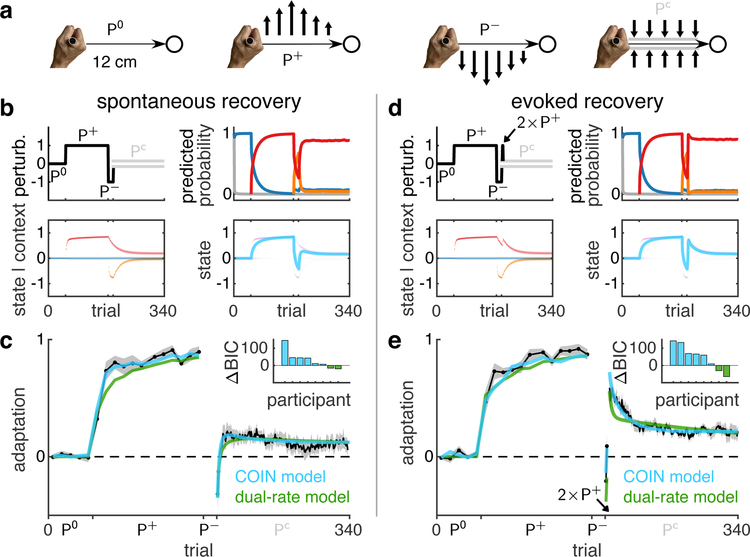
As an ideal litmus test of the contributions of contextual inference to memory creation and expression (Fig. 1b, arrows 1–2), we revisited a widely-used motor learning paradigm. In this paradigm (Fig. 2a and b, top left), participants learn a perturbation P+ applied by a robotic interface while reaching to a target. Adaptation is assessed using occasional channel trials, Pc, which remove movement errors and measure the forces participants use to counteract the perturbation (Fig. 2a, see Methods for details). Exposure to P+ is followed by brief exposure to the opposite perturbation, P−, bringing adaptation back, near to baseline. Finally, a series of channel trials is administered. As in previous studies1, our participants showed the intriguing feature of spontaneous recovery in this phase (Fig. 2c): a transient re-expression of P+ adaptation, rather than a simple decay towards baseline.
Fig. 2 |. Memory creation and expression accounts for spontaneous and evoked recovery.
a, Participants made reaching movements (thin horizontal arrows) to a target (circle) while holding the handle of a robotic manipulandum that could generate forces (thick vertical arrows). For clarity, schematic not to scale. The manipulandum could either be passive (null field, P0) or generate a velocity-dependent force field that acted to the left (P+) or right (P−) of the current movement direction. Channel trials (Pc) were used to assess adaptation by constraining the hand to a straight channel (grey lines) to the target and measuring the forces generated by the participant into the virtual channel walls. b, Simulation of the spontaneous recovery paradigm with the COIN model (parameters fit to average data in c & e simultaneously). Top left: perturbation (black) and channel-trial phase (grey). Bottom left: predicted state distributions of inferred contexts as in Fig. 1d (for clarity we omit the novel context here and in subsequent figures). Top right: predicted probability of contexts as in Fig. 1d. Bottom right: predicted state distribution (purple) and its mean (cyan) as in Fig. 1e. Note that full state distributions are inferred in bottom left and right but they appear narrow due to fitting to the average of all participants’ data (see Methods). c, Mean adaptation (black, ± SEM across n = 8 participants) on the channel trials of the spontaneous recovery paradigm. The cyan and green lines show model fits (mean of individual participant fits) of the COIN (7 parameters) and dual-rate models (5 parameters), respectively. Inset shows ΔBIC (nats) for individual participants, positive favours the COIN model. d-e, As in b-c for the evoked recovery paradigm (n = 8) in which the 3rd and 4th trials in the channel-trial phase were replaced by P+ trials (black arrow). For COIN model parameters see Extended Data Fig. 3.
Although this paradigm has no explicit sensory cues, according to our theory, contextual inference plays an important role. When simulated for this paradigm (Fig. 2b), the COIN model starts with a memory appropriate for moving in the absence of a perturbation (P0, blue Fig. 2b, bottom left) and creates new memories for the P+ (red) and P− (orange) perturbations. Spontaneous recovery arises due to the dynamics of contextual inference. As P+ has been experienced in most trials, it is quickly inferred to be active with a high probability during the channel-trial phase (Fig. 2b, top right). Therefore, as its state has not yet decayed (Fig. 2b bottom left), the memory of P+ is transiently expressed in the participant’s motor output (Fig. 2b bottom right). This mechanism is fundamentally different from that of a classical, single-context model of motor learning, the dual-rate model1. There, motor output is determined by a combination of individual memories that update at different rates (fast and slow) but whose expression does not change over time. Thus the dynamics of adaptation is solely determined by the dynamics of memory updating, i.e. proper learning. In contrast, in the COIN model, changes in motor output can occur without updating any individual memory, simply due to changes in the extent to which existing memories are expressed due to contextual inference, i.e. apparent learning. This mechanism allows the COIN model to account robustly for spontaneous recovery (Extended Data Fig. 4a), including elevated or reduced levels when the P+ phase is extended13 (Extended Data Fig. 5a–j) or when P− is experienced prior to the P+ phase14 (Extended Data Fig. 5k–o), respectively.
In order to distinguish between proper and apparent learning as the main mechanism underlying spontaneous recovery, we designed a novel ‘evoked recovery’ paradigm (similar to the reinstatement paradigm in classical conditioning15) in which sensorimotor evidence clearly indicates that a change in context has occurred. For this, two early trials in the channel-trial phase of the spontaneous recovery paradigm were replaced with P+ (‘evoker’) trials (Fig. 2d, top left, akin to trigger trials in visuomotor learning11). In this case, the COIN model predicts a strong and long-lasting recovery of P+-adapted behaviour (Fig. 2d, bottom right; Extended Data Fig. 4b), primarily due to the inference that the P+ context is now active (Fig. 2d, top right, red) and the gradual decay of the P+ state over subsequent channel trials (Fig. 2d, bottom left, red). In addition, our mathematical analysis suggested that evoked as well as spontaneous recovery are inherent features of the COIN model (Suppl. Inf. and Extended Data Fig. 6a–c). In contrast, the dual-rate model only predicts a transient recovery that rapidly decays due to the same underlying adaptation process with fast dynamics governing both recovery and decay (Extended Data Fig. 6d).
In line with COIN model predictions, participants showed a strong evoked recovery in response to the P+ trials (Fig. 2e). This recovery lasted for the duration of the experiment, defying models that predict a simple exponential decay to baseline4,11,16 (Extended Data Fig. 6e and Extended Data Table 1). We fit the COIN and dual-rate models to individual participants’ data in both experiments (Fig. 2c & e). The COIN model fit the data accurately, but the dual-rate model (and its multi-rate extensions, Extended Data Fig. 6d) showed a qualitative mismatch in the time course of decay of evoked recovery (insets in Fig. 2c & e). Formal model comparison provided strong support for the COIN model overall (Δ group-level BIC of 302.6 and 394.1 nats for the spontaneous and evoked recovery groups, respectively) and for the majority of participants (6 out of 8 for each experiment; individual fits shown in Extended Data Fig. 6f, Extended Data Fig. 2c–e).
The COIN model explains memory recovery by creating a new memory only when existing memories cannot account for a perturbation, such as on the abrupt introduction of P+ and P−, but not when a new perturbation is introduced gradually. This explains why deadaptation is slower following the removal of a gradually (vs. abruptly) introduced perturbation17 (Extended Data Fig. 5p–s).
Memory updating depends on contextual inference
In the COIN model, contextual inference also controls how each existing memory is updated, that is proper learning (Fig. 1b, arrows 3). In the COIN model all memories are updated, with the updates scaled by their respective inferred responsibilities (Fig. 1f3). This contrasts with models which only update a single memory11,12 or update multiple memories independent of context1,18. To test this prediction, we examined the extent to which memories for two contexts were updated when we modulated their responsibilities by controlling the sensory cue and state feedback – the two observations that determine context responsibilities (Fig. 1b).
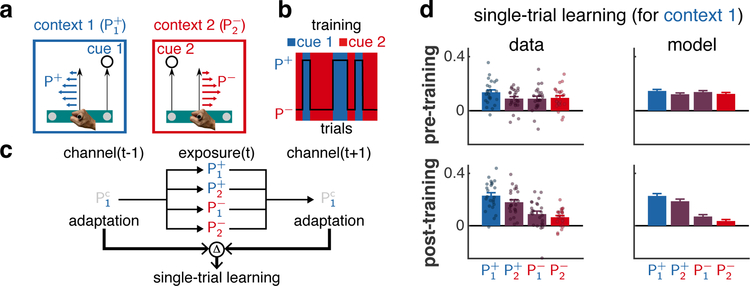
In many natural scenarios, sensory cues and state feedback provide consistent evidence about context (e.g. larger cups are heavier), and thus context responsibilities are approximately all-or-none (Fig. 1f3). Thus to test for graded memory updating, we created conflicts between cues and state feedback (akin to a light, large cup). Specifically, participants experienced an extensive training phase designed to form separate memories for two contexts associated with a distinct cue (target location) and perturbation (Fig. 3a; context 1 = and context 2 = , with sub- and superscript specifying sensory cue and perturbation sign, respectively). These contexts switched randomly (with probability 0.5; Fig. 3b). As expected19, participants formed separate memories for each context and expressed them appropriately based on the sensory cues (Extended Data Fig. 7a). In a subsequent test phase, we studied the updating of one of the memories, that associated with context 1, in response to exposure to a single trial of a potentially conflicting cue-feedback combination. To quantify single-trial learning for the memory associated with context 1, we assessed the adaptation of this memory using channel trials with the appropriate cue (cue 1) both before and after an exposure trial (Fig. 3c). The change in adaptation from the first to last channel trial of this ‘triplet’ (channel-exposure-channel) reflects single-trial learning in response to the exposure trial4,5. To bring adaptation back close to baseline before each triplet, we used sequences of washout trials, pairing P0 with the sensory cues ( and ).
Fig. 3 |. Memory updating depends on contextual inference.
a, Participants experienced two contexts defined by a sensory cue (right or left target) paired with a perturbation sign (P+ or P−). Participants moved a control point (right vs. left, grey disk) on a virtual bar to the corresponding target 19. For clarity, schematic not to scale. The colours of cues and perturbations indicate the context to which they are associated (blue and red for context 1 and 2, respectively). b, Training: cues (background colour) were consistently paired with perturbations (black line) randomly selected on each trial (only a few trials shown for clarity). c, Triplets: two channel trials (both with cue 1, ) bracket an ‘exposure’ trial that uses one of the four possible cue-perturbation combinations. Single-trial learning for the memory associated with context 1 is measured as the difference (Δ) in adaptation across the two channel trials. d Single-trial learning for context 1 before (top) and after (bottom) training. Experimental data (mean ± SEM, column 1) across n = 24 participants (dots). Positive values indicate single-trial learning consistent with the exposure trial perturbation (increase following P+ and decrease following P−). The average (± SEM across participants, column 2) of the individual COIN model fits (8 parameters each, Extended Data Fig. 3).
The COIN model predicted that the responsibility of context 1, and hence the updating of the corresponding memory (as reflected in single-trial learning; Fig. 3d, column 2, Extended Data Fig. 4c), should exhibit a graded pattern that arises over training (Extended Data Fig. 7b): it should be greatest when the cue and state feedback on the exposure trial both provide evidence of context 1 ( exposure trial), least when both provide evidence for context 2 ( exposure trial) and intermediate when the two sources of evidence are in conflict ( and exposure trials; see also Suppl. Inf. and Extended Data Fig. 7c–d for an analytical approximation). Comparing the two conditions with intermediate updating, due to the cues being paired with P0 in the washout trials, we also expected the cue to have a weaker effect than the perturbation and therefore less updating of the memory for context 1 following exposure with than with .
The pattern of single-trial learning in pre- and post-training confirmed the COIN model’s qualitative predictions (Fig. 3d, column 1). Prior to training, there was no significant difference in single-trial learning across exposure conditions (two-way repeated-measures ANOVA, F1,23 = 2.40, p = 0.135 for cue, F1,23 = 0.97, p = 0.335 for perturbation). After learning, single-trial learning showed a gradation across conditions with a significant modulatory effect for both the cue and the perturbation (F1,23 = 10.35, p = 3.82 × 10−3 for cue, F1,23 = 21.16, p = 1.26 × 10−4 for perturbation, with no significant interaction, F1,23 = 0.64, p = 0.432; Extended Data Fig. 7e). The modulatory effects of the cue and the perturbation were not confined to separate subsets of participants (Fisher’s exact test, odds ratio = 1.0, p = 1.00, see Methods and Extended Data Fig. 7f). After fitting to the data, the COIN model also accounted quantitatively for how single-trial learning changed during the training phase (Extended Data Fig. 7b). Taken together, the pattern of single-trial learning shows the gradation in memory updating (at an individual participant-level) predicted by the COIN model, with multiple memories updated in proportion to their responsibilities.
Apparent changes in learning rate
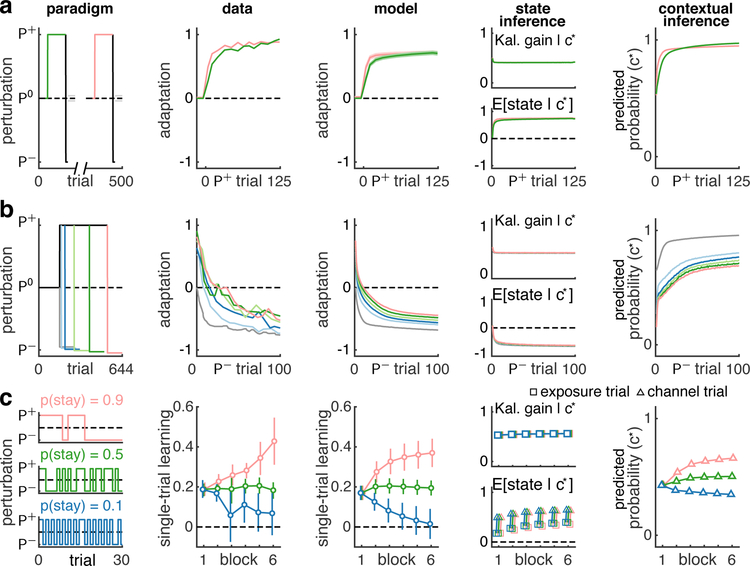
The COIN model also suggested an alternative account of classical results about apparent changes in learning rate under a variety of conditions. Fig. 4 shows three paradigms (column 1) with experimental data (column 2). What is common in all these cases is that the empirical finding of trial-to-trial changes in adaptation has been interpreted as proper learning, i.e. changes to existing memories (states). Thus differences between the magnitudes of these changes have been interpreted as differences in learning rate. For example, savings (Fig. 4a) refers to the phenomenon that learning the same perturbation a second time (even after washout) is faster than the first time1,2,20,21. In anterograde interference (Fig. 4b) learning a perturbation (P−) is slower if an opposite perturbation (P+) has been learned previously3, with the amount of interference increasing with the length of experience of the first perturbation. The persistence of the environment has also been shown to affect single-trial learning (Fig. 4c)4,5: more consistent environments lead to increased levels of single-trial learning.
Fig. 4 |. Contextual inference underlies apparent changes in learning rate.
The COIN model applied to three phenomena: savings (a), anterograde interference (b) and the effect of environmental consistency on single-trial learning (c). Column 1: experimental paradigms (lines as in previous figures, colours highlight key comparisons). Note the lines showing P− perturbations in b have been separated vertically for clarity. Column 2: experimental data replotted from Ref. 20 (a), Ref. 3 (b) and Ref. 4 (c). Column 3: output of COIN model averaged over 40 parameter sets obtained from fits to individual participants in the experiments shown in Figs. 2 and 3 (7 parameters, Extended Data Fig. 3). Error bars show SEM based on the number of participants in the original experiments (n = 46 in a, n = 50 in b and n = 27 in c). Columns 4–5: COIN model inferences with regard to the context (c∗) that is most relevant to the perturbation to which adaptation is measured. Specifically, c∗ is the context with the highest responsibility on the given trial (that associated with P+ in a and P− in b) or, as in Fig. 3d (also single-trial learning), the context with the highest predicted probability on the second channel trial of a triplet (that associated with P+, c). Column 4: Kalman gain (top) and mean of the predicted state distribution (bottom) for the relevant context c∗. Column 5: Predicted probability of the relevant context c∗. Grey lines in b represent initial adaptation to P+ and have been sign inverted in columns 2–3 and the bottom panel of column 4. Data in c shows averages within blocks, with the bottom panel in column 4 showing separate averages for exposure (squares) and subsequent channel trials (triangles).
The COIN model suggests that changes in adaptation can occur without proper learning, simply through apparent learning, that is by changing the way existing memories are expressed (Fig. 1d–f, blue vs. cyan arrows). Therefore, apparent changes in learning rate in these paradigms may be due to changes in memory expression rather than changes in memory updating. To test this hypothesis, we simulated the COIN model using the parameters obtained by fitting each of the 40 participants in our experiments (Extended Data Fig. 3), thus providing parameter-free predictions. The COIN model reproduced the pattern of adaptation and single-trial learning seen in these paradigms (Fig. 4 and Extended Data Fig. 8, column 3; Extended Data Fig. 4d–f). Crucially, differences in the apparent learning rate were not driven by differences in either the proper learning rate (Kalman gain, see Methods) or the underlying state (column 4). Instead, they were driven by changes in contextual inference (column 5). For example, according to the COIN model, in savings P+ is expected with higher probability during the second exposure after having experienced it during the first exposure. Similarly, anterograde interference arises as more extended experience with P+ makes it less probable that a transition to other contexts (i.e. P−) will occur. Finally, more (less) consistent environments lead to higher (lower) probabilities with which contexts are predicted to persist to the next trial, leading to more (less) memory expression, as reflected in single-trial learning. More generally, our analysis of the COIN model indicated that single-trial learning can be expressed mathematically as a mixture of two processes that both depend on contextual inference (see Suppl. Inf. and Extended Data Fig. 7c–d) and each of which can be dissected by the appropriate experimental manipulation: proper learning (as studied in Fig. 3) and apparent learning (as studied in Fig. 4c).
Cognitive mechanisms in contextual inference
In addition to providing a comprehensive account of the phenomenology of motor learning, the COIN model also suggests how specific cognitive mechanisms contribute to the underlying computations. For example, associating working memory with the maintenance of the currently estimated context probabilities explains how a working memory task can effectively lead to evoked recovery in a modified version of the spontaneous recovery paradigm22 (see Suppl. Inf. and Extended Data Fig. 9a–d). Furthermore, identifying explicit and implicit forms of visuomotor learning with inferences in the model about state (i.e. estimate of visuomotor rotation) versus a bias parameter (i.e. sensory recalibration between the proprioceptive and visual locations of the hand), respectively, explains the complex time courses of these components of learning23–25 (see Suppl. Inf. and Extended Data Fig. 9e–l).
Discussion
The COIN model puts the problem of learning a repertoire of memories — rather than a single motor memory — centre stage. Once this more general problem is considered, contextual inference becomes a key computation that unifies seemingly disparate data sets. By partitioning motor learning into two fundamentally different processes, contextual inference (Fig. 1b, top row) and state inference (Fig. 1b, bottom rows), the COIN model provides a principled framework for studying the neural bases of learning motor repertoires (see Suppl. Inf.).
In contrast to the COIN model, previous theories of motor learning typically did not have a notion of context1,4,18. In the few cases in which contextual motor learning was considered within a principled probabilistic framework11,16,26, the generative models underlying learning did not incorporate fundamental properties of the environment (e.g. context transitions, cues or state dynamics) that are critical for explaining a number of learning phenomena. Consequently, previous models can only account for a subset of the data sets we model (Extended Data Table 1), which they were often hand-tailored to address.
There are deep analogies between the context-dependence of learning in the motor system and other learning systems, both in terms of their phenomenologies and the computational problems they are trying to solve12,27–30. However, there is one important conceptual issue that has been absent from work on contextual learning in other domains that our work has brought to the fore – the distinction between proper learning and apparent learning. We have shown that many features of motor learning arise not from the updating of existing memories (proper learning) but from changes in the extent to which existing memories are expressed (apparent learning). This distinction, and the role of contextual inference in both proper and apparent learning, is likely to be relevant to all forms of learning in which experience can be usefully broken down into discrete contexts – in the motor system and beyond.
Methods
Here, we provide an overview of the methods. For full details see Suppl. Inf.
Participants
Forty right-handed, neurologically-healthy participants (18 males and 22 females; age 27.7 ± 5.6 yr, mean ± s.d.) participated in two experiments, which had been approved by the Cambridge Psychology Research Ethics Committee and the Columbia University IRB (AAAR9148). All participants provided written informed consent.
Experimental apparatus
Experiments were performed using a vBOT planar robotic manipulandum with virtual-reality system and air table31. Participants grasped the handle of the manipulandum with their right hand while their forearm was supported on an air sled and moved their hand in the horizontal plane.
The manipulandum controlled a virtual “object” that was displayed centred on the hand and translated with hand movements as participants made repeated movements from a home position to a target located 12 cm distally in the sagittal direction.
On each trial, the vBOT could either generate no forces (P0, null field), a velocity-dependent curl force field (P+ or P− perturbation depending on the direction of the field) or a force channel (Pc, channel trials). For the curl force field, the force generated on the hand was given by
| (1) |
where Fx, Fy, and are the forces and velocities at the handle in the x (transverse) and y (sagittal) directions respectively. The gain was set to ±15 N·s·m−1, with the sign specifying the direction of the curl field (counterclockwise or clockwise, which were assigned to P+ and P−, counterbalanced across participants). On channel trials, the hand was constrained to move along a straight line to the target by simulating channel walls on each side of the straight line as stiff springs (3,000 N·m−1) with damping (140 N·s·m−1)32,33.
Experiment 1: spontaneous and evoked recovery
Sixteen participants were assigned to either a spontaneous (n = 8) or evoked (n = 8) recovery group. The virtual object controlled by participants was simply a cursor.
Participants in the spontaneous recovery group performed a version of the standard spontaneous recovery paradigm1. A pre-exposure phase (50 trials) with a null field (P0) was followed by an exposure phase (125 trials) with P+. Participants then underwent a counter-exposure phase of 15 trials with the opposite perturbation (P−). This was followed by a channel-trial phase (150 channel trials, Pc). In the pre-exposure and exposure phases, to assess adaptation, each block of 10 trials had one channel trial (Pc) in a random location (not the first). A 45 s rest break was given after trial 60 of the exposure phase, followed by an additional 5 P+ trials prepended to the next block.
The evoked recovery group experienced the identical paradigm to the spontaneous recovery group except that the 3rd and 4th trials of the channel-trial phase were replaced with P+ trials (Fig. 2d).
Experiment 2: memory updating
Twenty-four participants performed the memory updating experiment. The paradigm is based on the control point experiment described in Ref. 19 in which perturbations , , , , and are presented with one of two possible sensory cues (different control points on a rectangular virtual object, denoted by subscripts). The experiment consisted of a pre-training, training and post-training phase. In the pre-training and post-training phases, participants performed blocks of trials consisting of a variable number (8, 10 or 12 in the pre-training phase and 2, 4 or 6 in the post-training phase) of washout trials (an equal number of and in a pseudorandom order) followed by 1 of 4 possible ‘triplets’. Each triplet consisted of 2 channel trials (both with cue 1, ) bracketing a cue-perturbation ‘exposure’ trial (, , or , see main text and Fig. 3c). Each of the 4 triplet types was experienced once every 4 blocks, using pseudorandom permutations, with a total of 16 blocks in the pre-training phase and 32 blocks in the post-training phase.
In the training phase (Fig. 3b), participants performed 24 blocks each consisting of 62–70 trials. The key feature of each block was that 32 force-field trials (equal number of and in a pseudorandom order) was followed by 2 triplets (with exposure trials of and ). Each triplet was preceded by a variable number of washout trials (equal number of and in a pseudorandom order) to bring adaptation back close to baseline. For full details of the block structure see Suppl. Inf.
The control point assigned to sensory cue 1 (used on all triplet channel trials) and sensory cue 2 was counterbalanced across participants as was the direction of force field assigned to P+ and P−.
Data analysis
On each channel trial, we linearly regressed the time series of actual forces generated by participants into the channel wall against the ideal forces that would fully compensate for the forces on a force-field trial1. The offset of the regression was constrained to zero, and we used the slope as our (dimensionless) measure of adaptation.
To identify changes in single-trial learning between triplets in the memory updating experiment, two-way repeated-measures ANOVAs were performed with factors of cue (2 levels: cue 1 and cue 2) and perturbation (2 levels: P+ and P−). To test whether the modulatory effects of cue and perturbation were confined to separate subsets of participants, we quantified the effect of each by computing, on an individual-participant basis, the following contrasts in single-trial learning: (cue effect) and (perturbation effect). We then split participants into 2×2 groups based on whether each effect was below or above the median of each effect and performed a Fisher’s exact test on the resulting 2×2 histogram (see Suppl. Inf. for details).
All statistical tests were two-sided with significance set to p < 0.05. Data analysis was performed using MATLAB R2020a.
COIN generative model
Fig. 1a shows the graphical model for the generative model. At each time step t = 1, …, T there is a discrete latent variable (the context) ct ∈ {1, …, ∞} that evolves as a Markov process:
| (2) |
where is the transition probability matrix and is its jth row containing the transition probabilities from context j to each context k (including itself). In principle, there are an infinite number of rows and columns in this matrix. However, in practice, generation and inference can both be accomplished using finite-sized matrices by placing a nonparametric prior on the matrix (see below).
Each context j is associated with a continuous (scalar) latent variable (the state, e.g. the strength of a force field) that evolves according to its own linear-Gaussian dynamics independently of all other states:
| (3) |
where a(j) and d(j) are the context-specific state retention factor and drift, respectively, and is the variance of the process noise (shared across contexts). Each state is assumed to have existed for long enough that its prior for the first time it is observed is its stationary distribution:
| (4) |
At each time step, a continuous (scalar) observation yt (the state feedback) is emitted from the state associated with the current context:
| (5) |
where is the variance of the observation noise (also shared across contexts).
In addition to the state feedback, a discrete observation (the sensory cue) qt ∈ {1, …, ∞} is also emitted. The distribution of sensory cues depends on the current context:
| (6) |
where is the cue probability matrix (which, in principle, is also doubly infinite in size but can be treated as finite in practice) and is its jth row containing the probability of each cue k in context j.
In order to make this infinite-dimensional switching state-space model well-defined, we place hierarchical Dirichlet process priors34 on the transition and cue probability matrices. The transition probability matrix is generated in two steps (Extended Data Fig. 1a). First, an infinite set of global probabilities for transitioning into each context (‘global transition probabilities’) is generated by sampling from a GEM (Griffiths, Engen and McCloskey) distribution:
| (7) |
where 0 ≤ βj ≤ 1 and , as required for a set of probabilities. The global transition probabilities decay exponentially as a function of j in expectation, with the hyperparameter γ controlling the rate of decay and thus the effective number of contexts: large γ implies a large number of small-probability contexts (slow decay from a relatively small initial probability), whereas small γ implies a smaller number of relatively large-probability contexts (fast decay from a relatively large initial probability).
Second, for each context (row of the transition probability matrix), an infinite set of local (context-specific) probabilities for transitioning into each context (‘local transition probabilities’) are generated via a ‘sticky’ variant35 of the Dirichlet process (DP):
| (8) |
where 0 ≤ πjk ≤ 1 and , as required for a set of probabilities, and δj is an infinite-dimensional one-hot vector with the jth element set to 1 and all other elements set to 0. The mean (base) distribution of the Dirichlet process is (αβ + κδj)/(α + κ), with large α + κ reducing variability around this mean (for a tutorial on the Dirichlet process see Ref. 36). Thus the concentration parameter α controls the resemblance of local transition probabilities to the global transition probabilities β. The self-transition bias parameter κ > 0 controls the resemblance of local transition probabilities to δj (i.e. a certain self-transition, ct = ct−1 = j). This self-transition bias expresses the fact that a context often persists for several time steps before switching (i.e. that contexts are ‘sticky’), such as when an object is manipulated for an extended period of time.
Note that the rows of the transition probability matrix are dependent as their expected values (the base distributions of the corresponding Dirichlet processes) contain a shared term, the global transition distribution β. This dependency, controlled by α, captures the intuitive notion that contexts that are common in general (i.e. have a large global transition probability) will be transitioned to frequently from all contexts.
The cue probability matrix is generated using an analogous (non-sticky) hierarchical construction:
| (9) |
where γe determines the distribution of the global cue probabilities βe, and αe determines the across-context variability of local cue probabilities around the global cue probabilities.
In order to allow full Bayesian inference over the parameters governing the state dynamics , we also place a prior on these parameters. For this, we use a bivariate normal distribution (truncated for a(j) between 0 and 1):
| (10) |
where μ = [μa 0]⊤ and is a diagonal covariance matrix. Here we have set the prior mean of d(j) to zero under the assumption that positive and negative drifts are equally probable.
Inference in the COIN model
At each time step t = 1, …, T, the goal of inference is to compute the joint posterior distribution of all quantities that are not directly observed by the learner: the current context ct, the current state of each context , the parameters governing the state dynamics in each context ω(j), the context transition parameters (global β and local Π transition probabilities) and the cue emission parameters (global βe and local Φ cue probabilities) based on the sequence of state feedback y1:τ and sensory cue observations . made until time τ and τ′, respectively (with τ and τ′ each being either t or t − 1, see below). In principle, this posterior is fully determined by the generative model defined in the previous section and can be obtained in a sequential manner by recursively propagating (‘filtering’) the joint posterior from one time point to the next after each new set of observations is made. As exact inference is infeasible, we use a sequential Monte Carlo method known as particle learning that computes an approximation to this filtered posterior37,38. We extensively validated the accuracy of this method (Extended Data Fig. 2a–b). The details of the inference method are given in Suppl. Inf. Here we only describe how the approximate posterior is used to obtain the main model-derived quantities plotted in the paper.
The predicted probability of context j ∈ {1, …, J,∅}, where J is the number of known contexts and ∅ is the novel context, on trial t (computed after observing the cue but before observing the state feedback; Fig. 1f1 and corresponding panels in later figures) is
| (11) |
where Θt\ct denotes the set Θt excluding ct and … represents all observations before time t (as in Fig. 1). The responsibility of context j on trial t (computed after observing both the cue and the state feedback; Fig. 1f2−3 and corresponding panels in later figures) is
| (12) |
The predicted state distribution for context j on trial t (computed before observing the state feedback; Fig. 1d and corresponding panels in later figures) is
| (13) |
where denotes the set Θt excluding . The mean of this distribution can be shown to evolve across trials (see Suppl. Inf.) as
| (14) |
where denotes the expected value of a(j) with respect to the distribution is the prediction error for context j and corresponds to the ‘Kalman gain’ for context j, which we plot in Fig. 4. Note that this update is scaled by the context’s responsibility p(ct = j | qt, yt,…), which underlies the effect of contextual inference on memory updating (arrows 3 in Fig. 1b).
The ‘overall’ predicted state distribution on trial t (i.e. the predicted state distribution of the context that is currently active, and of which the identity the learner cannot know with certainty; purple distribution in Fig. 1e and corresponding panels in later figures) is computed by integrating out the context from Eq. 13 using the predicted probabilities from Eq. 11 (arrow 1 in Fig. 1b):
| (15) |
The motor output ut of the learner (cyan line in Fig. 1e and corresponding panels in later figures) is the mean of this predicted state distribution:
| (16) |
Applying the COIN model to experimental data
Applying the COIN model to experimental data required solving two additional challenges. First, participants’ state feedback observations are hidden from the perspective of the experimenter, as they are noisy realisations of the ‘true’ underlying states (Eq. 5). To appropriately account for our uncertainty about the state feedback participants actually observed, we computed the distribution of COIN model inferences by integrating over the possible sequences of state feedback observations y1:T given the sequence of true states (experimentally-applied perturbations)39. Specifically, on each trial, was assigned a value of 0 (null-field trials), +1 (P+ perturbation trials) or −1 (P− perturbation trials) and yt was assumed to be distributed around with i.i.d. zero-mean Gaussian observation noise of variance (Eq. 5), except on channel trials (Pc) where we treated yt as unobserved, as the state (the magnitude of a force field) was not observed by the participants on those trials. Note that the distribution of state feedback given the true state shares the same parameters as those underlying the COIN model inferences as it is self-consistently defined by the generative model. All figures showing COIN model inferences applied to experimental data (i.e. all but Fig. 1) show the quantities described in the previous section after the state feedback has been integrated out (Fig. 1d–f shows COIN model inferences conditioned on the state feedback sequence shown in Fig. 1c).
Second, real participants’ behaviour can always be subject to influences not explicitly included in the COIN model. In order to account for these uncontrolled and unmodelled factors, we introduced a phenomenological ‘motor noise’ component that related the motor output ut of the COIN model (Eq. 16) to the experimentally measured adaptation at via i.i.d. zero-mean Gaussian noise:
| (17) |
where σm is the standard deviation of the motor noise.
Model fitting and model comparison
In Experiments 1 and 2, we fit the parameters of the COIN model ϑ to participants’ data by maximising the data log likelihood using Bayesian adaptive direct search (BADS)40. In Experiment 1, ϑ = {σq, μa, σa, σd, α, ρ, σm}, where
| (18) |
is the normalised self-transition bias parameter. In Experiment 2, which included sensory cues, an additional parameter αe was also fit. In Experiment 1, we also fit a two-state (dual-rate) and three-state state-space model to the data of individual participants by minimising the mean squared error using MATLAB’s fmincon and BADS. In all cases, optimisation was performed from 30 random initial parameter settings (see Suppl. Inf.).
To perform model comparison for individual participants, we calculated the Bayesian information criterion (BIC). A BIC difference of greater than 4.6 nats (a Bayes factor of greater than 10) is considered to provide strong evidence in favour of the model with the lower BIC value41. To perform model comparison at the group level, we calculated the group-level BIC, which is the sum of BICs over individuals42.
Parameter and model recovery
We used the parameters from the fits of the COIN and dual-rate models to the data of each participant in the spontaneous and evoked recovery experiments to generate 10 synthetic data sets per model class (COIN and dual-rate) for each participant from the corresponding experiment. In the dual-rate model, the only source of variability across the different synthetic data sets for a given participant was motor noise. In contrast, for the COIN model, sensory noise provided another source of variability in addition to motor noise. We fit both model classes to each synthetic data set as we did with real data (see above).
For parameter recovery (Extended Data Fig. 2c), we compared the COIN model parameters that were used to generate the synthetic data (‘true’ parameters) with the COIN model parameters fit to these synthetic data sets (‘recovered’ parameters).
For model recovery (Extended Data Fig. 2d–e), we examined the proportion of times the difference in BIC between the COIN and dual-rate fits favoured the true model class that generated the data.
Simulating existing data sets
We performed COIN model simulations on a diverse set of extant data in Fig. 4 (similarly Extended Data Figs. 5, 8 and 9) in a purely cross-validated manner, such that we used model parameters fitted to participants in our own experiments to make predictions for experiments conducted in other laboratories using other paradigms.
The paradigms in Fig. 4 and Extended Data Fig. 8 were simulated using the 40 sets of parameters fit to our individual participants’ data from both experiments. One hundred simulations (each conditioned on a different noisy state feedback sequence) were performed for each parameter set. The results shown are based on the average of all of these simulations.
The paradigms in Extended Data Fig. 5a–o and Extended Data Fig. 9 were variations of the standard spontaneous recovery paradigm. Therefore, we simulated these paradigms (as well as the paradigm in Extended Data Fig. 5p–s) using the parameters fit to the average spontaneous and evoked recovery data sets. One hundred simulations (each conditioned on a different noisy state feedback sequence) were performed. The results shown are based on the average of these simulations.
Modelling working memory
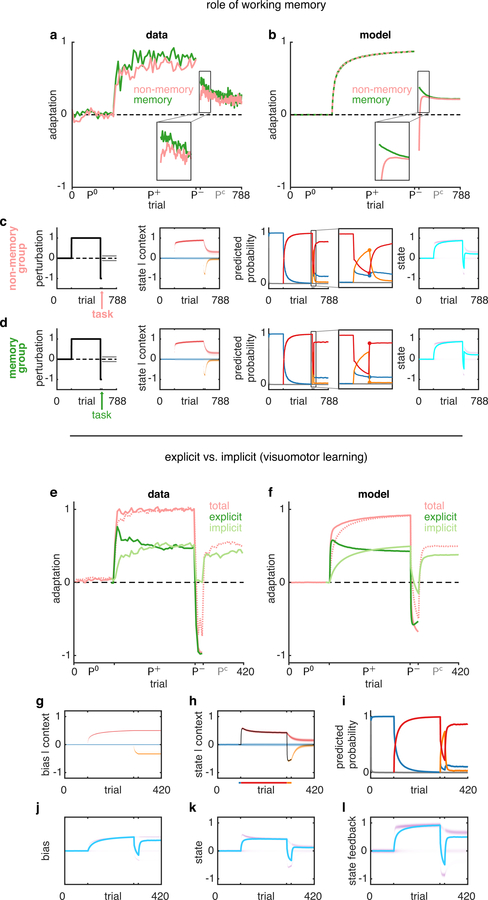
A working memory task performed after the last P− trial of a spontaneous recovery paradigm has been shown to interfere with spontaneous recovery, producing an effect that is reminiscent of evoked recovery on the first Pc trial (Extended Data Fig. 9a, Ref. 22). We modelled the effect of the working memory task as selectively abolishing the (working) memory of the responsibilities on the last P− trial (Extended Data Fig. 9b–d). This means that on the first Pc trial, the predicted probabilities are based on the expected context frequencies (the stationary probabilities).
Modelling visuomotor learning and its explicit and implicit components
In visuomotor rotation experiments, the cursor moves in a different direction to the hand (which is occluded from vision). Hence, visuomotor rotations introduce a discrepancy between the location of the hand as sensed by vision and proprioception. To model this discrepancy, we include a context-specific bias parameter in the state feedback (Eq. 5):
| (19) |
To support Bayesian inference, we place a normal distribution prior over this parameter:
| (20) |
We set μb to zero based on the assumption that positive and negative biases are equally probable and σb to 70−1 by hand to match the empirical data in Extended Data Fig. 9e. We extend and modify the inference algorithm accordingly (see Suppl. Inf.).
On each trial, the state feedback was assigned a value of 0 (no rotation trials), +1 (P+ rotation trials) or −1 (P− rotation trials) plus i.i.d. zero-mean Gaussian observation noise with variance . Visual error-clamp trials (Pc) were modelled in the same way as channel trials (i.e. with state feedback unobserved). Adaptation was modelled as the mean of the predicted state feedback distribution (Extended Data Fig. 5q and Extended Data Fig. 9f, dashed pink) plus Gaussian motor noise.
We also modelled an experiment in which an explicit judgement of the perturbation is obtained on every trial, and the implicit component is taken as the difference between adaption and the explicit judgement23. We hypothesised that participants have explicit access to the state representing their belief about the visuomotor rotation but do not have access to the bias in the state feedback, which is therefore implicit. Hence, we mapped the state of the context with the highest responsibility on the previous trial (Extended Data Fig. 9h, black line) onto the explicit component and the average bias across contexts weighted by the predicted probabilities (Extended Data Fig. 9j, cyan line) onto the implicit component. Adaptation is then, by definition, the sum of these two components (Extended Data Fig. 9e, solid pink) plus Gaussian motor noise. See Suppl. Inf. for full details.
Data availability
All experimental data are publically available at the Dryad repository (https://doi.org/10.5061/dryad.m63xsj42r). The data include the raw kinematics and force profiles of individual participants on all trials as well as the adaptation measures used to generate the experimental data shown in Fig. 2c,e and Fig. 3d.
Code availability
Code for the COIN model is available at GitHub (https://github.com/jamesheald/COIN).
Extended Data
Extended Data Fig. 1 |. Additional details of the COIN model (related to Fig. 1). a-b, Hierarchy and generalisation in contextual inference.
a, Local transition probabilities are generated in two steps via a hierarchical Dirichlet process. In the first step (top), an infinite set of global transition probabilities β are generated via a stochastic stick-breaking process (see Suppl. Inf.). Probabilities are represented by the width of bar segments with different colours indicating different contexts. In the second step (bottom), for each context (‘from context’), local transition probabilities to each other context (‘to context’) are generated (a row of Π) via a stochastic Dirichlet process and are equal to the global probabilities in expectation (bar a self-transition bias, which we set to zero here for clarity). (An analogous hierarchical Dirichlet process, not shown, is used to generate the global and local cue probabilities.) b, Contextual inference updates both the global and local transition probabilities. Context transition counts are maintained for all from-to pairs of known contexts and get updated based on the contexts inferred on two consecutive time points (responsibilities at time points t and t + 1). These updated context transition counts are used to update the inferred global transition probabilities . The updated global transition probabilities and context transition counts produce new inferences about the inferred local transition probabilities . Note that although the model infers full (Dirichlet) posterior distributions over both the global and local transition probabilities, for clarity here we only show the means of these posterior distributions (indicated by the hat notation). In the example shown, only row 3 of the context transition counts is updated (as context 3 has an overwhelming responsibility at time t), but all rows of the local transition probabilities are updated due to the updating of the global transition probabilities (if the model were non-hierarchical, there would be no global transition probabilities, and so the local transition probabilities would only be updated for context 3 via the updated context transition contexts). Thus inferences about transition probabilities generalise from one context (here context 3) to all other contexts (here contexts 1 and 2) due to the hierarchical nature of the generative model. Note that when a novel context is encountered for the first time, its local transition probabilities are initialised based on , thus allowing well-informed inferences about transitions to be drawn immediately. c-e, Parameter inference in the COIN model for the simulation shown in Fig. 1c–f. In addition to inferring states and contexts, the COIN model also infers transition (c) and cue (d) probabilities, as well as the parameters of context-specific state dynamics (e). c, Transition probabilities. Top: Estimated global transition probabilities (solid lines) to each known context (line colours) and the novel context (grey). Pale lines show estimated stationary probabilities of the same contexts representing the expected proportion of time spent in each context given the current estimate of the local transition probabilities (below). Bottom three panels: estimated local transition probabilities from each context (colours as in top panel). d, Estimated global (top panel) and local cue probabilities for the three known contexts (bottom three panels) and cues (line colours). Although the model infers full (Dirichlet) posterior distributions over both transition (c) and cue probabilities (d), for clarity here we only show the means of these posterior distributions. e, Posterior distribution of drift (left) and retention parameters (right) for the three known contexts (colours as in c, novel context not shown for clarity). Although the model infers the joint distribution of the drift and retention parameters for each context, for clarity here we show the marginal distribution of each parameter separately. Note that drift and retention are estimated to be larger for the red context that is associated with the largest perturbation.
Extended Data Fig. 2 |. Validation of the COIN model. a, Validation of the inference algorithm of the COIN model with a single context.
We computed inferences in the COIN model with a single context based on synthetic observations (state feedback) generated by its generative model (Fig. 1a). Plots show the cumulative distributions of posterior predictive p-values of the state variable (left), and the parameters governing its dynamics (retention, middle; drift, right). The posterior predictive p-value is computed by evaluating the cumulative distribution function of the model’s posterior over the given quantity at the true value of that quantity (as defined by the generative model). Empirical distributions of posterior predictive p-value were collected across 4000 simulations (with different true state dynamics parameters), with 500 time steps in each simulation (during which the true state changes, but the state dynamics parameters are constant). Note that although true state dynamics parameters do not change during a simulation, inferences in the model about them will still generally evolve, and so a new posterior p-value is generated in each time step even for these quantities. If the model implements well-calibrated probabilistic inference under the correct generative model, all these empirical distributions should be uniform. This is confirmed by all cumulative distributions (orange and purple curves) approximating the identity line (black diagonal). Orange curves show posterior predictive p-values under the corresponding marginals of the model’s posterior. To give additional information about the model’s joint posterior over state dynamics parameters, we also show the posterior predictive p-value (cumulative) distribution of each parameter conditioned on the true value of the other one (purple curves). b, Validation of the inference algorithm of the COIN model with multiple contexts. Simulations as in a but with additional synthetic observations (sensory cues) and multiple contexts allowed both during data generation and inference. Empirical distributions of posterior predictive p-value were collected across 2000 simulations (with different true retention and drift parameters), with 500 time steps in each simulation (during which not only states evolve but also contexts transition, and sometimes novel contexts are created). Left column shows the true distributions of sensory cues, contexts and parameters. Inset shows the growth of the number of contexts over time both during generation (blue) and inference (orange). Middle and right columns show the cumulative probabilities of the posterior predictive p-values (pooled across data sets and time steps) for the observations (top row), contexts and state (middle row) and parameters (bottom row). To calculate the posterior predictive p-values for the context, inferred contexts were relabelled by minimising the Hamming distance between the relabelled context sequence and the true context sequence (see Suppl. Inf.). For the parameters, the posterior predictive p-values were calculated with respect to both the marginal distributions (retention and drift) and the conditional distributions (retention | drift, and drift | retention) as in a. The cumulative probability curves approximate the identity line (thin black line) showing that the inferred posterior probability distributions are well calibrated. c, Parameter recovery in the COIN model related to Fig. 2. Plots show the COIN model parameters that were recovered (y-axes) from fits to 10 synthetic data sets generated with the COIN model parameters (true, x-axes) obtained from the fits to each participant in the spontaneous (n = 8) and evoked (n = 8) recovery experiments (Extended Data Fig. 3). Vertical bars show the interquartile range of the recovered parameters for each participant. While several parameters are recovered with good accuracy (σq, μa, σd, σm), others are not (α, and in particular σa and ρ). We expect that with richer paradigms and larger data sets, all parameters would be recovered accurately. Most importantly, despite partial success with recovering individual parameters, model recovery shows that recovered parameter sets taken as a whole can be used to accurately identify whether data was generated by the dual-rate or COIN model (d). Note that we make no claims about individual parameters in this study as our focus is on model class recovery. d-e, Model recovery for spontaneous (d) and evoked recovery experiments (e) related to Fig. 2. Synthetic data sets were generated using one of two models (COIN model, red; dual-rate model, blue). Parameters used for each model were those obtained from the fits to each participant in the spontaneous (n = 8) and evoked (n = 8) recovery experiments (Extended Data Fig. 3) – i.e. for the COIN model, these were the same synthetic data sets as those used in c. Then, the same model comparison method that we used on real data (Fig. 2c, e, insets) was used to recover the model that generated each synthetic data set (see Methods). Arrows connect true models (used to generate synthetic data, disks on top) to models that were recovered from their synthetic data (pie-chart disks at bottom). Arrow colour indicates identity of recovered model, arrow thickness and percentages indicate probability of recovered model given true model. Bottom disk sizes and pie-chart proportions show total probability of recovered model and posterior probability of true model given recovered model (assuming a uniform prior over true models), respectively, with percentages specifically indicating posterior probability of the correct model. These results show that the model recovery process is generally very accurate and actually biased against the COIN model in favour of the dual-rate model.
Extended Data Fig. 3 |. COIN model parameters.
Left column: Parameters for illustrating the COIN model (I: purple), model validation (V: brown) and fits to individuals in the spontaneous (S: blue) and evoked (E: green) recovery experiments, to the average of both groups (A: cyan), and individuals in the memory-updating experiment (M: red). Right: scatter plots for all pairs of parameters for the six groups. The overlap of data points suggest parameters are similar across experiments. σq: process noise s.d. (Eq. 3); μa, σa: prior mean and s.d. for context-specific state retention factors (Eq. 10); σd: prior s.d. for context-specific state drifts (Eq. 10); α: concentration of local transition probabilities (Eq. 8); ρ: self-transition bias parameter (Eq. 18); σm: motor noise s.d. (Eq. 17); αe: concentration of local cue probabilities (Eq. 9). Parameters used in the figures is as follows. I: Fig. 1 and Extended Data Fig. 1c–e. V: Extended Data Fig. 2a–b. S: Fig. 2c, Extended Data Fig. 6f (column 1) and Extended Data Fig. 2d. E: Fig. 2e, Extended Data Fig. 6f (column 3) and Extended Data Fig. 2e. S & E: Extended Data Fig. 2c. A: Fig. 2b & d, Extended Data Fig. 5 and Extended Data Fig. 9 (bias added for visuomotor rotation experiments: Extended Data Fig. 5a–j,p–s and Extended Data Fig. 9e–l). M: Fig. 3 and Extended Data Fig. 7a–d. S, E & M: (all parameters, but αe): Fig. 4 and Extended Data Fig. 8. The robustness analyses (Extended Data Fig. 4) used perturbed versions of the same parameters as the corresponding unperturbed simulations. To reduce the number of free parameters in the model, we set the parameters of the hierarchical Dirichlet process that determine the expected effective number of contexts or cues, γ (Eq. 7) and γe (Eq. 9), respectively, both to 0.1, the prior mean for context-specific state drifts, μd, to zero (Eq. 10), and the standard deviation of the sensory noise, σs, to 0.03 when fitting or simulating the model, with the variance of the observation noise (Eqs. 5 and 19) being set to . For visuomotor rotation experiments (Extended Data Fig. 5a–j,p–s and Extended Data Fig. 9e–l), we set the mean of the prior of the bias μb to zero (Eq. 20), and its s.d. σb to 70−1.
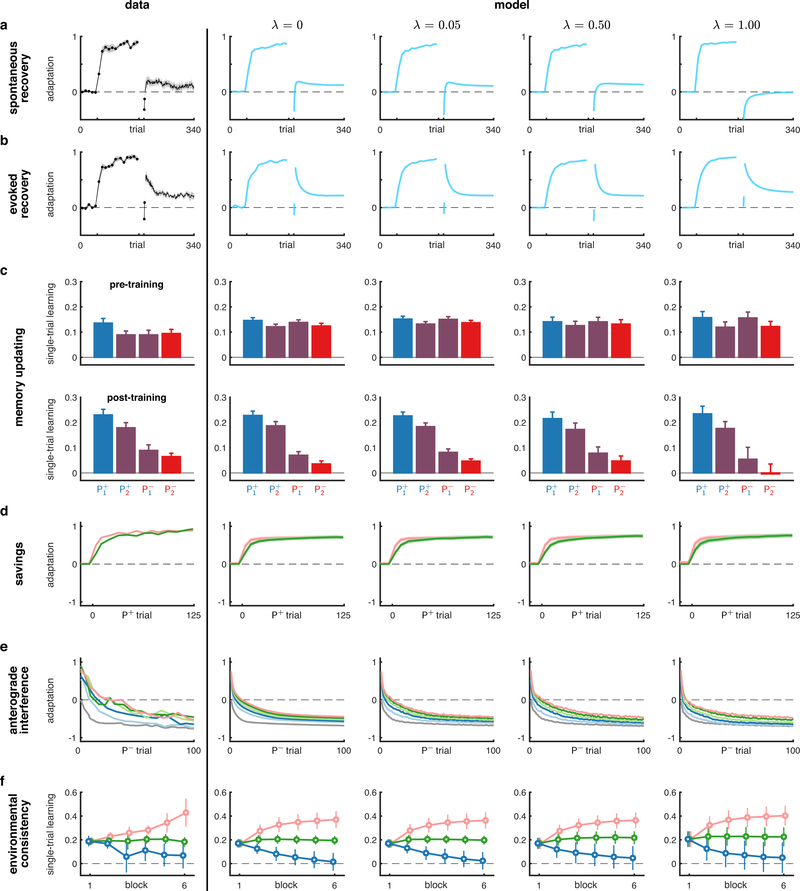
Extended Data Fig. 4 |. Robustness analysis of the main COIN model results.
To test how robust the behaviour of the COIN model is, we added noise to the parameters fit to the individual participants in the spontaneous and evoked recovery, and memory updating experiments and re-simulated the paradigms in Figs. 2 to 4: spontaneous recovery (a), evoked recovery (b), memory updating (c), savings (d), anterograde interference (e), and environmental consistency (f). For each experiment, we simulated the COIN model for the same participants as in Figs. 2 to 4 but perturbed each participant’s parameter values. That is, for each parameter (suitably transformed to be unbounded) we calculated the standard deviation across participants (relevant for the given paradigm or set of paradigms) and then perturbed each participant’s (transformed) parameter by zero-mean Gaussian noise whose standard deviation was a fraction (λ = 0, 0.05, 0.5, or 1.0) of this empirical standard deviation, after which we used the inverse transform to obtain the actual parameter used in these perturbed simulations. For parameters that are constrained to be non-negative (σq, σa, σd, α, αe, σm), we used a logarithmic transformation, whereas for parameters constrained to be on the unit interval (μa, ρ), we used a logit transformation. Column 1: experimental data (plotted as in Figs. 2 to 4). Columns 2–5: output of the COIN model for different amounts of noise added to the parameters. Note that the simulations were not conditioned on the actual adaptation data of individual participants (in contrast to the original simulations of Figs. 2 and 3) because these data are not available for the experiments shown in Fig. 4 (for which the original simulations were already performed using this ‘open-loop’ simulation approach). The robustness analysis shows that most predictions of the COIN model are robust to changes in the parameters, and only start to deviate for large parameter changes (λ = 1) in some of their quantitative details (such as the magnitude of spontaneous recovery). Note that λ = 1 leads to changes in parameters that are of the same magnitude as randomly shuffling the parameters across participants.
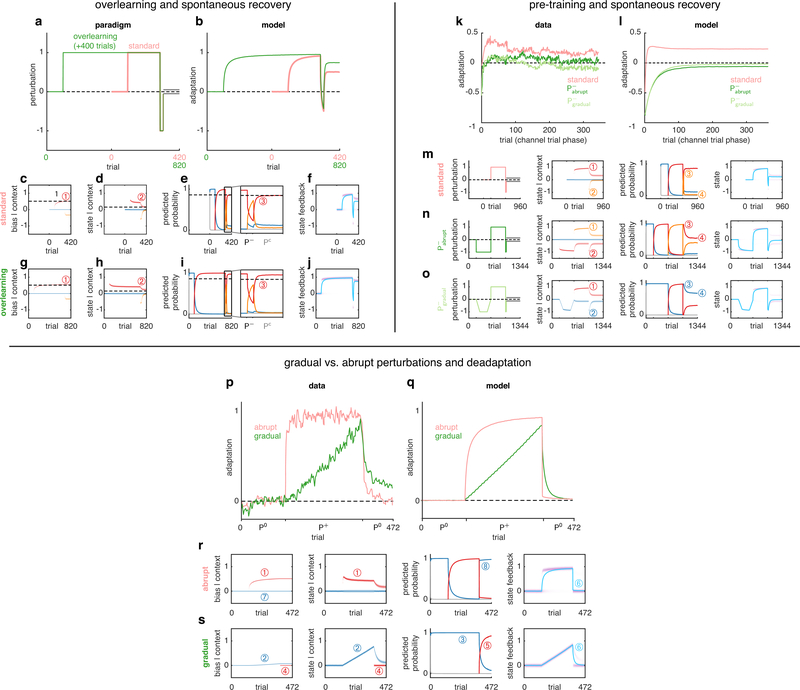
Extended Data Fig. 5 |. History dependence of contextual inference. a-j, Contextual inference underlies the elevated level of spontaneous recovery after ‘overlearning’.
a, Spontaneous recovery paradigm for visuomotor learning in which the length of the exposure (P+) phase is tripled from 200 trials (‘standard’ paradigm, pink) to 600 trials (‘overlearning’ paradigm, green). For comparison, paradigms are aligned to the end of the exposure phase. b, Adaptation in the COIN model for the standard and overlearning paradigms (same parameters as in Fig. 2b & d but with the addition of a bias parameter; see Suppl. Inf. and also Extended Data Fig. 3, parameter set A). Adaptation corresponds to reach angle normalised by the size of the experimentally-imposed visuomotor rotation. Note elevated level of spontaneous recovery after overlearning compared to the standard paradigm, qualitatively matching visuomotor learning data in Fig. 4A of Ref. 13. c-f, Internal representations of the COIN model for the standard paradigm. Inferred bias (c) and predicted state (d) distributions for each context (colours). e, Predicted probabilities of each context (with zoomed view starting from near the end of P+ exposure), colours as in c-d, grey is novel context as in Fig. 1f. f, Predicted state feedback (predicted state plus bias) distribution (purple), which is a mixture of the individual contexts’ predicted state feedback distributions (not shown) weighted by their predicted probabilities (e). Total adaptation (cyan line) is the mean of the predicted state feedback distribution. g-j, same as c-f for the overlearning paradigm. For comparison, the dashed horizontal lines in both paradigms show the final level of each variable for the red context in the standard paradigm. Note that overlearning leaves inferences about biases and states largely unchanged (compare 1 in c & g and 2 in d & h) but leads to higher predicted probabilities of the P+ context (red) in the channel-trial phase (compare 3 in e & i) reflecting the true statistics of the experiment in which P+ occurred more frequently. In turn, this makes the P+ bias and state contribute more to total adaptation in the channel-trial phase, thus explaining higher levels of spontaneous recovery. Therefore, differences between conditions are explained by contextual inference rather than by differences in bias or state inferences. The results are qualitatively similar when simulated as a force-field paradigm (i.e. without bias, not shown). k-o, Contextual inference underlies reduced spontaneous recovery following pre-training with P−. k, Adaptation in the channel-trial phase of a typical spontaneous recovery paradigm (standard, pink, as in Fig. 2b) and two modified versions of the paradigm in which the P+ phase is preceded by a P− (pre-training) phase in which P− is either introduced and removed abruptly (, dark green) or gradually (, light green). Data reproduced from Ref. 14. l-o, Simulation of the COIN model for the same paradigms (same parameters as in Fig. 2b and d; Extended Data Fig. 3, parameter set A), plotted as in Fig. 2b–c. In each paradigm, contexts are coloured according to their order of instantiation during inference (blue→red→orange). Note that pre-training with P− (either abrupt or gradual) leaves inferences about states within each context largely unchanged at the beginning of the channel-trial phase (compare corresponding numbers 1–2 in column 2 across m-o). However, the pre-training leads to higher predicted probabilities of the P− context initially (compare number 3 in m to 3 in n & o) and throughout the channel-trial phase (compare number 4 across m-o) reflecting the true statistics of the experiment in which P− occurred more frequently (compare column 1 across m-o). In turn, this makes the P− state contribute more to total adaptation, thus explaining the reduction in both the initial and final levels of adaptation during the channel-trial phase in the and groups. Therefore, as in Fig. 4, differences between conditions are explained by contextual inference rather than state inference. p-s, Contextual inference underlies slower deadaptation following a gradually-introduced perturbation. p, Adaptation (normalised reach angle, as in b) in a paradigm in which a visuomotor rotation is introduced abruptly (pink) or gradually (green) and then removed abruptly. Data reproduced from Ref. 17. q-s, Simulation of the COIN model on the abrupt (q, pink, and r) and gradual (q, green, and s) paradigms (same parameters as in Fig. 2b and d but with the addition of a bias parameter; Extended Data Fig. 3, parameter set A) plotted as in b-j. Note that contexts are coloured according to their order of appearance during inference (blue→red). In response to the abrupt introduction of the P+ perturbation, a new memory is created (1). In contrast, the gradual introduction of the P+ perturbation prevents the creation of a new memory, thus requiring changes in the inferred bias and state of the original memory associated with P0 (2, blue context) to account for the slowly increasing perturbation. Therefore, the ‘blue’ context is inferred to be active throughout the exposure phase (3) and becomes associated with a P+-like state. However, at the beginning of the abruptly introduced post-exposure (P0) phase, a new memory is created (4) which has a low initial probability that can only be increased by repeated experience with P0 (5). This leads to slower deadaptation in the post-exposure phase compared to the abrupt paradigm (6), in which the original context associated with P0 (blue) is protected (7) and can be reinstated quickly (8) as the P0 self-transition probability has been learned to be higher during the pre-exposure phase. Note that the smaller errors caused by the gradual perturbation relative to the abrupt condition are better accounted for by an error in the state rather than an error in the bias, and therefore the state is updated more than the bias. The results are qualitatively similar when simulated as a force field paradigm (without bias, not shown).
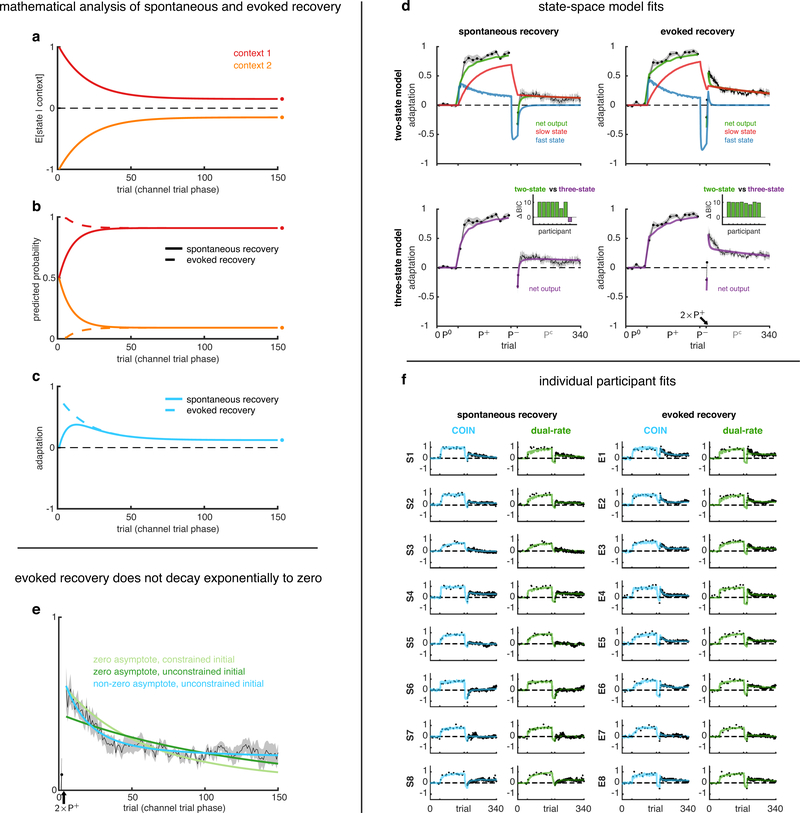
Extended Data Fig. 6 |. Additional analyses of spontaneous and evoked recovery related to Fig. 2. a-c, Mathematical analysis of spontaneous and evoked recovery.
The channel-trial phase of spontaneous and evoked (after the two P+ trials) recovery simulated in a simplified setting (Suppl. Inf.) with two contexts that are initialised to have equal but opposite state estimates (a) and equal (spontaneous recovery, solid) or highly unequal (evoked recovery, dashed) predicted probabilities (b). For the two contexts, the retention parameters are assumed to be constant and equal, and the drift parameters are assumed to be constant, of the same magnitude but opposite sign. Mean adaptation (c), which in the COIN model is the average of the state estimates (a) weighted by the corresponding context probabilities (b), shows the classic pattern of spontaneous recovery (solid, cf. Fig. 2b–c) and the characteristic abrupt rise of evoked recovery (dashed, cf. Fig. 2d–e). Note that although in the full model, state estimates are different between evoked and spontaneous recovery following the two P+ trials, here we assumed they are the same (no separate solid and dashed lines in a) for simplicity and to demonstrate that the difference in mean adaptation between the two paradigms (c) can be accounted for by differences in contextual inference alone (b, cf. Fig. 2b and d, top right insets). Circles on the right show steady-state values of inferences and the adaptation. Note that in both paradigms, adaptation is predicted to decay to a non-zero asymptote (see also e). d, State-space model fits to adaptation data from the spontaneous and evoked recovery groups. Solid lines show the mean fits across participants of the two-state model (5 parameters, top row) and the three-state model (7 parameters, bottom row) to the spontaneous recovery (left column) and evoked recovery (right column) data sets. Mean ± SEM adaptation on channel trials shown in black (same as in Fig. 2c and e). Insets show differences in BIC (nats) between the two-state model and the three-state model for individual participants (positive values in green indicate evidence in favour of the two-state model, and negative values in purple indicate evidence in favour of the three-state model). At the group level, the two-state model was far superior to the three-state model (Δ group-level BIC of 64.2 and 78.4 nats favour of the two-state model for the spontaneous and evoked recovery groups, respectively). Individual states are shown for the two-state model (top, blue and red). Both the fast and slow processes adapt to P+ during the extended initial learning period. The P− phase reverses the state of the fast process, but not of the slow process, so that they cancel when summed resulting in baseline performance. Spontaneous recovery during the Pc phase is then explained by the fast process rapidly decaying, revealing the state of the slow process that has remained partially adapted to P+. Note that this explanation is because in multi-rate models all processes contribute equally to the motor output at all times. This is fundamentally different from the expression and updating of multiple context-specific memories in the COIN model, which are dynamically modulated over time according to ongoing contextual inference. e, Evoked recovery does not decay exponentially to zero. According to the COIN model, adaptation in the channel-trial phase of evoked recovery can be approximated by exponential decay to a non-zero (i.e. positive) asymptote (a-c, Fig. 2e, Suppl. Inf.). To test this prediction, we fit an exponential function that either decays to zero (light and dark green) or decays to a non-zero (constrained to be positive) asymptote (cyan) to the adaptation data of individual participants in the evoked recovery group after the two P+ trials (black arrow). The two zero-asymptote models differ in terms of whether they are constrained to pass through the datum on the first (channel) trial (light green) or not (dark green). The mean fits across participants for the models that decay to zero (green) fail to track the mean adaptation (black, ± SEM across participants), which shows an initial period of decay followed by a period of little or no decay. The mean fit for the model that decays to a non-zero asymptote (cyan) tracks the mean adaptation well and was strongly favoured in model comparison (Δ group-level BIC of 944.3 and 437.7 nats compared to the zero-asymptote fits with constrained and unconstrained initial values, respectively). Note that fitting to individual participants excludes the confound of finding a more complex time course (e.g. one with non-zero asymptote) only due to averaging across participants that each show a different simple time course (e.g. all with zero asymptote but different time constants). f, COIN and dual-rate model fits for individual participants in the spontaneous and evoked recovery groups. Data and model predictions are shown for individual participants as in Fig. 2c and e for across-participant averages. Participants in the S and E groups are ordered by decreasing BIC difference between the dual-rate and COIN model (i.e. S1’s and E1’s data most favour the COIN model), as in insets of Fig. 2c and e. Note that the COIN model can account for much of the heterogeneity of spontaneous (e.g. from large in S1 to minimal in S6) and evoked recovery (e.g. from large in E1 to minimal in E7).
Extended Data Fig. 7 |. Additional analyses of memory updating experiment (related to Fig. 3). a-b, Memory updating experiment: time-course of learning.
a, Adaptation on channel trials at the end of each block of force-field trials in the training phase (purple), which occur before P0 washout trials, and on the first channel trial of triplets within each block (orange), which occurs after P0 washout trials. Data is mean ± SEM across participants and lines show mean of COIN model fits (8 parameters, Extended Data Fig. 3). b, Single-trial learning on triplets that were consistent with the training contingencies. Data (mean ± SEM across participants) with mean of COIN model fits across participants. Positive learning reflects changes in the direction expected based on the force field of the exposure trial (an increase following P+ and a decrease following P−). c-d, Mathematical analysis of single-trial learning. Single-trial learning in the COIN model (column 1) for the four cue-perturbation triplets in the pre-training phase (c) and the post-training phase (d) in the memory updating experiment. The COIN model was fit to each participant and model fits are shown as mean ± SEM (single-trial learning) or mean (dot product, posterior, prior and likelihood) across n = 24 participants. Single-trial learning (column 1) is approximately proportional to a dot product (column 2) between the vector of posterior context probabilities (responsibilities) on the exposure trial of the triplet and the vector of predicted context probabilities on the subsequent channel trial (see Suppl. Inf. for derivation). This dot product can be further approximated by collapsing the vector of predicted probabilities to a one-hot vector, i.e. by the responsibility p(ct = c∗|qt, yt,…) (column 3) of the context that is predominantly expressed on the subsequent channel trial (c∗, the context with the highest predicted probability), where … denotes all observations before time t (as in Fig. 1). This responsibility is proportional to a product of two terms. The first term is the prior context probability p(ct = c∗|qt,…) (column 4), i.e. the predicted context probability before experiencing the perturbation (as in Fig. 1f1), which is already conditioned on the sensory cue visible from the outset of the trial. The second term expresses the likelihood of the state feedback in that context p(yt|ct = c∗,…) (column 5). As prior to learning neither cues nor feedback are yet consistently associated with a particular context, the COIN model predicts that the prior and likelihood, and thus total single-trial learning should all be largely uniform across contexts before training. e-f, The effects of cue and perturbation on single-trial learning in individual participants. e, Single-trial learning (post-training) shown as a function of perturbation separated by cue (left) or as a function of cue separated by perturbation (right) for each participant (lines). Note a significant effect for both the perturbation and the cue. f, Scatter plot of cue effect against perturbation effect for each participant (dots). Solid lines show medians of corresponding effects. Note the lack of anti-correlation between two effects.
Extended Data Fig. 8 |. Additional analysis of the effect of environmental consistency on single-trial learning related to Fig. 4c.
Columns 1 & 2: experimental paradigm and data replotted from Ref. 5. Participants experienced repeating cycles of P+ trials of varying lengths (column 1: 20 P+ trials in P20, 7 in P7, 1 in P1 and 1 followed by 1 P− trial in P1N1) in between P0 trials. To assess single-trial learning (column 2) during exposure to the environments, channel trials were randomly interspersed before and after the first P+ trial in a subset of the force-field cycles. Columns 3 to 5 show the output and internal inferences of the COIN model in the same format as Fig. 4c (same parameters as in Fig. 4; Extended Data Fig. 3, parameter set S, E & M). The COIN model qualitatively reproduced the pattern of changes in single-trial learning seen over repeated cycles in this paradigm. As in Fig. 4, differences in the apparent learning rate were not driven by differences in either the proper learning rate (Kalman gain) or the underlying state (column 4) but were instead driven by changes in contextual inference (column 5).
Extended Data Fig. 9 |. Cognitive processes and the COIN model. a-d, Maintenance of context probabilities may require working memory.
a, Adaptation in a spontaneous recovery paradigm in which a non-memory (pink) or working memory task (green) is performed at the end of the P− phase before starting the channel-trial phase (data reproduced from Ref. 22). Initial adaptation in the channel-trial phase (inset) shows the working memory task abolishes spontaneous recovery and leads to adaptation akin to evoked recovery (cf. Extended Data Fig. 6a–c). b-d, COIN model simulation in which the working memory task abolishes the (working) memory of the context responsibilities on the last trial of the P− phase but not the context transition (and thus stationary) probabilities (same parameters as in Fig. 2b and d; Extended Data Fig. 3, parameter set A), plotted as in Fig. 2b–c. The circles on the predicted probability (zoomed view) show the values on the first trial in the channel-trial phase. d, as (c) but for the working memory task. The predicted probabilities on the first trial in the channel-trial phase are the values under the stationary distribution (shown on every trial in the simulation of Extended Data Fig. 1c). We calculate the stationary context distribution by solving for ψ (a row vector) subject to the constraint that ψ is a valid probability distribution (i.e. all elements of ψ are non-negative and sum to 1), where .is the expected local transition probability matrix. e-l, Explicit versus implicit learning in the COIN model. e, Results of a spontaneous recovery paradigm (as in Fig. 2b) for visuomotor learning. Adaptation is computed as participants’ reach angle normalised by the size of the experimentally imposed visuomotor rotation. Explicit learning (dark green) is measured by participants indicating their intended reach direction. Implicit learning (light green) is obtained as the difference between total adaptation (solid pink) and explicit learning. In the visual error-clamp phase (Pc), participants were told to stop using any aiming strategy so that the direction they moved was taken as the implicit component of learning. A control experiment (dashed pink) was also performed in which there was no reporting of intended reach direction. Data reproduced from Ref. 24. f-l, Simulation of the COIN model on the same paradigm (same parameters as in Fig. 2b and d but with the addition of a bias parameter; Extended Data Fig. 3, parameter set A). b, Predictions for experimentally observable quantities. Light green line: implicit learning is the average bias across contexts weighted by the predicted probabilities (cyan line in j). Dark green line: explicit learning is the state of the most responsible context on the previous trial (black line in h). Solid pink line: total adaptation for the reporting condition is the sum of explicit and implicit learning (as in experiments). Dashed pink line: total adaptation for the non-reporting condition is the average predicted state feedback across contexts weighted by the predicted probabilities (cyan line in l, as in all experiments that had no reporting element). g-h, Inferred bias (g) and predicted state (h) distributions for each context (colours), with black line showing the mean state of the most responsible context (coloured line below axis) for trials on which an explicit report was solicited. i, Predicted probability of each context. Colours as in g-h, grey is novel context as in Fig. 1f. j-k, Inferred bias (j) and predicted state (k) distributions (purple), obtained as mixtures of the respective distributions of individual contexts (g-h) weighted by their predicted probabilities (i), and their means (cyan lines). l, Predicted state feedback distribution (purple, computed as the the sum of bias, j, and predicted state, k) and its mean (cyan).
Extended Data Table 1 |. Comparison of the COIN model to other models.
Table shows which experimental phenomena (rows) can be explained by different single and multiple-context models (columns). Alphabetical superscripts index the key feature(s) missing from each model which are primarily responsible for their inability to explain a particular phenomenon. Note that we consider each model as described and implemented by its authors (although it might be possible to modify or extend these models to explain more features). Orange cross-ticks are for models that can partially explain a phenomenon.
| single-context models | multiple-context models | ||||||
|---|---|---|---|---|---|---|---|
| dual-rate Smith et al. 1 |
memory of errors Herzfeld et al. 4 |
source of errors Berniker & Körding 16 |
winner-take-all Oh & Schweighofer 11 |
DP-KF Gershman et al. 12 |
MOSAIC Haruno et al. 26 |
COIN | |
| spontaneous recovery | ✔ | ✘ a | ✘ b | ✘ b | ✘ c | ✘ d | ✔ |
| evoked recovery | ✘ e | ✘ e |
 f
f
|
 f
f
|
 f
f
|
✘ d | ✔ |
| memory updating | ✘ g | ✘ g | ✘ g | ✘ h | ✘ g,h | ✔ | ✔ |
| savings after full washout | ✘ i | ✔ | ✔ | ✔ | ✔ | ✔ | ✔ |
| anterograde interference | ✔ | ✘ a | ✘ b | ✘ b | ✔ | ✘ j | ✔ |
| environmental consistency | ✘ i | ✔ | ✘ b | ✘ b | ✘ k | ✔ | ✔ |
| explicit/implicit learning |
 m
m
|
✘ l | ✘ l | ✘ l | ✘ l | ✘ l | ✔ |
Spontaneous recovery, the gradual re-expression of P+ in the channel-trial phase (Fig. 2c), requires a single-context model to have multiple states that decay on different time scales or a multiple-context model that can change the expression of memories in a gradual manner based on the amount of experience with each context. Therefore, single-context models that have a single statea, or multiple-context models that do not learn context transition probabilitiesb or do not have state dynamicsd do not show spontaneous recovery. Models that learn transition probabilities but that do not represent uncertainty about the previous contextc (the ‘local’ approximation in DP-KF) can either include a self-transition bias or not. With a self-transition bias, the expression of memories changes in an abrupt manner (akin to evoked recovery) when, in the channel-trial phase, the belief about the previous context changes (e.g. from P− to P+), and thus such models fail to explain the gradual nature of spontaneous recovery. Without a self-transition bias, the change in expression of memories is gradual based on updated context counts, but this occurs too slowly relative to the time scale on which the rise of spontaneous recovery occurs.
Evoked recovery, the rapid re-expression of the memory of P+ in the channel-trial phase (Fig. 2e) that does not simply decay exponentially to baseline (Extended Data Fig. 6e), requires a model to be able to switch between different memories based on state feedback. Therefore, single-context modelse that cannot switch between memories are unable to show the evoked recovery pattern seen in the data. Multiple-context models with memories that decay exponentially to zero in the absence of observationsf (as during channel trials) can only partially explain evoked recovery, showing the initial evocation but not the subsequent change in adaptation over the channel-trial phase. Models with no state decayd cannot explain evoked recovery.
Memory updating requires a model to update memories in a graded fashion and to use sensory cues to compute these graded updates. Therefore, models that either have no concept of sensory cuesg or multiple-context models that only update the state of the most probable context in an all-or-none mannerh do not show graded memory updating.
Savings, faster learning during re-exposure compared to initial exposure, after full washout requires a single-context model to increase its learning rate or a multiple-context model to protect its memories from washout and/or learn context transition probabilities. Therefore, single-context models with fixed learning ratesi do not show savings.
Anterograde interference, increasing exposure to P+ leads to slower subsequent adaptation to P−, requires a single-context model to learn on multiple time scales or a multiple-context model to learn transition probabilities that generalise across contexts. Therefore, single-context models with a single statea, or multiple-context models that either do not learn transition probabilitiesb or that learn local transition probabilities independently for each row of the transition probability matrixj do not show anterograde interference.
Environmental consistency, the increase/decrease in single-trial learning for slowly/rapidly switching environments, requires a model to either adapt its learning rate or learn local transition probabilities based on context transition counts. Therefore, single-context models with fixed learning ratesi or multiple-context models that either do not learn transition probabilitiesb or that learn non-local transition probabilities based only on context countsk do not show the effects of environmental consistency on single-trial learning.
Explicit and implicit learning, the decomposition of visuomotor learning into explicit and implicit components, requires a model to have elements that can be mapped onto these components. For most models, there is no clear way to map model elements onto these componentsl. It has been suggested that the fast and slow processes of the dual-rate model correspond to the explicit and implicit components of learning, respectively. However, in a spontaneous recovery paradigm, this mapping only holds during initial exposure and fails to account for the time course of the implicit component during the counter-exposure and channel-trial phasesm (see Suppl. Inf.).
Supplementary Material
Acknowledgements
This work was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 726090 to M.L.), the Wellcome Trust (Investigator Awards 212262/Z/18/Z to M.L. and 097803/Z/11/Z to D.M.W.), Royal Society (Noreen Murray Professorship in Neurobiology to D.M.W), National Institutes of Health (R01NS117699 and U19NS104649 to D.M.W. ) and Engineering and Physical Sciences Research Council (studentship to J.B.H). For the purpose of open access, the authors have applied a CC-BY public copyright licence to any author accepted manuscript version arising from this submission. We thank J. Ingram for technical support and G. Hennequin for discussions.
Footnotes
Competing interests
The authors have no competing interests.
References
- 1.Smith MA, Ghazizadeh A & Shadmehr R Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol. 4, e179 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kitago T, Ryan S, Mazzoni P, Krakauer JW & Haith AM Unlearning versus savings in visuomotor adaptation: comparing effects of washout, passage of time, and removal of errors on motor memory. Front. Hum. Neurosci. 7, 307 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sing GC & Smith MA Reduction in learning rates associated with anterograde interference results from interactions between different timescales in motor adaptation. PLoS Comput. Biol. 6, e1000893 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Herzfeld DJ, Vaswani PA, Marko MK & Shadmehr R A memory of errors in sensorimotor learning. Science 345, 1349–1353 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gonzalez Castro LN, Hadjiosif AM, Hemphill MA & Smith MA Environmental consistency determines the rate of motor adaptation. Curr. Biol. 24, 1050–1061 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mcdougle SD et al. Credit assignment in movement-dependent reinforcement learning. Proc. Natl. Acad. Sci. 113, 6797–6802 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Donchin O, Francis JT & Shadmehr R Quantifying generalization from trial-by-trial behavior of adaptive systems that learn with basis functions: theory and experiments in human motor control. J. Neurosci. 23, 9032–9045 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thoroughman KA & Shadmehr R Learning of action through adaptive combination of motor primitives. Nature 407, 742–747 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shadmehr R, Smith MA & Krakauer JW Error correction, sensory prediction, and adaptation in motor control. Ann. Rev. Neurosci. 33, 89–108 (2010). [DOI] [PubMed] [Google Scholar]
- 10.Wolpert DM & Kawato M Multiple paired forward and inverse models for motor control. Neural Netw. 11, 1317–1329 (1998). [DOI] [PubMed] [Google Scholar]
- 11.Oh Y & Schweighofer N Minimizing precision-weighted sensory prediction errors via memory formation and switching in motor adaptation. J. Neurosci. 9237–9250 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gershman SJ, Radulescu A, Norman KA & Niv Y Statistical computations underlying the dynamics of memory updating. PLoS Comput. Biol. 10, e1003939 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hulst T et al. Cerebellar degeneration reduces memory resilience after extended training. bioRxiv (2020). [Google Scholar]
- 14.Pekny SE, Criscimagna-Hemminger SE & Shadmehr R Protection and expression of human motor memories. J. Neurosci. 31, 13829–13839 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rescorla RA & Heth CD Reinstatement of fear to an extinguished conditioned stimulus. J. Exp. Psychol.: Animal Behavior Processes 1, 88–96 (1975). [PubMed] [Google Scholar]
- 16.Berniker M & Körding K Estimating the sources of motor errors for adaptation and generalization. Nat. Neurosci. 11, 1454–1461 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Taylor JA, Wojaczynski GJ & Ivry RB Trial-by-trial analysis of intermanual transfer during visuomotor adaptation. J. Neurophysiol. 106, 3157–3172 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Körding KP, Tenenbaum JB & Shadmehr R The dynamics of memory as a consequence of optimal adaptation to a changing body. Nat. Neurosci. 10, 779–786 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Heald JB, Ingram JN, Flanagan JR & Wolpert DM Multiple motor memories are learned to control different points on a tool. Nat. Hum. Behav. 2, 300–311 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Coltman SK, Cashaback JGA & Gribble PL Both fast and slow learning processes contribute to savings following sensorimotor adaptation. J. Neurophysiol. 121, 1575–1583 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huang VS, Haith A, Mazzoni P & Krakauer JW Rethinking motor learning and savings in adaptation paradigms: model-free memory for successful actions combines with internal models. Neuron 70, 787–801 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Keisler A & Shadmehr R A shared resource between declarative memory and motor memory. J. Neurosci. 30, 14817–14823 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mcdougle SD, Ivry RB & Taylor JA Taking aim at the cognitive side of learning in sensorimotor adaptation tasks. Trends Cogn. Sci. 20, 535–544 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McDougle SD, Bond KM & Taylor JA Explicit and implicit processes constitute the fast and slow processes of sensorimotor learning. J. Neurosci. 35, 9568–9579 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Miyamoto YR, Wang S & Smith MA Implicit adaptation compensates for erratic explicit strategy in human motor learning. Nat. Neurosci. 23, 443–455 (2020). [DOI] [PubMed] [Google Scholar]
- 26.Haruno M, Wolpert DM & Kawato M MOSAIC model for sensorimotor learning and control. Neural Comput. 13, 2201–2220 (2001). [DOI] [PubMed] [Google Scholar]
- 27.Gershman SJ, Blei DM & Niv Y Context, learning, and extinction. Psychol. Rev. 117, 197–209 (2010). [DOI] [PubMed] [Google Scholar]
- 28.Sanders H, Wilson MA & Gershman SJ Hippocampal remapping as hidden state inference. eLife 9, e51140 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Collins A & Koechlin E Reasoning, learning, and creativity: frontal lobe function and human decision-making. PLoS Biol. 10, e1001293 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Collins AGE & Frank MJ Cognitive control over learning: creating, clustering, and generalizing task-set structure. Psychol. Rev. 120, 190–229 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Howard IS, Ingram JN & Wolpert DM A modular planar robotic manipulandum with end-point torque control. J. Neurosci. Methods 181, 199–211 (2009). [DOI] [PubMed] [Google Scholar]
- 32.Milner TE & Franklin DW Impedance control and internal model use during the initial stage of adaptation to novel dynamics in humans. J. Physiol. 567, 651–664 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Scheidt RA, Reinkensmeyer DJ, Conditt MA, Rymer WZ & Mussa-Ivaldi FA Persistence of motor adaptation during constrained, multi-joint, arm movements. J. Neurophysiol. 84, 853–862 (2000). [DOI] [PubMed] [Google Scholar]
- 34.Teh YW, Jordan MI, Beal MJ & Blei DM Hierarchical Dirichlet processes. J. Amer. Stat. Assoc. 101, 1566–1581 (2006). [Google Scholar]
- 35.Fox EB, Sudderth EB, Jordan MI & Willsky AS An HDP-HMM for systems with state persistence. In Proc. 25th Int. Conf. Machine Learning, 312–319 (2008). [Google Scholar]
- 36.Teh YW Dirichlet processes. In Encyclopedia of Machine Learning (Springer, 2010). [Google Scholar]
- 37.Carvalho CM, Johannes MS, Lopes HF & Polson NG Particle learning and smoothing. Stat. Sci. 25, 88–106 (2010). [Google Scholar]
- 38.Bernardo J et al. Particle learning for sequential Bayesian computation. Bayesian Statistics 9 9, 317 (2011). [Google Scholar]
- 39.Houlsby N et al. Cognitive tomography reveals complex, task-independent mental representations. Curr. Biol. 23, 2169–2175 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Acerbi L & Ji W Practical Bayesian optimization for model fitting with bayesian adaptive direct search. In Adv. Neural Inf. Proc. Sys., 1836–1846 (2017). [Google Scholar]
- 41.Jeffreys H The theory of probability (OUP Oxford, 1998). [Google Scholar]
- 42.Li J, Wang ZJ, Palmer SJ & McKeown MJ Dynamic Bayesian network modeling of fMRI: a comparison of group-analysis methods. Neuroimage 41, 398–407 (2008). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All experimental data are publically available at the Dryad repository (https://doi.org/10.5061/dryad.m63xsj42r). The data include the raw kinematics and force profiles of individual participants on all trials as well as the adaptation measures used to generate the experimental data shown in Fig. 2c,e and Fig. 3d.