The Learning of Prospective and Retrospective Cognitive Maps Within Neural Circuits

Abstract

Brain circuits are thought to form a “cognitive map” to process and store statistical relationships in the environment. A cognitive map is commonly defined as a mental representation that describes environmental states (i.e., variables or events) and the relationship between these states. This process is commonly conceptualized as a prospective process, as it is based on the relationships between states in chronological order (e.g., does reward follow a given state?). In this perspective, we expand this concept based on recent findings to postulate that in addition to a prospective map, the brain forms and uses a retrospective cognitive map (e.g., does a given state precede reward?). In doing so, we demonstrate that many neural signals and behaviors (e.g., habits) that seem inflexible and non-cognitive can result from retrospective cognitive maps. Together, we present a significant conceptual reframing of the neurobiological study of associative learning, memory, and decision-making.

It has long been recognized that animals, even insects, build internal models of their environment (Abramson, 2009; Chittka et al., 2019; Fleischmann et al., 2017; Giurfa, 2015; Webb, 2012; Wehner and Lanfranconi, 1981). For instance, in early 20^th century, Charles H Turner summarized his work on homing (ability of animals to return to an original location after a navigational bout) by stating that “After studying the subject from all possible angles, the conviction has been reached that neither the creeping ant, nor the flying bee, nor the hunting wasp is guided home by a mysterious homing instinct, or a combination of tropisms, or solely by muscular memory, but by something which each acquires by experience (Turner, 1923).” Perhaps the most striking example of such learning is found in Nobel prize winning work on honeybees. Honeybee foragers can return to the hive after outward journeys of tens of kilometers and can communicate the coordinates of the locations they visited to their nest mates using a symbolic waggle dance (Chittka et al., 1995; Dyer et al., 2008; von Frisch, 1967; Menzel et al., 2011). In work that is perhaps more familiar to neuroscientists, Edward Tolman showed that rats exposed to a maze without rewards can later flexibly take shortcuts in that maze to a reward or infer new paths when old ones were blocked (Tolman and Honzik, 1930; Tolman et al., 1946) (also shown earlier by (Hsiao, 1929)). These examples show that animals learn a spatial “cognitive map” of their environment (Tolman, 1948). In addition to spatial maps, animals (including humans) can also build cognitive maps for non-spatial information, by remembering a map of the sequence of events in their world (Aronov et al., 2017; Barron et al., 2020; Knudsen and Wallis, 2020; Theves et al., 2019). Brain regions such as the orbitofrontal cortex (OFC) and hippocampus represent such cognitive maps along space and time (Barron et al., 2020; Behrens et al., 2018; Eichenbaum, 2013, 2017; Ekstrom and Ranganath, 2018; Epstein et al., 2017; MacDonald et al., 2011; Manns and Eichenbaum, 2009; McNaughton et al., 2006; O’keefe and Nadel, 1978; O’Reilly and Rudy, 2001; Solomon et al., 2019; Spiers, 2020; Stachenfeld et al., 2017; Umbach et al., 2020; Whittington et al., 2020; Wikenheiser and Schoenbaum, 2016; Wilson et al., 2014). Prior work has primarily focused on cognitive maps for predicting future events (i.e., a prospective cognitive map).

In this perspective, we extend this framework in a significant new direction to propose that animals build both prospective and retrospective cognitive maps. We will illustrate the core intuition for a retrospective cognitive map using a simple example. Say that a reward is always preceded by a certain cue/action, but the cue/action is only followed by reward with a 10% probability. Here, the prospective relationship between the cue/action and the upcoming reward is very weak due to the low likelihood of reward. On the other hand, the retrospective relationship is perfect (100% of rewards are preceded by the cue/action). Thus, prospective and retrospective relationships are different and likely have distinct functions. Prospective reward expectation is especially useful for decisions. However, retrospective relationships are especially useful for learning: they help connect rare rewards to preceding cues/actions. Loosely, the prospective relationship measures whether the cue/action is sufficient for reward, but the retrospective relationship measures whether the cue/action is necessary for reward. When both relationships are perfect, the reward can only be obtained following the cue/action. In this perspective, we will build on this core intuition to formally define prospective and retrospective cognitive maps, discuss why they are both useful, and present behavioral and neural evidence supporting the existence of retrospective cognitive maps. Importantly, we will demonstrate that even behaviors that are commonly thought to be non-cognitive are nevertheless understandable as resulting from the interaction of prospective and retrospective cognitive maps. We will now first develop a formal definition of a cognitive map.

Cognitive maps and reinforcement learning

The most essential goal of animals is to obtain rewards such as food, water, or sex and to avoid punishments such as injury or death due to a predator. Hence, it follows that the sustained fitness of animals depends on predicting rewards and punishments. The process by which animals learn to predict rewards or punishments is studied in neuroscience using the mathematical theory of reinforcement learning. In keeping with RL theories, we will refer to “reward” as a general term for both rewards and punishments (Sutton and Barto, 2018). This is for the sake of brevity. While mathematical formalisms of RL first developed from theories in psychology (Rescorla and Wagner, 1972; Sutton and Barto, 2018), it was quickly adapted to computer science and showed great promise in solving real-world applications (e.g. Tesauro, 1995). The core algorithmic principle of RL is simple: keep updating one’s prediction of the world whenever there is a prediction error, i.e. if the prediction does not match reality (Sutton and Barto, 2018). The field of RL in neuroscience exploded following the discovery that the activity patterns of midbrain dopaminergic neurons resemble a reward prediction error signal (Schultz et al., 1997). This early discovery was explained by a rather simple form of RL — model-free RL

In model-free RL, the subjects’ goal is assumed to be to learn and memorize the value of being in any “state” based on possible future rewards. A state is defined as an abstract representation of a task, such that the structure of a task is the relationship between its various states (Niv, 2009; Sutton and Barto, 2018). For instance, in a simple Pavlovian task in which the presentation of a cue predicts a reward, both the cue and reward can be states, and the structure of the task may be that a cue is followed by a reward. The expected future value (or state value) of a state is defined as the sum of all possible future rewards from the state, discounted by how far in the future the rewards occur (to weigh sooner rewards higher than later rewards). In model-free RL, the animal only stores the values of each state in memory and does not store other statistical relationships between the states in memory.

The examples laid out in the introduction show that model-free RL is too simplistic of a view to fully describe animal learning. At the other extreme of the RL spectrum lies model-based RL (Box 1). In model-based RL, animals learn and remember not just the value of a state, but also the relationships between the various states in the environment (Daw et al., 2005; Sutton and Barto, 2018). The set of relationships between states, i.e., a model of the world, is mathematically formalized as a transition matrix. The transition matrix is the set of probabilities for transitioning in the next step from any given state to all possible states based on the action you perform (Sutton and Barto, 2018). Note that this transition matrix describes a one-step look ahead from any given state and tells you the probability that the immediate next state will be a given state. Multi-step look ahead requires repeated multiplication of the current state vector with this transition matrix. Thus, the “distance” between states can be estimated by the number of transitions required to move from one to the other. Such distance can either be in abstract state space, or time in continuous time models (Daw et al., 2006; Namboodiri, 2021).

Box 1: Model-free versus model-based reinforcement learning.

Numerous prior publications have highlighted the differences between model-free and model-based RL (e.g. Collins and Cockburn, 2020; Daw et al., 2005; Doll et al., 2012; Niv, 2009; Sutton and Barto, 2018). Given their importance for this perspective, we quickly summarize these differences here. In most conceptions of RL, the goal of the learning agent is to learn an estimate of future value for any given state of the world. Future value is commonly defined such that it obeys a convenient mathematical rule. Specifically, value of a given state can be written recursively as the expected reward for the given state plus the discounting factor multiplied by the value of the next state (Sutton and Barto, 2018). The key insight in model-free RL is that this recursive relationship allows value to be learned for each state by 1) only storing value in memory (and not other properties such as the probability or magnitude of rewards), and 2) local application of an error-rule at each time step. The purpose of this error rule is to get the value estimate closer and closer to obeying the recursive relationship.

In contrast, a model-based learning agent adopts a different strategy to learn value. Such an agent learns the transition matrix of the world (i.e., the set of probabilities of transitioning from any state to any other state), and separately learns the immediate expected reward for each state. Given these two pieces of information, the model-based agent calculates an estimate of value at decision time. This difference between model-based and model-free learning can be illustrated by considering what happens when the reward magnitude of a state changes in the environment. Since a model-free learning agent only stores the value estimates of all states in memory, it needs to relearn value using slow, local updates. On the other hand, a model-based agent can rapidly recalculate values of all states by simply updating the expected reward for the state that changed. Despite this flexibility of updating, the computational cost of estimating value at decision time is a lot higher for the model-based agent, as it does not store the decision variable (i.e., value) in memory like a model-free agent.

Due to the much larger representational richness and adaptive flexibility of model-based RL, model-based RL, but not model-free RL, is commonly considered to be cognitive learning. Nevertheless, we will show later in this perspective that even apparently inflexible, model-free-like behaviors may result from the use of cognitive maps.

This framework provides a formal notion of a cognitive map: in its most basic form, a cognitive map is a mental representation that describes the states in one’s environment and the transition rules between these states (Behrens et al., 2018; Wilson et al., 2014). A model-based value estimate is then defined as the sum of the reward associated with the current state and the discounted sum of value of the next states multiplied by the probability of transitioning to those states. Over the course of model-based RL, the goal of the agent is to iteratively improve its estimate of state values by enforcing consistency of the value estimate between adjacent states (Sutton and Barto, 2018). For further discussion of model-based RL versus model-free RL, see (Doll et al., 2012; Sutton and Barto, 2018).

Once a cognitive map is committed to memory by learning the set of states and the transition matrix between these states, it is possible to build a more complex representation of the world using these states. For instance, if there are two cues in a task and only one cue is paired with reward at any moment, animals can learn that the transition probabilities to reward from the cues are not independent, but sum up to 1 (Harlow, 1949). Thus, the cognitive map view of learning that we consider here proposes that animals learn about states in their world (including reward states, e.g. (Stalnaker et al., 2014; Takahashi et al., 2017)) and the transition probabilities between them, followed by additional properties of these states and transitions, such as temporal or spatial distances, sensory properties of the states (e.g. magnitude of reward associated with a reward state), or more abstract rules. Overall, the above view of a cognitive map ascribes a much more complex representational ability to animals than model-free RL. In the next section, we will critically examine an implicit assumption in the above presentation of the cognitive map framework.

Prospective and retrospective cognitive maps

So far, we have assumed, just like prior work, that the cognitive map is prospective. In other words, in assessing the relationships between states, the transition matrix is assumed to be calculated looking forward in time (i.e. what is the probability that state B follows state A?). However, statistical relations between two events—say a cue or an action predicting a reward, and the reward—can be both prospective and retrospective (Figure 1). We will mathematically describe the corresponding prospective cognitive map by the probability that a reward follows a cue (denoted symbolically by p(state_next=reward | state_current=cue) or p(cue→reward), i.e. a conditional probability, Box 2). Similarly, the retrospective cognitive map is defined by the probability that a cue precedes a reward (denoted symbolically by p(state_current=cue | state_next=reward) or p(cue←reward)).

Figure 1:

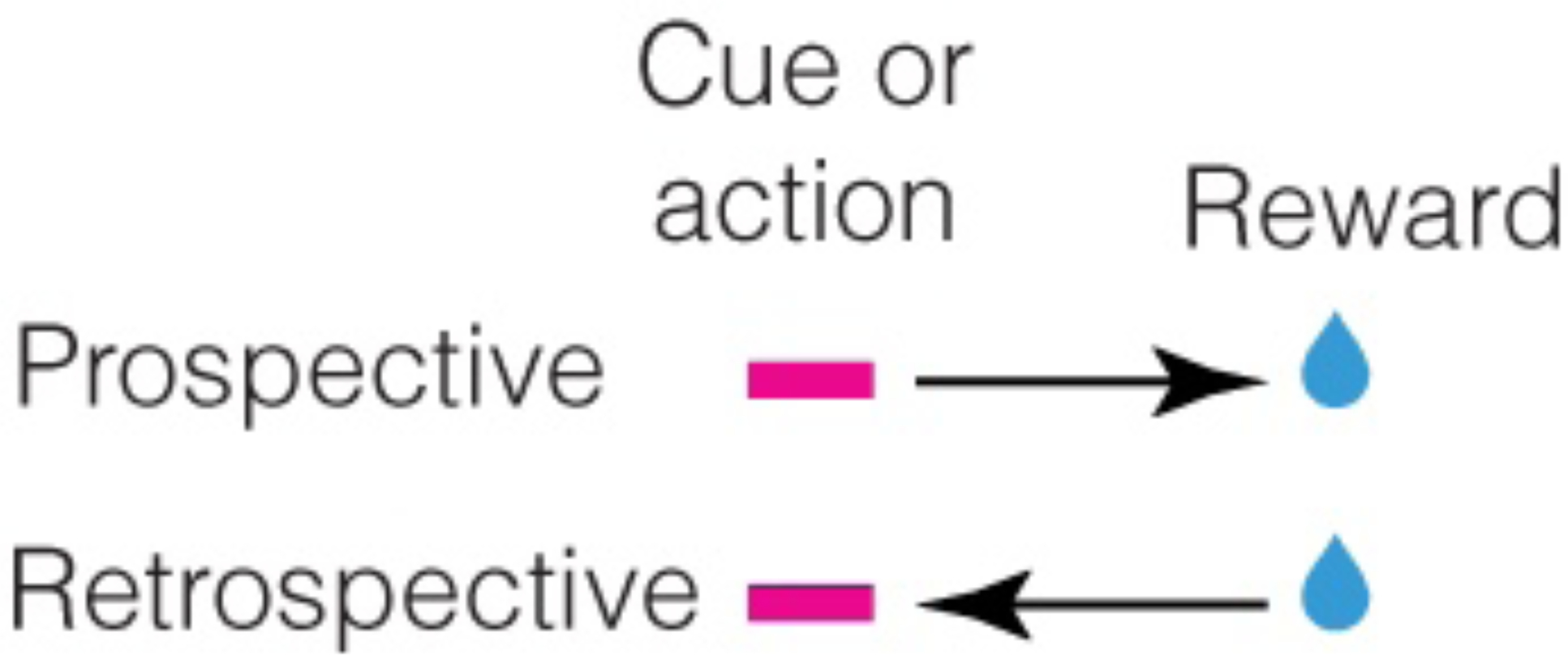
The causal relationship between reward predictors and rewards may be learned prospectively or retrospectively.

Box 2: Conditional probability, marginal probability, Bayes’ rule, and chain rule.

Here, we give a quick primer on probability. Intuitively, the probability of an event is defined as the ratio of the number of times that event occurs divided by the number of times any event occurs. Probability is thus a value between 0 and 1. When there are multiple types of events (denoted by A and B, say), then different types of probabilities can be defined. Conditional probability is the probability that one event occurs given that another event has occurred. Conditional probability is denoted by p(A|B) or p(B|A). These are read as the probability of event A given that event B has occurred or vice-versa. Another important measure of probability is the marginal probability. Marginal probability is simply the probability of either event happening and can be denoted by p(A) or p(B). For example, the conditional probability of someone being ill given that they are coughing is very high, but the marginal probability of someone being ill is low since most people are not sick. In general, p(A|B)≠p(B|A). For instance, the probability of someone being ill given that they are coughing is not the same as the probability that someone is coughing given that they are ill, as not all illnesses result in coughing. The marginal probability can be expressed in terms of the conditional probability as p(A)=p(A|B)p(B)+p(A|~B)p(~B), where ~B signifies that event B did not happen. Since event B can either happen or not happen, p(B)+p(~B)=1. Based on these relations, one can see that when the conditional probability (say p(A|B)) equals the marginal probability (p(A)), the event A does not depend on B as p(A|B)=p(A|~B). In other words, events A and B are statistically independent. For instance, the probability that someone is ill given that their favorite color is blue is practically the same as the probability that someone is ill, since knowing that someone’s favorite color is blue gives no information about whether they are likely to be ill.

Lastly, the joint probability is the probability of multiple events happening simultaneously. So, p(A,B), the joint probability of A and B, is the probability of both event A and event B occurring. This can be calculated by multiplying the probability that event B occurred (i.e. the marginal probability of event B occurring) and the conditional probability of event A occurring conditioned on event B occurring. Mathematically, p(A,B)=p(A|B)p(B). Similarly, p(B,A)=p(B|A)p(A). Since p(A,B)=p(B,A), i.e. the probability of event A and B occurring is the same as the probability of event B and A occurring, we get that p(A|B)p(B)=p(B|A)p(A). This relation is perhaps one of the most important rules in probability and is known as Bayes’ rule after Reverend Thomas Bayes. Written differently, we can express the conditional probability of A on B in terms of the conditional probability of B on A and the marginal probabilities by

$$p(A\mid B)=p(B\mid A)\frac{p(A)}{p(B)}$$

The joint probability can also be calculated for more than two events. For instance, the joint probability of events A, B and C can be thought of as the probability of C happening, and B happening given that C happened, and A happening given that both B and C happened. Mathematically, p(A,B,C)=p(A|B,C)p(B|C)p(C). Here, p(A|B,C) is the probability of A conditional on both B and C having occurred. This relationship is known as the chain rule of probability.

Importantly, prospective and retrospective transition probabilities are generally not the same (Figure 2). For instance, if the cue is followed by reward only 50% of the time, the reward is still preceded by the cue 100% of the time. Thus, in this case, the prospective association, i.e. p(cue→reward), is only half as strong as the retrospective association (p(cue←reward)). On the other hand, if the cue is followed by the reward 100% of the time but the reward is also available without the cue, the prospective association (p(cue→reward)) is stronger than the retrospective one (p(cue←reward)). Prospective and retrospective associations are therefore not identical. Hence, robust representations of causal relationships in the environment likely require representation of both prospective and retrospective associations. The central thesis of this perspective is that animals build a cognitive map of not only prospective associations, but also retrospective associations.

Figure 2:

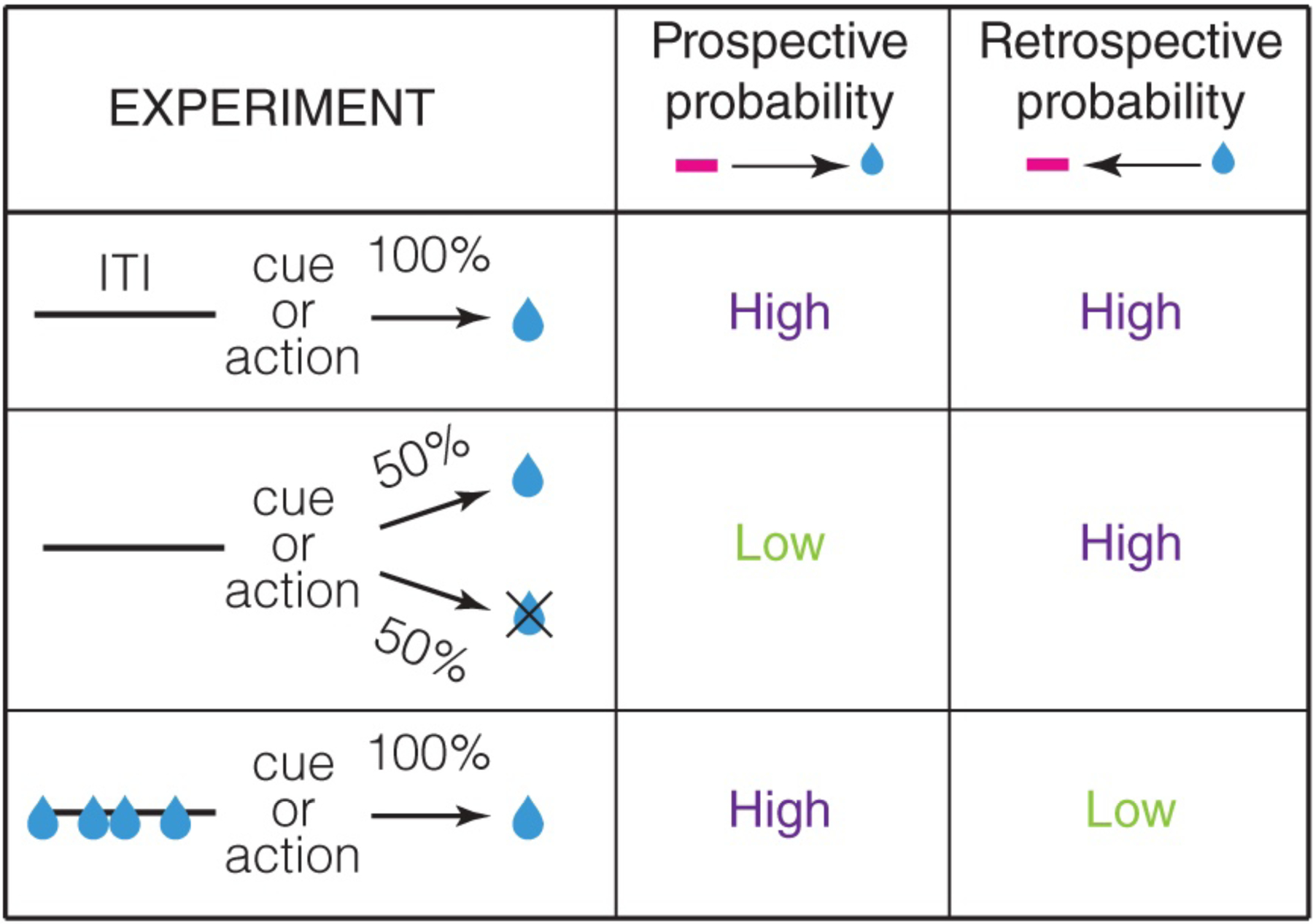
Schematic experiments illustrating prospective and retrospective transition probabilities. In the top experiment, there is a high prospective and retrospective probability between the reward predictor and reward. ITI stands for intertrial interval, i.e. the duration between a reward and the next reward predictor. In the middle experiment, the prospective probability is low since cue/action predicts reward only 50% of the time. However, retrospective probability is high since every reward is preceded by the cue/action. In the bottom experiment, prospective probability is high, as every cue/action is followed by a reward, but the retrospective probability is low since not every reward is preceded by the cue/action.

Why build retrospective cognitive maps?

Why might an animal build a retrospective cognitive map? For decision-making, retrospective cognitive maps may appear to be without any utility since a decision-maker needs to predict the future consequence of their action. A clue for the utility of learning the retrospective transition probability is that the prospective transition probability can be mathematically calculated from the retrospective transition probability. This is due to the following Bayes’ relationship (Box 2) between the two

$$p(cue\to reward)=\frac{p(cue\leftarrow reward)p(reward)}{p(cue)}$$ (1)

Here, p(reward) represents the marginal probability of the next state being the reward state (i.e. probability of the next state being the reward state if you know nothing about the current state) and p(cue) represents the probability of the previous state being the cue state if you know nothing about the current state.

This relationship points to a major utility of the retrospective association, p(cue←reward). Animals continuously experience a near-infinite number of sensory cues. Each of these cues could in principle be paired with future rewards. Directly learning p(cue→reward) requires computing the ratio between the number of cue presentations followed by reward, and the total number of cue presentations. Thus, this computation must be updated upon every presentation of the cue, for each of the infinite possible cues in the world. On the other hand, learning the retrospective transition probability, which is conditional on reward receipt, requires updates only upon reward receipt. Since rewards are much sparser in the world compared to the set of cues that could in principle predict a reward, updates triggered off a reward will be much sparser than updates triggered off a cue. Thus, learning the retrospective transition probability is computationally more efficient due to the ethological sparsity of rewards. More generally, the utility of learning the prospective association between any two states A and B (i.e. p(A→B)) by Bayesian inversion of the retrospective association (p(A←B)) will depend on the relative sparsity of A and B. If A is much sparser than B, the animal would be better positioned by directly estimating the prospective probability p(A→B). If B is sparser, Bayesian inversion of the retrospective probability is computationally more efficient. Therefore, a decision-maker can compute the prospective transition probability from a learned estimate of the retrospective transition probability in an efficient manner.

In addition to the above benefit, retrospective cognitive maps can also help a decision-maker plan a complex path of states leading to a reward by planning both in the forward and backward direction (Afsardeir and Keramati, 2018; Pohl, Ira, 1971). Such backward planning can result in an increase in the depth of prospective planning, thereby aiding in complex decisions involving sequential states (Afsardeir and Keramati, 2018; Pohl, Ira, 1971). We will discuss additional benefits of retrospective cognitive maps later. Collectively, we will show that they are useful for both learning and decision-making.

Sequence of states: successor and “predecessor” representations

We will next consider how a cognitive map can be generalized to a sequence of states (Box 3). Wild foragers know all too well that rewards are often predicted not by a single environmental cue, but by a sequence of cues. For instance, foraging honeybees can learn the sequence of environmental landmarks leading up to a reward location (Chittka et al., 1995). To decide whether it is worth it to take a path, the bee must expect the future reward at the beginning of the path. How does such learning occur? In other words, how do animals learn that a state results in reward only much later in the future, and not after the next state transition?

Box 3: Multiple maps for the same task?

An intriguing consequence of a cognitive map framework is that a given sequential task might have different underlying maps. For instance, in learning a cue→action→reward task (i.e. animal has to perform an action after a cue (also known as a discriminative stimulus) to obtain reward), animals could learn distinct cognitive maps for the task. Learning this task requires the animal to learn p(reward|cue,action). This transition probability can be written in two equivalent ways using Bayes’ rule

$$p(reward\mid cue,action)=p(reward\mid cue)\frac{p(action\mid cue,reward)}{p(action\mid cue)}$$

Or

$$p(reward\mid cue,action)=p(reward\mid action)\frac{p(cue\mid action,reward)}{p(cue\mid action)}$$

These two equations are mathematically equivalent. But they have different internal maps. For instance, imagine that one animal was taught the full task by first training on a cue→reward task (i.e. reward follows cue) and subsequently training that the reward now requires the performance of an action following the cue. This animal would be better served using the first equation since it learned p(reward|cue) first. On the other hand, imagine a different animal that was first taught that performing the action results in reward and then taught that only actions performed after the cue result in reward. Using the second equation would be better for this animal. Thus, behavior in the exact same task could be driven by different cognitive maps, depending on the training history. In fact, an even more profound implication is that these strategies may develop even if the training histories were identical. If both animals were instead trained on the full task from the outset, they may still have learned distinct cognitive maps to solve the task. Thus, assessing the latent causes of behavior may be extremely challenging, as the same behavior may be driven by distinct sets of prospective and retrospective memories. This suggests that erasing maladaptively strong real-world memories (e.g., using extinction therapy (Craske and Mystkowski, 2006; Maren and Holmes, 2016)) requires targeted degradation of the specific prospective and retrospective memories acquired by an individual.

It is possible to expect the future reward by iteratively estimating the future sequence of states and checking whether any of them is the reward state. For example, upon seeing the first landmark in a journey, the foraging bee could iteratively estimate that reward will be available after ten more landmarks. Thus, one-step transition probabilities are in principle sufficient to predict the future. However, such a sequential calculation of all possible future paths from the current state is exceedingly tedious and practically impossible as a general solution for most real-world scenarios (Momennejad et al., 2017). Hence, it is very likely that animals have evolved some computationally simpler approximations for prospective planning.

In RL, a quantity called the successor representation (SR) provides such an approximation (Dayan, 1993; Momennejad et al., 2017; Russek et al., 2017). Essentially, the SR, expressed in a similar form as the transition matrix, measures how often the animal transitions from a given state to any other state and exponentially discounts the number of steps required for these transitions (Dayan, 1993; Gershman, 2018; Gershman et al., 2012; Momennejad et al., 2017) (exact formula shown in Supplementary Information; Appendix 1). The utility of such a representation is especially obvious when thinking about transitioning to reward states. Calculating the SR of a state to the reward state will give a measure of how likely it is for this state to result in reward at some point in the future. Since the number of steps to reward is discounted (to weigh sooner reward visits more than later ones), it is also related to the number of states you must wait on average to enter a reward state.

To illustrate the concept of SR, we will use an example state space (Figure 3A). In this state space, the likelihood of visiting the reward state after state 1 is very low, as it requires two transitions of 10% probability each. Thus, the SR of state 1 to reward is very low (Figure 3B). The SR of state 2 to reward is comparatively higher. Similarly, for the foraging bee, the first of ten landmarks on the way to a reward state will have a much lower SR value to the reward state than the last landmark, since the reward state requires more transitions from the first landmark than the last landmark.

Figure 3.

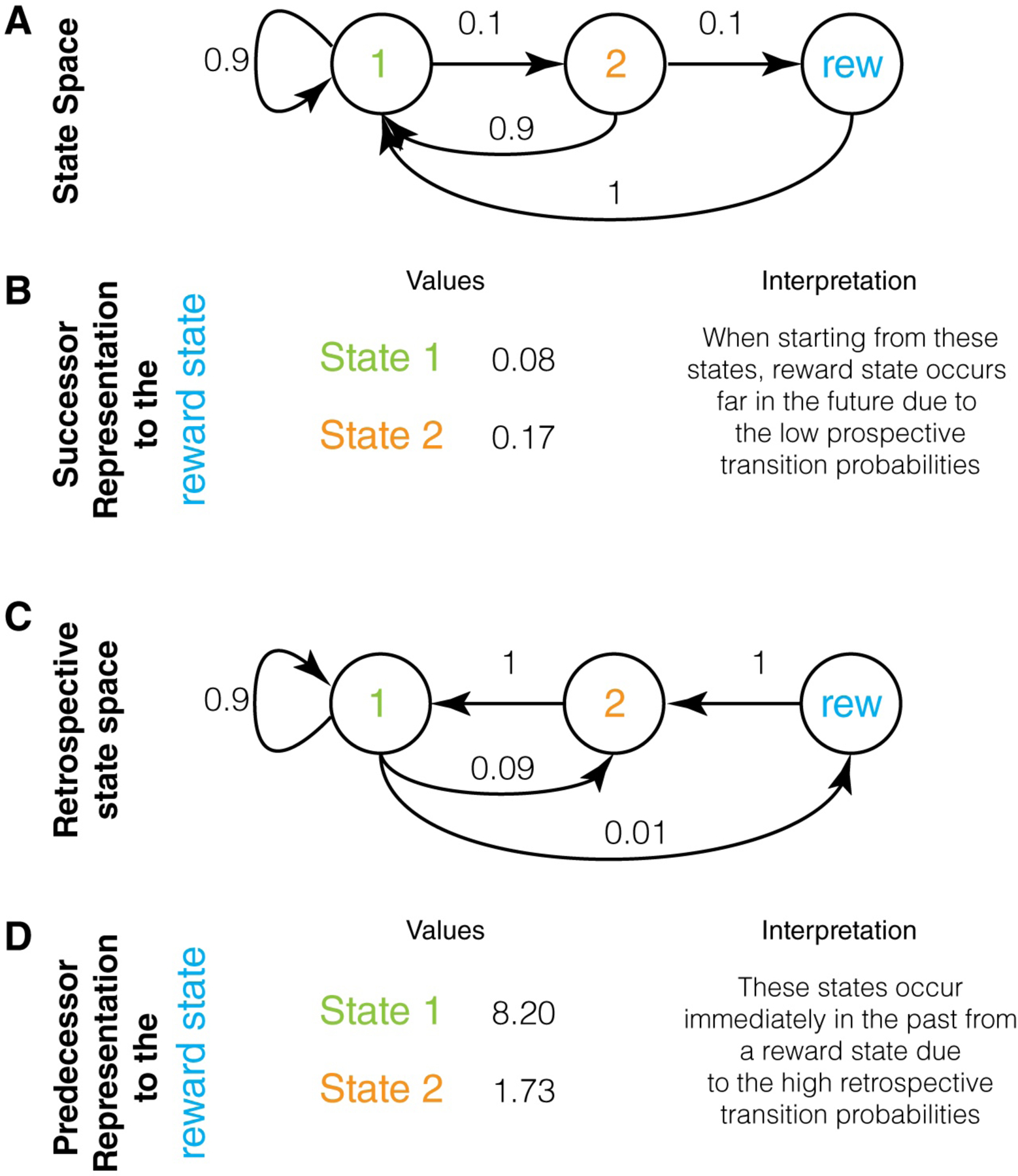
Successor and Predecessor representations: A. A state space that illustrates the key difference between successor and predecessor representations. Here, state 1 transitions with 10% probability to state 2, which then transitions with 10% probability to a reward state. Thus, obtaining reward is only possible by starting at state 1, even though the probability of reward is extremely low when starting at state 1 (1%). The challenge of an animal is to learn that the only feasible path to a reward state is by starting in state 1. B. The values of the successor representation to a reward state for states 1 and 2 are shown under the assumption of a discount factor of 0.9 (calculated in Appendix 1). These are very low and reflect the fact that reward states typically occur far into the future when starting in these states (due to low transition probabilities to reward state). Hence, these low values do not highlight that a reward state is only feasible if the animal starts in state 1. C. The retrospective state space for this example, showing that ending up in a reward state means that it is certain that the previous state was state 2 and that the second previous state was state 1. Thus, a retrospective evaluation makes it clear that a reward state is only feasible if one starts in state 1. D. The predecessor representation of the two states to the reward state. These values are very high compared to the SR and highlight the fact that a reward state is only feasible if the animal starts in state 1. PR is higher for state 1 because it is a much more frequent state (see text).

Just as a prospective transition probability has a corresponding retrospective transition probability (Figure 3C), the SR also has a corresponding retrospective version. We name this the predecessor representation (PR) (Figure 3D). The PR measures how often a given state is preceded by any other state and exponentially discounts the number of backward steps. Again, its utility is particularly apparent when the final state is a reward state. In this case, the PR measures how distant in the past any other state is from a reward state. To see the difference between the SR and PR, consider the state space shown in Figure 3A. If every available reward follows the state 1→state 2 sequence, the SR of state 1 will be very low (Figure 3B), but the PR of state 1 will be very high (Figure 3D). This is because whenever a reward is obtained, state 1 is always two steps behind. In fact, in this example, even though state 2 occurs one step behind the reward, the PR of state 1 is higher than the PR of state 2. This is because the states two or more steps behind reward are much more likely to be state 1, due to its higher relative frequency. In other words, PR is higher for state 1 from reward simply because state 1 is much more frequent.

This example highlights both an important advantage and a disadvantage of PR for learning. The advantage is that the higher the PR of a state to the reward state, the more likely it is for that state to be a key node in the path to reward, and thus, the more valuable it is to learn the path to reward from that state. The disadvantage is that the PR for more frequent states will be higher, regardless of whether they preferentially occur prior to a reward state. A solution for this problem is to calculate a quantity that we label the PR contingency. This quantity measures how much more frequently a state occurs before a reward state than it occurs before any random state (Box 4). Thus, if the PR contingency of a state from reward is high, that state occurs much more frequently before reward than expected by chance. We discuss the utility of PR contingency for learning in Box 4.

Box 4: Contingency.

It has long been recognized that the contingency between a reward and a predictor (i.e. a state in RL) is important for learning (Delamater, 1995; Jenkins and Ward, 1965). Contingency is an estimate of causality (Jenkins and Ward, 1965). The contingency between a reward predictor and reward is most commonly defined as the difference between the probability of reward in the presence of the predictor minus the probability of reward in the absence of the predictor (Gallistel et al., 2014; O’Callaghan et al., 2019). Calculation of these probabilities requires the assessment of whether the predictor is present or absent at a given moment in time. This calculation is very difficult to perform in the real word, however, as objectively measuring the absence of the predictor at a given moment in time is extremely challenging (Gallistel et al., 2014, 2019).

We will now develop an alternative definition. We will do so in multiple stages to eventually define a general measure of contingency. Since contingency is an estimate of causality, its value should be zero when two events are statistically independent. When a reward is statistically independent of a predictor state, the conditional probability that the reward follows the state should equal the marginal (i.e., the overall) probability of the reward (Box 2). Unlike the previous definition based on the probability of events at a given moment in time, we will use the transition probability to measure contingency. This is because we are interested in knowing whether the reward predictor is followed by the reward. Formally, we define a one-step contingency as the transition probability to reward from a given state minus the transition probability to reward from a random state (i.e., the marginal probability of reward). Thus, when contingency is zero, the given state is as good as a random state in predicting whether the next state is reward. This version of contingency is a prospective contingency which describes the probability of transitioning to a reward state. Our definition also allows us to reverse the order and define a retrospective one-step contingency as the transition probability between a given state and reward minus the retrospective transition probability between that state and a random state (i.e., the marginal probability of that state).

This transition probability-based definition largely avoids the challenges related to measuring the absence of a state at a given moment in time. This definition of contingency provides a one-step measure of relationships between states and rewards which we can then extend to a many step measure to account for the common situation where the path to reward passes through many states (e.g., Box Fig 1A). To this end, we can define a multi-step contingency based on the successor representation (SR). Briefly, the SR contingency is the SR of the future reward from a given state minus the SR of the future reward from a random state (Supplementary Information; Appendix 1). Thus, SR contingency measures how much more frequently reward follows a given state compared to chance. Similarly, the predecessor representation (PR) contingency is the PR of a state from reward minus the PR of that state from a random state. Thus, PR contingency measures how much more frequently a given state occurs before a reward compared to chance. In Box Fig 1, the PR contingency provides a quantitative measure that reflects that the only path to reward is through state 1. This highlights the utility of PR contingency for learning: the higher the PR contingency of a state to reward, the more valuable it is to learn the path to reward from that state.

The above definitions of SR and PR contingencies are defined for discrete time Markov state spaces. We can extend this framework to continuous time Markov state spaces, which are more appropriate for real animals (Namboodiri, 2021). We previously introduced a continuous time version of the SR contingency using the estimation of reward rate in a Markov renewal process model of the state space (Namboodiri, 2021). The continuous time SR contingency between a reward predictor and reward is defined as the difference between the conditional rate of rewards in a future look-ahead time period conditioned on the reward predictor, and the marginal rate of rewards from a random moment in time (Namboodiri, 2021). Similarly, the continuous time PR contingency is the difference between the PR for a predictor from reward minus the PR of the predictor from a random moment in time. We previously showed that the continuous time SR contingency between a cue and reward in a Pavlovian conditioning task depends positively on the intertrial interval and negatively on the cue-reward delay in such a way that scaling these intervals does not change the contingency (Namboodiri, 2021). We also show here that the continuous time PR contingency is much higher than the continuous time SR contingency for common instrumental action-reward tasks (Supplementary Information; Appendix 2).

Finally, we would like to point out that there are also other ways to define contingency based solely on the timing between events (Balsam et al., 2010; Gallistel et al., 2014, 2019; Ward et al., 2012). A full discussion of this body of work is beyond the scope of this perspective, but one theoretical postulate stands out. These papers propose that animals learn associations between reward predictors and rewards based on the information contained in the predictor on the timing of rewards. Using information theoretic principles, this timing contingency is defined as the normalized information gain of the timing of rewards and the timing of the predictors. In a simple Pavlovian conditioning paradigm in which a cue predicts a delayed reward, it has been shown that the above definition of contingency depends on the ratio of the intertrial interval (delay between reward to next cue) to the cue-reward delay. This definition also works retrospectively, since the retrospective contingency is the information contained in the reward of the timing of the previous predictor (Gallistel et al., 2019). Indeed, to the best of our knowledge, the idea of a retrospective contingency was first introduced by these authors (Gallistel et al., 2014). Overall, there are thus many ways to define statistical contingency. Considerable research is needed to identify the neuronal mechanisms underlying their computation.

Overall, we propose that the cognitive map of animals includes a prospective map comprising of the prospective one-step transition matrix and the SR, and a retrospective map comprising of the retrospective transition matrix and the PR. We propose that animals use these quantities to estimate statistical contingencies in the world for learning and decision-making. Though a retrospective cognitive map might superficially appear to be a simple reflection of the retrospective updating of a prospective cognitive map after an outcome, this is not the case. The retrospective cognitive map consisting of the retrospective transition matrix and the PR are altogether distinct representations. Crucially, these quantities are flexible cognitive representations measuring the retrospective transition dynamics of the world (Supplementary Information; Appendix 1). Nevertheless, we will show in the next section that these cognitive representations can produce behaviors that are apparently inflexible and non-cognitive.

Behavioral and neurobiological evidence supporting the existence of retrospective cognitive maps

Prior reviews have highlighted evidence supporting the existence of prospective cognitive maps, especially in the context of neurobiological investigations (Behrens et al., 2018; Wilson et al., 2014). Here, we present considerable behavioral and neural evidence supporting the hypothesis that animals use both prospective and retrospective cognitive maps for learning and decision-making. Together, we demonstrate that this conceptual framework captures key phenomena underlying multiple patterns of behavioral responding. Importantly, by rationalizing behaviors as being driven by both prospective and retrospective cognitive maps, we demonstrate that even apparently inflexible non-goal-directed behaviors can result from flexible cognitive processes.

Behavioral evidence:

Role of time intervals in initial learning: cognitive maps?

We will first discuss behavioral evidence consistent with the hypothesis that even simple learning procedures are driven by cognitive maps. As part of the cognitive map framework presented here, we propose that initial learning of cue-outcome or action-outcome associations is based on an estimation of a causal relationship between the outcome predictor and the outcome. Causality between events can be estimated by a contingency between them (Jenkins and Ward, 1965) (Box 4). Intuitively, contingency between a reward predictor and reward measures whether the occurrence of reward can be predicted based on the occurrence of the reward predictor better than chance. Thus, we hypothesize that during initial learning, animals evaluate whether the contingency between a reward predictor and reward is higher than a statistical threshold. A threshold crossing process implies that behavioral evidence for learning will appear rather suddenly with experience. Prior to the threshold crossing, there will be little to no evidence of learning. However, after the threshold crossing, the animals will have learned the statistical relationship between a reward predictor and reward. This framework contrasts with model-free RL algorithms, which propose that animals will show evidence of learning in proportion to their iteratively increasing estimate of value. For instance, in a simple Pavlovian conditioning paradigm in which a cue predicts a delayed reward, RL models predict that animals will slowly update their value estimates during initial learning and that behavior reflective of this value will show a similar gradual growth. Instead, animals often show a sudden appearance of learned behavior, consistent with evaluations of contingency (Gallistel et al., 2004; Morris and Bouton, 2006; Ward et al., 2012).

Learning driven by statistical contingency will be affected by the structure of the entire session and not just the trials. For instance, contingency between a cue and a reward in Pavlovian conditioning will depend positively on the intertrial interval (Namboodiri, 2021). Thus, increasing the intertrial interval should increase contingency and thus, reduce the number of trials required for conditioning to first appear. Similarly, when the intertrial interval and the delay to reward from the cue are both scaled up or down, there should be largely no difference in contingency (Namboodiri, 2021). Further, the learning of contingency will be based on the global structure of the task and will thus be independent of the ordering of trials (Madarasz et al., 2016). Considerable behavioral evidence supports these predictions (Gibbon and Balsam, 1981; Holland, 2000; Kalmbach et al., 2019; Madarasz et al., 2016). In contrast, these findings pose challenges to typical RL frameworks, as has been discussed in detail (Balsam et al., 2010; Gallistel and Gibbon, 2000; Gallistel et al., 2019; Namboodiri, 2021).

Variable interval instrumental conditioning:

A behavioral task in which a retrospective cognitive map or contingency seems especially important is the variable interval (VI) schedule of instrumental conditioning. In VI schedules, the reward is delivered on the first instrumental action performed after the lapse of a variable interval from the previous reward. In VI schedules, animals often perform the action at high enough rates that only an exceedingly small fraction of the actions are followed by reward. In many studies, a reward is delivered only after a hundred or more actions (Herrnstein, 1970). At that low a probability of reward per action, it is challenging to measure whether the rewards occur purely by chance or due to the performance of an action. Hence, from the commonly assumed view of a prospective contingency or a cognitive map, animals should not respond at such high rates on a VI schedule (Gallistel et al., 2019).

An intuition for why responding would nevertheless occur in VI schedules is that the rewards only occur if the subject performs the action. Thus, the occurrence of the reward is statistically dependent on the operant action. The challenge of the animal is to learn that there is indeed a statistical relationship between the two when the prospective contingency is low. This mystery is solved once we realize that the retrospective contingency is nearly perfect (Supplementary Information; Appendix 2). This is because every reward is preceded by an action. In words, this means that a reward is only obtained if the action precedes it. Hence, if contingency is the reason for VI responding, it must be the retrospective contingency that supports responding. Gallistel et al. tested this prediction by systematically degrading the retrospective contingency in a VI schedule and found that responding drops rapidly when the retrospective contingency drops below a critical value (Gallistel et al., 2019).

Habitual responding:

The retrospective cognitive map framework may also explain another observation about VI responding. With repeated training, animal behavior under the VI schedule becomes habitual relatively quickly (Adams, 1982; Dickinson and Balleine, 1994; Dickinson et al., 1983). A habitual behavior is one that is formally defined to be insensitive to the devaluation of the reward (e.g. due to satiation on the reward or a pairing of the reward with sickness) and separately, to a reduction in contingency (e.g. reducing the probability of reward following action or increasing unpredicted rewards) (Balleine and Dickinson, 1998; Dezfouli and Balleine, 2012; Robbins and Costa, 2017). The high rate of habitual behavior on VI schedules contrasts with responding on a different schedule known as a variable ratio (VR) schedule. In VR schedules, a reward is available after a variable number of actions. In typical VR schedules, animals remain sensitive to reward devaluation for considerably longer amounts of training (Adams, 1982; Dickinson and Balleine, 1994; Dickinson et al., 1983). The cognitive map framework provides an explanation for this result by postulating that responding in VI schedules is controlled by the retrospective contingency between action and reward (Supplementary Information; Appendix 3). The retrospective contingency between an action and a reward in a context is updated only upon receiving the reward in the experimental context. This contingency can be loosely thought of as p(action | reward, context) – p(action | context) (the technical definition is based on PR and not transition probabilities, Box 4). Here, the former term is updated only on the receipt of reward in the context. If the reward is altered by devaluation, retrospective contingency will not be updated until the experience of this new reward in the context, as supported experimentally (Balleine and Dickinson, 1991). Hence, behavior driven by a retrospective contingency is not based on the prospective evaluation of a (now) devalued reward. Further, a rational animal operating by Bayesian principles will evaluate drops in contingency in relation to its prior expectation of such a drop in the current context. The prior belief of a high contingency increases in strength with training in a fixed high contingency schedule. Thus, the more “overtrained” an animal is in the original high contingency, the less sensitive it will be to a drop in contingency (Supplementary Information; Appendix 3). Such an animal will appear insensitive to a drop in contingency and hence, appear habitual. Thus, habitual responding may simply be the result of behavior driven by a retrospective contingency with two separate mechanisms underlying insensitivity to reward devaluation and contingency reduction. Consistent with the presence of two separate mechanisms, many studies have found that sensitivity to reward devaluation and contingency degradation are neurally separable (Bradfield et al., 2015; Lex and Hauber, 2010a, 2010b; Naneix et al., 2009).

This framework makes at least five predictions, all of which have been verified experimentally. The first is that the longer the training history in a context, the higher the probability that the animal’s behavior will appear insensitive to a reduction in contingency. This has been experimentally verified numerous times (Adams, 1982; Dickinson et al., 1998). The second is that behavior will appear habitual only within a context. A change in context will make a habitual behavior appear goal-directed again, as the effect of prior beliefs about the context are eliminated. This has recently been tested and verified (Steinfeld and Bouton, 2020). Indeed, context dependence of habits has been used to test the same animals in separate VI (“habitual”) and VR (“goal-directed”) contexts (Gremel and Costa, 2013). The third is that behavior that appears insensitive to a drop in contingency will become sensitive to contingency if exposed for a long period of time. This is because the prior belief of a high contingency from overtraining will only reduce with a correspondingly long period of low contingency. This has also been recently verified (Dezfouli et al., 2014). The fourth is that behavior in a VI schedule will appear habitual more quickly than behavior in a VR schedule. This is because behavior in VI schedules is driven more by the retrospective contingency than in VR schedules (Supplementary Information; Appendix 3). This has been known for a long time (Adams, 1982; Dickinson and Balleine, 1994; Dickinson et al., 1983). Lastly, because habits are driven by a retrospective contingency, exposure to non-contingent rewards and the associated decrease in retrospective contingency should make the behavior become goal-directed. This has also been recently observed (Trask et al., 2020).

While some of these results are also predicted by other models (Dezfouli and Balleine, 2012; Miller et al., 2019), we would like to highlight that our retrospective cognitive map explanation is appealingly simple, and does not depend on many parameters. Indeed, the only parameters are a critical contingency below which responding ceases and a weighting of the prospective and retrospective contingencies for calculating the net contingency (Supplementary Information; Appendix 3). Perhaps more importantly, these results highlight the possibility that both “habitual” and “goal-directed” responding may result from the same underlying mechanism driven by contingency-based responding. It is the slowness of detecting a change in a retrospective contingency that makes behavior appear habitual. In this sense, habitual behavior is still goal directed (Dezfouli and Balleine, 2012; FitzGerald et al., 2014; Kruglanski and Szumowska, 2020). Finally, this framework can also be readily extended to sequences of actions, such that a chunked sequence of actions predictive of reward, later becomes repeated as a unit (Barnes et al., 2005; Dezfouli and Balleine, 2012; Graybiel, 1998).

Extinction:

It has long been known that extinction of the environmental association between a predictor and outcome does not extinguish the original memory of the association (Bouton, 2004, 2017; Bouton et al., 2020; Pavlov, 1927). For instance, animals reacquire a cue-outcome association after extinction much faster than the initial acquisition (Napier et al., 1992; Ricker and Bouton, 1996; Weidemann and Kehoe, 2003). The associative view of extinction is that extinction results in a new inhibitory association between the cue and outcome, and both the original excitatory association and the new inhibitory association are stored in memory (Bouton et al., 2020). The retrospective cognitive map framework posits a different explanation: after initial cue-outcome learning, both the prospective and retrospective transition probabilities between cue and outcome are learned. Extinction only reduces the prospective probability to zero. However, the retrospective probability remains high, as it is updated only upon the receipt of reward. Thus, a memory of the fact that the cue once preceded the outcome remains intact after extinction. One way to eliminate both prospective and retrospective contingencies is to present both cue and outcome in a randomly unpaired manner. Indeed, numerous studies have shown that such random unpaired presentations significantly reduce or erase the original memory (Andrew Mickley et al., 2009; Colwill, 2007; Frey and Butler, 1977; Leonard, 1975; Rauhut et al., 2001; Schreurs et al., 2011; Spence, 1966; Thomas et al., 2005; Vervliet et al., 2010). Thus, an effective means to extinguish cue-outcome associations would require extinguishing both the prospective and retrospective associations.

Pavlovian to instrumental transfer:

An intuitive role for a retrospective cognitive map can be seen in Pavlovian to instrumental transfer (PIT) (Cartoni et al., 2013, 2016; Holmes et al., 2010). Briefly, in PIT, an animal is separately trained that either cue1 or action1 predict reward1, and that either cue2 or action2 predict reward2 (of a different type than reward1) (this is known as outcome-specific PIT). In a subsequent extinction test, presentation of cue1 is sufficient to enhance the rate of execution of action1, but not action 2 (Cartoni et al., 2016). Similarly, cue2 enhances execution of action2, but not action1. Thus, animals appear to infer that cue1 predicts the same outcome as action1 and cue2 predicts the same outcome as action2. In the presence of a retrospective cognitive map, such inference is trivial: presentation of cue1 prospectively evokes a representation of reward1, which then retrospectively evokes a representation of action1. This view has recently received direct experimental support through some clever behavioral experiments (Alarcón et al., 2018; Gilroy et al., 2014). For a more detailed treatment of the role of retrospective planning in PIT, see (Afsardeir and Keramati, 2018).

Neurobiological evidence:

Mouse OFC neuronal recordings:

Our recent work showed that distinct subpopulations in the ventral/medial OFC of mice respond in a manner consistent with representing the prospective or retrospective transition probability between a cue and reward (Namboodiri et al., 2019). Such a study was only possible due to our ability to longitudinally track the activity of the same neurons across many days of behavior using two-photon calcium imaging. Due to this ability, we designed simple task conditions that systematically varied the prospective and retrospective associations as shown in Figure 2, while imaging from the same neurons.

Specifically, in one experiment, we reduced the probability of reward after a cue from 100% to 50%; every reward was delivered only after a cue. If a neuron represents the prospective probability of reward following a cue, its response should decrease in this experiment. If, on the other hand, the neuron represents the retrospective probability of a cue preceding reward, its response should not change in this experiment. We also performed another experiment in which after retraining animals at 100% reward probability, we introduced random unpredicted rewards during the intertrial interval. In this experiment, a neuron representing the prospective transition probability would not change its response. However, a neuron representing the retrospective transition probability should reduce its activity. Thus, these two contingency degradation experiments allow a dissociation of prospective and retrospective encoding.

To identify subpopulations of neurons with similar response patterns during behavior, we performed an unbiased clustering of neuronal responses during behavior and identified multiple subpopulations (Namboodiri et al., 2019). Such an approach has also been successfully used by other groups to identify neuronal subpopulations in OFC (Hirokawa et al., 2019; Hocker et al., 2021). We then used the above criteria to define whether a subpopulation of neurons encode prospective or retrospective transition probabilities. We found that the average activity of one subpopulation of OFC output neurons was consistent with a representation of the prospective transition probability, and that the average activity of two other subpopulations was consistent with a representation of the retrospective transition probability (Figure 4A, B). More strikingly, these subpopulations abided by the strongest prediction of a retrospective probability representation during extinction learning. After mice learned a retrospective transition probability p(cue←reward) during regular conditioning, we extinguished the cue-reward association such that cues were no longer followed by reward. In this case, the retrospective transition probability must remain high since its value is only updated when reward is received. On the other hand, a prospective transition probability p(cue→reward) will become zero since the cue no longer predicts reward. We found that OFC excitatory neurons from these subpopulations, especially those projecting to the ventral tegmental area (VTA), maintain high cue and trace interval responses even after complete behavioral extinction (Figure 4C–E). These results demonstrate that these OFC neuronal subpopulations represent the retrospective transition probability of a cue with respect to reward. In contrast to these results, we found that neurons in the subpopulation encoding the prospective association (cluster 2 in Figure 4B) reduced its activity after extinction of the cue-reward association.

Figure 4.

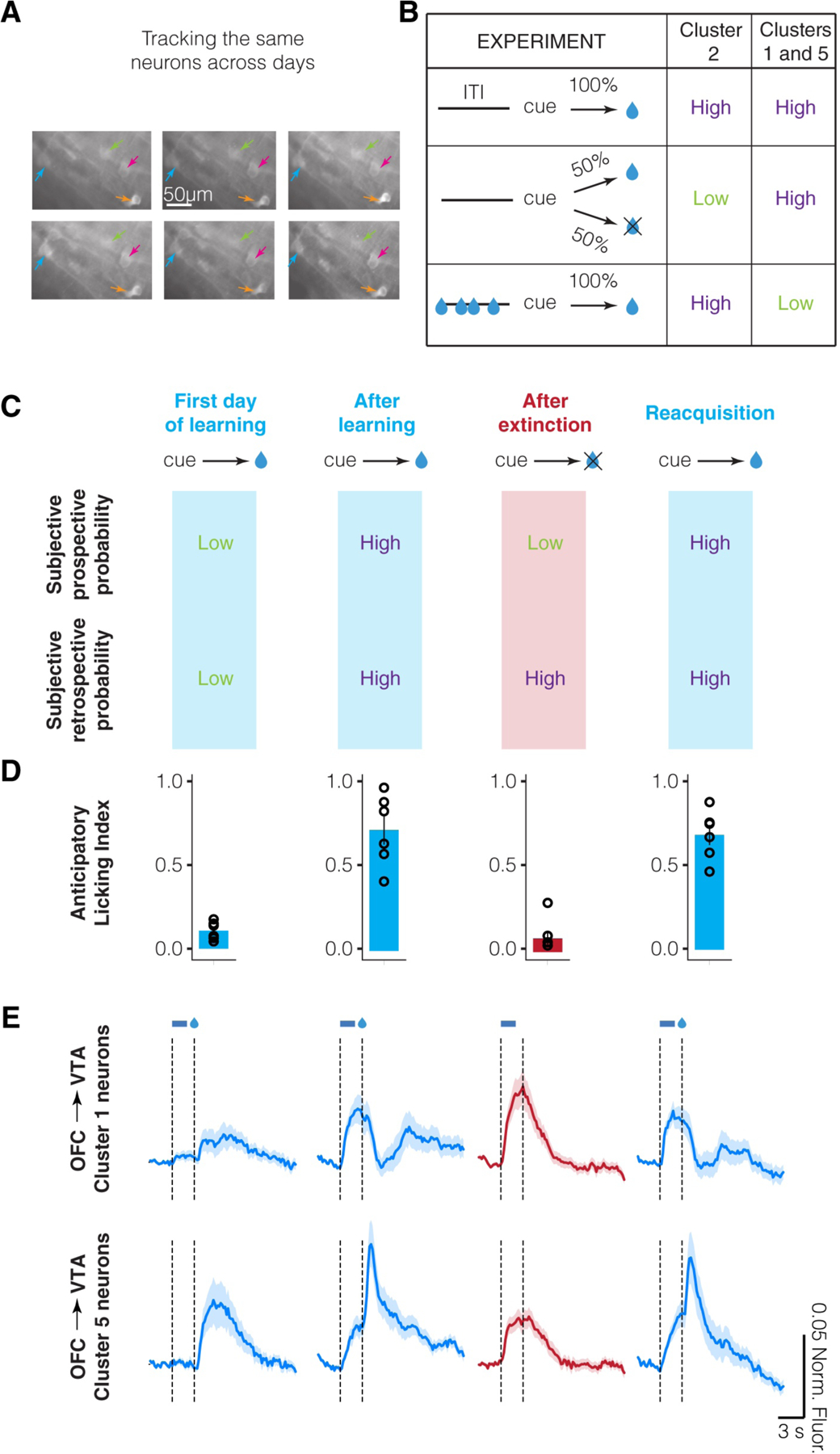
Neuronal activity in select OFC neuronal subpopulations is consistent with a representation of the retrospective transition probability A. Longitudinal tracking of the same neurons across many days using two-photon calcium imaging (reproduced from Namboodiri et al. 2019). Four example neurons are shown in different colored arrows. B. Qualitative summary of data from three separate subpopulations of neurons identified by clustering neuronal activity (summarized from Namboodiri et al. 2019). Comparison with Figure 2 shows qualitative correspondence of these groups with a representation of prospective and retrospective transition probabilities. C. Additional test of the representation of a retrospective transition probability using extinction of learned cue-reward pairing. The expected subjective probabilities are shown. D. Anticipatory licking induced by the cue, showing that animals learn extinction. E. Mean normalized fluorescence of longitudinally tracked OFC→VTA neurons (n=27 cluster 1, n=23 cluster 5) plotted against time locked to cue onset. Cue response (between the dashed lines) is high even after extinction, consistent with the expected subjective retrospective transition probability.

Importantly, these results show that even within a simple behavioral task that is commonly believed to be based on model-free learning, OFC neurons encode model-based/cognitive representations. Future experiments can test whether OFC neurons also form subpopulations based on the computation of prospective versus retrospective cognitive maps. If so, considering the Bayesian relationship between these quantities (see equation (1) and Supplementary Information; Appendix 1), it would also be interesting to test whether neurons encoding the retrospective cognitive map convey information to causally shape activity within the neurons encoding the prospective cognitive map.

OFC manipulation:

In the same study, we also performed a functional test of the representation of the retrospective transition probability. As shown in Equation 1, we hypothesized that a primary function of the retrospective probability is in updating the prospective transition probability. After extinction, animals should learn to stop responding to the cue since the prospective probability of transitioning to the reward state following the cue state is zero. Thus, disrupting the representation of the retrospective probability must disrupt this prospective probability update and hence, disrupt extinction learning and memory as well. To test this hypothesis, we disrupted OFC→VTA response following cue presentation during extinction. We measured behavioral learning of extinction by observing a reduction in anticipatory licking for reward during extinction (to near zero levels). We found that animals with a disruption of OFC→VTA responses learned extinction slower, but nevertheless learned by the end of the session. However, on the first few trials of the next day of extinction, these animals behaved as if they did not learn extinction and showed high anticipatory licking. These results can be explained by noting that in the absence of OFC signals conveying p(cue←reward), compensatory signals conveying p(reward) (i.e., transitioning to reward state in the behavioral context) could instruct the animals to lick less. However, once OFC comes back online, the non-updated value of p(cue→reward) (still high from before extinction) would drive behavior, thereby resulting in an apparent deficit in extinction memory. Thus, the deficit results from an inappropriate credit assignment: animals learn to expect no reward, but do not learn to attribute that reduction in expectation to the cue. Another study showed a similar hierarchical effect of OFC on the control of behavior (Keiflin et al., 2013).

Previous studies on nonhuman primates and humans have shown that OFC is indeed important for such credit assignment (Jocham et al., 2016; Noonan et al., 2010; Walton et al., 2010). These studies also showed that the brain uses three forms of learning to assign credit for a reward (Jocham et al., 2016). The first is contingency learning, in which the reward predictor that caused the reward is given credit for the reward through the calculation of contingency. The second form attributes credit to the cue/action immediately preceding the reward even though the true cause may have occurred further in the past. The last form attributes credit to the most common cue/action in the recent history prior to the reward. Similar retrospective credit assignment has been previously proposed as part of a “spread of effect” within Thorndike’s law of effect (Thorndike, 1933; White, 1989). All three forms of the above learning can be explained using simple constructs based on prospective and retrospective cognitive maps. Specifically, causal attribution of credit can be done by assigning credit to the cue/action with the highest prospective/retrospective contingency with reward. For example, PR contingency measures how much more likely a cue/action is to precede a reward above chance and thus, measures whether the cue/action contingently precedes a reward. It can also identify the first predictor in a sequence of cues/actions that leads to reward (see Box Fig 1). Attribution to the immediately preceding cue/action can be done by assigning credit to the cue/action with the highest retrospective transition probability. Since such attribution is not based on an explicit calculation of contingency, the cue/action receiving credit may or may not preferentially precede the reward (and thus may or may not be the true cause of the reward). Lastly, attribution to the most common cue/action in recent history can occur by assigning credit to the cue/action with the highest PR (and not PR contingency). This is because PR (and not PR contingency) reflects how common a cue/action is an environment (see Box Fig 1). Thus, all three forms of credit assignment can result from cognitive maps. Overall, the finding that OFC activity is specifically important for contingency learning suggests that OFC activity is especially useful to calculate prospective or retrospective contingency.

Box Fig 1.

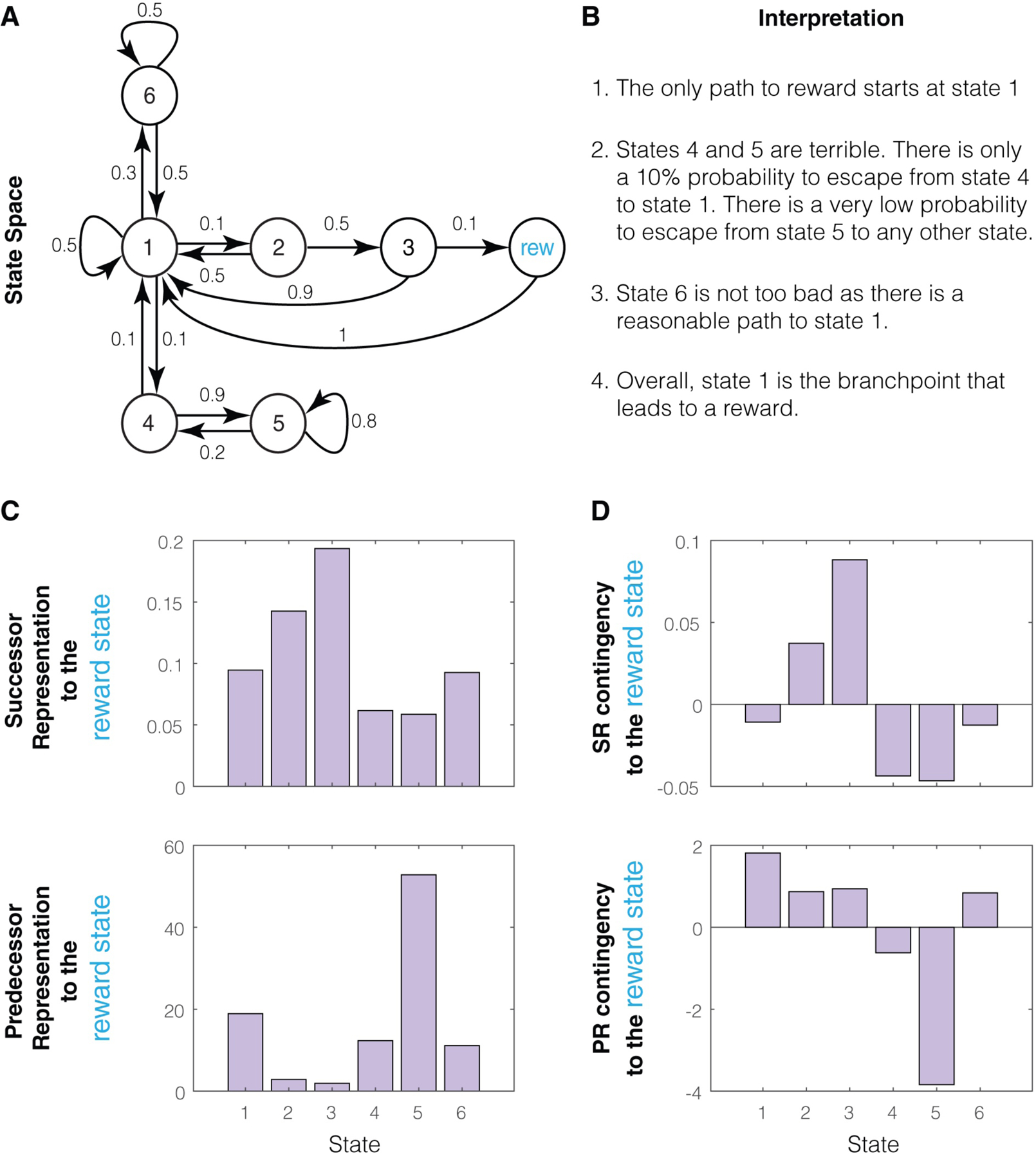
Illustration of SR and PR contingencies: A. An example high dimensional state space. All prospective transition probabilities are denoted by the corresponding arrows. B. Intuitive interpretation of the state space in A. Since the only path to reward goes through state 1, state 1 is the most important state to organize learning around. C. SR and PR for all states to the reward state. Here, the discounting factor was set to 0.99. Neither the SR nor the PR magnitudes highlight the fact that state 1 is the most important state for the path to reward. Note that the PR values here mostly reflect how frequent each state is, with state 5 being the most frequent state. This is also the reason why the mean SR value is much lower than the mean PR value, as the mean SR value reflects the relative frequency of the reward state. D. SR and PR contingencies for all states to the reward state. These quantities account for the relative frequencies of all states. SR contingency measures how much more frequently a given state occurs after reward compared to a random state. PR contingency measures how much more frequently a given state occurs before reward compared to a random state. PR contingency quantitatively measures all the important intuitive observations in B regarding the state space.

Since prospective and retrospective contingencies are mathematically related to each other, future work is needed to tease them apart and assess whether both calculations require the OFC. Prior work suggests that this is the case, with potential regional differences between the medial and lateral parts of OFC. Indeed, considerable support for the idea of prospective cognitive maps has come from studies of the lateral OFC (Gardner and Schoenbaum, 2020; Schuck et al., 2018; Wikenheiser and Schoenbaum, 2016; Wilson et al., 2014). On the other hand, medial OFC is comparatively much less studied. The fact that we observed retrospective encoding in ventral/medial OFC, a finding that has not yet been made in lateral OFC, suggests that this may be a unique function of some ventral/medial OFC neuronal subpopulations. Hence, a key difference between medial and lateral OFC may be the encoding of retrospective versus prospective cognitive maps. While this remains to be rigorously tested, the results of a previous lesion study in monkeys are qualitatively consistent with this hypothesis (Noonan et al., 2010). In this study, the authors found that after lesioning lateral OFC, the choice between two actions with a high difference in reward probability is disrupted. This is consistent with an approximation of p(action→reward) in the direction of p(reward); doing so would result in highly disparate reward probabilities to be approximated by their mean value. On the other hand, the authors found that after lesioning medial OFC, the discrimination between two actions with a low difference between their associated reward probabilities is reduced. Though the authors interpret this result as a disruption of decision-making, it is also consistent with an approximation of p(action←reward) in the direction of p(action); doing so would result in low discrimination between actions that have similar prior probabilities of occurrence. In sum, current studies suggest that there might be a functional difference between medial and lateral OFC in representing retrospective versus prospective cognitive maps. Nevertheless, future quantitative studies are required to adequately test this difference.

Birdsong HVC:

Vocal communication is built on sequences of sounds. Thus, measuring transition probabilities between different syllables is fundamental to communication. Songbirds are an ideal system to study such communication at the neural level. A previous study investigated the representations of transition probabilities of vocal sequences in the Bengalese finch (Bouchard and Brainard, 2013). In the learned song of Bengalese finches, there is considerable variability in the sequence of syllables (Bouchard and Brainard, 2013). Thus, it is an ideal system to measure how transition probabilities between different syllables are neurally represented. Bouchard and Brainard recorded from area HVC of the Bengalese finch, a homolog of the vocal premotor area in humans (Doupe and Kuhl, 1999). They found that the response of HVC neurons to a syllable depended linearly on the retrospective transition probability to the preceding sequence (Figure 5). They also demonstrated that these responses could not be explained by prospective transition probabilities or other variables. Thus, these data provide strong evidence for the representation of retrospective probabilities in sequence learning.

Figure 5.

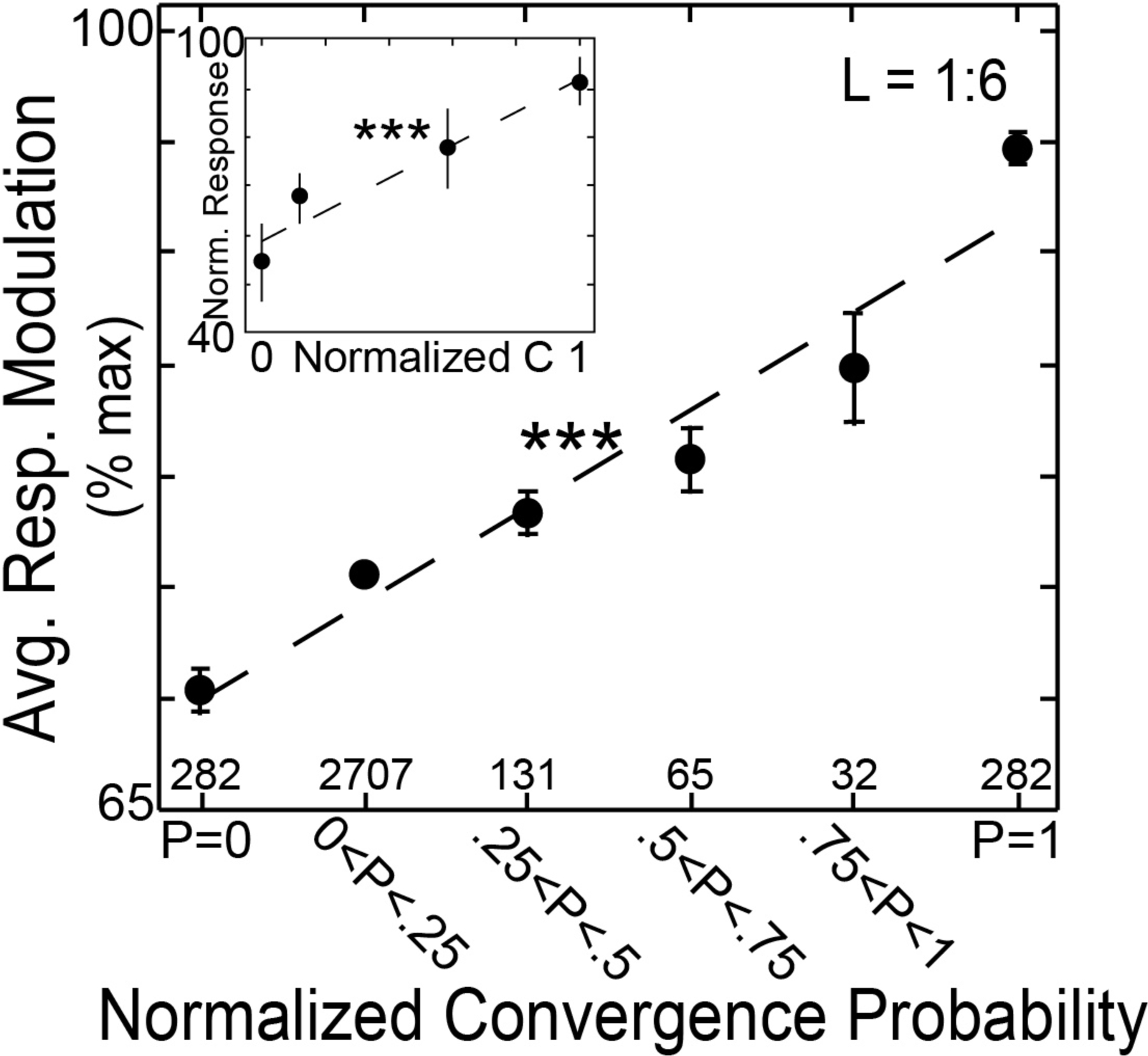
Representation of retrospective transition probability in a songbird brain: The y-axis measures the response modulation of neurons in area HVC of the Bengalese finch to a syllable (Bouchard and Brainard, 2013). The x-axis measures the retrospective transition probability from that syllable to the preceding sequence in the natural song of the bird. An increase in retrospective transition probability to the preceding stimulus causes a linear increase in response of HVC neurons. Reproduced here with permission (Fig 4G in original publication).

Rat Posterior thalamus:

A previous study found evidence for both prospective and retrospective encoding in the rat posterior thalamus (Komura et al., 2001). In rats that learned multiple cue-reward associations, this study found that an early onset cue response reflects the retrospective cue-reward association, and the late onset cue response reflects the prospective cue-reward association. These authors defined the retrospective association as the previously valid association after extinction (qualitatively similar to the results found in the mouse OFC, Figure 4). Though a direct test using the conditions laid out in Figure 2 was not performed, these observations are consistent with an encoding of the retrospective transition probability between a cue and reward.

Overall, the above results show that retrospective transition probability is neurally encoded across different brain regions of multiple species.

Reconceptualizing the function of many neural circuits

In this section, we proffer an overarching conceptual view of the function of many neural circuit elements in terms of representing, using, or learning prospective and retrospective cognitive maps (Figure 6). While we support our proposal using experimental evidence, we present this section to highlight hypotheses for future experimental testing in a wide range of brain areas.

Figure 6.

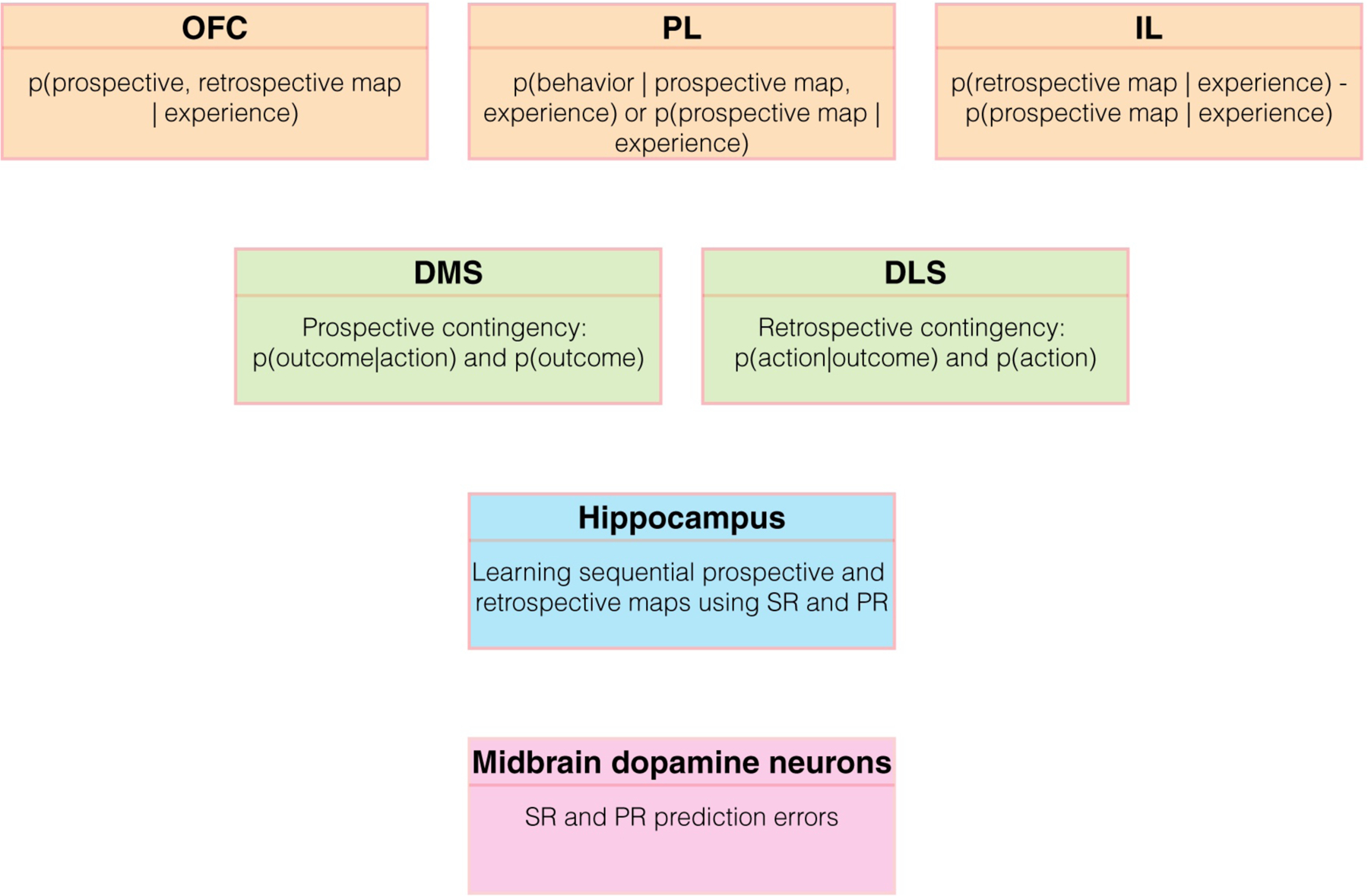
Reconceptualization of the function of several neural circuits. Here, we speculatively propose a reconceptualized framework of the function of several nodes of the neural circuits involved in associative learning. While we propose some evidence consistent with our framework in the text, we present this framework primarily to stimulate future experimental testing. For simplicity, we omit representations of reward value/magnitude. Further, we are not proposing that the listed functions completely describe a given node. Almost certainly, each node is involved in many other functions due to the heterogeneity of cell types.

Cognitive map hypothesis of OFC:

There are numerous theories of OFC function. Some prominent examples include the hypotheses that OFC represents a cognitive map of state space (Gardner and Schoenbaum, 2020; Stalnaker et al., 2015; Wilson et al., 2014), or value (Ballesta et al., 2020; Conen and Padoa-Schioppa, 2019; Enel et al., 2020; Padoa-Schioppa and Assad, 2006; Padoa-Schioppa and Conen, 2017; Rich and Wallis, 2016; Xie and Padoa-Schioppa, 2016), or confidence in one’s decision (Hirokawa et al., 2019; Kepecs et al., 2008; Masset et al., 2020), or flexible decision-making through prediction (Rolls, 2004; Rudebeck and Murray, 2014), or that it supports credit assignment (Noonan et al., 2010; Walton et al., 2010). One challenge in attributing global functions to a brain region is that these theories often assume that the OFC performs one primary function. Aside from the numerous regional differences within the OFC (Bradfield and Hart, 2020; Izquierdo, 2017; Lopatina et al., 2017; Rudebeck and Murray, 2011), it has also been shown that the same subregions of OFC contain distinct neuronal subpopulations with different representations (Hirokawa et al., 2019; Namboodiri et al., 2019). Hence, it is very likely that the function of a region as complex as OFC may be multipronged and not limited to a single representation. Nevertheless, the above proposed functions of OFC are consistent with the representation of prospective and retrospective cognitive maps.

To explain the role of OFC in generating behavior, we consider the following generative model for behavior.

$$p(behavior\mid experience)=\sum _{map}p(behavior\mid map,experience)p(map\mid experience)$$ (2)

Here, experience refers to recent experience, and map refers to a cognitive map (prospective and retrospective). This equation essentially states that the behavior of an animal results from the knowledge that it gains from experience (i.e., p(map|experience)) and its decision-making based on that knowledge (p(behavior|map,experience)). At any given moment, an animal can store multiple different maps of the world. For instance, during Pavlovian conditioning, the animal may store both the map that cue and reward are related, and the map that cue and reward are unrelated. Thus, in words, the above equation states that the probability of producing a behavior in response to recent experience is the probability of an internal cognitive map given that experience multiplied by the probability of producing behavior given that map and experience, summed over all possible cognitive maps.

We propose that OFC learns and represents p(map|experience). This proposal is consistent with all the functions described earlier. Since value is defined behaviorally (Hayden and Niv, 2020), i.e., based on the left hand side of equation (2), all the quantities on the right hand side could appear correlated with value. This may be part of the reason why OFC neurons appear correlated with economic value under some conditions (Padoa-Schioppa and Assad, 2006; Padoa-Schioppa and Conen, 2017; Rich and Wallis, 2016). Representing p(map|experience) is also consistent with confidence. For example, in a Pavlovian conditioning task, if the animal believes that the cue is predictive of reward, confidence is the probability that this belief is true, and is dependent on p(map|experience) (Pouget et al., 2016). Representing p(map|experience), especially its prospective component, is also important for flexible predictions of the future. Lastly, assigning the credit of an outcome to previous actions depends on representing the conditional probability that the outcome depended on the specific action, i.e., on representing p(map|experience).

A recent review presented an elegant and thorough discussion of the function of OFC under a cognitive map hypothesis (Gardner and Schoenbaum, 2020). Here, we have extended this framework in two important ways. First, we propose that OFC is important for not just learning the states of a task, but also the transition probabilities and relationships between them. Second, we propose that OFC learns both prospective and retrospective cognitive maps. To illustrate these changes, we will highlight a key set of findings discussed by the Gardner and Schoenbaum review. This centers on recent results questioning whether impairments in reversal learning, long thought to be a core deficit following OFC dysfunction, is a ubiquitous consequence of OFC dysfunction. Specifically, recent studies in monkeys have shown no deficit in reversal learning after fiber-sparing lesion of the OFC (Rudebeck et al., 2013, 2017). Similarly, as discussed in detail in the Gardner and Schoenbaum review, other studies suggest that OFC dysfunction produces effects primarily on the first reversal in serial reversal experiments (Boulougouris et al., 2007; Schoenbaum et al., 2002). To explain these results within a cognitive map framework, Gardner and Schoenbaum propose that OFC is important only for the formation and updating of a cognitive map, but not necessarily for its use.

Here, we present a different model for these results based on our proposal that OFC is important for learning and representing p(map|experience). In reversal learning, a previously learned predictor-outcome relationship is reversed. Here, there are two possible maps of the world: either the previous relationship is still true, or the previous relationship is not true. We will refer to these as map and ~map, respectively. In the absence of OFC, our proposal is that p(map|experience) and p(~map|experience) are not learned appropriately. There are many possible approximations to p(map|experience) in the absence of OFC. One is to approximate it by p(map). This prior belief is dependent on the long-term experience of the animal. So, for reversal learning in the absence of OFC, the animals will behave as if the cognitive map that has been the most active in the context (i.e., map and not ~map) is active and hence, will show delayed reversals of their behavior. Interestingly, this means that the largest learning deficit due to OFC dysfunction will be on the first reversal during repeated reversal learning. This is because the ratio of the priors (p(map)/p(~map)) is the highest during the first reversal. This may explain the nuanced role of OFC in reversal learning (Gardner and Schoenbaum, 2020). This is also consistent with Gardner and Schoenbaum’s proposal that fiber-sparing OFC lesions may not result in reversal learning deficits in monkeys that are often trained in many different tasks. This is because regions signaling p(map) and p(~map) may effectively compensate for the lesion under these settings. A similar reasoning in the context of retrospective associations may explain the role of OFC in mediating a shift between goal-directed and apparently habitual behavior (Supplementary Information; Appendix 3) (Gourley et al., 2013, 2016; Gremel and Costa, 2013; Gremel et al., 2016; Morisot et al., 2019; Renteria et al., 2018; Zimmermann et al., 2017).

Despite these arguments, representing p(map|experience) may be just one of the functions of OFC. For instance, we found that the reward responses of OFC neurons (and not cue responses) are more consistent with learning rate control (Namboodiri et al., 2021). A longer treatment on the role of OFC is beyond the scope of this perspective.

Hippocampal replay: a mechanism to learn prospective and retrospective cognitive maps?

How does the brain learn prospective and retrospective transition probabilities between different states? When sequences of states are minimally separated in time, Hebbian plasticity can be used to calculate prospective and retrospective transition probabilities (Box 5) (Bouchard et al., 2015). However, when states are separated by long delays (e.g., delays between cue and reward in Pavlovian trace conditioning), Hebbian plasticity is not sufficient for learning transition probabilities (Box 5). This is because Hebbian plasticity operates over millisecond timescales. In this case, prospective transition probabilities to rewards can be learned by Bayesian inversion of the corresponding retrospective transition probabilities (see “Why build retrospective cognitive maps?”). To learn prospective transition probabilities using Bayes’ rule (as shown in Equation 1), the retrospective transition probabilities must be updated upon receiving reward. This poses a challenge. To form a complete map for all states, the retrospective probabilities must be calculated for every single state (or stimulus or location) upon receiving reward. Hence, even for states experienced a long time ago (e.g. twenty years ago), the animal could update the retrospective probability (p(state|reward)). Updating the retrospective probability of a state experienced twenty years ago is almost never useful for current task needs. Therefore, the above update should be tailored to states that are currently relevant for behavior.

Box 5: Neuronal learning of prospective and retrospective transition probabilities.

How does the brain learn prospective and retrospective transition probabilities? An elegant theoretical paper offers a clue (Bouchard et al., 2015). It is generally believed that learning and memory requires the strengthening or weakening of synapses in the brain (Kandel et al., 2013). Such changes in synaptic strength are commonly referred to as synaptic plasticity. One form of such plasticity is Hebbian plasticity, memorialized by the aphorism “neurons that fire together wire together”. In Hebbian plasticity, when the activity of a presynaptic neuron precedes the activity of a postsynaptic neuron in close temporal proximity, the synaptic strength increases. In general, Hebbian plasticity is thought to occur along with competition between synapses, such that when some synapses get strengthened, others get weakened (Gütig et al., 2003; Miller, 1996; Sjöström et al., 2001). The key insight of (Bouchard et al., 2015) is this: if event A activates the presynaptic neuron and event B activates the postsynaptic neuron, Hebbian plasticity combined with presynaptic competition results in the synaptic strength approaching the prospective transition probability between event A and event B, i.e. p(A→B). Conversely, Hebbian plasticity combined with postsynaptic competition results in the synaptic strength approaching the retrospective transition probability between event A and event B, i.e. p(A←B). Thus, a biologically plausible synaptic learning mechanism can learn both prospective and retrospective transition probabilities between events close in time.

The challenge for a general learning mechanism is that events often do not occur in close temporal proximity. For instance, animals can learn the association between cues and outcomes over a timescale spanning five orders of magnitude (Etscorn and Stephens, 1973; Hinderliter et al., 2012; Kehoe and Macrae, 2002). However, the timescale needed for Hebbian plasticity is of the order of milliseconds. Thus, Hebbian plasticity cannot by itself result in the learning of transition probability between temporally distant states. One potential solution is to densely pack “microstates” between temporally distant states, such that there are always two microstates that occur in close temporal proximity (Namboodiri, 2021). However, this is impractical as a general solution for learning for numerous reasons (Namboodiri, 2021). How then does such learning occur over many timescales?

The observation that the brain can represent past experience in a timeline suggests a potential solution (Bright et al., 2020; Goh et al., 2021; Howard and Hasselmo, 2020; Shankar and Howard, 2012; Tiganj et al., 2018; Tsao et al., 2018). Our proposed solution is this: whenever highly salient events such as rewards occur, the brain operates on this timeline of experience and computes the retrospective transition probability between other states and the reward. Such learning will be sparse as rewards are ethologically sparse. Prospective transition probabilities are then learned by Bayesian inversion of the retrospective transition probability using Equation 1. A challenge in such updating is that upon receiving reward, the retrospective probabilities must be updated for every single state in the animal’s memory, regardless of when they happened in the past. Thus, there must be some mechanism to prioritize learning for states most relevant to current behavior. To this end, we propose that the hippocampus replays states by a rank ordering of their PR contingency with respect to reward states (see “Hippocampal replay: a mechanism to learn prospective and retrospective cognitive maps?”). Thus, hippocampal replay, which occurs over very short timescales (~milliseconds), could provide a means to produce sequential activation of states in a timescale that is close to that required for Hebbian plasticity. Thus, replay can be a mechanism for learning probabilities across timescales.

A simple solution to prioritizing states with currently relevant retrospective transition probabilities is to rank order states based on their PR contingency with respect to the reward state (Box 4). In other words, states that have recently occurred prior to rewards should be prioritized for the update of transition probabilities. We propose that the hippocampus is ideally situated to perform this function as it produces temporally compressed sequences of activity often reflecting past experience (referred to as replay) (Carr et al., 2011; Diba and Buzsáki, 2007; Foster, 2017; Foster and Wilson, 2006; Gillespie et al., 2021). We propose that hippocampal replay during immobility is scheduled by a rank order of the PR contingency of states to aid in the learning of prospective and retrospective relationships between states (Box 5). This is useful for learning relationships between both states that are separated in time, and for states that occur in close temporal proximity. When states are separated in time from reward, PR contingency identifies states that recently occurred before rewards. This is useful to rank order states for the update of retrospective probabilities conditioned on reward receipt. When states occur in close temporal proximity (e.g. in spatial navigation in small environments (Diba and Buzsáki, 2007; Foster and Wilson, 2006)), PR contingency can identify states that provide paths to rewards (Box Fig 1). Thus, rank ordering states by PR contingency provides a scheduling algorithm for learning across timescales.

We will highlight a few implications of this proposal by comparing our framework with a recent elegant explanation of hippocampal replay as prioritized memory access (Mattar and Daw, 2018). One is that our framework predicts that hippocampal replay during immobility will occur on reward delivery and not during instances of reward prediction errors such as the omission of a predicted reward. This is because retrospective transition probabilities are conditioned on reward delivery. In the Mattar and Daw framework, hippocampal replay is scheduled based on the balance between a gain and a need. The gain measures how much the update of the value of a state will change the action policy and the need measures how often a state will be visited in the future. Unlike our proposal, this scheduling should replay states that precede a predicted reward omission if it changes action policies (due to high gain). Most hippocampal replays during immobility are instead driven by reward receipt (Ambrose et al., 2016; Carr et al., 2011; Michon et al., 2019; Singer and Frank, 2009). Another important issue is that the gain-need based scheduling of memory access requires a scheduler that already knows that scheduling a state for replay will maximize future rewards by changing the action policy. In other words, the memory schedule for optimizing rewards is determined by an agent that already knows the optimal rewards. Our proposal is much simpler: memory access on reward receipt is scheduled by an ongoing estimate of the PR contingency of states with respect to reward. Consistent with our proposal, a recent study shows that hippocampal replay is not consistent with the planning of future paths, but is instead consistent with a maintenance of recently rewarded locations in memory (Gillespie et al., 2021). Lastly, planning future visits might be better served using a weighted average of the SR and PR contingencies of states with respect to reward and may underlie the observation of sequential activations of locations during movement (Kay et al., 2020; Wang et al., 2020). An exhaustive treatment of this framework is beyond the scope of this perspective, but the above implications show that prospective and retrospective cognitive maps may be important for understanding hippocampal replay. Lastly, similar considerations may also apply to reactivation events observed widely in the cortex (Euston et al., 2007; Ji and Wilson, 2007; Peyrache et al., 2009; Sugden et al., 2020; Xu et al., 2012).

Dorsolateral versus dorsomedial striatum: Retrospective vs prospective contingency?

Several key circuit nodes for behavioral control reside in the dorsal striatum (Graybiel, 2008; Graybiel and Grafton, 2015; Haber, 2016; Klaus et al., 2019; Kreitzer and Malenka, 2008; Nelson and Kreitzer, 2014; Schultz, 2016a). There is now considerable evidence that dorsolateral striatum (DLS)/putamen is more involved in apparent habitual behavior and dorsomedial striatum (DMS)/caudate is involved in goal-directed behavior (Corbit et al., 2012; Graybiel, 2008; Gremel and Costa, 2013; Redgrave et al., 2010; Yin and Knowlton, 2006; Yin et al., 2004). However, the mechanisms for this difference remain to be worked out. A common view of habit formation is that a habit results from a strengthening of cue-action responses (i.e. actions triggered by a cue without heeding their outcomes) (Robbins and Costa, 2017; Yin and Knowlton, 2006). A recent computational theory on habit formalized this hypothesis (Miller et al., 2019). Based on this view, a simple hypothesis could be that neurons in DLS are sensitive to cue-action associations but not outcomes, and that neurons in DMS are much more sensitive to outcomes. Recording studies show that this is not the case; both DLS and DMS neurons are sensitive to the outcome of actions (Berke et al., 2009; Burton et al., 2015; Isomura et al., 2013; Stalnaker et al., 2010; Thorn et al., 2010). Another hypothesis based on the above view is that since habits usually form with overtraining, the engagement of DMS in a task, measured by the strength of its neuronal responses, becomes weaker and weaker with training. However, this is also not true (Vandaele et al., 2019). Thus, the representations in these regions that contribute to their distinct functions remain to be fully worked out.

We proposed above that apparent habitual behavior may be controlled by a retrospective contingency. Hence, we propose that DLS preferentially represents the retrospective cognitive map (e.g., p(action|reward) and p(action)), whereas DMS preferentially represents the prospective cognitive map (e.g., p(reward|action) and p(reward)). Careful experiments are needed to dissociate these possibilities, as most experiments result in highly correlated prospective and retrospective transition probabilities. Nevertheless, some evidence of regional differences is consistent with our proposal. One study found a major difference between DLS and DMS activity patterns in a probabilistic choice task (Ito and Doya, 2015). In this study, DMS neurons were more sensitive than DLS neurons to the probability of the reward following an action. In contrast, DLS neurons were not significantly modulated by the prospective value of the upcoming action but were active immediately prior to the execution of an action, in a manner dependent on the propensity of performing that action in the presence of reward. These results are consistent with our proposal since reducing the probability of reward following an action would only affect the prospective probability and not the retrospective probability. Similarly, the retrospective probability of an action preceding a reward will be higher after the action was previously performed prior to reward. Another study in humans found that estimates of prospective transition probabilities for both contingent and non-contingent rewards are correlated with functional imaging responses in the caudate (similar to DMS in rodents), but not the putamen (similar to DLS in rodents) (Liljeholm et al., 2011). Another study found that only DMS activity (and not DLS activity) extends between consecutive trials in a task in which the probability of reward following an action increases whenever the alternative action is chosen(Kim et al., 2013). This is explainable if DMS is calculating p(reward|action, action history). This quantity depends on both the current action and the action history even if these variables are assumed to be independent by the animal. Thus, DMS activity would be expected to bridge information across trials. On the other hand, if animals treat the probability of the current action to be independent of action history when conditioned on reward, the retrospective transition probability p(action, action history|reward) = p(action|reward) p(action history|reward). Hence, calculation of the retrospective probability does not need to bridge activity between trials, as was observed in DLS neurons. Overall, these data support the parcellation of prospective and retrospective transition probabilities. Nevertheless, further studies are required to carefully delineate the information in these striatal subregions.

Prelimbic versus infralimbic cortex: linear combinations of prospective versus retrospective probabilities?

Extensive evidence demonstrates that the rodent prelimbic cortex (PL) is involved in the flexible control of anticipatory behavior related to positively and negatively valent outcomes (Balleine and Dickinson, 1998; Corcoran and Quirk, 2007; Giustino and Maren, 2015; Kim et al., 2017; Moorman et al., 2015; Murugan et al., 2017; Otis et al., 2017; Peters et al., 2009). PL contains distinct projection outputs that bidirectionally control reward seeking or punishment avoidance, both during and after learning (Kim et al., 2017; Lui et al., 2021; Otis et al., 2017; Parker et al., 2020; Vander Weele et al., 2018). Further, PL activity represents individual or linear combinations of prospective probabilities of upcoming reward (Bari et al., 2019). Overall, a proposal that rationalizes these findings is that PL represents either the probability of a prospective map given recent experience (i.e. p(prospective map|experience)) or the probability of behavior given a prospective map and experience (i.e. p(behavior|prospective map, experience)). Of course, similar models using successor representation (beyond one-step transition probability) can also fit these data.

In contrast, the infralimbic cortex (IL) that lies ventral to PL, appears especially important for extinction learning and habitual behaviors (Barker et al., 2014, 2017; Ghazizadeh et al., 2012; Milad and Quirk, 2002; Peters et al., 2009). A seminal discovery was that some IL neurons become active only after extinction of a previously learned cue-outcome relationship (i.e. when cue is no longer followed by the outcome) (Milad and Quirk, 2002). A relatively simple proposal to explain this finding is that IL represents the difference between the retrospective and prospective cognitive maps. For instance, if IL neurons represent the difference between p(predictor|outcome) and p(outcome|predictor), their activity will be high after extinction of a previously learned cue-outcome association. Based on the above hypothesis of habitual behavior being driven by retrospective contingencies, the above variable will signal that a behavior is under the control of a retrospective contingency, thereby making it appear habitual. Thus, this simple proposal is sufficient to provide a general model for the role of IL in both extinction and habitual behavior.

Midbrain dopaminergic neurons: prediction error in successor and predecessor representations?

The neurobiological findings that provide the strongest support to value based RL frameworks are the observations of reward prediction error (RPE) signals in midbrain dopaminergic neurons. Considerable evidence supports this claim (Chang et al., 2016; Cohen et al., 2012; Engelhard et al., 2019; Eshel et al., 2016; Kim et al., 2020; Mohebi et al., 2019; Schultz, 2016b; Schultz et al., 1997; Steinberg et al., 2013). In addition to cellular heterogeneity (Engelhard et al., 2019; Heymann et al., 2020; Lammel et al., 2012; Morales and Margolis, 2017), some recent findings related to sensory prediction in midbrain dopaminergic activity and function highlight that these neurons do not merely convey a value prediction error (Keiflin et al., 2019; Sharpe et al., 2017, 2020; Takahashi et al., 2017). Accordingly, a recent model has proposed that dopaminergic neurons convey errors in a successor representation, a postulate that readily incorporates sensory prediction errors (Gardner et al., 2018). Further, a linear function approximation of the successor representation with reward as a feature is mathematically equivalent to the classic temporal difference value signal (Gardner et al., 2018). Hence, here too, the prediction error can be thought of as related to the transition dynamics between states. Extending this framework to a predecessor representation and retrospective transition probabilities would immediately make dopamine prediction errors capable of traversing retrospectively to even sensory preconditioned cues following reward devaluation, as has been observed (Sharpe et al., 2017). Indeed, a previous study has found evidence of retrospective coding in dopamine release in the nucleus accumbens core (Fonzi et al., 2017). Dopamine is also important for contingency learning (Naneix et al., 2009). Nevertheless, it remains to be tested whether dopaminergic responses can reflect prospective and retrospective prediction errors.

Conclusions

Prediction of the future requires a knowledge of the causal structure of the world. Importantly, we showed that learning causal structure requires the learning of not just prospective relationships, but also retrospective relationships. Considering the importance of causal learning, it is perhaps not surprising that numerous behavioral and neurobiological phenomena are consistent with the formation and use of such cognitive maps. Causal learning of structural relationships is in many ways a signature of human cognition. By proposing that the behavior of much simpler animals is also understandable by the learning of such structure, we highlight that the difference between human and animal cognition may instead be related to the breadth of conditions in which humans can learn, infer, and communicate structure. Overall, our framework shows that adopting a causal cognitive view of neuronal processing may be required to better understand the neural circuit mechanisms of learning, memory and decision-making, across the animal kingdom (Cheng, 1997; Corrigan and Denton, 1996; FitzGerald et al., 2014; Gallistel, 2012, 2017; Goodman et al., 2011; Langille and Gallistel, 2020; Madarasz et al., 2016; Sawa, 2009; Tenenbaum et al., 2006, 2011). Further, given our demonstration that even apparently inflexible, “non-cognitive” behaviors can result from the use of retrospective cognitive maps, most animal learning may be model-based. This might explain the “ubiquity of model-based RL” (Doll et al., 2012).