Stability analysis and Hopf bifurcation in fractional order SEIRV epidemic model with a time delay in infected individuals

Abstract

Infectious diseases have been a constant cause of disaster in human population. Simultaneously, it provides motivation for math and biology professionals to research and analyze the systems that drive such illnesses in order to predict their long-term spread and management. During the spread of such diseases several kinds of delay come into play, owing to changes in their dynamics. Here, we have studied a fractional order dynamical system of susceptible, exposed, infected, recovered and vaccinated population with a single delay incorporated in the infectious population accounting for the time period required by the said population to recover. We have employed Adam–Bashforth–Moulton technique for deriving numerical solutions to the model system. The stability of all equilibrium points has been analyzed with respect to the delay parameter. Utilizing actual data from India COVID-19 instances, the parameters of the fractional order SEIRV model were calculated. Graphical demonstration and numerical simulations have been done with the help of MATLAB (2018a). Threshold values of the time delay parameter have been found beyond which the system exhibits Hopf bifurcation and the solutions are no longer periodic.

1. Introduction

Vaccination is one of the most effective measures in the prevention and control of highly contagious diseases like chicken pox, small pox, HIV, SARS, Swine flu, polio etc. It has been proved that vaccination may be considered as a key component in the anti-spread drive of such diseases. Among other measures, complete lockdown, semi lockdown, rationing, improvement of health services etc. may be mentioned. Considering the formidable challenge posed by the social, cultural, economic, demographic and geographical impact of such diseases on human population, it becomes necessary to discover methods of their prevention. From the inception of viral invasion into human community, scientists have constantly made efforts in the study of causes of newly infected cases of susceptible and exposed population, and the effect of vaccination on recovered population. Mathematical modeling of these epidemic diseases is very common in the related research where in the total population is primarily compartmentalized into the susceptible individuals $\left(S\right)$, the exposed individuals $\left(E\right)$, the infected individuals $\left(I\right)$ and the recovered individuals $\left(R\right)$. Another compartment of the population is considered to be the vaccinated individuals $\left(V\right)$. The dynamics of these variables are widely studied using integral order differential equations.[1], [2], [3], [4], [5], [6], [7], [8] In this communication, we have considered the Caputo derivative of order $0<\nu \le 1$ which is a special type of fractional order derivative to study the behavior of the spread of COVID-19 disease. Recently, an extensive investigation is being carried out to study the spread and prevention of corona virus disease which is reported to have a high fatality rate.[9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21] Kuang²² presents delay logistic equations, which are particularly applicable to epidemic systems. Mathematical models of epidemic systems with delay are discussed by Brauer and Chavez²³. Xu et al.²⁴ explore the effect of numerous time delays on fractional-order neural network bifurcation. For even more published articles, see Refs. [25], [26], [27], [28], [29], [30] Since it is quite natural that the infected population will take some time to recover, here, we have considered a single time delay in the infected population.

1.1. Motivation and novelties of the work

Fractional derivatives are an effective tool for understanding memory and inheritance in a variety of systems and situations. The essential information of a function is preserved in stacked format by fractional calculus. To study the dynamics of disease transmission, fractional-order modeling has been applied. Furthermore, whereas fractional derivative is not local, integer-order differentiation is. This tendency is beneficial in the modeling of epidemics. The Caputo derivative is extremely useful for discussing real-world situations since it enables conventional initial and boundary conditions to be used in the derivation, and the derivation of a constant is zero, which is not the fact with the Riemann–Liouville derivative. Epidemic models with time delay are more effective and realistic. Immunity period delays, infection period delays, latent period delays, and other delays are all frequent. Therefore, investigation of the role of delay is vital in the dynamics of epidemic models. Liu³¹ introduced a delayed $SEIS$ epidemic system and investigated the Hopf bifurcation by employing the time delay produced by the infected population’s cure period as the bifurcation parameter. Delay Differential Equations of epidemic models are also discussed in Refs. [32], [33], [34], [35], [36], [37], [38], [39], [40]. Motivated by early research, we explore the study of the disease’s impact using an appropriate mathematical model [$\mathit{SEIRV}$ model] in terms of the Caputo derivatives of the dynamical variables with a single delay parameter.

The objectives of the current work are:

• •To investigate the stability of a time-delayed fractional order $\mathit{SEIRV}$ model.
• •The basic reproduction number as well as the points of equilibrium are determined.
• •Existence of Hopf bifurcation at interior equilibrium point.
• •To obtain a numerical solution, the Adam–Bashforth–Moulton​ predictor–corrector technique is used.

1.2. Structure of the article

The construction of the $\mathit{SEIRV}$ model, as well as the establishing of non-negativity and boundedness of the solution and the calculation of the basic reproduction number, are all covered in Section 2. Section 3 comprises of the stability analysis of equilibrium points. Section 4 consists of the numerical solution of the model using Adam–Bashforth–Moulton method. Numerical Simulation using MATLAB is presented in Section 5. Section 6 consists of the conclusion.

2. Formulation

The total population $\left(N\right)$ is compartmentalized into five classes, namely, the susceptible individuals $\left(S\right)$, the exposed individuals $\left(E\right)$, the infected individuals $\left(I\right)$, the recovered individuals $\left(R\right)$ and the vaccinated individuals $\left(V\right)$ at any time $t\ge 0$. Thus

$$N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)+V\left(t\right).$$ (2.1)

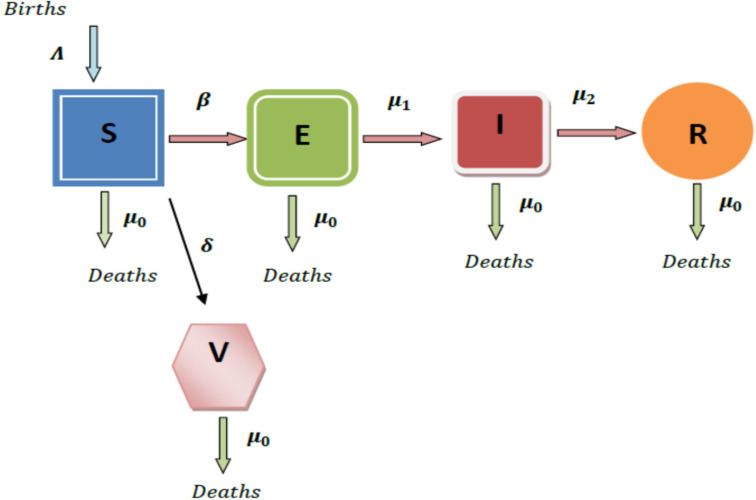
Fig. 1 depicts a flow diagram of the proposed $\mathit{SEIRV}$ model with vaccination.

Fig. 1.

Diagrammatic representation of the $\mathit{SEIRV}$ model.

The Caputo fractional derivative[41], [42], [43], [44], [45] of order $0<\nu \le 1$ is defined as

Definition 1

A function $h:{\mathbb{R}}^{+}\to \mathbb{R}$ with fractional order $0<\nu \le 1$, is defined as

$${}^C{I}_t^{\nu }\left(h\left(t\right)\right)=\frac{1}{\Gamma \left(\nu \right)}{\int }_0^t{(t-p)}^{\nu -1}h\left(p\right)dp,$$ (2.2)

here the Gamma function is denoted by $\Gamma \left(\right)$.

Definition 2

The Caputo derivative of order $0<\nu \le 1$, is defined as

$${}^C{I}_t^{\nu }\left(h\left(t\right)\right)=I^{n-\nu }{D}_t^{\nu }\left(h\left(t\right)\right)=\frac{1}{\Gamma \left(n-\nu \right)}{\int }_0^t{(t-p)}^{n-\nu -1}\frac{d^n}{d{p}^n}h\left(p\right)dp,$$ (2.3)

where $n-1<\nu <n$.

Definition 3

Let $h\in C\left[a,b\right],a<b$. The fractional derivative in Caputo sense or order $0<\nu \le 1$ is defined as

$${}^C{D}_t^{\nu }\left(h\left(t\right)\right)=\frac{M\left(\nu \right)}{(1-\nu )}{\int }_a^t{h}^{\prime }\left(p\right)exp\left(\text{–}\frac{\nu (t-p)}{1-\nu }\right)dp,$$ (2.4)

where the normalization function is denoted by $M\left(\nu \right)$ with $M\left(0\right)=M\left(1\right)=1$.

Definition 4

The Laplace transform for the fractional operator of order $0<\nu \le 1$ is defined as

$$L\left({}^C{D}_t^{\nu }\right)\left(h\left(t\right)\right)=p^{\nu }L\left(h\left(t\right)\right)-\sum _{i=0}^{k-1}{p}^{\nu -i-1}{h}^{\left(i\right)}\left(0\right),k-1<\nu \le k\in \mathbb{N}.$$ (2.5)

Definition 5

One-parametric and two-parametric Mittag-Leffler functions are described as follows: $E_{a_1}\left(p\right)={\sum }_{i=0}^{\infty }\frac{p^i}{\Gamma \left(a_{1}i+1\right)}$ and $E_{a_1,a_2}\left(p\right)={\sum }_{i=0}^{\infty }\frac{p^i}{\Gamma \left(a_{1}i+a_2\right)}$ where $a_1,a_2\in {\mathbb{R}}^{+}$.

Definition 6

For $a_1,a_2\in {\mathbb{R}}^{+}$ and $A\in {ℂ}^{n\times n}$ where $ℂ$ denotes complex plane, then

$$L\left\{t^{a_2-1}{E}_{a_1,a_2}\left(A{t}^{a_1}\right)\right\}=\frac{p^{a_1-a_2}}{p^{a_1}-A},\text{where}{E}_{a_1,a_2}:\text{Mittag-Leffler function}.$$ (2.6)

Lemma 1

Consider the following fractional order system:

$${}^C{D}_t^{\nu }\left(Y\left(t\right)\right)=\Phi \left(Y\right),Y_{t_0}=\left({y_{t_0}}^1,{y_{t_0}}^2,\dots ,{y_{t_0}}^n\right),{y_{t_0}}^j,j=1,2,\dots ,n$$

with $0<\nu <1,Y\left(t\right)=(y^1\left(t\right),y^2\left(t\right),\dots ,y^n\left(t\right))$ and $\Phi \left(Y\right):\left[t_0,\infty \right]\to {\mathbb{R}}^{n\times n}$ . For $\Phi \left(Y\right)=0$ , we get all the equilibrium points. These equilibrium points are locally asymptotically stable iff each eigen value ${\lambda }_j$ of the Jacobian matrix $J\left(Y\right)=\frac{\partial ({\Phi }_1,{\Phi }_2,\dots ,{\Phi }_n)}{\partial (y^1,y^2,\dots ,y^n)}$ calculated at the equilibrium points satisfies $|arg\left({\lambda }_j\right)|>\frac{\nu \pi }{2}$ .

Lemma 2

Let $h\left(t\right)\in {\mathbb{R}}^{+}$ be a differentiable function. Then, for any $t>0$ ,

$${}^C{D}_t^{\nu }\left[h\left(t\right)-h^{\ast }-h^{\ast }ln\frac{h\left(t\right)}{h^{\ast }}\right]\le \left(1-\frac{h^{\ast }}{h\left(t\right)}\right){}^C{D}_t^{\nu }\left(h\left(t\right)\right),h^{\ast }\in {\mathbb{R}}^{+},\forall \nu \in \left(0,1\right).$$

The integral order $\mathit{SEIRV}$ model ^{46 , 47} with vaccination as a dynamical variable is as follows:

$${\mathrm{D}}_{\mathrm{t}}\mathrm{S}\left(\mathrm{t}\right)=\Lambda -\beta S\left(t\right)I\left(t\right)-{\mu }_{0}S\left(t\right)-\delta S\left(t\right)$$

$${\mathrm{D}}_{\mathrm{t}}\mathrm{E}\left(\mathrm{t}\right)=\beta S\left(t\right)I\left(t\right)-({\mu }_0+{\mu }_1)E\left(t\right),$$ (2.7)

$${\mathrm{D}}_{\mathrm{t}}\mathrm{I}\left(\mathrm{t}\right)={\mu }_{1}E\left(t\right)-({\mu }_0+{\mu }_2)I\left(t\right)$$

$${\mathrm{D}}_{\mathrm{t}}\mathrm{R}\left(\mathrm{t}\right)={\mu }_{2}I\left(t\right)-{\mu }_{0}R\left(t\right)$$

$${\mathrm{D}}_{\mathrm{t}}\mathrm{V}\left(\mathrm{t}\right)=\delta S\left(t\right)-{\mu }_{0}V\left(t\right)$$

where

$\Lambda$ : birth rate of $S$ ,

$\beta$ : infection rate of $S$ ,

${\mu }_0$ : mortality rate of $I$ ,

$\delta$ : vaccination rate,

${\mu }_1$ : progression rate from $E$ to $I$ ,

${\mu }_2$ : recovery rate of $I$ .

In this presentation, we analyze the $\mathit{SEIRV}$ model with time delay using Caputo operator of order $0<\nu \le 1$.

$${}^C{D}_t^{\nu }S\left(t\right)={\Lambda }^{\nu }-{\beta }^{\nu }S\left(t\right)I\left(t\right)-{{\mu }_0}^{\nu }S\left(t\right)-{\delta }^{\nu }R\left(t\right),$$

$${}^C{D}_t^{\nu }E\left(t\right)={\beta }^{\nu }S\left(t\right)I\left(t\right)-({{\mu }_0}^{\nu }+{{\mu }_1}^{\nu })E\left(t\right),$$ (2.8)

$${}^C{D}_t^{\nu }I\left(t\right)={{\mu }_1}^{\nu }E\left(t\right)-{{\mu }_0}^{\nu }I\left(t\right)-{{\mu }_2}^{\nu }I\left(t\right),$$

$${}^C{D}_t^{\nu }R\left(t\right)={{\mu }_2}^{\nu }I\left(t\right)-{{\mu }_0}^{\nu }R\left(t\right),$$

$${}^C{D}_t^{\nu }\mathrm{V}\left(\mathrm{t}\right)={\delta }^{\nu }S\left(t\right)-{{\mu }_0}^{\nu }V\left(t\right).$$

The time dimension of the system (2.8) is confirmed to be valid, even though both sides have dimension ${\left(time\right)}^{-\nu }$. Let $t_0=0$ and ignore the super script $\nu$ and the system becomes:

$${}^C{D}_t^{\nu }\mathrm{S}\left(\mathrm{t}\right)=\Lambda -\beta S\left(t\right)I\left(t\right)-{\mu }_{0}S\left(t\right)-\delta S\left(t\right),$$

$${}^C{D}_t^{\nu }\mathrm{E}\left(\mathrm{t}\right)=\beta S\left(t\right)I\left(t\right)-({\mu }_0+{\mu }_1)E\left(t\right),$$ (2.9)

$${}^C{D}_t^{\nu }\mathrm{I}\left(\mathrm{t}\right)={\mu }_{1}E\left(t\right)-{\mu }_{0}I\left(t\right)-{\mu }_{2}I(t-{\eta }_1),$$

$${}^C{D}_t^{\nu }\mathrm{R}\left(\mathrm{t}\right)={\mu }_{2}I(t-{\eta }_1)-{\mu }_{0}R\left(t\right),$$

$${}^C{D}_t^{\nu }\mathrm{V}\left(\mathrm{t}\right)=\delta S\left(t\right)-{\mu }_{0}V\left(t\right),$$

where ${\eta }_1$ is the time delay describing the period of cure the infected individuals.

The initial conditions are

$$S\left(\phi \right)={\psi }_1\left(\phi \right),E\left(\phi \right)={\psi }_2\left(\phi \right),I\left(\phi \right)={\psi }_3\left(\phi \right),R\left(\phi \right)={\psi }_4\left(\phi \right),V\left(\phi \right)={\psi }_5\left(\phi \right),\left(-{\eta }_1\le \phi \le 0\right),$$ (2.10)

where $\psi$ =${\left({\psi }_1,{\psi }_2,{\psi }_3,{\psi }_4,{\psi }_5\right)}^T\in B$, such that ${\psi }_i\left(\phi \right)\ge 0,i=1,2,3,4,5$. Where $\mathrm{B}$ denotes the Banach space of continuous mapping from the interval $[-{\eta }_1,0]$ to ${\mathbb{R}}^5$. We presume, by biological meaning, that ${\psi }_i\left(\phi \right)>0$ for $i=1,2,3,4,5$.

Non-negativity and boundedness

Theorem 2.1

The closed region $\Omega =\{(S,E,I,R,V)\in {\mathbb{R}}^5:0<N\le \frac{\Lambda }{{\mu }_0}\}$ is non-negative invariant of system (2.9) for all $t\ge 0$ .

Proof

We have

$${}^C{D}_t^{\nu }(S+E+I+R+V)\left(t\right)=\lambda -{\mu }_0(S+E+I+R)\left(t\right).$$

• •
  $${}^C{D}_t^{\nu }N\left(t\right)=\lambda -{\mu }_{0}N\left(t\right)$$
• •
  $${}^C{D}_t^{\nu }N\left(t\right)+{\mu }_{0}N\left(t\right)=\lambda .$$ (2.11)

  Applying Laplace transforms, we get

  $$p^{\nu }L\left(N\left(t\right)\right)-p^{\nu -1}N\left(0\right)+{\mu }_{0}L\left(N\left(t\right)\right)=\frac{\lambda }{p}$$
• •
  $$L\left(N\left(t\right)\right)\left(p^{\nu +1}+{\mu }_0\right)=p^{\nu }N\left(0\right)+\lambda$$
• •
  $$L\left(N\left(t\right)\right)=\frac{p^{\nu }N\left(0\right)+\lambda }{p^{\nu +1}+{\mu }_0}=\frac{p^{\nu }N\left(0\right)}{p^{\nu +1}+{\mu }_0}+\frac{\lambda }{p^{\nu +1}+{\mu }_0}.$$ (2.12)

Taking inverse Laplace transform, we have

$$N\left(t\right)=N\left(0\right)E_{\nu ,1}\left(-{\mu }_0{t}^{\nu }\right)+\lambda t^{\nu }{E}_{\nu ,\nu +1}\left(-{\mu }_0{t}^{\nu }\right).$$ (2.13)

According to Mittag-Leffler function,

$$E_{c,d}\left(z\right)=z{E}_{c,c+d}\left(z\right)+\frac{1}{\Gamma \left(d\right)}$$

Hence,

$$N\left(t\right)=\left(N\left(0\right)-\frac{\lambda }{{\delta }_0}\right)E_{\nu ,1}\left(-{\mu }_0{t}^{\nu }\right)+\frac{\lambda }{{\mu }_0}$$

Thus

$$\underset{t\to \infty }{lim}SupN\left(t\right)\le \frac{\lambda }{{\mu }_0}.$$ (2.14)

And hence the model (2.9) is bounded above by $\frac{\lambda }{{\mu }_0}$.

Thus $S,E,I,R$, and $V$ are all non-negative, and the model (2.9) is non-negative invariant.

Basic reproduction number

The basic reproduction number ${\mathfrak{R}}_0$ provides the number of secondary cases induced by single susceptible individual.

Using next generation matrix method,^{48 , 49} ${\mathfrak{R}}_0$ can be determined from the maximum eigen value of $\mathcal{F}{V}^{-1}$ where,

$$\mathcal{F}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill \frac{\beta \Lambda }{{\mu }_0+\delta }\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{and}V=\left[\begin{array}{cc}\hfill {\mu }_0+{\mu }_1\hfill & \hfill 0\hfill \\ \hfill -{\mu }_1\hfill & \hfill {\mu }_0+{\mu }_2\hfill \end{array}\right].$$

Therefore, the reproduction number

$${\mathfrak{R}}_0=\frac{\beta \Lambda {\mu }_1}{\left({\mu }_0+\delta \right)\left({\mu }_0+{\mu }_1\right)({\mu }_0+{\mu }_2)}.$$ (2.15)

3. Stability analysis

The disease-free equilibrium points $E_0$ and the epidemic equilibrium point $E_1$ of are obtained from

$${}^C{D}_t^{\nu }S\left(t\right)={}^C{D}_t^{\nu }E\left(t\right)={}^C{D}_t^{\nu }I\left(t\right)={}^C{D}_t^{\nu }R\left(t\right)={}^C{D}_t^{\nu }V\left(t\right)=0.$$ (3.1)

We have $E_0=\frac{\Lambda }{{\mu }_0+\delta },0,0,0,\frac{\Lambda \delta }{{\mu }_0({\mu }_0+\delta )}$) and $E_1=(S^{\ast },E^{\ast },I^{\ast },R^{\ast },V^{\ast })$,

where $S^{\ast }=\frac{\left({\mu }_0+{\mu }_1\right)({\mu }_0+{\mu }_2)}{\beta {\mu }_1}$, $E^{\ast }=\frac{({\mu }_0+{\mu }_2)}{{\mu }_1}{I}^{\ast }$, $I^{\ast }=\frac{\Lambda {\mu }_1}{\left({\mu }_0+{\mu }_1\right)({\mu }_0+{\mu }_2)}-\frac{{\mu }_0+\delta }{\beta }$,

$R^{\ast }=\frac{{\mu }_2}{{\mu }_0}{I}^{\ast }$, $V^{\ast }=\frac{\left({\mu }_0+{\mu }_1\right)({\mu }_0+{\mu }_2)\delta }{\beta {\mu }_0{\mu }_1}$.

Now we consider the community matrix of the model (2.9) at $E_0$ is given by

$$J_0=P+Q{e}^{-\lambda {\eta }_1},$$

where

$$P=\left[\begin{array}{ccccc}\hfill P_{11}\hfill & \hfill 0\hfill & \hfill P_{13}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill P_{22}\hfill & \hfill P_{23}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill P_{32}\hfill & \hfill P_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill P_{44}\hfill & \hfill 0\hfill \\ \hfill P_{51}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill P_{55}\hfill \end{array}\right],Q=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill Q_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill Q_{43}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$$

with $P_{11}=-(\delta +{\mu }_0)$, $P_{13}=-\beta S_0$, $P_{22}=-({\mu }_1+{\mu }_0)$, $P_{23}=\beta S_0,P_{32}={\mu }_1$, $P_{33}=-{\mu }_0,P_{44}=-{\mu }_0,P_{51}=\delta ,P_{55}=-{\mu }_0,Q_{33}=-{\mu }_2,Q_{43}={\mu }_2$.

Theorem 3.1

When ${\mathfrak{R}}_0$ < 1, the equilibrium point $E_0$ of the model (2.9) is locally asymptotically stable, and when ${\mathfrak{R}}_0>1$ , it is unstable in the absence of time delay.

Proof

The characteristic equation of $J_0$ is given by determinant $\left(P+Q-\lambda I_5\right)=0$.

The roots of the characteristic equation are $-{\mu }_0$, $-{\mu }_0$, $-(\delta +{\mu }_0)$ and ${\lambda }^2-\lambda \left(P_{22}+P_{33}+Q_{33}\right)+\left(P_{22}{P}_{33}+P_{22}{Q}_{33}-P_{23}{P}_{32}\right)=0$.

The roots are negative if $\left(P_{22}+P_{33}+Q_{33}\right)<0$ and $\left(P_{22}{P}_{33}+P_{22}{Q}_{33}-P_{23}{P}_{32}\right)>0$, using Routh–Hurwitz Criterion.

Now $\left(P_{22}{P}_{33}+P_{22}{Q}_{33}-P_{23}{P}_{32}\right)>0$

$$=>\left({\mu }_1+{\mu }_0\right)\left({\mu }_0+{\mu }_2\right)-\frac{\beta \Lambda {\mu }_1}{\left({\mu }_0+\delta \right)}>0$$

$$=>{\mathfrak{R}}_0<1$$

Therefore the point $E_0$ is locally asymptotically stable or unstable according as ${\mathfrak{R}}_0<1$or ${\mathfrak{R}}_0>1$.

Theorem 3.2

The equilibrium point $E_0$ of the model (2.9) is locally asymptotically stable when ${\eta }_1\in [0,{{\eta }_1}^{\ast }]$ , ${{\eta }_1}^{\ast }=\frac{1}{k}si{n}^{-1}\left(\frac{vx+uy}{x^2+y^2}\right)$ .

Proof

The characteristic equation of $J_0$ is given by determinant $\left(P+Q{e}^{-\lambda {\eta }_1}-\lambda I_5\right)=0$.

Now

$$({\lambda }^5+P_4{\lambda }^4+P_3{\lambda }^3+P_2{\lambda }^2+P_1\lambda +P_0)+\left(Q_4{\lambda }^4+Q_3{\lambda }^3+Q_2{\lambda }^2+Q_1\lambda \right)e^{-\lambda {\eta }_1}=0$$ (3.2)

Where

$$P_4=-\left(P_{11}+P_{22}+P_{33}+P_{44}+P_{55}\right),$$

$$P_3=\left(P_{11}+P_{44}+P_{55}\right)\left(P_{22}+P_{33}\right)\left(P_{11}{P}_{44}+P_{11}{P}_{55}+P_{44}{P}_{55}\right)-(P_{22}{P}_{33}-P_{23}{P}_{32}),$$

$$P_2=\left[-P_{11}{P}_{44}{P}_{55}-\left(P_{11}{P}_{44}+P_{11}{P}_{55}+P_{44}{P}_{55}\right)\left(P_{22}+P_{33}\right)\right)-\left(\left(P_{11}+P_{44}+P_{55}\right)\left(P_{22}{P}_{33}-P_{23}{P}_{32}\right)\right],$$

$$P_1=[P_{11}{P}_{44}{P}_{55}\left(P_{22}+P_{33}\right)+(P_{11}{P}_{44}+P_{11}{P}_{55}+P_{44}{P}_{55})(P_{22}{P}_{33}-P_{23}{P}_{32})],$$

$$P_0=-P_{11}{P}_{44}{P}_{55}\left(P_{22}{P}_{33}-P_{23}{P}_{32}\right),$$

$$Q_4=-Q_{33},$$

$$Q_3=Q_{33}(P_{11}+P_{44}+P_{55}),$$

$$Q_2=-Q_{33}\left(P_{11}{P}_{44}+P_{11}{P}_{55}+P_{44}{P}_{55}\right),$$

$$Q_1=Q_{33}\left(P_{11}{P}_{44}{P}_{55}\right).$$

Let $\lambda =ik$ be a root of the Eq. (3.2), then we have

$$xcos\left(k{\eta }_1\right)+ysin\left(k{\eta }_1\right)=u,xsin\left(k{\eta }_1\right)-ycos\left(k{\eta }_1\right)=v,$$ (3.3)

where

$$x=Q_2{k}^2-Q_4{k}^4,y=Q_3{k}^3-Q_{1}k,u=P_4{k}^4-P_2{k}^2+P_0,v=k^5+P_3{k}^3-P_{1}k$$

We find that

$$x^2+y^2=u^2+v^2=>k^{10}+R_4{k}^8+R_3{k}^6+R_2{k}^4+R_1{k}^2+R_0=0,$$ (3.4)

where

$$R_4=2P_3+{P_4}^2-{Q_4}^2,R_3={P_3}^2-2P_1-2P_4{P}_2-{Q_3}^2+2Q_2{Q}_4,$$

$$R_2=-2P_1{P}_3+{P_2}^2+2P_0{P}_4+2Q_1{Q}_3-{Q_2}^2,$$

$$R_1={P_1}^2-2P_0{P}_2-{Q_1}^2,R_0={P_0}^2.$$

Putting $k^2=t$ in Eq. (3.4), then we have

$$t^5+R_4{t}^4+R_3{t}^3+R_2{t}^2+R_{1}t+R_0=0.$$ (3.5)

If ${t_1}^{\ast }$ is a positive root in Eq. (3.5), then $k=\sqrt{{t_1}^{\ast }}$ is a positive root in Eq. (3.4). Eliminating $cos\left(k{\eta }_1\right)$ from the Eq. (3.3), we obtain

$${{\eta }_1}^{\ast }=\frac{1}{k}si{n}^{-1}\left(\frac{vx+uy}{x^2+y^2}\right)$$

Theorem 3.3

When ${\mathfrak{R}}_0$ < 1, the equilibrium point $E_0$ of the model (2.9) is globally asymptotically stable, and unstable when ${\mathfrak{R}}_0>1$ for any positive ${\eta }_1$ .

Proof

Consider the suitable Lyapunov function:

$$\mathcal{F}\left(\mathrm{t}\right)={\mathcal{F}}_1+{\mathcal{F}}_2$$

where,

$${\mathcal{F}}_1=\left({\mu }_1\right)\mathrm{E}\left(\mathrm{t}\right)+\left({\mu }_0+{\mu }_1\right)\mathrm{I}\left(\mathrm{t}\right)\text{ and}{\mathcal{F}}_2=-{\int }_{\mathrm{t}-{\eta }_1}^{\mathrm{t}}\mathrm{I}\left(\mathrm{z}\right)\mathrm{dz}$$

Taking fractional derivative, we get

$${}^C{D}_t^{\nu }\mathcal{F}\left(t\right)={}^C{D}_t^{\nu }{\mathcal{F}}_1\left(t\right)+{}^C{D}_t^{\nu }{\mathcal{F}}_2\left(t\right)$$

From (2.5) we get,

$${}^C{D}_t^{\nu }\mathcal{F}\left(\mathrm{t}\right)=[{\mu }_1\beta S\left(t\right)I\left(t\right)-\left({\mu }_0+{\mu }_1\right)\left({\mu }_0+{\mu }_2\right)I\left(t\right)].$$ (3.6)

Now,

$${}^C{D}_t^{\nu }\mathcal{F}\left(\mathrm{t}\right)=[\beta S{\mu }_1-\left({\mu }_0+{\mu }_1\right)\left({\mu }_0+{\mu }_2\right)]I$$

Since $S=\frac{\Lambda }{{\mu }_0+\delta }$, it follows that

$${}^C{D}_t^{\nu }\mathcal{F}\left(t\right)=I\left[\left({\mu }_0+{\mu }_1\right)({\mu }_0+{\mu }_2)\right][\frac{\beta \Lambda {\mu }_1}{\left({\mu }_0+\delta \right)\left({\mu }_0+{\mu }_1\right)({\mu }_0+{\mu }_2)}-1]=I\left[\left({\mu }_0+{\mu }_1\right)({\mu }_0+{\mu }_2)\right][{\mathfrak{R}}_0-1].$$

Hence if ${\mathfrak{R}}_0<1$, then ${}^C{D}_t^{\nu }\mathcal{F}\left(\mathrm{t}\right)<0$. As a result of LaSalle’s extension to Lyapunov’s principle,^{50 , 51} $E_0$ is globally asymptotically stable and unstable if ${\mathfrak{R}}_0>1$.

Theorem 3.4

If ${\mathfrak{R}}_0>1$ , the equilibrium point $E_1=(S^{\ast },E^{\ast },I^{\ast },R^{\ast },V^{\ast })$ is locally asymptotically stable when ${\eta }_1=0$ .

Proof

The characteristic equation of the system (2.9) at the epidemic equilibrium $E_1$ is $\left(-{\mu }_0-\lambda \right)\left(-{\mu }_0-\lambda \right)$ (${\lambda }^3+A{\lambda }^2+B\lambda +C)=0$.

where

$$A=-\left(G_{11}+G_{22}+G_{33}+H_{33}\right),$$

$$B=G_{11}\left(G_{22}+G_{33}+H_{33}\right)+\left(G_{22}{G}_{33}-G_{23}{G}_{32}+G_{13}{G}_{21}{G}_{32}\right),$$

$$C=-G_{11}(G_{22}{G}_{33}-G_{23}{G}_{32}+G_{13}{G}_{21}{G}_{32}),$$

with

$$G_{11}=-\beta I^{\ast }-\delta -{\mu }_0,G_{22}=-{\mu }_0-{\mu }_1,G_{33}=-{\mu }_0,H_{33}=-{\mu }_2,G_{13}=-\beta S^{\ast },G_{23}=\beta S^{\ast },G_{32}={\mu }_1,G_{21}=\beta I^{\ast },G_{23}=\beta I^{\ast }.$$

Using Routh–Hurwitz Criterion, the system (2.9) is locally asymptotically stable at $E_1$ as $A>0,C>0,AB>C$.

Theorem 3.5

The epidemic equilibrium $E_1=(S^{\ast },E^{\ast },I^{\ast },R^{\ast },V^{\ast })$ of the system (2.9) is locally asymptotically stable when ${\eta }_1\in [0,{{\eta }_1}^{\ast }]$ , ${{\eta }_1}^{\ast }=\frac{1}{m_{10}}si{n}^{-1}\left(\frac{ad+bc}{a^2+b^2}\right)$ ; system (2.9) undergoes a Hopf bifurcation at $E_1$ when ${\eta }_1={{\eta }_1}^{\ast }$ .

Proof

The characteristic equation of the system (2.9) at the epidemic equilibrium $E_1$ is given by determinant $\left(G+H{e}^{-\lambda {\eta }_1}-\lambda I_5\right)=0$.

Now

$${\lambda }^5+A_4{\lambda }^4+A_3{\lambda }^3+A_2{\lambda }^2+A_1\lambda +A_0+\left(B_4{\lambda }^4+B_3{\lambda }^3+B_2{\lambda }^2+B_1\lambda +B_0\right)e^{-\lambda {\eta }_1}=0.$$ (3.7)

where

$$A_4=-\left(G_{11}+G_{22}+G_{33}+G_{44}+G_{55}\right),$$

$$A_3=(G_{11}{G}_{22}-G_{23}{G}_{32}+G_{11}{G}_{33}+G_{22}{G}_{33}+G_{11}{G}_{44}+G_{22}{G}_{44}+G_{33}{G}_{44}+G_{11}{G}_{55}+G_{22}{G}_{55}+G_{33}{G}_{55}),$$

$$A_2=\left[-G_{13}{G}_{21}{G}_{32}+G_{11}{G}_{23}{G}_{32}-G_{11}{G}_{22}{G}_{33}-G_{11}{G}_{22}{G}_{44}+G_{23}{G}_{32}{G}_{44}\right)-G_{11}{G}_{33}{G}_{44}-G_{22}{G}_{33}{G}_{44}-G_{11}{G}_{22}{G}_{55}+G_{23}{G}_{32}{G}_{55}-G_{11}{G}_{33}{G}_{55}-G_{22}{G}_{33}{G}_{55}+G_{44}{G}_{55}-G_{11}{G}_{44}{G}_{55}-\left(G_{22}{G}_{44}{G}_{55}-G_{33}{G}_{44}{G}_{55}\right],$$

$$A_1=[G_{13}{G}_{21}{G}_{32}{G}_{44}-G_{11}{G}_{23}{G}_{32}{G}_{44}+G_{11}{G}_{22}{G}_{33}{G}_{44}+G_{13}{G}_{21}{G}_{32}{G}_{55}-G_{11}{G}_{23}{G}_{32}{G}_{55}+G_{11}{G}_{22}{G}_{33}{G}_{55}+G_{11}{G}_{22}{G}_{44}{G}_{55}-G_{23}{G}_{32}{G}_{44}{G}_{55}+G_{11}{G}_{33}{G}_{44}{G}_{55}+G_{22}{G}_{33}{G}_{44}{G}_{55}],$$

$$A_0=-G_{13}{G}_{21}{G}_{32}{G}_{44}{G}_{55}+G_{11}{G}_{23}{G}_{32}{G}_{44}{G}_{55}-G_{11}{G}_{22}{G}_{33}{G}_{44}{G}_{55},$$

$$B_4=-H_{33},$$

$$B_3=G_{11}{H}_{33}+G_{22}{H}_{33}+G_{44}{H}_{33}+G_{55}{H}_{33},$$

$$B_2=-G_{11}{G}_{22}{H}_{33}-G_{11}{G}_{44}{H}_{33}-G_{22}{G}_{44}{H}_{33}-G_{11}{G}_{55}{H}_{33}-G_{22}{G}_{55}{H}_{33}-G_{44}{G}_{55}{H}_{33},$$

$$B_1=G_{11}{G}_{22}{G}_{44}{H}_{33}+G_{11}{G}_{22}{G}_{55}{H}_{33}+G_{11}{G}_{44}{G}_{55}{H}_{33}+G_{22}{G}_{44}{G}_{55}{H}_{33},$$

$$B_0=G_{11}{G}_{22}{G}_{44}{G}_{55}{H}_{33},$$

with $G=\left[\begin{array}{ccccc}\hfill G_{11}\hfill & \hfill 0\hfill & \hfill G_{13}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill G_{21}\hfill & \hfill G_{22}\hfill & \hfill G_{23}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill G_{32}\hfill & \hfill G_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill G_{44}\hfill & \hfill 0\hfill \\ \hfill G_{51}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill G_{55}\hfill \end{array}\right]$, $H=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill H_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill H_{43}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$,

where $G_{11}=-(\beta I^{\ast }+\delta +{\mu }_0)$, $G_{13}=-\beta S^{\ast }$, $G_{21}=\beta I^{\ast },G_{22}=-({\mu }_1+{\mu }_0)$, $G_{23}=\beta S^{\ast },G_{32}={\mu }_1$, $G_{33}=-{\mu }_0,G_{44}=-{\mu }_0,G_{51}=\delta ,G_{55}=-{\mu }_0,H_{33}=-{\mu }_2,H_{43}={\mu }_2$.

If we consider $\lambda$ $=i{m}_1$ to be a root of the Eq. (3.7), we get

$$acos\left(m_1{\eta }_1\right)+bsin\left(m_1{\eta }_1\right)=c,asin\left(m_1{\eta }_1\right)-bcos\left(m_1{\eta }_1\right)=d,$$ (3.8)

where

$$a=B_2{m_1}^2-B_4{m_1}^4-B_0,b=B_3{m_1}^3-B_1{m}_1,c=A_4{m_1}^4-A_2{m_1}^2+A_0,d={m_1}^5+A_3{m_1}^3-A_1{m}_1$$

Now we have

$$a^2+b^2=c^2+d^2=>{m_1}^{10}+L_4{m_1}^8+L_3{m_1}^6+L_2{m_1}^4+L_1{m_1}^2+L_0=0,$$ (3.9)

where

$$L_4=2A_3+{A_4}^2-{B_4}^2,L_3={A_3}^2-2A_1-2A_4{A}_2-{B_3}^2+2B_2{B}_4,$$

$$L_2=-2A_1{A}_3+{A_2}^2+2A_0{A}_4+2B_1{B}_3-{B_2}^2+2B_0{B}_4,$$

$$L_1={A_1}^2-2A_0{A}_2-{B_1}^2-2B_0{B}_2,$$

$$L_0={A_0}^2-{B_0}^2.$$

Put ${m_1}^2=j$ in Eq. (3.9), then we have

$$j^5+L_4{j}^4+L_3{j}^3+L_2{j}^2+L_{1}j+L_0=0.$$ (3.10)

Now consider that

Case-1: If $j_0$ is a positive root in Eq. (3.10), then $m_{10}=\sqrt{j_0}$ is a positive root in Eq. (3.9).

Eliminating $cos\left(m_1{\eta }_1\right)$ from (3.8) and substituting $m_1=m_{10}$, where $m_{10}$ is a positive root of Eq. (3.9), we have

$${{\eta }_1}^{\ast }=\frac{1}{m_{10}}si{n}^{-1}\left(\frac{ad+bc}{a^2+b^2}\right)$$

Now, by differentiating Eq. (3.7) with regard to ${\eta }_1$ and simplifying with $\lambda$ $=i{m}_{10}$, we get

$$\text{Re}{{\left[\frac{d\lambda }{d{\eta }_1}\right]}^{-1}}_{\lambda =i{m}_{10}}=\frac{f_1^{\prime }\left(j_0\right)}{a^2+b^2}$$ (3.11)

Therefore, Re ${{\left[\frac{d\lambda }{d{\eta }_1}\right]}^{-1}}_{\lambda =i{m}_{10}}\ne 0$ if the condition

$f_1^{\prime }\left(j_0\right)=\frac{d{f}_1\left(j\right)}{dj}\ne 0$ at $j=j_0$ holds, where $f_1\left(j\right)=j^5+L_4{j}^4+L_3{j}^3+L_2{j}^2+L_{1}j+L_0$.

Thus, according to the Hopf bifurcation theorem,⁵² we obtain the result of Theorem 3.5 if Case-1 hold.

Theorem 3.6

The epidemic equilibrium $E_1$ is globally asymptotically stable if ${\mathfrak{R}}_0>1$ .

Proof

Consider the non-linear Lyapunov function:

$$W\left(t\right)=\left(S\left(t\right)-S^{\ast }-S^{\ast }log\frac{S\left(t\right)}{S^{\ast }}\right)+\left(E\left(t\right)-E^{\ast }-E^{\ast }log\frac{E\left(t\right)}{E^{\ast }}\right)+Q\left(I\left(t\right)-I^{\ast }-I^{\ast }log\frac{I\left(t\right)}{I^{\ast }}\right).$$

Using Lemma 2 and taking the fractional derivative of $W\left(t\right)$ with respect to time is,

$${}^C{D}_t^{\nu }W\left(t\right)\le \left(1-\frac{S^{\ast }}{S\left(t\right)}\right){}^C{D}_t^{\nu }S\left(t\right)+\left(1-\frac{E^{\ast }}{E\left(t\right)}\right){}^C{D}_t^{\nu }E\left(t\right)+Q\left(1-\frac{I^{\ast }}{I\left(t\right)}\right){}^C{D}_t^{\nu }\mathrm{I}\left(\mathrm{t}\right).$$ (3.12)

Using system (2.9) we get,

$${}^C{D}_t^{\nu }W\left(t\right)\le \left(\Lambda -\beta S\left(t\right)I\left(t\right)-{\mu }_{0}S\left(t\right)-\delta S\left(t\right)-\frac{S^{\ast }(\Lambda -\beta S\left(t\right)I\left(t\right)-{\mu }_{0}S\left(t\right)-\delta S\left(t\right))}{S\left(t\right)}\right)+\left((\beta S\left(t\right)I\left(t\right)-\left({\mu }_0+{\mu }_1\right)E\left(t\right))-\frac{E^{\ast }(\beta S\left(t\right)I\left(t\right)-\left({\mu }_0+{\mu }_1\right)E\left(t\right))}{E\left(t\right)}\right)+Q\left(({\mu }_{1}E\left(t\right)-{\mu }_{0}I\left(t\right)-{\mu }_{2}I(\mathrm{t}-{\eta }_1))-\frac{I^{\ast }\left({\mu }_{1}E\left(t\right)-{\mu }_{0}I\left(t\right)-{\mu }_{2}I(\mathrm{t}-{\eta }_1)\right)}{I\left(t\right)}\right).$$ (3.13)

We have Eq. (2.9) in steady state,

$$\Lambda =\beta S^{\ast }{I}^{\ast }+{\mu }_0{S}^{\ast }+\delta S^{\ast }.$$ (3.14)

Substituting Eq. (3.14) into (3.13) we have,

$${}^C{D}_t^{\nu }W\left(t\right)\le \left(\beta S^{\ast }{I}^{\ast }+{\mu }_0{S}^{\ast }+\delta S^{\ast }-\beta S\left(t\right)I\left(t\right)-{\mu }_{0}S\left(t\right)-\delta S\left(t\right)\right)-\left(\frac{S^{\ast }(\beta S^{\ast }{I}^{\ast }+{\mu }_0{S}^{\ast }+\delta S^{\ast }-\beta S\left(t\right)I\left(t\right)-{\mu }_{0}S\left(t\right)-\delta S\left(t\right))}{S\left(t\right)}\right)+\left((\beta S\left(t\right)I\left(t\right)-\left({\mu }_0+{\mu }_1\right)E\left(t\right))-\frac{E^{\ast }(\beta S\left(t\right)I\left(t\right)-\left({\mu }_0+{\mu }_1\right)E\left(t\right))}{E\left(t\right)}\right)+Q\left(({\mu }_{1}E\left(t\right)-{\mu }_{0}I\left(t\right)-{\mu }_{2}I(\mathrm{t}-{\eta }_1))\right)\left(-\frac{I^{\ast }\left({\mu }_{1}E\left(t\right)-{\mu }_{0}I\left(t\right)-{\mu }_{2}I(\mathrm{t}-{\eta }_1)\right)}{I\left(t\right)}\right).$$

Further simplification gives,

$${}^C{D}_t^{\nu }W\left(t\right)\le \left(\beta S^{\ast }{I}^{\ast }+{\mu }_0{S}^{\ast }+\delta S^{\ast }-{\mu }_{0}S\left(t\right)-\delta S\left(t\right)\right)-\left(\frac{S^{\ast }(\beta S^{\ast }{I}^{\ast }+{\mu }_0{S}^{\ast }+\delta S^{\ast }-\beta S\left(t\right)I\left(t\right)-{\mu }_{0}S\left(t\right)-\delta S\left(t\right))}{S\left(t\right)}\right)+\left((-\left({\mu }_0+{\mu }_1\right)E\left(t\right))-\frac{E^{\ast }(\beta S\left(t\right)I\left(t\right)-\left({\mu }_0+{\mu }_1\right)E\left(t\right))}{E\left(t\right)}\right)+Q\left(({\mu }_{1}E\left(t\right)-{\mu }_{0}I\left(t\right)-{\mu }_{2}I(\mathrm{t}-{\eta }_1))\right)-\left(\frac{I^{\ast }\left({\mu }_{1}E\left(t\right)-{\mu }_{0}I\left(t\right)-{\mu }_{2}I(\mathrm{t}-{\eta }_1)\right)}{I\left(t\right)}\right).$$ (3.15)

Collecting all infected classes from (3.15) to zero without a single star (*):

$$S^{\ast }\beta I\left(t\right)-\left({\mu }_0+{\mu }_1\right)E\left(t\right)+Q\left({\mu }_{1}E\left(t\right)--{\mu }_{0}I\left(t\right)-{\mu }_{2}I(\mathrm{t}-{\eta }_1)\right)=0.$$ (3.16)

The steady state of equilibrium point (2.9), we get

$$Q=\frac{S^{\ast }\beta }{\left({\mu }_0+{\mu }_2\right)},\left({\mu }_0+{\mu }_1\right)=\frac{I^{\ast }{S}^{\ast }\beta }{E^{\ast }},{\mu }_1=\frac{({\mu }_0+{\mu }_2)I^{\ast }}{E^{\ast }}.$$ (3.17)

Substituting the expression from (3.17) into (3.15) gives:

$${}^C{D}_t^{\nu }W\left(t\right)\le \left(\beta S^{\ast }{I}^{\ast }+{\mu }_0{S}^{\ast }+\delta S^{\ast }-{\mu }_{0}S-\delta S\left(t\right)\right)-\left(\frac{S^{\ast }(\beta S^{\ast }{I}^{\ast }+{\mu }_0{S}^{\ast }-{\mu }_{0}S-\delta S)}{S}\right)+\left(-\frac{E^{\ast }\beta SI}{E}+I^{\ast }{S}^{\ast }\beta \right)+(-\frac{I^{\ast }{S}^{\ast }E\beta I^{\ast }}{I{E}^{\ast }}+\beta S^{\ast }{I}^{\ast }).$$

Using $A.M.\ge G.M.$, we get:

$$(2-\frac{s}{S^{\ast }}-\frac{S^{\ast }}{S})\le 0,(3-\frac{S^{\ast }}{S}-\frac{I^{\ast }E}{I{E}^{\ast }}-\frac{S{E}^{\ast }I}{E})\le 0.$$

Thus

$${}^C{D}_t^{\nu }W\left(t\right)\le 0\text{for}{\mathfrak{R}}_0>1$$

Therefore $E_1$ is globally asymptotically stable, according to LaSalle’s Invariance Principle.⁵¹

4. Adam–Bashforth–Moulton method for the $\mathit{SEIRV}$ model

For fractional order initial value situations, the Adams–Bashforth–Moulton​ approach is the most commonly used numerical technique.

Let

$${}^C{D}_t^{\nu }{L}_j\left(t\right)=g_j(t,L_j\left(t\right),L_j(t-{\eta }_1)),t\in \left[-{\eta }_1,0\right],L_j^r\left(0\right)=L_{j0}^r,$$ (4.1)

$r=0,1,2,\dots ,⌈\nu ⌉$, $j\in \mathbb{N}$

where $L_{j0}^r\in \mathbb{R}$, $\nu >0$ and ${}^C{D}_t^{\nu }$ is same as Volterra integral equation in the Caputo sense.

$$L_j\left(t\right)=\sum _{n=0}^{⌈\nu ⌉-1}{L}_{j0}^r\frac{t^n}{n!}+\frac{1}{\Gamma \left(\nu \right)}{\int }_0^t{(t-u)}^{\nu -1}{g}_j(u,L_j\left(u\right),L_j(u-{\eta }_1))du,j\in \mathbb{N}.$$ (4.2)

Let $h=\frac{T}{\hat{m}},t_n=nh,n=0,1,2,\dots ,\hat{m}$.

Corrector formulae:

$$S_{n+1}=S_0+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\left(\Lambda -\beta S_{n+1}^p{I}_{n+1}^p-{\mu }_0{S}_{n+1}^p-\delta S_{n+1}^p\right)+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\sum _{j=0}^n{\alpha }_{j,n+1}\left(\Lambda -\beta S_j{I}_j-{\mu }_0{S}_j-\delta S_j\right),$$

$$E_{n+1}=E_0+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\left(\beta S_{n+1}^p{I}_{n+1}^p-({\mu }_0+{\mu }_1)E_{n+1}^p\right)+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\sum _{j=0}^n{\alpha }_{j,n+1}(\beta S_j{I}_j-({\mu }_0+{\mu }_1)E_j),$$

$$I_{n+1}=I_0+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\left({\mu }_1{E}_{n+1}^p-({\mu }_0+{\mu }_2)I_{n+1}^p\right)+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\sum _{j=0}^n{\alpha }_{j,n+1}({\mu }_1{E}_j-({\mu }_0+{\mu }_2)I_j),$$

$$R_{n+1}=R_0+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\left({\mu }_2{I}_{n+1}^p-{\mu }_0{R}_{n+1}^p\right)+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\sum _{j=0}^n{\alpha }_{j,n+1}({\mu }_2{I}_j-{\mu }_0{R}_j),$$

$$V_{n+1}=V_0+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\left(\delta S_{n+1}^p-{\mu }_0{V}_{n+1}^p\right)+\frac{h^{\nu }}{\Gamma \left(\nu +2\right)}\sum _{j=0}^n{\alpha }_{j,n+1}(\delta S_j-{\mu }_0{V}_j).$$ (4.3)

Predictor formulae:

$$S_{n+1}^p=S_0+\frac{1}{\Gamma \left(\nu \right)}\sum _{j=0}^n{\Theta }_{j,n+1}\left(\Lambda -\beta S_j{I}_j-{\mu }_0{S}_j-\delta S_j\right),$$

$$E_{n+1}^p=E_0+\frac{1}{\Gamma \left(\nu \right)}\sum _{j=0}^n{\Theta }_{j,n+1}(\beta S_j{I}_j-({\mu }_0+{\mu }_1)E_j),$$ (4.4)

$$I_{n+1}^p=I_0+\frac{1}{\Gamma \left(\nu \right)}\sum _{j=0}^n{\Theta }_{j,n+1}({\mu }_1{E}_j-({\mu }_0+{\mu }_2)I_j),$$

$$R_{n+1}^p=R_0+\frac{1}{\Gamma \left(\nu \right)}\sum _{j=0}^n{\Theta }_{j,n+1}({\mu }_2{I}_j-{\mu }_0{R}_j),$$

$$V_{n+1}^p=V_0+\frac{1}{\Gamma \left(\nu \right)}\sum _{j=0}^n{\Theta }_{j,n+1}(\delta S_j-{\mu }_0{V}_j),$$

where

$${\nu }_{j,n+1}=\left\{\begin{array}{cc}{n}^{\nu +1}-\left(n-\nu \right){(n+1)}^{\nu },\hfill & ifj=0,\hfill \\ {(n-j+2)}^{\nu +1}+{(n-j)}^{\nu +1}-2{(n-j+1)}^{\nu +1},\hfill & if0\le j\le n,\hfill \\ 1,\hfill & ifj=1,\hfill \end{array}\right)$$

and

$${\Theta }_{j,n+1}=\frac{h^{\nu }}{\nu }\left[{(n+1-j)}^{\nu }-{\left(n-j\right)}^{\nu }\right],0\le j\le n.$$

5. Numerical simulation

We have studied and analyzed the dynamical behavior of the solutions of (2.9) using an extensive numerical simulation. In this section, we use MATLAB to analyze the solutions generated by Adams–Bashforth–Moulton scheme. The results of model simulations and the associated findings have been classified as follows:

Case - $\mathbf{I}$

In this case, we analyze the dynamical characteristics of all population for various fractional order with ${\eta }_1=0$.

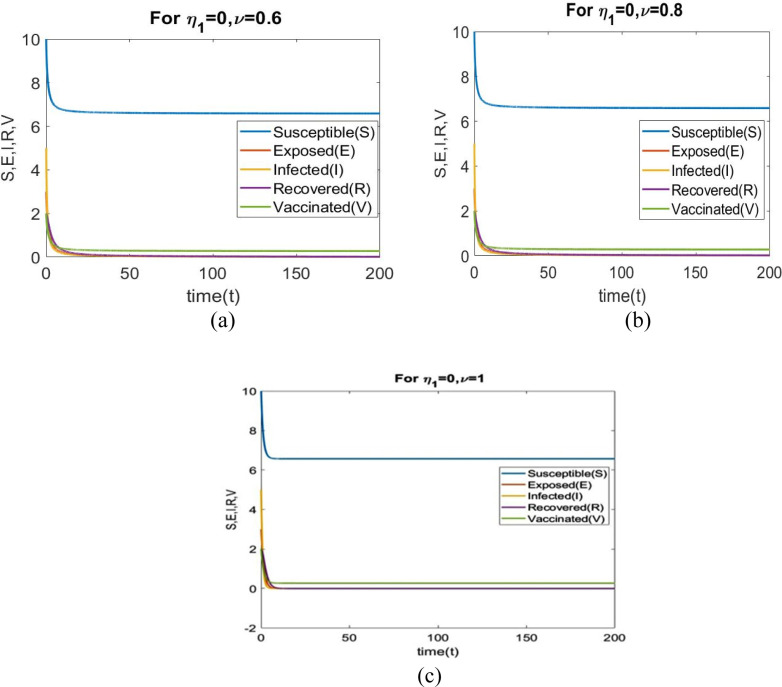
From Figs. 2(a) to 2(c) illustrate that when ${\mathfrak{R}}_0<1$, the number of exposed individuals, infected individuals and recovered individuals drops to zero. So the point $E_0$ is locally asymptotically stable when ${\mathfrak{R}}_0<1$ for different values of $\nu$. Table 1 displays the values of parameters.

Fig. 2.

Time series analysis corresponding to ${\eta }_1=0$ for (a) $\nu =0.6$ (b) $\nu =0.8$ (c) $\nu =1$.

Parameters	Value	Source
$\Lambda$	5	Estimated
$\beta$	0.01	Estimated
${\mu }_0$	0.731	Estimated
$\delta$	0.03	Model to fit
${\mu }_1$	0.015	Estimated
${\mu }_2$	0.5	Estimated
${\mathfrak{R}}_0$	0.0534	Estimated

Case - $\mathbf{II}$

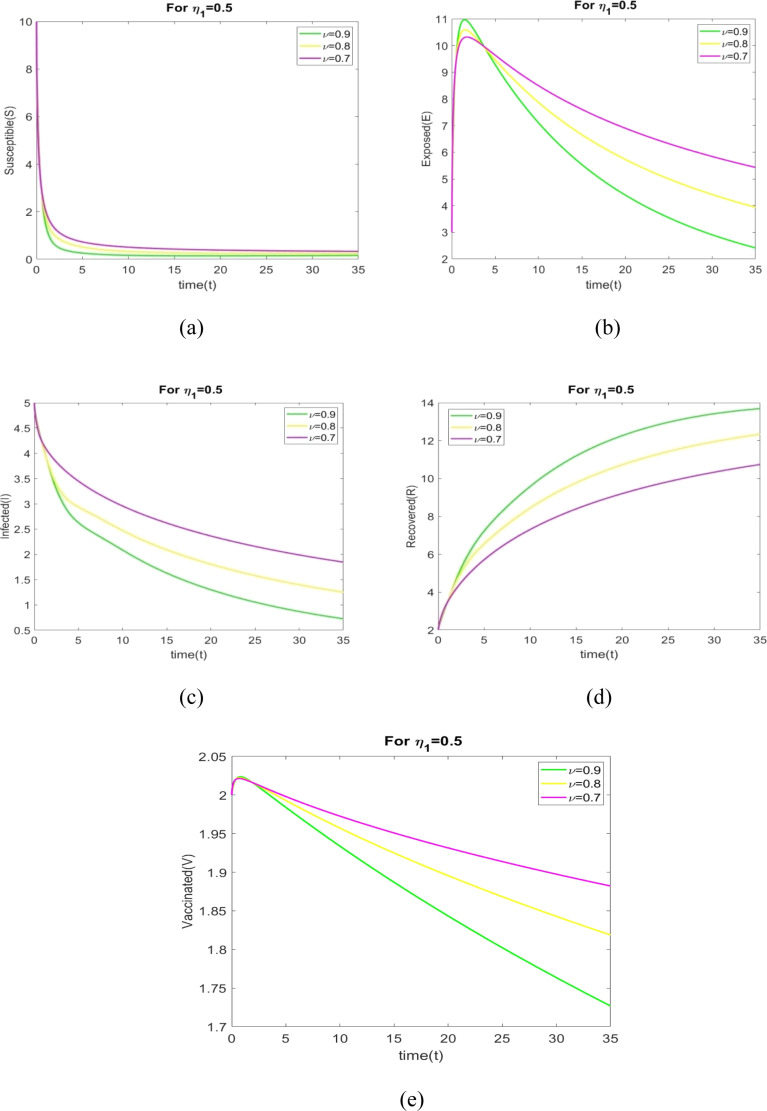
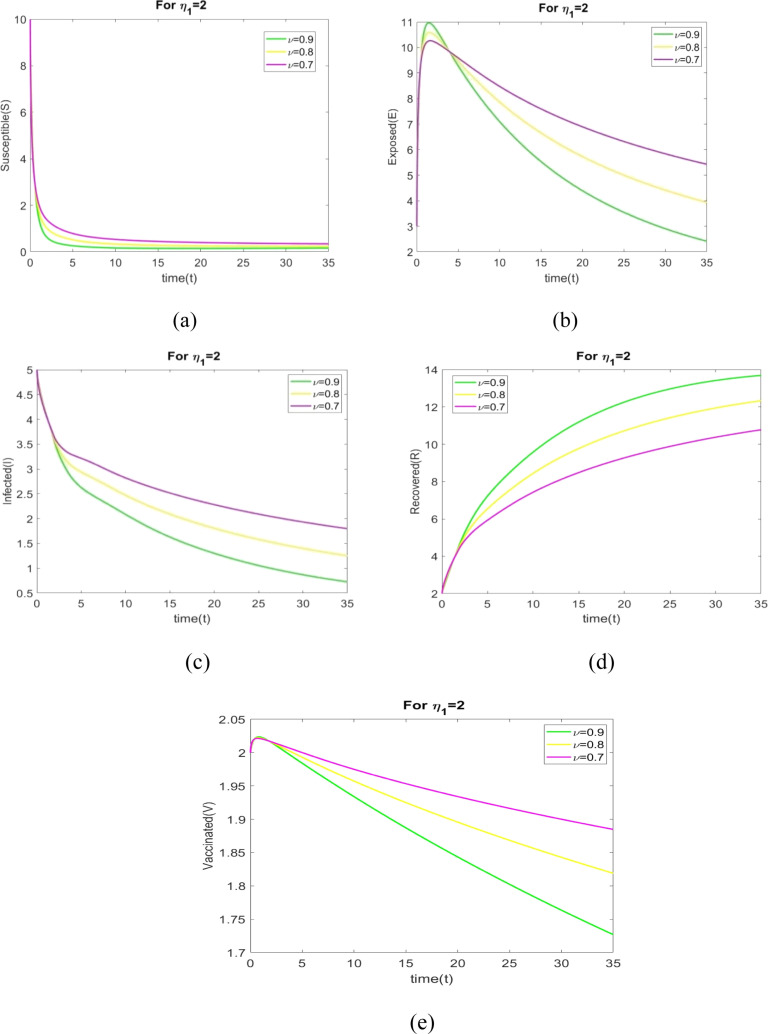
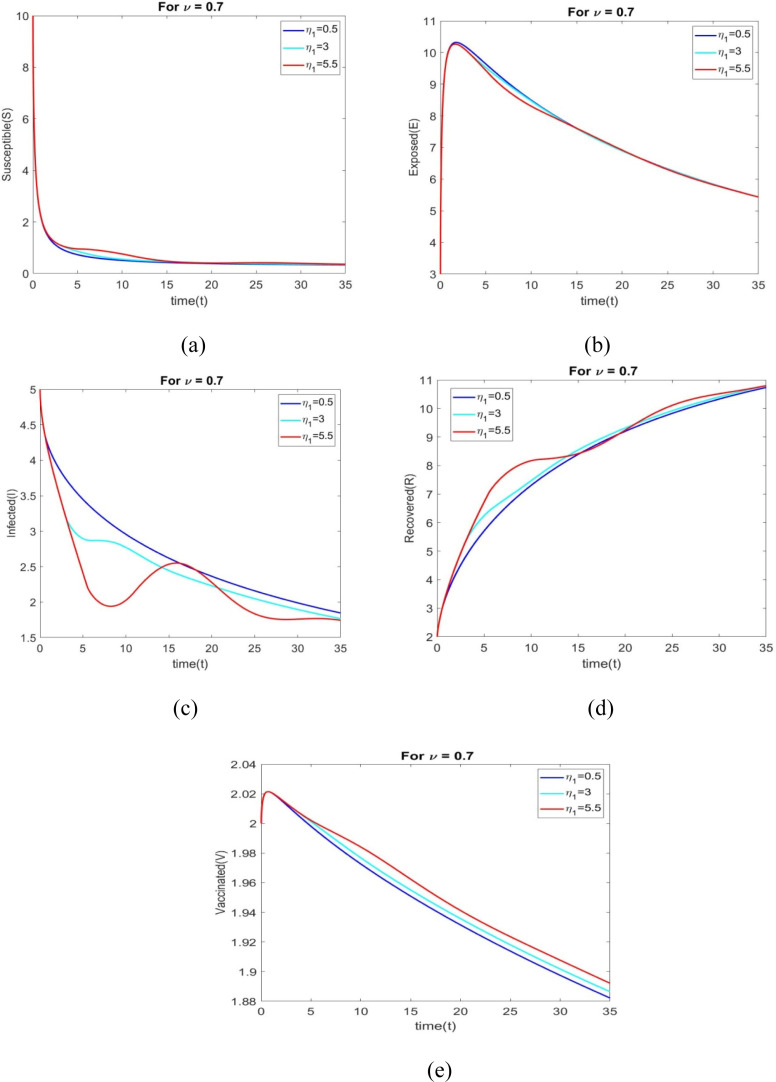
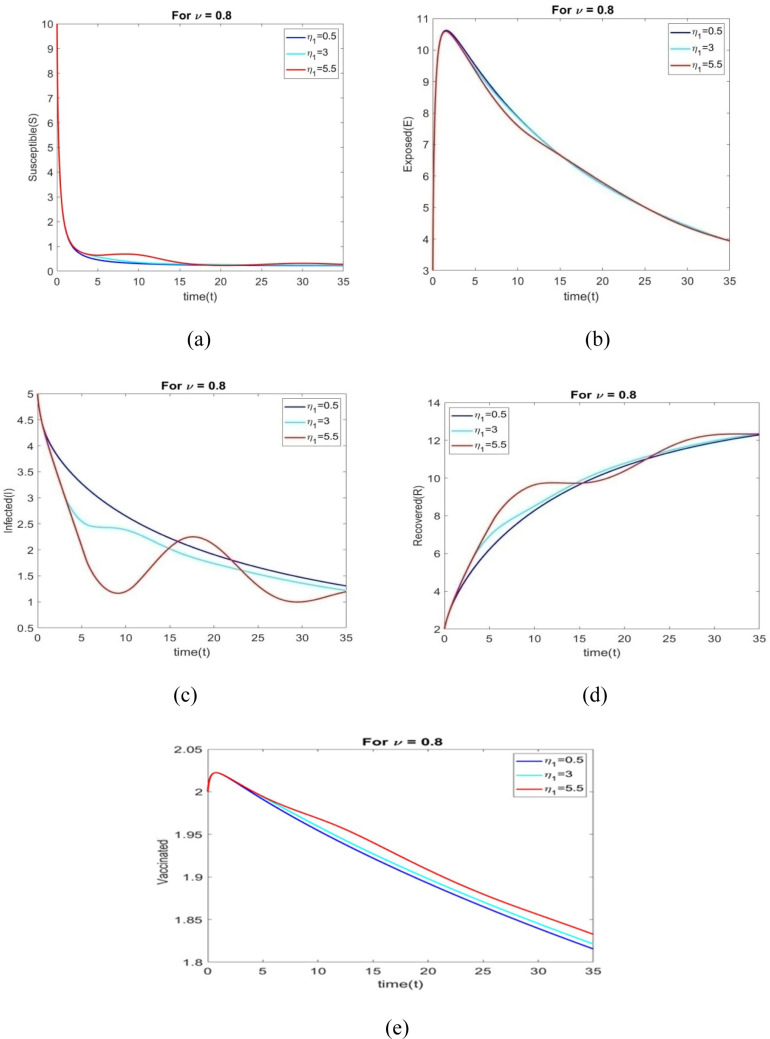
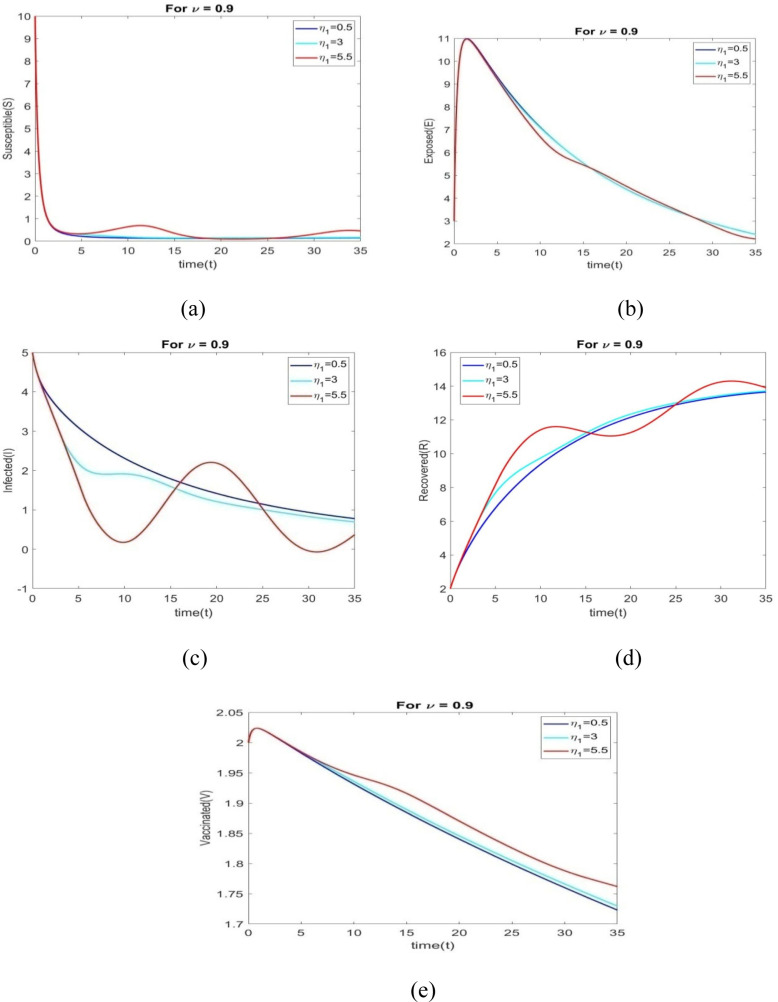
In this case, we analyze the dynamical characteristics of all population for various fractional order with ${\eta }_1=0$, ${\eta }_1=0.5$ and ${\eta }_1=2$.

The values of parameters in Table 2 are used to plot the figures in Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10. The behavior of all individuals with time corresponding to ${\eta }_1=0.5$ for different fractional order $\nu$ is shown in Figs. 3(a) through 3(e). The number of susceptible individuals and infected individuals decreases when $\nu$ increases. The number of recovered individuals increases when $\nu$ increases.

Parameters	Value	Source
$\Lambda$	0.0182	Estimated
$\beta$	0.476	Estimated
${\mu }_0$	0.0073	Estimated
$\delta$	0.01	Model to fit
${\mu }_1$	0.071	53,54
${\mu }_2$	0.286	53,54
${\mathfrak{R}}_0$	1.55	Estimated

Fig. 3.

The behavior of $S,E,I,R$ and $V$ for varied values of $\nu =0.9,0.8,0.7$ with ${\eta }_1=0.5$.

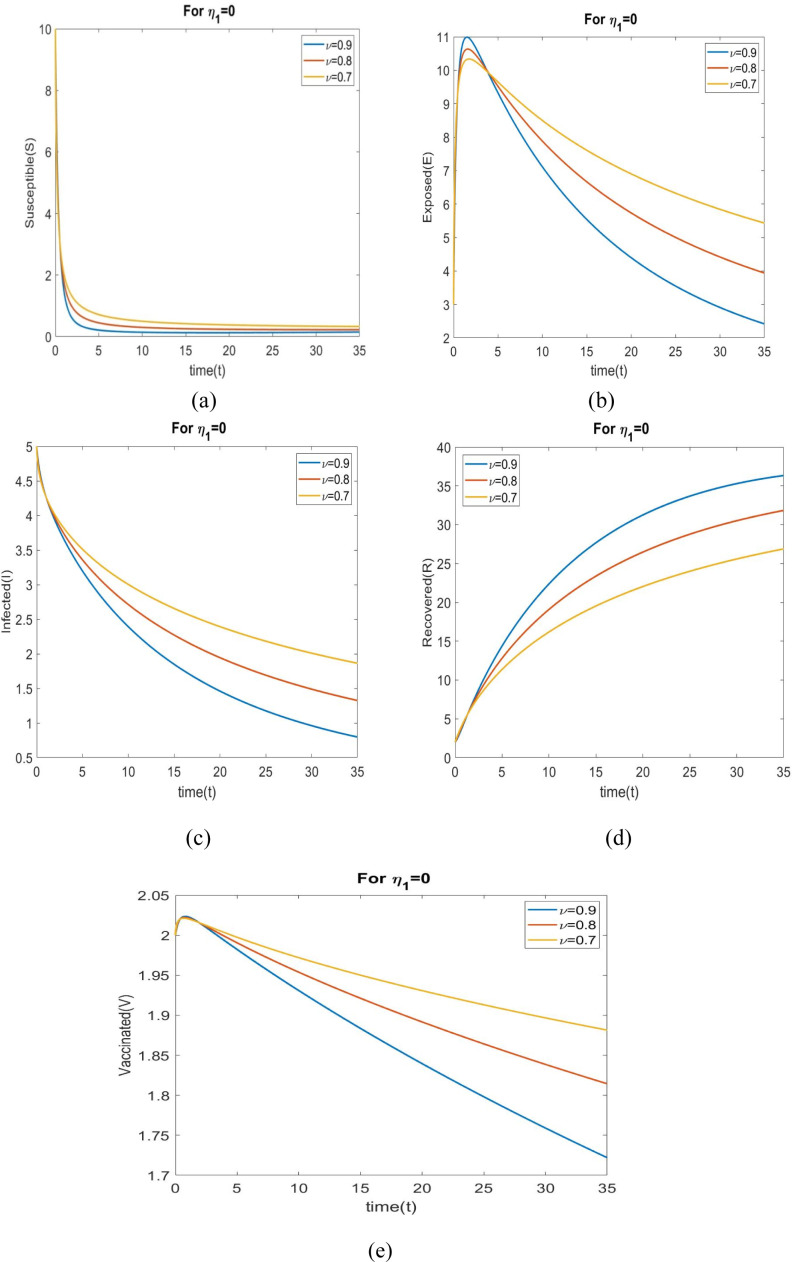
Fig. 4.

The behavior of all individuals for different values of $\nu =0.9,0.8,0.7$ with ${\eta }_1=0$.

Fig. 5.

The behavior of all individuals for values of $\nu =0.9,0.8,0.7$ and ${\eta }_1=2$.

Fig. 6.

Dynamical behavior of all individuals for $\nu =0.7$ and different values of ${\eta }_1=0$.5, 3, 5.5.

Fig. 7.

Dynamical behavior of all individuals for $\nu =0.8$ and different values of ${\eta }_1=0$.5, 3, 5.5.

Fig. 8.

The behavior of all individuals for $\nu =0.9$ and different values of ${\eta }_1=0$.5, 3, 5.5.

Fig. 9.

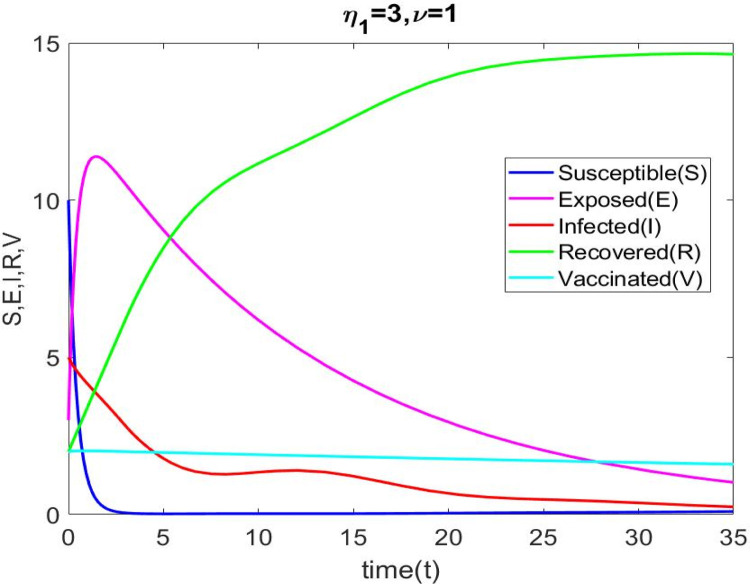
Time series analysis for ${\eta }_1=3$ and $\nu =1$ of Eq. (2.9).

Fig. 10.

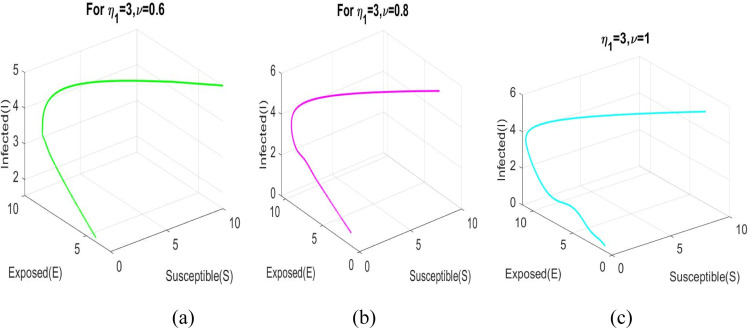
Phase diagram of the model (2.9) corresponding to ${\eta }_1=3$ and $\nu =0.6,0.8,1$.

Figs. 4(a) to 4(e) shows the behavior of all individuals with time corresponding to ${\eta }_1=0$ for different fractional order $\nu$. Fig. 4(a) depicts that the number of susceptible individuals increase when $\nu$ changes to 0.9 to 0.7. An increase value of $\nu$ leads to decrease in the exposed rate in the exposed population in Fig. 4(b). We see in Fig. 4(c) that number of infected individuals increase when $\nu$ changes to 0.9 to 0.7. Fig. 4(d) depicts that the number of recovered individuals increase with time when $\nu$ increases.

The behavior of all individuals with time corresponding to ${\eta }_1=2$ for different fractional order $\nu$ is shown in Figs. 5(a) through 5(e). Fig. 5(a) depicts that the number of susceptible individuals increase when $\nu$ increases. We see in Fig. 5(c) that number of infected individuals increase when $\nu$ changes to 0.9 to 0.7. Fig. 5(d) depicts that the number of recovered individuals increase when $\nu$ increases.

The behavior of all individuals with time corresponding to $\nu =0.7$ is shown in Figs. 6(a) through 6(e) for various time delays ${\eta }_1$.

Figs. 7(a) to 7(e) shows the behavior of all individuals with time corresponding to $\nu =0.8$ for different time delays ${\eta }_1$. The number of vaccinated individuals increase when ${\eta }_1$ changes to 0.5 to 5.5.

The performance of all individuals with time corresponding to $\nu =0.9$ is shown in Figs. 8(a) through 8(e) for various time delays ${\eta }_1$.

Case - $\mathbf{III}$

The existence of the Hopf bifurcation of the model system (2.9) with fractional order $\nu =1$ is discussed in this case. The following set of parametric values is chosen:

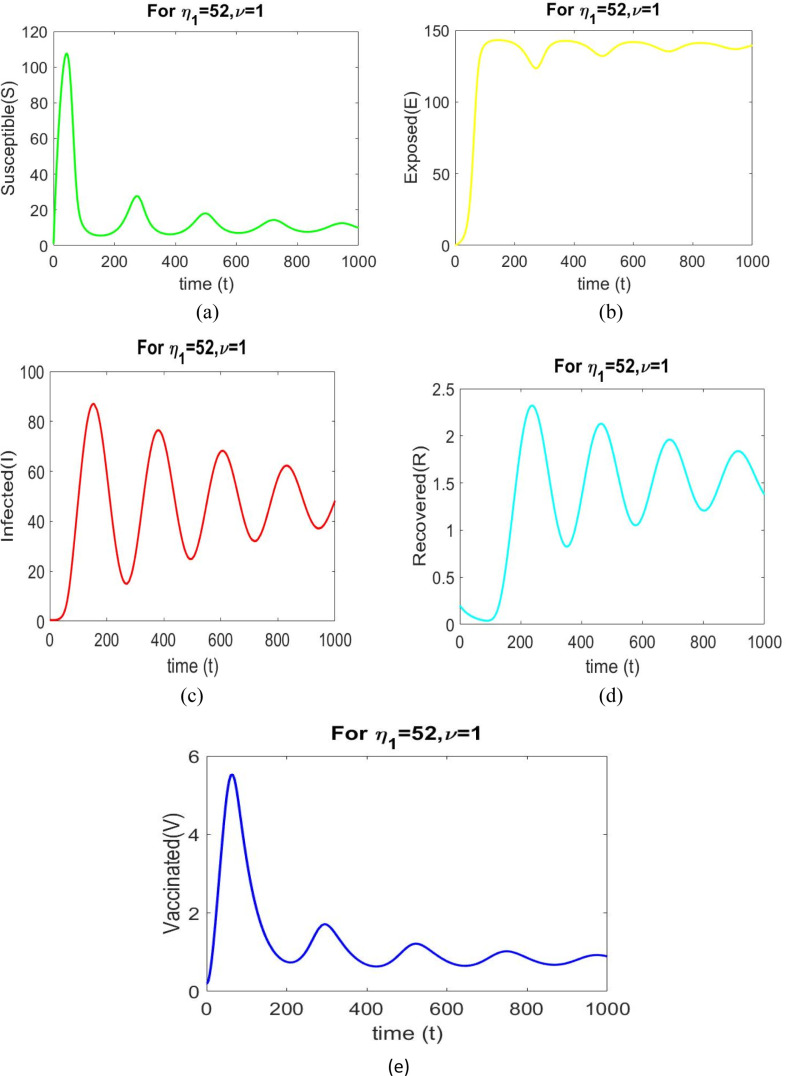
The values of the parameters in Table 3 are used to study the bifurcation analysis. The model system (2.9) is unstable at $E_1$, as shown in Fig. 11.

Parameters	Value	Source
$\Lambda$	5	For model fit
$\beta$	0.010	Estimated
${\mu }_0$	0.025	Estimated
$\delta$	0.002	Model to fit
${\mu }_1$	0.009	Estimated
${\mu }_2$	0.0008	For model fit

Fig. 11.

Time series solution of the model system (2.9) for ${\eta }_1>{{\eta }_1}^{\ast },\nu =1$ with different initial and parameter values as given in Table 3.

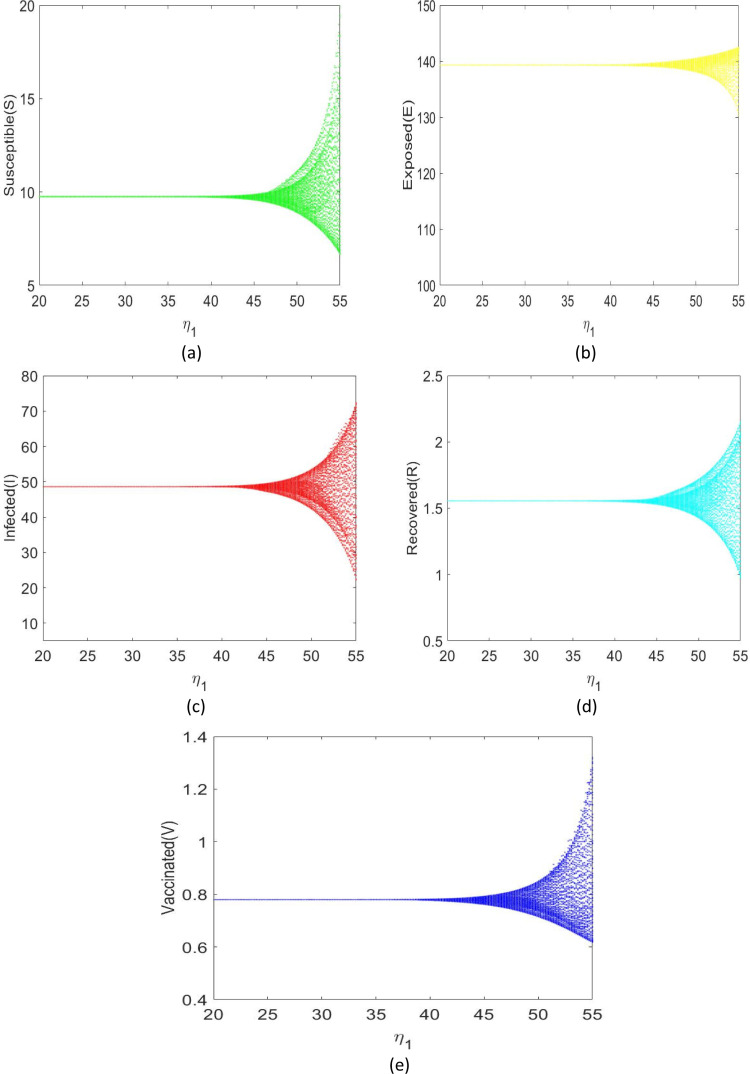
Using the parametric values in Table 3, the roots of the Eq. (3.10) are $-0.6240,-1.2724,0.1345,0.5832\pm 0.1750i$. Thus we obtain $f_1^{\prime }\left(0.1345\right)\ne 0$. The Hopf bifurcation diagram is shown in Fig. 12(a) through 12 (e). For ${\eta }_1=41.56$ and $m_{10}=0.3668$, we obtain $E_1=(9.7467,379.4148,132.3540,10.5883,0.7797)$. Now $E_1$ is locally asymptotically stable when ${\eta }_1\in [0,{{\eta }_1}^{\ast }]$, confirming our theoretical results in Theorem 3.5. The system (2.9) produces a Hopf bifurcation when ${\eta }_1={{\eta }_1}^{\ast }$.

Fig. 12.

Diagram of a single parameter bifurcation with respect to ${\eta }_1$.

6. Conclusion

We have studied the $\mathit{SEIRV}$ model (2.9) considering a single time delay parameter ${\eta }_1$. The stability analysis of the system depicts that point $E_0$ of the system (2.9) is locally asymptotically stable when ${\mathfrak{R}}_0$< 1, and unstable when ${\mathfrak{R}}_0>1$ in the absence of time delay. The endemic equilibrium $E_1=(S^{\ast },E^{\ast },I^{\ast },R^{\ast },V^{\ast })$ is locally asymptotically stable if ${\mathfrak{R}}_0>1$, when ${\eta }_1=0$. However, in the presence of time delay parameter ${\eta }_1$, both the points $E_0$ and $E_1$ are asymptotically stable in the interval $[0,{{\eta }_1}^{\ast }]$ where ${{\eta }_1}^{\ast }$ is given by ${{\eta }_1}^{\ast }=\frac{1}{m_{10,}}si{n}^{-1}\left(\frac{ad+bc}{a^2+b^2}\right)$. Numerical computations reveal that if ${\eta }_1>41.56$ then the system (2.9) exhibits Hopf bifurcation. Thus, it becomes apparent that beyond the value of ${{\eta }_1}^{\ast }=41.56$ the dynamics of the system becomes unstable. It may be recalled that the time delay parameter was incorporated in (2.9) to justify the argument that the infected population will take some time to recover. When the time delay owing to the time period required by the infected individuals to recover from the disease surpasses a threshold value, the model described here produces a Hopf bifurcation around the endemic equilibrium point.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.