Abstract
Theories of adult cognitive development classically distinguish between fluid abilities, which require effortful processing at the time of assessment, and crystallized abilities, which require the retrieval and application of knowledge. On average, fluid abilities decline throughout adulthood, whereas crystallized abilities show gains into old age. These diverging age trends, along with marked individual differences in rates of change, have led to the proposition that individuals might compensate for fluid declines with crystallized gains. Here, using data from two large longitudinal studies, we show that rates of change are strongly correlated across fluid and crystallized abilities. Hence, individuals showing greater losses in fluid abilities tend to show smaller gains, or even losses, in crystallized abilities. This observed commonality between fluid and crystallized changes places constraints on theories of compensation and directs attention toward domain-general drivers of adult cognitive decline and maintenance.
Counter to views that knowledge defies decline, cognitive aging generalizes across effortful processing and fact retrieval.
INTRODUCTION
Adult cognitive functioning is a key determinant of vocational performance, health behaviors, and the everyday functions necessary for independent living (1–3). Aging-related cognitive declines are tightly associated with declines in everyday functions and forecast both dementia onset and mortality (4). Cognitive functioning is multifaceted, itself constituting many different domains that vary in population-average age trends (5, 6). The classic fluid-crystallized model of individual differences in cognitive functioning makes the distinction between two broad classes of abilities (7). Fluid (Gf) abilities primarily require effortful processing at the time of assessment and encompass domains such as perceptual speed, working memory, abstract reasoning, and visuospatial reasoning. Crystallized (Gc) abilities primarily require the retrieval and application of previously acquired knowledge and encompass domains such as vocabulary knowledge, general information, and domain-specific skills. Population-average declines are observed across adulthood for fluid abilities, whereas population average increases are observed through the seventh decade of life for crystallized abilities (8, 9). The observations that average levels of fluid abilities are more sensitive to senescent neurobiological degeneration and that average levels of crystallized abilities increase in the face of such degeneration, have served as the basis for compensatory accounts of aging. Such compensatory accounts propose that individuals who decline precipitously in fluid abilities progressively shift their reliance to preserved, rote or automated, crystallized abilities, thereby prolonging independent functioning and cognitive status in later life (10–14).
Although the divergence in population-average age trends in fluid and crystallized abilities in adulthood is firmly established, the differentiation of individual variation in rates of change in different cognitive functions has only been the topic of relatively recent investigation (15, 16). Longitudinal data are necessary to test whether individual rates of change in fluid and crystallized abilities are indeed independent of one another; that is, whether individuals who decline precipitously relative to their peers in their fluid abilities are unaffected in their relative gains in crystallized abilities (17–19). Tucker-Drob et al. (15) reported meta-analytic evidence that longitudinal aging-related changes in different cognitive abilities are positively correlated, such that a general factor of change accounts for an average of approximately 60% of the variation in aging-related changes in each cognitive ability.
Thus, rather than representing altogether distinct or even opposing dimensions of adult cognitive development, changes in fluid and crystallized cognitive abilities may tap overlapping processes and/or be affected by overlapping sets of risk and protective factors. Here, we directly examined whether individual rates of general declines in fluid abilities are associated with individual rates of gain in crystallized ability using multivariate longitudinal data from two high-quality longitudinal studies of cognitive aging from early adulthood to old age: the Virginia Cognitive Aging Project (VCAP) (20) and the Betula Project (BETULA) (21), each of which measures crystallized ability and multiple fluid abilities across time.
RESULTS
We conducted parallel analyses in the VCAP and BETULA datasets, both of which included measures of the following ability domains: episodic memory, perceptual speed, visuospatial reasoning, and crystallized ability. VCAP additionally measured abstract reasoning. For VCAP, age at baseline assessment ranged from 18 to 99 years, and the data were most dense for baseline ages below approximately 85 years. For BETULA, age at baseline ranged from 25 to 86 years, and the data were most dense for baseline ages between approximately 40 and 85 years. For VCAP, the longitudinal time lag from baseline assessment ranged from 1 to 18 years. For BETULA, the longitudinal time lag ranged from 4 to 18 years.
In each dataset, we first fit multivariate growth curve models encompassing a general factor and domain-specific factors of static levels of fluid abilities and a general factor and domain-specific factors of rates of longitudinal changes in fluid abilities. We then extended our models, enabling levels and changes in crystallized ability to load on the previously established general factors of fluid levels and changes, as well as on their own domain-specific level and change factors. This allowed us to determine the extent to which individual differences in rates of domain-general aging-related (mostly negative) changes in fluid abilities are associated with individual differences in (mostly positive) changes in crystallized ability. All models included terms for nonlinear age trends and for practice effects, which are known to otherwise contaminate longitudinal estimates of cognitive decline (22, 23). Model parameter estimates for VCAP and BETULA are reported in Tables 1 and 2, respectively.
Table 1. Parameter estimates from step 1 and step 2 “factor of curves” models in VCAP.
ρFi,Fsa = −0.075 (P = 0.053), ρFi,Fqa = −0.963 (P < 0.001), and ρFs,Fqa = 0.086 (P = 0.305). The variances of Fi, Fs, and Fq were fixed to 1.0 to define the metrics of the latent growth factors. We specified age-based growth curve modeling, such that the basis coefficients for each of the five slopes were set to the age in decades of individual n at each assessment on variable w, centered at 50 years. Each of the five cognitive outcomes was standardized by subtracting the mean of all datapoints at the baseline occasion and dividing by the SD of the age and age-squared residuals of all the datapoints at baseline. Gf, abstract reasoning; Gv, visuospatial reasoning; Gm, memory; Gs, perceptual speed; Gc, crystallized ability. See Materials and Methods for explanation of model parameters.
|
Cognitive
domain |
Latent variable
means (SE) |
Unstandardized
loadings (SE) |
Standardized
loadings |
Residual variances and covariances (SE) | |||||||||||||
| μr | μi | μs | μq | Fi | Fs | Fq | Fi | F s | Fq | σ2e[t] | σ2ui | σ2us | σ2uq | σui,us | σui,uq | σus,uq | |
| Gf* | 0.118 (0.009) |
0.164 (0.015) |
−0.186 (0.007) |
−0.037 (0.003) |
0.867 (0.016) |
0.252 (0.016) |
0.064 (0.006) |
1.011 (0.007) |
1.022 (0.068) |
0.988 (0.002) |
0.115 (0.003) |
−0.016 (0.011) |
−0.003 (0.008) |
0.000 (0.000) |
0.007 (0.003) |
0.001 (0.004) |
0.001 (0.000) |
| Gv* | 0.175 (0.008) |
0.090 (0.015) |
−0.190 (0.007) |
−0.014 (0.003) |
0.696 (0.014) |
0.173 (0.014) |
0.050 (0.007) |
0.817 (0.009) |
0.875 (0.087) |
0.949 (0.015) |
0.107 (0.004) |
0.242 (0.011) |
0.009 (0.007) |
0.000 (0.000) |
−0.014 (0.003) |
−0.006 (0.004) |
0.000 (0.000) |
| Gm* | 0.116 (0.010) |
0.184 (0.015) |
−0.172 (0.007) |
−0.039 (0.003) |
0.576 (0.018) |
0.191 (0.011) |
0.060 (0.004) |
0.724 (0.014) |
0.776 (0.064) |
0.835 (0.028) |
0.137 (0.005) |
0.301 (0.013) |
0.024 (0.009) |
0.002 (0.000) |
0.004 (0.004) |
−0.020 (0.005) |
−0.001 (0.001) |
| Gs* | 0.100 (0.010) |
0.198 (0.014) |
−0.315 (0.006) |
−0.039 (0.003) |
0.453 (0.017) |
0.166 (0.010) |
0.047 (0.004) |
0.582 (0.017) |
0.764 (0.083) |
0.848 (0.045) |
0.133 (0.005) |
0.399 (0.015) |
0.020 (0.010) |
0.001 (0.000) |
−0.025 (0.005) |
−0.016 (0.005) |
0.001 (0.001) |
| G c † | −0.030 (0.006) |
0.117 (0.010) |
0.134 (0.004) |
−0.038 (0.002) |
0.713 (0.012) |
0.145 (0.006) |
0.046 (0.003) |
0.774 (0.009) |
0.933 (0.082) |
0.907 (0.033) |
0.050 (0.002) |
0.341 (0.012) |
0.003 (0.004) |
0.000 (0.000) |
−0.007 (0.003) |
−0.008 (0.002) |
0.000 (0.000) |
*First step: unconstrained factor of curves model excluding Gc.
†Second step: constrained factor of curves model including Gc.
Table 2. Parameter estimates from step 1 and step 2 “factor of curves” models in BETULA.
ρFi,Fsa = 0.233 (P = 0.063), ρFi,Fqa = −0.654 (P < 0.001), and ρFs,Fqa = −0.121 (P = 0.705). The variance of Fi, Fs, and Fq were fixed to 1.0 to define the metrics of the latent growth factors. We specified age-based growth curve modeling, such that the basis coefficients for each of the five slopes was set to the age in quarter centuries of individual n at each assessment on variable w, centered at 50 years. Each of the four cognitive outcomes was standardized by subtracting the mean of all datapoints at the baseline occasion and dividing by the SD of the age and age-squared residuals of all the datapoints at baseline.
|
Cognitive
domain |
Latent variable means (SE) |
Unstandardized
loadings (SE) |
Standardized
loadings |
Residual variances and covariances (SE) | ||||||||||||||
| μr | μi | μs | μq | Fi | Fs | Fq | Fi | F s | Fq | σ2e[t] | σ2ui | σ2us | σ2uq | σui,us | σui,uq | σus,uq | ||
| Gv* | 0.127 (0.016) |
0.544 (0.022) |
−0.871 (0.042) |
−0.525 (0.033) |
0.599 (0.032) |
0.298 (0.072) |
0.284 (0.068) |
0.643 (0.03) |
0.851 (0.088) |
0.825 (0.127) |
0.269 (0.007) |
0.511 (0.036) |
0.034 (0.02) |
0.038 (0.029) |
−0.02 (0.025) |
−0.107 (0.038) |
−0.01 (0.031) |
|
| Gm* | 0.195 (0.02) |
0.577 (0.02) |
−0.744 (0.041) |
−0.682 (0.035) |
0.477 (0.029) |
0.312 (0.066) |
0.285 (0.07) |
0.711 (0.036) |
0.748 (0.098) |
0.931 (0.034) |
0.517 (0.012) |
0.223 (0.028) |
0.077 (0.032) |
0.013 (0.003) |
0.057 (0.022) |
−0.035 (0.043) |
−0.03 (0.031) |
|
| Gs* | 0.185 (0.018) |
0.925 (0.027) |
−0.936 (0.058) |
−0.85 (0.043) |
0.65 (0.035) |
0.563 (0.08) |
0.346 (0.125) |
0.758 (0.033) |
0.819 (0.059) |
0.729 (0.136) |
0.21 (0.019) |
0.314 (0.04) |
0.156 (0.053) |
0.106 (0.026) |
0.011 (0.034) |
−0.076 (0.053) |
−0.125 (0.035) |
|
| G c † | 0.123 (0.013) |
0.319 (0.016) |
−0.033 (0.03) |
−0.58 (0.028) |
0.623 (0.025) |
0.425 (0.029) |
0.258 (0.05) |
0.763 (0.021) |
0.859 (0.024) |
0.461 (0.097) |
0.162 (0.006) |
0.278 (0.025) |
0.064 (0.012) |
0.247 (0.071) |
0.106 (0.029) |
−0.078 (0.033) |
−0.059 (0.056) |
|
*First step: unconstrained factor of curves model excluding Gc.
†Second step: constrained factor of curves model including Gc.
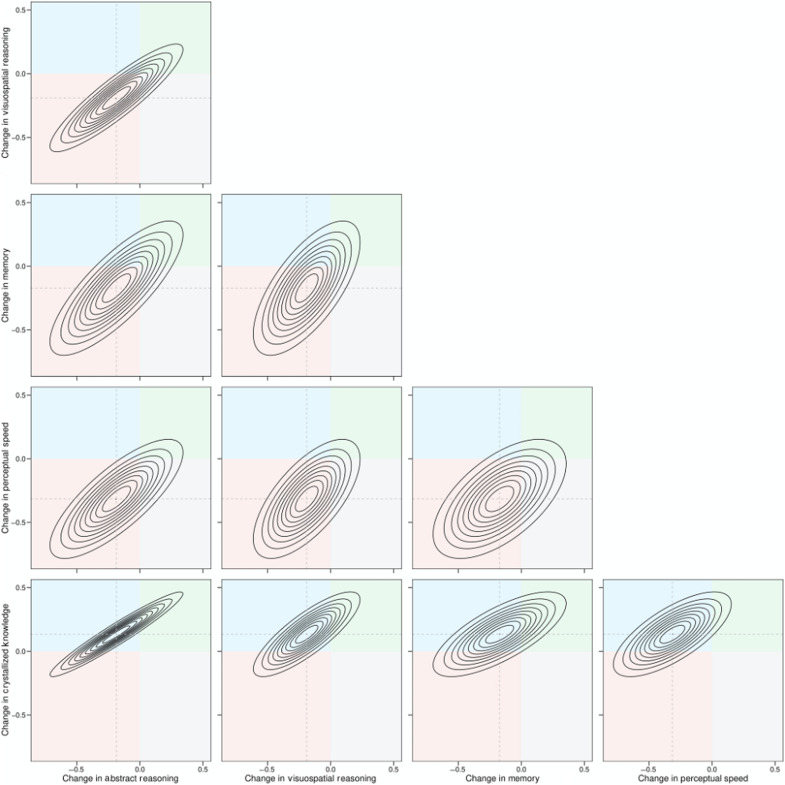
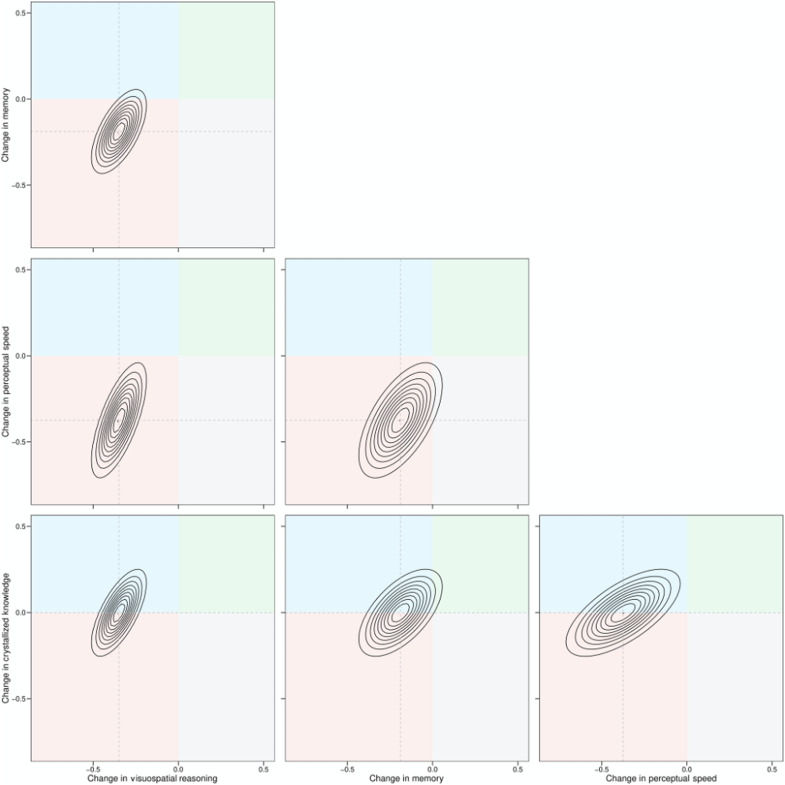
Our multivariate growth curve modeling revealed a strong dependency between changes in fluid abilities and crystallized ability, as displayed in Fig. 1 for VCAP and Fig. 2 for BETULA. These figures display the association between individual rates of per decade change in each domain at age 50 years, as implied by the multivariate growth curve model in the form of bivariate density plots, with quadrants colored to indicate regions of the distribution in which rates of change in the respective variables are positive or negative. We chose age 50 years, because it is the approximate age at which differences in mean trajectories of fluid declines and crystallized gains are most stark. For the associations between rates of change in different fluid abilities, it can be seen both that the changes are strongly correlated and that each distribution is centered over the red quadrant in which both abilities decline. By comparison, it can be seen that the associations between rates of change in crystallized ability and each fluid ability are also strong but that large portions of each distribution occupy the blue quadrant, in which the fluid ability declines and crystallized ability increases.
Fig. 1. Bivariate density plots of association between individual rates of change in different cognitive abilities in VCAP, as implied by the multivariate growth curve model.
Each concentric band represents 10% of the bivariate distribution of the linear rate of per decade change at age 50 years. The colored quadrants indicate regions of the distribution in which both abilities decline (bottom left quadrant; red), the ability on the x axis declines but the ability on the y axis increases (top left quadrant; blue), both abilities increase (top right quadrant; green), and the ability on the x axis increases and the ability on the y axis decreases (bottom right quadrant; gray). In all panels, strong positive associations between individual rates of change in different abilities are evident. For the associations between rates of change in different fluid abilities, it can be seen that each bivariate distribution is centered over the red quadrant in which both abilities decline. However, for the associations between rates of change in crystallized ability and each fluid ability (bottom row of panels), up to approximately half of each distribution occupies the blue quadrant, in which the fluid ability declines and crystallized ability increases.
Fig. 2. Bivariate density plots of association between individual rates of change in different cognitive abilities in the BETULA study, as implied by the multivariate growth curve model.
Each concentric band represents 10% of the bivariate distribution of the linear rate of per decade change at age 50 years. The colored quadrants indicate regions of the distribution in which both abilities decline (lower left quadrant; red), the ability on the x axis declines but the ability on the y axis increases (top left quadrant; blue), both abilities increase (top right quadrant; green), and the ability on the x axis increases and the ability on the y axis decreases (bottom right quadrant; gray). In all panels, strong positive associations between individual rates of change in different abilities are evident. For the associations between rates of change in different fluid abilities, it can be seen that each bivariate distribution is centered over the red quadrant in which both abilities decline. However, for the associations between rates of change in crystallized ability and each fluid ability (bottom row of panels), up to approximately half of each distribution occupies the blue quadrant, in which the fluid ability declines and crystallized ability increases.
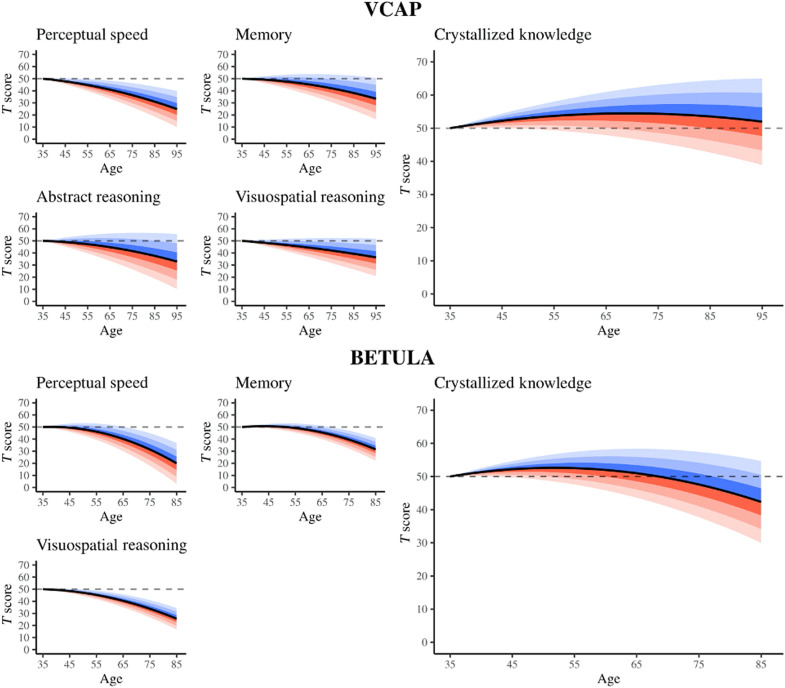
Figure 3 presents stratified trajectories of cognitive change in each of the domains of functioning across the full range of the distribution of the general factor of linear change in fluid abilities, holding the level at age 35 constant for clarity of presentation. As to be expected, for the individual fluid abilities, our results indicate that those experiencing the most negative general fluid change (red shading) exhibit particularly steep rates of decline in the individual fluid domains (perceptual speed, abstract reasoning, visuospatial reasoning, and memory) with age, whereas those experiencing the least negative general fluid change (blue shading) exhibit relatively modest rates of decline in the individual fluid domains with age. We can also observe a notable strong dependency between rates (of mostly gain) in crystallized ability and rates of general fluid decline. Individuals who exhibit relatively shallow rates of fluid decline (blue shading) exhibit some of the most positive rates of gain in crystallized ability, whereas individuals who exhibit relatively steep rates of fluid decline (red shading) exhibit very little gain, or even decline, in crystallized ability over the same period of time.
Fig. 3. Trajectories of change in each ability domain stratified across the distribution of variation in the general factor of fluid decline.
Trajectories are presented for the VCAP (top) and the BETULA study (bottom). The black curves represent the population average trajectories for each domain. Blue shading represents shallower-than-average rates of general fluid declines, whereas red shading represents steeper-than-average rates of general fluid declines. Each increment of shading corresponds to a 0.5 SD shift in the general factor of fluid decline. More saturated colors correspond to more densely concentrated regions of the distribution of change. All variables are on a T score metric, such that the mean of the age and age-squared residualized scores is 50, and the SD is 10. All trajectories were centered such that they begin at T score = 50 at age 35 years. It can be seen that individuals who exhibit relatively shallow rates of fluid decline exhibit some of the most positive rates of gain in crystallized ability, whereas those who exhibit relatively steep rates of fluid decline exhibit very little gain, or even decline, in crystallized ability over the same period of time.
We conducted a variety of sensitivity analyses to ensure the robustness of our inferences. First, we compared the fit of our primary models, in which linear and quadratic slopes for Gc were allowed to freely load on the respective general factors of changes in fluid abilities, to those in which these loadings were constrained to be 0. Supporting the inference that Gc changes are linked to Gf, the models in which the loadings were constrained to 0 fit substantially worse than those in which they were freely estimated [VCAP model with free loadings: −2loglikelihood = 92,348.54, scaling factor for likelihood ratio test = 1.3791, Akaike information criterion (AIC) = 92,378.544, and Bayesian information criterion (BIC) = 92,477.907; VCAP model with loadings fixed to 0: −2loglikelihood = 93,265.29, scaling factor for likelihood ratio test = 1.7029, AIC = 93,291.291, and BIC = 93,377.406; BETULA model with free loadings: −2loglikelihood = 64,094.88, scaling factor for likelihood ratio test = 1.2552, AIC = 64,122.877, and BIC = 64,208.381; and BETULA model with loadings fixed to 0: −2loglikelihood = 64,317.67, scaling factor for likelihood ratio test = 1.3115, AIC = 643,41.666, and BIC = 64,414.955]. Likelihood ratio tests indicated that the differences in model fit were highly significant (both P < 10−50). Second, to determine whether our decision to specify age-based growth curve models affected the key results, we specified time-based models (in which the basis coefficients for the linear and quadratic slopes were set to be equal to time since baseline). In these models, the linear slopes for all domains, including Gc, continued to load substantially on their corresponding general factors. Third, to determine whether our choice of functional form for the retest effects affected the results, we estimated models in which the retest function was freely estimated from the data [a so-called “latent basis” specification (24)], as well as models in which the function was set to be a logarithmic function of occasion [a monotonically increasing function with a slowing rate of growth, to reflect greater benefits after earlier exposures, as is generally found in research on learning (25), and commonly documented in the specific case of practice effects]. Again, the linear slopes for all domains, including Gc, continued to load substantially on their corresponding general factors. Last, to determine whether the documented dependency between changes in fluid and crystallized abilities was being driven by observations from later adulthood, in which both fluid and crystallized abilities exhibit mean declines, we refit the primary models using observations taken at ages 65 and younger. Again, the linear slopes for all domains, including Gc, continued to load substantially, although the confidence intervals for the parameters were considerably larger than those observed in the full dataset. Parameter estimates from these sensitivity analyses are reported in tables S7 to S14.
DISCUSSION
Fluid and crystallized abilities are well known to exhibit diverging population-average trajectories of change across adulthood: Whereas fluid abilities exhibit progressive mean declines beginning in early- to middle-adulthood, crystallized abilities exhibit age-related gains until approximately the seventh decade of life. This observation serves as the basis for prominent multicomponent theories of cognitive aging positing that the aging of fluid and crystallized abilities are independent (7). Counter to these proposals, in two large, independent longitudinal datasets that differ in the populations sampled, the cognitive measures, and the longitudinal protocols, we find that rates of change are strongly correlated across fluid abilities and crystallized abilities. Our results reveal that individuals showing greater losses in fluid abilities tend to show smaller gains, or even losses, in crystallized abilities.
What common biological mechanisms could account for our observation of a strong dependency between changes in fluid and crystallized abilities in aging? One dominating pattern was joint negative change among fluid and crystallized abilities at the particularly unhealthy region of the joint distribution of longitudinal change (Figs. 1 and 2, lower left quadrants in bottom rows). Such a pattern is consistent with underlying vascular dysregulation (26, 27) and broad, brain-wide patterns of cortical atrophy and white matter disconnection (28–30). Other patterns captured fluid decline along with positive rates of gain in crystallized ability (Figs. 1 and 2, top left quadrants in bottom rows) and even positive rates of gain for both fluid and crystallized abilities (Figs. 1 and 2, top right quadrants in bottom rows) at the particularly healthy region of the joint distribution of longitudinal change. These patterns are consistent with intact cellular and synaptic plasticity (31–33) and well-functioning attention and neurotransmission brain networks (34, 35). Multiple varied mechanisms are likely to contribute to common variation in fluid and crystallized changes. These mechanisms may themselves be correlated via pleiotropic genes (36, 37) and general epidemiological risk factors (38).
What common cognitive mechanisms might undergird shared rates of cognitive change across fluid and crystallized abilities? The cognitive processes associated with acquisition and retention of knowledge and skill have been well studied, and mathematically modeled, for over a century (25, 39, 40), but relatively little attention has been directed at understanding individual differences in these processes over prolonged developmental time scales. There is a rich body of theoretical empirical work indicating that different domains of cognitive function tap overlapping sets of core cognitive processes (41–44). Identifying and delineating the cognitive mechanisms that mediate shared individual differences in aging-related cognitive declines will be foundational to understanding, and—in combination with further scientific discoveries and advancements—postponing and ameliorating cognitive aging (45, 46).
The codependence between individual differences in aging-related fluid and crystallized changes documented here has important implications for lifespan theory and clinical practice. First, it implies that accounts of behavioral aging that exclusively invoke domain-specific mechanisms of change are inadequate, thereby strengthening the need to delineate both general and specific neural mechanisms and deterioration and maintenance (47). Second, it places constraints on the extent to which individuals can be expected to recruit crystallized abilities to compensate for decline in fluid abilities. In other words, it might be more difficult than previously acknowledged to individually tailor compensatory interventions that shift reliance from fluid to crystallized abilities, given that the individuals who experience particularly precipitous rates of fluid decline are likely to be those who exhibit the shallowest rate of gain, and perhaps even decline, in crystallized abilities. Directing attention toward identifying the domain-general mechanisms of adult cognitive decline and maintenance might help to reveal promising targets for individualized interventions (48).
MATERIALS AND METHODS
Sample characteristics
Virginia Cognitive Aging Project
The VCAP (20) is an institutional review board (IRB)–approved longitudinal study of a large community sample of adults from central Virginia, USA, focused on life-course trajectories of cognitive function, covering a wide range of domains of cognition. A total of 5566 participants from the first eight assessments (T1 to T8) of the VCAP study were included in the present study, 3663 females (65.81%). We did not include data for the handful of individuals with data beyond eight occasions so as to avoid model estimation problems that would result from the high degree of sparsity for those extended waves. Sample sizes across follow-up assessments are presented in table S1. Age at baseline ranged from 18 to 99 years (fig. S1). By design, assessments are conducted at variable retest intervals (table S2), with a mean total follow-up duration of 7.00 years (fig. S2).
Participants completed 16 cognitive tests covering five broad domains of cognitive function (Gf = abstract reasoning, Gv = visuospatial reasoning, Gm = memory, Gs = perceptual speed, and Gc = crystallized ability). For task descriptions, see table S3. Following Salthouse (49), we fit a confirmatory factor analysis (CFA) to verify the classifications of cognitive tests into the five ability domains. The CFA was fit to the age-residualized correlations (fig. S3) (47) among baseline cognitive test scores (fig. S4) in Mplus (50) using robust maximum estimation. The CFA model presented an adequate fit {χ2 (99) = 2317.91, comparative fit index (CFI) = 0.951, root mean square error of approximation (RMSEA) = 0.064 [90% confidence interval (CI) = 0.062 to 0.066], and standardized root mean square residual (SRMR) = 0.040}. All factor loadings were statistically significant (P < 0.001), with standardized estimates ranging from 0.68 to 0.856. On the basis of this factor structure, we produced unit-weighted composite scores for Gf, Gv, Gm, Gs, and Gc, which we used as the analytic variables in the multivariate growth curve models for VCAP.
The Betula prospective cohort study (BETULA)
The Betula study is an IRB-approved longitudinal study on aging, memory, and dementia, with repeated data collection between 1988 and 2014 in the university town of Umeå, northern Sweden (21). For the purpose of the present study, we focused on one task for each of the following abilities: episodic memory (Gm), perceptual speed (Gs), visuospatial reasoning (Gv), and crystallized ability (Gc) (table S4). We used data from four assessment occasions in each task, namely, the first four time points each individual was assessed. Participants were tested for perceptual speed up to 10 years later than for the other three abilities, because the letter-digit substitution task was introduced at wave 3 of the study. A total of 3320 BETULA participants from four assessments were included in the present study, 1803 females (54.3%). Age at baseline ranged from 25 to 95 years (fig. S5). Sample sizes across the follow-up assessments are presented in table S5. Assessments were conducted approximately every 5 years (table S6), with a mean total follow-up length of approximately 10 years (fig. S6).
A heatmap of age-residualized correlations among the four cognitive tests at baseline assessment is presented in fig. S7. To estimate loadings of static (rather than longitudinal) individual differences in the variables on a general factor, a CFA was conducted to fit a common factor model on the age-residualized correlations among the baseline cognitive test scores (fig. S8) in Mplus (50) using robust maximum likelihood estimation. The CFA model presented an adequate fit [χ2 (2) = 9.314, CFI = 0.998, RMSEA = 0.033 (90% CI = 0.014 to 0.056), and SRMR = 0.007]. All factor loadings were statistically significant (P < 0.001), with standardized estimates ranging from 0.662 to 0.839, indicating that each domain partly tapped a general dimension of individual differences in cognitive function.
Multivariate growth curve models
We used a multivariate growth curve approach in which we simultaneously modeled changes in multiple cognitive variables measured repeatedly over time. The growth curve portion of such a multivariate model can be written as
| (1) |
where Y[t]w,n is the score Y of person n on variable w at time t, iw,n is the level for person n on variable w, sw,n is the linear component of the longitudinal change for person n on variable w, qw,n is the nonlinear (quadratic) component of the longitudinal change, rw,n is a retest effect, and e[t]w,n is a disturbance for person n on variable w at time t. All righthand terms that vary across people (i.e., those with the subscript n) are allowed to have a nonzero mean, with the exception of the disturbance (e[t]), which has a mean of zero by definition. The term A[t]w,n is a set of growth curve basis coefficients that define the shape of the longitudinal changes over time. In our primary models, we specified age-based growth curve modeling, such that the basis coefficients were set to the age of individual n at each assessment on variable w. To facilitate model estimation, we centered age at 50 years and divided by 10 years for VCAP (such that change is expressed per decade) and by 25 years in BETULA (such that change is expressed per quarter century). Note that this choice of metric does not affect the standardized results or the levels of significance for our estimates of interest. Moreover, we transformed model parameters in T score units (mean = 50 and SD = 10) to plot model-implied trajectories. We also report results from sensitivity analyses in which the basis coefficients were set to be a function of time since baseline occasion. The basis coefficients for the retest effect, B[t], were set to be a function of number of occasions of measurement. In our primary models, we chose a parsimonious specification for the retest function in which we set B[t] to be equal to 0 for the first occasion of measurement for a particular individual and 1 for all subsequent occasions of measurement for that individual, so as to capture the performance benefits accruing from initial exposure to the test [cf. (23)]. We also report results from sensitivity analyses in which the retest basis coefficients were set to be logarithmic functions of occasion and those in which they were freely estimated from the data. As indicated by the subscript n on the r, we allowed for person-specific retest effects on each outcome when modeling both the VCAP and the BETULA data. When fitting the BETULA data, the estimates for between-person variance in retest effects were negative or zero, so we fixed them to zero. In VCAP, they were typically very small but remained freely estimated in the model. Note that while we estimated the quadratic component of change, q, with random effects to allow for individual differences in curvature, we focus our plots on variation in the linear component of change.
As the multivariate growth model allows for individual differences in levels and changes for each variable, we are able to test how these individual differences relate to one another. A conceptually straightforward approach is to estimate an unrestricted covariance matrix, taking the form
| (2) |
where Σi is a submatrix that includes level variances on its diagonal and level-level covariances off its diagonal, Σs is a submatrix that includes slope variances on its diagonal and slope-slope covariances off its diagonal, Σq is a submatrix that includes curvature variances on its diagonal and curvature-curvature covariances off its diagonal, Σi,s is a submatrix that includes within-variable level-slope covariances on its diagonal and cross-variable level-slope covariances off its diagonal, Σi,q is a submatrix that includes within-variable level-curvature covariances on its diagonal and cross-variable level-curvature covariances off its diagonal, and Σs,q is a submatrix that includes within-variable slope-curvature covariances on its diagonal and cross-variable slope-curvature covariances off its diagonal. When this covariance matrix is freely estimated, it is sometimes referred to as a “parallel process” model.
Such an unstructured approach to estimating associations among all components of variation in domain-specific levels and change can introduce a great deal of model complexity and produce estimates that are themselves so manifold that they may necessitate further post-modeling analysis. Rather than allowing the person-specific levels and slopes for each variable to covary freely, as in Eq. 2, we parsimoniously approximated the interrelations among levels (i) and among linear slopes (s) and curvatures (q) by common factors. The factor portions of such a “factor of curves” model (51) can be written as
| (3a) |
and
| (3b) |
| (3c) |
where τiw, τsw, and τqw are mean level, linear slope, and curvature for variable w; λiw is the loading of the person-specific level of variable w on the common factor of the levels, Fi,n; λsw is the loading of the person-specific slope of variable w on the common factor of the slopes, Fi,n; λqw is the loading of the person-specific slope of variable w on the common factor of the curvature components, Fq,n; uiw,n is a person-specific unique factor for the level of variable w; usw,n is a person-specific unique factor for the slope of variable w; and uqw,n is a person-specific unique factor for the curvature of variable w. We allow for within-variable covariances between level, slope, and quadratic unique factors to be freely estimated. To identify the metric of each of the common factors, we set their means to 0, and their variances to 1.0. All common factors are allowed to intercorrelate. Models were estimated as structural equation models with random slopes in Mplus (50) using the individually varying times of observation option, which we used to specify basis coefficients for age using the exact age of the participant (and in the case of sensitivity analyses, time lag using the time that had passed since baseline), without having to discretely bin observations.
Estimating models without allowing Gc to affect the structure of general Gf change
The explicit goal of our analyses was to stratify trajectories of Gc change by scores on a general factor of Gf change that has itself not been identified using Gc information in any way. We achieved this by estimating parameters from a multivariate model of Gf change that excluded Gc. In a subsequent step, we then fit the model again, including Gc, while fixing all parameters that overlapped with the first model to the estimates from that first model. Thus, the only parameters that we estimated in the second model were the loadings of Gc level and Gc slope on the general factor of Gf change, along with Gc-specific growth curve means, residual intercept and change variances, Gc-specific intercept-change residual covariance, and Gc-specific disturbance variances. Thus, we fitted a factor of curves model in two subsequent steps instead of fitting all parameters simultaneously. We did so to ensure that we are capturing Gc change as independent from Gf changes. If we had fitted all parameters of a factor of curves model as described by Eqs. 1, 3a, and 3b simultaneously, the general factor of change may have itself included information on the Gc change.
Deriving expected trajectories of change in a specific variable
Parameter estimates from the above-described factor of curves model (specified by simultaneously fitting a model described by Eqs. 1, 3a, and 3b) can be used to yield expectations for expected trajectories of change in each variable, stratified by general (cross-domain) change. When the metric of the common factor of slopes, Fs, is identified by fixing its variance to 1.0, such that its SD is , we can derive the expected mean of the slopes for individuals whose unobserved scores on the common factor are low (e.g., z SDs below the mean slope), average, and low (e.g., z SDs above the mean slope) by substituting their unobserved factor scores (e.g., −1, 0, or 1) into Eq. 3b as follows
| (4a) |
| (4b) |
| (4c) |
The expected mean trajectory in ability w (e.g., Gc) over time is then obtained for each unobserved score on the common factor of slopes, holding all other sources of variation constant, by substituting μsw,lowFs, μsw,averageFs, or μsw,highFs into Eq. 1, alongside the means of the other respective random terms of interest. Thus, the expected trajectories of change in variable w—stratified by low, average, and high scores of the common factor of slopes—are
| (5a) |
| (5b) |
| (5c) |
Note that we do not include terms in the above Eq. 5 (a to c) for retest effects, because we are specifically interested in the expected trajectories of cognitive change, decontaminated by retest effects.
Acknowledgments
We thank the participants in the VCAP and BETULA studies and T. A. Salthouse for providing the data from VCAP.
Funding: This work was supported by NIH grants R01AG054628, RF1AG073593, P30AG066614, and P2CHD042849 (to E.M.T.-D.); The Jacobs Foundation (to E.M.T.-D.); joint funding from the Max Planck Society and the Alexander von Humboldt Foundation (to E.M.T.-D.); The Max Planck Society (to U.L.); The European Commission as part of the Lifebrain Consortium grant 732592 within the Horizon 2020 program (to U.L., A.M.B., and Y.K.); and Knut and Alice Wallenberg’s Foundation (to L.N.).
Author contributions: E.M.T.-D., A.M.B., and U.L. jointly conceived of the idea, designed the study, and formulated the analytic plan. J.d.l.F. and Y.K analyzed the data and prepared the results, with contributions from E.M.T.-D., A.M.B., and U.L. L.N. directed data collection for the BETULA study. E.M.T.-D. wrote the paper, with contributions from U.L., A.M.B., L.N., J.F., and Y.K. All authors contributed to editing the paper.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: Code and output for the analyses reported in this paper are available on the Open Science Framework (OSF) at https://osf.io/j8qma/?view_only=c3de39b3d13143f9849703e2a901038e. All data needed to evaluate the conclusions in the paper are present in the paper, in the Supplementary Materials, and on OSF. Raw data from BETULA and VCAP were provided by the respective study administrators. Raw data from BETULA can be directly requested from the BETULA administrators at www.umu.se/en/research/projects/betula---aging-memory-and-dementia/collaboration-on-betula-data/. Raw data from VCAP can be directly requested from VCAP administrators, whose contact information can be found at https://uva.theopenscholar.com/vcap/.
Supplementary Materials
This PDF file includes:
Figs. S1 to S8
Tables S1 to S14
REFERENCES AND NOTES
- 1.Tucker-Drob E. M., Neurocognitive functions and everyday functions change together in old age. Neuropsychology 25, 368–377 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schmidt F. L., Hunter J. E., The validity and utility of selection methods in personnel psychology: Practical and theoretical implications of 85 years of research findings. Psychol. Bull. 124, 262–274 (1998). [Google Scholar]
- 3.Gottfredson L. S., Deary I. J., Intelligence predicts health and longevity, but why? Curr. Dir. Psychol. Sci. 13, 1–4 (2004). [Google Scholar]
- 4.Tucker-Drob E. M., Cognitive aging and dementia: A life-span perspective. Annu. Rev. Dev. Psychol. 1, 177–196 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Horn J. L., Cattell R. B., Age differences in fluid and crystallized intelligence. Acta Psychol. 26, 107–129 (1967). [DOI] [PubMed] [Google Scholar]
- 6.J. B. Carroll, Human Cognitive Abilities: A Survey of Factor-Analytic Studies (Cambridge Univ. Press, 1993). [Google Scholar]
- 7.J. L. Horn, Models of intelligence, in Intelligence: Measurement, Theory, Public Policy: Proceedings of a Symposium in Honor of Lloyd G. Humphreys (University of Illinois Press, 1989), pp. 29–73. [Google Scholar]
- 8.Baltes P. B., Staudinger U. M., Lindenberger U., Lifespan psychology: Theory and application to intellectual functioning. Annu. Rev. Psychol. 50, 471–507 (1999). [DOI] [PubMed] [Google Scholar]
- 9.U. Lindenberger, Lifespan theories of cognitive development, in International Encyclopedia of the Social and Behavioral Sciences, N. J. Smelser, P. B. Baltes, Eds. (Elsevier Science, 2001), pp. 8848–8854. [Google Scholar]
- 10.Salthouse T., Consequences of age-related cognitive declines. Annu. Rev. Psychol. 63, 201–226 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baltes P. B., Baltes P. B., On the incomplete architecture of human ontogeny. Selection, optimization, and compensation as foundation of developmental theory. Am. Psychol. 52, 366–380 (1997). [DOI] [PubMed] [Google Scholar]
- 12.P. B. Baltes, M. M. Baltes, Psychological Perspectives on Successful Aging: The Model of Selective Optimization with Compensation (Cambridge Univ. Press, 1990). [Google Scholar]
- 13.Reuter-Lorenz P. A., Cappell K. A., Neurocognitive aging and the compensation hypothesis. Curr. Dir. Psychol. Sci. 17, 177–182 (2008). [Google Scholar]
- 14.Stern Y., Cognitive reserve in ageing and Alzheimer’s disease. Lancet Neurol. 11, 1006–1012 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tucker-Drob E. M., Brandmaier A. M., Lindenberger U., Coupled cognitive changes in adulthood: A meta-analysis. Psychol. Bull. 145, 273–301 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ghisletta P., Rabbitt P., Lunn M., Lindenberger U., Two thirds of the age-based changes in fluid and crystallized intelligence, perceptual speed, and memory in adulthood are shared. Intelligence 40, 260–268 (2012). [Google Scholar]
- 17.P. B. Baltes, H. W. Reese, J. R. Nesselroade, Life-Span Developmental Psychology: Introduction to Research Methods (Psychology Press, 2014). [Google Scholar]
- 18.Lindenberger U., Von Oertzen T., Ghisletta P., Hertzog C., Cross-sectional age variance extraction: What’s change got to do with it? Psychol. Aging 26, 34 (2011). [DOI] [PubMed] [Google Scholar]
- 19.Rabbitt P., Does it all go together when it goes? The Nineteenth Bartlett Memorial Lecture. Q. J. Exp. Psychol. Sect. A. 46, 385–434 (1993). [DOI] [PubMed] [Google Scholar]
- 20.Salthouse T. A., Contributions of the individual differences approach to cognitive aging. J. Gerontol. Ser. B. 72, 7–15 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nyberg L., Boraxbekk C.-J., Sörman D. E., Hansson P., Herlitz A., Kauppi K., Ljungberg J. K., Lövheim H., Lundquist A., Adolfsson A. N., Biological and environmental predictors of heterogeneity in neurocognitive ageing: Evidence from Betula and other longitudinal studies. Ageing Res. Rev. 64, 101184 (2020). [DOI] [PubMed] [Google Scholar]
- 22.Salthouse T. A., Tucker-Drob E. M., Implications of short-term retest effects for the interpretation of longitudinal change. Neuropsychology 22, 800–811 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lövdén M., Ghisletta P., Lindenberger U., Cognition in the Berlin Aging Study (BASE): The first 10 years. Aging Neuropsychol. Cogn. 11, 104–133 (2004). [Google Scholar]
- 24.J. J. McArdle, J. R. Nesselroade, in Handbook of psychology: Research methods in psychology, Vol. 2, J. A. Schinka, W. F. Velicer, Eds. (John Wiley & Sons Inc., 2003), pp. 447–480. [Google Scholar]
- 25.H. Ebbinghaus, Über das Gedächtnis: Untersuchungen zur Experimentellen Psychologie (Duncker & Humblot, 1885). [Google Scholar]
- 26.Iturria-Medina Y., Sotero R. C., Toussaint P. J., Mateos-Pérez J. M., Evans A. C.; The Alzheimer’s Disease Neuroimaging Initiative , Early role of vascular dysregulation on late-onset Alzheimer’s disease based on multifactorial data-driven analysis. Nat. Commun. 7, 11934 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wåhlin A., Nyberg L., At the heart of cognitive functioning in aging. Trends Cogn. Sci. 23, 717–720 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Raz N., Lindenberger U., Rodrigue K. M., Kennedy K. M., Head D., Williamson A., Dahle C., Gerstorf D., Acker J. D., Regional brain changes in aging healthy adults: General trends, individual differences and modifiers. Cereb. Cortex 15, 1676–1689 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Cox S. R., Harris M. A., Ritchie S. J., Buchanan C. R., Valdés Hernández M. C., Corley J., Taylor A. M., Madole J. W., Harris S. E., Whalley H. C., McIntosh A. M., Russ T. C., Bastin M. E., Wardlaw J. M., Deary I. J., Tucker-Drob E. M., Three major dimensions of human brain cortical ageing in relation to cognitive decline across the eighth decade of life. Mol. Psychiatry 26, 2651–2662 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Madole J. W., Ritchie S. J., Cox S. R., Buchanan C. R., Hernández M. V., Maniega S. M., Wardlaw J. M., Harris M. A., Bastin M. E., Deary I. J., Tucker-Drob E. M., Aging-sensitive networks within the human structural connectome are implicated in late-life cognitive declines. Biol. Psychiatry 89, 795–806 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Morrison J. H., Baxter M. G., The ageing cortical synapse: Hallmarks and implications for cognitive decline. Nat. Rev. Neurosci. 13, 240–250 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Burke S. N., Barnes C. A., Neural plasticity in the ageing brain. Nat. Rev. Neurosci. 7, 30–40 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Gutchess A., Plasticity of the aging brain: New directions in cognitive neuroscience. Science 346, 579–582 (2014). [DOI] [PubMed] [Google Scholar]
- 34.T. P. Zanto, A. Gazzaley, Attention and ageing, in The Oxford Handbook of Attention, A. C. Nobre, S. Kastner, Eds. (Oxford Univ. Press, 2014), pp. 927–971. [Google Scholar]
- 35.A. Riekmann, L. Nyberg, Cognitive aging: The role of neurotransmitter systems, in Handbook of Cognitive Aging: A Life Course Perspective, A. K. Thomas, A. Gutchess, Eds. (Cambridge Univ. Press, 2020), pp. 82–100. [Google Scholar]
- 36.Grasby K. L., Jahanshad N., Painter J. N., Colodro-Conde L., Bralten J., Hibar D. P., Lind P. A., Pizzagalli F., Ching C. R. K., McMahon M. A. B., Shatokhina N., Zsembik L. C. P., Thomopoulos S. I., Zhu A. H., Strike L. T., Agartz I., Alhusaini S., Almeida M. A. A., Alnæs D., Amlien I. K., Andersson M., Ard T., Armstrong N. J., Ashley-Koch A., Atkins J. R., Bernard M., Brouwer R. M., Buimer E. E. L., Bülow R., Bürger C., Cannon D. M., Chakravarty M., Chen Q., Cheung J. W., Couvy-Duchesne B., Dale A. M., Dalvie S., de Araujo T. K., de Zubicaray G. I., de Zwarte S. M. C., den Braber A., Doan N. T., Dohm K., Ehrlich S., Engelbrecht H.-R., Erk S., Fan C. C., Fedko I. O., Foley S. F., Ford J. M., Fukunaga M., Garrett M. E., Ge T., Giddaluru S., Goldman A. L., Green M. J., Groenewold N. A., Grotegerd D., Gurholt T. P., Gutman B. A., Hansell N. K., Harris M. A., Harrison M. B., Haswell C. C., Hauser M., Herms S., Heslenfeld D. J., Ho N. F., Hoehn D., Hoffmann P., Holleran L., Hoogman M., Hottenga J.-J., Ikeda M., Janowitz D., Jansen I. E., Jia T., Jockwitz C., Kanai R., Karama S., Kasperaviciute D., Kaufmann T., Kelly S., Kikuchi M., Klein M., Knapp M., Knodt A. R., Krämer B., Lam M., Lancaster T. M., Lee P. H., Lett T. A., Lewis L. B., Lopes-Cendes I., Luciano M., Macciardi F., Marquand A. F., Mathias S. R., Melzer T. R., Milaneschi Y., Mirza-Schreiber N., Moreira J. C. V, Mühleisen T. W., Müller-Myhsok B., Najt P., Nakahara S., Nho K., Olde Loohuis L. M., Orfanos D. P., Pearson J. F., Pitcher T. L., Pütz B., Quidé Y., Ragothaman A., Rashid F. M., Reay W. R., Redlich R., Reinbold C. S., Repple J., Richard G., Riedel B. C., Risacher S. L., Rocha C. S., Mota N. R., Salminen L., Saremi A., Saykin A. J., Schlag F., Schmaal L., Schofield P. R., Secolin R., Shapland C. Y., Shen L., Shin J., Shumskaya E., Sønderby I. E., Sprooten E., Tansey K. E., Teumer A., Thalamuthu A., Tordesillas-Gutiérrez D., Turner J. A., Uhlmann A., Vallerga C. L., van der Meer D., van Donkelaar M. M. J., van Eijk L., van Erp T. G. M., van Haren N. E. M., van Rooij D., van Tol M.-J., Veldink J. H., Verhoef E., Walton E., Wang M., Wang Y., Wardlaw J. M., Wen W., Westlye L. T., Whelan C. D., Witt S. H., Wittfeld K., Wolf C., Wolfers T., Wu J. Q., Yasuda C. L., Zaremba D., Zhang Z., Zwiers M. P., Artiges E., Assareh A. A., Ayesa-Arriola R., Belger A., Brandt C. L., Brown G. G., Cichon S., Curran J. E., Davies G. E., Degenhardt F., Dennis M. F., Dietsche B., Djurovic S., Doherty C. P., Espiritu R., Garijo D., Gil Y., Gowland P. A., Green R. C., Häusler A. N., Heindel W., Ho B.-C., Hoffmann W. U., Holsboer F., Homuth G., Hosten N., Jack C. R., Jang M., Jansen A., Kimbrel N. A., Kolskår K., Koops S., Krug A., Lim K. O., Luykx J. J., Mathalon D. H., Mather K. A., Mattay V. S., Matthews S., J. Mayoral Van Son, McEwen S. C., Melle I., Morris D. W., Mueller B. A., Nauck M., Nordvik J. E., Nöthen M. M., O’Leary D. S., Opel N., Martinot M.-L. P., Pike G. B., Preda A., Quinlan E. B., Rasser P. E., Ratnakar V., Reppermund S., Steen V. M., Tooney P. A., Torres F. R., Veltman D. J., Voyvodic J. T., Whelan R., White T., Yamamori H., Adams H. H. H., Bis J. C., Debette S., Decarli C., Fornage M., Gudnason V., Hofer E., Ikram M. A., Launer L., Longstreth W. T., Lopez O. L., Mazoyer B., Mosley T. H., Roshchupkin G. V, Satizabal C. L., Schmidt R., Seshadri S., Yang Q.; Alzheimer’s Disease Neuroimaging Initiative; CHARGE Consortium; EPIGEN Consortium; IMAGEN Consortium; SYS Consortium; Parkinson’s Progression Markers Initiative, Alvim M. K. M., Ames D., Anderson T. J., Andreassen O. A., Arias-Vasquez A., Bastin M. E., Baune B. T., Beckham J. C., Blangero J., Boomsma D. I., Brodaty H., Brunner H. G., Buckner R. L., Buitelaar J. K., Bustillo J. R., Cahn W., Cairns M. J., Calhoun V., Carr V. J., Caseras X., Caspers S., Cavalleri G. L., Cendes F., Corvin A., Crespo-Facorro B., Dalrymple-Alford J. C., Dannlowski U., de Geus E. J. C., Deary I. J., Delanty N., Depondt C., Desrivières S., Donohoe G., Espeseth T., Fernández G., Fisher S. E., Flor H., Forstner A. J., Francks C., Franke B., Glahn D. C., Gollub R. L., Grabe H. J., Gruber O., Håberg A. K., Hariri A. R., Hartman C. A., Hashimoto R., Heinz A., Henskens F. A., Hillegers M. H. J., Hoekstra P. J., Holmes A. J., Hong L. E., Hopkins W. D., Hulshoff Pol H. E., Jernigan T. L., Jönsson E. G., Kahn R. S., Kennedy M. A., Kircher T. T. J., Kochunov P., Kwok J. B. J., Le Hellard S., Loughland C. M., Martin N. G., Martinot J.-L., McDonald C., McMahon K. L., Meyer-Lindenberg A., Michie P. T., Morey R. A., Mowry B., Nyberg L., Oosterlaan J., Ophoff R. A., Pantelis C., Paus T., Pausova Z., Penninx B. W. J. H., Polderman T. J. C., Posthuma D., Rietschel M., Roffman J. L., Rowland L. M., Sachdev P. S., Sämann P. G., Schall U., Schumann G., Scott R. J., Sim K., Sisodiya S. M., Smoller J. W., Sommer I. E., St Pourcain B., Stein D. J., Toga A. W., Trollor J. N., Van der Wee N. J. A., van ‘t Ent D., Völzke H., Walter H., Weber B., Weinberger D. R., Wright M. J., Zhou J., Stein J. L., Thompson P. M., Medland S. E.; Enhancing NeuroImaging Genetics through Meta-Analysis Consortium (ENIGMA)—Genetics working group , The genetic architecture of the human cerebral cortex. Science 367, eaay6690 (2020).32193296 [Google Scholar]
- 37.Tucker-Drob E. M., Reynolds C. A., Finkel D., Pedersen N. L., Shared and unique genetic and environmental influences on aging-related changes in multiple cognitive abilities. Dev. Psychol. 50, 152–166 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Plassman B. L., Williams J. W. Jr., Burke J. R., Holsinger T., Benjamin S., Systematic review: Factors associated with risk for and possible prevention of cognitive decline in later life. Ann. Intern. Med. 153, 182–193 (2010). [DOI] [PubMed] [Google Scholar]
- 39.A. Newell, P. S. Rosenbloom, Mechanisms of skill acquisition and the law of practice, in Cognitive Skills and Their Acquisition, J. R. Anderson, Ed. (Psychology Press, 1981), pp. 1–55. [Google Scholar]
- 40.Craik F. I. M., On the transfer of information from temporary to permanent memory. Philos. T. R. Soc. B 302, 341–359 (1983). [Google Scholar]
- 41.Laux L. F., Lane D. M., Information processing components of substitution test performance. Intelligence 9, 111–136 (1985). [Google Scholar]
- 42.J. B. Carroll, Human Cognitive Abilities: A Survey of Factor-Analytic Studies (Cambridge Univ. Press, 1993). [Google Scholar]
- 43.C. Spearman, The Abilities of Man (Macmillan, 1927). [Google Scholar]
- 44.Kovacs K., Conway A. R. A., Process overlap theory: A unified account of the general factor of intelligence. Psychol. Inq. 27, 151–177 (2016). [Google Scholar]
- 45.Lindenberger U., Human cognitive aging: Corriger la fortune? Science 346, 572–578 (2014). [DOI] [PubMed] [Google Scholar]
- 46.T. A. Salthouse, Steps toward the explanation of adult age differences in cognition, in Models of Cognitive Aging, T. J. Perfect, E. A. Maylor, Eds. (Oxford Univ. Press, 2000), pp. 19–49. [Google Scholar]
- 47.Nyberg L., Lövdén M., Riklund K., Lindenberger U., Bäckman L., Memory aging and brain maintenance. Trends Cogn. Sci. 16, 292–305 (2012). [DOI] [PubMed] [Google Scholar]
- 48.Lindenberger U., Lövdén M., Schellenbach M., Li S. C., Krüger A., Psychological principles of successful aging technologies: A mini-review. Gerontology 54, 59–68 (2008). [DOI] [PubMed] [Google Scholar]
- 49.Salthouse T. A., Localizing age-related individual differences in a hierarchical structure. Intelligence 32, 541–561 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.L. K. Muthén, B. O. Muthén, Mplus: Statistical Analysis with Latent Variables: User’s Guide (Version 8) (Muthén & Muthén, 1998–2017). [Google Scholar]
- 51.J. J. McArdle, Dynamic but structural equation modeling of repeated measures data, in Handbook of Multivariate Experimental Psychology, J. R. Nesselroade, Ed. (Springer, 1988), pp. 561–614. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figs. S1 to S8
Tables S1 to S14