DeepSENSE: Learning Coil Sensitivity Functions for SENSE Reconstruction Using Deep Learning

Abstract

Purpose:

To improve the estimation of coil sensitivity functions from limited auto calibration signals (ACS) in SENSE-based reconstruction for brain imaging.

Methods:

We propose to use deep learning to estimate coil sensitivity functions by leveraging information from previous scans obtained using the same RF receiver system. Specifically, deep convolutional neural networks (CNNs) were designed to learn an end-to-end mapping from the initial sensitivity to the high resolution counterpart; Sensitivity alignment was further proposed to reduce the geometric variation caused by different subject positions and imaging FOVs. Cross-validation with a small set of datasets was performed to validate the learned neural network. Iterative SENSE reconstruction was adopted to evaluate the utility of the sensitivity functions from the proposed and conventional methods.

Results:

The proposed method produced improved sensitivity estimates and SENSE reconstructions compared to the conventional methods in terms of aliasing and noise suppression with very limited ACS data. Cross-validation with a small set of data demonstrated the feasibility of learning coil sensitivity functions for brain imaging. The network learned on the spoiled GRE data can be applied to predicting sensitivity functions for spin-echo and MPRAGE datasets.

Conclusion:

A deep learning based method has been proposed for improving the estimation of coil sensitivity functions. Experimental results have demonstrated the feasibility and potential of the proposed method for improving SENSE-based reconstructions especially when the ACS data are limited.

1 |. INTRODUCTION

Parallel imaging has been widely used to accelerate MRI data acquisition in many research and clinical applications [1]. It exploits the spatial encoding effect of the RF receiver coil’s sensitivity functions to enable undersampling of k-space [2, 3, 4]. In image reconstruction, knowledge of the coil sensitivity functions is essential.

A common approach to determining high-quality coil sensitivity functions is to acquire a high-resolution data from a reference scan and use the sum of squares (SoS) or adaptive combine [5] method. But the sensitivity obtained may not be exactly aligned with the imaging data collected separately due to subject motion. A more desirable approach is to acquire a set of auto-calibration signals (ACS) within the imaging scan. However, due to scan time constraint, only a small set of ACS can be acquired with limited k-space coverage in practical imaging experiments, resulting in inaccurate sensitivity for SENSE reconstruction. To address this issue, several approaches have been developed in the previous literature: polynomial functions [3] were exploited to represent the coil sensitivity with reduced degrees of freedom and thus improve sensitivity estimation; Iterative reconstruction was developed to jointly estimate the sensitivity and image function with sparsity and smoothness constraints [4, 6]; GRAPPA was used to interpolate a larger k-space for sensitivity estimation [7]; and the ESPIRiT method [8] was developed to directly extract the coil sensitivity from the calibration matrix composed by the ACS data using its subspace structure. All these methods take advantage of prior knowledge within the current scan.

An alternative approach is to exploit redundancy between multiple scans, which has not been fully developed. For example, correlation imaging [9] was introduced to exploit the correlation of coil sensitivities and anatomical structures between multi-scans using a linear prediction function. Inspired by the recent success of deep learning (DL) in MR image reconstruction[10, 11, 12, 13, 14, 15, 16], we propose to use deep neural networks to predict high-quality coil sensitivity functions from limited ACS data. The main assumption is that variations of coil sensitivity for a given receiver system under various experimental conditions reside on a low dimensional manifold. Based on this premise, a 3D deep convolutional neural network (CNN) with the U-net [17] architecture was designed and trained to learn the manifold representation and the nonlinear mapping between the low-resolution and high-resolution sensitivities. Sensitivity alignment was further proposed to reduce the geometric variation induced by different subject positions and FOV settings. As a proof-of-concept study, we demonstrated the feasibility of the sensitivity learning idea for brain imaging at 3T. Experimental results have shown that the learning-based method can produce high-quality sensitivity maps with very limited ACS data, leading to improved SENSE reconstruction with less aliasing artifacts. A preliminary version of this work was previously reported in an abstract for the 2018 annual meeting of the International Society for Magnetic Resonance in Medicine [18]; a detailed description of the method is given in this paper.

2 |. METHODS

2.1 |. Subspace structure of coil sensitivity

According to the reciprocity principle, the coil receiving sensitivity can be approximated as proportional to the magnetic field $B_1^{-}(\mathbf{r})$ that would be generated by the coil element. in general, the geometry of the coil elements, the tissue electric property (e.g., permeability) and coil loading will all affect the $B_1^{-}$ field. In this study, we hypothesize that the $B_1^{-}$ field from in vivo brain scans should have variations that can be well captured by a low-dimensional representation [19]. More specifically, when the RF wavelength is much larger than the imaging object, the geometry of the $B_1^{-}$ field is hardly affected by the presence of the imaging object and can be calculated by Biot-Savart integration [20, 21]. As is well known, RF wavelength on average for in vivo brain imaging is 27 cm at 3 Tesla [22], which is greater than the typical human head sizes (16-24cm). Therefore, given a specific receiver system, the sensitivity from in vivo brain scan at 3T can be well approximated by Biot-Savart integration and mainly varies on subject related permeability and loading. Given well-defined range of permeability of in vivo brain tissues and limited geometric variation within the coil, we presume that the variation introduced by different subjects should yield a low-dimensional representation. The additional wave effects due to varying but similar head sizes may lead to additional sensitivity variations and slightly increase the dimensionality, but it will not invalidate the low-dimensional assumption. As shown in Fig. 1a, the 3D coil sensitivity functions acquired in this study exhibit a low-rank structure in the linear subspace. Based on these observations, we believe that the coil sensitivity functions should reside on a low-dimensional manifold and can be learned using deep learning from previous scans obtained from the same receiver system.

Figure 1.

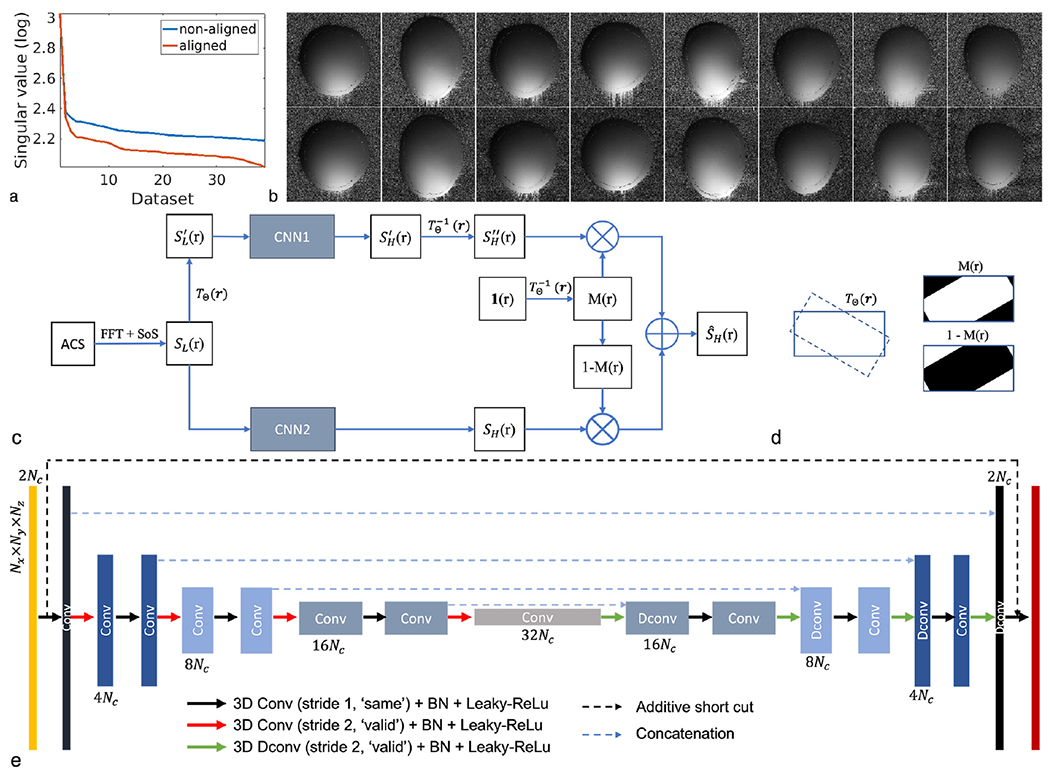
Main assumption and idea of DeepSENSE. a) Singular values of the Casorati matrix formed by stacking all the 3D sensitivity maps as its columns, demonstrating the low-dimensionality of the 3D coil sensitivity from the head coil. The 3D sensitivity maps are derived from the GRE dataset obtained from 15 subjects in this study. b) Example 2D sensitivity maps (i.e., same coil and same slice index) of each 3D volumes from eight different subjects before (top row) and after (bottom row) sensitivity alignment w.r.t. the first scan. With proper alignment, intensity variation in the sensitivity maps towards those in the first scan can be observed, leading to a lower-dimensional representation in the linear subspace. c) Workflow of the proposed method for improved sensitivity estimation from limited ACS data using deep learning; d) Illustration of spatial masks M (r) and 1 − M (r) to combine the predictions from the two CNNs in the case of a clockwise rotation. The mask M (r), calculated using 1 ($T_{\text{Θ}}^{-1}(\mathbf{r})$), indicates signals remaining in the FOV (intersected area between solid and dashed rectangles) that can be selected from the prediction of CNN1 while 1 − M (r), the area around the corner, corresponds to signals transformed out of the FOV, which can only be predicted from CNN2. e) The structure of the convolutional neural network used in the proposed method. The first orange and last red layers represent the input and output 3D sensitivity functions respectively. The intermediate layers are color coded differently at different scales. The number of feature maps is listed on the top or at the bottom of the corresponding layer. Layers from the same scale have the same size of feature maps. N_x × N_y × N_z and N_c denote the spatial dimension in 3D and the number of head coil channels respectively.

2.2 |. Sensitivity alignment

Due to variations in subject position and FOV settings, the sensitivity maps obtained from different scans will likely capture different 3D portions of the underlying sensitivity functions. In this study, we used a rigid-body motion T_Θ (r) to align the sensitivity functions to reduce such variation. The inverse transformation is defined as $T_{\text{Θ}}^{-1}(\mathbf{r})$. Given a set of 3D sensitivity S (r), the deformed sensitivity is denoted as S′ (r′) = S (T_Θ (r)). r and r′ indicate the spatial coordinates before and after the transformation, Θ contains the rotation and translation motion parameters. The mathematical description of the transformation T_Θ (r) and sensitivity alignment can be found in supplementary material. With proper alignment, the aligned sensitivity maps exhibited a lower-dimensional representation (Fig. 1a). Note that the 3D transformation can work for both 3D imaging and multi-slice imaging, as long as volumetric images are available.

2.3 |. Proposed workflow

The workflow of the proposed method is summarized in Fig. 1c. The ACS data was first zero-padded and Fourier transformed (ZP-FFT) to the image domain to generate low-resolution coil sensitivity functions S_L via dividing the individual coil images by the SoS coil combined image. Its high-resolution counterpart S_H was generated using fully sampled data. Sensitivity alignment was then performed to generate another set of sensitivity pairs (i.e., $S_L^{\prime }$ and $S_H^{\prime }$). Two 3D CNNs with identical architecture were trained separately using the original and the aligned sensitivity pairs respectively. The prediction from CNN1 using the aligned dataset was then inversely transformed to the original data space using $S_H^{″}=S_H^{\prime }(T_{\text{Θ}}^{-1}(\mathbf{r}))$. Note that a rigid-body transformation in 3D space may have signal moved out of the FOV (denoted by 1 − M (r) in Fig. 1d), which can not be recovered by the inverse transformation. Therefore, the predictions from the two CNNs were finally combined with corresponding spatial masks, yielding ${\hat{S}}_H=S_H^{″}·M+S_H·(1-M)$. An example was illustrated in Fig. 1d.

2.4 |. Network architecture

The 3D U-net architecture [23] was adopted for the CNNs described in the proposed method (Fig. 1e) with a few modifications. Specifically, to maintain effective encoding along with down sampling by a factor of 2, 3D convolutions with a stride of 2 were implemented replacing the max pooling used in the original segmentation task. An additive short cut was made between the input and output of the network for residual learning [24]. Leaky ReLU with a slope of 0.1 was employed. To avoid overfitting, ’dropout’ was employed [25] to randomly turn off neurons during training at a rate of 10%. L2 regularization with a parameter of 0.1 was also exploited. The training was generally done by minimizing the L2 loss function:

$$Loss={\Vert \rho \cdot \left[S_H-f\left(S_L;\omega \right)\right]\Vert }_2^2$$ (1)

where S_H and S_L are the corresponding input and output 3D sensitivity pairs, f (·) denotes the nonlinear mapping defined by the CNN with learnable parameters ω. · performs element-wise multiplication for each coil. ρ is the fully-sampled coil combined image, compensating for the spatially varying noise variation. In the spirit of reproducible research, the network code is available at: (https://github.com/stevepeng1120/DeepSENSE/).

2.5 |. Experimental set-up

In vivo brain experiments were conducted on a 3T MR scanner (SIEMENS Prisma) from 15 subjects using the standard 20-channel receive-only head/neck coil with 16 head coil elements activated and the other 4 neck elements turned off. Written informed consents were obtained from all the subjects with approval by the institutional IRB. A 3D spoiled gradient-echo (GRE) sequence (matrix size 160×160×36, FOV 240mm×240mm×72mm, FA 6°, TR 5.2ms, TE 2.3ms, Bandwidth 500Hz/pixel) was performed on each subject 2-3 times with axial slices along the anterior commissure (AC)-posterior commissure (PC) orientation. In between each scan, the subjects were asked to stand up and walk around before going back into the scanner, producing various head positions and FOV settings, in order to generate different permeability distributions within the coil, different sensitivity volumes, and probably different loading. To perform cross-validation, we randomly split our datasets into 5 groups. Each group contains data from 3 different subjects, yielding a set of 12 subjects (around 32 image volumes) and a set of 3 subjects (around 8 image volumes) for training and testing each time.

Conventional ZP-FFT with hamming filtering and the ESPIRiT [8] methods were also conducted. Sensitivity maps were compared given a various number of ACS lines (e.g., one central ,“k_y = 0”, phase encoding line plus additional 24, 16, 8, 4 surrounding PE lines) and evaluated by performing a subsequent iterative SENSE reconstruction [26] with uniform undersampling in the outer k-space. The ESPIRiT reconstruction were performed using the “SPIRiT_v0.3” Matlab code provided by the authors with kernel size either 6 or 5 (6 is preferred whenever feasible). Root mean square errors (RMSEs) were computed for both the sensitivity maps and SENSE reconstructions for quantitative assessment. To demonstrate the generalizability of the proposed technique to other sequences, an MPRAGE scan (matrix size 160×160×36, FA 9°, TR 1900ms, TE 3.06ms, TI 900ms, Bandwidth 200Hz/pixel) was performed on all 15 subjects and a multi-slice spin-echo scan (matrix size 192×192×36, TR 1500ms, TE 7.5ms, Bandwidth 250Hz/pixel) was carried out on five new subjects. All scans performed in this study had the same FOV.

2.6 |. Implementation details

Our current implementation forces the network to learn the inter-coil phase differences, which excludes any off-resonance and RF related phase and thus are still slowly varying functions residing on a low-dimensional manifold. More specifically, for both the input and output maps of all the training and testing datasets, we subtracted the phase of the 1st coil from all the coil sensitivities. The subtracted phase from the 1st coil, including the coil independent RF and off-resonance induced phase, will be absorbed into the final SENSE image. The 3D input and output labels to the network were formed by concatenating the real and the imaginary part of the corresponding coil sensitivity maps. Batch normalization [27] was employed right after each convolution and deconvolution layer to improve stability and training speed. Polynomial fitting with a order of 5 was applied to the sensitivity maps when estimating the motion parameters to improve motion estimation accuracy. The two CNNs were trained separately, where CNN2 was trained first using the original dataset, and CNN1 was trained afterwards using the aligned dataset with the learned weights from CNN2 as initialization. Predictions from different number of ACS lines were trained separately. The neural network was constructed in Tensorflow 1.5.0 and trained using stochastic gradient descent with an Adam optimizer [28] for 1000 epochs using the GeForce Titan XP graphics processing unit (GPU), taking approximately 20 hours. Before SENSE reconstruction, a rough background was estimated from the low-resolution image (using ACS data), and the predicted sensitivity values in such background were set to a very small constant number to further reduce image artifact.

3 |. RESULTS

The estimated sensitivity maps and SENSE reconstructions using 8 and 4 ACS lines were compared in Fig. 2 and Fig. 3 respectively. ZP-FFT with hamming filtering generated SENSE reconstructions with significant aliasing artifacts. The ESPIRiT method yielded inferior sensitivity estimation due to insufficient number of calibration data, especially with 4 ACS lines where a smaller kernel size (e.g., 5) could only be used (manifested by the distorted coil phase information), resulting in evident aliasing in the SENSE reconstruction. Our method provided consistently superior sensitivity estimation in both cases with very limited ACS data, leading to improved reconstruction with suppressed noise and aliasing artifacts. The RMSEs of the sensitivity and SENSE reconstructions with varying number of ACS lines were reported in Fig. 4. With moderate amount of calibration data (e.g., results from 24 ACS lines can be found in Fig. S2), ESPIRiT and the learning-based method produced comparable results. As the amount of ACS lines decreases, conventional methods degraded dramatically, while the learning-based method is much more robust since it takes advantage of information from previous scans. To demonstrate the applicability of the proposed method in handling rapid phase transitions, results from a bottom brain slice with air-tissue interface was also provided in supplementary material (Fig. S3).

Figure 2.

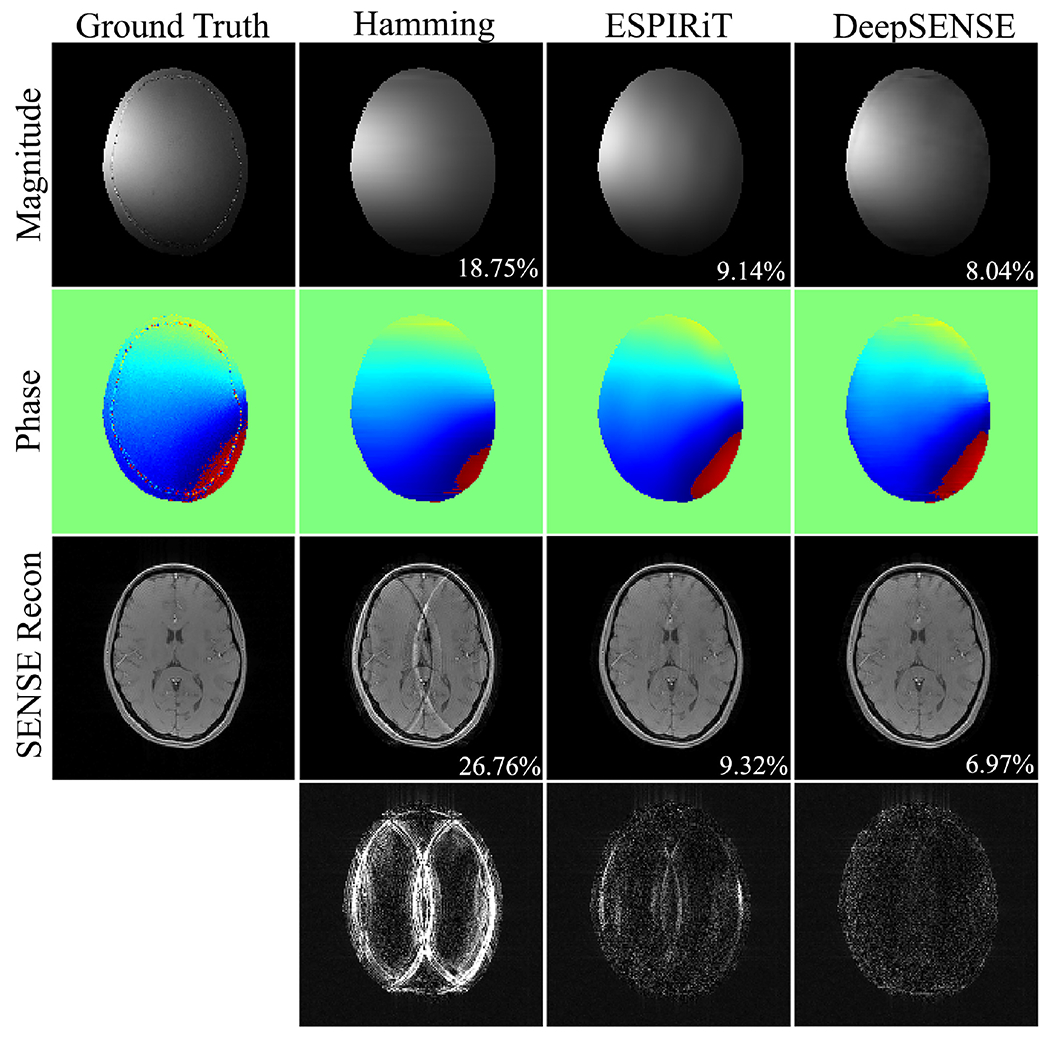
Comparison of the sensitivity maps (e.g., 6-th coil) estimated using 8 ACS lines and the subsequent iterative SENSE reconstructions at R=4 of a GRE testing dataset. RMSEs of the sensitivity maps and SENSE reconstructions are shown in the magnitude image. Error maps were scaled by 5 folds for better visualization.

Figure 3.

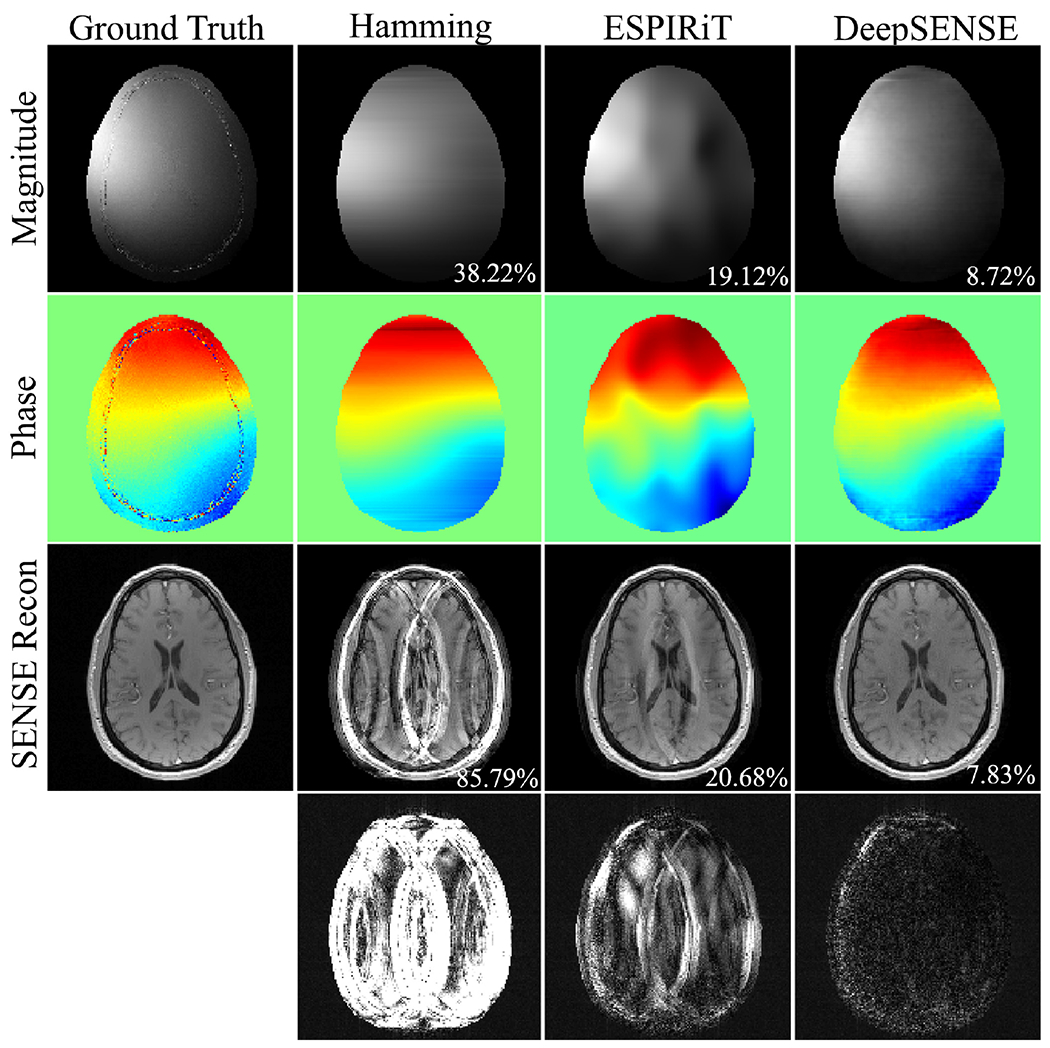
The coil sensitivity maps (e.g., 8-th coil) estimated using 4 ACS lines and the subsequent iterative SENSE reconstructions at R=4 of a GRE testing data from another subject. RMSEs of the sensitivity maps and SENSE reconstructions are shown in the magnitude image. Error maps were scaled by 5 folds for better visualization. The ESPIRiT method generated inferior coil sensitivity information due to insufficient calibration data and the smaller kernel size (e.g., 5) that could only be used.

Figure 4.

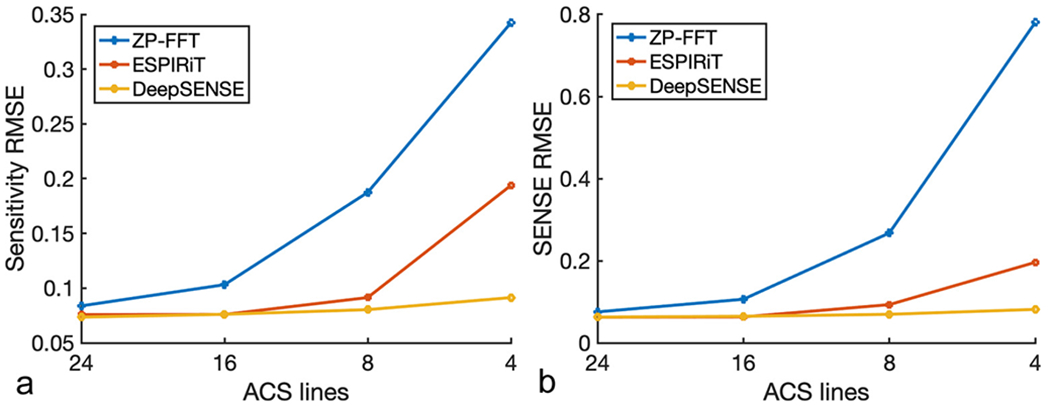
RMSEs of a) the estimated sensitivity maps and b) the subsequent SENSE reconstruction at R=4 with varying number of ACS lines from a testing GRE dataset. Conventional methods degraded dramatically as the number of ACS lines decreases, while the learning-based method is much more robust since it takes advantage of information from previous scans.

Results of the 5-fold cross-validation is shown in Fig. S4. Although we only employed a relatively small set of training data, the learned model was able to consistently improve the sensitivity to a similar level for all the validation groups, further validating our hypothesis that the coil sensitivity between scans reside on a low-dimensional manifold. Note that coil alignment may not be necessarily required in the case of small spatial misalignment (e.g., group 1-3), since the deep CNN should be able to handle certain extent of geometric variation due to its powerful representation capability. Lastly, the SENSE reconstructions of the spin-echo and MPRAGE datasets were carried out at various reduction factors (e.g., R=3, 4, 5) using sensitivity estimated from 8 ACS lines and compared in Fig. 5 and Fig. S5. Although the model was trained on GRE dataset, the proposed method still produced improved sensitivity estimation and superior SENSE reconstruction compared to the ESPIRiT method in terms of aliasing and noise suppression across all undersampling cases.

Figure 5.

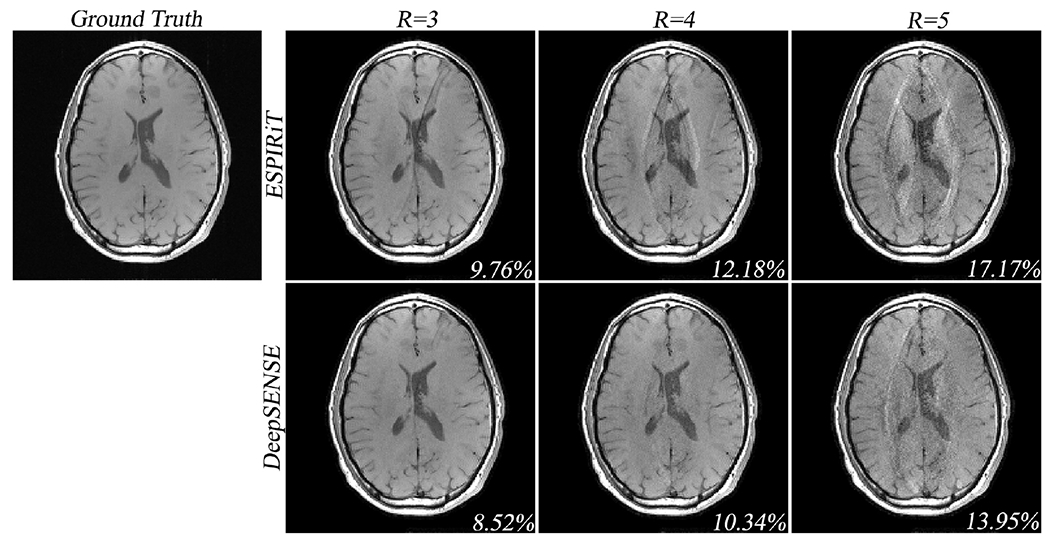
Iterative SENSE reconstructions of the multi-slice spin-echo dataset with uniform undersampling in the outer k-space at various reduction factors (i.e., R = 3, 4, 5). The ESPIRiT and the proposed DeepSENSE methods were used for sensitivity estimation from 8 ACS lines. Although the proposed model was trained on the GRE dataset, it still enables improved sensitivity estimation manifested by the reduced aliasing in the SENSE reconstruction across all reduction factors.

4 |. DISCUSSION

In this short proof of concept study, we focused on using a head coil to demonstrate the feasibility of coil sensitivity learning by taking advantage of previous scans produced from the same receiving coil. The key assumption is that coil sensitivities from the same RF receiver system should be highly correlated between scans and reside on a low dimensional manifold according to the underlying electromagnetic physics. The learning-based method has shown some robustness to data obtained in this study from a limited number of subjects and sequences. More comprehensive studies are still needed to evaluate the generalizability of the proposed method in different application scenarios, e.g., presence of large pathological features (such as gadolinium enhanced tumors) which may alter the sensitivity function.

Although our initial evaluation is limited to brain imaging, the idea of learning sensitivity variations and using deep neural network for accurate prediction can be applied to different types of coils and applications, provided the availability of quality training data. Furthermore, based on the sources of coil sensitivity variations, we think that it is actually beneficial to train separate network predictors for different coils, since the manifold structure of the sensitivities depends on the hardware. Adapting this idea for other body parts can be pursued in future research, for instance, the body coils without a fixed geometry and with certainly larger wave effects would be more challenging. Given a specific receiving coil, the variation of sensitivity could also be different in various practical scenarios and it would be better to train the network separately. For example, in high-field imaging, the geometry of the sensitivity map will contain more significant wave effects; in applications where the imaging space within the coil varies, the orientation of ACS lines changes, or the subject loading differs (e.g., pediatric imaging).

The current neural network has inherited features from the U-net, but is by no means optimal yet. Free parameters such as kernel size, number of layers, feature maps, type of activation function and loss function can be further adjusted and selected on a case-by-case basis. More advanced neural networks like the Generative Adversarial Neural Networks (GAN) [29, 30] certainly can lead to better performance. Our method would also depend on the quality of the input sensitivity maps. For example, starting with the ESPIRiT maps could be helpful in rejecting noise and ringing artefacts. Furthermore, the proposed network holds the potential to be integrated with other advanced image reconstruction models, including the most recent deep-learning based methods [31, 32, 33, 34, 35, 36] where sensitivity functions are required. Finally, it would also be worthwhile to build electromagnetics constraints into the learning model and explore the complementary power of physics-based and data-driven priors.

5 |. CONCLUSION

We proposed and evaluated a deep learning based method to improve the estimation of coil sensitivity functions from limited ACS data for brain imaging. A deep neural network is designed and trained to map low-resolution sensitivity maps to its high-resolution counterparts by exploiting the learnable coil geometry and subject-dependent sensitivity variations. Experimental results have demonstrated the ability of the proposed idea in producing high quality sensitivity functions with very limited ACS data. Future work may include network structure optimization and potential integration with deep learning based reconstruction methods.

Supplementary Material

supinfo

Figure S1 Estimated rotation and translation parameters of the sensitivity functions from the different GRE scans with respect to the first scan. The largest rotation occurs about the x-axis (pitch rotation), which is sensitive to both the head position and axial slices selection. The largest translation occurs along the z-axis (head foot direction).

Figure S2 The sensitivity maps estimated using 24 ACS lines and the subsequent iterative SENSE reconstructions at R=4 of a GRE testing dataset. RMSEs of the sensitivity maps and SENSE reconstructions are shown in the magnitude image.

Figure S3 The sensitivity maps estimated using 4 ACS lines and the subsequent iterative SENSE reconstructions at R=4 of a bottom brain slice with air-tissue interface. RMSEs of the sensitivity maps and SENSE reconstructions are shown in the magnitude image.

Figure S4 Sensitivity RMSEs from the 5-fold cross validation estimated using 8 ACS lines. Results showed that the learning-based method was able to improve the sensitivity estimation to a similar level (approximately a mean RMSE of 7.8%) for all the validation groups with a relatively small set of training data, further validating our hypothesis that the coil sensitivity between scans reside on a low-dimensional manifold. Note that coil alignment improved the sensitivity estimation for group 4 and 5 (possibly larger spatial misalignment), but may not be necessarily required in the case of small spatial misalignment (group 1-3), since the deep CNN should be able to handle certain extent of geometric variation due to its powerful representation capability.

Figure S5 Iterative SENSE reconstructions of the MPRAGE dataset with uniform undersampling in the outer k-space at various reduction factors (i.e., R = 3, 4, 5). The ESPIRiT and the proposed DeepSENSE methods were used for sensitivity estimation from 8 ACS lines. Error maps were scaled by 5 folds for better visualization. Although the proposed model was trained on the GRE dataset, it still enables improved sensitivity estimation manifested by the reduced aliasing and noise amplification in the SENSE reconstruction.