Describe Molecules by a Heterogeneous Graph Neural Network with Transformer-like Attention for Supervised Property Predictions

Abstract

Machine learning and deep learning have facilitated various successful studies of molecular property predictions. The rapid development of natural language processing and graph neural network (GNN) further pushed the state-of-the-art prediction performance of molecular property to a new level. A geometric graph could describe a molecular structure with atoms as the nodes and bonds as the edges. Therefore, a graph neural network may be trained to better represent a molecular structure. The existing GNNs assumed homogeneous types of atoms and bonds, which may miss important information between different types of atoms or bonds. This study represented a molecule using a heterogeneous graph neural network (MolHGT), in which there were different types of nodes and different types of edges. A transformer reading function of virtual nodes was proposed to aggregate all the nodes, and a molecule graph may be represented from the hidden states of the virtual nodes. This proof-of-principle study demonstrated that the proposed MolHGT network improved the existing studies of molecular property predictions. The source code and the training/validation/test splitting details are available at https://github.com/zhangruochi/Mol-HGT.

Introduction

Accurate prediction of chemical molecular properties is an essential and challenging topic in the area of high-throughput pharmaceutical screening.¹ The process of candidate drug screening could be substantially accelerated through the virtual prediction of the molecular properties. The rapid accumulation of experimentally confirmed molecular properties and the development of supervised learning algorithms continuously improve the prediction performances. The deployment of machine learning and deep learning techniques significantly improved the conventional ab initio computational modeling of molecular properties, including density functional theory,^2,3 GW approximation,⁴ quantum Monte Carlo,⁵ and so forth.

Graph-based models precisely captured the interatom correlations and demonstrated the state-of-the-art results for various prediction problems of molecular properties.⁶⁻¹⁷ Some open-source toolkits have been released to facilitate the graph-structured biomedical data.¹⁸ Wu et al. comprehensively evaluated the graph-based models on 17 data sets of various molecular properties and demonstrated the superior prediction performances over the conventional machine learning methods on 11 data sets.¹⁹

Most of the existing graph neural network (GNN) models assumed that there was only one type of graph node, which was connected through one type of edge. Gilmer et al. introduced the edge-dependent variations to the framework message passing neural network (MPNN) for the molecular property prediction problem.⁸ Their data demonstrated that the edge-level variations improved the molecular property prediction performances.

Such edge-level variations may be described by the heterogeneous graph neural networks,^20,21 which have been widely utilized in the graph data mining tasks, for example, link prediction,²² node classification,²³ and node clustering.²⁴ The heterogeneous graph attention network (HAN) introduced heterogeneous structures and semantic-level attentions to the graph attention networks.²⁵ Moreover, the heterogeneous graph network with the transformer-like attention mechanism outperformed the state-of-the-art graph networks by 9–21% on downstream tasks on the open academic graph data sets.²⁶

This research uses a heterogeneous graph network to represent the molecular graph structure and utilized MolHGT for the molecular property prediction problem. In summary, this study has three main contributions.

• 1.We created a new molecular heterogeneity setting for the graph neural network, including 11 types of nodes and 4 types of chemical bonds.
• 2.A virtual node transformer (VNT) readout function was introduced to aggregate all the structurally heterogeneous nodes to represent a molecule graph.
• 3.We proposed the MolHGT framework which represented both the atoms and interatom bonds of a chemical molecule with heterogeneous graph structures.

Results and Discussion

Tuning the Hyperparameters

The proposed graph MolHGT consisted of many hyperparameters, and different value choices may have a major influence on the model performance. The Bayesian hyperparameter optimization (BayesHyperOp) search demonstrated its superiority in optimizing a prediction model with an unknown objective function and a high computational complexity.²⁷ The BayesHyperOp search strategy estimated the posterior distribution of the objective function using the Bayes theorem and then selected the next value choice of the hyperparameters based on the distribution combination. Therefore, the BayesHyperOp search strategy was anticipated to make full use of the information from the previously evaluated value choices of the hyperparameters.

This study utilized the BayesHyperOp search strategy to find the best value choices of the three hyperparameters for all the 100 data sets, and the results are shown in Table 1. The max number of iterations was set to 20. Due to the time complexity and the computation cost, we cannot exhaustively screen all the hyperparameters. The following three hyperparameters were evaluated. Two values, 0.0005 and 0.0001, were evaluated for the hyperparameter learning rate (LRate). The hyperparameter dimension of hidden states (HiddenState) was set to be between the range [200, 800] with an internal 40. Three numbers of layers for the hyperparameter LayerNum were evaluated, that is, 2, 3, and 4. The best value choices of these three hyperparameters were calculated and are shown in Table 1. The following evaluation and ablation experiments were conducted using these best value choices of the three hyperparameters.

Table 1. Best Hyperparameter Combination for Each of the 10 Data Sets from the Bayesian Hyperparameter Optimization Search^a.

data set	LRate	HiddenState	LayerNum
ESOL	0.0001	400	4
FreeSolv	0.0005	240	3
Lipo	0.0001	560	3
HIV	0.0001	440	3
BACE	0.0001	400	2
BBBP	0.0005	680	4
Tox21	0.0001	560	3
ToxCast	0.0001	760	3
SIDER	0.0001	640	4
ClinTox	0.0005	720	2

^aThe column “data set” gave the data set name. The other three columns, “LRate”, “HiddenState”, and “LayerNum” gave the best value choices for the hyperparameters “Learning Rate”, “dimension of the hidden states”, and “the number of layers” of the graph neural network MolHGT.

Performance Comparison with the Existing Models

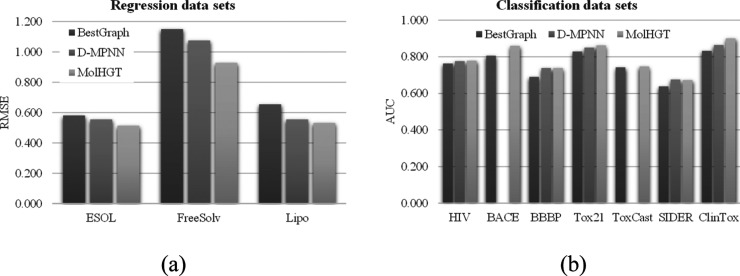
Figure 1 illustrates the performance comparison of the proposed MolHGT with the best graph-based model listed in the database MoleculeNet.¹⁹ The database MoleculeNet maintained the results of many graph-based models, including the graph convolutional network, weave network, directed acyclic graph network, deep tensor neural network, ANI-1 network, and MPNN. The data series “BestGraph” in Figure 1 was the performance measurements of the best graph-based models from the database MoleculeNet. The proposed network MolHGT achieved the average improvement of 16.49% on the three regression data sets and 4.84% on the seven classification data sets. The minimum improvement 0.67% was achieved by MolHGT on the data set ToxCast, and this data set may be difficult to be classified, since the minimum improvement of the other data set was at least 2.10%. A smaller RMSE suggested a better regression model, and the largest reduction 19.30% of RMSE was achieved by MolHGT on the data set FreeSolv.

Figure 1.

Performance comparison with the benchmark graph models in the database MoleculeNet and D-MPNN. The comparison was conducted on the (a) three regression data sets and (b) seven classification data sets. The horizontal axis gave the data set names, and the vertical axis gave the performance metrics, where RMSE is for the regression data sets and AUC is for the classification data sets. The data series “BestGraph” gave the best performance measurement of the graph-based models in the database MoleculeNet. In addition, the other data series, “D-MPNN”, gave the performance of the model D-MPNN.

The proposed model MolHGT was also compared with the D-MPNN model on eight of the ten data sets, as shown in Figure 1. The D-MPNN model was not evaluated on the two data sets BACE and ToxCast in its original study.¹⁹ MolHGT outperformed D-MPNN on seven out of the eight data sets except for SIDER. A minor decrease −0.59% of MolHGT was found on this data set SIDER. MolHGT achieved an averaged improvement 1.07% in AUC for the eight classification data sets and 8.40% for the three regression data sets. The largest improvement 13.67% in RMSE was achieved by MolHGT on the data set Lipo.

Recently, Chen et al. proposed to use algebraic graph-assisted bidirectional transformers to predict molecular properties.²⁸ They got an RMSE value of 0.994 on the data set FreeSolv. AUC-ROC of 0.555 and 0.763 were obtained, respectively, on Lipophilicity and BBBP data sets. Shen et al. proposed the MolMapNet model, which combined the potential of human expert knowledge of molecular representations and convolution neural networks to predict pharmaceutical properties.²⁹ They obtained an ROC-AUC of 0.739 on the BBBP data set, which is slightly better than the 0.738 of MolHGT. However, the results on the other eight data sets are all lower than MolHGT. Detailed data comparison is in Table 2.

Table 2. Detailed Performance Data Achieved Using the BestGraph Models, the D-MPNN Model, and the Proposed MolHGT Model^a.

Data set	split type	metric	MolNet best graph-based methods	D-MPNN	AGBT	MolMap	MolHGT features
ESOL	random	RMSE	MPNN: 0.580	0.555 ± 0.047		0.575	0.518 ± 0.021
FreeSolv	random	RMSE	MPNN: 1.150	1.075 ± 0.054	0.994	1.155	0.929 ± 0.121
lipophelicity	random	RMSE	GC: 0.655	0.555 ± 0.023	0.57	0.625	0.536±0.032
HIV	scaffold	ROC-AUC	GC: 0.763	0.776 ± 0.008		0.777	0.780 ± 0.026
BACE	scaffold	ROC-AUC	weave: 0.806			0.849	0.857±0.008
BBBP	scaffold	ROC-AUC	GC: 0.690	0.738 ± 0.001	0.763	0.739	0.738 ± 0.003
Tox21	random	ROC-AUC	GC: 0.829	0.851 ± 0.002		0.845	0.862±0.006
ToxCast	random	ROC-AUC	weave: 0.742				0.747±0.021
SIDER	random	ROC-AUC	GC: 0.638	0.676 ± 0.014		0.68	0.676 ± 0.013
ClinTox	random	ROC-AUC	weave: 0.832	0.864 ± 0.017		0.888	0.900±0.019

^aThe columns “data set” and “metric” gave the data set names and the performance metrics used by the data sets. The column “BestGraph” gave the best performance measurement of all the graph-based models listed in the database MoleculeNet. The column “D-MPNN” gave the performance measurement of the D-MPNN model. The column “AGBT” gave the performance measurement of the algebraic graph-assisted bidirectional transformer model. The column “MolMap” gave the performance measurement of MolMapNet. The column “MolHGT Features” gave the performance measurement of MolHGT on the 10 data sets, and the data were averaged over 10 random runs with the random seeds 0–9. The best model of each data set was highlighted in bold.

Overall, the proposed model MolHGT achieved the best results in most of the 10 evaluated data sets, as shown in Figure 1 and Table 2. MolHGT was the best model on all the three regression data sets, compared with the BestGraph model and the D-MPNN model. The D-MPNN model did not give the performance data on the two classification data sets BACE and ToxCast. Also, the proposed model MolHGT outperformed D-MPNN on seven out of the remaining eight data sets. The column “BestGraph” in Table 2 suggested that the existing graph models listed in the database MoleculeNet did not achieve consistently on all the 10 data sets. In addition, the D-MPNN model may deliver performance improvements in most cases.

Necessity of the Node Heterogeneity

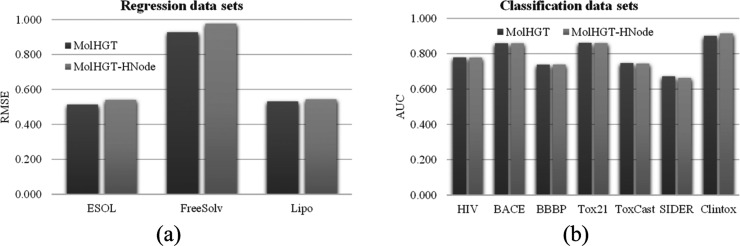
The node heterogeneity is one of the main contributions of MolHGT, and this section evaluated whether it is necessary to add the node heterogeneity to the graph network. The MolHGT model without the node heterogeneity learned the same weights for different types of atoms. The experimental results in Figure 2 showed that the node heterogeneity improved all the three regression data sets and an averaged improvement 4.01% in RMSE was achieved. Only the two data sets BBBP and ClinTox received the decreased classification AUC −0.14 and −1.53%, respectively. The node heterogeneity did not change the classification performance of MolHGT on the data set BACE. All the other five classification data sets were improved by node heterogeneity.

Figure 2.

Contribution evaluation of the node heterogeneity. The performance comparison between the MolHGT models with (MolHGT) and without (MolHGT-HNode) the settings of heterogeneous nodes for the (a) regression data sets and (b) classification data sets. The regression models were evaluated for the metric RMSE (the smaller, the better). Also, the classification models were evaluated for the metric AUC (the larger, the better).

Necessity of the Edge Heterogeneity

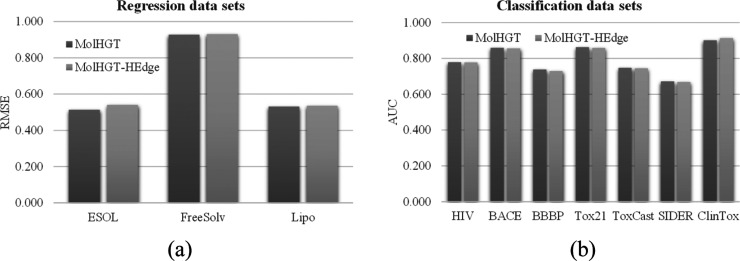
The edge heterogeneity is another main contribution of the proposed MolHGT model. Figure 3 illustrates the performance differences if the edge heterogeneity was not introduced to MolHGT. MolHGT improved nine out of the ten data sets with the edge heterogeneity, except for the classification data set ClinTox. The classification AUC of the data set ClinTox was decreased by 1.42%. The performance metric RMSE values of the three regression data sets were decreased by an average improvement 2.02%. Except for the data set ClinTox, MolHGT achieved an average improvement 0.48% in AUC values of the six classification data sets.

Figure 3.

Contribution evaluation of the node heterogeneity. The performance comparison between the MolHGT models with (MolHGT) and without (MolHGT-HEdge) the settings of heterogeneous edges for the (a) regression data sets and (b) classification data sets. The regression models were evaluated for the metric RMSE (the smaller, the better). Also, the classification models were evaluated for the metric AUC (the larger, the better).

Other Ablation Evaluations of MolHGT

The ablation experiments were conducted to evaluate the other MolHGT components, as shown in Table 3. The proposed model MolHGT gained performance improvements with the components’ metarelation, external features, and the modified gated recurrent unit (GRU) update function for all the three regression data sets. The additions of the component external features in the proposed model MolHGT contributed an average improvement 1.61% in AUC for the seven classification data sets. The addition of the component metarelation and the modified GRU introduced the positive contributions to many classification data sets and the minor decreases in the averaged classification AUC, by the averaged decreases of −0.25 and −0.07%, respectively.

Table 3. Ablation Evaluation of the Other MolHGT Components^a.

data set	MolHGT	MolHGT-MR	MolHGT-EF	MolHGT + GRU
ESOL	0.514	0.532	0.569	0.533
FreeSolv	0.928	0.95	0.965	0.946
Lipo	0.532	0.549	0.533	0.522
HIV	0.779	0.789	0.787	0.778
BACE	0.859	0.854	0.806	0.858
BBBP	0.738	0.741	0.703	0.74
Tox21	0.862	0.863	0.866	0.865
ToxCast	0.747	0.748	0.744	0.748
SIDER	0.672	0.668	0.669	0.666
ClinTox	0.901	0.91	0.898	0.909

^aThe column “MolHGT” gave the results of the proposed model MolHGT on all the 10 data sets. The column “MolHGT-MR” gave the results of the MolHGT model without the metarelations. The column “MolHGT-EF” gave the data of the MolHGT model without the external features. Also, the column “MolHGT + GRU” gave the data of the MolHGT model with the original version of a gated recurrent unit (GRU) as the update function. The performance metrics RMSE and AUC were used for the first three regression data sets and the other seven classification data sets, respectively.

Conclusions

This study proposed a novel graph network MolHGT with heterogeneous structures for different types of nodes and edges for the molecular property prediction problem. The transformer modules fused the features represented by these heterogeneous nodes and edges and passed the messages between these nodes and edges. The comprehensive ablation experiments demonstrated that the proposed network MolHGT delivered performance improvements on the 10 data sets with the major network components, and the heterogeneities in both nodes and edges were beneficial to the molecular property prediction problems. MolHGT also outperformed the existing graph-based molecular property prediction models in most cases, especially the regression data sets.

It is worth noting that the heterogeneity setting of the proposed MolHGT increases the model complexity and the largely increased number of parameters may potentially increase the possibility of model overfitting, as shown in Table S1. For example, MolHGT utilizes 11 node types and 4 edge types, and the numbers of model parameters to represent nodes and edges are increased to 11 and 4 times compared with the conventional graph neural network, respectively. This study splits the data set into the training/validating/testing sets by the ratio of 8:1:1 and carries 10 random runs of the experiments in order to reduce the overfitting bias. It will be important to further evaluate the proposed models using the future accumulation of more molecular samples.

Materials and Methods

Problem Settings and Data Sets

This study evaluated the proposed graph neural network MolHGT using 10 public data sets, as shown in Table 4. These 10 popular data sets retrieved the database MoleculeNet.¹⁹ All the data sets used the SMILES sequences to represent chemical molecules and consisted of less than 50,000 molecules. There were three regression data sets and the other seven data sets were classification problems. The three regression data sets investigated the physical chemistry properties. There were two classification data sets for the biophysical properties and the other five classification physiological properties.

Table 4. Descriptions of the 10 Data Sets Used in This Study^a.

category	data set	# molecules	# tasks	task type
physical chemistry	ESOL	1128	1	regression
	FreeSolv	642	1	regression
	Lipo	4200	1	regression
biophysics	HIV	41 127	1	classification
	BACE	1513	1	classification
physiology	BBBP	2039	1	classification
	Tox21	7831	12	classification
	ToxCast	8576	617	classification
	SIDER	1427	27	classification
	ClinTox	1478	2	classification

^aThe columns “# molecules” and “# tasks” gave the numbers of molecule samples and the number of tasks of each data set. The column “task type” gave whether this data set was a regression or classification task. Further details on the data sets are available in Wu et al.¹⁹

Performance Metrics

A receiver operating characteristic curve (ROC curve) is a graph showing the performance of a classification model at all classification thresholds. It plots TPR versus FPR at different classification thresholds. Lowering the classification threshold classifies more items as positive, thus increasing both false positives and true positives. AUC stands for “area under the ROC curve”. AUC measures the entire two-dimensional area underneath the entire ROC curve. Therefore, ROC-AUC provides an aggregate performance measure across all possible classification thresholds.³⁰

1

2

3

Root mean square error (RMSE) is the standard deviation of the residuals (prediction errors). Residuals measure how far from the regression line data points are; RMSE is a measure of how spreading out these residuals are. In other words, it tells how concentrated the data are around the line of best fit. RMSE is commonly used in climatology, forecasting, and regression analysis to verify experimental results.

4

where M is the number of the samples, y_i is the target variable of sample i, and 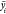is the prediction of sample i.

Data Set Splitting Strategy

For a fair comparison with the other studies, we downloaded the data sets in their original splitting strategy provided by MoleculeNet.¹⁹ That is to say, the splitting was carried out using 10 fixed random seeds (0–9) and the recommended splitting types (“random” or “scaffold”). Each data set was split into the ratio of 8:1:1 for the training/validation/testing data sets. The models were trained on the training data sets, and the hyperparameters were tuned on the validation data sets. The final performance was calculated on the testing data sets.

Heterogeneity Setting of a Molecule Graph

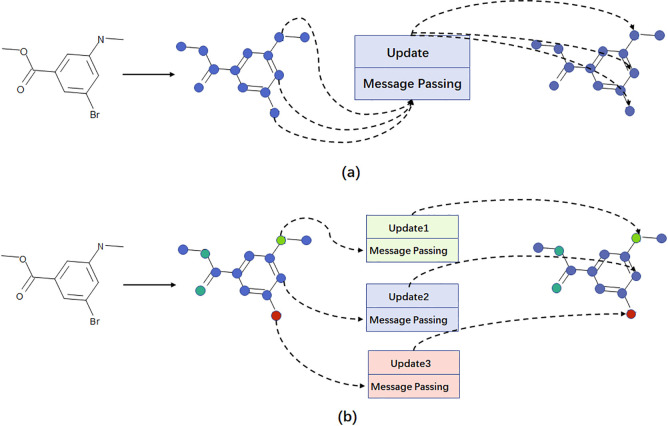
Heterogeneous graphs are composed of multiple types of nodes and edges and contain comprehensive information and rich semantics. A heterogeneous graph neural network will pass messages from source nodes to target nodes based on the specific nodes and edge types. While the message passing mechanism and neural network weights in the homogeneous graph network are the same, regardless of node types and edge types. Figure 4 illustrates the difference between homogeneous and heterogeneous graph neural networks. Our study introduced the heterogeneities in both nodes and edges into the graph-represented chemical compounds. A molecule was represented by a labeled graph with the nodes corresponding to the atoms and the edges corresponding to the chemical bonds between atoms of this molecule. There were many types of atoms and chemical bonds in a compound. This study defined 11 types of nodes, representing 10 common atoms (H, C, N, O, F, P, S, Cl, Br, and I) and the last type for all the other atoms rarely found in drug molecules. Five types of edges were defined, including four common types of chemical bonds (single, double, triple, and aromatic) and the last type for the self-connected edge. We hypothesized that this heterogeneity in the molecule graph may better represent a chemical molecule.

Figure 4.

Difference between homogeneous and heterogeneous graph neural networks. (a) Message passing mechanism is the same for different nodes in the homogeneous graph neural network. The different types of nodes have the same neural network weights. (b) Message passing mechanisms for different nodes in the heterogeneous graph neural network. Different types of nodes and different types of edges have different neural network weights.

Shui and Karypis introduced HMGNN, a graph representation learning model with two node types (one-body and two-bodies) and three edge types (1–1, 2–2, and 1–2), and fused the heterogeneous nodes by summing the node embeddings of each p-body module and concatenating them into an intermediate representation.³¹ HMGNN can capture complex geometric information of molecular graphs. For example, it can learn the rotation invariance of atoms. However, the heterogeneity of HMGNN lies in the construction strategies of new types of nodes and edges. HMGNN regards atom pairs and single atoms as two different types of nodes. For atoms such as C and O, they are still encoded into the same vector space by HMGNN. Different types of chemical bonds such as single bonds and double bonds are also encoded in the same vector space. We hypothesize that such a representation may cause the loss of some useful chemical information. MolHGT proposes a specifically designed framework to represent 11 node types and 4 edge types and directly encodes different types of atoms and edges into different vector spaces. MolHGT may better capture the rich chemical information of the target molecule. Moreover, the VNT readout function in this study facilitates a much more flexible and data-specific fusion interface for the heterogeneous graph structures.

Model Architecture of MolHGT

This study combined the graph neural network with the transformer module to represent the chemical molecules based on the previous observations that transformers may fuse the heterogeneous modules in graph neural networks. Yun et al. suggested that the graph transformer network may efficiently learn new graph structures based on the data and tasks without domain knowledge and deliver powerful node representations via convolution of the learned new graphs.³² Hu et al. demonstrated that the heterogeneous graph transformer outperformed the state-of-the-art graph neural network baseline models by 9–21% on various downstream tasks.²⁶

We followed the terminology of the study MPNN⁸ to separate the graph model into two phases, that is, the message passing phase and the readout phase, as shown in Figure 5. The message passing phase ran for L graph layers. The graph layer l ∈ [1, L] had the message function M^l and node update function U^l. The target node t aggregated the message from the source node s using the formula

5

Figure 5.

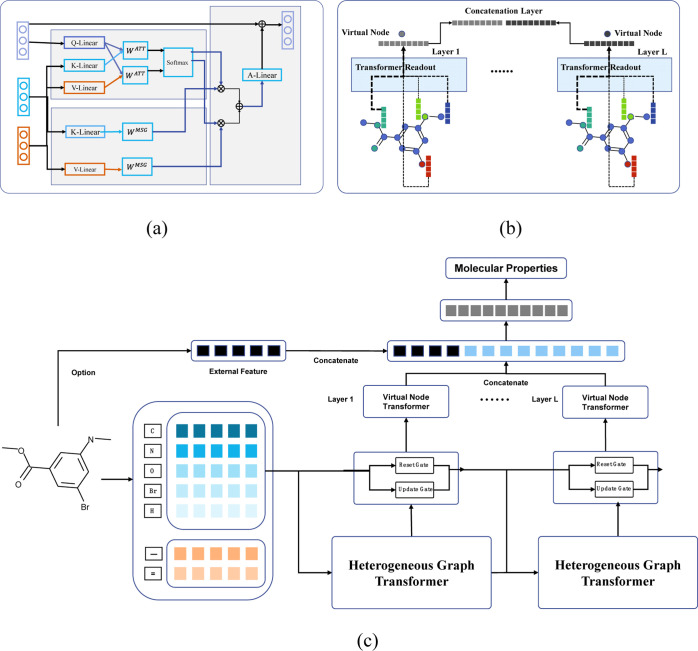
Submodules and overall architecture of the proposed graph network MolHGT. (a) Architecture of a heterogeneous graph transformer. (b) Architecture of the VNT. (c) Overall architecture of MolHGT. Molecules were loaded to train the graph network MolHGT, and the molecular properties were calculated as the output predictions.

The notations N(t) represent the neighbors of the target node t and the node t, e represents the type of the edge from the source node s to the target node t, and M^l represents the heterogeneous graph transformer message function.²⁶ The hidden states 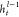were updated based on the message 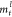using the formula

6

The notation U^l represents the GRU update function. The previous graph model MPNN got the graph features from the last graph layer.⁸ We introduced more flexibility by concatenating the node hidden states of all the graph layers into the graph feature h^l using the formula

7

and

8

The notations f() are a fully connected neural network and R^l represents the VNT readout function, which was described in the following section.

This study concatenated the graph features with the external features for the last fully connected output layer. The external features were defined in the same way as in the D-MPNN¹⁷ where the 2D molecular descriptors were calculated using the tool RDKit.³³

Heterogeneous Graph Transformer Message Function

The message function was inspired by the architecture design of the transformers³⁴ in the network HGT.²⁶ The main idea was to aggregate the multihead attention-weighted messages from the source nodes using the formulas

9

10

The notation h represented the number of attention heads, where this study set h = 10.

The ith head 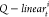function mapped the target node t into the ith head query vector Qⁱ(t) with the dimension R^d → 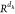, where d is the node hidden state dimension and 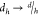is the vector dimension per head. Similarly, the functions 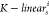and 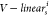mapped the source node into the ith head key vector Kⁱ(s) and value vector Vⁱ(s) using the mathematical formulas

11

12

13

Unlike the transformer vanilla, the parameters of the Q/K/V linear function depended on the node types they worked on. Therefore, this study defined them as the heterogeneous node parameters. There were 11 different heterogeneous node types, among which 10 for the common atoms (H, C, N, O, F, P, S, Cl, Br, and I) in the drug molecules and the last one for all the other atoms. Second, the ith head attention weight between the target node t and the source node s was calculated by

14

The notation 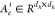is the ith head edge-based matrix, which was defined as the heterogeneous edge parameters. There were five different heterogeneous edge types, among which four represented the bond types (single, double, triple, and aromatic) and the last one represented the special self-connected edge type. The notation uⁱ[s,e,t] is the ith head learnable meta relation scalar, which was another heterogeneous parameter relying on the heterogeneities of both nodes and edges. Finally, the multihead message was calculated as

15

The notation 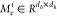is the ith head edge-based matrix, and it is also a heterogeneous edge parameter.

HGT is a general-purpose heterogeneous graph neural network, while MolHGT improves the HGT framework with molecule-specific features, as illustrated in Figures 4 and 5. Besides the heterogeneous definitions of node types and edge types, the GRU update function provides the more efficient capability to capture the messages when updating the node states from different graph layers. The VNT generates the final representation of the molecules and delivers satisfying performances of the molecular property prediction task.

GRU Update Function

The GRU update function was used in this study. GRU was first introduced in the graph model GG-NN, which was believed to be a strong baseline graph model.^35,36 GRU was an attention-like architecture with reset and update gates. We assumed that GRU may capture the important messages during updating the node states of different graph layers and compared it with the target node-dependent node update function in the HGT.²⁶ This study accompanied the GRU update function with layer normalization³⁷ using the following formula

16

The node hidden states were the hidden states of the GRU update function, and the message was the new input of GRU. Similar to the vanilla GRU in the recurrent neural networks,³⁸ the parameters of the GRU update function were shared across all the graph layers.

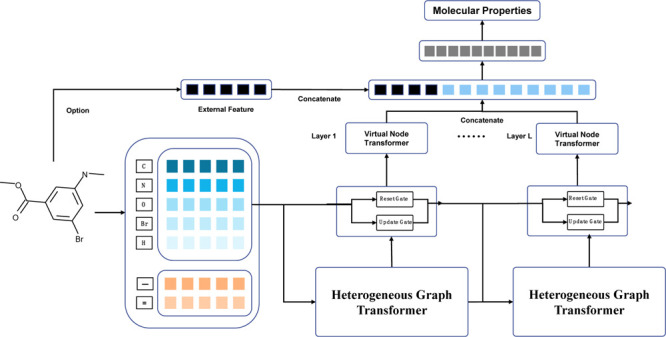
VNT Readout Function

This study used the VNT as the readout function. A set transformer³⁹ was a framework for the attention-based permutation-invariant neural networks and was specifically designed to handle set data, instead of summing the final node states. As similar in the pooling architecture of the set transformer, this study used one random initial virtual node 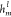to aggregate the attention-weighted messages from all the nodes in the graph network, where the attention was between the virtual node m and the source node s using the formula

17

18

19

20

21

The notations f(·) are a fully connected layer with ReLU activation, and 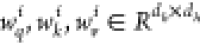. This study used the mean aggregation, instead of the summing one. The experimental data showed that MolHGT has better results when the VNT block uses different parameters in different graph layers. Therefore, VNT adopts the setting of nonsharing of parameters in this study.

Figure 5b shows that a virtual node combines the representation of each node in the molecular graph in a weighted form. Therefore, a virtual node carries the information from the entire molecular graph. MolHGT has L graph layers, and each graph layer contains a representation of a virtual node. We use a concatenation operator to merge them together and then load the concatenation to the final linear layer as the final representation of the molecular graph. The molecular data have to be encoded by the VNT layer, and it is difficult to remove the VNT module from the MolHGT framework. Therefore, VNT is not evaluated by the ablation experiment.

Implementation and Running Environment

All the experiments were implemented using the Python programming language version 3.6.12 with the package TensorFlow version 2.0.0. The experiments were conducted on a computing server with an Intel CPU (Intel(R) Xeon(R) Silver 4210 CPU 2.20 GHz), 4 GPU cards (Nvidia 2080Ti, 11 GB memory per card), and 128 GB system memory.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c06389.

• Number of parameters in different settings of HiddenState and LayerNum (PDF)

Author Contributions

D.D. and Z.L. contributed equally to this work. D.D., X.H., and F.Z. conceived and coordinated the project. X.H., R.Z., and Z.L. coded the analysis procedure and carried out the experiments. X.H., R.Z., and F.Z. drafted the manuscript. F.Z. formatted and polished the manuscript and handled the submission communications.

The authors declare no competing financial interest.