Single-Cell Multiomics Integration by SCOT

Abstract

Although the availability of various sequencing technologies allows us to capture different genome properties at single-cell resolution, with the exception of a few co-assaying technologies, applying different sequencing assays on the same single cell is impossible. Single-cell alignment using optimal transport (SCOT) is an unsupervised algorithm that addresses this limitation by using optimal transport to align single-cell multiomics data. First, it preserves the local geometry by constructing a k-nearest neighbor (k-NN) graph for each data set (or domain) to capture the intra-domain distances. SCOT then finds a probabilistic coupling matrix that minimizes the discrepancy between the intra-domain distance matrices. Finally, it uses the coupling matrix to project one single-cell data set onto another through barycentric projection, thus aligning them. SCOT requires tuning only two hyperparameters and is robust to the choice of one. Furthermore, the Gromov-Wasserstein distance in the algorithm can guide SCOT's hyperparameter tuning in a fully unsupervised setting when no orthogonal alignment information is available. Thus, SCOT is a fast and accurate alignment method that provides a heuristic for hyperparameter selection in a real-world unsupervised single-cell data alignment scenario. We provide a tutorial for SCOT and make its source code publicly available on GitHub.

1. INTRODUCTION

Single-cell measurements provide a fine-grained view of the heterogeneous landscape of cells in a sample, revealing distinct subpopulations and their developmental and regulatory trajectories. The availability of measurements capturing various genomic properties, such as gene expression, chromatin accessibility, and histone modifications, has increased the need for data integration methods for disparate data types. Owing to technical limitations, it is hard to obtain multiple types of measurements from the same cell, so data sets lack sample (i.e., cell-to-cell) correspondence. Furthermore, we cannot a priori identify correspondences between features in different domains. Accordingly, integrating two or more single-cell data modalities requires methods that do not rely on either cell-wise or feature-wise correspondences (Welch et al., 2017, 2019; Amodio and Krishnaswamy, 2018; Stuart et al., 2019).

Two unsupervised manifold alignment algorithms address this challenge in single-cell sequencing: (1) MMD-MA (Liu et al., 2019), which is based on the maximum mean discrepancy (MMD) measure, and (2) UnionCom (Cao et al., 2020), which performs topological alignment while emphasizing both local and global alignment. Although neither MMD-MA nor UnionCom requires any correspondence information, they require tuning three and four hyperparameters, respectively. Although hyperparameter values significantly affect the quality of the alignment for both methods, selecting the best hyperparameters is challenging in the completely unsupervised setting. One usually requires some correspondence information to pick the settings that provide the most accurate alignment.

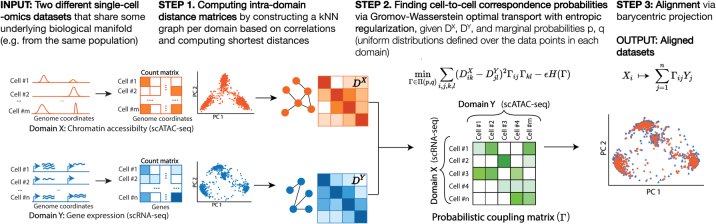
We present single-cell alignment using optimal transport (SCOT), an unsupervised learning algorithm that employs Gromov-Wasserstein optimal transport to align single-cell multiomics data sets while preserving local geometry (Fig. 1). When hyperparameter tuning with validation data on correspondences is possible, SCOT performs on par with state-of-the-art methods. It also converges faster than GPU implementations of MMD-MA and UnionCom, respectively. Unlike MMD-MA and UnionCom, our algorithm requires tuning only two hyperparameters and is robust to the choice of one.

FIG. 1.

Overview of the SCOT algorithm: SCOT takes in two data sets of single-cell genomics measurements in the form of count matrices to align them. For each data set, it first constructs k-nearest neighbor graphs based on correlations between samples and calculates the distance matrices capturing the intra-domain distances. Given these, it solves the Gromov-Wasserstein optimal transport formulation to find an ideal coupling (also known as “correspondence”) matrix, describing the probability of alignment between the samples across the two data sets. Finally, it completes the alignment by projecting the first domain onto the second one based on correspondence probabilities using barycentric projection. SCOT, single-cell alignment using optimal transport.

When there are no data available on correspondences, SCOT self-tunes its hyperparameters using a heuristic that picks hyperparameters by tracking Gromov-Wasserstein distance. Therefore, SCOT is the first algorithm to perform single-cell alignment in a completely unsupervised manner, without requiring any correspondence information to align data sets or select hyperparameters. A detailed tutorial on SCOT is available at https://rsinghlab.github.io/SCOT.

2. SCOT FUNCTIONS

We provide an implementation of SCOT in Python, using the Python Optimal Transport toolbox (Flamary and Courty, 2017). Our source code, along with example scripts and experiments, is available with an MIT license at http://github.com/rsinghlab/SCOT.

2.1. Data preprocessing

SCOT takes two sets of measurements to be aligned as input. It expects the input data sets to be in NumPy array format, with samples in rows and features in columns.

As an optional first step, the user can normalize the features; the default is L2 normalization, and the other options are no normalization, z-score, max value, or L1 normalization. Empirically, we found L2 normalization to work well with real-world sequencing data.

2.2. Hyperparameter tuning

SCOT has two hyperparameters: k, the number of neighbors in the k-NN graph, and ɛ, the regularization coefficient. The hyperparameter k determines how much of the neighborhood will be accounted for when preserving local geometry. We set the default k value to 50 but recommend users to try values in the range k∈[20, n/5], where n is the number of samples in the smallest data set. Although the optimal k varies between data sets, it is not advisable to go too high (above n/5) to avoid losing local geometry information.

The hyperparameter $\in$ determines how much to split correspondence probabilities across samples. Lower values of $\in$ will split fewer masses, leading closer to a 1-1 correspondence between domains, but is more computationally complex. Higher values of $\in$ split correspondence probabilities across more samples and makes the optimization problem more convex and, therefore, faster to converge. We set the default value of ɛ to le − 3 but recommend trying out values in the range ɛ∈[5e–4, 5e − 2]. In general, SCOT is robust to the choice of k and requires more tuning in $\in$.

If the user has access to some labels on the data that would indicate alignment such as cell types, we recommend using that information to pick hyperparameters (see Section 2.4 for guidance). Otherwise, we provide a heuristic to pick hyperparameters based on which ones achieve the lowest Gromov-Wasserstein distance between the aligned data sets. To use this heuristic, it suffices to set the parameter selfTune = True.

2.3. Output

By default, SCOT returns the aligned domains projected onto the second domain through a barycentric projection. Similar to the inputs, the output data sets are in NumPy array format with samples in rows and features in columns. However, a user may instead receive the coupling matrix as output from the SCOT object for further downstream analysis, by setting the input parameter returnCoupling = True.

2.4. Evaluation

We provide metrics that can be used to evaluate the alignment and choose hyperparameters when orthogonal information such as true correspondences or cell-type labels exist. For cases where 1-1 cell correspondences exist (such as for co-assayed data sets, which can be used to benchmark alignment algorithms), the “fraction of samples closer than the true match” (FOSCTTM) metric introduced by Liu et al. (2019) can be used to measure the alignment error. If the only information available is cell-type labels, “label transfer accuracy,” a metric used by Cao et al. (2020) can assess the quality of alignment between cells of the same cell type.

2.5. Tutorial and examples

We provide tutorials, as well as example data sets and scripts on our documentation page at rsinghlab.github.io/SCOT. Users can find information on how to set up SCOT, as well as detailed descriptions and suggestions on model parameters. We also provide example scripts for several scenarios such as aligning co-assayed data sets, aligning separately sequenced data sets with varying sample sizes, and automatically picking hyperparameters in an unsupervised manner.

AUTHOR DISCLOSURE STATEMENT

The authors declare they have competing financial interests.

FUNDING INFORMATION

W.S.N.'s contribution to this study was funded by NIH award U54 DK107979. B.S. was partially supported by NSF awards 1714429 and 1740741. R.S. is supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1644760.