Three small vesicular pools in sequence govern synaptic response dynamics during action potential trains

Significance

Short-term changes in the strength of synaptic connections underlie many brain functions. The strength of a synapse in response to subsequent stimulation is largely determined by the remaining number of synaptic vesicles available for release. We developed a methodological approach to measure the dynamics of various vesicle pools following synaptic activity. We find that the readily releasable pool, which comprises vesicles that are docked or tethered to release sites, is fed by a small-sized pool containing approximately one to four vesicles per release site at rest. This upstream pool is significantly depleted even after a short stimulation train. Therefore, regulation of the size of the upstream pool emerges as a key factor in determining synaptic strength during and after sustained stimulation.

Abstract

During prolonged trains of presynaptic action potentials (APs), synaptic release reaches a stable level that reflects the speed of replenishment of the readily releasable pool (RRP). Determining the size and filling dynamics of vesicular pools upstream of the RRP has been hampered by a lack of precision of synaptic output measurements during trains. Using the recent technique of tracking vesicular release in single active zone synapses, we now developed a method that allows the sizes of the RRP and upstream pools to be followed in time. We find that the RRP is fed by a small-sized pool containing approximately one to four vesicles per docking site at rest. This upstream pool is significantly depleted by short AP trains, and reaches a steady, depleted state for trains of >10 APs. We conclude that a small, highly dynamic vesicular pool upstream of the RRP potently controls synaptic strength during sustained stimulation.

Synaptic depression is primarily due to the exhaustion of a finite pool of synaptic vesicles (SVs), the readily releasable pool (RRP) (1). In several preparations, it has been suggested that the RRP is not homogeneous (2–4). At the calyx of Held synapse, the response to presynaptic depolarization originates from two pools of equivalent sizes, the slowly releasing pool (SRP) and the fast releasing pool (FRP) (5); the FRP has been further split into primed FRP and superprimed FRP (6–9). Likewise, in cerebellar mossy fiber synapses (10–12) and in hippocampal mossy fiber synapses (13), two subpools resembling the FRP and SRP of the calyx of Held have been identified. In each of these two types of synapses, recent studies using total internal reflection fluorescence microscopy have indicated the presence of several subpools of SVs within 100 nm from the active zone (AZ) membrane (14, 15). The organization of these various pools and their roles during sustained or repeated synaptic stimulations have been extensively examined but remain uncertain (review: refs. 16–19). In particular, it remains unclear whether the SRP, the primed FRP, and the superprimed FRP release their SVs according to a parallel scheme, to a sequential scheme, or to a mixed parallel-sequential scheme (5, 8, 12, 20–25), even though recent studies often favor sequential schemes (9, 26, 27). In certain additional synapses [cerebellar parallel fiber to molecular layer interneuron (28, 29), molecular layer interneuron to molecular layer interneuron (30), and hippocampal mossy fiber to interneuron (31)], studies carried out at the level of individual AZs (“simple synapse recording”: ref. 32) suggest a sequential binding of incoming SVs to a “replacement site” and an associated “docking site” before release. These results suggest two sequentially arranged pools of up to one docked SV and one replacement SV per release site. Altogether, it is plausible that central synapses involve a common basic scheme where two to three subpools constitute the RRP or are closely associated with the RRP. However, the exact structure of these pools and their respective roles during synaptic activity remain to be established.

The standard method to distinguish RRP-related subpools has been to measure the kinetics of SV release during sustained presynaptic depolarization (5, 7, 11–13, 20). However, recent studies have suggested that the pattern of responses to individual action potentials (APs) in a train also gives information on the originating subpools of the released SVs (9, 28). In addition, several lines of evidence indicate that modifications of RRP-related subpools are accompanied by changes in release kinetics during a train. For instance, the well-known shift from synchronous to asynchronous release that accompanies synaptic depression (33) has been proposed to be linked to RRP depletion (34–36). Furthermore, it has been shown that after each AP in a train, the latency distribution of synchronous release is biphasic, with a fast component reflecting the release of docked SVs and a slow component reflecting an uninterrupted sequence of docking followed by release of SVs initially located in replacement sites (“two-step release”: ref. 29). As the proportion of fast vs. slow release changes markedly during a train, it provides information on the dynamics of docked and replacement vesicular pools. Altogether, a study of the pattern of release as a function of AP number, together with a quantitative assessment of release kinetics during trains, may provide decisive information on RRP-related subpools.

In the present work, we take advantage of simple synapse recordings at cerebellar parallel fiber–molecular layer interneuron (PF–MLI) synapses, together with modeling, to investigate changes in RRP-related subpools during AP trains. Our results indicate the existence of an unexpectedly small-sized pool (intermediate pool; 1.2 to 4 SVs per release site) located upstream of replacement SVs. We propose that in this preparation, three pools of comparable sizes (intermediate, replacement, and docked SVs) are placed sequentially to guide SVs toward exocytosis.

Results

Biphasic Recovery of Cumulative Synaptic Vesicle Numbers after an Action Potential Train.

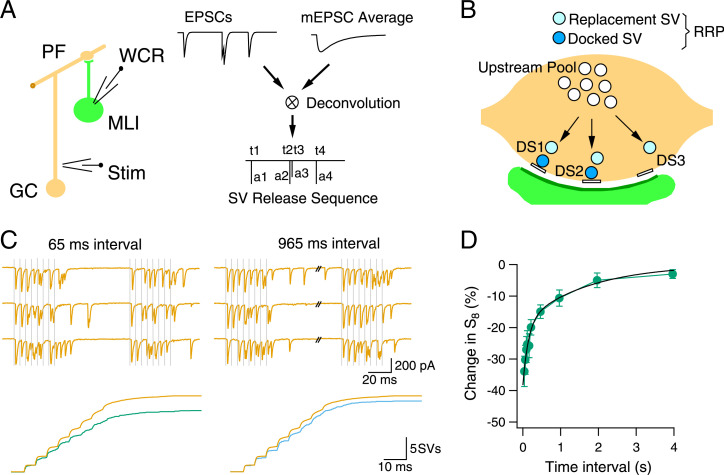
In order to study vesicular pools’ dynamics, it is important to measure accurately the consumption of SVs during synaptic function. At large multisite synapses, measurements of excitatory postsynaptic current (EPSC) amplitudes are prone to errors linked to receptor saturation and desensitization, as well as to receptor activation by neurotransmitter spillover, particularly during high-frequency trains of presynaptic stimulation (10, 11, 37, 38). By contrast, individual quantal EPSCs can be reliably identified in responses obtained from synapses containing only a few release sites (39, 40). Such an approach has been developed at synapses formed between PFs and MLIs (32). Extracellular stimulation of a single granule cell (GC) and associated PF elicits a series of quantal EPSCs in a postsynaptic MLI (Fig. 1 A, Left). The EPSC trace is deconvolved using an average miniature EPSC (mEPSC) trace for the same recording as template. This yields an SV release sequence where each released SV is represented by a couple of values (t_i and a_i) (Fig. 1 A, Right). In each couple, t_i marks the time of release, and a_i is the peak amplitude of the corresponding (monovesicular) EPSC.

Fig. 1.

Recovery kinetics of cumulative SV release after an 8-AP train. (A) Experimental protocol. (A) Whole-cell recording (WCR) was obtained from a MLI. A single PF-MLI connection is established by positioning an extracellular stimulation pipette (Stim) near a GC soma. Synaptic responses are analyzed by deconvolution using the average mEPSC as template. This transforms the EPSC trace into an SV release sequence where paired (time, amplitude) results are obtained for each released SV. (B) Diagram of SV pools at a PF-MLI synapse. Each synapse contains a single AZ where several docking/release sites (here three: DS_1–3) can release SVs in parallel. Each docking site is associated with a replacement site. Docking and replacement sites may or may not be occupied by a docked SV and a replacement SV, respectively. Together, docked SVs and replacement SVs constitute the RRP. Replacement sites are supplied by SVs located in an upstream pool. (C, Top) Exemplar traces showing EPSCs evoked by a pair of 8-AP trains (gray vertical lines), with 65- or 965-ms interval between trains. (Bottom) Superimposed cumulative histograms of SV counts for the first train (yellow; averaged from 200 repeats) and the second train (green/blue; averaged from 20 repeats) of the same synapse. (D) Time course of recovery of the total response to the second train as a function of intertrain interval. The recovery curve is fitted with a double-exponential function with time constants of 0.15 (46%) and 1.7 s (54% of total amplitude). Error bars indicate the SEM. n = 9 to 15 synapses, among which 6 synapses had recordings for all intertrain intervals, while the remaining had recordings for at least four intertrain intervals.

Single PF-MLI synapses typically comprise a single active zone (AZ) and an associated postsynaptic density, and they are called for this reason “simple synapses” (32). Work on simple synapses indicates that each AZ comprises several docking/release sites (32, 41). At PF-MLI synapses, the number of docking sites ranges from two to eight (42) (three such sites are depicted in Fig. 1B). Each site can accommodate up to two SVs: one docked SV (deep blue SVs in Fig. 1B) and one replacement SV (light blue SVs) (28). Together, docked SVs and replacement SVs form the RRP (mean RRP size per AZ: 7.5 SVs) (28). Following an AP, docked SVs are released in a parallel manner at each docking site, so several SVs can be released simultaneously from a single AZ (“multivesicular release”: refs. 43, 44). In addition to triggering release, the calcium rise elicited by AP-induced calcium entry promotes the translation of replacement SVs to vacated docking sites (26, 45). In PF-MLI synapses, this transition occurs within a few milliseconds only, so that replacement SVs rapidly fill empty docking sites during repetitive stimulation (28, 29). Finally, replacement SVs are themselves renewed by recruitment of SVs from the pool upstream of replacement SVs (white SVs in Fig. 1B).

In the present work, we investigate changes in the numbers of docked SVs, replacement SVs, and upstream SVs following intense synaptic activity. To force a strong SV flux along the various pools, we applied AP trains (usually eight APs) at high frequency (200 Hz) under conditions of high release probability (3-mM external calcium concentration). Fig. 1 C, Upper shows an exemplar experiment in which we compare EPSCs between two consecutive AP trains separated by an intertrain interval of 65 or 965 ms. In the average cumulative SV release obtained for this synapse (Lower), the response to the second train is depressed for the 65-ms interval (Left, green), and it has partially recovered for the 965-ms interval (Right, blue). Importantly, compared to the cumulative response to the first train (yellow), the cumulative response after either the 65-ms interval or the 965-ms interval is indistinguishable for the first AP, and it only starts to deviate after the second AP. Thus, while inhibition of synaptic release is usually associated with a decrease in short-term depression, the transient inhibition of the response seen following the first train is paradoxically associated with increased short-term depression. Group results across experiments indicate that the cumulative SV number (S₈) at the end of the second 8-AP train recovers with a biexponential function as a function of the intertrain interval (fast time constant of 150 ms and slow time constant of 1.7 s; Fig. 1D; n = 9 to 15 synapses for each intertrain interval; 6 out of 13 synapses tested with ≥965-ms intertrain intervals displayed a slow recovery component with a time constant >1 s). This indicates that synaptic recovery is a complex process, possibly involving different kinetics for the different SV pools.

s_1f, s_2f, and S_5–8 Are Proxies for the Numbers of Docked SVs, Replacement SVs, and Upstream SVs, Respectively.

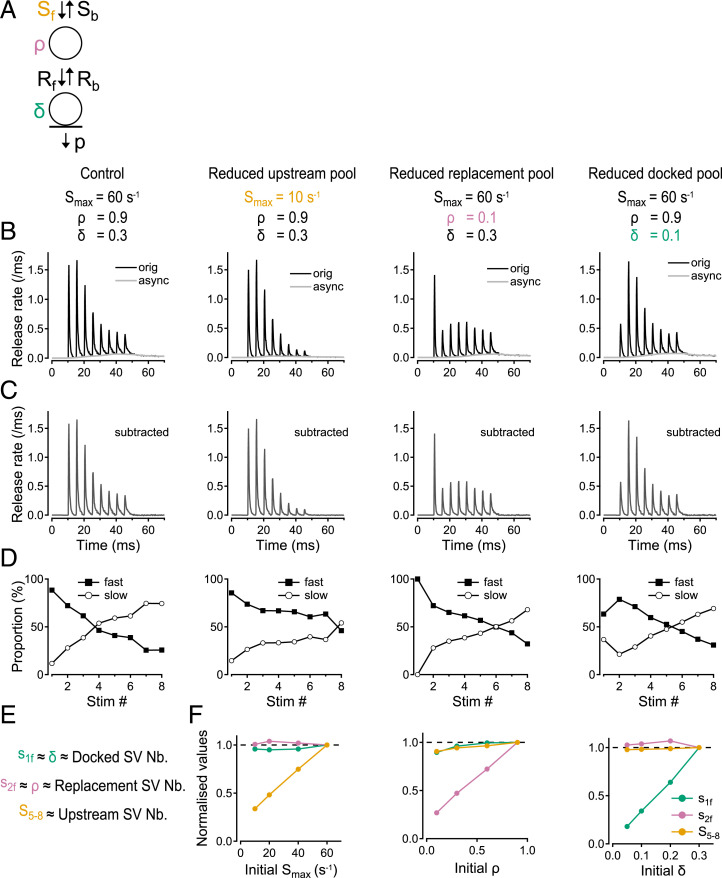
To gain insight into how SV release during the test train is affected by the sizes of various SV pools at the onset of this train, we performed simulations using a previously developed docking/release model (Fig. 2A) (28, 29). In this model, each replacement site is linked to the upstream pool by two rate constants, S_f and S_b. Likewise, each docking site is linked to the corresponding replacement site by the rate constants R_f and R_b. Finally, docked SVs are released with a rate p. S_f, R_f, and p vary during an AP train, as they are driven by changes in the presynaptic calcium concentration. These calcium concentration changes can be calculated from a realistic spatiotemporal model of PF terminals incorporating calcium entry, buffering, and diffusion, as explained before (28, 29).

Fig. 2.

Fast component responses to first and second APs represent docked vesicle and replacement vesicle numbers, while cumulative response to the fifth to the eighth AP represents the upstream pool size. (A) Kinetic model depicting SV exchange between upstream, replacement, and docked SV pools (from ref. 28). (B–D) Monte Carlo simulations showing the effect of changing the size of various SV pools on the response pattern to an 8-AP train. Control simulations are depicted in the first column. The second to fourth columns show the effect of reducing S_max, ρ, and δ, respectively, representing reductions of the upstream pool, the replacement pool, and the docked pool. (B) Total release rate (orig) together with asynchronous release component (async). (C) Synchronous release obtained from the subtraction of the two traces in B. (D) Fast and slow components of synchronous release as a function of AP number. (E) Proposed correspondence between the number (Nb.) of SVs in the upstream pool (represented by S_max) and cumulative SV release number for fifth to eighth APs (S_5–8); between the replacement pool size (represented by ρ) and fast SV release number for the second AP (s_2f); and between the docked pool size (represented by δ) and fast SV release number for the first AP (s_1f). (F) Effect of reducing separately S_max, ρ, and δ on the synaptic parameters S_5–8, s_2f, and s_1f.

As detailed in Materials and Methods, the calcium dependency of S_f is reflected by a simple binding equation with a maximum value S_max at high calcium levels. In addition to its sensitivity to calcium, S_f is proportional to the number of SVs present in the upstream pool. The same applies to S_max. Therefore, in the model, the size of the upstream pool was changed by changing S_max. Calling N the number of docking sites per AZ, the size of the replacement pool is Nρ, where ρ represents the replacement site occupancy (the probability that a replacement site is occupied with an SV) under basal conditions. Likewise, the size of the docked pool is Nδ, where δ represents the basal docking site occupancy. Therefore, replacement and docked pool sizes are respectively proportional to ρ and δ. Fig. 2B illustrates the simulated time course of SV release with normal SV pools (first column: control), or with a reduction in the size of either the upstream pool (second column: S_max reduced from 60 s⁻¹ to 10 s⁻¹), the replacement SV pool (third column: ρ reduced from 0.9 to 0.1), or the docked SV pool (fourth column: δ reduced from 0.3 to 0.1). In each of the last three simulations, a single parameter representing a specific pool size was altered immediately before the start of the 8-AP train, leaving all other parameters unchanged. Therefore, before the train, the system was at steady state under control conditions (first column), but it was not so for any of the perturbed conditions (second to fourth columns). Previous Monte Carlo simulations show that responses to the first few APs rely on SVs that are initially in the docked and replacement pools, while late responses mainly depend on SVs initially in the upstream pool (28). A similar conclusion was reached using nonnegative matrix factorization at the calyx of Held synapse (9). Accordingly, reducing the upstream pool has little effect at the beginning of the train, but it induces a marked reduction near the end of the train, especially for the fifth to eighth APs (Fig. 2B, second column). This result suggests that the total number of SVs released between the fifth and the eighth APs, noted S_5–8, is related to the upstream pool size. Reducing the replacement SV pool leaves the first response almost unchanged, but produces a reduction in synaptic output that is very marked for the second AP and that gradually recovers toward control values thereafter (Fig. 2B, third column). This suggests that s₂ is a candidate to represent ρ. Finally, reducing the docked SV pool affects primarily s₁, the response to the first AP (Fig. 2B, last column). To explain the tight link between δ and s₁, we note that in our recording conditions, the probability of release of docked SVs is high (0.6: ref. 46), so that a large proportion of initially docked SVs are released after the first AP, and few are left at the time of the second AP.

The above analysis suggests S_5–8, s₂, and s₁ as candidate proxies for the sizes of the upstream pool, the replacement pool, and the docked pool, respectively. We previously found that, after each AP, release occurs in three distinct kinetic components (29). The first release component, with latencies distributed along an exponential with a time constant τ_fast around 0.5 ms, represents the rapid release of previously docked SVs. The second release component, with latencies distributed along an exponential with a time constant τ_slow around 2 ms, represents the slower release of SVs that were in the replacement site at the time of the AP. Provided that the corresponding docking site is free, such SVs can undergo a two-step release, which involves an uninterrupted sequence of docking and then release; the additional delay due to docking largely explains the distinctive slow latency of two-step release events. Apart from two-step release, accumulation of calcium near release sites, as well as a gradual decrease of responsiveness of release due to synaptic fatigue, are both thought to contribute to the slowing of release during a train (29). Finally, the third component of SV release, with latencies of 5 ms or more, represents asynchronous release.

Although the majority of SV release after a single AP has short latencies, both slow and asynchronous release appear and become increasingly prominent during a high-frequency AP train. Therefore, by removing asynchronous release and separating the remaining (synchronous) release events between fast and slow components (corresponding to τ_fast of 0.5 ms and τ_slow of 2 ms), as illustrated in Fig. 2 C and D, we improve our choice of parameters representing ρ and δ values. Whereas the fast component of s₁, noted s_1f, directly reflects δ, the slow component s_1s is related to ρ, as it reflects two-step release after the first AP. For this reason, s_1f is a better representation of δ than s₁. Likewise, both s_2f and s_2s contain a contaminating component coming from the upstream pool, and this component is larger for s_2s than for s_2f. For this reason, s_2f is a better representation of ρ than s₂. Altogether, we propose the following representation of the pool sizes (Fig. 2E): for the docked SV pool, the count of fast SV release following the first AP, s_1f; for the replacement SV pool, the count of fast SV release following the second AP, s_2f; and for the upstream pool, the cumulative SV count for the fifth to eighth APs, S_5–8. Fig. 2F shows the plots of the synaptic parameters S_5–8, s_2f, and s_1f as functions of the pool size parameters S_max, ρ, and δ, respectively. The plot of each synaptic parameter as a function of the corresponding pool size parameter is roughly linear. Equally importantly, when changing the size of an individual pool, the two synaptic parameters representing the other two SV pools remain essentially unchanged. This shows that the representation of the three SV pool sizes with the parameters S_5–8, s_2f, and s_1f is almost completely exclusive—there is no significant cross-talk between the three pool reporters.

In conclusion, measurements of S_5–8, s_2f, and s_1f provide reliable indicators of changes in S_max, ρ, and δ, which respectively represent the sizes of the upstream pool, of the replacement pool, and of the docked pool. Fig. 2 F, Right indicates that δ is directly proportional to s_1f. Left and Middle show linear relations that intersect the ordinate axis near 20% of the control values. This indicates that roughly 80% of the values of S_5–8 and s_2f under control conditions covary with the upstream pool size and the replacement pool size, respectively, while 20% of S_5–8 and s_2f remain insensitive to the two corresponding pool sizes.

While the present analysis provides a much-needed tool to distinguish between SV pools, its applicability rests on important underlying assumptions. In the simulations of Fig. 2, only pool sizes are allowed to change, while all other model parameters retain their control values. In particular, presynaptic calcium concentration profiles are assumed to be the same for the second train as those for the first train, and the same applies to all rate constants of the model in Fig. 2A except for S_f. As further discussed below, these assumptions may not be valid when analyzing consecutive trains with short intertrain intervals.

Recovery Kinetics of s_1f, s_2f, and S_5–8 after an 8-AP Train.

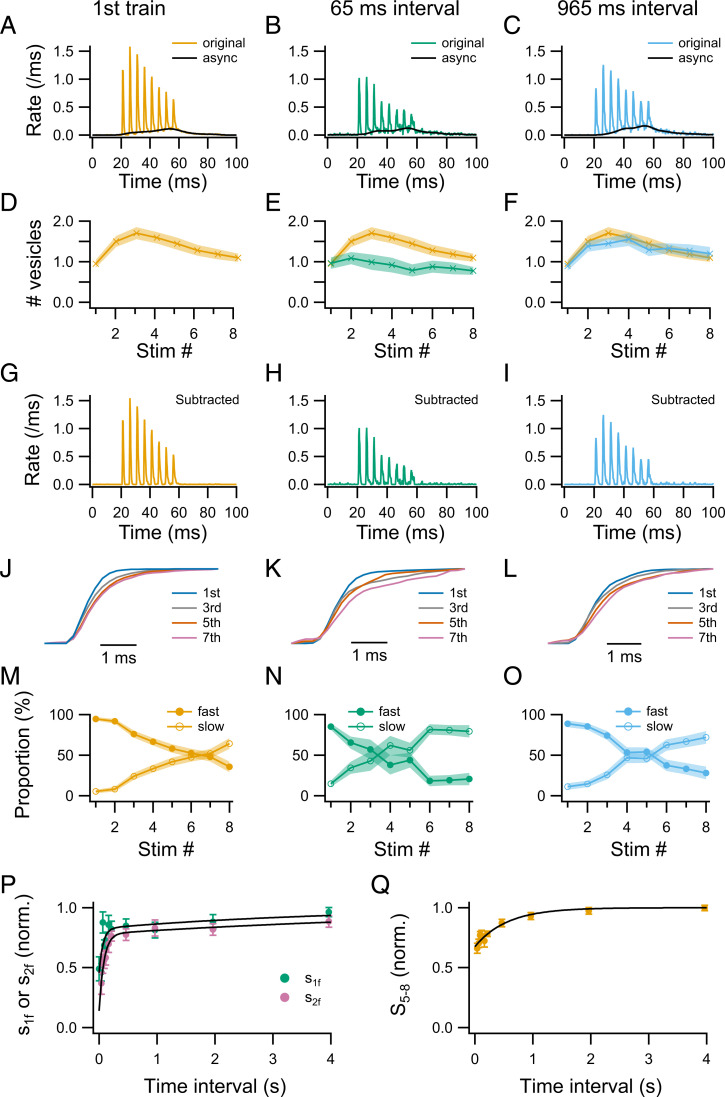
Having used simulations to establish a relation between S_max, ρ, and δ on one side, and S_5–8, s_2f, and s_1f on the other side, we next employed this relation to analyze recorded synaptic responses to a pair of 8-AP trains separated by different time intervals.

Fig. 3 A–C compares the average release rate during the first 8-AP train with that during the second 8-AP train after an intertrain interval of 65 or 965 ms (n = 9 to 15 synapses). As already noted for the exemplar experiment shown in Fig. 1C, the total amount of SV release during the second train is markedly reduced with the 65-ms interval, but it has largely recovered for the longer intertrain interval of 965 ms. In addition, whereas in the control train and in the second train with the 965-ms interval, the peak release rate is smaller for the first AP than for the second or third AP (Fig. 3 A and C), following the 65-ms interval, the peak release rate for the first AP is similar to that for the second AP and larger than that for the third AP (Fig. 3B). Consequently, the integrated numbers of released SVs after individual APs display facilitation in control (Fig. 3D, yellow) and after the 965-ms interval (Fig. 3F, blue), but facilitation is almost absent after the 65-ms interval (Fig. 3E, green). This indicates a deeper relative decrease for the replacement pool than for the docked pool after the 65-ms interval.

Fig. 3.

Recovery kinetics of s_1f, s_2f, and S_5–8 after an 8-AP train. (A–C) The overall release rates (original) and the associated asynchronous component (async), averaged from 15 (A), 9 (B), and 13 (C) synapses. The first AP train serves as control (A). Test trains at different intervals (B: 65 ms; C: 965 ms) examine the time course of recovery of different SV pools. (D–F) The number of released SVs following individual APs. Control data are shown together with test 65- and 965-ms intervals for comparison. (G–I) The synchronous release component, obtained by subtracting the asynchronous component from the overall release rate in A–C. (J–L) Overlay of cumulative synchronous release for AP number 1, 3, 5, and 7. Traces have been scaled vertically to have the same amplitude so that the release kinetics after individual APs can be compared. (M–O) Fast and slow components of synchronous release as a function of AP number. (P) The numbers of rapidly releasing SVs after the first AP (s_1f, representing δ) and after the second AP (s_2f, representing ρ) of the second train plotted against intertrain interval. All values had been normalized to those of the first train. Plots were fitted with a double-exponential function with time constants 67 ms (68%) and 4.0 s (32% of the total amplitude) for s_1f, and 83 ms (64%) and 6.6 s (36% of the total amplitude) for s_2f. (Q) The summed number of SVs released between AP 5 and 8 of the second train (S_5–8, representing the upstream pool size), normalized to that during the first train, and plotted against intertrain interval. Plot was fitted with a single exponential function having a time constant of 550 ms. n = 9 to 15 synapses for each time interval.

To be able to determine the recovery of s_1f and s_2f, the asynchronous release component (async; black traces in Fig. 3 A and C) was removed from the original traces to obtain the rate of synchronous release (Fig. 3 G–I). The cumulative synchronous release after individual APs (Fig. 3 J–L) was then fitted with a double-exponential function with τ_fast = 0.5 ms and τ_slow = 2 ms to yield the corresponding proportions of fast vs. slow synchronous release (Fig. 3 M–O). In agreement with our earlier work (29), the proportion of slow release during the first train is initially small, but it increases as a function of AP number, while the proportion of fast release decreases (Fig. 3 J and M). Following the 65-ms interval, the proportion of slow release is increased throughout the second 8-AP train compared to the control train (Fig. 3K), and the cross-over point where slow and fast components have the same proportion shifts to near AP number 3 (Fig. 3N), compared to AP number 7 in the control (Fig. 3M). Even after a recovery period of 965 ms, the proportion of slow release remains higher than in the control (Fig. 3L), and the cross-over point is still left shifted (around AP number 5 instead of 7: Fig. 3O). These results indicate that the proportion of two-step release increases after the conditioning train, and that this proportion recovers slowly as the interval increases between the conditioning and the test trains.

Group results showing the recovery of s_1f (representing δ) and s_2f (representing ρ) are shown in Fig. 3P. Both recovery curves are biphasic, with an initial phase of large amplitude having a time constant of 67 ms for s_1f and 83 ms for s_2f, and a second phase of small amplitude with a time constant in the range of several seconds. The recovery of s_2f trails that of s_1f throughout the time period examined (4 s). Back extrapolation to 0-time interval indicates amounts of depression of 54% for s_1f and 86% for s_2f.

The recovery of S_5–8 (representing the upstream pool size) follows a single exponential component with a time constant of 550 ms (Fig. 3Q), markedly slower than the time constants of the main component of recovery for δ or ρ (Fig. 3P). Back extrapolation of the recovery curve for S_5–8 indicates an initial amount of inhibition of 32%, substantially smaller than the corresponding numbers for δ or ρ. Nevertheless, these results clearly indicate a significant reduction of S_5–8, and by implication, of the upstream pool size, at the end of the conditioning 8-AP train.

Marked Inhibition of Synchronous Release during Prolonged AP Trains.

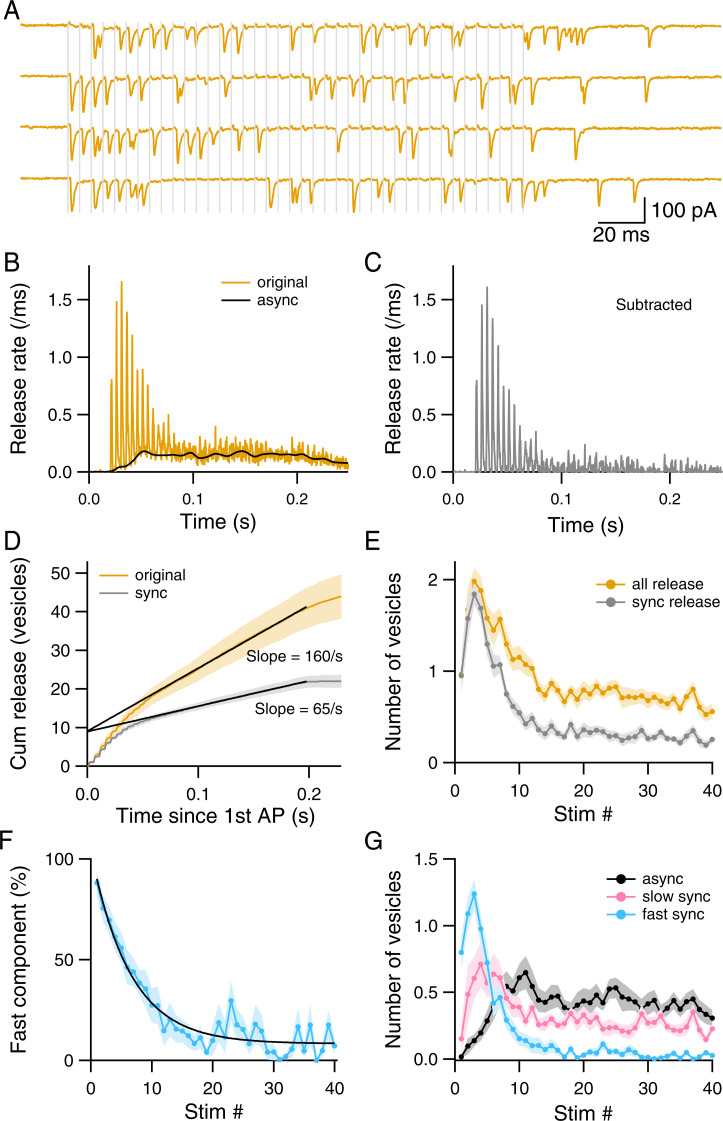
Our results so far indicate that following an 8-AP train, the RRP (containing both replacement and docked SVs) is severely depleted and recovers quickly, while the upstream pool is moderately depressed and recovers slowly. These results suggest that the processes regulating the number of replacement and docked SVs have faster kinetics than those regulating the upstream pool. They raise the question as to whether prolonged AP trains would further deplete the upstream pool size. To address these issues, we next investigated the effects of a longer depressing AP train (a 40-AP train at 200 Hz). As shown in the representative recording of Fig. 4A, and in the summary results of Fig. 4 B–G (n = 14 synapses), synchronization of SV release is dominant at the beginning but not at the end of the AP train. As synchronous release is reduced (Fig. 4 B and C), it is replaced with a continuous flow of vesicular release (asynchronous release) that proceeds with little immediate change even after the end of the train. The cumulative plot of released SVs during the train becomes linear for AP numbers >10, with a limiting slope of 160 SV/s (yellow curve in Fig. 4D). By contrast, the limiting slope for synchronous release is less than half of this value (65 SV/s; gray curve in Fig. 4D). When plotted as a function of AP number, the share of synchronous release in global release drops from near 100% for the first AP to less than 50% at the end of the train (Fig. 4E). Within the shrinking share of total SV number attributable to synchronous release, the percentage of fast release gradually decreases from an initial value near 90% for the first AP down to a steady-state value of 8% near the end of the train (Fig. 4F).

Fig. 4.

Dynamic redistribution of three components of SV release during a 40-AP train. (A) Exemplar recordings showing EPSCs in response to trains of 40 APs evoked at 200 Hz (gray vertical lines). (B) Average release rate from 14 experiments. (C) Synchronous release rate, obtained by subtracting asynchronous release from total release in B. (D) Cumulative release curves for synchronous and total release. Linear fits to the late parts of the curves yield limiting slopes of 65 SV/s for synchronous release and 160 SV/s for total release. (E) The number of released SVs associated with synchronous release and with total release plotted against AP number. (F) Fast component of synchronous release as a function of AP number. Plot was fitted with an exponential function with a time constant of 6.4 stimuli and a steady-state value of 8%. (G) The number of released SVs associated with fast synchronous release, slow synchronous release, and asynchronous release, plotted against AP number.

As predicted by previous Monte Carlo simulations (29), the three components of release have strikingly different time courses (Fig. 4G). Fast synchronous release peaks for AP number 3 and descends to very low levels past AP number 10 (0.03/AP). Slow synchronous release peaks for AP number 4. Finally, asynchronous release is initially very small but grows in size gradually before reaching a plateau level after AP number 10.

According to previous models (28, 29), the amplitude of the fast synchronous component after AP number i is N δ_i p, where δ_i is the docking site occupancy, and p is the release probability per docked SV (assumed constant at 0.6). Since the average number of docking sites in this set of experiments (N) is 5, the product N p is 3. Therefore, δ_i can be deduced from the blue plot in Fig. 4G by scaling down the vertical axis by a threefold ratio. From the steady-state value of the fast synchronous component, the corresponding estimate for δ is 0.03/3 = 0.01. Thus, docking sites are largely depleted at the end of the train. Likewise, the occupancy of replacement sites is low, since equilibration between replacement sites and docking sites is rapid. For both replacement sites and docking sites, incoming SVs rapidly move forward toward exocytosis, preventing accumulation of the SVs at these sites. As previously suggested (34, 36), it is then the supply of replacement SVs from the upstream pool that limits the release rate. Since the total release rate remains constant at 160/s (Fig. 4D), these results indicate that the size of this upstream pool reaches a stable value at the end of the train, so that the system is at steady state.

Recovery Kinetics of δ, ρ, and Upstream Pool Size after a 40-AP Train.

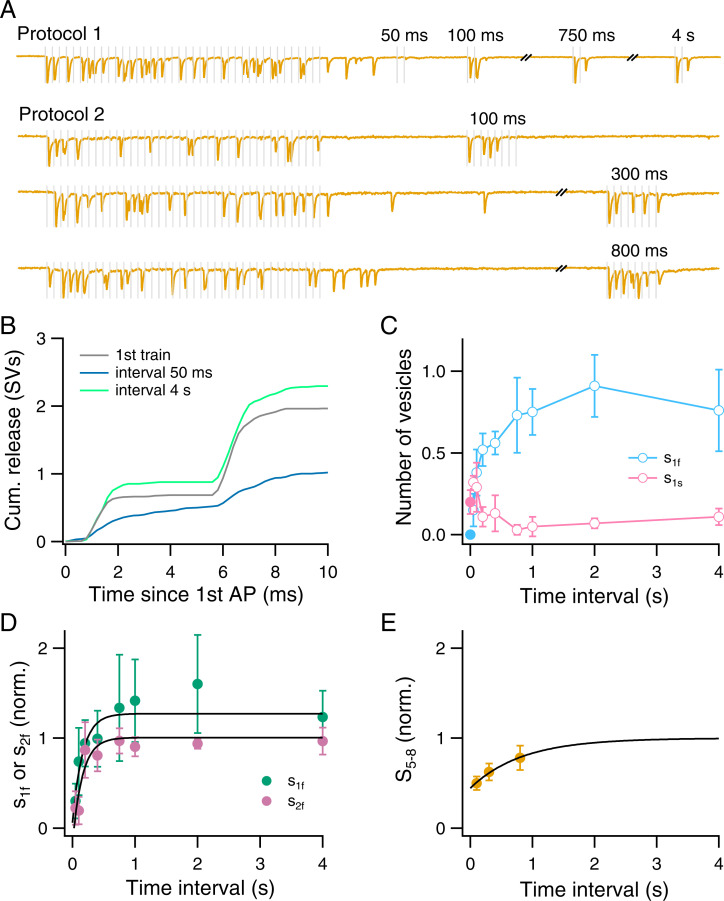
We studied the recovery of pool sizes after the 40-AP train with two distinct protocols. The first protocol aimed at studying the recovery of s_1f and s_2f. It employed a series of twin test stimuli applied at various intervals (Fig. 5A). The average profile of cumulative synchronous release at an intertrain interval of 50 ms (Fig. 5B, blue curve) shows a severe depression of the fast component and a relatively large slow component of release, compared to the control or to the longer interval of 4 s (Fig. 5B, gray and green curves, respectively; n = 4 synapses). The recovery curve of the fast component is monotonous (Fig. 5C, blue), but that of the slow component is biphasic, with a peak at 50 ms (Fig. 5C, pink; closed circle represents SV release after the last AP of the 40-AP train; open circles correspond to release after the first AP of the twin test stimulation). This biphasic recovery may be understood by the double requirement of two-step release for a sufficient supply of replacement SVs and for a free downstream docking site. Extrapolation of s_1f and s_2f recovery curves at short intervals indicates a deep depression for both parameters at the end of the train, to less than 10% of the control values (Fig. 5D). These results are consistent with our previous conclusion that δ and ρ reach low values near the end of the train. Both s_1f and s_2f recover with a time constant of 160 ms after the 40-AP train (Fig. 5D), slightly larger than those observed after the 8-AP train (Fig. 3P). These results suggest that δ and ρ likewise recover with time constants on the order of 160 ms.

Fig. 5.

s_1f and s_2f recover more quickly than S_5–8 after a 40-AP train. (A) Two protocols were used to study the recovery of SV pools after the 40-AP train. In the first protocol, double AP stimulations with a 5-ms inter-AP interval were given after various delay periods following the end of the 40-AP train. This protocol was used to assess the recovery of s_1f and s_2f. In the second protocol, a single 8-AP test train was given at variable intervals following the end of the 40-AP train. This protocol was used to assess the recovery of S_5–8. (B) Cumulative release following the two test APs used to study the recovery of s_1f and s_2f. Traces with test intervals of 50 ms and 4 s were averaged from four synapses and superimposed with the control from the beginning of the conditioning train. Note the reduced fast component and the enhanced slow component of release for the 50-ms recovery interval. (C) Recovery kinetics for s_1f and of s_1s. Closed symbols show values after the last AP of the 40-AP train. (D) s_1f and s_2f, normalized to that of the conditioning 40-AP train and plotted against test interval. Plots were fitted with single exponential functions having a time constant of 160 ms. (E) S_5–8, normalized to that of the conditioning train and plotted against test interval. Plot was fitted with a single exponential function having a time constant of 830 ms. n = 4 synapses for each protocol.

To examine the recovery kinetics of S_5–8, representing the upstream pool size, we performed additional experiments using a single 8-AP test train following each 40-AP train with various time intervals (protocol 2 in Fig. 5A). This revealed that S_5–8 was less reduced than s_1f or s_2f by the 40-AP train (Fig. 5E; to about 45% of the control value for S_5–8, compared to <10% for either s_1f or s_2f). However, compared to those after the 8-AP train, the extent of reduction of S_5–8 was larger following the 40-AP train (respectively to 68% and to 45% of the control), and the recovery of S_5–8 was slower (respective recovery time constants: 550 and 830 ms; compare Fig. 5E with Fig. 3Q). These results suggest that the amount of depression of the vesicular pool upstream of the replacement sites increases with the duration of the AP train.

Modeling SV Pool Changes during AP Trains.

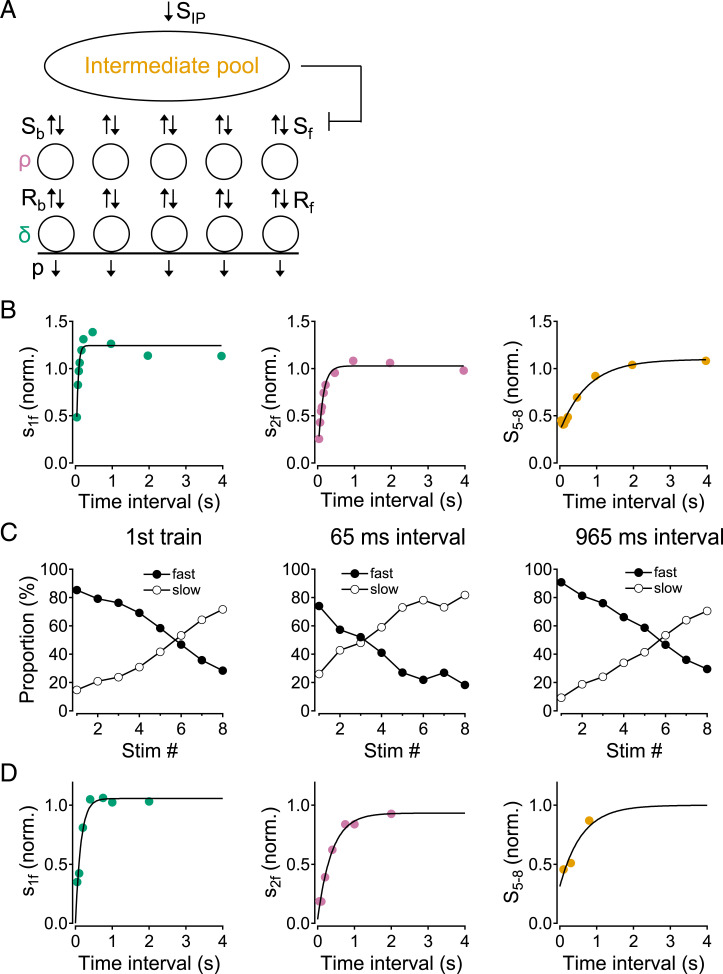
The standard view of SV recycling assumes a recycling pool with relatively large capacity upstream of the RRP (46). This view is at odds with the results of experiments with two 8-AP trains (Fig. 3). These experiments suggest that the upstream SV pool feeding the RRP had a low capacity, since this upstream pool was significantly reduced at the end of a relatively short AP train (on average, a total of 11 SVs were released during the first 8-AP train). Therefore, we introduced an intermediate pool (IP) with a limited size between the recycling pool (assumed of infinite size) and the replacement sites (Fig. 6A). This introduced two new parameters: the size of the IP at rest, and the replenishment rate of this pool (S_IP). Like the other replenishment rates S_f and R_f, S_IP was assumed to be calcium dependent (see detailed numerical assumptions and simulations in SI Appendix, Fig. S1 for paired 8-AP trains, in SI Appendix, Fig. S2 for 40-AP trains, and in Materials and Methods; also see below). The IP was assumed to contain eight SVs at rest. Following partial IP depletion, like in the simulation of Fig. 2, the entry rate S_f into individual replacement sites was scaled proportionally to the current IP size (pictured as a brake on S_f in Fig. 6A; see Materials and Methods). With these assumptions, the simulations could replicate many features of the experimental data (Fig. 6). Specifically, following an 8-AP train, the simulation predicted a time constant for recovery of 46, 131, and 760 ms for δ, ρ, and the IP size (Fig. 6B), compared to experimental values of 67, 83, and 550 ms, respectively (Fig. 3 P and Q). The model also replicated the reduced facilitation during the test 8-AP train when preceded by a conditioning 8-AP train with short intervals (compare simulations in SI Appendix, Fig. S3 with experimental data in Fig. 3 A–F). Moreover, for this set of experiments, the model correctly predicted the increase in slow release during the test 8-AP train, as well as the left shift of the cross-over point where the proportions of fast and slow release are equal (compare simulations in Fig. 6C with data in Fig. 3 M–O). Similarly, simulations of 40-AP train experiments accurately reproduced the loss of time dependence of the release process during the train (compare Left and Middle in SI Appendix, Fig. S2E with Fig. 4 B and C, and SI Appendix, Fig. S2F with Fig. 4F), and the slope of the steady-state release near the end of the train (143 s⁻¹ in the model vs. 160 s⁻¹ in the average measurement: Right in SI Appendix, Fig. S2E and Fig. 4D). Finally, the model yielded reasonable estimates of the recovery time constants for the three pools after prolonged stimulation (compare Fig. 6D with Fig. 5 D and E).

Fig. 6.

Simulating synaptic responses to train stimulations using a sequential SV pool model. (A) Sequential SV model. On their way toward exocytosis, SVs transit sequentially from an infinitely large recycling pool (above, not shown) to an intermediate pool (resting pool size: eight SVs), followed by replacement sites and to docking sites (five sites each per AZ). All pool replenishment rates (downward arrows) are assumed to be calcium dependent (see numerical values in SI Appendix, Figs. S1B and S2B). (B) Recovery kinetics of s_1f, s_2f, and S_5–8 after an 8-AP train. Recovery time constants are similar to experimental values (compare with Fig. 3 P and Q). (C) Fast and slow components of synchronous release during 8-AP trains. The simulation reproduces the leftward shift of the cross-over point between the two curves at short intertrain intervals (compare with experimental data in Fig. 3 M–O). (D) Recovery kinetics of s_1f, s_2f, and S_5–8 after a 40-AP train (compare with Fig. 5 D and E).

A key feature of our model is that the SV pool upstream of replacement SVs (IP) is small. As already mentioned, the small size of this pool accounts for the significant depression of S_5–8 in experiments with two 8-AP trains. Remarkably, the same assumption brought a solution to an otherwise intractable problem of an entirely different nature. With a large size upstream pool (such as the infinite recycling pool assumed in ref. 29), the large residual calcium concentration following an 8-AP train resulted in a large (severalfold) rebound of δ over its basal value, due to a rapid refilling of replacement and docking sites from the upstream pool (SI Appendix, Fig. S4). By contrast, on average, the experimental values of s_1f remained smaller than the control value following the 8-AP train (Fig. 3P), and only a small potentiation was apparent after the 40-AP train (to about 120% of the control value: Fig. 5D). We were unable to remove this discrepancy as long as the upstream pool was kept large. However, with a basal IP size as small as 8, the IP size was reduced to about two SVs after the end of an 8-AP train, or to 1/4 of the basal value (SI Appendix, Fig. S1D). Consequently, the refilling rate of the RRP after the first 8-AP train was reduced by a factor of 4, and the δ rebound was likewise reduced (SI Appendix, Fig. S4).

To understand the interplay among vesicular pools, it is instructive to follow the evolution during intertrain intervals of the global calcium concentration, of the calcium-dependent replenishment rates R_f, S_f, and S_IP, as well as of the replacement, docked, and intermediate SV pools (SI Appendix, Fig. S1 B–D and F–H; Fig. S2 B–D). It can be seen that the order R_f > S_f > S_IP was always respected. δ and ρ varied roughly in parallel, even though δ always remained below ρ, and varied with somewhat faster kinetics than ρ (SI Appendix, Fig. S1C; Fig. S2C); by contrast, the evolution of the IP was markedly slower (SI Appendix, Fig. S1D; Fig. S2D). This indicates that the RRP equilibrates rapidly compared to the IP. Finally, in conformity with the predictions of Fig. 2, the recovery kinetics of s_1f, s_2f, and S_5–8, respectively, mimicked those of δ, ρ, and the IP size (compare SI Appendix, Fig. S1 G and H with Fig. 3 P and Q or with Fig. 6B; and SI Appendix, Fig. S2 C and D with Fig. 5 D and E or with Fig. 6D).

The model predicts that S_IP, the calcium-dependent entry rate into the IP, reaches a maximum value near 30 SVs/s per SV site in the IP (amounting to ∼240 SVs/s per AZ) during the late part of a 40-AP train (SI Appendix, Fig. S2 B, Bottom). During this time, δ and ρ are <0.1 while the IP is reduced to 3.2 SVs (SI Appendix, Fig. S2 C and D). Although the downstream on-rate constants S_f, R_f, and P_r are all higher than S_IP (SI Appendix, Fig. S2 A and B), due to its proportionality with the current IP size, the actual flux associated with S_f (= 74/s × 5 docking sites × 3.2/8 = 148/s) becomes equal to that of S_IP (= 240/s × 4.8/8 = 144/s; SI Appendix, Fig. S2 B and D), thereby limiting the flow of SVs. This accounts for the similarity between these fluxes and the slope of the cumulative release plot (143/s, SI Appendix, Fig. S2 E, Bottom).

SI Appendix, Fig. S5 illustrates the effects of the calcium dependence of S_IP. If the value of S_IP was calcium independent and small (∼23 SVs/s per AZ), the model was able to predict the results of paired 8-AP experiments, but failed to reproduce the high steady-state output observed at the end of a 40-AP train (SI Appendix, Fig. S5A). If S_IP was still calcium independent but an order of magnitude larger (∼230 SVs/s per AZ), the model was able to predict the high steady-state output observed at the end of a 40-AP train, but failed to reproduce the results of paired 8-AP experiments (SI Appendix, Fig. S5B). A similar situation was found when using a Michaelis–Menten equation to relate S_IP to the intracellular calcium concentration ([Ca²⁺]_i) (SI Appendix, Fig. S5C). To redeem this problem, it was necessary to assume a delayed increase of S_IP as a function of [Ca²⁺]_i, as implemented in the model by introducing a cooperative activation of S_IP by [Ca²⁺]_i (SI Appendix, Fig. S5D).

The dependence of key parameters of synaptic responses as a function of the IP size is shown in SI Appendix, Fig. S6. The optimal IP size is close to 20 when examining the y intercept of S_5–8 (SI Appendix, Fig. S6A), and it is around 6 to 8 when examining either the horizontal asymptote of s_1f, the time constant of s_1f recovery, or the slope of the release rate at the end of 40-AP trains (SI Appendix, Fig. S6 C–E). By contrast, the time constant of S_5–8 recovery was largely unaffected by a basal IP size between 6 and 40 SVs (SI Appendix, Fig. S6B). Therefore, while a small IP size accounts both for the lack of δ overshoot and for the depression of S_5–8, the optimal IP size differs somewhat, depending on the synaptic parameter that is considered. Overall, the simulations suggest a range of 6 to 20 for the IP size for a standard synapse with five release sites, corresponding to 1.2 to 4 SVs per release site (gray zones in SI Appendix, Fig. S6).

Discussion

The main conclusion from this work is the existence of a small pool of SVs upstream of replacement SVs. This conclusion is based on the finding that a single 8-AP train, which releases around 2 SVs per release site, significantly reduces S_5–8, a parameter reporting the size of the upstream pool. This indicates that the upstream pool is significantly depleted after losing at most 2 SVs per release site, so that its size cannot be larger than a few SVs per release site. Modeling release kinetics suggests a pool size of 1.2 to 4 SVs per release site, or 6 to 20 SVs per AZ.

The classical view of SV pools places a recycling pool upstream of the RRP, with a size 5 to 20 times larger than the RRP (47). As our estimate of the RRP size is 7/AZ, the upstream pool is only one to three times larger than the RRP. For this reason, we call the upstream pool “intermediate pool” (IP); determining the relation between the IP and the actual recycling pool will need further investigation.

Following Changes in Vesicular Pool Sizes.

One of the advances of the present work is to propose a method to follow changes of various SV pool sizes based on the number of released SVs elicited by an 8-AP test train. As shown in Fig. 2, s_1f, s_2f, and S_5–8, respectively, represent the size of the docked pool, the replacement pool, and the IP. This approach rests on the assumption that only pool sizes change between the control and test conditions. In particular, it requires the profile of calcium concentration to remain unchanged between the conditioning train and the test train. For intertrain intervals of a few hundred milliseconds or less, this condition may not be met, as the tail of the calcium rise associated with the conditioning train overlaps with the calcium rise elicited by the test train (29). On the other hand, such errors are unlikely to affect our key finding that the replenishment rate from the IP (rate constant S_f in the scheme of Fig. 2A) is reduced after an AP train. This is because the IP reduction is observed for intertrain intervals extending beyond 500 ms, for which the tail of the calcium transient has subsided close to baseline levels (ref. 29 and see SI Appendix, Fig. S1F).

To identify the pools of origin of released SVs, we have used in the present work a higher external calcium concentration than normal (3 mM). In these conditions, when taking an initial IP size of eight SVs, we estimate the decrease in the IP size to be slightly smaller than 50% after an 8-AP train (Fig. 3Q), and slightly larger than 50% after a 40-AP train (Fig. 5E). One could expect smaller effects under normal calcium concentration conditions (1.5 mM), because of a smaller number of total SV release. However, due to the differential sensitivities of synaptic facilitation and synaptic depression on external calcium, differences in the number of released SVs between high and low calcium conditions diminish as a function of stimulus number (46). As a result, the cumulative number of released SVs shows a weak dependence on the external calcium concentration. Specifically, the total number of released SVs at the end of an 8-AP train are only 10% lower in 1.5 mM calcium compared to 3 mM calcium (29). Therefore, our results suggest a significant reduction of the IP size during train activity also under physiological calcium conditions (SI Appendix, Fig. S7).

Recovery of the Three Subpools after a Train.

Our data indicate that after a train, the IP size recovers with a time constant comprised between 500 ms and 1 s (Fig. 3Q and Fig. 5E). This time constant reflects the refilling rate of the IP from a further upstream pool (presumably the recycling pool). Recovery kinetics for docking sites and replacement sites are clearly faster (Fig. 3P and Fig. 5D). They represent a downward flux of SVs coming from the IP. s_1f and s_2f, respectively, representing the occupancy of docking sites (δ) and of replacement sites (ρ), have similar recovery kinetics. This indicates that equilibration within the RRP is rapid, so that the entire RRP (the sum of docked and replacement SVs) recovers as a single unit. However, the time constants of s_1f and s_2f recovery are in the time window where the assumptions underlying the analysis of Fig. 2 may not be valid. Therefore, a definitive description of the recovery kinetics of δ and ρ will need further investigations.

A Small-Sized Pool between Replacement SVs and Recycling Pool.

Our simulations showed that not only does a small IP size account for the significant reduction of S_5–8 after a short AP train, but it also prevents a severalfold overshoot of δ during the test trains. However, it remains possible that after a conditioning train, inhibition of S_5–8 during the test train could result from a reduction of the rate constant S_f, independently from a reduction of the IP size. Thus, we cannot exclude the alternative possibility that S_f becomes inactivated after the conditioning train and thereby suppresses late release during the test trains. Nonetheless, it is unlikely that S_f inactivation also prevents δ overshoot during the test trains (Fig. 2 F, Left). Therefore, our proposal of a small-sized IP appears as the most parsimonious interpretation of the data.

In vivo recordings indicate that, during sensory input such as whisker stimulation, granule cells typically fire short or moderate bursts of APs (<100 ms) (48). Our results suggest that during moderate duration trains, IP recruitment slows RRP depletion and maintains synaptic output. In particular, during an 8-AP train, the number of released SVs originally in the IP can be roughly estimated in our simulations from the reduction of the IP size, which amounts to six SVs in 3 mM external calcium concentration (SI Appendix, Fig. S1D) and to five SVs in 1.5 mM external calcium concentration (SI Appendix, Fig. S7D). These numbers represent about 60% of the synaptic output in both cases, showing that the IP is a potent contributor to synaptic output in these conditions.

Our results also suggest that the IP is quickly depleted (to <1/2 of the control during an 8-AP train: SI Appendix, Figs. S1D and S7D). In order to restore the initial IP size, a resting period of >1 s is necessary. As shown in SI Appendix, Fig. S4, the persistent IP depletion resulting from the first AP train prevents subsequent overfilling of the docking sites. The lack of overfilling enables the response to the first AP of the second train to be restored to a level similar to that observed with the first train after a waiting time as short as 65 ms and allows the response to an 8-AP train to be restored to the original response after a waiting time on the order of 1 s (SI Appendix, Fig. S4D). Thus, IP depletion contributes to preserving the pattern of response to AP trains separated in time, particularly for the first stimuli within trains.

Ambiguities in the Separation between RRP and IP.

Our finding of a small-sized pool upstream of the RRP raises questions about the reliability of standard methods of RRP measurements. We find that in our conditions (3 mM external calcium), δ is 0.5 and ρ is 0.9 (29, 46), so that an AZ containing five release sites has 2.5 docked SVs and 4.5 replacement SVs at rest. As both docked and replacement SVs are released during a short AP train, we assign both of them to the RRP, with a total RRP size of 7/AZ. Together with the 8 SVs that we found optimal for the IP, the total size of the RRP-related pools is 15/AZ, or 3/release site. An RRP size of 9/AZ was obtained using the classical back-extrapolation method of cumulative release, performed on the data of Fig. 4D. However, this method actually measures the drop in the pool size during the train, and it gives an underestimate of the total pool size (49). Accordingly, the 9/AZ value obtained with the extrapolation method is consistent with a total pool size of 15/AZ, and not with a total pool of 7/AZ. Therefore, this method does not distinguish the RRP from the IP in our synapses. Likewise, an RRP size estimate using capacitance measurements of PF-MLI synapses in culture gave 20/AZ (50). This number is markedly larger than our present RRP size estimate, but it is only slightly larger than the sum of RRP and IP sizes found here (15/AZ); the difference is likely explained by a bias toward selecting large presynaptic boutons for capacitance recording. Altogether, the rapid replenishment kinetics of the RRP by the IP make the separation between these two pools difficult when using standard pool measurements.

Comparison with Other Synapses.

The sequential model proposed here is in agreement with previous studies at the PF-MLI synapses (28, 29). Such a model can account for many aspects of short-term synaptic plasticity and may have general validity (26, 51–53). In the calyx of Held, a recent study suggests that the FRP can be subdivided into primed and superprimed components, placed sequentially (9). These components act similarly to the replacement and docked pools of the present study. Furthermore, the SRP can replenish the FRP after synaptic depression (7, 23), so that SRP, primed, and superprimed SVs may be organized in sequence. As the sizes of SRP and FRP in the calyx of Held are similar (54), and the sizes of the IP and the RRP are likewise similar in the present study, it is tempting to draw a parallel between the IP proposed here and the SRP of the calyx of Held. However, in the calyx of Held, following prolonged presynaptic stimulation, recovery is faster for the SRP than for the FRP (5), whereas we find a slower recovery for the IP than for the RRP at PF-MLI synapses. The reasons for this apparent discrepancy remain to be investigated.

The exact geometric arrangement of replacement SVs and docked SVs is still uncertain (review: ref. 55), making the position of IP vesicles also uncertain. If replacement SVs are located in a second row of SVs, behind docked SVs, IP vesicles would be placed further back, at a distance of >80 nm from release sites. If, however, replacement and docked SVs are all located within the first row of SVs above the plasma membrane, as suggested by the “two-state model” (26), IP vesicles would correspond to the second row of vesicles and could be attached to the plasma membrane by Munc13 links (55).

Materials and Methods

Preparation.

The use and care of experimental animals complied with guidelines of Université de Paris (approval no. D 75-06-07). Tissue harvesting was carried out as described previously (56). See SI Appendix for details.

Electrophysiology.

A single PF-MLI connection was established as described previously (31, 41). See SI Appendix for details.

Decomposition of EPSCs.

The time of occurrence and the amplitude of individual release events were determined based on deconvolution analysis, as described previously (31). See SI Appendix for details.

Simulation of AP-Evoked Ca²⁺ Transients.

All simulations were performed using CalC (version 7.9.4) (57). The simulation parameters are as described in ref. 29. See SI Appendix for details.

Simulation of SV Release.

We performed Monte Carlo simulations of SV release using the two-step model as described previously (29). Refer to SI Appendix for details.

Data Availability

Data for replication of the figures are publicly available via the Open Science Framework (OSF) (https://osf.io/mwfdj/). All other study data are included in the article and/or the SI Appendix.