Surface NMR using quantum sensors in diamond

Significance

Many of the functions and applications of materials in catalysis, energy conversion, drug delivery, bioanalysis, and electronics are based on their interfacial properties and structures. The characterization of their molecular properties under ambient or chemically reactive conditions is a fundamental scientific challenge. Here, we develop a surface-sensitive magnetic resonance technique that combines the nanoscale-sensing capabilities of defects in diamond with a high precision and versatile protocol for diamond surface modification. We demonstrate the functionality of this method for probing the molecular properties and kinetics at surfaces and interfaces under ambient conditions.

Abstract

NMR is a noninvasive, molecular-level spectroscopic technique widely used for chemical characterization. However, it lacks the sensitivity to probe the small number of spins at surfaces and interfaces. Here, we use nitrogen vacancy (NV) centers in diamond as quantum sensors to optically detect NMR signals from chemically modified thin films. To demonstrate the method’s capabilities, aluminum oxide layers, common supports in catalysis and materials science, are prepared by atomic layer deposition and are subsequently functionalized by phosphonate chemistry to form self-assembled monolayers. The surface NV-NMR technique detects spatially resolved NMR signals from the monolayer, indicates chemical binding, and quantifies molecular coverage. In addition, it can monitor in real time the formation kinetics at the solid–liquid interface. With our approach, we show that NV quantum sensors are a surface-sensitive NMR tool with femtomole sensitivity for in situ analysis in catalysis, materials, and biological research.

The characterization of surface processes at the molecular level is essential for understanding fundamental processes in industrial catalysis, energy conversion, electronic circuits, targeted drug delivery, and biosensing (1). However, many analytical techniques used in surface science are inaccessible under ambient or chemically relevant conditions. Therefore, it remains challenging to perform chemical analysis under the conditions in which these processes occur (2, 3). Commonly used surface sensitive methods, such as X-ray photoelectron spectroscopy (XPS), Auger electron spectroscopy, and secondary ion mass spectroscopy can perform chemical analysis but require ultra-high vacuum and expensive equipment (4). Great efforts have been devoted to extending XPS analysis to near ambient conditions (2). Indeed, both near-ambient pressure XPS and extended X-ray absorption fine structure have significantly expanded the applicability of these X-ray–based techniques for understanding reaction mechanisms at chemically active interfaces (2, 5). However, both methods require intense synchrotron radiation to achieve high sensitivity and resolution, which limits their practical accessibility and increases their cost. State-of-the-art surface-sensitive spectroscopy techniques, such as sum frequency generation and second harmonic generation, can perform analysis under ambient conditions but require technically complex equipment such as femtosecond lasers (6). Even with all these techniques available, molecular dynamics or chemical reaction kinetics at surfaces are still challenging to probe experimentally (7) (SI Appendix, Supplementary Note 1).

NMR spectroscopy is one of the major tools for chemical and structural analysis in chemistry, biology, and materials science. Solid-state NMR in particular (8) has advanced understanding of a range of systems, including metal organic frameworks (9), batteries (10), and catalysts (11). However, sensitivity remains a challenge for traditional NMR spectroscopy, making studies at surfaces difficult because of the limited numbers of nuclear spins. Recently, surface-enhanced NMR spectroscopy (DNP-SENS) relying on hyperpolarization such as dynamic nuclear polarization (12, 13) or xenon-based techniques (14) gained research momentum and enabled probing spins located at surfaces. However, even in highly porous materials with greater than 1,000 m²/g surface area, the concentration of NMR-active nuclei of interest often remains low (e.g., 1 mmol of surface atoms/g), which requires long averaging times to obtain solid-state NMR spectra with reasonable signal-to-noise ratios (SNR) (12) (SI Appendix, Supplementary Note 2).

Here, we demonstrate the use of quantum sensors in diamond as a surface-sensitive spectroscopy technique that works at ambient conditions and can probe planar interfaces on the microscopic length scale with far greater sensitivity (femtomoles, see Materials and Methods) than conventional NMR. The spectroscopic technique relies on the nitrogen vacancy (NV) point defect, consisting of a nitrogen impurity (N) and an adjacent vacancy (V) in the carbon lattice of diamond. These spin-1 defects allow for optical detection of magnetic resonance and have been established as highly sensitive nanoscale magnetic field sensors (15, 16). Near-surface NV centers are sensitive to magnetic fields from the Larmor precession of nuclei from samples positioned outside of the diamond. This enables nanoscale NMR detection—even down to a single molecule (17) or spin (18, 19). The measurement volume of such NV sensors (20, 21) corresponds to a hemisphere whose radius is roughly their depth below the surface in the diamond lattice (e.g., 5 to 10 nm). At this small length scale, the thermal polarization of the nuclear spins can be neglected since spin noise dominates for a small number of spins (22, 23). For that reason, the NMR signal strength is independent of the applied magnetic field B₀, reducing experimental complexity and costs, which makes the technique accessible to a broader community. Previously published nanoscale NV-NMR experiments detected NMR signals from either bulk samples [such as viscous oils (21, 22, 24)] or samples tethered to (17) or placed directly on the diamond surface (25). In this work, we propose the use of NV centers in diamond combined with state-of-the-art thin film deposition techniques as a general platform to detect NMR signals with high sensitivity and spatial resolution even from nondiamond surfaces. This approach is general and allows for the probing of a variety of surfaces and interfaces with NMR, thereby enabling their chemistry to be explored. Here, we use atomic layer deposition (ALD), a technology that can be applied to synthesize films of a wide variety of materials with high thickness precision to coat the diamond with amorphous aluminum oxide (Al₂O₃). Al₂O₃ provides an exemplary surface of high technical relevance in optoelectronic applications and acts as structural support in various catalytic processes (26). In a proof-of-concept study for this surface-sensitive spectroscopic technique, we probe the chemical modification of the Al₂O₃ surface with phosphonate anchoring during the formation of a self-assembling monolayer (SAM) (27).

Results

Surface NV-NMR.

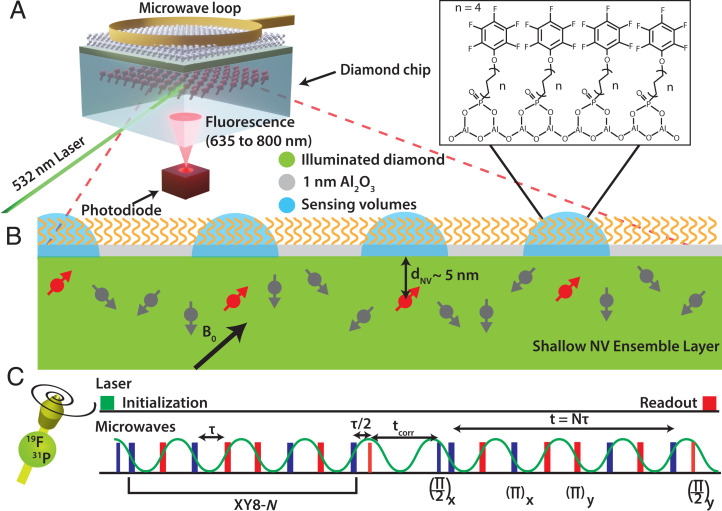
The surface NV-NMR technique is performed on a diamond chip in which ¹⁵N was implanted with a particle fluence of 2 × 10¹²/cm² and with an energy of 2.5 keV (Fig. 1A) (SI Appendix, Supplementary Notes 3 and 4), resulting in a distribution of near-surface NV centers 4.5 ± 1.9 nm below the surface (SI Appendix, Supplementary Note 5). For these implant conditions, we estimate an NV density of ∼50 to 100 NVs/µm² (28–30), corresponding to 2 to 4 × 10⁵ NV centers for the ∼4,000 µm² spot used in our experiments as shown in Fig. 2C (SI Appendix, Supplementary Note 6). These defects can have four different orientations in the tetrahedral diamond lattice; thus, one in four is aligned with the external magnetic field B₀. Consequently, an effective ensemble of ∼0.5 to 1 × 10⁵ NV centers allows for random NMR sampling of the diamond surface within the laser spot. The NMR detection volume of each NV center is determined by its depth, indicated schematically as blue hemispheres in Fig. 1B. The quantum-sensing scheme for detecting NMR signals with NV centers in diamond has been described in detail before (22, 31–33). In brief, the electronic ground state of the NV center is a spin triplet with the Zeeman states m_s = 0 and ± 1, which are separated by ∼2.87 GHz at zero magnetic field. The degenerate m_s = ± 1 states are typically split by a static external magnetic field B₀, and transitions between the Zeeman split states can be addressed by microwave fields. The spin state of the NV center can be initialized in the m_s = 0 state with laser excitation at a wavelength of 532 nm and optically read out because of spin-dependent photoluminescence (PL), which is weaker for the m_s = ± 1 states compared to the m_s = 0 state. After optical excitation, nearly all the NV spins are in the m_s = 0 state. Subsequently, transitions between the m_s = 0 and m_s = ± 1 can be coherently controlled with microwave pulses. Dynamic decoupling sequences optimized for nuclear spin noise detection (such as XY8-N) are used because synchronized pulse schemes (such as the coherently averaged synchronized readout [CASR] protocol) detects thermal NMR signals (34, 35) inefficiently. These sequences are sensitive to frequencies corresponding to 1/(2τ), where τ is the spacing between the π pulses (Fig. 1C). Sweeping the time t_corr between two XY8-N sequences correlates oscillating magnetic fields such as spin noise from the Larmor precession of nanoscale nuclear spin ensembles (measured in B_rms²). The detected spin noise appears as oscillations in the PL readout as a function of t_corr and resembles the free induction decay in traditional NMR spectroscopy. However, this nanoscale NMR spectroscopy can be performed without strong magnets due to the detection of spin noise. Notably, there is no need to excite the nuclear spins with radiofrequency pulses or to wait for nuclear spin–lattice relaxation during signal acquisition.

Fig. 1.

Surface NV-NMR spectroscopy on a functionalized metal oxide surface. (A) Scheme of the experiment. Near surface NV centers in a 2 × 2 × 0.5 mm diamond chip are excited with a 532-nm laser in a total internal reflection geometry. The resulting spin-dependent photoluminescence from the NV defects is detected with an avalanche photodiode. The microwave pulses for quantum control of the spin state of the defects are delivered through a small wire loop. (B) NV centers aligned with the magnetic field have sensing volumes with a radius determined by their distance to the surface, 4.5 ± 1.9 nm in our case. (Inset) Schematic of an organic monolayer formed from PFPDPA on 1 nm Al₂O₃ deposited on the diamond surface by ALD. (C) Correlation spectroscopy pulse sequence. Two blocks of dynamic decoupling XY8-N sequences are correlated by sweeping the time between them (t_corr). The time spacing τ between the π pulses is set to half the period of the Larmor frequency of the nuclear spin being sensed. The NV spin state is initialized with a 532-nm laser pulse, and photoluminescence detection with a photodiode occurs after the microwave pulse sequence.

Fig. 2.

Surface NV-NMR and validation with complementary analytical surface techniques. (A) Diamond coated with an Al₂O₃ layer. The thickness of the ALD-deposited Al₂O₃ layer was determined by AFM scratching measurements. The height profile along the segment indicated by a blue arrow was used to determine the Al₂O₃ film thickness of 0.9 ± 0.1 nm. (B) Functionalized Al₂O₃ surface on diamond. The presence of PFPDPA molecules on the surface is confirmed with XPS by the appearance of F 1s and P 2s peaks (blue), which are absent on the clean diamond (yellow). (C) Surface NV-NMR spectroscopy. (Top) Image of the laser spot (∼4,000 µm²) on the diamond and time domain correlation signal of ¹⁹F. (Bottom) Surface NV-NMR spectrum of ³¹P detected from the monolayer measured at 174 mT and ¹⁹F nuclei detected at 31 mT. The clean diamond reference is shown in yellow.

Characterization of the Metal Oxide Layer.

In prior works, NMR signals from samples directly on the diamond surface have been detected (22, 29). Here, the goal is to probe nondiamond surfaces and interfaces. This requires the preparation of a material of interest on top of the diamond substrate. Our proof-of-concept study uses an Al₂O₃ film prepared by ALD (36), whose surface modification with organophosphonate chemistry shall be investigated through the surface NV-NMR technique. First, we optimized the thickness of the ALD layer by keeping it as thin as possible, allowing the NV centers to sense the surface modification while also ensuring that it was thick enough to create a closed film onto which a dense molecular monolayer could be bound. The formation of the fluorinated monolayer on the Al₂O₃ surface increases the surface hydrophobicity, which can be investigated with static water contact angle (SWCA) measurements. The minimal ALD layer thickness required to facilitate the formation of a dense SAM was determined using SWCA measurements as a function of Al₂O₃ thickness from 0.5 to 3 nm. The saturation of the SWCA signal appears for ALD layers of 1 nm and beyond (SI Appendix, Supplementary Note 7), which indicated that we reached the minimal thickness required for the organic monolayer to be fully formed. The hardness of the diamond chip allows for a scratching experiment to corroborate the thickness of the Al₂O₃ layer on the diamond using atomic force microscopy (AFM) (Fig. 2A). Removing the Al₂O₃ with the AFM tip revealed two different surfaces—the Al₂O₃ with an RMS roughness of 0.71 nm and the underlying diamond with a roughness of 0.25 nm. A vertical cut showed a step height of 0.9 ± 0.1 nm, confirming the thickness expected for 10 ALD cycles (37). Second, we ensure that the material preserves the NV center properties by quantifying the coherence times before and after depositing the Al₂O₃ film on the diamond. We observe a small reduction in the spin–lattice relaxation T₁ and spin–spin relaxation T₂ times (Table 1), with only a minor influence on the NV-NMR sensitivity.

Table 1.

Influence of Al₂O₃ on NV center relaxation properties

	T2 (µs)	T1 (ms)
Clean diamond (n = 5)	5.59 ± 0.13	0.80 ± 0.28
After ALD (n = 8)	4.19 ± 0.24	0.73 ± 0.30

Chemical Characterization of the Functionalized Metal Oxide Support.

Following thickness optimization, we analyzed the chemical composition of the functionalized Al₂O₃ layer. We selected a C₁₂ chain phosphonic acid (PA) terminated with a fluorinated phenolic ring (12-Pentafluorophenoxydodecylphosphonic acid [PFPDPA]) for chemical modification of the Al₂O₃ surface. The functionalization occurs via the binding of phosphonic acid groups to the hydroxy groups of the Al₂O₃ surface. Fig. 1B illustrates the bridged bidentate-binding motif. We note, however, that multiple binding modes might be present on the surface (38). These fluorinated monolayers can be easily prepared by soaking the Al₂O₃/diamond in the PA solution. X-ray photoelectron spectroscopy (XPS) confirmed the presence of the F 1s peak and P 2s peaks from the monolayer (Fig. 2B). Corresponding spectra from the bare substrate prior to functionalization did not contain any detectable fluorine or phosphorous. Thus, the phosphorous and fluorine peaks originate from the PFPDPA molecules at the Al₂O₃ surface. The surface NV-NMR technique is capable of providing chemical information from the SAM-functionalized Al₂O₃ surface with high sensitivity, much like XPS but under ambient conditions. The ¹⁹F correlation spectroscopy data provides a time domain NMR signal (Fig. 2C), clearly showing an oscillation at the ¹⁹F Larmor frequency that decays. The Fourier transform of these data results in the ¹⁹F NMR spectrum with a resonance at 1.247 MHz, which agrees with the theoretical Larmor frequency at 31 mT (details can be found in Materials and Methods). Similarly, we can detect the ³¹P signal from the functionalized surface, which results in a peak at 3 MHz at 174 mT (SI Appendix, Supplementary Note 8). The signal is weaker since the number of spins per molecule and the gyromagnetic ratio are lower compared to ¹⁹F. Both signals were taken from the same monolayer and laser spot.

We note that other NMR-active nuclei are present in this system, most notably ²⁷Al and ¹H. However, the strong ¹³C signals naturally occurring within the diamond is likely precluding the detection of the ²⁷Al resonance in the current experiment. This can be overcome in the future by using an isotopically enriched ¹²C diamond. ¹H signal is ubiquitously observed on a clean diamond and cannot be unambiguously attributed to a characteristic of our system. Therefore, it has been excluded from the present analysis.

Probing the Spatial Homogeneity of the Phosphonate Monolayer.

The spatial resolution (Fig. 2C) is a considerable advantage of our technique which we utilized to probe the homogeneity of the phosphonate monolayer. The ¹⁹F signal from the monolayer was measured in multiple areas within the MW loop and normalized to a constant reference signal generated by an external radiofrequency source, which allows the quantification of ¹⁹F nuclei at each spot. It reveals gradient-like local differences rather than spot-by-spot differences, which may be caused by inhomogeneity in the ALD process (Fig. 3). Because of the microwave delivery, experiments can only be performed within the loop, whose position can be scanned together with the laser spot across the entire diamond. We avoid repositioning the loop because of possible scratching and damaging the SAM layer. This approach allows for correlating optical images with spatially resolved NMR signals.

Fig. 3.

Probing the homogeneity of the phosphonate monolayer. (A) Optical image of the diamond with marked measurement positions (color-coded, the laser spot for the green position is shown). The microwave loop for quantum control appears in black, the NV fluorescence of the excitation laser spot in white. (B) Normalized ¹⁹F spectra of the different positions that are indicated in A.

Detection of Molecular Dynamics at the Surface.

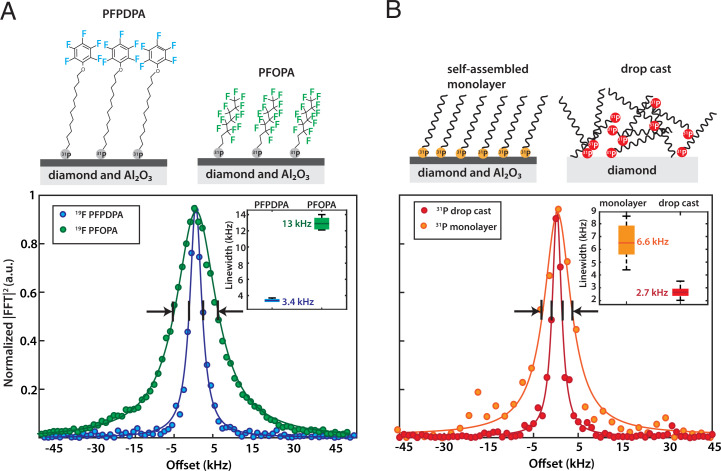
From our measurement of the PFPDPA monolayer, a resonance linewidth of ∼3 kHz was observed, which is narrower than the linewidths observed in previous NV-NMR experiments of solid samples (24). For that reason, we performed a second set of experiments in which the Al₂O₃ surface was functionalized with a shorter but perfluorinated PA molecule (1H,1H,2H,2H-peruoroctanephosphonic acid [PFOPA]) (Fig. 4A). The resonance linewidth is much broader (∼12 kHz) than for the case of the monolayer made from PFPDPA. In the solid state, the linewidth is typically limited by dipolar broadening, which can be minimized by local molecular dynamics such as rotations. The fluorinated phenolic moiety attached to a long carbon chain is more mobile than the ¹⁹F nuclei in the perfluorinated chain of PFOPA, which likely reduces the linewidth (39, 40).

Fig. 4.

Spectroscopic characterization of the SAM layer. (A) Influence of molecular structure on ¹⁹F resonance linewidth. The ¹⁹F linewidth of a monolayer made from PFOPA is approximately four times broader than that of PFPDPA. This is likely caused by local dynamics of the fluorinated phenolic moiety, which lead to line narrowing of the NMR signal. (Inset) Statistics over three experiments. The green and blue bars show one SD for the PFPDPA and PFOPA monolayers. The darker green and blue lines indicate the mean. The black lines are the minimum and maximum obtained linewidths. (B) Comparison of the ³¹P linewidth for a SAM layer (Left) and a drop cast sample (Right). The ³¹P linewidth in the case of a SAM layer is more than two times broader than that of the drop cast sample. (Inset) Statistics over eight repeated experiments. The orange and red bars show one SD for the monolayer and drop cast, respectively. The darker orange and red lines indicate the mean. The black lines are the minimum and maximum obtained linewidths.

Spectroscopic Investigation for Binding of the Phosphonate Head Group to the Al₂O₃ Surface.

Following characterization of the phosphonate monolayer, we studied the molecular interaction between the phosphonate head group and the Al₂O₃ surface. This was explored in a set of experiments in which the ³¹P resonance linewidth was measured for a monolayer and on a drop cast sample on the diamond surface. Drop casting results in a random distribution of the molecules on the diamond surface with no chemical binding to the surface. The resonance linewidth of the monolayer (∼7 kHz) is significantly broader than for the drop cast molecules (∼3 kHz) (Fig. 4B). In an additional set of experiments, we also monitored the linewidth of the ¹⁹F signal, which broadened to a much lesser extent compared to the ³¹P signal upon binding (SI Appendix, Supplementary Note 9). These results imply that the broadening effect is mainly on the phosphorus headgroup, indicating an interaction with the Al₂O₃ layer.

Quantification of the Molecular Coverage.

An advantage of the quantum-sensing detection scheme is the facile quantification of the molecular coverage. The signal size (i.e., B_rms²) is proportional to the spin density, which can be described by the following equation (41):

$$B_{\mathit{rms}}{}^2= 5\mathit{\pi }/96{\left({\mathit{\mu }}_{0}h{\gamma }_{\mathit{nuc}}/4\pi \right)}^2\mathit{\rho }\left[1/d^3{}_{NV}- 1/{\left(d_{NV}+h_{\mathit{spins}}\right)}^3\right],$$ [1]

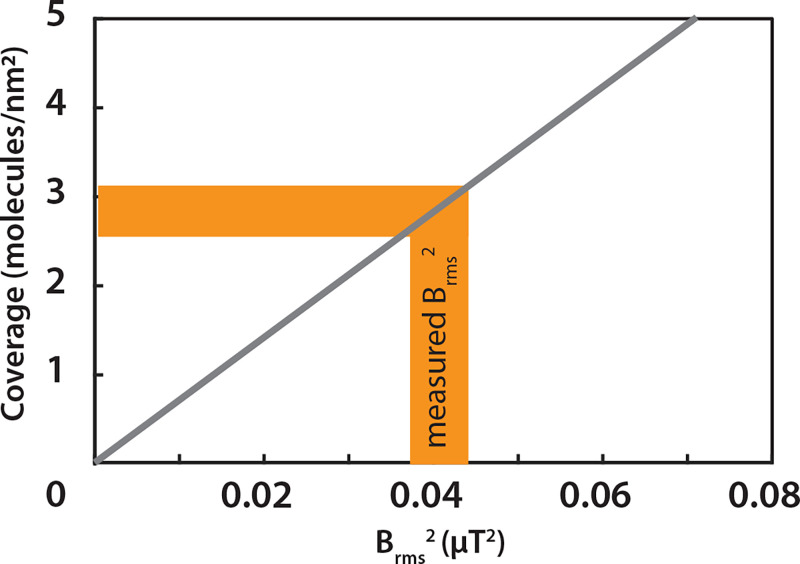
where μ_o = 4π × 10⁷m × T/A is the vacuum permeability, h = 6.626 10³⁴J × s is the Planck constant, γ is the nuclear gyromagnetic ratio in MHz/T (40.05 MHz/T for ¹⁹F), ρ is the nuclear spin density, h_spins is the thickness of the nuclear spin layer, and d_NV is the depth of the NVs. With a known NV depth distribution and defined sample geometry (SI Appendix, Supplementary Notes 6 and 10), the equation correlates the measured signals (B_rms²) to the spin density and the corresponding molecular coverage as shown in Fig. 5. With a reference signal, we calibrated our experiment and obtain 0.041 ± 0.003 μT² as the signal strength B_rms² for the monolayer ¹⁹F. This corresponds to a coverage of circa 3 molecules/nm², which is in good agreement with a dense monolayer (42).

Fig. 5.

Quantification of the molecular coverage. The gray curve shows the molecular coverage as a function of sensed fluctuating magnetic field (B_rms²). Experimentally obtained B_rms² of ∼0.04 μT² corresponds to a molecular coverage of ∼3 molecules/nm² shown in yellow shading for a monolayer.

Monitoring Surface Chemistry in Real Time.

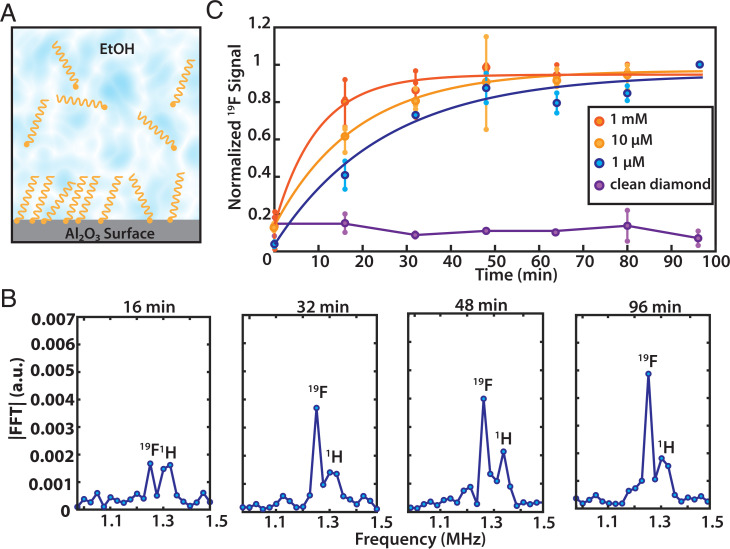
In contrast to other surface-sensitive techniques, surface NV-NMR allows for measurements under chemically relevant conditions, for example, at the solid–liquid interface. In the present case, this enables the observation of the binding of the phosphonate-anchoring group to the Al₂O₃ support at the solid/liquid interface depicted in Fig. 6A. The chemical reaction kinetics were directly detected by the addition of PFPDPA solution onto a freshly prepared Al₂O₃ layer on a diamond and measurement of the surface NV-NMR signal as a function of time. Fig. 6B shows individual surface NV-NMR spectra at different times after adding the PFPDPA solution. The ¹⁹F resonance signal grows on a time scale of tens of minutes and plateaus after approximately half an hour. The broad resonance at 1.325 MHz next to the ¹⁹F signal originates from ¹H, which is present from the beginning and is not characteristic of the surface chemistry. We repeated the experiment using solutions of different concentrations of the PFPDPA displaying an increase in the monolayer formation rate at higher concentration (Fig. 6C). The kinetics of the ¹⁹F signal can be modeled with an exponential growth function (SI Appendix, Supplementary Note 11) (43–45). As a reference, we repeated the experiment with a clean diamond without an Al₂O₃ layer. In this case, we did not observe a signal at the expected ¹⁹F resonance, which indicates that the monolayer is inefficiently formed on diamond surfaces.

Fig. 6.

Probing surface chemistry in situ. (A) Schematic of monolayer formation on Al₂O₃ in PA solution. (B) Individual spectra of ¹⁹F showing the time evolution for a 1-µM solution. The peak around 1.35 MHz can be assigned to protons (¹H) which are known to be ubiquitous on or within the diamond and are not characteristic of the surface chemistry. (C) Real-time monitoring of the ¹⁹F NMR signal amplitude growth in solution for three different PA concentrations shows a decrease in formation rate for lower concentrations. Small markers are measured data points of repeated experiments connected with a vertical line, averaged data are shown with the large points. Data points are fitted with a single exponential. Background signal of a clean, non-Al₂O₃–coated diamond in a 10-µM PA solution shows no ¹⁹F signal. Note that due to the absolute value of the Fourier transformation, the noise floor is always positive.

Discussion

The surface NV-NMR technique has been successfully demonstrated to detect microscopic NMR signals down to submonolayer coverages, by observing real-time formation of molecular monolayer assembly on Al₂O₃. The use of a diamond-based sensor that is chemically inert and can withstand high temperatures and high pressures is advantageous, especially for chemical applications and catalysis. It will not only bridge the “pressure gap” in surface science but has the resilience to probe chemical reactions even under harsh conditions in situ (3). Although this study used ALD-deposited Al₂O₃ thin films, this technique is not limited to this material. A variety of surfaces or thin films and its associated processes can be investigated ranging from lipid bilayers (46), two-dimensional (2D) materials (25), to metal organic frameworks and covalent organic frameworks as electrocatalysts in the form of thin films on conductive substrates (47).

Nevertheless, the technique is still in its infancy and has many possible avenues for improvement. The main challenge is the lack of molecular structural information due to dipolar broadening in the solid state that causes resonance linewidths on the order of a few kilohertz. Such a problem is well known in the field of solid-state NMR and has been solved by spinning the sample at the magic angle. Such a solution may be adopted for NV-NMR too, although with significant engineering challenges (48). Alternatives are decoupling pulse sequences, which reduce sensitivity and cannot fully recover high-resolution spectra (24). In order to resolve chemical shifts, the magnetic field B₀ must be increased up to ∼1 Tesla, which is feasible but technically demanding due to Q-band microwave electronics. Another approach is to utilize quadrupolar nuclei such as ¹⁴N, ²D, etc., which have been shown to convey detailed structural information despite their broad lines, making them ideal targets for surface NV-NMR at low fields (40).

Although the sensitivity did not limit this study, future analysis with faster temporal resolution of reaction kinetics or the detection of nuclei with low gyromagnetic ratios would benefit from further improvement. Advanced NV generation techniques (49, 50) or the growth of preferentially orientated NV centers (51) can significantly improve the sensitivity. Additionally, an improved readout scheme of the NV quantum state has been shown to increase the sensitivity for single NV centers over an order of magnitude (17). Finally, it should be noted that NV centers are strongly influenced by magnetic noise. Consequently, paramagnetic samples will deteriorate the NV coherence times and preclude surface NV-NMR studies of this type. However, other quantum-sensing schemes are available to study these types of materials (52).

In summary, the results from this study demonstrate the use of NV centers in a surface-sensitive and spatially resolved magnetic resonance technique for probing the chemical composition, binding to surfaces, and quantifying molecular coverage. Moreover, it can monitor chemical reactions in real time at the solid–liquid interface. In contrast to other surface analysis techniques, signals can be detected under chemically relevant conditions quantitatively in a low-cost experimental setup (31). We are convinced that this presented technique will facilitate further understanding and probing of a variety of surface phenomena and materials. Not only does this method offer the noninvasive benefit of NMR spectroscopy but its functionality under chemically relevant conditions and low technical complexity also makes it a practical and sensitive technique for advanced studies in important areas of catalysis, materials science, biological sensing, or 2D materials research.

Materials and Methods

Diamond Preparation.

An electronic grade diamond (natural ¹³C abundance, Element Six) was implanted with ¹⁵N at an energy of 2.5 keV with an off-axis tilt of 7° and with a fluence of 2 × 10¹²/cm² by Innovion. Then, the implanted sample was annealed under vacuum in a home-built oven for over 32 h (SI Appendix, Fig. S1) with a Tectra BORALECTRIC sample heater. The diamond was cleaned before every Al₂O₃ deposition with a triacid cleaning protocol involving equal parts boiling sulfuric, nitric, and perchloric acid according to Brown et al. (53).

Atomic Layer Deposition.

ALD was performed using a Veeco Fiji G2 system. Prior to deposition, the diamond surface was cleaned in situ by 5× 0.15 s cycles of ozone, which was generated via electrical discharge in O₂. For the deposition of Al₂O₃ thin films, the ozone-treated diamond substrates were sequentially exposed to trimethyl aluminum (TMA) (98-1955, STREM Chemicals) followed by H₂O at 200 °C cyclically. Each ALD cycle followed the sequence: TMA pulse/Ar purge/H₂O pulse/Ar purge. This was repeated for 10 cycles to achieve a final thickness of ∼1 nm (nominal growth per cycle of 0.1 nm/cycle). To achieve a reproducible surface hydroxyl surface termination suitable for monolayer assembly by phosphonate chemistry, the sample was exposed to a remote oxygen plasma within the ALD system. In particular, the radiofrequency (13.64 MHz) inductively coupled plasma source of the Fiji G2 system was operated at 300 W for a total of 1 min exposure. For repeated use of diamond substrates, the Al₂O₃ was removed by soaking overnight in a 5% NaOH solution (SI Appendix, Supplementary Note 12) before the next ALD deposition.

Phosphonic Acid Surface Functionalization.

For the fully formed monolayer shown in Figs. 2–4, the following procedure was used. After the ALD process, the diamond is immersed in a 10 mM solution of either 12-pentafluorophenoxydodecylphosphonic acid (CAS number 1049677–16-8, Sigma-Aldrich) or 1H,1H,2H,2H-Perfluorooctanephosphonic acid (CAS number 252237–40-4, Sigma-Aldrich) for 2 d to allow the monolayer formation to equilibrate. Then, the diamond is sonicated for 5 min in ethanol to remove all physisorbed molecules, after which the sample was dried with flowing nitrogen.

Surface NV-NMR Setup.

The experiment is based on a modified version of the setup described in Bucher et al. (31). The diamond was positioned in the middle of two neodymium magnets, which were rotated and tilted for alignment of the B₀ field with one of the four possible NV center orientations. For quantum control of the NV centers, microwave frequencies were generated with a signal source (SynthHD, Windfreak Technologies, LLC.) and fed into a phase shifter (ZX10Q-2–27-S+, Mini-Circuits) and two switches (ZASWA-2–50dRA+, Mini-Circuits) to generate X and Y pulses and then combined (ZX10-2–442-s+, Mini-Circuits) and amplified by a microwave amplifier (ZHL-16W-72+, Mini-Circuits). The initialization of the NV ensemble was achieved by using a 532-nm laser (Verdi G5, Coherent) at a power of around 200 mW at the diamond. The laser pulses were controlled by an acousto-optic modulator (Gooch and Housego, model 3260–220) with pulse durations of 5 µs. The diamond was glued to a thin glass slide (48393026, VWR). In order to increase the light collection efficiency, a 6-mm glass hemisphere (TECHSPEC N-BK7 Half-Ball Lenses, Edmund Optics) was glued to the other side of the cover slide. This assembly was then taped to a 30-mm cage plate (CP4S, Thorlabs) and mounted onto the experiment 1.2 cm above the top condenser lens (ACL25416U-B, Thorlabs). This coupled in the focused laser (LA1986-A-M, Thorlabs) in a total internal reflection geometry. The photoluminescence (PL) was collected and collimated by two condenser lenses, the bottom one placed right above a large area avalanche photodiode (ACUBE-S3000-10, Laser Components GmbH) below the diamond. The excitation wavelength was removed from the PL light with a long-pass filter (Edge Basic 647 Long Wave Pass, Semrock) placed immediately between the bottom condenser lens and the photodiode. The photo voltage was digitized with a data acquisition unit (USB-6229 DAQ, National Instruments). The electron spin resonance frequency measured from the dip in PL was used to determine the magnetic field strength and the NV resonance frequency to perform a Rabi experiment, which then determined the π and π/2 pulse durations for the correlation spectroscopy pulse sequences (Fig. 1C). The correlation spectroscopy sequence has the highest performance for sensing frequencies between ∼1 to 4 MHz, limited by 1) the T₂ relaxation time of the NVs and 2) finite π pulse durations. For that reason, we chose to work at 31 mT for ¹⁹F (∼1.3 MHz) and at 174 mT for ³¹P (∼3 MHz). The magnetic field strength B₀ can be adjusted by changing the distance between the magnets.

Surface NV-NMR and Sensitivity Estimate.

Correlation spectroscopy was performed using XY8-4 blocks (a total of 32 π pulses) with t_corr swept starting from 2 µs to obtain the spectra. For ¹⁹F detection, t_corr was swept until 160 µs in 801 points. The time domain data were then Fourier transformed and the absolute value plotted using MATLAB. Each spectrum shown in Fig. 2C is zero filled with 801 points. For the ¹⁹F signal shown in Fig. 2C, we obtain an SNR of 95 as calculated by dividing the signal value by the SD of the noise floor within a region without signal. For our laser spot area of 4,000 µm² and a monolayer coverage of 15 ¹⁹F spins/nm², we obtain for 6 × 10¹⁰ (100 femtomoles) ¹⁹F spins an SNR of 2.5 after 1 s integration. For ³¹P detection, t_corr was swept until 80 µs in 801 points. The ³¹P signal was averaged twice to obtain an SNR of 15. The ¹⁹F and ³¹P NMR signals were obtained in 25 and 32 min, respectively.

For linewidth measurements as shown in Fig. 4 A and B, each monolayer ³¹P signal was measured to 2,501 points, and t_corr swept to 0.25 ms, and each spectrum averaged 10 times (20 h) and zero filled to 5,001 points. For each drop cast measurement, the ³¹P signal was measured to 5,001 points, and t_corr swept to 0.5 ms and zero filled to 10,001 points. The ¹⁹F signals for the linewidths were measured to 2,501 points, t_corr swept to 0.5 ms and zero filled to 5,001 points (45 min). After zero filling, each fast Fourier transform (FFT) power spectrum (|FFT|²) is plotted, and the linewidth of the resonance is fit with a Lorentzian model (34).

For the homogeneity study, the t_corr was swept until 160 µs in 801 points again to obtain the ¹⁹F signal with only one average (25 min). For the 1-MHz reference signal the t_corr was swept until 80 µs in 401 points.

Imaging of Diamond and Laser Spot.

The laser spots for the homogeneity study shown in Fig. 3 were imaged using a Basler a2A1920-160umBAS camera. The signal was normalized with a 1-MHz reference signal generated with an arbitrary waveform generator (DG 1032, Rigol), amplified (LZY-22+, Mini-Circuits), and then delivered through a wound coil fixed close to the diamond. The t_corr was swept until 80 µs in 401 points to obtain the reference signal. The described procedure was manually performed as a proof of principle but can be converted to a systematic scan of the surface by simply motorizing the optics with standard piezo components to obtain microscale control of the laser spot position.

Determining the Molecular Coverage.

To simulate spin noise, we use an oscillating magnetic field with tunable strength. This signal is generated with an arbitrary waveform generator (DG 1032, Rigol) and amplified (LZY-22+, Mini-Circuits) and then delivered through a large wound coil fixed close to the diamond. The NMR signal from the monolayer can be calibrated by comparing it to this reference signal to determine the B_rms² (54). A simple model was set up to quantify the molecular coverage of the SAM layer from the signal size measured in the experiments. The alkyl chain length l_mol = 1.5 nm was added to the NV depth d_NV, and h_spins = 0.5 nm was considered to be the thickness of the layer with nuclear spins (fluorinated benzene ring). The sensed fluctuating magnetic field (B_rms²) corresponding to different nuclear spin densities was calculated applying Eq. 1 and the value weighted according to a Gaussian probability function utilizing d_NV = 4.5 nm and σ_NV = 1.9 nm as mean and SD. These values were obtained from the SRIM simulation as reported in SI Appendix, Supplementary Note 6 (55). The nuclear spin density ρ was multiplied by the thickness of the spin layer h_spins, converting it to a coverage (spins/nm²), and then divided by the number of fluorine spins in each molecule, obtaining the final molecular coverage as in the curve reported in Fig. 5.

In Situ Kinetics of Monolayer Formation.

The triacid-cleaned diamond was first coated with 1 nm Al₂O₃ and activated with oxygen plasma as described in Atomic Layer Deposition. Subsequently, the diamond was glued down to a watertight liquid sample holder made from a 30-mm cage plate (CP4S, Thorlabs) with a thin round cover slide (100493678, VWR) glued to the bottom and the top fitted with a threaded lens tube (SM30L03, Thorlabs). The cage plate was then mounted to the surface NV-NMR experiment. ¹⁹F is detected with 24 time traces, which were continuously acquired by sweeping t_corr to 40 µs with 201 points. Each data point in Fig. 6B was an average of four time traces, which were then Fourier transformed and the ¹⁹F signal amplitude plotted, resulting in six points for the kinetic dataset. Each of these experiments are repeated three times (1 mM, 10 µM) and two times (1 µM), and the signal amplitudes are averaged and then fit. Each time trace is normalized to 1 for the time point at 96 min. The first point at t = 0 min is set to the mean of the noise floor of the Fourier-transformed spectra. The background signal is the value at the ¹⁹F frequency within spectra obtained with a clean diamond measured in the intermediate concentration 10-µM solution. As there is no ¹⁹F, the background data are normalized to the final ¹⁹F signal of a 10-µM growth kinetics data set.

Static Water Contact Angle Measurements.

SWCA measurements were performed on an OCA 15Pro contact angle system (DataPhysics Instruments). Data acquisition and evaluation were realized with SWCA 20—contact angle (DataPhysics Instruments, version 2.0). For quantifying an average Young’s contact angle (θγ), 2 µL deionized H₂O (18.2 M Ωcm at 25 °C, Merck Millipore) was dispensed with a rate of 0.2 µLs⁻¹ from a 500-µL Hamilton syringe onto the sample surface. After allowing the droplet to settle for ∼3 s, an image was acquired for further processing. The procedure was repeated at least three times on different spots on the surface, and the SD was calculated.

Atomic Force Microscopy.

A MultiMode 8 (Bruker Corp.) was used in tapping mode and in contact mode under ambient conditions using NSG30 (TipsNano) for standard characterization and to estimate the Al₂O₃ layer thickness. Scratching in contact mode was performed over areas of 1 × 1 µm² with a deflection set point of 5 V. Amplitude modulation (tapping mode) AFM was done with an amplitude set point of 0.3 V (at a free amplitude of 0.5 V). The surface roughness was evaluated via the RMS average of height deviations taken from the mean image data plane of 2 × 2 µm² tapping mode micrographs. The roughness and step heights were analyzed using Gwyddion 2.56.

X-ray Photoelectron Spectroscopy.

XPS measurements were performed with an Axis Supra (Kratos) spectrometer. The monochromatized Al K_α (1486.9 eV) X-ray tube source was operated at an emission current of 15 mA. The data were recorded with a circular acceptance area of Al source, and the analyzed area was 700 × 300 µm in diameter. Spectra were processed with CasaXPS (Casa Software Ltd, version 2.3.17).

Data Availability

Raw data have been deposited in Zenodo (https://zenodo.org/record/5836776#.Yd1cmS-B1QI). All other study data are included in the article and/or SI Appendix.