On Training Deep 3D CNN Models with Dependent Samples in Neuroimaging

Abstract

There is much interest in developing algorithms based on 3D convolutional neural networks (CNNs) for performing regression and classification with brain imaging data and more generally, with biomedical imaging data. A standard assumption in learning is that the training samples are independently drawn from the underlying distribution. In computer vision, where we have millions of training examples, this assumption is violated but the empirical performance may remain satisfactory. But in many biomedical studies with just a few hundred training examples, one often has multiple samples per participant and/or data may be curated by pooling datasets from a few different institutions. Here, the violation of the independent samples assumption turns out to be more significant, especially in small-to-medium sized datasets. Motivated by this need, we show how 3D CNNs can be modified to deal with dependent samples. We show that even with standard 3D CNNs, there is value in augmenting the network to exploit information regarding dependent samples. We present empirical results for predicting cognitive trajectories (slope and intercept) from morphometric change images derived from multiple time points. With terms which encode dependency between samples in the model, we get consistent improvements over a strong baseline which ignores such knowledge.

1. Introduction

The use of machine learning methods to perform classification or regression tasks with brain imaging data, in the last decade or so, has demonstrated that the clinical manifestation of various diseases such as Alzheimer’s disease (AD) and Parkinson’s disease (PD) can be reliably identified and predictive features obtained from such models are consistent with scientific hypotheses based on post-mortem studies [8]. In the last five years, following the broad adoption of convolutional neural networks for learning tasks in vision, we have seen the deployment of such architectures for brain imaging data as well [7]. While the diagnosis of various diseases using brain images remains important within brain image analysis, many scientific questions such as understanding brain development, evaluating normal aging trends or assessing the course of disease progression requires moving beyond cross-sectional analysis [17]. In other words, instead of one scan per participant, answering a number of key questions involves studies that need multiple scans per person. While sometimes, the setting may be longitudinal (gap between scans is 1–2 years), in other cases, the temporal relation between the scans may not be important. What is relevant, however, is that when each subject in a study provides more than one scan (or sample), the samples are no longer i.i.d. – instead, scans from each person are dependent.

Consider a simple regression task using brain imaging data, motivated by applications in Alzheimer’s disease (AD) research. Let us assume that structural magnetic resonance (MR) images are the predictor variables $\mathcal{X}$. In AD research, cognitive trends are an important outcome variable. So, the slope and intercept (calculated over multiple years) of an appropriate measure of cognition, say the Auditory Verbal Learning Test (AVLT) [14], can be the response variable $\mathcal{Y}$. This is a simple regression model which seeks to estimate $f:\mathit{x}\in {\mathbf{R}}^p\to \mathit{y}\in {\mathbf{R}}^2$, where x denotes the brain image and y is the multi-valued response: AVLT cognition intercept together with its slope over multiple years. The task of estimating the parameters that map the independent variable $x\in \mathcal{X}$ to the dependent variables $y\in \mathcal{Y}$ can be approached via deep methods. If one were to use recent deep learning advances, one choice could be convolutional neural networks.

Notice that most regression models in vision and machine learning, including standard CNNs, assume that the samples are independent and identically distributed (i.i.d.). This usually allows a relatively simple model derivation that does not need to take the dependency between the samples into account. We know how to analyze the behavior of such models and tractable inference schemes are also available. Under the i.i.d assumption, standard regression techniques have one model for a dataset which maps all the samples in the same way. These models are called fixed effects models [18]. For instance, a linear regression as well as non-linear (or deep) regression models involve a set of fixed coefficients for the full set of examples. However, in the applications with dependent measurements, the i.i.d. assumption does not hold and fixed effects models are often suboptimal. For instance, longitudinal data or any study with multiple samples for a subject involve data that are dependent and affected by certain subject-specific terms. This is called a random effect. In such situations, to accurately model global trends, the random effects should be properly utilized.

Dependent samples in regression are modeled using mixed effects models [18]. Mixed effects models handle the fixed effects and random effects by explicitly leveraging the “group” (dependent samples) information to handle the inherent non-independence in the data. Many brain imaging studies have repeated measurements and non-independence with a hierarchical structure of data. We know that CNNs have been shown to be highly effective in a variety of medical imaging problems [2]. But CNNs for non-i.i.d samples are far less explored. This paper studies how CNNs can be modified to incorporate terms that account for dependent samples, motivated by neuroimaging applications.

The main goal of our work is to use random effects within 3D convolutional neural networks, and use this 3D CNN model to predict cognitive performance on multiple brain image scans per subject with visual interpretation. Our main contributions are: 1) We use random effects within 3D convolutional neural networks (RE-CNN) built on inverted residual blocks. 2) We show that our proposed RE-CNN works well for brain imaging datasets with dependent samples and outperforms a strong baseline (which does not incorporate random effects) by significant margins. 3) We provide a module for visual interpretation of voxels that are relevant for the prediction task. Experiments suggest that regions identified are consistent with existing hypotheses (i.e., cognitive performance affected by gross brain atrophy).

Related work:

Various approaches have been proposed to analyze repeated measurements. A model with RE-EM tree was presented in [15] to combine mixed effects models for longitudinal and clustered data with the flexibility of tree-based estimation methods. In [6], mixed-effects random forest was developed to analyze clustered data consisting of individuals nested within groups. Riemannian nonlinear mixed effects models are developed in [9] for longitudinal brain data analysis. In [1], non-linear mixed effects statistical model was proposed to estimate alteration of the shape of the hippocampus during the course of Alzheimer’s disease. Separately, visual interpretation methods are developed to help understand and indicate the spatial attention of convolutional neural network when making predictions. [20] shows that the visualization genuinely corresponds to the image structure that stimulates that feature map by performing occlusion sensitivity. [16] proposed the visualization of deep convolutional neural network based on computing the gradient of the class score with respect to the input image. In [5], a perturbation scheme was developed to find where highly complicated neural networks look in an image for evidence. Class Activation Mapping (CAM) in [21] is developed to visualize the linear combination of a late layer’s activation and class-specific weights.

2. Preliminaries

In this section, we briefly review the basic concepts and properties of linear mixed-effects models and nonlinear mixed-effects model to setup the rest of our presentation for AVLT cognition prediction. For simplicity, we introduce models with a univariate response variable (also called labels or dependent variable).

Fixed effect models can be considered as a linear or non-linear global model. An example for fixed effect models is a standard linear regression model,

$$y={\mathit{x}}^T\mathit{\beta }+ϵ,ϵ~\mathcal{N}(0,\mathit{\Sigma })$$ (1)

where y ∈ R is the response, $\mathit{x}={[1,x_1,x_2,\dots ,x_p]}^T\in {\mathbf{R}}^{p+1}$ are the covariates, $\mathit{\beta }={[{\beta }_0,\dots ,{\beta }_p]}^T\in {\mathbf{R}}^{p+1}$ are fixed effects coefficients shared over all subjects.

Mixed effect models explicitly incorporates subject information by introducing a set of parameters for each subject (or group) to yield subject-specific adjustments. Recall that AVLT cognition prediction for AD research is a function fitting problem, mapping a single input brain image to AVLT cognition. We observe from (1) that all subjects have the exactly same estimation function to map an input 3D brain image to AVLT cognition output and the noise permitted in the estimation function also comes from a distribution identical to every subject. However, with multiple measurements from each subject, these 3D brain image scans are not independent and each subject may have a slightly different estimation function. Therefore, our goal is to use fixed effects for a global model but also incorporate random effects for flexible specific-subject adjustments, yielding slightly different mapping function of AVLT cognition prediction. By adding random effects to (1) for each participant, the linear mixed effects (LME) model can be written as,

$$y={\mathit{x}}^T\mathit{\beta }+{\mathbf{z}}^T{\mathbf{b}}_i+{ϵ}_i,{\mathbf{b}}_i~\mathcal{N}(0,\mathit{D})\text{and}{ϵ}_i~\mathcal{N}(0,{\mathit{\Sigma }}_{{ϵ}_i}),i=1,2,\dots ,N$$ (2)

where N is the number of subjects, $\mathit{\beta }=[{\beta }_0,\dots ,{\beta }_p]\in {\mathbf{R}}^{p+1}$ are the fixed effects (population parameters) shared over the entire population and ${\mathbf{b}}_i=[b_0^i,\dots ,b_q^i]\in {\mathbf{R}}^{q+1}$ are the subject-specific random effects (individual parameters) for i^th subject for subject-specific adjustment, x and z are the associated fixed effects and random effects covariates, D and ${\mathit{\Sigma }}_{{ϵ}_i},i=1,2,\dots ,N$, are the variance components of linear mixed effects model, ϵ_i is the measurement error, drawn from a subject-specific unknown zero mean Gaussian distribution with covariance structure, $\mathcal{N}(0,{\mathit{\Sigma }}_{{ϵ}_i})$, for dealing with the non-i.i.d. nature. When covariance matrices, D and ${\mathit{\Sigma }}_{{ϵ}_i}$, are unknown, no closed form solution for estimation of fixed and random effects is available and EM algorithms are proposed for estimation [18].

Nonlinear mixed effects models (NLME) [18] is a generalization of a LME model. Given a nonlinear link function η, the NLME model is,

$$y=\eta (\mathit{x},\mathit{\beta },\mathbf{z},{\mathbf{b}}_i)+{ϵ}_i,{\mathbf{b}}_i~\mathcal{N}(0,\mathit{D}),{ϵ}_i~\mathcal{N}(0,{\mathit{\Sigma }}_{{ϵ}_i}),i=1,2,\dots ,N$$ (3)

where β are fixed effects vector and b_i are random effects vector for i^th subject.

3. Random effects 3D Convolutional Neural Networks

Linear mixed effects model assumes a linear parametric form, and sometimes, this assumption might be too restrictive. Assuming a linear model may not be the best option when the parametric form is unknown. Further, when the number of covariates are large (e.g., 3D brain image), including all of the attributes may lead to overfitting and poor predictions. Therefore, we generalize linear mixed effects model to nonlinear mixed effects model using convolutional neural networks: we will learn the mapping from the input 3D brain image to AVLT cognition intercept and slope while being cognizant to individual level differences of the subjects, denoted as random effects 3D convolutional neural network (RE-CNN). The cognition slope and intercept may be provided for each sample, or may be the same for all samples for a participant. To specify nonlinear mixed effects models, we write the model as a sum of fixed and random components,

$$\eta =f_{\text{fix}}(\mathit{x},\mathit{\beta })+f_{\text{rnd}}(\mathbf{z},{\mathbf{b}}_i)$$ (4)

where f_fix is a nonlinear link function for fixed effects and f_random is a nonlinear link function for random effects. Generalized from the random intercept and random slope model [4], individually varying subject-specific intercept and slope, we define our nonlinear mixed effects model as

$$\eta =h(\mathit{x})\mathit{\beta }+h(\mathit{x}){\mathbf{b}}_i$$ (5)

where h is a nonlinear link function, h(x)β represents the fixed component and h(x)b_i represents the random component. Here, (5) can be considered in the following way: we apply a nonlinear transformation h(·) first and then learn the fixed effects and random effects on top of the output features from h.

3.1. Architecture of RE-CNN

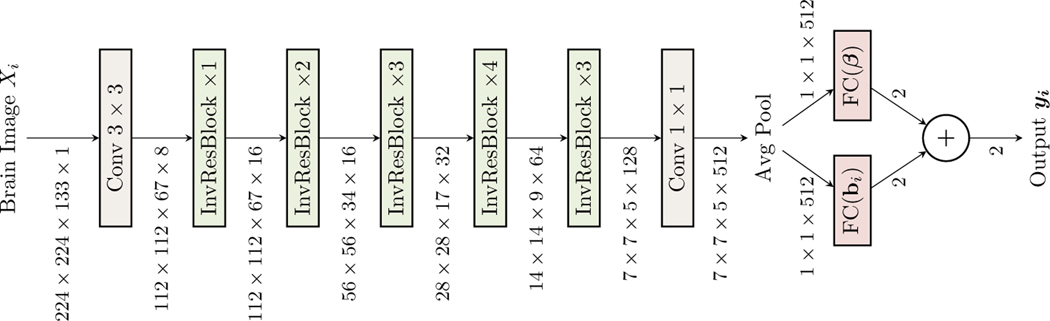
Our model is based on the efficient MobileNetV2 architecture and a sequence of inverted residual blocks, to represent nonlinear transformation h. To predict AVLT cognition prediction from 3D brain images, our model uses an adapted 3D MobileNetV2 architecture (see Fig 1) for h, followed by a linear mixed regression loss after average pooling (Avg Pool).

Fig. 1:

An overview of 3D convolutional neural network structure incorporating linear mixed effects model, RE-CNN. InvResBlock denotes adapted 3D inverted residual block from 2D MobileNetV2 and it can be seen in Fig 2. InvResBlock ×1/2/3/4 means the number of repeated layers within InvResBlock. The output of average pooling is denoted as h(x), which is the input for the mixed effects models, f_fix(x) = h(x)β for fixed effects estimation and f_random = h(x)b_i is for random effects estimation. The output of the network is a 2D vector, the sum of fixed effects estimation and random effects estimation.

RE-CNN can be viewed as a linear mixed effects regression for AVLT cognition prediction on the average pooling layer, h(·), output from 3D MobileNetV2. In Fig 1, we can see that the top network learns the nonlinear fixed effects component, h(·)β, and the bottom network learns the nonlinear random component, h(·)b_i. Therefore, learning the nonlinear mixed effects model (see (4)) represented by RE-CNN (see Fig 1) can be considered as an optimization where we train the network with the loss,

$$\underset{f_{\text{fix}},f_{\text{rnd}}}{\min }\sum _{\mathit{x}}\mathit{loss}(y,f_{\text{fix}}(\mathit{x})+f_{\text{rnd}}(\mathit{x}))=\sum _{\mathit{x}}{\Vert y-f_{\text{fix}}(\mathit{x})-f_{\text{rnd}}(\mathit{x})\Vert }^2,$$ (6)

where $f_{\text{fix}}(\mathit{x})=h(\mathit{x})\mathit{\beta }\text{and}{f}_{\text{rnd}}(\mathit{x})=h(\mathit{x}){\mathbf{b}}_i$

3.2. Parameter estimation of RE-CNN

Given N subjects, each subject with $n_i\left({\sum }_{i=1}^N{n}_i=n\right)$ observations, our goal is to estimate the parameters of our nonlinear mixed effects regression model.

$$\begin{gathered} {\mathit{y}}_i=h({\mathit{X}}_i)\mathit{\beta }+h({\mathit{X}}_i){\mathbf{b}}_i+{\mathit{ϵ}}_i, \\ {\mathbf{b}}_i~\mathcal{N}(0,\mathit{D})\text{and}{\mathit{ϵ}}_i~\mathcal{N}(0,{\mathit{\Sigma }}_{{\mathit{ϵ}}_i}),i=1,2,\dots ,N \end{gathered}$$ (7)

where ${\mathit{y}}_i={[y_{i1},\dots ,y_{i{n}_i}]}^T$ is a n_i × 1 vector of observations of the i^th subject, ${\mathit{X}}_i={[{\mathit{x}}_{i1},\dots ,{\mathit{x}}_{i{n}_i}]}^T$ is a n_i × p covariates matrix, $h({\mathit{X}}_i)={[h({\mathit{x}}_{i1}),\dots ,h({\mathit{x}}_{i{n}_i})]}^T$, and ${\mathit{ϵ}}_i={[{ϵ}_{(i1)},\dots ,{ϵ}_{(i{n}_i)}]}^T$ is a n_i × 1 measurements error vector.

When the variance components of (7), D and ${\mathit{\Sigma }}_{{\mathit{ϵ}}_i},i=1,2,\dots ,N$, and the nonlinear transformation, h, are known, the estimates of fixed effects parameters β and random effects parameters b_i, i = 1,2,...,N can be solved by minimizing the following generalized log-likelihood loss function [18],

$$\begin{gathered} loss(\mathit{\beta },{\mathbf{b}}_i|\mathit{y})=\sum _{i=1}^N[{({\mathit{y}}_i-h({\mathit{X}}_i)\mathit{\beta }-h({\mathit{X}}_i){\mathbf{b}}_i)}^T{\mathit{\Sigma }}_{{\mathit{ϵ}}_i}^{-1} \\ ({\mathit{y}}_i-h({\mathit{X}}_i)\mathit{\beta }-h({\mathit{X}}_i){\mathbf{b}}_i)+{\mathbf{b}}_i^T{\mathit{D}}^{-1}{\mathbf{b}}_i+\log |\mathit{D}|+\log |{\mathit{\Sigma }}_{{\mathit{ϵ}}_i}|] \end{gathered}$$ (8)

The minimization of the loss in (8) can be performed by solving the so-called mixed model equation [13] with known D, ${\mathit{\Sigma }}_{{\mathit{ϵ}}_i}$ and h,

$$\left[\begin{array}{cc}h{(\mathit{X})}^T{\mathit{\Sigma }}_{\mathit{ϵ}}^{-1}h(\mathit{X})& h{(\mathit{X})}^T{\mathit{\Sigma }}_{\mathit{ϵ}}^{-1}h(\mathit{X})\\ h{(\mathit{X})}^T{\mathit{\Sigma }}_{\mathit{ϵ}}^{-1}h(\mathit{X})& h{(\mathit{X})}^T{\mathit{\Sigma }}_{\mathit{ϵ}}^{-1}h(\mathit{X})+{\mathit{D}}_c^{-1}\end{array}\right]\left[\begin{array}{l}\mathit{\beta }\hfill \\ \mathbf{b}\hfill \end{array}\right]=\left[\begin{array}{l}h{(\mathit{X})}^T{\mathit{\Sigma }}_{\mathit{ϵ}}^{-1}\mathit{y}\hfill \\ h{(\mathit{X})}^T{\mathit{\Sigma }}_{\mathit{ϵ}}^{-1}\mathit{y}\hfill \end{array}\right].$$ (9)

where $\mathit{y}={[{\mathit{y}}_1^T,\cdots ,{\mathit{y}}_N^T]}^T$, $h(\mathit{X})={[h{({\mathit{X}}_1)}^T,\cdots ,h{({\mathit{X}}_N)}^T]}^T$, $\mathbf{b}={[{\mathbf{b}}_1^T,\cdots ,{\mathbf{b}}_N^T]}^T$, ${\mathit{D}}_c=\mathit{diag}(\mathit{D},\cdots ,\mathit{D}),{\mathit{\Sigma }}_{\mathit{ϵ}}=\mathit{diag}({\mathit{\Sigma }}_{{\mathit{ϵ}}_1},\cdots ,{\mathit{\Sigma }}_{{\mathit{ϵ}}_N})$.

Since the covariance matrices, D and ${\mathit{\Sigma }}_{{ϵ}_i},i=1,\cdots ,N$, are unknown, we need to estimate them for solving (9). Similar to [18], we maximize the following log-likelihood function for estimating these matrices,

$$\log \mathbf{L}\left({\mathit{D}}_c,{\mathit{\Sigma }}_{\mathit{ϵ}}|\mathit{y}\right)=-\frac{1}{2}[n\log 2\pi -\log |\mathit{V}|-{(\mathit{y}-h(\mathit{X})\mathit{\beta })}^T{\mathbf{V}}^{-1}(\mathit{y}-h(\mathit{X})\mathit{\beta })]$$ (10)

where ${\mathit{V}}_i=h({\mathit{X}}_i)\mathit{D}h{({\mathit{X}}_i)}^T+{\mathit{\Sigma }}_{{\mathit{ϵ}}_i},i=1,\cdots ,N\text{and}\mathit{V}=\mathit{diag}({\mathit{V}}_1,\cdots ,{\mathit{V}}_N)$.

Based on (9) and (10), the last step in parameter estimation for our model (7) is to estimate the nonlinear transformation h, represented by a 3D MobileNetV2 (see Fig. 1). Stochastic gradient algorithm (SGD) is a popular scheme to optimize neural networks. We thus directly apply SGD for training h.

When the covariance matrices are replaced by the current available values, their updated values can be obtained by (9) and (10). Therefore, we use an EM algorithm for parameter estimation for our RE-CNN, denoted as RE-EM. Assume ${\mathit{\Sigma }}_{{ϵ}_i}={\sigma }^2{I}_{n_i},i=1,\cdots ,N$. Let t index the number of iterations and ${\widehat{\mathit{\beta }}}^{\{t\}},{\widehat{\mathbf{b}}}_i^{\{t\}},h^{\{t\}},{\widehat{\sigma }}^{2\{t\}}$ and ${\widehat{\mathit{D}}}^{\{t\}}$ be the estimates of β, b_i, h σ² and D at t^th iteration. The major update equations in our RE-EM procedure are,

1. Solving (9),

   $$\begin{gathered} {\widehat{\mathbf{b}}}_i^{\{t\}}={\widehat{\mathit{D}}}^{\{t-1\}}{\widehat{h}}^{\{t\}}{({\mathit{X}}_i)}^T{\widehat{\mathit{V}}}_i^{-1\{t-1\}}({\mathit{y}}_i-{\widehat{h}}^{\{t\}}({\mathit{X}}_i){\widehat{\mathit{\beta }}}^{\{t\}}) \\ {\widehat{\mathit{ϵ}}}_i^{\{t\}}={\mathit{y}}_i-h^{\{t\}}({\mathit{X}}_i){\widehat{\mathit{\beta }}}^{\{t\}}-h^{\{t\}}({\mathit{X}}_i){\widehat{\mathbf{b}}}_i^{\{t\}} \end{gathered}$$ (11)

   where ${\widehat{\mathit{V}}}_i^{\{t-1\}}=h^{\{t\}}({\mathit{X}}_i){\widehat{\mathit{D}}}^{\{t-1\}}{h}^{\{t\}}{({\mathit{X}}_i)}^T+{\widehat{\sigma }}^{2\{t-1\}}{I}_{n_i}$.
2. Solving (10),

   $$\begin{gathered} {\widehat{\sigma }}^{2\{t\}}=\frac{1}{n}\sum _{i=1}^N\left[{\widehat{\mathit{ϵ}}}_i^{T\{t\}}{\widehat{\mathit{ϵ}}}_i^{\{t\}}+{\widehat{\sigma }}^{2\{t-1\}}(n_i-{\widehat{\sigma }}^{2\{t-1\}}\mathrm{trace}({\widehat{\mathit{V}}}_i^{\{t-1\}}))\right] \\ {\widehat{\mathit{D}}}^{\mathit{\left\{}t\mathit{\right\}}}=\frac{1}{N}\sum _{i=1}^N[{\widehat{\mathbf{b}}}_i^{\mathit{\left\{}t\mathit{\right\}}}{\widehat{\mathbf{b}}}_i^{T\mathit{\left\{}t\mathit{\right\}}}+({\widehat{\mathit{D}}}^{\mathit{\{}t-1\mathit{\}}}-{\widehat{\mathit{D}}}^{\mathit{\{}t-1\mathit{\}}}{\widehat{h}}^{\mathit{\left\{}t\mathit{\right\}}}{({\mathit{X}}_i)}^T{\widehat{\mathit{V}}}_i^{-1\mathit{\{}t-1\mathit{\}}}{\widehat{h}}^{\mathit{\left\{}t\mathit{\right\}}}({\mathit{X}}_i){\widehat{\mathit{D}}}^{\mathit{\{}t-1\mathit{\}}})] \end{gathered}$$ (12)

Then, the RE-EM algorithm for our regression task can be written formally in Algorithm 1. When the training of Algorithm 1 has been completed, we can fix h and learn a fully connected layer, g, based on the hidden representation of h to approximate ${\widehat{f}}_{\text{rnd}}(\mathit{x})$ only based on input 3D brain image without knowing the subject “id” for cognition measures estimate (AVLT slope or intercept).

4. Experiments

In this section, we discuss the task of predicting AVLT cognition prediction (intercept and slope) using brain images and evaluate the effectiveness of our RE-CNN model. First, we briefly review a representation that measures local morphometric changes of brains over time for each subject. Using this representation as input, we compare our model with various schemes and evaluate generalization power on unseen subjects. Further, we demonstrate how to interpret the learned model showing activation maps in the image space by a visual explanation approach [21], which allows identifying brain regions that are correlated with cognitive trajectories.

Algorithm 1.

Parameters estimation of RE-CNN for AVLT cognition prediction

0:	procedure RE-CNN Training
1:	#iter t = 0, Let ${\widehat{\mathbf{b}}}_{\text{i}}^{\{\text{0}\}}\text{=0},{\widehat{\sigma }}^{\text{2}\{\text{0}\}}\text{=1},{\widehat{\mathit{D}}}^{\{\text{0}\}}\text{=}{I}_p$, and denote ${\mathit{X}}_i,i=1,\cdots ,N$, the input 3D brain samples for training RE-CNN.
3:	Update ${\widehat{\mathbf{b}}}_i^{\{t\}}$ and ${\widehat{\mathit{ϵ}}}_i^{\{t\}}$ using expressions 11.
4:	Update variance ${\widehat{\sigma }}^{2\{t\}}$ and ${\widehat{\mathit{D}}}^{\{t\}}$ using expressions 12.
5:	Repeating steps 2, 3, and 4 until convergence.
5:	procedure RE-CNN AVLT cognition Prediction
6:	For an input 3D brain scan, x, taking the sum of corresponding fixed part RE-CNN AVLT cognition prediction and predicted random part RE-CNN AVLT cognition prediction, $\widehat{h}(\mathit{x})\widehat{\beta }+\widehat{g}(\widehat{h}(\mathit{x}))$

4.1. RE-CNN on longitudinal CDT images for cognition prediction

Our model uses longitudinal brain images and cognitive scores. In our experiments, morphometric change maps are used as input to the network architecture – these maps are obtained using multiple registration steps.

Morphometric change maps (given by determinant of Cauchy Deformation Tensor) brain images are subject-specific warps derived from a longitudinal neuroimaging study. In this paper, they are derived from a preclinical Alzheimer’s disease (AD) cohort at Wisconsin. The longitudinal warps (or deformations) are with-in subject registrations of T₁-weighted images between two consecutive time points, ${\Phi }_{i,j}:{\mathcal{I}}_{i,j}\to {\mathcal{I}}_{i,j+1}$. At each voxel, a CDT Det is a determinant of Cauchy-Deformation Tensor derived from the spatial derivatives $\nabla {\Phi }_{i,j}(vox)$ of the deformation field, i.e., $det(\sqrt{\nabla {\Phi }_{i,j}{(vox)}^T\nabla {\Phi }_{i,j}(vox)})$. For downstream analysis, CDT calculation should be spatio-temporally unbiased and registered in a common coordinate system for voxel-wise analysis. Our pipeline is as follows. First, we estimate an unbiased global template space. Following [9], we estimate a temporally unbiased subject-specific average for each subject and then use the averages to generate the global template space. The averages are obtained by Advanced Normalization Tools (ANTS) [3]. Within-subject deformations (longitudinal changes) are transported to the global template space by the parallel transport of stationary velocity fields (SVFs) by Lorenzi and Pennec [11], Specifically, all brain images are registered in the global template space by a rigid transformation and then nonlinear symmetric diffeomorphic deformations are obtained by [10]. Thus brain images registered pairwise between two consecutive time points lead to a SVF, representing a longitudinal morphometric change between visits i + 1 and i. In our cohort, 88 subjects had at least three visits (CDT Dets brain image computed from scans at two time points, see Fig 3) and a total of 202 samples (CDT Det images) are generated. Some subjects had two visits whereas a few had four visits.

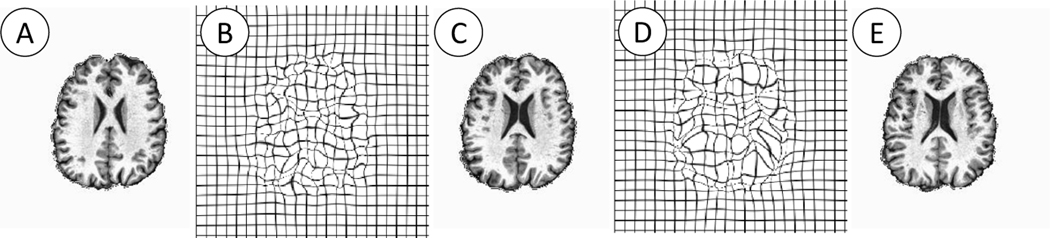
Fig. 3:

Examples of input brain images and warps in AVLT cognition prediction. (A, C, E) the brain images are collected at three time points for one participant. (B) Warped spatial grid to move (A) to (C), (D) Warped spatial grid to move (C) to (E). Our CDT Det features are derived from the Jacobian of the deformations (C, E).

RE-CNN on longitudinal CDT Dets

We now discuss how to use morphometric change maps (multiple images per subject) to predict cognition slope and intercept, i.e., subjects’ multiple morphometric maps → their cognition intercept and slope. Here $x_{ij}\in {\mathbf{R}}^{H\times W\times C}$ represents the CDT determinant brain image between two consecutive visits of each subject and $y_{ij}\in {\mathbf{R}}^2$. Given the small sample size, we split the data with 8 subjects/split and perform 11-fold cross validation. Then, Alg. 1 is used for training RE-CNN. Table 1 summarizes the comparisons of our RE-CNN and other baseline methods. Our model achieved the lowest root mean squared error. It shows that even if the subject id (group information) is not available at test time, our method leads to a more accurate fixed effects model by controlling for random effects during training. Our model performs better against a standard 3D CNN architecture for cognition slope and intercept prediction.

Table 1:

Comparison of RE-CNN and other baseline methods for AVLT cognition slope and intercept prediction. Our approach offers the smallest Root Mean Squared Error (RMSE) and the highest Pearson correlation score between AVLT cognition intercept and the predicted cognition intercept > 0.6 and the highest Pearson correlation score between AVLT cognition slope and the predicted cognition slope > 0.6. It means our model predicts more accurately than other baselines. Surprisingly, without any group information at test time, RE-CNN achieves better results than standard 3D CNNs that are not trained with group information. Even only using fixed effects part of RE-CNN, RE-CNN_fix performs better than standard 3D CNN. It empirically shows that modeling random effects during training using group information may help learn better fixed effects models and leads to better generalization on unseen subjects.

Method	RE-CNN	RE-CNNfix	3D CNN	GPR[12]	SVR
RMSE	2.7	2.9	3.1	4.8	5.2

4.2. Visual Interpretation of RE-CNN on Brain Image

In this subsection, we describe our methods for explaining the predictions of RE-CNN in detail and then visually check heatmaps generated by a visual explanation method. There are two major ways to explain the predictions of 2D deep convolutional neural network. One scheme applies perturbations to data and conducts sensitivity analysis. Another strategy is to use architectural properties of CNNs to heuristically track the attention of convolutional neural networks. We extend 2D visual explanation methods [5,21] to 3D visual explanation.

Sensitivity analysis methods suffer from the problem that each time we only get an output change for one voxel, which makes this extremely computationally intensive for a brain image of size 224 × 224 × 133. To avoid the issues of one-at-a-time sensitivity analysis, we focus on a method based on the architectural properties of our 3D CNN, visualizing the activation map of convolutional layers directly when predictions are made [21,19]. We extend 2D activation mapping to 3D using the idea that the last convolution layer of the CNN contains spatial information indicating discriminative regions for making prediction. Thus, the activation mapping creates a spatial heatmap out of the activations from the last convolutional layer for visualizing discriminative parts. Assume we are given a 3D CNN, e.g., RE-CNN, and one brain image V and denote $f_u(x,y,z)$ to be the activation of unit u in the last convolutional layer at location (x, y, z). The global average pooling for unit u is $G_u=\frac{1}{N}\sum _{x,y,z}{f}_u(x,y,z)$, where N is the number of voxels in the corresponding convolutional layer. Notice that our RE-CNN is trained for regressing on AVLT cognition intercept and slope and the global average pooling layer is directly connected to the output layer, we extend the AVLT cognition intercept score as,

$$\text{Score}(\text{INT})=\sum _u{w}_u^{\text{INT}}{G}_u=\frac{1}{N}\sum _{x,y,z}\sum _u{w}_u^{\text{INT}}{f}_u(x,y,z)$$ (13)

where ${\sum }_u{w}_u^{\text{INT}}{f}_u(x,y,z)$ is defined for every spatial location (x,y,z) and their sum is proportional to the AVLT cognition intercept score. With the intercept score, we define our regression activation mapping (RAM) for AVLT cognition intercept as ${\text{sRAM}}_{x,y,z}(\text{INT})=|{\sum }_u{w}_u^{\text{INT}}{f}_u(x,y,z)|$, where $|\cdot |$ is the absolute value. The activation mapping for AVLT cognition intercept can be taken as a heatmap of weighted sum of activations in every location (x,y,z) and can be computed by one forward pass given one brain image. Similarly, we can define the regression activation mapping (RAM) for AVLT cognition slope as ${\text{RAM}}_{x,y,z}(\text{SLOPE})=|{\sum }_u{w}_u^{\text{SLOPE}}{f}_u(x,y,z)|$. The regression activation mapping (RAM) for AVLT total cognition can be defined as,

$${\text{RAM}}_{x,y,z}(\text{TOT})=|\sum _u\left(w_u^{\text{INT}}+w_u^{\text{SLOPE}}\right)f_u(x,y,z)|$$ (14)

Our goal is to obtain visual explanations for highlighting brain regions important for cognition prediction. In our experiments, we take the morphometric change brain images from the test set for visual explanation/interpretation analysis and generate the heatmap from the horizontal, sagittal, and coronal sections. We present the highlighted regions which indicate that overall brain atrophy is associated with cognitive slope and intercept. The regression activation mapping heatmaps of RE-CNN are presented in Figure 4.

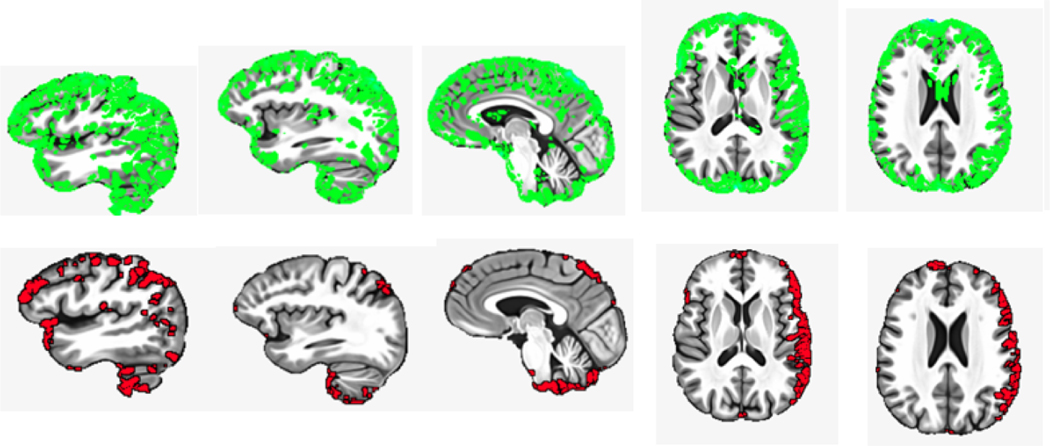
Fig. 4:

Visual explanation heatmaps of brain images. RE-CNN takes CDT Dets images to associate the morphometric change of brain images with AVLT cognition scores. The regions which have relatively large morphometric change are highlighted in grean in Row 1. The red highlights in Row 2 represent the activation map learned RE-CNN computed by RAM visual approach. Its activation shows the relevant regions for predicting AVLT cognition slope and intercept for each subject.

5. Conclusion

This paper proposes a 3D convolutional neural network that is able to handle dependent brain imaging data (multiple samples per subject) for predicting cognitive measures. By respecting the dependencies, we present a 3D MobileNetV2 based architecture with random effects terms, RE-CNN, to exploit the representation power of 3D CNNs but systematically deal with dependencies in the samples. We develop a RE-EM algorithm for parameter estimation. Experimentally, our RE-CNN achieves promising results. We applied visual explanations to interpret the learned RE-CNN model by assessing regression activation maps, which allows identifying brain regions that are associated with cognition in this observational study focused on better understanding Alzheimer’s disease (AD).

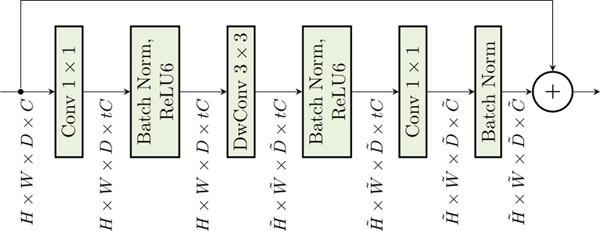
Fig. 2:

The 3D inverted residual block is adapted from 2D inverted residual block of MobileNetV2. Similarly, if the output resolution of the block differs from the input resolution, the residual connection of the block is skipped.