SUMMARY
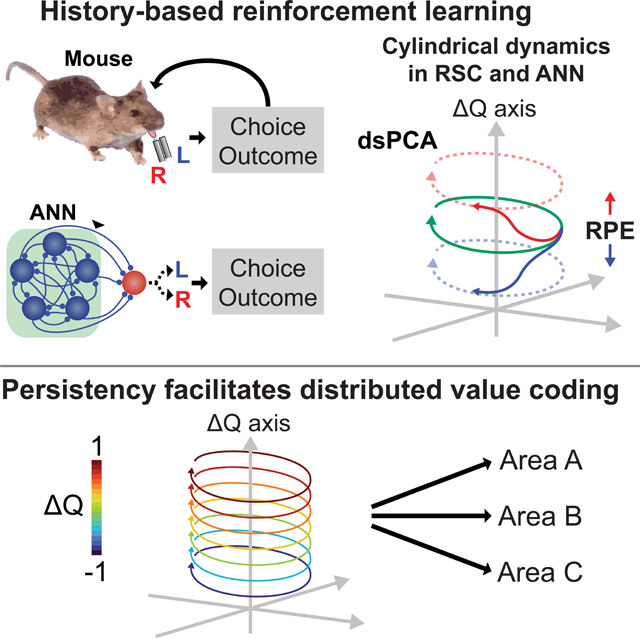
Task-related information is widely distributed across the brain with different coding properties, such as persistency. We found in mice that coding persistency of action history and value was variable across areas, learning phases, and task context, with the highest persistency in the retrosplenial cortex of expert mice performing value-based decisions where history needs to be maintained across trials. Persistent coding also emerged in artificial networks trained to perform mouse-like reinforcement learning. Persistency allows temporally untangled value representations in neuronal manifolds where population activity exhibits cyclic trajectories that transition along the value axis after action outcomes, collectively forming cylindrical dynamics. Simulations indicated that untangled persistency facilitates robust value retrieval by downstream networks. Even leakage of persistently maintained value through non-specific connectivity could contribute to the brain-wide distributed value coding with different levels of persistency. These results reveal that context-dependent untangled persistency facilitates reliable signal coding and its distribution across the brain.
eTOC blurb
Hattori et al. showed that highly persistent value coding emerges in the mouse retrosplenial cortex and artificial recurrent neural network in a learning- and context-dependent manner. Persistency ensures untangled value representations in neural population dynamics and facilitates distributed value coding across the brain, highlighting the benefits of persistent coding.
Graphical Abstract
INTRODUCTION
The parallel distributed processing (PDP) theory (McClelland et al., 1986; Rogers and McClelland, 2014; Rumelhart et al., 1986) highlights computational advantages of distributed information coding in neural networks and has had a profound impact on our understanding of cognition and deep learning. Growing evidence revealed that information coding in the brain is highly distributed across neurons and distinct brain areas (Allen et al., 2019; Hattori et al., 2019; Koay et al., 2020; Musall et al., 2019; Steinmetz et al., 2019; Stringer et al., 2019). Even neurons in the primary sensory cortex, which were classically thought to process only sensory information of a single modality, have been found to encode diverse information such as other sensory modalities (Hattori and Hensch, 2017; Hattori et al., 2017; Iurilli et al., 2012), spontaneous movements (Musall et al., 2019; Stringer et al., 2019), actions (Hattori et al., 2019; Koay et al., 2020; Steinmetz et al., 2019), reward (Hattori et al., 2019; Koay et al., 2020), event history (Hattori et al., 2019; Koay et al., 2020), and value (Hattori et al., 2019; Serences, 2008). Although these signals are widely distributed, activity perturbations of a brain area typically affect only a subset of behavioral outputs that are associated with the information encoded in the area. These results suggest that, although information coding is highly distributed, not all of the information represented in neural activity may be used in each area.
A clue to understand the utility of encoded information may lie in the temporal dynamics of the information coding. In working memory tasks where information is maintained for several seconds in a trial, information can be maintained as either persistent neural activity or sequential transient activity across a neural population that tiles the memory period (Cavanagh et al., 2018; Fuster and Alexander, 1971; Masse et al., 2019; Miller et al., 1996; Murray et al., 2017; Orhan and Ma, 2019; Romo et al., 1999; Zhu et al., 2020). Recently, it was shown that certain brain areas in mice such as the retrosplenial cortex (RSC) (Hattori et al., 2019) and the medial prefrontal cortex (Bari et al., 2019) encode action values with exceptional persistency during history-dependent value-based decision making tasks where values need to be stably maintained across trials. Inactivation of either area impaired the ability to use the action value for their decision making. These results suggest that persistent value coding is critical for animals to exploit value for decision making when the value needs to be maintained for extended periods of time. Similar persistent coding is prevalent across the brain and species, ranging from coding of motor planning (Guo et al., 2017; Inagaki et al., 2019; Li et al., 2016), internal states (Allen et al., 2019; Marques et al., 2020) to emotions (Jung et al., 2020; Kennedy et al., 2020), yet the computational advantages of persistent coding has not been fully established quantitatively.
Here we investigated the neural dynamics of action history and value coding in 6 areas of the mouse cortex and artificial recurrent neural network (RNN) agents to understand the computational advantages of persistent coding and its impact on distributed coding.
RESULTS
Learning- and context-dependence of coding persistency across cortical areas
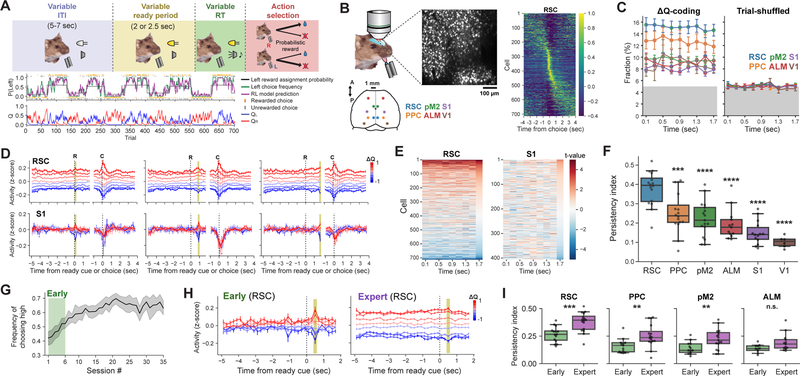
We first used the neural activity data recorded in mice performing decision making based on history-dependent action value we reported previously (Hattori et al., 2019). Each trial consisted of a ready period, an answer period, and an inter-trial-interval (ITI). The duration of each period was variable from trial to trial, making the task more naturalistic than a fixed temporal sequence (Figure 1A). During the ready period (LED cue), mice needed to withhold licking to enter the answer period. This ensured that the neural activity during the ready period was free of licking-related motor activity. Mice were allowed to freely choose either left or right lickport after a go cue tone. Different reward probabilities were assigned to the 2 lickports, and the reward probabilities changed every 60–80 trials without cue. Therefore, mice were encouraged to dynamically estimate the underlying reward probabilities of the 2 options on a trial-by-trial basis by forming subjective action values based on their recent choice outcome history using reinforcement learning (RL) (Sutton and Barto, 2018). The action values need to be stably maintained within each trial and updated after each trial based on the action and its outcome. Neural activity was collected with in vivo 2-photon calcium imaging from transgenic mice that express GCaMP6s (Chen et al., 2013) in excitatory neurons (Wekselblatt et al., 2016) (Figure 1B), and the calcium signals were converted to estimated spike rates by non-negative deconvolution (Friedrich et al., 2017; Pachitariu et al., 2018). The recording data were from 6 cortical areas including 2 association (RSC: retrosplenial; PPC: posterior parietal), 2 premotor (pM2: posterior secondary motor; ALM: anterior-lateral motor), and 2 primary sensory (S1: primary somatosensory; V1: primary visual) cortex. We estimated the 2 action values on each trial (QL and QR) by fitting a RL model to the choices of mice, and we focused our analyses on the neural coding of the policy value (ΔQ = QL - QR: the value difference between the 2 actions) on which animals rely their decision making.
Figure 1. Persistency of action value coding across mouse cortex is area- and learning-dependent.
(A) Schematic of the value-based decision task and an example expert behavior.
(B) Neural activity was recorded from 6 cortical areas. The heatmap is the trial-averaged z-scored deconvolved activity of an example RSC population. The activity of each neuron was normalized to its peak. A half of the recorded trials were used to sort cells by the peak time, and the mean activity of the other half are shown.
(C) Fractions of cells with significant ΔQ coding during ready period based on the mean activity within each of the non-overlapping 200 ms bins (Regression, P < 0.05, 2-sided t-test). The fractions with filled circles are significantly above the chance fraction of 5% (P < 0.05, one-sided t-test). ΔQ values were shuffled across trials for the right panel.
(D) Activity of ΔQ coding neurons that were identified at different time windows (yellow shadings) for example RSC and S1 populations. Trials were binned according to the ΔQ of each trial, and the activity in each trial bin was averaged.
(E) t-values for ΔQ coding at each time bin of ready period for example populations of RSC and S1 (Regression). Neurons were sorted based on the t-values at the last time bin.
(F) ΔQ coding persistency of each population as quantified by the persistency index (0: chance persistency, 1: maximum-possible persistency, Methods, ***P < 0.001, ****P < 0.0001, one-way ANOVA with Tukey’s HSD).
(G) Fraction of trials when mice chose the side with higher reward assignment probability across training sessions (n = 9 mice, mean ± CI). The first 6 sessions were treated as early sessions.
(H) Activity of ΔQ coding RSC neurons that were identified from the activity within the specified time bin (yellow shadings) in early and late sessions (same RSC population between the 2 sessions) indicating an increase in persistency during learning.
(I) ΔQ coding persistency of each population as quantified by the persistency index for early and expert sessions (**P < 0.01, ***P < 0.001, mixed effects model with population as the fixed intercept).
All error bars are s.e.m.
Regression analysis of the activity of individual neurons at different time bins within the ready period identified significant fractions of neurons that encode ΔQ in all 6 areas, with the highest fraction in RSC (Figure 1C). ΔQ coding in these neurons was independent of upcoming choice directions (Figure S1), and reliably updated at single-trial resolution (Figure S2), indicating that these neurons faithfully encoded ΔQ on a trial-by-trial basis across all 6 areas. Despite the widespread ΔQ coding, the temporal stability of ΔQ coding within the ready period differed across areas. Only in RSC, the ΔQ-coding neurons identified at different time bins reliably encoded ΔQ throughout the trial and across trials, while the encoding was temporally unstable in the other 5 areas (Figure 1D and S1H). This was because the way individual neurons encoded ΔQ across time differed across areas (Figure 1E and S1I). We quantified the temporal stability of ΔQ coding by defining the persistency index which reflects the coding persistency relative to the chance level (Methods). The analysis revealed RSC as the area with the highest ΔQ coding persistency (Figure 1F).
We next examined whether the coding persistency is a fixed property of individual areas or changes with learning. We analyzed the population activity from RSC, PPC, pM2 and ALM during early stages of training (< 1 week from training start, Figure 1G). We compared their value coding persistency between early and expert sessions. We found that the ΔQ coding persistency significantly increases in RSC, PPC and pM2 during training (Figure 1H–I), indicating that coding persistency can change during task learning.
The coding persistency may have increased during learning because the value-based decision task requires stable value maintenance for an extended period of time across trials. Therefore, we tested whether coding persistency differs in another task that does not require long maintenance of value. We trained 9 mice in the alternate choice task in which a reward was given when mice made a choice that was the opposite to the previous action (Figure 2A). Thus, the correct action depended only on the immediately preceding trial, in contrast to the value task in which history from multiple past trials was informative. All other task conditions were identical between the 2 tasks. camk2-tTA::tetO-GCaMP6s transgenic mice were trained in the alternate choice task for at least 2 weeks to achieve a plateau-level performance (~80% correct) (Figure 2B). We then performed 2-photon calcium imaging of 8,524 RSC cells, 3,186 PPC cells, 7,915 pM2 cells and 4,911 ALM cells (RSC: 14 populations, 608.9 ± 18.1 cells, PPC: 7 populations, 455.1 ± 25.1 cells, pM2: 14 populations, 565.4 ± 34.6 cells, ALM: 10 populations, 491.1 ± 36.8 cells, mean ± s.e.m per population). The coding persistency of action history in the alternate choice task was significantly weaker than in value-based task for the 4 imaged areas (Figure 2C, D). These results indicate that the coding persistency in the cortex is context-dependent.
Figure 2. Persistency of history coding is task-dependent.
(A) Schematic of the alternate choice task. The choice opposite to the choice in the previous trial was rewarded regardless of reward outcome in the previous trial.
(B) Fraction of trials of correctly choosing the side with reward across training sessions (n = 9 mice, mean ± 95% CI).
(C) Activity of RSC neurons that significantly encoded the action history from previous trial in alternate choice task and value-based decision task. These neurons were identified using the activity within the specified time bin (yellow shadings). The activity of the identified action history coding neurons was separately averaged according to the choice on the previous trial.
(D) Persistency of action history coding in each population as quantified by the persistency index for the alternate choice task (Alt) and the value-based decision task (Value) (*P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001, mixed effects model with population as the fixed intercept).
Persistent value coding in RSC forms cylindrical dynamics
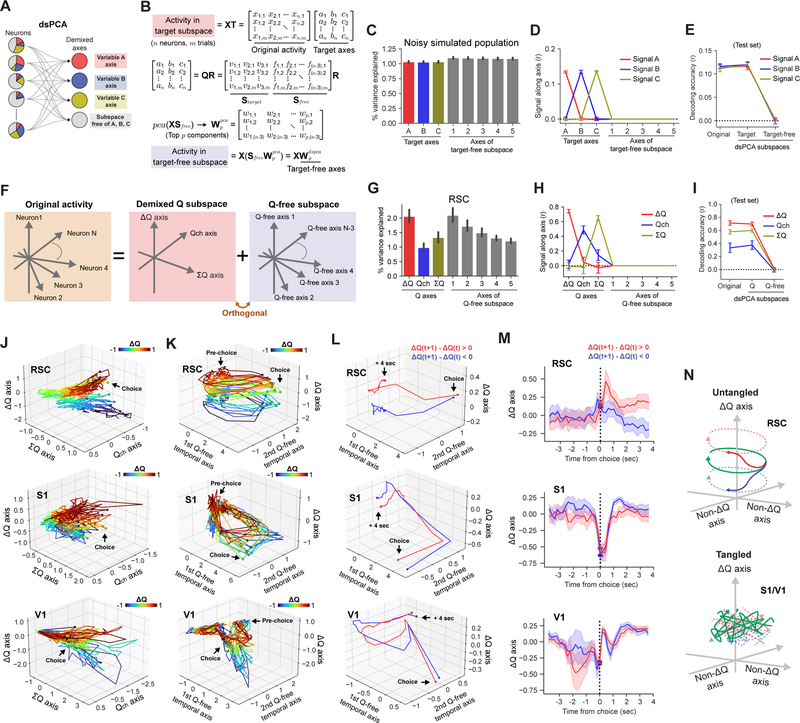
In the value-based task, ΔQ coding in RSC is temporally stable within each trial. However, this does not necessarily mean that RSC population activity is static during these periods. In fact, individual neurons in RSC showed heterogeneous and rather dynamic activity patterns (Figure 1B). To investigate how the coding of different information temporally interacts, we sought to decompose population activity into the demixed neural subspaces where different task-related signals are separated into distinct dimensions. Specifically, we sought to define 3 demixed axes each encoding ΔQ, Qch (value of selected action, e.g. QL on left choice trial), or ΣQ (sum of 2 values), and the remaining Q-free subspace that retains all the activity variance that is not explained by the 3 Q-related axes. A previous study reported demixed principal component analysis (dPCA) (Kobak et al., 2016) as a method to decompose population activity into demixed target-dependent and independent dimensions. However, dPCA is only designed to identify dimensions for discrete variables and cannot be applied for continuous variables such as Q-related signals. In addition, dPCA splits each targeted signal into multiple linear axes, which makes the signal interpretation difficult. To overcome these limitations, we developed a novel dimensionality reduction method that is more generally applicable, which we term demixed subspace principal component analysis (dsPCA) (Figure 3A). dsPCA identifies demixed dimensions for targeted signals and dimensions for target-independent activity, similarly to dPCA. However, unlike dPCA, it groups each of the target signals along a single linear coding dimension and can identify such dimensions for both discrete and continuous target variables. The first step of dsPCA identifies the best demixed linear axes for the target variables using a regression-based approach, similarly to (Mante et al., 2013). This step involves fitting a multiple linear regression model of the form x(trail) = βAA(trail) + βBB(trail) + βCC(trail) to the activity of individual neurons for the targeted variables, A, B and C. The regression coefficients, βA, β𝐵 and βC are the partial derivatives of the neural activity by each target variable, and the vectors that consist of the coefficients from all neurons are the linearly demixed coding directions of the neural population for the 3 targeted variables. We defined the targeted coding axes as the unit vectors of these coding directions. By definition, these demixed coding vectors capture all linear information of targeted variables in a population. Next, dsPCA identifies the remaining target-free subspace that is orthogonal to these targeted axes and captures all the remaining activity variance. The target-free orthogonal subspace is identified by performing full QR decomposition of the matrix with the coding axis vectors. Then the axes of the target-free subspace are further realigned based on the principal components of the activity within the target-free subspace to define axes that contain large fractions of remaining variance. (Figure 3B). Therefore, dsPCA can be viewed as a general extension of PCA by combining the regression-based supervised target axis identifications and the PCA-based unsupervised dimensionality reduction of the target-free population dynamics.
Figure 3. dsPCA reveals cylindrical dynamics with untangled value representation in RSC.
(A) dsPCA decomposes the activity of a population of individual neurons that exhibit mixed selectivity for multiple variables into demixed dimensions and the remaining subspace that is free of the targeted signals.
(B) Matrix operations to identify the target-free axes. Full QR decomposition of a matrix with target axes (T) identifies a set of basis vectors that spans the target-free subspace (Sfree). These target-free axes are realigned based on the principal component vectors (, matrix with top p PCA loadings) of the activity in the target-free subspace. The target-free axes in the original n-dimensional space are the columns of .
(C) Fraction of activity variance along each target axis and the top 5 PC axes from the target-free subspace. dsPCA was performed on noisy simulated data with target signals A, B, and C (10 repeated simulations). The amount of variance is similar between the 5 target-free axes because only Gaussian noise remained in the target-free subspace.
(D) Signals A, B, and C along each dimension identified with dsPCA for the simulated data. Pearson correlations between the projected activity and each signal are shown.
(E) Decoding accuracy of target signals from original population activity, activity in the target subspace (3 dimensions), and activity in the target-free subspace (n-3 dimensions). 50,000 and 10,000 trials for training and test sets.
(F) We applied dsPCA to decompose the original population activity into the demixed Q subspace that consists of ΔQ, Qch, and ΣQ dimensions, and the Q-free subspace which is orthogonal to the Q subspace.
(G) Fraction of activity variance along each Q-related axis and the top 5 PC axes from the Q-free subspace for RSC populations. Unlike simulated data (C), the amount of variance between axes of the Q-free subspace differ, indicating that non-targeted correlated signals exist in the Q-free subspace.
(H) Q-related signals along each dsPCA dimension for RSC populations. Pearson correlations between the projected activity and each signal are shown.
(I) Decoding accuracy of Q signals from the original RSC population activity, activity in the Q subspace (3 dimensions), and activity in the target-free subspace.
(J-K) Example RSC, S1, and V1 population activity dynamics in neuronal manifolds where ΔQ axis is paired with Qch and ΣQ axes (J), or axes that reflect major within-trial temporal activity variance of Q-free subspace (K). dsPCA was applied on the activity between −2 and −1 sec from choice, and the activity between ±4 sec from choice was projected onto the identified axes. Circles indicate the choice time. Projected activity was temporally downsampled to non-overlapping 200 ms bins.
(L) Activity state transitions along ΔQ axis according to the updated action values in RSC, whereas S1 and V1 activity draw complex trajectories that lead to tangling in the geometry. Post-action selection trajectory was separately averaged according to the sign of ΔQ update.
(M) Activity state transitions in (L) shown along the ΔQ axis.
(N) Population activity in RSC forms cylindrical dynamics where within-trial cyclic dynamics can transition along ΔQ axis across trials according to the RPE, while in the other areas ΔQ representation is tangled.
All error bars are 95% CI.
We evaluated the demixing performance of dsPCA using noisy simulated neural populations (200 neurons / population with Gaussian noise) where graded signals A, B and C are linearly encoded in 20% of the neurons. Each target signal was uniquely encoded only along the single, target axis (Figure 3C–D), and linear decoders failed to decode any A, B and C signals in the remaining target-free subspace (Figure 3E). We next applied dsPCA on the cortical population activity time-averaged over the ready period to identify demixed coding axes for ΔQ, Qch, and ΣQ, and the remaining, Q-free subspace (Figure 3F). For all 6 areas, most of the targeted information was confined to each of the coding axes, and the remaining subspace completely lacked any of the targeted information even though this subspace contained the highest activity variance (Figure 3G–I, and S3). Although we detected some Qch signal along the ΣQ axis (Figures 3H and S3B), this is expected because Qch is a component of ΣQ (ΣQ = Qch + unchosen Q). However, note that ΣQ signal is not detectable along the Qch axis, indicating that the demixing of activity variance worked correctly. Thus, dsPCA successfully identified demixed coding axes for Q-related variables and the remaining Q-free subspace.
With dsPCA, we examined how ΔQ coding temporally interacts with other dynamics. The activity dynamics around the choices (between ±4 sec from the choice) was visualized in the neuronal manifold consisting of the ΔQ coding axis and the other value-related axes (Figure 3J), or the manifold consisting of the ΔQ coding axis and 2 largest temporal activity variance axes within the Q-free subspace (Figures 3K). We found in both manifolds that activity trajectories in RSC from trials with different ΔQ values do not cross with each other across time. In the manifold with the largest temporal dynamics (Figures 3K, S4 and S5), RSC population remained in the initial positions linearly segregated along ΔQ axis according to ΔQ of the trial (‘Pre-choice’ in the figures). Around the go cue time, the RSC population diverged from these initial positions and drew rotational dynamics. After a choice, the population returned towards the initial positions following a circular geometry. The return geometry was warped along ΔQ axis, reflecting the reward prediction error (RPE) on each trial depending on the choice and its outcome, which updates the ΔQ representation in the population (Figure 3L–M). The RPE-dependent, bidirectional transition of the activity state ensures that the neural population closely represents and updates the ΔQ coding online in each trial. In contrast, the dynamics in S1 and V1 were highly tangled over time, and similar ΔQ values could accompany different activity states at different time. Therefore, although ΔQ coding is widely distributed across the cortex, the different levels of persistency confer different levels of tangling in ΔQ coding (Figure 3N). The exceptionally high ΔQ coding persistency in RSC allows a temporally untangled value representation with the within-trial cyclic dynamics that transitions along the value axis to reflect value updates. These dynamics across trials collectively form cylindrical dynamics during task performance.
Untangled, persistent value coding emerges in the RNN trained with the mouse RL strategy
The persistent and untangled ΔQ coding in RSC, together with our previous observation that RSC inactivation impairs value-based decision (Hattori et al., 2019), raises the possibility that persistent value coding is advantageous in the task. We investigated this possibility by training artificial RNN agents to perform RL in the same task and subsequently examining the ΔQ coding scheme in the trained network. The training of RNNs was done without constraining the activity dynamics. We reasoned that, if persistent coding is advantageous, trained RNN agents may use persistent coding to perform the task.
First, we trained RNNs to perform RL optimally by teaching them the ideal choices of each trial based on the reward assignment rule. In this task, once a reward is assigned to a choice, the reward remains assigned until the choice is selected. As a result, the actual reward probability of a choice cumulatively increases if the choice is not selected in the recent trials. Therefore, an optimal choice would depend on the current reward assignment probabilities, which are unknown to mice and RNN agents, and past choice history. By using the optimal choices as the teacher, we trained synaptic weights of RNNs such that the RNNs use only history of choice and reward to make near-optimal decisions (Figures 4A and 4B). The durations between decisions were made variable, similarly to the task structure in mice. The RNNs receive action outcome information only at the time step after choice and need to maintain the information through recurrent connectivity across time steps and trials. These optimally trained networks (“optimal RNN agents”) achieved higher reward rate than expert mice (Figure 4E). Furthermore, the choice patterns of optimal RNN agents diverged from the RL model that has been optimized to describe the behavior of expert mice (Figure 4E), indicating that the optimal RNN acquired a RL strategy that is distinct from mice. Accordingly, a regression analysis showed that the dependence of optimal RNN agents on choice and reward history differed from that of expert mice (Figure 4F).
Figure 4. Untangled persistency emerges in the artificial RNNs trained to perform ‘mouse-like’ RL.
(A) Optimal RNN agent was trained by updating its synaptic weights to minimize the discrepancy in decisions (cross-entropy error) between the teacher (optimal choice generator) and the student (RNN).
(B) Behaviors of the trained optimal RNN agent in an example session. The agent ran the task by itself using its recurrent activity dynamics to implement RL. The left choice probability of the RNN agent was taken from its output neuron activity. Left (QL) and right (QR) action values were estimated by fitting a RL model to the behaviors.
(C) Mouse-like RNN agent was trained by updating its synaptic weights to minimize the discrepancy in decisions (cross-entropy error) between the teacher (expert mice) and the student (RNN).
(D) Behaviors of the trained mouse-like RNN agent in an example session.
(E) Frequency of rewarded trials (left) and choice predictability by a RL model optimized to describe expert mouse behaviors (right, 5-fold cross-validation). n = 82 sessions for mice, 500 sessions (5 trained networks, each ran 100 sessions of 500 trials/session) each for the optimal and mouse-like RNN agents.
(F) Decision dependence on history from past 10 trials, quantified by a regression model (Methods). RewC: rewarded choice, UnrC: unrewarded choice, C: outcome-independent choice history. n = 82 sessions for mice, 5 sessions (5 trained networks, each ran 10,000 trials) each for the optimal and mouse-like RNN agents. The regression weights were normalized by the model accuracy. Error bars are 95% CI.
(G) Activity of ΔQ coding neurons that were identified using the activity at the highlighted time bin (yellow shading, −1 time step before choice) in the recurrent layer of a trained mouse-like RNN agent (left), and the t-values of ΔQ after choice for the activity in each time bin (right). Each trial had 10 time steps, and 0 corresponds to the choice time. t-values were sorted based on the last time step (+9). The t-values in RNNs are higher than in mice due to smaller amount of activity noise. Error bars are s.e.m.
To obtain a network model that better mimics the mouse strategy, we trained RNNs to imitate expert mouse behaviors using behavioral cloning, a form of imitation learning (Osa et al., 2018). We used 50,472 decision making trials of expert mice as the teaching labels to train the synaptic weights of the RNN. The goal of this training was for the RNN to make the same decisions as expert mice with its recurrent activity dynamics based on the same history of choice and outcome in the past trials (Figure 4C). The trained RNNs (“mouse-like RNN agents”) performed RL using their recurrent activity (Figure 4D), and the reward rate and the RL model accuracy were equivalent to those of expert mice (Figure 4E). Furthermore, the mouse-like RNN agents used history from previous trials for its decisions in a similar way as expert mice (Figure 4F). Therefore, the RL strategy of expert mice was successfully transferred to the synaptic weights of the trained RNN agents, and the trained RNNs could implement mouse-like RL using its recurrent activity dynamics without updating synaptic weights from trial to trial.
We then examined how the mouse-like RNN agents encoded ΔQ. We found that RSC-like persistent ΔQ coding emerged in their recurrent activity (Figures 4G). This observation is significant as the training procedure did not impose a priori constraints on the coding scheme of the RNN. We also examined how the population activity dynamics evolved during training. We had RNN agents at 3 stages of training run the task (before training, intermediate (after 1 epoch of training), and fully trained) and analyzed their recurrent activity during the task performance. dsPCA revealed that untrained networks with random connectivity exhibit highly tangled ΔQ coding, while training gradually shaped the networks to form stacked circular dynamics (Figure 5A). Unlike RSC that formed cylindrical dynamics (Figure 3K), the diameter of rotational trajectory varied across different ΔQ states in the trained networks, suggesting that additional biological constraints that were not considered for RNN training may have imposed a constant diameter in the mouse brain. In addition to the analysis of ΔQ estimates from a RL model fit to behaviors, we examined the coding persistency of the ground truth ΔQ which is available as the activity of the action output neuron in each RNN agent. We confirmed that the ground truth ΔQ was also persistently encoded in both optimal and mouse-like RNN agents (Figure S6).
Figure 5. Cylindrical dynamics emerges in mouse-like RNN agents and mice during training.
(A) Population activity dynamics of the recurrent layer of mouse-like RNN agents in neuronal manifolds where ΔQ axis is paired with axes that reflect major within-trial temporal activity variance in Q-free subspace. Agents at each training stage ran the task for 10,000 trials. dsPCA was applied on the activity averaged between −5 and −1 time steps from choice, and the population activity between ±5 time steps from choice was projected onto the identified axes. 4 independently trained mouse-like RNN agents are shown. Circles indicate the choice time.
(B) Population activity dynamics of example RSC, PPC, pM2, and ALM populations in early and expert sessions. The same population of neurons was longitudinally compared for each area. dsPCA was applied on the activity averaged between −2 and −1 sec from choice, and the population activity between ±4 sec is visualized. Circles indicate the choice time.
Persistency facilitates reliable and robust value retrieval by downstream neural networks
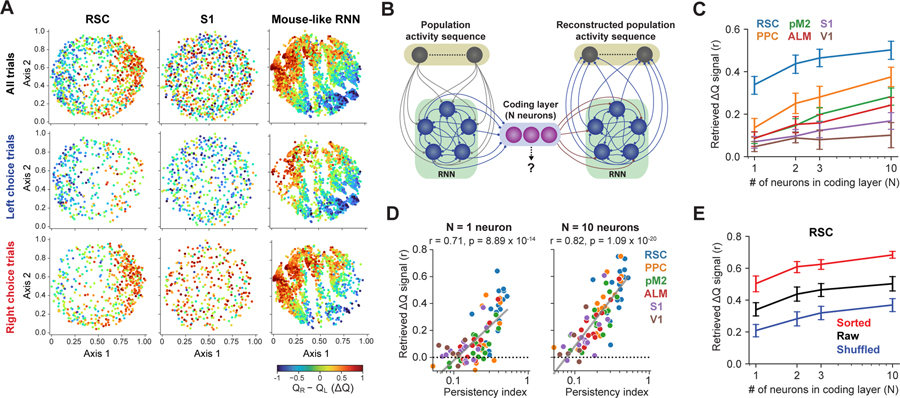
The emergence of ΔQ coding persistency in RNN agents suggests that persistent coding is a preferred solution in the task. What would be the advantage of persistent coding? One possibility is that untangled persistency may allow a more reliable signal retrieval by the downstream network to guide the action selection. We tested this possibility by training artificial RNNs to retrieve the ΔQ signal from different temporal patterns of simulated population activity (Figure 6A). For this purpose, RNNs are biologically relevant as they receive time-varying inputs sequentially, as opposed to other decoder models (e.g. regression models).
Figure 6. Persistency in value coding facilitates reliable and robust value retrieval by downstream neural networks.
(A) RNN (40 recurrent units) was trained to retrieve ΔQ from the input population activity sequence with either persistent or non-persistent ΔQ coding.
(B) Artificial population activity with either persistent or non-persistent ΔQ coding in the 200-cell sequence. 3 types of non-persistent mode were considered (2 rate coding, 1 binary coding; Methods). In the rate coding populations, the color indicates the Pearson correlation between the activity and ΔQ (20 % of neurons at each bin encode ΔQ). Example populations were visualized by either clustering ΔQ-coding neurons at each time bin (top) or sorting neurons based on the correlation at the last time bin (bottom). In the binary coding population, ΔQ is encoded by a unique activity sequence across time for each bin of ΔQ values (ten evenly spaced bins between ±1). 20% of neurons at each time bin participate in each sequence. In the example, cells are sorted for either sequence 1 or 2. Time bins that are active in both sequences are colored black.
(C) Mean ΔQ retrieval accuracy by the downstream RNNs from populations with different coding modes and varying SNR (10 simulations for each).
(D) The ΔQ retrieval accuracy at the 5th time step with different SNR in the input activity. The purple dashed line indicates the median SNR of ΔQ coding in imaged RSC populations.
(E) Robustness of trained RNNs. Simulations were performed using artificial population activity with SNR of 1. Noise to synaptic weights was given by Gaussian noise with the standard deviation relative to the standard deviation of the weight distribution of each connection type. Error bars in (D) and (E) are 95% CI.
(F) Artificial manipulations of ΔQ coding persistency illustrated in an example PPC population during ready period. Error bars are s.e.m.
(G) ΔQ retrieval accuracy before and after the persistency manipulations (subsampled 240 cells were used, **P < 0.01, ****P < 0.0001, one-way ANOVA with Tukey’s HSD).
(H) Gain in retrieval accuracy by sorting correlates with the original ΔQ coding persistency.
(I) Loss in retrieval accuracy by shuffling correlates with the original ΔQ coding persistency.
We created artificial population activity encoding ΔQ in 4 different patterns: persistent, and 3 types of non-persistent coding (Figure 6B). In persistent coding, 20% of cells encode ΔQ as rate coding persistently. The slope of ΔQ tuning curve for each neuron was taken from its distribution among RSC neurons (Figure S7). For the first 2 types of non-persistent coding, the cellular identity of the persistent coding pattern was shuffled independently at each time bin to alter the ΔQ persistency of each neuron without altering the population-level ΔQ signal in each time bin. Non-persistent 1 allowed each neuron to encode ΔQ in multiple time points, while non-persistent 2 was constrained that each neuron encodes ΔQ in only one of the 5 time points. In the third non-persistent coding scheme, binary signals (active or inactive) at each time bin were used to encode ΔQ by activating distinct sequences of neurons across time for different values of ΔQ. We prepared 10 different sequences for 10 bins of ΔQ values.
Using these activity patterns as inputs, we trained RNNs to retrieve ΔQ. Various levels of noise were added to the input activity to test a range of signal-to-noise ratio (SNR). The RNN trained with the persistent ΔQ codes was able to retrieve ΔQ better than those trained with non-persistent codes, especially when the input activity noise was high (Figure 6C–D). This indicates that persistent coding facilitates reliable information retrieval by downstream circuits. Furthermore, the RNNs that were trained to retrieve ΔQ from persistent coding were more robust to changes in the synaptic weights, loss of synapses and cells (Figure 6E).
To investigate the impact of persistency in the brain activity, we next examined how ΔQ could be retrieved from the neural activity with different levels of persistency recorded from the 6 cortical areas (Figure 6F). In addition to the original recorded activity (‘Raw’), we artificially increased or decreased ΔQ coding persistency by temporally sorting (‘Sorted’) or shuffling (‘Shuffled’) the cell identity in each area. These persistency manipulations simply changed the neuron ID of activity and thus did not alter the total amount of ΔQ signal in each time bin. Using these sets of neural activity as inputs, we trained RNNs to retrieve ΔQ. There was a general trend that an increase in persistency (sorted activity) improved retrieval accuracy, while a decrease in persistency (shuffled activity) impaired retrieval accuracy (Figure 6G). However, the effect size differed across different cortical areas. We found that the increase in retrieval accuracy by sorting was larger when the original persistency in the population was lower, and the decrease in retrieval accuracy by shuffling was larger when the original persistency was higher (Figures 6H–I). These results further support the notion that coding persistency is a critical determinant that enhances the accuracy of information retrieval by the downstream network.
The results above indicate that persistent codes can be read out by the downstream more effectively than non-persistent codes when the artificial neural network is allowed to train its synaptic weights by minimizing the difference between its output and the target (ΔQ) as supervised learning. However, in the real brain, such an explicit supervised target label to guide the shaping of network connectivity is rarely available. Another approach to shape the connectivity to retrieve particular information is unsupervised learning where errors are computed using information readily available to the local network such as the input itself (Lillicrap et al., 2020). Therefore, we next considered the possibility that coding persistency may also affect signal retrieval processes that do not necessitate a supervised target label for each information. It has been suggested that the brain may implement unsupervised learning in a similar way to autoencoder networks in which the target is the input itself (Lillicrap et al., 2020). Autoencoders extract the most dominant signals from the input activity and represent them in the activity of a small number of neurons in the coding layer. The networks shape their connectivity by reconstructing the input activity from the coding layer and minimizing the reconstruction error between the input and the reconstructed activity. To examine what information in the input population activity can be extracted in an unsupervised manner by downstream recurrent networks, we used a recurrent denoising autoencoder (RDAE) (Maas et al., 2012; Vincent et al., 2010) that sequentially processes input activity and extracts the latent representations embedded in the input activity sequence, which are sufficient to reconstruct the original population activity sequence with noise robustness (Figure 7B; Methods). When the RDAE was trained on RSC population activity, ΔQ was extracted in the most dominant dimensions of neural activity in the coding layer (Figure 7A). The ΔQ representation in the coding layer was independent of upcoming choice directions, indicating that the dimensions reflect value and not motor plans. Other task-related signals were not represented as the dominant signals in the coding layer (Figure S8). Similar results were observed in the activity dynamics of the mouse-like RNN agent but not in S1. Systematic comparisons among 6 cortical areas revealed that extracted ΔQ in the coding layer was especially high from RSC, and the amount of extracted ΔQ showed a high correlation with the ΔQ coding persistency in the input population activity (Figures 7B–D). To directly test the effect of persistency, we artificially manipulated the persistency of ΔQ coding in RSC without changing the total amount of ΔQ signals in the population. We found that artificial increases in the persistency by sorting the cell identity improved the ΔQ extraction, while artificial decreases in the persistency by shuffling the cell identity worsened the ΔQ extraction (Figure 7E). These results indicate that high persistency in the input activity can allow ΔQ retrieval by the downstream network even without supervised learning.
Figure 7. Persistency in value coding also facilitates unsupervised value retrieval by downstream neural networks.
(A) Representation of input population activity in the coding layer of denoising recurrent autoencoder networks (RDAE). Each network was trained to extract major signals from example populations of RSC, S1, or a trained mouse-like RNN agent (5,000 trials). Population activity sequence during ready period was used as the input. Each data point corresponds to a trial, with the colors indicating the ΔQ of the trial. Trials were separated according to the choice directions in the upcoming answer period in the bottom 2 rows. The dominant signals extracted in the activity of coding neurons (10 neurons) were visualized in 2 dimensions by multidimensional scaling.
(B) RDAEs extract major signals of the input population activity into the activity of N neurons in the coding layer by unsupervised learning.
(C) Decoding accuracy of ΔQ from the activity of N neurons in the coding layer. A simple feedforward neural network (N neurons in the coding layer are connected to a single output neuron with tanh activation function) was used to decode from the coding layer. Input populations were subsampled 240 cells.
(D) Decoding accuracy of ΔQ from the activity of neurons in the coding layer (N = 1 and 10) positively correlates with the ΔQ coding persistency of the input population activity.
(E) Artificial manipulations of ΔQ coding persistency in the input RSC population bi-directionally alter the amount of extracted ΔQ signal in the coding layer.
All error bars are s.e.m.
Taken together, these analyses indicate that the persistency of value coding facilitates a robust and accurate readout of value by downstream networks.
Signal leakage can contribute to distributed value coding with varying levels of persistency
The results so far indicate computational advantages of persistent coding. However, in the mouse brain, ΔQ coding was widely distributed across the 6 cortical areas with different levels of persistency (Figures 1C–F). We asked whether anatomical connectivity among cortical areas relates to the persistency levels of value coding. We analyzed the connectivity among imaged areas using the dataset from the Allen Mouse Brain Connectivity Atlas (Oh et al., 2014). Focusing on the projections from each of the 3 areas with high ΔQ persistency (RSC, PPC, pM2), we quantified their axon projection density in each of the other 5 imaged areas (Figure 8A). We found that RSC, PPC, and pM2 predominantly project to each other, with smaller amounts of direct projections to ALM, S1, and V1 (Figures 8B–C and S9). Thus, 3 areas with persistent and strong ΔQ coding densely connect with each other, while they send less direct projections to the other 3 areas with weaker and less persistent ΔQ coding. Based on this observation, we hypothesized that the weak ΔQ persistency in ALM, S1 and V1 could result from a signal leakage from the areas that maintain ΔQ as persistent activity. To test this hypothesis, we built RNNs with multiple recurrent layers that receive RSC activity through non-specific synaptic connectivity and examined how ΔQ coding changes along the downstream hierarchy of layers (Figure 8D). We found that the fractions of neurons with ΔQ coding gradually decreased as the signal leaked through layers of recurrent connectivity (Figures 8E–F). Concurrently, ΔQ coding became increasingly less persistent (Figure 8G), and the temporal tangling of ΔQ coding in neuronal manifolds gradually increased in the downstream (Figure 8H). Furthermore, artificial manipulations of ΔQ coding persistency in the input RSC activity revealed that persistency in ΔQ coding can affect the robust distribution of ΔQ coding with graded levels of persistency across the downstream layers (Figures 8F–G). We obtained similar results using PPC and pM2 as the input activity (Figure S10A–H), and the decreases in the ΔQ coding neurons and the ΔQ coding persistency in the downstream layers were more dramatic when the direct neural projections from layer to layer were sparse (Figure S10I–K). These results indicate that, even without specific connectivity to selectively route particular information, persistently encoded information can propagate thorough layers of non-specific connectivity to lead to a wide distribution of the information encoded with lower levels of persistency in downstream areas.
Figure 8. Non-specific signal leakage can contribute to widely distributed value coding with graded persistency.
(A) Injection coordinates for anterograde tracing virus. RSC (red, n = 60 experiments), PPC (blue, n = 9), and pM2 (yellow, n = 33). Experiments with left hemisphere injections were mirrored horizontally. Experiments with both WT mice and Cre-transgenic mice were included (See Figure S9 for WT only). White squares indicate the imaging FOVs used for our neural activity analyses.
(B) Mean projection density of axons from each source area. Black dots indicate the injection coordinates.
(C) Connectivity matrix with the mean projection density from each source area to the 6 target areas that we used for our neural activity analyses (500μm × 500μm white squares).
(D) RSC population activity sequences were processed through 5 recurrent layers with non-specific connectivity. Connection probability from layer to layer was set to 20% (Other probabilities in Figure S10).
(E) Fractions of ΔQ coding neurons at each of the 200 ms time bins during ready period (Regression, P < 0.05, 2-sided t-test). Error bars are s.e.m.
(F) Mean fractions of ΔQ coding neurons at each layer during ready period. Fractions of time bins within the ready period were averaged for each population. Artificial manipulations of ΔQ coding persistency in RSC does not affect the fractions of ΔQ coding neurons in RSC, but affect the fractions in the downstream.
(G) ΔQ coding persistency at each layer. Persistency progressively decreases in the downstream. Artificial manipulations of ΔQ coding persistency affect the persistency in the downstream. Error bars in (F) and (G) are 95% CI.
(H) Temporal dynamics of population activity states visualized with dsPCA applied at each layer. Cylindrical dynamics gradually collapses into highly tangled dynamics in downstream layers.
DISCUSSION
Brain-wide distribution of task-related information has emerged as a common principle in recent years. In many cases, such as what we observed for ΔQ coding (Figure S1), task-related signals are encoded by a heterogeneous population with some cells increasing but others decreasing their activity. Such information coding may not be identified with classical large-scale recording techniques such as fMRI, EEG and ECoG that quantify population average responses. Even though information coding is wide-spread, the way by which information is encoded differs across areas (Hattori et al., 2019). In the present study, the big data of >100k mouse decisions and the activity from >100k neurons in 2 behavioral tasks allowed us to investigate the potential origin of the distributed information coding and the computational advantages of persistent coding using data-driven machine learning approaches. Coding persistency was both learning- and context-dependent, and the persistent coding emerged during task learning in both mouse brain and artificial network agents performing the same task. Persistency facilitates an untangled maintenance of information as well as its reliable retrieval by downstream circuits. The observation that persistency is context-dependent suggests that certain cortical areas such as RSC can adjust coding persistency depending on behavioral demands. For example, persistency may be especially preferred when the task context requires extended maintenance of the information, or the maintained information is graded as in the case of value, so that information can be stably maintained and robustly retrieved by downstream areas. Furthermore, we showed that persistent coding in key areas such as RSC could also contribute to the wide distribution of ΔQ coding across the mouse brain even through non-specific signal leakage. The same principle may also apply to other task-related signals in various task conditions, providing a possible explanation for the widespread phenomenon of distributed coding across the brain. In other words, a wide distribution of information is expected across the interconnected network of the brain, unless specific connectivity restricts the propagation of particular information. We note that non-specific leakage is one of potential mechanisms for signal distribution and it remains to be shown how much such a mechanism contributes to the phenomenon. Furthermore, this mechanism is agnostic to whether the propagated information has a function in the downstream areas — leaked information could contribute to various computations performed in downstream areas.
We trained artificial RNNs to imitate the mouse behavioral strategy using behavioral cloning and investigated the activity dynamics that emerged in the RNNs that were trained without activity constraints. Previous studies trained task-performing artificial neural networks either by using the correct action labels which are defined in each task structure (e.g. action A must be taken after stimulus A) (Masse et al., 2019; Orhan and Ma, 2019) or by RL (Banino et al., 2018; Song et al., 2017; Tsuda et al., 2020; Wang et al., 2018). Both approaches train the networks to learn the optimal strategy in the respective task, independent of the actual behavioral strategy that animals learn in the environment. In our value-based decision task, animals learn to use behavioral history for decisions during training, but the RL strategy that animals develop was suboptimal (Figure 4E–F). The origins of the sub-optimality likely include 1) limited memory capacity, 2) low sample efficiency, 3) limited amount of training trials, and 4) inductive bias inherent to each species. Deep RL, an artificial network that learns to solve a task with RL, does not always have these constraints, and thus it learns a near-optimal strategy unlike animals. These artificial networks may not reflect the mechanisms used by the brain. In another common approach, simpler mathematical models (e.g. regression, classical RL models) directly fit to animal behaviors are useful to understand the behavioral strategies. However, they do not provide insights into potential neural activity dynamics that may mediate the behaviors. To overcome these issues, we trained artificial RNNs, using mice as the teachers, to acquire the sub-optimal RL strategy that mice develop during training. The big data of ~50k decisions collected from expert mice allowed us to successfully train RNNs to imitate mouse behavioral strategy. This data-driven approach to train RNNs to implement animal/human-like behaviors would be a useful approach to obtain the neural network models and analyze what kind of activity dynamics allows the animal strategy in a particular task. Similarly to our approach, convolutional neural networks has been trained in visual object recognition tasks. The training was done to perform the task optimally, as opposed to our approach using behavioral cloning. Nevertheless these networks have been shown to develop some neural activity characteristics that resemble the neural activity in the visual system of animals (Kriegeskorte, 2015; Yamins and DiCarlo, 2016). These deep learning approaches will be a powerful approach to understand what kind of neural activity may mediate given behaviors.
In this study, we developed dsPCA, a novel dimensionality reduction method which combines the strengths of supervised and unsupervised algorithms. The supervised aspect allows us to identify the best demixed linear coding dimensions for targeted task-related variables, and the unsupervised aspect allows us to identify non-targeted correlated signals in the remaining population activity. Therefore, dsPCA is a generally applicable method to understand both the signals of interest and other non-targeted correlational structures in high-dimensional data. Using dsPCA, we found that both mouse brain and artificial RNN agents develop cylindrical dynamics, which consists of within-trial cyclic dynamics and its across-trial transition along ΔQ axis. Similar within-trial dynamics have been well-studied in monkey motor cortex during arm movement (Churchland et al., 2012; Russo et al., 2018, 2020). The studies showed that the population activity state draws untangled rotational dynamics during movements. They also showed that the activity state draws a simple cyclic trajectory in the primary motor cortex, while the supplementary motor area draws a helical trajectory that unfolds along a single direction by reflecting the ‘context’ of the movement (Russo et al., 2020). The activity trajectory that we observed had cylindrical geometry, and the activity state repeatedly transitioned along the ΔQ axis based on the RPE. These spatially confined geometries ensure the untangled representation of ΔQ, which contributes to a robust ΔQ representation in the brain. dsPCA and other RNN-based approaches in this study would facilitate the geometric understanding of population dynamics in both biological and artificial networks.
STAR Methods
Resource availability
Lead Contact
Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Takaki Komiyama (tkomiyama@ucsd.edu).
Materials Availability
This study did not generate new unique reagents.
Data and code availability
Data reported in this paper are available from the lead contact upon reasonable request.
dsPCA code has been deposited at Zenodo and is publicly available. The DOI and the link to the latest code in the GitHub repository are listed in the key resource table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE.
Experimental model and subject
Animals
The experimental data in the value-based decision task were first reported in ref. (Hattori et al., 2019). The data in the alternate choice task were newly collected for the current study. Both male and female mice were included in both datasets because we did not observe obvious sex-dependent differences in their neural activity patterns. Mice were originally obtained from the Jackson Laboratory (CaMKIIa-tTA: B6;CBA-Tg(Camk2a-tTA)1Mmay/J [JAX 003010]; tetO-GCaMP6s: B6;DBA-Tg(tetO-GCaMP6s)2Niell/J [JAX 024742]). All mice (6 weeks or older) were implanted with glass windows above their dorsal cortex for in vivo two-photon calcium imaging. All mice were water-restricted at ~1ml/day during training.
Method details
Surgery
Mice were continuously anesthetized with 1–2% isoflurane during surgery after subcutaneous injection of dexamethasone (2mg/kg). After exposing the dorsal skull and removing the connective tissue on the skull surface using a razor blade, we marked on the skull with black ink at the coordinates of [AP from bregma, ML from bregma] = [+3.0 mm, 0 mm], [+2.0 mm, 0 mm], [+1.0 mm, 0 mm], [0 mm, 0 mm], [−1.0 mm, 0 mm], [−2.0 mm, 0 mm], [−3.0 mm, 0 mm], [0 mm, ±1.0 mm], [0 mm, ±2.0 mm], [0 mm, ±3.0 mm], [−2.0 mm, ±1.0 mm], [−2.0 mm, ±2.0 mm], [−2.0 mm, ±3.0 mm]. We then applied saline on the skull and waited for a few minutes until the skull became transparent enough to visualize vasculature patterns on the brain surface. We took a photo of the vasculature patterns along with marked coordinates and used it to find target cortical areas for two-photon microscopy. A large craniotomy was performed to expose 6 cortical areas, and a hexagonal glass window was implanted on the brain. The glass window was secured on the edges of the remaining skull using 3M Vetbond (WPI), followed by cyanoacrylate glue and dental acrylic cement (Lang Dental). After implanting the glass window, a custom-built metal head-bar was secured on the skull above the cerebellum using cyanoacrylate glue and dental cement. Mice were subcutaneously injected with Buprenorphine (0.1 mg/kg) and Baytril (10 mg/kg) after surgery.
Behavior task and training
Mice were water-restricted at 1–2 ml/day after a minimum of 5 days of recovery after surgery. We began animal training in pre-training tasks after at least a week of water restriction. We used BControl (C Brody), a real-time system running on Linux communicating with MATLAB, to control behavioral apparatus. We placed 2 lickports in front of head-fixed mice to monitor their licking behaviors and give water rewards. Licking behaviors were monitored by IR beams running in front of each water tube. We used an amber LED (5mm diameter) as the ready cue and a speaker for auditory cues. Each trial begins with a ready period (2 or 2.5 sec with the amber LED light), followed by an answer period with an auditory go cue (10 kH tone). The 10 kHz tone was terminated when animals made a choice (the first lick to a lickport) or when the answer period reached the maximum duration of 2 sec. Mice received a 50 ms feedback tone (left: 5 kHz, right: 15 kHz) after a choice. ~2.5 μl water was provided to mice on each rewarded trial from a lickport.
Before running in the alternate choice task or value-based decision task, mice were trained in 2 pre-training tasks. In the 1st pre-training task, mice were rewarded for either choice during the answer period. We gradually increased the mean ITI from 1 sec to 6 sec with ±1 sec jitter. Through training in this task (2–3 days), mice learn that they can obtain water rewards from the 2 lickports if they lick during the answer period. In the 2nd pre-training task, reward location alternated every trial irrespective of their choice directions. Furthermore, licking during ready period was punished by 500 ms white noise alarm sound and trial abort with an extra 2 sec ITI in addition to the regular 5–7 sec ITI. Through training in this 2nd pre-training task (2–3 days), mice learned to lick from both lickports and withhold licking during the ready period.
Alternate choice task
In the alternate choice task, mice need to change their choice from a previous trial to get a water reward. For example, if a mouse chose left on one trial, regardless of whether the mouse received a reward or not, a water reward is available only from the right choice on the next trial. The mouse will not get any rewards by repeating left choices for many trials because a reward will not be assigned to the left until the mouse collects the assigned reward on the right side. Mice need to rely on which side they chose in the previous trial to make the correct choice. ITI was 5–7 sec, and the trials with licking during ready period were classified as alarm trials (500 ms white noise alarm sound and extra 2 sec ITI). Mice were trained for at least 2 weeks before starting 2-photon calcium imaging.
Value-based decision task
In the value-based decision task, a reward is probabilistically assigned to each choice. On each trial, a reward may be assigned to each choice according to the reward assignment probabilities that are different between two choices. Once a reward was assigned to a lickport, the reward remained assigned until it was chosen. As a result, the probability that a reward is assigned to a choice gradually increases if the choice has not been selected in the recent past trials. The combinations of reward assignment probabilities were either [60 %, 10 %] or [52.5 %, 17.5 %] in a trial, and reward assignment probabilities switched randomly every 60–80 trials in the order of [Left, Right] = …, [60 %, 10 %], [10 %, 60 %], [52.5 %, 17.5 %], [17.5 %, 52.5 %], [60 %, 10 %], …. The probability switch was postponed if the fraction of choosing the lickport with higher reward assignment probability was below 50 % in recent 60 trials until the fraction reached at least 50 %. ITI was 5–7 sec, and the trials with licking during ready period were classified as alarm trials (500 ms white noise alarm sound and extra 2 sec ITI). Trials in which mice licked during ready period (‘alarm trials’, 5.15 %) and the trials in which mice failed to lick during the answer period (‘miss trials’, 4.68 %) were not rewarded. We did not include alarm and miss trials in neural activity analyses to ensure that the ready periods we analyzed were free of licking behaviors and that mice were engaged in the task in the trials.
Two-photon calcium imaging
We used a two-photon microscope (B-SCOPE, Thorlabs) with a 16× objective (0.8 NA, Nikon) and 925 nm excitation wavelength (Ti-Sapphire laser, Newport) for in vivo calcium imaging. Images were acquired using ScanImage (Vidrio Technologies) running on MATLAB. All calcium imaging was performed using camk2-tTA::tetO-GCaMP6s double transgenic mice that express GCaMP6s in camk2-positive excitatory neurons. Each field-of-view (FOV) (512 × 512 pixels covering 524 × 524 μm) was scanned at ~29 Hz. Areas within the FOV that were not consistently imaged across frames were discarded from analyses (Typically 10 pixels from each edge of the FOV). We imaged and analyzed layer 2/3 neurons of 6 cortical areas in this study: retrosplenial (RSC, 0.4 mm lateral and 2 mm posterior to bregma), posterior parietal (PPC, 1.7 mm lateral and 2 mm posterior to bregma), posterior premotor (pM2, 0.4 mm lateral and 0.5 mm anterior to bregma), anterior lateral motor (ALM, 1.7 mm lateral and 2.25 mm anterior to bregma), primary somatosensory (S1, 1.8 mm lateral and 0.75 mm posterior to bregma), and primary visual (V1, 2.5 mm lateral and 3.25 mm posterior to bregma) cortex. Images from these areas were collected from both hemispheres. We collected only 1 population from each hemisphere for each cortical area of a single mouse. We imaged both hemispheres in two different behavioral sessions if the FOVs on both hemispheres were clear at the time of imaging.
Image processing
Images from 2-photon calcium imaging were processed using a custom-written pipeline (Hattori, 2021). The pipeline corrects motion artifacts using pyramid registration (Mitani and Komiyama, 2018), and slow image distortions were further corrected by affine transformations based on enhanced correlation coefficients between frames (Evangelidis and Psarakis, 2008). We used Suite2P (Pachitariu et al., 2017) to define regions of interests (ROIs) corresponding to individual neurons and extract their GCaMP fluorescence. We selected only cellular ROIs using a user-trained classifier in Suite2P and by manual inspections. At the step of signal extraction from each cellular ROI, we excluded pixels that overlap with the other ROIs.
Neural activity
The neural activity data for the value-based decision task were first reported in ref. (Hattori et al., 2019). We also additionally collected new neural activity data from mice running the alternate choice task. The activity was continuously recorded with in vivo two-photon calcium imaging at ~29 Hz from mice during the task performance. GCaMP fluorescence time series were deconvolved to obtain signals that better reflect the kinetics of neural spiking activity using a non-negative deconvolution algorithm (Friedrich et al., 2017; Pachitariu et al., 2018). The deconvolved signal of each neuron was z-score normalized using the activity time series during the entire imaging session before performing all the activity analyses in this study.
For the alternate choice task, we collected and analyzed the activity of 8,524 RSC neurons (14 populations), 3,186 PPC neurons (7 populations), 7,915 pM2 neurons (14 populations) and 4,911 ALM neurons (10 populations) from 9 expert mice while they were running the alternate choice task. For the value-based decision task, we analyzed the activity of 9,254 RSC neurons (15 populations), 6,210 PPC neurons (13 populations), 7,232 pM2 neurons (13 populations) and 5,498 ALM neurons (10 populations) from early sessions (≤ 6th session), and 9,992 RSC neurons ( populations), 7,703 PPC neurons ( populations), 9,759 pM2 neurons (populations), 6,721 ALM neurons (populations), 7,576 S1 neurons (14 populations) and 2,767 V1 neurons (6 populations) from expert sessions of the data used in ref. (Hattori et al., 2019).
Reinforcement learning model for mouse behaviors
The reinforcement learning model that we used to estimate the action values in each trial was taken from ref. (Hattori et al., 2019). This model was optimized specifically for mouse behaviors and not necessarily ideal for describing the RL action policy of artificial neural network agents (e.g. Optimal RNN agents). Action values of chosen (Qch) and unchosen (Qunch) options in each trial were updated as follows:
| [eq. 1] |
| [eq. 2] |
where αrew and αunr are the learning rates for rewarded and unrewarded trials respectively, δ is the forgetting rate for the unchosen option, and R(t) is reward outcome in trial t (1 for rewarded, 0 for unrewarded trials). The learning rates and the forgetting rate were constrained between 0 and 1. In alarm and miss trials, values of both options were discounted by δ. The probability of choosing left (PL) on trial t is estimated using left (QL) and right (QR) action values as follows:
| [eq. 3] |
where β0 is the value bias which is constant within each session, and βΔQ reflects the behavioral sensitivity to ΔQ. The RL model was fit to the behavioral choice patterns with maximum likelihood estimation.
ΔQ-coding neurons
ΔQ-coding neurons in the value-based decision task were identified with the following multiple linear regression model.
| [eq. 4] |
where ai(t) is the mean activity of ith neuron within each 200 ms time bin on trial t (except for some analyses (Figures S1 and S2) where the mean activity within the first 2 sec of ready period was used instead), C(t) is the choice on trial t (1 if contralateral choice, −1 if ipsilateral choice), ΔQ(t) is the value difference between contralateral and ipsilateral options on trial t, Q𝑐ℎ(t) is the value of the chosen option on trial t, and ∑Q (t) is the sum of values of both options on trial t. The regression weights were estimated by the ordinary least squares method. ΔQ-coding neurons were identified with two-tailed t-test for the βΔQ regression weight (statistical threshold of either P < 0.05 or P < 0.01 as indicated in the figure legend of each analysis). The t-value for βΔQ(t) is where se(βΔQ) is an estimate of the standard error of βΔQ.
Action history coding neurons
Neurons that encode action history from an immediately preceding trial in the alternate choice task and the value-based decision task were identified with the following multiple linear regression model.
| [eq. 5] |
where ai(t) is the mean activity of ith neuron within each 200 ms time bin on trial t, C(t) is the choice on trial t (1 if contralateral choice, −1 if ipsilateral choice), C(t − 1) is the choice on trial (t − 1) (1 if contralateral choice, −1 if ipsilateral choice, 0 otherwise). The regression weights were estimated by the ordinary least squares method. Action history coding neurons were identified with two-tailed t-test for the regression weight (statistical threshold of P < 0.05). The t-value for is where is an estimate of the standard error of .
Persistency index
Persistency index to quantify the mean persistency of ΔQ coding or action history coding in a population of neurons was defined as follow;
| [eq. 6] |
where is the time series of t-values for βΔQ or that was obtained by fitting the [eq. 4] or [eq. 5] to the activity of each of the non-overlapping 200 ms time bins between 5 sec before the ready cue and 2 sec after the ready cue. The across-time standard deviation of the was summed across all n neurons in the population (including neurons with non-significant t-values), and this summed standard deviation was normalized by min-max normalization such that the persistency index ranges between 0 (chance level persistency of a target population) and 1 (maximum persistency of a target population). The maximum persistency of a target population, , was obtained by independently sorting the cell identity at each time bin according to the βΔQ t-values of each cell in the time bin. The chance level persistency of a target population, , was obtained by independently shuffling the cell identity at each time bin. To minimize the effect of randomness in the shuffling procedure, we iterated the shuffling m times (m = 10) and took the mean of the 10 iterations. This persistency index describes how persistent the target signal coding is above chance and how far the persistency is from the maximum persistency that the target population activity could achieve.
Demixed subspace principal component analysis (dsPCA)
Supervised dimensionality reduction algorithms can identify dimensions that encode targeted signals in high-dimensional data. However, they do not provide any information about signals that are not targeted by the users. As a result, these supervised analyses may miss important signals that exist in the original high-dimensional data. On the other hand, unsupervised dimensionality reduction algorithms can find dimensions for the major signals in the high-dimensional data, but they do not automatically reveal what kind of signals are reflected along each dimension. Furthermore, unsupervised methods may miss the signals of interest if the target signals are much weaker than the other dominant signals in the data.
We developed a novel dimensionality reduction algorithm that combines the strengths of both supervised and unsupervised methods. The demixed subspace principal component analysis (dsPCA) identifies demixed coding axes for targeted variables in a supervised manner, and then identify axes that capture the remaining variance in the data using an unsupervised method. Although previously reported demixed principal component analysis (dPCA) has similar objectives (Kobak et al., 2016), dPCA can only identify targeted coding axes for discrete variables. In contrast, dsPCA can identify demixed axes for both discrete and continuous variables. Furthermore, although dPCA splits each targeted signal into multiple linear axes, dsPCA identifies a single linear coding dimension for each of the target signals, and all the linear information for the target signals are contained within the dimensions identified by these single coding axes.
The input to the algorithm is a 3rd-order tensor of population activity with dimensions of Trial (m) × Time (t) × Neuron (n).
| [eq. 7] |
The tensor Xm×t×n is first averaged over time axis elements within a specified time range, and we get a 2nd-order tensor of .
| [eq. 8] |
To identify the demixed linear coding axes that encode ΔQ, Qch, or ΣQ in the population activity, we fit the following multiple linear regression model to the mean activity of individual neurons during the ready period;
| [eq. 9] |
where βi,ΔQ, , and are the regression coefficients of the ith neuron. For a population of n neurons, we obtain n regression coefficients for each type of Q-related signal. These regression coefficients are used to define the coding axes as follows;
| [eq. 10] |
| [eq. 11] |
| [eq. 12] |
Note that these coding axes are ‘demixed’ coding axes where the activity variance for partially correlated variables are demixed into one of the axes for the partially correlated variables thanks to the linear demixing in the regression model ([eq. 9]). Although some previous studies further orthogonalized these demixed coding axes (Mante et al., 2013), we did not orthogonalize between the coding axes because further orthogonalization would remix these best demixed coding axes.
Next, our goal is to identify a neural subspace that does not encode any of the targeted Q-related signals. To identify the neural subspace that is free of the 3 targeted Q-related signals, we solve the following full QR decomposition of an n × 3 matrix with the 3 coding axis vectors using Householder reflections;
| [eq. 13] |
where R is an upper triangular matrix, SQ is a neural subspace that captures all Q-related signals, and Sfree is the Q-free subspace that is orthogonal to the SQ. SQ is formed by 3 orthonormal basis vectors , and these basis vectors and the 3 coding axis vectors span the identical neural subspace. On the other hand, Sfree is formed by (n – 3) target-free orthonormal vectors and capture all the remaining population activity variance that were not captured by the subspace SQ. The representation of the population activity in Sfree is given by
| [eq. 14] |
Lastly, we further realign the dimensions of the Q-free subspace Sfree such that minimum numbers of dimensions are necessary to explain the remained activity variance as much as possible. This realignment is done using the principal component vectors from PCA on . The top p principal component vectors (p ≤ n - 3) can be used as the major Q-free subspace dimensions for dimensionality reduction purpose as follows;
| [eq. 15] |
where the m-by-p matrix Fp′ is the top p principal components of the activity within the Q-free subspace, the (n-3)-by-p matrix Wppca is the loadings matrix of the PCA, and the n-by-p matrix Wpdspca is the loadings matrix of the dsPCA. The columns of Wpdspca are the Q-free axis vectors in the raw n-dimensional population activity space. More generally, the neural subspace that is free of k targeted variables can be obtained by the same [eq. 15] with p ≤ n – k.
Through these steps ([eq. 7] ~ [eq. 15]), dsPCA identified the 3 linearly demixed coding axes for the targeted Q-related signals , and (n - 3) target-free axes (column vectors of Wn−3dspca). We confirmed that none of the targeted signals could be linearly decodable from the population activity within the obtained target-free subspace (Figures 3E, 3I and S3C).
In this manuscript, we decomposed neural population activity into demixed Q subspace and Q-free subspace using dsPCA. The Q subspace consists of demixed linear coding axes for ΔQ, Qch and ΣQ, and all activity variance that linearly relates to these Q-related signals are included in this subspace. On the other hand, all the other activity variance that did not remain in the Q subspace is included in the Q-free subspace. The activity state of the neural population changes across trials within the Q subspace depending on how each of the Q-related signals is updated by choice and its outcome. We also identified the axes that capture the major with-intrial temporal activity variance in the Q-free subspace by performing PCA on the 2nd-order tensors that are obtained by averaging over trial axis elements.
Quantification of Q-related signals in subspaces from dsPCA
dsPCA decomposed population activity into Q subspace and Q-free subspaces. We examined the amount of Q-related signals in each subspace. The strength of Q-related signals in a full population activity with n neurons was quantified using linear decoders given by
| [eq. 16] |
| [eq. 17] |
| [eq. 18] |
where ai(t) is the activity of the ith neuron on trial t, is the regression weight for ai(t), and is the constant term. The decoder was trained with an L2 penalty by selecting the regularization parameter by 5-fold cross-validation. The decoding accuracy was obtained with 5-fold cross-validation by separating trials into training and test sets. Similarly, the strength of Q-related signals in the 3-dimensional Q subspace and the (n - 3)-dimensional Q-free subspaces were quantified using linear decoders on the projected population activity in each subspace as follows;
| [eq. 19] |
| [eq. 20] |
| [eq. 21] |
where si(t) is the population activity along the ith dimension of the subspace on trial t, is the regression weight for si(t), and is the constant term. x = 3 for Q subspace while x = n − 3 for Q-free subspace. These analyses revealed that all Q-related signals were captured by the Q-subspace, while Q-related signals were completely absent in the Q-free subspace (Figures 3E, 3I and S3C).
RNN agents with optimal or mouse-like RL strategy
The RNN agents trained to perform RL in this study consisted of 2 neurons in the input layer, 100 neurons in the recurrent layer, and 1 neuron in the output layer. The agents were trained to perform RL in the same behavior task environment with 10 time steps per trial. The 2 input neurons receive choice and reward outcome information only at the time step immediately after choice, and the history of the choice outcome information was maintained through the recurrent connectivity in the downstream recurrent layer. The sequence of activity fed into the input neurons was given as vectors with either choice or reward history labels in their elements. The elements that correspond to the time steps immediately after choice took 1 for left choice and −1 for right choice in the choice history vector, and the elements took 1 for reward outcome and −1 for no-reward outcome in the reward history vector. These elements took 0 in miss trials. The other elements of the vectors were all zeros. We sequentially fed 100 time steps of sequences into these input neurons, and the network training was done with unroll length of 100 time steps for backpropagation through time. The choice input neuron and reward input neuron connect with neurons in the recurrent layer. The neurons in the recurrent layer are connected with each other through recurrent connections, which allows each recurrent neuron to receive outputs of the previous time steps. The output of the recurrent layer is given by
| [eq. 22] |
where tanℎ(∙) is a hyperbolic tangent activation function of the form , x(t) is a 2 × 1 vector containing the choice and reward information from a previous time step, y(t−1) is a 100 × 1 vector containing the layer’s outputs at time step t, Wx is a 100 × 2 matrix containing the connection weights for the inputs of the current time step, Wy is a 100 × 100 matrix containing the connection weights for the outputs of the previous time step, and b is a 100 × 1 vector containing each neuron’s bias term. The recurrent neurons send their outputs to the output neuron. The output neuron calculates the probability of selecting left action in the trial with a sigmoid activation function of the form . The agent then selects an action for the trial probabilistically by following the choice probability from the output neuron. This 3-layer RNN agent was trained to perform either an optimal RL strategy or the RL strategy that mice develop after training using its recurrent activity dynamics.
To train the RNNs to perform optimal RL in the task environment, we directly utilized the reward assignment rule of the task. In the value-based decision task, a reward is assigned to each choice according to the reward assignment probabilities of each choice on each trial. Once a reward was assigned to a lickport, the reward was maintained on the choice until it was chosen by the animal. As a result, the probability that a reward is assigned to a choice gradually increases if the choice has not been selected in the recent trials. The actual cumulative reward probabilities of left and right choices are given by
| [eq. 23] |
| [eq. 24] |
where Ac(x) is the reward assignment probability of choice c on trial x, Nc(t) is the number of successive c choices before trial t (e.g. NR(t) = 3 when the choice on (t-4) was left and the choices on (t-3), (t-2), (t-1) were right). Therefore, an optimal choice generator would select a choice with higher cumulative reward probability on each trial as follows;
| [eq. 25] |
We used this optimal choice generator as the teacher to train RNNs to learn a near-optimal RL strategy. Unlike the optimal choice generator that knows the exact reward assignment probabilities (Ac(x)) and the reward assignment rule, the RNNs are agnostic to these hidden variables. Therefore, our goal is to train the RNNs to use only the past choice and reward history to make choices that are similar to the choices made by the optimal choice generator. To train the RNNs to imitate the behaviors of the optimal choice generator, we calculated binary cross-entropy as the loss function to be minimized. The cross-entropy is given by
| [eq. 26] |
where M is the total number of training trials, is 1 or 0 when the optimal choice generator selected left or right action on the ith trial respectively, and is the left choice probability of the RNN agent from its output neuron.
To train RNNs to perform mouse-like RL that is suboptimal in the task environment, we used 50,472 decision making trials of expert mice in the task environment. We fed the choice and reward history that expert mice experienced into the RNNs, and trained the RNNs to imitate the choice patterns of expert mice. To do this, we calculated the binary cross-entropy as the loss function to be minimized. The cross-entropy is given by
| [eq. 27] |
where M is the total number of training trials, . is 1 or 0 when the expert mouse selected the left or right action in the ith trial respectively, and is the left choice probability of the RNN agent from its output neuron.
For the training of both the optimal RNN agents and mouse-like RNN agents, the cross-entropy loss was calculated at variable time steps for each trial to reflect the temporal variability of the timing of decision making in this task (variable ITI, variable ready-period, variable reaction time), and all the synaptic weights of the RNN agent were trained with backpropagation through time. The training was optimized using mini-batch gradient descent with Nesterov momentum optimization (learning rate of 0.001 and momentum of 0.9, batch size of 128), and the training was terminated when the loss for a validation set (1/5 of trials) stopped decreasing for the consecutive 50 epochs as a form of regularization (Early stopping). The trained RNN agents ran the task in a simulated environment with the length of 500 trials/session, and the RL behavioral strategy in the simulated environment was quantified by a RL model optimized to describe expert mouse behaviors [eq. 1–3] and a logistic regression model [eq. 28].
Quantification of history-dependent behavioral strategy
The quantification of behavioral strategy for mice and RNN agents was performed with either a RL model [eq. 1–3] or a logistic regression model [eq. 36]. The logistic regression model predicts an action in each trial based on 3 types of history from the past 10 trials. The model is given by
| [eq. 28] |
where PL(t) is the probability of choosing left on trial t, RewC(t − i) is the rewarded choice history on trial t − i (1 if rewarded left choice, −1 if rewarded right choice, 0 otherwise), UnrC(t − i) is the unrewarded choice history on trial t − i (1 if unrewarded left choice, −1 if unrewarded right choice, 0 otherwise), C(t − i) is the outcome-independent choice history on trial t − i (1 if left choice, −1 if right choice, 0 otherwise). βRewC(t−i), βUnrC(t−i), and βC(t−i) are the raw regression weights of each history predictor, and β0 is the history-independent constant bias term. The sizes of these raw weights reflect the relative contribution of each history variable to decision making in a behavior session. However, the weight size does not reflect the absolute strength of the contribution to decision making because the strength of each history effect on decision making is determined by not only the regression weight but also the choice prediction accuracy of the regression model. Therefore, we normalized the regression weights by the choice predictability of the regression model as follows;
| [eq. 29] |
where is the number of choice trials in the session, and .is the number of choice trials that were correctly predicted by the [eq. 36]. Each regression weight is divided by the sum of absolute values of all the regression weights before being multiplied by the choice prediction accuracy. This normalization turns raw regression weights to reflect the fraction of choice predictability by each of the history variable. These normalized weights are comparable across different behavior sessions or mice because they reflect the absolute strength of each history event on decision making. We used these normalized weights to compare the history dependence of expert mice and trained RNN agents for their decision making.
Artificial population activity sequence
Artificial population activity sequences with either persistent or non-persistent rate coding of ΔQ were created based on the distributions of the tuning curves of ΔQ coding among RSC neurons. Each population consisted of 200 neurons with 5 time bins, and we assigned 20% of neurons at each time bin to encode ΔQ. The tuning curve slope of ΔQ coding of each RSC neuron (βΔQ) was measured by fitting [eq. 4] to the activity during ready period. We defined across-trial standard deviation of βΔQΔQ(t) from [eq. 4] as the signal standard deviation of ΔQ coding. To derive the noise standard deviation, we first subtracted βΔQΔQ(t) from the ready period activity sequence of each trial. The residual ready period activity sequences were then concatenated across trials. The standard deviation of the concatenated activity sequence was defined as the noise standard deviation. The SNR of ΔQ coding was defined as the ratio of the signal standard deviation to the noise standard deviation. The tuning curve slope for each activity time bin was randomly sampled without replacement from the distributions of ΔQ-coding neurons. The ΔQ signal was linearly encoded at each time bin according to the sampled tuning curve slope, and additional Gaussian noise was added to the neural activity. The other non-ΔQ coding activity time bins simply exhibited Gaussian noise. We created populations with 3 different types of rate coding modes (Persistent, Non-persistent 1, Non-persistent 2). In the populations with Persistent mode, the identical 20% of neurons encoded ΔQ at all 5 time bins. In the populations with Non-persistent 1 mode, we randomly selected 20% of neurons at each time bin as the ΔQ-coding neurons and allowed each neuron to encode ΔQ with different tuning curve slopes at different time bins. Non-persistent 2 mode is similar to Non-persistent 1, except that each neuron in the population encoded ΔQ at only one of the time bins.
In addition to the 3 rate coding schemes, we also considered a coding mode that encodes ΔQ as specific sequential activity patterns across cells in a population. In this 3rd non-persistent coding mode (Non-persistent 3), neural activity at each time bin can take only binary states (0: inactive, 1: active). Therefore, this population encodes ΔQ using only the identity of active cells. We encoded 10 different sequences in a population such that each sequence uniquely corresponds to one of the 10 binned ΔQ (−1 to 1 with binning of 0.2 width). For each sequence, we randomly assigned 20% of neurons at each time bin as active neurons with a constraint that each neuron can be active only at a single time step in a sequence. After encoding the 10 different sequences in a population, we added Gaussian noise to the activity of each neuron. We defined the SNR of this coding scheme as the ratio of the across-time standard deviation of the activity of a neuron to the standard deviation of its added Gaussian noise.
ΔQ retrieval by RNN
RNNs were trained to retrieve ΔQ information from the input population activity sequence. The RNN had 40 recurrent neurons with tanh activation functions and an output neuron with linear activation function. The network weights were updated by backpropagation through time with RMSprop to minimize mean-squared-error (MSE) between the network outputs and ΔQ values of the trials in a training set. The network training was terminated when the MSE of a validation set stopped decreasing for the consecutive 20 epochs as a form of regularization (Early stopping). For each training iteration, we used 20% of available trials as a test set to calculate the ΔQ retrieval accuracy by the trained network, and the remaining 80% of the trials were further split into validation set (10%) and training set (70%). We repeated the network training 5 times by using different sets of trials as the test set such that we can obtain ΔQ predictions by the trained networks for all available trials in a cross-validated way. The ΔQ retrieval accuracy was calculated by comparing the ΔQ predictions to the true ΔQ from the RL model. For the ΔQ retrieval from cortical activity, we used only 240 cells as the inputs to match the number of cells across different cortical areas. For each neural population, we subsampled 240 cells in each iteration allowing repetitions with the smallest number of iterations to include every cell at least once for decoding, and the ΔQ retrieval accuracy from the iterations were averaged.
Denoising recurrent autoencoder
Autoencoder is an artificial neural network that learns to extract efficient coding of its input without supervision. It consists of an encoder network and a decoder network, and they are sequentially connected through a coding layer with small number of neurons. In a trained autoencoder, the encoder extracts essential signals in the input into the coding layer, while the decoder tries to reconstruct the original input from activity in the coding layer. When the number of neurons in the coding layer is smaller than the dimensions of the input, only signals that are dominant in the input remains in the coding layer of a trained autoencoder network. Among various types of autoencoders, we used denoising recurrent autoencoders (Maas et al., 2012; Vincent et al., 2010) to extract dominant signals embedded in each population activity sequence. Although autoencoders with only feedforward connections or convolutional neural networks can also extract latent signals in a population activity sequence, we used recurrent neural networks that sequentially process the input activity because the neural networks in a brain also process input activity sequentially. Our goal is to understand whether such biologically relevant recurrent networks can extract signals from input activity without explicit teaching labels (i.e. unsupervised learning). The latent signals extracted by a recurrent autoencoder represent the latent signals from the perspective of a recurrent network that processes input activity sequentially through its recurrent connectiviy.
The autoencoders that we used to visualize extracted dynamics from example populations (Figure 7A) consisted of 3 hidden layers with recurrent connectivity (1st: 50 neurons, 2nd: 10 neurons, 3rd: 50 neurons), and the activity of all neurons in a population was used as the input to the autoencoder. On the other hand, the autoencoders that we used for quantitative across-area comparisons (Figure 7B–E) consisted of 3 hidden layers with recurrent connectivity (1st: 20 neurons, 2nd: N neurons, 3rd: 20 neurons) and processed input activity of subsampled 240 cells. Note that 3 layers are the minimum number of layers that are required for an autoencoder network. All recurrent neurons in the hidden layers had tanh activation functions. All neurons except for the neurons in the middle hidden layer (coding layer) sent activity sequentially to the neurons in the next layer. However, the neurons in the coding layer sent only the activity at the last time step to the next hidden layer. The last-time-step activity is the result of the temporal integration of the original population activity sequence through recurrent connectivity, and the activity reflects the latent representations in the original population activity sequence. The hidden layers after the coding layer reconstructed the original population activity sequence from the latent representations in the coding layer. The network weights were updated by backpropagation through time with RMSprop to minimize mean-squared-error (MSE) between the original population activity sequence and the reconstructed population activity sequence. To ensure stable training of network weights, we clipped the gradients of network weights if their L2 norms were greater than 1 (Gradient clipping (Pascanu et al., 2012)). To add noise robustness to the autoencoders, we applied dropout (Hinton et al., 2012; Srivastava et al., 2014) to the connections between the input neurons and the neurons in the 1st hidden layer such that 50% of randomly selected connections are ablated at each training step. The network training was terminated when the MSE of a validation set (20% of trials for Figure 7A, 10% of trials for Figure 7B–E) stopped decreasing for the consecutive 20 epochs as another form of regularization (Early stopping). The activity of the 10 coding neurons for Figure 7A were further reduced to 2 dimensions with multidimensional scaling to visualize the dominant population activity states. To quantify the strength of ΔQ signal in the activity of N coding neurons for Figures 5B–E, we performed decoding of ΔQ from the activity of N coding neurons using a simple feedforward neural network where all the N coding neurons are connected to an output neuron with tanh activation function. For each training iteration, we used 20% of available trials as a test set to calculate the ΔQ decoding accuracy by the trained network, and the remaining 80% of the trials were further split into validation set (10%) and training set (70%). We repeated the network training 5 times by using different sets of trials as the test set such that we can obtain ΔQ predictions by the trained networks for all available trials in a cross-validated way. For these ΔQ decoding analyses, we also matched the number of cells included in the inputs to the autoencoders across different decoding by subsampling 240 cells from the original population. For each neural population, we subsampled 240 cells in each iteration allowing repetitions with the smallest number of iterations to include every cell at least once for decoding, and the ΔQ decoding accuracy from the iterations were averaged.
Deep RNN with non-specific connectivity
Neural networks with 5 recurrent layers were used to simulate how the input population activity transforms in the downstream recurrent layers when the synaptic weights are non-specific throughout the networks. Each recurrent layer had 1,000 neurons with tanh activation functions, and the 5 recurrent layers were sequentially connected through feedforward connections. All neurons of a recorded cortical population were directly connected to the 1st recurrent layer. Each neuron in a recurrent layer was connected with all the other neurons in the same layer, but we made the connections between successive layers sparse by setting the connection probability of a neuron to the neurons in the next layer to 1%, 5%, 10%, 20%, or 50%. The non-specific synaptic weights were randomly drawn from a uniform distribution on [−1, 1).
Anatomical connectivity analyses
We analyzed neural projections from the areas with high ΔQ coding persistency (RSC, PPC, pM2) using the neural tracing data available in the Allen Mouse Brain Connectivity Atlas (Oh et al., 2014). These projection data were originally acquired by injecting adeno-associated virus (AAV) encoding EGFP into various target brain areas and scanning EGFP-labelled axons throughout the brain with high-throughput serial 2-photon tomography. We used their software development kit (SDK), allensdk, to access and process their data in Python.
Dorsal view of the Allen Reference Atlas
Allen Reference Atlas is a high-resolution anatomical 3D reference atlas for the adult mouse brain. Different brain structures are colored differently in this atlas. All projection data in the Connectivity Atlas are registered to this reference atlas. We created a dorsal view of the Allen Reference Atlas to indicate the virus injection coordinates and cortical projection density in the dorsal cortex. First, we downloaded the 3D RGB-colored atlas at the resolution of 25 μm/pix. At each anterior-posterior (AP) and medial-lateral (ML) coordinate of the 3D atlas, we picked up the RGB value of the most dorsal brain surface. We obtained a dorsal view of the atlas by projecting these dorsal RGB values onto a single 2D plane.
Selection of injection data
In the Allen Mouse Brain Connectivity Atlas, each injection experiment is labelled with the name of the injected structure. First, we narrowed injection experiments using these annotations. We selected experiments with virus injections into retrosplenial area (RSP), anterior area (VISa) of posterior parietal association area (PTLp), and secondary motor area (MOs). Then, we further narrowed down injection experiments based on the exact injection coordinates. As we indicated in Figure S9, we isolated medial RSP injections, anterior VISa injections, and posterior MOs injections for RSC, PPC, and pM2, respectively. The database contains experiments that were performed on wild-type mice and Cre transgenic mice for cell-type specific tracing. We used experiments from only WT mice or combined data (WT + Cre). The projection patterns were similar in both cases (Figure S9).
Axon projection density in dorsal cortex
We analyzed the axon projection density from RSC, PPC, and pM2 in the dorsal cortex. For each injection experiment, we calculated the projection density at each AP-ML coordinate as [# of positive pixels] / [# of all pixels] in the volume of 25μm (AP axis) × 25μm (ML axis) × 1000μm (DV axis, from dorsal surface at each AP-ML coordinate). To create a mean projection density map, experiments with left hemisphere injections were mirrored relative to midline before averaging. We also quantified mean projection density within each imaging FOV that we used for in vivo 2-photon calcium imaging. Although our imaging FOVs were based on stereotactic coordinates from the bregma in the Paxinos’ atlas (Paxinos and Franklin, 2004), the Allen Reference Atlas does not include coordinates from the bregma. To register our imaging FOVs to the Allen Reference Atlas Coordinate, we calculated the scaling factors for the AP and ML dimensions of the mouse brain to match the brain in the Paxino’s atlas to the brain in the Allen Reference Atlas. Using the scaling factors, we estimated the coordinates of each imaging FOV on the Allen Reference Atlas. We calculated the mean signal density within each imaging FOV of the size 500 μm × 500 μm. The mean signal density of each FOV was used to construct the connectivity matrix in Figure 8C.
Data analysis and statistics
All data analyses and network simulations were performed in Python3.7 with libraries of TensorFlow (Abadi et al., 2016), scikit-learn (Pedregosa et al., 2011), NumPy (Harris et al., 2020), SciPy (Virtanen et al., 2020), and Statsmodels (Seabold and Perktold, 2010). Statistical tests were performed either in Python with SciPy and Statsmodels or in R with its statistics libraries. All accuracy measures reported in this study were obtained with cross-validation. Unless otherwise noted, we split trials into training set (70%), validation set (10%), and test set (20%) for each iteration of decoding, and repeated the network training 5 times by using different sets of trials as the test set. When we compared ΔQ retrieval/decoding accuracy across different cortical populations, we matched the number of cells in the input population activity by subsampling 240 cells in each iteration allowing repetitions with the smallest number of iterations to include every cell at least once for decoding, and the accuracies from the iterations were averaged. For all the simulations with artificial population activity, we created 10 distinct populations for each of the 3 types of coding modes by independently sampling tuning curve slopes from RSC neurons. These repetitions allowed us to tell the variability that originates from the randomness of ΔQ signal assignments and randomness of network trainings. All figure plots were created using Matplotlib (Hunter, 2007) and seaborn (Waskom, 2021) in Python.
Supplementary Material
Highlights.
Coding persistency in the cortex is learning- and context-dependent
Highly persistent value coding emerged in RSC and ANN during reinforcement learning
Persistency ensures untangled value representation within cylindrical geometry
Coding persistency facilitates brain-wide distributed information coding
Acknowledgements
We thank Marcus Benna and the Komiyama lab members for discussions and comments. This work was supported by NIH (R01 NS091010, R01 EY025349, R01 DC014690, and P30 EY022589), NSF (1940181), and David & Lucile Packard Foundation to T.K., and the Uehara Memorial Foundation Postdoctoral Fellowship, JSPS Postdoctoral Fellowship for Research Abroad, and the Research Grant from the Kanae Foundation for the Promotion of Medical Science to R.H.
Footnotes
Declaration of Interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, et al. (2016). TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. 2th USENIX Symp. Oper. Syst. Des. Implement. (OSDI 16), USENIX Assoc. 265–283. [Google Scholar]
- Allen WE, Chen MZ, Pichamoorthy N, Tien RH, Pachitariu M, Luo L, and Deisseroth K (2019). Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science (80-. ). 364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banino A, Barry C, Uria B, Blundell C, Lillicrap T, Mirowski P, Pritzel A, Chadwick MJ, Degris T, Modayil J, et al. (2018). Vector-based navigation using grid-like representations in artificial agents. Nature 557, 429–433. [DOI] [PubMed] [Google Scholar]
- Bari BA, Grossman CD, Lubin EE, Rajagopalan AE, Cressy JI, and Cohen JY (2019). Stable Representations of Decision Variables for Flexible Behavior. Neuron 103, 922–933.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D, Machler M, Bolker B, and Walker S (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw 67, 1–48. [Google Scholar]
- Cavanagh SE, Towers JP, Wallis JD, Hunt LT, and Kennerley SW (2018). Reconciling persistent and dynamic hypotheses of working memory coding in prefrontal cortex. Nat. Commun 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen TW, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, Shenoy KV, and Shenoy KV (2012). Neural population dynamics during reaching. Nature 487, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evangelidis GD, and Psarakis EZ (2008). Parametric image alignment using enhanced correlation coefficient maximization. IEEE Trans. Pattern Anal. Mach. Intell. 30, 1858–1865. [DOI] [PubMed] [Google Scholar]
- Friedrich J, Zhou P, and Paninski L (2017). Fast online deconvolution of calcium imaging data. PLoS Comput. Biol 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuster JM, and Alexander GE (1971). Neuron activity related to short-term memory. Science (80-. ). 173, 652–654. [DOI] [PubMed] [Google Scholar]
- Guo ZV, Inagaki HK, Daie K, Druckmann S, Gerfen CR, and Svoboda K (2017). Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545, 181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ, et al. (2020). Array programming with NumPy. Nature 585, 357–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hattori R (2021). PatchWarp. Zenodo. 10.5281/zenodo.5590965. [DOI] [Google Scholar]
- Hattori R, and Hensch TK (2017). Developmental dynamics of cross-modality in mouse visual cortex. bioRxiv doi: 10.1101/150847. [DOI] [Google Scholar]
- Hattori R, Südhof TC, Yamakawa K, and Hensch TK (2017). Enhanced cross-modal activation of sensory cortex in mouse models of autism. bioRxiv doi: 10.1101/150839. [DOI] [Google Scholar]
- Hattori R, and Komiyama T (2021). PatchWarp: Corrections of non-uniform image distortions in two-photon calcium imaging data by patchwork affine transformations. bioRxiv doi: 10.1101/2021.11.10.468164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hattori R, Danskin B, Babic Z, Mlynaryk N, and Komiyama T (2019). Area-Specificity and Plasticity of History-Dependent Value Coding During Learning. Cell 177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinton GE, Srivastava N, Krizhevsky A, Sutskever I, and Salakhutdinov RR (2012). Improving neural networks by preventing co-adaptation of feature detectors. ArXiv. [Google Scholar]
- Hunter JD (2007). Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 9, 90–95. [Google Scholar]
- Inagaki HK, Fontolan L, Romani S, and Svoboda K (2019). Discrete attractor dynamics underlies persistent activity in the frontal cortex. Nature 566, 212–217. [DOI] [PubMed] [Google Scholar]
- Iurilli G, Ghezzi D, Olcese U, Lassi G, Nazzaro C, Tonini R, Tucci V, Benfenati F, and Medini P (2012). Sound-Driven Synaptic Inhibition in Primary Visual Cortex. Neuron 73, 814–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung Y, Kennedy A, Chiu H, Mohammad F, Claridge-Chang A, and Anderson DJ (2020). Neurons that Function within an Integrator to Promote a Persistent Behavioral State in Drosophila. Neuron 105, 322–333.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy A, Kunwar PS, Li L. yun, Stagkourakis S, Wagenaar DA, and Anderson DJ (2020). Stimulus-specific hypothalamic encoding of a persistent defensive state. Nature 586, 730–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koay SA, Thiberge S, Brody CD, and Tank DW (2020). Amplitude modulations of cortical sensory responses in pulsatile evidence accumulation. Elife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobak D, Brendel W, Constantinidis C, Feierstein CE, Kepecs A, Mainen ZF, Qi XL, Romo R, Uchida N, and Machens CK (2016). Demixed principal component analysis of neural population data. Elife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N (2015). Deep Neural Networks: A New Framework for Modeling Biological Vision and Brain Information Processing. Annu. Rev. Vis. Sci. 1, 417–446. [DOI] [PubMed] [Google Scholar]
- Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lillicrap TP, Santoro A, Marris L, Akerman CJ, and Hinton G (2020). Backpropagation and the brain. Nat. Rev. Neurosci. 21, 335–346. [DOI] [PubMed] [Google Scholar]
- Maas A, Le Q, O’Neil T, Vinyals O, Nguyen P, and Ng A (2012). Recurrent neural networks for noise reduction in robust ASR. INTERSPEECH. [Google Scholar]
- Mante V, Sussillo D, Shenoy KV, and Newsome WT (2013). Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques JC, Li M, Schaak D, Robson DN, and Li JM (2020). Internal state dynamics shape brainwide activity and foraging behaviour. Nature 577, 239–243. [DOI] [PubMed] [Google Scholar]
- Masse NY, Yang GR, Song HF, Wang XJ, and Freedman DJ (2019). Circuit mechanisms for the maintenance and manipulation of information in working memory. Nat. Neurosci. 22, 1159–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland J, Rumelhart D, and PDP Research Group (1986). Parallel Distributed Processing (MIT Press; ). [Google Scholar]
- Miller EK, Erickson CA, and Desimone R (1996). Neural mechanisms of visual working memory in prefrontal cortex of the macaque. J. Neurosci. 16, 5154–5167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitani A, and Komiyama T (2018). Real-time processing of two-photon calcium imaging data including lateral motion artifact correction. Front. Neuroinform. 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray JD, Bernacchia A, Roy NA, Constantinidis C, Romo R, and Wang XJ (2017). Stable population coding for working memory coexists with heterogeneous neural dynamics in prefrontal cortex. Proc. Natl. Acad. Sci. U. S. A. 114, 394–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nat. Neurosci. 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, et al. (2014). A mesoscale connectome of the mouse brain. Nat 2014 5087495 508, 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orhan AE, and Ma WJ (2019). A diverse range of factors affect the nature of neural representations underlying short-term memory. Nat. Neurosci. 22, 275–283. [DOI] [PubMed] [Google Scholar]
- Osa T, Pajarinen J, Neumann G, Bagnell JA, Abbeel P, and Peters J (2018). An Algorithmic Perspective on Imitation Learning. Found. Trends Robot. 7, 1–179. [Google Scholar]
- Pachitariu M, Stringer C, Dipoppa M, Schröder S, Rossi LF, Dalgleish H, Carandini M, and Harris K (2017). Suite2p: beyond 10,000 neurons with standard two-photon microscopy. bioRxiv doi: 10.1101/061507. [DOI] [Google Scholar]
- Pachitariu M, Stringer C, and Harris KD (2018). Robustness of spike deconvolution for neuronal calcium imaging. J. Neurosci. 38, 7976–7985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascanu R, Mikolov T, and Bengio Y (2012). On the difficulty of training Recurrent Neural Networks. 30th Int. Conf. Mach. Learn. ICML 2013 2347–2355. [Google Scholar]
- Paxinos G, and Franklin KBJ (2004). The Mouse Brain in Stereotaxic Coordinates, 2nd edition. Acad. Press; 360 p. [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. (2011). Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 12, 2825–2830. [Google Scholar]
- Rogers TT, and McClelland JL (2014). Parallel distributed processing at 25: Further explorations in the microstructure of cognition. Cogn. Sci 38, 1024–1077. [DOI] [PubMed] [Google Scholar]
- Romo R, Brody CD, Hernández A, and Lemus L (1999). Neuronal correlates of parametric working memory in the prefrontal cortex. Nature 399, 470–473. [DOI] [PubMed] [Google Scholar]
- Rumelhart D, McClelland J, and PDP Research Group (1986). Parallel Distributed Processing (MIT Press; ). [Google Scholar]
- Russo AA, Bittner SR, Perkins SM, Seely JS, London BM, Lara AH, Miri A, Marshall NJ, Kohn A, Jessell TM, et al. (2018). Motor Cortex Embeds Muscle-like Commands in an Untangled Population Response. Neuron 97, 953–966.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russo AA, Khajeh R, Bittner SR, Perkins SM, Cunningham JP, Abbott LF, and Churchland MM (2020). Neural Trajectories in the Supplementary Motor Area and Motor Cortex Exhibit Distinct Geometries, Compatible with Different Classes of Computation. Neuron 107, 745–758.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seabold S, and Perktold J (2010). Statsmodels: Econometric and Statistical Modeling with Python. PROC. 9th PYTHON Sci. CONF. [Google Scholar]
- Serences JT (2008). Value-Based Modulations in Human Visual Cortex. Neuron 60, 1169–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song HF, Yang GR, and Wang XJ (2017). Reward-based training of recurrent neural networks for cognitive and value-based tasks. Elife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava N, Hinton G, Krizhevsky A, and Salakhutdinov R (2014). Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 15, 1929–1958. [Google Scholar]
- Steinmetz NA, Zatka-Haas P, Carandini M, and Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science (80-. ). 364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, and Barto AG (2018). Reinforcement Learning: An Introdcution (2nd ed.) (MIT Press; ). [Google Scholar]
- Tsuda B, Tye KM, Siegelmann HT, and Sejnowski TJ (2020). A modeling framework for adaptive lifelong learning with transfer and savings through gating in the prefrontal cortex. Proc. Natl. Acad. Sci. U. S. A. 117, 29872–29882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent P, Larochelle H, Lajoie I, Bengio Y, and Manzagol P-A (2010). Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 11, 3371–3408. [Google Scholar]
- Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. (2020). SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang JX, Kurth-Nelson Z, Kumaran D, Tirumala D, Soyer H, Leibo JZ, Hassabis D, and Botvinick M (2018). Prefrontal cortex as a meta-reinforcement learning system. Nat. Neurosci. 21, 860–868. [DOI] [PubMed] [Google Scholar]
- Waskom ML (2021). seaborn: statistical data visualization. J. Open Source Softw. 6, 3021. [Google Scholar]
- Wekselblatt JB, Flister ED, Piscopo DM, and Niell CM (2016). Large-scale imaging of cortical dynamics during sensory perception and behavior. J. Neurophysiol. 115, 2852–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamins DLK, and DiCarlo JJ (2016). Using goal-driven deep learning models to understand sensory cortex. Nat. Neurosci 2016 193 19, 356–365. [DOI] [PubMed] [Google Scholar]
- Zhu J, Cheng Q, Chen Y, Fan H, Han Z, Hou R, Chen Z, and Li CT (2020). Transient Delay-Period Activity of Agranular Insular Cortex Controls Working Memory Maintenance in Learning Novel Tasks. Neuron 105, 934–946.e5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data reported in this paper are available from the lead contact upon reasonable request.
dsPCA code has been deposited at Zenodo and is publicly available. The DOI and the link to the latest code in the GitHub repository are listed in the key resource table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.