Solubility of favipiravir (as an anti-COVID-19) in supercritical carbon dioxide: An experimental analysis and thermodynamic modeling

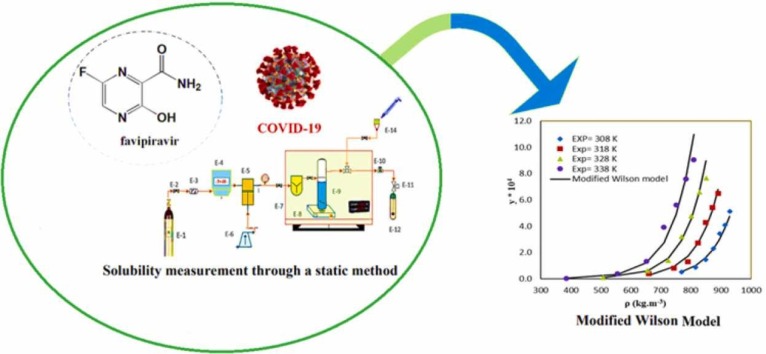
Abstract

Favipiravir is one of the most commonly prescribed drugs in the treatment of COVID-19 in the early stages of the disease. In this work, the solubility of favipiravir was measured in supercritical CO₂ at temperatures ranging from 308 to 338 K and pressures ranging from 12 to 30 MPa. The mole fraction solubility of favipiravir was in the range of 3.0 × 10^-6 to 9.05 × 10^-4. The solubility data were correlated with three types of methods including; (a) density-based models (Chrastil, Garlapati and Madras, Sparks et al., Sodeifian et al., K-J and Keshmiri et al.), (b) Equations of states SRK with quadratic mixing rules) and (c) expanded liquid theory (modified Wilson model). According to the results, modified Wilson and K-J models are generally capable of providing good correlation of solubility. Finally, the approximate values of total (${\Delta H}_{\mathit{total}}$), vaporization (${\Delta H}_{\mathit{vap}}$), and solvation (${\Delta H}_{\mathit{sol}}$) enthalpies were computed.

Graphical Abstract

Nomenclature

${\mathit{a}}_{\mathit{0}}-{\mathit{a}}_{\mathit{5}}$

Adjustable parameters of model

$\mathit{AARD}\%$

Average absolute relative deviation

$\mathit{a}(\mathit{T})$

Energy parameter of the cubic EoS (Nm⁴ mol⁻²)

$\mathit{B}$

Volume parameter for equations of state (m³ mol⁻¹)

$\mathit{C}$

Solubility of solute (g/L)

${\mathit{c}}_{\mathit{s}}$

Concentration of solute (g/L) in the collection vial

${\mathit{H}}_{\mathit{f}}^{\mathit{2}}$

Molar heat of fusion

${\mathit{K}}_{\mathit{ij}}$

Binary interaction parameter

${\mathit{K}}_{\mathit{ij}}$

Binary interaction parameter in the mixing rules

${\mathit{L}}_{\mathit{ij}}$

Binary interaction parameter in the mixing rules

${\mathit{M}}_{\mathit{w}}$

Solute molecular weight (g/mol)

${\mathit{M}}_{{\mathit{co}}_{\mathit{2}}}$

CO₂ molecular weight (g/mol)

$\mathit{N}$

Number of data points, dimensionless

$\mathit{P}$

Pressure

${\mathit{P}}_{\mathit{c}}$

Critical pressure

$\mathit{P}\mathit{r}$

Reduced pressure

${\mathit{P}}_{\mathit{ref}}$

Reference pressure

${\mathit{P}}_{\mathit{sub}}$

Sublimation pressure (Pa)

$\mathit{Q}$

Number of independent variables

$\mathit{R}$

Gas constant, Jmol⁻¹ K⁻¹

${\mathit{R}}_{\mathit{adj}}$

Adjusted correlation coefficient

$\mathit{S}$

Equilibrium solubility

$\mathit{T}$

Temperature, K

${\mathit{T}}_{\mathit{b}}$

Boling point

${\mathit{T}}_{\mathit{c}}$

Critical temperature

${\mathit{T}}_{\mathit{r}}$

Reduced temperature

${\mathit{y}}_{\mathit{2}}$

Mole fraction solubility

${\mathit{V}}_{\mathit{s}}$

Volume of the collection vial (L)

${\mathit{V}}_{\mathit{L}}$

Volume of the sampling loop (L)

$v^s$

Solid molar volume

$\mathit{Z}$

Number of adjustable parameters

Greek symbols

$\mathit{\alpha }(\mathit{Tr},\mathit{\omega })$

Temperature-dependent function of the considered parameter of the EoS

$\mathit{\alpha }$

Regressed parameter of the Wilson’s model

$\mathit{\beta }$

Regressed parameter of the Wilson’s model

$\mathit{\delta }$

Solubility parameter (cal/cm³)^0.5

$\mathit{\rho }$

Density, kg.m⁻³

${\mathit{\rho }}_{\mathit{c}}$

Critical density

${\mathit{\rho }}_{\mathit{r}}$

Reduced density

${\mathit{\rho }}_{\mathit{ref}}$

Reference density

${\mathit{\upsilon }}_{\mathit{1}}$,${\mathit{\upsilon }}_{\mathit{2}}$

Volumes of the SCF and the solid solute, respectively

$\mathit{\lambda }$

Energies of interaction between the molecules designated in the subscripts

${\mathit{\gamma }}_{\mathit{2}}^{\mathit{\infty }}$

The activity coefficient of the solid solute at infinite dilution

$\mathit{\Phi }$

Fugacity coefficient

$\mathit{w}$

Acentric factor

Superscripts

Cal

Calculated

Exp

Experimental

i,j

Component

Sub

Sublimation

1. Introduction

In December 2019, a new coronavirus (COVID-19) emerged whose quick outbreak led to a pandemic according to the World Health Organization (WHO) classification. COVID-19 was initially discovered in Wuhan, Hubei Province, China. Coronavirus can cause drastic acute respiratory syndrome (SARSCoV-2) [1]. SARS CoV-2 belongs to the coronaviridae family with a positive-strand RNA (+RNA) genome. An RNA-dependent RNA polymerase (RdRp) and proteases are encoded by this single-stranded RNA beta-coronavirus [2]. Quarantine and antiviral medicines significantly reduced the ultimate size of the prevalence and peak incidence [3]. Favipiravir, remdesivir, umifenovir, oseltamivir, immune globulin, lopinavir, azithromycin, and ivermectin have been employed for the treatment of COVID-19 [4].

Favipiravir (FAV) was endorsed by the Food and Drug Administration (FDA) in 2014 to cure new and re-emerging influenza viruses [3]. Thanks to their antiviral features, favipiravir and its derivatives have been approved as a prodrug and support in the treatment of the influenza virus [5]. FAV belongs to class II in the Biopharmaceutics Classification System (BCS). High permeability and low water solubility are two major characteristics of favipiravir. The poor solubility of the favipiravir in the aqueous media of the human body has decreased its effectiveness and bioavailability [6]. Recently, Abd Elkodous et al. [4] reviewed nanomaterial-based drug delivery systems for the treatment of COVID-19 to increase the bioavailability of current drugs, reduce their toxicity, and increase their efficiency. They reported that favipiravir-encapsulated nano-emulsions as prospective carriers of COVID-19 drug delivery. Biodegradable nano-emulsions have a kinetically persistent structure and can be dispersed both in oil and water. Small particles with a diameter range of 5–200 nm make up nano-emulsion formulae.

Various approaches have been developed to enhance the aqueous solubility and bioavailability of drugs among which, co-crystallization, salt formation, encapsulation/impregnation, and particle size reduction in micro/nano-scale can be mentioned. Furthermore, supercritical fluid technology could be a viable option to overcome the drawbacks of conventional techniques for enhancing the solubility of poor water-soluble formulas. Traditional processes suffer from temperature sensitivity and impurity contamination. Non-toxicity, eco-friendliness, and adaptability are among the benefits of SCF technology, making it an ideal route in green chemistry. SCF has been used to improve solubility and increase the bioavailability of poorly soluble drugs [7], [8], [9], [10]. The bioavailability of drugs is highly dependent on their solubility and dissolution. In this regard, the production of nano/microparticles of drugs through the SCF method is of paramount significance. Concerning particle development, SCF technology is an alternative technique for particle production which can avoid most of the disadvantages associated with conventional approaches such as crushing, milling, crystallization, and precipitation. More advanced technologies, such as microencapsulation, coating, and composite particle creation, can be developed by SCF technology [11], [12], [13], [14], [15], [16], [17], [18]. The solubility of drugs in SC-CO₂ is the main parameter I reduction of the particle size, highlighting the significance of measuring drug solubility. Several methods have been introduced for the measurement of solubility among which, gravimetric, spectrometric, chromatographic, and miscellaneous methods can be mentioned.

Experimental measurement of drug solubility in SC-CO₂ at different temperatures and pressures is time-consuming, costly, and in some cases impossible. Therefore, various correlative models such as the equation of states (EoSs; (e.g. Peng-Robinson (PR) and Soave- Redlich-Kowang (SRK)), empirical models, and expanded liquid models (e.g. universal quasi-chemical (UNIQUAC) and modified Wilson's models) have been considered to correlate the solubility of solid at different pressures and temperatures in SC-CO₂. Prediction and correlation via EoS and expanded liquid require the calculation of the physicochemical properties of solid (pharmaceutical components) such as acentric factor, critical pressure, temperature, and sublimation pressure. These properties are not in literature and are usually determined by different group contribution (GC) methods. In return, the empirical models (density-based model), only require pressure, temperature, and SC-CO₂ density. The correlative model has indicated the best fitting with the experimental data [8], [9], [13], [19].

In the current research, the solubility of favipiravir was measured in the temperature range of 308 − 338 K and the pressure range of 12 − 30 MPa. For this purpose, solubility data were correlated with three types of methods including (1) Empirical density-based models (Chrastil, Garlapati and Madras, Sparks et al., Sodeifian et al., K-J, and Keshmiri et al.) (2) Equations of states (EoSs) (Soave–Redlich–Kwong (SRK) with vdW2 mixing rule), and (3) expanded liquid theory (modified Wilson model). The mentioned models were evaluated based on mean absolute deviation (AARD%) and adjusted correlation coefficient (R_adj).

2. Experiments

2.1. Materials

Favipiravir (CAS No. 259793–96–9) has been procured through the Tofigh Darou pharmaceutical corporation (Tehran, Iran), at the minimum purity of 99%. Carbon dioxide (CO₂) was prepared by Oxygen Novin Company (Shiraz, Iran) with a purity of 99.99%. Analytical-grade methanol was supplied by Merck (Darmstadt, Germany). The structure of favipiravir (drug) and the information of all components are presented in Table 1.

Table 1.

Structure and details of favipiravir.

Compound	Formula	CAS number	Structure	Mw (g/mol)	Tm (K)	λmax (nm)
Favipiravir	C5H4FN3O2	259793–96–9		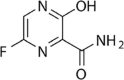157.1	465.9	323

2.2. Experimental apparatus

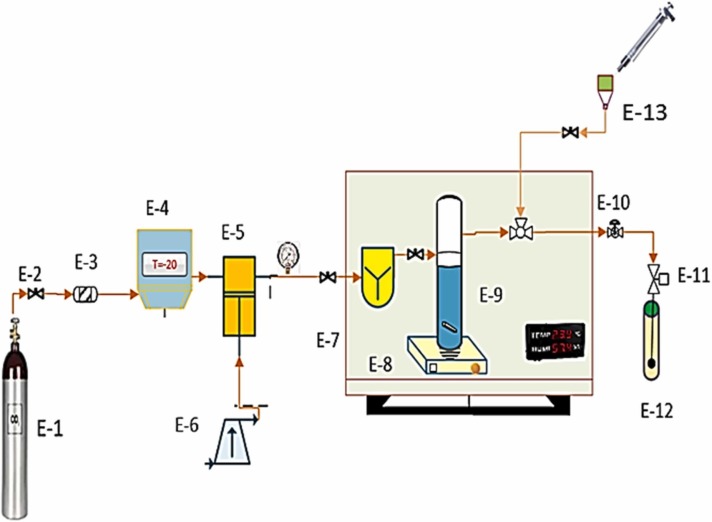
The applied laboratory setup with a spectrophotometer is presented in Fig. 1 which encompassed a CO₂ cylinder (E-1), a needle valve (E-2), a molecular sieve filter (E-3), a refrigerator unit (E-4), a high-pressure pump (E-5, air driven liquid pump, type-M64, Shineeast Co., Shandong, China), an air compressor (E-6), an incubator (E-7, shimaz), magnetic stirrer (100 rpm) (E-8, Alfa, D-500 180,), a high-pressure equilibrium cell (E-9), a back-pressure valve (E-10, Xi'an Shelok Instrument Technology Co., Shaanxi, China), a micrometer valve (E-11), a collection vial (E-12), a Syringe (E-13). In this high-pressure system, all equipment, piping and connections were made from stainless steel 316 at 1/8″ in size. The CO₂ flow from the cylinder first enters the molecular sieve filter (pore size of 1 µm) to prevent impurities. It then flows to the refrigerator. The temperature inside the refrigerator is about − 15 °C, liquifying the CO₂ flow. The liquid CO₂ at the pressure in the CO₂ tank (about 60 bar) entered the high-pressure reciprocating pump. Using the pressure gauge and transmitter, measurements were performed at a precision of ± 1 bar.

Fig. 1.

Process diagram of experimental apparatus used for measuring favipiravir solubility. E-1: CO₂ cylinder, E-2: Needle valve, E-3: Filter, E-4: Refrigerator unit, E-5: High-pressure pump, E-6: Compressor, E-7: Oven, E-8: Magnetic stirrer, E-9: Equilibrium cell, E-10: Backpressure, E-11: Micrometer valve, E-12: Collection vial, E-13: syringe.

In the next step, 3000 mg favipiravir was mixed in SC-CO₂ using a magnetic stirrer to establish an equilibrium phase into a cell with a capacity of 300 mL. The temperature was maintained at the desired level by an oven equipped with a digital display with temperature measurements at an accuracy of ± 0.1 K. A sintered filter (1 µm) was used on both sides of the cell to hold the drug. Carbon dioxide was pressurized and then transferred to the cell at the appropriate pressure. The static time, i.e. the time to reach equilibrium, was considered 120 min based on the preliminary experiments. After 120 min, 600 µL of saturated SC-CO₂ was introduced into the injection loop using a three-valve two-position device. By redirecting the injection valve, the loop was depressurized into the collection vial containing a certain volume of methanol (solvent). In this part, the micrometer valve was used for controlling the flow.

In the final step, about 1 mL of solvent was injected through an external needle valve for washing the loop and the solution is collected in the vial. The final volume of the solution was 5 mL. Each experiment was repeated three times (triplicates). The favipiravir solubility values were determined by measuring the absorbance at λ_max on a Shimadzu UV-Vis spectrophotometer with a 1 cm long quartz cell. The solubility was calculated from the concentration of solute using the calibration curve (with regression coefficient 0.998) and the UV-absorbance.

At different sets of temperature and pressure, the equilibrium mole fraction, y ₂, and solubility, S (g/L), in SC-CO₂ were computed as follows [20]:

$$y_2=\frac{n_{solute}}{n_{solute}+n_{C{O}_2}},$$ (1)

where:

$$n_{solute}=\frac{C_s\left(\frac{g}{L}\right)V_s\left(L\right)}{M_s\left(\frac{g}{mol}\right)},$$ (2)

and

$$n_{C{O}_2}=\frac{V_l\left(L\right)\rho \left(\frac{g}{L}\right)}{M_{C{O}_2}\left(\frac{g}{mol}\right)}$$ (3)

where n _solute and n _CO2 are moles of solute (favipiravir) and CO₂ in the sampling loop, respectively, C _s denotes the solute concentration (g/L) in the collection vial as obtained from the calibration curves. The volumes of the collection vial and sampling loop are Vs(L)= 5 × 10^-3 and V _l(L)= 600 × 10^-6 respectively. M _s also represents the molecular weight of the solute while M _CO2 is the molecular weight of CO₂. The accuracy of the mentioned volumes (500 µL and 5 mL) was 0.5% and 0.2% respectively.

The equilibrium solubility, S (g/L), of the solute in the SC-CO₂ can be obtained by Eq. (4):

$$S=\rho \frac{M_2}{M_1}\frac{y_2}{\left(1-y_2\right)}$$ (4)

3. Modeling studies

In this research, three types of models were considered to correlate the experimental solubility data of Favipiravir in SC-CO₂: (1) EoS-based SRK, (2) empirical density-based models (Chrastil, Garlapati and Madras, Sparks et al., Sodeifian et al., K-J, and Keshmiri et al.,), and (3) expanded liquid theory (modified Wilson's model).

3.1. Equation of state-based (EoS) models

For solubility measurements of the solid (component 2) in SC-CO₂ (component 1) under the thermodynamic equilibrium condition, the following equation can be used:

$$y_2=\frac{P_2^{sub}\left(T\right)}{P}\frac{{\varphi }_2^{sat.s}\left(T\right)}{{\varphi }_2\left(T,P,y\right)}\exp \left[\frac{v_2^s\left(P-P_2^{sub}\left(T\right)\right)}{RT}\right]$$ (5)

where P, R, T, $P_2^{sub}\left(T\right)$, ${\varphi }_2^{sat.s}\left(T\right)$, ${\varphi }_2\left(T,P,y\right)$, and $v_2^s$ are pressure, gas constant, temperature, sublimation pressure of the drug, saturation fugacity coefficient of the solute, fugacity coefficient of the solute in supercritical phase, and the solid molar volume, respectively. According to Eq. (5), solubility (y₂) depends on the physicochemical properties of the pure components. Since the physicochemical and critical properties of pharmaceutical compounds are not available in the literature; the group contribution methods were used to determine these properties. Different group contribution methods have been developed to estimate the critical and physicochemical properties of the solid compounds (drug). Table 2 reports the critical and other physicochemical properties of favipiravir. Selection of the proper mixing and combining rules to calculate the thermodynamic characteristics of the mixtures and parameters of the EoS is of crucial importance. In the current work, the quadratic mixing rules was applied for EoS.

Table 2.

Critical and physicochemical properties of favipiravir.

Component	Tb (K)	Tc (k)	Pc (bar)	ω	Vs (cm3/mol)	T (K)
						308	318	328	338
						Psuba (bar)
Favipiravir	589.73b	878.71b	66.82b	0.5799c	97.53d	2.43 × 10-8	8.86 × 10-8	2.94 × 10-7	9 × 10-7
Carbon dioxide		304.18	73.8	0.224

^aEstimated by Grain-Watson method.

^bMarrero and Gani.

^cEstimated by the Ambrose–Walton corresponding states method.

^dEstimated by Immirzi–Perini method.

3.1.1. Soave–Redlich–Kwong equation

The reduced residual Helmholtz energy of the SRK model can be expressed as follows [21]:

$$P=\frac{\mathit{RT}}{v-b}-\frac{a\left(T\right)}{v\left(v+b\right)}$$ (6)

Where $R$, $T$, and $v$ are the universal gas constant, absolute temperature, and molar volume, respectively.

The parameters of a and b depend on the critical and physical properties of pure components and can be determined by the following equation (for a single-component system):

$$\mathrm{a}\left(\mathrm{T}\right)=\frac{\mathrm{0.42747}{R}^2{T}_c^2}{P_c}\times \mathrm{\alpha }\left({\mathrm{T}}_{\mathrm{r},\mathrm{\omega }}\right)$$ (7)

$$\mathrm{\alpha }\left({\mathrm{T}}_{\mathrm{r},\mathrm{\omega }}\right)={\left[\mathrm{1}+\mathrm{m}\left({\mathrm{1}-\mathrm{T}}_r^{\mathrm{0.5}}\right)\right]}^2$$ (8)

$$\mathrm{m}=0.480+1.574\mathrm{\omega }-0.176{\mathrm{\omega }}^2$$ (9)

$$\text{b=}\frac{0.08664\text{R}{\text{T}}_{\text{c}}}{{\text{P}}_{\text{c}}}$$ (10)

The quadratic mixing rules in mole fraction for $a\left(T\right)$ and $b$ are used as follows:

$$a\left(T\right)=\sum _i\sum _j{y}_i{y}_j{a}_{ij}\left(T\right)$$ (11)

$$b=\sum _i\sum _j{y}_i{y}_j{b}_{ij}$$ (12)

Where $a_{ij}\left(T\right)$ and $b_{ij}$ are the cross energetic and the cross-co-volume parameters, respectively. $a_{ij}\left(T\right)$ and $b_{ij}$ can be calculated by:

$$a_{ij}\left(T\right)=\sqrt{a_{ii}\left(T\right)a_{jj}\left(T\right)}\left(1-k_{ij}\right)$$ (13)

$$b_{ij}=\frac{b_i+b_j}{2}\left(1-l_{ij}\right)$$ (14)

3.2. Expanded liquid theory

The density of the supercritical fluid is very close to the typical liquid and its phase can be considered as an expanded liquid [22]. As a result, the thermodynamic phase equilibrium of solid and supercritical fluid can be defined by solid-liquid equilibrium and activity coefficients. The activity coefficients are required to calculate the solid solubility in the supercritical phases. In this regard, the equilibrium between the pure solid and the supercritical phase is expressed as follows [23], [24]:

$$f_2^s=f_2^{\mathit{SCF}}=f_2^L$$ (15)

Where ${\mathrm{ƒ}}_2^S$ and ${\mathrm{ƒ}}_2^{\mathit{ScF}}$ are the fugacity of the solid solute in the solid phase and the supercritical phase, respectively.

The fugacity of solute in the supercritical phase can be expressed by:

$$f_2^L={\gamma }_2{y}_2{f}_2^{0L}$$ (16)

and

$$f_2^{\mathit{os}}={\gamma }_2{y}_2{f}_2^{0L}$$ (17)

Where ${\gamma }_2$is the activity coefficient,$y_2$ is the mole fraction of solid solubility and ${\mathrm{ƒ}}_2^{0S}$ is and the fugacity of the pure solid solute in the expanded liquid phase.

According to Prausnitz et al. [25]:

$$\mathit{ln}\frac{{\mathrm{ƒ}}_2^{0S}}{{\mathrm{ƒ}}_2^{0L}}=\frac{-∆{\mathrm{H}}_2^f}{R}\left(\frac{1}{T}-\frac{1}{T_m}\right)-\frac{∆\mathit{Cp}}{\mathit{RT}}\left(\frac{T-T_m}{T}\right)+\frac{∆\mathit{Cp}}{R}\mathit{ln}\left(\frac{T}{T_m}\right)$$ (18)

The heat capacity terms can be neglected [25], so:

$$y_2=\frac{1}{{\gamma }_2}\mathit{exp}\left(\frac{-∆H_2^f}{R}\left(\frac{1}{T}-\frac{1}{T_m}\right)\right)$$ (19)

Where $∆H_2^f$ is the enthalpy of fusion and $T_m$ shows the melting point of the solid (drug). The solid solubility in the supercritical fluid is very low (~ infinite dilution). Therefore, the activity coefficient of the solid solute is one at infinite dilution. Thus, Eq. (19) becomes:

$$y_2=\frac{1}{{\gamma }_2^{\mathrm{\infty }}}\mathit{exp}\left[\frac{-∆H_2^f}{R}\left(\frac{1}{T}-\frac{1}{T_m}\right)\right]$$ (20)

3.2.1. Modified Wilson model

Wilson equation can be utilized for determining the activity coefficient of the solid solute at infinite dilution. This equation consists of two parts, a combinatorial contribution based on Flory’s theory, and a term based on the Gibbs excess energy, which can be written as follows [23]:

$$\frac{G^E}{RT}=-\sum _i{x}_i\ln \left(\sum _j{x}_j{\Lambda }_{ij}\right)$$ (21)

Where G ^E is the excess Gibbs energy, and ${Ʌ}_{12}$ and ${Ʌ}_{21}$ represent adjustable parameters.

$$\ln {\gamma }_i=-\ln \left(\sum _j{x}_j{\Lambda }_{ij}\right)+1-\sum _k\frac{x_k{\Lambda }_{ki}}{\sum _j{x}_j{\Lambda }_{kj}}$$ (22)

According to the theory proposed by Assael et al., [26], Eq. (22) can be rewritten to the following form:

$$\ln {\gamma }_2^{\infty }=1-{\Lambda }_{12}-\ln {\Lambda }_{21},$$ (23)

where ${Ʌ}_{12}$and ${Ʌ}_{21}$ are defined at infinite dilution conditions:

$${\Lambda }_{12}={\upsilon }_2{\rho }_c{\rho }_r\exp \left(-\frac{{\lambda }_{12}^{\prime }}{T_r}\right),$$ (24)

and

$${\Lambda }_{21}=\frac{1}{{\upsilon }_2{\rho }_c{\rho }_r}\exp \left(-\frac{{\lambda }_{21}^{\prime }}{T_r}\right)$$ (25)

Where ${\rho }_c$ is the critical density of SCF, ${\rho }_r({\rho }_r=\frac{\rho }{{\rho }_c})$ represents the reduced density of the SCF, ${\upsilon }_2$denotes the molar volume of the solid solute. The dimensionless energies of interaction are as follows:

$${\lambda \prime }_{12}=\frac{{\lambda }_{12}}{R{T}_{1c}}$$ (26)

and

$${\lambda \prime }_{21}=\frac{{\lambda }_{21}}{R{T}_{1c}}$$ (27)

To address the effect of high pressures and simplify the prediction process, Wilson model was introduced by an empirical expression that linearly correlates the molar volume and the reduced density [23]:

$${\upsilon }_2=\alpha {\rho }_r+\beta$$ (28)

where$\alpha$, $\beta$, ${\lambda \prime }_{12}$ and${\lambda \prime }_{21}$ are the regressed parameters of the model.

3.3. Semi-empirical density-based models

Density-based correlations are common techniques for modeling solid solubility in SCFs. Empirical models do not require estimation of the physicochemical properties of solid as they only depend on temperature, pressure, and density of SCF (independent variables) as well as several adjustable parameters (constants). In the current work, empirical density-based models (proposed by Chrastil, Garlapati, and Madras, Sparks et al., Sodeifian et al., K-J, and Keshmiri et al.) were applied for correlating the experimental solubility data.

The constants in the empirical models were determined by regression of experimental data. The adjustable parameters were optimized by simulated annealing (MATLAB software). The average absolute relative deviation ($\mathrm{AARD}\%$) was used to compare the precision of the model with experimental data which can be defined by:

$$\mathit{AARD}\%=\frac{100}{N_t-Z}\sum _{i=1}^{N_t}\frac{\left|y_2^{\mathit{cal}}-y_2^{\mathit{exp}}\right|}{y_2^{\mathit{exp}}}$$ (29)

Where Z and $N_t$ are the number of fitted parameters for each model and the number of data points in each set, respectively. As another criterion for comparing different models, R _adj has the following expression [27], [28]:

$$R_{adj}=\sqrt{\left|R^2-(Q(1-R^2)/(N-Q-1))\right|}$$ (30)

Where N shows the number of data points in each set, Q is the number of independent variables in each equation.

4. Results and discussion

4.1. Experimental data

Solubility of favipiravir in SC-CO₂ was experimentally measured at the temperature range of 308–338 K and pressure range of 10–30 MPa. Solubility data of favipiravir is collected in Table 3. The SC-CO₂ density was calculated by Span-Wanger EoS [29]. Furthermore, each data point was repeated three times to increase the reliability of the measurements; relative standard uncertainties were lower than 5%. The expanded uncertainty with the mole fractions is also reported in Table 3.

Table 3.

The favipiravir solubility experimental data in SC-CO₂. The y₂ and S are mole fractions and solubility of solute in the SC-CO₂, respectively.^a.

Temperature (K)	Pressure (MPa)	Density (kg/m3)	Binary
			y2 × 104 (Mole Fraction)	Standard deviation of the mean, SD (ȳ) × (104)	Expanded uncertainty × 104	S× 101 (Solubility (g/L))
308	12	768.42	0.53	0.014	0.027	1.46
	15	816.06	0.87	0.041	0.047	2.54
	18	848.87	1.44	0.023	0.017	4.37
	21	874.40	2.31	0.023	0.011	7.22
	24	895.54	3.42	0.046	0.014	10.95
	27	913.69	4.09	0.023	0.007	13.35
	30	929.68	5.13	0.069	0.014	17.04
318	12	659.73	0.37	0.041	0.110	0.87
	15	743.17	0.80	0.014	0.018	2.13
	18	790.18	1.30	0.046	0.036	3.67
	21	823.70	2.72	0.047	0.018	8.01
	24	850.10	4.29	0.093	0.022	13.03
	27	872.04	5.41	0.047	0.010	16.86
	30	890.92	6.48	0.116	0.018	20.63
328	12	506.85	0.08	0.001	0.019	0.15
	15	654.94	0.60	0.003	0.008	1.41
	18	724.13	1.39	0.047	0.034	3.60
	21	768.74	3.21	0.070	0.022	8.82
	24	801.92	4.75	0.068	0.015	13.61
	27	828.51	6.58	0.117	0.018	19.48
	30	850.83	7.65	0.092	0.012	23.26
338	12	384.17	0.03	0.008	0.270	0.04
	15	555.23	0.37	0.014	0.037	0.74
	18	651.18	1.32	0.023	0.018	3.07
	21	709.69	3.92	0.070	0.019	9.95
	24	751.17	5.6	0.043	0.009	15.03
	27	783.29	7.57	0.115	0.016	21.19
	30	809.58	9.05	0.163	0.018	26.18

The experimental standard deviation and the experimental standard deviation of the mean (SD) were calculated by $\mathrm{S}\left({\mathrm{y}}_{\mathrm{k}}\right)=\sqrt{\frac{{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\mathrm{y}\right)}^2}{\mathrm{n}-1}}$ and $\mathrm{SD}\left(\stackrel{\circledR }{\mathrm{y}}\right)=\frac{\mathrm{S}\left({\mathrm{y}}_{\mathrm{k}}\right)}{\sqrt{\mathrm{n}}}$ respectively. The relative combined standard uncertainty was obtained by ${\mathrm{U}}_{\mathrm{combined}}/\mathrm{y}=\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\left({\mathrm{P}}_{\mathrm{i}}\mathrm{U}\left({\mathrm{x}}_{\mathrm{i}}\right)/{\mathrm{x}}_{\mathrm{i}}\right)}^2}$. The expanded uncertaint U is $\mathrm{k}\times {\mathrm{U}}_{\mathrm{combined}}$. ^bStandard uncertainty u are (T) = 0.1 K; u(p) = 0.1 MPa. The relative standard uncertainties are calculated below 0.05 for solubilities and mole fractions. ^c Data from the Span–Wagner equation of state ¹⁸.

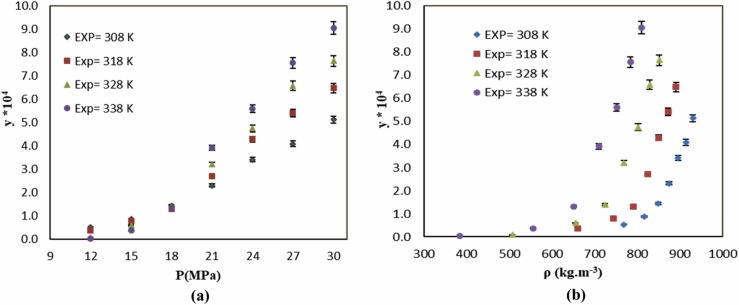
Fig. 2 shows the mole fraction solubility of favipiravir vs. pressure and density at different temperatures. In general, the density of SC-CO₂ and its solvating power increased with increasing the pressure. Therefore, favipiravir solubility in SC-CO₂ rose with increasing pressure (Table 3 and Fig. 2). As indicated in Fig. 2, at the pressure range of 12–18 MPa, the solubility of favipiravir in SC-CO₂ decreased with increasing the temperature. At pressures below 18 MPa, favipiravir solubility showed a decremental trend with increasing temperature. Above this pressure (18 MPa), the solubility increased with elevating the temperature. The mentioned trend can be also observed in Fig. 2, where the solubility curve showed the crossover region between 15 and 18 MPa. At pressures lower than the crossover region, the density effect is predominant and as a result, the solubility increases with decreasing temperature. However, at pressures above the crossover point, the vapor pressure of the solution was the main factor and the solubility increased at higher temperatures. The crossover point of various pharmaceutical compounds in SC-CO₂ have been investigated by some other researchers, that crossover point of some of these compounds was reported in Table 4.

Fig. 2.

The influence of (a) pressure and (b) density of SC-CO₂ on favipiravir solubility at different temperatures.

Table 4.

Review of some articles on the crossover points of various pharmaceutical compound in SC-CO₂.

Compound	Pressure range (MPa)	Temperature range (K)	Crossover (MPa)	Mole fraction (y)	Ref
Clobetasol Propionate (C25H32ClFO5)	15.5–30.5	315–345	24.5	1 × 10−6 to 2.1 × 10−5	[30]
Desoxycorticosterone acetate ( C21H30O3)	15.5–30.5	315–345	24.5	5 × 10−6 to 1.03 × 10−4	[30]
Esomeprazole (C17H19N3O3S)	12–27	308.2–338.2	22	1.11 × 10-5 to 9.10 × 10-4	[31]
Amiodarone hydrochloride (C25H29I2NO3. Hcl)	12–30	313.2–343.2	19	2.510 × 10−5 to 1.012 × 10−3	[32]
Ketotifen fumarate (C23H23NO5S)	12–30	308.2–338.2	20	2.11 × 10−5 to 1.07 × 10−3	[33]
Aprepitant (C23H21F7N4O3)	12–33	308.15–338.15	15–18	4.50 × 10−6 to 7.67 × 10−5	[34]
Imatinib mesylate (C30H35N7O4S)	12–27	308.2–338.2	18–21	1.0 × 10−7 to 4.4 × 10−6	[35]
Coumarin-7 (C20H19N3O2)	9–33	308–338	13–16	4.15 × 10−6 to 1.00 × 10−5	[36]
Loratadine (C22H23N2O2Cl)	12–27	308.15–338.15	18–21	4.50 × 10−6 to 1.30 × 10−3	[37]
Cefixime trihydrate (C16H15N5O7S2.3 H2O)	18.3–33.5	308–328	NO	1.6 × 10−7 to 3.02 × 10−7	[38]
Oxymetholone (C21H32O3)	18.3–33.5	308–328	18	1.6 × 10−5 to 1.49 × 10−4	[38]
Atorvastatin (C33H33FN2O4)	12.16–35.46	308–348	17	1.12 × 10−6 to 1.45 × 10−3	[39]
Simvastatin (C25H38O5)	12.16–35.46	308–348	17	2 × 10−6 to 5.35 × 10−4	[39]
Lovastatin (C24H36O5)	12.16–35.46	308–348	17	1. 10 × 10−5to 1.14 × 10−4	[39]
Rosuvastatin (C22H28FN3O6S)	12.16–35.46	308–348	17	3 × 10−6 to 2.44 × 10−4	[39]
Fluvastatin (C24H26FNO4)	12.16–35.46	308–348	17	5 × 10−6 to 6 × 10−4	[39]
Azithromycin (C38H72N2O12)	12.2–35.5	308–348	13.8–14	6.9 × 10−5 to 2.73 × 10−4	[40]
Erythromycin (C37H67NO13)	12.2–35.5	308–348	16.8–17	4.3 × 10−5 to 3.12 × 10−4	[40]
Clindamycin (C18H33ClN2O5S)	12.2–35.5	308–348	14.8–15.2	1.77 × 10−4 to 1.146 × 10−3	[40]
Clarithromycin (C38H69NO13)	12.2–35.5	308–348	15–15.2	1.31 × 10−4 to 3.28 × 10−4	[40]
Loxoprofen (C15H18O3)	12–40	308–338	20	1.04 × 10−5 to 1.28 × 10−3	[41]
Cyproheptadine (C21H21N)	16–40	308–338	20	3.35 × 10−5 to 3.09 × 10−3	[42]
2,4,7-Triamino-6-phenylpteridine (Triamterene) (C13H13N7)	12–27	308–338	19.2–19.5	0.03 × 10−5 to 2.89 × 10−5	[43]
Tolmetin (C15H15NO3)	12–40	308–338	16	5.00 × 10−5 to 2.59 × 10−3	[44]
Busulfan(C6H14O6S2)	12–40	308–338	16	3.27 × 10 − 5–8.65 × 10 − 4	[45]
Sunitinib malate (C26H33FN4O7)	12–27	308–338	NO	0.5 × 10−5 to 8.56 × 10−5	[46]
Fenoprofen ( C15H14O3)	12–40	308–338	16	2.01 × 10−5 to 4.20 × 10−3	[47]
Azathioprine (C9H7N7O2S)	12–27	308–338	12–15	0.27 × 10−5 to 1.83 × 10−5	[48]
Sorafenib tosylate (C28H24ClF3N4O6S)	12–27	308–338	NO	0.68 × 10−6 to 12.57 × 10−6	[49]
spiroindolinonaphthoxazine photochromic dye (1,3-dihydro-3,3-dimethyl-1-isopropyl-6 -(2,3)- (dihydroindole-1-yl)spiro[2 H-indole-2,3 − 3 H-naphtho[2,1- b][1,4]oxazine])	10–26	308–328	17	2.2 × 10-7 to 5.05 × 10-6	[50]
Flurbiprofen(C15H13FO2)	8–25	303–323	12	2.170 × 10-5 to 19.683 × 10-5	[51]
Artemisinin(C15H22O5)	10–25	303–328	13–17	10-4 to 10-3	[52]
Juglone (5-hydroxy-1,4-naphthoquinone) (C10H6O3)	9.2–24.4	308.2–328.2	21–22	2.0 × 10−5 to 1.6 × 10−3	[53]
Diflunisal (5-(2,4-difluorophenyl)− 2-hydroxybenzoic acid)( C13H8F2O3)	9–25	308.2–328.2	15	0.54 × 10-6 to 8.07 × 10-6	[54]
Norfloxacin (C16H18FN3O3)	10–30.3	308.2–328.2	NO	1.4 × 10−6 to 24.4 × 10−6	[55]
Ofloxacin (C18H21ClFN3O4)	10–30.3	308.2–328.2	NO	0.4 × 10−6 to 1.3 × 10−6	[55]
Meloxicam sodium (C14H12N3NaO4S2)	14.9–25.5	303–323	15–17	4.41 × 10−6 to 12.76 × 10−6	[56]
CIBA photoinitiator Irgacure® 2959 2-Hydroxy-4'-(2-hydroxyethoxy)− 2-methylpropiophenone(C12H16O4)	10–26	308.2–328.2	14	5.17 × 10−6 to 2.83 × 10−4	[57]

The crossover pressure was investigated by several articles which proposed some methods to predict the crossover pressure region [58], [59], [60], [61]. Investigation of these methods showed the crossover region depends on the critical properties of solutes, sublimation pressure, enthalpy of sublimation, partial molar enthalpy, and molar volume of the solute. Minimum and maximum favipiravir solubility were seen at the temperature of 338 K and pressures of 12 and 30, respectively. As indicated in Table 3, the mole fraction of favipiravir in the binary system (favipiravir-SC-CO₂) ranged in 3.0 × 10^-6-9.05 × 10^-4. The mole fraction of drugs in Table 4 shows a wide range of values. These values were reported between 10^-3 and 10^-7 according to the experimental conditions. The mole fraction of favipiravir also was in this range. The results present that high mole fraction values were obtained in the order of 10^-4. As above mentioned some researchers reported that the solubility of solutes in SC-CO₂ can be dependent on the critical properties of solutes, sublimation pressure values, enthalpy of sublimation, partial molar enthalpy, and molar volume of solute. This experimental data can be used to develop the method for the production of favipiravir nanoparticles using SCF. This information can be also employed for the incorporation of polar co-solvent to increase the solubility.

4.2. Expanded liquid theory - Modified Wilson model

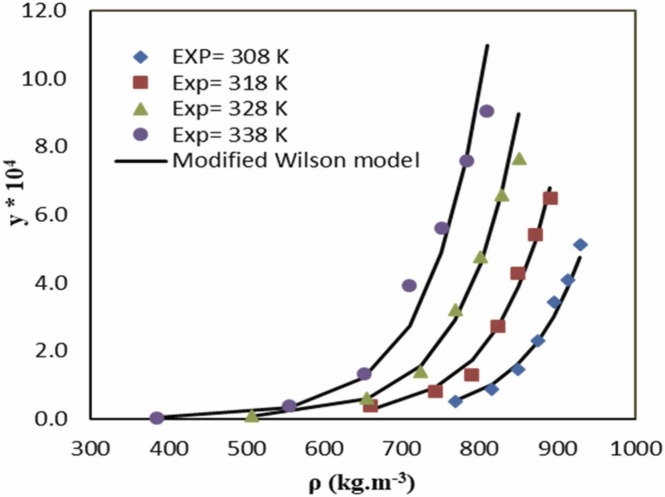
The modified Wilson model was studied to model the favipiravir solubility in SC-CO₂. The modified Wilson model parameters ($\alpha$, $\beta$, ${\lambda \prime }_{12}$ and${\lambda \prime }_{21}$) were optimized for binary system favipiravir-SC-CO₂. The results on the solubility of favipiravir in SC-CO₂ are listed in Table 5. Fig. 3 shows the experimental data and model of solubility of favipiravir in SC-CO₂. As indicated in Fig. 3, the model exhibited a proper agreement with experimental solubility data of favipiravir in SC-CO₂. According to Table 5, the values of AARD% and R_adj were 10.09% and 0.9658. Therefore, the modified Wilson model can correlate the solubility of favipiravir at proper accuracy.

Table 5.

Modified Wilson model parameters for solubility of favipiravir in SC-CO2.

$\mathrm{\alpha }$	$\mathrm{\beta }$	${\mathrm{\lambda }\prime }_{12}$	${\mathrm{\lambda }\prime }_{21}$	AARD%	Radj
-0.000027	0.000929	0.2525	15.021	10.09	0.9658

Fig. 3.

Comparison of experimental data (point) and calculated (line) solubility of favipiravir in SC-CO₂ based on modified Wilson model.

4.3. Correlation of the solubility data with semi-empirical models

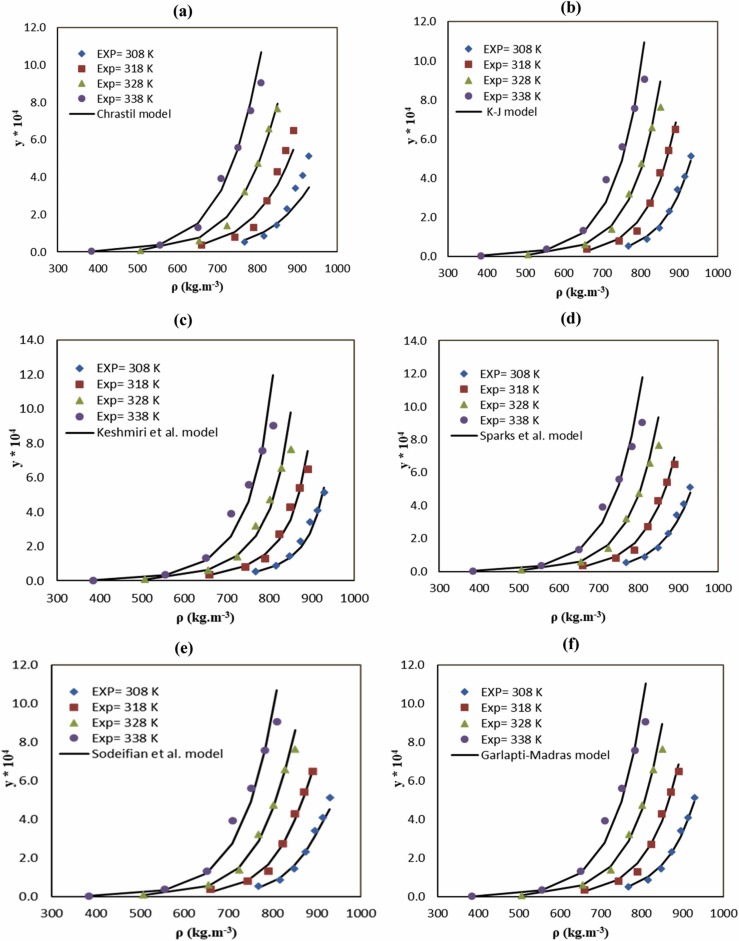
As presented in Table 6, six empirical density-based models (Chrastil, K-J, Keshmiri et al., Sparks et al., Sodeifian et al., and Garlapati- Madras) were used to correlate favipiravir solubility experimental data in a binary system (favipiravir-SC-CO₂). The results and adjustable parameters of each empirical model are listed in Table 7.

Table 6.

Semi-empirical modela.

Name	Formula
Chrastil	$\ln \mathrm{S}={\mathrm{a}}_0\ln \mathrm{\rho }+{\mathrm{a}}_1+\frac{{\mathrm{a}}_2}{\mathrm{T}}$
K-J	$\ln {\mathrm{y}}_2={\mathrm{a}}_0+{\mathrm{a}}_1\mathrm{\rho }+\frac{{\mathrm{a}}_2}{\mathrm{T}}$
Keshmiri et al.	$\ln {\mathrm{y}}_2={\mathrm{a}}_0+\frac{{\mathrm{a}}_1}{\mathrm{T}}+{\mathrm{a}}_2{\mathrm{P}}^2+\left({\mathrm{a}}_3+\frac{{\mathrm{a}}_4}{\mathrm{T}}\right)\ln \mathrm{\rho }$
Sparks et al.	${\mathrm{S}}_2^{*}={\mathrm{\rho }}_{\mathrm{r},1}^{\left({\mathrm{a}}_0+{\mathrm{a}}_1{\mathrm{\rho }}_{\mathrm{r},1}+{\mathrm{a}}_2{\mathrm{\rho }}_{\mathrm{r},1}^2\right)}\exp \left({\mathrm{a}}_3+\frac{{\mathrm{a}}_4}{{\mathrm{T}}_{\mathrm{r}}}+\frac{{\mathrm{a}}_5}{{\mathrm{T}}_{\mathrm{r}}^2}\right){\mathrm{S}}_2^{*}=\frac{\mathrm{S}}{{\mathrm{\rho }}_{\mathrm{c},1}}\mathrm{S}=\frac{\mathrm{\rho }{\mathrm{M}}_{\mathrm{w\; solute}}{\mathrm{y}}_2}{{\mathrm{M}}_{\mathrm{w\; SCF}}\left(1-{\mathrm{y}}_2\right)}$
Sodeifian et al.	$\ln {\mathrm{y}}_2={\mathrm{a}}_0+{\mathrm{a}}_1\frac{{\mathrm{P}}^2}{\mathrm{T}}+{\mathrm{a}}_2\ln \left(\mathrm{\rho }\mathrm{T}\right)+{\mathrm{a}}_3\left(\mathrm{\rho }\ln \mathrm{\rho }\right)+{\mathrm{a}}_4\mathrm{P}\ln \mathrm{T}+{\mathrm{a}}_5\frac{\ln \mathrm{\rho }}{\mathrm{T}}$
Garlapati and Madras	$\ln {\mathrm{y}}_2={\mathrm{a}}_0+\left({\mathrm{a}}_1+{\mathrm{a}}_2\mathrm{\rho }\right)\ln \mathrm{\rho }+\frac{{\mathrm{a}}_3}{\mathrm{T}}+{\mathrm{a}}_4\ln \left(\mathrm{\rho }\mathrm{T}\right)$

a a₀ −a₅, adjustable parameters of models.

Table 7.

The correlation results of the favipiravir – CO₂ system provided by semi-empirical models.^a.

Model	${\mathrm{a}}_0$	${\mathrm{a}}_1$	${\mathrm{a}}_2$	${\mathrm{a}}_3$	${\mathrm{a}}_4$	${\mathrm{a}}_5$	${\mathrm{a}}_6$	AARD%	Radj
Chrastil	10.01	-8267.85	-40.35	–	–	–	–	18.61	0.966
K-J	7.35	-8593.17	0.014	–	–	–	–	10.55	0.957
Keshmiri et al.	-43.11	-4486.03	0.0000129	7.99	-253.79	–	–	15.55	0.954
Sparks et al.,	4.98	2.74	16.41	-29.65	4358.15	11.14	–	11.10	0.976
Sodeifian et al.,	-16.03	-0.00506	1.58	0.0021	0.012	-1177.91	–	13.45	0.966
Garlapati and Madras	-61.13	-8.1	0.0016	-5595.52	9.29	–	–	11.31	0.956

^aa₀ −a₆, adjustable parameters of models.

The equation developed by K-J (AARD = 10.55%) presented the best fit compared to the other equation with three parameters namely Chrastil (AARD = 18.61%). K-J provided a relationship between the logarithm of the mole fraction of a solute has a linear dependence on the density of the SCF phase. On the other hand, Chrastil described one of the first density-based models, based on the solvato complex formed between the solute and solvent molecules at equilibrium. However, it has some limitations in high solubility [62]. Therefore, the model described by Chrastil underwent several modifications, deriving in different equations like Adachi- Lu [63] and del Valle and Aguilera [64]. Moreover, Sparks et al. combined Adachi-Lu and del Valle- Aguilera models considering the effect of the density in the association number k and the change of the enthalpy of vaporization with the temperature. The results in Table 7 showed that Sparks et al. (AARD = 11.10%) was more adequate than Chrastil model.

Keshmiri et al. introduced a semi-empirical model based on the effect of pressure, density, and temperature. This model is expressed by a linear relationship between the logarithm of the solid solubility and the density of the CO₂ and it has a strong relationship with pressure. Keshmiri’s model (AARD= 15.55%) with more parameters, but the fit was worse compared to K-J and better than Chrastil. In this model, the relationship of solubility to pressure, density, and temperature are complicated.

Sodeifian et al. and Garlapti- Madras models were developed by reviewing the laboratory data and models presented. Both of them included more combined terms than K-J, but the AARDs obtained with these models were 13.45% and 11.31% respectively. The main conclusion obtained from Table 7 is that the best models for correlating favipiravir solubility were the equation developed by K-J and Sparks et al.”

Furthermore, experimental data and favipiravir solubility calculated by empirical models are compared in Fig. 4. As seen, the models showed satisfactory agreement with experimental data. Using the model, total heat (ΔHtotal = 70.09 KJ mol^-1), vaporization heat (ΔHvap = 90.12 KJ mol^-1), and solvation heat (ΔHsol = 20.04 KJ mol^-1) can be calculated for binary system.

Fig. 4.

Comparison of experimental (points) and calculated (line) values of favipiravir solubility based on the (a) Chrastil, (b) K-J, (c) Keshmiri (d) Sparks et al., (e) Sodeifian et al., and (f) Garlapati and Madras models at different temperatures.

4.4. Solubility correlation with EoS model

In this study, the SRK EoS with quadratic mixing rules was employed. Interaction parameters (k_ij, l_ij) are used to calculate the parameters of the SRK equation for the binary system. As previously mentioned, different group contribution (GC) methods are used to calculate the physico-chemical and critical properties of solids (drug), which can affect the correlation results (AARD) for solubility data in SC-CO₂ by EoS, but in many cases the results were not significantly different [65]. In the current research, the Ambrose-Walton equation [66], Immirzi and Perini [67], Edmister [66] and Marrero and Gani [68], methods were applied to determine the sublimation pressure, solid molar volume, acentric factor, critical temperature and pressure, respectively. The results of estimating of drug properties are presented in Table 2.

Moreover, interaction parameters can be written as a function of temperature:

$$l_{\mathit{ij}}=AT+B$$ (32)

$$k_{\mathit{ij}}=\mathit{CT}+D$$ (33)

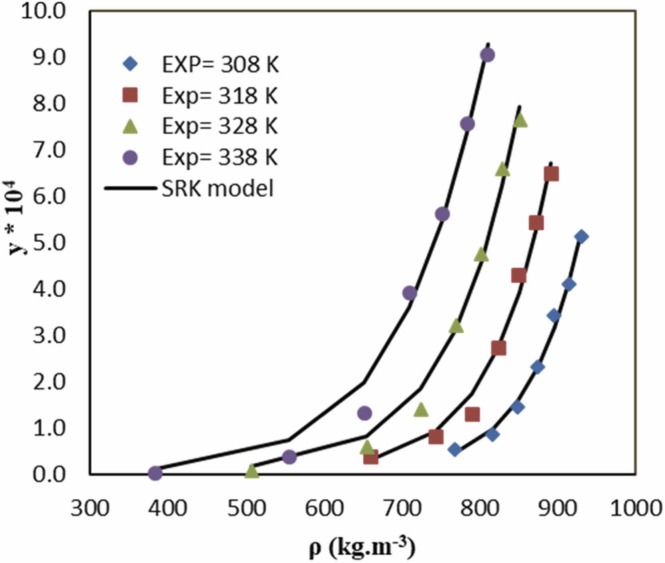
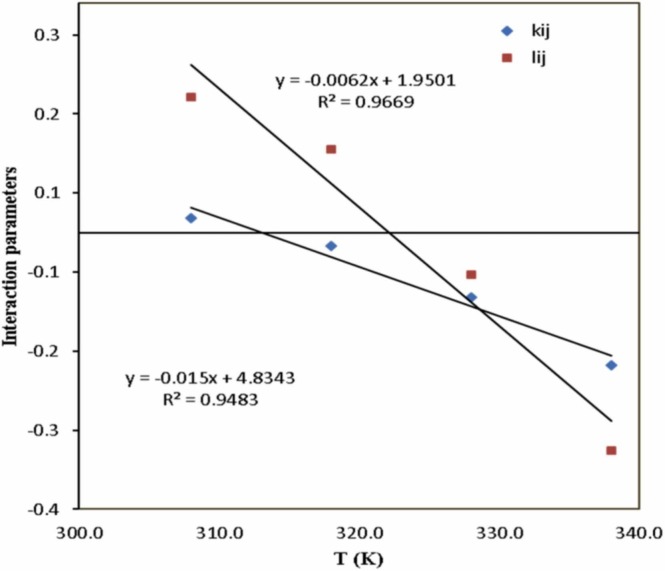
The corresponding values of interaction parameters were optimized by the simulated annealing (SA) method. The correlation results obtained with the SRK-EoS and quadratic mixing rules at four temperatures are reported in Table 8. According to AARD% values in Table 8, the interaction parameters were calculated with acceptable accuracy. However, it can be said that the accuracy of the data obtained at low temperatures (308 K) is higher than those determined at high temperatures (338 K). Fig. 5 shows the experimental solubility of favipiravir in SC-CO₂ at four temperatures (308, 318, 328, and 338 K) and those predicted by SRK-EoS. As indicated in Fig. 5, the SRK EoS with quadratic mixing rules was capable of corrolating solubility data. The coefficients of A, B, C, and D (Eq. (33), (34)) were calculated via linear regression analysis ( Fig. 6).

Table 8.

Correlation results of the SRK for solubility of favipiravir in SC-CO₂, interaction parameters.

Model	Parameter	T = 308 K	T = 318 K	T = 328 K	T = 338 K
SRK	${\mathrm{k}}_{12}$	0.018	-0.0168	-0.0818	-0.168
	${\mathrm{l}}_{12}$	0.1717	0.1052	-0.053	-0.2758
	$\mathrm{AARD}$	6.08	11.59	15.04	17.65
	${\mathrm{R}}_{\mathrm{adj}}$	0.996	0.986	0.975	0.965

Fig. 5.

Comparison of experimental and calculated solubilities of favipiravir base on SRK- with quadratic mixing rules EoS.

Fig. 6.

The influence of temperature on the binary interaction parameters for the favipiravir SC–CO₂ system, SRK model.

5. Conclusion

Proper knowledge of drug’s solubility in a supercritical fluid is essential in the production of pharmaceutical micro and nanoparticles using supercritical fluids. In this study, the solubility of favipiravir in SC-CO₂ was explored at the temperature range 308 − 338 K and pressure range 12–30 MPa. The solubility of favipiravir in SC-CO₂ varying from 0.004 to 2.618 g/L was obtained. The minimum and maximum values for favipiravir solubility were observed in the temperature of 338 K and pressures of 12 and 30 MPa. After experimental measurement of the solubility, three models including expanded liquid theory (modified Wilson model), semi-empirical density-based models (Chrastil, K-J, Keshmiri et al., Sparks et al., Sodeifian et al., and Garlapati- Madras), and equation of state (SRK with quadratic mixing rules) were used to correlate the generated solubility data. According to the results, K-J (AARD% = 10.55), Sparks et al. (AARD% = 11.1), and Garlapati and Madras (AARD% = 11.31) showed a better agreement with solubility data of favipiravir compared to SRK model (12.59%). Comparison of the models showed that the best model for correlating favipiravir solubility is the modified Wilson (AARD% = 10.09) and K-J (AARD% = 10.55).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.