Keywords: acute lung injury, cationic rhodamine dyes, computational modeling, electrochemical transmembrane potential, fluorescence imaging
Abstract
Dissipation of mitochondrial membrane potential (Δψm) is a hallmark of mitochondrial dysfunction. Our objective was to use a previously developed experimental-computational approach to estimate tissue Δψm in intact lungs of rats exposed to hyperoxia and to evaluate the ability of duroquinone (DQ) to reverse any hyperoxia-induced depolarization of lung Δψm. Rats were exposed to hyperoxia (>95% O2) or normoxia (room air) for 48 h, after which lungs were excised and connected to a ventilation-perfusion system. The experimental protocol consisted of measuring the concentration of the fluorescent dye rhodamine 6 G (R6G) during three single-pass phases: loading, washing, and uncoupling, in which the lungs were perfused with and without R6G and with the mitochondrial uncoupler FCCP, respectively. For normoxic lungs, the protocol was repeated with 1) rotenone (complex I inhibitor), 2) rotenone and either DQ or its vehicle (DMSO), and 3) rotenone, glutathione (GSH), and either DQ or DMSO added to the perfusate. Hyperoxic lungs were studied with and without DQ and GSH added to the perfusate. Computational modeling was used to estimate lung Δψm from R6G data. Rat exposure to hyperoxia resulted in partial depolarization (−33 mV) of lung Δψm and complex I inhibition depolarized lung Δψm by −83 mV. Results also demonstrate the efficacy of DQ to fully reverse both rotenone- and hyperoxia-induced lung Δψm depolarization. This study demonstrates hyperoxia-induced Δψm depolarization in intact lungs and the utility of this approach for assessing the impact of potential therapies such as exogenous quinones that target mitochondria in intact lungs.
NEW & NOTEWORTHY This study is the first to measure hyperoxia-induced Δψm depolarization in isolated perfused lungs. Hyperoxia resulted in a partial depolarization of Δψm, which was fully reversed with duroquinone, demonstrating the utility of this approach for assessing the impact of potential therapies that target mitochondria such as exogenous quinones.
INTRODUCTION
Acute lung injury (ALI) and its most severe form, acute respiratory distress syndrome (ARDS), are characterized by rapidly progressing hypoxic respiratory failure and carry high morbidity and mortality rates (1). These high rates are attributable to multiple factors, but key are the lack of clinical means for early detection and effective therapies to supplement supportive care (2).
Rat exposure to normobaric hyperoxia (>95% O2) results in lung injury reproducing the cardinal features of human ALI, including increased pulmonary vascular permeability, low-pressure pulmonary edema, and hypoxemia (3–11). Crapo et al. (5) showed that rats exposed to hyperoxia (100% O2) display the first clinical evidence of lung injury after >40 h of exposure with worsening at 60 h and death by 72 h. Oxidative stress, inflammation, and mitochondrial dysfunction are key pathways in the pathogenesis of hyperoxia-induced ALI (6, 12), with the lung capillary endothelium a primary and early site of injury (5, 12, 13).
Previous studies have reported hyperoxia-induced mitochondrial changes in the lungs, isolated lung mitochondria, and cultured pulmonary endothelial cells (13–20). For instance, Sepehr et al. (20) reported a 77% decrease in complex I activity in lung tissue from rats exposed to hyperoxia (>95% O2 for 48 h). In the same study, they showed using surface fluorometry that hyperoxia decreased rotenone-induced changes in NADH signal, as an index of lung tissue complex I activity, by 63% compared with that of normoxic lungs. In addition, they reported a 63% decrease in lung tissue complex II activity with hyperoxia. Based on these decreases in complex I and II activity, they concluded that the lung tissue electron transport chain (ETC) upstream from complex III is more reduced in isolated perfused hyperoxic lungs than in normoxic lungs. These hyperoxia-induced decreases in mitochondrial complex I and II activity would be expected to alter mitochondrial bioenergetics and respiration.
Mitochondrial membrane potential (Δψm) is a major component of the proton motive force, which plays a key role in mitochondrial bioenergetics, metabolism, and signaling functions (16, 21). For pulmonary endothelial cells in isolated perfused lungs, mitochondria produce 80%–85% of ATP needed for normal cellular functions (22, 23). Dissipation of Δψm is a hallmark of mitochondrial dysfunction observed in various cell types, including pulmonary endothelial cells exposed to oxidative stress (16, 24, 25). Previous studies have assessed the impact of hyperoxia on Δψm in mitochondria isolated from lungs of rats exposed to hyperoxia or in cultured pulmonary endothelial cells exposed to hyperoxia (11, 16), but not in intact functioning lungs.
Lungs have a high capacity for reducing exogenous amphipathic quinones such as duroquinone (DQ) and coenzyme Q1 (CoQ1) and for oxidizing their hydroquinones (15, 26). Audi et al. (26) showed that rat lungs reduce DQ to its hydroquinone form (DQH2) and oxidize DQH2 back to DQ, and that the dominant site for DQ reduction in lungs is the phase 2 cytosolic enzyme NAD(P)H:quinone oxidoreductase 1 (NQO1). Furthermore, they showed that mitochondrial complex III is the predominant site for DQH2 oxidation on passage through the pulmonary circulation (26). Audi et al. (15) also assessed the disposition of the ubiquinone analog coenzyme Q1 (CoQ1) on passage through the rat pulmonary circulation. They showed that the dominant sites of CoQ1 reduction to its hydroquinone form (CoQ1H2) are mitochondrial complex I and NQO1 and that the predominant site for CoQ1H2 oxidation is complex III (15). Using DQ, CoQ1, and indicator dilution methods, a hyperoxia-induced decrease in lung complex I activity in intact lungs, with no change in complex III or IV activity, was demonstrated (14, 15).
In addition to the utility of these quinone compounds for probing the activities of NQO1, complexes I and III in intact functioning lungs and cultured endothelial cells, they can also be used to reverse the effect of decreased complex I and/or II activity on mitochondrial respiratory and bioenergetic functions (22, 26–28). For instance, Audi et al. (26) showed that the inhibition of complexes I and II decreased lung O2 consumption by ∼60% and that this decrease was fully reversible with the addition of DQ to the recirculating lung perfusate. This observation is consistent with DQ reduction to DQH2 followed by the oxidation of DQH2 via complex III, thereby forming an electron bypass around complexes I and II and thus restoring O2 consumption. The effect of hyperoxia on Δψm associated with decreased function of complexes I and II in intact lungs, however, is not known.
Fluorescent lipophilic cations such as rhodamine dyes have been used for monitoring Δψm, largely in cultured cells and isolated mitochondria (16, 29–34). Only a small number of studies have utilized these dyes to monitor Δψm in organs (33, 35, 36). Recently, Audi et al. (36) presented an experimental and computational approach for measuring Δψm (in mV) in intact functioning lungs using the rhodamine dye rhodamine 6 G (R6G). The objective of the present study was to use this approach to assess Δψm in lungs from rats exposed to hyperoxia as a model of human ALI and to evaluate the ability of DQ to reverse hyperoxia-induced depolarization of Δψm. We hypothesized that rat exposure to hyperoxia depolarizes lung Δψm mainly due to a decrease in mitochondrial complex I and II activity and that this depolarization can be detected in isolated perfused lungs using R6G.
MATERIALS AND METHODS
Materials
R6G, verapamil hydrochloride, carbonyl cyanide 4-(trifluoromethoxy) phenylhydrazone (FCCP), DQ, glutathione (GSH), and all other reagents used in experiments were purchased from Sigma-Aldrich (St. Louis, MO).
Rat Exposure to High Oxygen (Hyperoxia) as a Model of ALI
All animal protocols used in the present study and described below were approved by the Institutional Animal Care and Use Committees of the Veterans Affairs Medical Center and Marquette University (Milwaukee, WI).
For normoxia (control) studies, adult male Sprague–Dawley rats (Charles River; 344 ± 4 (SE) g, n = 25) were exposed to room air in chambers side by side with those exposed to hyperoxia. For normobaric hyperoxia studies, rats within the same weight (329 ± 4 g, n = 9) and age range of normoxia rats were housed in a Plexiglass chamber maintained at >95% O2 for 48 h, as previously described (11). This exposure period was chosen, as it is relatively early in the pathogenesis of hyperoxia-induced ALI, before clinical evidence of respiratory distress (5, 8, 11).
Isolated Perfused Rat Lung Preparation
Each rat was anesthetized with sodium pentobarbital (40–50 mg/kg ip). The trachea was surgically isolated and cannulated, the chest opened and heparin (0.7 IU/g body wt) injected into the right ventricle, as previously described (37). The pulmonary artery and the pulmonary venous outflow were accessed via cannulas, then the heart/lungs were removed and connected to a ventilation-perfusion system. The Krebs-Ringer bicarbonate perfusate contained (in mM): 4.7 KCl, 2.51 CaCl2, 1.19 MgSO4, 2.5 KH2PO4, 118 NaCl, 25 NaHCO3, and 5.5 glucose. The perfusate also contained 0.5% bovine serum albumin (BSA) plus 2.5% Ficoll to maintain consistent oncotic pressure (36). The perfusion system was primed with the perfusate maintained at 37°C and equilibrated with 15% O2, 6% CO2, balance N2 gas mixture resulting in perfusate Po2, Pco2, and pH of ∼105 Torr, 40 Torr, and 7.4, respectively. The lung was ventilated (40 breaths/min) with the above gas mixture with end-inspiratory and end-expiratory pressures of ∼6 and 3 mmHg, respectively. The pulmonary artery and airway pressures were referenced to atmospheric pressure at the level of the left atrium and monitored continuously during the course of the experiment.
Experimental Protocols
The single-pass perfusion system was primed with the perfusate and ∼30 mL of the perfusate was passed through the system until the lungs were clear of blood with the flow rate set at 10 mL/min.
The experimental protocol to probe Δψm in intact lungs was developed by Audi et al. (36). It consists of three phases, a loading phase during which the lung perfusate contained R6G (0.25 µM) and the multidrug efflux pump P-glycoprotein (Pgp) inhibitor verapamil (100 µM), a washing phase in which the perfusate contained verapamil but without R6G, and an uncoupling phase in which the perfusate contained the uncoupler FCCP (67 µM) with verapamil but no R6G. Before each phase, the flow was stopped and the reservoir emptied and then refilled with the appropriate perfusate. For each phase, a 2-mL reservoir sample was collected before restarting the flow. For the loading phase, the lung was perfused for 10 min (single pass) at 10 mL/min during which 2-mL venous effluent perfusate samples were collected every 40 s during the first 2 min and every minute for the remaining 8 min. For the washing phase, the lungs were perfused (single pass) for 5 min during which 2-mL venous effluent samples were collected every minute. For the uncoupling phase, the lungs were perfused (single pass) for 7 min during which 2-mL venous effluent samples were collected every 20 s for the first 2 min and every minute for the last 5 min. All collected samples were centrifuged for 1 min (13,000 g, 4°C) to remove cellular components and debris (36). The sample supernatant was then transferred to plastic cuvettes to measure R6G emission fluorescence using a RatioMaster fluorescence system (Photon Technology International, HORIBA Scientific, NJ) at excitation and emission wavelengths of 525 nm and 565 nm, respectively (36). The R6G emission signal was then converted to R6G venous effluent concentration using a standard curve (36). At the end of each experiment, the lungs were weighed, dried, and reweighed to obtain their dry weight. The above protocol was carried out in lungs from normoxic (n = 5) and hyperoxic (n = 5) rats.
Rotenone-induced Δψm depolarization.
Inhibition of complex I with rotenone would be expected to depolarize Δψm. Thus, to assess the ability of the above protocol to detect rotenone-induced Δψm depolarization, we repeated the protocol in lungs from a separate group of normoxic rats (n = 4) in which mitochondrial complex I was inhibited by adding rotenone (complex I inhibitor, 40 µM) to the perfusate for all three phases.
Ability of DQ to reverse rotenone-induced Δψm depolarization.
To assess the ability of DQ to reverse rotenone-induced Δψm depolarization, we repeated the above R6G protocol in a separate group of normoxic lungs (n = 8) with rotenone and either DQ (100 µM) or its vehicle alone (DMSO, 0.05% volume) added to the perfusate for all three phases.
DQ can potentially be reduced to durosemiquinone on passage through the pulmonary circulation (26, 38), which in turn autooxidizes to generate hydrogen peroxide (H2O2) or disproportionate to DQH2 and DQ (38). To counter the potential prooxidant effects of durosemiquinone, we repeated the protocol in a separate group of normoxic lungs (n = 8) with rotenone, glutathione (GSH, 16 µM) (39), and either DQ or its vehicle (DMSO) added to the perfusate for all three phases.
Ability of DQ to reverse hyperoxia-induced Δψm depolarization.
To assess the ability of DQ to reverse hyperoxia-induced Δψm depolarization and to determine the role of hyperoxia-induced decrease in lung complex I and II activities in this depolarization, we repeated the above R6G protocol in a separate group of lungs from hyperoxic rats (n = 4) with DQ (100 µM) and GSH (16 µM) added to the perfusate for all three phases.
Standard curve.
For each experimental day, a standard curve was obtained and used to convert R6G emission signal in collected samples to R6G concentrations (36). Six tubes containing perfusate with known concentrations of R6G (0.5, 0.25, 0.125, 0.0625, and 0.03125 µM) were prepared. For each tube, a 2-mL sample was collected then processed the same way as the samples collected from the lung’s venous effluent.
Computational Model
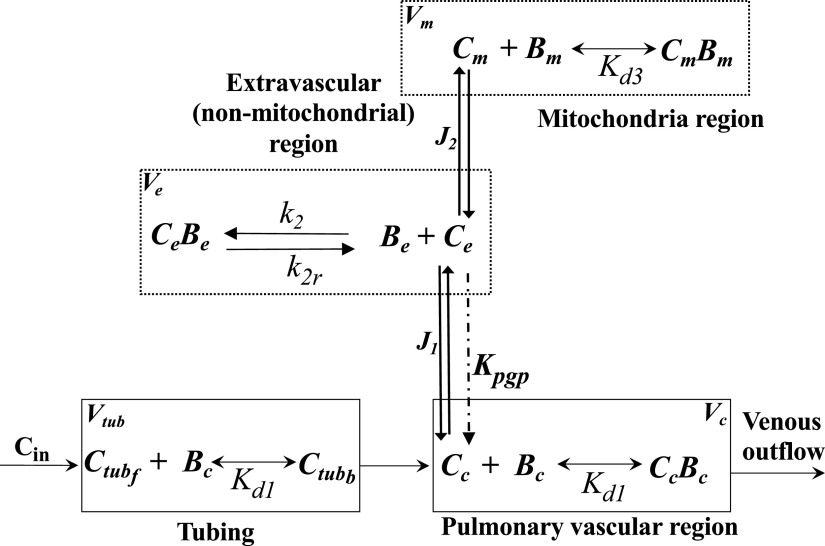
For mechanistic and quantitative interpretation of the R6G dynamic data, we used a previously developed physiologically based pharmacokinetic (PBPK) model (36). The PBPK model (Fig. 1) includes four regions, namely the tubing connecting the reservoir to the pulmonary artery, lung vasculature, extravascular (intracellular, nonmitochondrial) region, and mitochondria, each with volume Vtub, Vc, Ve, and Vm, respectively. The model accounts for the dominant vascular and/tissue processes that determine the lung uptake and retention of R6G on passage through the pulmonary circulation, including the electrochemical gradients that drive the uptake of R6G from the vascular region to the extravascular region and from the extravascular to the mitochondrial region (36). See appendix for the model’s governing ordinary differential equations (ODEs).
Figure 1.
Physiologically based pharmacokinetic (PBPK) model of R6G lung uptake and retention on passage through the rat pulmonary circulation. The model consists of four regions: tubing, vascular, extravascular (nonmitochondrial), and mitochondrial with volumes Vtub, Vc, Ve, and Vm, respectively. See appendix and Table 1 for definitions of various symbols and parameters.
The volumes of the four regions, the dissociation constant for R6G binding to protein (bovine serum albumin, BSA) in the vascular region (Kd1), the mitochondrial permeability-surface area product for R6G (P2S2), and the plasma membrane potential (Δψp) were fixed to previously estimated values (36). In addition, the rate of efflux of R6G via Pgp pump from cytoplasm to the vascular region (Kpgp) was set to zero, as the Pgp inhibitor verapamil was added to the perfusate for all three phases of the protocol in all experiments (36). Thus, for each lung, the unknown model parameters Δψm, Kd3, , k2r, and P1S1, (Table 1) were estimated by fitting the solution of the ODEs to the corresponding R6G dynamic data. The model fitting was done in MATLAB (MathWorks Inc.) using the “lsqcurvefit” function to implement the trust-region-reflective algorithm, an iterative optimization algorithm that readily incorporates bounds on the values of the parameters. At each iteration, the ODEs were solved numerically using the MATLAB function “ode45”, which is based on an explicit Runge-Kutta formula.
Table 1.
Unknown model parameters
| Symbol | Description | Units |
|---|---|---|
| Apparent rate constant for R6G-Bc binding within the cytoplasm region | min−1 | |
| k2r | Dissociation rate constant of R6G-Bc binding within the cytoplasm region | min−1 |
| Dissociation constant for R6G-Bm binding within the mitochondria region | ||
| P1S1 | R6G permeability-surface area product across the plasma membrane | mL/min |
| Δψm | Mitochondrial membrane potential | mV |
Statistical Analysis
The number of rats (n) studied was four to five for each of the eight experimental groups. This number was chosen based on our experience with these experiments and on power analysis of normoxia and hyperoxia mean R6G data (Fig. 2, uncoupling phase), which demonstrated that n > 3 allows detection of significant differences (P < 0.05) of 25% between means of the R6G data with a power value of 0.85.
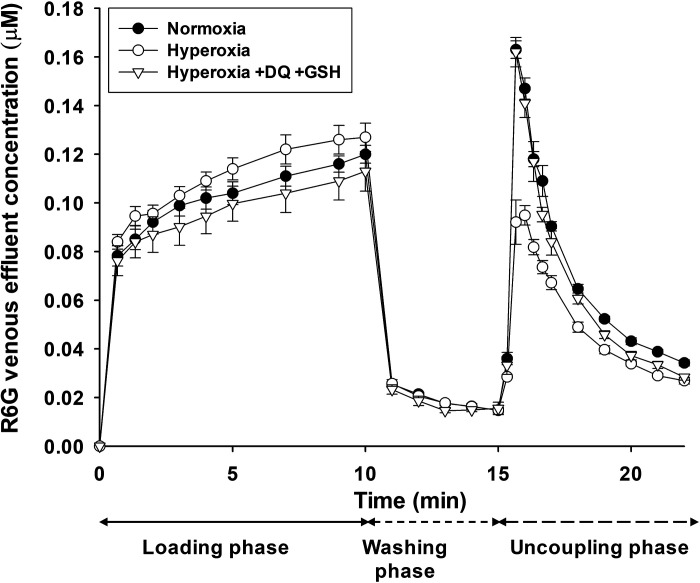
Figure 2.
R6G venous effluent concentration in normoxic lungs (closed circles, n = 5), hyperoxia lungs (open circles, n = 5), and hyperoxia lungs with duroquinone (DQ) and glutathione (GSH) (open triangles, n = 4) added to the perfusate for all three phases of the protocol. Values are means ± SE; n, number of rats.
Statistical evaluation of data was carried out using SigmaPlot version 12.0 (Systat Software Inc., San Jose, CA). Values from different groups were compared using unpaired t tests. The level of statistical significance was set at P < 0.05. Values are means ± SE unless otherwise indicated.
RESULTS
Experimental Results
For normoxic lungs, the addition of rotenone, DQ, and/or GSH to the perfusate had no significant effect on lung wet weight, wet/dry weight ratio, or pulmonary artery pressure.
Hyperoxic rats lost ∼2% of body weight during the 48-h exposure period (from 336 ± 3 g to 329 ± 4 g). Exposure to hyperoxia also increased lung wet weight by ∼22% (1.58 ± 0.05, n = 9) compared with normoxic lungs (1.30 ± 0.03, n = 24), with no effect on lung wet/dry weight ratio. These observations are consistent with our previously published data and the hyperoxia-induced increase in lung wet weight being mainly due to cellular infiltration rather than edema (11). The addition of DQ and GSH to perfusate had no significant effect on the lung wet weight, wet/dry wt ratio, or pulmonary artery pressure of hyperoxic lungs. There was no difference in pulmonary artery pressure between normoxic and hyperoxia lungs.
R6G venous effluent dynamic data from normoxic and hyperoxic lungs.
Figure 2 shows dynamic R6G venous effluent concentrations from normoxic and hyperoxic lungs. For normoxic lungs, R6G venous effluent concentration decreased from ∼0.13 µM during the loading phase to ∼0.02 µM during the washing phase, and perfusing the lungs with perfusate containing FCCP resulted in a rapid increase in the concentration of R6G in the venous effluent samples (uncoupling phase). This increase is consistent with the uncoupling of lung tissue mitochondria and the release of R6G that accumulated in the mitochondria during the loading phase, driven by Δψm. The results also show that for hyperoxic lungs, R6G venous effluent concentrations tended to be higher during the loading phase, but significantly lower during the uncoupling phase compared with normoxic lungs. These results are consistent with less uptake of R6G by hyperoxic lungs due to partial depolarization of Δψm.
Effect of rotenone-induced Δψm depolarization on R6G venous effluent dynamic data.
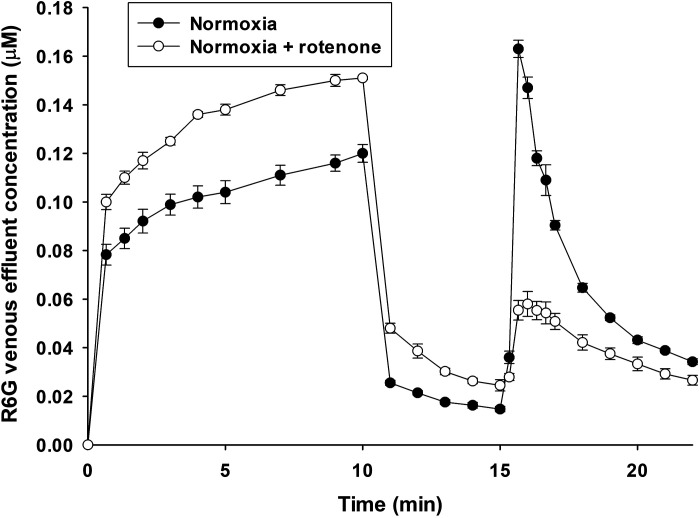
Figure 3 shows that inhibiting complex I with rotenone increased R6G venous effluent concentrations from normoxic lungs during the loading and washing phases, but decreased R6G concentrations during the uncoupling phase as compared with R6G concentration in the absence of rotenone. These results are consistent with a decrease in R6G lung uptake due to rotenone-induced Δψm depolarization.
Figure 3.
R6G venous effluent concentration in normoxic lungs without (closed symbols, n = 5) or with (open symbols, n = 4) rotenone (complex I inhibitor) added to the perfusate for all three phases of the protocol. Values are means ± SE; n, number of rats.
Ability of DQ to reverse rotenone-induced Δψm depolarization as reflected by R6G venous effluent dynamic data.
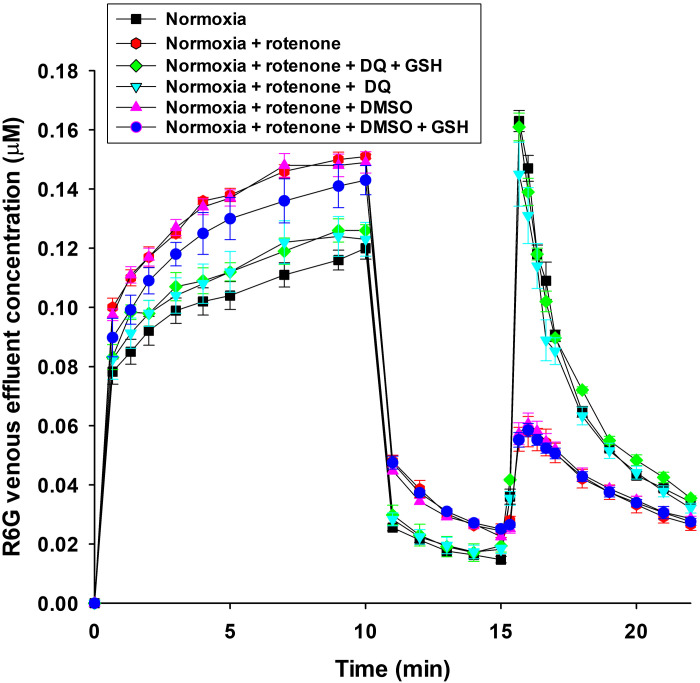
Figure 4 shows that adding DQ to perfusate during the three phases completely reversed the effect of rotenone on R6G concentration, consistent with the ability of the lungs to reduce DQ to its hydroquinone form (DQH2), which in turn bypasses complexes I and II to reduce complex III and restores Δψm and mitochondrial respiration and bioenergetics (26). Figure 4 also shows that the addition of DQ vehicle (DMSO) had no effect on rotenone-induced changes in R6G concentration and hence rotenone-induced Δψm depolarization. Results in Fig. 4 also show that the addition of GSH had no effect on the ability of DQ to reverse rotenone-induced changes in R6G, hence rotenone-induced Δψm depolarization.
Figure 4.
R6G venous effluent concentration in normoxic lungs without anything added to the perfusate (n = 5) or with either rotenone (complex I inhibitor) (n =4), rotenone + duroquinone (DQ) (n = 4), rotenone + DQ + glutathione (GSH) (n = 4), rotenone + DMSO (DQ vehicle) (n = 3), or rotenone + DMSO + GSH (n = 3) added to the perfusate for all three phases of the protocol. Values are means ± SE; n, number of rats.
Ability of DQ to reverse hyperoxia-induced Δψm depolarization.
Figure 2 shows that adding DQ to perfusate during the three phases almost completely reversed differences in R6G concentrations between normoxic and hyperoxic lungs. These results are consistent with the ability of the reduced form of DQ, namely DQH2, to bypass complexes I and II to reduce complex III and in the process reverse hyperoxia-induced changes in R6G concentration, presumably due to Δψm depolarization. GSH was also added to the perfusate along with DQ to mitigate the potential prooxidant effects of durosemiquinone.
Computational Modeling Results
Figure 5 shows representative model fits to data from individual normoxia, hyperoxia, and normoxia + rotenone lungs. The estimated model parameters obtained from all data (Table 2) show that rat exposure to hyperoxia depolarized lung tissue Δψm from −140 to −107 mV. Furthermore, exposure to hyperoxia decreased the values of Kd3 (29%) and k2r (45%), but had no significant effect on the values of and P1S1. As expected, inhibition of complex I activity with rotenone-depolarized Δψm from −140 to −57 mV. Furthermore, rotenone decreased the values of (48%), k2r (42%), and Kd3 (60%), but increased the value of P1S1 (5%). Lung perfusion with DQ or DQ + GSH fully reversed the rotenone effect on the values of Δψm and other model parameters. These results suggest that GSH has no effect on the pulmonary disposition of R6G or the ability of DQ to reverse rotenone-induced Δψm depolarization. Additional results show that adding DMSO (DQ vehicle) to the perfusate along with rotenone had no significant effect on the model parameters. The addition of DQ + GSH to the recirculating perfusate fully reversed hyperoxia-induced depolarization of Δψm and the effect of hyperoxia on the values of Kd3 and k2r.
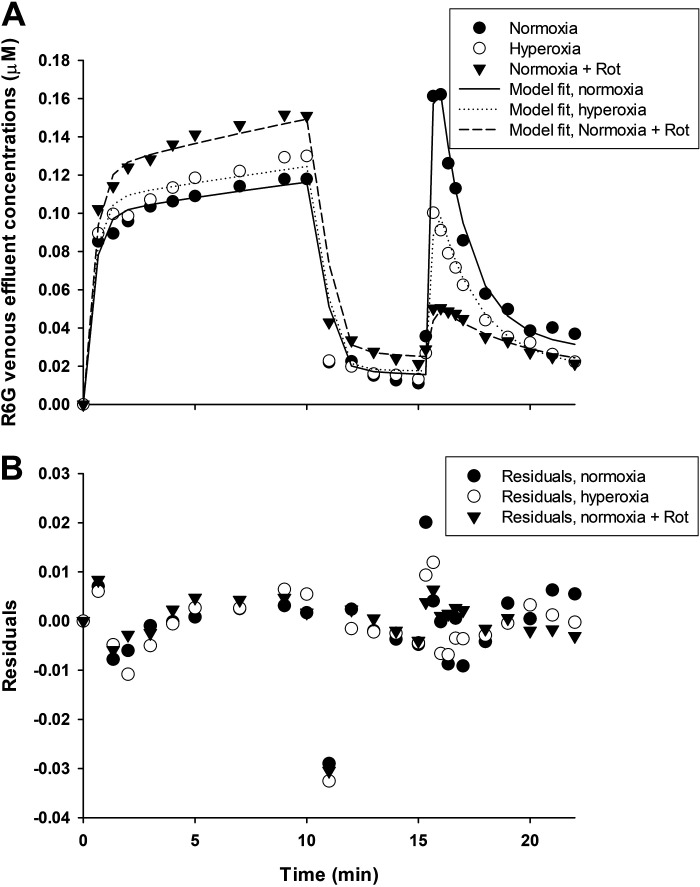
Figure 5.
A: R6G venous effluent concentration from representative normoxic lung (closed circles), hyperoxia lung (open circles), and normoxic lung with rotenone (closed triangles) added to the perfusate for all three phases of the protocol. Lines are model fits to data. B: residuals of the model fit to each of the three data sets in A. Rot, rotenone.
Table 2.
Estimated values of model parameters estimated by fitting the model to kinetic data from individual normoxic and hyperoxic lungs for each of the different experimental conditions
| Experimental Condition | n | , min−1 | k2r, min−1 | Δψm, mV | P1S1 , mL/min | CV, % | |
|---|---|---|---|---|---|---|---|
| Normoxia | 5 | 8.99 ± 0.99 | 0.113 ± 0.009 | 0.0136 ± 0.0004 | −139.6 ± 8.7 | 50.4 ± 0.2 | 13.8 ± 0.8 |
| Hyperoxia | 5 | 7.34 ± 0.99 | 0.062 ± 0.009* | 0.0092 ± 0.0003* | −106.8 ± 9.1* | 51.2 ± 1.0 | 14.6 ± 1.0 |
| Normoxia + Rotenone | 4 | 4.62 ± 0.39 * | 0.065 ± 0.010* | 0.0054 ± 0.0005* | −57.1 ± 2.3 | 52.8 ± 0.5* | 11.2 ± 0.3 |
| Normoxia + Rotenone + DQ + GSH | 4 | 8.46 ± 0.43 | 0.139 ± 0.011 | 0.0137 ± 0.0005 | −120.9 ± 4.6 | 50.5 ± 0.21 | 13.8 ± 1.6 |
| Normoxia + Rot + DQ | 4 | 9.45 ± 0.95 | 0.107 ± 0.005 | 0.0129 ± 0.0003 | −126.9 ± 14.9 | 50.5 ± 0.5 | 13.0 ± 1.2 |
| Normoxia + Rot + DMSO | 4 | 4.45 ± 0.38* | 0.062 ± 0.005 * | 0.0050 ± 0.0006* | −60.3 ± 3.1 * | 53.4 ± 0.5* | 10.9 ± 0.7 |
| Normoxia + Rot + DMSO + GSH | 4 | 6.38 ± 1.03 | 0.075 ± 0.003* | 0.0060 ± 0.0007* | −61.8 ± 4.2* | 53.1 ± 0.3* | 10.0 ± 0.6 |
| Hyperoxia + DQ + GSH | 4 | 9.72 ± 1.30 | 0.092 ± 0.004 | 0.0149 ± 0.0005 | −147.5 ± 12.0 | 50.5 ± 0.2 | 14.8 ± 0.9 |
Values are means ± SE; n, number of rats. *Different from normoxia (t test, P < 0.05). DQ, duroquinone; Rot, rotenone.
Figure 5 (bottom) shows the residuals of the model fits to the data in Fig. 5 (top) and reveals some systematic differences between model fits and data, especially during the loading phase (see discussion for potential reasons for this behavior). One global measure of the model fit to R6G data from an individual lung is the coefficient of variation (CV) (40) given by
| (1) |
where and are the measured and model fit R6G venous effluent concentrations, respectively, and N and P are the number of data points and model parameters, respectively. The CV for individual lungs ranged between 10% and 15% (Table 2) for the eight experimental conditions studied.
Measures of the estimability of the unknown model parameters from R6G dynamic data.
The estimability of the model parameters was evaluated with a Monte Carlo approach and sensitivity analysis (41, 42). For the Monte Carlo approach, the model solution was fit to the mean R6G data 100 times with random initial parameter values sampled from a uniform distribution within ± 30% of the mean of the optimal values in Table 2 obtained from either the normoxia group (Table 3) or the corresponding experimental group (Table 4). The resulting mean of the estimates are virtually the same regardless of the initial values used and very close to the means of the values of the estimates from individual lungs (Table 2). Tables 3 and 4 also show that for each model parameter, the standard deviation of the estimated 100 values is small relative to the mean.
Table 3.
Estimated values of model parameters for each of the different experimental conditions (Monte Carlo approach) along with estimated 95% confidence intervals (in parenthesis)
| ExperimentalCondition | , min−1 | k2r, min−1 | Δψm, mV | P1S1, mL/min | |
|---|---|---|---|---|---|
| Normoxia | 8.89 ± 0.98 (7.34, 10.72) | 0.108 ± 0.016 (0.085, 0.130) | 0.0136 ± 0.0008 (0.0125, 0.0153) | −141.0 ± 11.7 (−128.6, −165.5) | 50.9 ± 8.6 (37.3, 59.2) |
| Hyperoxia | 7.05 ± 0.87 (5.75, 8.69) | 0.057 ± 0.001 (0.042, 0.078) | 0.0090 ± 0.0005 (0.0082, 0.0099) | −105.6 ± 6.8 (−96.5, −118.6) | 51.5 ± 9.3 (37.8, 67.8) |
| Normoxia + Rot | 4.52 ± 0.40 (4.01, 5.31) | 0.061 ± 0.007 (0.051, 0.076) | 0.0054 ± 0.0003 (0.0049, 0.0061) | −57.0 ± 1.93 (−54.0, −60.9) | 56.2 ± 9.3 (39.4, 70.5) |
| Normoxia + Rot + DQ + GSH | 6.70 ± 0.93 (5.20, 8.78) | 0.136 ± 0.022 (0.097, 0.184) | 0.0129 ± 0.0012 (0.011, 0.016) | −120.7 ± 7.3 (−106.8, −136.7) | 52.6 ± 8.9 (38.5, 66.8) |
| Normoxia + Rot + DQ | 6.78 ± 1.18 (4.84, 9.51) | 0.113 ± 0.023 (0.073, 0.163) | 0.0126 ± 0.0012 (0.0103, 0.0149) | −120.2 ± 8.9 (−107.7, −142.9) | 51.7 ± 8.9 (37.5, 68.0) |
| Normoxia + Rot + DMSO | 4.38 ± 0.39 (3.81, 5.06) | 0.061 ± 0.007 (0.050, 0.072) | 0.0050 ± 0.0003 (0.0045. 0.0056) | -60.7 ± 2.2 (−57.4, −65.0) | 54.3 ± 9.7 (39.8, 71.1) |
| Normoxia + Rot + DMSO + GSH | 6.12 ± 0.61 (5.33, 7.35) | 0.073 ± 0.009 (0.062, 0.092) | 0.0058 ± 0.0004 (0.0053. 0.0066) | −61.3 ± 2.6 (−57.7, −67.1) | 55.0 ± 9.6 (38.5, 70.1) |
| Hyperoxia + DQ + GSH | 9.70 ± 0.83 (8.27, 11.31) | 0.092 ± 0.012 (0.073, 0.117) | 0.0148 ± 0.0008 (0.0136, 0.0163) | −147.0 ± 9.8 (−130.1, −166.7) | 52.2 ± 8.5 (36.3, 66.0) |
Values are means ± SD of estimated values of model parameters (Monte Carlo approach). For each experimental condition, the model solution was fit to the mean R6G data 100 times with random initial parameter values sampled from a uniform distribution within ± 30% of the mean of the optimal values obtained from the normoxia group (Table 2). DQ, duroquinone; Rot, rotenone.
Table 4.
Estimated values of model parameters for each of the different experimental conditions (Monte Carlo approach)
| ExperimentalCondition | , min−1 | k2r, min−1 | Δψm, mV | P1S1, mL/min | |
|---|---|---|---|---|---|
| Normoxia | 8.89 ± 0.98 | 0.108 ± 0.016 | 0.0136 ± 0.0008 | −141.0 ± 11.7 | 50.9 ± 8.6 |
| Hyperoxia | 7.13 ± 1.15 | 0.059 ± 0.014 | 0.0091 ± 0.0007 | −105.2 ± 7.2 | 52.2 ± 9.5 |
| Normoxia + Rot | 4.50 ± 0.40 | 0.060 ± 0.007 | 0.0054 ± 0.0003 | −58.8 ± 2.0 | 53.7 ± 8.9 |
| Normoxia + Rot + DQ + GSH | 6.89 ± 1.07 | 0.135 ± 0.023 | 0.0129 ± 0.0013 | −123.7 ± 11.03 | 53.6 ± 9.2 |
| Normoxia + Rot + DQ | 6.97 ± 1.22 | 0.116 ± 0.023 | 0.0127 ± 0.0012 | −122.1 ± 11.4 | 50.9 ± 9.1 |
| Normoxia + Rot + DMSO | 4.27 ± 0.40 | 0.058 ± 0.0070 | 0.0049 ± 0.0003 | −62.2 ± 2.1 | 54.8 ± 9.2 |
| Normoxia + Rot + DMSO + GSH | 6.18 ± 0.74 | 0.073 ± 0.011 | 0.0059 ± 0.0004 | −63.5 ± 2.8 | 53.2 ± 9.7 |
| Hyperoxia + DQ + GSH | 9.59 ± 0.73 | 0.092 ± 0.011 | 0.0147 ± 0.0007 | −149.2 ± 10.5 | 50.3 ± 9.1 |
Values are means ± SD of estimated values of model parameters (Monte Carlo approach). For each experimental condition, the model solution was fit to the mean R6G data 100 times with random initial parameter values sampled from a uniform distribution within ± 30% of the mean of the optimal values obtained from the corresponding experimental group (Table 2). DQ, duroquinone; Rot, rotenone.
The Monte Carlo approach was also used to estimate the 95% confidence intervals (Table 3) for the estimated values of the various parameters, as described by Buckland (43). For n independently estimated values of a given parameter (µ), sort the estimates from smallest to largest, then an estimate of the 95% confidence interval for µ [100 (1 − 2α)%, where α = 0.025] is provided by the estimated values that correspond to the rounded jth and kth sorted values where j = (n + 1)α and k = (n + 1)(1 − α). Table 3 shows that for most parameters, the confidence intervals are relatively narrow. For Δψm, there is no overlap between the confidence intervals of the normoxia and hyperoxia groups or between the normoxia and normoxia + rotenone groups.
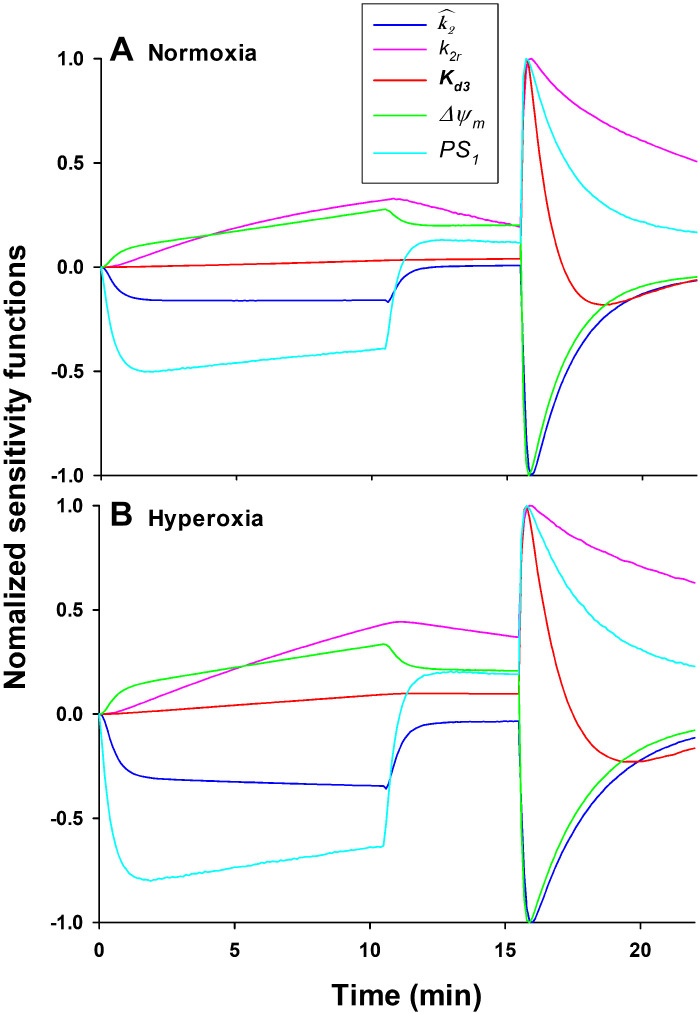
The estimability of the model parameters was also evaluated with sensitivity analysis (42). For the ith model parameter µi, the sensitivity function Si(t) = , where is the simulated lung venous effluent R6G concentration, was approximated by the change in resulting from a 1% change in µi divided by the change in µi (42). Comparison of these normalized sensitivity functions reveals the extent and the time epoch to which the optimized model parameters contribute to the model fit. The shape of a given sensitivity function relative to the others reveal how independent/dependent the contribution of that parameter is to the model fit. Figure 6 shows that for each parameter, the shape of its sensitivity function is different from those of the other parameters during at least one of the three phases of the experimental protocol. This suggests that the R6G data from individual lungs has enough information to separately estimate the values of all five model parameters.
Figure 6.
Model parameter sensitivity functions for model parameters estimated from R6G data from a representative normoxia (A) and hyperoxia (B) lung. The sensitivity functions show the change in the model solution given a 1% increase in the value of a given model parameter. Each plot is normalized to its maximum value.
DISCUSSION
The present study demonstrates the utility of a previously developed experimental-computational approach for quantifying hyperoxia-induced depolarization of Δψm in isolated perfused rat lungs. The results show that rat exposure to hyperoxia resulted in a partial depolarization (−33 mV or 24%) of Δψm, consistent with hyperoxia-induced decrease in activities of lung tissue mitochondrial complexes I and II. The robustness of the approach was assessed by perfusing normoxic lungs with the complex I inhibitor rotenone, resulting in depolarization of Δψm from –140 to −57 mV (or 60%). The results also demonstrate the ability of the exogenous quinone compound DQ to fully reverse both rotenone-induced and hyperoxia-induced lung tissue Δψm depolarization. As discussed below, Δψm depolarization appears to be predominantly due to hyperoxia-induced decrease in the activities of mitochondrial complexes I and II (20).
The results of the present study are consistent with results from previous studies, which also demonstrated hyperoxia-induced lung mitochondrial changes that in turn could alter Δψm (11, 15, 20, 44). Sepehr et al. (20) reported decrease in complex I (77%) and complex II (63%) activity in lung tissue from rats exposed to >95% O2 for 48 h. Audi et al. (15) reported that rat exposure to 85% O2 for 48 h decreased lung tissue complex I activity by ∼50% with no effect on complex III activity. Das et al. (44) showed that exposure of mice to 90% O2 for 48 h decreased the activities of lung tissue complex I (44%) and II (∼20%) with no effect on complex IV. Audi et al. (11) showed that Δψm recovery from ADP-induced depolarization (state 3) in mitochondria isolated from hyperoxic lungs was substantially slower than that from normoxic lungs.
Decreased activities of mitochondrial complexes I and II and the resulting depolarization of Δψm could impair mitochondrial bioenergetics and respiration functions. Fisher (45) reported that rat exposure to 100% O2 for 48 h increased lung lactate production rate (78%) and lactate to pyruvate ratio (105%) as an index of glycolytic ATP production. In the same study, hyperoxia had no significant effect on total lung tissue ATP content, with the conclusion that the increase in glycolytic ATP production could compensate for a decrease in ATP production via mitochondrial oxidative phosphorylation. Bassett et al. (46) reported a 52% increase in the rate of glucose utilization and 99% increase in the rate of lactate + pyruvate production in lungs of rats exposed to 100% O2 for just 24 h, consistent with the need of cells to increase glycolytic ATP production to compensate for decreased ATP production via mitochondrial oxidative phosphorylation, potentially due to hyperoxia-induced partial depolarization of lung tissue Δψm. Das et al. (44) showed that exposure of mice to 90% O2 for 48 h decreased basal, state 3 and uncoupled state 3 respiratory rates in mitochondria isolated from lungs, consistent with a decrease in mitochondrial respiratory functions. These results suggest potentially significant functional implications for the hyperoxia-induced partial depolarization of lung tissue Δψm measured in the present study.
Previous studies have assessed the impact of inhibiting complex I and/or II activity on mitochondrial respiration and bioenergetics in intact lungs and in cultured endothelial cells and the ability of exogenous quinones (e.g., DQ and coenzyme Q1) to counter this impact (22, 26–28, 47). For instance, Audi et al. (26) showed that inhibition of complexes I and II decreased rat lung O2 consumption by ∼60% and that this decrease was fully reversible with the addition of DQ to the recirculating lung perfusate. These data are consistent with the ability of DQH2 to bypass complex I and II and reduce cytochrome c at complex III. Bongard et al. (22) showed that inhibition of complex I with rotenone decreased lung ATP by ∼ 60%, increased lactate/pyruvate ratio by ∼200%, as an index of the glycolic pathway, and that CoQ1 was able to fully reverse these rotenone-induced mitochondrial changes. Using cultured rat pulmonary microvascular endothelial cells, Bongard et al. (27) showed that rotenone decreased ATP by 75%, depolarized Δψm from −129 to −93 mV, decreased O2 consumption by 85%, and increased cell monolayer permeability, all of which were completely reversed when CoQ1 was added to the cell medium. The effect of rotenone on cellular Δψm in these previous studies is qualitatively consistent with the results in the present study in isolated perfused lungs.
The results from the present study do not provide information about the individual contributions of hyperoxia-induced decrease in complex I versus complex II activity to the measured partial depolarization of Δψm. For the electron transport chain, protons are pumped from the mitochondrial matrix into the intermembrane space at complexes I, III, and IV, generating a proton gradient and membrane potential (Δψm) across the inner mitochondrial membrane. Normally, 10 H+ are pumped via the complex I-III-IV versus 6 H+ via the complex II-III-IV pathway. Based on this, one would expect a decrease in complex I activity to have a larger impact on Δψm than a similar decrease in complex II activity.
In addition to partial depolarization of Δψm, rotenone and hyperoxia decreased the values of the model parameters descriptive of R6G binding (, k2r, and Kd3) within the nonmitochondrial and mitochondrial regions (Table 2). This could be due to the effect of rotenone or hyperoxia on the number of R6G binding sites within the nonmitochondrial and mitochondrial regions and/or on the R6G-binding kinetics due to changes in the redox states within these regions resulting from the partial depolarization of Δψm (48). The fact that the addition of DQ to perfusate fully reversed the effects of hyperoxia and rotenone on all model parameters (Table 2), including , k2r, and Kd3 suggests that the changes in these parameters with rotenone or hyperoxia (Table 2) are likely due to changes in R6G binding kinetics rather than the number of binding sites.
In addition to durohydroquinone (DQH2), DQ can be reduced by various mammalian enzymes to durosemiquinone, which in turn can either autooxidize back to DQ with superoxide as by-product, which in turn dismutates to form H2O2, or disproportionate to DQH2 and DQ (Table 5) (26, 38). Audi et al. (26) showed that the reduction of DQ on passage through the rat and mouse pulmonary circulations is predominantly via NQO1, which is a two-electron reduction. For the present study, to counter any potential prooxidant effect due to durosemiquinone, GSH was added along with DQ to the lung perfusate.
Table 5.
DQ cellular redox reaction
| NQO1-mediated two electron DQ reduction to DQH2 |
| Complex III-mediated DQH2 oxidation to DQ |
| One electron DQ reduction to |
| autooxidation, superoxide dismutation to H2O2 |
| Peroxidase-mediated DQH2 oxidation to DQ |
| disproportionation to DQH2 and DQ |
RH and R+ are the reduced and oxidized forms of electron donor(s) for one-electron DQ reductases; is durosemiquinone. CytCo and CytCr are the oxidized and reduced forms of cytochrome C, respectively.
In addition to reducing complex III, DQH2 can serve as an antioxidant by reducing H2O2 to H2O (Table 4) (38). The fact that the addition of GSH alone to perfusate did not have an effect on the rotenone-induced Δψm depolarization (Fig. 3) suggests that the ability of DQ to fully reverse rotenone-induced Δψm depolarization is not due to the antioxidant effect of DQH2, but rather to the ability of DQH2 to bypass complexes I and II and reduce complex III.
Limitations of Experimental-Computational Approach
The lung consists of more than 40 different resident cell types (49, 50). In addition, other cell types (e.g., leukocytes) are recruited to the lungs following exposure to hyperoxia (5, 8, 11). For the present study, the results provide no direct information regarding the contributions of the different cell types to the measured hyperoxia-induced change in R6G lung uptake and the estimated Δψm depolarization. However, endothelial cells would be expected to dominate because of their large surface area and high fraction (∼50%) of total cells in normal lungs, and their direct contact with R6G in perfusate (5). Furthermore, pulmonary endothelial cells are a primary and early target of hyperoxia-induced acute lung injury (5, 14–16, 18, 19). However, we cannot exclude the potential significant contribution of other cell types to the measured hyperoxia-induced change in R6G lung uptake and the estimated Δψm depolarization.
The proposed PBPK model accounts for the dominant vascular and tissue processes hypothesized to determine the pulmonary disposition of R6G. However, it does not account for spatial heterogeneity of the concentrations of various species (compartmental vs. distributed in time and space model) or for perfusion kinematics (51). These factors could account for the nonrandom behavior of the model fit residuals during the loading phase (Fig. 5). Also, in the PBPK model, the lung vascular volume was assumed to be unaffected by exposure to hyperoxia, based on results from several previous studies (5, 14, 15, 52). We note that simulations using the PBPK model predict that a 15% decrease in vascular volume, in contrast to our assumption of constant, results in only a 1.4% decrease in Δψm. In addition, the value of the plasma membrane potential (Δψp) was fixed to that estimated by Gan et al. (16) from cultured pulmonary endothelial cells, although Δψp could be altered by hyperoxia and model simulations show that depolarization of Δψp could partially alias for depolarization of Δψm as far as its effect on venous effluent R6G data. Nonetheless, the addition of DQ to the lung perfusate fully reversed hyperoxia-induced changes in the R6G concentration data (Fig. 2) and the model parameters (Table 2), including Δψm, suggests that the assumption of no difference in the values of Δψp (and vascular volume) between normoxic and hyperoxic lungs is reasonable.
Potential Clinical Implications and Conclusions
Increased vascular permeability is a cardinal feature of clinical ALI (1). Previously, we showed that rat exposure to hyperoxia increased the pulmonary endothelial filtration coefficient, Kf, a sensitive measure of endothelial barrier function, by approximately twofold (8). Bongard et al. (22) showed that inhibiting lung complex I with rotenone, which decreased lung ATP by ∼ 60%, increased Kf by ∼2.8 fold, and hence established a connection between mitochondrial bioenergetics and Kf. Furthermore, the addition of coenzyme Q1 (CoQ1) to the perfusate fully reversed the effect of rotenone on lung ATP and Kf. These results suggest the potential utility of exogenous quinones such as DQ or CoQ1 as potential therapies for ALI/ARDS to mitigate mitochondrial dysfunction leading to microvascular permeability and lung injury associated with clinical administration of high fractions of oxygen.
In conclusion, this study is the first to measure hyperoxia-induced Δψm depolarization in intact lungs and to demonstrate the utility of this experimental-computational approach for assessing the impact of potential therapies that target mitochondria in isolated perfused lungs.
GRANTS
This study was funded by NIH 2R15HL129209-02 and Department of Veterans Affairs Merit Review Award BX001681.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.H.A. and E.R.J. conceived and designed research; S.H.A., S.G., and P.T. performed experiments; S.H.A., S.G., X.Z., and R.K.D. analyzed data; S.H.A., S.G., A.V.C., and E.R.J. interpreted results of experiments; S.H.A. prepared figures; S.H.A. drafted manuscript; S.H.A., S.G., P.T., X.Z., R.K.D., A.V.C., and E.R.J. edited and revised manuscript; S.H.A., S.G., P.T., X.Z., R.K.D., A.V.C., and E.R.J. approved final version of manuscript.
APPENDIX
The previously developed PBPK model describing the pulmonary disposition of R6G includes four regions (Fig. 1), namely the tubing connecting the reservoir to the pulmonary artery, the lung vasculature, the extravascular (intracellular, nonmitochondrial) region, and the mitochondria, with volumes Vtub, Vc, Ve, and Vm, respectively (36). Within the vasculature, the model accounts for binding of R6G to BSA. The model also accounts for electrochemical gradients that drive the uptake of R6G from the vascular to the extravascular region and from there to the mitochondria region. Within the extravascular region, the model allows for slowly equilibrating interactions for R6G. Within the mitochondrial region, the model accounts for the binding of R6G to protein.
The rates of change in the concentrations of R6G in each of the four regions are described by the following system of ordinary differential equations (ODEs), which were derived using the laws of mass balance and mass action.
Tubing Region
| (A1) |
where [Cin] and [Ctub] are total (free + bound) concentration of R6G in reservoir and tubing regions, respectively, and Q is the pump flow rate.
Vascular Region
| (A2) |
where , Kd1 is the R6G to BSA binding dissociation constant, and [Cc] and [CcBc] are the respective concentrations of free and BSA-bound R6G within the vascular region, S1 is the vascular surface area, where Δψp is plasma membrane potential, and α = ZF/RT is a constant dependent on the universal gas constant (R), Faraday constant (F), R6G valence (Z = 1), and absolute temperature (T).
Extravascular Region
Rates of change in the concentrations of free, [Ce], and protein-bound, [CeBe], R6G within this region are:
| (A3) |
| (A4) |
where , [Be] is the concentration of extravascular R6G binding sites, S2 is the mitochondrial surface area, and .
Mitochondrial Region
Rate of change in the concentration of free R6G, [Cm], within this region:
| (A5) |
where is the apparent volume of the mitochondrial region, is R6G and Bm binding dissociation constant, and [Bm] is the protein concentration within the mitochondrial region, and k3 and k3r are the association and dissociation rate constants of R6G-Bm binding in the mitochondrial region, respectively.
REFERENCES
- 1.Matthay MA, Zemans RL. The acute respiratory distress syndrome: pathogenesis and treatment. Annu Rev Pathol 6: 147–163, 2011. doi: 10.1146/annurev-pathol-011110-130158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fanelli V, Vlachou A, Ghannadian S, Simonetti U, Slutsky AS, Zhang H. Acute respiratory distress syndrome: new definition, current and future therapeutic options. J Thorac Dis 5: 326–334, 2013. doi: 10.3978/j.issn.2072-1439.2013.04.05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fisher AB, Beers MF. Hyperoxia and acute lung injury. Am J Physiol Lung Cell Mol Physiol 295: L1066; author reply L1067, 2008. doi: 10.1152/ajplung.90486.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kallet RH, Matthay MA. Hyperoxic acute lung injury. Respir Care 58: 123–141, 2013. doi: 10.4187/respcare.01963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Crapo JD, Barry BE, Foscue HA, Shelburne J. Structural and biochemical changes in rat lungs occurring during exposures to lethal and adaptive doses of oxygen. Am Rev Respir Dis 122: 123–143, 1980. doi: 10.1164/arrd.1980.122.1.123. [DOI] [PubMed] [Google Scholar]
- 6.Reiss LK, Uhlig U, Uhlig S. Models and mechanisms of acute lung injury caused by direct insults. Eur J Cell Biol 91: 590–601, 2012. doi: 10.1016/j.ejcb.2011.11.004. [DOI] [PubMed] [Google Scholar]
- 7.Chu CH, David Liu D, Hsu YH, Lee KC, Chen HI. Propofol exerts protective effects on the acute lung injury induced by endotoxin in rats. Pulm Pharmacol Ther 20: 503–512, 2007. doi: 10.1016/j.pupt.2006.03.006. [DOI] [PubMed] [Google Scholar]
- 8.Audi SH, Clough AV, Haworth ST, Medhora M, Ranji M, Densmore JC, Jacobs ER. 99MTc-hexamethylpropyleneamine oxime imaging for early detection of acute lung injury in rats exposed to hyperoxia or lipopolysaccharide treatment. Shock 46: 420–430, 2016. doi: 10.1097/SHK.0000000000000605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fiala A, Slagle C, Legband N, Aghabaglou F, Buesing K, Borden M, Harris S, Terry B. Treatment of a rat model of LPS-induced ARDS via peritoneal perfusion of oxygen microbubbles. J Surg Res 246: 450–456, 2020. doi: 10.1016/j.jss.2019.09.017. [DOI] [PubMed] [Google Scholar]
- 10.Wheeldon EB, Walker ME, Murphy DJ, Turner CR. Intratracheal aerosolization of endotoxin in the rat: a model of the adult respiratory distress syndrome (ARDS). Lab Anim 26: 29–37, 1992. doi: 10.1258/002367792780809020. [DOI] [PubMed] [Google Scholar]
- 11.Audi SH, Jacobs ER, Zhang X, Camara AK, Zhao M, Medhora MM, Rizzo B, Clough AV. Protection by inhaled hydrogen therapy in a rat model of acute lung injury can be tracked in vivo using molecular imaging. Shock 48: 467–476, 2017. doi: 10.1097/SHK.000000000000872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bannerman DD, Goldblum SE. Mechanisms of bacterial lipopolysaccharide-induced endothelial apoptosis. Am J Physiol Lung Cell Mol Physiol 284: L899–L914, 2003. doi: 10.1152/ajplung.00338.2002. [DOI] [PubMed] [Google Scholar]
- 13.Merker MP, Audi SH, Lindemer BJ, Krenz GS, Bongard RD. Role of mitochondrial electron transport complex I in coenzyme Q1 reduction by intact pulmonary arterial endothelial cells and the effect of hyperoxia. Am J Physiol Lung Cell Mol Physiol 293: L809–L819, 2007. doi: 10.1152/ajplung.00448.2006. [DOI] [PubMed] [Google Scholar]
- 14.Audi SH, Bongard RD, Krenz GS, Rickaby DA, Haworth ST, Eisenhauer J, Roerig DL, Merker MP. Effect of chronic hyperoxic exposure on duroquinone reduction in adult rat lungs. Am J Physiol Lung Cell Mol Physiol 289: L788–L797, 2005. doi: 10.1152/ajplung.00064.2005. [DOI] [PubMed] [Google Scholar]
- 15.Audi SH, Merker MP, Krenz GS, Ahuja T, Roerig DL, Bongard RD. Coenzyme Q1 redox metabolism during passage through the rat pulmonary circulation and the effect of hyperoxia. J Appl Physiol (1985) 105: 1114–1126, 2008. doi: 10.1152/japplphysiol.00177.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gan Z, Audi SH, Bongard RD, Gauthier KM, Merker MP. Quantifying mitochondrial and plasma membrane potentials in intact pulmonary arterial endothelial cells based on extracellular disposition of rhodamine dyes. Am J Physiol Lung Cell Mol Physiol 300: L762–L772, 2011. doi: 10.1152/ajplung.00334.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gan Z, Roerig DL, Clough AV, Audi SH. Differential responses of targeted lung redox enzymes to rat exposure to 60 or 85% oxygen. J Appl Physiol (1985) 111: 95–107, 2011. doi: 10.1152/japplphysiol.01451.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Merker MP, Audi SH, Bongard RD, Lindemer BJ, Krenz GS. Influence of pulmonary arterial endothelial cells on quinone redox status: effect of hyperoxia-induced NAD(P)H:quinone oxidoreductase 1. Am J Physiol Lung Cell Mol Physiol 290: L607–L619, 2006. doi: 10.1152/ajplung.00302.2005. [DOI] [PubMed] [Google Scholar]
- 20.Sepehr R, Audi SH, Staniszewski KS, Haworth ST, Jacobs ER, Ranji M. Novel flurometric tool to assess mitochondrial redox state of isolated perfused rat lungs after exposure to hyperoxia. IEEE J Transl Eng Health Med 1: 1500210, 2013. doi: 10.1109/JTEHM.2013.2285916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Duchen MR, Surin A, Jacobson J. Imaging mitochondrial function in intact cells. Methods Enzymol 361: 353–389, 2003. doi: 10.1016/s0076-6879(03)61019-0. [DOI] [PubMed] [Google Scholar]
- 22.Bongard RD, Yan K, Hoffmann RG, Audi SH, Zhang X, Lindemer BJ, Townsley MI, Merker MP. Depleted energy charge and increased pulmonary endothelial permeability induced by mitochondrial complex I inhibition are mitigated by coenzyme Q1 in the isolated perfused rat lung. Free Radic Biol Med 65: 1455–1463, 2013. doi: 10.1016/j.freeradbiomed.2013.07.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fisher AB. Intermediary metabolism of the lung. Environ Health Perspect 55: 149–158, 1984. doi: 10.1289/ehp.8455149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ma C, Beyer AM, Durand M, Clough AV, Zhu D, Norwood Toro L, Terashvili M, Ebben JD, Hill RB, Audi SH, Medhora M, Jacobs ER. Hyperoxia causes mitochondrial fragmentation in pulmonary endothelial cells by increasing expression of pro-fission proteins. Arterioscler Thromb Vasc Biol 38: 622–635, 2018. doi: 10.1161/ATVBAHA.117.310605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ruchko M, Gorodnya O, LeDoux SP, Alexeyev MF, Al-Mehdi AB, Gillespie MN. Mitochondrial DNA damage triggers mitochondrial dysfunction and apoptosis in oxidant-challenged lung endothelial cells. Am J Physiol Lung Cell Mol Physiol 288: L530–L535, 2005. doi: 10.1152/ajplung.00255.2004. [DOI] [PubMed] [Google Scholar]
- 26.Audi SH, Bongard RD, Dawson CA, Siegel D, Roerig DL, Merker MP. Duroquinone reduction during passage through the pulmonary circulation. Am J Physiol Lung Cell Mol Physiol 285: L1116–L1131, 2003. doi: 10.1152/ajplung.00185.2003. [DOI] [PubMed] [Google Scholar]
- 27.Bongard RD, Townsley MI, Merker MP. The effects of mitochondrial complex I blockade on ATP and permeability in rat pulmonary microvascular endothelial cells in culture (PMVEC) are overcome by coenzyme Q1 (CoQ1). Free Radic Biol Med 79: 69–77, 2015. doi: 10.1016/j.freeradbiomed.2014.09.030. [DOI] [PubMed] [Google Scholar]
- 28.Chan TS, Teng S, Wilson JX, Galati G, Khan S, O’Brien PJ. Coenzyme Q cytoprotective mechanisms for mitochondrial complex I cytopathies involves NAD(P)H: quinone oxidoreductase 1(NQO1). Free Radic Res 36: 421–427, 2002. doi: 10.1080/10715760290021270. [DOI] [PubMed] [Google Scholar]
- 29.Farkas DL, Wei MD, Febbroriello P, Carson JH, Loew LM. Simultaneous imaging of cell and mitochondrial membrane potentials. Biophys J 56: 1053–1069, 1989. [Erratum in Biophys J 57: following 684, 1990]. doi: 10.1016/S0006-3495(89)82754-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Perry SW, Norman JP, Barbieri J, Brown EB, Gelbard HA. Mitochondrial membrane potential probes and the proton gradient: a practical usage guide. Biotechniques 50: 98–115, 2011. doi: 10.2144/000113610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Aiuchi T, Daimatsu T, Nakaya K, Nakamura Y. Fluorescence changes of rhodamine 6G associated with changes in membrane potential in synaptosomes. Biochim Biophys Acta 685: 289–296, 1982. doi: 10.1016/0005-2736(82)90070-0. [DOI] [PubMed] [Google Scholar]
- 32.Johnson LV, Walsh ML, Bockus BJ, Chen LB. Monitoring of relative mitochondrial membrane potential in living cells by fluorescence microscopy. J Cell Biol 88: 526–535, 1981. doi: 10.1083/jcb.88.3.526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Scaduto RC Jr, Grotyohann LW. Measurement of mitochondrial membrane potential using fluorescent rhodamine derivatives. Biophys J 76: 469–477, 1999. doi: 10.1016/S0006-3495(99)77214-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fu C, Dai X, Yang Y, Lin M, Cai Y, Cai S. Dexmedetomidine attenuates lipopolysaccharide-induced acute lung injury by inhibiting oxidative stress, mitochondrial dysfunction and apoptosis in rats. Mol Med Rep 15: 131–138, 2017. doi: 10.3892/mmr.2016.6012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hough RF, Islam MN, Gusarova GA, Jin G, Das S, Bhattacharya J. Endothelial mitochondria determine rapid barrier failure in chemical lung injury. JCI Insight 4, 2019. doi: 10.1172/jci.insight.124329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Audi SH, Cammarata A, Clough AV, Dash RK, Jacobs ER. Quantification of mitochondrial membrane potential in the isolated rat lung using rhodamine 6G. J Appl Physiol (1985) 128: 892–906, 2020. doi: 10.1152/japplphysiol.00789.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Audi SH, Friedly N, Dash RK, Beyer AM, Clough AV, Jacobs ER. Detection of hydrogen peroxide production in the isolated rat lung using Amplex red. Free Radic Res 52: 1–11, 2018. doi: 10.1080/10715762.2018.1511051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Merker MP, Bongard RD, Krenz GS, Zhao H, Fernandes VS, Kalyanaraman B, Hogg N, Audi SH. Impact of pulmonary arterial endothelial cells on duroquinone redox status. Free Radic Biol Med 37: 86–103, 2004. doi: 10.1016/j.freeradbiomed.2004.02.078. [DOI] [PubMed] [Google Scholar]
- 39.Adams JD Jr, Lauterburg BH, Mitchell JR. Plasma glutathione and glutathione disulfide in the rat: regulation and response to oxidative stress. J Pharmacol Exp Ther 227: 749–754, 1983. [PubMed] [Google Scholar]
- 40.Ramakrishna M, Gan Z, Clough AV, Molthen RC, Roerig DL, Audi SH. Distribution of capillary transit times in isolated lungs of oxygen-tolerant rats. Ann Biomed Eng 38: 3449–3465, 2010. doi: 10.1007/s10439-010-0092-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dutta S, Ebling WF. Parameter estimability of biphasic response models. J Pharm Sci 86: 44–51, 1997. doi: 10.1021/js960248f. [DOI] [PubMed] [Google Scholar]
- 42.Bassingthwaighte JB, Chaloupka M. Sensitivity functions in the estimation of parameters of cellular exchange. Fed Proc 43: 181–184, 1984. [PMC free article] [PubMed] [Google Scholar]
- 43.Buckland ST. Monte Carlo confidence intervals. Biometrics 40: 811–817, 1984. doi: 10.2307/2530926. [DOI] [Google Scholar]
- 44.Das KC. Hyperoxia decreases glycolytic capacity, glycolytic reserve and oxidative phosphorylation in MLE-12 cells and inhibits complex I and II function, but not complex IV in isolated mouse lung mitochondria. PLoS One 8: e73358, 2013. doi: 10.1371/journal.pone.0073358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fisher AB. Energy status of the rat lung after exposure to elevated PO2. J Appl Physiol Respir Environ Exerc Physiol 45: 56–59, 1978. doi: 10.1152/jappl.1978.45.1.56. [DOI] [PubMed] [Google Scholar]
- 46.Bassett DJ, Bowen-Kelly E, Reichenbaugh SS. Rat lung glucose metabolism after 24 h of exposure to 100% oxygen. J Appl Physiol (1985) 66: 989–996, 1989. doi: 10.1152/jappl.1989.66.2.989. [DOI] [PubMed] [Google Scholar]
- 47.Erb M, Hoffmann-Enger B, Deppe H, Soeberdt M, Haefeli RH, Rummey C, Feurer A, Gueven N. Features of idebenone and related short-chain quinones that rescue ATP levels under conditions of impaired mitochondrial complex I. PLoS One 7: e36153, 2012. doi: 10.1371/journal.pone.0036153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Dell’Antone P, Colonna R, Azzone GF. The membrane structure studied with cationic dyes. 1. The binding of cationic dyes to submitochondrial particles and the question of the polarity of the ion-translocation mechanism. Eur J Biochem 24: 553–565, 1972. doi: 10.1111/j.1432-1033.1972.tb19718.x. [DOI] [PubMed] [Google Scholar]
- 49.Kotton DN, Morrisey EE. Lung regeneration: mechanisms, applications and emerging stem cell populations. Nat Med 20: 822–832, 2014. doi: 10.1038/nm.3642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dinh PC, Cores J, Hensley MT, Vandergriff AC, Tang J, Allen TA, Caranasos TG, Adler KB, Lobo LJ, Cheng K. Derivation of therapeutic lung spheroid cells from minimally invasive transbronchial pulmonary biopsies. Respir Res 18: 132, 2017. doi: 10.1186/s12931-017-0611-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Audi SH, Linehan JH, Krenz GS, Dawson CA. Accounting for the heterogeneity of capillary transit times in modeling multiple indicator dilution data. Ann Biomed Eng 26: 914–930, 1998. doi: 10.1114/1.138. [DOI] [PubMed] [Google Scholar]
- 52.Block ER, Fisher AB. Depression of serotonin clearance by rat lungs during oxygen exposure. J Appl Physiol Respir Environ Exerc Physiol 42: 33–38, 1977. doi: 10.1152/jappl.1977.42.1.33. [DOI] [PubMed] [Google Scholar]