Detection and analysis of cortical beta bursts in developmental EEG Data

Abstract

Developmental EEG research often involves analyzing signals within various frequency bands, based on the assumption that these signals represent oscillatory neural activity. However, growing evidence suggests that certain frequency bands are dominated by transient burst events in single trials rather than sustained oscillations. This is especially true for the beta band, with adult ‘beta burst’ timing a better predictor of motor behavior than slow changes in average beta amplitude. No developmental research thus far has looked at beta bursts, with techniques used to investigate frequency-specific activity structure rarely even applied to such data. Therefore, we aimed to: i) provide a tutorial for developmental EEG researchers on the application of methods for evaluating the rhythmic versus transient nature of frequency-specific activity; and ii) use these techniques to investigate the existence of sensorimotor beta bursts in infants. We found that beta activity in 12-month-olds did occur in bursts, however differences were also revealed in terms of duration, amplitude, and rate during grasping compared to adults. Application of the techniques illustrated here will be critical for clarifying the functional roles of frequency-specific activity across early development, including the role of beta activity in motor processing and its contribution to differing developmental motor trajectories.

Highlights

• •Transient bursts rather than oscillations dominate sensorimotor beta activity
• •Lagged coherence indicates the rhythmicity of a signal
• •The p-episode method can be used to identify beta bursts in developmental EEG data
• •Infant sensorimotor beta has a lower peak frequency than adults and consists of longer duration, higher amplitude bursts

1. Introduction

Classical analyses of frequency-specific activity in magneto/electroencephalography (M/EEG) data from developmental and adult populations start with the assumption that such activity is oscillatory, with amplitude time series in various frequency bands then averaged over trials. Recently, however, it has become clear that such trial-averaged analyses can mask the temporal structure of frequency-specific activity in individual trials, and moreover, that activity in certain frequency bands may occur as discrete, transient bursts rather than as oscillations (Jones, 2016, Lundqvist et al., 2018, Quinn et al., 2019, Seedat et al., 2020, Sherman et al., 2016, Tal et al., 2020, van Ede et al., 2018).

Evidence for the occurrence of bursts versus oscillations in the beta frequency band in particular is accumulating rapidly (Feingold et al., 2015, Jones et al., 2009, Little et al., 2019, Murthy and Fetz, 1996, Murthy and Fetz, 1992, Sherman et al., 2016, Shin et al., 2017, Spitzer and Haegens, 2017). When beta amplitude is averaged over trials, systematic changes are observed before, during, and after movement, including a slow decrease in beta amplitude prior to movement followed by a post-movement rebound (Cassim et al., 2000, Cheyne, 2013, Fetz, 2013, Jurkiewicz et al., 2006, Müller et al., 2003, Pfurtscheller, 1981, Pfurtscheller et al., 1996, Pfurtscheller and Lopes da Silva, 1999). Recent animal and human research, however, suggests that these slow, sustained changes in averaged beta activity do not accurately reflect trial-wise dynamics that occur in this band (Little et al., 2019, Sherman et al., 2016). Instead, these studies indicate that cortical beta activity in sensorimotor regions is characterized by transient bursts of activity, and that beta activity only appears to be temporally sustained if it is averaged over multiple trials (Jones, 2016, Little et al., 2019, Sherman et al., 2016). ‘Beta bursts’ have a stereotyped, wavelet-like shape in the time domain (Bonaiuto et al., 2021, Little et al., 2019, Sherman et al., 2016), occur much more focally in space than temporally averaged beta amplitude (Little et al., 2019), and interestingly, their timing in adults is a better predictor of motor behavior than slow changes in average beta amplitude (Hannah et al., 2020, Jana et al., 2020, Little et al., 2019, Shin et al., 2017, Sporn et al., 2020, Wessel, 2020). Such fine-grained temporal and spatial structure is obscured by trial- and temporal-averaging, but due to the strong relationship between burst timing and behavior, this information may be of vital importance for understanding the role of beta activity in motor processing.

In this case, looking at beta bursts in younger populations may also be critical for clarifying how early changes in this frequency band could underlie typical versus atypical motor development. No developmental research thus far has analyzed beta activity in terms of bursts, with developmental studies focused on the beta band severely lacking in general (Cuevas et al., 2014, Perone and Gartstein, 2019). A few EEG studies have looked at sensorimotor beta power during action observation in infants and young children (Meyer et al., 2011, van Elk et al., 2008), and EEG and MEG research with older children and adults have demonstrated that the peak frequency of beta changes over the lifespan (Johnson et al., 2019, Rossiter et al., 2014, Trevarrow et al., 2019). However, infant studies have typically used the canonical adult beta frequency band or one just above infant alpha (e.g. Niemarkt et al., 2011; Samson-Dollfus et al., 1983), and much remains unknown about the development and early function of this band.

The ability to apply techniques used to investigate the structure of frequency-specific activity may be particularly useful for developmental EEG studies, both for clarifying the functional role of sensorimotor beta activity but also of other frequency bands in which activity may occur in bursts (e.g. gamma; Cheyne and Ferrari, 2013; Lundqvist et al., 2018). Therefore, the two main objectives of this paper are as follows: 1) to provide a tutorial for developmental researchers on how to apply techniques for evaluating the rhythmicity (i.e. periodicity, a primary characteristic of oscillatory activity) of frequency-specific activity and for detecting bursts of activity; and 2) to apply these methods to infant and adult EEG datasets collected during the same grasping task in order to provide evidence for infant sensorimotor beta bursts, and to compare burst properties and their modulation in infants and adults. Specifically, we illustrate the use of power spectral densities combined with lagged coherence to determine frequency band limits and examine the rhythmicity of beta band activity, and a variant of the widely-used ‘p-episode method’ (Caplan et al., 2001, Hannah et al., 2020, Little et al., 2019, Lundqvist et al., 2016, Sherman et al., 2016, Shin et al., 2017, Tal et al., 2020, Wessel, 2020) for the identification of beta burst timing, duration, and amplitude. All source code used for tutorial and subsequent analyses have been made publically available.

2. Tutorial

In the following section, we demonstrate how to determine frequency band limits, how to evaluate the rhythmicity of activity within a frequency band, and how to identify transient burst events occurring in that band. These techniques can be used to analyze burst events within any frequency range, but here we focus on activity within the beta band, measured from electrodes over the sensorimotor cortex, as this signal is dominated by transient bursts of activity (Little et al., 2019). In this tutorial section, data are analyzed from an example adult participant, averaged within an electrode cluster centered on the C3 electrode (E16, E20, E21, E22). All source code for these analyses is available at https://github.com/danclab/dev_burst_analysis. These analyses were run using EEGLAB v14.1.1 (Delorme and Makeig, 2004) and FieldTrip v20190329 (Oostenveld et al., 2011) on MatLab 2015b.

2.1. Determining beta peak frequency

Before identifying transient bursts of activity within a frequency band, it is first necessary to identify the frequency limits of that band. The power spectral density (PSD) of a signal is the measure of signal power over different frequency bands. Frequency band limits can be identified by looking for prominent peaks in the PSD. There are several methods that can be used to compute power spectra, but Welch’s method (Welch, 1967) is one of the most commonly used. This method computes the PSD by dividing data into temporally overlapping segments. Each segment is then windowed using a Hamming window in order to give emphasis to the data at the center of the segment. The discrete Fourier transform is then applied to the windowed segments and the magnitude of the result is squared to yield the power in each frequency bin within each segment. Finally, the power spectra for all segments are averaged.

The power spectrum includes both periodic and aperiodic activity, which can bias estimates of frequency band limits (Donoghue et al., 2020). The aperiodic activity typically has a 1/f-like distribution. We therefore fit a 1/f function to the spectrum and identify frequency bands using the residuals of this fit, representing the periodic component of the spectrum (see Discussion). Band peak frequencies are identified as local maxima, and the full width half maximum (FWHM) is computed for each band.

The code for computing the PSD and identifying frequency bands for the C3 electrode cluster in an example adult participant can be found in the Github repository in the script tutorial_1.m (Code segment 1). The EEGLAB function spectopo is used to compute the PSD. The MatLab function fit_lm with ‘RobustOpts’ on is used to fit the 1/f function to the spectrum using robust linear regression to reduce the influence of the periodic component peaks. The MatLab function findpeaks is used to find peaks in the periodic spectrum component. The resulting alpha and beta ranges for the C3 cluster in this example participant are 9–12 Hz and 19.25–22.75 Hz.

Code segment 1

: Determining beta frequency band limits.

Lines 31–86 of tutorial_1.m. The sampling rate of the EEG data is used to compute the window size and overlap. The EEGLAB function spectopo returns the spectra and vector of frequencies for each cluster. The MatLab function fitlm returns the fitted model including coefficient estimates and residuals, and findpeaks returns the local maxima of the spectrum residuals and the indices of the frequencies vector where they occur.

2.2. Evaluating rhythmicity

Having determined that the data contain prominent beta band activity, how can we assess whether this activity is periodic and oscillatory versus transient and ‘bursty’? To do this, a measure of signal rhythmicity is required. Lagged coherence is one such measure (Fransen et al., 2015), where rhythmicity is quantified based on the ability to predict the future phase of a signal based on the present one; that is, the consistency of the phase between different time intervals (‘lags’). If the underlying rhythmicity of a signal is high, lagged coherence will be high across a range of lags, with phase highly predictable far into the future. If the signal consists of transient, arrhythmic bursts, however, lagged coherence will be lower, or only high at very short lags, with future phase highly unpredictable. Lagged coherence involves splitting the data up into segments, computing the Fourier coefficients within those segments, comparing the phase of the signal between segments, and then summarizing the consistency of phase differences across segment pairs (Fransen et al., 2015).

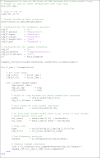
The script tutorial_2.m computes lagged coherence within the C3 electrode cluster across a range of frequencies and lags for an example adult participant (Code segment 2). It uses FieldTrip functions, therefore the EEGLAB-formatted data must first be converted to FieldTrip format (see the create_ft_data function). For a range of frequencies and cycle lags, the script uses the FieldTrip functions ft_freqanalysis to compute the complex Fourier spectra, and ft_connectivity_laggedcoherence to compute lagged coherence.

Code segment 2

: Computation of lagged coherence.

Lines 33–93 of tutorial_2.m. The EEGLab data is converted to FieldTrip format. After setting up the configuration structure for the frequency analysis and lagged coherence, the function loops through the list of frequencies (foi), and for each frequency, loops through the list of lag cycles (lags). For each frequency and lag, the time windows for phase comparison are computed, and the FieldTrip functions ft_freqanalysis and ft_connectivity_lagged_coherence are used to get the phase of the signal within each window, and compare phase between windows.

2.3. Identifying beta bursts

Having confirmed that beta activity appears non-oscillatory and ‘bursty’, we now demonstrate one technique to detect and extract these bursts. Known as the ‘p-episode method’ (Caplan et al., 2001, Hannah et al., 2020, Little et al., 2019, Lundqvist et al., 2016, Sherman et al., 2016, Shin et al., 2017, Tal et al., 2020, Wessel, 2020), this involves first computing the amplitude or power of a signal within a frequency range, and then detecting when amplitude or power fluctuations exceed a threshold. There are several versions of this method that use power rather than amplitude and differ in how the threshold is determined (Sherman et al., 2016, Shin et al., 2017), but the version we demonstrate below uses the amplitude envelope rather than power in order to keep the data as raw as possible, and empirically estimates subject-specific thresholds.

There are several methods that can be used for computing the amplitude of a signal within a given frequency band. The filter-Hilbert method is one such method useful for narrowband data, such as the restricted beta band range considered here. The data is first bandpass filtered, then the amplitude envelope is extracted after applying the Hilbert transform to the filtered data. Different types of filters can be used, but it is important to use a two-pass rather than a single-pass causal filter to avoid temporally distorting the amplitude. The result of the Hilbert transform is a complex-valued signal including the amplitude envelope and phase of the signal, from which we extract the amplitude envelope. Code for computing signal amplitude using the filter-Hilbert method within the alpha and beta ranges derived above can be found in the script tutorial_3.m (Code segment 3). In order to avoid filter-related edge artifacts, the data are padded using the DC offset before applying the filter and Hilbert transform. This padding is then removed from the resulting amplitude envelope. The FieldTrip function ft_preproc_bandpass_filter is used to perform bandpass filtering, and the Hilbert transform is applied using MatLab function hilbert.

Code segment 3

The filter-Hilbert method for computing signal amplitude.

Lines 31–80 of tutorial_3.m. The DC component of the data for each trial (data) is computed, and then used to pad the data on either side. The FieldTrip function ft_preproc_bandpassfilter is used to bandpass filter the data within the frequency range, the amplitude is derived from the Hilbert transform, and the padding is removed.

Having computed the amplitude envelope of the beta band in each trial, we now need some criteria which can be applied to this signal to detect transient beta activity. Here, we use an empirically derived relative threshold on beta amplitude. This threshold is computed based on multiple standard deviations above the median beta amplitude, with the median representing a robust measure of centrality for skewed distributions. This measure is subject-specific, with the absolute threshold set per subject based on their amplitude distribution. More specifically, for each subject we compute the nonparametric correlation (Spearman’s ρ) between the number of bursts per trial (number of threshold crossings) and the mean amplitude per trial. This is done using a range of thresholds computed from the median and standard deviation of beta amplitude in all time points across all trials for that subject. We then determine the standard deviation multiple that maximizes the mean of this correlation (Code segment 4). For the C3 cluster in this example participant, this results in a threshold of 1.6 SDs above the median.

Code segment 4

: Determining the optimal threshold for burst detection.

Lines 76–108 of tutorial_4.m. For each relative threshold (SDs above the median), the absolute threshold is computed, and the number of bursts per trial is computed as the number of times the amplitude crosses the threshold. The relative threshold is chosen as that which maximizes the correlation between the number of bursts and mean amplitude per trial.

2.4. Extracting beta bursts for further analysis

Given the beta amplitude envelopes and threshold, beta bursts can be extracted from the data. The script tutorial_5.m (Code segment 5) extracts the duration, peak amplitude, and peak time of each burst for every trial from an example adult participant. First, times at which beta amplitude crosses the absolute, subject-specific threshold are identified. Second, for each threshold-crossing, the time at which beta amplitude returns below the threshold is found. The difference between these two times points gives the duration of the burst, and from within these, burst onset and offset times, peak amplitude, and the time at which this peak is reached can be identified. The timing of the bursts can then be compared to changes in beta amplitude and between epochs to determine if it is modulated by the task.

Code segment 5

The p-episode method for burst identification.

Lines 82–131 of tutorial_5.m. The outer loop iterates over each trial. The inner loop finds each time where the amplitude within a trial crosses the threshold. For each of these times, the next time where the amplitude returns below the threshold is found and used to compute the burst duration, amplitude, and peak time.

3. Investigation of infant beta bursts

In this section, we use the techniques described in the tutorial to provide evidence for infant sensorimotor beta bursts, and to compare the properties of these bursts in a sample of 12-month-old infants and a sample of adults. EEG was recorded as both infants and adults performed the same grasping task.

3.1. Material and methods

3.1.1. Participants

Forty-six full-term 12-month-old infants (26 females, age range 11.2–12.93 months) and 23 adults (10 females, age range 18–22 years) were recruited for a study about the neural bases of reaching and grasping. Sixteen infants were excluded due to unusable EEG data before preprocessing (N = 8), being distressed shortly after applying EEG electrodes net (N = 7), and recording failure (N = 1). One adult was also excluded due to an error in data recording. Therefore, the final sample included 30 infants and 22 adults. All infants were typically developing with no known or suspected neurodevelopmental or medical diagnoses. Prior to an infant’s participation in the study, informed consent was obtained from the infant’s parents. All adults had normal or corrected to normal vision and did not have any neurological disorder. They provided informed consent before participating in the study. The experiment was approved by the University of Maryland Institutional Review Board.

3.1.2. Procedure and task

Infants and adults performed the same task. Infants sat on their caregiver's lap, and adults sat in a chair approximately 40 cm from the front of a black puppet stage (99 cm [W] × 61 cm [L] × 84 cm [H]) placed on a table. Black panel curtains covered the areas immediately surrounding the stage to hide the experimenter and the equipment from the participant’s view. A video camera was placed behind the presenter focused on the participant and the presenter to capture events of interest during testing. Infant caregivers were instructed to remain passive.

A trial consisted of an observation and an execution condition. A curtain was raised and lowered at the start and end of each observation and execution portion of the trial. To begin the observation condition, the curtain was raised, revealing a female presenter. The presenter made eye contact with the participant then shifted their gaze towards a toy that was placed at the centre of the stage, but not within the participant’s grasp. The presenter then reached for the toy with a hand‐operated claw-like tool, picked up the toy, brought the toy to themselves, and gave the toy a brief shake. The curtain was lowered to mark the end of this event, which lasted approximately 4–s. To begin the execution condition, a toy was placed on the table, and the presenter hiding from the participant’s view pushed the tabletop towards the participant within reaching distance as the curtain was raised. Participants were then given around 60 s to reach for the toy. The tabletop was retracted and the curtain lowered to mark the end of this event. Baseline events were recorded during a short period of rest preceding each observation and execution event. Thus, one complete trial consisted of an observation epoch, an execution epoch, and two baseline epochs. The order of the observation and execution conditions was pseudo‐randomized.

Ten unique toys were used, with each toy used for two observation and two execution events. For adults, there were twenty trials in which the observation condition was first, and twenty in which the execution condition was first (40 trials per adult). For infants, there were ten trials in which the observation condition was first and ten trials in which execution condition was first (maximum 20 trials per infant). On average, infants each completed 12 trials (SD = 5).

3.1.3. EEG recording and preprocessing

EEG was recorded using a 65-channel HydroCel Geodesic Sensor Net (Electrical Geodesics, Inc., Eugene, OR). The vertex (Cz) electrode was used as online reference. EEG data were sampled at 500 Hz using EGI’s Net Station (v4.5.4) software. Impedances were kept below 100 kΩ. After recording, EEG data were exported to a MatLab compatible format using Net Station software for offline processing. Both infant and adult datasets were preprocessed using the MADE pipeline (https://github.com/ChildDevLab/MADE-EEG-preprocessing-pipeline; Debnath et al., 2020) and MatLab 2015b. The data were highpass filtered at 0.3 Hz and lowpass filtered at 50 Hz using EEGLAB v14.1.1 (Delorme and Makeig, 2004) FIR filters. Artifact-laden channels were identified and removed using the EEGLAB plug-in FASTER (infants: 0–5 channels, M = 1.81, SD = 1.33; adults: 0–3 channels, M = 1.77, SD = 0.81; Nolan et al., 2010). For preprocessing of the infant data, six channels (23, 55, 61, 62, 63, 64) on the boundary of the electrode net were also excluded from analyses since they were heavily susceptible to eye, face and head movements. Then, independent component analysis (ICA) was performed on an identical copy of the dataset. Before ICA, this copied dataset was highpass filtered at 1 Hz and segmented into 1 s epochs. In the copied dataset, noisy segments were rejected using a combined voltage threshold of ± 1000 μV and spectral threshold (range −30 dB to +100 dB) within the 24–40 Hz frequency band to remove EMG-like activity. After ICA decomposition, independent components (ICs) were transferred from the ICA copied dataset to the original dataset, which was used from then on. Artifactual ICs were removed from the original dataset using the EEGLAB ADJUST plugin (infants: 7–31 components, M = 15.68, SD = 6.94; adults: 4–21 components, M = 12.91, SD = 4.61; Mognon et al., 2011) and via visual inspection of individual ICs. The data were then segmented into 3 s (from −1.5 s to 1.5 s) epochs time-locked to four event markers: execution baseline, execution object contact, observation baseline, and observation object contact. In both execution and observation conditions, time 0 therefore represents the time at which the hand first contacted the toy, and the time window from 0 to 1.5 s is when the grasp is completed and the toy is brought to the body and shook. After segmenting data into 3-second epochs, a voltage threshold of + /− 200 µV was used to remove epochs contaminated by artifacts (infants: 1–40 epochs, M = 9.42, SD = 7.62; adults: 0–7 epochs, M = 1.14, SD = 1.91). After artifact rejection, missing channels were interpolated. Finally, a current source density (CSD) transformation was applied to the epoched data using the CSD toolbox (Kayser and Tenke, 2006).

3.1.4. Burst analyses

This analysis included all participants with at least 5 trials following preprocessing (infants: 30 participants, trials per participant, M = 13.73, SD = 6.87; adults: 22 participants, trials per participant, M = 36.59, SD = 6.37).

All source code for these analyses is available at https://github.com/danclab/dev_burst_analysis. These analyses were run using EEGLAB v14.1.1 (Delorme and Makeig, 2004) and FieldTrip v20190329 (Oostenveld et al., 2011) on MatLab 2015b, and lme4 v1.1.26 (Bates et al., 2015) on R v3.6.1 (R Core Team, 2020).

Power spectral densities (PSDs) were computed from 0.5 to 40 Hz using Welch’s method (Welch, 1967) with a window size of 1 s, 50% overlap, and zero-padding to 2 s, resulting in a frequency resolution of 0.5 Hz. For each subject (infant and adult), this was applied to all data (i.e. from both the observation and execution conditions). For each channel, the periodic component of the spectra was isolated by fitting a 1/f function to the PSD using robust linear regression, and taking the raw residuals of this fit. The periodic components were than averaged within the C3 (E16, E20, E21, E22) and C4 (E41, E49, E50, E51) electrode clusters, located centrally in the left and right hemispheres, and then across subjects within each age group. For each cluster, spectral peaks in the periodic component from 5 to 40 Hz were identified using the MatLab function findpeaks, and for each peak, the frequency band limits were determined by computing the full width half maximum (FWHM) of the peak power.

Lagged coherence was computed for all data from each subject (e.g. from both the observation and execution conditions) from 5 to 40 Hz in 1 Hz increments and 2–7 cycles in increments of 0.1 cycles (Fransen et al., 2015). We used overlapping epochs with lag- and frequency-dependent widths. Fourier coefficients were then obtained for each epoch using a Hann-windowed Fourier transform.

Beta amplitude was computed by bandpass filtering the raw data (6th order two-pass Butterworth filter, reducing the order when instability is detected), and taking the amplitude of the Hilbert transformation of the bandpass filtered data. The data were padded with 1 s on either side using the DC offset before applying the filter and Hilbert transform. The relative threshold for beta burst detection was computed separately for C3 and C4 for the infant and adult participants. This was defined as a multiple of the standard deviation of beta amplitude above the median amplitude. We determined the standard deviation multiple that maximized the mean of the nonparametric correlation between the number of beta bursts detected in each trial (number of times beta amplitude crossed the threshold) and the average beta amplitude, averaged across participants. This yielded a relative threshold of 1.1 and 1.2 standard deviations for C3 (Spearman’s ρ = 0.85) and C4 (ρ = 0.85) of the adult participants (Fig. S1A, B), and 1.5 and 1.2 standard deviations for C3 (ρ = 0.73) and C4 (ρ = 0.77) of infants (Fig. S1C, D), which we then used to extract bursts.

Bursts were extracted from the baseline and grasp execution epochs of the execution task by detecting times at which the beta amplitude envelope, averaged within the C3 or C4 cluster electrodes, crossed the threshold. The burst ending times were taken as the time when the amplitude envelope next fell below the threshold. Burst duration was defined as the difference between these time points, amplitude as the maximum amplitude within them, and peak time as the time point at which the maximum amplitude was reached. Bursts lasting a single time point (2 ms) were discarded.

To compare burst rate to beta amplitude, we baseline-corrected the amplitude and a smoothed measure of burst rate. The amplitude was baseline corrected by subtracting the mean amplitude over the whole baseline epoch. The burst rate was obtained by binning the burst event timings using 10 ms bins, smoothing using a two-pass Gaussian convolution with a width of 25 bins, and then baseline correcting by subtracting the mean burst rate over the whole baseline epoch.

Burst frequency was compared between the baseline and grasp performance epochs in each cluster, for infants and adults. We used a generalized linear mixed model with a Poisson distribution and log link function. This included epoch as a fixed effect, and subject-specific offsets as a random effect. Burst duration and amplitude were compared between infants and adults for each cluster using linear mixed models with age as a fixed effect and subject-specific random offsets.

3.2. Results

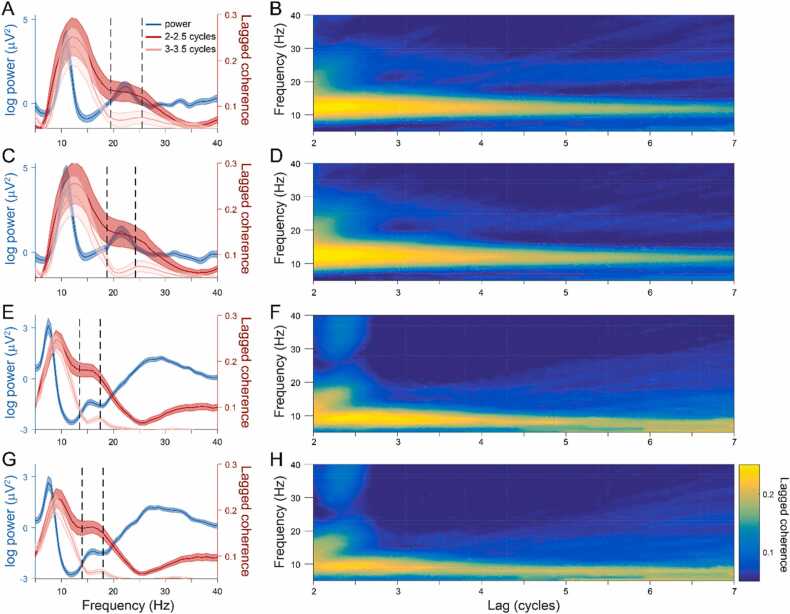
To remove the bias of aperiodic activity from the power spectral density (PSD) and isolate the periodic activity, we fit a 1/f function to the spectra from each electrode cluster and analyzed the residuals of this fit (Donoghue et al., 2020; see Discussion). In the C3 and C4 electrode clusters, a prominent alpha peak is evident in the adult (11 Hz, FWHM = 3 Hz; Fig. 1A, C; Fig. S2A, B) and the infant (C3: 7.5 Hz, FWHM = 2 Hz; C4: 7.5 Hz, FWHM = 3 Hz; Fig. 1E, G; Fig. S2C, D) periodic spectra. Beta was identified as the next highest peak frequency, which was lower in infants (C3: 15.5 Hz, FWHM = 4 Hz, range = 13.5 – 17.5 Hz; C4: 16 Hz, FWHM = 4 Hz; range = 14 – 18 Hz; Fig. 1E, G; Fig. S2C, D) compared to adults (C3: 22.5 Hz, FWHM = 6 Hz, range = 19.5 – 25.5 Hz; C4: 21.5 Hz, FWHM = 5.5 Hz, range = 18.75 – 24.25 Hz; Fig. 1A, C; Fig. S2A, B). These ranges were used in the following analyses of beta activity.

Fig. 1.

Sensorimotor beta activity is dominated by transient bursts. A) The power spectral density (blue) after removing the 1/f aperiodic component and lagged coherence averaged over 2 – 2.5 (dark red) and 3 – 3.5 (light red) cycles in the C3 cluster of the adult participants. Dark lines show the mean across participants and the shaded areas indicate the standard error. A prominent peak appears in the alpha range in the power spectrum and lagged coherence at 2 – 2.5 and 3 – 3.5 cycles, whereas a beta peak is visible in the power spectrum and only in lagged coherence at 2 – 2.5 but not 3 – 3.5 cycles. B) Mean lagged coherence over all adult participants in the C3 cluster over a range of lags. There is high lagged coherence in the alpha band over a large range of lags, but beta lagged coherence rapidly decreases after 2 cycles. This same pattern of power and lagged coherence in the alpha and beta bands was also apparent in the adult C4 cluster (C and D), as well as the 12 m infant C3 (E and F) and C4 (G and H) clusters, but each band was evident at a lower peak frequency in the infant data. (For interpretation of the references to colour in this figure, the reader is referred to the web version of this article.)

We then used lagged coherence, a measure of signal rhythmicity (Fransen et al., 2015), to determine which frequencies contained “bursty” or arrhythmic activity. The alpha and beta peaks found in the adult and infant periodic spectra were also present in the lagged coherence at 2 – 2.5 cycles, but only the alpha peak (slightly shifted in peak frequency) was still present at 3 – 3.5 cycles (Fig. 1A, C, E, G; Fig. S3). In both the adults and infants, lagged coherence in the alpha frequency range remained relatively high over a range of lags up to 7 cycles, but rapidly diminished after 2 cycles in the beta range (Fig. 1B, D, F, H). Activity in the alpha band, therefore, appears to be rhythmic and oscillatory, whereas lagged coherence confirms that in both adults and infants, beta activity occurs predominantly as burst events.

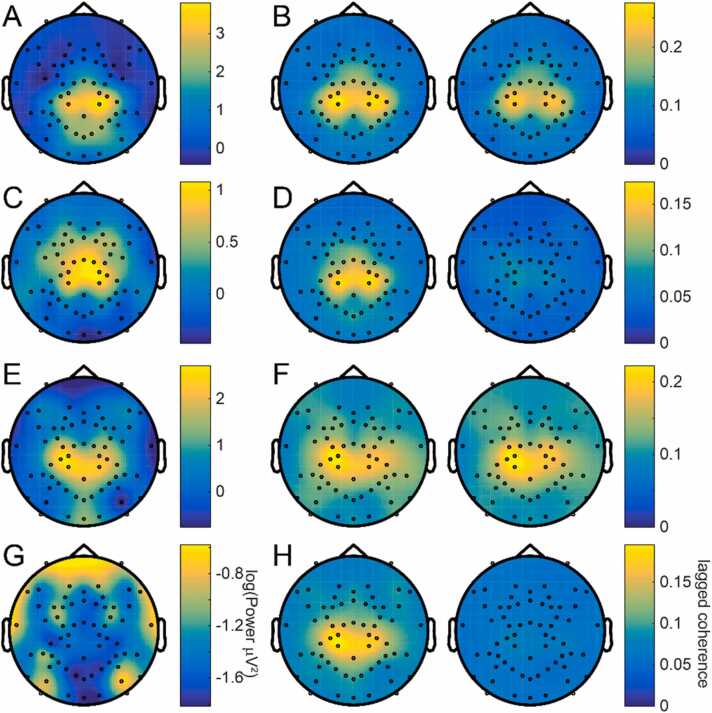
The choice of the C3 and C4 electrode clusters is further justified by the topographic distribution of power and lagged coherence in the alpha and beta bands. In adults, alpha power is centered over the central electrodes (Fig. 2A), and so is beta (Fig. 2C). Lagged coherence in the alpha (Fig. 2B) and beta (Fig. 2D) bands also localizes centrally. Infant alpha power is also centered over central electrodes (Fig. 2E), but infant beta power is strongest in the peripheral electrodes (Fig. 2G). However, both infant alpha (Fig. 2F) and beta (Fig. 2H) lagged coherence localizes centrally. In both adults and infants, alpha lagged coherence remained roughly unchanged as the lag was increased from 2 to 2.5–3–3.5 cycles, whereas beta lagged coherence was high in central electrodes at 2–2.5 cycles but decreased to nearly 0 at 3–3.5 cycles.

Fig. 2.

Lagged coherence localizes beta activity to central electrode clusters. A) Topography of power in the alpha band, averaged over adult participants. Alpha power is most prominent in central electrodes. B) Alpha lagged coherence topography averaged between 2 and 2.5 cycles (left) and 3 – 3.5 cycles (right), averaged over adult participants. Alpha lagged coherence also localizes to central electrodes, and remains high over several cycles. C) As in (A), for the beta band in adult participants. As with alpha, adult beta power is highest in central electrodes. D) As in (B), for the beta band in adult participants. Lagged coherence in the beta band localizes to central electrodes, but lagged coherence drops off more rapidly with increasing cycles. E) Topographic distribution of power in the alpha band, averaged over infant participants. Infant alpha power localizes to the central and occipital electrodes. F) Topography of alpha lagged coherence averaged between 2 and 2.5 cycles (left) and 3 – 3.5 cycles (right), averaged over infant participants. As in adults, lagged coherence in infant alpha localizes centrally and does not greatly decrease with increasing cycles. G) As in (E), for the beta band in infant participants. Unlike adults, infant beta power is highest in frontal and temporal electrodes. H) As in (F), for beta lagged coherence in infant participants. As in adults, beta lagged coherence is strongest in central electrodes and decreases with increasing cycles.

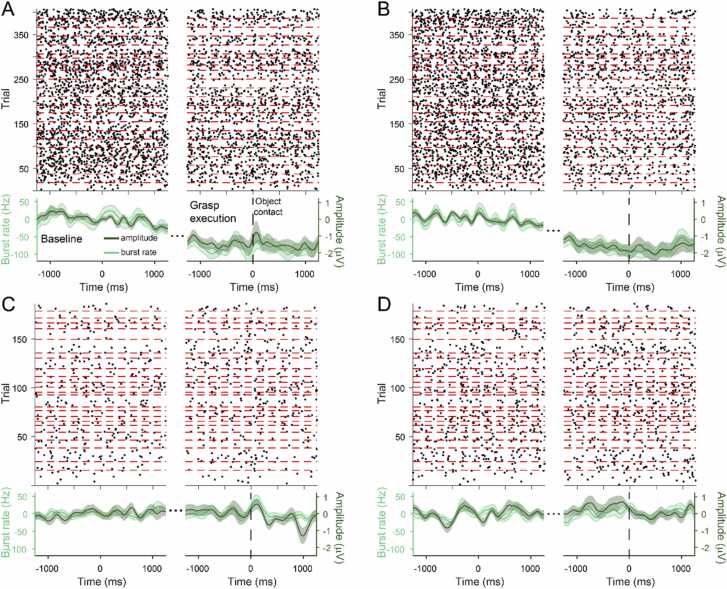
Having demonstrated that sensorimotor beta activity is largely arrhythmic, we then identified bursts of beta activity in the C3 and C4 electrode clusters during the execution condition. In both adults and infants, the beta probability time series closely tracked changes in beta amplitude (Fig. 3). There was a clear difference in burst rate and beta amplitude between the baseline and grasp execution epochs in the adult subjects in both clusters (Fig. 3A,B), with a higher number of bursts occurring during baseline compared to grasp execution (C3: baseline M = 3.36, SD = 2.17, grasp execution M = 1.96, SD = 1.98, Χ²(1) = 148.03, p < 0.001; C4: baseline M = 3.17, SD = 1.99, grasp execution M = 1.69, SD = 1.66, Χ²(1) = 178.93, p < 0.001). No changes in burst rate or beta amplitude were evident in the infant data (Fig. 3C,D). While fewer bursts occurred during grasp execution than baseline (C3: baseline M = 1.45, SD = 1.17, grasp execution M = 1.32, SD = 1.11; C4: baseline M = 2.06, SD = 1.49, grasp execution M = 1.89, SD = 1.41), this difference was not statistically significant (C3: Χ²(1) = 1.09, p = 0.297; C4: Χ²(1) = 1.39, p = 0.238).

Fig. 3.

Beta burst probability tracks changes in beta amplitude. A) Bursts extracted from the C3 cluster of adult subjects during the baseline and grasp execution epochs of all trials. A raster plot of bursts in each trial (top panel; dashed red lines denote the trials from each subject) shows that bursts occurred more frequently during the baseline epoch. The burst rate (light green) closely tracked changes in beta amplitude (dark green). Solid lines show the mean across participants and shaded regions indicate the standard error. B) Beta amplitude and burst rate also decreased in the C4 cluster of adult subjects during grasp execution. Time zero in the grasp execution epoch represents the first contact of the hand with the object. Burst rate in the C3 (C) and C4 (D) clusters of infants also closely tracked changes in beta amplitude, but neither were modulated by grasp execution. (For interpretation of the references to colour in this figure, the reader is referred to the web version of this article.)

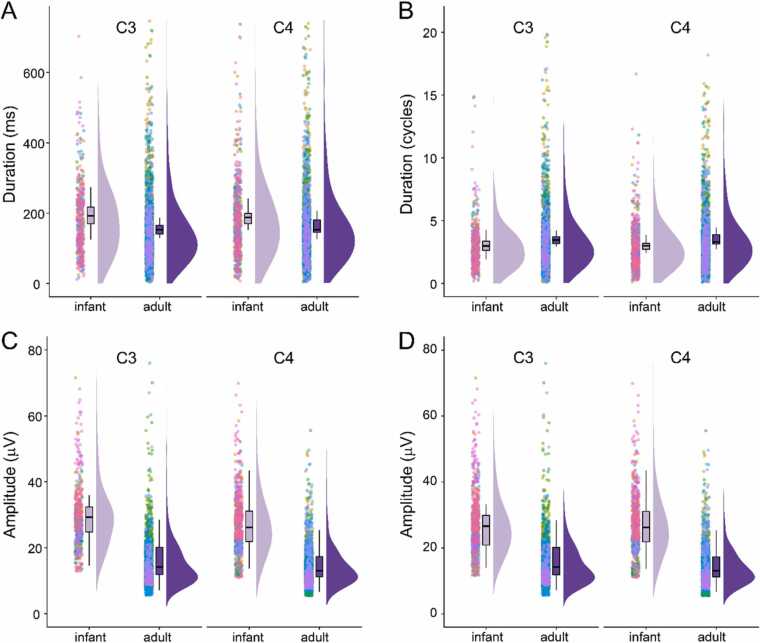
In addition to differential modulation by grasp execution, infants and adult bursts differed in terms of duration and amplitude. Infant bursts lasted ~20–30 ms longer than adult bursts (C3: infant M = 188.23, SD = 122.32 ms, adult M = 153.13, SD = 127.86 ms, Χ²(1) = 16.57, p < 0.001; C4: infant M = 184.71, SD = 126.92 ms, adult M = 162.48, SD = 118.95 ms, Χ²(1) = 7.10, p = 0.007; Fig. 4A). In order to ensure that this difference was not a simple consequence of infants having a lower beta peak frequency, we compared burst duration in terms of the number of cycles per bursts, thus correcting for differences in peak frequency. In fact, infant bursts were ~0.5 cycles shorter than adult bursts (C3: infant M = 2.92, SD = 1.90 cycles, adults M = 3.45, SD = 2.88 cycles, Χ²(1) = 9.47, p = 0.002; C4: infant M = 2.96, SD = 2.03 cycles, adult M = 3.49, SD = 2.56 cycles, Χ²(1) = 9.56, p = 0.002; Fig. 4B). Infant bursts also tended to have higher amplitudes than adult bursts (C3: infant M = 29.34, SD = 10.01 μV, adult M = 15.04, SD = 8.18 μV, Χ²(1) = 30.39, p < 0.001; C4: infant M = 26.53, SD = 9.41 μV, adult M = 14.00, SD = 6.17 μV, Χ²(1) = 32.22, p < 0.001; Fig. 4C), and this was true even after using the lower adult threshold to detect infant bursts (C3: infant M = 26.86, SD = 9.56 μV, Χ²(1) = 21.04, p < 0.001; C4: infant M = 26.53, SD = 9.31 μV, Χ²(1) = 32.22, p < 0.001; Fig. 4D).

Fig. 4.

Infant and adult beta bursts differ in duration and amplitude. A) Infant beta bursts in C3 and C4 have longer duration than adult beta bursts. Each dot shows the duration of an individual beta burst, color-coded by subject. B) When expressed in terms of cycles rather than absolute duration, infant beta bursts in C3 and C4 lasted fewer cycles than adult bursts. C) Infant beta bursts in C3 and C4 tended to have a higher amplitude than adult bursts. D) Even when using the lower threshold identified for burst detection in adults, C3 and C4 infant beta bursts had a higher amplitude than in adults.

4. Discussion

Here, we illustrated how recently developed methods to examine the structure of frequency-specific activity and identify transient bursts of activity can be applied to developmental EEG data, and provided the first evidence that infant sensorimotor beta activity is dominated by transient bursts, as in adults. We also demonstrated that infant and adult beta bursts differ in terms of peak frequency, duration, amplitude, and task-modulation. Of note, while our focus was on the beta band, activity in other frequency bands can also occur in bursts (Lundqvist et al., 2016, Schaworonkow and Voytek, 2021), and the techniques demonstrated here can be readily applied to activity in any frequency band via the use of lagged coherence and power spectra to define frequency limits, and using these boundaries with the filter-Hilbert method to compute signal amplitude. Going forward, utilizing such techniques to investigate beta band activity specifically will likely be vital for clarifying the developmental trajectory of this particular band and its potential role in motor skill development.

We found that the sensorimotor beta band in 12 month old infants had a lower peak frequency compared to adults. Such an increase in peak frequency has been widely observed in the alpha band (Henry and Greulich, 1944, Lindsley, 1939, Lindsley, 1938, Marshall et al., 2002, Smith, 1938). While changes in beta peak frequency have also been observed from late childhood through adulthood (Johnson et al., 2019, Rossiter et al., 2014, Trevarrow et al., 2019), it is unclear whether a clear beta peak in the power spectra can even be observed in the first year of life (Cuevas et al., 2014, Xie et al., 2018). Our data are cross-sectional, but our results do suggest an age-related increase in beta peak frequency from 12 months to adulthood.

One difficulty in examining infant beta activity is that infant jaw and arm movements cause an increase in power at approximately 15 Hz over peripheral sites (Georgieva et al., 2020), which overlaps our estimate of the infant beta range. The spatial distribution of beta power that we found in infants is in line with these findings (Fig. 2G), but the spatial topography of beta lagged coherence (Fig. 2H) suggests that these movement-related artifacts may obscure motor cortical beta activity which occurs around the same frequency range. A combination of lagged coherence and power spectra could therefore be a powerful way to identify and automatically remove artifactual components in ICA-based EEG preprocessing.

Computational modeling suggests that beta burst peak frequency is determined by their waveform shape in the temporal domain (Jones, 2016, Sherman et al., 2016), itself reflecting a combination of synaptic inputs to deep and superficial cortical layers (Bonaiuto et al., 2021, Sherman et al., 2016). Differences in the peak frequency of infants compared to adults could therefore arise from differences in the temporal dynamics, amplitude, or timing of either or both of these inputs, which could also account for infant – adult differences in burst duration and amplitude. While the absolute duration of infant and adult beta bursts in our data matches that previously reported in adults (Bonaiuto et al., 2021, Echeverria-Altuna et al., 2021a, Little et al., 2019, Little et al., 2012, Seedat et al., 2020), the fewer number of cycles in infant bursts might suggest that they differ in waveform shape. Future studies could use techniques such as empirical mode decomposition (Fabus et al., 2021, Quinn et al., 2021), in combination with computational modeling (Bonaiuto et al., 2021), to characterize and temporally align beta burst waveforms and identify the patterns of inputs that account for differences between infant and adult bursts.

Interestingly, sensorimotor beta burst rate decreased bilaterally during grasp execution in adults, but did not change compared to baseline in infants. The burst rate decrease in adults is characteristic of the event-related “desynchronization” commonly observed in motor regions prior to action performance (Cassim et al., 2000, Doyle et al., 2005, Heinrichs-Graham and Wilson, 2016, Kaiser et al., 2001, Neuper et al., 2006, Pfurtscheller, 1981, Stancák and Pfurtscheller, 1996), now understood to reflect the averaging of burst occurrence over trials (Brady et al., 2020, Little et al., 2019, Wessel, 2020). Such a pre-movement decrease in sensorimotor beta power has not previously, to our knowledge, been reported in infants, and we failed to find a change in burst rate. This could be for several reasons: 1) sensorimotor beta activity is not functionally related to movement performance at such a young age, 2) sensorimotor beta bursts are tightly linked to all movements and infants make more movements during the baseline period than adults, 3) the SNR of the infant data biases burst detection toward larger bursts. It has been suggested that beta bursts in motor cortex are related to movement planning (Little et al., 2019), and therefore they might emerge as functionally relevant motor signals only after later developmental motor milestones have been reached. Alternatively, infants may have been making many additional, uncaptured movements during the baseline period (Georgieva et al., 2020), obscuring any potential modulation by grasp performance. Finally, lower amplitude beta bursts may be modulated by grasp performance, but could be undetectable in the data we analyzed (Bonaiuto et al., 2021). This would be consistent with the higher threshold we found for infants compared to adults. These possibilities point to the need for a longitudinal study across infancy and early childhood, utilizing motion tracking to capture all infant movements (Karashchuk et al., 2021, Mathis et al., 2018, Nakano et al., 2020, Pereira et al., 2018), and EEG alternatives such as newly developed, cryogen-free MEG sensors (Boto et al., 2018, Boto et al., 2017, Boto et al., 2016, Iivanainen et al., 2019, Iivanainen et al., 2017, Knappe et al., 2014) which have to potential to allow acquisition of high SNR data from developmental populations.

The specific version of the burst detection method presented here (Bonaiuto et al., 2021, Little et al., 2019) uses the filter-Hilbert technique to compute the amplitude envelope, and therefore one limitation is that information about the peak frequency of each burst is lost which may potentially be informative (Zich et al., 2020). However, there are also a number of other techniques that can be used to identify transient bursts of activity. For example, hidden Markov models (HMMs) have been used to identify bursts (Quinn et al., 2019, Seedat et al., 2020), which have the advantage they can model bursting dynamics over a wide frequency range, but require specification of the number of hidden states. Another approach involves analyzing the signal cycle-by-cycle in the time domain (Cole and Voytek, 2019). This avoids the assumption of the Fourier and Hilbert transforms that the signal is sinusoidal, but also introduces a new set of hyperparameters, and it is not clear how to set these empirically. Finally, empirical mode decomposition has recently been used to identify beta bursts, which has greater temporal resolution than Fourier-based methods (Echeverria-Altuna et al., 2021b). An interesting avenue for future research is to compare these methods for extracting beta bursts from developmental datasets.

We determined the infant beta band at 12 months via examination of the PSD and lagged coherence, but the PSD includes both periodic and aperiodic activity. The aperiodic component changes with age (Schaworonkow and Voytek, 2021), and thus can bias estimates of frequency band peaks in periodic activity (Donoghue et al., 2020). We plotted the residuals after fitting the PSD to a 1/f function, but there are more sophisticated ways to decompose and model power spectra (Donoghue et al., 2020). An important next step for developmental research will be to longitudinally investigate and identify changes in peak beta frequency across early development.

Additionally, to illustrate the techniques presented here, we focused on C3/C4 electrodes only as these are located over motor cortex, the primary source of prominent modulations of movement-related beta activity (Jurkiewicz et al., 2006, Parkes et al., 2006), particularly beta bursts (Echeverria-Altuna et al., 2021b, Little et al., 2019). However, beta activity is implicated in a variety of functions across a network of cortical regions (Brovelli et al., 2004, Chandrasekaran et al., 2019, Chung et al., 2017, Fischer et al., 2016, Lundqvist et al., 2016, Michalareas et al., 2016), with beta bursts also found in somatosensory and prefrontal cortices (Hannah et al., 2020, Jana et al., 2020, Lundqvist et al., 2016, Sherman et al., 2016, Wessel, 2020). In future empirical work, activity over other regions will also need to be examined to determine the spatial specificity of beta activity at different ages.

5. Conclusion

In this paper, we illustrated how to apply techniques for assessing the rhythmic versus transient nature of frequency-specific activity, specifically, lagged coherence, as well as methods for identifying and extracting bursts of activity within a frequency band. We then used these techniques to show that infant sensorimotor beta activity is dominated by short bursts, and that these bursts consist of more cycles and have a higher amplitude than adult beta bursts. In future developmental research, such methods will enable probing of the functional role of highly dynamic cortical activity across frequency bands. In terms of the beta band, applying the methods described here to developmental datasets coupling neural data with behavioral kinematics will be critical for determining the role of cortical beta activity in motor development, including how aberrant beta activity may relate to atypical motor outcomes.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material.

.