Automatic quantification of white matter hyperintensities on T2- weighted fluid attenuated inversion recovery magnetic resonance imaging

Abstract

White matter hyperintensities (WMH) are areas of increased signal visualized on T2-weighted fluid attenuated inversion recovery (FLAIR) brain magnetic resonance imaging (MRI) sequences. They are typically attributed to small vessel cerebrovascular disease in the context of aging. Among older adults, WMH are associated with risk of cognitive decline and dementia, stroke, and various other health outcomes. There has been increasing interest in incorporating quantitative WMH measurement as outcomes in clinical trials, observational research, and clinical settings. Here, we present a novel, fully automated, unsupervised detection algorithm for WMH segmentation and quantification. The algorithm uses a robust preprocessing pipeline, including brain extraction and a sample-specific mask that incorporates spatial information for automatic false positive reduction, and a half Gaussian mixture model (HGMM). The method was evaluated in 24 participants with varying degrees of WMH (4.9–78.6 cm³) from a community-based study of aging and dementia with dice coefficient, sensitivity, specificity, correlation, and bias relative to the ground truth manual segmentation approach performed by two expert raters. Results were compared with those derived from commonly used available WMH segmentation packages, including SPM lesion probability algorithm (LPA), SPM lesion growing algorithm (LGA), and Brain Intensity AbNormality Classification Algorithm (BIANCA). The HGMM algorithm derived WMH values that had a dice score of 0.87, sensitivity of 0.89, and specificity of 0.99 compared to ground truth. White matter hyperintensity volumes derived with HGMM were strongly correlated with ground truth values (r=0.97, p=3.9e-16), with no observable bias (−1.1 [−2.6, 0.44], p-value=0.16). Our novel algorithm uniquely uses a robust preprocessing pipeline and a half-Gaussian mixture model to segment WMH with high agreement with ground truth for large scale studies of brain aging.

1. Introduction

White matter hyperintensities (WMH) are areas of increased signal intensity visualized on T2-weighted magnetic resonance imaging (MRI), including fluid attenuated inversion recovery (FLAIR) sequences. In the context of aging, WMH are typically considered a common marker of small vessel cerebrovascular disease and are associated with risk for cognitive decline, dementia, mood disorders, gait abnormalities, migraine headache, and many other clinical conditions [1–4].

There has been appreciation for decades for the importance of capturing the severity and distribution of white matter lesions [5]. Early visual rating scales [6, 7] required users to rate the WMH severity in different brain regions based on visual inspection of scans. These scales necessitate expert knowledge in neuroanatomy and clinical radiology, and, although yielding reliable data with adequate training [8], only provide ordinal, not truly quantitative, values. More recent manual approaches in which an expert labels hyperintense voxels based on visual inspection of regional intensities [9], yield quantitative volumes and are considered ground truth, but still require advanced training and are labor and time intensive. Manual quantitative approaches are also not feasible for large scale efforts in which hundreds or thousands of scans require WMH quantification. Several imaging laboratories have developed semi- or fully-automated quantitative approaches for WMH segmentation [10–15], which can be implemented efficiently in large scale studies by individuals with minimal training. However, there is currently no “industry standard” nor consensus on which approaches work best.

Several methods have been proposed that provide either a semi-automatic or fully automatic processing stream with T2-weighted scans and, in some cases, T1-weighted scans for additional anatomical information. Semi-automated approaches typically involve a priori selection of an initial segmentation intensity threshold for whole brain [13, 14, 16, 17] or from different anatomical regions of interests (ROIs) [18, 19]. For example, Sheline et al. [19] used fuzzy class means to segment white matter, grey matter, cerebrospinal fluid (CSF), and WMH by placing centroids in manually selected ROIs on multimodal T1- and T2-weighted scans. Kawata et al. [20], introduced a region growing method for adaptive selection of segmentation by using a support vector machine (SVM) with image features extracted from initially identified WMH candidates. Fully automated algorithms [3, 10–13, 21–25] have the advantage of reducing operator bias, facilitating replicable delineation of WMH, and allowing for higher throughput processing of larger datasets.

The Lesion Segmentation Tool’s Lesion Growing Algorithm (LGA) from the Statistical Parametric Mapping (SPM) toolbox in MATLAB [13] uses an a priori WMH map and multimodal data (T1-weighted and T2-weighted FLAIR images), and grows the initial WMH map along adjacent hyperintense voxels. The Lesion Segmentation Tool’s Lesion Prediction Algorithm (LPA) from the SPM toolbox in MATLAB [13] uses a similar a priori WMH map and a single modality data (T2-weighted FLAIR image) to estimate the probability that a given voxel is hyperintense based on a logistic regression model that includes spatial covariates. A default probability threshold is then used to classify voxels with high probabilities as being WMH. The FSL’s Brain Intensity AbNormality Classification Algorithm (BIANCA) algorithm can use multimodal data (T1-weighted and T2-weighted FLAIR) to estimate the probability that a given voxel is hyperintense based on k-nearest neighbors that includes spatial features. A default probability threshold is then used to classify voxels with high probabilities of being WMH.

In this paper, we introduce a fully automatic, unsupervised segmentation method for WMH quantification that implements a robust preprocessing pipeline, a sample specific exclusion mask for restricting the labeling of WMH to white matter, and a half Gaussian mixture model (HGMM). We evaluate the validity of our method by comparing it to values derived via manual segmentation by two expert raters, considered here as the ground truth. We also compare the performance of our method to open source software packages including LPA, LGA, and BIANCA [12].

2. Materials and Methods

2.1. Participants

Magnetic resonance imaging data from a subset of participants in the Washington Heights Inwood Columbia Aging Project (WHICAP) were used to validate our methodology [26]. WHICAP is an ongoing study of aging and dementia that includes a representative cohort of older adults from a racially and ethnically diverse community in northern Manhattan, New York. Beginning in 2004 a random subset of WHICAP participants without dementia received MRI scanning at 1.5T [27]; starting in 2008, a random subset of WHICAP participants received MRI scanning at 3T [27]. For the current effort, we selected a random subset of MRI scans acquired at 3T representing a range of WMH severity. These data came from 24 older adults (77 ± 6.55 years old (67–91 years old), 17 women), 10 Hispanic/Latinx, 11 Non-Hispanic/Latinx Black, and 3 Non-Hispanic/Latinx White [28]. At the time of imaging, 4 were classified as having mild cognitive impairment, and 4 were diagnosed with dementia [28]. T1-weighted MRI were collected for ROI delineation and T2-weighted FLAIR images were collected for WMH segmentation in each participant. All participants provided informed consent according to the Declaration of Helsinki and study procedures were approved by the local Institutional Review Board.

2.2. Scan Parameters

MRI scanning was completed on a 3T Philips Achieva scanner at Columbia University. T1-weighted magnetization prepared rapid gradient echo (MPRAGE) structural images had the following scan parameters: repetition time (TR) = 6.6 ms, echo time (TE) = 3 ms, scan mode = 3D, resolution =1×1×1 mm³. T2-weighted FLAIR images were acquired with the following parameters: TR = 8000 ms, TE = 1337 ms, inversion time (TI) = 2400 ms, scan mode = 2D, resolution = 1×1×1 mm³.

2.3. Volumetric Agreement

The performance of all automated segmentation methods was evaluated against values derived from ground truth manual segmentation. Manual segmentation of WMH was conducted with MRICron (https://people.cas.sc.edu/rorden/mricron/index.html) [16]. A region-of-interest (ROI) defined by an unambiguous region of WMH was visually selected, an intensity threshold was applied based on the intensity values within the initial ROI, and the threshold was adjusted until all voxels appearing as hyperintense were labeled. Next, an ROI drawing tool was used to remove false positive labels (e.g., high intensity voxels in the cortical ribbon). This method of initially overlabeling and then deleting false positive labels was chosen over hand-tracing WMH to reduce manual segmentation time and difficulty in tracing exact borders. Manual segmentation was performed by two expert raters (KCI, AB).

2.4. White matter hyperintensity quantification

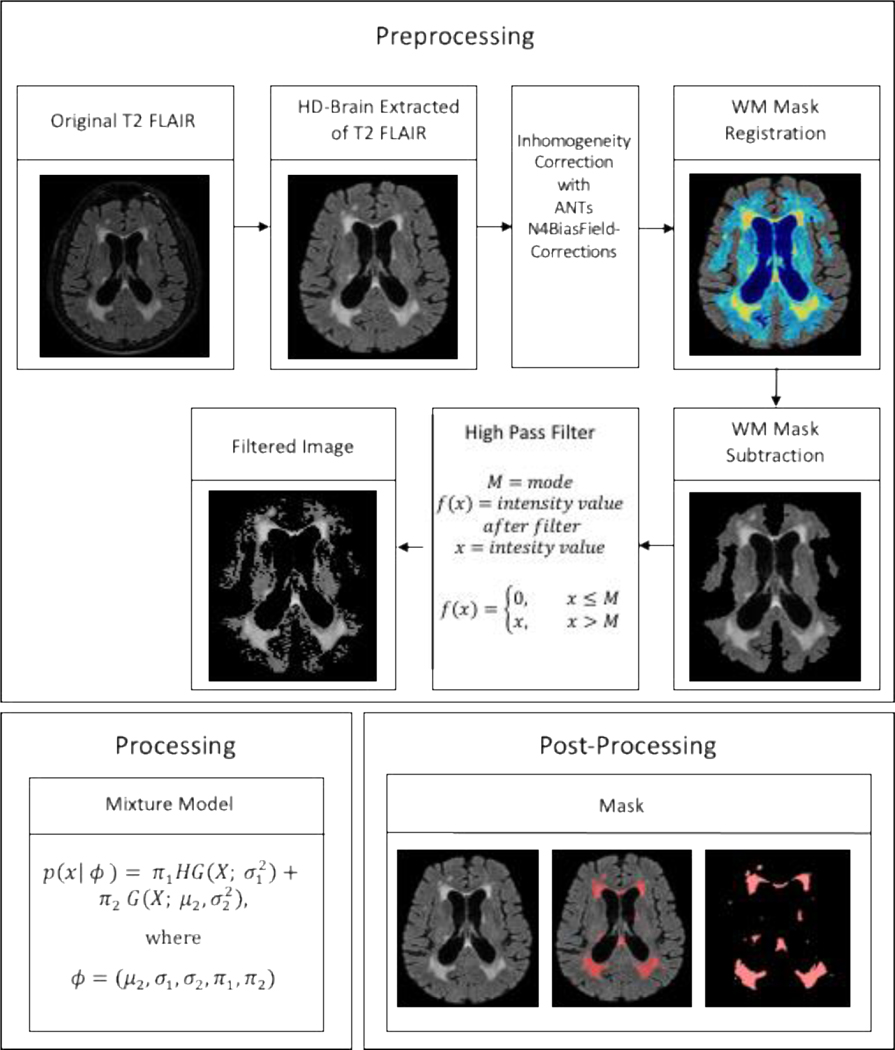
Our novel WMH quantification approach has several steps, described in detail below, which were applied to the test dataset. The WMH segmentation method can be divided into the following four steps: 1) preprocessing of the FLAIR images, 2) segmentation of WMH, 3) (optional) visual inspection and manual correction for false positive errors, and 4) postprocessing quantification of WMH volumes based on anatomical areas of interest. The preprocessing step can be further broken down into four steps: 1) brain extraction, 2) bias correction, 3) high pass filter, and 4) exclusion mask. An overview of this process is presented in Figure 1.

Figure 1.

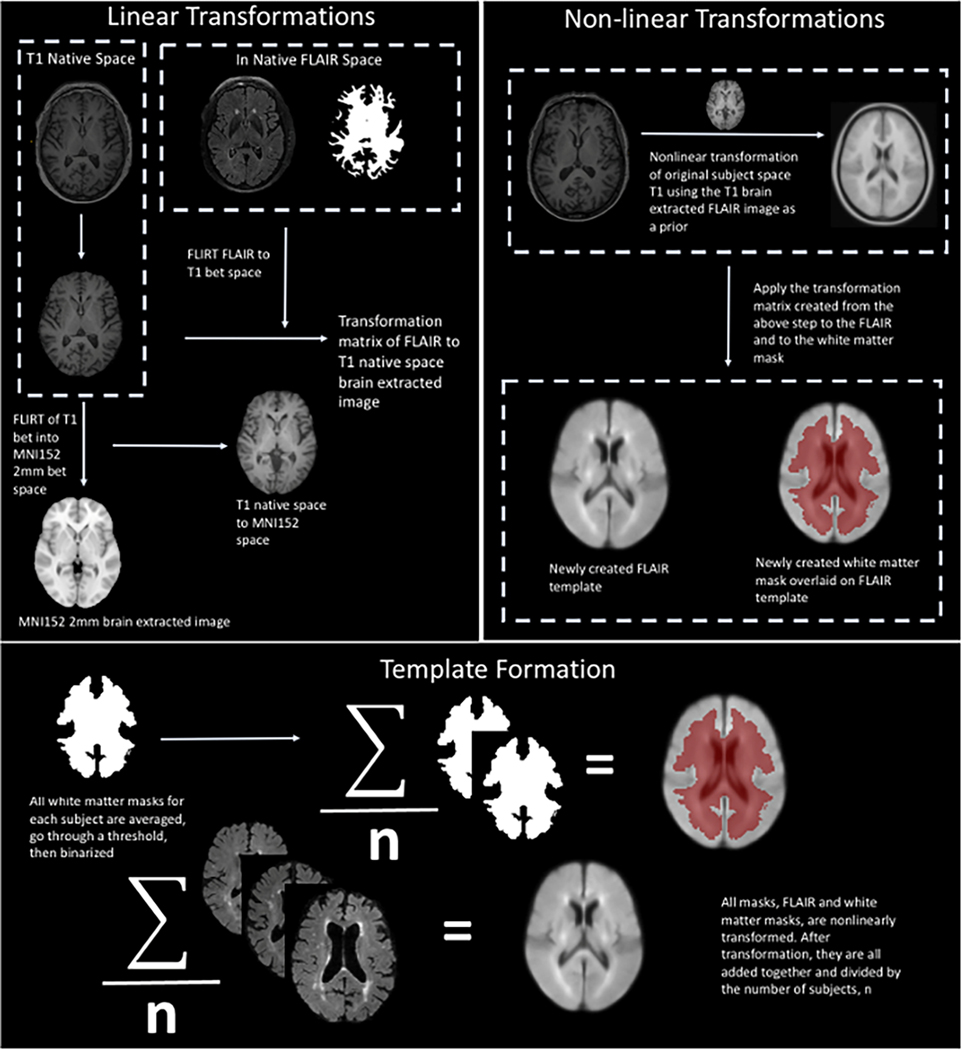
Cortex exclusion mask. A labeled subject specific anatomical brain region segmentation mask was coregistered into T2 FLAIR space. The T2 FLAIR was linearly coregistered, using FSL’s FLIRT, to T1 brain extracted space, and the transformation matrix from this registration was applied to the brain region anatomical brain region segmentation mask. Next, the brain-extracted T1-weighted image was non-linearly transformed to MNI T1 brain extracted space. The transformation matrix was then applied to the FLAIR and the labeled subject specific brain region atlas. Next, the cerebellum, brain stem, and cortex from each atlas was extracted. The resulting mask was then averaged with all of the 328 masks and then thresholded and binarized to create the final exclusion mask.

2.4.1. Preprocessing

In order to increase accuracy, fully automated WMH algorithms require the removal of non-brain tissue and correction of intensity inhomogeneities. Readily available, open-source packages were used for these steps. First, the robust, deep learning-based brain extraction tool (HD-BET) of Isensee et. al. [29] was used on FLAIR images. Then we used ANTS N4BiasFieldCorrection [30] for intensity inhomogeneity correction. A high pass filter was applied to the FLAIR intensity histogram for search space reduction. In MATLAB, we calculated the mode of the voxel intensity values (excluding zeros), and removed voxels (i.e., set to zero) whose intensity values were equal to or below the mode. This step removes the normal appearing white matter, CSF, and half of the grey matter intensity distributions.

The signal intensity of the cortex can have similar values to that of WMH. This issue is dependent on the contrast of the image. Therefore, we chose to remove cortical ribbon, brainstem, and cerebellum from the segmentation of the WMH automatically by creating an exclusion mask from 328 randomly selected scans from the WHICAP study [26], which did not include scans that were used in validating the method. Briefly, a brain extracted T1-weighted scan and subject specific anatomical mask from FreeSurfer v6 [31] were linearly transformed to T2-weighted FLAIR native space. The coregistered brain extracted T1-weighted scan, subject specific anatomical mask, and FLAIR were non-linearly transformed to MNI152 (2 mm) space [32]. The cortical ribbon, brain stem, and cerebellum were removed from each anatomical mask, and the resulting anatomical masks were averaged across subjects, thresholded, and binarized to create the final exclusion mask. Figure 1 illustrates the pipeline used to construct the exclusion mask. This FreeSurfer-based exclusion mask was used after applying HD-BET, bias correction, and the high pass filter to ensure that voxels used for determining that intensity values are classified as WMH do not come from the cortical ribbon, brain stem, or cerebellum.

The only manual work involved is the recommended editing of FreeSurfer segmentations. There are otherwise no manual corrections necessary for the preprocessing steps. FreeSurfer segmentation can take 1–2 hours per scan to run, and manual editing can take up to 10–15 minutes per scan. However, once the exclusion mask is created, applying HD-BET, ANTS N4BiasFieldCorrection, the high pass filter, and the exclusion mask takes approximately 5 minutes per scan on a CPU and less than 2 minutes per scan on a GPU. The FreeSurfer steps are not required for running HGMM, although it contributes to increased accuracy.

2.4.2. Processing: Segmentation

The goal was to identify voxels that fell within an intensity distribution that represented WMH by using a mixed Gaussian approach, which can capture multiple voxel intensity distributions within an image. Each tissue type has a characteristic intensity distribution in FLAIR scans. Grey matter values are higher (i.e., appear bright) than white matter intensity values (i.e., appear dark), WMH appear bright (by definition), while ventricle intensity values are suppressed on a FLAIR image. After the application of the high pass filter in the third preprocessing step, the intensity histogram was left with two distributions: a lower half-Gaussian representing grey matter intensities and normal appearing white matter above the mode and an upper full Gaussian representing WMH. Before segmentation, the intensity values were log-transformed to provide a larger separation between the two distributions while preserving the peak values in the histogram and therefore an easier delineation of the two distributions, outlined in Figure 2.

Figure 2.

Outline of the Processing Stream. The processing stream includes the pre-processing, processing, and post-processing steps used to create a WMH segmented mask. In pre-processing, T2-weighted FLAIR scans are brain extracted, intensity corrected, high pass filtered, and restricted to regions within the exclusion mask. In processing, HGMM is applied to create the WMH mask. Finally, in post-processing, after optional erasure of potential false positives, the result is a manually edited WMH mask.

The probability density function (PDF) of the half-Gaussian distribution is then represented by

$$p_{HG}\left(x_i\right)=\frac{2}{\sigma \sqrt{2\pi }}exp\left(\frac{-x_i^2}{2{\sigma }_1^2}\right)=HG\left(X;{\sigma }_1^2\right),ifx\ge 0,$$ 1.

where $p_{HN}\left(x_i\right)$ denotes the PDF of the half-Gaussian distribution, x denotes an independent and identically distributed (i.i.d.) random variable represented by the set ${\text{x}}_1,{\text{x}}_2,{\text{x}}_3,\dots ,{\text{x}}_{\text{i}}$ for each tissue type intensity value, and σ² is the variance.

Voxels that represent WMH are modeled by the full Gaussian distribution. The PDF of the Gaussian distribution is represented by

$$p_G\left(x_i\right)=\frac{2}{\sigma \sqrt{2\pi }}exp\left(\frac{-{\left(x_i-{\mu }_2\right)}^2}{2{\sigma }_2^2}\right)=G\left(X;{\mu }_2,{\sigma }_2^2\right),$$ 2.

where $p_G\left(x_i\right)$ denotes the PDF of the Gaussian distribution, an, i.i.d. random variable X is represented by the set, [33 …., xi], the tissue intensity values, σ² is the variance, and μ₂ denotes the mean of the Gaussian distribution.

Our mixture model is then given by

$$p(x\mid \varphi )={\pi }_{1}HG\left(X;{\sigma }_1^2\right)+{\pi }_{2}G\left(X;{\mu }_2,{\sigma }_2^2\right),$$

where

$$\varphi =\left({\mu }_2,{\sigma }_1,{\sigma }_2,{\pi }_1,{\pi }_2\right)$$

and ${\pi }_{1,2}>0$ are the mixing proportions for each distribution. A K-means classifier was used to for initial clustering in order to derive starting values, including the mean and variances, $\left({\mu }_2,{\sigma }_1,{\sigma }_2\right)$, for the model. Next, expectation-maximization was used to estimate the parameters of HGMM, predicting the final values represented by ϕ. The distribution with intensity values within the upper full Gaussian was labeled as WMH, given that each cluster of labeled voxels included at least 5 voxels.

The HGMM algorithm takes approximately 8 minutes on a CPU for automatic WMH segmentation and up to an additional 10 minutes for visual inspection and manual editing if necessary. This processing time compares to up to 60 minutes for WMH segmentation of a scan with 1×1×1 mm³ resolution using manual approaches.

In typical analyses, WMH masks would be visually inspected and manually corrected for false positive errors; however, for the purposes of this methodological assessment, we did not perform manual correction for false positive errors in any of the methods evaluated, including HGMM, to ensure that comparisons across methods were not biased. We include the description here for completeness.

2.4.3. Postprocessing: Quantification Options

White matter hyperintensity volume can be quantified globally, by lobar regions, by white matter tracts, and/or as a function of proximity to the walls of the lateral ventricles (so-called “periventricular” versus “deep” distributions). Our method quantifies WMH volume in all supratentorial brain regions and in each lobe separately, but there is often interest in the anatomical distribution of these lesions [34, 35]. For example, some authors have hypothesized that periventricular versus deep distributions of WMH have different etiologies and promote distinct behavioral phenotypes [36, 37]. Various types of anatomical segmentation software or anatomical atlases can be used to quantify WMH volume by subject-specific or population-specific ROIs, respectively. With our method, to derive deep versus periventricular WMH, FreeSurfer [31], is first run on the subject’s T1-weighted MRI, and the resulting segmentation is co-registered to the FLAIR. Using the ventricular ROIs defined by FreeSurfer, the 3D Euclidean distance between each voxel labeled as a WMH and the nearest ventricular surface is computed, and the total volume of voxels lying within a range specified by the user is calculated.

Similarly, regional anatomical distribution based on gross lobar distribution, specific white matter regions, or white matter tracts can be derived by counting the labeled voxels and multiplying by the voxel dimensions to yield a total volume in cm³ withina given region. For this approach, a regional lobar atlas can be coregistered to each FLAIR scan. Then, all of the voxels in a given region of the lobar mask are added and multiplied by the voxel dimension to give the regional WMH volume [38].

2.5. Statistical Analysis

We used several approaches to evaluate the accuracy of our method and to compare it to other approaches commonly used in the extant literature. To define our ground truth metric, we first confirmed adequate inter-rater reliability with intraclass correlation coefficients. Then we used the average total volume derived from each of the manual ratings as ground truth. Each method, as in [39], was then compared in terms of the following metrics: (a) the number of true positives (TP, i.e. voxels labeled by both the ground truth and algorithm); (b) the number of false positives (FP, i.e. voxels not labeled by the ground truth but labeled with the algorithm); (c) the number of true negatives (TN, i.e. voxels not labeled by the ground truth or the algorithm); (d) and the number of false negatives (FN, i.e. voxels labeled by the ground truth, but not the algorithm). These metrics were then used to measure the spatial agreement, sensitivity and specificity of each model. The dice similarity coefficient, given by the formula $\mathit{\text{Dice}}=\frac{2\text{TP}}{2\text{TP}+\text{FP}+\text{FN}}$, was used to measure spatial agreement between the ground truth and each output. According Zou et. al. [40], a dice score of Dice >0.7 shows good overlap between the two images being compared [40]. Sensitivity was measured using the equation, $Sensitivity=\frac{TP}{TP+FN}$. Finally, specificity was measured using the equation, $Specificity=\frac{TN}{TN+FP}$.

The agreement of each algorithm with the ground truth was quantified with Pearson’s r correlation, and the bias of each method compared to ground truth was quantified using Bland-Altman analyses. The smaller the bias, the more the output from a given method agreed with the ground truth. A p-value <0.05 in a Pearson’s correlation indicated that the agreement from a method with ground truth was reliable, while in a Bland-Altman a p-value<0.05 indicated that the output from a method differed systematically from the ground truth. All statistical analysis was performed using the IBM Statistical Product and Service Solutions (SPSS v26) software.

3. Results

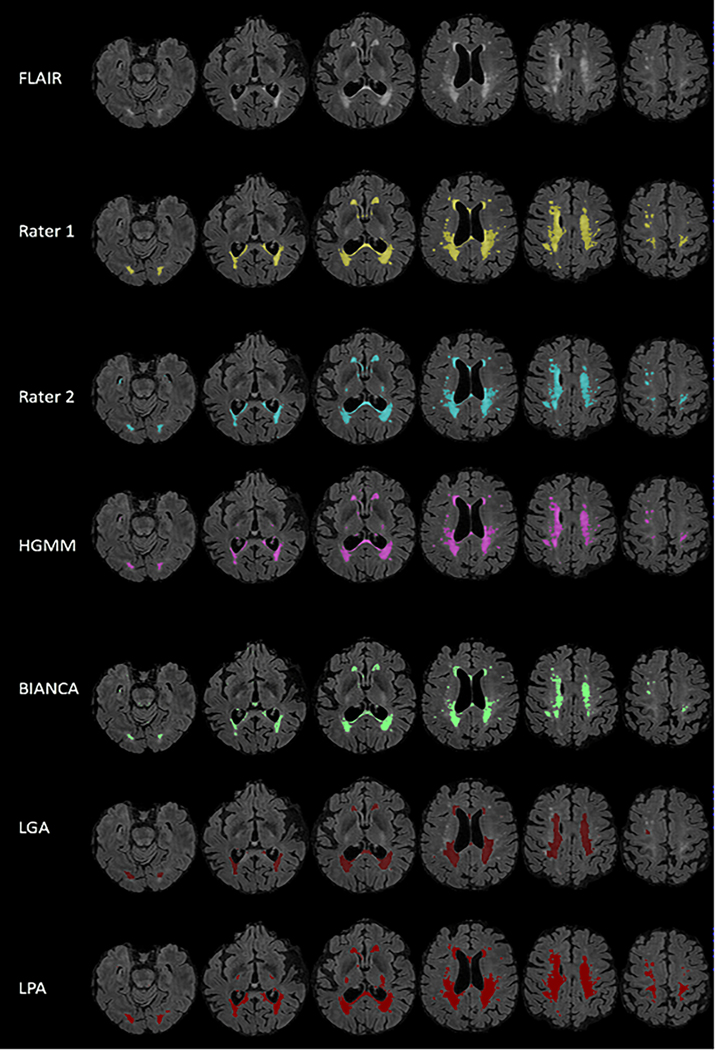
The two expert raters showed adequate dice and inter-rater reliability (dice=0.92, intraclass correlation coefficient (ICC)=0.92) and the total volumes from each rater were averaged to derive the ground truth manual segmentation of WMH volume. Figure 3 shows the output WMH masks of each algorithm on one representative scan. On visual inspection there were no obvious differences in labeling between HGMM and BIANCA, suggesting that they performed similarly across the range of WMH volumes in this sample. The range of WMH volumes from each segmentation algorithm are plotted against ground truth manual segmentation, with a pooled range across methods of 4.9 – 78.6 cm³. Most participants (17/24, 71%) had WMH volumes of less than 20 cm³, demonstrating the typical right skew for older populations. Algorithms differed most in their labeling of small punctate WMH. HGMM and BIANCA labeled punctate WMH, whereas LPA tended to combine nearby small punctate WMH into a single large WMH and LGA did not label some punctate WMH. Figure 4 illustrates the similarity metrics between manual segmentation and each algorithm. In terms of spatial similarity (i.e., dice coefficient), HGMM had the greatest overlap with ground truth, followed by BIANCA, LPA, and finally LGA. LPA had the highest sensitivity, followed by HGMM, BIANCA, and LGA. All methods had excellent specificity, with HGMM having the highest.

Figure 3.

WMH segmentation on representative T2-weighted FLAIR. The performance of each algorithm on one representative scan compared with each rater (i.e., ground truth). LGA and BIANCA are both shown to under labeled slightly, while LPA over labels more than HGMM. LPA tends towards clustering smaller hyperintense areas that are close to large hyperintense areas. However, all algorithms are highly specific, as a majority of labeled voxels are also identified in ground truth.

Figure 4.

Agreement between ground truth and fully automated white matter hyperintensity (WMH) segmentation algorithms. Ground truth was manual segmentation, while segmentation algorithms included Lesion Probability Algorithm (LPA); Lesion Growing Algorithm (LGA); spell out Brain Intensity AbNormality Classification Algorithm (BIANCA); and Half-Gaussian Mixture Model (HGMM). Agreement metrics include the (a) dice coefficient, (b) sensitivity, and (c) specificity.

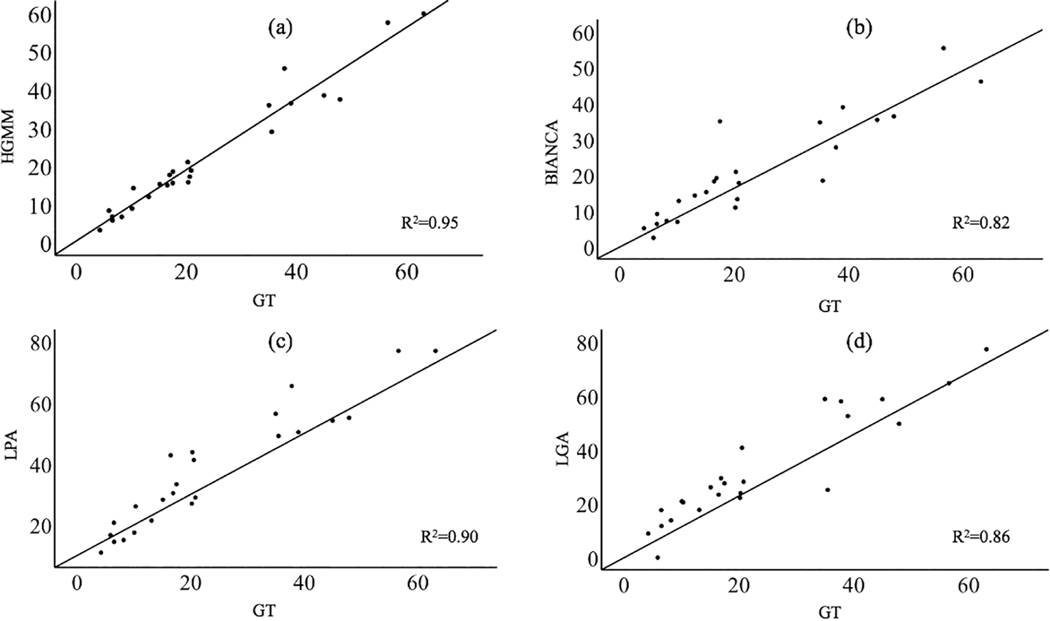
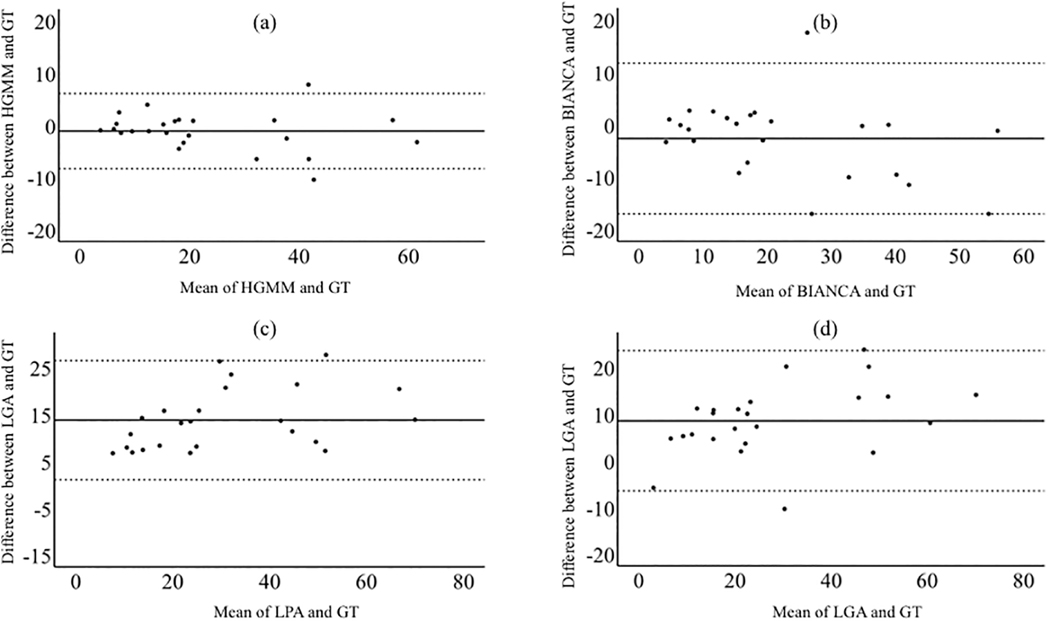
The correlation with manual segmentation values was strongest using HGMM (r=0.97, p=3.9e-16), weakest using BIANCA (r=0.91, p=1.3e-9) and intermediate using LPA (r=0.95, p=2.6e-12) and LGA (r=0.93, p=6.1e-11 Figure 5). Additionally, there was no reliable bias using HGMM or BIANCA compared to manual segmentation; descriptively, HGMM slightly underlabeled WMH (mean=−1.1, CI= [−2.6, 0.44], p=0.16), while BIANCA underlabeled WMH to a greater extent (mean=−2.65, CI= [−5.7, 0.44], p=0.089). There was bias using LGA and LPA compared to manual segmentation such that LGA overlabeled WMH (mean=−8.6, CI= [5.3, 11.8], p=1.5e-5) and LPA overlabeled WMH (mean=−13.8, CI= [11.0, 16.5], p=3.5e-10; Figure 6).

Figure 5.

Relationship between ground truth (GT) measurements and each of the WMH segmentation approaches tested, including HGMM (a), BIANCA (b), LPA (c), and LGA (d). Values are in cm³. The R² is also shown in each plot.

Figure 6.

Bland-Altman plots testing for systematic bias of each technique against ground truth. HGMM slightly under labeled WMH and BIANCA underlabeled WMH to a greater extent. LGA and LPA reliably over labeled WMH relative to ground truth.

4. Discussion

We developed and validated a novel fully automated WMH segmentation algorithm that uses a HGMM on 3T T2-weighted FLAIR images. The HGMM and BIANCA methods were similarly able to detect WMH when compared with the ground truth. The purpose of our analyses was not to compare accuracy explicitly or statistically across WMH segmentation algorithms, but rather to describe the development and validation of in-house methodology, demonstrate that its accuracy is similar to that of other, commonly used protocols, and show in descriptive terms the relative strengths and weaknesses of the approaches. The HGMM, BIANCA, LGA, and LPA methods all yielded values that had strong positive relationships with values derived by the ground truth method, although there was some bias observed in LGA and LPA, such that they tended to overlabel voxels as WMH. Our observations indicate that HGMM can be implemented in large datasets and yields values that are in line with ground truth, derived through manual segmentation from expert operators.

The results showed that HGMM had numerically higher spatial agreement with ground truth segmentations than BIANCA, LPA, and LGA, although both HGMM and BIANCA had strong volumetric agreement when compared to ground truth (Dice > 0.7) [40]. Descriptively, LGA performed relatively worse than the other approaches and resulted in the highest number of false negatives, and LPA tended to overlabel voxels as hyperintense and to cluster small groups of small punctate areas of hyperintense voxels into a single WMH. Additionally, we used a Pearson’s r correlation to test correlations with the ground truth WMH volumes and Bland-Altman analyses to test systematic overlabeling or underlabeling compared to ground truth WMH volumes. All algorithms were highly correlated with ground truth, but LGA and LPA systematically overlabeled compared to ground truth.

Several preprocessing steps were incorporated to optimize performance of the algorithm, including intensity inhomogeneity correction, brain extraction, a high pass filter, and the exclusion masking step. It is crucial to have a robust brain extraction method when using intensity-based algorithms. We used HD-BET instead of the more widely used FSL’s Brain extraction tool (FSL-BET). While FSL-BET is not optimized for images that have large amounts of extratentorial tissue or for images with large clusters of pathology [29], such as WMH, HD-BET is robust to brain pathology, MRI sequence (i.e., not restricted to T1-weighted scans), hardware and scan parameters (i.e., tested from scans from 37 institutions and validated in three independent datasets) [29]. The high pass filter reduced the search space for the algorithm, producing the half Gaussian distribution. This filter reduced the number of potential intensity distributions found in the original histogram from four different distributions that represented white matter, grey matter, cerebral spinal fluid (CSF), and WMH to two different distributions representing grey matter and WMH. The addition of an exclusion mask further helped exclude grey matter voxels from being misclassified as WMH. False positive labeling of hyperintense voxels as WMH can commonly occur because certain regions, such as the cortical ribbon and choroid plexus, are prone to having higher intensities on T2-weighted FLAIR scans. The exclusion mask automatically removes areas with high likelihood of false positive labeling. As with any automatic labeling or segmentation approach, visual inspection is always recommended with manual correction, if necessary.

One limitation is that HGMM was tested using FLAIR scans from one type of scanner, a 3T Philips Achieva. Potential issues could arise from different scanner manufacturer and/or model, image contrast, or image acquisition parameters. HGMM can overcome these issues through the implementation of the robust ANTs intensity inhomogeneity correction, the log transform of the image intensity histogram prior to applying the HGMM, and the exclusion mask to automatically remove potential false positives based on anatomical location, respectively. Future work will need to test the accuracy of the approach across scanner platforms.

In conclusion, we developed and validated a segmentation method for the quick and robust quantification of WMH volume with minimal software (i.e., freely available imaging software), and expertise requirements (i.e., automatic). Comparison to ground truth manual segmentations revealed that HGMM can segment brain WMH equally well with high correlation and small bias across a range of WMH volumes commonly observed with aging and disease.