Abstract
In this paper, we present the impact of migration on the spread of HIV and AIDS cases. A simple model for HIV and AIDS that incorporates migration and addresses its contributions to the spread of HIV and AIDS cases was constructed. The model was calibrated to HIV and AIDS incidence data from Malaysia. We explore the use of Markov chain Monte Carlo (MCMC) simulation method to estimate uncertainty in all the unknown parameters incorporated in our proposed model. Among the migrant population, 1.5572e-01 were susceptible to HIV transmission, which constituted 67,801 migrants. A proportion of migrants, 6.3773e-04, were estimated to be HIV infected, constituting 278 migrants. There were 72 (per 10,000) migrants estimated to have had AIDS, representing a proportion of 1.6611e-08. The result suggests that the disease-free steady state was unstable since the estimated basic reproduction number was 2.0906 and 2.3322 for the models without and with migration, respectively. This is not a good indicator from the public health point of view, as the aim is to stabilize the epidemic at the disease-free equilibrium. The advantage of introduction of migration to the simple model validated the true and the transmission rate associated with HIV and AIDS epidemic disease in Malaysia. It also indicates an approximately 12 percentage points increase in the rate of HIV infection with migration.
Keywords: Migration, Mathematical transmission modeling, HIV/AIDS, Parameter estimation, Basic reproduction number
1. Introduction
The spread of the human immunodeficiency virus (HIV), which progresses into the acquired immunodeficiency syndrome (AIDS), has created a new global threat. In Malaysia alone, there have been 101,672 (0.4%) cases of HIV infection, 20,235 (0.07%) cases of AIDS and 16,360 (0.05%) HIV/AIDS deaths reported between 1986 and 2013. Currently, there are 85,332 (0.3%) Malaysians living with HIV/AIDS (MOH, 2015). Prior mathematical models describing HIV transmission have concentrated mainly on populations of specific sexual orientation, i.e., homosexual or heterosexual. The AIDS epidemic has tremendously stimulated the development of mathematical models describing infectious diseases. The transmission dynamics of HIV infection and its eventual development into AIDS has taken a central role in many mathematical models. Various improvements have been made since the initial HIV and AIDS models by May and Anderson (R M Anderson et al., 1986; Roy M. Anderson, 1988; May & Anderson, 1987), including specific issues that have been well discussed in the literature (Jansson et al., 2014; Kelly & Wilson, 2015; Merli et al., 2006; Mukandavire et al., 2011; Naresh et al., 2011; Nyabadza and Mukandavire, 2011a, Nyabadza and Mukandavire., 2011b; Zhang et al., 2011). Similar to other infectious diseases (e.g., hepatitis B, chlamydia, gonorrhea, syphilis, and genital herpes), HIV is transmitted by unsafe sexual interaction between individuals. Sinka et al. (Sinka et al., 2003) presented a theoretical framework that described the effect of migrants from HIV-prevalent Sub-Saharan Africa on HIV incidence in the United Kingdom. Kibona et al. (Kibona et al., 2011) studied the effect of HIV-infected migration using a deterministic model of HIV/AIDS with vertical transmission. McGinn et al., concluded that migration affected the transmission of HIV, as well as other sexually transmitted diseases, in California, USA (McGinn et al., 2001). There have been several statistical models that have described the impact of migration on disease spread (Roy M. Anderson, 1988; Brookmeyer & Liao, 1990; Brummer, 2002; Coffee et al., 2007; Salomon & Murray, 2001; Sinka et al., 2003). Recent events in Malaysia indicate that there is an increase in migration issues in the country that could pose a high risk of the spread of disease. For the past decades, the migration of health experts from Malaysia has been a cause for concern due to the fact that those who stay for longer periods contribute to the impact on the health care system (Chuah et al., 2018; Pottie et al., 2017). Relatively few studies have examined how the role of migration has impacted on HIV/AIDS in various countries. Therefore, migration should also be considered in the modelling of HIV/AIDS, especially in Asian countries such as Malaysia. Globally, migration is a defining challenge. The countries of the world are interconnected through migration, which has an economic impact on the countries that receive migrants. Migration also has health implications for the countries that migrants have left. On the other hand, apart from the increased potential for the spread of HIV/AIDS, there is also a rising concern that migrants’ health needs are not always adequately met.
To the best of our knowledge, the use of a mathematical model to determine the effect of migration on HIV/AIDS cases has not been studied in Malaysia. The few research works did not use mathematical models (Coffee et al., 2007; Sani & Kroese, 2008; Yang et al., 2007). Many people who traveled to another country are involved in sexual activity (L. Agustín, 2006; Cooper et al., 2003; Ratliff, 1999; Richens, 2006). As they find these activities more accessible and affordable compared to sexual services in their home country (Anarfi, 1993), the spread of HIV and AIDS is equally inevitable (L. M. Agustín, 2007; Corno & de Walque, 2012; Nishigaya, 2002; Parrado et al., 2004). Migration is directly linked to the numerous spread of epidemics worldwide (Deane et al., 2010). The primary objective of our study is to understand the impact of migration on the spread of HIV and AIDS in Malaysia. Sound statistical analysis methods require that mathematical models be supplemented by fitting the model to an observed data to account for uncertainties and to ascertain the accuracy of the model. The statistical analyses used to determine these uncertainties are detailed in (Blum, 2010; Haario et al., 2006; Laine, 2008; Solonen et al., 2013). Here, a constrained least-squares fitting method was used to estimate the epidemiological parameters. The estimated parameters are then used to calculate the basic reproduction number. The uncertainties in both the model parameters and the model output are handled using the Markov chain Monte Carlo (MCMC) simulation method (Sun et al., 2013). The mathematical models constructed and their fitting to the data are validated using the Bayesian inference via MCMC sampling of the posterior distribution (Apenteng & Ismail, 2014; Höhle, 2008; Mahani & Sharabiani, 2015). These findings may improve the understanding of the HIV and AIDS epidemic in Malaysia and demonstrate the importance of monitoring migration in order to reduce the spread of HIV/AIDS.
2. Materials and methods
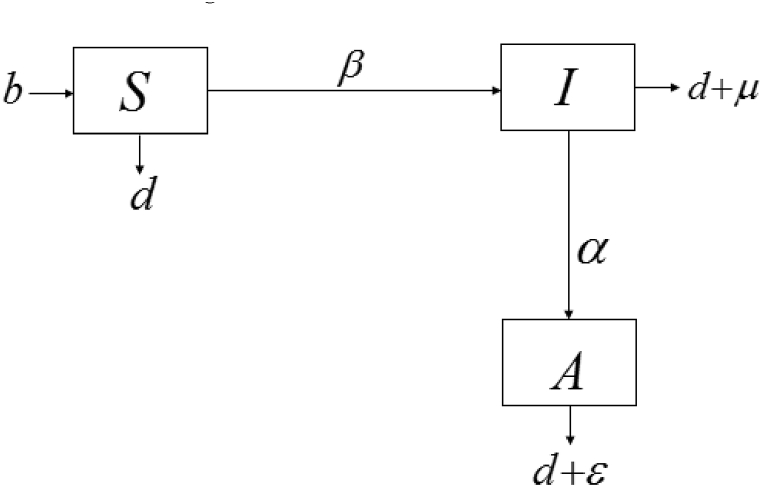
The aim is to keep the model as simple as possible while incorporating two essential elements, sexual behaviour, and migration of the HIV/AIDS-infected population. The simplest HIV/AIDS model without migration is shown in Fig. 1.
Fig. 1.
Flow diagram of HIV transmission.
2.1. Model without migration
Key Model Assumptions.
We assume that once an individual becomes infected with HIV/AIDS, the individual remained infectious for life. The total population is divided into three categories: susceptible, HIV, and AIDS individuals, and the model is based on the following assumptions:
-
•
The sexually active population susceptible to infection is represented by .
-
•
Justification. Although we wished to model a sexually active population at risk of acquiring HIV/AIDS, the recruitment rate of the susceptible compartment is the birth rate, , which was independent of vertical transmission and hence unstable. Therefore, the natural death rate, , was constant across all compartments.
-
•
Infection is classified into two categories to represent those who are infected and diagnosed with HIV and AIDS, respectively. That is, represents sexually active individuals who are infected and diagnosed with HIV, while represents those who are diagnosed with AIDS.
-
•
HIV-infected individuals progress to AIDS at a rate .
-
•
The rate of HIV transmission to a susceptible population is , and the probability of transmission is which was assumed to be frequency dependence.
-
•
A disease-induced mortality rate is assumed for the HIV population, and AIDS population ; , and respectively.
Based on these assumptions, the model is represented by the following equations:
| (1) |
| (2) |
| (3) |
The total population is described by
| (4) |
We solve (1), (2), (3) using the following steps:
Lemma 1. The equations maintain positive solutions.
Proof. The vector field obtained by the right-hand side of (1), (2), (3) pointed inward on the boundary of . For instance, if , then . The same results can be obtained for the other compartmental variables.
Lemma 2. All solutions of (1), (2), (3) are bounded.
Proof. In the absence of disease, (4) is . Assume that for all , where , . Suppose that if the assumption is not true, then there exists a such that
| (5) |
| (6) |
| (7) |
| (8) |
Equation (8) contradicts our assumption of falsehood by indicting that the assumption is true. Therefore, for all .
The basic reproduction number is very important in disease modelling. It determines the transmission potential of a disease. It describes the number of individuals, on average, to whom one infected person will pass on the disease to another person. Furthermore, to determine whether the disease was either epidemic or endemic, we needed to find the reproduction number of the model. The is either a threshold value or a number that determines the stability of the disease-free equilibrium. If , then, an epidemic of AIDS occurs, and if , then, the disease-free equilibrium is locally and asymptotically stable. One useful approach to compute the is by using the next-generation method (Diekmann et al., 2009; Jones, 2013; Roberts & Heesterbeek, 2007; Van Den Driessche & Watmough, 2002). Thus, the basic reproduction number of the system of equations (1), (2), (3) is obtained as follows:
2.2. Model with migration
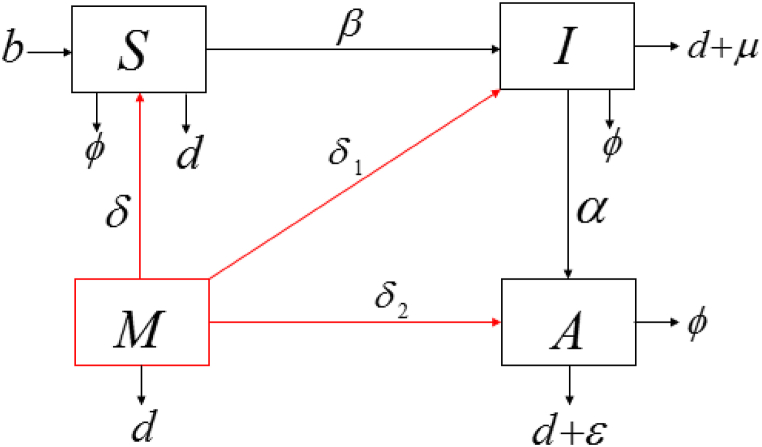
As a second step, we extend the simplest HIV/AIDS model to include the impact of migration, as shown in Fig. 2.
Fig. 2.
Flow diagram of HIV transmission with migration.
Key Model Assumptions.
-
•
denotes the immigration of individuals to the host country (Malaysia).
-
•
Justification. The HIV and AIDS status was unknown for the immigrant population. was assumed to contain susceptible as well as HIV- and AIDS-infected individuals. The proportion of migrants in each compartmental level cannot be calculated with precision as there are no real demographic data available. Therefore, we have assumed that a fraction , and were recruited into , and , respectively. We also assumed that migrants left the country at the rate of from the , and populations.
The model takes the following form:
| (9) |
| (10) |
| (11) |
| (12) |
The total population is described by
| (13) |
of the system is obtained as follows. Using the next-generation method as was done in section 2.1, From (12), at equilibrium Thus, .
2.3. Data
Data for the model were collected and collated by the Ministry of Health (MOH, 2012). The formulated model was used to analyse the annually reported HIV and AIDS cases for Malaysia between 1986 and 2011. In 1986, the total Malaysian population was 16,329,400. From (MOH, 2012), three and one were infected with HIV and AIDS, respectively, representing and . Because , there are 16,329,396 individuals who are susceptible to infection. In 1986, the total number of migrants in Malaysia was 435,408 (Lim, 1996).
2.4. Estimation of parameters and data fitting
The proposed models are fitted and validated using the HIV and AIDS incidence cases data from Malaysia. There are six and ten parameters to be estimated for without and with epidemiological migration models, respectively. It is worth noting that the model parameters for both models may not be uniquely identifiable based on only HIV and AIDS incidence data available. We addressed this problem by using a constrained least-squares approach and local sensitivity analysis (Soetaert & Petzoldt, 2010) to obtain suitable initial parameter estimates for the two proposed models. To determine these parameters, each of the models was fitted using the data (MOH, 2012). The estimated parameter values obtained from the best fit are given in Table 1, Table 2. Fig. 3, Fig. 5 may be considered as the basic classical goodness-of-fit for without and with the migration model, respectively.
Table 1.
Estimated parameters without migration with their respective uncertainties.
| Parameter description | Symbol | Estimate | 95% CI |
|---|---|---|---|
| HIV transmissibility | 9.7847e-01 | (9.7805e-01, 9.7888e-01) | |
| Rate of HIV progression to AIDS | 7.7416e-02 | (7.7322e-02, 7.7511e-02) | |
| Natural mortality rate | 3.9060e-01 | (3.9056e-01, 3.9064e-01) | |
| Recruitment rate of birth | 4.2249e-10 | (-1.6762e+00, 1.6762e+00) | |
| HIV mortality rate | 1.7396e-12 | (-4.6967e-04, 4.6967e-04) | |
| AIDS mortality rate | 4.8233e-07 | (-5.5380e-04, 5.5476e-05) |
Table 2.
Estimated parameters with migration together with their uncertainties.
| Parameter description | Symbol | Estimates | 95% CI |
|---|---|---|---|
| HIV transmissibility | 6.0786e-01 | (6.0780e-01, 6.0792e-01) | |
| Rate of HIV progression to AIDS | 7.4165e-02 | (7.4139e-02, 7.4192e-02) | |
| Natural mortality rate | 3.0475e-01 | (3.0472e-01 3.0477e-01) | |
| Recruitment rate of birth | 8.6480e-09 | (5.1205e-09 1.2175e-08) | |
| HIV mortality rate | 4.3164e-09 | (-3.9676e-05, 3.9684e-05) | |
| AIDS mortality rate | 4.3603e-05 | (3.3791e-05, 5.3414e-05) | |
| Proportion of migrants recruited into | 1.5572e-01 | (1.5561e-01, 1.5583e-01) | |
| Proportion of migrants recruited into | 6.3773e-04 | (6.3727e-04, 6.3818e-04) | |
| Proportion of migrants recruited into | 1.6611e-08 | (-8.0299e-07, 8.3621e-07) | |
| The rate migrant at which leaves the population | 3.0110e-02 | (3.0083e-02, 3.0137e-02) |
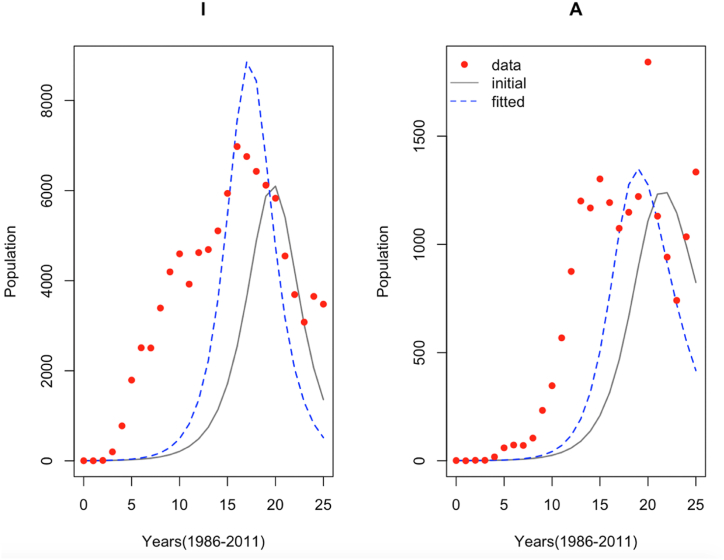
Fig. 3.
Simple model fit of epidemiological data with initial and estimated parameters for the HIV and AIDS populations.
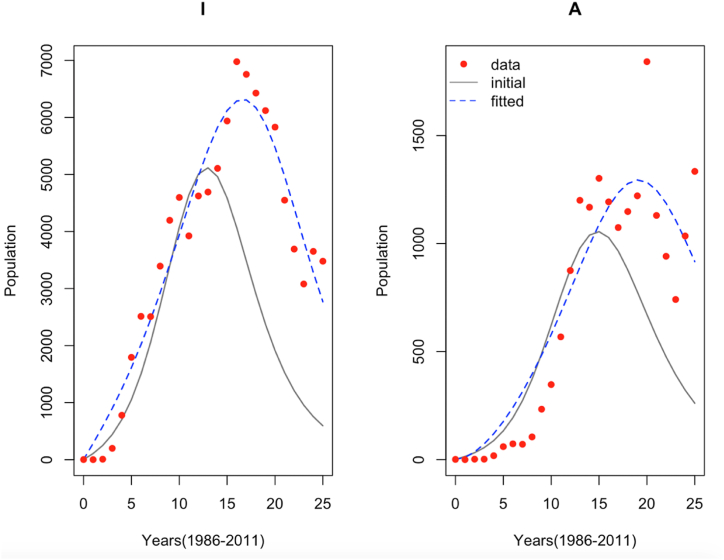
Fig. 5.
Model fit of epidemiological data with initial and estimated migration parameters for the HIV and AIDS populations.
3. Results
This section discusses the various results of the proposed models. The mathematical models were calibrated to the Malaysian HIV incidence data from 1986 to 2011.
3.1. Without migration
We begin by considering a simple mathematical model without migration and analyse its impact on the dynamics of HIV and AIDS incidence cases during the data calibration period. The incidence of data and its model fitting are given in Fig. 3.
Fig. 3 depicts an overlay of annually reported HIV case counts and simulations with initial and fitted parameters during the 25-year (1986–2011) calibration period. The highest peak infection rate occurred during year 16, which corresponds to 2002 when there were 6978 infected individuals. We observe that in general, both the HIV and AIDS incidence data do not have a good fit. Furthermore, the HIV and AIDS incidence cases are overfitted using the simple model. It is worth noting that while both fittings of HIV and AIDS cases have relatively a good fit at the start of the 25-year period, it is poorly fitted between the fifth and twentieth years. This suggests that the simple model without migration is not an appropriate model for the HIV and AIDS incidence data during the years 1986–2011.
The estimated epidemiological parameters, together with their 95% credible intervals, are given in Table 1. Generally, credible intervals widths are narrower for all the estimated parameters. Interestingly, the lower limits of the parameters , and are less than zero. This is not surprising since the system of equations is underdetermined.
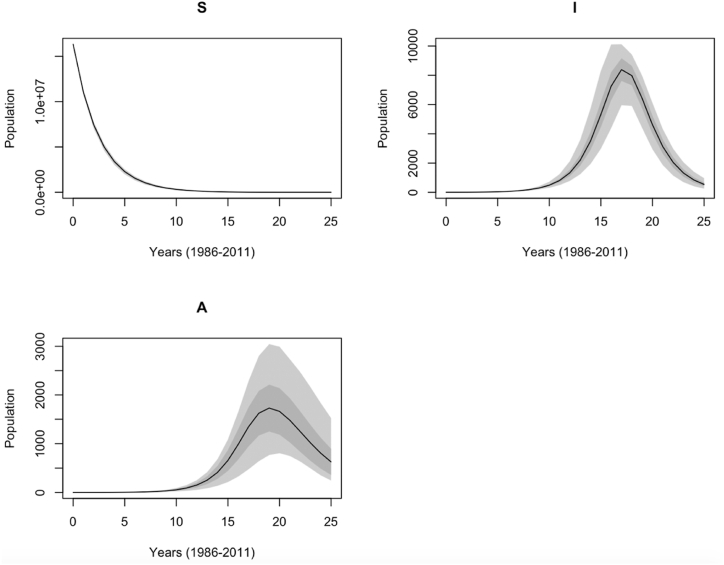
The effect of the parameter uncertainty on the model output can be estimated and visualized on the unobserved variables , , and . It should be noted that these ranges only represent the distribution of the model response as a function of the parameter values as shown in Fig. 4.
Fig. 4.
Predictive ranges of the simple model without migration. The light and dark shaded areas describe the sensitivity range of the estimated parameters.
Fig. 4 shows the sensitivity range of annually reported HIV cases based on parameter distribution as generated with the MCMC method during the 25-year calibration period. The light grey area represents the minimum and maximum model response at each time step, and the dark grey area (Mean sd) illustrates the mean model response plus or minus one standard deviation. Among the compartment populations, the variance increases in the following order: . The large variance is due to either the uncertainties in the model or noise in data collection.
3.2. The impact of migration
We extended the simple mathematical model to a more realistic one by including the impact of migration on the spread of HIV and AIDS cases. In order to validate this extension, we fitted the model to the same HIV and AID incidence data from Malaysia. The result of the model validation is given in Fig. 5.
Fig. 5 shows the fitting of the epidemiological model incorporating the effect of migration with initial and estimated parameters for the HIV and AIDS incidence cases over period of 25 years. We can see that there is an improved model fitting compared with the simple model without migration.
Table 2 presents the estimated parameters, together with their 95% credible intervals. The widths of the intervals are shorter for all the estimated parameters. The lower limits of the parameters and are less than zero and this again shows that the system of nonlinear differential equations is underdetermined (Apenteng et al., 2020) as in the case of the model without migration.
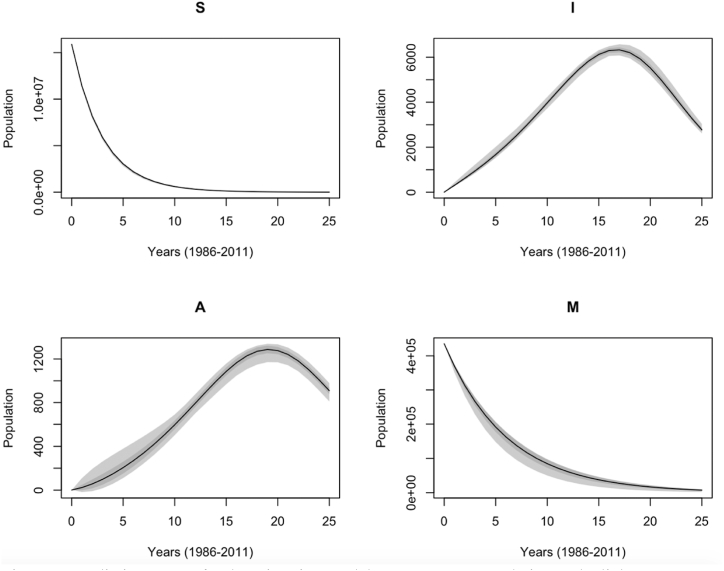
Fig. 6 shows the variance in annually reported compartment populations from the migration-based model. The variance increased in the following compartment order: . The variance of the predictive distribution demonstrates the predictive accuracy of the migration model. The large variance is due to either the uncertainties in the model or noise in the data collection. The model fits the noisy data sufficiently well.
Fig. 6.
Predictive ranges for the migration model compartment populations. The light grey area represents the minimum and maximum model response at each time step, and the dark grey area refers to the mean model response with and without one standard deviation.
3.3. The impact of migration on HIV and AIDS
The addition of migration to the simple model reduces the transmission rate from 0.9785 to 0.6079. The basic reproduction number, on the other hand, rises from 2.0906 to 2.3322. This shifted the disease away from the steady-state disease equilibrium due to the proportions of migrants recruited into susceptible, HIV, and AIDS at rates of 1.5572e-01, 6.3773e-04, and 1.6611e-08, respectively. It also indicates that the rate of HIV infection speeds up with an increase of approximately 12% with migration over the model without migration. Thus, introduction of migration to the simple model identifies the pitfalls in estimating the true transmission rate and the basic reproduction number. It validated the true transmission rate beta and the basic reproduction number associated with HIV and AIDS epidemic disease in Malaysia.
4. Summary and discussion
In this paper, we formulated a simple model and its extension to study the dynamics of HIV and AIDS disease spread. We applied the models to the Malaysian HIV and AIDS epidemiological data that represented a nationwide homogeneous mix of infected migrants and susceptible citizens to study the HIV epidemic. We demonstrated how immigration impacted the spread of HIV and AIDS in Malaysia. As with all mathematical models, these results must be interpreted within the context of the model assumptions and the quality of epidemiological data available. While the estimated parameter sensitivity analysis offered robust results, we caution against over-interpretation of these predictions due to the uncertainty in the parameter describing migrant inflow and due to the structural limitations of the proposed model. The Bayesian approaches were used to derive a data-dependent probability distribution of the parameters to facilitate the implementation of the MCMC method. This approach was used to identify the parameter ranges and for parameter fitting.
Our findings highlight the important role that immigrant, susceptible, and sexually active, HIV-positive, and AIDS-infected populations play in the HIV/AIDS model. From Table 2, we observe that the proportion of migrants recruited to susceptible was 1.5572e-01, which constituted 67,801 migrants. Of the migrants, a proportion of 6.3773e-04 was estimated to be HIV infected, constituting 278 migrants. There were 72 (per 10,000) migrants estimated to have had AIDS, representing a proportion of 1.6611e-08. The estimated parameter correlations and uncertainty, as well as the uncertainty in the model prediction curves (Fig. 4, Fig. 6), were used to assess the accuracy of the model. Fig. 1, Fig. 2 showed that the estimate was not accurate but satisfied the given assumptions. This was an acceptable flaw because the data themselves can be questionable. The results suggested that a susceptible individual not exposed to migration becomes HIV infected at a rate of 9.7846e-01, which was greater than the 6.0786e-01 rate of transmission in a population interacting with migrants. This reduction in transmission rate is due to an increase in the number of parameters to be estimated which makes the migration model underdetermined.
The disease-free steady state for the proposed models were unstable since the basic reproduction number were estimated to be 2.0906 and 2.3322, respectively, for the models without and with migration. The advantage of introduction of migration to the simple model validated the true and the transmission rate associated with HIV and AIDS epidemic disease in Malaysia. This is not a good indicator from the public health point of view, as the aim is to stabilize the epidemic at the disease-free equilibrium. However, the introduction of migration pushes the disease away from the disease-free equilibrium state compared with the model without migration. It also indicates that the rate of HIV infection speeds up with an increase of approximately 12% with migration over the model without migration. The disease instability further implies that HIV will continue to infect the susceptible population because the rate of transmission was very high among HIV- and AIDS-infected migrants. The results of this study suggested that existing Malaysian intervention strategies may not be sufficient to reduce the spread of HIV and AIDS. Insights into future HIV/AIDS prevalence are useful for decision making in the public health sector. We believe that MCMC analysis could yield significant advances in our understanding of HIV/AIDS. Finally, there must be effective intervention measures to continue to minimize the spread of the HIV/AIDS epidemic within the unaffected population.
Declaration of competing interest
Dear Editor.
We hereby submit a manuscript entitled “Analysing the impact of migration on HIV/AIDS cases using epidemiological modelling to guide policy makers” by Ofosuhene O. Apenteng, Prince P. Osei, Noor Azina Ismail and Aline Chiabai to be considered for an original publication in Infectious Disease Modelling.
The authors have no conflict of interest to declare, because we obtained our data from Ministry of Health, Malaysia. This is secondary data that can be found at http://ptfmalaysia.org/v2/hiv-sti-info/hivaids-in-malaysia/
We declare that this manuscript is original, has not been submitted elsewhere before and is not currently being considered for publication elsewhere.
We wish to confirm that there are no known conflicts of interest associated with this paper.
We hope you find our manuscript suitable for publication and looking forward to hear from you soon.
Handling editor: Dr Y. Shao
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Contributor Information
Ofosuhene O. Apenteng, Email: ofap@food.dtu.dk.
Prince P. Osei, Email: prinpep@gmail.com.
Noor Azina Ismail, Email: nazina@um.edu.my.
Aline Chiabai, Email: aline.chiabai@bc3research.org.
References
- Agustín L. The disappearing of a migration category: Migrants who sell sex. Journal of Ethnic and Migration Studies. 2006;32(1):29–47. doi: 10.1080/13691830500335325. [DOI] [Google Scholar]
- Agustín L.M. Book; 2007. Sex at the margins: Migration, labour markets and the rescue industry. [Google Scholar]
- Anarfi J.K. Health transition review. Vol. 3. National Center for Epidemiology and Population Health (NCEPH), The Australian National University; 1993. Sexuality, migration and AIDS in Ghana - a socio-behavioural study; pp. 45–67. [DOI] [Google Scholar]
- Anderson R.M. The epidemiology of HIV infection: Variable incubation plus infectious periods and heterogeneity in sexual activity. Journal of the Royal Statistical Society: Series A. 1988;151(1):66. doi: 10.2307/2982185. [DOI] [Google Scholar]
- Anderson R.M., Medley G.F., May R.M., Johnson A.M. IMA journal of mathematics applied in medicine & biology. Vol. 3. 1986. A preliminary study of the transmission dynamics of the Human Immunodeficiency Virus (HIV), the causative agent of AIDS.http://imammb.oxfordjournals.org/ [DOI] [PubMed] [Google Scholar]
- Apenteng O.O., Ismail N.A. The impact of the wavelet propagation distribution on SEIRS modeling with delay. PLoS One. 2014;9(6) doi: 10.1371/journal.pone.0098288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apenteng O.O., Osei P.P., Oduro B., Kwabla M.P., Ismail N.A. The impact of implementing HIV prevention policies therapy and control strategy among HIV and AIDS incidence cases in Malaysia. Infectious Disease Modelling. 2020;5 doi: 10.1016/j.idm.2020.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blum M. Academic.Oup.Com; 2010. HIV with contact tracing: A case study in approximate Bayesian computation.https://academic.oup.com/biostatistics/article-abstract/11/4/644/372055 [DOI] [PubMed] [Google Scholar]
- Brookmeyer R., Liao J. Biometrics; 1990. Statistical modelling of the AIDS epidemic for forecasting health care needs.https://www.jstor.org/stable/2532455 [PubMed] [Google Scholar]
- Brummer D. 2002. Labour migration and HIV/AIDS in Southern Africa. [Google Scholar]
- Chuah F.L.H., Tan S.T., Yeo J., Legido-Quigley H. The health needs and access barriers among refugees and asylum-seekers in Malaysia: A qualitative study. International Journal for Equity in Health. 2018;17(1) doi: 10.1186/s12939-018-0833-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffee M., Lurie M., Garnett G. Modelling the impact of migration on the HIV epidemic in South Africa. AIDS. 2007 doi: 10.1097/QAD.0b013e328011dac9. https://journals.lww.com/drug-monitoring/00002030-200701300-00008.fulltext [DOI] [PubMed] [Google Scholar]
- Cooper A., Månsson S.A., Daneback K., Tikkanen R., Ross M.W. Predicting the future of Internet sex: Online sexual activities in Sweden. Sexual and Relationship Therapy. 2003;18(3):277–291. doi: 10.1080/1468199031000153919. [DOI] [Google Scholar]
- Corno L., de Walque D. Mines, migration and HIV/AIDS in Southern Africa. Journal of African Economies. 2012;21(3):465–498. doi: 10.1093/jae/ejs005. [DOI] [Google Scholar]
- Deane K.D., Parkhurst J.O., Johnston D. Linking migration, mobility and HIV. Tropical Medicine and International Health. 2010;15(12):1458–1463. doi: 10.1111/j.1365-3156.2010.02647.x. [DOI] [PubMed] [Google Scholar]
- Diekmann O., Heesterbeek J.A.P., Roberts M.G. 2009. Compartmental epidemic models the construction of next-generation matrices for References Subject collections the construction of next-generation matrices for compartmental epidemic models. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haario H., Laine M., Mira A., Saksman E. DRAM: Efficient adaptive MCMC. Statistics and Computing. 2006;16(4):339–354. doi: 10.1007/s11222-006-9438-0. [DOI] [Google Scholar]
- Höhle M. Elsevier; 2008. RLadyBug—an R package for stochastic epidemic models.https://www.sciencedirect.com/science/article/pii/S0167947306004221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansson J., Kerr C.C., Wilson D.P. Predicting the population impact of increased HIV testing and treatment in Australia. Sexual Health. 2014;11(2):146. doi: 10.1071/SH13069. [DOI] [PubMed] [Google Scholar]
- Jones J.H. 2013. Notes on R 0 1 the basic reproduction number in a Nutshell. [Google Scholar]
- Kelly S., Wilson D. HIV cascade monitoring and simple modeling reveal potential for reductions in HIV incidence. JAIDS Journal of Acquired Immune Deficiency Syndromes. 2015 doi: 10.1097/QAI.0000000000000655. https://journals.lww.com/jaids/fulltext/2015/07010/HIV_Cascade_Monitoring_and_Simple_Modeling_Reveal.1.aspx [DOI] [PubMed] [Google Scholar]
- Kibona I., Mahera W., Makinde D., Mango J. A deterministic model of HIV/AIDS with vertical transmission in the presence of infected immigrants. International Journal of the Physical Sciences. 2011;6(23):5383–5398. doi: 10.5897/IJPS11.452. [DOI] [Google Scholar]
- Laine M. 2008. Adaptive MCMC methods with applications in environmental and geophysical model. [Google Scholar]
- Lim L.L. The migration transition in Malaysia. Asian and Pacific Migration Journal. 1996;5(2–3):319–337. doi: 10.1177/011719689600500209. [DOI] [PubMed] [Google Scholar]
- Mahani A.S., Sharabiani M.T. 2015. SIMD parallel MCMC sampling with applications for big-data Bayesian analytics.http://www.nvidia.com/object/what-is-gpu-computing.html [Google Scholar]
- May R., Anderson R. Transmission dynamics of HIV infection. Nature. 1987 doi: 10.1038/326137a0. [DOI] [PubMed] [Google Scholar]
- McGinn T., Purdin S., Krause S., Jones R. 2001. Forced migration and transmission of HIV and other sexually transmitted diseases: Policy and programmatic responses. [Google Scholar]
- Merli M.G., Hertog S., Wang B., Li J. Modelling the spread of HIV/AIDS in China: The role of sexual transmission. Population Studies. 2006;60(1):1–22. doi: 10.1080/00324720500436060. [DOI] [PubMed] [Google Scholar]
- MOH . 2012. Global AIDS response country progress report. Malaysia. 2012. [Google Scholar]
- MOH . 2015. The global AIDS response progress report, 2014. Malaysia. [Google Scholar]
- Mukandavire Z., Das P., Chiyaka C., Gazi N.H., Das K., Shiri T. HIV/AIDS model with delay and the effects of Stochasticity. Journal of Mathematical Modelling and Algorithms. 2011;10(2):181–191. doi: 10.1007/s10852-010-9148-7. [DOI] [Google Scholar]
- Naresh R., Tripathi A., Sharma D. A nonlinear HIV/AIDS model with contact tracing. Applied Mathematics and Computation. 2011 https://www.sciencedirect.com/science/article/pii/S009630031100590X [Google Scholar]
- Nishigaya K. Female garment factory workers in Cambodia: Migration, sex work and HIV/AIDS. Women & Health. 2002;35(4):27–42. doi: 10.1300/J013v35n04_03. [DOI] [PubMed] [Google Scholar]
- Nyabadza F., Mukandavire Z. Modelling the HIV/AIDS epidemic trends in South Africa: Insights from a simple mathematical model. Nonlinear Analysis: REAL: Yearbook of Research in English and American Literature. 2011 https://www.sciencedirect.com/science/article/pii/S1468121810003342 [Google Scholar]
- Nyabadza F., Mukandavire Z. Modelling HIV/AIDS in the presence of an HIV testing and screening campaign. Journal of Theoretical Biology. 2011 doi: 10.1016/j.jtbi.2011.04.021. https://www.sciencedirect.com/science/article/pii/S0022519311002219 [DOI] [PubMed] [Google Scholar]
- Parrado E.A., Flippen C.A., McQuiston C. Use of commercial sex workers among hispanic migrants in North Carolina: Implications for the spread of HIV. Perspectives on Sexual and Reproductive Health. 2004;36(4):150–156. doi: 10.1111/j.1931-2393.2004.tb00016.x. [DOI] [PubMed] [Google Scholar]
- Pottie K., Hui C., Rahman P., Ingleby D., Akl E., Russell G., Ling L., Wickramage K., Mosca D., Brindis C. Building responsive health systems to help communities affected by migration: An International Delphi consensus. International Journal of Environmental Research and Public Health. 2017;14(2):144. doi: 10.3390/ijerph14020144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratliff E.A. Women as “sex workers,” men as “boyfriends”: Shifting identities in Philippine go-go bars and their significance in STD/AIDS control. Anthropology & Medicine. 1999;6(1):79–101. doi: 10.1080/13648470.1999.9964575. [DOI] [Google Scholar]
- Richens J. Sexually transmitted infections and HIV among travellers: A review. Travel Medicine and Infectious Disease. 2006;4(3–4):184–195. doi: 10.1016/j.tmaid.2005.06.010. [DOI] [PubMed] [Google Scholar]
- Roberts M.G., Heesterbeek J.A.P. Model-consistent estimation of the basic reproduction number from the incidence of an emerging infection. Journal of Mathematical Biology. 2007;55(5–6):803–816. doi: 10.1007/s00285-007-0112-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salomon J., Murray C. Modelling HIV/AIDS epidemics in sub-Saharan Africa using seroprevalence data from antenatal clinics. Bulletin of the World Health Organization. 2001 https://www.scielosp.org/article/bwho/2001.v79n7/596-607/en/ [PMC free article] [PubMed] [Google Scholar]
- Sani A., Kroese D.P. Controlling the number of HIV infectives in a mobile population. Mathematical Biosciences. 2008;213(2):103–112. doi: 10.1016/j.mbs.2008.03.003. [DOI] [PubMed] [Google Scholar]
- Sinka K., Mortimer J., Evans B., Morgan D. Impact of the HIV epidemic in sub-Saharan Africa on the pattern of HIV in the UK. AIDS. 2003 doi: 10.1097/00002030-200307250-00013. https://journals.lww.com/greenjournal/00002030-200307250-00013.fulltext [DOI] [PubMed] [Google Scholar]
- Soetaert K., Petzoldt T. Inverse modelling, sensitivity and Monte Carlo analysis in R using package FME. Garr.Tucows.Com. 2010 [Google Scholar]
- Solonen A., Haario H., Tchuenche J.M., Rwezaura H. Studying the identifiability of epidemiological models using MCMC. International Journal of Biomathematics. 2013;6(2) doi: 10.1142/S1793524513500083. [DOI] [Google Scholar]
- Sun X., Xiao Y., Peng Z., Wang N. Modelling HIV/AIDS epidemic among men who have sex with men in China. BioMed Research International. 2013 doi: 10.1155/2013/413260. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Den Driessche P., Watmough J. 2002. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission.www.elsevier.com/locate/mbs [DOI] [PubMed] [Google Scholar]
- Yang X., Derlega V.J., Luo H. Migration, behaviour change and HIV/STD risks in China. AIDS Care. 2007;19(2):282–288. doi: 10.1080/09540120600909414. [DOI] [PubMed] [Google Scholar]
- Zhang T., Jia M., Luo H., Zhou Y., Wang N. Applied Mathematical Modelling; 2011. Study on a HIV/AIDS model with application to Yunnan province, China.https://www.sciencedirect.com/science/article/pii/S0307904X11001247 [Google Scholar]