A tutorial on the use of temporal principal component analysis in developmental ERP research – Opportunities and challenges

Abstract

Developmental researchers are often interested in event-related potentials (ERPs). Data-analytic approaches based on the observed ERP suffer from major problems such as arbitrary definition of analysis time windows and regions of interest and the observed ERP being a mixture of latent underlying components. Temporal principal component analysis (PCA) can reduce these problems. However, its application in developmental research comes with the unique challenge that the component structure differs between age groups (so-called measurement non-invariance). Separate PCAs for the groups can cope with this challenge. We demonstrate how to make results from separate PCAs accessible for inferential statistics by re-scaling to original units. This tutorial enables readers with a focus on developmental research to conduct a PCA-based ERP analysis of amplitude differences. We explain the benefits of a PCA-based approach, introduce the PCA model and demonstrate its application to a developmental research question using real-data from a child and an adult group (code and data openly available). Finally, we discuss how to cope with typical challenges during the analysis and name potential limitations such as suboptimal decomposition results, data-driven analysis decisions and latency shifts.

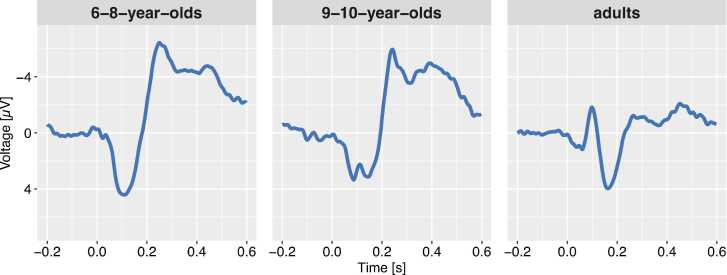
Electroencephalography (EEG) is a widely used time sensitive and noninvasive method to measure brain activity. More specifically, to enhance the understanding of neuronal and cognitive development throughout the lifetime, developmental researchers are often interested in event-related potentials (ERPs) as a measure of brain activity occurring time-locked to an event of interest (e.g., the presentation of a stimulus). ERPs undergo considerable developmental changes throughout childhood; for instance, there are substantial differences in amplitudes, polarities, latencies, and topographies of ERPs to auditory stimuli between newborns, toddlers, children, and adults (for a review, see Wunderlich et al., 2006). Fig. 1 depicts the ERPs to an auditory stimulus in two groups of children and an adult group. The children’s ERPs are characterized by a dominant positive peak which is followed by a negative peak whereas the adults’ ERP shows a prototypical series of peaks including two positive and two negative peaks (i.e., P1-N1-P2-N2). With increasing age, children’s ERPs develop more and more towards the prototypical mature adult ERP. As different cognitive functions are associated with different components in the ERP (e.g., Luck and Kappenman, 2012), ERPs allow for profound insights into the development of cognitive functions and their underlying neuronal networks.

Fig. 1.

Event-related potentials to a to-be-ignored auditory stimulus for two groups of children (left panel: 6–8-year-olds, middle-panel: 9–10-year-olds) and a group of adults (right panel). Negative amplitudes are displayed upwards. In the youngest children a broad positive deflection is followed by a large negative deflection. This pattern changes typically with age and results in an alternating sequence of positive and negative deflections.

A typical ERP analysis proceeds in the following steps (e.g., Luck, 2014): After recording a continuous EEG from multiple electrode sites during an experiment, the continuous EEG signal is filtered and cleaned from frequent artifacts such as eye-movement and blink activity (e.g., Chaumon et al., 2015) to reduce the amount of non-neural activity in the EEG signal. The EEG signal is then cut into epochs around the events of interest and averaged across all repetitions of each event separately for each event type (e.g., different stimuli) and electrode site per participant. The resulting ERP dataset containing data from each sampling point × participant × electrode × event type combination is then subjected to subsequent statistical analyses to identify amplitude, latency, polarity, or topographic differences between events. When this ERP dataset is further averaged across participants (especially for data visualization purposes), the resulting sampling point × electrode × event type dataset is referred to as the grand-average ERP (dataset). Before statistical inference is conducted, the ERP dataset is typically further aggregated to reduce noise and complexity. For instance, ERP amplitudes are commonly averaged within specific time windows and across specific electrode sites (i.e., region of interest, ROI) to quantify the activity of the ERP component of interest. This aggregated amplitude measure is then used as dependent variable for statistical inference (e.g., via ANOVAs).

This “traditional” data-analytic approach for ERPs suffers from two major, partially related problems: (1) The definition of analysis time windows as well as ROIs often proceeds in a relatively arbitrary manner (please see Luck and Gaspelin, 2016; for a thorough discussion) or is potentially afflicted by double dipping (Kriegeskorte et al., 2009). (2) The observed signal at the scalp is a mixture of underlying signals generated in the brain. The underlying signals overlap to an unknown extent both in the temporal domain (i.e., multiple sources contribute to the voltage at a specific sampling point) and in the spatial domain (i.e., multiple sources contribute to the voltage at a specific electrode site) – making the peaks of the observed signal a poor indicator of the underlying signals. Together, these problems can considerably bias estimates of amplitude, latency, and topography, especially when these estimates are based on the peaks of the observed signal. Therefore, researchers interested in ERPs can benefit a lot from using multivariate decomposition methods. These methods aim to describe the observed ERP data as a function of a set of underlying signals and provide objective characterizations of the time courses of these underlying signals. Here, we focus on temporal principal component analysis (PCA) which belongs to a class of procedures decomposing the data based on statistical properties such as the covariance between the voltages at the sampling points (Dien and Frishkoff, 2005, Donchin and Heffley, 1978). Temporal PCA for ERP data aims (a) to identify and disentangle the constituent components of the ERP and (b) to provide dependent measures for statistical analyses which are derived in an objective and transparent way. PCA is particularly suited for the investigation of ERPs in developmental populations reducing problems due to the enhanced noise level (Dien, 2012).

The overarching goal of this article is to enable the reader to conduct a PCA-based ERP analysis of amplitude differences between two age groups on his or her own and to cope with specific challenges when comparisons between children’s and adults’ ERPs are of interest for the research question. To this end, (1) we will introduce the benefits of a PCA-based approach using a simplistic simulated ERP for illustrative purposes, (2) we will demonstrate a real-data PCA analysis in a step-by-step manner using open source software (including example code and an open dataset), (3) we will explain the challenges which arise from differential ERP structures between age groups and provide recommendations how to cope with them, and lastly, (4) we will briefly compare PCA to other decomposition approaches and discuss potential limitations. In the following, we assume that the reader is familiar with essentials of the ERP technique such as its neural origin, typical research objectives, and pre-processing pipelines (for more basic introductions, see, e.g., Bradley and Keil, 2012, Luck, 2014). In addition, to work with the accompanying R code, we recommend that the reader is proficient in at least one high-level programming language (e.g., MATLAB, R, or Python).

1. Benefits of PCA-based ERP analyses

1.1. ERPs versus underlying components

The observed ERP signal at the scalp reflects simultaneous activity – mostly post-synaptic potentials – from a large number of neurons in the brain (Nunez and Srinivasan, 2006). Much like a movie is a time series of 2-dimensional images of a 3-dimensional world, an ERP signal can be construed as a time series of the electric potential across the electrode grid on the scalp surface – which is only a projection of the 3-dimensional signal in the brain. Because multiple sources can be active at a certain point in time and can project to the same electrode sites, the signal measured at the scalp suffers from considerable temporal and spatial overlap. Furthermore, the source signal is transmitted to the sensors via volume conduction through several layers with differential resistive properties resulting in the signal at the scalp being “smeared” spatially but also temporally because the spatial overlap of source activity at the sensors also limits the temporal precision which can be achieved in practice (see Burle et al., 2015; for more detailed discussion and possible remedies). In addition, ERPs are typically computed by averaging over many repetitions of the event of interest assuming strict temporal coherence with the event of interest (i.e., no latency jitter). Because brain maturation is not necessarily on the same level in children of the same age, this can have an even greater impact in developmental studies. Therefore, in sum, ERP data are a spatially and temporally imprecise representation of the source activity in the brain (Burle et al., 2015). The inherent loss of information regarding time courses, 3-dimensional position and direction of the source signals makes an exact reconstruction of the source signal impossible (that is, without further information and assumptions – this is typically referred to as the inverse problem of M/EEG). To appreciate this state of facts and avoid conceptual confusion, we will refer to the ground truth signals at the scalp electrodes that would be recovered by a decomposition technique under ideal circumstances as ERP components. The term ERP component has been used with many different connotations. In a broad sense, we define a component as coherent voltage deflection which contributes to the observed ERP at the scalp in a replicable way across experiments. A component can be characterized based on: the time of its occurrence within the epoch, its typical amplitude, its sources in the brain and/or its functional interpretation (i.e., its typical behavior under experimental manipulations).

Without further detailed knowledge regarding potential sources in the brain and how the signal spreads through brain, skull, and scalp, the best that researchers can hope for is to gain knowledge regarding functional interpretations of these components. Therefore, a certain functional independence, which can, for instance, be established by unique sensitivity towards certain experimental manipulations, is often considered a defining property of a component (e.g., Luck, 2014b). The spatial and temporal superposition of underlying components poses a great challenge for researchers who want to interpret the results from ERP experiments because it conceals how many components constitute the observed ERP and how much each individual component contributes to the electric potential at a specific time point and electrode site. That is, temporal and spatial overlap biases the functional interpretation of the ERP. Consequently, inferences regarding differences in component activity between events can be substantially biased when they are based on the observed ERP (Luck, 2005a). In the worst case, this might even lead to erroneous conclusions regarding functional interpretations and underlying processes.

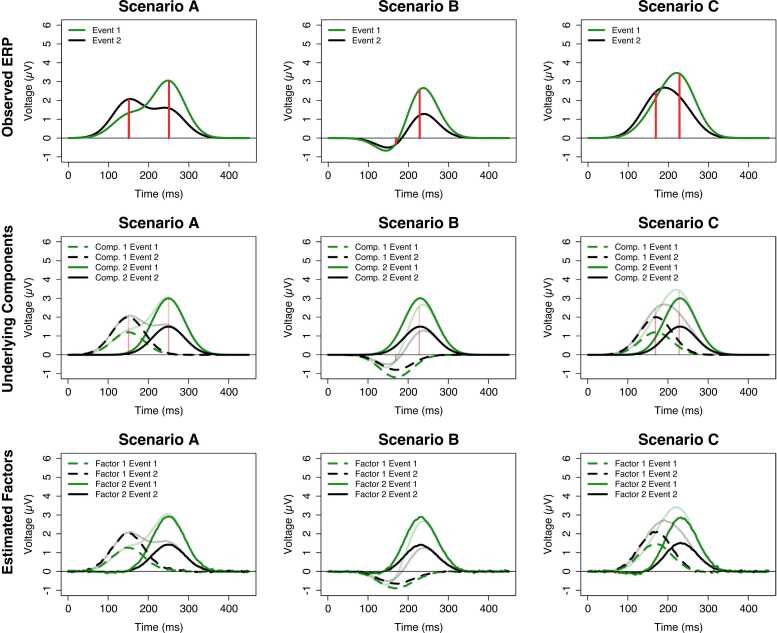
Fig. 2 illustrates three scenarios which mimic typical ERPs in a simplistic manner. These ERPs (upper panel) were simulated so that it is known that there are two underlying components (middle panel). Suppose there are two events for which we wish to investigate differences in ERPs. Due to the simulated nature of the example, we know that both components have reverse response patterns to the events: Component 1 has a more positive response to Event 2 compared to Event 1 whereas Component 2 has a more negative response to Event 2 compared to Event 1. When the overlap between components is mild (Scenario A), the observed ERP reflects the underlying components sufficiently because the two peaks of the signal roughly resemble the two peaks of the components and the condition effects resemble the reversed pattern of the underlying components. However, when the overlap between components is large (Scenarios B & C), this is not the case. Although the presence of a positive and a negative peak in Scenario B could be interpreted as a hint towards more than one underlying component, the peaks of the signal are poor indicators of the peaks of the underlying components (marked by the vertical red lines). Consequently, any analysis of amplitude and latency differences based on the peaks would suffer from severe biases. This is especially apparent for Component 1 for which both its true amplitude difference between Events and its latency deviates considerably from the peak-based measure. Scenario C illustrates a case in which peak-based measures are even more fallible because the ERP consists of one broad peak instead of two. In this case, neither the number of underlying components nor the nature of the event effect are as obvious. Solely based on the shape of the ERP, one might easily conclude that there is only one component and that its latency rather than its amplitude differs between events. This conclusion would severely misrepresent the ground truth and would probably result in inappropriate conclusions regarding the functional interpretation of the effect.

Fig. 2.

Illustration of three simplistic ERPs with mild (A) and severe (B & C) temporal overlap of the underlying components. The upper panel depicts the simulated ERPs “elicited” by two events (black and green lines); the vertical red lines mark the true peak of the underlying components shown in the middle panel. The lower panel depicts the factors estimated by the temporal PCA approach explained in the upcoming sections. The estimated factors (lower panel) resemble the underlying components (middle panel) well. Please note that results may be less optimal under more challenging circumstances (e.g., more temporal overlap).

The three scenarios in Fig. 2 demonstrate the central limitation of a data-analytic approach that is based on the observed peaks of the signal (e.g., averaging in a time window of interest): It assumes that the observed peaks are valid indicators of number, time course, and topography of the underlying components. This is only true when we can assume sufficient temporal and/or spatial separation of components. This limitation is well-known and severe (Luck, 2014a) because it is easily conceivable that many ERP components are never elicited in sufficient isolation to investigate them appropriately. In absence of sufficient separation, the choice of analysis time windows is arbitrary and prone to capitalizing on chance (Luck and Gaspelin, 2016), resulting in reduced reliability (and therefore, reduced statistical power) and potentially in erroneous conclusions regarding experimental effects of interest (Beauducel et al., 2000, Beauducel and Debener, 2003).

1.2. Theoretical introduction to temporal PCA

1.2.1. The temporal PCA model

These outlined limitations of peak-based approaches motivated a search for better suited analytic approaches for ERPs which explicitly acknowledge the mixture of underlying signals. Several multivariate analysis methods have been proposed with the purpose of estimating the unobserved underlying components based on combined statistical properties of ERP datasets. Among these methods are Principal Component Analysis (PCA), Independent Component Analysis (ICA), Wavelet-based decompositions, multimode PCAs, and source reconstruction methods (Achim and Bouchard, 1997, Chapman and McCrary, 1995, Dien, 2012, Donchin, 1966, Donchin and Heffley, 1978, Groppe et al., 2008, Möcks, 1988b, Mørup et al., 2006a, Slotnick, 2005). Here, we focus on temporal PCA which decomposes the observed ERPs based solely on the statistical associations between the sampling points. We will briefly discuss the relationship between temporal PCA and other proposed approaches in the last section of this article.

The aim of temporal PCA is to decompose the observed signal into a set of underlying factors summarizing sampling points with a similar/coherent activity pattern across participants, electrodes, and conditions. Ideally, one would like to view these factors as estimates of the true underlying components. However, there is no guarantee that the decomposition is always successful in disentangling all underlying components. To avoid any confusion about this fact, we refer to the estimated underlying signals as factors and to the ideally recovered signals as components throughout this article (deviating from the typical use of the term “component” in PCA and ICA).

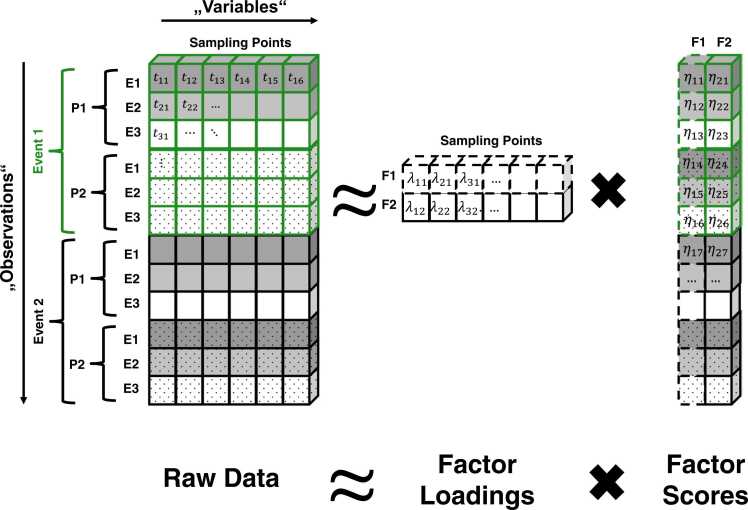
The lowest panel in Fig. 2 illustrates a 2-factor temporal PCA solution for each scenario. The transparent lines show the grand-average ERP for both events and the opaque lines are the factor-wise reconstruction of the ERP – summed together, both factors reconstruct the observed ERP. When comparing the estimated factors (lowest panels) with the underlying components from which the data were simulated (middle panels), one can clearly see that temporal PCA was quite successful in recovering the underlying components because the factors resemble the components very well even under severe temporal overlap (Scenarios B & C). Although the decomposition is not always perfect, especially in the presence of strong temporal and spatial overlap (Beauducel and Debener, 2003, Dien, 1998, Dien et al., 2005, Kayser and Tenke, 2003, Möcks and Verleger, 1986, Scharf and Nestler, 2018), one should keep in mind that a simple peak-based approach would have obscured the nature of the underlying amplitude effects, especially in Scenario C. We hope to convince the reader that this data-driven and therefore much more objective characterization of the underlying signals makes temporal PCA a valuable tool for ERP researchers. Furthermore, previous research indicates that temporal PCA can provide more reliable quantifications of ERPs and more accurate estimates of experimental effects (Arruda et al., 1996, Beauducel et al., 2000, Beauducel and Debener, 2003). How does temporal PCA achieve this decomposition? A fully-fledged technical introduction into the mathematical foundations of PCA is beyond the scope of this article but bottom-up introductions including all necessary mathematical basics are available elsewhere (e.g., Gorsuch, 1983; Mulaik, 2010). In the following, we want to provide the reader with an intuitive understanding of the PCA parameters, their estimation and the central assumptions underlying temporal PCA. Temporal PCA typically operates on an individual average dataset (i.e., averaged across trials within participants during pre-processing) in which each row represents a specific electrode site from an individual participant and from a specific experimental condition, and the columns contain the sampling points. Each cell defined by row and column reflects the mean voltage averaged across trials for a specific participant, electrode, condition, and latency. That is, the sampling points are treated as variables of interest and electrode sites, conditions, and participants are stacked as observations in the rows. Note that this is a variation of how PCA is taught in typical statistics 101 courses in which variables are answers to items in questionnaires and the observations are participants. Fig. 3 illustrates the data structure which enters the computation of a temporal PCA.

Fig. 3.

Prototypical data structure and decomposition into factor loadings and factor scores. P = Participant, E = Electrode, t = voltage at a specific sampling point for a specific observation, F = Factor, λ = factor loading (representing the time course of the activity for each factor), η = factor score (representing the level of activity of each factor for a specific observation). The residuals were left out for the sake of comprehensibility; but typically loadings and scores reconstruct the participant average data only approximately.

The temporal PCA model decomposes the participant average data into two sets of coefficients called factor loadings and factor scores, respectively (see Fig. 3). Roughly, the factor loadings describe the time course of a factor and are fixed across all electrodes, participants, and conditions. The factor scores describe the contribution (i.e., level of activity) of the factor to the voltage for each observation. Mathematically, this can be summarized in the fundamental equation of PCA in which the voltage at each sampling point is denoted as $t_{\mathit{ij}}$ where the indices represent any specific observation i and any specific sampling point j. The voltage at each sampling point is approximated by a weighted linear combination of the factor scores ${\eta }_{\mathit{ki}}$ of a fixed number of m factors (with k indicating any specific factor). That is, the factor scores are multiplied with the respective factor loading of a sampling point and summed up:

$$t_{\mathit{ij}}\approx {\lambda }_{j1}\cdot {\eta }_{1i}+{\lambda }_{j2}\cdot {\eta }_{2i}+\dots +{\lambda }_{\mathit{jm}}\cdot {\eta }_{\mathit{mi}}$$ (1)

The factor loadings λ_jk are weights which describe how much and with which sign a specific factor contributes to the voltage at sampling point j (“variable” t_⋅j): high loadings indicate a strong influence, and zero loadings indicate no influence of the factor. The factor scores reflect how much a specific factor contributes to the voltage at a specific electrode site for a specific participant in a specific experimental condition and are usually normalized to have unit variance. The unstandardized factor loadings can be interpreted as regression weights indicating by how many microvolts the predicted voltage at a sampling point changes when the score of the respective factor is increased by 1 standard deviation (while keeping all other factor scores constant). The factor scores can be directly used as quantifications of a factor’s contribution to the observed ERP. That is, they can be subjected to statistical tests, or they can be averaged across participants to compute a “grand-average” factor score for each electrode and condition, for instance, to illustrate the topography of a factor.

The signs and scales of factor loadings and factor scores are arbitrary and some identifying restrictions are necessary (Mulaik, 2010). In the context of ERP analyses, some specific conventions regarding the factor loadings and factor scores have been established (see also Dien and Frishkoff, 2005) in order to have an interpretable relationship between the signs of the factor scores and the polarity of the ERP signal: (1) the majority of the factor loadings of each factor should be positive, (2) the factor loadings are reported in the original unit µV (i.e., unstandardized5), (3) the factor scores are normalized6 (i.e., have unit variance) but they are not centered (i.e., they have a non-zero mean), and (4) the mean (or intercept) of the voltage at a sampling point is zero when no factor is active (i.e., when all loadings and/or scores are zero). This identification strategy maintains an interpretable relationship between factor scores and raw voltage (see, e.g., Kline, 2016, for a thorough explanation in the context of structural equation modeling): That is, for sampling points with a positive loading, a positive/negative factor score reflects positive/negative voltage of the factor at the respective electrode site in a specific participant and condition, and a factor score of zero indicates that a factor is inactive for a certain observation.

A very important implication of the model described above is that factor loadings are assumed to be constant across participants, electrodes, and conditions whereas the factor scores may vary. This assumption is typically referred to as measurement invariance in the factor analysis literature and its violation can have severe consequences for the performance of temporal PCA (Beauducel and Hilger, 2018, Meredith, 1993, Möcks, 1986). In general, equal factor loadings across electrode sites can be assumed due to the electrophysiological nature of the ERP signal and it is physiologically plausible to describe the ERP signal as weighted linear combination of the factors (Nunez and Srinivasan, 2006). However, systematic latency differences, latency jitter, or even different component structures can make it implausible to assume equal time courses across participants, conditions, or groups (see Molenaar and Campbell, 2009; for a general discussion).

Whenever measurement invariance is justifiable, it is preferable to analyze data in a combined PCA across all observation, because this naturally allows for mean comparisons of the factor scores (Beauducel and Hilger, 2018, Mellenbergh, 1989, Meredith, 1993, Nesselroade, 2007, Van De Schoot et al., 2015). When substantially different component structures are conceivable, separate PCAs can help to evaluate in how far the factor structures differ. The analyst should proceed with separate PCAs in case of major differences between component structures (e.g., different number of factors, some factors are only present in one PCA, strong latency shifts, etc.). Specific examples in which conducting separate PCAs might be beneficial include comparisons across different modalities (e.g., auditory vs. visual ERPs; see Dien, 2012; for a similar argument), comparisons across experimental conditions with very different factor structures (e.g., Barry et al., 2016), and comparisons between groups with expectably different ERP component structures such as children versus adults or patients versus healthy controls (e.g., Barry et al., 2014).

Separate PCAs violate the assumption of measurement invariance making it difficult to decide which mean comparisons are meaningful. In principle, there are strong theoretical reasons to believe that at least some factors from separate PCAs actually represent the same underlying component (see Nesselroade and Molenaar, 2016b, Nesselroade and Molenaar, 2016a; for a detailed discussion). For instance, both adults and children can be expected to have a P2 component in their ERPs and a factor representing the P2 component should occur in the adult as well as in the child PCA. If such matching factors can be identified based on theoretical considerations, quantitative comparisons between both groups can be conducted. Separate PCAs can provide some insights into differential factor structures (e.g., due to latency shifts), but they must be interpreted with caution due to the rotational indeterminacy. Different factor structures could either be caused by different component structures or be an artifact of differential rotated solutions. For instance, the P2 component could be conflated with a P3 component in one group but not in the other (cf. section Challenges). Despite these complications, separate PCAs can provide unique analysis opportunities when measurement invariance is unlikely fulfilled. This is especially relevant in developmental populations where ERP structures can vary tremendously between age groups.

1.2.2. Estimation of the temporal PCA model

A large and still growing variety of methods exists to estimate the factor loadings and factor scores (Conti et al., 2014, Mulaik, 2010, Trendafilov, 2014) which differ in many details of their implementation. However, some basic tasks for an estimation procedure can be identified: (1) determination of the number of factors, (2) estimation of the factor loadings, and (3) estimation of the factor scores. In the following, we will describe how these tasks have been solved traditionally in a stepwise manner.

Determination of the Number of Factors. The most fundamental question when estimating PCA is how many factors should be extracted. Ideally, the number of factors would coincide with the number of underlying components so that each factor is an estimate of one underlying component. Because the number of components is typically unknown to ERP researchers, extraction criteria can be used to decide how many factors should be extracted (Mulaik, 2010). Most of these criteria are based on the overall fit of the model, for instance, the amount of variance explained by each individual factor or all factors together. Put simply, a factor model is estimated with as many factors as sampling points in which the factors are sorted in descending order of explained variance. The number of factors is then chosen so that each individual factor explains a substantial amount of variance. A popular criterion to identify substantial factors is the so-called Parallel Analysis (Horn, 1965). This procedure compares the variance explained by each factor with the variance explained by the corresponding factor from a simulated dataset of uncorrelated variables. The rationale behind this is that a substantial factor should explain more variance than a factor that was extracted from random (white) noise with no underlying factors.

Despite its simplicity and rather heuristic nature, Parallel Analysis has been shown to perform remarkably well under certain conditions and is therefore an extremely popular extraction criterion (Auerswald and Moshagen, 2019, Buja and Eyuboglu, 1992, Crawford et al., 2010). With respect to applications of PCA to ERP data, two opposing views seem to exist in the literature: On the one hand, it has been suggested to apply a restricted solution with as many factors as suggested by Parallel Analysis (Dien, 1998, Dien, 2006). On the other hand, it has been suggested to use an unrestricted solution, that is, to extract as many factors as sampling points (Kayser and Tenke, 2003, Kayser and Tenke, 2006). Both recommendations have influenced researchers applying PCA and both practices can be found in published research (e.g., Fogarty et al., 2018; Kieffaber and Hetrick, 2005). Restricted solutions have the advantage of parsimony because they reduce the number of factors to be considered for interpretation (and statistical tests). Extracting too many factors can result in large factors such as slow wave components being split up artificially (Wood et al., 1996). However, unrestricted solutions could be preferable because effect size estimates converge towards a stable value with increasing number of factors (Kayser and Tenke, 2003, Kayser and Tenke, 2006). In addition, the amount of variance explained is of limited relevance in temporal PCA because factors which are active for a shorter amount of time always explain less variance (because they load on fewer sampling points) – but this does not automatically mean they are also negligible from a substantive perspective.

These seemingly contradictory recommendations can be reconciled in the light of recent research on factor extraction criteria. Indeed, extracting too few factors (underextraction) goes along with much stronger biases than extracting too many factors (overextraction; De Winter and Dodou, 2012; Fava and Velicer, 1992; Wood et al., 1996). Put simply, when the number of factors is too small, PCA represents separate components in conflated factors, but when too many factors are extracted, PCA can represent each component correctly as one factor. When extracting too many factors, PCA often results in additional small factors connecting a few sampling points which are negligible for substantive purposes (based on their weak loadings and topography). The findings of Kayser and Tenke (2003) make a strong case for avoiding underextraction: their estimated effects varied dramatically between solutions when only a few (e.g., 1–8) factors were extracted. When extracting more factors, results stabilized – even when extracting extremely many factors (i.e., severe overextraction). Nevertheless, an unrestricted solution is both computationally inefficient and makes the solution harder to interpret. Furthermore, the use of an unrestricted solution poses a massive multiple comparison problem because as many factors as sampling points need to be analyzed. A restricted solution with fewer factors suffers from this problem to much less extent. Considering this, the call for unrestricted solutions could be rephrased to read: Use a restricted solution, but when in doubt, prefer solutions with too many factors over solutions with too few factors.

Unfortunately, Parallel Analysis tends to extract too few factors in cases of highly correlated factors (Beauducel, 2001, Green et al., 2012, Lim and Jahng, 2019). Correlated factors are very common in temporal PCA because factors with similar topography are necessarily highly correlated (Dien, 2010a, Scharf and Nestler, 2018) – validating concerns regarding underextraction expressed in previous research (Kayser and Tenke, 2003). The reason for this is that Parallel Analysis is not a formally valid test but rather a heuristic for factors beyond the first factor (Saccenti and Timmerman, 2017). In the initial solution used to determine the number of factors, the variance explained by later factors can easily fall below that of random white noise factors when the factors are substantially correlated (Beauducel, 2001). Alternative extraction criteria such as the Empirical Kaiser Criterion perform better under these circumstances (EKC; Braeken and Van Assen, 2017; Li et al., 2020). Therefore, we tend to recommend against relying on Parallel Analysis (alone) to determine the number of factors and will consider the EKC in our step-by-step guide.

Estimation of the Factor Loadings. When a decision was made regarding the number of factors to be extracted, the final estimates of the factor loadings (and scores) need to be obtained. The factor loadings are typically estimated from the covariance matrix of the sampling points. Eq. (1) implies that these covariances are a function of the factor loadings and factor correlations (Gorsuch, 1983, Mulaik, 2010, Muthén, 2004):

$$\mathrm{\Sigma }\approx \mathrm{\Lambda }\mathrm{\Phi }{\mathrm{\Lambda }}^{\prime }$$ (2)

Σ is called model-implied covariance matrix of the sampling points, it contains the variances and covariances of the sampling points that would be predicted based on the factor model. It can be computed from the factor loading matrix Λ and the factor correlation matrix Φ. Put simply, the PCA model implies that two sampling points should be more correlated the more the same factors contribute to their voltage. This fact can be utilized to estimate the factor loadings, factor correlations and residual variances by minimizing the difference between the model-implied covariance matrix and the observed covariance matrix of the dataset. Alternatively, the standardized correlation matrix could be used but research on PCA for ERPs suggests that the unstandardized covariance matrix is preferable (Dien, 1998, Dien et al., 2005, Kayser and Tenke, 2003) because all sampling points are measured in the same meaningful unit (i.e., microvolts).

An important property of the outlined model is its rotational indeterminacy. That is, any specific ERP can be reconstructed by an infinite set of different factor loadings and factor scores. All these solutions fit the data equally well (see, e.g., Fig. 1 in Dien, 1998, for an illustration) and can be transformed into another by an operation called rotation (Asparouhov and Muthén, 2009, Gorsuch, 1983, Mulaik, 2010, Scharf and Nestler, 2019a). Rotational indeterminacy can only be overcome by additional assumptions. Typically, an initial or unrotated solution is estimated in which a set of restrictions with desirable computational properties is applied (e.g., uncorrelated factors which are extracted in descending order of explained variance). The unrotated solution is then subjected to a factor rotation procedure to obtain a rotated solution which is used for substantive interpretations. In the box Some details about factor rotation, we provide further details regarding this mathematical operation.

Factor rotation aims at transforming the initial unrotated solution into an alternative rotated solution which optimizes a certain rotation criterion. Modern rotation algorithms allow the use of virtually any criterion that can be computed from the factor loadings (Jennrich, 2004b). In the context of ERP research, a simple structure rotation criterion is typically applied. Simple structure rotation aims to rotate the factor loadings so that the voltage at each sampling point is attributed to as few factors as possible and so that each factor contributes to a set of sampling points as uniquely as possible (Dien, 2010a, Dien et al., 2007, Kayser and Tenke, 2003, Thurstone, 1935). Although simple structure rotation has difficulty in disentangling factors when temporal and spatial overlap are high (Möcks and Verleger, 1986; Wood and McCarthy, 1984), there is general consensus that the underlying components can be conceived as transient and temporally distinct enough for simple structure rotated results to be useful (Dien, 2010a, Dien and Frishkoff, 2005). For the sake of completeness, we would like to make the reader aware of two relevant alternatives: First, it is possible to rotate towards a user-defined target structure in a more confirmatory manner when sufficient previous data is available (Arruda et al., 1996, Zhang et al., 2018). Second, there are promising recent efforts to apply ERP-specific rotation criteria instead of general simple structure rotation (Beauducel, 2018a, Haumann et al., 2020).

In the following, we will assume that the user wants to apply a simple structure rotation. A variety of rotation techniques exists which differ in the technical criterion of simplicity being optimized (Browne, 2001) and can be roughly divided into orthogonal rotation methods and oblique rotation techniques. Orthogonal rotation assumes that the factors are strictly uncorrelated whereas oblique rotation allows the factors to be correlated. The factor correlation measures how much the factor scores covary across observations (i.e., across participants, electrode sites, and experimental conditions). Due to the specific data structure (cf. Fig. 3), the factor correlation is a hardly interpretable mix of contributions from participants, electrodes and experimental conditions (Scharf and Nestler, 2018) and the factors in temporal PCA are necessarily substantially correlated as a consequence of functional and topographic overlap (Dien, 1998, Dien, 2010a, Dien et al., 2005, Scharf and Nestler, 2018). Therefore, we strongly recommend applying oblique rotation methods in PCA for ERP data. Among the oblique rotation techniques, Promax (Hendrickson and White, 1964) has long been the gold standard based on its good performance in simulation studies (Dien, 2010a). Recent research revealed that Geomin (Yates, 1987) and Componentloss rotations (Jennrich, 2004a, Jennrich, 2006) may be able to disentangle highly overlapping factors that would be conflated by Promax (Scharf and Nestler, 2018, Scharf and Nestler, 2019a).

To sum up, when estimating the factor loadings, temporal PCA must cope with the rotational indeterminacy of the factor model implying that an infinite set of factors can fit the data equally well. To resolve this indeterminacy, rotation is applied which estimates the factor loadings based on the assumption that the components are transient and at least to some extent temporally separable. Since solutions from different rotation techniques cannot be evaluated by model-fit criteria, substantive/physiological considerations should be made to choose among rotated solutions. Recommendations how to detect and improve problematic results of the rotation step will be discussed later in this article (cf. section Challenges).

Estimation of the Factor Scores. After the factor loadings are estimated, the factor scores can be estimated. Several factor scoring methods have been proposed in the context of PCA for psychometric applications (Hershberger, 2014, Mulaik, 2010).7 We compute scores using the Regression method (Thomson, 1938, Thurstone, 1935) following the formula provided by DiStefano et al. (2009; Appendix 2):

$$\hat{\eta }=T{S}^{-1}\mathrm{\Lambda }\mathrm{\Phi }$$ (3)

Here, T is the raw data matrix, S is the observed covariance matrix of the sampling points (and S⁻¹ is its inverse), and Λ and Φ are the factor loading and factor correlation matrix, respectively, as estimated in the previous step. In other research contexts, the standardized raw data along the correlation matrix instead of the covariance matrix are usually used in Eq. 3 which results in standardized factors scores with zero mean and a variance of 1. Deviating from this procedure, we use the unstandardized (and non-centered) raw data along the covariance matrix. This results in factors scores which obey the restrictions outlined in the section on the temporal PCA model, that is, the factor scores are normalized with a variance of 1 but have a non-zero mean.

The factor scores provide a summary statistic for the activity of the factors in each observation (i.e., per electrode, condition, and participant; cf. Fig. 3). The factor scores can be used to reconstruct the data in a factor-wise manner, or they can be directly used as dependent measures, for instance, they can be subjected to ANOVAs to test for condition effects. In addition, average factor scores at each electrode site can be used to plot the topography of a factor. As a simple intuition, one can imagine factor scores as weighted averages of the voltage across the whole epoch in which the highest weight is given to the sampling points with high factor loadings (or vice versa: peak-based measures can be seen as extremely simplistic factor scores, see Beauducel and Debener, 2003; DiStefano et al., 2009; Donchin, 1966).

1.2.3. Factor-wise reconstruction of the ERP

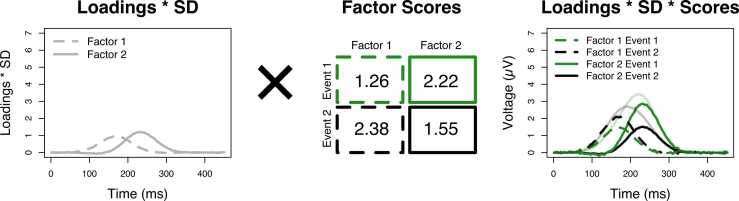
The factor loadings and scores can be used to provide a factor-wise decomposition of the average ERPs. Fig. 4 illustrates how we computed the factor-wise reconstruction of the ERP in Scenario C (right-most column, lowest-panel in Fig. 2). The left-most panel illustrates the unstandardized factor loadings reflecting the time course of the activity of the factors. By convention, many software packages return standardized factor loadings, referring to both the voltages at the sampling points and the factor scores in z-standardized units much like standardized regression weights. Unstandardized factor loadings are scaled in µV units.8 For ERP applications, it is preferable to report unstandardized loadings because the original unit of the voltage (i.e., µV) is meaningful and interpretable for researchers and unstandardized factor loadings thus provide a better link to the original ERP (Dien, 1998, Dien, 2012, Dien et al., 2005). To compute the unstandardized factor loadings from the standardized loadings, the standardized factor loading at a sampling point needs to be multiplied with the standard deviation of the voltage at the respective time point (Dien, 1998, Dien et al., 1997, Muthén and Muthén, 2004).9

Fig. 4.

Factor-wise reconstruction of the observed ERP in Scenario C. The unstandardized factor loadings (left-most panel) represent the time courses of the factors’ activities and are fixed across all participants, electrodes, and conditions. The factor scores (middle panel) vary across participants, electrodes and conditions and represent how much and with which sign a factor contributes to the voltage for a specific combination of participant, electrode, and condition. The factor scores can be used to analyze condition effects and to illustrate a factors’ topography – by averaging these scores across participants separately for each condition and electrode site. By multiplying the factor loadings and scores, the original data can be reconstructed in a factor-wise manner resulting in an estimate of the underlying components (cf. right-most panel and right-most low panel in Fig. 2).

To reconstruct the ERP in a factor-wise manner, the unstandardized loadings need to be multiplied with the factor scores (see middle panel in Fig. 4). The factor scores in the illustrative example were computed by averaging the factor scores across all participants separately for each event, that is, these are the grand-average factor scores. Multiplying these with the factor loadings results in the factor-wise reconstruction of the ERP in the right-most panel of Fig. 4. Similarly, the averaged factor scores across participants (per condition) at a specific electrode site can be used to reconstruct the ERP at a specific electrode site. The factor-wise reconstructions of the ERP provide a dependent variable in the original unit µV which is comparable across different PCA solutions, and which can be subjected to any further analysis.

2. Step-by-step analysis of an ERP dataset

In this section, we proceed with a step-by-step guide through a PCA analysis of real ERP data (see Fig. 5 for an overview). Extending previous treatments (Boxtel, 1998, Dien, 2012, Dien and Frishkoff, 2005, Donchin, 1978), we provide openly available R scripts (R Core Team, 2020) and an example dataset which can be adapted for further use by the reader. Some important code sections are also highlighted in code boxes to provide a link between the code and the corresponding explanations. We would like to make the reader aware of the ERP PCA Toolkit (Dien, 2010b) which is a MATLAB-based software specifically for PCA analyses with a graphical user interface. We did not want the user to depend on any commercial software to apply the methods described here. Therefore, our choice should rather be interpreted as a decision in favor of maximal accessibility rather than against the ERP PCA Toolkit. All codes and data are available from GitHub (https://github.com/FlorianScharf/PCA_Tutorial/).

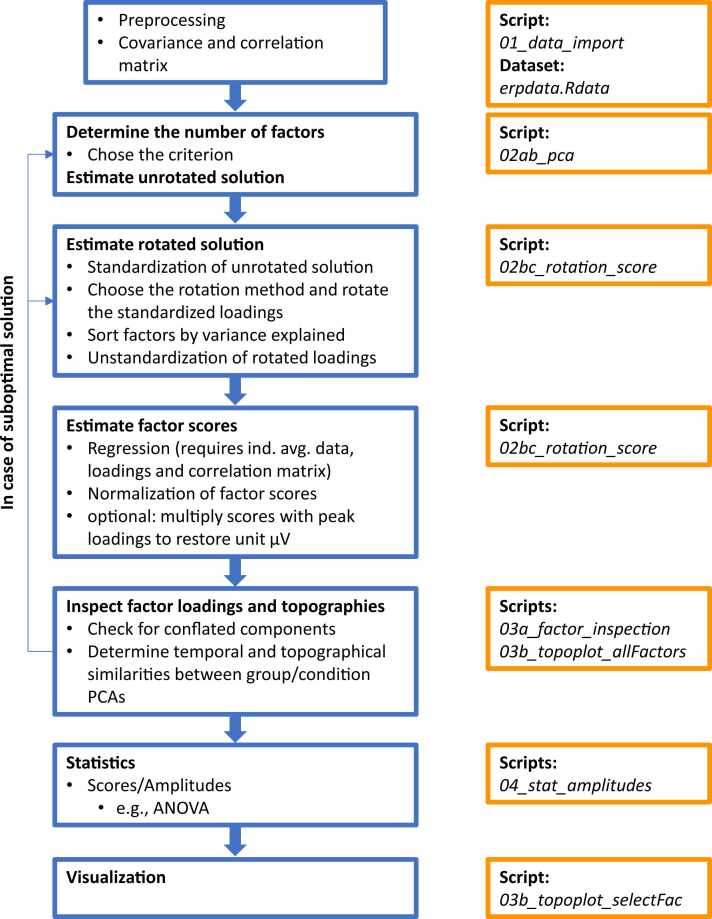
Fig. 5.

Overview of all processing steps and accompanying scripts in our step-by-step guide.

2.1. Prerequisites

We assume that the EEG dataset has already undergone basic pre-processing such as filtering, artifact cleaning, epoching, and averaging across trials within participants. That is, we apply temporal PCA to a dataset with an average ERP per electrode site, participant, and condition in each row. As for any ERP analysis, pre-processing might have beneficial or adverse effects depending on the extent to which the signal is isolated from noise and/or confounding influences. Systematic investigations of pre-processing choices in the context of temporal PCA are scarce but it is known that re-referencing or centering of the data has profound consequences because it can remove variance sources from the data. For instance, some variability across participants can be removed by applying an average reference within participants (Dien, 2012, Dien et al., 2005, Möcks and Verleger, 1985). In addition, one should be aware that slow-wave potentials can substantially confound the solutions because it is hard for temporal PCA to disentangle factors which are perfectly overlapping (Beauducel, 2018a, Verleger and Möcks, 1987; Wood and McCarthy, 1984). Similarly, filtering could affect the PCA solution because high-pass and low-pass filters are known to reduce or increase, respectively, the auto-correlation of the signal (i.e., the correlation of the voltage between adjacent sampling points entering PCA; Piai et al., 2015). Whether this is beneficial or harmful should depend on the extent to which the signal-to-noise ratio is improved (Widmann et al., 2015), but we are not aware of systematic investigations in the context of the PCA model.

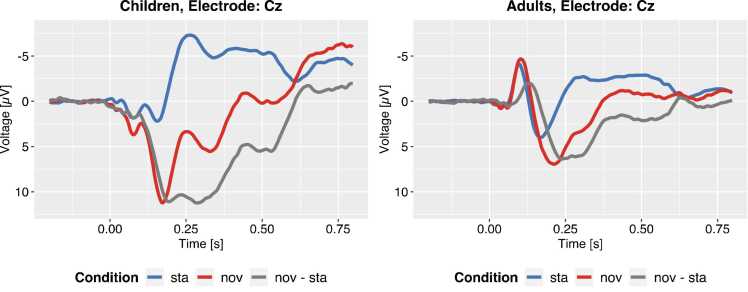
In the following, we re-analyze an ERP dataset from a passive auditory oddball task that was previously reported by Bonmassar et al. (2020). A child group (N = 32, 7–10-years, mean 8 years and 10 months) and an adult group (N = 32, 18–36-years, mean 26 years and 6 months) watched a silenced video while a sequence of sounds was being presented to them. The sound sequence consisted of 80% standard sounds and 20% novel sounds (i.e., environmental novel sounds which were presented only four times during the experiment). Half of the novel sounds was categorized as “emotional” whereas the other half was categorized as “neutral”. Participants were instructed to ignore the stream of sounds. The authors investigated amplitude and latency differences between adults and children regarding multiple ERP components. For the sake of comprehensibility, we will focus on the early P3a component and ignore the emotional content of the sounds when we illustrate each specific analysis step in the application of a temporal PCA. Fig. 6 depicts the grand averages across all participants in both groups.

Fig. 6.

Grand-average ERPs to standards and novels at Cz for children and adults. Very similar to the simplistic illustrations before, the observed ERPs are characterized by a series of peaks with different amplitudes and polarities. Nevertheless, it is hard to tell from the observed ERP which sampling points reflect specific underlying components. Note that all novel sounds were analyzed together irrespective of their emotional content.

We import the pre-processed ERP data from the file erpdata.Rdata (also available as a human-readable file in erpdata.csv). One could also import the data from toolboxes such as ERPLAB (Lopez-Calderon and Luck, 2014), EEGLAB (Delorme and Makeig, 2004), or FieldTrip (Oostenveld et al., 2011) – or consider conducting the pre-processing in R (see the R package eegUtils by Craddock, 2021).

2.2. Combined or separate analysis of groups?

First, one should consider whether it is justified to conduct a combined PCA over all available data, that is, measurement invariance can be assumed. In the following, we will analyze data from different stimulus types in combined PCAs and data from children and adults in separate PCAs, demonstrating how the analysis is conducted in any of the two cases. Therefore, most of the analysis scripts contain a variable to indicate for which group the specific analysis step should be conducted.

2.3. Estimation of the PCA model

In the next step, the parameters of the factor model need to be estimated. That is, the number of factors needs to be determined, the factor loadings and the factor scores need to be estimated. In this section, we go through these steps separately for the adult and child data. The presented code boxes are taken from the accompanying scripts 02ab_pca.R and 02bc_rotation_score.R.

2.3.1. Determination of the number of factors

We applied the EKC to determine the number of factors (Braeken and Van Assen, 2017). A user-friendly implementation of the EKC is available from the package EFAtools (Steiner and Grieder, 2020). The correlation matrices of the sampling points need to be computed for adults and children separately and are then used to compute the EKC.

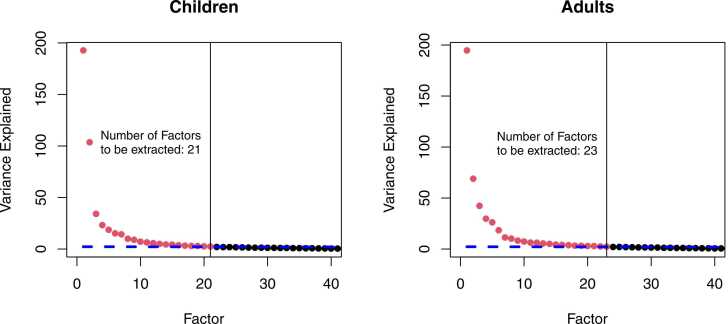
Fig. 7 depicts the variance explained by each unrotated factor in descending order and the value of the EKC with which it is compared. Remember that the number of factors in the initial unrestricted solution is equal to the number of sampling points. That is, there are 500 factors in our example. The number of factors m is the number of factors (red dots) lying above the EKC reference line. In the child PCA, 21 factors were extracted compared to 23 factors in the adult PCA. The number of factors is typically high for ERP data (e.g., > 10), which may still be challenging to interpret. We recommend reflecting on components of interest and their potential time range before the analysis. For instance, if the main research question focuses on an N100 component, one would focus on factors in a time range around 100 ms. The plausibility of the solution cannot be judged at this point. We will discuss how to detect potential under- and overextraction when we address common challenges.

Fig. 7.

Variance explained by each factor in the initial solution for adults and children. Note. Remember that the factors are extracted in descending order of variance explained in the initial solution. The dots in the figures illustrate the variance explained by each factor in the initial solution for all factors (so-called Scree-Plot). There are 500 factors in the initial solution (as many as sampling points in the epoch), but we cut the plot at 40 factors to focus on the comparison with the reference line (blue line) for the EKC. The number of factors is marked by the last factor lying above the reference line (additionally marked by the vertical line). The red dots are above the reference line, the black dots are below the reference line. For the child PCA, the EKC indicates that 21 factors should be extracted, compared to 23 factors in the adult PCA.

2.3.2. Factor loading estimation

We proceed with the estimation of the factor loadings. We first compute an unrotated solution and perform the factor rotation in a separate step. We estimate the unrotated solution using a custom10 version of a function11 from the package psych (Revelle, 2021). We note that the estimation of the unrotated model can take some time depending on the size of the dataset. To improve computation speed, the user can consider reducing the sampling rate. The correlation between adjacent sampling points is typically extremely high (e.g., between .97 and 1 in our dataset) so that reducing the sampling rate would not remove much information. However, one should make sure that the sampling rate is high enough to represent each theoretically expected component with multiple sampling points.

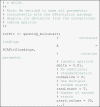
Before we subject the unrotated loadings to the rotation algorithm, we standardize them, that is, we divide the factor loadings by the standard deviations of the sampling points. It is common to standardize the factor loadings before rotation to prevent large factors from dominating the results of the rotation step (Asparouhov and Muthén, 2009; Appendix B; Dien et al., 2005; Grieder and Steiner, 2020; Mulaik, 2010). There is evidence that this can lead to better rotation results (Cureton, 1976, Mulaik, 2010) and that rotating unstandardized loadings is suboptimal in the context of ERP data (Dien et al., 2005). The standardized unrotated factor loadings are then subjected to factor rotation. We applied a Geomin rotation (Yates, 1987) with the rotation parameter ϵ set to 0.01.

The estimation of the rotated solution is done with Gradient Projection as implemented in the R package GPArotation (Bernaards and Jennrich, 2005, Jennrich, 2004b). Gradient projection can be used to rotate the factor loadings optimizing any mathematical criterion calculated from the factor loadings – enabling researchers to choose from a variety of rotation criteria. However, the user must be aware of the occurrence of local optima (Hattori et al., 2017, Nguyen and Waller, 2022, Weide and Beauducel, 2019). In simplified terms, Gradient projection proceeds as follows: (1) Choose a random rotation matrix for a start; (2) Compute the rotated factor loadings for this starting rotation matrix; (3) Evaluate the rotation criterion for these intermediate rotated factor loadings; (4) Compute a new rotation matrix to achieve a more optimal value of the rotation criterion; (5) Re-iterate through steps (2) to (4) until the value of the rotation criterion does not change substantially any more between iterations; (6) The rotated factor loadings from the last iteration are the final rotated solution. This estimation procedure is "short-sighted", that is, it tends to pick a solution optimizing the rotation criterion in close proximity to the starting value (local) while overlooking (globally) more optimal solutions “further away”. One might imagine a soapbox race car on a street which – on average – descends a hill but every now and then there is a minor ascent. If the soapbox car is too slow, it may get stuck due to one of these ascents and never reach the real valley. This leads to a strong dependence of the solution on the random starting value, especially for Geomin rotation (Hattori et al., 2017). When random starting values are used, it could even be that re-running the rotation procedure with the same data yields a different result every time. That is, our soapbox car might end up in different places depending on our starting point along the hill.

To increase the probability of finding the global optimum, the procedure outlined above should be repeated from many (e.g., 30) different random starting points and the globally optimal solution among all random starts should be used. With respect to the soapbox car, we just restart from different places on the hill and declare the deepest point that we have reached in all runs the “global valley”. Even relatively few random starts (usually between 30 and 100) can suffice to find the global optimum (Hattori et al., 2017). When in doubt, the user can check for global optimality by increasing the number of random starts. If the solution does not change after considering (many) more random starts, it is very likely globally optimal. We provide a custom implementation of the Geomin rotation with multiple starts based on the package GPArotation. We set the number of random starts to 30 for computational efficiency but we made sure that more random starts (we tested as many as 500) do not change the results. The validity of the rotated solution can only be judged by careful inspection of the solution and will be discussed later.

As mentioned before, ordering and signs or the factors are generally arbitrary. That is, after rotation, the factors can appear in an arbitrary order and can have mainly negative loadings. As the ERP PCA Toolkit (Dien, 2010b), we reorder the factors in descending order of variance explained. This makes visual inspection easier because large factors (e.g., P3 components) tend to appear among the first factors. We also reverse the signs of factors with mainly negative loadings so that a positive factor score indicates positive polarity at least for sampling points with positive loadings.

2.3.3. Factor score estimation

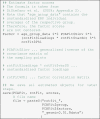
Using the original data (and their covariance matrix), the unstandardized rotated factor loadings, and the estimated factor correlations, we estimate the factor scores using the regression method (Thomson, 1935, Thurstone, 1935). We subject the unstandardized original data to the factor scoring step (Dien and Frishkoff, 2005). This results in factor scores with a non-zero mean and unit-variance. For instance, the first factor from the adult PCA has a mean of −0.20 and a standard deviation of 1.

2.4. Visual inspection of time courses and topography

Before conducting further analyses of condition effects or group differences, it is important to inspect the rotated solution, judge its substantive plausibility and interpret the factors based on their time courses and topography. We recommend looking at the time courses (i.e., the unstandardized factor loadings) first and inspect the topographies afterwards. We generated a series of plots (Fig. 8, Fig. 9, Fig. 10) that can be used to conduct these steps and provide the code to create them in the scripts. We also provide a script 03b_topoplot_selectFactor.R which generates a combined plot of time course and topography of a selected factor as a service to the reader. All topography plots rely on the package eegUtils (Craddock, 2021).

Fig. 8.

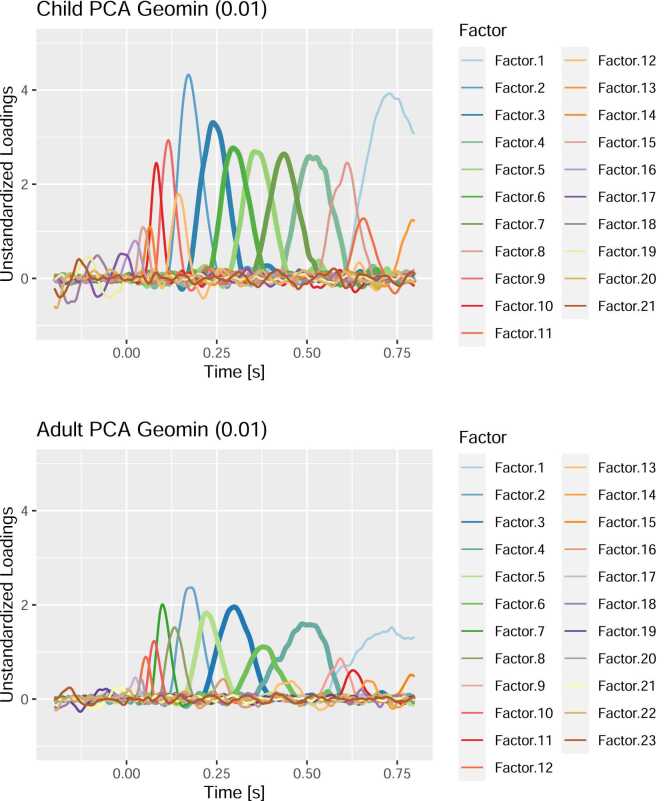
Unstandardized Factor Loadings after Geomin (0.01) Rotation in both PCAs. Each colored line represents the factor loadings of a factor. Higher factor loadings implicate that the factor contributes more to the voltage at a sampling point. Thus, one can conceive the loadings as a representation of the time course of a factor’s activity. Please note that the factors are numbered by the amount of variance they explain – not by their temporal order. Thicker lines were used to highlight factors in the typical P300 time range. This plot can be created using the script 03a_factor_inspection.R.

Fig. 9.

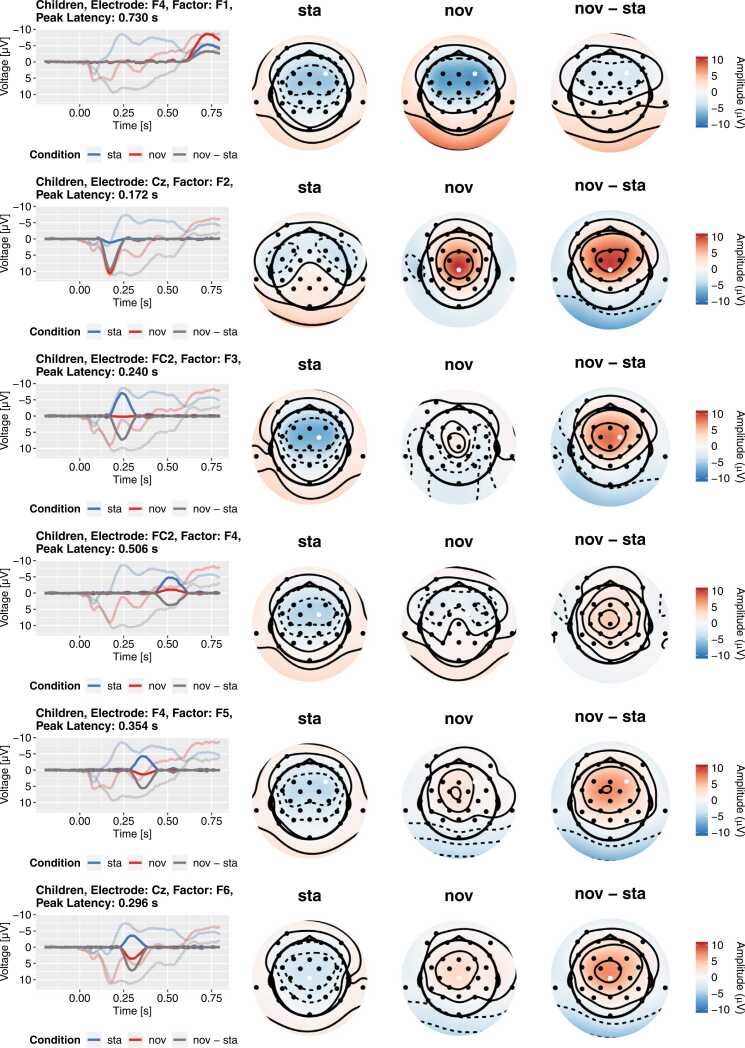
Topographies and reconstructed ERPs for the first six factors from the child PCA. Each row represents a factor in the rotated solution. The left-most column depicts the contribution of the factor to the grand-average ERP (transparent lines) at the maximum electrode (marked by white dot). The other columns present the factors’ topographies separately for all conditions. Please note that the extrapolated topography becomes unreliable outside the area covered by electrodes and tends towards extreme values due to the simplistic biharmonic interpolation. This plot is created in the script 03b_topoplot_allFactors.R.

Fig. 10.

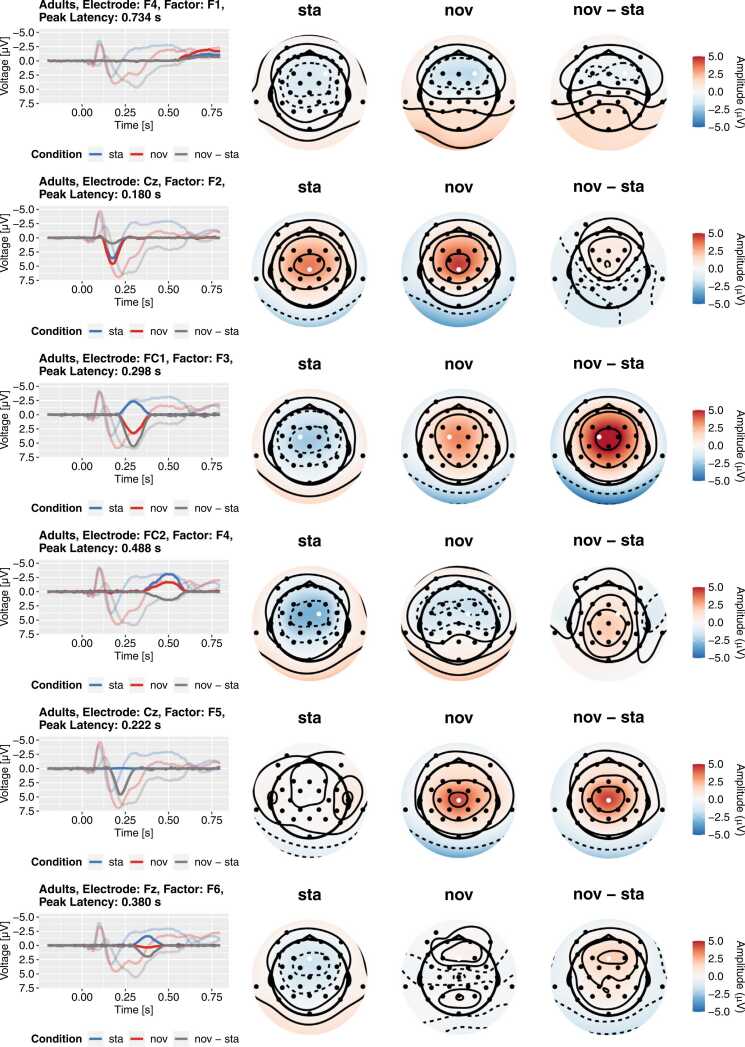
Topographies and reconstructed ERPs for the first six factors from the adult PCA. Each row represents a factor in the rotated solution. The left-most column depicts the contribution of the factor to the grand-average ERP (transparent lines) at the maximum electrode (marked by white dot). The other columns present the factors’ topographies separately for all conditions. Please note that the extrapolated topography becomes unreliable outside the area covered by electrodes and tends towards extreme values due to the simplistic biharmonic interpolation. This plot is created in the script 03b_topoplot_allFactors.R.

Fig. 8 depicts the unstandardized rotated factor loadings for the child and adult PCA, respectively. As expected, the factor solutions between adults and children differ profoundly. The loadings in the child PCA were generally higher – reflecting the typically larger ERPs and larger variability in children compared to adults. Although major factors were extracted in similar time ranges, the relative contributions of these factors differ considerably between both groups. For instance, Factor 1 has much lower peak loadings (e.g., relative to Factor 2) in the adult group than in the child group. Finally, a close look reveals that there could also be some latency differences (e.g., for Factor 2) between both groups.

The depicted solutions are quite typical of a PCA solution for ERP data. There are often about 8–12 major factors with large peak loadings and many minor factors which explain only a small proportion of the variation in the data. In our experience, meaningful ERP components are most often represented among the major factors (see also Dien, 2010b, Dien, 2012). The interpretation of minor factors is difficult and often unnecessary regarding the actual research questions. These factors could represent remaining autocorrelations in the noise, minor latency jitter between participants or idiosyncrasies in the ERPs of certain individuals among the participants (Dien, 2012, Dien, 2018, Möcks, 1986). Unless there are specific substantive hypotheses regarding a small but established component which must be identified among the minor factors, it is not essential to specifically explain the occurrence of every factor in the solution. Nevertheless, we want to emphasize again that the extraction of minor factors can improve the overall solution and that overextraction is typically preferable to underextraction. Even if only a subset of the major factors is relevant for further analyses, we recommend to always report the rotated loadings of all extracted factors. This ensures that readers (and reviewers) can evaluate the adequacy of the conclusions and that potential problems with the rotated solutions can be detected (cf. section Challenges).

To derive substantive interpretations, the topography of the factors needs to be considered in addition to the loadings. As in the ERP PCA Toolkit (Dien, 2010b), we computed the average factor scores across participants at each electrode site, for each stimulus type, and for each group and multiplied these scores with the factor loadings. The resulting factor-wise reconstructions of the grand-average ERP served as the basis for the topography plots. Specifically, we plotted the time courses at the electrode site with the maximal factor score and the topography at the sampling point with the maximal factor loading. Please note that this heuristic is not always optimal (e.g., for bipolar factors) and that the automatically chosen electrode site may not always be theoretically reasonable. In the following, we focus on the identification of the early P3a among the factors in both groups for the sake of comprehensibility. In a complete analysis, the topographies of all factors should be inspected, and we encourage authors to always make them available in the spirit of transparency. The full topography plots for our example dataset are available from the online supplement.

There are several major factors in a typical P300 time range between 200 and 400 ms in each PCA (highlighted in Fig. 8). Based on the loadings alone, these factors are candidates to represent the early P3a. Figs. 9 and 10 depict the topographies and reconstructed grand-average ERPs for the child and adult PCA, respectively. For both groups, there are two factors in the time range between 200 ms and 400 ms with a central, positive topography for novel sounds (child PCA: F5 and F6; adult PCA: F3 and F5). All remaining candidates are characterized by a negative topography which excludes them as early P3a factors (Escera et al., 2000). Based on their peak latencies, we labeled the adult factor F5 (peak loading at 222 ms) and the child factor F6 (peak loading at 296 ms) as “early P3a” and the respective other factor as “late P3a”. Despite their considerably different latency, we think that comparing these factors between groups is substantively justified because it is known that the respective components occur later in children compared to adults (Riggins and Scott, 2020). While the considerable latency differences support the appropriateness of separate PCAs in this case, they also demonstrate that detailed substantive reasoning is mandatory when matching factors from separate PCAs (Nesselroade, 2007, Nesselroade and Molenaar, 2016b).

In general, researchers must face several challenges when matching factors from separate PCAs: (1) the order in which the factors were extracted can vary, (2) systematic latency shifts of factors can occur, (3) matching factors solely based on visual inspection can be very subjective, and (4) the number of factors to compare is typically very large. Quantitative similarity measures for the factor loadings and topographies such as Pearson’s correlation or Tucker’s congruency coefficient can support the search for matching factors (Lorenzo-Seva and ten Berge, 2006). These measures are regularly applied in simulation studies to quantify the similarity of loading patterns (De Winter and Dodou, 2016, Dien, 1998, Scharf and Nestler, 2018, Scharf and Nestler, 2019a, Scharf and Nestler, 2019b). Therefore, we think that they can be helpful to researchers applying PCA as well. Specifically, we recommend matching the factors by temporal similarity first followed by topographic similarity because factors tend to be more distinct with respect to their time courses than to their topographies (Dien, 2010a). In our experience, this procedure allows to identify clearly corresponding factors very easily. However, we note that factors with systematic latency shifts cannot be matched based on temporal similarity. In the accompanying scripts, we provide a detailed demonstration how Pearson’s correlation can be used to match the corresponding factors from the child and adult PCA (see script 03a_factor_inspection.R).

A closer inspection of the contributions of early and late P3a to the grand average ERPs (Fig. 6, Fig. 9, Fig. 10) underlines the usefulness of the temporal PCA approach. Both factors overlap considerably in time and space with each other and with the P2 factor and are hardly distinguishable based on the grand average ERP alone. That is, there is no obvious time-window (or baseline-to-peak relation) that could be utilized to disentangle these factors. Given that these separate factors could not even be identified without statistical decomposition, any analysis based on the observed waveform would suffer from a considerable risk of false conclusions due to the conflation of separable factors. To be clear, we do not claim that all such analyses are wrong – to what extent a conflation of factors biases the results is highly specific for a given dataset – but the risk of missing important features of an ERP is much higher without decomposition approaches.

2.5. Analysis of amplitude effects

Either the factor scores or a factor-wise reconstruction of the ERPs could be used for inferential statistics. In a combined PCA, the choice does not matter – at least not for the results of a general linear model (i.e., t-tests, ANOVAs, regressions) – because common amplitude measures (e.g., peak amplitude or time window averages) are only rescaled factor scores. This can be shown very easily: The peak amplitudes of the reconstructed ERPs are just the factor scores of the respective factor multiplied with the peak factor loading: ${\hat{t}}_{\mathit{peak}}={\lambda }_k^{\left(\mathit{peak}\right)}\cdot {\eta }_k$. Similarly, one can show that the average reconstructed voltage in a time window is simply the average factor loading in that time window multiplied by the factor scores:

$${\overline{\hat{t}}}_{\mathit{timewindow}}=\frac{\sum _{i\in \mathit{timewindow}}{\lambda }_{\mathit{ik}}\cdot {\eta }_k}{\mathit{length}(\mathit{timewindow})}={\eta }_k\frac{\sum _{i\in \mathit{timewindow}}{\lambda }_{\mathit{ik}}}{\mathit{length}(\mathit{timewindow})}={\eta }_k\cdot {\overline{\lambda }}_{\mathit{timewindow},k}$$

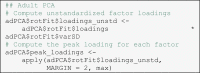
These considerations underline that both approaches are equally valid and will eventually lead to the same conclusions in a combined PCA. However, in separate PCAs only the analysis of reconstructed ERPs ensures a shared scale (i.e., µV) – directly comparing the factor scores between children and adults would be problematic because both scores were normalized relative to the variability within the respective dataset. A natural way to bring them back to a shared scale is the factor-wise reconstruction of the ERP. After this rescaling, again, it does not matter whether the reconstructed peak amplitudes are used or a measure of the area under the curve. In the following, we will use the peak of the reconstructed ERP ${\hat{t}}_{\mathit{peak}}$ as dependent variable in our analyses. We generally recommend this approach because it reinstates the original unit µV which ERP researchers are most familiar with. We compute the peaks of the reconstructed ERPs in the script 04_stat_amplitudes.R:

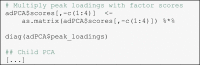
For the sake of simplicity, we conduct further amplitude analyses on a single electrode site for each factor, but it would also be possible to average across a spatial region of interest instead. It should be noted that the electrode site should be chosen a-priori to avoid capitalization on chance or “double dipping” (Kriegeskorte et al., 2009, Luck and Gaspelin, 2016). For each of the four selected factors, we conducted the same statistical analyses: (1) Compute descriptive statistics using the package psych (Revelle, 2021), (2) conduct an analysis of variance with the between factor “group” and the within factor “condition”, and (3) conduct some selected pairwise comparisons of interest. This should be read as a basic suggestion; the reader is free to use the (rescaled) factor scores for any analysis for which peak-based ERP scores could have been used. We demonstrate frequentist inferential statistics using the package afex (Singmann et al., 2021) as well as Bayesian inferential statistics as implemented in the packages BayesFactor (Morey and Rouder, 2018) and bayestestR (Makowski et al., 2019). We report generalized η² (${\eta }_{\mathit{gen}}^2$) as effect size measure (Bakeman, 2005).

In the following, we briefly go through the results of these steps for the early P3a factor. As illustrated in Figs. 9 and 10 (child PCA: F6; adult PCA: F5), the voltage of the early P3a factor at electrode site Cz is negative for standard sounds in both groups (Children: M = −3.58 µV, SD = 2.35 µV; Adults: M = −0.064 µV, SD = 1.60 µV). For novel sounds, the voltage was more positive compared to standard sounds (Children: M = 3.56 µV, SD = 3.82 µV; Adults: M = 4.52 µV, SD = 2.90 µV). The ANOVA revealed a significant main effect of condition, indicating generally more positive voltage of the factor for novels, F(1,62) = 235.97, p < .001, ${\eta }_{\mathit{gen}}^2$ = 0.533. There was also a significant main effect of group, F(1,62) = 14.68, p < .001, ${\eta }_{\mathit{gen}}^2$ = 0.142, and a significant group × condition interaction, F(1,62) = 11.26, p = .001, ${\eta }_{\mathit{gen}}^2$ = 0.052. Both effects were most likely driven by the more negative voltage of the factor for standards in children – but we did not follow up on them to keep this demonstration simple. Most importantly, both in adults, t(31) = 10.15, p < .001, and in children, t(31) = 11.61, p < .001, paired t-tests revealed significant differences in the voltage between standards and novels.

To sum up, amplitude differences in the voltage of a specific factor can be analyzed either using the factor scores directly or based on the reconstructed participant average data. Both yield equivalent test results in combined PCAs but the reconstructed ERP approach offers the advantage of restoring the original unit µV and enabling comparisons across separate PCAs. The factor score based measures can be used for any further analysis as a quantification of a factor’s contribution.

3. Challenges in developmental studies

In the previous sections, we have introduced the PCA model and its potential merits for ERP researchers and we have provided a step-by-step guide through a PCA-based analytic approach demonstrating how amplitude effects can be analyzed. In this section, we want to address several common challenges and discuss how the data-analyst can cope with them: (1) How can the visual inspection be used to reveal suboptimal decomposition results and what can be done about it? (2) How can “double dipping“ be avoided? (3) Further considerations on measurement non-invariance: What are possible reasons for different results from separate PCAs? What should one do when quantitative comparisons seem unreasonable? (4) How can PCA be used to analyze longitudinal data with multiple measurement occasions for each participant? (5) How can separate PCAs be used to investigate latency differences?

3.1. How to detect and handle suboptimal PCA results

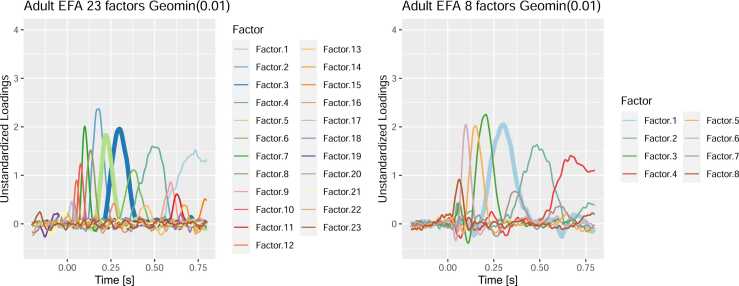
Careful visual inspection of the PCA solution is essential to make the substantive decision whether a specific PCA solution is “reasonable”. The most likely reasons for suboptimal solutions are under- or overextraction of factors and difficulty of the rotation method in disentangling highly overlapping factors. A very common symptom are conflated factors (Scharf and Nestler, 2019a), that is, factors occur in the solution which seem to be a mixture of established (sub-) components. The likelihood of this happening increases with temporal and spatial overlap. To illustrate this, Fig. 11 contrasts the loadings from the adult PCA presented before (23 factors) with a suboptimal solution with only 8 factors. The extraction of too few factors forces PCA to conflate separable components into a single factor. In this case, the early and late P3a factors from the left panel (Factors 3 and 5) are conflated into a single factor in the right panel (Factor 1). The reason for this is that both factors overlap in time and have very similar topographies. Such a conflation of prominent separate components is a clear warning sign that the solution is not optimal and is often also recognizable in the topographies which are also a mixture of the conflated factors’ typical topographies.

Fig. 11.

Comparison of the reported solution with two suboptimal solutions. The left-hand panel contains our reported solution. The right-hand panel contains a suboptimal solution. The thicker lines highlight the factors mentioned in the text. In the right-hand panel, early and late P3a (Factors 3 and 5 in left panel) are conflated into a single factor.

In general, temporal PCA tends to err in the direction of conflating factors which should be separated rather than splitting factors artificially (but see Wood et al., 1996). The spatial and temporal overlap which make it hard to identify these factors by visual inspection of the original ERP also make it hard to separate them based on statistical properties of the data. Although conflated factors cannot always be treated successfully, there are some systematic steps researchers can try to improve suboptimal solutions: (1) Try to increase the numbers of random starts and iterations for the rotation algorithm in case the suboptimal solution was due to a local optimum of the rotation criterion. (2) Investigate whether the solution improves when the number of factors is increased to rule out underextraction. (3) Adapt the rotation procedure. Promax has been the gold standard for a long time, but alternative rotation techniques such as Geomin and Componentloss rotation can sometimes achieve better results (Scharf and Nestler, 2019a). Alternatively, some rotation techniques have a tuning parameter that can be changed. For instance, increasing the Geomin ϵ improves the ability of the rotation to separate overlapping factors (but at the risk of splitting other factors artificially). (4) When none of the above options is viable, the assumptions of PCA may simply not fit the present purpose and alternative decomposition methods could help (see below).12

3.2. How can “double dipping” be avoided?

Although such data-driven adaptations of the analysis procedure can improve the physiological plausibility of the decomposition, one must be aware of the considerable risk of “double dipping” (Kriegeskorte et al., 2009). Technically, data-driven adaptations of the analyses present a case of selective inference in which statistical tests are applied after the statistical “model” has been chosen based on the same dataset (Benjamini, 2010, Kriegeskorte et al., 2009, Luck and Gaspelin, 2016). Strictly speaking, any post-hoc model modification is potentially problematic and may inflate the type I error rate – be it a change of the number of factors or a change of the rotation method. A simple and effective strategy to avoid this is a strict separation of the model specification step from the statistical inference step. Preregistrations can be used to decide on the parameters for PCA before beginning the analysis and to make all deviations from the original analysis scheme transparent. A preregistration of a PCA-based analysis should at least contain the following aspects:

• (1)How are the data pre-processed and cleaned?
• (2)Which subsets of the data are submitted to combined versus separate PCAs?
• (3)How is the number of factors determined?
• (4)Is the analysis based on standardized data (i.e., a correlation matrix) or unstandardized data (i.e., a covariance matrix)?
• (5)Which rotation technique is applied? (if applicable, including the values of rotation parameters and standardization scheme of loadings during rotation)
• (6)How will a substantive interpretation of the factors be derived?
• (7)How will factors from separate PCAs be matched?
• (8)How will statistical inference be conducted? Which electrode sites/ROIs will be included in the analysis for each presumed factor?

To increase the objectivity of interpretations, we also encourage groups of cooperating researchers to interpret the results independently in a first step and to discuss deviating interpretations in a second step.

Even for very experienced researchers, it is hardly possible to anticipate all characteristics of ERP data with sufficient accuracy to always make ideal a-priori choices. Instead of avoiding modifications at all costs, we think that it is important to make transparent which decisions were made post-hoc. Ultimately, each exploratory modeling decision increases the need for confirmatory replication studies to establish the robustness of the findings. If the sample size is sufficient, researchers may consider data splitting (i.e., tuning analysis parameters in one half of the data and conducting statistical inference on the other half). Data splitting is an effective, easily implemented and non-parametric method to assure the validity of statistical inference after model selection (Rinaldo et al., 2019, Wasserman and Roeder, 2009), although we acknowledge that sufficiently large samples are hard to collect in a developmental context. Nevertheless, replication studies and studies trying to manipulate certain factors in isolation are essential next steps to validate the decomposition results (Widmann et al., 2018). Alternatively, when many analyses have been tried out, it may even be best to make their results transparent and to show which of the results is sensitive towards specific data-analytic choices (Steegen et al., 2016). In sum, none of these threads for replicability is specific to temporal PCA; peak-based analyses suffer from the very same issues, and the same strategies can (and should) be applied to maximize the chance of replicable findings.

3.3. Further considerations on measurement invariance

As we have seen, equality of the factor loadings across all observations is arguably one of the most questionable assumptions of the temporal PCA model. Apart from differences between groups, systematic latency shifts may also occur between experimental conditions (Barry et al., 2016) or between participants resulting in additional factors (Möcks, 1986). We recommend the use of separate PCAs whenever measurement invariance is questionable. Specifically, developmental researchers should conduct separate PCAs for different age groups because the evidence for fundamentally different component structures between different age groups is strong (Wunderlich et al., 2006). With respect to experimental conditions, separate PCAs should be conducted when substantial latency differences are expected. Otherwise, separate PCAs can be conducted to check for unanticipated latency shifts. In the presence of very strong latency jitter, PCA might not be an appropriate analysis model and alternative decomposition methods might be considered (see below).

When separate PCAs reveal different factor patterns, this may either be an artifact of the rotation step or indicate genuinely different component structures. That is, measurement non-invariance does not inevitably imply different component structures (see Welzel et al., 2021; for a similar discussion in the context of psychometric data). For instance, PCA may conflate certain factors in one group but not in the other. This possibility can hardly be ruled out using a single dataset, although isolated cases of conflated factors could be identified as outlined in the previous section. Nevertheless, measurement non-invariance can be a hint towards qualitative differences between the groups and there is no guarantee that separate PCAs map as well as in our example dataset – and it is therefore not a failure of the analyst if a specific factor from one group cannot be matched with any factor from the other group. For instance, it is well-known that babies have very different ERPs from school children and adults (Wunderlich et al., 2006) and it would not be surprising if separate PCAs in these groups yielded very different results. Quantitative comparisons may be unreasonable in such situations, and we suggest that potential explanations for the qualitative differences should be discussed instead of enforcing a quantitative comparison of fundamentally different entities.

3.4. Longitudinal designs

In the present article, we focused on an example of a cross-sectional temporal PCA in which independent age groups were compared. However, developmental researchers could also use longitudinal designs with repeated measurement occasions for the same group of participants. Two specific challenges occur in the context of longitudinal designs: First, researchers should reflect on the plausibility of measurement invariance across measurement occasions, and second, they need to account for the dependencies between measurements occasions from the same participant. With respect to the first challenge, temporal proximity between measurement occasions is crucial. Assuming that the main driver of different factor structures is cognitive and neuronal development, the plausibility of measurement invariance largely depends on the time lag between measurements. For instance, when ERPs are recorded from a group of children twice within one week, it is unlikely that fundamental development has taken place in these areas, and one would expect to observe the same factor structure across both measurement occasions. However, if the time lag between measurements would be a year or longer, substantial developmental changes could have occurred and all considerations on measurement invariance from the previous sections apply.

When measurement invariance can be assumed, researchers can conduct a combined PCA across all measurement occasions. Importantly, for statistical inference, the measurement occasions need to be considered a within-person factor, essentially in the same way as we did it with stimulus type in our example. When measurement invariance cannot be assumed, researchers could combine separate PCAs with so-called target rotations (for an overview, see Browne, 2001). For instance, a separate PCA with simple structure rotation could be applied for the first measurement occasion. For the second measurement occasion, this rotated loading matrix could serve as a target for the rotation – aiming for as similar factor structures as possible. We think this approach is most reasonable when the time lag is substantial but not too large. In this case, factor structures may still be relatively similar with some specific changes (e.g., latency shifts of certain factors). In such cases, target rotation could help to uncover the nature of the developmental changes. More recent approaches to longitudinal analyses such as latent growth models can be applied in the context of exploratory structural equation models (Asparouhov and Muthén, 2009, Marsh et al., 2009, Marsh et al., 2013, Marsh et al., 2014, Morin et al., 2013, Scharf and Nestler, 2019b) including a more general approach to rotate towards a similar factor structure between multiple measurement occasions (Marsh et al., 2017). Please note that further methodological evaluations of these approaches are necessary because we are not aware of any previous applications of these recently developed methods to ERP data.

3.5. Analysis of latency effects

Apart from the analysis of amplitude differences between conditions, ERP researchers are often interested in latency differences between groups or conditions. Some methods have been proposed which are able to provide individual factor-wise latency estimates for participants (e.g., Möcks et al., 1988; Tuan et al., 1987) but these methods have not been widely adopted to our knowledge. In a combined PCA, latency differences are mostly concealed due to the strict measurement invariance assumption, but extreme latency differences may result in split-up factors representing different latencies. Separate PCAs can be used to detect latency differences assuming that none of the solutions is affected by rotation artifacts such as conflated factors – but they do not quantify the uncertainty of the estimated latencies. In the original analysis, we adopted an established Jackknife approach to test for latency effects (Kiesel et al., 2008, Miller et al., 1998, Ulrich and Miller, 2001). Instead of applying this resampling approach to the observed ERP, we applied it to the factor loadings re-estimating the rotated loading for each re-sampled dataset (Bonmassar et al., 2020). Systematic evaluations of the utility of this approach are not yet available but we provide an implementation and documentation of this approach as a supplement in the GitHub repository for any interested reader. In sum, despite the aforementioned and other methodological efforts to lift this limitation (De Munck et al., 2004, Ouyang et al., 2017, Truccolo et al., 2003), using temporal PCAs to analyze latency effects remains challenging and no validated wide-spread solution is available so far.

4. Comparison with alternative decomposition methods

The challenges described above demonstrate that PCA is a data-analytic approach with strengths and weaknesses as any other approach (Delorme et al., 2012, Dien et al., 2007). Since the original proposal of PCA decompositions for ERP data (Donchin, 1966, Donchin and Heffley, 1978), its usefulness has been demonstrated many times (Chapman and McCrary, 1995, Dien, 2012, Dien et al., 2003, Dien and Frishkoff, 2005). But there have also been lively debates regarding its weaknesses (Achim and Marcantoni, 1997, Beauducel and Debener, 2003, Collet, 1989, Dien, 1998, Dien et al., 2005, Donchin, 1989, Kayser and Tenke, 2003, Kayser and Tenke, 2005, Möcks, 1989, Möcks and Verleger, 1986; Wood and McCarthy, 1984). The term variance misallocation has been coined by Wood and McCarthy (1984) to describe the fact that condition effect estimates based on PCA can be biased. The reason for this is that the loading estimates can be biased which is a result of a partial mismatch between the goal of the rotation technique and the ground truth (Möcks and Verleger, 1986). Specifically, orthogonal rotations must be avoided because they always estimate uncorrelated factors which is not appropriate (Dien, 1998, Dien, 2010a, Dien et al., 2005, Scharf and Nestler, 2018). In addition, when the ground truth is characterized by components with high spatial and temporal overlap, especially in the presence of slow-wave components, simple structure rotation can by definition not achieve perfect separation but will conflate, for instance, slow-wave components with other components (Scharf and Nestler, 2018, Scharf and Nestler, 2019a, Verleger and Möcks, 1987). ERP-specific rotations and estimation algorithms could further reduce this problem (Beauducel, 2018b, Haumann et al., 2020) but more experience is needed with applications of these methods for further evaluation.

Despite this methodological progress and the wide-spread use of decomposition methods such as ICA for artifact removal (e.g., Chaumon et al., 2015), the use of decomposition techniques during the actual quantitative analysis step is sometimes met with skepticism. Some of these concerns have been expressed in popular introductory treatments for ERP analysis (Luck, 2005b).13 Therefore, we would like to put some arguments made there into perspective:

The PCA technique, in particular, is problematic because it does not yield a single, unique set of underlying components without additional assumptions (see, e.g., Rösler and Manzey, 1981). That is, PCA really just provides a means of determining the possible set of latent component waveshapes, but additional assumptions are necessary to decide on one set of component waveshapes (and there is typically no way to verify that the assumptions are correct). (Luck, 2005b, p. 22).

It is true that the PCA model needs restrictions to identify the model parameters. However, this is not a property of the method itself but rather of the inverse problem in ERP research. We try to make inferences regarding the functional significance of components (or even the sources in source localization analyses) from the limited information provided by the ERP observed at the scalp. From a mathematical perspective, this problem is ill-posed. That is, the ERP signal at the scalp does not contain sufficient information to recover the ground truth uniquely. Consequently, it is impossible to infer the components without additional assumptions or additional knowledge (e.g., co-registered fMRI). Importantly, mean amplitudes in time-windows, peak- or area-based measures make even more restrictive assumptions: All these measures can be conceived as extremely simplistic factor scores (e.g., with rectangular factor loadings in case of mean amplitude time-windows) assuming that the voltage in the analyzed time-window is uniquely due to one factor, that is, that there is zero temporal or spatial overlap with other components (DiStefano et al., 2009, Donchin and Heffley, 1978). Because these methods are simply naïve scoring methods, it is not surprising that they suffer from even worse variance misallocation than PCA (Beauducel and Debener, 2003). The appropriateness of simple structure rotations is certainly up to discussion in many contexts but we see it as an advantage of PCA that we can explicitly name and discuss this assumption rather than simply making it implicitly by using naïve scoring methods.

Another common concern is that decomposition techniques fail in the presence of latency shifts and latency jitter:

[A]ny correlation-based method will have significant limitations. One limitation is that when two separate cognitive processes covary, they may be captured as part of a single component even if they occur in very different brain areas and represent different computational functions. […] Another very important limitation is that, when a component varies in latency across conditions, both PCA and ICA will treat this single component as multiple components (Luck, 2005b, p. 22).

It is true that temporal PCA tends to conflate components which overlap temporally, spatially and/or functionally (i.e., when they have the similar condition effects; but see below for potential solutions). It is also true that latency jitter can result in artificial additional factors (Möcks, 1986) and that a combined PCA cannot represent latency shifts but, as we have demonstrated, separate PCAs can be used to improve this situation to some extent. In the context of exploratory structural equation models, measurement invariance can even be tested formally (Asparouhov and Muthén, 2009, Putnick and Bornstein, 2017, Scharf and Nestler, 2019b). Furthermore, for measures based on the observed ERP it is by no means clear whether ERP differences are due to amplitude differences or latency shifts as is apparent even in a simplistic example such as Scenario C in Fig. 2. PCA offers a much more objective way to disentangle these scenarios than visual inspection of observed ERPs. An additional advantage of PCA-based analyses is that we know the direction in which PCA tends to err and we know the symptoms: Conflated factors and artificial “jitter-factors” are well-documented (Möcks, 1986, Verleger and Möcks, 1987) and it is possible to inspect the PCA solution for these signs of suboptimal solutions – offering much deeper insight into the potential component structure.

Ultimately, researchers must decide – based on their knowledge on the subject matter – which assumptions can be made and, hence, which analytic method is appropriate. In that sense, we agree with (Luck’s 2005b, p.22) conclusion that PCA “[does] not provide a magic bullet for determining which components an experimental manipulation influences” but neither do the “traditional” approaches which are based on the observed ERP. Hence, we strongly advocate that researchers carefully reflect on the assumptions and make them explicit. To support these reflections, we briefly want to make the reader aware of some further decomposition methods and when they could be helpful. A detailed treatment of these methods is beyond the scope of this introductory tutorial, but we strongly encourage the reader to explore them following the familiarization with the temporal PCA approach.

Instead of the sampling points as in temporal PCA, the electrode sites can be treated as variables in a spatial PCA (Dien, 2010a, Dien et al., 2004, Dien et al., 2007, Dien and Frishkoff, 2005). Spatial PCA assumes equal topographic weights across participants, time points, and conditions but allows the time courses to vary. Whereas measurement invariance of the topography is clearly plausible in many situations (Delorme et al., 2012), spatial PCA requires the use of special rotation techniques because factors typically contribute to the voltage at all electrode sites. These rotation techniques (e.g., Infomax) are closely related to independent component analysis (ICA; Dien et al., 2007), and they aim to extract factors which are as stochastically independent as possible instead of rotating towards a simple structure (for mathematical introductions and tutorial treatments, see, e.g., De Lathauwer et al., 2000; Groppe et al., 2008; Huster and Raud, 2018; Makeig et al., 1996; Stone, 2004). Please note that there is an ongoing debate regarding the use of restricted versus unrestricted solutions for spatial decompositions as well (Artoni et al., 2018).

A further noteworthy analytic approach is to combine spatial and temporal PCA. That is, first, a temporal PCA is applied, followed by a spatial PCA on the temporal PCA results in a second step. This is called temporospatial PCA or spatiotemporal PCA when the PCAs are conducted in reversed order (Dien, 2010a, Dien et al., 2004, Spencer et al., 2001). The main idea is to complement the strengths of both approaches: Temporal PCA benefits from the fact that many of the factors are temporally separable but it fails to separate factors with identical time courses but separable topography. Spatial PCA suffers from the strong spatial overlap and could conflate factors with identical topography but separable time courses. A combination of these approaches could therefore considerably reduce the risk of conflating factors. In addition, spatial PCA offers an aggregated quantification across all electrodes which uses more of the available information compared to factor scores from single electrodes or averages across regions of interest. Alternatively, a trilinear decomposition of the ERP dataset has been proposed as an advancement of the PCA model which acknowledges the role of electrode sites and sampling points as measurement occasions instead of treating one or the other as “observations” (Achim and Bouchard, 1997, Cong et al., 2015, Möcks, 1988b, Möcks, 1988a, Wang et al., 2000). There have even been proposals how latency shifts can be directly acknowledged within such a model (Harshman et al., 2003, Harshman and Lundy, 1994, Mørup et al., 2008, Mørup et al., 2011). Apart from modifications of the PCA model to ERP data, it has been suggested that PCA can also be helpful when conducted on typical transformations of ERP data such as scalp current density (Kayser and Tenke, 2015b, Kayser and Tenke, 2015a), time-frequency decompositions (Barry et al., 2019), or wavelet-transformations (Mørup et al., 2006b).

In sum, a variety of methods has been proposed to address certain limitations of the temporal PCA explained in this article or to adapt it to other use cases. All these methods are either direct modifications of the outlined approach or they estimate a very similar mathematical model. In that sense, the reader could see the temporal PCA approach as an entry point to the world of decomposition methods. The limitations of peak-based methods have been acknowledged for a long time. We are convinced that a basic understanding of decomposition methods is crucial for ERP researchers and that it will contribute to further progress in the field of developmental cognitive neuroscience. We hope that this tutorial and the provided code encourage the readers to apply this method to learn more about the development of the brain.

5. Conclusion

We set out from the fact that observed ERP data are a mixture of latent signals and that ignoring this issue can considerably bias substantive conclusions drawn from ERP data. Decomposition methods such as temporal PCA aim to model the latent signals. Although there are common challenges one must be aware of, temporal PCA is an effective tool for ERP researchers, especially in a developmental context where the noise level is typically high and the comparability of the ERP signals from different age groups is always at stake due to maturational changes. Extending previous tutorial treatments, the analytic procedure outlined here explicitly acknowledges that ERPs differ systematically between children and adults. We conclude that the use of decomposition methods in ERP analysis can substantially improve research on the development of neuronal network activity underlying cognitive functions.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.