Dark-field tomography of an attenuating object using intrinsic x-ray speckle tracking

Abstract.

Purpose

We investigate how an intrinsic speckle tracking approach to speckle-based x-ray imaging is used to extract an object’s effective dark-field (DF) signal, which is capable of providing object information in three dimensions.

Approach

The effective DF signal was extracted using a Fokker–Planck type formalism, which models the deformations of illuminating reference beam speckles due to both coherent and diffusive scatter from the sample. Here, we assumed that (a) small-angle scattering fans at the exit surface of the sample are rotationally symmetric and (b) the object has both attenuating and refractive properties. The associated inverse problem of extracting the effective DF signal was numerically stabilized using a “weighted determinants” approach.

Results

Effective DF projection images, as well as the DF tomographic reconstructions of the wood sample, are presented. DF tomography was performed using a filtered back projection reconstruction algorithm. The DF tomographic reconstructions of the wood sample provided complementary, and otherwise inaccessible, information to augment the phase contrast reconstructions, which were also computed.

Conclusions

An intrinsic speckle tracking approach to speckle-based imaging can tomographically reconstruct an object’s DF signal at a low sample exposure and with a simple experimental setup. The obtained DF reconstructions have an image quality comparable to alternative x-ray DF techniques.

1. Introduction

X-rays have been utilized in a variety of applications since their discovery by Röntgen.¹ Their ability to pass through matter makes x-rays highly useful in a broad range of applications, particularly in medical imaging. X-rays are attenuated, scattered, and refracted when traversing a material. As a result, the wavefield at the exit surface of the object contains encoded information regarding that object. X-ray imaging directly visualizes differing densities, and therefore refractive indices, of materials within a sample. The refractive index for x-rays travelling through matter is given as $n({\mathbf{r}}^{\prime })=1-\delta ({\mathbf{r}}^{\prime })+i\beta ({\mathbf{r}}^{\prime })$, where ${\mathbf{r}}^{\prime }$ is the three-dimensional position vector and $\delta ({\mathbf{r}}^{\prime })$ and $\beta ({\mathbf{r}}^{\prime })$ describe refraction and attenuation of the x-ray beam, respectively. In many x-ray imaging techniques, these functions provide the relative image contrast; for example, conventional radiography is attenuation-based imaging and hence depends on $\beta ({\mathbf{r}}^{\prime })$.

Phase-contrast imaging (PCI)² is an x-ray imaging technique that exploits the refraction of x-rays in material. PCI is especially useful for imaging objects that are weakly attenuating, for example, soft tissues in mammography. Propagation-based PCI (PB-PCI)^3–6 is a PCI technique that achieves phase contrast by making use of sufficiently spatially coherent illumination and subsequent downstream free space propagation of the exit surface wavefront. PB-PCI is a refraction- and attenuation-based radiography technique that is easily implemented as no additional optical elements are required. PB-PCI can be used to noninvasively study samples at micrometer and sub-micrometer length scales. The downstream propagation in PB-PCI allows for the extraction of phase information, relating to $\delta ({\mathbf{r}}^{\prime })$, via suitable phase retrieval algorithms. This phase information is lost in attenuation-based x-ray imaging techniques. Paganin et al.⁷ demonstrated a simple phase retrieval algorithm for a single-material object using PB-PCI that is based on the transport-of-intensity equation.⁸

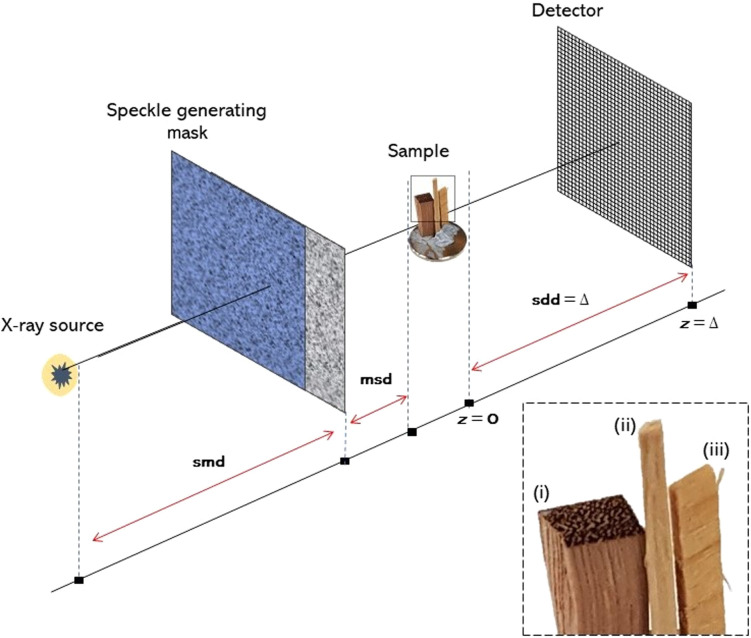
Some methods achieve phase contrast by introducing additional optical elements, for example, grating interferometry,^9–14 single-grid PCI,¹⁵ Bonse–Hart interferometry,^16–18 edge-illumination PCI,^19,20 and analyzer-based PCI.^21–25 Speckle-based x-ray imaging (SBXI), first introduced in 2012 by Berujon et al.²⁶ and Morgan et al.,²⁷ uses a spatially random mask placed between the x-ray source and detector (see Fig. 1). This mask acts as a random phase and intensity modulator to generate a near-field speckle pattern. In this technique, information regarding the sample is inferred by studying how the speckles, first measured in the absence of the object, are altered by the introduction of the object. Using such an approach, SBXI is capable of reconstructing phase gradients, attenuation, and small-angle scattering information.²⁸

Fig. 1.

Schematic of SBXI experimental setup. Here, smd is the source-to-mask distance, msd is the mask-to-sample distance, and $\mathrm{sdd}=\mathrm{\Delta }$ is the sample-to-detector distance.

Spatial resolution in PCI is limited by the size of the detector pixels and the size of the x-ray source. As a result, microstructure smaller than the resolution of the imaging system, and hence smaller than the pixel size, cannot be imaged directly. Dark-field (DF) x-ray imaging provides information about such spatially unresolved microstructures. DF thereby enables complementary structural information to be obtained at subpixel scales. Image contrast in DF imaging is generated by position-dependent small-angle x-ray scattering (SAXS) of the incident beam by the sample. SAXS²⁹ is the diffusive scattering of an x-ray beam from the unresolved microstructures that are smaller than the width of a pixel and are found within an object. This position-dependent SAXS influences the measured PCI data, leading to the associated inverse problem³⁰ of how information regarding the spatially unresolved microstructure (e.g., a position-dependent correlation length) may be inferred from one or more measured PCI images.

Currently, there are a variety of DF-PCI techniques, for example, propagation-based DF-PCI,^31,32 grating-based DF-PCI,^33–36 edge-illumination DF-PCI,^37,38 and analyzer-based DF-PCI.^25,39–42 Grating-based PCI has regular gratings placed between the source and detector, for example, the so-called Talbot-Lau interferometer reported by David et al.⁹ and Momose et al.¹⁰ In such techniques, the attenuation, differential phase, and DF signal are extracted by measuring the intensity variations caused by introducing the sample in the path of the beam. However, to do so, several different image acquisitions are required to reconstruct a single projection. This is done using different transverse positions of the gratings, relative to one another. Single-grating-based methods have also been reported,^43,44 aiming to reduce the x-ray exposure relative to multigrating-based approaches. Analyzer-based imaging, similar to grating-based imaging, requires multiple image acquisitions to reconstruct a single projection of the object. In this technique, an analyzer crystal is introduced to selectively measure angular components of the x-ray beam. Kitchen et al.^45–47 and Ando et al.⁴¹ used a Laue geometry to simultaneously collect transmitted and diffracted images to reconstruct both the absorption and phase images in a single exposure. As a result, both the exposure time and radiation dose were considerably reduced compared with alternative techniques that rotate the analyzer crystal.

SBXI techniques are also capable of extracting DF images through speckle tracking.^48–51 Berujon and Ziegler⁵¹ used “x-ray speckle-vector tracking” (XSVT), and Zdora et al.⁴⁹ employed the formalism of “unified modulated pattern analysis” (UMPA). XSVT and UMPA each apply an explicit, pixelwise tracking approach to extract the DF signal by analyzing multiple SBXI images. However, single-image multimodal recovery is also possible using a correlation-based approach.^27,50 Pavlov et al.^52,53 recently developed “multimodal intrinsic speckle tracking” (MIST), an algorithm that retrieves a sample’s DF signal in SBXI. MIST⁵² utilizes intrinsic speckle tracking within a SBXI setup to recover an object’s phase and DF signal simultaneously, in a deterministic manner. MIST combines a Fokker–Planck^31,54,55 description of paraxial x-ray optics with a geometric flow formalism for x-ray speckle tracking.⁵⁶ The MIST⁵² formalism only requires two sets of projection data, for two different transverse positions of the mask, suggesting that the technique may be suitable for clinical applications in which dose should be minimized. DF images have proven highly advantageous in the study of soft tissues,⁵⁷ and the success of SBXI techniques in PCI has also been highlighted.⁵⁸

The speckle tracking variant of obtaining the DF signal published by Pavlov et al.⁵² assumes that (a) the sample is nonattenuating and (b) the position-dependent SAXS fans that emanate from the exit surface of the object are rotationally symmetric. Here, we extend the MIST formalism⁵² to consider a monomorphous attenuating object, while maintaining the assumption of rotationally symmetric SAXS fans. Such generalizations are crucial for the broader utility of this technique—for example, in possible future applications to disciplines such as metallurgy, paleontology, soils science, and structural failure prediction—since typical samples in such contexts are often strongly attenuating.

2. Theory

Here, we extend the MIST⁵² formalism to the case of a monomorphous attenuating object, by first formulating the forward problem and then solving the corresponding inverse problem.³⁰ The forward-finite-difference Fokker–Planck equation is first obtained; it is used to model optical energy conservation as the speckles are formed and then deformed due to propagation through a SAXS-inducing object. The inverse problem for a monomorphous attenuating object is then considered to retrieve both (a) the effective DF signal and (b) projected thickness (which can be related to the object-induced phase shifts). We also consider two approaches to numerically stabilize the mildly ill-posed inverse problem.

2.1. Scalar-Diffusion Fokker–Planck Formalism for X-Ray Speckle Tracking: Monomorphous Attenuating Object Approximation

We begin by assuming that a monomorphous attenuating object is placed in a spatially well-resolved reference speckle field, as shown in Fig. 1. The reference speckle field, together with the corresponding images in the presence of the sample, obeys the Fokker–Planck⁵⁵ generalization^31,54 of the geometric flow formalism⁵⁶ for speckle tracking. Now, following Pavlov et al.⁵² and Paganin and Morgan,^31,54 we have the Fokker–Planck equation for SBXI, which models coherent flow and diffusive flow for a phase object described by its phase shift, ${\varphi }_{\mathrm{ob}}(\mathbf{r})$, and effective scalar diffusion coefficient, $D_{\mathrm{eff},\hspace{0.17em}\mathrm{Phase}}(\mathbf{r};\mathrm{\Delta })$, as

$$I_R(\mathbf{r})-I_S(\mathbf{r})=\frac{\mathrm{\Delta }}{k}{\nabla }_{\perp }·[I_R(\mathbf{r}){\nabla }_{\perp }{\varphi }_{\mathrm{ob}}(\mathbf{r})]-\mathrm{\Delta }{\nabla }_{\perp }^2[D_{\mathrm{eff},\hspace{0.17em}\mathrm{Phase}}(\mathbf{r};\mathrm{\Delta })I_R(\mathbf{r})].$$ (1)

This expression relates the reference speckle image intensity, $I_R(\mathbf{r})$, obtained with no sample in the beam, to the encoded form of the speckle image, $I_S(\mathbf{r})$, which is obtained in the presence of the sample. Here, $(\mathbf{r})\equiv (x,y)$ denotes the Cartesian coordinates in planes perpendicular to the optical axis $z$, $\mathrm{\Delta }$ is the sample-to-detector distance (a plane-wave illumination is assumed), $k$ is the wavenumber of the x-rays, ${\nabla }_{\perp }=(\partial /\partial x,\partial /\partial y)$ is the transverse gradient operator in the $(x,y)$ plane, and ${\nabla }_{\perp }^2$ is the transverse Laplacian operator. Next, we consider equation (9) from Pavlov et al.,⁵⁸ which gives the variation in registered intensity of a well-resolved speckle field due to an attenuating object as

$$\frac{I_S}{I_R}\approx I_{\mathrm{ob}}(\mathbf{r})-\frac{\mathrm{\Delta }}{k}{\nabla }_{\perp }·[I_{\mathrm{ob}}(\mathbf{r}){\nabla }_{\perp }{\varphi }_{\mathrm{ob}}(\mathbf{r})].$$ (2)

Here, $I_{\mathrm{ob}}(\mathbf{r})$ describes the intensity at the exit surface of the sample, $z=0$, after the object has attenuated the incident x-ray beam of unit intensity. It should be noted that the above expression only models the coherent flow of x-rays through the sample. We now combine this with the Fokker–Planck equation for a phase object, Eq. (1), to give the Fokker–Planck equation for an attenuating object as

$$I_R(\mathbf{r})I_{\mathrm{ob}}(\mathbf{r})-I_S(\mathbf{r})=\frac{\mathrm{\Delta }}{k}{\nabla }_{\perp }·[I_R(\mathbf{r})I_{\mathrm{ob}}(\mathbf{r}){\nabla }_{\perp }{\varphi }_{\mathrm{ob}}(\mathbf{r})]-\mathrm{\Delta }{\nabla }_{\perp }^2[D_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })I_R(\mathbf{r})I_{\mathrm{ob}}(\mathbf{r})].$$ (3)

This forward-finite-difference continuity equation is formulated on the basis of local energy conservation within the system. The first term on the right side describes coherent energy flow, and the second describes the diffusive component. The coherent term models local absorption, lensing, and prism-like effects,³¹ which are also seen in the transport-of-intensity equation.⁸ The diffusion term describes the position-dependent local blurring, which is associated with the SAXS fans at the exit surface of the object. Here, we remind the reader that the position-dependent SAXS fans are approximated as rotationally symmetric.

We now assume that the effective DF signal, $D_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })$, is a slowly varying function of the transverse positions, so it approximately commutes with the transverse Laplacian operator. Moreover, we neglect the transverse spatial derivatives of $D_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })$ as they will be small compared with the retained terms. Several components arise when the second derivative of the second term in Eq. (3) is evaluated. Many of these can be neglected, using an approximation employed by Pavlov et al.:^52,58 an average of the scalar product of a rapidly varying random vector field with a more slowly changing gradient of a non-random function, can be neglected. Then,

$$\frac{I_S(\mathbf{r})}{I_R(\mathbf{r})}=I_{\mathrm{ob}}(\mathbf{r})-\frac{\mathrm{\Delta }}{k}{\nabla }_{\perp }·[I_{\mathrm{ob}}(\mathbf{r}){\nabla }_{\perp }{\varphi }_{\mathrm{ob}}(\mathbf{r})]+\frac{\mathrm{\Delta }{D}_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })I_{\mathrm{ob}}(\mathbf{r}){\nabla }_{\perp }^2{I}_R(\mathbf{r})}{I_R(\mathbf{r})}+\mathrm{\Delta }{D}_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta }){\nabla }_{\perp }^2{I}_{\mathrm{ob}}(\mathbf{r}).$$ (4)

We proceed using the projection approximation for a single-material object⁵⁹

$${\varphi }_{\mathrm{ob}}(\mathbf{r})=-k\delta t(\mathbf{r}),$$ (5)

$$I_{\mathrm{ob}}(\mathbf{r})=e^{-2k\beta t(\mathbf{r})}=e^{-\mu t(\mathbf{r})},$$ (6)

where $\mu =2k\beta$ is the linear attenuation coefficient of the single-material object and $t(\mathbf{r})$ is the projected thickness of the object along the direction of the x-rays, to give

$$\frac{I_S(\mathbf{r})}{I_R(\mathbf{r})}=(1-\frac{\gamma \mathrm{\Delta }}{2k}{\nabla }_{\perp }^2)I_{\mathrm{ob}}(\mathbf{r})+\frac{\mathrm{\Delta }{D}_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })I_{\mathrm{ob}}(\mathbf{r}){\nabla }_{\perp }^2{I}_R(\mathbf{r})}{I_R(\mathbf{r})}+\mathrm{\Delta }{D}_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta }){\nabla }_{\perp }^2{I}_{\mathrm{ob}}(\mathbf{r}).$$ (7)

This expression models the forward problem of encoding a given well-resolved reference speckle field by putting an attenuating object in the beam path, where $\gamma =\delta /\beta$.

We now turn to the inverse problem and define the additional functions as follows:

$$G_1(\mathbf{r})=(1-\frac{\gamma \mathrm{\Delta }}{2k}{\nabla }_{\perp }^2)I_{\mathrm{ob}}(\mathbf{r})+\mathrm{\Delta }{D}_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta }){\nabla }_{\perp }^2{I}_{\mathrm{ob}}(\mathbf{r}),$$ (8)

$$G_2(\mathbf{r})=\mathrm{\Delta }{D}_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })I_{\mathrm{ob}}(\mathbf{r}),$$ (9)

$$G(\mathbf{r})=(1-\frac{\gamma \mathrm{\Delta }}{2k}{\nabla }_{\perp }^2)I_{\mathrm{ob}}(\mathbf{r}).$$ (10)

The function $G(\mathbf{r})$, which describes the coherent component of the optical flow, is written in terms of the defined functions $G_1(\mathbf{r})$ and $G_2(\mathbf{r})$, that is, we apply the Laplacian operator to $G_2(\mathbf{r})$, once again assuming $D_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })$ to be slowly varying, to give

$${\nabla }_{\perp }^2{G}_2(\mathbf{r})=\mathrm{\Delta }{D}_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta }){\nabla }_{\perp }^2{I}_{\mathrm{ob}}(\mathbf{r}).$$ (11)

Hence,

$$G(\mathbf{r})=G_1(\mathbf{r})-{\nabla }_{\perp }^2{G}_2(\mathbf{r}).$$ (12)

Equation (7) is now expressed in terms of the defined functions $G_1(\mathbf{r})$ and $G_2(\mathbf{r})$ to give

$$\frac{I_S(\mathbf{r})}{I_R(\mathbf{r})}=G_1(\mathbf{r})+\frac{G_2(\mathbf{r}){\nabla }_{\perp }^2{I}_R(\mathbf{r})}{I_R(\mathbf{r})}.$$ (13)

Here, it is important to note that the functions $G_1(\mathbf{r})$ and $G_2(\mathbf{r})$ are independent of the illuminating speckle field, so they are unaffected by the transverse position of the speckle generating mask. Hence, if two independent measurements of $I_S(\mathbf{r})$ and $I_R(\mathbf{r})$ are taken, for example, using two different positions of the mask, a system of linear equations is obtained. These linear equations are solved for the attenuation term, $I_{\mathrm{ob}}(\mathbf{r})$, and the effective DF signal, $D_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })$.

Specifically, if $I_{S1,S2}(\mathbf{r})$ and $I_{R1,R2}(\mathbf{r})$ denote the sample image and well-resolved speckle image for positions 1 and 2 of the mask, respectively,

$$\{\begin{array}{l}\frac{I_{S1}(\mathbf{r})}{I_{R1}(\mathbf{r})}=G_1(\mathbf{r})+\frac{G_2(\mathbf{r}){\nabla }_{\perp }^2{I}_{R1}(\mathbf{r})}{I_{R1}(\mathbf{r})},\\ \frac{I_{S2}(\mathbf{r})}{I_{R2}(\mathbf{r})}=G_1(\mathbf{r})+\frac{G_2(\mathbf{r}){\nabla }_{\perp }^2{I}_{R2}(\mathbf{r})}{I_{R2}(\mathbf{r})}.\end{array}$$ (14)

Solving these equations gives

$$G_1(\mathbf{r})=\frac{I_{S1}(\mathbf{r})}{I_{R1}(\mathbf{r})}-\frac{G_2(\mathbf{r}){\nabla }_{\perp }^2{I}_{R2}(\mathbf{r})}{I_{R2}(\mathbf{r})},$$ (15)

$$G_2(\mathbf{r})=\frac{I_{R1}(\mathbf{r})I_{S2}(\mathbf{r})-I_{R2}(\mathbf{r})I_{S1}(\mathbf{r})}{I_{R1}(\mathbf{r}){\nabla }_{\perp }^2{I}_{R2}(\mathbf{r})-I_{R2}(\mathbf{r}){\nabla }_{\perp }^2{I}_{R1}(\mathbf{r})}.$$ (16)

Using the approach presented in Paganin et al.⁷ and the definition of $G_2(\mathbf{r})$, the effective DF signal $D_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })$ and projected thickness $t(\mathbf{r})$ of a SAXS-inducing attenuating object are given as

$$t(\mathbf{r})=\frac{-1}{\mu }{\log }_e{\mathcal{F}}^{-1}\left[\frac{\mathcal{F}\hspace{0.17em}G(\mathbf{r})}{1+\gamma \mathrm{\Delta }\lambda \pi (u^2+v^2)}\right],$$ (17)

$$D_{\mathrm{eff},\mathrm{Atten}}(\mathbf{r};\mathrm{\Delta })=\frac{G_2(\mathbf{r})}{\mathrm{\Delta }{I}_{\mathrm{ob}}(\mathbf{r})}.$$ (18)

In Eq. (17), $\mathcal{F}$ denotes Fourier transformation with respect to $x$ and $y$, for which the corresponding Fourier-space variables are $u$ and $v$, respectively, and $\lambda$ is the x-ray wavelength. It should be highlighted that the expression for the effective DF of an attenuating object, namely Eq. (18), is equivalent to equation (7) from Pavlov et al.,⁵² for the special case of a phase object.

2.2. Numerical Stabilization of Recovered DF Images

DF images are intrinsically noisy,^31,32 in the sense that the diffuse scattering that underpins them is due to extremely small unresolved spatially random features within the sample. This leads to finely fluctuating unresolved speckle variations over individual pixels. By spatially averaging these high-frequency variations across pixels, the DF signal is obtained. Gureyev et al.³² developed a model based on the assumption of a single-material sample for which the projected linear attenuation coefficient, ${\mu }_p(\mathbf{r})$, is a composite of a rapidly varying component ${\mu }_{\mathrm{fast},p}(\mathit{r})$ and a slowly varying component ${\mu }_{\mathrm{slow},p}(\mathit{r})$

$${\mu }_p(\mathbf{r})={\mu }_{\mathrm{fast},p}(\mathbf{r})+{\mu }_{\mathrm{slow},p}(\mathbf{r}).$$ (19)

Here, ${\mu }_{\mathrm{slow},p}(\mathit{r})$ results from density variations over length scales larger than the pixel size, which can be resolved in a typical phase-contrast image. Conversely, ${\mu }_{\mathrm{fast},p}(\mathit{r})$ is associated with the unresolved microstructure in the sample, which fluctuates rapidly throughout the sample and hence across one detector pixel. The spatially averaged fast-varying component of the projected linear attenuation coefficient, $\overline{{\mu }_{\mathrm{fast},\mathrm{p}}(\mathbf{r})}$, is connected to the effective DF signal by³²

$$D_{\mathrm{eff}}(\mathbf{r};\mathrm{\Delta })=\frac{\delta }{\beta k}\hspace{0.17em}\overline{|{\mu }_{\mathrm{fast},p}(\mathbf{r}){|}^2}.$$ (20)

Here, the overline denotes spatial averaging over a single detector pixel. Since the above expression is obtained via a spatial average of an intrinsically rapidly varying and often spatially random quantity, the effective DF signal is typically inherently noisy.

This “intrinsic noise” is closely related to the evident numerical division-by-zero instability in Eq. (18). To deal with this instability, we propose two alternative approaches to numerically stabilize this expression. Each is considered in turn below.

2.2.1. Tikhonov regularization

This is a well-known mathematical technique^60–62 and can easily be implemented by making the replacement for any numerator and denominator $A(\mathbf{r})$ and $B(\mathbf{r})$ of

$$\frac{A(\mathbf{r})}{B(\mathbf{r})}\to \frac{A(\mathbf{r})B(\mathbf{r})}{[B(\mathbf{r}){]}^2+ϵ}.$$ (21)

Here, $ϵ$ is a positive regularization parameter.

2.2.2. Weighted determinants

This method utilizes the determinant of the system of linear equations, Eq. (14). Moreover, the determinant is used as a weighting factor for the appropriate pairs of mask positions, $a$ and $b$. The proposed method can be thought of as a type of the “weighted mean”⁶³ approach often used in the practice of statistics. The determinant of the system of linear equations is

$${\mathrm{Det}}_{a,b}(\mathbf{r})=\frac{{\nabla }_{\perp }^2{I}_{Rb}(\mathbf{r})}{I_{Rb}(\mathbf{r})}-\frac{{\nabla }_{\perp }^2{I}_{Ra}(\mathbf{r})}{I_{Ra}(\mathbf{r})}.$$ (22)

The determinant of a system of linear equations characterizes the stability of the solution. A system of linear equations has a unique and stable solution if the determinant is nonzero. Therefore, as the determinant approaches zero, the solution becomes unstable. The determinant of Eq. (14) is an array equal to the size of the input projection images, and its elements will give a pixelwise measure of how much to “trust” the corresponding element in the DF image. Then, given $N$ different mask positions, we calculate $[N(N-1)/2]$ effective DF projection images for each distinct pair of mask positions. The determinant of the appropriate system of linear equations is then calculated using Eq. (22). The effective DF projection images can subsequently be weighted by their appropriate squared determinant, summed, and normalized to give what we term the “weighted determinant” effective DF projection image, $\mathrm{WD}[D_{\mathrm{eff}}(\mathbf{r};\mathrm{\Delta })]$. To demonstrate this approach, we present the weighted determinant expression for three transverse positions of the mask, $N=3$, however, this can be easily extended to a larger number of mask positions:

$$\mathrm{WD}[D_{\mathrm{eff}}(\mathbf{r};\mathrm{\Delta })]=\frac{|{\mathrm{Det}}_{\mathrm{1,2}}(\mathbf{r}){|}^2{D}_{\mathrm{eff}}^{\mathrm{1,2}}(\mathbf{r})+|{\mathrm{Det}}_{\mathrm{2,3}}(\mathbf{r}){|}^2{D}_{\mathrm{eff}}^{\mathrm{2,3}}(\mathbf{r})+|{\mathrm{Det}}_{\mathrm{1,3}}(\mathbf{r}){|}^2{D}_{\mathrm{eff}}^{\mathrm{1,3}}(\mathbf{r})}{|{\mathrm{Det}}_{\mathrm{1,2}}(\mathbf{r}){|}^2+|{\mathrm{Det}}_{\mathrm{2,3}}(\mathbf{r}){|}^2+|{\mathrm{Det}}_{\mathrm{1,3}}(\mathbf{r}){|}^2}.$$ (23)

3. Experimental Data/Procedure

The experimental x-ray data analyzed throughout this work were collected at the Imaging and Medical Beamline (IMBL) at the Australian Synchrotron in Melbourne. This set of SBXI data was collected in hutch 3B, which is often used for large-sample x-ray imaging and computed tomography (CT), due to its large x-ray beam size. We used a custom-designed x-ray imaging detector (similar to a Ruby detector⁶⁴) using a pco.edge camera and a tandem lens system giving an effective pixel size of $12.3\mu \mathrm{m}$. The x-ray capture element was a $\text{25\hspace{0.17em}\hspace{0.17em}}\mu \mathrm{m}$ thick Gadox (Gd₂O₂S: Tb2+; P43) phosphor. The detector’s pixelation is $2560\times 2160$. The distance between the source and beam entrance window for hutch 3B, smd, was 135.8 m, the distance between the mask and sample, msd, was 1.019 m, and the propagation distance between the sample and detector, $\mathrm{sdd}=\mathrm{\Delta }$, was 2.000 m. The speckle generating mask had a typical grain size of 30 to $45\mu \mathrm{m}$. The position of the mask was transversely shifted in the direction perpendicular to the beam to acquire a total of six different sets of raw intensity projection data.

The sample investigated throughout was a wood sample, as shown in Fig. 1. This sample has three different wood types, (i)–(iii), mounted onto a metal cylindrical disk. The exact wood type of these samples was unknown; however, key characteristics can be observed from Fig. 1.

SBXI was carried out on the wood sample with a monochromatic x-ray beam of energy 30 keV. Raw intensity projection data, namely three data sets, were collected: sample projections, mask reference projections, and dark-current projections. Sample projections included intensity variations arising from phase and attenuation differences introduced by both the sample and specified mask, whereas the reference speckle projections showed just the image of the mask. The dark-current projection images were collected in the absence of x-rays used to correct for the detector. The acquired projection images were then processed within a Python3 script to calculate the attenuation, projected thickness, and DF images.

The projected thickness, and hence attenuation, of the wood sample was calculated using equation (18) from Pavlov et al.,⁵⁸ with $\gamma ={\delta }_{\mathrm{wood}}/{\beta }_{\mathrm{wood}}=2990$, assuming a generic composition of wood. The phase object approximation for the effective DF image was then calculated using a Tikhonov-regularized weighted determinant variant of equation (7), that is, the two methods in conjunction, from Pavlov et al.,⁵² or equivalently

$$D_{\mathrm{eff},\mathrm{Phase}}(\mathbf{r};\mathrm{\Delta })=\frac{G_2(\mathbf{r})}{\mathrm{\Delta }},$$ (24)

as derived in this paper. From there, the attenuating object approximation of the DF image was calculated using, once again, a Tikhonov-regularized weighted determinant form of Eq. (18). As we had SBXI data for six different well-resolved reference speckle fields, $N=6$ in Eq. (23), these were all utilized to calculate the effective DF. All of the speckle fields were included to maximize the DF signal quality and robustness to noise, following Pavlov et al.⁵²

4. Discussion/Analysis

We experimentally implemented the phase object approximation to MIST⁵² and then extended this to consider a monomorphous attenuating object, by utilizing the already-presented multimodal x-ray Fokker–Planck-based speckle tracking approach.³¹ Figures 2(b) and 2(c) demonstrate how the proposed extension of MIST⁵² to consider an attenuating object, rather than a phase object, more accurately models objects that attenuate the x-ray beam significantly. An example of this is the feature at the bottom center of Figs. 2(b) and 2(c), namely Blu Tack, which has strong attenuating and small-angle scattering characteristics. In the phase object approximation [see Fig. 2(b)], the effective DF is significantly suppressed in inner regions of the wood samples due to strong x-ray attenuation. However, this effective DF is corrected in the attenuating object approximation [see Fig. 2(c)] as the object attenuation term, $I_{\mathrm{ob}}(\mathbf{r})$, was considered.

Fig. 2.

Top row: Projection images, in the direction of the optical axis, $z$, of (a) projected thickness, (b) effective DF signal generated using a phase object approximation, and (c) attenuating object approximation of the wood sample. Bottom row: CT reconstructions of (d) attenuation coefficient, $\beta ({\mathbf{r}}^{\prime })$, (e) phase object approximation for the DF, and (f) attenuating object approximation for the DF. Wood labeling, (i)–(iii), refers to that in Fig. 1. All of the DF images, (b), (c), (e), and (f), were postprocessed with a five pixel standard deviation Gaussian filter.

The effective DF projection images were numerically stabilized using the “weighted determinant” approach and Tikhonov regularization, as given by Eqs. (21) and (23). We utilized the entirety of the data set available, that is, six transverse mask positions, $N=6$, to maximize the signal-to-noise ratio in the extracted DF signal. However, fewer mask positions were also investigated using the same approach, and the results agreed with that of Pavlov et al.,^52,53 demonstrating that two mask positions are sufficient for extracting a measurable DF signal. The quality of the reconstructed DF signal was clearly improved using the Tikhonov-regularized weighted determinant method. This optimization of effective DF projection images [Figs. 2(b) and 2(c)] then allowed for standard CT algorithms to be used to reconstruct axial slices [Figs. 2(e) and 2(f)]. Here, XTRACT⁶⁵ software was used to implement a filtered back projection CT reconstruction algorithm, with a Hamming filter being used for noise suppression.⁶⁶ The weighted determinant variant of numerical stabilization was less computationally expensive, giving a reduction of a factor of 100 in computation time, compared with other trialed techniques, for example, having a pixelwise matrix inversion to obtain the solution in a least-squares⁶⁷ sense.

Figures 2 and 3 demonstrate the differing structural information obtained in bright field, standard PCI and DF imaging, as well as how the presented monomorphous attenuating object description compares with the previously published⁵² phase object approach. The projected thickness, Fig. 2(a), displays the fiber-like features in the wood: these run horizontally in sample (iii) and vertically in sample (i). Such features are also resolvable in the DF images, Figs. 2(b) and 2(c), alongside further variations in structural characteristics. It is interesting to note that, although sample (iii) has the weakest contrast of the three samples in the attenuation coefficient image in Fig. 2(d), it has the strongest contrast of the three samples in the DF images shown in Figs. 2(e) and 2(f). The power of DF imaging is accentuated in Fig. 2, particularly the complementary information for samples (ii) and (iii). Moreover, although the projected thickness is equal for these two samples, sample (iii) has a factor of 2 greater effective DF signal than sample (ii). These characteristics are also shown in the CT reconstructions. Indeed, there is further structural information about the wood sample that is revealed in the CT reconstructions and not seen in the projection images. For example, as previously mentioned, in the axial slice shown in Fig. 2, sample (ii) has the largest effective DF signal, yet the lowest attenuation coefficient, $\beta ({\mathbf{r}}^{\prime })$. An unseen structural feature also appears in the DF-CT reconstruction of wood sample (i) that is not in the PCI-CT, as marked in red.

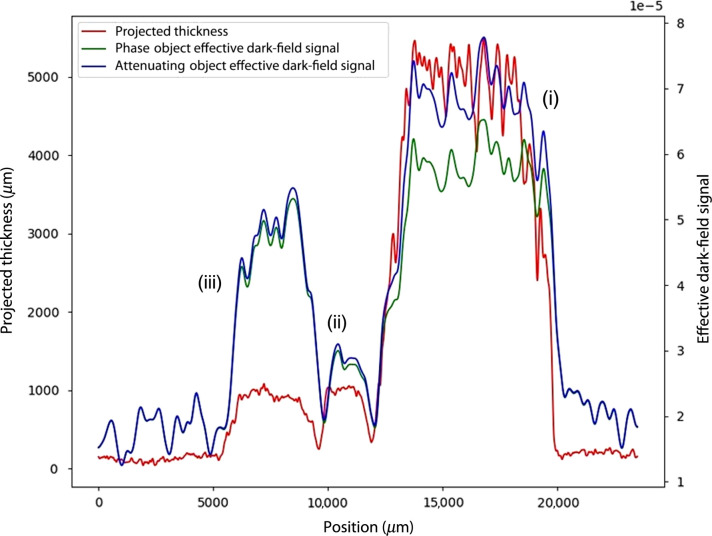
Fig. 3.

Line profiles taken across each of the wood samples in the projection images of (red) projected thickness, (green) phase object approximation DF image, and (blue) attenuating object approximation DF image. Wood labeling, (i)–(iii), refers to that in Fig. 1.

Equation (18) was used to calculate the effective DF signal, shown in Fig. 2, which was derived under the assumption that the SAXS fans emanating from the exit surface of the sample are rotationally symmetric. However, the sample studied within (wood) typically has anisotropic scattering structures, and thus one might think that the key assumption (i.e., rotational symmetry of the position-dependent SAXS fans that underpin the DF signal) is violated. However, as shown in Figs. 2 and 3, the isotropic attenuating object approximation, which improves upon the isotropic phase object approximation, extracts a first approximation (i.e., rotationally symmetric) of the DF signal that well represents the wood sample. Stated differently, the locally elliptical position-dependent SAXS fans may be reasonably approximated as rotationally symmetric, to give lowest-order position-dependent information regarding this scattering channel. This suggests that the formalism presented in our paper is capable of providing directionally averaged DF information, for objects that may violate the underlying assumptions of rotationally symmetric position-dependent SAXS fans.

Equation (18) is also, in theory, restricted to monomorphous objects. This arises from the definition of $\gamma$ used for phase-contrast signal extraction, which is used to calculate $I_{\mathrm{ob}}(\mathbf{r})$, which is then required to calculate the DF of an attenuating object. This single-material restriction can be extended to a two-component sample by taking the difference between the real and imaginary components of refractive index for each material.⁶⁸ This representation of $\gamma$ results in correctly phase-retrieved interfaces between the two materials. In multimaterial samples, if $\gamma$ for specific interfaces between two materials deviates too far from the inputted value, then the phase-contrast signal will be either over- or under-compensated.⁶⁹ However, Gureyev et al.⁷⁰ report that an incorrect choice of $\gamma$ does not affect the extracted $\beta$ far away from the interface. Hence, this underlying monomorphous restriction would only be detrimental to the reconstructed DF if the sample had many composite materials that had greatly differing attenuation and refraction properties. In such cases, there would be a large range of $\gamma$ values for specific interfaces within the sample; hence, edge effects would exist in both the PCI and DF reconstructions. The described case is unlikely in applications, and this is further supported by wide adoption of Paganin’s single-material TIE-Hom phase retrieval algorithm⁷ in various disciplines. We refer the reader to the introduction in Paganin et al.,⁷¹ in which the utility domain of the single-material approach is discussed in-depth. Many objects can be viewed as being locally composed of a single material, in three dimensions, even though such materials may not contain a single material in projections. It is possible to apply a fast localized 3D reconstruction for such isolated single-material regions.⁷² Also, in biomedical applications, the single-material assumption is still appropriate at high x-ray energies at which biomedical samples, such as soft tissues, can be considered to be a single material,⁷³ that is, a cloud of electrons.

DF imaging provides complementary information to both conventional attenuation-based imaging, which is currently employed in clinics, and PCI. SBXI is experimentally simple and requires fewer sample exposures than alternative x-ray imaging techniques that extract multimodal signals. We have demonstrated that an intrinsic speckle tracking approach to SBXI allows for both projection and tomographic reconstruction of phase contrast and DF signals for a monomorphous attenuating object, which when considered in parallel provide complementary information. In a clinical/biomedical setting, the additional information provided by DF tomography could prove to be highly useful in diagnostic studies. A recent publication, Willer et al.,⁷⁴ demonstrates x-ray DF imaging in a clinical application, namely chest imaging. Willer et al.⁷⁴ used a grating interferometry x-ray imaging technique, which requires a precisely aligned experimental setup but also enables the use of large pixels for large-area imaging. SBXI utilizes a less demanding setup, but it must directly resolve changes to the speckle pattern; hence it is best suited for smaller samples.

5. Conclusion

We have developed a monomorphous attenuating object variant of the phase object MIST x-ray speckle tracking method proposed in 2020 by Pavlov et al.⁵² Our method has been demonstrated on experimental data to achieve speckle-based x-ray DF tomography. A numerical stabilization approach, namely the “weighted determinant” method, together with Tikhonov regularization, was used to stabilize the intrinsic noise of DF images. These reconstructions are based on six sets of images acquired at different transverse positions of the speckle mask. However, reconstructions based on two images, as reported also by Pavlov et al.,⁵² give comparable reconstructions, albeit with higher noise because of the smaller number of measurements that are required.

Biographies

Samantha J. Alloo is a Doctor of Philosophy (PhD) student in medical physics at the University of Canterbury, New Zealand, under the supervision of K. M. Pavlov, D. M. Paganin, and K. S. Morgan. Her research primarily focuses on developing theoretical approaches to speckle-based x-ray imaging, specifically dark-field and phase-contrast tomography. She also has research experience in alternative phase-contrast techniques, such as propagation-based phase-contrast x-ray imaging.

David M. Paganin is an adjunct researcher within the School of Physics and Astronomy, Monash University, Australia. He is an optical physicist whose research focuses on phase-retrieval inverse problems, ghost imaging and coherent optics using x-rays, electrons, neutrons and visible light. Together with Daniele Pelliccia, he is currently authoring a book on “The Physics of Synchrotron Light.”

Kaye S. Morgan is an Australian Research Council Future Fellow within the School of Physics and Astronomy at Monash University. Since completing her PhD in 2011, she has been continuously supported by fellowships including a DECRA, a Veski VPRF and a Hans Fischer Fellowship at the Technical University of Munich. Her research focuses on developing new methods of x-ray phase and dark-field imaging and applying these to enable new directions of biomedical research.

Konstantin M. Pavlov is a senior lecturer at the School of Physical and Chemical Sciences (University of Canterbury, New Zealand). He also holds Adjunct positions at Monash University (Australia) and University of New England (Australia). He has developed new theoretical approaches in diffraction tomography, deterministic coherent diffractive imaging, phase-contrast imaging/tomography and extended the statistical dynamical x-ray diffraction theory to multilayer structures and nanostructures. These approaches were successfully used at numerous laboratory and synchrotron radiation sources.

Biographies of the other authors are not available.

Disclosures

All authors of the presented manuscript report no relevant conflicts of interest or financial interests with respect to this work.