Abstract
Nuclear pore complexes (NPCs) embedded within the nuclear envelope (NE) mediate rapid, selective, and bidirectional traffic between the cytoplasm and the nucleoplasm. Deciphering the mechanism and dynamics of this process is challenged by the need for high spatial and temporal precision. We report here a multi-color imaging approach that enables direct 3D visualization of cargo transport trajectories relative to a super-resolved octagonal double-ring structure of the NPC scaffold. The success of this approach is enabled by the high positional stability of NPCs within permeabilized cells, as verified by a combined experimental and simulation analysis. Hourglass-shaped translocation conduits for two cargo complexes representing different nuclear transport receptor (NTR) pathways indicates rapid migration through the permeability barrier on or near the NPC scaffold. Binding sites for cargo complexes extend over 100 nm from the pore openings, consistent with a wide distribution of the FG-polypeptides that bind NTRs.
Keywords: nuclear pore complex, 3D super-resolution microscopy, astigmatism imaging, nucleocytoplasmic transport
INTRODUCTION
The NPCs perforating the nuclear envelope (NE) enable the nucleocytoplasmic exchange of ~1000 molecules per NPC per second1 with typical protein transit times of ~10 ms.2–4 How the permeability barrier is able to selectively accommodate cargos with dramatically different physical characteristics (e.g., from small proteins up to pre-ribosomal subunits) moving in both directions is a heavily studied, but still unsolved, problem.5,6 An attractive notion is that distinct high probability paths through the permeability barrier exist for the different NTR-dependent pathways, and that these could be segregated for import and export.7–9 While evidence exists for some partial separation of transport paths, overlap also exists.10,11 Binding assays, sequence analysis and structure modeling predict that NTR binding motifs are asymmetrically distributed within the permeability barrier, consistent with the notion of distinct translocation conduits.12–15 Whereas electron microscopy reveals high-resolution snapshots of translocation events and simultaneously visualizes the translocation pore,10,16 it lacks the capability to visualize rapid dynamics in three dimensions (3D). 3D models of transport pathways have been deduced from two-dimensional (2D) light microscopy videos.11,17 However, the direct 3D tracking of cargo translocation with high time resolution in the context of well-resolved NPCs necessary to accurately decipher the geometrical and physical properties of translocation conduits has not been reported.
The human NPC scaffold has an outer diameter of ~110 nm, and the hourglass-shaped central pore has a minimum constriction of ~50 nm.18,19 Nonetheless, the NPC is largely impermeable to molecules larger than ~4-5 nm that are not bound to NTRs.20,21 The permeability barrier is generated by a network of ~200-250 largely intrinsically disordered polypeptide chains that occupy the central pore and decorate its cytoplasmic and nucleoplasmic openings.14,22 These disordered polypeptides contain, in aggregate, 3,000-4,000 phenylalanine-glycine (FG) repeats to which NTRs transiently bind as they carry cargos through NPCs.14,23–25 Both peripheral and central translocations pathways through this FG-network have been identified,11,26 though the rules by which cargo complexes partition into distinct locales and the extent to which pathways overlap remains unsettled. Our goal was to develop an approach that would allow us to characterize the real-time dynamics of cargo translocation in the context of a well-resolved NPC scaffold. In most super-resolution imaging studies on NPC scaffold structures reported to date, NEs were stabilized via fixation (e.g., see 27–30), thus eliminating the possibility of exploring the dynamics of key aspects of the translocation process. We demonstrate here using unfixed NEs that NPCs are sufficiently positionally stable over ~10 min in permeabilized cells such that 3D transport trajectories can be aligned with a highly-resolved NPC scaffold with 8-fold rotational symmetry. We thus report a substantially improved approach for investigating the dynamics of nucleocytoplasmic transport.
RESULTS
Overview of the Experimental Design
While numerous 3D light microscopy methods have been developed over the last few decades, single molecule astigmatism imaging31 provides high temporal resolution from a single image, high spatial precision in x, y, and z, and its useful z-range matches very well to that necessary to monitor cargo trafficking through NPCs.32,33 Though the simplest approach to achieve astigmatism imaging is via a cylindrical lens,31 we used an adaptive optics (AO) system (Fig. 1a), which enabled optimization of the astigmatism for the needs of the experiment as well as correction of the focal mismatch arising from chromatic aberrations in multi-color applications. Fluorescence was recovered from NPCs within the largely flat bottom NE of the nuclei of permeabilized U-2 OS cells (Fig. 1b) using a narrow-field epifluorescence scheme.2 NPCs tagged on NUP96 with mEGFP were first decorated with dye-labeled anti-GFP nanobodies, and then transport mix was added to begin the import experiments. The NPC scaffold and cargo complexes were imaged separately but sequentially with no reagent changes (Fig. 1c). Individual fluorescent spots were localized with z- and photon count-dependent localization precisions in each of the three dimensions (Figs. 1d–g).
Figure 1. 3D Super-resolution Microscope and Experimental Workflow.
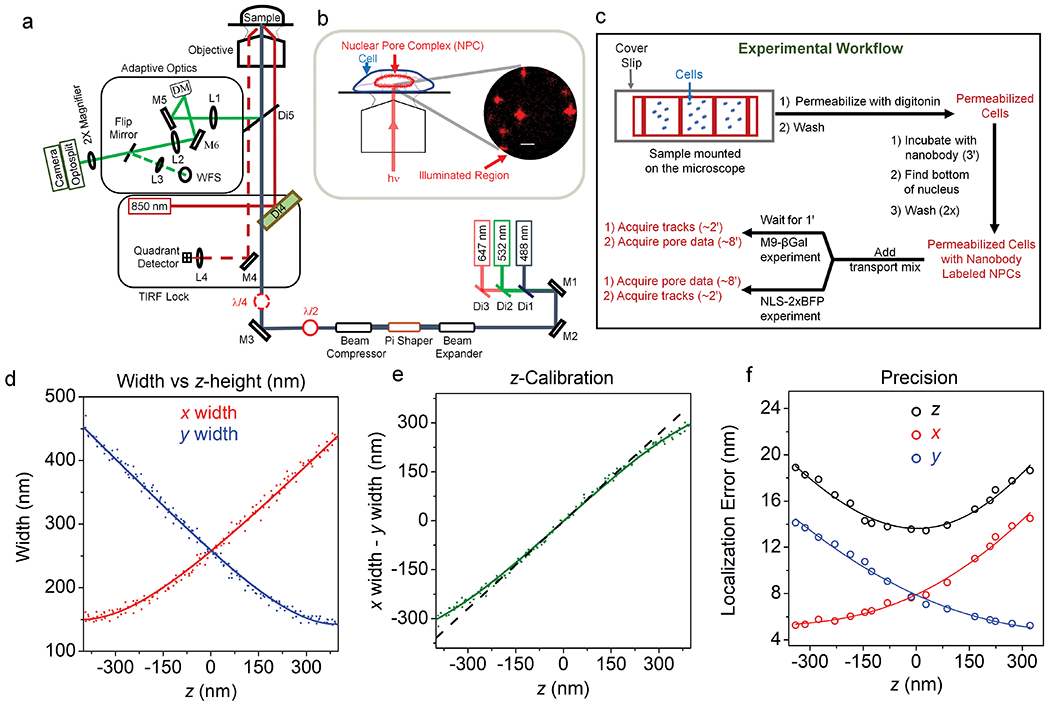
a, The 3D microscope setup used to obtain super-resolved positional information for single dyes on the NPC scaffold and for individual diffusing cargo complexes. Fluorescence was collected by an EMCCD camera after passing through a home-built adaptive optics (AO) system. The deformable mirror (DM) was used to first correct optical aberrations via a feedback algorithm with the wavefront sensor (WFS), and then introduce the astigmatism needed for 3D imaging. A self-configured TIRF-lock system ensured a z-stability of < 3 nm. Lenses (L), mirrors (M), and dichroic mirrors (Di) are indicated. b, Imaging plane. The bottom surface of nuclei contained NPCs within a nearly flat NE that was perpendicular to the narrow-field illumination beam. The image shows the fluorescence from single HMSiR dye molecules on NPCs (see Fig. 2) using astigmatism imaging, in which z-information is retrieved from the elongation of the spot in x or y. Bar = 1 μm. c, Experimental workflow. The total time for sample preparation and data acquisition was ~20 min after cell permeabilization. Data collection at room temperature required ~10 min via Approach 1 (cargo complexes tracked first, NPCs localized second) or Approach 2 (reverse order). d-f, Microscope z-calibration and precision using a 60 nm root mean square (rms) astigmatism introduced with the DM. The z-dependence of x- and y-spot widths (d) was obtained from z-stack images (100 ms/frame, 41 steps, step size = 25 nm) of five different 0.1 μm beads embedded in 2% agarose (λex = 647 nm; ~2500-3500 photons/spot). The difference between the x- and y-widths was approximately linearly dependent on z (e, dashed black line). The fits in d,e were described earlier,31 although the data obtained for NPCs used the improved algorithm implemented by ThunderStorm.66 The localization errors (precisions) were defined as the standard deviation of the position in x, y, and z over 100 images of 0.1 μm beads embedded in 2% agarose (f). Precision values obtained at various excitation intensities (~1500-4500 photons/spot; 50 ms/frame), and z positions were scaled to the 3000 photon level by multiplication by (Np/3000)1/2, where Np = the number of photons, and were fit with Eqs. 5, 6, and 7b. These data illustrate that the three spatial measurement precisions for each fluorescent spot depends on the photons collected and the position in z. See Online Methods for additional details. Source numerical data are provided in source data.
A Highly-Resolved NPC Scaffold in 3D
An averaged 8-fold rotationally symmetric NPC scaffold was obtained as described in Fig. 2. Nanobodies34 tagged with the spontaneous blinking dye HMSiR35 were bound to the GFP domains on chromosomally expressed NUP96-mEGFP (Figs. 2a–d, Extended Data Fig. 1a, Supplementary Video 1).28 Fluorescence spots arising from HMSiR molecules were curated to those with N ≥ 3000 photons, yielding initial super-resolved images of NPCs (Fig. 2e). Clusters arising from at least 10 spots were fit to a double-circle distribution (Figs. 2f,g). Clusters surviving the double-circle fitting routine – i.e., with centroids of z = 0±200 nm, diameters of 80-135 nm, and ring-spacing of 40-65 nm – were considered well-localized NPCs (Fig. 2h, Extended Data Fig. 2). The photon- and z-selection applied yielded average single particle precisions of ~7 nm in x and y and ~12 nm in z. These precision values are the weighted statistical averages considering the photon and z-distributions for the final curated localizations (calculated with Supplementary Data 1_Software File 1 using the data in Fig. 1f over the volume and photon levels analyzed). Initial cluster alignments of well-localized NPCs, assuming no tilt from the z axis, yielded a clear double-ring structure (Figs. 2i,j), consistent with the known positions of the 32 molecules of NUP96 within the NPC scaffold (Fig. 2a). The angles of individual localizations relative to the cluster centroid were estimated and binned (0-45°), assuming an 8-fold rotationally symmetric distribution. The estimated phase angle was then used to realign the individual pore clusters, resulting in an easily recognizable 8-fold symmetric structure in both rings (Figs. 2k,l and Supplementary Video 2) consistent with structural studies.18,19 Despite the poor angle fits due to the low number of points distributed in 5° bins, this approach worked surprisingly well (Extended Data Fig. 3). The ring radius of 52.4 nm (Fig. 2m) and ring spacing of 51.2 nm (Fig. 2n) agree well with the known positions of NUP96 (Fig. 2a), especially considering the 6-7 nm distance between the dye and the NUP96 attachment point (Fig. 2b).
Figure 2. Localization of the NPC Scaffold.
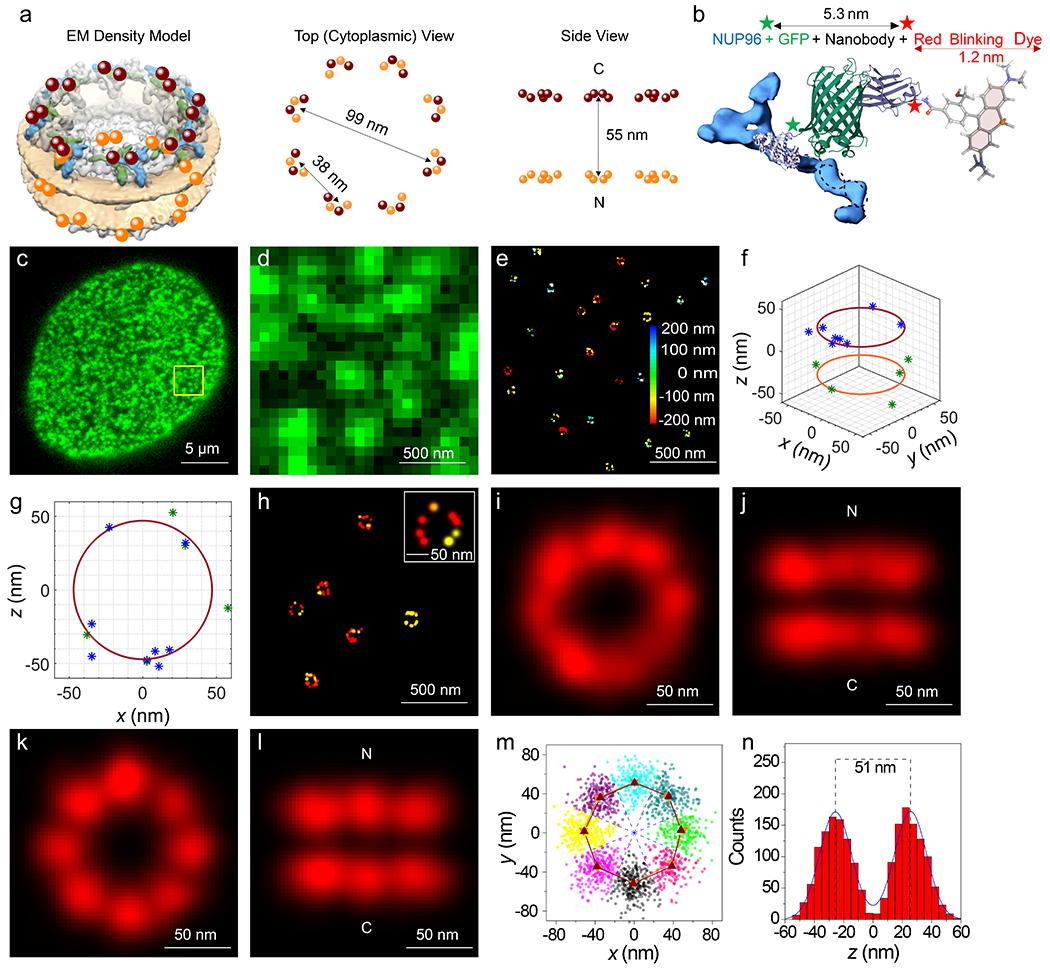
a, Schematic of the NUP96 distribution within NPCs. The maroon and orange dots (cytoplasmic (C) and nucleoplasmic (N) rings, respectively) indicate the 3D position of the C-termini of the 32 NUP96 molecules within the EM density map (EMD-3103).67 b, The HMSiR blinking dye labeling approach of the mEGFP domain on NUP96 (not to scale). c,d, Wide-field fluorescence emission of mEGFP from the bottom NE of a permeabilized U-2 OS-CRISPR-NUP96-mEGFP28 cell (λex = 488 nm). Spots (green) are individual NPCs. Similar results were observed for N = 100 cells. (d) represents an expanded view of the square region identified in (c). e, First pass images of individual super-resolved NPCs. These dye clusters remained after applying photon and z filters. The color bar represents z-height. The total acquisition time per nucleus was ~8 min (50 ms/frame, λex = 647 nm, 3 kW/cm2). f,g, Representative double-circle fit for determining NPC centroids. h, 3D-super-resolution images of individual well-localized NPCs. These clusters survived the double-circle fitting routine, and were selected for alignment into the NPC scaffold. See Extended Data Fig. 2 for selection workflow. i,j, Composite NPC images from aligned but unrotated clusters (1872 localizations obtained from 142 clusters from 10 nuclei; each nucleus was an independent biological replicate). k,l, Composite NPC images from rotated clusters revealing the 8-fold rotational symmetry. These images were constructed from a single dataset. Images from a duplicate dataset are shown in Fig. 5a,b and a quantitative comparison is provided in Table 1. See Supplementary Video 2 for rotated views. m, Localizations from all NPCs separated into 8 segments for each ring based on an angular global fit (Extended Data Fig. 3). The angular centroid within each segment was calculated from a sinusoidal fit to the angle distribution. The difference between the angular centroids of the two rings for the 8 segments is 0.9±3.8°. n, The distribution of z values from all NPCs. The symmetric double Gaussian fit (centered at 0) indicates that the distance between the two rings is 51.2 nm. Simulated distributions and errors are modeled in Fig. 3. Source numerical data are provided in source data.
Positional Stability of the NPCs
The total time over which localizations for individual NPCs was collected was ~8 min, providing ample opportunity for the NPCs to move within the NE or for the NE itself to undergo large-scale fluctuations. To better understand the errors in the scaffold structures generated (Figs. 2k,l), we simulated distributions of stochastically-distributed NUP96 localizations based on potential sources of error and experimentally-determined constraints. In addition to the experimentally-determined xyz localization errors (σx, σy, and σz), potentially significant error sources are the cluster centroid localization errors (σcx, σcy, and σcz), the axial tilt of the NPC (σat), and the NE/NPC positional (cartesian) instability (collectively termed the ‘jiggle’), i.e., the axial fluctuations in NE/NPC position (σNPCz), and the lateral NPC movements within the NE (σNPCx and σNPCy). Physical instability errors (e.g., chamber movements) are assumed to be subsumed into the localization errors. A comparison of z and radial distribution widths obtained for experimental and simulated data revealed that the axial tilt is ≤ ~10°, the jiggles in x and y are < ~8-9 nm, and the axial NE/NPC fluctuations are < ~6 nm (Fig. 3). The positional immobility of NPCs within the NE is well-known, enabled by the nuclear lamin structure,36 and essential for the success of particle tracking measurements on transiting cargos.2,37 The comparison of experimental and simulated data reported here provides quantitative limits on NPC movements within permeabilized cells. Since the NE is more mobile in live cells,38 a significant increase in the stability of the system must have ensued as a result of the permeabilization procedure and the subsequent wash steps. These procedures removed the bulk of the soluble material, including the energy and regulatory systems responsible for controlling cytoskeletal polymerization and depolymerization. Since the nuclei were not directly attached to the glass coverslip, stabilized cytoskeletal filaments likely contributed to providing structural stability to the NE.
Figure 3. Effect of Tilt and Jiggle on Resolving the NPC Scaffold.
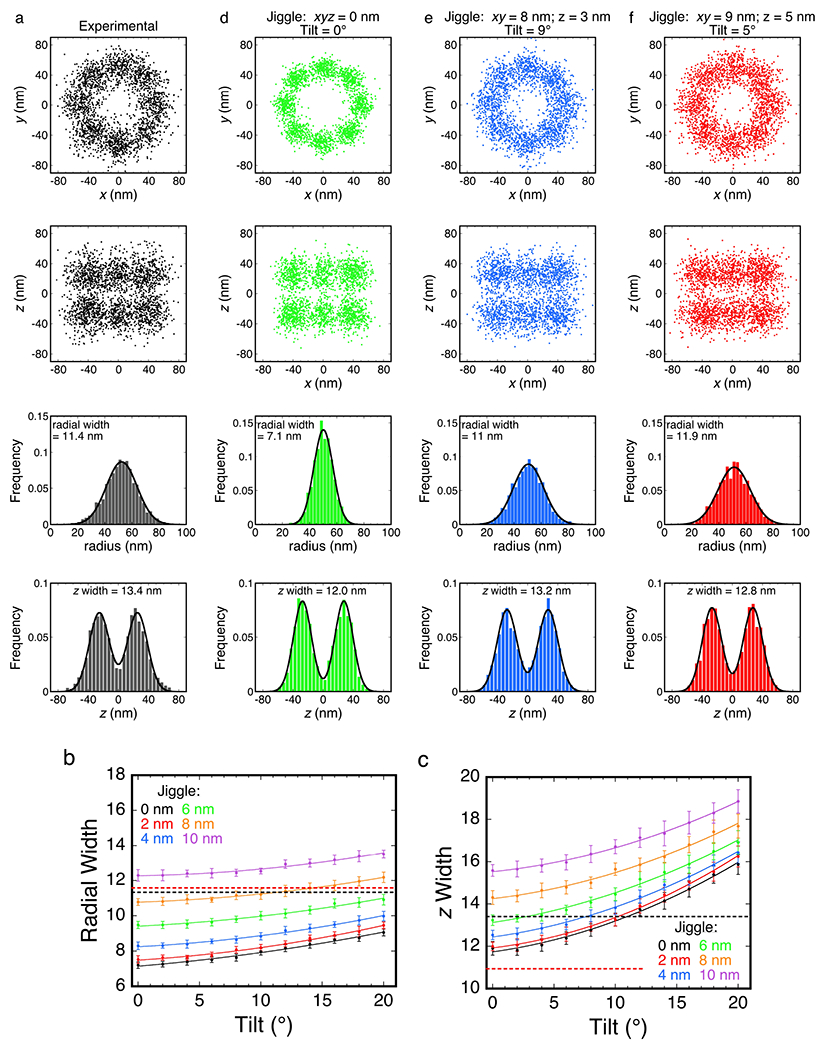
a, An expanded version of the data set used to construct Figs. 2k,l. For comparison with the simulations, these data underwent less selection before rotationally-corrected alignment (corresponding to the clusters in Extended Data Fig. 3c without filtering the diameter and the distance between the rings, but with a z-centroid = 0±200 nm), and thus, there are significantly more localizations (N = 2362 localizations from 181 clusters; the distribution of localizations/cluster is given in Extended Data Fig. 2e). The radial width (σrw) and z width (σzw) are key parameters for comparing distributions, and reflect standard deviations of Gaussian and double Gaussian fits, respectively. b,c, Effect of tilt and jiggle. Average (±SD) radial (b) and z (c) widths from 20 independent simulations. The horizontal black dashed lines indicate the experimental radial and z widths from (a), and the red lines indicate these values for the localization data used to make Figs. 2k,l. The data in (c) indicate that the tilt is ≤ ~10°, and the total jiggle in z is < ~6 nm. While the x, y, and z jiggles were identical in (b,c), they largely independently influence radial- or z-width. With this in mind, the jiggles in x and y are 8-9 nm (b). d,e,f, Simulated distributions based on various jiggle and tilt values. As an initial reference, a simulated distribution with no tilt or jiggle (d) reveals the data scatter expected based on the current localization precision. Considering the results in (b,c), a minimal non-zero z jiggle of 3 nm was asssumed, which suggested a maximum reasonable tilt of 9° and x and y jiggles of 8 nm (e). Alternatively, considering that the z jiggle is potentially larger, a more moderate tilt (5°) suggests a z jiggle of 5 nm and x and y jiggles of 9 nm (f). Both (e) and (f) reasonably reproduced the experimental data. The simulations reported here do not include centroid localization errors – these would be identical in effect to the jiggles. By applying the two-circle fit algorithm to simulated data, the centroid localization errors were estimated as 4-5 nm in x, y, and z. See Online Methods for additional details. Source numerical data are provided in source data.
Cargo Complex Tracking Strategies
Due to the high positional stability of NPCs, we used a two-color approach to combine the well-localized NPCs with 3D particle trajectories of cargo complexes undergoing transport. As indicated in Fig. 1c, the NPC scaffold data were either collected before or after the cargo transport data. In both cases, the only changes to switch between imaging modes were software-driven changes in illumination wavelength and an AO chromatic correction (see Online Methods). These two approaches had distinct advantages and disadvantages. When cargo transport was imaged first (Approach 1), nuclear background fluorescence was low since the transport reaction was recently initiated. However, the camera integration time for the cargo trajectories was minimally ~3 ms, as the higher 532 nm excitation intensities required for faster image acquisition resulted in unacceptable photobleaching of the HMSiR dye, which was visualized later. In contrast, when the NPC scaffold data were obtained first (Approach 2), acquisition speed during cargo imaging was limited by the photon collection efficiency of the system. However, a significant background fluorescence arose from inside the nucleus from already imported molecules, requiring photobleaching before the signal-to-noise ratio was high enough for data collection. For Approach 1, we followed the strategy of our previous work,39 beginning the accumulation of trajectory data ~1 min after the cargo, transport factors and RanGTP (transport mix) were added and continuing for ~2 min. After collecting cargo trajectory data, we then switched to localization of the NPC scaffolds for ~8 min. For Approach 2, scaffold data collection (~8 min) began shortly after addition of transport mix, and when completed, cargo trajectory data were collected (~2 min). In both cases, the total time elapsed for data collection in an individual experiment was ~10 min, although data acquisition was delayed for ~1 min for Approach 1, as indicated earlier. The mEGFP fluorescence was photobleached by ~2 s of 532 nm excitation (Extended Data Fig. 1b) before collecting cargo trajectory data.
Approach 1 – Import of M9-βGal/Transportin Complexes
We first examined transport of a previously characterized large tetrameric model cargo M9-βGal40 (~500 kDa; fullname ‘M9-βGal-8C’) labeled on the eight accessible cysteine residues with Atto542. M9-βGal(Atto542) requires the transportin NTR for import (Extended Data Fig. 4). Single molecule transport experiments were conducted in the presence of an excess of transportin. The M9-βGal cargo tracking strategy is illustrated in Fig. 4 and Supplementary Videos 3 and 4. Due to the narrow-field illumination scheme2 used, diffusing cargo complexes underwent some level of photobleaching before encountering an NPC. Consequently, spots were curated to those with N ≥ 1000 photons, yielding average single particle precisions of ~12 nm in x and y and ~21 nm in z. All cargo localizations within a 400 nm cube centered on an NPC centroid were identified and aligned to the averaged NPC scaffold, using the same rotational matrix used for the NPC that the cargo was associated with (Figs. 4a,b). The NPC scaffold data in Fig. 4 is the same as that reported in Fig. 2 since these NPC data were collected immediately after the M9-βGal cargo trajectory data. As freely diffusing molecules were expected to be only transiently present, whereas cargo complexes that interact with NPCs were expected to have an average residence time of ~9 ms,40 we curated the data to include only those molecules present for three or more consecutive frames. This approach yielded a distribution (Figs. 4c,d) with a substantially clarified NE region, except at the location occupied by the pore.
Figure 4. 3D Tracking of M9-βGal Cargo Complexes Interacting with and Transiting Through NPCs.
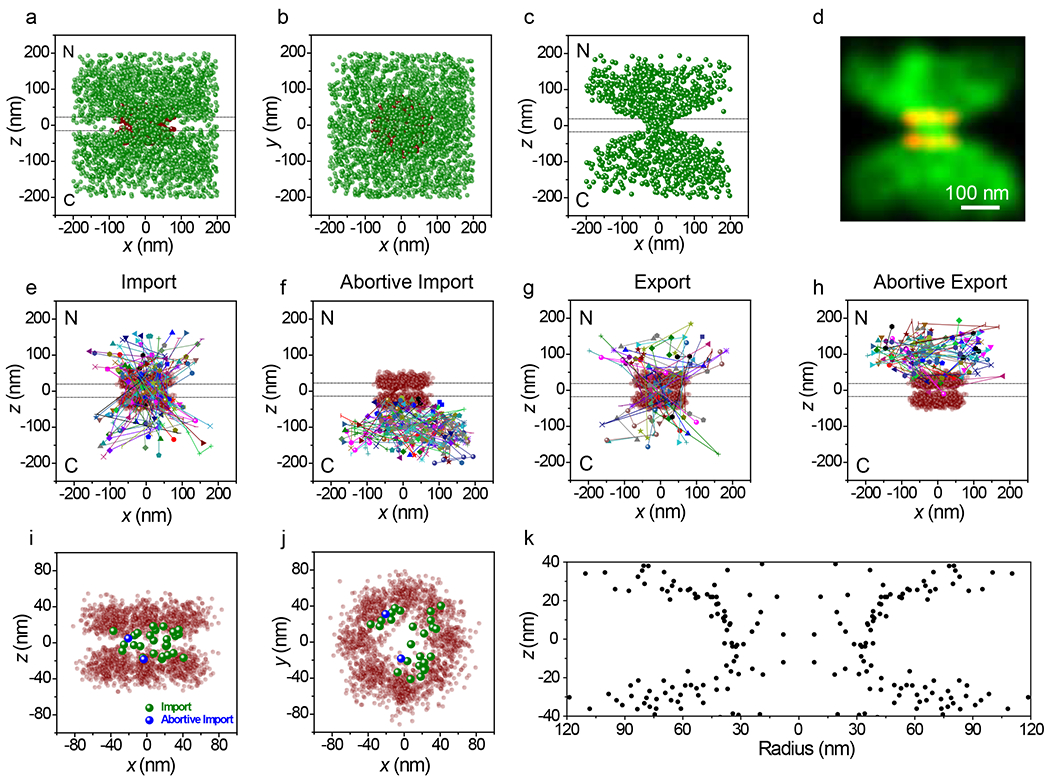
a,b, All M9-βGal(Atto542) localizations (N = 2665 localizations from 142 NPCs from 10 nuclei; each nucleus was an independent biological replicate, green) within a 400 nm cube centered on NPC clusters (from Fig. 2, red), shown from the side (a) and from the cytoplasm (b). Total acquisition time per nucleus for cargo localizations was ~2 min (3 ms/frame, λex = 532 nm, 50 kW/cm2). The two horizontal dashed lines (0±20 nm) in a indicate the approximate location of the NE membranes. [M9-βGal(Atto542)] = 1 nM, [transportin] = 1.0 μM, [RanGDP] = 0.5 μM, [NTF2] = 1 μM, [GTP] = 1 mM. c,d, Localizations for cargos detected in three or more consecutive frames (N = 1077 localizations selected from the data in a,b) in localization (c) and Gaussian rendered (d) maps. Eliminated localizations appear randomly distributed (Extended Data Figs. 5a,b,e). e-h, Representative trajectories. Select trajectories (from N = 239 trajectories obtained from the data in a,b) separately identified as (e) Import (39%), (f) Abortive Import (27%), (g) Export (18%), and (h) Abortive Export (16%). i,j, Distribution map of localizations from import and abortive import trajectories within the NPC scaffold (z = 0±20 nm), shown from the side (i) and from the cytoplasm (j). k, The z-dependent radial distribution of the localizations from import and abortive import trajectories within the central pore region. Values are duplicated by reflection through r = 0 to generate an image representative of a pore cross-section, thus illustrating the hourglass shape of the translocation conduit. Source numerical data are provided in source data.
The large clouds near both the cytoplasmic and nucleoplasmic openings suggested that the cargo complexes had interactions with structures well beyond the translocation pore. To further explore this possibility, the interactions were separated into import and export trajectories, and whether transport occurred or did not occur (Figs. 4e–h). Both abortive import and abortive export trajectories yielded broad clouds at the cytoplasmic and nucleoplasmic openings, respectively (Figs. 4f,h). These data are consistent with the presence of binding sites extending over 100 nm from the scaffold double-ring structure that impede translational mobility. Such a dispersed interaction scaffold is consistent with the network of intrinsically disordered FG-polypeptides, which are known to provide binding sites for NTRs,6,24,41,42 and which can extend significantly into the cytoplasmic and nucleoplasmic compartments.43–45
Considering the large M9-βGal cargo and the absence of endogenous export factors, the observed export trajectories (18% of total, Fig. 4g) were surprising. Possibilities include: i) the NTR-free cargo can export on its own (unlikely, as it cannot undergo import; Extended Data Fig. 4); ii) the bound transportin was not completely dissociated from M9-βGal-8C in the nucleus, and the cargo complex was re-exported; or iii) an unidentified exportin was present in sufficient quantity such that export of single cargos was detectable.
To probe the nature of the import channel, the export events were removed to generate a distribution of M9-βGal cargo localizations within the pore when entering from the cytoplasmic side (import + abortive import trajectories). While there were relatively few particle localizations obtained between the two scaffold rings, these were largely localized near the periphery of the pore (Figs. 4i–j). To further explore the nature of the translocation conduit, the radial distribution of the particles was examined in the vicinity of the pore. The radial distribution was narrowest with the smallest average radius near the center of the pore (~30 nm) and wider and more diffuse (average radius > 50 nm) near the pore exits (Fig. 4k).
Approach 2 – Import of NLS-2xBFP/Imp α/Imp β Complexes
We next examined the importin α/importin β (Imp α/Imp β) pathway by monitoring the import of NLS-2xBFP/Imp α/Imp β complexes (Fig. 5 and Supplementary Videos 5 and 6). The NLS-2xBFP cargo (~57 kDa; fullname ‘NLS-2xBFP(4C)’) was modeled after the previously characterized NLS-2xGFP(4C).47 The color of the tandem fluorescent protein was changed to eliminate the interference of weak GFP fluorescence within the cargo complex imaging channel (Extended Data Fig. 1b). Imp α was labeled on the four accessible cysteine residues48 with Atto542, resulting in a cargo complex approximately half as bright as the M9-βGal cargo complex. Control experiments with Imp α and Imp β alone revealed essentially no bulk import of Imp α and a substantially lower interaction frequency with NPCs than in the presence of NLS-2xBFP (Table 1; Extended Data Fig. 4c). This was expected since the Imp β binding domain of Imp α is auto-inhibitory, binding to the NLS binding pocket in the absence of cargo.49,50 Thus, in the absence of cargo, Imp α cannot bind to Imp β; therefore, the localizations in Fig. 5 represent fully intact cargo complexes despite the fluorescent dyes being on Imp α. The imaging strategy was similar to that described for Approach 1 (Fig. 4), except that since the NPC scaffold data were collected first, a higher time resolution could be used. The higher temporal resolution (2 ms/frame) and dimmer cargo necessitated an ~2-fold higher excitation intensity. Spots were again curated to those with N ≥ 1000 photons, yielding average single particle precisions similar to those observed for M9-βGal. The highly resolved octagonal double-ring structure of the NPC scaffold was reproducibly demonstrated (Figs. 5a,b; Table 1). Cargo complex localization data were again filtered to those molecules present in the imaging region for 3 frames, although due to the faster imaging speed this corresponds to ≥ 6 ms (Figs. 5c,d) instead of the 9 ms threshold for Approach 1. As for M9-βGal cargo complexes, large clouds near both the cytoplasmic and nucleoplasmic openings for import and export trajectories were observed (Figs. 5e–h). NLS-2xBFP cargo complex localizations obtained within the center of the NPC scaffold were largely localized near the periphery of the pore (Figs. 5i–j), and a radial distribution map (Fig. 5k) resembled that obtained earlier for the M9-βGal cargo (Fig. 4k). In short, the M9-βGal and NLS-2xBFP cargo complex tracking data yielded very similar results.
Figure 5. 3D Tracking of NLS-2xBFP Cargo Complexes Interacting with and Transiting Through NPCs.
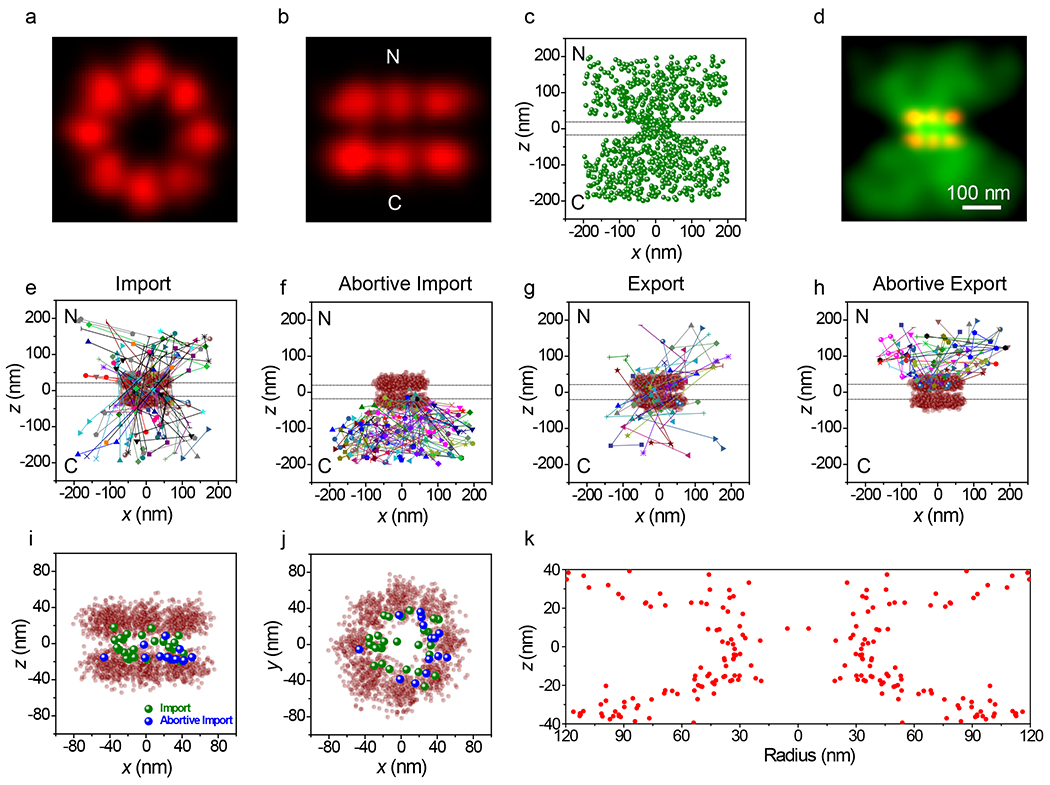
a,b, Composite NPC images, shown from the cytoplasm (a) and from the side (b). Visual comparison with Fig. 2k,l reveals the structural reproducibility. A quantitative comparison is given in Table 1. c,d, Localizations for NLS-2xBFP/Imp α/Imp β cargo complexes detected in three or more consecutive frames (N = 882 localizations from 115 NPCs from 10 nuclei; each nucleus was an independent biological replicate) in localization (c) and Gaussian rendered (d) maps. Total acquisition time per nucleus for cargo complex localizations was ~2 min (2 ms/frame, λex = 532 nm, 100 kW/cm2). Eliminated localizations (particles visible for 1 or 2 frames) appear randomly distributed (Extended Data Figs. 5c,d). The two horizontal dashed lines (0±20 nm) in c indicate the approximate location of the nuclear envelope membranes. [Imp α(Atto542)] = 1 nM, [Imp β] = 0.5 μM, [NLS-2xBFP] = 0.5 μM, [RanGDP] = 1.5 μM, [NTF2] = 1 μM, [GTP] = 1 mM. e-h, Representative trajectories. Select trajectories (from N = 196 trajectories a selected from the data in c,d) separately identified as (e) Import (34%), (f) Abortive Import (36%), (g) Export (13%), and (h) Abortive Export (17%). i,j, Distribution map of localizations from import and abortive import trajectories within the NPC scaffold (z = 0±20 nm), shown from the side (i) and from the cytoplasm (j). k, The z-dependent radial distribution of the localizations from import and abortive import trajectories within the central pore region (compare with Fig. 4k). Source numerical data are provided in source data.
Table 1.
Parameters for NPC Scaffold Localizations and Cargo Trajectory Frequenciesa
| Complex | Cells | NPCs | HMSiR Localizations | Mean Radius, μr (nm)b | Radial Width, σrw (nm)b | z-spacing between rings, 2μz (nm)b | z-Width, σrw (nm)b | Cargo trajectories/min of videoc |
|---|---|---|---|---|---|---|---|---|
| M9-βGal(Atto542)/Transportin | 10 | 142 | 1872 | 52.4 | 11.6 | 51.2 | 10.9 | 18.5 |
| NLS-2xBFP/Imp α(Atto542)/Imp β | 10 | 115 | 1498 | 52.2 | 12.1 | 49.4 | 10.7 | 13.8 |
| Imp α(Atto542)/Imp β | 3 | 30 | - | - | - | - | - | 0d |
With the exception of the cargo trajectories/min, the first two rows were calculated from the data used to generate Figs. 2k,l and 5a,b.
See Fig. 3 and Online Methods for the definitions of terms.
A trajectory was defined as ≥ 3 sequential localizations.
No trajectories; 11 single points were observed.
Import Pathway Overlap
The M9-βGal/transportin and NLS-2xBFP/Imp α/Imp β translocation pathways were directly compared by overlaying their radial distribution maps (Fig. 6a). Since this 2D representation does not account for the larger volumes available at higher radii, volume-corrected heatmaps were generated (Fig. 6b). This analysis revealed a strong similarity between the radial distributions of the transportin and Imp α/Imp β cargo complexes within the central pore, with minor deviations/differences appearing before entering or after exiting the pore. In both cases, the cargo complexes exhibited a strong preference to transport near the NPC scaffold, minimally ~32 nm from the center of the pore (for z = 0±20 nm; see Figs. 6c,d). This transport near the periphery of the pore is consistent with previous results.10,11,17 Importantly, however, the current data reveal an hourglass-shape to the translocation paths (Fig. 6). As this hourglass-shape closely resembles the inner surface of the NPC scaffold structure,15,18,19 these data are consistent with both cargo complexes diffusing along the NPC scaffold surface,51 or following a channel or annular path that is close to this surface.13,26 Notably, our data predict a central channel width of ~60 nm, consistent with recent reports of ‘dilated’ pores (57-64 nm diameter) as a more physiologically relevant structure.52,53 And finally, abortive import trajectories for both cargo complexes almost never penetrated the NPC-midplane (Figs. 4f, 5f and 6e,f), suggesting that transport almost invariably occurred once the complex entered the central pore. In contrast, previous work indicated that a significant percentage of molecules penetrated quite deeply into the FG-network, even across the pore, before aborting transport.40,46 The most likely explanation is that the better localization of individual NPCs reported here provides a more accurate picture from the current data.
Figure 6. Overlap of the Transportin and Imp α/Imp β Import Pathways.
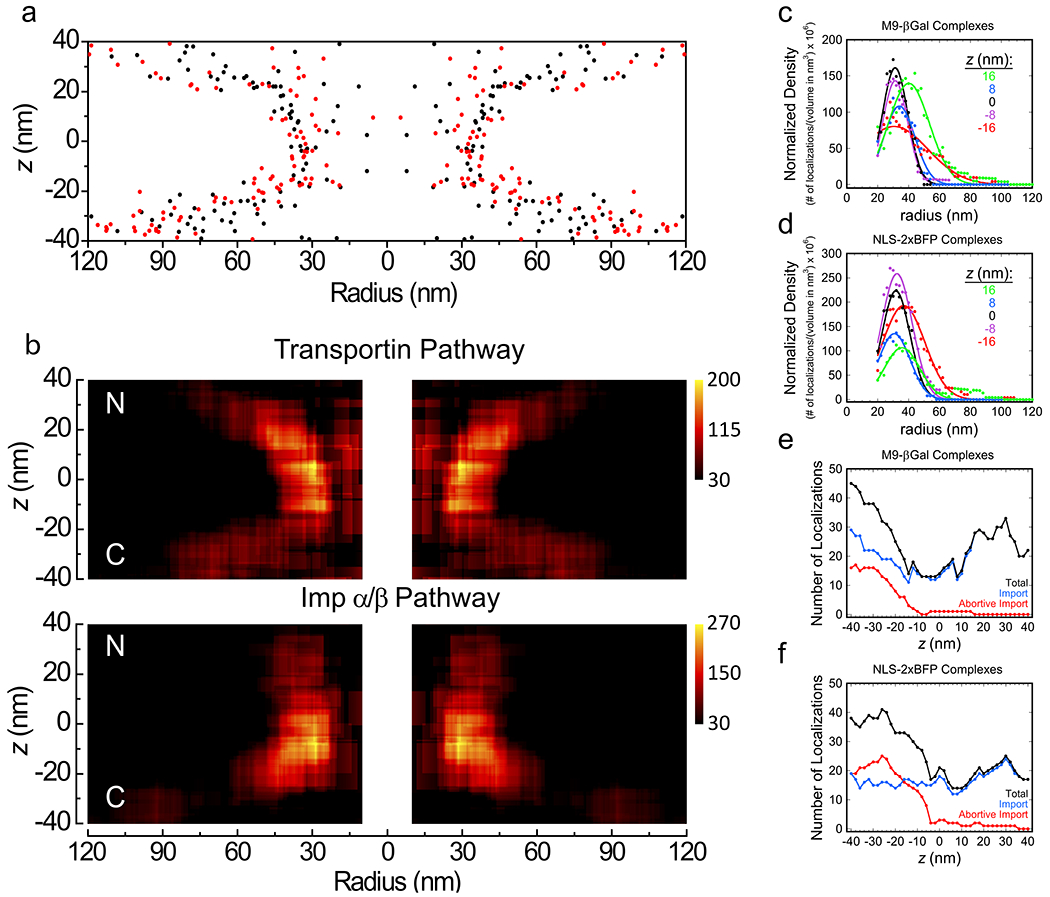
a, Overlap of z-dependent radial distribution maps. Data are from Fig. 4k (black, M9-βGal import complexes) and Fig. 5k (red, NLS-2xBFP import complexes). b, Volume-corrected heat maps for the transportin and Imp α/Imp β import pathways. The particle distributions in a were volume corrected by calculating the particle densities within annular cylinders. At each (r,z) coordinate, the number of localizations within an annular cylinder (r = ±10 nm and z = ±10 nm) were determined, and divided by the total volume of the region to yield the density. The color scale represents the particle density (number of localizations per volume in nm3 x 106). c,d, Radial density distributions at different z-heights. Data from b were plotted for the indicated z-values and fit with a Gaussian function. While a few localizations were observed at small radii, individual localizations in such locations had large effects on density values due to the small volumes; these values were deemed unreliable, and therefore were eliminated from the analysis. For both cargo complexes, the peak density for z = 0±20 nm is at r ≈ 32 nm. e,f, Number of localizations in different z-sections. The total number of localizations obtained within 20 nm thick z-sections (over all radii) are indicated. These data indicate that cargo complexes that abort transport are largely rejected before the middle of the pore (z = 0). Source numerical data are provided in source data.
DISCUSSION
In live cells, the NE undergoes shape fluctuations on the order of hundreds of nanometers in seconds.38 In contrast, the well-resolved octagonal double-ring structure of NPCs obtained here via super-resolution imaging reveals that the NPCs and the NE are quite stable over ~10 min within permeabilized cells. This stability most likely results from a substantial rigidification of the cytoskeletal structure(s) interacting with the NE during permeabilization. While the precise explanation for the very low NPC mobility requires further study, the stability of the system is truly remarkable, as an entirely rigid framework must exist from the coverslip, through the poly-L-lysine layer, through the fragmented plasma membrane, most likely through a stably polymerized cytoskeletal structure to the NE, which must itself prevent both lateral and axial motion of the individual NPCs. It is now apparent that fixation is not necessary for obtaining super-resolved structural information on the NPC, eliminating the potential for artifacts introduced by such sample preparation, which is of particular concern for the highly flexible permeability barrier. Moreover, true 3D particle tracking of rapid real-time nucleocytoplasmic transport processes is now feasible, eliminating the mathematical complications that arise when extrapolating 3D distributions from 2D data,54,55 and allowing more challenging questions to be addressed, such as relating densities to affinities, identifying discrete binding sites, and determining whether transport occurs through distinct peripheral channels.
Though the NPCs in our permeabilized cells could certainly retain some NTRs and/or transport cargos, we assume that they were largely devoid of other transport traffic. Therefore, the peripheral bias that was observed for import complexes likely represents an inherent preference for this region of the permeability barrier rather than the result of competition with other transiting cargos. While the distribution of different types of FG repeat motifs (e.g., FG, FxFG, and GLFG) and FG density provide a likely mechanism to generate preferred translocation conduits through the FG-network,7–9,15 other potential contributing mechanisms exist. For example, electrostatic potential can influence diffusional path,12 and structural organization within the permeability barrier can provide open (or, more likely, less dense) channels to bias translocation paths.13,26 In addition, considering that the observed translocation paths seemingly follow the contour of the NPC scaffold, the potential for NTR binding sites on or near the surface of this scaffold is a reasonable consideration. The direct binding of GLFG repeats to scaffold nucleoporins56 could contribute to ensuring that such binding sites are present. While a translocation path following the contours of the NPC scaffold is a prediction of the reduction-of-dimensionality model,51 this finding does not exclude other models.13,57–59 However, it does challenge a prediction of the Kap-centric model, which suggests that strongly bound NTRs are embedded near the scaffold where the FG repeat density is highest, leaving a single central channel through the FG-network for cargo translocation.60
While the radial distribution data for transiting import complexes provide one constraint on the shape of the translocation conduits, the current data does not allow conclusions to be drawn regarding the angular distribution of the translocating cargo complexes relative to the NPC scaffold. Further experimental improvements are needed to distinguish between an annular-shaped translocation path or discrete channels. In the case of eight separate discrete conduits (consistent with the 8-fold rotational symmetry), distinct transportin and Imp α/Imp β pathways could be maximally spaced by ~12 nm (assuming a 32 nm radius and 22.5° arc between channels). Considering that the import complexes used had average diameters of ~13 and ~8 nm (~900 kDa and ~200 kDa for the M9-βGal and NLS-2xBFP import complexes, respectively), competitive influences are expected if both cargo complexes were simultaneously transporting within neighboring channels. Thus, despite the potential for at least a partial distinction between discrete translocation channels, high transport fluxes will undoubtedly introduce competitive effects. Competition within a single annular translocation conduit would also, of course, be expected.
The large number of cargo complex localizations outside the central pore of the NPC (> 90%; Extended Data Figs. 5f,g) reflects a large accessible volume with numerous binding sites (Figs. 4c and 5c). Verification that this entire volume is accessible to rapid confined movement requires a true 3D approach, such as that reported here. The diffusion constant of the tracked M9-βGal and Imp α molecules was ~25-fold less in the vicinity of an NPC relative to free diffusion (Extended Data Fig. 6), an expected consequence of numerous transient binding events for the assembled cargo complexes. While we suggest that the largest contributor to the necessary binding sites on the cytoplasmic and nucleoplasmic sides of the pore were the FG repeats on extended FG-polypeptides,12,43–45 the cytoplasmic filaments and nuclear basket structure are additional likely binding site contributors.61–63 In addition, the current data cannot rule out non-NPC binding sites, such as cytoskeletal and nucleoskeletal structures.64,65
The described super-resolution approaches can be improved and applied in multiple ways. A third cargo imaging approach in which the NPC scaffold is labeled with a bluer blinking dye with appropriate photophysics and photon output would enable cargo transport to be imaged first at a faster frame rate without bleaching of the NPC tags, which could then be imaged second. Data quantity can be increased with alternating or parallel acquisition of the different colors. Looking beyond the NPC, these rapid 3D super-resolution strategies can be applied to address numerous cell biological questions. Trapped complexes within the rigid structural framework generating the NPC positional stability can likely be examined with exogenous probes and super-resolution microscopy.
ONLINE METHODS
A step-by-step protocol describing the 3D microscopy imaging method reported in this paper is provided at Nature Protocol Exchange.68
Experimental Methods
Protein Mutation, Expression and Purification.
The expression and purification of RanGDP,40,69–71 NTF2,71,72 transportin,73 M9-βGal-8C,40 and a mutated version of the anti-GFP nanobody LaG-934 largely followed the approaches in the indicated work. A C-terminal cysteine on the LaG-9 nanobody was generated by mutation (S151C) using the QuikChange protocol (Agilent Technologies) to produce plasmid pET21b-LaG9(S151C). Plasmid pNLS-2xBFP(4C), encoding NLS-2xBFP(4C), was created by a Y66H mutation74 in each of the GFP genes of pNLS-2xGFP(4C)47 via the QuikChange method. For simplicity, the M9-βGal-8C and NLS-2xBFP(4C) proteins are referred to as M9-βGal and NLS-2xBFP, respectively, throughout this paper. All plasmids were confirmed by DNA sequencing. Plasmids pM9-βGal-8C, pET21b-LaG9(S151C), and pNLS-2xBFP(4C) are available from Addgene (ID#172489, ID#172490 and ID#176151, respectively). For clarity, descriptions of all protein expressions and purifications are provided in the following sections. When used, antibiotics were 50 μg/mL for ampicillin (Amp) and 30 μg/mL for kanamycin (Kan). All purified proteins were stored at −80°C until use.
RanGDP.
BL21(DE3) cells transfected with pQE32-Ran70 were inoculated into 5 mL of LB with 2% glucose + Amp, and cultured overnight at 37°C. The following day, the starter culture was transferred to 1 L of LB with 2% glucose + Amp, grown at 37°C until an OD600 of ~0.8, induced with 1 mM isopropyl β-D-1-thiogalactopyranoside (IPTG) and grown for another 4 h at 27°C before pelleting the culture (4,000xg, 20 min, 4°C). Cells were resuspended in 20 mL of 20 mM potassium phosphate (K-Phos), 200 mM NaCl, 0.5 mM MgCl2, 10 mM imidazole, 4 mM β-mercaptoethanol (βME), pH 7 + protease inhibitors (PI; 10 mM phenylmethane sulfonyl fluoride, 100 μg/mL trypsin inhibitor, 20 μg/mL leupeptin, and 100 μg/mL pepstatin), and lysed by French press (3X at 16,000 psi). The lysate was centrifuged (15,000xg, 20 min, 4°C), and the supernatant was mixed with 0.5 mL Ni-NTA resin. After incubation for 30 min at 4°C, the suspension was transferred to a gravity column. The resin was washed with 15 mL of 20 mM K-Phos, 500 mM NaCl, 0.5 mM MgCl2, 20 mM imidazole, 0.1% TX-100, pH 7.0 + PI and then 15 mL of 20 mM K-Phos, 50 mM NaCl, 0.5 mM MgCl2, 20 mM imidazole, pH 8. Fractions (1 mL) were eluted with 20 mM K-Phos, 50 mM NaCl, 0.5 mM MgCl2, 250 mM imidazole, pH 8. Major elution fractions were combined and then subjected to cation exchange chromatography in 20 mM K-Phos, 50 mM NaCl, 0.5 mM MgCl2, pH 8 using a MonoS column (GE Pharmacia Biotech, #17-0547-01) and linear NaCl gradient (with 500 mM NaCl in the second buffer) to separate RanGDP (first peak at ~150 mM NaCl) from RanGTP (second peak at ~250 mM NaCl).
NTF2.
BL21(DE3) cells transfected with pET15b-NTF275 were inoculated into 5 mL of LB + Amp, and incubated at 37°C overnight. This starter culture was transferred to 2 L LB + Amp, grown at 37°C for ~5 h (until OD600 ≈ 0.8), and then grown an additional 4 h at 27°C after inducing with 1 mM IPTG. Cells were resuspended in 20 mL of 20 mM Tris, 200 mM NaCl, 5 mM MgCl2, 10 mM imidazole, pH 8.0 + PI, and then lysed as was done during the Ran purification. NTF2 was precipitated from the cleared lysate with saturated ammonium sulfate (at ~40-50% saturation), and recovered by centrifugation (4,000xg, 20 min, 4°C). The pellet was dissolved in 5 mL of 50 mM Tris, pH 8 over 1 h. The NTF2 solution was then purified using an HiPrep Q FF Anion Exchange Resin column (GE Healthcare Bioscience, #17-5190-01) with the dissolution buffer and a linear NaCl gradient, followed by Superdex 75 size exclusion chromatography (GE Healthcare Bioscience, #17-5174-01) in the dissolution buffer.
Transportin.
BL21-Gold(DE3) cells transfected with pGEX4TT3-TEV-KapBeta273 were inoculated into 20 mL of LB + Amp and grown overnight at 37°C. The starter culture was transferred to 2 L of LB + Amp, grown to an OD600 of ~0.6 at 25°C, and then induced with 0.5 mM IPTG for 12 hours at 25°C. The cells were resuspended in 15 mL of transportin lysis buffer (50 mM Hepes, 150 mM NaCl, 15% glycerol, 2 mM dithiotheitol (DTT), 2 mM EDTA, pH 7.4 + PI) per liter of original culture, and then lysed as was done during the Ran purification. The cleared lysate was mixed with 500 μL glutathione Sepharose resin (GE Healthcare, #17-0756-01) and loaded onto a gravity column, which was washed with 20 mL of transportin lysis buffer, 25 mL of 50 mM Hepes, 100 mM NaCl, 1 mM EGTA, 10 mM MgOAc2, 2 mM DTT, 15% glycerol, 5 mM ATP, pH 7.4 + PI, and 25 mL of 20 mM Hepes, 20 mM NaCl, 2 mM EDTA, 10% glycerol, 2 mM DTT, pH 7.4. The GST tag was cleaved by incubating the Sepharose resin with 20 mM Hepes, 20 mM NaCl, 2 mM EDTA, 10% glycerol, 2 mM DTT, 0.5 units/μL TEV protease (ThermoFisher Scientific, #12575015), pH 7.4 for 2 h at room temperature, and the solution was then collected (0.5 mL fractions). The transportin protein was further purified by Enrich Sec 650 size exclusion chromatography (Biorad, #7801650) in 20 mM Hepes, 110 KOAc, 5 mM NaOAc, 2 mM MgOAc2, 2 mM DTT, pH 7.4.
M9-βGal.
BL21(DE3) cells transfected with pET30a-M9-βGal-8C40 were inoculated into 4 mL of LB + Kan and cultured overnight at 37°C. The starter culture was transferred into 1 L of LB + Kan, grown at 37°C for 2-3 hrs (until OD600 ≈ 0.8), and then induced overnight at 22°C with 0.15 mM IPTG. The cells were resuspended in 15 mL of 5 mM Tris, 500 mM NaCl, 5 mM MgCl2, 4 mM βME, 10% glycerol, pH 8.0 + PI and a pinch of DnaseI, and then lysed as was done during the Ran purification. The cleared lysate was incubated with 0.5 mL Ni-NTA resin for 30 min at 4°C, and the suspension was then transferred to a gravity column. The resin was washed with 15 mL of 5 mM Tris, 500 mM NaCl, 5 mM MgCl2, 4 mM βME, 0.1% TX-100, pH 8 and then 15 mL of 5 mM Tris, 100 mM NaCl, 10 mM imidazole, pH 8. Fractions (0.5 mL) were eluted with 5 mM Tris, 100 mM NaCl, 250 mM imidazole, pH 8. The most concentrated fraction was further purified by Enrich Sec 650 size exclusion chromatography using 20 mM Hepes, 150 mM NaCl, pH 7.3.
LaG-9(S151C).
BL21(DE3) cells transfected with pET21b-LaG9(S151C) were inoculated into 5 mL of LB + Amp, and cultured overnight at 37°C. The starter culture was transferred into 1 L of LB + Amp, which was grown at 37°C until the OD600 was ~0.8, and then induced with 0.1 mM IPTG for 20 h at 20°C. The cells were resuspended in 10 mL ice cold 20 mM Tris, 0.5 mM EDTA, 500 mM sucrose, 10 mM βME, 0.3 mM MgSO4, pH 8.0 + PI, and then lysed as was done during the Ran purification. The cleared lysate was incubated with 0.5 mL Ni-NTA resin for 30 min at 4°C, and the suspension was then transferred to a gravity column. The resin was washed with 15 mL of 20 mM Tris, 900 mM NaCl, 10 mM βME, 0.1% TX-100, pH 8.0, and then 15 mL of 20 mM Tris, 150 mM NaCl, 10 mM imidazole, pH 8.0. Fractions (0.5 mL) were eluted with 20 mM Tris, 150 mM NaCl, 250 mM imidazole, pH 8.0. The most concentrated fraction was further purified by Superdex 75 size exclusion chromatography (GE Healthcare Bioscience, #17-5174-01) using 20 mM Hepes, 150 mM NaCl, pH 7.3.
Imp α.
BL21(DE3) cells transfected with pRSET-hSRPα76 were inoculated into 5 mL of LB + Amp, and cultured overnight at 30°C. The starter culture was then transferred into 2 L of LB + Amp, grown at 37°C until the OD600 was ~0.8, and then induced with 0.8 mM IPTG for 4.5 h at 28°C. The cells were resuspended in 10 mL of 20 mM Tris, 200 mM NaCl, 5 mM MgSO4, 10 mM imidazole, 4 mM βME, pH 8.0 + PI, and then lysed as was done during the Ran purification. The cleared lysate was incubated with 0.6 mL Ni-NTA resin for 30 min at 4°C, and the suspension was then transferred to a gravity column. Next, the resin was washed with 20 mL of 20 mM Tris, 1 M NaCl, 5 mM MgSO4, 10 mM imidazole, 4 mM βME, 0.1% TX-100, pH 8.0 + PI, and then 20 mL of 20 mM Tris, 100 mM NaCl, 10 mM imidazole, pH 8. Fractions (0.5 mL) were eluted with 20 mM Tris, 100 mM NaCl, 250 mM imidazole, pH 8.0. The most concentrated fraction was further purified by Superdex 200 size exclusion chromatography (GE Healthcare Bioscience, #28-9909-44) using 20 mM Hepes, 150 mM NaCl, pH 7.3.
Imp β.
BL21(DE3) cells transfected with pQE9-Imp β69 were inoculated into 5 mL of LB with 2% glucose + Amp and cultured overnight at 37°C. The starter culture was then transferred into 1 L of LB with 2% glucose + Amp, grown at 37°C until the OD600 was ~0.8, and then induced with 0.7 mM IPTG for 3 h at 37°C. The cells were resuspended in 6 mL of 5 mM Tris, 500 mM NaCl, 5 mM MgSO4, 10 mM imidazole, 4 mM βME, pH 8.0 + PI, and then lysed as was done during the Ran purification. The cleared lysate was incubated with 0.5 mL Ni-NTA resin for 30 min at 4°C, and the suspension was then transferred to a gravity column. The resin was washed with 20 mL of 5 mM Tris, 500 mM NaCl, 5 mM MgSO4, 10 mM imidazole, 4 mM βME, 0.1% TX-100, pH 8.0 + PI, and then 20 mL of 5 mM Tris, 100 mM NaCl, 10 mM imidazole, pH 8. Fractions (0.5 mL) were eluted with 5 mM Tris, 100 mM NaCl, 250 mM imidazole, pH 8.0. The most concentrated fraction was further purified by Superdex 200 size exclusion chromatography using 20 mM Hepes, 110 KOAc, 5 mM NaOAc, 2 mM MgOAc2, 2 mM DTT, pH 7.4.
NLS-2xBFP.
JM109 cells transfected with pNLS-2xBFP(4C) were inoculated into 5 mL of LB + Amp, and cultured overnight at 37°C. The starter culture was then transferred into 1 L of LB + Amp, grown at 37°C until the OD600 was ~0.8, and then induced with 0.7 mM IPTG for 14 h at 25°C. The cells were resuspended in 6 mL of 5 mM Tris, 500 mM NaCl, 5 mM MgSO4, 10 mM imidazole, 4 mM βME, pH 8.0 + PI, and then lysed as was done during the Ran purification. The cleared lysate was incubated with 0.5 mL Ni-NTA resin for 30 min at 4°C, and the suspension was then transferred to a gravity column. The resin was washed with 20 mL of 5 mM Tris, 500 mM NaCl, 5 mM MgSO4, 10 mM imidazole, 4 mM βME, 0.1% TX-100, pH 8.0 + PI, and then 20 mL of 5 mM Tris, 100 mM NaCl, 10 mM imidazole, pH 8.0. Fractions (0.5 mL) were eluted with 5 mM Tris, 100 mM NaCl, 250 mM imidazole, pH 8.0. The most concentrated protein fraction was further purified by Superdex 200 size exclusion chromatography using 20 mM Hepes, 110 KOAc, 5 mM NaOAc, 2 mM MgOAc2, 2 mM DTT, pH 7.4.
Protein Labeling.
The spontaneously blinking dye HMSiR35 (SaraFluor 650B-maleimide; Goryo Chemical, Japan, #A209-01) or Alexa568 (Thermo Fischer Scientific, #A20341) was attached to the C-terminal cysteine on LaG-9(S151C) by incubating with a 15-fold molar excess of the maleimide derivatives at room temperature for 15 min. Excess dye was removed by adding the dye-protein mixture to 0.1 mL Ni-NTA resin (30 min incubation), washing the resin-bound protein with 20 mL of 20 mM Hepes, 500 mM NaCl, 0.1% TX-100, 4 mM βME, pH 7.3, and then eluting the labeled nanobody with 20 mM Hepes, 150 mM NaCl, 250 mM imidazole, pH 7.3.
The eight surface cysteines on M9-βGal were labeled with Atto542 maleimide (Atto-Tec, #AD 542) using a 150-fold molar excess of dye dissolved in DMSO. To label the four surface cysteines on Imp α, a 70-fold molar excess of Atto542 maleimide was used. Excess dye was removed by adding the dye-protein mixture to 0.1 mL Ni-NTA resin (30 min incubation), washing the resin-bound protein with 5 mL of 20 mM Hepes, 150 mM NaCl, 0.1% TX-100, 4 mM βME, pH 7.3 and eluting with 20 mM Hepes, 150 mM NaCl, 250 mM imidazole, pH 7.3.
Protein Concentrations.
Protein concentrations were determined by the densitometry of bands on SDS-PAGE gels stained with Coomassie Blue R-250 using bovine serum albumin as a standard and a ChemiDoc MP imaging system (Bio-Rad Laboratories). The purity of dye-labeled proteins was assayed by direct in-gel fluorescence imaging using the same ChemiDoc imaging system, and was > 95%.
Cell Culture.
U-2 OS-CRISPR-NUP96-mEGFP clone #195 (300174, CLS GmbH) and U-2 OS (300364, CLS GmbH) cells28 were obtained in January 2020, and were used without authentication. Cells were grown in McCoy’s 5A (modified) media (Thermo Fisher Scientific, #16600082) supplemented with 100 U/mL penicillin-streptomycin (Thermo Fisher Scientific, #15140148), 1 mM sodium pyruvate (Thermo Fisher Scientific, #11360070), 1X MEM non-essential amino acids solution (Thermo Fisher Scientific, #11140050), and 10% (v/v) fetal bovine serum (Thermo Fisher Scientific, #A3160401) in 5% (v/v) CO2 enriched air at 37°C. Cells were typically grown to ~95% confluency, were split using Accutase (Thermo Fisher Scientific, #A1110501), and were tested monthly for mycoplasma contamination (InvivoGen, #rep-pt1). For microscopy experiments, freshly split cells were grown overnight (< 3% confluence) on coverslips pre-treated with 0.01% poly-L-lysine (Sigma, #P4832) for 5 min, which reduced cell-detachment after permeabilization.
Single Molecule Transport Experiments.
Flow chambers (~10 μL) were constructed by inverting a small coverslip (10.5x35 mm; Electron Microscopy Sciences, #72191-35) with beads of high-vacuum grease parallel to its short edges over a #1.5 coverslip (24x60 mm; VWR, #16004-312) on which U-2 OS cells were grown overnight. Cells were permeabilized by incubating with 40 μg/mL digitonin in import buffer (IB; 20 mM Hepes, 110 mM KOAc, 5 mM NaOAc, 2 mM MgOAc2, 1 mM EGTA, pH 7.3) for 2 min. Permeabilized cells were washed once with 10 μL IB containing 1.2% (w/v) polyvinylpyrrolidone (PVP, 360,000 g/mol; Sigma, #P5288).2 Then, 10 μL of 100 nM nanobody-HMSiR in IB + 1.2% PVP (IB-PVP) was flowed onto the permeabilized cells and incubated for 3 min. The cells were washed twice (2x 10 μL?) with IB-PVP. The cells were then ready for single molecule nuclear transport experiments. The LaG9(S151C) nanobody showed high specificity towards the GFP domain in U-2 OS-CRISPR-NUP96-mEGFP cells (Extended Data Fig. 1a, Supplementary Video 1).
For Approach 1, the ‘transport mix’ consisting of 0.5 μM RanGDP, 1 μM NTF2, 1 mM GTP, 1 μM transportin, and 1 nM M9-βGal(Atto542) in IB-PVP was added to the permeabilized nanobody-tagged cells. As it takes ~1 min for the Ran concentration at the NE to become established and reach steady-state,39 this time was used to find the bottom surface of the cell and prepare for image acquisition. Approximately 2 min was used for imaging cargo transport (3 ms/frame, thirty 1000-frame movies), and ~8 min for acquiring nanobody localizations (50 ms/frame, fourteen 500-frame movies with a 5 s gap between movies).
For Approach 2, ‘transport mix’ consisted of 1.5 μM RanGDP, 1 μM NTF2, 1 mM GTP, 0.5 μM Imp β, 0.5 μM NLS-2xBFP, and 1 nM Imp α(Atto542) in IB-PVP. In the first ~8 min, nanobody localizations were acquired (50 ms/frame, fourteen 500-frame movies with a 5 s gap between movies), and then, the next ~2 min was used to image cargo complexes (2 ms/frame, fifty 1000-frame movies). The first 2-3 movies were not included in the analysis because of the significant background fluorescence from already transported cargo complexes. After this time, sufficient photobleaching had occurred allowing for single particle detection.
2D Microscope for Bulk Transport.
Bulk import of M9-βGal(Atto542) and Imp α(Atto542) (Extended Data Fig. 4) was measured using wide-field fluorescence with a Nikon Eclipse Ti equipped with a 100X oil-immersion objective (Nikon Apo TIRF, 1.49 NA). Epifluorescence excitation from a white-light lamp (532±5 nm) was selected (Chroma zet532/10x, zt532rdc-UF2, and ET550LP), and emission was recorded using a Prime 95B camera. For these assays, the permeabilized cells were washed twice with IB-PVP before adding transport mix.
3D Super-Resolution Microscope.
The core of our 3D microscope set-up (Fig. 1a) was a Zeiss Axiovert 200M equipped with an oil-immersion objective (Zeiss Alpha Plan-Apochromat, 1.40 NA) on a vibration isolation table. A nearly flat sample plane illumination was obtained with a π-shaper (Edmund Optics, #12-644) using diode lasers (0.7-0.8 mm initial diameter; 488, 532 and 647 nm with 400, 300, and 120 mW maximum power, respectively) directed through the epifluorescence excitation path from which all manufacturer-installed optics before the dichroic mirror were removed, except for the tube lens. The flattened beam profiles exiting the π-shaper were compressed 7X and converted to circularly polarized light with half (λ/2) and a quarter (λ/4) waveplates (Newport, #10RP42-1 and #10RP44-1) before entering the microscope as a slightly converging illumination beam. A self-configured adaptive optics (AO) system (Imagine Optic, MicAO) was incorporated into the emission path between the microscope and the EMCCD camera (Photometrics Evolve 128 Delta). A 400 mm focal length tube lens (L1; Thorlabs, TL400-A) increased the diameter of the objective exit pupil (~5 mm) to ~12 mm, which was directed by a mirror to the center of an ~15 mm diameter deformable mirror (DM; Imagine Optic, Mirao 52-e). Considering the 165 mm focal length of the microscope tube lens, this represents an exit pupil magnification of ~2.42. A second lens, L2 (identical to L1), re-created the sample image with the wavefront corrected by the DM. A 2X lens magnifier (Edmund Optics, #54-356) was used to magnify the image ~2-fold. Image magnification was determined using a calibration slide (Amscope, #MR095), and yielded 118 nm square pixels. A flip mirror (FM) diverted the beam from the DM to a Shack-Hartman wavefront sensor (WFS; Imagine Optic, HASO4), which was positioned in a conjugate plane to the DM after a 100 mm focal length tube lens (L3; Thorlabs, TL100-A), which compressed the pupil diameter 4X to ~3 mm. All introduced lenses were chromatically corrected. An Optosplit III (Cairn Research) was incorporated before the camera to enable simultaneous multi-color imaging, though this option was not used here due to the different imaging timescales for the two-colors. Both green and red emission channels were collected with a double-bandpass filter set (Chroma, ZT532/640/NIR-RPC-UF2 and zet532/640m). A self-configured TIRF-Lock system (Mad City Labs) installed using an infra-red (IR) laser (850 nm, 20 mW; Thorlabs, #LDM850) provided a z-stability for the coverslip of < 3 nm for the duration of the experiment. This system measures the deflection of the total internally reflected IR laser beam focused with a 50 mm lens (L4; Edmund Optics, #88-724) on a quadrant detector, which then enables z-positional correction of the coverslip via a feedback loop with a z-nanostage. Microscope coverslips were mounted within a home-built aluminum frame and held in place with high-vacuum grease. The mounted coverslip was suspended within the piezo-stage (MadCityLabs, #Nano-LPS200) opening with a manufacturer provided scaffold, and covered with a glass plate during acquisition to reduce air current drift. The AO system was used to correct the aberrations introduced by the microscope imaging optics using two approaches enabled by software provided by the manufacturer (Imagine Optic). First, the emission from a 1 μm fluorescent bead (ThermoFisher Scientific, #T7282) embedded in 2% agarose (Sigma Aldrich, #A7174) was directed to the WFS. The shape of the DM was then altered in an iterative process to achieve a substantially flattened wavefront. Next, the emission beam from a diffraction limited 0.1 μm bead (ThermoFisher Scientific, #T7279) embedded in 2% agarose was directed to the camera, and the DM was adjusted to achieve the highest quality image, using an iterative algorithm based on an intensity-based merit factor.77 This second correction has the advantage that it utilized the exact optical path used for eventual imaging, unlike the first approach where the beam was diverted to the WFS. When satisfied with the corrected point spread function (PSF), 60 nm root mean square (rms) astigmatism was added to generate the z-dependent spot ellipticity needed for 3D information.31 The microscope was then ready for imaging. This two-step correction was always done in the red channel, and the optimized shape of the DM obtained for the red channel was also used as the primary correction for the green channel. However, when acquiring movies in the green channel, a 30 nm rms defocus was additionally applied, which made the z-foci of the green and red channels very close (within ~30 nm). Immediately after imaging cargo transport and obtaining NPC localizations, z-stack image sequences (100 ms/frame, 41 steps, step size of 25 nm) from five different 0.1 μm beads embedded in 2% agarose were obtained in both green and red channels to generate 3D calibration curves (Fig. 1d).31 Image sequences (100 frames, 50 ms/frame) were also acquired to calculate the image alignment matrix between the two imaging channels.
3D Diffusion Constant.
The diffusion constant for isotropic motion in three dimensions can be estimated using a step size probability distribution. In one dimension, the step sizes follow a Gaussian (normal) distribution.78 Assuming all jump distances are positive (to more readily compare with 2D and 3D cases), the normalized 1D step size probability distribution is:
| (Eq. 1) |
where D is the translational diffusion constant, t is the camera integration time, b is the bin size, and the factor of 2 accounts for the fact that the data are plotted using |x|. The 2D step size probability distribution is:
| (Eq. 2) |
where r2 = x2 + y2, 2πrdr is the volume element for a circle, and the bin size is included.79 Similarly, the 3D step size probability distribution is:
| (Eq. 3) |
where R2 = x2 + y2+ z2, 4πR2dR is the volume element for the surface of a sphere, and the bin size is included. Assuming three distinct molecular populations with different diffusion constants,
| (Eq. 4) |
where A, B, and 1-A-B are weighting factors for the three distributions.
Computational Methods
Software.
The Nikon microscope was controlled by NIS-Elements AR 5.02.01 (Nikon Instruments, Tokyo, Japan). The Zeiss microscope was controlled by Metamorph 7.7.7 (Molecular Devices, San Jose, CA). The DM and WFS were controlled by MicAO 1.3 and CasAO 1.0, respectively (Imagine Optic, Orsay, France). The TIRF-lock system was controlled by a standalone LabVIEW 2015 program (National Instruments, Austin, TX) provided by Mad City Labs. Data were visualized, analyzed and plotted using ImageJ (Fiji 1.52P), Origin 8.5 (OriginLab Corporation, Northampton, MA), Kaleidagraph 4.5.2 (Synergy Software, Reading, PA), Microsoft Excel 16.16.20 (200307) (Microsoft Corp., Redmond, WA), and SnapGene 5.3.2 (GSL Biotech LLC, San Diego, CA). With the exception of the simulations and the initial determination of 3D coordinates, all data were analyzed with programs written in Matlab R2018a (Mathworks, Natick, MA), which are summarized in Supplementary Table 1.Simulations. Two different types of simulations were used to guide the analyses and assist with the interpretation of the results, both of which used Microsoft Excel. Supplementary Data 1_Software File 1 models the random appearance in 3D of fluorescent spots from labeled NUP96 molecules based on coordinates from the EM density map of the human NPC.67 The centroid of the localizations was assumed to be located at the C-terminus of NUP96. Though the position of the dye labels relative to this density map are not known, they are within ~6-7 nm of the labeled site (Fig. 2b). Options are included that allow the localization precision to be either static (fixed) or experimentally determined z-dependent values. The model NPC scaffold can be stochastically rotated, translated or tilted from the z-axis to encompass the range of possibilities for localized structures within the NE. For rotations and translations, values were randomly selected from a linear distribution function. For tilts and static localization precisions, values were randomly selected from normal distributions defined by the provided standard deviation (mean = 0). For each localization, a photon count was randomly selected from a log-normal distribution with scale and shape parameters determined from experimental measurements (Extended Data Fig. 2f). The photon count was used to generate the z-dependent localization precision of the spot, as defined by experimentally determined fit curves (Fig. 1f). Since Supplementary Data 1_Software File 1 generates average precision values over input z and photon ranges, it was used to estimate average experimental single particle precision values.
Supplementary Data 2_Software File 2 models the random appearance of fluorescence spots appearing in the cytoplasmic and nucleoplasmic compartments and within the NPC central pore. This is a coarse simulation of the experimental model, as it does not include detailed structural information for the NPC or dynamic information on particle trajectories, which could have significant effects on spatial densities. The intention of this simulation was to verify that localizations of single point trajectories within the NE region could arise from the localization error (Extended Data Fig. 5e). The z-dependent localization precisions were generated as in Supplementary Data 1_Software File 1. Spot densities in the various regions are variable parameters, as are the annular diameter and width of the central channel localizations.
Major Errors in Resolving the NPC Scaffold.
Using the experimental data as a guide, limits on significant errors in resolving the NPC scaffold were obtained through simulations (Supplementary Data 1_Software File 1), and summarized in Figure 3. While particle localization precisions are the largest individual errors in resolving the NPC scaffold in our current imaging strategy, the largest potential sources of additional significant errors are biological movements (natural fluctuations in NPC location either due to moment of the NE or NPC movement within the NE). Instrument stability errors (e.g., movements of the sample holder) are assumed to be subsumed into the localization errors. All of the cartesian (xyz) movements are collectively referred to as the ‘jiggle’ and the only angular movement considered is the tilt of the cylindrical scaffold from the normal to the NE. We have not taken into account the error in the rotational alignment of clusters (i.e., we assumed that all clusters are perfectly aligned) – the parameters used here for error comparisons are largely independent of this rotational alignment due to the small tilt angles. The radial distribution histograms were fit with a Gaussian function, y = A*exp[−(r-μr)2/2σrw2], and the z height histograms were fit with a symmetric double Gaussian centered on the origin, y = B*{exp[−(z-μz)2/2σzw2] + exp[−(x+μ)2/2σzw2]}. Average (±SD) radial and z widths were determined for various tilt and jiggle values from 20 independent simulations of ~2300-2400 localizations (reduced from 2500 by z selection), a fixed cluster size of 13, and a z centroid of 0±200 nm (to model the variable precision in the experiments).
Spot Identification and 3D Localization.
All image sequences were analyzed using Fiji80 with the Thunderstorm66 plug-in. The maximum likelihood method was used for all single molecule localizations, yielding spot centroids (x and y positions) and widths in x and y. The z-coordinates were obtained from calibration curves obtained with 0.1 μm beads, and were fit as described earlier31 for display purposes (Figs. 1d,e) or as implemented by ThunderStorm66 for image analysis. For pore localization data, two post-processing options were used: “Remove duplicates” (eliminates overlapping molecules) and “Density filters” (eliminates most spots between NPC clusters).
Alignment of the Green (Atto542) and Red (HMSiR) Channels.
The accurate alignment of images in distinct color channels is essential to any super-resolution multi-color imaging scheme. Chromatic aberration is a common alignment issue since different wavelengths are focused at different spots along the optical axis. While we were careful to choose lenses designed to reduce these effects, chromatic mis-matches still remained and introduced significant errors in nanometer-scale precision estimates. The AO system was a major advantage here, as it was used to roughly align the z-focus of the two channels. Fine tuning of the z-position was obtained through use of distinct z-calibration curves for the two color channels. We have used the red channel (NUP96 localizations) as the reference, and corrected the green channel (cargo localizations) coordinates to the red channel coordinate system. This was accomplished by applying two successive corrections to the green channel coordinates, first to x and y and then to z.
Image Alignment in x and y.
To determine the alignment matrix between the two imaging channels, five different 0.1 μm beads were successively imaged in the red and green channels without changing the DM settings (100 frames each; 50 ms/frame), and the mean xy positions for each bead were determined. The alignment matrix to transform the x and y green channel coordinates into red channel coordinates was obtained as described earlier,81 using rotational and translational corrections. This process was repeated for each nucleus using images collected immediately after the NPC localization measurements. The standard deviation of the differences between the transformed green channel coordinates and the red channel coordinates was considered the alignment precision in x and y (σa,x and σa,y), and was typically ~0.1-2 nm for both x and y.
Image Alignment in z.
From repeated experiments, it became apparent that the green and red emission foci differed by ~100 nm. However, since the two-step AO PSF corrections were performed for each experiment, there was some variation in the distance between the foci. Thus, an ~100 nm correction was introduced with the DM by applying a 30 nm rms defocus when switching from the red channel to the green channel so as to more closely position the green and red emission foci. The 30 nm rms defocus was removed when switching back to the red channel. The remaining correction needed for each experiment was obtained by measuring the mean z-position for five 0.1 μm nm beads in each channel (± the 30 nm rms defocus, as appropriate) to accurately determine the distance between the green and red z-calibration curves. With these independent channel calibrations, the standard deviation of the difference between the five mean z-position measurements was ~3-7 nm, which was considered to be the z-alignment precision (σa,z).
Precision.
The precision in x, y, and z was determined as the standard deviation of the measured position over 100 images of 0.1 μm beads embedded in 2% agarose. Precision was measured at various z positions for various excitation intensities and integration times. The z-dependent precisions in x, y, and z were fit using the following equations (Fig. 1f):
| (Eq. 5) |
| (Eq. 6) |
| (Eq. 7a) |
| (Eq. 7b) |
where g1-g10 are fit constants, whose experimentally determined values (Fig. 1f) are used in Supplementary Data 1_Software File 1 and Supplementary Data 2_Software File 2. Eqs. 5 and 6 were modified from Huang et al.31 Eq. 7b is identical to Eq. 7a, except for the minor shift in the minimum provided by g10. To compare values obtained under different conditions, all experimental precision values were normalized to 3000 photons by multiplying the measured precision by (Np/30001/2,82 where Np is the average number of photons per frame over the measurement. To ensure convergence of the fits, g2 and g6 were typically set to −450 and 450 nm.
Localization of the NPC Scaffolds.
The x, y, and z coordinates and photon counts from Thunderstorm analysis for all fluorescence spots were saved within an Excel spreadsheet (“raw image data.csv”). Regions of interest (ROIs) that contained spot clusters likely arising from NPCs were saved in a text file (“cluster details.txt”). The Matlab script “photonandz_filter” was used to curate the data, retaining only those localizations (Extended Data Fig. 2) with z = 0±300 nm, and for which the photon count was ≥ 3000 (output file: “roi_photon_filtered.txt”).
Using “circular_roi”, the individual clusters were size selected, retaining only those with distributions wider than 59 nm and smaller than 153 nm (pairwise point distances 0.5 and 1.3 times the 118 nm camera pixel size, respectively). This process was simplified by plotting the points in a 11.8 nm pixel grid (1/10th of the original camera pixels), where the inter-spot distances were straightforward to determine visually. Clusters that were not round were also rejected, as they would not survive the circle fitting algorithm used later. In practice, this process was fairly straightforward to implement as usable clusters yielded circular shapes of fairly consistent diameter. Occasional random spots not associated with clusters (background) were rejected, and closely spaced clusters were separated. The coordinates for all selected clusters were stored within the text file “roi_all_combine.txt’ and an image file “all clusters.fig” (Extended Data Fig. 2c) was generated for visualization. Using “separate_pores”, the coordinates for individual clusters were extracted into separate text files.
The localizations in each of the individual clusters were then fit to a double circle model, reflecting the double ring structure of NUP96 within the NPC. Since the flatness of the NE suggested minimal tilt of the NPCs (see also Fig. 3), we assumed that the two circles were both parallel to the xy-plane with centers defining an axis parallel to the z-axis. The “double-circle fit” algorithm minimized the the sum of the absolute values of the residuals in the radial- and z-directions. The “estimate_cylinder” script generated the xyz centroid, height and diameter of the cylinder defined by the best-fit double-circle. The “select_pores” script was used to select those clusters having at least 10 points with a diameter of 80-135 nm, a height of 40-65 nm, and z-center of 0±200 nm, according to the double-circle fit (Extended Data Fig. 2d). This double-circle fitting routine was a key step of the process to build the well-resolved NUP96 scaffold in Fig. 2.
To further improve the chosen localization datasets, outlier localizations were removed as follows. “Circlefit_bisquare” was used to fit all cluster localizations to a circle in the xy-plane, i.e., ignoring the z-values. Then, the mean distance to the circle for all localizations was determined (residuals), as well as the standard deviation of the residuals. Those localizations whose residual was more than two standard deviations away from the circle were eliminated, and the “double-circle fit” and “select_pores” scripts were re-run with the remaining points. In practice, very few clusters had points eliminated by this circle fitting process. The localizations for all clusters were then combined based on their xyz centroid to yield the initial NPC scaffold (Figs. 2i,j).
Since the rotational orientation of NPCs in the NE is expected to be random, the alignment of clusters was expected to yield a double torus distribution, which it did (Fig. 2i,j). Though a non-flat angular distribution provides some evidence for non-randomness (Extended Data Fig. 3b), this likely arises from undersampling (N = 10 nuclei) as it is difficult to explain how this could be recovered from different cells on different slides and days. To recover the 8-fold rotationally symmetric distribution of NUP96, the angles of the individual localizations relative to the centroid determined from the double-circle fit were estimated and binned (0-45°), assuming an 8-fold periodicity. The distributions for each individual cluster were then fit to a sinusoidal function with a 45° period and a variable phase. The best-fit phase angle was then used to rotate the individual pore clusters about their xyz centroid, which were then all aligned based on their xyz centroids (Fig. 2k,l). This rotational algorithm was the second key step of the process to building the well-resolved NUP96 scaffold in Fig. 2. Considering the very low number of angle values (~13 on average, Extended Data Fig. 2e) placed in 9 bins, the fits generally were quite poor (Extended Data Fig. 3a). Nonetheless, the result of the rotated and centered individual clusters yielded surprisingly well-isolated clusters clearly revealing the expected 8-fold rotational symmetry (Fig. 2k and Extended Data Fig. 3c).
Cargo Localizations and the Identification of Tracks.
As for the labeled nanobody localizations in the red channel, the multiple movies acquired for cargo trajectories were combined, and the xyz coordinates and photon counts for all fluorescence spots were identified via ThunderStorm (output file: “all green spots.csv”). Due to the substantially faster imaging speed (2 or 3 ms vs. 50 ms for the nanobody), the data were curated with “photon_based_filter”, retaining only those localizations for which the photon count was ≥ 1000 (output file: “spots_photon_filtered.txt”). To correct for the localization mis-match between the green and red channels, the xyz coordinates were corrected using the xyz alignment procedure described earlier using “green_localization_in_red_channel” and (output file: “spots_photon_filtered_calib.txt”). After this coordinate correction, all cargo localizations within a 400 nm cube centered on an NPC centroid (from the double-circle fits of nanobody clusters) were identified using “track_localize_whole_roi”. To align the cargo localizations with the averaged NPC scaffold, localizations were xyz translated and then rotated based on the pore that they were closest to using “centering_tracks_wrt_whole” and “track_rotation_in_whole”. Cargo localizations identified in successive frames and linked to the same NPC were considered to represent the same molecule, and three successive localizations were linked to generate trajectories.
Statistics and Reproducibility.
No statistical method was used to predetermine sample size. Statistical methods, measurement precision, data included in the analysis, and the repeatability of measurements are discussed throughout the text, and supported by simulated data. The “N” values for all the reported measurements and simulations are indicated and defined within the figure legends.
Extended Data
Extended Data Fig. 1. Nanobody Specificity and Fluorescence Background.
a, Specificity of the LaG-9 anti-GFP nanobody. Alexa568-labeled nanobody (100 nM) was added to permeabilized cells, incubated for 3 min and washed twice with IB + PVP. Cells were imaged at the nuclear equator. The top row shows the strong GFP fluorescence (λex = 488 nm) obtained from the mEGFP-tagged NPCs of U-2 OS NUP96-mEGFP cells. The Alexa568 fluorescence (λex = 561 nm) from the tagged nanobody matches the GFP fluorescence. In the bottom row, the wild type U-2 OS cells exhibited no fluorescence in the GFP channel and no nanobody binding. The range of the fluorescence images in the bottom row is 10 times smaller than in the top row, emphasizing the very low signal. These data indicate the high specificity of the nanobody for the GFP domain. Similar results were observed for N = 20 cells over 4 independent experiments. b, Fluorescence background and photobleaching of mEGFP. For all images, permeabilized U-2 OS NUP96-mEGFP cells labeled with HMSiR-labeled nanobodies were excited with λex = 532 nm and emission was collected by a dual bandpass (545-623 nm, 656-763 nm). The mEGFP fluorescence (left) was photobleached after ~2 s of illumination, allowing diffusing M9-βGal(Atto542) cargo complexes to be readily visualized (top right). The HMSiR dye was not detectable (bottom right). Similar results were observed for N = 20 cells over 4 independent experiments.
Extended Data Fig. 2. Workflow for NPC Cluster Selection.
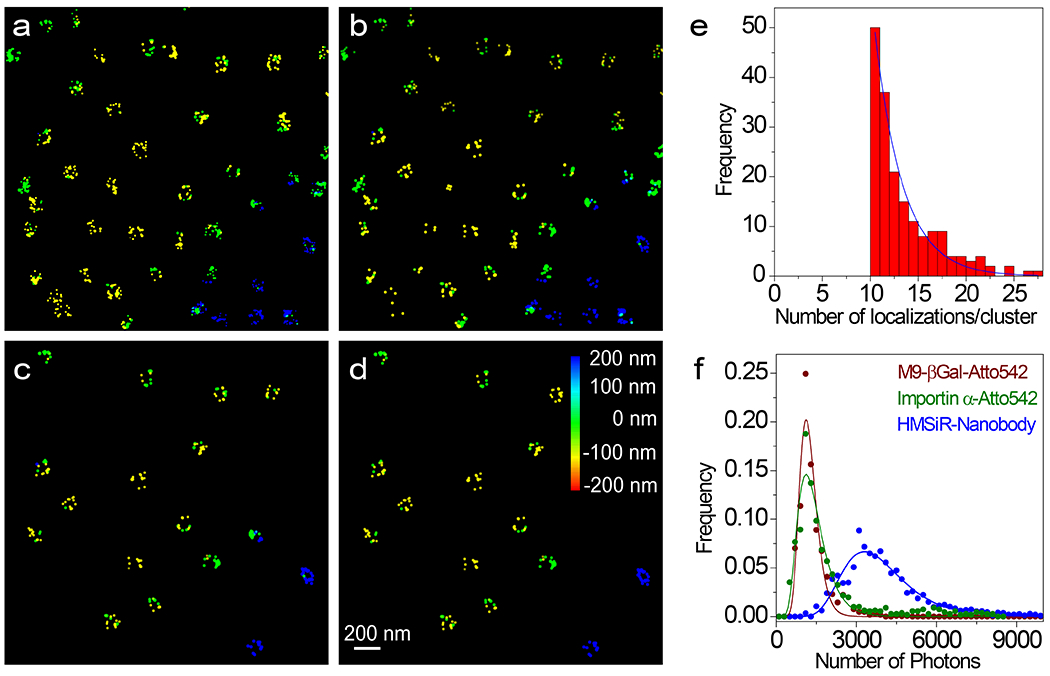
a, Initial image obtained from ThunderSTORM. b, Image after photon filtering (≥ 3000 photons) and z filtering (0±300 nm) (corresponds to Fig. 2e). c, Clusters remaining after applying a rough diameter threshold (59-153 nm) and with ≥ 10 localizations/cluster. d, Clusters remaining after the double-circle fit and subsequent curating (fit diameter = 80-135 nm; distance between the rings = 40-65 nm; z-centroid = 0±200 nm). These remaining clusters are considered well-localized NPCs (image corresponds to Fig. 2h), and were used to construct the composite images in Figs. 2i–l. Dye localizations are color-coded based on z-height. e, Distribution of the number of localizations per cluster for the experiment in Fig. 2. The number of localizations per cluster followed an approximately exponential distribution (decay constant = 2.9) with an average of 13.2 following the filtering described in (a-c) and with a z-centroid = 0±200 nm (N = 2362 total localizations obtained from 142 clusters from 10 nuclei; each nucleus was an independent biological replicate). f, Photon frequency histograms. The HMSiR-labeled nanobody was bound to NPCs (Fig. 2) and the Atto542-labeled M9-βGal and Imp α were undergoing transport (Figs. 4 and 5). The log-normal fit parameters were used for the simulations in Supplementary Data 1_Software File 1 and Supplementary Data 2_Software File 2. Source numerical data are provided in source data.
Extended Data Fig. 3. Rotation of Individual NPC Clusters.
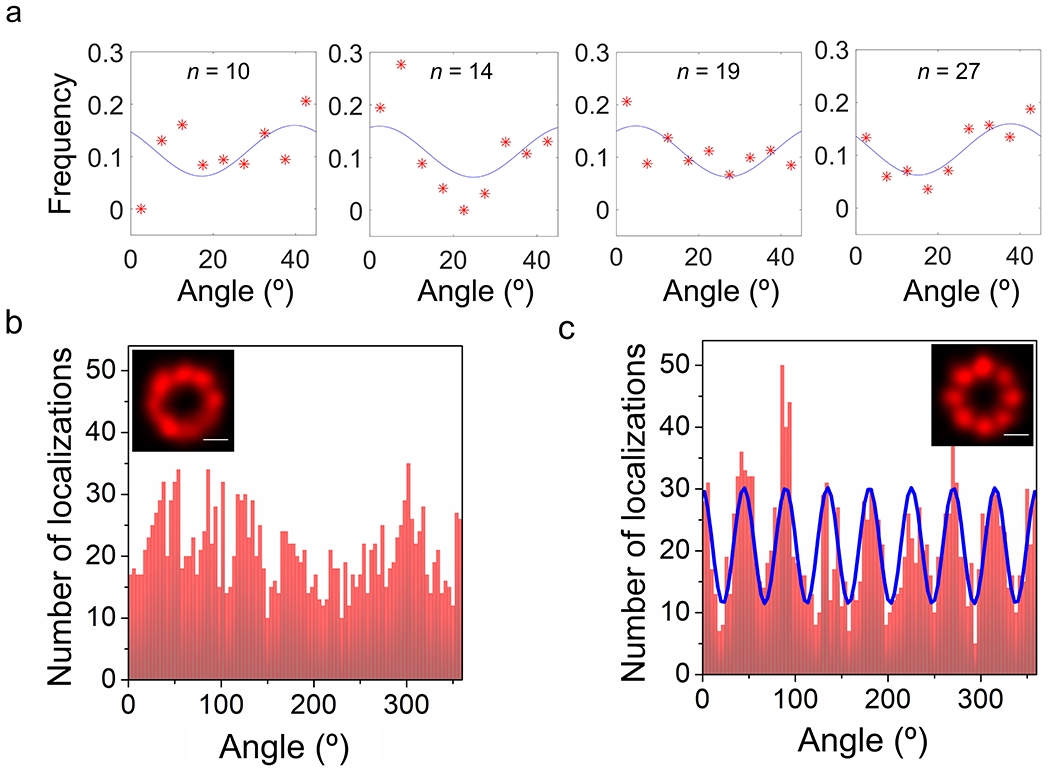
a, Estimating the rotational phase angle (φ). The angles of individual localizations relative to the double-circle centroid of well-localized NPC clusters (Extended Data Fig. 2d) were estimated and binned (5° bins, θ = 0-45°). Four examples are shown here for a range of localizations/cluster (the number of localizations/cluster, n, is given in each figure panel). Distributions were fit to y = 1/9 + (1/20.6)*cos[8(θ-φ)]. The 1/9 term reflects the 9 bins, and the cosine scaling factor is a reasonable average based on simulations. This amplitude scaling factor is insensitive to the goodness-of-fit due to orthogonality – the phase angle shifts the curve laterally, and identical phase angles are obtained by the fitting routine regardless of the scaling factor. The fixed scaling factor enables rapid convergence of the fit. The phase angles from these fits were used to rotate pore clusters before aligning them based on their centroids. b, Angular distribution of localizations in the initially aligned pore clusters (Fig. 2i). Inset: Fig. 2i, bar: 50 nm. c, Angular distribution of rotationally-corrected localizations (Fig. 2k). Inset: Fig. 2k, bar: 50 nm. Pore clusters were rotated based on the phase angle as determined in (a) before aligning. The distribution was fit to y = y0 + c1*sin(8(x-ϕ)), where y0, c1 and ϕ are fit parameters. The minima define the angles of the dashed spokes in Fig. 2m. Source numerical data are provided in source data.
Extended Data Fig. 4. Nuclear Accumulation of M9-βGal and Imp α in Permeabilized U-2 OS NUP96-mEGFP Cells.
a, Nuclear import of M9-βGal(Atto542). The M9-βGal cargo is an ~500 kDa tetramer with four M9 nuclear localization sequences (NLSs) that are recognized by the transportin NTR. Transport reactions were monitored using wide-field fluorescence (λex = 532 nm) in the presence or absence of transportin or RanGTP (RanGDP + GTP) as indicated. The ‘transport mix’ was flowed in at t = 0.5 min. Representative images from four time points are shown (N = 20 cells from 4 independent experiments). [M9-βGal] = 0.25 μM, [transportin] = 0.25 or 1.0 μM, [RanGDP] = 0.5 μM, [NTF2] = 1 μM, [GTP] = 1 mM. b, Kinetics of nuclear import of M9-βGal. Average nuclear fluorescence (±SD) was quantified over time for N = 15 (-transportin), 17 (-RanGTP), or 20 (high and low transportin) cells from 4 independent experiments). Background refers to an area far from the cells. c, Cargo-dependent nuclear uptake of Imp α. Robust accumulation of Imp α(Atto542) into the nucleus (λex = 532 nm) occurs in the presence of the NLS-2xBFP cargo (top row) but not in its absence (bottom row). The range of the fluorescence images in the bottom row is 5 times smaller than in the top row, emphasizing the very low nuclear accumulation (N = 18 cells over 4 independent experiments). [Imp α(Atto542)] = 0.5 μM, [Imp β] = 0.5 μM, [NLS-2xBFP] = 0.5 μM, [RanGDP] = 1.5 μM, [NTF2] = 1 μM and [GTP] = 1 mM. Source numerical data are provided in source data.
Extended Data Fig. 5. Localizations of M9-βGal and NLS-2xBFP Complexes.
a,b, Brief M9-βGal complex appearances. Shown are the localizations from Fig. 4a that remained visible for one (a) or two (b) 3 ms frames. c,d, Brief NLS-2xBFP complex appearances. Shown are the localizations from the experiment in Fig. 5 that remained visible for one (c) or two (d) 2 ms frames. Localizations shown in (a-d) appear randomly distributed, consistent with particles that are largely diffusing and not interacting with the NPC. e, Simulated distribution of particles penetrating a barrier. In this simulation (Supplementary Data 2_Software File 2), particles appeared randomly within two compartments separated by a 50 nm thick barrier with a 100 nm diameter pore. This distribution models the M9-βGal complex localizations in Fig. 4a. The localizations appearing within the barrier result from the precision error, indicating that the localizations observed within the NE region in Fig. 4a are likely a consequence of localization error. For a-e, the N values are the number of localizations from 142 NPCs from 10 nuclei; each nucleus was an independent biological replicate. f,g, Localizations along the transport axis. Distribution of z values for M9-βGal complexes (f; from Figs. 4e,f) and NLS-2xBFP complexes (g; from Figs. 5e,f) undergoing import or abortive import. Distributions are fit to a double Gaussian function yielding mean values (±SD) of −100±48 nm and 68±56 nm for M9-βGal complexes, and −104±82 nm and 122±47 nm for NLS-2xBFP complexes. Source numerical data are provided in source data.
Extended Data Fig. 6. Cargo Complex Diffusion Constants.
a, 3D step-size histogram for M9-βGal complexes. Step sizes of M9-βGal complexes were calculated from consecutive localizations in the trajectories of Fig. 4c (N = 824 total jump distances from 10 nuclei; each nucleus was an independent biological replicate). Data were fit using Eq. 4, yielding three distinct diffusion constants of 0.2 (18%), 0.8 (50%) and 2.6 (32%) μm2/s, or a weighted average diffusion constant of 1.3 μm2/s. b, 3D step-size histogram for NLS-2xBFP complexes. Step sizes of NLS-2xBFP complexes were calculated from consecutive localizations in the trajectories of Fig. 5c (N = 660 total jump distances from 10 nuclei; each nucleus was an independent biological replicate). Fitting the histogram yielded two distinct diffusion constants of 0.6 (25%) and 2.7 (75%) μm2/s, or a weighted average diffusion constant of 2.2 μm2/s. Due to the highly confined, irrregular volume sampled by the cargo complexes, these average diffusion constant estimates are considered both approximate and an underestimate. For comparison, the diffusion constant of the M9-βGal and NLS-2xBFP cargo complexes in aqueous buffer are approximated as ~34 and 55 μm2/s, respectively, using the Stokes-Einstein equation and a protein density of ~1.35 g/cm3.83 Source numerical data are provided in source data.
Supplementary Material
Blinking of the HMSiR Dye on Nanobody-Decorated NPCs. The LaG-9 anti-GFP nanobody labeled with HMSiR was added to permeabilized U-2 OS-CRISPR-NUP96-mEGFP cells, incubated for 3 min and then washed twice. Cells were imaged (50 ms/frame) at the nuclear equator using excitation at 488 nm (GFP fluorescence, green) and 647 nm (HMSiR fluorescence, red). The blinking of HMSiR molecules was observed mostly along the NE. [pixel size = 118 nm]
360° Rotation of the NPC Scaffold. 3D representation of the NPC scaffold from Fig. 2k,l showing the 8-fold rotational symmetry for each of the two rings, constructed using the 3D Viewer plugin in Fiji.1 The image of the NPC is tilted for visualization purposes. The difference in the rotation angles between successive frames is 2°.
Nuclear Import of M9-βGal(Atto542). The M9-βGal(Atto542) cargo (red) was tracked in 3D as in Fig. 4 (3 ms/frame, λex = 532 nm) with an astigmatic PSF. For reference, this video was overlaid onto a 2D AO-corrected wide-field image of the NE showing the location of NPCs tagged with NUP96-mEGFP as in Fig. 2d (λex = 488 nm). This raw image data illustrates the spot shape of the cargo fluorescence changing from elongated in y, to symmetric, to elongated in x as the particle migrates from negative to positive z. [pixel size = 118 nm]
Supplementary Video 4: 3D Super-resolved Nuclear Export of M9-βGal(Atto542)
The position of an NPC scaffold was determined as in Fig. 2f,g from HMSiR localizations. An M9-βGal(Atto542) cargo undergoing nuclear export (approach of Fig. 4) was determined via successive localizations. On the left, the x- and y-coordinates are reflected by the two spatial dimensions, and the color indicates position along the z-coordinate (transport axis). Inset: z-color scale. On the right, the same trajectory is presented in the xz plane, the NPC is identified in red, and the cargo is in green. The abscissa is the x-axis in both cases. Spot widths correspond to the average localization precision based on photon counts. [pixel size = 2.95 nm].
Supplementary Video 5: 3D Super-resolved Nuclear Import of an NLS-2xBFP/Imp α(Atto542)/Imp β Complex
The position of an NPC scaffold was determined as in Fig. 2f,g from HMSiR localizations. An NLS-2xBFP cargo complex undergoing nuclear import (approach of Fig. 5) was determined via successive localizations. On the left, the x- and y-coordinates are reflected by the two spatial dimensions, and the color indicates position along the z-coordinate (transport axis). Inset: z-color scale. On the right, the same trajectory is presented in the xz plane, the NPC is identified in red, and the cargo is in green. The abscissa is the x-axis in both cases. Spot widths correspond to the average localization precision based on photon counts. [pixel size = 2.95 nm].
Supplementary Video 6: 3D Super-resolved Nuclear Abortive Import of an NLS-2xBFP/Imp α(Atto542)/Imp β Complex
The position of an NPC scaffold was determined as in Fig. 2f,g from HMSiR localizations. An NLS-2xBFP cargo complex undergoing abortive import (approach of Fig. 5) was determined via successive localizations. On the left, the x- and y-coordinates are reflected by the two spatial dimensions, and the color indicates position along the z-coordinate (transport axis). Inset: z-color scale. On the right, the same trajectory is presented in the xz plane, the NPC is identified in red, and the cargo is in green. The abscissa is the x-axis in both cases. Spot widths correspond to the average localization precision based on photon counts. [pixel size = 2.95 nm].
This Excel file was used to model the random appearance in 3D of fluorescent spots from labeled NUP96 molecules based on coordinates from the EM density map of the human NPC. The ‘final coordinates’ (output) will automatically recalculate after any of the input parameters are changed. Additional outputs are the average single particle precisions, which are estimated over input z and photon ranges (the photon range is determined by the minimum photons and the log-normal distribution used). See Online Methods and the file itself for additional details.
This Excel file was used to model the random appearance of fluorescence spots appearing in the cytoplasmic and nucleoplasmic compartments and within the NPC central pore (see Extended Data Fig. 5e). See Online Methods and the file itself for additional details.
List of Matlab scripts used for data analysis. All scripts are available at GitHub under https://github.com/npctat2021/npc3d2021
ACKNOWLEDGEMENTS
We thank M. Rout, Y.M. Chook, M.S. Moore, and D. Görlich for the LaG-9 anti-GFP nanobody, transportin, Imp α, and Imp β expression plasmids, respectively, and Jerry Chao for assisting with the double-circle fit Matlab script. This research was supported by the National Institutes of Health (GM126190 to SMM).
Footnotes
COMPETING INTERESTS
The authors declare no competing interests.
CODE AVAILABILITY
The Matlab scripts used to analyze the data are summarized in Supplementary Table 1, and are available at GitHub under https://github.com/npctat2021/npc3d2021.
DATA AVAILABILITY
Raw image and movie data are available from the corresponding author upon reasonable request. All other data supporting the findings of this study are available within the paper and its supplementary information files. Source data are provided with this paper.
REFERENCES
- 1.Ribbeck K & Görlich D Kinetic analysis of translocation through nuclear pore complexes. EMBO J. 20, 1320–1330 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yang W, Gelles J & Musser SM Imaging of single-molecule translocation through nuclear pore complexes. Proc. Natl. Acad. Sci. USA 101, 12887–12892 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kubitscheck U et al. Nuclear transport of single molecules: dwell times at the nuclear pore. J. Cell Biol 168, 233–243 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tu L-C & Musser SM Single molecule studies of nucleocytoplasmic transport. Biochim. Biophys. Acta - Mol. Cell Res 1813, 1607–1618 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Beck M & Hurt E The nuclear pore complex: understanding its function through structural insight. Nat. Rev. Mol. Cell Biol 18, 73–89 (2017). [DOI] [PubMed] [Google Scholar]
- 6.Dickmanns A, Kehlenbach RH & Fahrenkrog B Nuclear pore complexes and nucleocytoplasmic transport: from structure to function to disease. Int. Rev. Cell Mol. Biol 320, 171–233 (2015). [DOI] [PubMed] [Google Scholar]
- 7.Strawn LA, Shen T, Shulga N, Goldfarb DS & Wente SR Minimal nuclear pore complexes define FG repeat domains essential for transport. Nat. Cell Biol 6, 197–206 (2004). [DOI] [PubMed] [Google Scholar]
- 8.Bayliss R, Littlewood T, Strawn LA, Wente SR & Stewart M GLFG and FxFG nucleoporins bind to overlapping sites on importin-β. J. Biol. Chem 277, 50597–50606 (2002). [DOI] [PubMed] [Google Scholar]
- 9.Allen NPC, Huang L, Burlingame A & Rexach M Proteomic analysis of nucleoporin interacting proteins. J. Biol. Chem 276, 29268–29274 (2001). [DOI] [PubMed] [Google Scholar]
- 10.Fiserova J, Richards SA, Wente SR & Goldberg MW Facilited transport and diffusion take distinct spatial routes through the nuclear pore complex. J. Cell Sci 123, 2773–2780 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ma J, Goryaynov A & Yang W Super-resolution 3D tomography of interactions and competition in the nuclear pore complex. Nat. Struct. Mol. Biol 23, 239–247 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang K, Tagliazucchi M, Park SH, Rabin Y & Szleifer I Nanocompartmentalization of the nuclear pore lumen. Biophys. J 118, 219–231 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yamada J et al. A bimodal distribution of two distinct categories of intrinsically-disordered structures with separate functions in FG nucleoporins. Mol. Cell. Proteomics 9, 2205–2224 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Peleg O & Lim RY Converging on the function of intrinsically disordered nucleoporins in the nuclear pore complex. Biol. Chem 391, 719–730, doi: 10.1515/BC.2010.092 (2010). [DOI] [PubMed] [Google Scholar]
- 15.Kim SJ et al. Integrative structure and functional anatomy of a nuclear pore complex. Nature 555, 475–482 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Beck M, Lucic V, Förster F, Baumeister W & Medalia O Snapshots of nuclear pore complexes in action captured by cryo-electron tomography. Nature 449, 611–615 (2007). [DOI] [PubMed] [Google Scholar]
- 17.Ma J & Yang W Three-dimensional distribution of transient interactions in the nuclear pore complex obtained from single molecule snapshots. Proc. Natl. Acad. Sci. USA 107, 7305–7310 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Maimon T, Elad N, Dahan I & Medalia O The human nuclear pore complex as revealed by cryo-electron tomography. Structure 20, 998–1006 (2012). [DOI] [PubMed] [Google Scholar]
- 19.Bui KH et al. Integrated structural analysis of the human nuclear pore complex scaffold. Cell 155, 1233–1243 (2013). [DOI] [PubMed] [Google Scholar]
- 20.Mohr D, Frey S, Fischer T, Güttler T & Görlich D Characterization of the passive permeability barrier of nuclear pore complexes. EMBO J. 28, 2541–2553 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Timney BL et al. Simple rules for passive diffusion through the nuclear pore complex. J. Cell Biol 215, 57–76 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Suntharalingam M & Wente SR Peering through the pore: nuclear pore complex structure, assembly, and function. Dev. Cell 4, 775–589 (2003). [DOI] [PubMed] [Google Scholar]
- 23.Milles S et al. Plasticity of an ultrafast interaction between nucleoporins and nuclear transport receptors. Cell 163, 734–745 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schmidt HB & Görlich D Transport selectivity of nuclear pores, phase separation, and membraneless organelles. Trends Biochem. Sci 41, 46–61 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Zahn R et al. A physical model describing the interaction of nuclear transport receptors with FG nucleoporin domain assemblies. eLife 5, e14119 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Eibauer M et al. Structure and gating of the nuclear pore complex. Nat. Comm 6, 7532 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Löschberger A et al. Super-resolution imaging visualizes the eightfold symmetry of gp210 proteins around the nuclear pore complex and resolves the central channel with nanometer resolution. J. Cell Sci 125, 570–575 (2012). [DOI] [PubMed] [Google Scholar]
- 28.Thevathasan JV et al. Nuclear pores as versatile reference standards for quantitative superresolution microscopy. Nat. Meth 16, 1045–1053 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schlichthaerle T et al. Direct visualization of single nuclear pore complex proteins using genetically-encoded probes for DNA-PAINT. Angew. Chem. Int. Ed 58, 13004–13008 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yoo TY & Mitchison TJ O-GlcNAc modification of nuclear pore complexes accelerates bidirectional transport. J. Cell Biol 220, e202010141 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huang B, Wang W, Bates M & Zhuang X Three-dimensional super-resolution imaging by stochastic optical reconstruction microscopy. Science 319, 810–813 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sahl SJ, Hell SW & Jakobs S Fluorescence nanoscopy in cell biology. Nat. Rev. Mol. Cell Biol 18, 685–701 (2017). [DOI] [PubMed] [Google Scholar]
- 33.von Diezmann A, Shechtman Y & Moerner WE Three-dimensional localization of single molecules for super-resolution imaing and single-particle tracking. Chem. Rev 117, 7244–7275 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fridy PC et al. A robust pipeline for rapid production of versatile nanobody repertoires. Nat. Meth 11, 1253–1260 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Uno S et al. A spontaneously blinking fluorophore based on intramolecular spirocyclization for live-cell super-resolution imaging. Nat. Chem 6, 681–689 (2014). [DOI] [PubMed] [Google Scholar]
- 36.Daigle N et al. Nuclear pore complexes form immobile networks and have a very low turnover in live mammalian cells. J. Cell Biol 154, 71–84 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Musser SM & Grünwald D Deciphering the structure and function of nuclear pores using single-molecule fluorescence approaches. J. Mol. Biol 428, 2091–2119 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chu F-Y, Haley SC & Zidovska A On the origin of shape fluctuations of the cell nucleus. Proc. Natl. Acad. Sci. U.S.A 114, 10338–10343 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yang W & Musser SM Nuclear import time and transport efficiency depend on importin β concentration. J. Cell Biol 174, 951–961 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tu L-C, Fu G, Zilman A & Musser SM Large cargo transport by nuclear pores: implications for the spatial organization of FG-nucleoporins. EMBO J. 32, 3220–3230 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Grossman E, Medalia O & Zwerger M Functional architecture of the nuclear pore complex. Annu. Rev. Biophys 41, 557–584 (2012). [DOI] [PubMed] [Google Scholar]
- 42.Chook YM & Blobel G Karyopherins and nuclear import. Curr. Opin. Struct. Biol 11, 703–715 (2001). [DOI] [PubMed] [Google Scholar]
- 43.Ananth AN et al. Spatial structure of disordered proteins dictates conductance and selectivity in nuclear pore complex mimics. eLife 7, e31510 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pulupa J, Rachh M, Tomasini MD, Mincer JS & Simon SM A coarse-grained computational model of the nuclear pore complex predicts Phe-Gly nucleoporin dynamics. J. Gen. Physiol 149, 951–966 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fiserova J, Spink M, Richards SA, Saunter C & Goldberg MW Entry into the nuclear pore complex is controlled by a cytoplasmic exclusion zone containing dynamic GLFG-repeat nucleoporin domains. J. Cell Sci 127, 124–136 (2014). [DOI] [PubMed] [Google Scholar]
- 46.Ma J et al. High-resolution three-dimensional mapping of mRNA export through the nuclear pore. Nat. Comm 4, 2414 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yang W & Musser SM Visualizing single molecules transiting through nuclear pore complexes with narrow-field epifluorescence microscopy. Methods 39, 3316–3328 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sun C, Yang W, Tu L-C & Musser SM Single molecule measurements of importin α/cargo complex dissociation at the nuclear pore. Proc. Natl. Acad. Sci. USA 105, 8613–8618 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kobe B Autoinhibition by an internal nuclear localization signal revealed by the crystal structure of mammalian importin α. Nat. Struct. Biol 6, 388–397 (1999). [DOI] [PubMed] [Google Scholar]
- 50.Lott K & Cingolani G The importin β binding domain as a master regulator of nucleocytoplasmic transport. Biochim. Biophys. Acta 1813, 1578–1592 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Peters R Translocation through the nuclear pore complex: selectivity and speed by reduction-of-dimensionality. Traffic 6, 421–427 (2005). [DOI] [PubMed] [Google Scholar]
- 52.Schuller AP et al. The cellular environment shapes the nuclear pore complex architecture. Nature, Advance online publication (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zila V et al. Cone-shaped HIV-1 capsids are transported through intact nuclear pores. Cell 184, 1032–1046 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tu L-C, Huisman M, Chung Y-C, Smith CS & Grunwald D Deconstructing transport-distribution reconstruction in the nuclear-pore complex. Nat. Struct. Mol. Biol 25, 1061–1062 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ruba A, Kelich J, Ma J & Yang W Reply to ‘Deconstructing transport-distribution reconstruction in the nuclear-pore complex’. Nat. Struct. Mol. Biol 25, 1061–1064 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Onischenko E et al. Natively unfolded FG repeats stabilize the structure of the nuclear pore complex. Cell 171, 904–917.e919 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rout MP, Aitchison JD, Magnasco MO & Chait BT Virtual gating and nuclear transport: the hole picture. Trends Cell Biol. 13, 622–628 (2003). [DOI] [PubMed] [Google Scholar]
- 58.Frey S, Richter RP & Görlich D FG-rich repeats of nuclear pore proteins form a three-dimensional meshwork with hydrogel-like properties. Science 314, 815–817 (2006). [DOI] [PubMed] [Google Scholar]
- 59.Lim RYH et al. Nanomechanical basis of selective gating by the nuclear pore complex. Science 318, 640–643, doi: 10.1126/science.1145980 (2007). [DOI] [PubMed] [Google Scholar]
- 60.Kapinos LE, Schoch RL, Wagner RS, Schleicher KD & Lim RYM Karyophein-centric control of nuclear pores based on molecular occupancy and kinetic analysis of multivalent binding with FG nucleoporins. Biophys. J 106, 1751–1762 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Strambio-de-Castillia C, Niepel M & Rout MP The nuclear pore complex: bridging nuclear transport and gene regulation. Nat. Rev. Mol. Cell Biol 11, 490–501 (2010). [DOI] [PubMed] [Google Scholar]
- 62.Walther TC et al. The cytoplasmic filaments of the nuclear pore complex are dispensable for selective nuclear protein import. J. Cell Biol 158, 63–77 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ben-Efraim I, Frosst PD & Gerace L Karyopherin binding interactions and nuclear import mechanism of nuclear pore complex protein Tpr. BMC Cell Biol. 10, 74 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Goldberg MW Nuclear pore complex tethers to the cytoskeleton. Semin. Cell Dev. Biol 68, 52–58 (2017). [DOI] [PubMed] [Google Scholar]
- 65.Simon DN & Wilson KL The nucleoskeleton as a genome-associated dynamic ‘network of networks’. Nat. Rev. Mol. Cell Biol 12, 695–708 (2011). [DOI] [PubMed] [Google Scholar]
- 66.Ovesný M, Křížek P, Borkovec J, Švindrych Z & Hagen GM ThunderSTORM: a comprehensive ImageJ plugin for PALM and STORM data analysis and super-resolution imaging. Bioinformatics 30, 2389–2390 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.von Appen A et al. In situ structural analysis of the human nuclear pore complex. Nature 526, 140–143 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Chowdhury R, Sau A & Musser SM Super-resolved 3D tracking of cargo transport through nuclear pore complexes by astigmatism imaging. Protocol Exchange, [DOI to be added when available] (2021). [Google Scholar]
ONLINE METHODS REFERENCES
- 69.Kutay U, Izaurralde E, Bischoff FR, Mattaj IW & Görlich D Dominant-negative mutants of importin-beta block multiple pathways of import and export through the nuclear pore complex. EMBO J. 16, 1151–1163 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Görlich D, Prehn S, Laskey RA & Hartmann E Isolation of a protein that is essential for the first step of nuclear protein import. Cell 79, 767–778 (1994). [DOI] [PubMed] [Google Scholar]
- 71.Ribbeck K, Lipowsky G, Kent HM, Stewart M & Görlich D NTF2 mediates nuclear import of Ran. EMBO J. 17, 6587–6598 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lyman SK, Guan T, Bednenko J, Wodrich H & Gerace L Influence of cargo size on Ran and energy requirements for nuclear protein import. J. Cell Biol 159, 55–67 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Yoshizawa T et al. Nuclear import receptor inhibits phase separation of FUS through binding to multiple sites. Cell 173, 693–705 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Heim R, Prasher DC & Tsien RY Wavelength mutations and posttranslational autooxidation of green fluorescent protein. Proc. Natl. Acad. Sci. USA 91, 12501–12504 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Kent HM, Clarkson WD, Bullock TL & Stewart M Crystallization and preliminary X-ray diffraction analysis for nuclear transport factor 2. J. Struct. Biol 116, 326–329 (1996). [DOI] [PubMed] [Google Scholar]
- 76.Schwoebel ED, Talcott B, Cushman I & Moore MS Ran-dependent signal-mediated nuclear import does not require GTP hydrolysis by Ran. J. Biol. Chem 273, 35170–35175 (1998). [DOI] [PubMed] [Google Scholar]
- 77.Débarre D, J. BM & Wilson T Image based adaptive optics through optimization of low spatial frequencies. Opt. Express 15, 8176–8190 (2007). [DOI] [PubMed] [Google Scholar]
- 78.Berg HC Random Walks in Biology. (Princeton University Press, 1993). [Google Scholar]
- 79.Kues T, Peters R & Kubitscheck U Visualization and tracking of single protein molecules in the cell nucleus. Biophys. J 80, 2954–2967 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Schindelin J et al. Fiji: an open-source platform for biological-image analysis. Nat. Meth 9, 676–682 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Fu G, Tu L-C, Zilman A & Musser SM Investigating molecular crowding within nuclear pores using polarization-PALM. eLife 6, e28716 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Mortensen KI, Churchman LS, Spudich JA & Flyvbjerg H Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat. Meth 7, 377–381 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Fischer H, Polikarpov I & Craievich AF Average protein density is a molecular-weight-dependent function. Protein Sci. 13, 2825–2828 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Blinking of the HMSiR Dye on Nanobody-Decorated NPCs. The LaG-9 anti-GFP nanobody labeled with HMSiR was added to permeabilized U-2 OS-CRISPR-NUP96-mEGFP cells, incubated for 3 min and then washed twice. Cells were imaged (50 ms/frame) at the nuclear equator using excitation at 488 nm (GFP fluorescence, green) and 647 nm (HMSiR fluorescence, red). The blinking of HMSiR molecules was observed mostly along the NE. [pixel size = 118 nm]
360° Rotation of the NPC Scaffold. 3D representation of the NPC scaffold from Fig. 2k,l showing the 8-fold rotational symmetry for each of the two rings, constructed using the 3D Viewer plugin in Fiji.1 The image of the NPC is tilted for visualization purposes. The difference in the rotation angles between successive frames is 2°.
Nuclear Import of M9-βGal(Atto542). The M9-βGal(Atto542) cargo (red) was tracked in 3D as in Fig. 4 (3 ms/frame, λex = 532 nm) with an astigmatic PSF. For reference, this video was overlaid onto a 2D AO-corrected wide-field image of the NE showing the location of NPCs tagged with NUP96-mEGFP as in Fig. 2d (λex = 488 nm). This raw image data illustrates the spot shape of the cargo fluorescence changing from elongated in y, to symmetric, to elongated in x as the particle migrates from negative to positive z. [pixel size = 118 nm]
Supplementary Video 4: 3D Super-resolved Nuclear Export of M9-βGal(Atto542)
The position of an NPC scaffold was determined as in Fig. 2f,g from HMSiR localizations. An M9-βGal(Atto542) cargo undergoing nuclear export (approach of Fig. 4) was determined via successive localizations. On the left, the x- and y-coordinates are reflected by the two spatial dimensions, and the color indicates position along the z-coordinate (transport axis). Inset: z-color scale. On the right, the same trajectory is presented in the xz plane, the NPC is identified in red, and the cargo is in green. The abscissa is the x-axis in both cases. Spot widths correspond to the average localization precision based on photon counts. [pixel size = 2.95 nm].
Supplementary Video 5: 3D Super-resolved Nuclear Import of an NLS-2xBFP/Imp α(Atto542)/Imp β Complex
The position of an NPC scaffold was determined as in Fig. 2f,g from HMSiR localizations. An NLS-2xBFP cargo complex undergoing nuclear import (approach of Fig. 5) was determined via successive localizations. On the left, the x- and y-coordinates are reflected by the two spatial dimensions, and the color indicates position along the z-coordinate (transport axis). Inset: z-color scale. On the right, the same trajectory is presented in the xz plane, the NPC is identified in red, and the cargo is in green. The abscissa is the x-axis in both cases. Spot widths correspond to the average localization precision based on photon counts. [pixel size = 2.95 nm].
Supplementary Video 6: 3D Super-resolved Nuclear Abortive Import of an NLS-2xBFP/Imp α(Atto542)/Imp β Complex
The position of an NPC scaffold was determined as in Fig. 2f,g from HMSiR localizations. An NLS-2xBFP cargo complex undergoing abortive import (approach of Fig. 5) was determined via successive localizations. On the left, the x- and y-coordinates are reflected by the two spatial dimensions, and the color indicates position along the z-coordinate (transport axis). Inset: z-color scale. On the right, the same trajectory is presented in the xz plane, the NPC is identified in red, and the cargo is in green. The abscissa is the x-axis in both cases. Spot widths correspond to the average localization precision based on photon counts. [pixel size = 2.95 nm].
This Excel file was used to model the random appearance in 3D of fluorescent spots from labeled NUP96 molecules based on coordinates from the EM density map of the human NPC. The ‘final coordinates’ (output) will automatically recalculate after any of the input parameters are changed. Additional outputs are the average single particle precisions, which are estimated over input z and photon ranges (the photon range is determined by the minimum photons and the log-normal distribution used). See Online Methods and the file itself for additional details.
This Excel file was used to model the random appearance of fluorescence spots appearing in the cytoplasmic and nucleoplasmic compartments and within the NPC central pore (see Extended Data Fig. 5e). See Online Methods and the file itself for additional details.
List of Matlab scripts used for data analysis. All scripts are available at GitHub under https://github.com/npctat2021/npc3d2021
Data Availability Statement
Raw image and movie data are available from the corresponding author upon reasonable request. All other data supporting the findings of this study are available within the paper and its supplementary information files. Source data are provided with this paper.


