Tutorial on Directed Acyclic Graphs

Abstract

Directed acyclic graphs (DAGs) are an intuitive yet rigorous tool to communicate about causal questions in clinical and epidemiologic research and inform study design and statistical analysis. DAGs are constructed to depict prior knowledge about biological and behavioral systems related to specific causal research questions. DAG components portray who receives treatment or experience exposures; mechanisms by which treatments and exposures operate; and other factors that influence the outcome of interest or which persons are included in an analysis. Once assembled, DAGs — via a few simple rules — guide the researcher in identifying whether the causal effect of interest can be identified without bias and, if so, what must be done either in study design or data analysis to achieve this. Specifically, DAGs can identify variables that, if controlled for in the design or analysis phase, are sufficient to eliminate confounding and some forms of selection bias. DAGs also help recognize variables that, if controlled for, bias the analysis (e.g., mediators or factors influenced by both exposure and outcome). Finally, DAGs help researchers recognize insidious sources of bias introduced by selection of individuals into studies or failure to completely observe all individuals until study outcomes are reached. DAGs, however, are not infallible, largely owing to limitations in prior knowledge about the system in question. In such instances, several alternative DAGs are plausible, and researchers should assess whether results differ meaningfully across analyses guided by different DAGs and be forthright about uncertainty. DAGs are powerful tools to guide the conduct of clinical research.

1. Introduction: DAGs represent sets of hypothesized or assumed causal relationships

In clinical epidemiology, domains of inquiry include characterization of diagnostic tests, generation of prediction models for prognosis, and evaluation of the efficacy/effectiveness of treatments, including why they work and for whom they work best. These latter domains more generally fall into the objectives of causation, mediation, and interaction. The pursuit of research questions with these three objectives has been greatly aided in recent decades by the development of an intuitive yet rigorous tool for communication called directed acyclic graphs (DAGs) (1,2).

DAGs depict an investigator’s hypotheses or assumptions about the biological or behavioral systems that determine who receives treatment; mechanisms by which treatment operates on a specific outcome; factors that influence which patients are included in a data analysis; and other determinants of the outcome of interest (Figure 1). DAGs are composed of variables (also called nodes; e.g., representing treatments, exposures, health outcomes, or patient characteristics) and arrows (also called edges), which depict known or suspected causal relationships between variables. To create a DAG one must specify: 1) the causal question of interest, thus necessitating inclusion of exposure/treatment (which we call E) and outcome of interest (D); 2) variables that might influence both E (or a mediator of interest) and D; 3) discrepancies between the ideal measures of the variables and measurements actually available to researchers; 4) selection factors that influence which patients are represented in the study population; and 5) potential causal relationships among these variables (depicted as arrows connecting variables). Even if a variable was not measured in the available data (or cannot be measured in most practical settings), it should nonetheless be represented in the DAG. Because the list of potential unmeasured variables can be long, a common convention visually simplifies by representing all unmeasured variables with the same causal structure (i.e., the same arrows in and out) as a single node.

Figure 1:

Directed acyclic graph illustrating key concepts and terms.

• Paths are sequences of arrows, of any direction, connecting two variables and may be causal or non-causal.
• Paths are causal if each variable causes the subsequent variable (all the arrows point in the same direction).
• Paths are non-causal if the arrows do not all point in the same direction. They contain confounders and/or colliders.
• Confounding occurs because of common (shared) causes (e.g., C) of E and D. To estimate the effect of E on D, it is necessary to control for such common causes or other variables along the non-causal path. For example, control for either C or G would be adequate to eliminate the confounding due to C. G may be preferable, for example if it is easier to obtain a high-quality measurement of G.
• Mediators (e.g., M) are caused by E and, in turn, cause D. They should not be controlled for to estimate the total effect of E on D.
• Colliders (e.g., S) are so named because they have two arrows pointing into them. Colliders on a path block that path unless they are conditioned on (e.g., by controlling for them) or a consequence of the collider is conditioned on.
• Analyses should not adjust for, stratify on, or in any way condition on descendants of D (e.g., Z).
• Instrumental variables (e.g., I) are variables related to the exposure of interest that have no association with the outcome except through the exposure. Instrumental variables analysis (a technique common in the economics literature) can be used to derive effect estimates when there is intractable confounding of E and D.
• Effect modifiers (e.g., J) are variables that cause D and modify the effect of other causes of D, such as E. If E and J both cause D, then J modifies the effect of E on D on at least one effect-measure scale (additive or multiplicative).

2. A simple set of rules for interpreting DAGs makes them useful to guide study design and analyses

Studies intended to estimate the causal effect of E on D must eliminate other, non-causal sources of association between E and D. To accomplish this, the essential insight is that after ruling out the role of chance, we expect an association between E and D if any of the following is true: E causes D; D causes E; some third factor (called a “common” cause in DAG terminology) influences both E and D (i.e., confounding); or, least intuitively, we have selected or controlled for a third factor (a “collider” in DAG terminology) that is caused by both E and D or by causes of E and D. Accordingly, to estimate the casual effect of E on D, we must specify a study design or analytic plan so all and only non-causal paths on the DAG connecting E and D are “blocked”. A path can be blocked by controlling for a variable that is a common cause (e.g., C in Figure 1, ←C→) or intermediary mechanism (e.g., G in Figure 1, →G→) on the path. A path is also blocked if there is a collider on the path (e.g., a variable with two arrows pointing into it, S in Figure 1, →S←) that has not been controlled or adjusted for in any way. If the DAG correctly represents all confounding, measurement error, and selection processes, blocking all non-causal paths eliminates these biases. If all and only non-causal paths are blocked, then any statistical association found between E and D can be considered an unbiased estimate of a causal effect of E on D.

3. DAGs enable clear communication

Narrative explanations of research questions are open to different interpretations. Does the claim: “W accounts for the association between E and D” mean that W is a confounder of the relationship between E and D or that W is a mediator between E and D? Drawing a DAG lays it bare. “E is a risk factor for D” might mean that E causes D or that E is associated with D only because of confounding by some other factor. DAGs are particularly useful in distinguishing causation vs. prediction objectives. DAGs foster communication between colleagues and are especially beneficial for interdisciplinary understanding (e.g., between subject matter experts and those responsible for study design and data analysis). We consider drawing DAGs the first step when conceiving research questions and believe a DAG is often the appropriate Figure 1 in research proposals and papers. While especially useful for observational studies, DAGs can also represent potential biases in randomized trials, such as loss-to-follow-up, unexpected mechanisms of effects, or measurement error (3).

4. DAGs inform us about how to avoid bias due to confounding

Researchers commonly grapple with how to define confounding and what variables must be accounted for via study design or statistical analysis to eliminate confounding. In the past, change-in-estimate methods, statistical criteria, and other techniques have all been popular to identify confounders, but these approaches may not fully capture all variables required to control confounding and could erroneously introduce bias by suggesting control for the wrong variables (4). In contrast, DAGs have greatly clarified confounding by depicting it as the consequence of common causes of the exposure and outcome under study. DAGs also shed light on how to control for confounding by blocking confounding paths, even if the common cause itself is unmeasured (see explanation of C and G in Figure 1). Furthermore, use of DAGs can help investigators recognize multiple alternative variable sets that would be sufficient to estimate the causal effect of interest; some sets of variables may be preferable for reasons such as ease or quality of measurement.

When no set of measured variables is sufficient to control confounding, DAGs can aid in recognition of novel approaches, such as instrumental variables (I in Figure 1). Instrumental variables are constructs that are related to the exposure of interest but have no association with the outcome except through the exposure. Instrumental variables can sometimes rescue observational studies when conventional means of confounding management are intractable. Mendelian Randomization studies are an increasingly popular type of instrumental variable study, in which a genetic variant is used to evaluate effects of a phenotype it influences. DAGs also allow critical evaluation of instrumental variables, as in the discussion around Mendelian Randomization (5). Finally, users can integrate prior knowledge about the signs (positive or negative) or plausible strength of paths in a DAG to guide bias analysis and anticipate the sign or magnitude of bias due to uncontrolled confounding (6,7).

Some investigators believe there is little harm in adjusting for extra variables — it seems the longer the list, the more thorough the control. However, DAGs expose the hazards of indiscriminate adjustment (8). Specifically, DAGs illustrate how adjustment for mediators of causal pathways of interest (M in Figure 1); variables that are affected by both E and determinants of D under study (S in Figure 1); or descendants of outcomes (Z in Figure 1) can induce bias. Even rules that seem clear in theory (“don’t adjust for anything downstream of the exposure”) are sometimes violated in practice. For example, in a study of the effect of stroke on functional decline, researchers may be inclined to control for stroke severity as measured by the National Institutes of Health Stroke Scale (Figure 2a). However, items on this scale (e.g. level of consciousness) are consequences of stroke rather than causes of it. Thus, controlling for scale score is likely to block part of the effect of stroke on functional decline, attenuating effect sizes. By forcing researchers to be explicit about their causal beliefs, DAGs help researchers avoid such violations.

Figure 2:

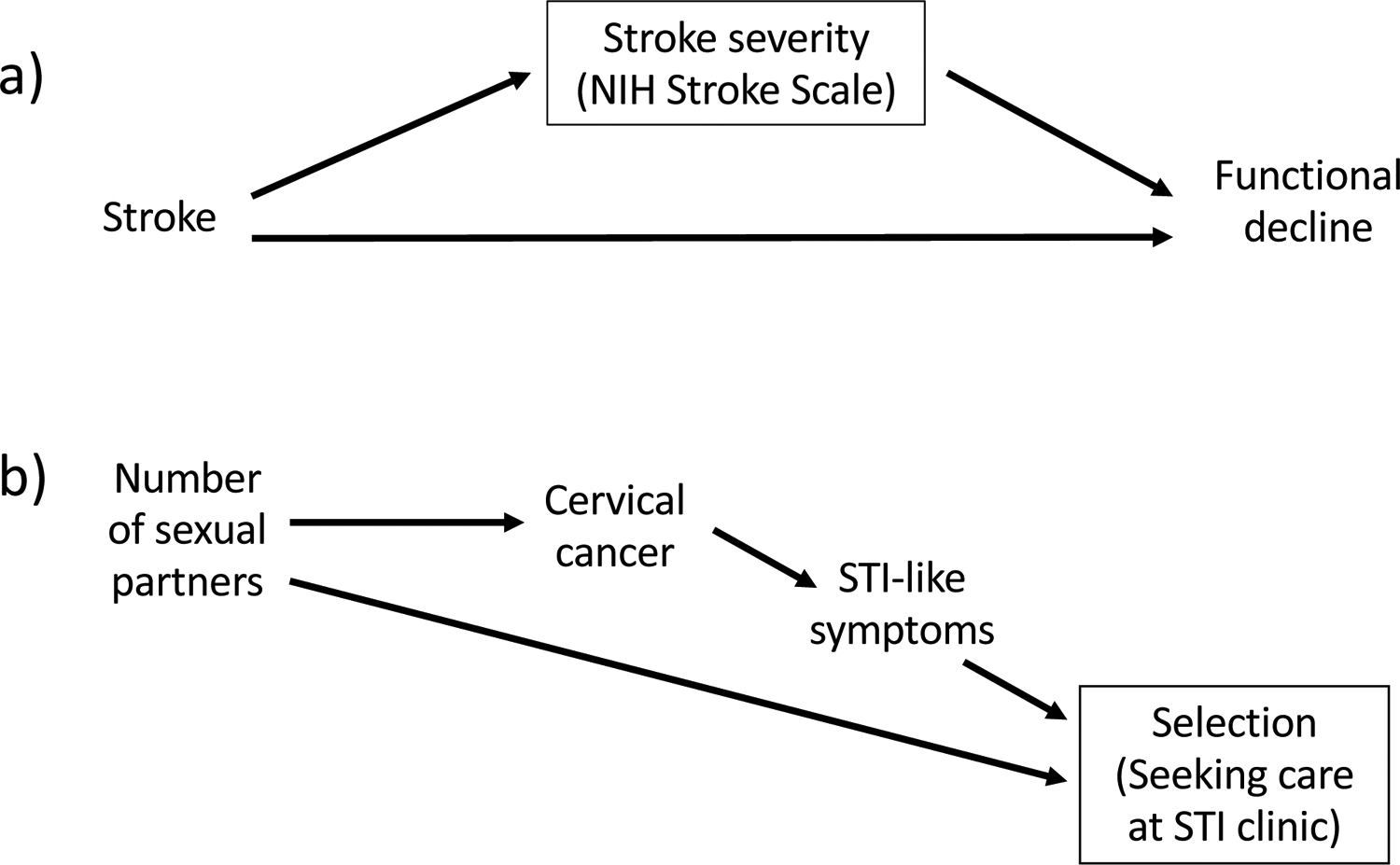
Examples of settings in which controlling for or restricting on a variable can introduce bias. A box around a variable denotes conditioning on that variable.

Panel a) Depiction of controlling for a mediating variable. Stroke severity is a consequence of stroke and adjusting for it blocks one pathway through which stroke causes functional decline, attenuating the estimated effect size.

Panel b) Depiction of selection bias in a study estimating the effect of the number of sexual partners on cervical cancer. Here, to be included in the study, participants had to have sought care at an STI clinic. Because seeking care at an STI clinic is influenced by both the exposure and the outcome (i.e., it is a collider), the estimate of the causal effect of interest will be biased.

5. DAGs aid in recognition of potential selection bias

Selection due to initial recruitment or subsequent retention or survival can be represented on a DAG as a variable whose range is effectively restricted (e.g., participation in the study is a variable that must be “yes” for all people included in the analysis) (9,10). If selection into the study is influenced by both E and D (or an early manifestation of D), DAGs reveal that this selection process can create a spurious association between exposure and disease. For example, suppose a study aiming to estimate the effect of number of sexual partners on cervical cancer enrolled participants from a clinic specializing in treating sexually transmitted infections (STIs). Because number of sexual partners influences risk of STIs, the exposure of interest in the study will affect the likelihood an individual is included in the study. Similarly, particularly in resource-limited settings, symptoms of cervical cancer may be misinterpreted as STI symptoms, leading a patient to seek care at an STI clinic. These two processes — both E and D influencing selection into the study — can be represented in a DAG (Figure 2b) to reveal that bias would potentially occur with enrollment from an STI clinic. In this example, the bias would tend to attenuate any true effect of number of sexual partners on cervical cancer. Similar selection processes have been implicated in many conundrums previously described as “paradoxes”, including the birthweight paradox (11) and the obesity paradox (12).

6. Limitations of DAGs

Although greatly outweighed by their strengths, DAGs do have limitations. First, drawing DAGs forces us to admit that, often, because of limitations in our prior knowledge, we may not know which of several possible DAGs is correct. In this case, it is useful to assess whether results differ meaningfully across analyses guided by different DAGs and be honest about our uncertainty. Second, DAGs do not convey information about magnitude or functional form of causal relationships and therefore are not ideal tools to definitively represent effect-measure modification or moderators. For example, in Figure 1, J causes D. J therefore modifies the effect on D of any other cause of D on at least one scale (additive or multiplicative). However, the DAG does not represent information about the scale, magnitude, or even direction of the interaction (13). To definitively evaluate for the presence of effect-measure modification, an empiric analysis of data must be performed. Third, to display feedback loops, time-ordering must be explicitly represented on DAGs (e.g., weight at age 50 may cause stroke at age 60 which may cause weight at age 70) (7). Such DAGs can be overwhelmingly complicated and do not well-represent processes for which feedback occurs more quickly than the time scale of data collection (e.g., level of SARS-CoV-2 antigen and antibody response). Fourth, most work using DAGs assumes that treatment of one individual does not influence outcomes of another individual, so modifications must be made to study processes like population immunity or contagion (14). Fifth, DAGs are primarily applied in settings with causal questions, rather than prediction problems such as diagnostic tests or prognostic models. The role of DAGs in these settings is evolving, however, for example with recent applications in evaluating unfair discrimination in machine learning algorithms (15). Finally, DAGs are not an analysis approach and do not replace the need for numerous statistical modeling decisions (7).

7. Conclusion

DAGs are powerful and easy-to-learn tools to sharpen communication and guide the conduct of research. DAGS also reveal the weakest links or most questionable assumptions in any study. Additional examples of applications of DAGs can be found in (16–18). Adopting DAGs as the standard language for all research related to causation, mediation and interaction would foster precise and efficient communication and improve the quality of many clinical research efforts.