Big Data to Knowledge: Application of Machine Learning to Predictive Modeling of Therapeutic Response in Cancer

Abstract

Background

In recent years, the availability of high throughput technologies, establishment of large molecular patient data repositories, and advancement in computing power and storage have allowed elucidation of complex mechanisms implicated in therapeutic response in cancer patients. The breadth and depth of such data, alongside experimental noise and missing values, requires a sophisticated human-machine interaction that would allow effective learning from complex data and accurate forecasting of future outcomes, ideally embedded in the core of machine learning design.

Objective

In this review, we will discuss machine learning techniques utilized for modeling of treatment response in cancer, including Random Forests, support vector machines, neural networks, and linear and logistic regression. We will overview their mathematical foundations and discuss their limitations and alternative approaches in light of their application to therapeutic response modeling in cancer.

Conclusion

We hypothesize that the increase in the number of patient profiles and potential temporal monitoring of patient data will define even more complex techniques, such as deep learning and causal analysis, as central players in therapeutic response modeling.

1. INTRODUCTION

In recent years, the availability of high throughput technologies, the establishment of large molecular patient data repositories such as TCGA [1], SU2C [2], TARGET [3], etc., and advancement in computing power and storage [4, 5] have allowed elucidation of complex mechanisms implicated in cancer progression and therapeutic response [2, 6-15], building a foundation for the development of personalized medicine and precision therapeutics. Such molecular data, spanning clinical information, human genome, epigenome, and transcriptome, is referred to as Big Data and, if utilized effectively, holds a promise to make individualized predictions of therapeutic response directly at diagnosis and in real time [7, 13, 16, 17], enhancing clinical decision making and improving patient outcomes.

The volume and depth of such data, alongside experimental noise and missing values, requires a sophisticated human-machine interaction that would allow effective learning from complex data and accurate predictions of the future outcomes based on the learning experiences even in the presence of noise, ideally embedded in the core of machine learning (ML) design. In 1950, “Turing test” evaluated machine's ability to exhibit intelligent behavior equivalent to a human [18]. Following its success, machine learning officially originated in 1956, when John McCarthy organized the infamous Dartmouth Conference, coining the term artificial intelligence [19] (i.e., the ability of a computer to perform learning and reasoning similar to the human mind) and in 1959, when Andrew Samuel introduced the term machine learning (i.e., “field of study that gives computers the ability to learn without being explicitly programmed”) [20]. After the success of the Dartmouth conference, in 1958, Frank Rosenblatt introduced the first neural network (i.e., perceptron) [21], followed by Widrow and Hoff in 1960, who developed a single layer neural network (known as ADALINE) and a multilayer neural network MADALINE - a three-layered (input, hidden and output layers) feed forward neural network, with ADALINE units in their hidden and output layers [22, 23], applied to detect binary patterns and eliminate echo from phone lines, respectively. The machine learning experienced further expansion throughout 60’s via works by Hunt et al. [24] in symbolic learning, Nilsson [25] in statistical methods and Rosenblatt [26] in neural networks, laying the solid foundation for the field.

After the initial bricks for the field were laid out, late 1960s welcomed significant enhancement in ML. Some of the iconic algorithms introduced during that time included the nearest neighbor algorithm [27], k-means clustering [28], and cross-validation technique [29]. To improve the neural network accuracy, in 1974, Werbos first described neural network specific back propagation [30], which was then implemented in 1982, leading to a surge in the interest for the field in the years to follow. In 1979, Fukushima introduced neocognitron, a hierarchical multilayered neural network, which was for the first time capable of performing multilayer network training/learning to recognize patterns. In 1982, Hopfield proposed the idea of building a bidirectional network, which later became popularly known as Hopfield network [31], one of the first types of recurrent neural networks. Following these discoveries, in 1983, Hinton and Sejnowski introduced Botlzmann machine, which was stochastic in nature and could be utilized to determine optimal solution (by optimizing the weights in the network) for the associated problem [32]. The earlier discovery of neocognitron by Fukushima in 1979 inspired the development of convolutional neural networks (a type of deep neural network utilized for image processing at the time) in late 80’s to 90’s, including LeNet-1, LeNet-4, and LeNet-5 [33-36].

Alongside these developments, several groups significantly contributed to the field, laying the foundation for theoretical machine learning, including work by Vapnik and Chervonenkis [37] (VC) in 1971, which introduced the concept of VC dimension, a measure of capacity for a classifier to accurately classify data points in a sample, where VC dimension along with training error was utilized to compute the upper bound of the test error. Following this, Valiant in 1984 introduced a probably approximately correct (PAC) learning model, where a model was learned by applying an approximation function [38]. Furthermore, several mathematical methods have been effectively adopted into the ML field to improve its accuracy and precision, including Fisher’s Linear Discriminant Analysis [39], Naive Bayes [40], Least squares [41], Markov Chains [42], etc. The 80s and 90s also witnessed massive development in broad areas of ML, including classification and regression decision trees [43, 44], and boosting techniques [45].

Late 90s and the beginning of the 21^st century further contributed to significant advances in machine learning. In fact, 90s introduced advanced algorithms such as support vector machines (SVM) [46], Random Forests [47], bagging technique [48], least absolute shrinkage and selection operator (LASSO) [49], etc., whereas the 21^st century witnessed a surge in popularity of algorithms for deep (representation) learning due to the exceptionally good performance of AlexNet on the ImageNet image recognition task [50]. Some of the algorithms introduced since AlexNet included ResNet [51], U-net [52], Google Brain [53], DeepFace [54] etc., revolutionizing the field and creating an arsenal of computational tools to analyze real-life data, efficiently dealing with noise, missing values, and data sparsity.

With high-throughput patient molecular data becoming accessible came the true manifestation of machine learning, with its effective applications in making decisions that can affect patient lives, undoubtedly including its significant-impact utilization in cancer therapeutic response. While relatively recent in its application to treatment response in cancer, machine learning has already established itself as a major player in predictive therapeutic modeling, with significant promise for high impact on patients’ lives and clinical decision making. In particular, most recent applications in this field have included utilization of Random Forests to predict response to chemotherapy in oral squamous cell carcinoma patients [55], support vector machines to predict response to chemotherapy across 19 cancer types available in TCGA [56], and regression-based modeling to predict response to first generation androgen-deprivation therapy in prostate cancer [6], among others [8, 57-62]. This review will focus on the machine learning algorithms that have already been utilized to successfully predict therapeutic response in cancer and will describe mathematical and statistical foundations of their implementation, discuss their limitations and advantages over other methods, and explore future avenues to enhance personalized treatment predictions and precision therapeutics.

2. DATA SOURCES FOR PREDICTING THERAPEUTIC RESPONSE

Predictive modeling of therapeutic response aims to learn relationships between two essential components: predictor variables and response variables and then subsequently utilize predictor variables to predict therapeutic response. Further, predictor variables recapitulate clinical and molecular patient characteristics, where clinical data involves age, gender, race, demographics, initial disease aggressiveness, accompanied treatments, etc., and molecular data includes gene expression, alternative splicing, mutations, epigenomic changes, etc., and is obtained from biopsies, tumor-removing surgery, or blood/urine samples. At the same time, response variables recapitulate treatment-related disease progression, which for example, includes time to treatment failure (e.g., where treatment failure can be defined as detection of minimal residual disease, change in blood markers, tumor re-occurrence, local or distant metastasis, cancer-related death, etc.) or an indication if treatment response was good or poor (often defined for a specific time frame, for example within 6 months, 1-year, or 5-year period).

In recent years, advancements in high throughput technologies have significantly increased the availability of clinical and molecular data in cancer therapeutic response experimental systems. Yet, interpretability and compatibility of different in vitro and in vivo models with human samples have been a long-standing problem, especially for advancing predictive modeling of therapeutic response. In fact, it has been reported that these systems differ in their ability to capture genomic and transcriptomic features of the primary tumors of patients [63], including their microenvironment [64]. Thus, in this review, we specifically focus on data sources derived from therapeutic administration to patients (Fig. 1, Table 1). Examples of such resources include (i) The Tumor Genome Atlas (TCGA) database [1]; (ii) Stand Up To Cancer (SU2C) East Coast project [2, 9, 65, 66]; (iii) Stand Up To Cancer (SU2C) West Coast project [67-69]; (iv) PROstate Cancer Medically Optimized Genome Enhanced ThErapy (PROMOTE) [70]; (v) Cancer Genome Characterization Initiative (CGCI) [71]; (vi) Therapeutically Applicable Research To Generate Effective Treatments (TARGET) [3,72-74]; (vii) Molecular Taxonomy of Breast Cancer International Consortium (METABRIC) database [75]; alongside cohorts from GEO repository, such as (viii) GSE6532 [76]; (ix) GSE1379 [77]; (x) GSE1456 [78]; (xi) GSE78870 [79]; (xii) GSE41994 [80] etc. Some of these resources have already been utilized to study therapeutic response using non- machine learning approaches, including work of (i) Abida et al. [9], which utilized Whole Exome Sequencing data from SU2C East Coast prostate cancer cohort to identify alterations in TP53, RB1 and AR as associated with resistance to androgen receptor signaling inhibitors (ARSI) in metastatic castration-resistant prostate cancer patients; (ii) Epsi et al. [8], which integrated RNA Sequencing and DNA Methylation data from TCGA to identify pathways that govern chemotherapy response in lung adenocarcinoma; and (iii) Oshi et al. [81], which utilized RNA Sequencing data from METABRIC to identify E2F pathway as a predictive marker governing response to neoadjuvant chemotherapy in ER+/HER2- breast cancer.

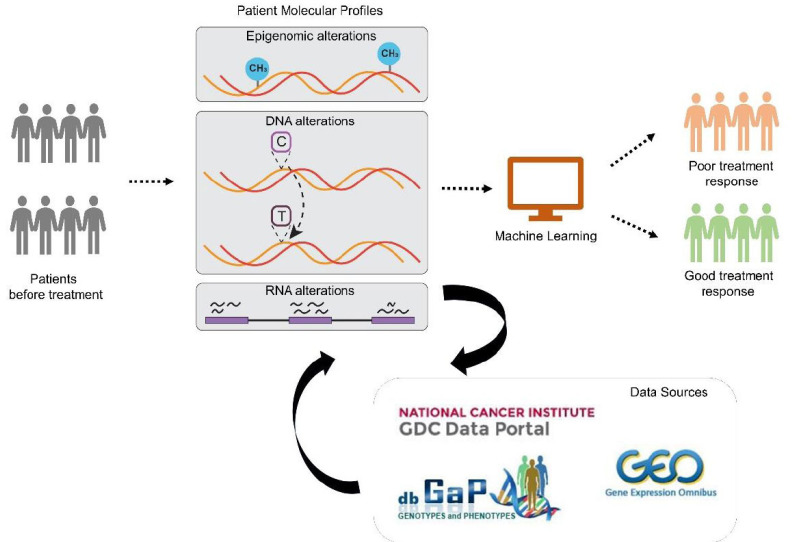
Fig. (1).

Schematic representation of the workflow for predictive modeling of therapeutic response: Patient clinical information alongside molecular profiles (e.g., Epigenomic alterations, DNA alterations, RNA alterations) are utilized as input to machine learning for predictive modeling of patient therapeutic response. (A higher resolution / colour version of this figure is available in the electronic copy of the article).

Table 1.

Description of data sources for therapeutic response. Detailed description of data sources for predictor variables (e.g., RNA sequencing, DNA methylation, etc.) and response variables (e.g., treatment response etc.).

Data Sources	Data Types	Cancer Types	Response Variables	Sources
TCGA [1]	DNA Methylation	33 cancer types (including Lung, Breast, Colon, Prostate, etc.)	Overall survival, Disease progression, Treatment response	Genomics Data Commons (GDC) (https://portal.gdc.cancer.gov/)
	RNA Sequencing
	miRNA Sequencing
	Whole Exome Sequencing
	ATAC Sequencing
	Genotyping Array
SU2C East Coast [9, 65, 66, 82]	RNA Sequencing	Prostate cancer, Pancreatic cancer, Lung cancer	Overall survival, Treatment response	dbGaP phs000915.v2.p2
	Whole Exome Sequencing
	Single Nucleotide Variation
SU2C West Coast [67-69]	Bisulfite Sequencing	Prostate cancer, Pancreatic cancer	Treatment response	Genomics Data Commons (GDC) (https://portal.gdc.cancer.gov/projects/WCDT-MCRPC)
	RNA Sequencing
	Whole Genome Sequencing			dbGap phs001648.v2.p1
PROMOTE [70]	RNA Sequencing	Prostate cancer	Treatment response	dbGaP phs001141.v1.p1
	Whole Exome Sequencing
	Single Nucleotide Polymorphism
Cancer Genome Characterization Initiative (CGCI) [71]	RNA Sequencing	Cervical cancer	Overall survival, Disease progression, Treatment response	Genomics Data Commons (GDC) (https://portal.gdc.cancer.gov/projects/CGCI-HTMCP-CC)
	miRNA Sequencing
	Whole Genome Sequencing
	Targeted Sequencing
TARGET [3, 72-74]	RNA Sequencing	Acute myeloid leukemia, Acute lymphoblastic leukemia, Neuroblastoma, kidney, Osteosarcoma, Rhabdoid tumor, Wills tumor, Clear cell sarcoma	Overall survival, Treatment response	Genomics Data Commons (GDC) https://portal.gdc.cancer.gov/
	miRNA Sequencing
	Whole Exome Sequencing
	Whole Genome Sequencing
	Genotyping Array
METABRIC [75]	Copy Number Variation	Breast cancer	Overall survival, Disease specific survival, Treatment response	https://www.synapse.org/#!Synapse:syn1688369/wiki/27311
	mRNA Expression (Illumina HT 12 arrays)
GSE6532 [76]	mRNA Expression (Affymetrix)	Breast cancer	Treatment response	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE6532
GSE1379 [77]	mRNA Expression (Arcturus 22k human oligonucleotide microarray)	Breast cancer	Treatment response	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE1379
GSE1456 [78]	mRNA Expression (Affymetrix)	Breast cancer	Treatment response	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE1456
GSE78870 [79]	miRNA Expression (TaqMan microRNA Low-Density Array pools A and B version 2.0)	Breast cancer	Treatment response	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE78870
GSE41994 [80]	mRNA Expression (Agilent_ human_DiscoverPrint_15746)	Breast cancer	Treatment response	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE41994

3. MACHINE LEARNING FOR TREATMENT RESPONSE: RATIONALE AND STUDY DESIGN

Since the ultimate goal of machine learning in therapeutic predictive modeling is to learn features (i.e., inputs/predictor variables) associated with treatment response (i.e., called outcomes, outputs/response variables, or labels in classical machine learning) and then utilize this knowledge to predict future therapeutic response for new incoming patients, supervised learning (i.e., where outputs are known as ground truth and are actively utilized in the learning process) has earned its solid place in the state-of-the-art therapeutic response modeling. In fact, while unsupervised learning (e.g., k-means [28], Principal Component Analysis [83], etc.) has been widely applied in cancer-related research, it only discovers associations among input variables and does not utilize their relationship to the outputs. On the other hand, supervised learning (e.g., decision tree [84], Random Forests [85], support vector machines [46], regression-based models [86], etc.) utilizes outputs as ground truth and learns relationships between input and output variables so that the final model can be used to predict the outputs for a new set of inputs (e.g., in new patients).

Generally speaking, supervised learning estimates a function f that maps input variable/s X (i.e., predictor) to output variable/s Y (i.e., outcome/response variables), so that,

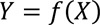
As mentioned above, in predictive modeling of therapeutic response, predictor variables could include clinical patient data (i.e., age, gender, race, initial disease aggressiveness, etc) and molecular data (i.e., gene expression, mutations, epigenomic changes such as DNA methylation, etc) obtained from biopsies, tumor-removing surgery, blood or urine samples, etc. Outcomes/response variables include time to treatment failure (e.g., defined as tumor re-occurrence, local or distant metastasis, or cancer-related death etc) or simply an indication, if treatment response was good or poor (defined using a specific clinical test or time-related threshold, such as a 1-year or a 5-year relapse or survival) [2, 9]. Depending on the type of outcome/response data, supervised learning can either utilize (a) regression model (i.e., output data is continuous, such as time to treatment failure) or (b) classification model (i.e., output data is categorical, such as good or poor response).

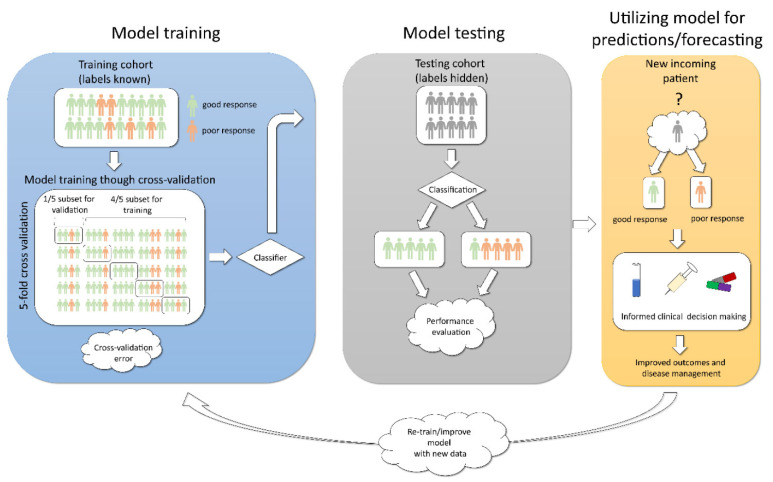
In a clinical setting, supervised learning tailored for predictive modeling of therapeutic response utilizes the following three steps: training (i.e., the model is learned/trained), testing (i.e., evaluating the ability of the model to predict outcomes), and forecasting (i.e., outcomes are predicted for new incoming cases) (Fig. 2). To successfully implement the first two steps, supervised learning divides available data into training and test sets (usually training set constitutes 2/3^rd and test set 1/3^rd of the available data). Training data is utilized to learn the model (function f), while test data is utilized to test the ability of such model to effectively predict outputs. In training step, inputs and outputs (labels) are known to the model and their relationships are actively learned (Fig. 2, Left), while in the test step, the outputs are hidden on purpose and are only uncovered at the end in order to evaluate if the predictions were correct (Fig. 2, Middle). The culmination of such model training and testing results in the third, most important step in clinical decision making - forecasting - predicting outputs/labels for new incoming patients (Fig. 2, Right). If such predictions are later proven to be accurate, these additional data are utilized to re-train and improve the original model.

Fig. (2).

Schematic representation of steps in supervised machine learning to build a predictive model for classification problem. Left: Build/learn the model using training patient cohort. Cross-validation is employed to reduce model variance and improve robustness. Middle: Test and evaluate the model’s performance using the test patient cohort. Right: Forecasting/predicting outcomes for new incoming patients, with subsequent model re-training/improvement. (A higher resolution / colour version of this figure is available in the electronic copy of the article).

One of the essential sub-steps in the training step of supervised learning is cross-validation. Cross-validation allows to mitigate overfitting (where the model can perform well by chance due to the nature of the training set selected) and evaluate how the model is expected to perform on the unseen data. This technique is also utilized to tune parameters when necessary (e.g., for supervised learning methods that require parameter estimation to define f, called parametric models, e.g., linear regression). To achieve this, the training set is divided into k folds/subsets (as for example in Fig. 2, Left, k = 5), so that one of the subsets is kept on-hold and the model is trained on the k-1 subsets. Once trained, the subset on-hold is used to evaluate (i.e., validate) model’s expected accuracy using Mean Squared Error (i.e., the average of the sum of squared difference between actual response and predicted response, MSE), which reflects how far our predictions are from the actual output values. The process is repeated k times, combining MSEs for all folds, followed by averaging it over k, which results in the estimation of cross- validation error. This error is used to evaluate how the constructed model is expected to perform on unseen data or (when parameter tuning) which parameters result in the lowest error and should be selected for optimal model performance.

As a part of supervised learning, the machine learning field has adopted two main methods on how to learn/estimate parameters from training data for prediction purposes: frequentist and conditionalist (i.e., Bayesian) [87]. Frequentists’ viewpoint estimates a parameter that is a constant and assume no prior knowledge for this process [88]. In Bayesian viewpoint, a parameter is viewed as a variable with its own distribution (set of values), utilized to make predictions with degrees of certainty, and prior knowledge is considered for this process [88]. The main difference between these viewpoints is in the way they measure uncertainly in parameter estimation [89]. When frequentist methods obtain a point estimate of the parameters, they do not assign probabilities to possible parameter values. To measure uncertainty, they rely on confidence intervals, where at least 95% of estimated confidence intervals (from enough population samples) are expected to include the true value of the parameter [90]. At the same time, when Bayesian methods estimate a full posterior distribution over the parameters (or point estimates that maximize the posterior distribution), this allows them to get uncertainty of the estimate by integrating the full posterior distribution [91]. In large, utilization of any of these approaches depends on the philosophy, type of prediction we want to achieve (point estimate or probability of potential values) and data availability of appropriate data (i.e., where we have prior knowledge that can be used in the modeling process) [92]. Classical examples of supervised machine learning models that utilize a frequentist approach include logistic and linear regression [93, 94] and those that utilize the Bayesian approach include Bayesian Neural Networks [95], Markov Chain Monte Carlo [96], Bayesian linear regression [97], etc.

These general principles of supervised learning design are utilized as essential building blocks by different machine learning algorithms for predictive modeling of therapeutic response, including tree-based methods (e.g., decision trees and Random Forests), support vector machines, artificial neural networks, and classical regression-based models (e.g., linear regression and logistic regression). Here, we will discuss their mathematical foundations, advantages, disadvantages, and clinical applications, specifically in modeling therapeutic response in cancer patients.

4. SURVEY OF MACHINE LEARNING IN TREATMENT RESPONSE MODELING

4.1. Random Forests

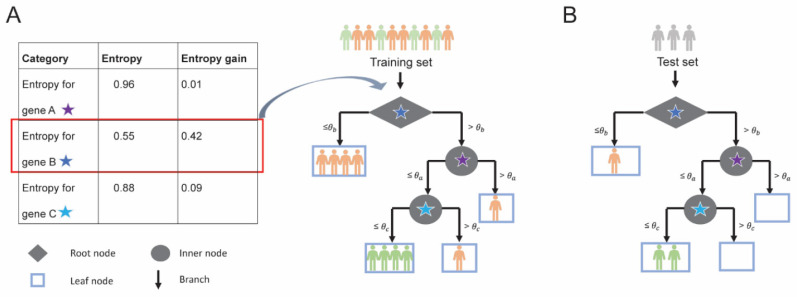
Random Forests is a collection of decision trees [47, 84, 98-101], which have been highly popular in healthcare and medical research due to their interpretability and decision- making capability. A typical decision tree consists of root node, inner nodes, and leaf nodes, all connected by tree branches (Fig. 3). In a decision tree, features/inputs are utilized for each tree split (represented by the root node and internal nodes), allowing to make a decision about the output categorization (outputs or “decisions” are stored at the leaf nodes). For example, in a classical classification example (Fig. 3A), in a dataset with n = 10 patients (i.e., four patients with good response and six patients with poor response) and M = 3 features (i.e., gene A, B, and C), expression level θ_b of gene B is selected at the root as the most important feature to best split/classify the patients (four patients for the left branch with the expression level of gene B ≤ θ_b and six patients for the right branch with the expression level of gene B > θ_b ).

Fig. (3).

Training and testing of a decision tree; (A) Decision tree built using 3 genes A, B and C for 6 poor responders (patients in orange) and 4 good responders (patients in green). At a single expression threshold, entropy gain for each gene is calculated and gene with highest entropy gain is selected as a node for splitting. For example, entropy gain for each gene is calculated (Table, left) and gene B is selected as it has the highest entropy gain (highlighted in red) for the root node. The root node is denoted by a diamond and the intermediate nodes are denoted by a circle. At threshold θ_b, gene B splits (black arrows) the training set such that 6 patients have gene B expression less than or equal to threshold θ_b and the 4 patients have expression above threshold θ_b. All 4 patients with gene B expression less than or equal to threshold θ_b belong to the poor responder category and, therefore, are represented in leaf node (light blue rectangle). (B) The predictive ability of the decision tree model is evaluated using a test set. (A higher resolution / colour version of this figure is available in the electronic copy of the article).

In general, to select the most important feature at each node split, a decision tree evaluates all provided features and calculates a so-called node purity, which for example, can be estimated by minimizing the residual sum of squares (for regression models), Gini Index or entropy (for classification models). Entropy (E), which conceptually measures the randomness associated with the outcome at each node, is calculated as:

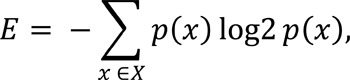
where p(x) is the probability of a category X (i.e., patients with poor or good treatment response) in the training set. It is calculated for each available feature at each node split (starting from the root), so that a feature with the highest entropy gain (compared to the entropy for the entire set) is selected at each split, as described in Fig. (3A) (where expression levels of gene B are selected for a root node split due to its highest gain in entropy - for simplicity, we assume a single expression threshold available for each gene). This principle is employed at each node split until all the samples have been classified or until a certain threshold set by the user or estimated by a tuning parameter is reached (we will touch on Random Forests’ parameters that can be tuned later). Once built, such decision tree is utilized to either make predictions for out-of-bag patients or forecasting for new patients (Fig. 3B).

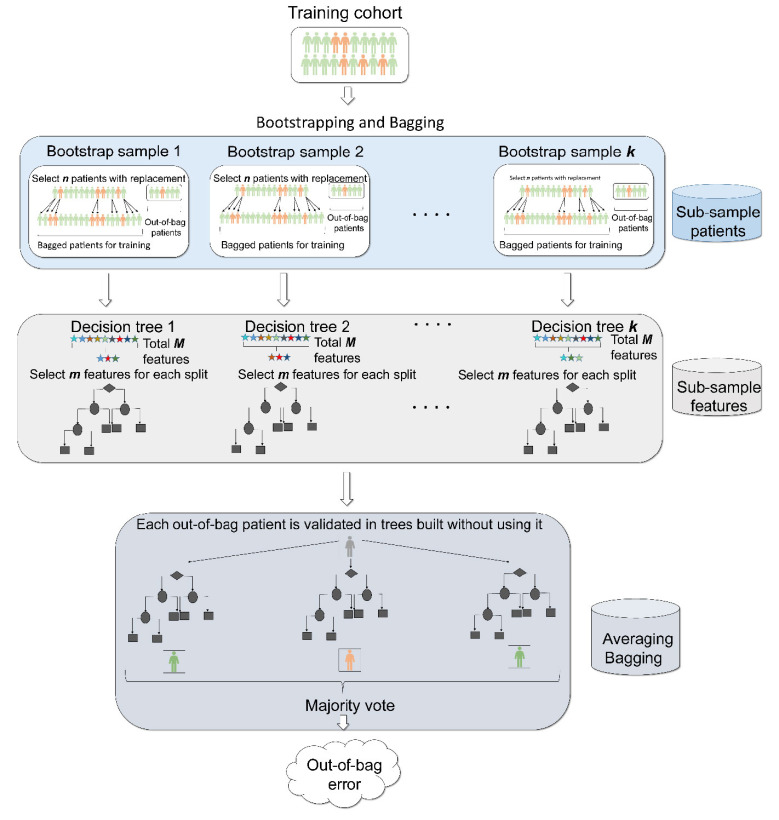
While a single decision tree is prone to overfitting, an ensemble of decision trees, known as Random Forests, has been widely utilized to increase prediction accuracy [101, 102]. In particular, to reduce variance and increase model robustness, Random Forests utilizes several important techniques, including (i) bootstrapping (where patients are sub- sampled with replacement multiple times and each sub-sample is utilized to build a decision tree) (Fig. 4, top); (ii) feature sub-sampling (only a specific number of features are selected for each tree split) (Fig. 4, middle); (iii) bagging (where the output of sample and feature sub-sampling is integrated and averaged for predictive purposes) (Fig. 4, bottom). Bootstrapping employs sampling with replacement, producing a bagged subset (n bagged patients, sampled with replacement from a patients’ set of size n) and an out-of-bag subset (similar to hold-on cross-validation subset in Fig. 2). On average, during bootstrapping 2/3^rd of the training set is utilized to build a bagged subset and 1/3^rdof the training set for out-of-bag subset. Each k^th round of bootstrapping produces a decision tree, resulting in k decision trees overall (Fig. 4, middle).

Fig. (4).

Schematics for Random Forests. Random Forests has three unique features (i) bootstrapping (top), feature selection (middle) and bagging (bottom). First Random Forests performs bootstrapping whereby n random patients are chosen with replacement from a patient set of size n. This process is continued k times, producing k different patient subsets. Each patient subset (known as bootstrap sample) is used to build a decision tree. Patients considered for building a tree are known as bagged patients and patients that are left out of the bootstrap samples are known as out-of bag samples. Next, to build a tree, at each split, out of total M features available, a subset of m features is considered. This process is known as feature selection. Finally, after building k decision trees, Random Forests performs a procedure called bagging whereby each patient from out of bag subsets is validated across trees that did not use that specific patient while building their trees. The final output by the Random Forests is the prediction from each tree is recorded and the vote is selected as the final output of the model, known as average bagging. Finally, to evaluate the predictive ability of the Random Forests, out of bag error is calculated. (A higher resolution / colour version of this figure is available in the electronic copy of the article).

To ensure that all decision trees in the Random Forests are uncorrelated, each tree split feature sub-sampling is employed. If a total number of features is M, it is recommended that features selected for classification lie within the range of 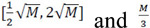features are selected for the regression model (Fig. 4, middle). Finally, bagging utilizes outputs from bootstrapping and feature sub-sampling so that each sample from the out-of-bag subsets (from each bootstrap round) is validated using decision trees built without utilizing this specific sample. After predictions are made for each sample/patient, bagging utilizes a majority vote to make a final prediction, used to calculate Mean Squared Error or classification error (average misclassifications) (Fig. 4, bottom), thus minimizing model variance. To control for bias- variance trade-off, important parameters in Random Forests to consider and thus tune are the number of trees, tree depth (or number of samples at the leaf nodes), number of features at each tree split etc.

One of the clinically relevant and most widely used outputs in Random Forests is feature importance, which is often used to evaluate which clinical or molecular determinant/s are most important for predicting therapeutic response. It is calculated using the average of the total decrease in Gini Index/ entropy for each feature across all trees (for classification model) or the average of the total decrease in residual sum of squares across all trees (for regression models). Yet, when evaluating feature importance, one should be careful about the presence of collinear features. While not affecting model performance per se, they can reduce the importance of one another and could be easily misinterpreted in the clinical setting.

Due to its robustness and ability to perform well even in moderate-sized datasets, Random Forests has been actively utilized for predictive modeling of treatment response in cancer patients [55, 103-122]. In a classic example by Tsuji et al. [59], Random Forests was implemented to identify gene expression markers to stratify patients based on their response to mFOLFOX therapy in colorectal cancer. A total of 83 patients with colorectal cancer without prior treatment were enrolled and received mFOLFOX6 treatment after sample collection. Out of 83 samples, 54 samples (2/3^rd of 83) were selected for training purposes and 29 (1/3^rd of 83) for testing. Gene expression profiles (i.e., 17,920 probes) were used as inputs/features. Response to the therapy (outcomes/labels) was assessed through computer tomography (for the appearance of lesions) and evaluated after 4 cycles of the treatment. The multi-layered analysis identified 14 most important genes, which successfully predicted 12 out of 15 (80%) patients with good response and 13 out of 14 (92.8%) patients with poor response in the test set, establishing Random Forests as a robust, reliable method for therapeutic response modeling.

4.2. Support Vector Machines

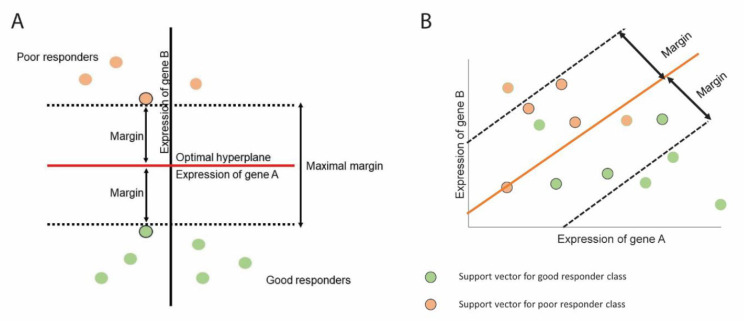
Support vector machines or SVMs [46, 123, 124] are popularly used for binary classification problems (yet their recent extensions can handle multi-class [125, 126] and regression modeling [127, 128]). Conceptually, SVM is a generalization of the optimal separating (i.e., maximal margin) classifier and support vector (i.e., soft margin) classifier, with the advantage of allowing for misclassified samples and non-linear class boundaries. The main objective of SVM is to identify an optimal hyperplane which would effectively separate classes from each other (e.g., poor responders and good responders). The SVM hyperplane is defined in a way such that the distance between the separating hyperplane and training data observations is maximized (such distance is also known as a margin) (Fig. 5). One can think about the hyperplane as the widest/maximal ribbon that can fit between the two classes (this is classically known as a maximal margin classifier, Fig. 5A). Yet, an advancement over the maximal margin classifier - support vector classifier - allows a margin to be “soft” and have some observations inside a margin or even have some observations (i.e., mismatches) on a wrong part of the hyperplane, having at most epsilon deviation from the hyperplane (Fig. 5B). In support vector classifier, samples that lie directly on the margin are known as support vectors as they “support” the hyperplane (only these observations affect the hyperplane and if they move, the hyperplane would move as well). It is interesting that SVM classification is only based on a small number of observations (i.e., support vectors) and is robust to the observations that are far from the hyperplane/margin. The size of the margin (and the corresponding support vectors) is a parameter to optimize in SVM.

Fig. (5).

Support vector machines determine a hyperplane that can separate patients into two classes. (A) SVM identifies a hyperplane such that it can maximize the margin and no patients lie inside the margin. (B) SVM can also identify hyperplane where patients lie inside the margin. This is known as soft margin. (A higher resolution / colour version of this figure is available in the electronic copy of the article).

A unique and valuable characteristic of SVM in addition to utilizing a support vector classifier is that it works not only with linear but also with non-linear observations. In order to accommodate non-linear boundaries between the classes, SVM enlarges the feature space through kernels (widely used non-linear kernels include polynomial [129], radial [130], and hyperbolic tangent kernels [131]). However, utilization of kernels could be computationally expensive, as it turns optimization involved in SVM in a quadratic programming problem [132-134]. This might cause a computational challenge, especially as data depth and breadth increase, as is the case with Big Data [135-141].

The mathematical way to define a hyperplane (which is M-1 dimensional) is,

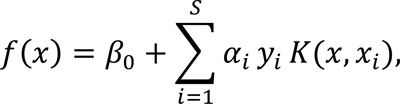
where β₀ is the intercept, S is the number of support vectors, α_i is the Lagrange multiplier, y_i is the class label for a support vector i so that y₁…y_s are in {-1,1} (where 1 represents one class/good response and -1 the other class/poor response), K(x, x_i) is a kernel function, and x_i is a feature vector of size M for a support vector i. One can think of hyperplane as an entity that divides M-1 dimensional space into two parts, so that all points/samples with ƒ(x) > 0 lie to one side of the hyperplane and points/samples with ƒ(x) < 0 lie to the other side of the hyperplane [141, 142].

Once SVM classifier is built, the samples to be evaluated/predicted are subjected to ƒ(x) and their class is predicted/assigned based on the sign of the ƒ(x) (i.e., if it is positive, the sample is assigned to class 1 and if it is negative, to class -1). Interestingly, the magnitude of ƒ(x) can suggest how far the observation is from the hyperplane and thus how confident we are in assigning a class membership [143] (i.e., the further away from the hyperplane a sample is, the more confident we are in its predicted membership).

Given its flexibility in allowing mismatches and ability to work with non-linear relationships, SVM have been widely utilized for predictive modeling of treatment response in cancer patients in the last decade [144-164]. One of the bright examples is the work of Huang et al. [60], which developed an open sourced SVM to predict drug response to seven chemotherapeutic drugs using gene expression data across 60 human cancer cell lines. To increase performance accuracy and reduce the number of features (especially important for SVM and discussed later in the Limitations and alternative approaches section), they utilized recursive feature elimination (RFE) approach. The model was tested on 273 ovarian cancer patients and showed significant predictive ability, when compared to previous reports. In addition, the same group later demonstrated that utilization of the SVM-RFE model (i.e., SVM model along with recursive feature elimination approach) when employed on 152 patients with different cancers from TCGA produced predictions of treatment response to gemcitabine and 5-flurouracil with high accuracy > 80% [56].

4.3. Artificial Neural Networks

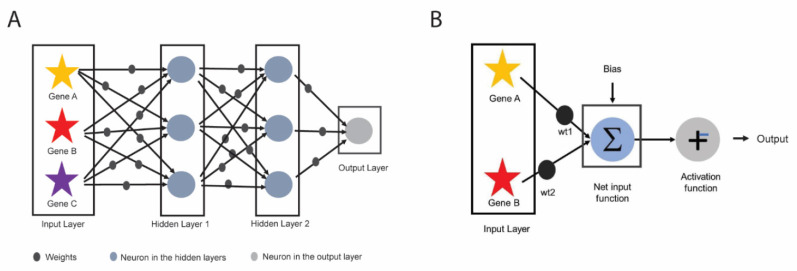
Artificial neural network (ANN) is an algorithm inspired by the biological neural network of the human brain and has been widely utilized in pattern recognition and image processing [165]. Generally, ANN consists of three parts: one input layer, multiple hidden layers, and one output layer (Fig. 6A). The hidden layers allow for processing of the data that are not linearly separable and if more than one hidden layer is present, the neural network is commonly known as a deep neural network. Inputs to the input layer are predictors (e.g., molecular or clinical features), which are then assigned weights that either amplify or dampen the inputs thus indicating input significance. Value for each predictor (e.g., expression level for a gene) multiplied by its weight (called weighted nodes) along with a bias (which also has its own weight) are summed up in a summation function (also known as Net input function) (Fig. 6B). The output of the summation function is then sent to an activation function which is an important step of the ANN as it directly affects its output, accuracy, convergence, and computational efficiency. Activation function can be as simple as a binary step function (i.e., based on a threshold, determines if a neuron is activated or repressed) or account for non-linear relationships and data complexity utilizing sigmoid, hyperbolic tangent, rectified linear unit, soft-max, swish functions, etc [166-169].

Fig. (6).

Schematics of Artificial Neural Network (ANN). (A) An example of deep neural network which has three components: input layer, 2 hidden layers, and output layer. (B) Each of the predictors in input layer (red and yellow stars) is multiplied by its corresponding weights (black balls) and along with bias is input to net input function (also known as summation function). The output of the summation function is passed through the activation function (i.e., stepwise function), to determine the output of ANN. (A higher resolution / colour version of this figure is available in the electronic copy of the article).

The objective of the training step in ANN is to find the best/optimal set of weights for inputs and bias to solve a specific problem (i.e., treatment response prediction). This is often implemented as a backpropagation [169], where weights for input and bias are optimized to minimize the difference between the actual and the predicted output values (e.g., measured as sum of squared errors or entropy), although this solution is not always global. To control for bias-variance trade-off, the model could be tuned for the number of units in hidden layer and amount of weight decay.

ANN has been utilized by several groups to study treatment response in cancer [170-175]. One of the bright examples is the study of Tadayyon et al. [61], which built an artificial neural network classifier based on quantitative ultrasound imaging to predict response to neoadjuvant chemotherapy for 100 breast cancer patients. The ANN classifier could predict response to the treatment with an accuracy of 96 ± 6%.

4.4. Linear and Logistic Regression

Linear and logistic regressions have earned their historical foundational role in statistical inference and learning and have been widely utilized in treatment response modeling in the recent decade [115, 120, 176-183].

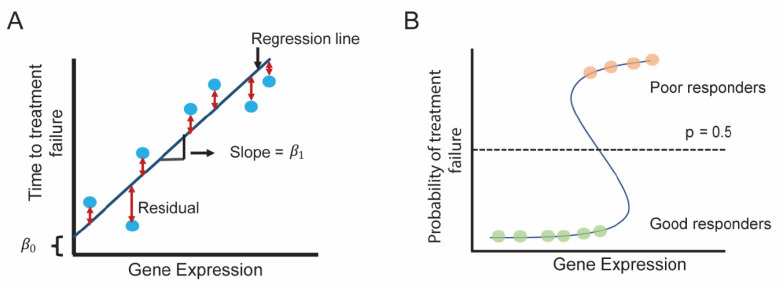
Linear regression estimates linear relationship between input and output variables and fits a so-called regression line (Fig. 7A) in a way so that the sum of the squares of the distances between the line and the data points (i.e., residuals) is minimized. In mathematical terms, function f for a regression line can be re written as:

Fig. (7).

Schematics for linear and logistic regression. (A) Simple linear regression between gene expression (input/predictor variable) and time to treatment response (output/dependent variable) is shown. The regression determines the regression line with slope β ₁ and β ₀ y-intercept . (B) Logistic regression between gene expression (predictor/independent variable) and response to treatment (response/dependent variable). At a threshold (p=0.5), if the probability of belonging to a specific class is p ≥ 0.5, patients belong to a class (i.e., poor responders) and if p < 0.5, patients belong to another class (i.e., good responders). (A higher resolution / colour version of this figure is available in the electronic copy of the article).

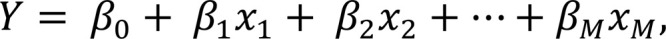
where M is the number of input variables/predictors, β ₀ is the y-intercept and β₁, β₂, ... β _M are the slope coefficients for input variables x₁, x₂, ... x_M (reflecting how much each predictor affects the outcome Y). If only one input/predictor variable is present, it is referred to as a simple linear regression and when more than one input/predictor variable is present, it is referred to as a multiple (or multivariable) linear regression. One of the significant extensions of linear regression is Cox proportional hazards modeling, particularly important in modeling therapeutic response, where the outcomes are represented by treatment-related survival time: time to treatment failure or time to latest follow-up (i.e., for censored patients).

In logistic regression, the output is a binary variable (i.e., class membership) and if p is the probability of belonging to a specific output class (e.g., good or poor response), then f takes the following form:

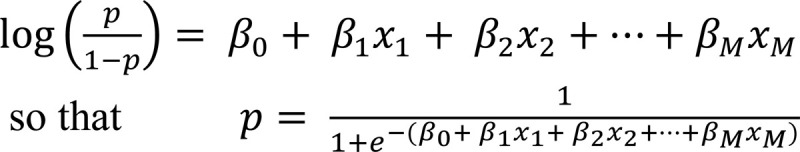
For example, if the probability threshold is p = 0.5, patients with probability p ≥ 0.5 are classified as poor responders and p < 0.5 as good responders (Fig. 7B).

Due to their interpretability and wide dissemination, linear and logistic regression have been widely utilized to model treatment response in cancer [115, 120, 178-183]. For example, Jahani et al. [62], analyzed DCA-MR images of 132 locally advanced breast cancer patients after being treated with neoadjuvant chemotherapy. Voxel-wise changes in morphologic, kinetic, and structural features were quantified using image registration technique. Strength of identified features in determining pathological complete response was evaluated using logistic regression analysis first on a baseline model which included age, race, hormone receptor status, and tumor volume as explanatory variables. Following this, voxel-wise features were added to the baseline model and were shown to improve early prediction of response to neoadjuvant chemotherapy in locally advanced breast cancer patients.

Recently, a series of regression-based methods have been utilized for integration of different data types in predictive therapeutic response modeling. In particular, in Panja et al. [6], linear regression-based analysis was employed to elucidate relationships between epigenomic (i.e., DNA methylation) and transcriptomic (i.e., gene expression) determinants of response to first generation androgen-deprivation therapy in prostate cancer. To specifically study primary resistance, localized primary prostate cancer tumors (at radical prostatectomy) from The Cancer Genome Atlas (TCGA-PRAD) patient cohort, not receiving any treatment prior to sample collection, but treated with adjuvant (post-operative) androgen deprivation therapy, were specifically selected. Linear regression analysis between DNA methylation sites (independent variable) and gene expression of the site-harboring genes (dependent variable) identified 5 site-gene pairs with functional importance in therapeutic response. These markers were shown to differentiate patients at risk of resistance to androgen deprivation therapy in prostate cancer with 90% accuracy and were demonstrated to be active in patients that failed androgen-deprivation with metastatic disease.

In Epsi et al. [8], and Rahem et al. [17], molecular determinants of therapeutic response were evaluated not as single independent entities, but as groups of genes connected by their biological function - biological pathways. These studies utilized logistic regression-based methods and Cox proportional hazard modeling to establish relationship between activity levels of biological pathways (used as features) and therapeutic response to carboplatin + paclitaxel in lung adenocarcinoma [8] and to tamoxifen in breast cancer [17]. Identified pathway markers were shown to accurately stratify patients at risk of resistance across multiple independent patient cohorts (82%-94% accuracy) and have been shown to outperform non-pathway-based methods.

5. LIMITATIONS AND ALTERNATIVE APP- ROACHES

As more clinical and molecular data from cancer patients become available for computational use, machine learning is becoming a backbone for predictive modeling of treatment response. Yet, some of the limitations inherent to its design needs special attention, especially when applied to therapeutic response modeling.

Big Data provides the necessary breadth and depth for the elucidation of complex mechanisms that govern treatment response, yet since its single determinants are used as features/inputs in a machine learning setting, their magnitude can easily overwhelm the system, resulting in overfitting. In fact, it is recommended that the number of features should be significantly less compared to the number of samples/patients M<<n. Given that the thousands of molecular features are routinely profiled using high-throughput technologies, it would require even more patient samples and might not be feasible. To overcome this limitation, various feature selection techniques have been proposed and utilized, including (i) wrapper methods [184-186], which evaluates all possible combination of features to identify optimal set of features that maximize model performance, where commonly used wrapper methods include forward [187], backward [188], stepwise selection [189], simulated annealing [190], genetic algorithms [191], etc.; (ii) filter methods [192-195], which evaluate relevance of predictors outside of the training model (i.e., usually features are evaluated individually), where commonly used filter methods include correlation [196], information theory [197], rough set theory [198], distance measures [199], etc.; (iii) hybrid methods [200-202], which identify features using a combination of both filter and wrapper methods, with most popular being F-score and Supported Sequential Forward Search (FSSFS) method [203], which utilizes F-score (i.e., filter method) to first preprocess and identify a subset of features which is then subjected to supported sequential forward search (i.e., a wrapper method) to identify the final list of features; and (iv) embedded methods [204-206], where feature selection is a part of model selection process, including L1 - regularization based methods such as Least Absolute Shrinkage and Selection Operator (LASSO) [49], which is a regularized linear regression model that penalizes all features equivalently, shrinking unimportant ones (i.e., features which are unlikely to impact response variable) to zero. Apart from LASSO, another commonly used embedded method for feature selection is Smoothly Clipped Absolute Deviation Penalty (SCAD) [207], which penalizes both important and unimportant features, shrinking unimportant features to zero whereas having a lesser impact on important features compared to LASSO. Besides computational methods, feature selection can also be performed through feature masking based on domain knowledge, where users can utilize their domain knowledge to facilitate feature selection. A classic example of such feature selection was described by Yan et al. [208], incorporating prior knowledge of staining pattern to identify texture based features that can help quantify cellular phenotype.

It is possible to pre-select features even prior to feature selection, as is referred to as feature screening, such as (i) Sure Independence Screening (SIS) [209], which determines the association between each predictor and response variable through correlation analysis to determine the important features; (ii) Sure Independence Ranking and Screening (SIRS) [210], which utilizes expectation of squared correlation between a predictor and an indicator function of the response variable to determine a minimum number of important features; (iii) Distance Correlation Sure Independence Screening (DC-SIS) method [211] which screens features based on their distance correlation with response variable (by computing distance between simultaneous observations of each predictor, and as well as simultaneous observations of response variable), etc.

The large number of predictors can also lead to the substantial presence of non-informative features. While this can be easily overcome with some machine learning algorithms (e.g., Random Forests), it might substantially affect the performance of other methods such as multiple linear and logistic regression, SVM and neural networks. One of the solutions is to filter features based on their data cross-integration or biological relevance (e.g., biological pathways, like in Epsi et al. [8] and Rahem et al. [17]) and for their association with therapeutic response ahead of time. Additional advantage in reducing the feature space to informative features only is in the fact that fewer corresponding model terms/parameters need to be optimized, thus improving model performance.

Furthermore, the presence of multiple co-occurring molecular features or a correlation between clinical and molecular features (often observed in therapeutic response data) could lead to feature co-linearity, which can substantially interfere with model performance (e.g., in neural networks and SVM) and could substantially affect its interpretation (e.g., Random Forests’ feature importance is not interpretable in cases of feature co-linearity). To overcome these limitations, in addition to feature selection techniques described above, it is recommended to test for feature co-linearity ahead of time and keep the most important representative feature or the most biologically relevant feature from the group, “eliminating” non-important features. Alternatively, co-linear features could be represented as a group and utilized in the analysis as one entity.

While high throughput techniques to generate Big Data have brought significant advantages to our understanding of cancer progression and therapeutic response, they could be prone to experimental noise or missing values [212]. While some machine learning algorithms are relatively immune to noise or missing data (e.g., Random Forests), others will suffer in terms of their model performance. To address this problem, in the last two decades, several methods have been developed to deal with noise in the data [213-215], including robust regression methods such as M-estimation, S-estimation and MM-estimation [216, 217] and domain knowledge (e.g., pathology expertise) [218]. M-estimation minimizes a function of residuals to estimate coefficients for a regression model, in the presence of outliers (i.e., noise), specifically in response variables [219], yet not taking into account outliers from predictor variables [219]. Thus to overcome this limitation, S-estimation was developed, which modified the residual function of M-estimation by introducing the standard deviation of residuals, being able to handle more diverse sources of noise [220]. However, S-estimation has a major drawback as it requires a large number of samples to accurately estimate coefficients for regression model (i.e., has low efficiency) [220]. Therefore, to compensate for the efficiency and at the same time to have a model which can consider outliers from both predictor and response variables, MM-estimation, a combination of M- and S-estimation, was introduced [220].

At the same time, missing data can substantially affect model performance and accuracy of prediction [221] and can be tackled with (i) expectation-maximization (EM) algorithms [222-224], utilized to estimate missing data from expected complete data by maximizing a likelihood function; (ii) matrix completion-based methods such as simple, complex optimization program [225, 226], which compute a complete low rank matrix from a matrix with missing data by minimizing the nuclear norm.

Furthermore, even though molecular Big Data has produced a lot of features (i.e., M is large), the available datasets for therapeutic response modeling still offer cohorts of relatively small sizes (i.e., n is smaller than M), thus limiting possible machine learning applicability and performance. This is especially important for methods that requires estimation of parameters for each hidden layer (thus the number of parameters is further amplified) such as neural networks, while other methods perform relatively well even in moderate-sized patient cohorts (i.e., linear and logistic regression, Random Forests, etc.). Finally, while linear relationships are the most natural way to start data explorations, molecular Big Data’s complexity and its association with therapeutic response often require non-linear solutions. In such settings, machine learning methods that account for such relationships are preferred, such as Random Forests, SVM with non-linear kernels, or neural nets.

6. DISCUSSION

Recent advancements in Big Data high throughput technology hold a promise to move the field of therapeutic predictive modeling fast forward. Techniques such as CRISPR, ChIP-Seq, HI-C etc. have been widely utilized in cancer research [227-229], with great potential to be effectively expanded to predicting treatment response. One of the most promising shifting paradigms, which has revolutionized cancer research in recent years, is single-cell sequencing [230]. Not only such technique is utilized to analyze complexities of biological systems at single cell level, it also reflects tumor heterogeneity [231-233], clonality [234, 235], and epithelial-stromal interactions [236, 237], opening doors to better precision therapeutics and in-depth monitoring of treatment response, perfectly suited for complex machine learning tasks [238].

While such advances have significantly improved the treatment response investigation, several challenges in the field of therapeutic monitoring remain to be thoroughly addressed. First of all, access to available molecular data in the public domain pose significant challenges when rapid predictions need to be made or results reproduced/validated [239]. Furthermore, the access to facilities and cost of the tumor molecular profiling at the time of biopsy and surgery remain substantial obstacles for many patients and institutions [240] and pose a substantial challenge for subsequent effective application of predictions from multi-omic integrative machine learning techniques [241]. Moreover, this challenge is further amplified if such samples need to be obtained repeatedly, for treatment monitoring [242]. One of the ways to overcome this problem and effectively monitor disease and treatment progression is through utilizing liquid biopsies, a rapid non-invasive technique, which can analyze cancer cells from tumors circulating in the blood [243] and can be applied repeatedly. Such technique has been widely utilized by the cancer community [244, 245] and holds a promise for effective therapeutic monitoring and analyses, providing plethora of data for effective machine learning utilization and accurate predictions.

As the therapeutic monitoring becomes more accessible and molecular datasets become larger (i.e., n increase), we foresee the utilization of more advanced machine learning techniques, which require sufficient number of samples for their optimal performance. One such example is deep learning [57, 246]. The advantage of deep learning is in its ability to capture the biological complexities at a more granular level compared to other machine learning algorithms. One of the algorithms widely utilized for deep learning is deep neural networks (i.e., neural networks with multiple hidden layers), where its additional hidden layers allow for a “deeper” learning. Given the complexity of mechanisms and molecular cross-talks implicated in therapeutic response, deep learning is ideally suited to elucidate mechanisms and markers of therapeutic response, yet in large-sized patient cohorts.

Even though deep learning might offer an elucidation of more complex deep relationships in the data, it often suffers from output interpretability [247, 248], when knowledge about the prediction is essential for a well-informed decision [249, 250]. In deep neural network, tracing which variables are combined to make the prediction could become too complex and hides conditions at which the models can fail (i.e., black box model) [251]. Several alternative solutions have been proposed to overcome this problem, where a complex model is followed by the subsequent explanatory model [252, 253], yet not fully providing an accurate representation [252].

Another example of machine learning algorithms ideally suited for therapeutic modeling is causal methods [254-256]. Causal methods look for causal rather than accidental associations among data points, essential in identifying mechanisms underlying treatment response and novel therapeutic targets. Causal models and analysis have already been used in a clinical setting, such as establishing a causal relationship between lower lipid levels in the body and higher bone mineral density [257], in epidemiology [258], or in cancer progression [259]. Yet, the absolute beauty of causal analysis is obtained with time series data, established by Kleinberg et al. [254, 256, 260], and later applied to cancer progression using cross-sectional data by Ramazzotti et al., [261]. As the availability of time-series monitoring data for therapeutic response in cancer patients is underway, its pressing need, importance, and interpretability will undoubtedly benefit from causal analysis.

We foresee that future utilization of currently utilized approaches for predictive modeling alongside causal analysis, as machine learning paradigm for modeling of therapeutic response, will not only overcome limitations of finding simple association relationships, but will also provide outputs easily interpretable by the clinicians and pave a road to interpretable precision therapeutics.

CONCLUSION

Over the last decade, there has been a significant increase in the utilization of machine learning in predictive modeling of treatment response in cancer patients. In this review, we have discussed machine learning algorithms currently utilized for this purpose, their mathematical foundations, and specific applications in a practical setting. Volume and heterogeneity of Big Data in therapeutic modeling allows for elucidation of complex mechanisms implicated in treatment response, yet requires special considerations due to the large number of unfiltered determinants/features it provides. We have discussed these limitations and approaches to overcome them. We conclude that as patient datasets become larger and better characterized, we foresee effective utilization of deep learning and causal analysis in therapeutic modeling in cancer patients, paving a road to interpretable precise outcomes.

LIST OF ABBREVIATIONS

ML

Machine Learning

DNA

Deoxyribonucleic Acid

RNA

Ribonucleic Acid

SVM

Support Vector Machine

ANN

Artificial Neural Network

TCGA

The Cancer Genome Atlas

PRAD

Prostate Adenocarcinoma

ICGC

International Cancer Genome Consortium

RFE

Recursive Feature Elimination

CONSENT FOR PUBLICATION

Not applicable.

FUNDING

This work was supported by New Jersey Commission on Cancer Research (DCHS20PPC028) and Rutgers School of Health Professions, USA, start-up funds.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.