Abstract
Purpose:
To compare different optimization approaches for choosing the spin-lock times (TSLs), in spin-lattice relaxation time in the rotating frame (T1ρ) mapping.
Methods:
Optimization criteria for TSLs based on Cramér-Rao lower bounds (CRLB) are compared with matched sampling-fitting (MSF) approaches for T1ρ mapping on synthetic data, model phantoms, and knee cartilage. The MSF approaches are optimized using robust methods for noisy cost functions. The MSF approaches assume that optimal TSLs depend on the chosen fitting method. An iterative non-linear least squares (NLS) and artificial neural networks (ANN) are tested as two possible T1ρ fitting methods for MSF approaches.
Results:
All optimized criteria were better than non-optimized ones. However, we observe that a modified CRLB and an MSF based on the mean of the normalized absolute error (MNAE) were more robust optimization approaches, performing well in all tested cases. The optimized TSLs obtained the best performance with synthetic data (3.5–8.0% error), model phantoms (1.5–2.8% error), and healthy volunteers (7.7–21.1% error), showing stable and improved quality results, comparing to non-optimized approaches (4.2–13.3% error on synthetic data, 2.1–6.2% error on model phantoms, 9.8–27.8% error on healthy volunteers).
Conclusion:
A modified CRLB and the MSF based on MNAE are robust optimization approaches for choosing TSLs in T1ρ mapping. All optimized criteria allowed good results even using rapid scans with 2 TSLs when a complex-valued fitting is done with iterative NLS or ANN.
Keywords: T1ρ relaxation, Cramér-Rao bounds, spin-lock times, quantitative MRI
1. INTRODUCTION
The spin-lattice relaxation time in the rotating frame (T1ρ) has shown sensitiveness to loss of proteoglycan content in the cartilage (1,2) and T1ρ relaxation mapping can be useful for early detection of osteoarthritis (OA) (3). To produce good and stable T1ρ maps, many T1ρ-weighted images must be acquired, taking a long acquisition time if a good signal-to-noise ratio (SNR) and small variance in the estimated parameters are desired.
The quality of T1ρ mapping can be improved if the SNR of the acquired data is improved (4). This can be achieved by using different pulse sequences (5), by averaging multiple acquisitions, or even by using multiple receiving coils (6). Specifically, in T1ρ mapping, improved quality can also be obtained by optimally choosing the spin-lock times (TSLs), also called optimal TSL sampling schedules (7). Efficient choices can reduce the overall acquisition time while maintaining a good quality of the estimated parameters.
The choice of the sampling schedules is important in quantitative MRI in general. This has been discussed for T1ρ mapping (7), for spin-lattice relaxation time (T1) and spin-spin relaxation time (T2) mapping (8–12), for magnetic resonance (MR) fingerprinting (13,14). Typically, this problem is handled with optimization of the Cramér-Rao lower bounds (CRLB) (15). Improving the CRLB using better signal sampling is related to the improvement of the stability of unbiased statistical estimators. In (16,17), the similarity in construction of the Fisher information matrix (FIM), used in the CRLB optimizations, and the Hessian matrix (or its approximations using the Jacobian matrix), used by fitting algorithms based on non-linear least squares (NLS) (18), is demonstrated for the case of Gaussian noise and differentiable fitting models. Essentially, this implies that optimizing the sampling schedule using CRLB leads to a “regularization by discretization” of the NLS problem (19), improving the condition number of the matrix used in the non-linear system solved by these algorithms and, consequently, stabilizing the non-linear inverse problem (17). Even though NLS methods had direct benefit from the optimized sampling schedule, other aspects of the estimation algorithms are not considered when using CRLB, such as the type of iterative algorithm, constraints, step-sizes, number of iterations, or initial guess. However, these choices are relevant for the effectiveness of the fitting algorithm. Data-driven approaches, such as those used to optimize the k-space sampling pattern in MRI (20–22) and flip-angles in T1 mapping (16), can consider the specific strategies of a fitting algorithm. These approaches claim that effective sampling patterns depend on the recovering method and expected signal parameters. They are called here as matched sampling-fitting (MSF) because they include the fitting algorithm in their criterion for optimal sampling.
While curve fitting is classically solved with NLS, other approaches, such as artificial neural networks (ANNs)(23–27) can be exploited. Curve fitting with ANNs is not a novelty (23), but the topic has been revived in MRI (28–30) due to the good results of deep learning with relaxometry (31,32). An ANN is usually trained with sample data of the expected exponential relaxation process. The input signals are non-linearly processed by the ANN to obtain the parameters of the relaxation model. Since ANN works differently from unbiased estimators, it is not known if optimization of the sampling schedules with CRLB is useful for T1ρ mapping with ANNs.
Both approaches, CRLB and MSF, consider a specific distribution of relaxation parameters for the optimization process, which should correspond to the distribution expected on the scanned subjects. Besides, there are many possible cost functions to compose a criterion. The cost function objectively defines what the best sampling schedules are (considering a given distribution of relaxation parameters is expected). All these choices lead to different optimal sampling schedules, which may have different performances in practical applications.
In this study, we compare four different criteria. Two CRLB criteria are compared: one based on the sum of the CRLB for each parameter, and the other one based on the sum of the squared root of the CRLB normalized by its parameter value. Also, two MSF criteria are compared: one based on the mean squared error (MSE), and the other one based on the mean of the normalized absolute error (MNAE). All approaches consider the monoexponential complex-valued signal model, the expected distribution of parameters in the human knee cartilage, and complex-valued Gaussian noise. Besides, MSF criteria also consider the fitting method. Because MSF leads to the optimization of noisy cost functions, we optimize it with subset selection algorithms for noisy problems, such as (33).
We observe that different optimal TSLs are obtained from different criteria and, in general, they are always better than non-optimized TSLs. However, the Modified CRLB and the MSF criterion based on MNAE described later in this work are more robust approaches, being insensitive if the model of choice considers the optimization of T1ρ or its inverse, the spin-lattice relaxation rate in the rotating frame (R1ρ). These optimizing approaches obtained TSLs that are stable across the test problems, enabling good T1ρ mapping results for synthetic data, model phantoms, and healthy volunteer’s knee cartilage.
2. METHODS
2.1. 3D-T1ρ-Weighted Data Acquisition and Reconstruction
The 3D-T1ρ-weighted datasets were acquired with various TSLs (optimized and non-optimized) using a modified 3D Cartesian low flip-angle fast gradient-echo sequence (34). Fourier Transform is applied in the readout (frequency-encoding) direction, denominated kx, to separate 3D Cartesian data into multiple 2D slices on the ky-kz plane.
The MRI scans were performed using a 3T clinical MRI scanner (Prisma, Siemens Healthcare, Erlangen, Germany) with a 15-channel Tx/Rx knee coil (QED, Cleveland OH). The T1ρ preparation module P uses spin-lock frequency=500Hz and TSL defined by the TSL sampling schedule. The 3D imaging module A acquires 64 k-space lines (with 256 samples each) of the data matrix per preparation pulse, using a steady-state sequence with TR/TE=7.60ms/3.86ms and flip-angle=8°, and receiver bandwidth=510 Hz/pixel. A longitudinal magnetization restoration module R with delay=1000ms is used after the imaging module A and before the repetition of the next set of modules P-A-R, which are repeated 128 times to capture a data matrix of size 256×128×64 per TSL. The slice thickness=2mm, the field of view (FOV)=140mm×140mm. This T1ρ pulse sequence is illustrated in Figure 1. Each module P takes approximately the TSL (between 1 and 55 ms), each module A takes approximately 64×TR=486.4ms, and each module R takes 1000ms. Each shot is composed of one set of modules P-A-R and takes 1.5 sec. The shots are repeated 128 times to collect all k-space data for one specific TSL, taking 3.28 minutes per TSL. The more TSLs are captured, the longer is the total acquisition time.
Figure 1:
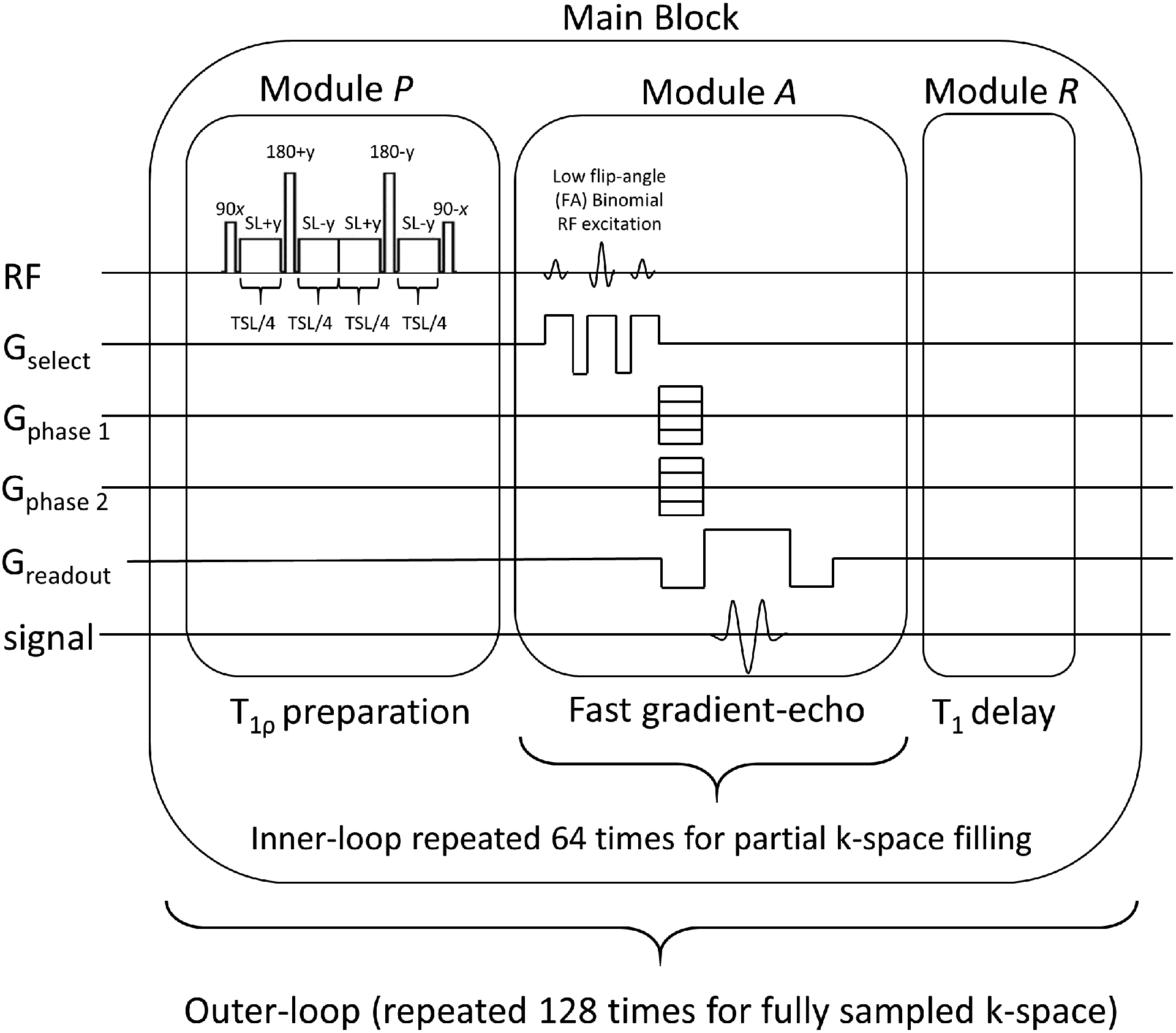
Pulse sequence used to capture one T1ρ-weighted 3D volume (one TSL). The pulse sequence is composed of a T1ρ preparation module P, that applies the T1ρ weighting, a 3D imaging module A, that acquires 64 k-space lines of the entire 3D k-space, and the longitudinal magnetization restoration module R, which recovers the main magnetization before the sequence be repeated until all 3D k-space lines are acquired.
After separation of 2D slices, each slice is reconstructed with SENSE (35), that minimizes:
| [1] |
where xt is a complex-valued vector that represents an image with TSLt, with size Ny × Nz = 128 × 64, with Ny being the image size in the y-axis and Nz the size in the z-axis. The vector yt represents the captured k-space with size Ny × Nz× Nc, where Nc = 15 is the number of coils. The matrix B contains the coil sensitivities and phase compensation (36,37), F the Fourier transforms of all sensitivity-weighted images. The is the squared l2-norm or Euclidean norm of e = yt − FBxt.
The T1ρ magnetization-preparation pulses in this study accept TSLs between 1 and 55 ms, spaced by 1 ms. In this study, two non-optimized choices of TSL, one logarithmically spaced and one linearly spaced within the range of possible TSLs were used to compare against optimized TSLs.
The T1ρ-weighted scans were performed in model phantoms and human volunteers. The model phantoms are composed of 2%, 3%, 4%, 5%, and 6% agar gel. The human knee data were acquired in the sagittal plane from five healthy volunteers (males, mean age 31±8 years). Each scanning session acquired 16 TLSs for agar gel model phantoms and 15 TSLs for healthy volunteers, with an acquisition time of 3.28 minutes per TSL. The scanning session of model agar gel phantoms and one human volunteer was repeated for repeatability evaluation. This study was approved by the institutional review board (IRB) and all the volunteers consented before scanning.
2.2. Exponential Models:
The T1ρ relaxation is represented using a complex-valued exponentially decaying process (38), described as:
| [2] |
with complex-valued θ1(n), real-valued relaxation time θ2(n), and complex-valued white Gaussian noise η(t, n) at spin-lock time t and spatial position n with voxel [xt]n = x(t, n). The model in Equation 2 is the same for all spatial positions, then we will omit n from the following equations. Also, the observed signal will be acquired using K spin-lock times t = [t1, … , tK]T, where tk ∈ T which is a finite set containing all possible TSLs one can set in the MRI scanner (between 1 and 55 ms, spaced by 1 ms), x = [x(t1), … , x(tK)]T, and the parameters are shown as θ = [θ1 θ2]T. We may write x(t, θ) = [x(t1, θ), … , x(tK, θ)]T, to emphasize the dependence Equation 2 on the TSL sampling schedule t and parameters θ.
The model based on the R1ρ, which is the inverse of the T1ρ value, is described as:
| [3] |
where . Unless explicitly noted, we will use the T1ρ model from Equation 2.
2.3. Fitting Algorithms:
Two methods were used for T1ρ fitting. The first method uses NLS, according to:
| [4] |
where f (tk, θ) = θ1 exp(−tk/θ2), and Θ is a set that contains the relaxation parameters.
Equation 4 is minimized using the conjugate gradient Steihaug’s trust-region (CGSTR) algorithm (39), stopping at a maximum of 2500 iterations or when the normalized update is lower than 10−9. The set Θ constrains the parameter θ2, the T1ρ relaxation time, within the range of 10 and 100 ms, while θ1 is not constrained.
The second fitting method is a shallow ANN (23), with one hidden layer of fully connected components of dimension 12, hyperbolic tangent sigmoid transfer function as the non-linear element, and a linear output layer. The number of inputs is 2K where the magnitude and phase of the complex numbers are used as separated inputs for each of the K TSLs. There are 3 real-valued outputs: the magnitude and phase of the θ1 and the real-valued θ2. The output θ2 is constrained between 10 and 100 ms as in the NLS fitting.
To use an ANN for fitting, the following training process needs to be performed:
| [5] |
where represents the ANN, with parameters w (learned during training) and input signal xp, such as used in (23). The index p is the index of the sample of the parameters θ ∈ Θ. The learning problem in Equation 5 is performed using 400 iterations of the Levenberg-Marquadt algorithm (18), using P=20000 samples of the exponential signal xp artificially generated according to Equation 2. From the parameters θp = [θ1 θ2]T, θ2 is taken from a uniform distribution between 10 and 100 milliseconds, and the parameter θ1 is a random complex number with normalized magnitude. The additive Gaussian noise η is independent and identically distributed with zero mean and a standard deviation selected to obtain an SNR of 30. The SNR of 30 was the lowest value obtained from measuring SNR in model phantoms and in vivo knee cartilage data, as described next in section 2.4. When the fitting is applied to model phantoms or healthy volunteer data, the signal x is normalized and the normalization constant integrated into parameter θ1.
2.4. T1ρ and SNR Statistics:
For the TSL optimization procedure, it is necessary to give sample values for θ1, θ2, and noise. For this purpose, we use reference values from the literature (7) for synthetic experiments and measured values from the model agar gel phantoms and human knee experiments. For synthetic experiments, following (7), we used T1ρ values for θ2 as a uniform distribution between 20 and 70 ms, θ1 values as random complex-valued numbers with normalized magnitude, and Gaussian noise with fixed standard deviation to obtain SNR values of 30 and 125 (from our measurements on human volunteers).
For the optimization of the TSLs for model phantoms and knee cartilage, we used data obtained using a non-optimized sequence. First, the noise standard deviation was estimated using the Marchenko–Pastur principal component analysis (MP-PCA) (40). The MP-PCA reshapes the 3D volumes of all K TSLs into a matrix X, of size (K×256)×(128×64), and uses the singular value decomposition X = UΛVT, with singular values . The MP-PCA detects the thresholding 1 ≤ p ≤ M, where the noise standard deviation is
| [6] |
To obtain values for θ1 and θ2, a fitting algorithm was applied voxel-wise in a region of interest (ROI) of the model phantoms and the knee cartilage. The pairs of parameters θ1 (complex-valued amplitudes) and θ2 (T1ρ values) were stored. Note that in model phantoms and human knee images, the SNR is variable voxel-wise, and can be computed as
| [7] |
where n is the spatial position. The SNR=30 was the lowest SNR obtained in knee cartilage measurements, and SNR=125 was the mean value. The SNR values were fixed in the synthetic experiments.
2.5. Optimizing Spin-Lock Times using Cramér-Rao Lower Bounds:
The CRLB asserts a lower bound on the variance of any unbiased estimator (15). In multi-parameter estimators, the Cramér-Rao matrix (CRM), defined as V (t, θ), is given by:
| [8] |
where I (t, θ) is the Fisher information matrix (FIM), given by:
| [9] |
where x(t, θ) = [x(t1, θ), … , x(tK, θ)]T and ρ (x(t, θ)) ln is the natural logarithm of the probability density function of the signal given by Equation 2 or 3. Explicit forms of the FIM for the models in Equations 2 and 3 are in the Appendix. The i-th diagonal element of the CRM in Equation 8 represents the lower bound of the variance of the estimated i-th parameter, written as:
| [10] |
The CRM depends on the TSLs t used in the acquisition and the model parameters θ. The parameters depend on the expected values according to the anatomy, such as knee cartilage. We used in the optimization the values obtained with the procedure from section 2.4.
We are interested in t that minimizes the CRLB averaged over the parameters θ expected in the cartilage. The optimization of the weighted averaged CRLB is stated as:
| [11] |
where ωi is the weight of a particular parameter, and it is used to weigh the importance of the parameters. In this work, we are just interested in improving the T1ρ value of the exponential model, given by θ2, regardless of θ1, using ω1 = 0 and ω2 = 1. The TSLs t should be in a pre-defined grid T. In this study, T corresponds to a grid of possible TSLs between 1 and 55 ms, spaced by 1 ms. Where θs is the s-th sample drawn from the distribution of the parameters of the anatomy or object.
We are particularly interested in the following Modified CRLB criterion that resembles the mean of the normalized absolute error (NAE), which leads to:
| [12] |
This is the squared root of the magnitude of the element in the CRM weighted by the magnitude of the component, which favors equal relative precision across the components (11), and is more robust since it avoids that large V (t, θ) dominates the overall cost (41). This is also connected to the mean of coefficient of variations (CV) over a set of possible parameters.
Because the optimization of the CRLB is an exact (i.e. non-noisy) optimization, any method for combinatorial problems can be used. We used recently-developed subset selection methods such as Pareto Optimization for Subset Selection (POSS) (42,43).
2.6. Matched Sampling-Fitting Optimization:
CRLB criteria are connected to the use of unbiased estimation methods for fitting (16,17) and optimize the lower bound for the variance of the estimated parameters (15). This does make the Hessian matrix (or its approximation using the Jacobian matrix) involved in NLS methods more stable, with a better condition number (19,44). However, this does not necessarily mean that the chosen t will provide the best performance on a particular fitting method. Note that iterative fitting methods for NLS, such as CGSTR (39) or Levenberg-Marquardt (18), are not necessarily unbiased estimators. They have their approaches to deal with the ill-conditioning of the non-linear system (18). This means that CRLB may not be a fundamental bound in this context. Besides, fitting methods based on ANNs may have no benefit by using CRLB-optimized TSLs.
Following the arguments of data-driven approaches for MRI that optimizes the k-space sampling according to the recovery method (20–22), where it was observed that a matched sampling-reconstruction is more effective, we decided to modify the TSLs optimization to include the fitting algorithm. CRLB is partially symbolic, using the model derivative and statistical expectation of the second-order moment of the noise, and partially numerical, using numerical values of θ. In contrast, sampling-fitting approaches are purely numerical, even though the data can be generated from analytical models, as we did in this work.
Considering θs as the s-th sample of the expected parameters, and xs is the noisy signal generated with θs from Equation 2, the fitting algorithm returns the estimated , assuming that the TSL schedule t was used to generate xs. The proposed criterion considers the following minimization problem:
| [13] |
being:
| [14] |
where is a measurement of the distance between the exact parameters θ and its estimation . One possible choice for is the weighted squared error, given by:
| [15] |
leading Equation 13 to the optimization of the mean squared error (MSE), where ωi is the weight on the i-th element of θ, which we denominated MSF-MSE. Another possible cost function is to use the normalized absolute error (NAE) of each parameter, given by:
| [16] |
leading Equation 13 to the optimization of the mean of the normalized absolute error (MNAE), denominated MSF-MNAE, which is also related to the coefficient of variations.
The learning problem in Equation 13 uses samples of the signal xs, generated according to Equation 2, considering the current t, η, and θ = [θ1 θ2]T. We used values obtained with the procedure described in section 2.4.
Note that the cost function in Equation 13 is noisy (33), because the cost d(θs, R(t, xs)) requires to compute R(t; xs), where the signal xs is generated with random noise. This makes the optimization problem also noisy, and the optimization algorithm must be aware of it.
Algorithm 1 is a modification of Pareto Optimization for Noisy Subset Selection (PONSS) (33,42), denoted here as Modified PONSS. Similar to PONSS, a group of candidate solutions is stored in the set C. At each iteration of Algorithm 1, one element of C, defined as t, is selected (in line 5) and modified (in line 6) by changing one of its elements in the composition of a new candidate as t′. The modification is a random switch of one of its time points to a new point in a pre-defined grid T. The new candidate t′ will be accepted in the set C if F (t′) < F (tbest) + 2b.
Because F (t) is noisy, one needs to include the dispersion of the values of the cost function, represented by b. In the same way as PONSS, good candidates in the ±b range are not discarded. However, since the size of the set C may grow significantly, a new evaluation of the cost function is done between lines 12 and 15 of Algorithm 1, also called a tie-break in (33). In the regular PONSS, in (33), a new sample of F (t) is drawn from each t ∈ C, while previous F (t)’s are forgotten. Here, in the Modified PONSS, the new samples are proportionally averaged to the mean F (t), (in line 14), leading the optimization to the mean value of the noisy cost function. As more tie-breaks are done, more samples of F (t) are drawn, producing better estimations of the mean F (t)’s.

2.7. Analysis of Estimated T1ρ Values:
To validate the results, we compare the estimated T1ρ values obtained with different TSLs against reference values. In the synthetic experiments, the exact T1ρ values are known. For the other cases, the reference values are estimated using all TSLs acquired in each scanning session. We used the MNAE:
| [17] |
and normalized root MSE (NRMSE):
| [18] |
The sums consider the voxels n in the region of interest (ROI), where |ROI| is the number of voxels in the ROI. The ROI was manually segmented. Also, θ2 (n) is the reference value of a particular voxel, and is its estimation using the TSL schedule being evaluated.
To assess repeatability, we evaluate the coefficient of variations (CV), which corresponds to RMS CV used in (45). For agar gel phantoms the sessions were repeated one after the other without moving the phantom. We also assessed linear predictability between agar gel concentrations and R1ρ values by using the coefficient of determination (R2). For healthy volunteer scans, motion correction was used to register the knees in the same position.
3. RESULTS
3.1. Illustration of Noisy Cost Functions and Stability of the Modified CRLB:
In Figure 2 we illustrate the issue with noisy cost functions and the stability of the modified CRLB using curves related to small problems (K=2). Figure 2(a) shows CRLB and Modified CRLB for optimizing TSLs targeting the models in Equations 2 and 3. If the objective is improving T1ρ, then the FIM, shown in Equation A1 in theAppendix, has its components as in Equation A2. On the other hand, if the objective is improving R1ρ, then the components of FIM should be as in Equation A3. Note that when the T1ρ value is estimated, the R1ρ value is automatically obtained. However, from the point of view of the CRLB optimization, they are different things and have different optimal TSLs. In this sense, the Modified CRLB has the advantage of being invariant to this choice, as seen in Figure 2(a). No matter if one is interested in improving T1ρ or R1ρ estimation, the optimal TSL sampling schedule is the same. Figure 2(b) shows a comparison of the two (non-noisy) CRLB criteria for T1ρ values (CRLB and the Modified CRLB) and the mean cost function (averaged from 15 realizations) of the two (noisy) MSF criteria (MSF-MSE and MSF-MNAE). Note that the optimal solutions for the Modified CLRB and MSF-MNAE are much closer to one another than the CRLB and MSF-MSE. Figures 2(a) and 2(b) illustrate the stability of the Modified CRLB.
Figure 2:
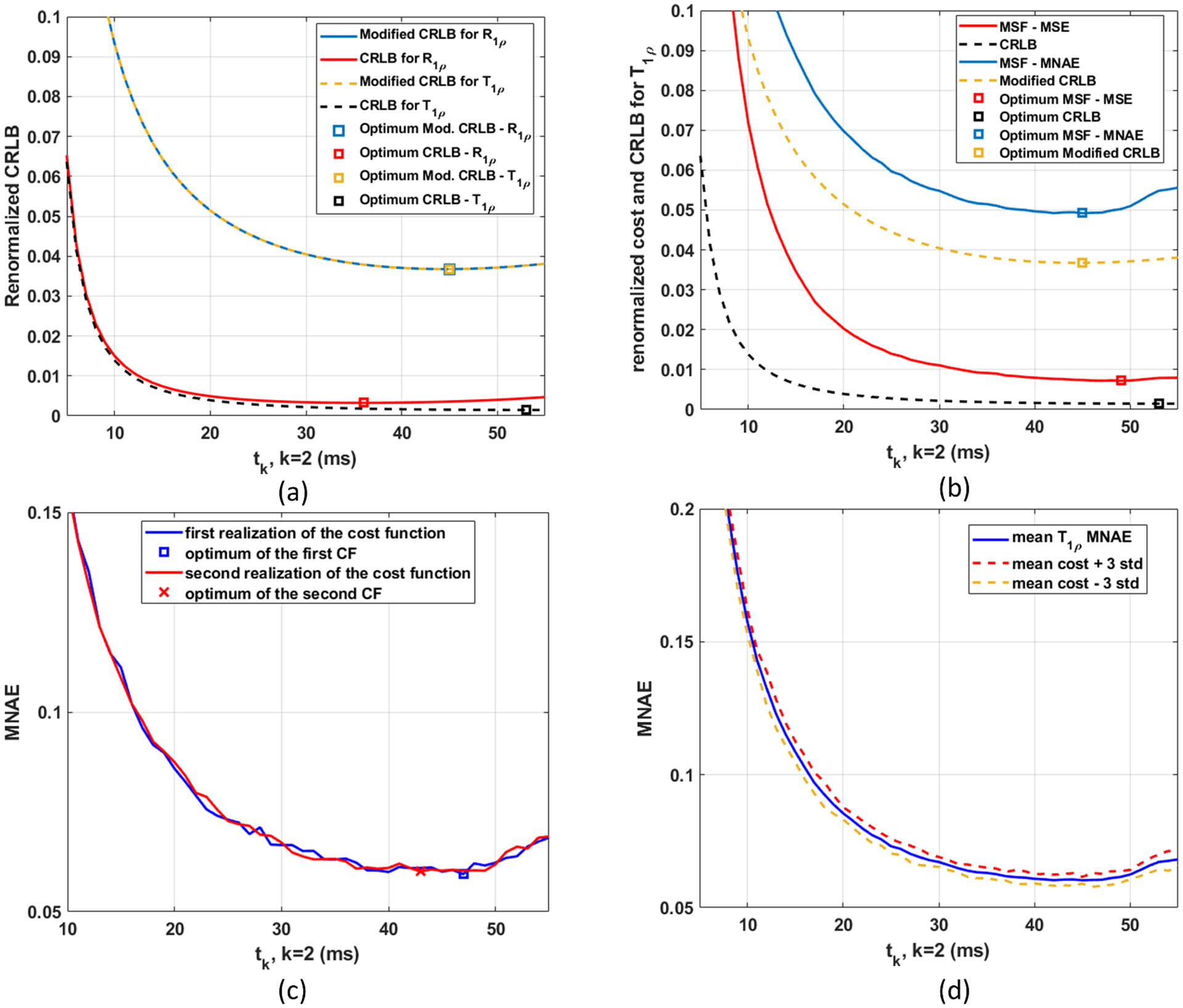
In (a), the comparison of the renormalized costs of CRLB and Modified CRLB when optimizing T1ρ values or R1ρ values, using 2 TSLs, with t = [t1 t2]T, where t1=1 millisecond (ms) and t2 is the optimizing variable. In (b), Modified CRLB has its shape and minimum very close to the MSF-MNAE, while CRLB and MSF-MSE are not so close to one another. In (c) two different realizations of the noisy cost function (for MSF-MNAE) are shown with their corresponding minima. In (d) the mean cost function (averaged from 15 realizations) for MSF-MNAE and the range of ± 3 standard deviations are shown, illustrating where 99.73% of the realizations are expected to be.
Because the MSF cost functions are noisy, each realization may have a different minimum. In Figure 2(c), it is shown the curves for two different realizations. Optimization methods for exact cost functions are likely to converge to the optimum of one realization because they expect the evaluations of F(t) to be exact. Since they are not exact, we need a method able to converge to the optimal solution of the mean cost function. To achieve this, the optimization method needs to average among multiple measures of F(t). Also, the value of b in Modified PONSS should be chosen considering the dispersion of the noisy cost function around its mean value. This can be seen in Figures 2(d), which shows the mean cost function and a range of values (±3 st.dev.) where 99.73% of the realizations are expected to be.
3.2. Evaluation of the Optimized TSLs for Synthetic Data:
The evaluation of the methods with synthetic data is composed of 15 repetitions of the sampling-fitting, using S=5000 samples of exponential functions generated according to the model from Equation 2, with parameters (θ1 and θ2) obtained as described in section 2.4.
The non-optimized and optimized TSLs, for different K, are shown in Table 1 for SNR=30 and in Supporting Information Table S1 (in the supplemental information) for SNR=125 showing the MNAE and NRMSE, in percentages. Note that optimized TSLs with K=2 are approximately equal in quality to non-optimized with K=3, and optimized TSLs with K=3 are equivalent to non-optimized with K=4. In Figure 3, we see the performance of some TSL schedules for individualized T1ρ values in the range used in this experiment. This figure shows an average of 500 repetitions for each T1ρ value. The resulting curve (with lower MNAE) shows the reduced estimation error for T1ρ values (with low MNAE) in the expected range. Note that the estimation error is different for each T1ρ and each TSL schedule favors some T1ρ values.
Table 1:
Optimized and non-optimized spin lock times, in milliseconds (ms) for the various criteria and sizes K, with SNR=30.
| MNAE | NRMSE | MNAE | NRMSE | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Non-Optimized log. spaced | NLS | ANN | NLS | ANN | Non-Optimized linearly spaced | NLS | ANN | NLS | ANN | ||||||||||
| K=2 | 1 | 20 | 8.6% | 9.3% | 12.6% | 13.3% | K=2 | 1 | 25 | 7.4% | 7.9% | 10.5% | 11.2% | ||||||
| K=3 | 1 | 3 | 30 | 6.6% | 6.9% | 9.0% | 9.5% | K=3 | 1 | 20 | 40 | 5.4% | 5.5% | 7.5% | 7.7% | ||||
| K=4 | 1 | 2 | 9 | 40 | 5.8% | 5.9% | 7.9% | 7.8% | K=4 | 1 | 15 | 30 | 45 | 4.7% | 4.8% | 6.6% | 6.6% | ||
| K=5 | 1 | 2 | 5 | 16 | 50 | 5.2% | 5.2% | 7.0% | 6.8% | K=5 | 1 | 13 | 26 | 39 | 52 | 4.2% | 4.2% | 6.0% | 5.6% |
| MNAE | NRMSE | MNAE | NRMSE | ||||||||||||||||
| CRLB | NLS | ANN | NLS | ANN | Modified CRLB | NLS | ANN | NLS | ANN | ||||||||||
| K=2 | 1 | 53 | 6.7% | 6.5% | 7.9% | 7.8% | K=2 | 1 | 45 | 6.0% | 6.3% | 7.6% | 8.0% | ||||||
| K=3 | 1 | 55 | 55 | 4.7% | 4.8% | 5.6% | 5.7% | K=3 | 1 | 47 | 48 | 4.5% | 4.7% | 5.7% | 5.9% | ||||
| K=4 | 1 | 55 | 55 | 55 | 3.9% | 4.1% | 4.8% | 4.9% | K=4 | 1 | 49 | 50 | 50 | 3.9% | 4.0% | 4.9% | 5.0% | ||
| K=5 | 1 | 55 | 55 | 55 | 55 | 3.5% | 3.6% | 4.3% | 4.4% | K=5 | 1 | 51 | 51 | 51 | 52 | 3.5% | 3.6% | 4.4% | 4.5% |
| MNAE | NRMSE | MNAE | NRMSE | ||||||||||||||||
| MSF-MSE for NLS | NLS | ANN | NLS | ANN | MSF-MNAE for NLS | NLS | ANN | NLS | ANN | ||||||||||
| K=2 | 1 | 49 | 6.2% | 6.3% | 7.5% | 7.8% | K=2 | 1 | 44 | 6.1% | 6.3% | 7.7% | 8.0% | ||||||
| K=3 | 1 | 51 | 54 | 4.6% | 4.7% | 5.6% | 5.8% | K=3 | 1 | 46 | 47 | 4.5% | 4.7% | 5.7% | 5.9% | ||||
| K=4 | 1 | 53 | 55 | 55 | 3.9% | 4.0% | 4.8% | 4.9% | K=4 | 1 | 47 | 48 | 52 | 3.9% | 4.0% | 4.9% | 5.0% | ||
| K=5 | 1 | 54 | 54 | 55 | 55 | 3.5% | 3.7% | 4.3% | 4.5% | K=5 | 1 | 46 | 48 | 52 | 54 | 3.5% | 3.6% | 4.4% | 4.5% |
| MNAE | NRMSE | MNAE | NRMSE | ||||||||||||||||
| MSF-MSE for ANN | NLS | ANN | NLS | ANN | MSF-MNAE for ANN | NLS | ANN | NLS | ANN | ||||||||||
| K=2 | 1 | 50 | 6.4% | 6.4% | 7.6% | 7.8% | K=2 | 1 | 43 | 6.1% | 6.3% | 7.8% | 8.0% | ||||||
| K=3 | 1 | 51 | 55 | 4.7% | 4.7% | 5.6% | 5.8% | K=3 | 1 | 43 | 44 | 4.6% | 4.7% | 5.9% | 6.0% | ||||
| K=4 | 1 | 50 | 55 | 55 | 4.0% | 4.0% | 4.8% | 4.9% | K=4 | 1 | 37 | 52 | 54 | 3.9% | 4.0% | 5.0% | 5.1% | ||
| K=5 | 1 | 49 | 55 | 55 | 55 | 3.6% | 3.6% | 4.3% | 4.4% | K=5 | 1 | 32 | 52 | 54 | 55 | 3.6% | 3.6% | 4.6% | 4.6% |
Figure 3:
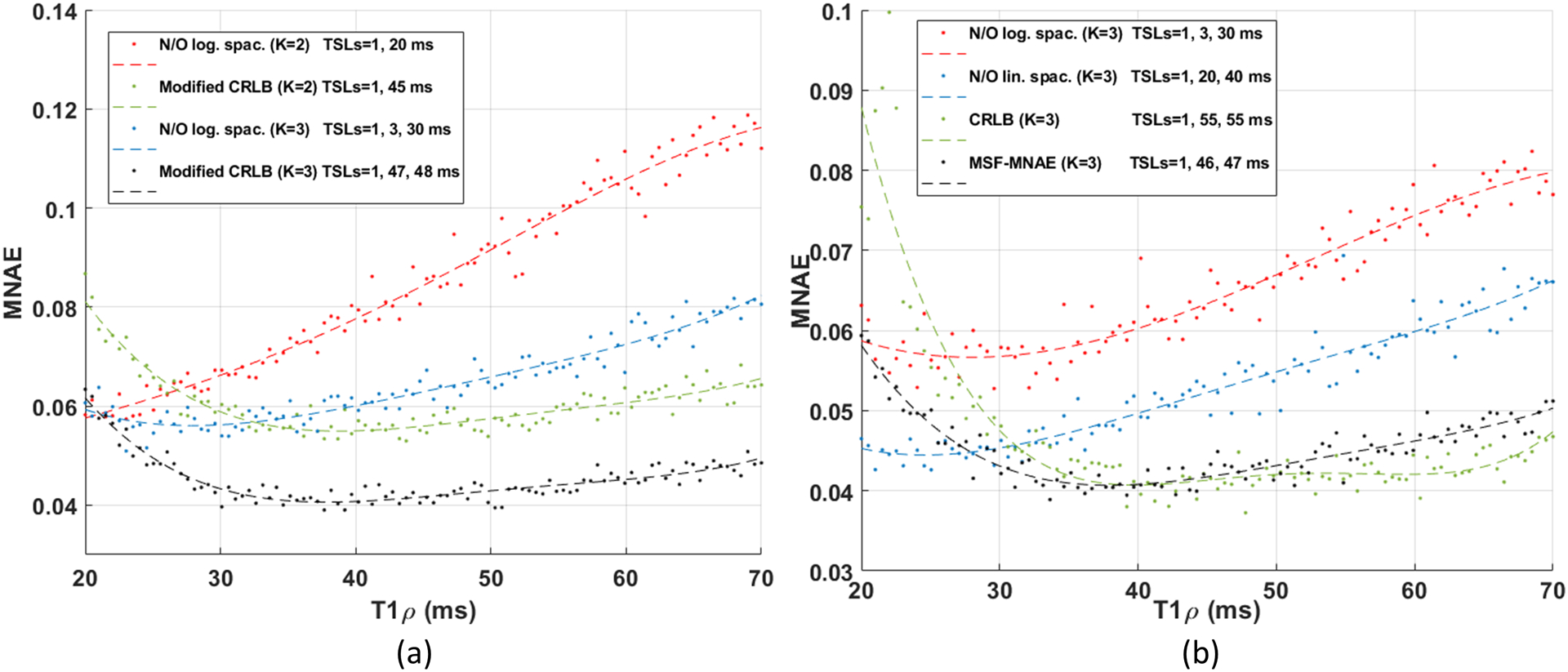
Performance of different choices of TSL in the synthetic experiments with SNR=30 for each expected T1ρ value, measured by MNAE. This curve considers that the measured signal was generated by the specified T1ρ value (in the range of 20 and 70 ms). In (a), increasing K lowers the curve of MNAE. In (b), the optimization finds the best TSL sampling schedules for an expected range of T1ρ values using the same K.
3.3. Experiments with T1ρ Model Phantoms:
The reference T1ρ map of the model phantom (composed of tubes with 2%, 3%, 4%, 5%, and 6% agar gel) is shown in Figure 5(a). It was computed using all the 16 TSLs acquired in the session (1, 1, 3, 10, 20, 25, 30, 32, 32, 34, 34, 38, 40, 40, 42, 55 ms). Figures 4 shows the linear regression between agar gel concentrations and R1ρ values. The strong coefficient of determination (R2) with R1ρ values shows the linear predictability between agar gel concentrations and R1ρ values. One-dimensional histograms of the T1ρ values for the first and second scans of the phantom are shown in Figure 5(b). Some illustrative examples of T1ρ maps and their voxel-wise error related to the reference are shown in Figure 5(c)–(f). These examples illustrate the improvement in the maps and reduction of error with optimization of the TSLs. Table 2 shows all the results with model phantoms computed from 10 slices of the T1ρ phantom.
Figure 5:
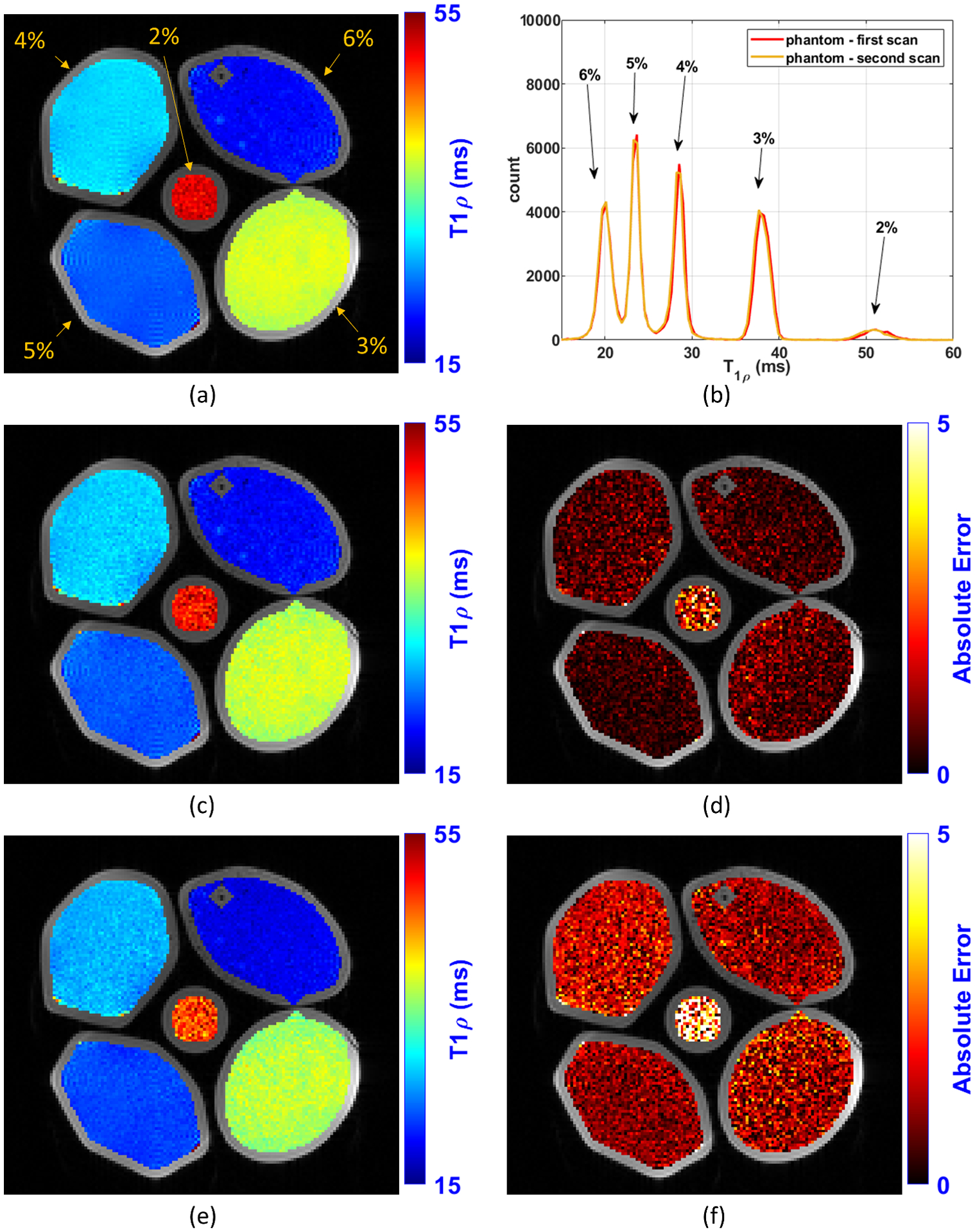
Illustration of the T1ρ maps obtained with the T1ρ agar gel model phantoms experiment. In (a) is shown the reference map obtained using all the 16 TSLs acquired in a phantom scan session (1, 1, 3, 10, 20, 25, 30, 32, 32, 34, 34, 38, 40, 40, 42, 55 ms). In (b) is shown the histogram of the T1ρ values of the phantom (histogram CV=5.9%). In (c) and (d) are shown respectively the T1ρ map and error map obtained with K=2 optimized TSLs: 1, 32 ms (optimal TSLs for Modified CRLB and MSF-MNAE when K=2). In (e) and (f) are shown respectively the T1ρ map and error map obtained with K=2 non-optimized logarithmic scaled TSLs: 1, 20 ms.
Figure 4:
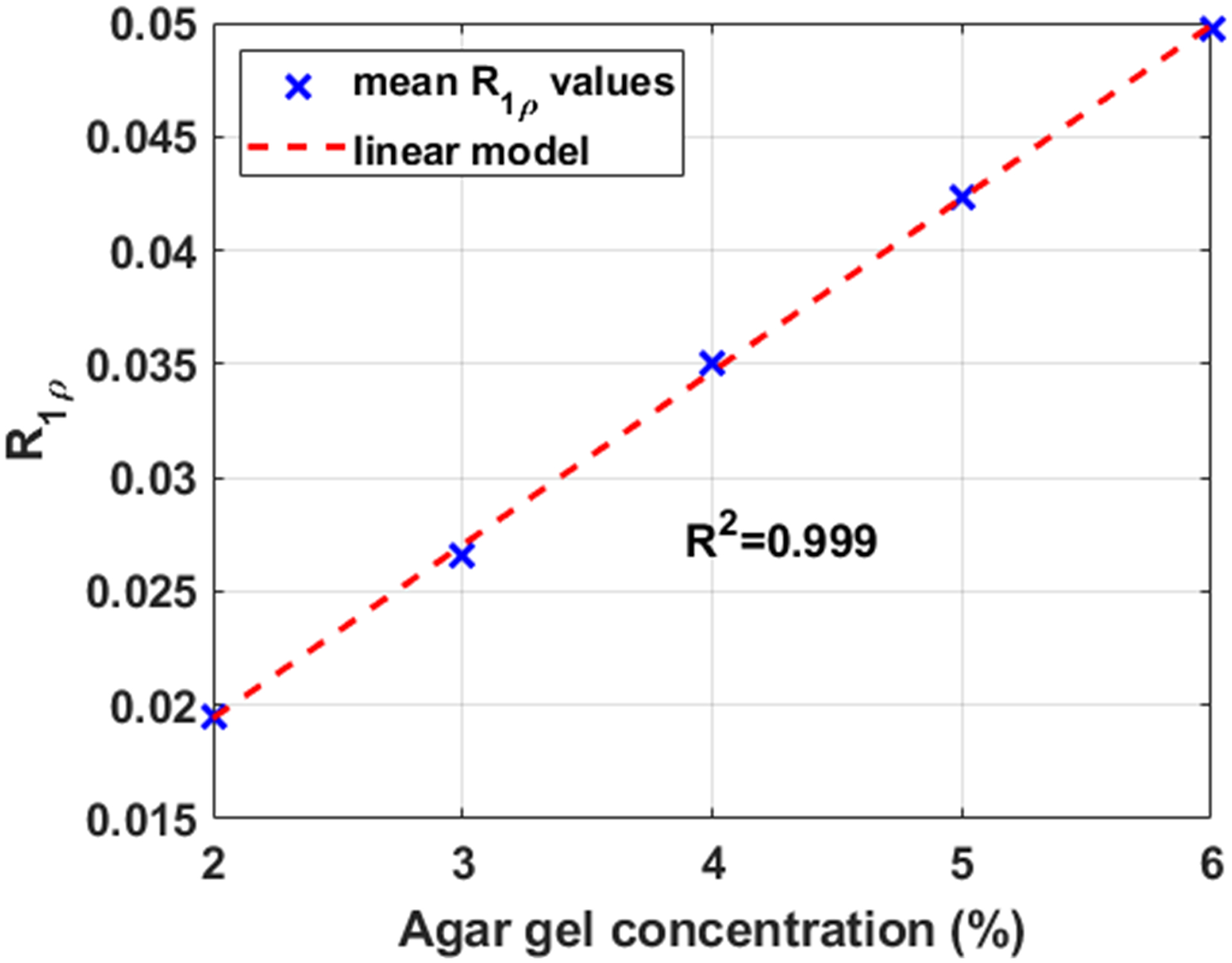
Correlation between R1ρ values and agar gel concentration in the model phantoms.
Table 2:
Optimized and non-optimized spin lock times, in milliseconds (ms) for the various criteria and K=2 and 3 with the T1ρ agar gel model phantoms in a 3T MRI scanner.
| Comparison with the Reference (MNAE and NRMSE), Repeatability (CV), and regression with agar gel (R2) |
MNAE | NRMSE | CV | Regression of R1ρ (R2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NLS | ANN | NLS | ANN | NLS | ANN | NLS | ANN | |||||
| Non-Optimized log. spaced | K=2 | 1 | 20 | 5.3% | 4.4% | 6.2% | 5.2% | 1.7% | 1.9% | 0.996 | 0.996 | |
| K=3 | 1 | 3 | 30 | 2.3% | 2.2% | 3.2% | 2.9% | 1.5% | 1.7% | 0.998 | 0.998 | |
| Non-Optimized linearly spaced | K=2 | 1 | 25 | 3.6% | 3.2% | 4.6% | 4.0% | 1.6% | 1.7% | 0.997 | 0.997 | |
| K=3 | 1 | 20 | 40 | 2.2% | 2.1% | 2.6% | 2.5% | 1.2% | 1.4% | 0.998 | 0.998 | |
| CRLB | K=2 | 1 | 38 | 2.2% | 2.3% | 2.7% | 2.8% | 1.6% | 1.7% | 0.998 | 0.998 | |
| K=3 | 1 | 40 | 40 | 2.0% | 2.1% | 2.3% | 2.4% | 1.3% | 1.3% | 0.998 | 0.998 | |
| Modified CRLB | K=2 | 1 | 32 | 2.1% | 2.0% | 2.8% | 2.7% | 1.6% | 1.7% | 0.998 | 0.998 | |
| K=3 | 1 | 34 | 34 | 1.5% | 1.5% | 2.1% | 2.0% | 1.2% | 1.3% | 0.998 | 0.998 | |
| MSF-MSE for NLS | K=2 | 1 | 38 | 2.2% | 2.3% | 2.7% | 2.8% | 1.6% | 1.7% | 0.998 | 0.998 | |
| K=3 | 1 | 38 | 42 | 2.0% | 2.0% | 2.3% | 2.3% | 1.3% | 1.3% | 0.998 | 0.998 | |
| MSF-MSE for ANN | K=2 | 1 | 40 | 2.4% | 2.5% | 2.8% | 2.8% | 1.7% | 1.7% | 0.998 | 0.998 | |
| K=3 | 1 | 34 | 55 | 2.3% | 2.3% | 2.3% | 2.6% | 1.3% | 1.4% | 0.998 | 0.998 | |
| MSF-MNAE for NLS | K=2 | 1 | 32 | 2.1% | 2.0% | 2.8% | 2.7% | 1.6% | 1.7% | 0.998 | 0.998 | |
| K=3 | 1 | 32 | 34 | 1.5% | 1.5% | 2.2% | 2.0% | 1.2% | 1.3% | 0.998 | 0.998 | |
| MSF-MNAE for ANN | K=2 | 1 | 38 | 2.2% | 2.3% | 2.7% | 2.8% | 1.6% | 1.7% | 0.998 | 0.998 | |
| K=3 | 1 | 25 | 55 | 1.6% | 1.8% | 2.2% | 2.4% | 1.3% | 1.4% | 0.998 | 0.998 | |
| REFERENCE | K=16 | 1, 1, 3, 10, 20, 25, 30, 32, 32, 34, 34, 38, 40, 40, 42, 55 | 0.6% | 0.7% | 0.999 | 0.999 | ||||||
3.4. Experiments with In Vivo Knee Cartilage Data:
In-vivo knee cartilage data from five volunteers were acquired. A non-optimized scan of one of the volunteers was used to obtain parameters for training, as described in section 2.4. In Figure 7(e) a 2D histogram showing the pair of T1ρ and SNR (as defined in Equation 7) values of the volunteer used for training is presented. The 2D histogram of one of the other volunteers is shown in Figure 7(m), with its respective 1D versions for each repeated scan in Figures 6(e) and 6(m).
Figure 7:
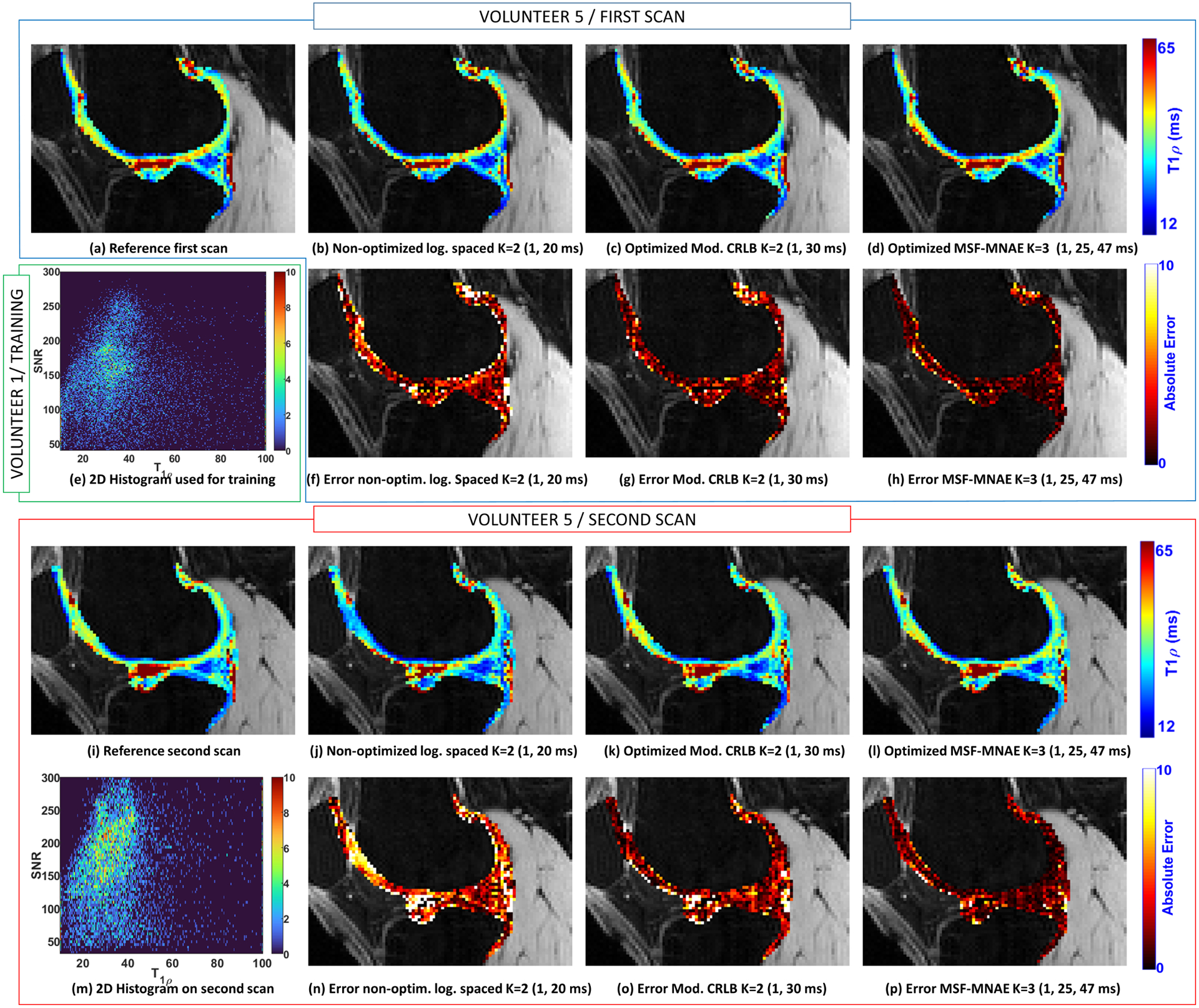
Illustration of the T1ρ maps of the lateral cartilage obtained with the volunteer 5. The reference map obtained using all the TSLs (K=15, TSLs=1, 1, 3, 10, 20, 25, 30, 31, 32, 36, 37, 40, 42, 47, 55 ms) from the first scan is shown in (a) and from the second scan in (i). T1ρ map obtained with volunteer 5 in the first scan with non-optimized TSLs (K=2, TSLs=1, 20 ms) is shown in (b), with TSLs optimized for Mod. CRLB (K=2, TSLs=1, 30 ms) in (c), and MSF-MNAE (K=3, TSLs=1, 25, 47 ms) in (d). T1ρ maps of the second scan of the same volunteer are shown in (j)-(l). In (f)-(h) and (n)-(p) the corresponding errors related to the reference are shown. The 2D histogram obtained with volunteer 1, which was used for the optimization, is shown in (e). The 2D histogram obtained after optimization, with volunteer 5 is shown in (m).
Figure 6:
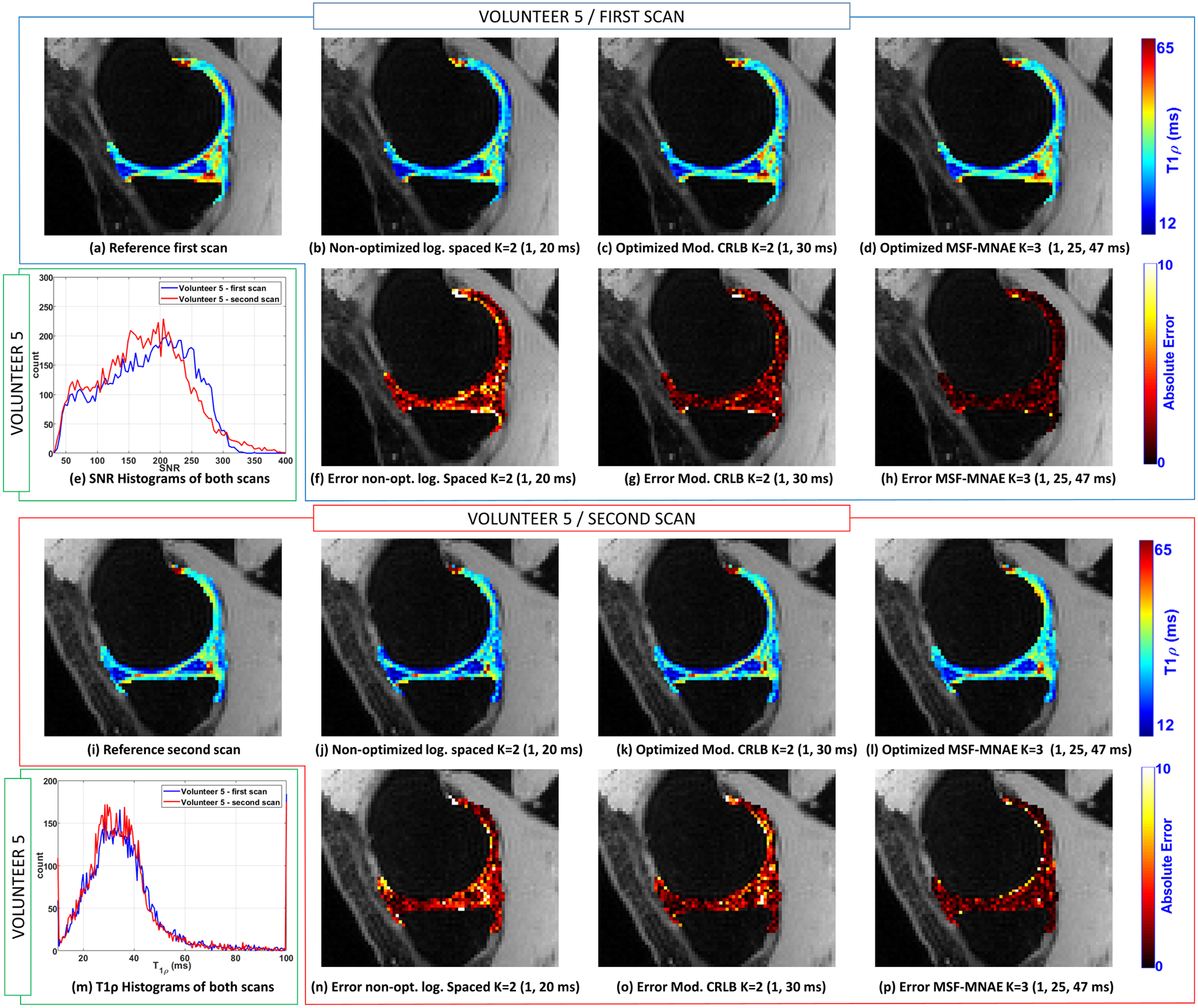
Illustration of the T1ρ maps of the medial cartilage obtained with the volunteer 5. The reference map obtained using all the TSLs (K=15, TSLs=1, 1, 3, 10, 20, 25, 30, 31, 32, 36, 37, 40, 42, 47, 55 ms) from the first scan is shown in (a) and from the second scan in (i). T1ρ map obtained with volunteer 5 in the first scan with non-optimized TSLs (K=2, TSLs=1, 20 ms) is shown in (b), with TSLs optimized for Mod. CRLB (K=2, TSLs=1, 30 ms) in (c), and MSF-MNAE (K=3, TSLs=1, 25, 47 ms) in (d). T1ρ maps of the second scan of the same volunteer are shown in (j)-(l). In (f)-(h) and (n)-(p) the corresponding errors related to the reference are shown. The histograms obtained in the first and second scans are shown in (e) for the SNR (CV=10.9%) and in (m) for T1ρ values (CV=8.6%).
In each scanning session, a total of 15 TSLs were acquired to compose all optimized and non-optimized TSLs needed for the comparison (only K =2 and K =3 were compared to avoid long scanning sessions). The reference T1ρ map was computed using the values measured from all the 15 TSLs (TSLs=1, 1, 3, 10, 20, 25, 30, 31, 32, 36, 37, 40, 42, 47, 55 ms). One of the volunteers was scanned twice, one week apart, for repeatability evaluation. The MNAE, NRMSE, and CV are shown in Table 3. Figure 6 shows some illustrative T1ρ maps and voxel-wise errors (related to the reference) to compare optimized and non-optimized TSLs for medial cartilage. Also, the first and second scans of one volunteer are shown (same slice) to illustrate the repeatability. Figure 7 shows similar results for the lateral cartilage.
Table 3:
Optimized and non-optimized spin lock times, in milliseconds (ms) for the various criteria and K=2 and K=3 on healthy volunteers in a 3T MRI scanner.
| Comparison with the Reference (MNAE and NRMSE) and Repeatability (CV and ROI CV) | MNAE | NRMSE | CV | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NLS | ANN | NLS | ANN | NLS | ANN | |||||
| Non-Optimized log. spaced | K=2 | 1 | 20 | 17.9% | 18.1% | 27.5% | 27.8% | 3.7% | 3.8% | |
| K=3 | 1 | 3 | 30 | 10.5% | 10.6% | 17.5% | 16.7% | 3.1% | 3.3% | |
| Non-Optimized linearly spaced | K=2 | 1 | 25 | 13.1% | 13.1% | 21.5% | 20.8% | 3.5% | 3.6% | |
| K=3 | 1 | 20 | 40 | 9.8% | 10.4% | 17.0% | 16.6% | 3.0% | 3.2% | |
| CRLB | K=2 | 1 | 42 | 12.7% | 12.8% | 19.8% | 20.1% | 2.9% | 3.0% | |
| K=3 | 1 | 36 | 55 | 9.9% | 9.9% | 16.3% | 16.4% | 2.8% | 2.9% | |
| Modified CRLB | K=2 | 1 | 30 | 11.0% | 11.1% | 18.2% | 18.3% | 2.9% | 2.9% | |
| K=3 | 1 | 30 | 32 | 8.0% | 8.3% | 14.2% | 14.3% | 2.8% | 2.8% | |
| MSF-MSE for NLS | K=2 | 1 | 37 | 12.6% | 12.7% | 19.8% | 19.9% | 3.0% | 3.0% | |
| K=3 | 1 | 36 | 55 | 9.9% | 9.9% | 16.3% | 16.4% | 2.8% | 2.9% | |
| MSF-MSE for ANN | K=2 | 1 | 42 | 12.7% | 12.8% | 19.8% | 20.1% | 2.9% | 3.0% | |
| K=3 | 1 | 42 | 47 | 10.0% | 10.2% | 14.5% | 15.6% | 2.9% | 2.9% | |
| MSF-MNAE for NLS | K=2 | 1 | 31 | 10.3% | 10.7% | 16.6% | 16.6% | 2.9% | 2.9% | |
| K=3 | 1 | 32 | 37 | 7.7% | 7.9% | 12.8% | 12.9% | 2.7% | 2.7% | |
| MSF-MNAE for ANN | K=2 | 1 | 32 | 10.1% | 10.2% | 16.5% | 16.2% | 2.8% | 2.8% | |
| K=3 | 1 | 25 | 47 | 7.7% | 7.9% | 13.9% | 13.7% | 2.7% | 2.7% | |
| REFERENCE | K=15 | 1, 1, 3, 10, 20, 25, 30, 31, 32, 36, 37, 40, 42, 47, 55 | 2.5% | 2.5% | ||||||
4. DISCUSSION
4.1. Fitting with Non-Linear Least Squares and Artificial Neural Networks:
The T1ρ mapping results using NLS or ANN are very similar in terms of quality, as seen in Tables 1, 2, 3, and Supporting Information Table S1, more than previously reported (23). ANNs are computationally advantageous when a large number of voxels are to be fitted. Even though the training process takes some time (0.2~1 hours), the fitting process of new data is fast (2~10 sec).
While the difference in quality according to the fitting method is not large in this problem, the difference in quality according to the chosen TSL is. Using optimal TSLs improved both fitting approaches, NLS and ANN, by larger margins, especially for small K, as seen in the tables.
4.2. Difficulties of the Optimization of MSF and Advantages of CRLB:
Algorithms like POSS can find the optimal solution for CRLB criteria relatively quickly, taking from 10 minutes to 1 hour in our problems, because the cost function only needs to be evaluated once for a particular t. On the other hand, optimizing any of the MSF criteria is more difficult. Cost functions are more expensive to evaluate since it requires to perform the fitting process, and they have to be evaluated multiple times for improved precision. The finer the precision of the grid T, the more evaluations are needed to properly resolve which t is optimal. Because of these issues, algorithms like the Modified PONSS require a longer optimization time, in the order of 10 to 100 times more cost function evaluations than with exact cost functions (from 1 day to a couple of weeks in our problems). This long optimization time is not always worthwhile, considering that CRLB criteria, which is easier to optimize, obtain very close quality results.
4.3. Robustness of the Modified CRLB and MSF-MNAE:
As seen in Figure 2(a), the CRLB is sensitive to the exponential model used, leading to different optimal TSLs for T1ρ and R1ρ. In contrast, the Modified CRLB was insensitive to choice for T1ρ or R1ρ. The MSF-MNAE also shares the same robustness property, as seen in Figure 2(b), producing stable results across the different experiments than the ordinary CRLB and MSF-MSE.
4.4. Stability and Unicity of the Optimal TSLs:
Note that the optimization of the TSLs is a non-convex problem. In this sense, there is no guarantee of uniqueness. On top of it, the optimal TSLs are usually in a plateau in the cost function (a plateau is a region of the cost function where the cost is approximately equal), as seen in Figure 2, particularly in Figure 2(a) and 2(b). This explains why different TSL schedules performed almost equally well in most experiments, particularly with large K. In this sense, the resulting TSLs provided in Tables 1, 2, and 3 and Supporting Information Table S1 should not be taken as the unique optimal TSL because other non-tested TSLs schedules may perform equally well. Note also that, as shown in Figure 3, that a particular choice of TSL schedule may perform better for some T1ρ values than the others. This usually depends on the given distribution T1ρ values of and the chosen criterion.
4.5. Comparison with Previous Studies:
In (7) only linear fitting in the magnitude values was considered. Here we rely on the fact that complex-valued fitting, being it done by NLS or ANNs, is more precise, and we also assessed different optimization criteria. Even though the precision of the grid T in (7) is small (TSLs spaced by 10 ms), some similarities among optimal values are observed: the first TSL is usually in the smallest position of the grid while the others are clustered nearby in mid to large positions. Similar results have already been shown in (46). In some sense, the optimal TSLs we obtained contradicted our previous intuition that good TSLs should be spread in time (34,47). Plots like in Figure 3 can help to check if certain expected T1ρ values are well-covered by the chosen TSL schedule.
In (8,9) the worst-case of the CRLB for the expected range of parameters was optimized, instead of the mean-case considered in Equations 11. Worst-case optimization focus on reducing the cost for the worst parameter in the range of expected parameter values. The mean of the CRLB, on the other hand, depends on the expected distribution of parameters, giving more importance to more frequent parameters. Mean-case is more accurate when the distribution is known and stable across different scanned subjects.
In (11) worst-case of the Modified CRLB for the expected range of parameters was optimized. This is the same modification of the CRLB parameters done in Equation 12, except that in Equation 12 the mean is optimized. In (13), the mean-case optimization with a cost function similar to Equations 11 was used for MR fingerprinting. To the best of our knowledge, no other study compared different CRLB approaches and different MSF approaches with various fitting methods to find which one is better for choosing the TSL sampling schedules.
4.6. Limitations of This Study and Future Directions
In this study, we considered Gaussian noise in complex-valued fitting algorithms, assuming the image reconstruction returns a complex-valued image. Magnitude-only fitting, outliers, and problems with motion other than translation motion are not considered here. For the magnitude-only fitting, Rician noise is more adequate than Gaussian noise (48). Under outliers and complex motion, approaches based on robust statistics (46) can perform better. Also, ANN can be trained with these problems, possibly overcoming them in a more simplified and advantageous computational manner than robust fitting methods.
The approaches discussing here can also be applied to other quantitative mapping techniques, such as T1 and T2 mapping (8–12,16), and diffusion measurements (49). Also, these approaches can be extended with sophisticated multi-compartment models such as biexponential (34,50), stretched exponential (51,52) models.
We did not discuss k-space undersampling as a way to reduce scan time for T1ρ mapping in this study, only the scan time reduction by reducing the number of TSLs. In this sense, we observe that the TSLs optimized by the Modified CRLB and MSF-MNAD performed well even when 2 TSLs were used. Nevertheless, k-space undersampling, specially optimized k-space undersampling (22), can be combined with optimized TSL for even faster and stable T1ρ mapping.
5. CONCLUSION
In this work, different optimization criteria for choosing the spin-lock times in T1ρ mapping were compared. According to our results in synthetic data, model phantoms, and healthy volunteers, a modified CRLB and the MSF based on MNAE were the most robust optimization approaches for choosing TSLs. The Modified CRLB was easier to optimize since this criterion has exact (non-noisy) cost functions. The optimized TSLs with these methods allowed robust results with improved quality when using only 2 TSLs and complex-valued fitting with iterative NLS or ANN.
Supplementary Material
Supporting Information Table S1: Optimized and non-optimized spin lock times, in milliseconds (ms) for the various criteria and sizes K, with SNR=125.
Acknowledgment
This study was supported by NIH grants, R21-AR075259-01A1, R01-AR068966, R01-AR076328-01A1, R01-AR076985-01A1, and R01-AR078308-01A1 and was performed under the rubric of the Center of Advanced Imaging Innovation and Research (CAI2R), an NIBIB Biomedical Technology Resource Center (NIH P41-EB017183).
APPENDIX
Fisher Information Matrix used in CRLB optimization:
The FIM for CRLB optimization with the T1ρ model from Equation 2 can be written as
| [A1] |
with
| [A2] |
where J (tk, θ)H is the transpose and complex-conjugate version of J (tk, θ). Note that the R1ρ model from Equation 3 can also be used. In this case
| [A3] |
REFERENCES
- 1.Akella SVS, Reddy Regatte R, Gougoutas AJ, et al. Proteoglycan-induced changes in T1ρ-relaxation of articular cartilage at 4T. Magn. Reson. Med 2001;46:419–423 doi: 10.1002/mrm.1208. [DOI] [PubMed] [Google Scholar]
- 2.Nishioka H, Nakamura E, Hirose J, Okamoto N, Yamabe S, Mizuta H. MRI T1ρ and T2 mapping for the assessment of articular cartilage changes in patients with medial knee osteoarthritis after hemicallotasis osteotomy. Bone Jt. Res 2016;5:294–300 doi: 10.1302/2046-3758.57.BJR-2016-0057.R1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.MacKay JW, Low SBL, Smith TO, Toms AP, McCaskie AW, Gilbert FJ. Systematic review and meta-analysis of the reliability and discriminative validity of cartilage compositional MRI in knee osteoarthritis. Osteoarthr. Cartil 2018;26:1140–1152 doi: 10.1016/j.joca.2017.11.018. [DOI] [PubMed] [Google Scholar]
- 4.Redpath TW. Signal-to-noise ratio in MRI. Br. J. Radiol 1998;71:704–707 doi: 10.1259/bjr.71.847.9771379. [DOI] [PubMed] [Google Scholar]
- 5.Bernstein M, King K, Zhou X. Handbook of MRI pulse sequences. Academic Press; 2004. [Google Scholar]
- 6.Ohliger MA, Sodickson DK. An introduction to coil array design for parallel MRI. NMR Biomed. 2006;19:300–315 doi: 10.1002/nbm.1046. [DOI] [PubMed] [Google Scholar]
- 7.Johnson CP, Thedens DR, Magnotta VA. Precision-guided sampling schedules for efficient T1ρ mapping. J. Magn. Reson. Imaging 2015;41:242–250 doi: 10.1002/jmri.24518. [DOI] [PubMed] [Google Scholar]
- 8.Funai A, Fessler JA. Cramér Rao bound analysis of joint B1/T1 mapping methods in MRI. In: IEEE International Symposium on Biomedical Imaging. IEEE International Symposium on Biomedical Imaging IEEE; 2010. pp. 712–715. doi: 10.1109/ISBI.2010.5490075. [DOI] [Google Scholar]
- 9.Nataraj G, Nielsen J-F, Fessler JA. Optimizing MR Scan Design for Model-Based T1, T2 Estimation From Steady-State Sequences. IEEE Trans. Med. Imaging 2017;36:467–477 doi: 10.1109/TMI.2016.2614967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hernando D, Kramer JH, Reeder SB. Multipeak fat-corrected complex R2* relaxometry: Theory, optimization, and clinical validation. Magn. Reson. Med 2013;70:1319–1331 doi: 10.1002/mrm.24593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Teixeira RPAG, Malik SJ, Hajnal JV. Joint system relaxometry (JSR) and Crámer-Rao lower bound optimization of sequence parameters: A framework for enhanced precision of DESPOT T 1 and T 2 estimation. Magn. Reson. Med 2018;79:234–245 doi: 10.1002/mrm.26670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shrager RI, Weiss GH, Spencer RGS. Optimal time spacings for T2 measurements: monoexponential and biexponential systems. NMR Biomed. 1998;11:297–305 doi: . [DOI] [PubMed] [Google Scholar]
- 13.Zhao B, Haldar JP, Liao C, et al. Optimal Experiment Design for Magnetic Resonance Fingerprinting: Cramér-Rao Bound Meets Spin Dynamics. IEEE Trans. Med. Imaging 2019;38:844–861 doi: 10.1109/TMI.2018.2873704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Assländer J A Perspective on MR Fingerprinting. J. Magn. Reson. Imaging 2021;53:676–685 doi: 10.1002/jmri.27134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kay SM. Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory. Prentice Hall; 1993. [Google Scholar]
- 16.Lewis CM, Hurley SA, Meyerand ME, Koay CG. Data-driven optimized flip angle selection for T1 estimation from spoiled gradient echo acquisitions. Magn. Reson. Med 2016;76:792–802 doi: 10.1002/mrm.25920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Basu S, Bresler Y. The stability of nonlinear least squares problems and the Cramer-Rao bound. IEEE Trans. Signal Process 2000;48:3426–3436 doi: 10.1109/78.887032. [DOI] [Google Scholar]
- 18.Madsen K, Nielsen HB, Tingleff O. Methods for Non-Linear Least Squares Problems. 2nd ed. Technical University of Denmark, DTU; 2004. [Google Scholar]
- 19.Kirsch A Regularization by Discretization. In: An Introduction to the Mathematical Theory of Inverse Problems. An Introduction to the Mathematical Theory of Inverse Problems.; 2011. pp. 63–119. doi: 10.1007/978-1-4419-8474-6_3. [DOI] [Google Scholar]
- 20.Gözcü B, Sanchez T, Cevher V. Rethinking Sampling in Parallel MRI: A Data-Driven Approach. In: European Signal Processing Conference. European Signal Processing Conference IEEE; 2019. pp. 1–5. doi: 10.23919/EUSIPCO.2019.8903150. [DOI] [Google Scholar]
- 21.Gözcü B, Mahabadi RK, Li YH, et al. Learning-based compressive MRI. IEEE Trans. Med. Imaging 2018;37:1394–1406 doi: 10.1109/TMI.2018.2832540. [DOI] [PubMed] [Google Scholar]
- 22.Zibetti MVW, Herman GT, Regatte RR. Fast data-driven learning of parallel MRI sampling patterns for large scale problems. Sci. Rep 2021;11:19312 doi: 10.1038/s41598-021-97995-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bishop CM, Roach CM. Fast curve fitting using neural networks. Rev. Sci. Instrum 1992;63:4450–4456 doi: 10.1063/1.1143696. [DOI] [Google Scholar]
- 24.Jung S, Lee H, Ryu K, et al. Artificial neural network for multi‐echo gradient echo–based myelin water fraction estimation. Magn. Reson. Med 2021;85:380–389 doi: 10.1002/mrm.28407. [DOI] [PubMed] [Google Scholar]
- 25.Bertleff M, Domsch S, Weingärtner S, et al. Diffusion parameter mapping with the combined intravoxel incoherent motion and kurtosis model using artificial neural networks at 3 T. NMR Biomed. 2017;30:e3833 doi: 10.1002/nbm.3833. [DOI] [PubMed] [Google Scholar]
- 26.Domsch S, Mürle B, Weingärtner S, Zapp J, Wenz F, Schad LR. Oxygen extraction fraction mapping at 3 Tesla using an artificial neural network: A feasibility study. Magn. Reson. Med 2018;79:890–899 doi: 10.1002/mrm.26749. [DOI] [PubMed] [Google Scholar]
- 27.Balasubramanyam C, Ajay MS, Spandana KR, Shetty AB, Seetharamu KN. Curve fitting for coarse data using artificial neural network. WSEAS Trans. Math 2014;13:406–415. [Google Scholar]
- 28.Liu F, Feng L, Kijowski R. MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping. Magn. Reson. Med 2019;82:174–188 doi: 10.1002/mrm.27707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn. Reson. Med 2018;79:3055–3071 doi: 10.1002/mrm.26977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Knoll F, Hammernik K, Zhang C, et al. Deep-learning methods for parallel magnetic resonance imaging reconstruction: A survey of the current approaches, trends, and issues. IEEE Signal Process. Mag 2020;37:128–140 doi: 10.1109/MSP.2019.2950640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu F, Kijowski R, El Fakhri G, Feng L. Magnetic resonance parameter mapping using model‐guided self‐supervised deep learning. Magn. Reson. Med 2021;85:3211–3226 doi: 10.1002/mrm.28659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Feng L, Ma D, Liu F. Rapid MR relaxometry using deep learning: An overview of current techniques and emerging trends. NMR Biomed. 2020:e4416 doi: 10.1002/nbm.4416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qian C, Shi JC, Yu Y, Tang K, Zhou ZH. Subset selection under noise. In: Advances in Neural Information Processing Systems. Vol. 2017-Decem. Advances in Neural Information Processing Systems.; 2017. pp. 3561–3571. [Google Scholar]
- 34.Sharafi A, Xia D, Chang G, Regatte RR. Biexponential T 1ρ relaxation mapping of human knee cartilage in vivo at 3 T. NMR Biomed. 2017;30:e3760 doi: 10.1002/nbm.3760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med 1999;42:952–962 doi: . [DOI] [PubMed] [Google Scholar]
- 36.Lustig M, Donoho DL, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med 2007;58:1182–1195 doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 37.Zibetti MVW, De Pierro AR. Improving compressive sensing in MRI with separate magnitude and phase priors. Multidimens. Syst. Signal Process 2017;28:1109–1131 doi: 10.1007/s11045-016-0383-6. [DOI] [Google Scholar]
- 38.Hernando D, Levin YS, Sirlin CB, Reeder SB. Quantification of liver iron with MRI: State of the art and remaining challenges. J. Magn. Reson. Imaging 2014;40:1003–1021 doi: 10.1002/jmri.24584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Steihaug T The conjugate gradient method and trust regions in large scale optimization. SIAM J. Numer. Anal 1983;20:626–637 doi: 10.1137/0720042. [DOI] [Google Scholar]
- 40.Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016;142:394–406 doi: 10.1016/j.neuroimage.2016.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Huber P, Ronchetti E. Robust statistics. 1981.
- 42.Qian C, Yu Y, Zhou ZH. Subset selection by Pareto optimization. In: Advances in Neural Information Processing Systems. Vol. 2015-Janua. Advances in Neural Information Processing Systems.; 2015. pp. 1774–1782. [Google Scholar]
- 43.Zhou Z-H, Yu Y, Qian C. Evolutionary learning: Advances in theories and algorithms. Singapore: Springer Singapore; 2019. doi: 10.1007/978-981-13-5956-9. [DOI] [Google Scholar]
- 44.Hansen PC. Rank-Deficient and Discrete Ill-Posed Problems. Philadelphia, PA: Society for Industrial and Applied Mathematics; 1998. doi: 10.1137/1.9780898719697. [DOI] [Google Scholar]
- 45.Mosher TJ, Zhang Z, Reddy R, et al. Knee articular cartilage damage in osteoarthritis: Analysis of MR image biomarker reproducibility in ACRIN-PA 4001 multicenter trial. Radiology 2011;258:832–842 doi: 10.1148/radiol.10101174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zibetti MVW, Sharafi A, Regatte R. Robust Statistics for T1ρ-Mapping of Knee Cartilage on Mono- and Bi-Exponential Models : Optimal Spin-Lock Times and Fitting Methods. In: Proc. Intl. Soc. Mag. Res. Med. Proc. Intl. Soc. Mag. Res. Med; 2020. [Google Scholar]
- 47.Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Accelerated mono- and biexponential 3D-T1ρ relaxation mapping of knee cartilage using golden angle radial acquisitions and compressed sensing. Magn. Reson. Med 2020;83:1291–1309 doi: 10.1002/mrm.28019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bouhrara M, Spencer RG. Fisher information and Cramér-Rao lower bound for experimental design in parallel imaging. Magn. Reson. Med 2018;79:3249–3255 doi: 10.1002/mrm.26984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Brihuega-Moreno O, Heese FP, Hall LD. Optimization of diffusion measurements using Cramer-Rao lower bound theory and its application to articular cartilage. Magn. Reson. Med 2003;50:1069–1076 doi: 10.1002/mrm.10628. [DOI] [PubMed] [Google Scholar]
- 50.Sharafi A, Chang G, Regatte RR. Biexponential T2 relaxation estimation of human knee cartilage in vivo at 3T. J. Magn. Reson. Imaging 2018;47:809–819 doi: 10.1002/jmri.25778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Reiter DA, Magin RL, Li W, Trujillo JJ, Pilar Velasco M, Spencer RG. Anomalous T2 relaxation in normal and degraded cartilage. Magn. Reson. Med 2016;76:953–962 doi: 10.1002/mrm.25913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Johnston DC. Stretched exponential relaxation arising from a continuous sum of exponential decays. Phys. Rev. B 2006;74:184430 doi: 10.1103/PhysRevB.74.184430. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Table S1: Optimized and non-optimized spin lock times, in milliseconds (ms) for the various criteria and sizes K, with SNR=125.


