Abstract

We have quantum chemically investigated how solvation influences the competition between the SN2 and E2 pathways of the model F– + C2H5Cl reaction. The system is solvated in a stepwise manner by going from the gas phase, then via microsolvation of one to three explicit solvent molecules, then last to bulk solvation using relativistic density functional theory at (COSMO)-ZORA-OLYP/QZ4P. We explain how and why the mechanistic pathway of the system shifts from E2 in the gas phase to SN2 upon strong solvation of the Lewis base (i.e., nucleophile/protophile). The E2 pathway is preferred under weak solvation of the system by dichloromethane, whereas a switch in reactivity from E2 to SN2 is observed under strong solvation by water. Our activation strain and Kohn–Sham molecular orbital analyses reveal that solvation of the Lewis base has a significant impact on the strength of the Lewis base. We show how strong solvation furnishes a weaker Lewis base that is unable to overcome the high characteristic distortivity associated with the E2 pathway, and thus the SN2 pathway becomes viable.
Introduction
One of the fundamental challenges in chemistry is the rational design of chemical reactions. Understanding the processes that control reactivity in chemistry paves the way for the tailor-made design of reactions and can open up avenues to discover new chemistry. Two elementary reactions in organic chemistry that are used in many synthetic routes are the bimolecular nucleophilic substitution (SN2) and base-induced bimolecular elimination (E2) reactions.1 In principle, these reactions are always in competition (Scheme 1). This intrinsic competition requires active tuning of the reactivity of the system toward the desired pathway to avoid unwanted side reactions, which can hamper the use of these reactions in synthetic endeavors. The competition between SN2 and E2 has been experimentally2 and computationally3 extensively studied, and valuable insights have emerged from these studies.
Scheme 1. Computationally Analyzed SN2 and E2 Pathways of Sn···F– with C2H5Cl, in which S = CH2Cl2 and H2O and n = 0–3.
In general, strong Lewis bases (e.g., F–, HO–) will follow an E2 pathway (i.e., protophilic attack) because the strong acid–base-like interaction with the substrate can overcome the highly destabilizing characteristic distortivity that intrinsically accompanies the E2 reaction.3f−3h The characteristic distortivity is always more destabilizing for the more distortive E2 pathway compared to SN2 as a result of the two bonds that are being broken during this pathway (Cα–Y and Cβ–H), while for the latter, only one bond is being broken (Cα–Y). In contrast, weak Lewis bases (e.g., I–, HS–) are, due to their weak acid–base-like interaction with the substrate, unable to overcome the characteristic distortivity of the E2 pathway and prefer the less distortive SN2 reaction (i.e., nucleophilic attack). In contrast, the nature of the leaving group generally affects both reaction pathways in a similar fashion, in which good leaving groups result in high reactivity for both the SN2 and E2 pathways, and poor leaving groups cause a low reactivity for both reaction pathways.3h
In all, the strength of the Lewis base is decisive on whether it will react as either a nucleophile (SN2 reaction) or protophile (E2 reaction), and has a vital role in the SN2/E2 competition. Solvation can have a dramatic impact on the Lewis base strength, and, in turn, the SN2/E2 competition. Nonetheless, limited quantitative data are available regarding the exact underlying mechanism of the effect of solvation.3f,4 With the aim to eclipse these phenomenological observations, we now reexamine and provide concrete quantitative insights into the solvent effects, and their underlying mechanism, on the SN2/E2 competition.
Herein, we have quantum chemically investigated how exactly solvation influences the competition between SN2 and E2 pathways in the F– + C2H5Cl model reaction system, by going stepwise from the gas phase, via different extents of microsolvation (1–3 solvent molecules H2O or CH2Cl2) to bulk solvation (simulated with COSMO), using relativistic density functional theory at ZORA-OLYP/QZ4P (Scheme 1). We selected dichloromethane (ε = 9, nonpolar aprotic) and water (ε = 78, polar protic) as solvents because they represent realistic extremes of solvent polarity, and are often used in experimental reactions and studies. The activation strain model (ASM)5 and Kohn–Sham molecular orbital (KS-MO)6a theory in combination with the matching energy decomposition analysis (EDA)6b,6c were used to provide quantitative insight into the effect of solvation on the SN2/E2 preference. This methodological approach enables the investigation of the potential energy surface and the activation barrier by decomposing the system’s total energy into chemically intuitive terms, proving to be valuable for understanding chemical reactivity.3h,7
Results and Discussion
Table 1 and Figure 1 summarize the computed reaction profiles with the energies relative to the separate reactants (reactivity trends are consistent for ΔE and ΔG; see SI Table S1) and structural data of the SN2 and E2 reactions of Sn···F– + C2H5Cl (see Table S2 for additional data). In our following detailed analysis, we transition in a stepwise manner from the gas phase to microsolvation then to bulk solvation. In general, the reactions proceed via a reactant complex (RC), and a transition state (TS), toward a product complex (PC), which can eventually dissociate into the products (P). Analyzing the reaction profiles, several apparent trends emerge. First of all, the reactant complexes (RC), formed upon the interaction between the Lewis base and the substrate, systematically become less stabilized when increasing the number of explicit solvent molecules interacting with the Lewis base F– (i.e., increasing the solvation strength).4g In other words, the Lewis base–substrate reactant complexes are destabilized relative to the separate reactants of the reaction (i.e., Sn···F– + C2H5Cl) as solvation is increased. This observation is regardless of the nature of the solvent. When going to bulk solvation, simulated with COSMO, these stationary points are no longer stable. This is the result of the increasingly stronger interaction between the solvent and the Lewis base, which weakens the Lewis base–substrate interaction until the point it is unbound. In parallel, the reaction barriers, for both the SN2 and E2, also systematically rise along with this series, however, to a more significant degree. The reaction barriers rise more rapidly when increasing the number of explicit solvent molecules coordinating with the Lewis base F–, for the E2 than for the SN2 reaction pathway. This can be found for both solvents, while more pronounced in the systems with water compared to dichloromethane. For example, along F–, (H2O)···F–, (H2O)2···F–, (H2O)3···F–, the reaction barrier for SN2 moderately increases from −14.9, to +0.1, to +9.0, to +16.4 kcal mol–1, respectively, whereas the E2 barrier rises more steeply from −20.5, to −3.0, to +8.4, to +18.0 kcal mol–1 (i.e., ΔΔE‡ = +5.6, +3.1, +0.6, −1.6 kcal mol–1 for SN2 relative to E2). This ultimately causes the mechanistic preference to switch from E2 to SN2 in water. For the systems in dichloromethane, this trend is also present; however, it is not sufficiently strong to induce a switch from E2 to SN2 along F–, (CH2Cl2)···F–, (CH2Cl2)2···F–, (CH2Cl2)3···F– (i.e., ΔΔE‡ = +5.6, +3.5, +2.0, +1.8 kcal mol–1 for SN2 relative to E2).
Table 1. Energies Relative to Reactants (in kcal mol–1) of the Stationary Points of the SN2 and E2 Reactions of Sn···F– + C2H5Cl along the PES, in which S = CH2Cl2 and H2O, and n = 0–3a.
| Sn···F– | RC | SN2-TS | E2-TS | SN2-PC | E2-PC | SN2-P | E2-P |
|---|---|---|---|---|---|---|---|
| F– | –20.6 | –14.9 | –20.5 | –44.7 | –48.8 | –37.5 | –46.2 |
| (CH2Cl2)···F– | –10.0 | 1.6 | –1.9 | –26.8 | –29.3 | –20.9 | –8.0 |
| (CH2Cl2)2···F– | –7.4 | 9.0 | 7.0 | b | –21.4 | –15.2 | –2.3 |
| (CH2Cl2)3···F– | –5.4 | 15.4 | 13.6 | b | b | –12.1 | 0.9 |
| COSMO(CH2Cl2)···F– | b | 19.9 | 18.4 | b | b | –13.5 | –3.0 |
| COSMO(CH2Cl2)-(CH2Cl2)3···F– | b | 21.1 | 19.3 | b | b | –8.4 | 1.9 |
| (H2O)···F– | –11.3 | 0.1 | –3.0 | –20.2 | –29.3 | –20.9 | –8.0 |
| (H2O)2···F– | –8.7 | 9.0 | 8.4 | –18.4 | –19.6 | –13.1 | –0.2 |
| (H2O)3···F– | –6.9 | 16.4 | 18.0 | b | –13.0 | –8.5 | 4.4 |
| COSMO(H2O)···F– | b | 23.1 | 22.4 | b | b | –11.1 | –0.8 |
| COSMO(H2O)-(H2O)3···F– | b | 26.7 | 28.1 | b | b | –4.3 | 6.0 |
Electronic energies computed at ZORA-OLYP/QZ4P or COSMO-ZORA-OLYP/QZ4P.
Nonexistent: Stationary point is not stable.
Figure 1.

Transition state structures with key bond lengths (in Å) for the SN2 and E2 reactions of F–, (CH2Cl2)3···F–, and (H2O)3···F– + C2H5Cl. Computed at ZORA-OLYP/QZ4P. Atom colors: carbon (gray), hydrogen (white), fluorine (green), chlorine (cyan), and oxygen (red).
Next, when going from microsolvation to bulk solvation by using COSMO, i.e., COSMO(H2O)-(H2O)3···F– and COSMO(CH2Cl2)-(CH2Cl2)3···F–, the reaction barriers of both the SN2 and E2 pathway rise further. Bulk solvation in COSMO without any microsolvation results in slightly lower barriers than the systems with microsolvation in combination with COSMO. Again, also for COSMO-only solvation, the barrier for E2 increases more rapidly than that for SN2. Note that solvation by only COSMO, which does not account for covalent solute–solvent interactions (vide infra), is not able to fully induce the mechanistic switch from E2 to SN2 as discussed for the microsolvation. Similar to the situation with microsolvation, bulk solvation in water (i.e., strong solvation) leads to a larger shift in the SN2/E2 competition than bulk solvation in dichloromethane (i.e., weak solvation). Thus, every form of solvation erodes the intrinsic E2 preference of the system; however, the extent to which it does so strongly depends on the solvation strength. Altogether, if no competing E2 channel exists then solvation always leads to a weaker nucleophile.4g This is the “intrinsic nucleophilicity”, which systematically decreases when increasing the solvation strength. However, we also previously showed3h that if a competing E2 pathway exists, this is slowed more, going to a weaker Lewis base, than SN2. This is the “apparent nucleophilicity”, in which weaker Lewis bases or, in the context of solvation, more strongly solvated Lewis bases, prefer an SN2 mechanism (vide infra).
To gain quantitative insight into the effect of solvation on the Lewis base, we turned to the activation strain model (ASM) of reactivity.5 The ASM decomposes the electronic energy (ΔE) into two distinct energy terms, namely, the strain energy (ΔEstrain) and the interaction energy (ΔEint).
The strain energy results from the required deformation of the individual reactants, and the interaction energy consists of all mutual interactions between the deformed reactants along the intrinsic reaction coordinate (IRC) which we project in the resulting activation strain diagrams (ASD) onto the Cα···Cl leaving-group bond distance. In the ASD of Figure 2a, we show the SN2 reaction of Sn···F– + C2H5Cl in the gas phase, i.e., bare F–, and with F– microsolvated by three H2O molecules, i.e., (H2O)3···F–, as representative systems. Note that the ASM/EDA results of all systems (i.e., S = H2O and CH2Cl2, and n = 0–3) of both the SN2 and E2 reaction provided in Figure S1 exhibit the same characteristics (see Table S3 and S4 for the ASM/EDA data on consistent geometries extracted from the IRC). As found in Table 1, we observe that the reaction barriers always rise by the microsolvation of Lewis base F–.4g This trend in reactivity is traced back to a less stabilizing interaction energy between the Lewis base and the substrate (i.e., C2H5Cl) for systems in which the Lewis base is microsolvated. The magnitude of this effect depends on the nature and amount of the solvent molecules, i.e., the solvation strength. Increasing the number of solvent molecules coordinating to the Lewis base results in a systemic decrease in stabilizing interaction energy (see Figure S1 and Table S2). In contrast, solvation of the leaving group will lead to a less destabilizing strain energy for the more strongly solvated systems, which can directly be related to the donor–acceptor interaction between the leaving group and the solvent. This stabilizes the evolving negative charge localizing on the leaving group atom. Thus, in other words, the solvation of the leaving group renders a “better leaving group” and therefore lowers the activation strain of both reaction pathways.
Figure 2.
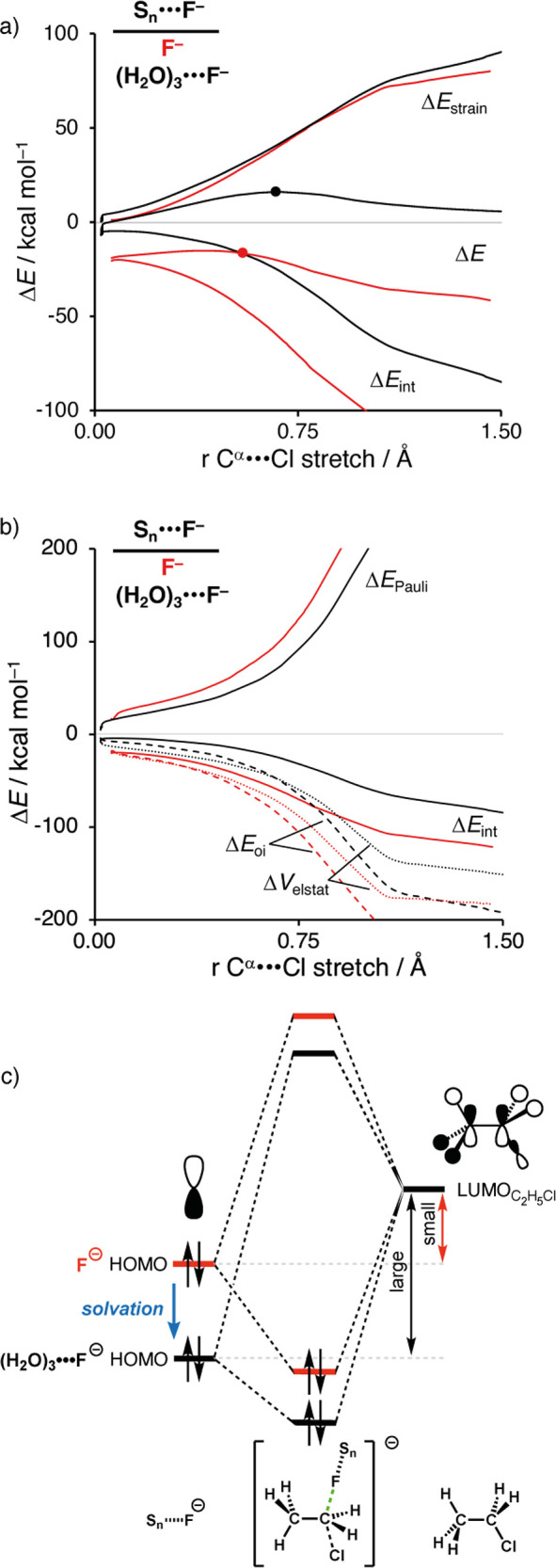
(a) Activation strain analysis and (b) energy decomposition analysis of the SN2 reactions between Sn···F– (S = none, n = 0, red; S = water, n = 3, black) + C2H5Cl, along the IRC projected on the Cα···Cl bond stretch. (c) Schematic molecular orbital diagram of the most important HOMOSn···F––LUMOC2H5Cl orbital interaction. Computed at ZORA-OLYP/QZ4P.
To understand the less stabilizing interaction energy of the solvated Lewis base with the substrate, we employ an energy decomposition analysis (EDA).6b,6c Our canonical EDA decomposes the ΔEint between the deformed reactants into the following three chemically intuitive energy terms: steric (Pauli) repulsion (ΔEPauli), classical electrostatic interactions (ΔVelstat), and orbital interaction (ΔEoi). Herein, ΔEPauli includes the destabilizing interaction between the occupied orbitals of the reactants, due to the Pauli exclusion principle, and is a measure for steric repulsion. The ΔVelstat is the electrostatic interaction between the unperturbed charge distributions of the (deformed) reactants. The orbital interaction energy, ΔEoi, accounts for, among others, charge transfer between the reactants, such as HOMO–LUMO interactions.
We find that both the electrostatic attraction and, even more so, the orbital interactions are significantly less stabilizing for (H2O)3···F– than F– reacting with C2H5Cl (Figure 2b). The less stabilizing orbital interaction between (H2O)3···F– and C2H5Cl can be ascribed to the difference in the orbital energies of their interacting lone pair HOMOs. As shown in Figure 2c, the HOMO of (H2O)3···F– is lower (i.e., more stable) than that of bare F–. This makes (H2O)3···F– a weaker Lewis base which hence engages in a weaker HOMO–LUMO interaction with the substrate. As a consequence, the TS is less stable, and therefore we arrive at a higher reaction barrier (see Table S5 for more data on the key occupied orbitals of the Lewis base–solvent complexes). This working mechanism is also operational when going from microsolvation to bulk solvation, in which COSMO also stabilizes the HOMO of the Lewis base resulting in a weaker HOMO–LUMO interaction with the substrate (vide infra).
Next, we turn to the ASM analysis of the SN2 and E2 reactions of (CH2Cl2)3···F– + C2H5Cl and (H2O)3···F– + C2H5Cl, where (CH2Cl2)3···F– still favors the E2 mechanism while (H2O)3···F– prefers the SN2 pathway (Table 1). In the previous section, we established that solvation reduces the basicity of the Lewis base. But how does this affect the competition between SN2 and E2? By applying the ASM, we find a switch from the preferential E2 to SN2 reactivity if one goes from weak solvation in the case of (CH2Cl2)3···F– to strong solvation in the case of (H2O)3···F–, i.e., going from an effectively stronger to an effectively weaker Lewis base (see also Table 1). This mechanistic switch is the direct result of the weaker interaction between the Lewis base and the substrate for (H2O)3···F– compared to (CH2Cl2)3···F– (Figure 3a and 3b). The weaker interaction of (H2O)3···F– cannot anymore overcome the higher characteristic activation strain for the more distortive E2 reaction, and therefore, the reaction follows the less distortive SN2 pathway. This effect is best observed in the ASDs in Figure 3a and 3b, after the TS: the strain curves of both systems are almost superimposed, while the interaction energies for (H2O)3···F– is significantly less stabilizing.
Figure 3.

Activation strain analyses of the (a) SN2 and (b) E2 reactions between Sn···F– + C2H5Cl for S = CH2Cl2 (green) and S = H2O (black), n = 3, along the IRC projected on the Cα···Cl bond stretch. (b) Schematic molecular orbital diagram of the most important interaction between the HOMOSn···F– and LUMOC2H5Cl. (c) Schematic molecular orbital diagram of the most important HOMOSn···F––LUMOC2H5Cl orbital interaction. Computed at ZORA-OLYP/QZ4P.
The origin of the less stabilizing interaction energy upon microsolvation is again traced back to the more stabilized HOMO (i.e., lower energy HOMO) of the Lewis base (Figure 3c). The low-energy HOMO of (H2O)3···F– engages in a less stabilizing HOMO–LUMO interaction with the substrate which results in a less stabilizing interaction energy. The weakening in the Lewis base–substrate interaction is more disadvantageous for the highly distortive E2 pathway (2 bonds breaking in the substrate) than for the less distortive SN2 pathway (only 1 bond breaking in the substrate). Again, this also holds when going from microsolvation to bulk solvation. Altogether, our analyses thus show that the stronger a solvent interacts with the Lewis base the higher the tendency to switch from protophilic attack (E2) to nucleophilic attack (SN2).
Finally, we wish to understand how solvation of the Lewis base lowers its HOMO energy and, therefore, causes the aforementioned weakening in the HOMO–LUMO interaction with the substrate and the concomitant rise in barriers and reduced preference from E2 (in dichloromethane) or even switch to SN2 (in water). In order to rationalize this, we investigated the strength and nature of the interaction between the Lewis base and the solvent. The total complexation energy between the Lewis base and the solvent becomes more stabilizing when the number of solvent molecules increases. This trend is exclusively determined by the interaction energy between the Lewis base and the solvent (see Table S6). This is the case for both solvents but more pronouncedly so for water than for dichloromethane. For example, along (CH2Cl2)···F–, (CH2Cl2)2···F–, (CH2Cl2)3···F–, the interaction energy moderately becomes more stabilizing from −28.1, to −42.2, to −52.4 kcal mol–1, respectively, whereas the corresponding systems with water decrease more steeply from −29.0, to −47.5, to −61.7 kcal mol–1 (see Table S5).
Both the orbital interaction and, even more so, the electrostatic interaction play an important role in the complexation energy (i.e., strength of the Lewis base–solvent interaction), and become more stabilizing along with the stepwise introduction of solvent molecules. The electrostatic attraction is mainly the result of the partially positively charged H-atom of the polarized Yδ−–Hδ+ bond of the solvent molecule (Y = O, C for water and dichloromethane, respectively) being coordinated toward the anionic Lewis base F– resulting in favorable interaction, i.e., Yδ−–Hδ+···F–. This stabilization is substantially stronger between water and the Lewis base than for dichloromethane. Thus, ΔVelstat goes from −49.0, to −72.2, to −90.2 kcal mol–1 along (H2O)···F–, (H2O)2···F– and (H2O)3···F–, and only goes from −48.2, to −57.7, to −66.8 kcal mol–1 along (CH2Cl2)···F–, (CH2Cl2)2···F– and (CH2Cl2)3···F– (see Table S5). In parallel, our Kohn–Sham molecular orbital analysis shows that the frontier orbital interaction in the formation of the microsolvated Sn···F– complex is the HOMO–LUMO interaction of the fluoride lone-pair orbital with the σ* (O–H or C–H) antibonding LUMO of the solvent molecules. This explains the saturation effect associated with the stepwise addition of the solvent molecules: each additional solvent molecule will interact with F– in a less stabilizing manner than the previously added solvent molecule (vide supra, also see Table S5). The reason is that the F– HOMO is stabilized upon coordination of a solvent molecule and, thus, becomes a less capable electron-donating orbital for the HOMO–LUMO interaction with the next solvent molecule. Also, the electrostatic interaction with the next solvent molecule effectively levels off as the charge of F– decreases upon coordination of each solvent molecule.
To interrogate the role of the stabilizing HOMOLewis base–LUMOsolvent donor–acceptor orbital interaction on the stability of the HOMO of the Lewis base–solvent complex, we performed an additional bonding analysis of the interaction between the Lewis base and the solvent complex in Sn···F– where the empty acceptor orbitals on the solvent fragment were artificially removed (see Table S7). Indeed, in the absence of the unoccupied orbitals on the solvent, and thus without the stabilizing donor–acceptor interactions, the HOMO of the Lewis base–solvent complex is significantly less stabilized (i.e., less lowered in energy compared to bare F–) by the solvent. This analysis confirms that by removing the unoccupied orbitals of the solvent, the Lewis base regains a significant amount of its original Lewis base strength. Hence, this charge transfer mechanism is indeed causing a part of the reduction of the Lewis base strength by the stabilization of the HOMO of the Lewis base (see Figure 4a). Taken altogether, the solvent can be viewed as a weak Lewis acid that interacts with the Lewis base and renders an overall weaker Lewis base as a result.
Figure 4.
(a) Schematic diagram for the orbital interaction between the 2p HOMO of F– and the LUMO of the discrete solvent, forming a more stabilized HOMOSn···F–. (b) Schematic diagram for the stabilization of the 2p HOMO of the Lewis base by the positive external potential of the solvent, which can be found for discrete (microsolvation) and continuum solvent models (e.g., COSMO). Energy decomposition analysis of the Sn···F– interaction for (c) S = CH2Cl2 (green) and S = H2O (red), n = 1, and (d) S = H2O, n = 1 (red) and n = 3 (black) projected on the Y–H···F– bond length (Y = O, C for water and dichloromethane, respectively). The fragments were kept fixed in their equilibrium geometry. The equilibrium bond lengths are indicated by a vertical line. Computed at ZORA-OLYP/QZ4P.
On removing the unoccupied orbitals of the solvent fragment, the HOMO of the Lewis base did not fully regain its original Lewis base strength of bare F– (see Table S6). This can be traced back to the positive external potential of the solvent, which, aside from the charge-transfer mechanism, also stabilizes the HOMO of the Lewis base (see Figure 4b).8 This is, as the electrostatic interactions, originating from the polarized Yδ−–Hδ+ bonds of the solvent introducing an apparent positive potential. This general phenomenon is observed for many other chemical systems, in which a (partial) positive charge will pull down the molecular orbitals (i.e., stabilize), in contrast, a (partial) negative charge will push up the orbitals (i.e., destabilize).8 Importantly, without the charge-transfer mechanism, the HOMO of the F– solvated by water is still significantly more stabilized than by dichloromethane (see Table S6), which can be directly related to the more stabilizing electrostatic interactions between water and F–. This mechanism is also operational for the systems that are bulk solvated by only COSMO, which accounts for electrostatic interactions between the Lewis base and solvent. Thus, solvation of the Lewis base with water by COSMO also stabilizes the HOMO of Lewis base significantly more than with dichloromethane (see Table S6).
To ultimately understand why these Lewis base–solvent interactions (Figure 4a and 4b) result for water in strong solvation and for dichloromethane in weak solvation, we employed a canonical energy decomposition analysis as a function of the Sn···F–distance. On the basis of the EDA results in Figure 4c, one would be tempted to conclude that dichloromethane (green) can engage in a more stabilizing interaction with the Lewis base than water (red) because, at a given bond distance, it goes with a significantly more stabilizing orbital interaction. However, dichloromethane is also sterically more demanding than water, and therefore experiences a significantly more destabilizing steric (Pauli) repulsion with the Lewis base. This results in a weaker overall interaction ΔEint, and more importantly, in a longer Sn···F– equilibrium distance for dichloromethane than water, which in turn leads to substantially less stabilizing electrostatic and orbital interactions. As previously discussed, each additional solvent molecule interacts with a less stabilizing orbital and electrostatic interaction with F– than the previously added solvent molecule (Figure 4d). Importantly, however, each additional solvent molecule will engage in practically a similar destabilizing steric (Pauli) repulsion with the Lewis base, which pushes the solvent molecules increasingly further away from the Lewis base (Figure 4d and Figure S2 for data on the dichloromethane system). As expected, this effect is more apparent for the larger dichloromethane resulting in an overall weak solvation. The smaller water molecules can interact at a shorter distance, and thus, stronger with the Lewis base, enabling to significantly stabilize the HOMO of the Lewis base resulting in strong solvation. Bulk solvation by COSMO can mimic this effect by its larger effective solvent radius for dichloromethane (2.94 Å for CH2Cl2 versus 1.93 Å for H2O), and thus a larger cavity for the solute in the continuum. These effects will be even more apparent progressing in the SN2/E2 reaction, when also steric interactions between the solvent and the substrate will push the solvent molecules further away, which again will be more pronounced for the larger dichloromethane.
Conclusions
Solvation raises all reaction barriers for our studied systems and shifts the mechanistic preference from E2 elimination toward SN2 substitution, as we show in our relativistic DFT computations. This tendency already appears upon monosolvation, by water and dichloromethane, and continues along higher orders of microsolvation up to bulk solvation, as follows from our quantum chemical activation strain analyses for gas phase, microsolvated, and bulk-solvated model reactions of F– + C2H5Cl. If solvation is strong enough, e.g., for water, not for dichloromethane, the overall mechanistic preference indeed switches from E2 (intrinsically preferred for F– + C2H5Cl) to the SN2 pathway (for the SN2/E2 competition in the gas phase, see ref (3h)).
Our activation strain and Kohn–Sham MO analyses reveal the causal physical mechanisms behind the above reactivity trends. Solvation stabilizes the HOMO of the Lewis base F– (i.e., lowers the HOMO) and, if modeled using discrete solvent molecules, it reduces the negative charge on the Lewis base through HOMO–LUMO interactions with the solvent. Thus, effectively, solvation reduces the basicity of the Lewis base F– and, consequently, it weakens the orbital and the electrostatic interactions with the substrate C2H5Cl in the SN2/E2 reaction. Therefore, the TS is less stabilized and reaction barriers rise. This effect is more apparent for the E2 pathway which suffers extra from a high characteristic activation strain associated with the more distortive character of the E2 reaction (2 bonds are breaking in substrate) than the SN2 pathway (only 1 bond is breaking). Thus, solvation pushes the mechanistic preference from E2 toward SN2.
Finally, we have found that the biggest steps from the gas phase to solution phase behavior happen upon introducing the first few solvent molecules. Thereafter, the trend continues but levels off. This saturation effect finds its origin in the aforementioned solute–solvent interaction between Lewis base and solvent. Introducing the first solvent molecule stabilizes the lone-pair HOMO and withdraws charge from the Lewis base. Thus, the next solvent molecule experiences a larger HOMO–LUMO gap and a reduced charge density on the Lewis base and, thus, engages in weaker orbital interactions and weaker electrostatic attraction. COSMO can mimic the stabilization of the Lewis base’s lone-pair HOMO, by exposing it to a stabilizing potential of the mirror charges on the surface of the cavity, while it lacks the effect of charge transfer from solute to solvent. In all, we find that already upon the introduction of three discrete solvent molecules, we achieve the order of magnitude of bulk solvation effects.
Methods
Computational Details
All density functional theory (DFT) calculations were performed using the Amsterdam Density Functional (ADF2018.105) software package.9 The generalized gradient approximation (GGA) exchange-correlation functional OLYP was used for all computations, which consists of the optimized exchange (OPTX) functional proposed by Handy and co-workers,10a and the Lee–Yang–Parr (LYP) correlation functional.10b Our benchmark studies have shown that OLYP reproduces SN2 barriers from highly correlated ab initio within only a few kcal mol–1.11 Scalar relativistic effects are accounted for using the zeroth-order regular approximation (ZORA).12 The basis set used, denoted QZ4P, is of quadruple-ζ quality for all atoms and has been improved by four sets of polarization functions.13 This large basis set is required for small anionic species (e.g., F–).11 All solution phase calculations used COSMO to simulate bulk solvation. For these calculations, the optimized stationary points in the gas phase were fully reoptimized at COSMO-ZORA-OLYP/QZ4P.14 The accuracies of the fit scheme (Zlm fit) and the integration grid (Becke grid) were, for all calculations, set to VERYGOOD.15 No symmetry constraints were used for all computations. All calculated stationary points have been verified by performing a vibrational analysis calculation,16 to be energy minima (no imaginary frequencies) or transition states (only one imaginary frequency). The character of the normal mode associated with the imaginary frequency of the transition state has been inspected to ensure that it is associated with the reaction of interest. The potential energy surfaces of the studied SN2 and E2 reactions were obtained by performing intrinsic reaction coordinate (IRC) calculations,17 which, in turn, were analyzed using the PyFrag 2019 program.18 The optimized structures were illustrated using CYLview.19
Activation Strain and Energy Decomposition Analysis
The activation strain model (ASM) of chemical reactivity,5 also known as the distortion/interaction model,20 is a fragment-based approach in which the potential energy surface (PES) can be described with respect to, and understood in terms of the characteristics of, the reactants. It considers the rigidity of the reactants and to which extent they need to deform during the reaction, plus their capability to interact with each other as the reaction proceeds. With the help of this model, we decompose the gas phase total energy, ΔE(ζ), into the strain and interaction energy, ΔEstrain(ζ) and ΔEint(ζ), respectively, and project these values onto the reaction coordinate ζ (eq 1).
| 1 |
In this equation, the strain energy, ΔEstrain(ζ), is the penalty that needs to be paid to deform the reactants from their equilibrium to the geometry they adopt during the reaction at the point ζ of the reaction coordinate. On the other hand, the interaction energy, ΔEint(ζ), accounts for all the chemical interactions that occur between these two deformed reactants along the reaction coordinate.
The interaction energy between the deformed reactants can be further analyzed in terms of quantitative Kohn–Sham molecular orbital (KS-MO)6a theory together with a canonical energy decomposition analysis (EDA).6b,6c The EDA decomposes the ΔEint(ζ) into the following three energy terms (eq 2):
| 2 |
Herein, ΔVelstat(ζ) is the classical electrostatic interaction between the unperturbed charge distributions of the (deformed) reactants and is usually attractive. The steric (Pauli) repulsion, ΔEPauli(ζ), includes the destabilizing interaction between the fully occupied orbitals of both fragments due to the Pauli principle. The orbital interaction energy, ΔEoi(ζ), accounts for, among others, charge transfer between the fragments, such as HOMO–LUMO interactions.
In the herein presented activation strain and accompanied energy decomposition diagrams, the intrinsic reaction coordinate (IRC) is projected onto the carbon–leaving group (Cα···Cl) distance. This critical reaction coordinate undergoes a well-defined change during the reaction from the reactant complex via the transition state to the product and is shown to be a valid reaction coordinate for studying SN2/E2 reactions.3h,7
Acknowledgments
We thank The Netherlands Organization for Scientific Research (NWO) for financial support.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.joc.1c02354.
Additional computational results; Cartesian coordinates, energies, and the number of imaginary frequencies of all stationary points (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- a Carey F. A.; Sundberg R. J.. Advanced Organic Chemistry, Part A, 5th ed.; Springer: New York, 2007; pp 389–577. [Google Scholar]; b Smith M. B.March’s Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, 7th ed.; Wiley: New York, 2013; pp 425–656. [Google Scholar]
- a DePuy C. H.; Bierbaum V. M. Gas-Phase Elimination Reactions of Ethers Induced by Amide and Hydroxide Ions. J. Am. Chem. Soc. 1981, 103, 5034–5038. 10.1021/ja00407a011. [DOI] [Google Scholar]; b Jones M. E.; Ellison G. B. A Gas-Phase E2 Reaction: Methoxide Ion and Bromopropane. J. Am. Chem. Soc. 1989, 111, 1645–1654. 10.1021/ja00187a017. [DOI] [Google Scholar]; c DePuy C. H.; Gronert S.; Mulin A.; Bierbaum V. M. Gas-Phase SN2 and E2 Reactions of Alkyl Halides. J. Am. Chem. Soc. 1990, 112, 8650–8655. 10.1021/ja00180a003. [DOI] [Google Scholar]; d Lum R. C.; Grabowski J. J. Intrinsic Competition between Elimination and Substitution Mechanisms Controlled by Nucleophile Structure. J. Am. Chem. Soc. 1992, 114, 9663–9665. 10.1021/ja00050a059. [DOI] [Google Scholar]; e Carrascosa E.; Meyer J.; Michaelsen T.; Stei M.; Wester R. Conservation of direct dynamics in sterically hindered SN2/E2 reactions. Chem. Sci. 2018, 9, 693–701. 10.1039/C7SC04415A. [DOI] [PMC free article] [PubMed] [Google Scholar]; f Carrascosa E.; Meyer J.; Zhang J.; Stei M.; Michaelsen T.; Hase W. L.; Yang L.; Wester R. Imaging dynamic fingerprints of competing E2 and SN2 reactions. Nat. Commun. 2017, 8, 25. 10.1038/s41467-017-00065-x. [DOI] [PMC free article] [PubMed] [Google Scholar]; g Garver J. M.; Fang Y.-R.; Eyet N.; Villano S. M.; Bierbaum V. M.; Westaway K. C. A Direct Comparison of Reactivity and Mechanism in the Gas Phase and in Solution. J. Am. Chem. Soc. 2010, 132, 3808–3814. 10.1021/ja909399u. [DOI] [PubMed] [Google Scholar]; h Villano S. M.; Kato S.; Bierbaum V. M. Deuterium Kinetic Isotope Effects in Gas-Phase SN2 and E2 Reactions: Comparison of Experiment and Theory. J. Am. Chem. Soc. 2006, 128, 736–737. 10.1021/ja057491d. [DOI] [PubMed] [Google Scholar]; i Meyer J.; Tajti V.; Carrascosa E.; Győri T.; Stei M.; Michaelsen T.; Bastian B.; Czakó G.; Wester R. Atomistic dynamics of elimination and nucleophilic substitution disentangled for the F– + CH3CH2Cl reaction. Nat. Chem. 2021, 13, 977–981. 10.1038/s41557-021-00753-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Gronert S.; Merrill G. N.; Kass S. R. Fluoride-Induced Elimination of Ethyl Fluoride. The Importance of High-Level Optimizations in ab Initio and DFT Studied. J. Org. Chem. 1995, 60, 488–489. 10.1021/jo00108a005. [DOI] [Google Scholar]; b Minato T.; Yamabe S. Theoretical Studies on Gas-Phase Reactions of Fluoride Ion with Fluoroethance: E2 and SN2 Reactions. J. Am. Chem. Soc. 1985, 107, 4621–4626. 10.1021/ja00302a004. [DOI] [Google Scholar]; c Gronert S.; Kass S. R. Theoretical Studies of Eliminations. 6. The Regiochemistry and Stereochemistry of the Gas-Phase Reactions of 3-Halocyclohexenes with Fluoride. An ab Initio Study. J. Org. Chem. 1997, 62, 7991–8000. 10.1021/jo970626g. [DOI] [PubMed] [Google Scholar]; d Gronert S. Theoretical Studies of Elimination Reactions. 4. Gas Phase Reactions of F– with Cyclopentyl and Cyclohexyl Chloride. Stereochemical Preferences of E2 Eliminations. J. Org. Chem. 1994, 59, 7046–7050. 10.1021/jo00102a032. [DOI] [Google Scholar]; e Gronert S.; Freed P. Theoretical Studies of Eliminations. 5. Intermolecular vs Intramolecular Eliminations: An ab Initio Study of the Gas-Phase reaction between NH2– with CH3CH2SCH3. J. Org. Chem. 1996, 61, 9430–9433. 10.1021/jo961482t. [DOI] [Google Scholar]; f Bickelhaupt F. M.; Baerends E. J.; Nibbering N. M. M. The Effect of Microsolvation on E2 and SN2 Reactions: Theoretical Study of the Model System F– + C2H5F + nHF. Chem. - Eur. J. 1996, 2, 196–207. 10.1002/chem.19960020212. [DOI] [Google Scholar]; g Hamlin T. A.; Swart M.; Bickelhaupt F. M. Nucleophilic Substitution (SN2): Dependence on Nucleophile, Leaving Group, Central Atom, Substituents, and Solvent. ChemPhysChem 2018, 19, 1315–1330. 10.1002/cphc.201701363. [DOI] [PMC free article] [PubMed] [Google Scholar]; h Vermeeren P.; Hansen T.; Jansen P.; Swart M.; Hamlin T. A.; Bickelhaupt F. M. A Unified Framework for Understanding Nucleophilicity and Protophilicity in the SN2/E2 Competition. Chem. - Eur. J. 2020, 26, 15538–15548. 10.1002/chem.202003831. [DOI] [PMC free article] [PubMed] [Google Scholar]; i Ryding M. J.; Debnarova A.; Fernandez I.; Uggerud E. Nucleophilic substitution in reactions between partially hydrated superoxide anions and alkyl halides. J. Org. Chem. 2015, 80, 6133–6142. 10.1021/acs.joc.5b00651. [DOI] [PubMed] [Google Scholar]
- a Eyet N.; Melko J. J.; Ard S. G.; Viggiano A. A. Effect of higher order solvation and temperature on SN2 and E2 reactivity. Int. J. Mass Spectrom. 2015, 378, 54–58. 10.1016/j.ijms.2014.07.011. [DOI] [Google Scholar]; b Liu X.; Zhang J.; Yang L.; Hase W. L. How a solvent molecule affects competing elimination and substitution dynamics. Insight into mechanism evolution with increased solvation. J. Am. Chem. Soc. 2018, 140, 10995–11005. 10.1021/jacs.8b04529. [DOI] [PubMed] [Google Scholar]; c Oh Y. H.; Im S.; Park S. W.; Lee S. Y.; Chi D. Y. SN2/E2 Branching in Protic Solvents: A Mechanistic Study. Bull. Korean Chem. Soc. 2009, 30, 1535–1538. 10.5012/bkcs.2009.30.7.1535. [DOI] [Google Scholar]; d Hu W. P.; Truhlar D. G. Modeling transition state solvation at the single-molecule level: Test of correlated ab Initio predictions against experiment for the gas-phase SN2 reaction of microhydrated fluoride with methyl chloride. J. Am. Chem. Soc. 1994, 116, 7797–7800. 10.1021/ja00096a041. [DOI] [Google Scholar]; e O’Hair R. A.; Davico G. E.; Hacaloglu J.; Dang T. T.; DePuy C. H.; Bierbaum V. M. Measurements of solvent and secondary kinetic isotope effects for the gas-phase SN2 reactions of fluoride with methyl halides. J. Am. Chem. Soc. 1994, 116, 3609–3610. 10.1021/ja00087a061. [DOI] [Google Scholar]; f Hirao K.; Kebarle P. SN2 reactions in the gas phase. Transition states for the reaction: Cl– + RBr = ClR + Br–, where R = CH3, C2H5, and iso-C3H7, from ab initio calculations and comparison with experiment. Solvent effects. Can. J. Chem. 1989, 67, 1262–1267. 10.1139/v89-192. [DOI] [Google Scholar]; g Hamlin T. A.; van Beek B.; Wolters L. P.; Bickelhaupt F. M. Nucleophilic Substitution in Solution: Activation Strain Analysis of Weak and Strong Solvent Effects. Chem. - Eur. J. 2018, 24, 5927–5938. 10.1002/chem.201706075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Vermeeren P.; van der Lubbe S. C. C.; Fonseca Guerra C.; Bickelhaupt F. M.; Hamlin T. A. Understanding Chemical Reactivity Using the Activation Strain Model. Nat. Protoc. 2020, 15, 649–667. 10.1038/s41596-019-0265-0. [DOI] [PubMed] [Google Scholar]; b Bickelhaupt F. M.; Houk K. N. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem., Int. Ed. 2017, 56, 10070–10086. 10.1002/anie.201701486. [DOI] [PMC free article] [PubMed] [Google Scholar]; Angew. Chem. 2017, 129, 10204 - 10221.10.1002/ange.201701486
- a Bickelhaupt F. M.; Baerends E. J.. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. In Reviews in Computational Chemistry; Lipkowitz K. B., Boyd D. B., Eds.; Wiley-VCH: New York, 2000; Vol. 15, pp 1–86. [Google Scholar]; b van Meer R.; Gritsenko O. V.; Baerends E. J. Physical Meaning of Virtual Kohn-Sham Orbitals and Orbital Energies: An Ideal Basis for the Description of Molecular Excitations. J. Chem. Theory Comput. 2014, 10, 4432–4441. 10.1021/ct500727c. [DOI] [PubMed] [Google Scholar]; c Zhao L.; von Hopffgarten M.; Andrada D. M.; Frenking G. Energy Decomposition Analysis. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1345. 10.1002/wcms.1345. [DOI] [Google Scholar]
- a Hansen T.; Vermeeren P.; Yoshisada R.; Filippov D. V.; van der Marel G. A.; Codée J. D.; Hamlin T. A. How Lewis Acids Catalyze Ring-Openings of Cyclohexene Oxide. J. Org. Chem. 2021, 86, 3565–3573. 10.1021/acs.joc.0c02955. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Galabov B.; Koleva G.; Schaefer H. F.; Allen W. D. Nucleophilic Influences and Origin of the SN2 Allylic Effect. Chem. - Eur. J. 2018, 24, 11637–11648. 10.1002/chem.201801187. [DOI] [PubMed] [Google Scholar]; c Hansen T.; Vermeeren P.; Bickelhaupt F. M.; Hamlin T. A. Origin of the α-Effect in SN2 Reactions. Angew. Chem. 2021, 133, 21008–21016. 10.1002/ange.202106053. [DOI] [PMC free article] [PubMed] [Google Scholar]; Angew. Chem., Int. Ed. 2021, 60, 20840 - 20848.10.1002/anie.202106053
- Svatunek D.; Hansen T.; Houk K. N.; Hamlin T. A. How the Lewis Base F– Catalyzes the 1,3-Dipolar Cycloaddition between Carbon Dioxide and Nitrilimines. J. Org. Chem. 2021, 86, 4320–4325. 10.1021/acs.joc.0c02963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]; b Fonseca Guerra C.; Snijders J. G.; te Velde G.; Baerends E. J. Towards an Order-N DFT Method. Theor. Chem. Acc. 1998, 99, 391–403. 10.1007/s002140050353. [DOI] [Google Scholar]; c ADF2018.105. SCM Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands. http://www.scm.com.
- a Handy N. C.; Cohen A. J. Left-right correlation energy. Mol. Phys. 2001, 99, 403–412. 10.1080/00268970010018431. [DOI] [Google Scholar]; b Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Swart M.; Solà M.; Bickelhaupt F. M. Density Functional Calculations of E2 and SN2 Reactions: Effects of the Choice of Method, Algorithm, and Numerical Accuracy. J. Chem. Theory Comput. 2010, 6, 3145–3152. 10.1021/ct100454c. [DOI] [PubMed] [Google Scholar]
- van Lenthe E.; Baerends E. J.; Snijders J. G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. 10.1063/1.467943. [DOI] [Google Scholar]
- van Lenthe E.; Baerends E. J. Optimized Slater-Type Basis Sets for the Elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
- a Klamt A.; Schüürmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc., Perkin Trans. 2 1993, 5, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]; b Klamt A. Conductor-like screening model for real solvents: a new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. 10.1021/j100007a062. [DOI] [Google Scholar]
- a Franchini M.; Philipsen P. H. T.; van Lenthe E.; Visscher L. Accurate Coulomb Potentials for Periodic and Molecular Systems through Density Fitting. J. Chem. Theory Comput. 2014, 10, 1994–2004. 10.1021/ct500172n. [DOI] [PubMed] [Google Scholar]; b Franchini M.; Philipsen P. H. T.; Visscher L. The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite. J. Comput. Chem. 2013, 34, 1819–1827. 10.1002/jcc.23323. [DOI] [PubMed] [Google Scholar]
- a Bérces A.; Dickson R. M.; Fan L.; Jacobsen H.; Swerhone D.; Ziegler T. An Implementation of the Coupled Perturbed Kohn-Sham Equations: Perturbation due to Nuclear Displacement. Comput. Phys. Commun. 1997, 100, 247–262. 10.1016/S0010-4655(96)00120-8. [DOI] [Google Scholar]; b Jacobsen H.; Bérces A.; Swerhone D. P.; Ziegler T. Analytic Second Derivatives of Molecular Energies: a Density Funtional Implementation. Comput. Phys. Commun. 1997, 100, 263–276. 10.1016/S0010-4655(96)00119-1. [DOI] [Google Scholar]; c Wolff S. K. Analytical Second Derivatives in the Amsterdam Density Functional Package. Int. J. Quantum Chem. 2005, 104, 645–659. 10.1002/qua.20653. [DOI] [Google Scholar]
- a Fukui K. The Path of Chemical Reactions - the IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. 10.1021/ar00072a001. [DOI] [Google Scholar]; b Deng L.; Ziegler T.; Fan L. A. Combined Density Functional and Intrinsic Reaction Coordinate Study on the Ground State Energy Surface of H2CO. J. Chem. Phys. 1993, 99, 3823–3835. 10.1063/1.466129. [DOI] [Google Scholar]; c Deng L.; Ziegler T. The Determination of Intrinsic Reaction Coordinates by Density Functional Theory. Int. J. Quantum Chem. 1994, 52, 731–765. 10.1002/qua.560520406. [DOI] [Google Scholar]
- Sun X.; Soini T. M.; Poater J.; Hamlin T. A.; Bickelhaupt F. M. PyFrag 2019–Automating the Exploration and Analysis of Reaction Mechanisms. J. Comput. Chem. 2019, 40, 2227–2233. 10.1002/jcc.25871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legault C. Y.CYLview, 1.0b; Université de Sherbrooke: Sherbrooke, QC, Canada, 2009. http://www.cylview.org.
- a Ess D. H.; Houk K. N. Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity. J. Am. Chem. Soc. 2007, 129, 10646–10647. 10.1021/ja0734086. [DOI] [PubMed] [Google Scholar]; b Ess D. H.; Houk K. N. Theory of 1,3-Dipolar Cycloadditions: Distortion/Interaction and Frontier Molecular Orbital Models. J. Am. Chem. Soc. 2008, 130, 10187–10198. 10.1021/ja800009z. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




