Abstract
Objectives
The lung nodule volume determined by CT is used for nodule diagnoses and monitoring tumor responses to therapy. Increased image noise on low-dose CT degrades the measurement accuracy of the lung nodule volume. We compared the volumetric accuracy among deep-learning reconstruction (DLR), model-based iterative reconstruction (MBIR), and hybrid iterative reconstruction (HIR) at an ultra-low-dose setting.
Methods
Artificial ground-glass nodules (6 mm and 10 mm diameters, −660 HU) placed at the lung-apex and the middle-lung field in chest phantom were scanned by 320-row CT with the ultra-low-dose setting of 6.3 mAs. Each scan data set was reconstructed by DLR, MBIR, and HIR. The volumes of nodules were measured semi-automatically, and the absolute percent volumetric error (APEvol) was calculated. The APEvol provided by each reconstruction were compared by the Tukey-Kramer method. Inter- and intraobserver variabilities were evaluated by a Bland-Altman analysis with limits of agreements.
Results
DLR provided a lower APEvol compared to MBIR and HIR. The APEvol of DLR (1.36%) was significantly lower than those of the HIR (8.01%, p = 0.0022) and MBIR (7.30%, p = 0.0053) on a 10-mm-diameter middle-lung nodule. DLR showed narrower limits of agreement compared to MBIR and HIR in the inter- and intraobserver agreement of the volumetric measurement.
Conclusions
DLR showed higher accuracy compared to MBIR and HIR for the volumetric measurement of artificial ground-glass nodules by ultra-low-dose CT.
Advances in knowledge
DLR with ultra-low-dose setting allows a reduction of dose exposure, maintaining accuracy for the volumetry of lung nodule, especially in patients which deserve a long-term follow-up.
Introduction
The characterization of the properties of pulmonary nodules involves the estimation of nodule volume doubling time on follow-up CT.1–3 In the CT examinations conducted for the follow-up of lung cancer, computer-aided semi-automated volumetric measurements of pulmonary nodules are used to guide the diagnostic strategy.4,5 Repeated follow-up CT examinations in clinical practice can provide excessive radiation exposure. Therefore, it is necessary to reduce the radiation exposure dose of CT while maintaining the diagnostic ability. Model-based iterative reconstruction (MBIR) and hybrid iterative reconstruction (HIR) are widely used to reduce radiation exposure and improve diagnostic ability, because these techniques have lower image noise and fewer artefacts.6–9 However, the image texture and spatial resolution of these images obtained by MBIR or HIR are inadequate, especially on low-dose CT.10
A novel reconstruction algorithm, deep-learning reconstruction (DLR), was recently developed. It incorporates noise and artefact reduction by a deep convolutional neural network.11,12 The DLR method incorporates a noise and artefact reduction filter with a deep convolutional neural network which is trained with noise-contaminated and noise-free training pairs to extract true signals from noisy images.11 DLR reduces the image noise and increases the spatial resolution simultaneously, unlike conventional noise reduction methods with trade-offs between spatial resolution and noise reduction.11 Compared to other traditional reconstruction methods, the DLR technique help improve the image quality, especially at low-dose settings.13 We have thus speculated that DLR is a suitable reconstruction method for ultra-low-dose CT and that the use of DLR could improve the accuracy of measurements of the volume of pure ground-glass nodules (GGNs) compared to HIR and MBIR. We conducted the present study to compare the accuracy of HIR, MBIR, and DLR in the volumetric measurement of artificial pure GGNs by ultra-low-dose CT.
Methods and materials
Phantom
A chest phantom used for lung cancer screening CT (LSCT-001 chest phantom, Kyoto Kagaku Co. Ltd., Kyoto, Japan) was used14 (Figure 1). The lung parenchyma of the phantom consists of a combination of urethane foam and styrene resin that shows a CT value of approx. −900 HU. Two sets of spherical artificial pure GGNs (6 mm and 10 mm diameters, −660 HU) were placed at the lung apex level and the middle lung field level of the phantom. Thus, a total of four artificial were placed in the phantom. The volume of the 6-mm-diameter GGN was 113.1 mm3, and that of the 10-mm-diameter GGN was 523.6 mm3.
Figure 1.
LSCT-001 chest phantom.
Image acquisition
The chest phantom with artificial pure GGNs was scanned on a 320-row detector CT system (Aquilion ONE/PRISM Edition: Canon Medical Systems, Otawara, Japan). The following scanning parameters were used: X-ray tube voltage, 120 kV; detector configuration, 0.5 mm × 80 rows, beam pitch, 0.8; gantry rotation time, 0.5 second ; X-ray tube current, 160, 80, and 10 mA. The effective milliampere-second (mAs) values were thus set at 100, 50, and 6.3 mAs. All acquisitions were repeated six times consecutively with shifting the scan start position by 60 degrees each to compensate for random errors in data measurements. Each set of raw data was subjected to HIR (Adaptive Iterative Dose Reduction 3D [AIDR 3D] Standard FC13), MBIR (Forward projected model-based Iterative Reconstruction SoluTion [FIRST] BODY Standard), and DLR (Advanced intelligent Clear-IQ Engine [AiCE] BODY Standard). The lung kernel is generally adopted on detection of lung nodules. However, Wang Y et al reported that the soft tissue kernel was appropriate for accurate quantitative evaluation in lung nodule volume measurement.15 We thus adopted the soft tissue kernel in this study.
Assessment of radiation doses
Radiation doses of each scan were recorded in terms of the volume CT dose index (CTDIvol [mGy]) and the total dose-length product (DLP [mGy cm]). CTDIvol and DLP values were obtained from the dose page provided from the CT scanner. The effective dose was estimated from the DLP using a normalized effective dose constant of 0.014. The relative percentage compared with the average effective dose of 1.5 mSv in the low-dose screening of National Lung Screening Trial (NLST) in United States were calculated for each tube current.16
Volumetric protocols
Two radiological technologists experienced in CT examinations (7 and 10 years experience) performed volumetric measurements for the chest phantom data. A total of 216 nodules (2 size nodules × 2 locations × 3 tube currents × 6 repeated scans × 3 reconstruction algorithms = 216 nodules) were measured, and the measurements of six repeated scans were averaged at each reconstruction algorithm. The volumetric measurements for the artificial pure GGNs were performed independently at the same lung window setting (window level, −600 HU; window width, 1500 HU) using a semi-automated method on CT workstation (Synapse Vincent; Fujifilm Medical, Tokyo, Japan).
In the volumetric measurement, a level of the maximum diameter of an artificial pure GGN was selected and the GGN volume measurement was performed semi-automatically by the CT workstation by drawing its major axis. In clinical practice, the growth rate of lung nodules is managed based on the nodules' volume doubling time, and we therefore defined the absolute percent volumetric error (APEvol) of the artificial pure GGN by the following equation.
APEvol = |Vm − Vt | / Vt × 100 [%]
where Vm is the measured nodule volume and Vt is the true nodule volume.
The volumes of the artificial pure GGNs once again with the same set 1 month later for the assessment of intraobserver variability.
Image noise
The image noise for HIR, MBIR, and DLR at each dose setting were assessed by measuring the standard deviation of the CT values for each corresponding pixel between six consecutive scans. Circular regions of interest (20-pixel-diameter) were placed in the 10-mm-diameter middle lung GGN at the same location in all of the image sets (Figure 2). The average standard deviation value was measured as an estimate of the image noise.
Figure 2.

The Yellow circular regions of interest on 10-mm-diameter GGNs at the middle lung of the chest phantom (a), and the enlarged image (b).
Statistical analyses
An one-way analysis of variance (ANOVA) was used to test the APEvol and image noise data among the three reconstruction methods, followed by post hoc pair-wise comparisons based on the Tukey-Kramer method to account for multiple comparisons. Dunnett’s test was performed to assess the differences in the APEvol between MBIR with the low-dose-setting (which is similar to the exposure dose in the NLST) and all reconstruction methods with the ultra-low-dose setting. Statistical significance was accepted at p-values < 0.05.
The inter- and intraobserver agreements for the APEvol data were evaluated using Bland-Altman analyses and intraclass correlation coefficients (ICCs). The interobserver variability was assessed by using the mean results from each observer. In the Bland-Altman analysis, the 95% confidence interval for the limits of agreement was determined.17 Each ICC was calculated by using two-way random single measures with an absolute agreement condition (ICC1,2) for interobserver agreement and one-way random single measures (ICC1,1) for intraobserver agreement. Inter- and intraobserver agreement was interpreted in the following way: ICC <0.20 = slight agreement, ICC 0.21–0.40 = fair agreement, ICC 0.41–0.60 = moderate agreement, ICC 0.61–0.80 = substantial agreement, ICC 0.81–1.0 = perfect agreement. All statistical analyses were performed with the JMP Pro 15.0.0 program (SAS Institute, Cary, NC, USA).
Results
Radiation doses
Table 1 presents the results with the CTDIvol, DLP, ED, and percentage compared with NLST mean ED at each dose settings. The relative percentage doses to the low-dose screening of NLST in United States were 212.8%, 104.5%, and 14.9% at 100, 50, and 6.3 mAs setting, respectively. Kim et al set the percentage of dose reduction compared to the radiation doses of 6.74 mGy at 120 kV, 100 mAs setting.8 In addition, a radiation dose was compared to the average effective dose of 1.5 mSv in a low-dose scan of NLST.8,12 We therefore defined the dose of 5.7 mGy at 100 mAs as the standard-dose, 2.8 mGy at 50 mAs as the low-dose, and 0.4 mGy at 6.3 mAs as the ultra-low-dose settings.
Table 1.
Descriptive statistics for the radiation dose protocols.
| Setting | Tube current-time product (mAs) | CTDIvol (mGy) | DLP (mGy ・cm) | ED (mSv) | Percentage compared with NLST mean ED (%) |
|---|---|---|---|---|---|
| ultra-low | 6.3 | 0.4 | 16 | 0.2 | 14.9 |
| low | 50 | 2.8 | 112 | 1.6 | 104.5 |
| standard | 100 | 5.7 | 228 | 3.2 | 212.8 |
CTDIvol, volume CT dose index; DLP, dose-length product; ED, effective dose; NLST, National Lung Screening Trial.
Radiation dose of each CT scan was compared to the average ED of NLST, which was 1.5 mSv.
Comparisons of APEvol
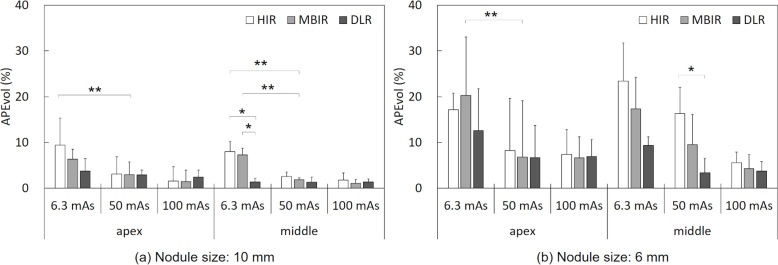
Images of the artificial pure GGNs scanned at each dose setting are provided as Figure 3. The results of the comparison of APEvol values obtained with the HIR, MBIR, and DLR methods are summarized in Table 2 and illustrated in Figure 4. In all reconstruction methods, the APEvol was larger at low-dose CT compared to standard-dose CT. For the 10-mm artificial pure GGN, DLR showed a smaller APEvol than the other two reconstruction methods in the low-dose scanning.
Figure 3.
CT images of the scanned chest phantom and artificial pure ground-glass nodules (GGNs). The lung apex of the chest phantom at the standard dose of 100 mAs with HIR (a) and at the ultra-low-dose of 6.3 mAs with HIR (b), MBIR (c), and DLR (d). The middle lung of the chest phantom at the standard dose of 100 mAs with HIR (e) and at the ultra-low-dose of 6.3 mAs with HIR (f), MBIR (g), and DLR (h). The 10-mm-diameter GGNs at the middle lung of the chest phantom at the standard dose of 100 mAs with HIR (i) and at the ultra low dose of 6.3 mAs with HIR (j), MBIR (k), and DLR (l). The overlay images for volume extraction in semi-automatic measurement of the 10-mm-diameter GGNs at the middle lung of the chest phantom at the standard dose of 100 mAs with HIR (m) and at the ultra-low-dose of 6.3 mAs with HIR (n), MBIR (o), and DLR (p).
Table 2.
Comparison of APEvol values among HIR, MBIR, and DLR at each dose setting for 10 and 6-mm-diameter artificial pure GGNs.
| Size | Dose setting | Level of GGN | HIR | MBIR | DLR | One-way ANOVA | Tukey-Kramer test | ||
|---|---|---|---|---|---|---|---|---|---|
| HIR vs MBIR | HIR vs DLR | MBIR vs DLR | |||||||
| Mean ± SD | p-value | p-value | p-value | p-value | |||||
| 10 mm | Ultra-low-dose 6.3 mAs |
Lung apex | 9.4 ± 5.9 | 6.3 ± 2.2 | 3.7 ± 2.7 | 0.0755 | 0.3964 | 0.0819 | 0.5929 |
| Middle lung | 8.0 ± 3.8 | 7.3 ± 2.8 | 1.4 ± 1.0 | 0.0014 | 0.8968 | 0.0022 | 0.0053 | ||
| Low-dose 50 mAs |
Lung apex | 3.1 ± 3.2 | 3.0 ± 2.6 | 2.9 ± 1.6 | 0.9822 | 0.9978 | 0.981 | 0.9917 | |
| Middle lung | 2.5 ± 2.2 | 1.9 ± 1.5 | 1.3 ± 0.8 | 0.4319 | 0.7476 | 0.4008 | 0.824 | ||
| Standard-dose 100 mAs |
Lung apex | 1.5 ± 1.0 | 1.4 ± 0.4 | 2.4 ± 1.1 | 0.1404 | 0.9783 | 0.2278 | 0.1655 | |
| Middle lung | 1.8 ± 1.5 | 1.1 ± 0.9 | 1.3 ± 0.7 | 0.5111 | 0.4854 | 0.7544 | 0.894 | ||
| 6 mm | Ultra-low-dose 6.3 mAs |
Lung apex | 17.2 ± 3.6 | 20.3 ± 12.8 | 12.6 ± 9.1 | 0.9703 | 0.8343 | 0.6795 | 0.3533 |
| Middle lung | 23.4 ± 11.4 | 17.3 ± 12.3 | 9.3 ± 7.1 | 0.4329 | 0.5872 | 0.0838 | 0.4076 | ||
| Low-dose 50 mAs |
Lung apex | 8.2 ± 5.4 | 6.8 ± 4.6 | 6.7 ± 3.7 | 0.8098 | 0.8515 | 0.8289 | 0.9989 | |
| Middle lung | 16.3 ± 8.3 | 9.5 ± 6.9 | 3.4 ± 1.9 | 0.0106 | 0.1864 | 0.0079 | 0.2447 | ||
| Standard-dose 100 mAs |
Lung apex | 7.4 ± 5.7 | 6.6 ± 6.5 | 6.9 ± 3.2 | 0.1651 | 0.9677 | 0.9887 | 0.9944 | |
| Middle lung | 5.6 ± 2.3 | 4.2 ± 3.1 | 3.7 ± 2.1 | 0.3814 | 0.6333 | 0.4214 | 0.9292 | ||
ANOVA, analysis of variance; DLR, deep learning reconstruction;HIR, Hybrid iterative reconstruction; MBIR, Model-based iterative reconstruction.
Figure 4.
The APEvol for the 10 mm-diameter (a), and 6 mm diameter (b) GGNs placed at the lung apex and the middle-lung field level. *p < 0.05, Tukey-Kramer method; **p < 0.05, Dunnett’s test.
At 6.3 mAs ultra-low-dose setting, there were significant differences in the APEvol for the 10-mm-diameter middle-lung artificial pure GGN (ANOVA, p = 0.0014) among each reconstructed image. The post hoc analysis showed that the 6.3 mAs ultra-low-dose setting images with DLR (1.4 ± 1.0) had a significantly lower APEvol for the 10-mm-diameter middle-lung GGN compared to those obtained with HIR (8.0 ± 3.8, p = 0.0022) and MBIR (7.3 ± 2.8, p = 0.0053).
At the 50 mAs low-dose setting, there were significant differences in the APEvol values for the 6-mm-diameter middle lung-GGN (ANOVA, p = 0.0106) among each reconstructed image. The post hoc analysis showed that the 50 mAs low-dose setting images with DLR (3.4 ± 1.9) had a significantly lower APEvol for the 6-mm-diameter middle-lung GGN compared to that obtained with HIR (16.3 ± 8.3, p = 0.0079).
At the 100 mAs standard-dose setting, there was no significant difference in the APEvol for the lung-apex or middle-lung GGNs with 10-and 6 mm diameters among the reconstructed images.
Dunnett’s test showed that the ultra-low-dose setting with MBIR or HIR resulted in significantly higher APEvol values for the 10-mm-diameter GGN compared to the low-dose setting with MBIR (p < 0.05). For the 6 mm GGN, the ultra-low-dose setting with MBIR provided a significantly higher APEvol compared to the low-dose setting with MBIR (p < 0.05). However, there was no significant difference in the APEvol for the 10- or 6-mm GGNs between the ultra-low-dose setting with DLR and the low-dose setting with MBIR.
Variabilities of volumetric measurements
The Bland-Altman plots for the inter- and intraobserver agreement at ultra-low-dose setting regarding volumetric measurements of the 10 mm nodule are shown in Figures 5 and 6, and those for the 6 mm nodule volumetric measurements are shown in Figures 7 and 8. Table 3 presents the results with mean differences and limits of agreement in the variabilities of the volumetric measurements. Both the intra- and interobserver volumetric measurement agreement results for DLR were better than those for MBIR and HIR, and the corresponding Bland-Altman plots indicated no bias. The mean differences in the inter- and intraobserver agreement ranged from 1.8 to 5.8% and from −0.6 to 2.5% for the 10 mm nodule, and from 3.0 to 9.8% and from 0.2 to 2.3% for the 6 mm nodule, respectively. The mean differences in the intra- and intraobserver agreement results for DLR were the minimum values compared to MBIR and HIR for both nodule sizes. The inter- and intraobserver agreements for the volumetric measurements by DLR showed narrower limits of agreement compared to MBIR and HIR (Figures 5–8). The ICCs for the inter- and intraobserver agreement ranged from 0.03 to 0.63 and from 0.18 to 0.51 for the 10 mm nodule and from 0.12 to 0.54 and from 0.39 to 0.80 for the 6 mm, respectively. The DLR method thus showed a higher ICC for inter- and intraobserver agreement compared to HIR and MBIR.
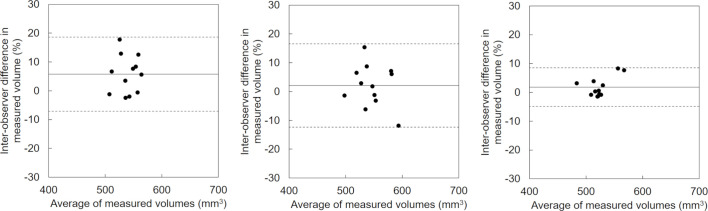
Figure 5.
Interobserver variability in the measured volume of the 10 mm nodule by ultra-low-dose CT at 6.3 mAs with HIR (a), MBIR (b), and DLR (c). The variability of DLR was less one-half of that of MBIR. The mean difference is shown by a continuous line; the upper and lower limits of agreement are shown by dashed lines.
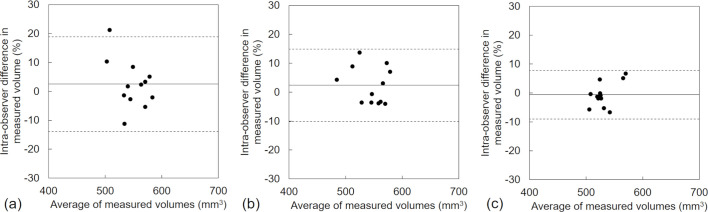
Figure 6.
Intraobserver variability in the measured volume of the 10 mm nodule by ultra-low-dose CT at 6.3 mAs with HIR (a), MBIR (b), and DLR (c). The mean difference is shown by a continuous line; the upper and lower limits of agreement are shown by dashed lines.
Figure 7.
Interobserver variability in the measured volume of the 6 mm nodule by ultra-low-dose CT at 6.3 mAs with HIR (a), MBIR (b), and DLR (c). The variability of DLR was less one-half of that of HIR. The mean difference is shown by a continuous line; the upper and lower limits of agreement are shown by dashed lines.
Figure 8.
Intraobserver variability in the measured volume of the 6 mm nodule by ultra-low-dose CT at 6.3 mAs with HIR (a), MBIR (b), and DLR (c). The mean difference is shown by a continuous line; the upper and lower limits of agreement are shown by dashed lines.
Table 3.
Inter- and intra observer agreement of the GGNs' volumes on ultra-low dose CT image reconstructed with each algorithm.
| Nodule size | Type of agreement | Type of agreement | Mean differencea (limits of agreement, %) | ICCb |
|---|---|---|---|---|
| 10 mm | Inter observer | HIR | 5.8 (-7.1, 18.7) | 0.0307 |
| MBIR | 2.1 (-12.3, 16.6) | 0.2999 | ||
| DLR | 1.8 (-4.9, 8.5) | 0.6354 | ||
| intra observer | HIR | 2.5 (-13.9, 18.9) | 0.1834 | |
| MBIR | 2.4 (-10.2, 14.9) | 0.4436 | ||
| DLR | −0.6 (-9.0, 7.8) | 0.5143 | ||
| 6 mm | Inter observer | HIR | 9.8 (-38.7, 58.3) | 0.2763 |
| MBIR | 6.8 (-27.2, 40.7) | 0.1241 | ||
| DLR | 3.0 (-18.3, 24.3) | 0.5417 | ||
| intra observer | HIR | 2.3 (-31.9, 36.5) | 0.6049 | |
| MBIR | 1.5 (-25.6, 29.0) | 0.3935 | ||
| DLR | 0.2 (-17.2, 17.5) | 0.7967 |
HIR, Hybrid iterative reconstruction; MBIR, Model-based iterative reconstruction; DLR, deep learning reconstruction; ICC, intraclass confidence coefficient.
Bland-Altman analysis.
random single measures with an absolute agreement condition (ICC [1,1], [2, 1]).
Image noise
The image noise was compared among the three reconstruction algorithms, and the results are summarized in Table 4. At the 6.3 mAs ultra-low-dose setting, there was no significant difference in the image noise among the three reconstructed sets of data (ANOVA, p = 0.1811). A significant difference was observed at the 50 mAs low-dose setting (ANOVA, p < 0.0001); the post hoc analysis showed that the 50 mAs low-dose setting images with HIR (11.1 ± 3.6) had significantly greater image noise compared to those with MBIR (9.2 ± 3.3, p < 0.0001) and those with DLR (8.9 ± 3.2, p < 0.0001). At the 100 mAs standard-dose setting, another significant difference was observed (ANOVA, p < 0.0001); the post hoc analysis showed that the 100 mAs standard setting images with HIR (9.2 ± 2.9) had significantly greater image noise compared to those with MBIR (5.5 ± 1.8, p < 0.0001) and DLR (6.9 ± 2.4, p < 0.0001). DLR had significantly greater image noise compared to those with MBIR (p < 0.0001).
Table 4.
The image noise provided by HIR, MBIR, and DLR at each dose setting.
| Dose setting | HIR | MBIR | DLR | One-way ANOVA | Tukey-Kramer test | ||
|---|---|---|---|---|---|---|---|
| HIR vs MBIR | HIR vs DLR | MBIR vs DLR | |||||
| Mean ± SD | p-value | p-value | p-value | p-value | |||
| Ultra-low-dose | 16.3 ± 5.5 | 17.1 ± 6.2 | 16.3 ± 5.8 | 0.1811 | - | - | - |
| Low-dose | 11.1 ± 3.6 | 9.2 ± 3.3 | 8.9 ± 3.2 | <0.0001 | <0.0001 | <0.0001 | 0.7274 |
| Standard-dose | 9.2 ± 2.9 | 5.5 ± 1.8 | 6.9 ± 2.4 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
ANOVA, analysis of variance; DLR, deep learning reconstruction;HIR, Hybrid iterative reconstruction; MBIR, Model-based iterative reconstruction.
Discussion
Our present findings suggest that unlike other IR algorithms, DLR could be applied to ultra-low-dose CT for the volumetric measurement of lung nodules without compromising measurement reliability. We observed that the semi-automated lung nodule volumetric measurements were significantly affected by the reconstruction algorithms from the aspect of measurement accuracy and reproducibility, especially at low-dose settings.
Our results demonstrated that at ultra-low-dose levels, significantly lower lung nodule volumetric measurement errors could be obtained by DLR compared to MBIR and HIR. At the low- and ultra-low-doses of 50 and 6.3 mAs, DLR provided a lower APEvol compared to MBIR and HIR in artificial pure GGNs with diameters 10 mm and 6 mm. There were significant differences in the APEvol for the 10-mm-diameter nodule at the middle lung between DLR and MBIR (1.4 and 7.3%, p = 0.0053) at the ultra-low-dose setting of 6.3 mAs. This may be because MBIR tends to be remarkably degraded due to low-frequency noise, particularly at low radiation dose settings,18 and because DLR could improve the image contrast between artificial pure GGNs and lung parenchyma due to its superior noise reduction without a loss of spatial resolution.13,19 We observed that at the standard dose setting, the image noise was lowest on MBIR images, whereas at ultra-low-dose settings, DLR provided the lowest image noise because the low-frequency noise component was effectively reduced.13 Regarding CT radiation doses, most studies have reported that the accuracy of lung nodule volumetric measurements would decrease in low-dose CT.8,9,20–22 The excessive noise on a low-dose chest CT image can cause inaccurate results for lung nodule volumetric measurement.23 DLR is thus a suitable reconstruction method for lung nodule follow-up CT that requires reduction of the cumulative dose due to repeated radiation exposure.
Our present findings demonstrate that DLR contributes to measurement reliability, especially in ultra-low-dose follow-up CT. In our Bland-Altman analysis of the data obtained at the ultra-low-dose setting, DLR showed a mean difference of volumetric measurement <3% in the inter- and intraobserver agreements, and these were smaller compared to those provided by HIR and MBIR. Similarly, the limits of agreement with DLR was less than ± 25% and narrower compared to those of MBIR and HIR in the inter- and intraobserver agreements. The lung cancer screening trials commonly use a follow-up CT schedule of third to fourth/year to evaluate the growth of nodules, based on a minimum increase of 25%.1,24,25 The DLR algorithm thus enables ultra-low-dose CT screening to confirm lung nodule growth. In addition, the ICCs of DLR showed moderate or substantial agreement in this study, whereas there was only slight inter- and intraobserver agreements for HIR and MBIR. Padole et al noted that the blurring of lung structures would be due to an increased or pronounced blotchy and pixelated appearance related to noise reduction processing on MBIR, and that lung abnormalities would thus be missed on MBIR images at submillisievert dose levels.26 In addition, the increased low-frequency noise in low-dose images reconstructed by MBIR or HIR induces a degradation of image texture (such as blurry or plastic-like images).27,28 In semi-automatic volumetric measurements drawing both ends of the lung nodule, the blurring of the contour by MBIR or HIR might induce larger measurement error between observers. Conversely, Higaki et al reported that the noise power spectral curve of DLR images was superior especially for low-frequency components because the teaching images were scanned at relatively high radiation doses and reconstructed with MBIR whose parameters were adjusted to obtain the best image quality. We thus speculate that the deterioration of the ultra-low-dose image quality on MBIR and HIR reduced the inter- and intraobserver agreement compared to that on DLR in our present investigation.
DLR has the potential for an 85% reduction in exposure compared to the effective dose used in the NLST. Our present results demonstrate that compared to other reconstruction algorithms, DLR can improve the accuracy of volumetric measurements of pure GGNs and reduce volumetric measurement variability, especially at the ultra-low-dose setting. There was no significant difference between the APEvol of MBIR with the low-dose-setting (which is similar to the exposure dose in the NLST) and that of DLR with the ultra-low-dose setting. Dose reduction is especially important for the follow-up of pure GGNs, because these nodules require repeated CT examinations due to their slower growth compared to solid or part-solid nodules. A further exposure dose reduction would thus be achievable for the volumetric measurement of pure GGNs while maintaining diagnostic accuracy by using the DLR algorithm.
This study has several limitations. It was a phantom study, and the shape and CT value of the targeted artificial pure GGNs was limited to spherical and −660 HU, respectively. These values differ from those of pure GGNs examined in vivo. In addition, the number of nodules was limited. We believe that a larger number of nodules with various diameters, attenuations, and margin characteristics are required for a more precise evaluation of measurement feasibility. Second, multiple parameters (noise reduction level) for each reconstruction algorithm were not evaluated. In this study, only one set of parameters for each algorithm was evaluated. We focused on the effect elicited by the difference in the reconstruction algorithm rather than the noise reduction level in the reconstruction parameter. However, it is possible that adjusting the parameters to match the noise and spatial resolution of the three algorithms may provide results that differ from those of our present study. A validation study is necessary to determine whether the noise reduction level for each reconstruction algorithm affects the volumetric measurement of GGNs. Finally, only one software package was used for the semi-automated method, and only one CT scanner of a single vendor was used. Further studies comparing various software packages are needed, and the influence of different CT scanners should be identified.
Conclusion
DLR was superior to both MBIR and HIR for the volumetric measurement of pure GGNs by ultra-low-dose CT. Substantial dose reductions might be achieved in lung CT screening for the volumetric measurement of pure GGNs by adapting DLR.
Footnotes
Competing interests: The authors have no conflicts of interest directly relevant to the content of this article.
Funding: This work was supported by grant from the Clinical Research Promotion Foundation (2020).
Contributor Information
Ryoji Mikayama, Email: mikayama.ryoji.923@m.kyushu-u.ac.jp.
Takashi Shirasaka, Email: shirasaka.takashi.154@m.kyushu-u.ac.jp.
Tsukasa Kojima, Email: kojima.tsukasa.929@m.kyushu-u.ac.jp.
Yuki Sakai, Email: sakai.yuki.592@m.kyushu-u.ac.jp.
Hidetake Yabuuchi, Email: h-yabu@med.kyushu-u.ac.jp.
Masatoshi Kondo, Email: kondou.masatoshi.074@m.kyushu-u.ac.jp.
Toyoyuki Kato, Email: kato.toyoyuki.715@m.kyushu-u.ac.jp.
REFERENCES
- 1. van Klaveren RJ, Oudkerk M, Prokop M, Scholten ET, Nackaerts K, Vernhout R, et al. Management of lung nodules detected by volume ct scanning. N Engl J Med 3, 2009; 361: 2221–29. doi: 10.1056/NEJMoa0906085 [DOI] [PubMed] [Google Scholar]
- 2. de Margerie-Mellon C, Ngo LH, Gill RR, Monteiro Filho AC, Heidinger BH, Onken A, et al. The growth rate of subsolid lung adenocarcinoma nodules at chest ct. Radiology October 2020; 297: 189–98. doi: 10.1148/radiol.2020192322 [DOI] [PubMed] [Google Scholar]
- 3. Park S, Lee SM, Kim S, Lee J-G, Choi S, Do K-H, et al. Volume doubling times of lung adenocarcinomas: correlation with predominant histologic subtypes and prognosis. Radiology June 2020; 295: 703–12. doi: 10.1148/radiol.2020191835 [DOI] [PubMed] [Google Scholar]
- 4. de Koning HJ, van der Aalst CM, de Jong PA, Scholten ET, Nackaerts K, Heuvelmans MA, et al. Reduced lung-cancer mortality with volume ct screening in a randomized trial. N Engl J Med February 6, 2020; 382: 503–13. doi: 10.1056/NEJMoa1911793 [DOI] [PubMed] [Google Scholar]
- 5. Silva M, Milanese G, Sestini S, Sabia F, Jacobs C, van Ginneken B, et al. Lung cancer screening by nodule volume in lung-rads v1.1: negative baseline ct yields potential for increased screening interval. Eur Radiol 2021; 31: 1956–68. doi: 10.1007/s00330-020-07275-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Ohno Y, Yaguchi A, Okazaki T, Aoyagi K, Yamagata H, Sugihara N, et al. Comparative evaluation of newly developed model-based and commercially available hybrid-type iterative reconstruction methods and filter back projection method in terms of accuracy of computer-aided volumetry (cadv) for low-dose ct protocols in phantom study. Eur J Radiol 2016; 85: 1375–82. doi: 10.1016/j.ejrad.2016.05.001 [DOI] [PubMed] [Google Scholar]
- 7. Katsura M, Matsuda I, Akahane M, Yasaka K, Hanaoka S, Akai H, et al. Model-based iterative reconstruction technique for ultralow-dose chest ct: comparison of pulmonary nodule detectability with the adaptive statistical iterative reconstruction technique. Invest Radiol 2013; 48: 206–12. doi: 10.1097/RLI.0b013e31827efc3a [DOI] [PubMed] [Google Scholar]
- 8. Kim H, Park CM, Song YS, Lee SM, Goo JM. Influence of radiation dose and iterative reconstruction algorithms for measurement accuracy and reproducibility of pulmonary nodule volumetry: a phantom study. Eur J Radiol 2014; 83: 848–57. doi: 10.1016/j.ejrad.2014.01.025 [DOI] [PubMed] [Google Scholar]
- 9. Sakai N, Yabuuchi H, Kondo M, Kojima T, Nagatomo K, Kawanami S, et al. Volumetric measurement of artificial pure ground-glass nodules at low-dose ct: comparisons between hybrid iterative reconstruction and filtered back projection. Eur J Radiol 2015; 84: 2654–62. doi: 10.1016/j.ejrad.2015.08.018 [DOI] [PubMed] [Google Scholar]
- 10. Millon D, Vlassenbroek A, Van Maanen AG, Cambier SE, Coche EE. Low contrast detectability and spatial resolution with model-based iterative reconstructions of mdct images: a phantom and cadaveric study. Eur Radiol 2017; 27: 927–37. doi: 10.1007/s00330-016-4444-x [DOI] [PubMed] [Google Scholar]
- 11. Tatsugami F, Higaki T, Nakamura Y, Yu Z, Zhou J, Lu Y, et al. Deep learning-based image restoration algorithm for coronary ct angiography. Eur Radiol 2019; 29: 5322–29. doi: 10.1007/s00330-019-06183-y [DOI] [PubMed] [Google Scholar]
- 12. Kang E, Min J, Ye JC. A deep convolutional neural network using directional wavelets for low-dose x-ray ct reconstruction. Med Phys 2017; 44: e360–75. doi: 10.1002/mp.12344 [DOI] [PubMed] [Google Scholar]
- 13. Higaki T, Nakamura Y, Zhou J, Yu Z, Nemoto T, Tatsugami F, et al. Deep learning reconstruction at ct: phantom study of the image characteristics. Acad Radiol 2020; 27: 82–87. doi: 10.1016/j.acra.2019.09.008 [DOI] [PubMed] [Google Scholar]
- 14. Muramatsu Y, Tsuda Y, Nakamura Y, Kubo M, Takayama T, Hanai K. The development and use of a chest phantom for optimizing scanning techniques on a variety of low-dose helical computed tomography devices. J Comput Assist Tomogr 2003; 27: 364–74. doi: 10.1097/00004728-200305000-00012 [DOI] [PubMed] [Google Scholar]
- 15. Wang Y, de Bock GH, van Klaveren RJ, van Ooyen P, Tukker W, Zhao Y, et al. Volumetric measurement of pulmonary nodules at low-dose chest ct: effect of reconstruction setting on measurement variability. Eur Radiol 2010; 20: 1180–87. doi: 10.1007/s00330-009-1634-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. National Lung Screening Trial Research Team, Aberle DR, Adams AM, Berg CD, Black WC, Clapp JD, et al. Reduced lung-cancer mortality with low-dose computed tomographic screening. N Engl J Med 4, 2011; 365: 395–409. doi: 10.1056/NEJMoa1102873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Martin Bland J, Altman D. STATISTICAL methods for assessing agreement between two methods of clinical measurement. The Lancet 1986; 327: 307–10. doi: 10.1016/S0140-6736(86)90837-8 [DOI] [PubMed] [Google Scholar]
- 18. Racine D, Ba AH, Ott JG, Bochud FO, Verdun FR. Objective assessment of low contrast detectability in computed tomography with channelized hotelling observer. Phys Med 2016; 32: 76–83. doi: 10.1016/j.ejmp.2015.09.011 [DOI] [PubMed] [Google Scholar]
- 19. Akagi M, Nakamura Y, Higaki T, Narita K, Honda Y, Zhou J, et al. Deep learning reconstruction improves image quality of abdominal ultra-high-resolution ct. Eur Radiol 2019; 29: 6163–71. doi: 10.1007/s00330-019-06170-3 [DOI] [PubMed] [Google Scholar]
- 20. Xu Y, He W, Chen H, Hu Z, Li J, Zhang T. Impact of the adaptive statistical iterative reconstruction technique on image quality in ultra-low-dose ct. Clin Radiol 2013; 68: 902–8. doi: 10.1016/j.crad.2013.03.024 [DOI] [PubMed] [Google Scholar]
- 21. Chen B, Barnhart H, Richard S, Robins M, Colsher J, Samei E. Volumetric quantification of lung nodules in ct with iterative reconstruction (asir and mbir). Med Phys 2013; 40(11): 111902. doi: 10.1118/1.4823463 [DOI] [PubMed] [Google Scholar]
- 22. Ko JP, Rusinek H, Jacobs EL, Babb JS, Betke M, McGuinness G, et al. Small pulmonary nodules: volume measurement at chest ct--phantom study. Radiology 2003; 228: 864–70. doi: 10.1148/radiol.2283020059 [DOI] [PubMed] [Google Scholar]
- 23. Scholten ET, Jacobs C, van Ginneken B, Willemink MJ, Kuhnigk J-M, van Ooijen PMA, et al. Computer-aided segmentation and volumetry of artificial ground-glass nodules at chest ct. AJR Am J Roentgenol 2013; 201: 295–300. doi: 10.2214/AJR.12.9640 [DOI] [PubMed] [Google Scholar]
- 24. Wang Y, van Klaveren RJ, van der Zaag-Loonen HJ, de Bock GH, Gietema HA, Xu DM, et al. Effect of nodule characteristics on variability of semiautomated volume measurements in pulmonary nodules detected in a lung cancer screening program. Radiology 2008; 248: 625–31. doi: 10.1148/radiol.2482070957 [DOI] [PubMed] [Google Scholar]
- 25. Rampinelli C, De Fiori E, Raimondi S, Veronesi G, Bellomi M. In vivo repeatability of automated volume calculations of small pulmonary nodules with ct. AJR Am J Roentgenol 2009; 192: 1657–61. doi: 10.2214/AJR.08.1825 [DOI] [PubMed] [Google Scholar]
- 26. Padole A, Singh S, Ackman JB, Wu C, Do S, Pourjabbar S, et al. Submillisievert chest ct with filtered back projection and iterative reconstruction techniques. AJR Am J Roentgenol 2014; 203: 772–81. doi: 10.2214/AJR.13.12312 [DOI] [PubMed] [Google Scholar]
- 27. Ehman EC, Yu L, Manduca A, Hara AK, Shiung MM, Jondal D, et al. Methods for clinical evaluation of noise reduction techniques in abdominopelvic ct. Radiographics 2014; 34: 849–62. doi: 10.1148/rg.344135128 [DOI] [PubMed] [Google Scholar]
- 28. Geyer LL, Schoepf UJ, Meinel FG, Nance JW Jr, Bastarrika G, Leipsic JA, et al. State of the art: iterative ct reconstruction techniques. Radiology 2015; 276: 339–57. doi: 10.1148/radiol.2015132766 [DOI] [PubMed] [Google Scholar]