3 T: the good, the bad and the ugly

Abstract

It is around 20 years since the first commercial 3 T MRI systems became available. The theoretical promise of twice the signal-to-noise ratio of a 1.5 T system together with a greater sensitivity to magnetic susceptibility-related contrast mechanisms, such as the blood oxygen level dependent effect that is the basis for functional MRI, drove the initial market in neuroradiology. However, the limitations of the increased field strength soon became apparent, including the increased radiofrequency power deposition, tissue-dependent changes in relaxation times, increased artifacts, and greater safety concerns. Many of these issues are dependent upon MR physics and workarounds have had to be developed to try and mitigate their effects. This article reviews the underlying principles of the good, the bad and the ugly aspects of 3 T, discusses some of the methods used to improve image quality and explains the remaining challenges and concerns.

Introduction

In his contribution to the History of MRI, Paul Bottomley¹ recounts the story that on moving to GE’s Corporate Research and Development Centre (GE-CRD) in upstate New York in 1980, the team set about trying to obtain the highest field strength whole-body MRI magnet they could to perform whole-body magnetic resonance spectroscopy. The agreement with Oxford Instruments was for a superconducting magnet with a target field of 2.0 T with 1.5 T as an absolute minimum. Despite several theoretical arguments that MRI could not be performed above about 0.3 T, the GE-CRD team demonstrated head and body MR imaging and spectroscopy results, using the delivered 1.5 T magnet, at the second annual meeting of the Society of Magnetic Resonance in Medicine (SMRM) meeting in San Francisco in August 1983. Bottomley notes that the published literature against high-field MRI meant that the patent that GE held for MRI systems above 0.7 T² for the period 1985–2005 was probably quite financially lucrative. Clinically, 1.5 T whole-body systems started to become commercially available from the mid-1980s. As the science and engineering of MRI continued to develop, the signal-to-noise advantage of even higher field strengths systems, led the major MRI manufacturers to investigate the capabilities of a small number of 4 T systems in the late 1980s.^3–6 However, the anticipated benefits failed to materialise, probably due to the hardware limitations of the time, and the projects were abandoned.⁷ However, in 1993 the University of Nottingham convinced Oxford Instruments to develop a 3 T magnet which could be used to demonstrate the quality of images obtained using the echoplanar imaging (EPI) technique pioneered in Nottingham.^8,9 The success of the Nottingham 3 T system led to a renewed interest in high-field MRI by the system vendors and commercial 3 T systems were first FDA approved between 1999 and 2002. In 2017 it was estimated that about 33% of MRI system sales per annum were 3 T, with 1.5 T sales representing around 60% and 6% of systems below 1.5 T.¹⁰ Recent figures (2020) from the UK show that approximately 17% of the MRI installed base comprises 3 T systems (Personal communication NHS England). As it is now around 20 years since the first 3 T systems were introduced, this article will review some of the physics-based advantages and limitations of 3 T.

The good

Signal-to-noise

A major driver for increased field strength was the associated increase in the signal-to-noise ratio (SNR). This arises from two mechanisms, firstly the increase in sample magnetisation or polarisation and secondly, the increase in the precessional (Larmor) frequency. The equilibrium magnetisation $M_0$ is proportional to the thermal equilibrium spin polarisation $\left(P\right)$, which in the case of spin-half nuclei such as the single proton in the nucleus of hydrogen (¹H), is the difference in the number of spins in the two energy states; spin up $\left(N_{\uparrow }\right)$ and spin down $\left(N_{\downarrow }\right)$ . $M_0$ is directly proportional to $B_0$ and is given by the following relationship $M_0\propto P=∆N_{\uparrow \downarrow }=N_T\frac{\hslash \bullet \gamma \bullet B_0}{2\bullet k\bullet T}$ , where $N_T$ is the total number of nuclei in a specified volume, $\hslash$ is the reduced Planck’s constant (${\displaystyle \hslash =\frac{h}{2\pi }=1.054\mathsf{x}{10}^{-32}J\cdot s}$), $\gamma$ is the gyromagnetic ratio of the nucleus, e.g. for ¹H, ${\displaystyle \gamma /2\pi =42.58\mathsf{x}{10}^{6}Hz\cdot T^{-1}}$ for protons, ${\mathrm{B}}_0$ is the static magnetic field strength, $k$ is Boltzmann’s constant ${\displaystyle \left(k=1.38\mathsf{x}{10}^{-23}J\cdot K^{-1}\right)}$ and $T$ is the absolute temperature (human body temperature = 310 K). For example, if $B_0=$ 3 T and $T$ = 310 K then the thermal polarisation is approximately p = 0.001%.

The precessional frequency ${\omega }_0$ is given by Sir Joseph Larmor’s 1897 equation ¹¹ , that was originally derived to explain the precessional frequency of electrons in a magnetic field and hence pre-dates the discovery of NMR in 1946. However, it applies to any charged particle and therefore tells us that $M_0$ precesses about $B_0$ at an angular frequency, generally known as the Larmor frequency ${\omega }_0=\gamma \bullet B_0$ , where $\gamma$ is the gyromagnetic ratio of the relevant nucleus. At the field strengths used in MRI the Larmor frequency lies in the radiofrequency (RF) part of the electromagnetic spectrum. To create a signal $\left(S\right)$ , it is necessary to tip all, or part, of the equilibrium magnetisation $M_0$ by a desired flip angle from the longitudinal direction into the transverse plane. From Faraday’s law of electromagnetic induction, the magnitude of the signal $S$, detected in an RF receiver coil, is proportional to the product of the Larmor frequency and the equilibrium magnetisation, which are both proportional to $B_0$ , i.e. $S\propto {\omega }_0{\bullet M}_0\propto B_0^2$. The noise $\left(N\right)$ arises from two sources, the electronic noise from the electrical resistance of the RF receiver coil which is proportional to $\sqrt{B_0}$ and the electronic noise from dielectric and inductive losses in the sample, i.e. the patient, that is proportional to $B_0$.¹² The SNR is given by the ratio of the signal to the noise. At high field, e.g. >0.5 T, the noise is primarily from the sample hence the $SNR=\frac{S}{N}\propto \frac{B_0^2}{B_0}\propto B_0$. There is therefore a theoretical doubling of the SNR from 1.5 to 3 T. However, in vivo measurements of SNR in different tissues at 1.5 T and 3 T have only resulted in increases of the order of 30–60%,¹³ that have been attributed to the lengthening of the T₁ relaxation time and increased signal losses due to the magnetic susceptibility of iron in certain brain tissues at 3 T.¹³ In terms of imaging, SNR is proportional to the voxel size and the acquisition time and is often expressed by the following relationship for a basic 2D pulse sequence with a single echo per repetition time (TR)

$$SNR\propto B_0\bullet \frac{∆x\bullet ∆y\bullet ∆z\bullet \sqrt{N_x\bullet N_y\bullet NSA}}{\sqrt{RBW}}$$ (1)

where $∆x,∆y$ and $∆z$ are the individual imaging voxel dimensions, with $∆z$ being the slice thickness. $N_x\text{and}{N}_y$ are the number of samples in the frequency and phase encoding directions, respectively. NSA is the number of signal averages, i.e. repeated acquisitions and $RBW$ is the receiver bandwidth across the whole image. The main benefit of the increase in SNR provided by a 3 T system is the ability to acquire data with improved image quality, including the ability to trade SNR for higher spatial resolution. Figure 1 shows the SNR improvement in a 3D FLAIR acquisition performed at 3 T in comparison to 1.5 T. Several consensus documents are now recommending 3T over 1.5 T, e.g. multiparametric MRI (mpMRI) of the prostate,¹⁴ myocardial perfusion and late gadolinium enhanced cardiac imaging,¹⁵ and the use of MRI in multiple sclerosis.¹⁶ Alternatively, the improved SNR can be traded for shorter examination times, either by simply reducing the NSA, including the use of partial Fourier acquisitions, or by using advanced acquisition and reconstruction algorithms.^17–20 One downside of having a higher SNR is that artifacts may also have a higher signal and therefore may appear more visually distracting at 3 T.²¹

Figure 1.

Improved SNR in a 3D FLAIR acquired at (a) 3 T compared to (b) 1.5 T using the same imaging parameters, (TI/TR/TE = 1900 ms/7000 ms/104 ms), in the same subject. FLAIR, fluid attenuated inversion recovery

Relaxation times

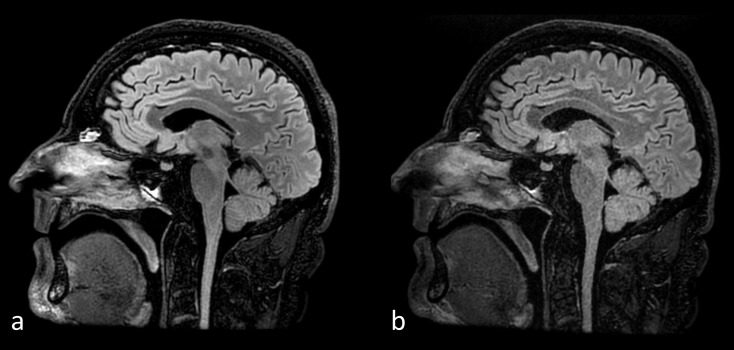
The longitudinal (T₁) and transverse (T₂) relaxation times of biological tissue depend on the physical and chemical environments of the protons as well as the static magnetic field strength. Whilst there are generally no significant differences between T₂ values at 3 T compared to 1.5 T, the T₁ values for tissues are generally longer at 3 T.²² A disadvantage of this increase in T₁ relaxation times is reduced contrast on traditional T₁ weighted spin echo acquisitions which have been replaced by T₁ weighted fluid attenuated inversion recovery (T1 FLAIR) sequences, particularly for neuroimaging.²³ In addition to the improved SNR at 3 T, three-dimensional time-of-flight (3D TOF) MR angiography also benefits from the longer T₁ relaxation times in brain parenchyma resulting in improved saturation of the stationary spins and better vessel-to-background contrast.²⁴ Figure 2 shows the improved vessel visualisation in a 3D TOF study acquired at 3 T compared to 1.5 T.

Figure 2.

3D time-of-flight MRA acquired at 3 T (a, c) and 1.5 T (b, d) using the same imaging parameters, (TR/TE/Flip = 24 ms/6.8 ms/20°), in the same subject. The single section image at 1.5 T (b) has a lower SNR but incidentally better grey/white matter tissue contrast compared to 3T (a). The top-down maximum intensity projection image at 3 T (c) shows better background suppression and hence distal vessel visualisation that the MIP at 1.5 T (d). MRA, MR angiography; SNR, signal-to-noise ratio; TE, echo time; TR, repetition time.

The longer T₁ relaxation times at 3 T also provide a slight advantage for the use of gadolinium-based contrast agents (GBCA). The longer the native (pre-contrast) T₁ relaxation time, the greater the T₁ shortening effect of the GBCA. The overall effect is a greater T₁ reduction post-contrast at 3.0 T, resulting in improved tumour-to-brain contrast.²⁵ This effect can also be seen in the improved image quality of contrast-enhanced MR angiography at 3 T compared to 1.5 T.²⁶

Spectroscopy/X-nuclei

Nuclear magnetic resonance (NMR) was first discovered and demonstrated in ordinary materials by Bloch²⁷ and Purcell,²⁸ separately, in 1946. By 1950, several researchers had identified that the NMR frequency of a given element was slightly shifted depending upon its chemical form. The electrons surrounding the molecule slightly shielded the NMR active nucleus creating a “chemical shift”. A molecule with an NMR active nucleus in different positions produces an NMR spectrum with several distinct resonances, hence the now widely used analytical chemistry technique of NMR spectroscopy was born. Chemical shifts are reported in terms of ppm which are independent of the static magnetic field strength. Multiplying the chemical shift by the resonant frequency of the nuclei in a specific molecule at a given field strength returns the shifts in terms of frequency. As the field strength increases the spectral separation of the peaks also increases, so at 3 T the shifts would be twice those at 1.5 T. The greater the range of frequency shifts the easier it is to identify the multiple peaks in complex molecules or tissues in vivo.

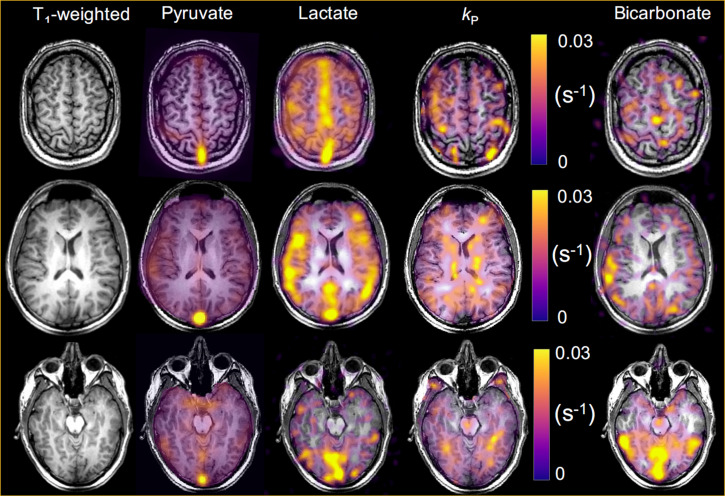
In addition to protons (¹H), there are several other NMR active nuclei that are of interest in studying in vivo metabolism including ¹³C, ¹⁵N and ³¹P. Each nucleus has a different gyromagnetic ratio ($\gamma$) and hence a different resonant frequency $\left({\omega }_0\right)$ depending upon the static magnetic field strength ($B_0$) as given by the Larmor equation. Therefore, to be able to investigate these so-called X-nuclei the MR system needs to be equipped with a broadband RF amplifier and receiver chain as well as dedicated transmit and receive coils tuned to the desired frequency. Initially, these capabilities could be purchased at additional cost as extras to many 1.5 T systems but the development of 3 T, with its improved SNR and greater chemical shifts, has led the major MRI system and RF coil vendors to no longer support such capabilities at 1.5 T. Hyperpolarisation techniques enhance the nuclear spin polarisation in certain gases or small molecules by several orders of magnitude in comparison to the thermal equilibrium polarisation described above. There are various methods of hyperpolarising materials, including spin exchange optical pumping for creating hyperpolarised noble gases, e.g. ¹²⁹Xe for lung imaging²⁹ and dynamic nuclear polarisation (DNP) for hyperpolarising small molecules, e.g. ¹³C-pyruvic acid to track the conversion of pyruvate to lactate, particularly in cancer.³⁰ Figure 3 shows metabolic imaging of a normal human brain at 3 T following intravenous injection of hyperpolarised ¹³C-labelled pyruvate.³¹ In hyperpolarised samples the SNR is relatively independent of the static magnetic field strength, but there are certain advantages, e.g. in lung imaging using hyperpolarised ¹²⁹Xe, where performing the studies at a lower field strength would reduce the T₂^* signal dephasing.^32,33

Figure 3.

Metabolic imaging of the normal human brain at 3 T with hyperpolarised carbon-13 MRI following intravenous injection of hyperpolarised carbon-13 labelled pyruvate. The formation of hyperpolarised carbon-13 labelled lactate is shown along with the apparent exchange rate constant (kP measured in s^-1) describing the reaction catalysed by the enzyme LDH. Hyperpolarised carbon-13 labelled bicarbonate can also be detected due to mitochondrial metabolism of the pyruvate. Figure adapted from Grist et al³¹. LDH, lactate dehydrogenase.

Susceptibility effects

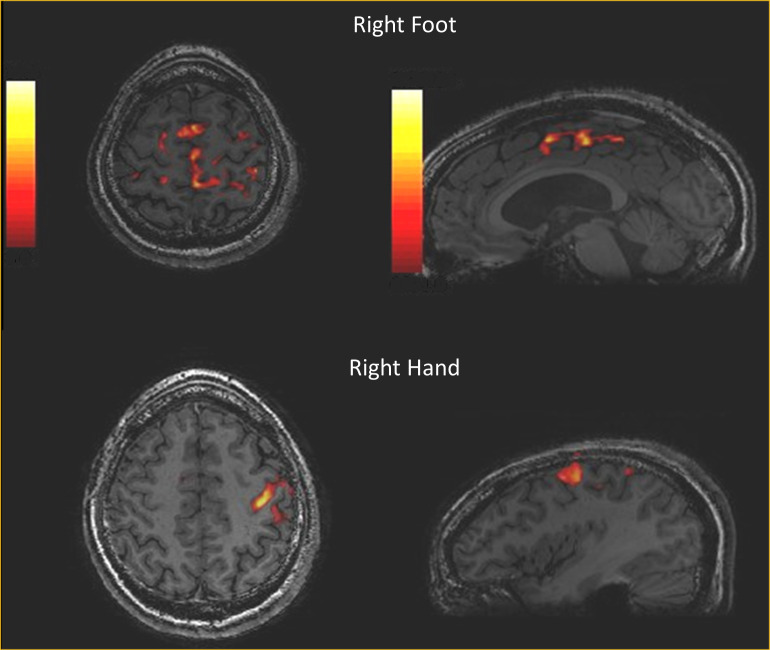
The magnetic susceptibility $\left(\chi \right)$ is a measure of how magnetised a material will become in the presence of an external magnetic field. Materials that become magnetised can be classified as diamagnetic, paramagnetic, superparamagnetic, or ferromagnetic, based on their susceptibilities. Nearly all biological tissues are weakly diamagnetic due to the large abundance of water ($\chi =-9.05ppm)$), however some tissues may contain focal accumulations of metals such as calcium, iron, copper, or manganese that have much larger susceptibilities. The magnetic susceptibility causes a variation in the uniformity of the static magnetic field ${\displaystyle \left(\mathrm{\Delta }{B}_0\right)}$ proportional to $B_0$ , i.e. ${\displaystyle \mathrm{\Delta }{B}_0=\chi \cdot B_0}$ . Hence the static field non-uniformity is doubled at 3 T compared to 1.5 T. A greater non-uniformity results in a shortening of the T₂^* relaxation time and a relative decrease in signal in T₂^* -weighted imaging. This is a double-edged sword. Whilst a greater static field non-uniformity is often undesirable in terms of signal loss, there are also applications where magnetic susceptibility is an important contrast mechanism. Where susceptibility effects are desirable then 3 T has a greater sensitivity compared to 1.5 T. In addition to T₂^* weighted magnitude images, it is also possible to create quantitative images of signal phase (and frequency) and T₂^* relaxation. Combining T₂* weighted imaging with phase/frequency information has been used to create so-called susceptibility weighted images (SWI) that enhance the susceptibility contrast in several body areas and pathologies.^34,35 Furthermore, it is possible to post-process the susceptibility data to obtain quantitative maps of tissue susceptibility.³⁶ Functional MRI (fMRI) is based upon the blood oxygen level dependent (BOLD) contrast mechanism, where a specific neuronal activation task results in a surfeit of oxyhaemoglobin beyond that of the local, to the activation, brain tissues immediate metabolic need. This results in a relative increase in the concentration of weakly diamagnetic oxyhaemoglobin over paramagnetic deoxyhaemolgobin during the activation, i.e. on a microscopic scale the magnetic environment becomes more uniform and provides a higher signal. Since the difference in magnetic susceptibilities is greater at 3 T, several studies have shown that fMRI at 3 T produces a greater BOLD signal change and area of activation compared to 1.5 T.^37–39 Figure 4 shows an fMRI study at 3 T demonstrating the BOLD effect in a subject performing a foot and finger motor activation task.

Figure 4.

An fMRI motor function study performed at 3 T. The colour overlay on a 3D T₁ weighted gradient echo acquisition represents the correlation between the BOLD signal change and a simple boxcar (on/off) reference activity, in this case 30 s of foot or finger tapping and then 30 s of rest repeated for 5 minutes. BOLD, blood oxygen level dependent.

The bad

Susceptibility effects

We shall continue with the negative effects of spatial variations in magnetic susceptibility. Firstly, $∆B_0$ will cause a change in resonant frequency, which will give rise to spatial misregistration and distortion depending upon the spatial variation of $∆B_0$ . In the case of metal implants, these field non-uniformities are responsible for the most severe artifacts that include variously signal loss, signal pile-ups and through plane displacement. As expected, these artifacts are worse at 3 T, and therefore initially it could not be used for the imaging of patients with prosthetic implants. Fortunately, the development of new MRI methods such as SEMAC⁴⁰ and MAVRIC,⁴¹ have addressed these issues and are equally effective at both 1.5 T and 3 T.^42,43 However, there are still issues with the use of 3 T for high accuracy stereotactic procedures.⁴⁴

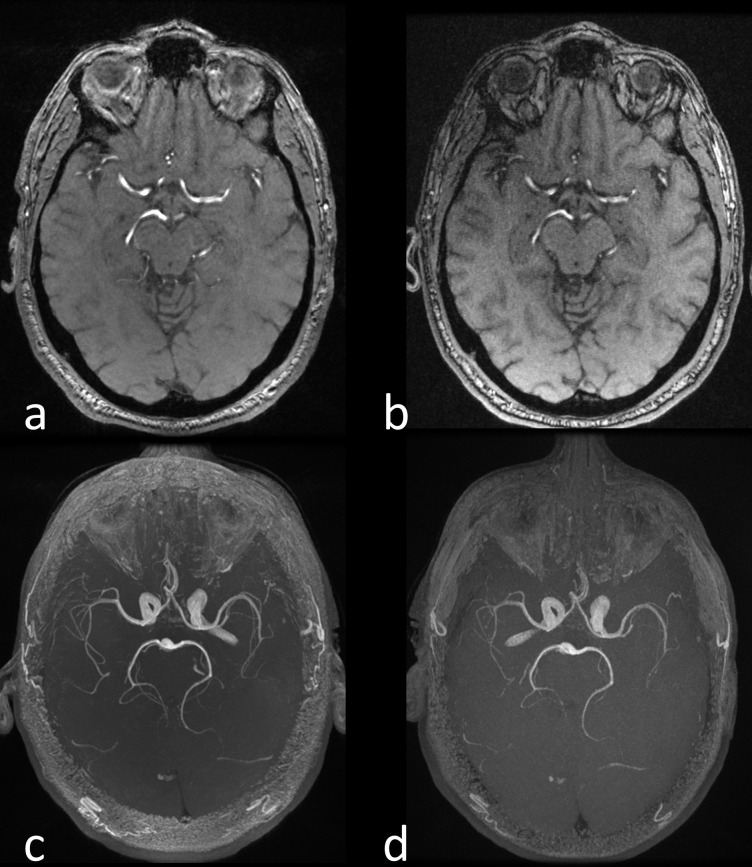
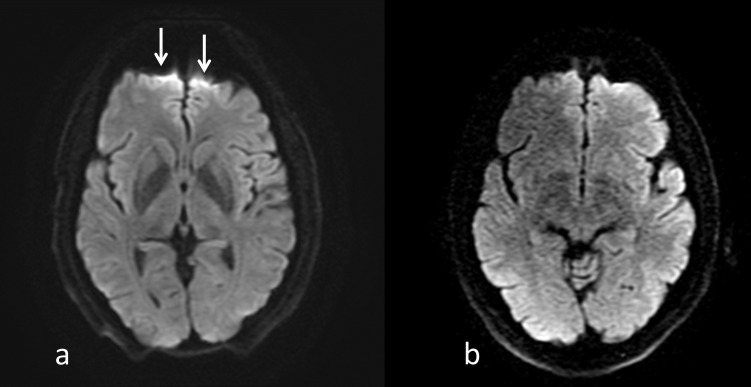
Another artifact can occur where there is an interface between two materials of different magnetic susceptibilities $\left(∆\chi \right)$ , thereby creating an intrinsic variation in the magnetic field $\left(∆B_0\right)$ , across a voxel of size $\left(∆r\right)$ . The resulting phase dispersion $\left(∆\varphi \right)$ is given by $∆\varphi =\gamma \bullet ∆B_0\bullet ∆r\bullet TE$. If the phase dispersion is large enough then signal loss can be seen, typically at air/tissue boundaries, e.g. mastoid air cells, nasopharynx, etc. Although these artifacts can be eliminated using spin echo imaging, it is not possible to do so in gradient echo acquisitions. In this case, it is necessary to either decrease the voxel size, or more commonly, to reduce the TE through increasing the receiver bandwidth ($RBW$). Increasing $RBW$ will reduce the sampling time of each echo, and hence the TE, but as shown in Eq. 1, this will also have the effect of reducing the SNR by a factor of $\frac{1}{\sqrt{RBW}}$ . For example, increasing the $RBW$ from ±15.63 kHz to ±31.25 kHz for a readout of 256 samples will reduce the sampling time from 8.2to 4.1 ms, whilst reducing the SNR by 29%. EPI, as originally developed by Mansfield, is particularly sensitive to differences in magnetic susceptibility. This is due to the extended sampling time in phase encoding rather than frequency encoding, which results in a very low encoding bandwidth in the phase encoding direction. Therefore, any frequency offset due to magnetic susceptibility results in image distortion. Figure 5 shows the distortion in the frontal lobe at 3 T compared to 1.5 T in a diffusion-weighted single-shot EPI acquisition.⁴⁵

Figure 5.

DW-EPI obtained at 3 T (a) and 1.5 T (b) using the same imaging parameters, (TR/TI/b-value = 5000 ms/62.1 ms/1000 s mm^-2) in the same subject. Note the better SNR at 3T but the greater image distortion and signal pile-up in the frontal lobe due to the susceptibility differences between the brain tissue and the air in the frontal sinus (arrows). DW-EPI, diffusion weighted echoplanar imaging; TE, echo time; TR, repetition time.

Chemical shift

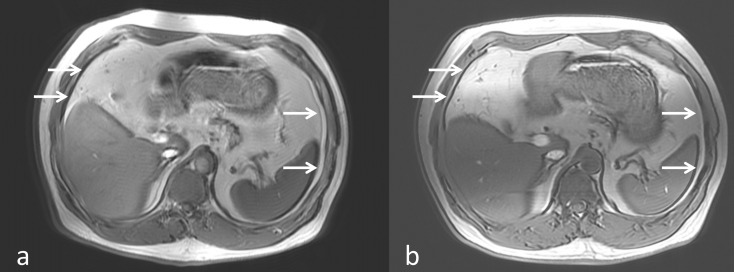
There is an approximately 3.4 ppm chemical shift between water and fat, meaning that the frequency difference will be twice as large at 3 T (440 Hz) compared to 1.5 T (220 Hz). This has two main implications. Firstly, the spatial shift of the adipose tissue in the frequency encoding direction will be twice as big for the same frequency encoding gradient amplitude at 1.5T. Using the example above for a $RBW$ of ±15.63 kHz the water/fat shift will be 1.8 pixels at 1.5 T and 3.6 pixels at 3.0 T. Hence, it is usual to acquire images with a higher $RBW$ at 3.0 T to avoid large spatial shifts, and/or to use fat suppression. Figure 6 shows the increased water/fat chemical shift at 3 T compared to 1.5 T in the abdomen for the same $RBW$. Similarly, when acquiring images in- and out-of-phase for applications such as Dixon imaging for water and fat separation⁴⁶ the TEs at 3 T will be half the values at 1.5 T.

Figure 6.

Gradient echo images in the abdomen acquired at 3 T (a) and 1.5 T (b) with TR/TE = 180 ms/4.2 ms and a readout bandwidth of 65 Hz pixel^-1. This results in a water/fat chemical shift in the frequency encoding direction (arrows) of 6.8 pixels at 3 T and 3.4 pixels at 1.5 T. TE, echo time; TR, repetition time.

RF power deposition

As discussed in the Signal-to-noise section above, an RF pulse of amplitude $B_1$ is used to tip $M_0$ through the desired flip angle. Less than 1% of the power is used to tip $M_0$ , with the rest resulting in undesirable tissue heating. From Faraday’s law of induction, we know that the RF magnetic field will induce electric fields inside the tissue. Since the tissues are electrically conducting this will result in the deposition of electrical power resulting, over time, in heating. At radiofrequencies, the power deposition is measured by the specific absorption rate (SAR) in W/kg. The SAR is proportional to

$SAR\propto \frac{\sigma }{\rho }\bullet \frac{{B_1}^2\bullet {\omega }_0^2\bullet t_{rf}}{TR}$, where $\sigma$ is the tissue conductivity (S m^-1), $\rho$ is the tissue density (kg m^-3), TR is the sequence repetition time and $t_{rf}$ is the duration of the RF pulse.

We can therefore see that the power deposition is proportional to ${\omega }_0^2$ , i.e. the static magnetic field strength squared since ${\omega }_0=\gamma \bullet B_0$ . Therefore, an identical RF pulse will deposit approximately four times more power at 3 T compared to 1.5 T. The SAR is limited by local regulatory limits, e.g. the Food and Drug Administration (FDA) in the US⁴⁷ and the International Electrotechnical Commission (IEC) in Europe.⁴⁸ The estimation of SAR in human subjects is complex and different MR system vendors have their own methods of making such estimates, often using simplified head/body models based on weight, possibly height and the selected anatomical landmark. For example, a T₁ weighted multi slice spin echo sequence with TE/TR = 15/500 ms acquired at 1.5 T and 3 T has MR system reported head-SAR values of 0.9 W/kg and 3.37 W/kg respectively.

A further issue at 3 T is the shorter RF wavelength compared to 1.5 T. The wavelength $\left(\lambda \right)$ of an electromagnetic wave in a particular material is given by $\lambda =\frac{c}{f\bullet \sqrt{\epsilon }}$ , where c is the speed of light (3.0 x 10⁸ m s^-1), $f$ is the frequency and $\epsilon$ is the relative permittivity of the material. Assuming a value of $\epsilon$ = 81 for tissue/water the wavelength at 1.5 T is approximately 52 cm and at 3 T approximately 26 cm. At 26 cm, the wavelength starts to be commensurate with the dimensions of the human body and wave interference occurs, potentially resulting in localised SAR ‘hot-spots’. In recent years, the vendors have started to use computational electromagnetic (EM) modelling⁴⁹ to derive the B-fields and E-fields in anatomically realistic, high resolution, human voxel models.⁵⁰ These models contain many tissues/organs each with their own conductivity and relative permittivity values. Together with models of the RF transmit coil, the B-fields and E-fields can be iteratively calculated. The SAR can then be calculated from the E-field. Note that these EM models are used to try to improve the SAR estimates for a given anatomical landmark, e.g. the neck where the anatomical narrowing can result in an underestimation of SAR based on simple geometric models.

RF intensive pulse sequences such as 3D fast or turbo spin echo (FSE/TSE) that utilise many RF refocusing pulses usually modulate the flip angle of the pulses across the echo-train. The use of pulses less than 180° can substantially reduce both the SAR as well as reducing the effects of T₂ decay across the echo-train and hence image blurring. Gradient echo sequences may either require a lengthening of TR or a reduction in the excitation flip angle to ensure SAR is not exceeded.^51,52

Static magnetic field uniformity

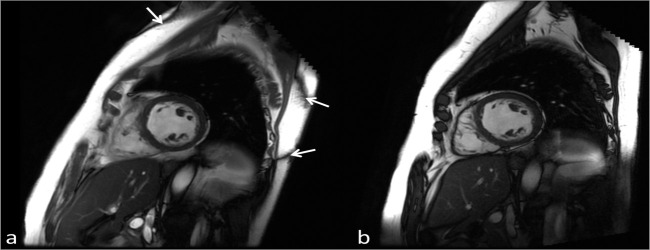
The uniformity of the static magnetic field, measured in ppm, is generally the same for both 1.5 T and 3 T. However, this means that the actual frequency variation is twice as large at 3 T. For example, an average homogeneity over a 45 cm diameter spherical volume may be around 1.5 ppm at 1.5 T and 3 T, however this translates into an average frequency variation of 96 Hz and 192 Hz, respectively. The peak-to-peak variations can be much higher. One application where this can cause issues is when using a balanced steady state free precession (bSSFP) sequence, typically for cardiac cine imaging. One characteristic of this sequence is its sensitivity to off-resonance effects, due to both field non-uniformity as well as patient susceptibility, which can cause banding artifacts in the images.⁵³ These and other off-resonance flow artifacts present challenges for bSSFP cine cardiac imaging at 3T.⁵⁴ Figure 7 shows typically bSSFP banding artifacts at 3 T in comparison to 1.5 T.

Figure 7.

Single diastolic frames from a cardiac cine bSSFP acquisition performed at 3 T (a) and 1.5 T (b) acquired with the same imaging parameters, (TR/TE/Flip = 3.8 ms/1.9 ms/4$5°$), in the same subject. Due to the poorer field uniformity at 3 T compared to 1.5 T the characteristic bSSFP banding artifacts can be seen (arrows). Due to localised shimming over the heart the artifacts are displaced to the edges of the body. Note the improved SNR at 3 T. bSSFP, balanced steady state free precession; SNR, signal-to-noise ratio; TE, echo time; TR, repetition time.

The increased field non-uniformity can also affect quantitative T₂^* relaxation time measurements. T₂^* is related to T₂ by $\frac{1}{T_2^{*}}=\frac{1}{T_2}+\gamma \bullet ∆B_0$ , where $∆B_0$ is the variation in the magnetic field due to the non-uniformity of the static magnetic field as well as tissue susceptibility. This is particularly problematic when attempting to use T₂^* measurements to monitor, for example, tissue iron concentrations. One study reported that the R₂^* (=1/T₂^*) values for both heart and liver approximately doubled between 1.5 T and 3 T with more artifacts and lower reproducibility at 3 T.⁵⁵ This makes the quantification of T₂^* in tissues with a high iron content more difficult at 3 T compared to 1.5 T. Ultrashort echo time methods are typically required to quantify massive iron overload at both 1.5 T and 3 T.⁵⁶

The ugly

RF non-uniformity

As discussed above in RF Power Deposition, the RF wavelength at 3 T is approximately 26 cm in tissue. It has been proposed that due to this shorter wavelength, standing electric waves may develop that can interfere with each other resulting in constructive and destructive interference.⁵⁷ This spatially varying transmit B-field produces corresponding variations in the flip angle within the body and subsequent intensity variations across the image.⁵⁸ Such brightening and darkening artifacts have sometimes been incorrectly attributed to dielectric resonance, which is strictly a function of frequency rather than position.⁵⁹ Abdominal MRI often suffers from regions of central darkening with body habitus often influencing the degree of artifact. Obese patients do not necessarily produce worse shading because a) the lower dielectric constant of fat compared to muscle causes the RF wavelength to be 2–3 times longer in fat, ²¹ and b) they have a more circular cross-section. Whereas artifacts can be substantially worse in thin patients because of less fat and a more elliptical cross-section. Patients with ascites are also problematic due to the high relative permittivity of the fluid as well as the high conductivity if it also has a high salt concentration.^58,60

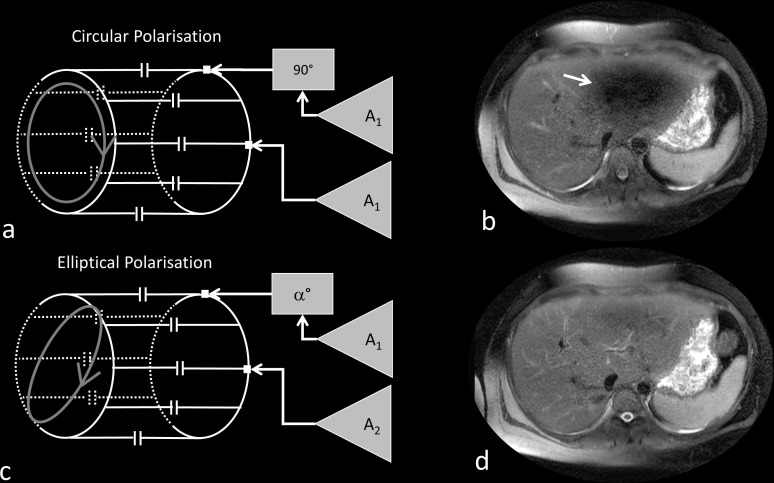
The initial attempt to reduce this shading artifact involved the use of so-called “dielectric pads”,^61–63 that were placed over the patient’s abdomen. An alternative and, in many cases, a more successful approach to reducing dielectric shading artifacts is the use of a dual channel transmit body coil rather than the standard single channel body transmit coil. An RF body coil for 1.5 T or 3 T is usually of the birdcage design.⁶⁴ This comprises a pair of circular end rings connected by a number of straight conductors called ‘rungs’. The birdcage is designed to create a current varying with the sine of the azimuthal angle around the coil, thereby creating a uniform magnetic field within the coil. This is normally achieved by driving the coil via two ports that are physically 90° apart. Each port is driven by the same voltage from the RF amplifier but with a 90° phase shift between them. This creates a circularly polarised alternating magnetic field that rotates in the same sense as $M_0$ , often referred to as $B_1^{+}$ , that tips the magnetisation through the desired flip angle. Whilst circular polarisation has served 1.5 T very well since the mid-1980s it is not optimal at 3 T when the subject geometry is more elliptical.⁵⁸ It is relatively straightforward to create an elliptically polarised RF excitation, by driving the two ports of the birdcage coil with different voltage amplitudes and phases. Initially, vendors used pre-set ratios of amplitude and phase to create specific elliptical polarisations for different body areas without the need to determine patient-specific values. However, this approach was found to be too simplistic and improved image quality was found when using patient specific values.^65–67 The optimisation of the B₁ transmit field for individual patients is known as ‘B₁-shimming’ to show the similarity with patient specific optimisation of the static magnetic field uniformity using B₀-shimming. B₁-shimming involves the use of special pulse sequences^68–70 that spatially determines the B₁-field (effectively the flip angle variation) across the patient. A computer algorithm then calculates the optimal amplitude and phase ratios to minimise the B₁-variation. In addition to improving the excitation uniformity, B₁-shimming also provides a more reliable estimate, and commensurate reduction, of the local SAR.^71,72 Figure 8 shows the arrangement of a dual channel transmit body coil in quadrature and elliptical polarisation mode, and the use of elliptical polarisation.

Figure 8.

Dual channel transmit RF coil in quadrature excitation mode uses the same RF amplitude A₁ and a 90º phase shift between the channels (a). Quadrature excitation results in reduced signal in the left lobe of the liver (arrow) due to dielectric effects (b). Using optimised elliptical polarisation with two different RF amplitudes, A₁ and A₂, and an $\alpha °$phase shift between the channels (c) results in an improved image uniformity (d).

Ferromagnetic attraction and torque

The translational or attractive force on a ferromagnetic object is proportional to the strength of the static magnetic field $B_0$ , or the objects saturation flux density $B_s$ , and the spatial field gradient (SFG) represented by $\nabla B_0$ . A material becomes saturated when an increase in the external magnetic field cannot increase the magnetisation of the object any further. The $B_s$ in ferromagnetic objects ranges from about 0.25 to 2.5 T.⁵⁷ The SFG is the variation in the static magnetic field with distance from the isocentre. The SFG can be quite large due to magnets being actively shielded, resulting in a rapid decrease in the strength of the magnetic field with distance. The force is proportional to $F\propto min\left(B_0,B_s\right)\bullet \nabla B_0$.⁷³ The MRI vendors provide maps of their specific magnet $\nabla B_0$ isocontours so the MR operator can ensure that any patient with an MR-conditional implant, that has a SFG condition, can be appropriately managed. The SFG of a 3 T magnet is approximately twice that of a 1.5 T.

Whilst the attractive force on a ferromagnetic object is proportional to the SFG, a highly asymmetric object may also experience a torque, or twisting motion, that tries to align the object with the direction of $B_0$ . The torque $T$, on an object with a magnetic moment (m) aligned at an angle $\theta$ to the direction of $B_0$ is given by $T=m\bullet B_0\bullet \sin \theta .$ The torque on an unsaturated soft ferromagnetic material of volume V with magnetic permeability ${\mu }_0$ , diameter d and length l is given by $T=\frac{1}{2\bullet {\mu }_0}\bullet V\bullet B_0^2\bullet \frac{d-l}{d\bullet l}\bullet \sin \left(2\theta \right)$.⁷³ Hence the torque is proportional to the field strength squared.

Heating of conducting materials

Loops of wire, either positioned on or in the body, can result in inductive heating and burns when exposed to RF. Straight wires can also result in burns due to the antenna effect when the RF electric field is aligned along the direction of the wire. As described in RF Power Deposition the RF wavelength in tissue at 3 T is dependent upon tissue electrical properties, but is typically around 26 cm. A length of wire that is equal to half the RF wavelength can create a standing wave potentially resulting in significant heating in the tissues at the ends of the wire. Temperature increases from 20 to 60°C have been recorded in experiments with a variety of devices that include wires; deep brain stimulators, vagus nerve stimulators, pacemakers, guide wires, and EEG electrodes.^57,73 However, due to the RF wavelength, it is not necessarily the case that 3 T systems are always worse for heating than 1.5 T.⁷⁴

Summary

MRI at 3T offers an SNR advantage over lower field strengths that can be traded for resolution and/or acquisition speed. Other factors, such as the increase in T₁ relaxation time, mean that clinically you cannot achieve the expected doubling in SNR from 1.5 to 3 T. However, the increased sensitivity to magnetic susceptibility effects at 3 T yields advantages in fMRI and other susceptibility weighted imaging methods. The main limitations of 3 T are the necessity to control the increased RF power deposition, dealing with the RF non-uniformity challenges, particularly in thoracic and abdominal imaging and the appropriate management of patients with implanted devices. Over the last 20 years, the quality of 3 T (and 1.5 T) imaging has improved due to developments in RF and gradient hardware as well as new pulse sequences and image reconstruction algorithms, but have those changes made a diagnostic impact? Unfortunately, there is a paucity of objective evidence that proves a definitive clinical advantage of 3 T over, say 1.5 T, in the literature. In 2012 Wardlaw et al⁷⁵ performed a systematic review of the utility of 1.5 T and 3 T in neuroimaging and found little evidence of improved diagnosis at 3 T. A 2018 review by Cheng and Zhao, comparing 1.5 T and 3 T for the evaluation of lesions in the knee, showed that 3 T MRI provided greater diagnostic accuracy but only for articular cartilage lesions.⁷⁶ Difficulties in making such comparisons include ensuring that the MR systems being compared are of equivalent technical performance; a particular challenge given the rapid development of image acquisition/reconstruction software and RF coil and gradient hardware. However, these improvements are independent of field strength, and it is of interest that in addition to the trend in increasing magnetic field strength,⁷⁷ with 7 T systems now approved for clinical use, that the advantages of high-performance systems based on lower field strength magnets, e.g. 0.55 T are now being investigated.⁷⁸ Over the last 20 years 3 T MRI systems have become well established clinically, particularly for neuroimaging, and the commercial market for 3 T systems will continue to grow, mainly driven by the simple consensus that ‘bigger is better’. My expectation is that 3 T systems will gradually replace 1.5 T systems as the clinical field strength of choice despite the limitations discussed in this article.