Voltage-mediated mechanism for calcium wave synchronization and arrhythmogenesis in atrial tissue

Abstract

A wide range of atrial arrythmias are caused by molecular defects in proteins that regulate calcium (Ca) cycling. In many cases, these defects promote the propagation of subcellular Ca waves in the cell, which can perturb the voltage time course and induce dangerous perturbations of the action potential (AP). However, subcellular Ca waves occur randomly in cells and, therefore, electrical coupling between cells substantially decreases their effect on the AP. In this study, we present evidence that Ca waves in atrial tissue can synchronize in-phase owing to an order-disorder phase transition. In particular, we show that, below a critical pacing rate, Ca waves are desynchronized and therefore do not induce substantial AP fluctuations in tissue. However, above this critical pacing rate, Ca waves gradually synchronize over millions of cells, which leads to a dramatic amplification of AP fluctuations. We exploit an underlying Ising symmetry of paced cardiac tissue to show that this transition exhibits universal properties common to a wide range of physical systems in nature. Finally, we show that in the heart, phase synchronization induces spatially out-of-phase AP duration alternans which drives wave break and reentry. These results suggest that cardiac tissue exhibits a phase transition that is required for subcellular Ca cycling defects to induce a life-threatening arrhythmia.

Significance

In this study, we identify a novel mechanism that explains how molecular scale defects within cells can induce an arrhythmia in the heart. The main finding is that heart cells can synchronize via an order-disorder phase transition driven by the coupling between chemical and electrical activity. By exploiting the symmetries inherent in a periodically driven heart tissue, we show that this transition can be mapped to a well-studied phase transition observed in ferromagnetic systems. Finally, we demonstrate that this phase transition provides a mechanism for molecular scale defects to induce dangerous electrical excitations in the heart.

Introduction

Atrial fibrillation is the most common cardiac arrhythmia, and it is associated with a high degree of mortality (1). However, despite decades of work, the underlying mechanisms are still not fully understood (2). This is because atrial fibrillation involves a breakdown of tissue-scale electrical activity, and it is difficult to identify the molecular scale processes that promote this condition. This difficulty arises because a cardiac cell is regulated by the coordination of tens of thousands of individual proteins within each cell. Each protein fluctuates between conformational states on the submillisecond time scale, and it is the behavior of large populations of interacting proteins that dictates the cellular response. Furthermore, cells are electrically coupled in cardiac tissue, and it is the aggregate behavior of hundreds of thousands of coupled cells that determines the tissue response. Thus, it is crucial to understand cause and effect relationships across a vast range of space and time scales to uncover the mechanisms underlying life-threatening cardiac arrhythmias.

In a cardiac cell, the coordination between electrical activity and cell contraction is mediated by calcium (Ca), a ubiquitous signaling messenger that cycles between intracellular stores to regulate a multitude of cellular processes (3). There is now an extensive body of work linking Ca cycling abnormalities to atrial fibrillation (1,4,5). At the center of these studies is the ryanodine receptor 2 (RyR2), which controls the flow of Ca from the main intracellular store called the sarcoplasmic reticulum (SR) (6). RyR2s are Ca sensitive and transition from a closed to open state at a nonlinear rate that increases with the local Ca concentration. Thus, a small Ca concentration change in the vicinity of an RyR2 can be amplified by stimulating more Ca release. In a cardiac cell, RyR2s form clusters such that Ca release from one receptor typically induces all other receptors in the cluster to fire. In turn, RyR2 clusters are spatially distributed within the three-dimensional (3D) volume of the cell, and under certain conditions, a Ca release at one cluster can ignite neighboring clusters to form an expanding front of Ca release that can propagate across the cell. This process is referred to as a Ca wave, and it is well established that these waves play a crucial role in cardiac arrhythmias (7, 8, 9). It is generally believed that the Ca released during a wave can activate depolarizing currents, such as the sodium-Ca exchanger (NCX), and thus perturb the action potential (AP). It is these perturbations that are believed to cause ill-timed electrical excitations that can propagate and induce atrial fibrillation.

Ca waves have been studied extensively within single cells, and it is known that their timing and magnitude is stochastic and highly variable from cell to cell (7,10,11). This is because Ca wave nucleation depends on both the fluctuations of individual RyR2s and on the local arrangement of RyR2 clusters within the cell. In cardiac tissue, cells are electrically coupled via gap junctions so that electrical perturbations at the cellular scale are averaged over a large population of cells. Thus, at a given beat, cells that exhibit Ca waves are electrically coupled to cells that are quiescent. This coupling will substantially decrease the depolarizing effect of those cells in tissue that exhibit Ca waves since quiescent cells will act as a current sink. Therefore, it is unclear how these stochastic Ca waves can induce electrical excitations that can substantially perturb the voltage time course. This is a fundamental problem that must be addressed in all attempts to explain arrhythmias that are caused by a subcellular defect in the Ca cycling system (12).

In this article, we show that, in paced atrial tissue, Ca waves can be synchronized by the bidirectional coupling between membrane voltage and subcellular Ca. This transition occurs at a critical pacing rate, above which Ca waves synchronize and form coherent structures over millions of cells in cardiac tissue. We show further that this transition is robust, and it depends only on a few physiological relationships that are experimentally known. Also, we demonstrate that in paced cardiac tissue, the synchronization of Ca waves leads to large AP perturbations that induce wave break and the formation of reentrant activity. Thus, our results demonstrate that Ca waves become arrhythmogenic only above the critical point of a phase transition in atrial tissue.

Methods

Spatially distributed model of the atrial myocyte

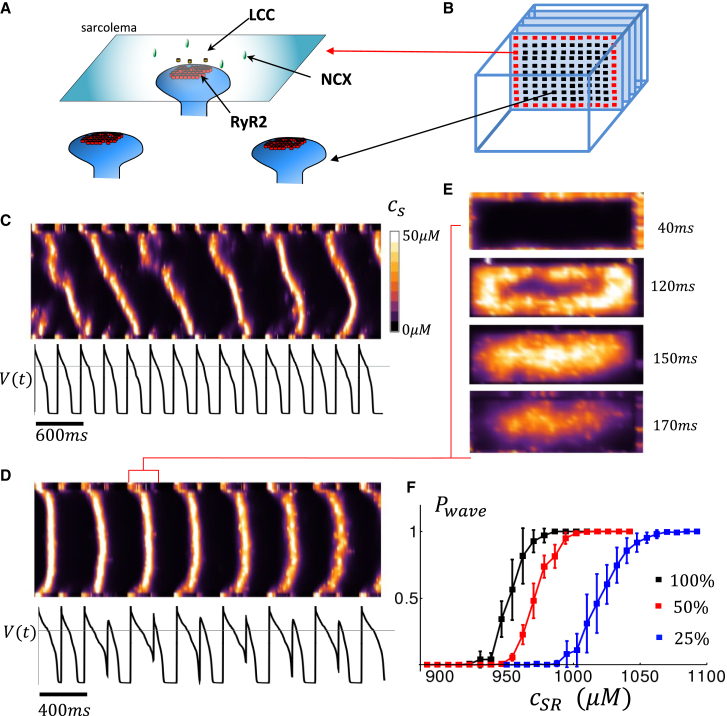
To model Ca dynamics, we apply a spatially distributed cell model originally attributed to Restrepo and Karma (13), which we have previously extended to describe atrial myocytes (14,15). In this approach, the cell interior is divided into compartments that contain the key Ca cycling ion channels (Fig. 1 A and B). The basic unit of the model is referred to as a Ca release unit (CRU), which is composed of the main compartments that surround a RyR2 cluster in the cell along with an array of membrane bound ion channels, such as the L-type Ca channel (LCC) and the NCX. To account for channel stochasticity, the RyR2 and LCC are described using experimentally based Markovian models. To describe an atrial myocyte, we note that the cell membrane forms invaginations into the cell referred to as t-tubules (TTs). In atrial myocytes, these TTs are sparse and do not penetrate fully into the cell, in sharp contrast with ventricular myocytes, where the TTs extend deep into the cell interior. To account for this feature, we allow membrane-bound channels to penetrate the cell a distance that is taken from an exponential distribution. In this manner, we allow some degree of invagination that is representative of an atrial myocyte. Details of our computational model, and the statistical modeling of the TT system, are given in a recent study (14).

Figure 1.

(A) An illustration of the ion channels and transporters involved in Ca signaling. RyR2s form clusters on synapse-like protrusions of the SR network that are near LCC and NCX on the membrane. A small amount of Ca injected into the junctional space by an LCC opening will trigger an autocatalytic release from the cluster, which can diffuse and activate neighboring clusters. The NCX transporter extrudes excess Ca in the vicinity of an RyR2 cluster near the membrane. (B) Spatial architecture of the distribution of Ca-V signal transduction in atrial or Purkinje ventricular myocytes. In these cells, the bulk of the Ca-voltage signaling occurs at junctions at the cell periphery (red squares) while the cell interior contains an array of RyR2 clusters (black squares) that can sustain wave propagation when the SR load is elevated. (C) A line scan image of a $40\times 20\times 20$ computational cell model that is paced to steady state at $T=300ms$. The line scan is located at the center of the cell and oriented along the long axis of the cell. Ca release is visualized by plotting the average Ca concentration, denoted as $c_s$, in the vicinity of RyR2 clusters on the computational grid. Ca waves are visualized as diagonal lines on the line scan. Bottom trace corresponds to the voltage time course $V\left(t\right)$. (D) A line scan image when the cell is paced at $T=200ms$. Ca waves, which appear as U-shaped excitations, occur only on alternate beats. (E) Visualization of 2D image of subcellular Ca for the time duration indicated, showing that the U-shaped trace on the line scan corresponds to a centripetal Ca wave that propagates from the cell periphery to the cell interior. (F) Plot of the probability that a Ca wave propagates $\left(P_{wave}\right)$ vs SR load, for three different values of the strength of $I_{Ca}$. In this simulation, all LCCs have been removed except within a $20\times 20$ sarcomere at one end of the cell. An AP is applied to the cell to initiate wave propagation from one end, and $I_{Ca}$ strength is modulated by changing the conductance of LCC channels. The default ion channel strength which was tuned to reproduce experimentally measured Ca release in atrial myocytes is shown in black (16). The red and blue curve correspond to reductions in $I_{Ca}$ conductance to $50\%$ and $25\%$.

A phenomenological model of Ca cycling

A limitation of the detailed spatial model shown in Fig. 1 A and B is that it is computationally expensive to model cardiac tissue composed of tens of thousands of cells. Thus, we will apply a phenomenological model of subcellular Ca that captures the main features of the detailed model. This model was developed in a previous publication, and it is based on experimental line scan imaging of Ca release in atrial myocytes (15). In this approach, we keep track only on the total number of Ca sparks at the cell boundary and the cell interior. The nucleation and extinction rate of sparks is then described using phenomenological functions of the Ca concentration in the cytosol and SR. By tuning the magnitude and rate of these events, we can then reproduce the qualitative features of Ca wave nucleation and propagation during pacing, as observed using the detailed spatial model, and experimentally. A summary of the phenomenological model is presented in the supporting material.

Simulations of two-dimensional cardiac tissue

In this study, we explore the dynamics of electrical propagation in a two-dimensional (2D) tissue of cells described by our phenomenological model of atrial tissue. To model electrical propagation, we apply the cable equation

$$\frac{\partial V}{\partial t}=-\frac{I_{ion}}{C_m}+D_V\left(\frac{{\partial }^{2}V}{\partial x^2}+\frac{{\partial }^{2}V}{\partial y^2}\right),$$ (Eq. 1)

where $C_m=1\mu F/c{m}^2$ is the membrane capacitance, $D_V=2.5\times {10}^{-4}c{m}^2/ms$ is the effective voltage diffusion coefficient, and $I_{ion}$ is the total transmembrane current (17). Ion currents that determine the AP are modeled using an established model for the atrial myocyte from Grandi et al. (18). The cable equation is integrated using an operator splitting approach (19), with a space step $\text{Δ}x=0.015cm$, and with a variable time step in the range $dt=0.01-0.1ms$.

Results

The phenomenology of Ca waves in electrically paced cardiac cells

In Fig. 1 C, we show a simulated line scan image of a $40\times 20\times 20$ array of CRUs representing an atrial cell model, along with the membrane voltage, that is paced for 15 beats at $300ms$ (Fig. 1 C) and $200ms$ (Fig. 1 D). At a pacing rate of $300ms$, we find that Ca wave propagation is stochastic and occurs intermittently over several beats (Fig. 1 C). However, when the pacing cycle length is decreased, we find that Ca waves tend to propagate only on alternate beats (Fig. 1 D) and that this sequence can be sustained over several beats. A closer examination reveals that the large Ca release beat is due to a Ca wave that originates at the cell boundary and propagates to the cell interior in a centripetal fashion (Fig. 1 E). Note also that the alternating sequence of a wave followed by quiescence corresponds with a long and short AP duration (APD). This is because, when a Ca wave occurs, it stimulates an inward current owing to NCX, which slows AP repolarization and increases the APD on that beat. Subsequently, on the next beat, the SR is depleted so that the cell interior is refractory, no waves occur, and the APD is short. Thus, the APD alternates with the same phase as the subcellular Ca waves propagating into the cell interior.

Alternating Ca release and their association with Ca waves have been well studied experimentally. Their behavior is attributed to the fact that the probability of a Ca wave occurring has a nonlinear dependence on the SR load (20, 21, 22). In Fig. 1 F, we compute the probability of wave propagation, denoted as $P_{wave}$, by stimulating one side of the cell and computing the probability that a Ca wave forms and propagates 15 sarcomeres along the long axis of the cell. Indeed, we find a sigmoid dependence of $P_{wave}$ on the SR load, where the probability of wave propagation increases from 0 to 1 over a range of SR concentrations that is much smaller than the dynamic range of SR concentration during pacing. This nonlinear dependence has been experimentally confirmed in a variety of cell types and conditions and is believed to drive the nonlinear beat-to-beat behavior (20,23). The initiation of Ca waves also depends on the number of Ca sparks that are ignited at the cell boundary in response to the AP upstroke. This release of Ca is mostly dictated by the whole cell LCC current $\left(I_{Ca}\right)$, since more Ca entry triggers more Ca sparks at the cell periphery. In fact, it is well known that the amount of Ca released in the cell increases in proportion to the Ca entry via $I_{Ca}$. This is a basic relation in excitation-contraction coupling, and it is referred to as graded release (24). Thus, the probability that a Ca wave is ignited depends on how much $I_{Ca}$ triggers Ca release in the cell. In Fig. 1 F, we have plotted $P_{wave}$ as a function of SR load for three different strengths of the boundary $I_{Ca}$ current. Indeed, we find that $P_{wave}$ shifts to the left with increasing $I_{Ca}$ since the necessary threshold for Ca wave nucleation is decreased. Thus, Ca wave propagation into the cell interior is sensitive to both the SR load and the amount of $I_{Ca}$ inducing Ca release in the cell.

Electrical coupling in tissue suppresses the effect of Ca waves

In this section, we apply our phenomenological model to study the spatial distribution of Ca waves in cardiac tissue. This phenomenological model captures the essential features of Ca release owing to triggered Ca sparks and Ca waves, and can be used to determine how these events are distributed in cardiac tissue. As a starting point we will first consider tissue sizes such that spatial variations in voltage are small, so that all cells are driven by the same voltage time course. Note that during the APD voltage will diffuse in cardiac tissue a distance of $l\sim \sqrt{D_{V}APD}$, where $APD$ denotes the AP duration. Taking values in the range $APD\sim 100-300ms$ gives $l\sim 2mm-6mm$. For simplicity, we will approximate cells in the tissue to be a square with side $d\sim 70\mu m$, which is roughly the average of a typical cardiac cell diameter $\sim 20\mu m$ and length $\sim 120\mu m$. Thus, the length $l$ corresponds to roughly $30-80$ cells. Thus, for square tissue smaller than $30\times 30$ cells, the voltage is effectively spatially uniform and can be described using a single voltage that satisfies

$$\begin{array}{l}\frac{dV}{dt}=\frac{1}{C_m}\left(I_{Na}+I_K+\frac{1}{N}\sum _{kl}{I}_{Ca}^{kl}+I_{NCX}^{kl}\right),\hfill \end{array}$$ (Eq. 2)

where $C_m$ is the membrane capacitance, and the superscripts $k,l$ run over an $N=L\times L$ lattice of cells. Note that only Ca-sensitive currents such as $I_{Ca}$ and $I_{NCX}$ differ from cell to cell, so that the voltage is dictated by the spatial average of these currents in the tissue. To keep track of the Ca activity in the tissue, we compute the average Ca concentration in the cell interior defined as

$$\begin{array}{l}\overline{c}=\frac{1}{N}\sum _{kl}{c}_{kl},\hfill \end{array}$$ (Eq. 3)

where $c_{kl}$ denotes the Ca concentration $c_i$ in the interior of cell $kl$. To characterize the response of the tissue to pacing, we measure the maximum value of $\overline{c}$, denoted as ${\overline{c}}_{peak}$, during each paced beat. In Fig. 2 A, we plot the ${\overline{c}}_{peak}$ for the last 15 beats, after a tissue of $N=30\times 30$ cells is paced to steady state (100 beats) at a cycle length $T.$ Here, we find that the ${\overline{c}}_{peak}$ undergoes a period-doubling bifurcation at a cycle length of $T_c\sim 375ms$. To analyze the underlying dynamics, we plot $\overline{c}$ and $V\left(t\right)$ for the last 15 beats after pacing at $T=385ms$ and $T=370ms$. As expected, for $T>T_c$ the average Ca in tissue $\left(\overline{c}\right)$ and the AP is periodic from beat to beat (Fig. 2 B). In contrast, for $T<T_c$, both the average Ca and the APD alternate from beat to beat (Fig. 2 C). To understand how the single cell activity generates the spatially averaged alternating signal, we plot the internal Ca concentration ($c_{kl}$) of three cells in the tissue in Fig. 2 Bi–iii and Ci–iii. At the cellular level, we find that cells exhibit a large-small-large release pattern that corresponds with a beat-to-beat alternating pattern of a large Ca release representing a Ca wave, which we will designate as "w," followed by a beat with no Ca wave in the cell interior, which is designated as "n," Thus, each cell exhibits a transient pattern of alternating sequences of the form $\dots nwnw\dots$. However, it is unclear why the Ca transient, averaged over all cells in tissue, alternates below, and not above, the critical pacing rate $T_c$.

Figure 2.

(A) Plot of steady-state average peak Ca ${\overline{c}}_{peak}$ of a $30\times 30$ array of cells as a function of the pacing period $T$. A steady state is achieved after 100 beats and the peak of the Ca transient of the last 15 beats is plotted as a function of $T$. (B) The average voltage and Ca concentration of the array of cells shown for the last 10 beats when the tissue is paced at $T=385ms$. (i–iii) The interior Ca concentration within cells $\left(\mathrm{5,5}\right),\left(\mathrm{10,10}\right)$ and $\left(\mathrm{20,20}\right)$. A large Ca release with $c_i>1\mu M$ is designated as a Ca wave and indicated with a red "w," while a small internal $(c_i<1\mu M)$ release is denoted by a blue "n." (C) Same simulation as (B), but where the array of cells is paced at $T=370ms$. Steady state APD and average Ca alternate with the same phase. APD alternates in a pattern of …LSLS…, where L(S) denotes a long(short) APD.

Ca waves in atrial tissue synchronize via a phase transition

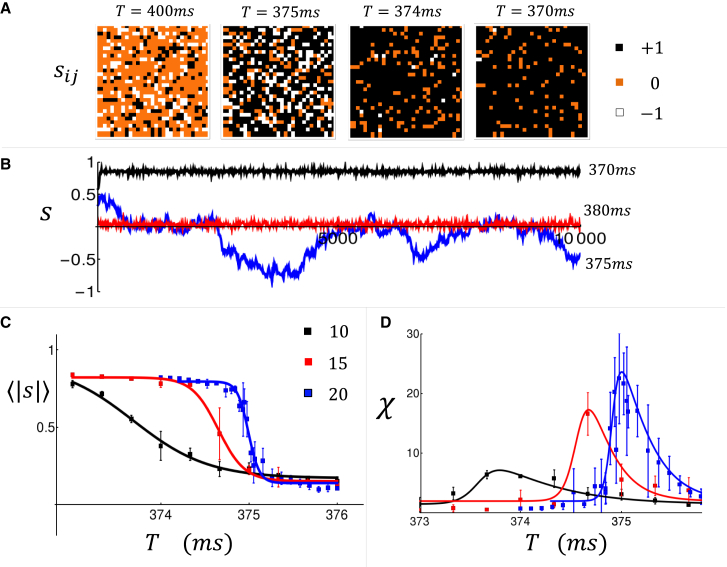
To analyze the nature of the period doubling bifurcation, we introduce an order parameter that captures the degree of synchronization of Ca waves in cardiac tissue. To proceed in this direction, we follow previous studies (25,26) and define a quantity

$$\begin{array}{l}{s}_{ij}\left(n\right)=\left\{\begin{array}{l}+1\text{Δ}{c}_{ij}^p\left(n\right)>\xi \hfill \\ 0\left|\text{Δ}{c}_{ij}^p\left(n\right)\right|\le \xi \hfill \\ -1\text{Δ}{c}_{ij}^p\left(n\right)<-\xi \hfill \end{array}\right\}\hfill \end{array}$$ (Eq. 4)

where

$$\begin{array}{l}\Delta c_{ij}^p\left(n\right)={\left(-1\right)}^n\left(c_{ij}^p\left(n\right)-c_{ij}^p\left(n-1\right)\right),\hfill \end{array}$$ (Eq. 5)

and where $c_{ij}^p\left(n\right)$ is the peak of the interior Ca transient at beat $n$ and cell $ij$. Here, we have introduced a factor ${\left(-1\right)}^n$ to keep track of the phase of the alternating response owing to Ca waves i.e., a sequence $\dots nwnw\dots$ is assigned a value $s_{ij}=+1$, while the opposite phase $\dots wnwn\dots$ is assigned $s_{ij}=-1$. Also, in the absence of Ca waves, the difference in Ca transient from one beat to the next, given by $\left|\text{Δ}{c}_{ij}\left(n\right)\right|$, is small, and we assign a phase of $s_{ij}=0$. In this study, we fix $\xi =0.5\mu M$, although, as we will see later, our key findings are independent of the precise value of this choice of parameter In Fig. 3 A, we show a snapshot of the spatial distribution of $s_{ij}$ when the tissue is paced to steady state at the indicated cycle length ($T$). Here, we find that, above $T_c$, the tissue is dominated by cells that did not exhibit Ca waves so that most cells have phase $s_{ij}=0$ (orange). However, as the cell was paced faster, more cells acquire the phase $s=+1$ (black), indicating that Ca waves are more synchronized from beat to beat. In Fig. 3 B, we plot the beat-to-beat evolution of the average phase at each beat defined as

$$\begin{array}{l}s\left(n\right)=\frac{1}{N}\sum _{ij}{s}_{ij}\left(n\right).\hfill \end{array}$$ (Eq. 6)

Here, we see that $s\left(n\right)\sim 0$ above the transition ($T=380ms$, red line), and $s\left(n\right)\sim 1$ below the transition ($T=370ms$, black line). However, close to the transition ($T=375ms,$ blue line) the average phase exhibits large fluctuations over the 10,000 beats shown. This feature is reminiscent of the phenomenon of critical slowing down, which is known to occur near a continuous phase transition (27). To characterize the dependence of the order parameter on the pacing rate, we have also computed

$$⟨\left|s\right|⟩=\frac{1}{M}\sum _{k=1}^M\left|s\left(k\right)\right|,$$ (Eq. 7)

where the sum is over $M=\mathrm{20,000}$ paced beats. In Fig. 3 C, for system sizes of $L=$ 10, 15, and 20 cells, we plot $⟨\left|s\right|⟩$ vs $T$, which shows a gradual increase in the average phase as the cycle length is decreased. In Fig. 3 D, we plot the susceptibility, defined as $\chi =L^2\left(⟨s^2⟩-{⟨s⟩}^2\right)$, which increases with system size $L$ close to $T_c$. This result indicates that the susceptibility diverges in the thermodynamic limit, which is a hallmark of a phase transition. These numerical results provide evidence that Ca waves in atrial tissue can synchronize above a critical pacing rate $T_c$ via an order-disorder phase transition.

Figure 3.

(A) Snapshot of the order parameter in our tissue of $30\times 30$ cells. Tissue is paced at the indicated cycle lengths, and the order parameter $s_{ij}$ is computed at steady state after 100 paced beats. (B) The average order parameter $s\left(n\right)$ plotted as a function of beat number $n$. (C) The order parameter averaged more than $\mathrm{20,000}$ beats for system sizes $L=\mathrm{10,15}$ and $20$. Error bars are estimated by computing the standard deviation of 4 sets of 5000 beats. (D) The susceptibility $\chi$ as a function of pacing period for the same system sizes.

Coupled map reduction and critical exponents

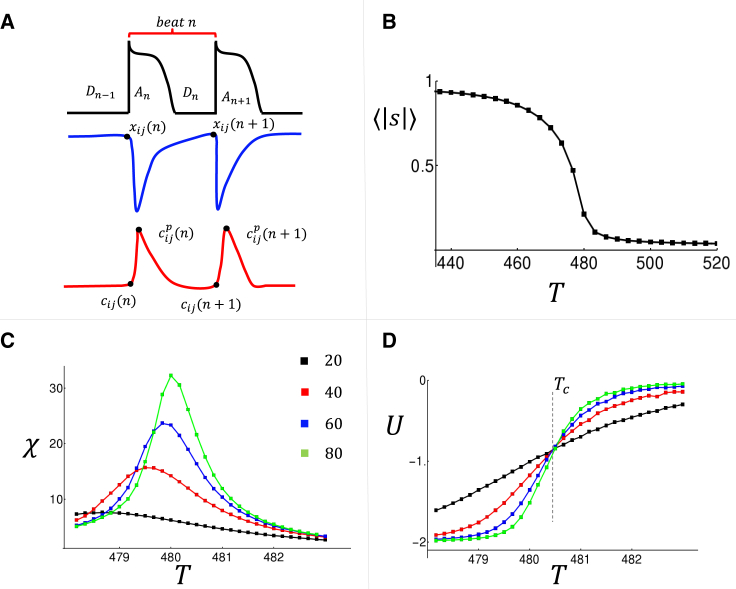
In this section, we develop a coupled map model that captures the beat-to-beat dynamics of Ca waves and voltage. The motivation for this map is two-fold. First, the phenomenological model applied in the previous section is computationally demanding, and therefore it is not suited to analyze dynamics near T_c, which requires averaging over tens of thousands of paced beats. Second, the detailed computational model involves numerous physiological ion currents and Ca fluxes, which makes it difficult to isolate the essential features that underlie the synchronization transition. Thus, we follow our previous work (28) and develop a coupled map model that will yield insight into the mechanism driving the synchronization transition. To proceed, we introduce a new variable $x_{ij}\left(n\right)$ to be the total amount of Ca ions in the SR at cell $ij$, and at the beginning of beat $n$ (see Fig. 4 A). In addition, $c_{ij}\left(n\right)$ represents the total Ca in the cytosol before Ca is released. Here, we will assume for simplicity that total Ca is conserved from beat to beat so $c_{ij}\left(n\right)+x_{ij}\left(n\right)=1$. Also, the voltage dynamics of the tissue is characterized by the APD and the diastolic interval (DI), which are denoted at a given beat $n$ as $A_n$ and $D_n$, respectively. The beat-to-beat evolution of the SR load is given by

$$\begin{array}{l}{x}_{ij}\left(n+1\right)=x_{ij}\left(n\right)-R_{ij}\left(n\right)+U_{ij}\left(n\right),\hfill \end{array}$$ (Eq. 8)

where $R_{ij}\left(n\right)$ is the total Ca released during beat $n$, and $U_{ij}\left(n\right)$ is the total Ca pumped back into the SR. To describe Ca waves, we will describe Ca release into the cell using

$$\begin{array}{l}{R}_{ij}\left(n\right)=r{\eta }_{ij}\left(n\right)x_{ij}\left(n\right),\hfill \end{array}$$ (Eq. 9)

where $r$ is a constant, and where ${\eta }_{ij}\left(n\right)$ is a random variable generated at each beat that satisfies

$$\begin{array}{l}{\eta }_{ij}\left(n\right)=\{\begin{array}{l}1withprobability{P}_{wave}\left(D_{n-1},x_{ij}\left(n\right)\right)\hfill \\ 0withprobability1-P_{wave}\left(D_{n-1},x_{ij}\left(n\right)\right)\hfill \end{array},\hfill \end{array}$$ (Eq. 10)

where $P_{wave}$ denotes the probability that a wave occurs during beat $n$. Here, we have included a dependence on the SR load $x_{ij}\left(n\right)$ and the previous DI $D_{n-1}$. The later dependence is because the DI determines the strength of the L-type Ca current $\left(I_{Ca}\right)$, which triggers Ca release on the next beat. For simplicity, we will consider a functional form

$$P_{wave}=P_V\left(D_{n-1}\right)P_{sr}\left(x_{ij}\left(n\right)\right),$$ (Eq. 11)

where the function $P_{sr}$ describes the SR load dependence and $P_V$ describes the dependence on the membrane voltage. Following our previous work, we model the voltage dependence to have the form $P_V\left(D\right)=1/(1+A\exp (-D/{\tau }_R))$, where ${\tau }_R$ is determined by the time scale of the recovery of $I_{Ca}$, and where $A$ is an adjustable constant that depends on the details of the current kinetics. To model the SR load dependence, we use a sigmoid curve that is motivated by our numerical computation of $P_{wave}$ from the detailed subcellular model (Fig. 1 D). Thus, we use $P_{sr}\left(x_{ij}\right)=1/\left(1+{\left(x^{\ast }/x_{ij}\right)}^{\delta }\right)$ where $\delta$ is the Hill coefficient that controls the strength of the nonlinearity and where $x^{\ast }$ is the threshold SR load. Now, once Ca is released into the cell owing to a wave, the SR Ca²⁺-ATPase pumps Ca back into the SR during one pacing interval $T$. It is well known that the total uptake increases in proportion to the peak of the Ca transient and the period $T$ over which Ca is pumped back into the SR. Thus, we use $U_{ij}\left(n\right)=aT{c}_{ij}^{peak}\left(n\right)$, where $a$ is a proportionality constant and $c_{ij}^{peak}\left(n\right)=c_{ij}\left(n\right)+R_{ij}\left(n\right)$. The last step of our nonlinear map determines how the Ca release couples to the APD on that beat. This is given by $A_n=F_V\left(D_{n-1}\right)+\sigma \overline{R}\left(n\right)$ where

$$\begin{array}{l}\overline{R}\left(n\right)=\frac{1}{N}\sum _{ij}{R}_{ij}\left(n\right),\hfill \end{array}$$ (Eq. 12)

and where $\sigma$ is a constant that determines the sign of the coupling between Ca release and the APD, i.e., whether or not a large Ca release increases $(\sigma >0)$ or decreases $(\sigma <0)$ the APD. Note that this coupling is largely dictated by the NCX current, which provides a depolarizing current in response to Ca release in the cell. In most physiological conditions (29), a large Ca release tends to induce an increase in the APD, so we will take $\sigma >0$.

Figure 4.

(A) The map variables used to describe the beat-to-beat evolution of the $APD$$\left(A_n\right)$, the DI $\left(D_n\right)$, the SR load $x_{ij}\left(n\right)$, and the diastolic Ca $c_{ij}\left(n\right)$. The peak of the internal Ca concentration is denoted as $c_{ij}^p\left(n\right)$. (B) The average order parameter $⟨\left|s\right|⟩$ as a function of pacing rate. (C) The susceptibility $\chi$ computed for the indicated system size $L$. (D) A plot of the Binder cumulant $U$. Intersection point is indicative of a phase transition at $T_c$. All averages are computed using ${10}^8$ beats with a standard error that is smaller than the symbol size.

To analyze the spatiotemporal behavior of this coupled map model, we will introduce an order parameter defined as

$$\begin{array}{l}{s}_{ij}\left(n\right)=\left\{\begin{array}{l}+1\text{Δ}{\eta }_{ij}\left(n\right)>0\hfill \\ 0\left|\text{Δ}{\eta }_{ij}\left(n\right)\right|=0\hfill \\ -1\text{Δ}{\eta }_{ij}\left(n\right)<0\hfill \end{array}\right\}\hfill \end{array}$$ (Eq. 13)

where

$$\begin{array}{l}\text{Δ}{\eta }_{ij}\left(n\right)={\left(-1\right)}^n\left({\eta }_{ij}\left(n\right)-{\eta }_{ij}\left(n-1\right)\right).\hfill \end{array}$$ (Eq. 14)

This choice is more suited for this discrete approach because it keeps track directly of the phase of release events without reference to the Ca transient. In Fig. 4 B, we plot $⟨\left|s\right|⟩$ versus $T$ for a system of size $L=40$, and where the average is computed over ${10}^8$ beats. In Fig. 4 C, we show the susceptibility $\chi =L^2\left(⟨s^2⟩-{⟨s⟩}^2\right)$ for a range of system sizes, which indicates that this quantity diverges near $T_c$ in the thermodynamic limit.

The main advantage of the coupled map is that we can now average over many more beats and thus identify the critical exponents of the phase transition. To proceed, we first assume a finite size scaling ansatz

$$\begin{array}{l}⟨s^k⟩=L^{-\frac{k\beta }{\gamma }}F\left[\left(T-T_c\right)L^{\frac{1}{\nu }}\right],\hfill \end{array}$$ (Eq. 15)

where the critical exponents dictate the system behavior near criticality in the thermodynamic limit $(L\to \infty )$ (27). The scaling ansatz predicts that the Binder cumulant $U=-3+⟨s^4⟩/{⟨s^2⟩}^2$ is independent of system size. In Fig. 4 D, we have computed the Binder cumulant by averaging over ${10}^8$ beats for system sizes $L=20-80$, indicating that there is indeed a clear intersection point at $T_c$. At the critical point, finite size scaling predicts that $⟨\left|s\right|⟩\sim L^{-\beta /\nu }$, $\chi \sim L^{\gamma /\nu }$ and ${\left[\partial U/\partial T\right]}_{T_c}\sim L^{1/\nu },$ where $\beta ,\gamma ,\nu$ are critical exponents that characterize the universality class of the phase transition (30,31). Numerical evaluation of these exponents is straight forward and gives $\beta /\nu =0.487\pm 0.021,\gamma /\nu =1.017\pm 0.022,1/\nu =0.986\pm 0.016,$which describes the phase transition in the thermodynamic limit.

Statistical mechanics analogy and universality

The presence of a phase transition suggests that it will be fruitful to find a mapping to an equivalent statistical mechanics system. A natural starting point is to map the order parameter defined in Eq. (13) to an $L\times L$ lattice of spin-1 particles. In this regard, we point out that the two alternating sequences

$$\begin{array}{l}\dots n,w,n,w,\dots \hfill \end{array}$$ (Eq. 16)

$$\begin{array}{l}\dots w,n,w,n,\dots \hfill \end{array}$$ (Eq. 17)

differ by a shift of one beat so that both responses are dynamically equivalent (28). Thus, a paced cardiac cell possesses an exact Ising symmetry, so that at steady state pacing, the probability of an $L\times L$ spin configuration is the same as that with all the spins reversed. This symmetry was first pointed out by Restrepo and Karma (32), and it has been applied previously to show that Ca alternans within a cardiac cell can occur via an Ising phase transition (26). In cardiac tissue, this symmetry suggests that the probability of a spin configuration is dictated by a Hamiltonian, $H\left[s_{ij}\right]$, which possesses an Ising symmetry, so that $H\left[s_{ij}\right]=H[-s_{ij}]$. To determine how the spins interact, it is necessary to refer to the bidirectional coupling between Ca and voltage that can be determined from the coupled map model. The key couplings at the cellular level are (i) a Ca wave on a given beat will tend to prolong the APD on that beat since $\sigma >0$, and (ii) the prolonged APD will lead to a short DI on that beat, which will decrease the probability of wave propagation on the next beat. This sequence of events ensures that the APD changes can amplify the phase of the subcellular Ca waves, which induce that change. Now, in tissue, the APD is spatially averaged over many cells so that the phase of APD alternans is simply proportional to the average phase $⟨s⟩=(1/N){\sum }_{ij}{s}_{ij}$. These interactions between Ca and voltage in tissue can be described using an effective Hamiltonian

(Eq. 18)

where $ϵ$ is a constant that captures the effective coupling between Ca and voltage. Here, we note that the APD, which is proportional to $⟨s⟩$, will seek to align local spins $s_{ij}$ via the coupling between voltage on Ca. This coupling is governed by the dependence of $I_{Ca}$ on the previous $DI$, so that a longer DI will favor a higher probability of Ca release on the next beat. Thus, energetically, we require that $ϵ\sim \partial P_{wave}/\partial D$, so that the phase of local Ca is driven by the global signal proportional to $⟨s⟩$. Likewise, $ϵ$ is also proportional to the coupling between Ca on voltage, which is governed by the extent to which Ca release, on a given beat, prolongs the APD on that beat. Now, since $\sigma >0$ then an alternating pattern of Ca will drive an alternating pattern of APD with the same phase. Thus, energetically we require that $ϵ\propto \sigma$ to favor spin alignment. Thus, it is the bidirectional coupling between Ca and voltage that dictates the sign of $ϵ$, which in turn determines the nature of the transition. Interestingly, for $ϵ>0$, the Hamiltonian given in Equation 18 corresponds to the Curie-Weiss model (33), which has a well-known ferromagnetic transition at temperature $T_c=2ϵ/3$, in units where the Boltzman constant is taken to be $k=1$. Indeed, this model is exactly solvable, and the critical exponents for this model are in the mean-field universality class where $\beta /\nu =1/2,\gamma /\nu =1,\nu =1$. These exponents are consistent with our coupled map computation, which indicates that the phase transition is in the mean-field universality class.

Synchronization transition leads to the formation of spatially out-of-phase alternans and arrhythmogenesis in heart tissue

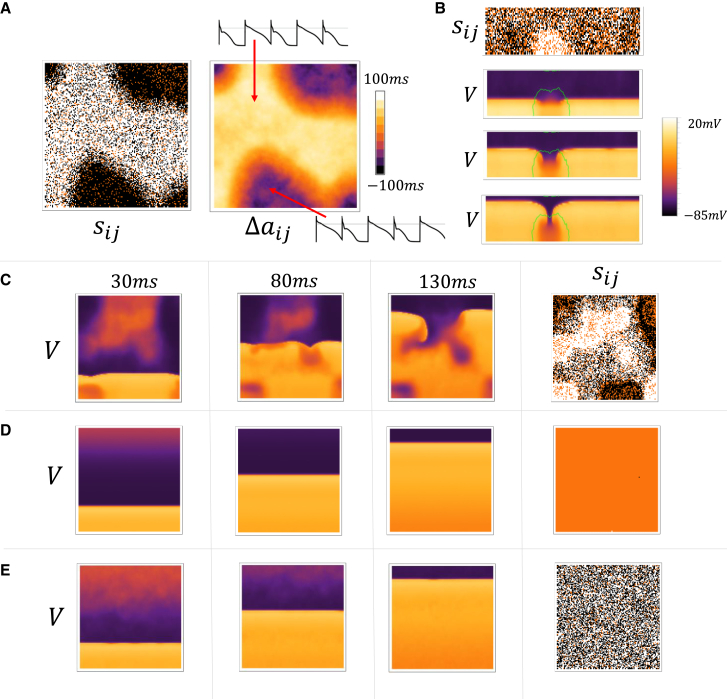
In cardiac tissue with dimension larger than the length scale $l\sim 2-6mm$, the voltage distribution will not be spatially uniform. To explore this regime, we have applied our stochastic model of Ca waves to explore the dynamics of a large 2D tissue composed of $150\times 150$ cells ($\sim 10mm\times 10mm$). To measure the spatial distribution of the phase of the APD we compute

$$\Delta a_{ij}={\left(-1\right)}^n\left(A_{ij}\left(n\right)-A_{ij}\left(n-1\right)\right),$$ (Eq. 19)

where $A_{ij}\left(n\right)$ is the APD at cell $ij$ at beat $n$. Simultaneously, we also measure the spatial organization of Ca waves by computing the order parameter $s_{ij}$ in tissue. In Fig. 5 A, we show $s_{ij}$ and $\text{Δ}{a}_{ij}$ in a cardiac tissue where all the cells are paced simultaneously at $T=360ms$ until a steady state is reached. Our simulations indicate that at steady state the tissue settles into a pattern of spatially out-of-phase APD alternans, where the APD alternates in opposite phase in different regions of tissue (see inset). This pattern is driven by the underlying synchronization of Ca waves where $s_{ij}=+1\left(black\right)$ or $s_{ij}=-1\left(white\right)$ (on average) within the corresponding regions of tissue. The length scale of the observed pattern is determined by voltage diffusion, which smooths the APD over a length scale roughly $l\sim 5mm$. Thus, within this length scale Ca waves are synchronized locally, but can be spatially out-of-phase on longer length scales.

Figure 5.

Spatial distribution of voltage and Ca in large tissue sizes. (A) Snapshot of $s_{ij}$ and $\text{Δ}{a}_{ij}$ on a tissue of $150\times 150$ cells. All cells are paced simultaneously at $T=360ms$ and the snapshots shown are computed using the 99th and 100th beats. Insets show the AP for the last 4 beats at the indicated cells on the array. (B) A $150\times 50$ strip paced at the bottom edge. A snapshot of $s_{ij}$ is computed using the Ca transients at beat 30 and 31. The three images below are voltage snapshots at 2-ms intervals following the 30th paced beat. The green line denotes the APD nodal line where $\text{Δ}{a}_{ij}=0$. (C) Snapshots of the voltage distribution on a $150\times 150$ cell tissue that is paced on a five-cell strip at the bottom edge. The snapshots shown are at the indicated times during the 30th paced beat. The snapshot for $s_{ij}$ is computed using the 31st and 30th beats. (D) Same simulation but Ca waves have been eliminated by increasing the threshold for Ca wave nucleation by increasing the parameter $p_b^{\ast }$ (see Supporting material for a detailed description) from $0.45$ to $0.9.$ The parameter $p_b^{\ast }$ denotes the threshold for Ca sparks, which are triggered at the cell boundary, to nucleate a Ca wave that propagates to the cell interior. (E) Same simulation but where the recovery from inactivation of $I_{Ca}$ has been reduced by a factor of two.

In our tissue simulations, we have also found that an AP wave front is unstable to localized wave break when the system is paced at a period $T$ that is less than $T_c$. In Fig. 5 B, we show a tissue of $150\times 50$ cells that is driven at $T=350ms$ along a five-cell strip at the bottom edge of the tissue. After 30 beats of pacing, we find that a local region in the tissue becomes out-of-phase with the surrounding tissue. This region is demarcated by a nodal line (green curve), where $\text{Δ}{a}_{ij}=0$, which separates the out-of-phase regions. In this case, we find that the 31st excitation front undergoes conduction block within the demarcated region, which occurs because the APD in that region was large owing to the summation of synchronized Ca waves on that beat. Thus, once local synchronization of Ca waves has occurred, then the AP perturbations owing to these waves are dramatically amplified within local regions in tissue. Thus, when cardiac tissue is driven at cycle lengths $T<T_c$, then local synchronization will destabilize the propagation of AP wavefronts. To confirm this insight, in Fig. 5C we plot the spatial distribution of voltage in a large tissue of $150\times 150$ cells. Here, we show snapshots of the voltage distribution at times 30 ms, 80 ms, and 130 ms after the 30th paced beat. Indeed, we find that the spatially out-of-phase APD distribution promotes wave break and leads to the induction of reentrant excitations in the tissue. To confirm that the resulting wave break arises from the underlying Ca waves, in Fig. 5 D, we show snapshots of the same time points, but where the threshold for Ca waves has been increased. In this case, Ca waves do not occur within cells and the AP propagation is indeed spatially uniform. Alternatively, Ca wave synchronization can be eliminated by adjusting model parameters so that the onset of synchronization is shifted to higher rates. A convenient way to do this is to decrease the rate of recovery from inactivation of $I_{Ca}$, which decreases the coupling between voltage and Ca. In Fig. 5 E, we show that when the recovery from inactivation of $I_{Ca}$ is decreased by $50\%$, then AP wave propagation is spatially uniform for many beats, even though cells in tissue readily exhibit Ca waves that are not synchronized in tissue. These results demonstrate that a synchronization transition at $T_c$, which is sensitive to the bidirectional coupling between Ca and voltage, dictates the onset of wave break and reentry in cardiac tissue.

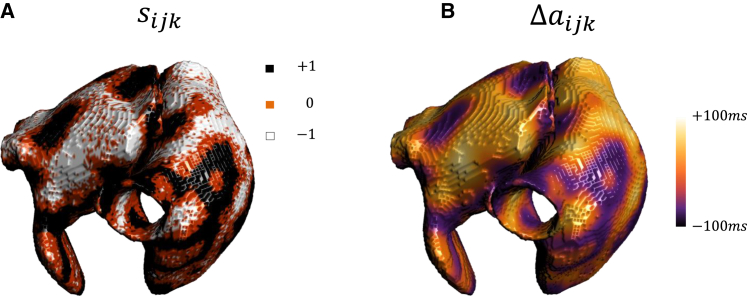
The spatiotemporal properties of spatially out-of-phase Ca waves should be sensitive to the geometry of cardiac tissue. To explore the effect of tissue curvature, and the effect of curved boundary conditions, we have also implemented our phenomenological model of voltage and Ca in an anatomically accurate 3D model of the atria. The model that will be used has been developed previously by Harrild and Henriquez (34), and details of the 3D simulation method used have been presented elsewhere (35,36). In Fig. 6 A and B, we show the distribution of $s_{ijk}$ and $\text{Δ}{a}_{ijk}$ on the surface of the 3D rabbit atria. In this simulation, all cells in the atria are paced simultaneously at $T=380ms$, and $s_{ijk}$ and $\text{Δ}{a}_{ijk}$ are computed using the 15th and 16th beats. When the atria is paced rapidly we have found that, similar to the 2D case, wavebreak and reentry occur in this 3D model. Thus, our simulations suggest that wave break and reentry in 3D is likely dictated by the formation of spatially out-of-phase alternans that occur at pacing rates $T<T_c$. However, it is difficult to identify the sites of wave break in the 3D atria, and a clear association between the synchronization transition and the initiation of reentry will require further investigation.

Figure 6.

Spatiotemporal distribution of Ca waves in an anatomically accurate 3D model of the atria. (A) Distribution of $s_{ijk}$ and (B) $\text{Δ}{a}_{ijk}$ on the surface of the rabbit atria. The atria is paced simultaneously at $T=380ms$ and beat-to-beat differences are computed using the 15th and 16th beats. The global time step was taken to be $25\mu s$, and the spatial discretization size was $0.7mm$. A uniform isotropic diffusion of $7\times {10}^{-4}c{m}^2/ms$ was assumed for the tissue. Simulations were performed using WebGL 2.0 as detailed in Ref. (35). All computations, as well as visualization and post-processing of the results, were carried out simultaneously and interactively on a Radeon RX 5700 XT graphic card.

Discussion

It is now well established that a variety of cardiac arrhythmias have been linked to defects in the Ca cycling machinery. However, it is still not understood how these Ca waves summate to induce dangerous electrical activity in a large population of electrically coupled cells. In particular, since Ca waves occur randomly and are uncoordinated between cells, cells without Ca waves will act as a current sink and decrease the depolarizing effect of those cells which exhibit Ca waves. Thus, voltage depolarization in electrically coupled tissue will be substantially diminished, and it is unclear how Ca waves can induce a tissue scale arrhythmia. In this study, we show that indeed for $T>T_c$ Ca waves are uncoordinated and thus cannot induce AP heterogeneities in tissue. However, for $T<T_c$ Ca waves can synchronize gradually over millions of cells in tissue and induce large beat-to-beat AP perturbations in tissue. We have analyzed the mechanism for this transition in detail to show that it is robust, and it depends only on several known properties of cardiac cells. These are:

• i.A nonlinear sigmoid dependence on the SR load of the probability that a Ca waves occurs on a given beat: The sensitivity of Ca wave propagation on the SR load is well-known, and it has been experimentally measured in cardiac cells (23). This functional relationship is because the nucleation of a Ca wave is highly sensitive to the Ca content in the SR (21,37).
• ii.A dependence of the Ca wave probability on the DI: This coupling arises from the fact that, during an AP, LCCs open and initiate Ca release in the cell. Thus, the probability of Ca wave propagation will increase with the amount of Ca entry owing to $I_{Ca}$. Now, it is well known that $I_{Ca}$ inactivates, and its strength on the next beat depends on recovery from inactivation, which is sensitive to the DI. Thus, the probability that a Ca wave occurs on a given beat will increase with the DI from the previous beat.
• iii.An increase of the APD in response to Ca released during a Ca wave: This coupling is attributed to the NCX, which is an electrogenic pump which produces a depolarizing membrane current in response to a rise in the Ca transient in the cell (38, 39, 40).

The results of this study demonstrate that these three properties of cardiac cells are sufficient to provide a mechanism for Ca waves to synchronize in cardiac tissue. Furthermore, we have mapped our system to the Curie-Weiss model in statistical mechanics, which has been used to describe ferromagnetic spin systems with long-range coupling (33). This mapping indicates that the synchronization transition observed here exhibits universal properties that are common to a wide range of physical system in nature, and can be studied using the framework of equilibrium statistical mechanics. The universal nature of the transition indicates that the driving mechanism is robust and depends only on the underlying Ising symmetry and qualitative features of the coupling between voltage and Ca. In particular, the Ising Hamiltonian given in Equation 18 suggests that it is the sign of the Ca-V coupling that is crucial to the existence of the transition. Thus, even though the synchronization transition is demonstrated using a specific computational model, our analysis suggests that the mechanism for the transition is largely model independent.

In this study, we have demonstrated that the synchronization transition at $T_c$ is highly arrhythmogenic since it provides a mechanism for Ca waves to fire in unison, and thus, substantially perturb the AP in tissue. This result suggests that it may be possible to develop pharmacological interventions that specifically target the onset of Ca wave synchronization. Our work suggests that a potential target to prevent synchronization is the rate of recovery from inactivation of $I_{Ca}$. In particular, decreasing the time scale for recovery should decrease the dependence on the previous DI and, therefore, abolish wave synchronization in tissue. Indeed, we find, in Fig. 5 E, that when the recovery from inactivation of $I_{Ca}$ is decreased, then AP wave propagation is spatially uniform, even though cells in tissue readily exhibit Ca waves. Thus, our finding suggests that shortening the recovery from inactivation of $I_{Ca}$ should prevent Ca wave synchronization, and therefore decrease the likelihood of arrythmias. This approach to target Ca wave synchronization has not been proposed previously and may hold promise as an antiarrhythmic strategy.

In this study, we have shown that when cardiac tissue is paced at $T>T_c$, Ca waves are spatially desynchronized and spatial averaging substantially dampens electrical perturbations. Thus, at these pacing rates, a subcellular defect that makes cells prone to Ca waves is unlikely to induce AP fluctuations that can cause an arrhythmia. In contrast, when subcellular Ca waves are synchronized, they can have a substantial effect on the voltage distribution in tissue. In particular, AP wavefronts propagating in tissue can undergo localized conduction block in regions formed by spatially out-of-phase APD alternans that are induced by Ca wave synchronization. These regions of out-of-phase APD alternans are generated by regions of tissue that synchronize to the opposite phase. We point out here that there is a global Ising symmetry so that a region of tissue, of size smaller than $l$, with average phase $⟨s⟩$, and APD alternans amplitude $a$, is dynamical equivalent to tissue with phase $-⟨s⟩$ and alternans amplitude $-a$. Thus, since regions separated by $d>l\sim 2-6mm$ are independent, then these regions have an equal likelihood of being out-of-phase rather than in-phase. Thus, we expect Ca waves in cardiac tissue to coarsen into regions of spatially out-of-phase regions separated by a length scale $l$. This effect has been previously reported in numerical studies where unstable Ca cycling induces alternans at the cellular scale (41). However, it was not understood that this effect is due to a synchronization transition that occurs only above a critical pacing rate $T_c$. Interestingly, similar complex patterns of out-of-phase Ca and voltage in cardiac cells have been observed experimentally in the rabbit ventricle (42,43). In particular, in the study of Uzelac et al. (43) Langendorff-perfused rabbit hearts were paced at gradually decreasing cycle lengths and spatially discordant patterns of Ca release were detected at cycle lengths in the range 350–140 ms. They found that the complexity of the spatial pattern increased with pacing rate until conduction block and reentry was initiated in the 150–130 ms range. However, further experimental work is needed to confirm that the spatial patterns observed in this study are due to the phase transition identified here. Also, it is not established whether the onset of reentry is directly related to the spatial heterogeneity that is caused by these spatially discordant patterns. Thus, further work is needed to determine if the spatial patterns observed in these rabbit hearts are caused by the phase transition reported here.

Author contributions

D.G., A.K., A.W., F.F., and Y.S. designed research; performed research; contributed analytic tools; analyzed data and wrote the paper.

Editor: Arthur Sherman.