CNN-based Deformable Registration Facilitates Fast and Accurate Air Trapping Measurements at Inspiratory and Expiratory CT

Abstract

Purpose

To develop a convolutional neural network (CNN)–based deformable lung registration algorithm to reduce computation time and assess its potential for lobar air trapping quantification.

Materials and Methods

In this retrospective study, a CNN algorithm was developed to perform deformable registration of lung CT (LungReg) using data on 9118 patients from the COPDGene Study (data collected between 2007 and 2012). Loss function constraints included cross-correlation, displacement field regularization, lobar segmentation overlap, and the Jacobian determinant. LungReg was compared with a standard diffeomorphic registration (SyN) for lobar Dice overlap, percentage voxels with nonpositive Jacobian determinants, and inference runtime using paired t tests. Landmark colocalization error (LCE) across 10 patients was compared using a random effects model. Agreement between LungReg and SyN air trapping measurements was assessed using intraclass correlation coefficient. The ability of LungReg versus SyN emphysema and air trapping measurements to predict Global Initiative for Chronic Obstructive Lung Disease (GOLD) stages was compared using area under the receiver operating characteristic curves.

Results

Average performance of LungReg versus SyN showed lobar Dice overlap score of 0.91–0.97 versus 0.89–0.95, respectively (P < .001); percentage voxels with nonpositive Jacobian determinant of 0.04 versus 0.10, respectively (P < .001); inference run time of 0.99 second (graphics processing unit) and 2.27 seconds (central processing unit) versus 418.46 seconds (central processing unit) (P < .001); and LCE of 7.21 mm versus 6.93 mm (P < .001). LungReg and SyN whole-lung and lobar air trapping measurements achieved excellent agreement (intraclass correlation coefficients > 0.98). LungReg versus SyN area under the receiver operating characteristic curves for predicting GOLD stage were not statistically different (range, 0.88–0.95 vs 0.88–0.95, respectively; P = .31–.95).

Conclusion

CNN-based deformable lung registration is accurate and fully automated, with runtime feasible for clinical lobar air trapping quantification, and has potential to improve diagnosis of small airway diseases.

Keywords: Air Trapping, Convolutional Neural Network, Deformable Registration, Small Airway Disease, CT, Lung, Semisupervised Learning, Unsupervised Learning

Supplemental material is available for this article.

© RSNA, 2021

An earlier incorrect version of this article appeared online. This article was corrected on December 22, 2021.

Summary

Convolutional neural network–based deformable registration is fast, accurate, and fully automated, facilitating clinical quantification of air trapping to improve diagnosis and severity assessment of small airway diseases.

Key Points

• ■ For deformable registration of chest CT, the proposed convolutional neural network (CNN)–based algorithm achieved greater lobar overlap and faster runtime (418 times) than an iterative reference method.

• ■ Incorporation of a Jacobian determinant constraint in a hybrid loss function during CNN training reduced voxel folding and improved colocalization of lung landmarks.

• ■ Application of the CNN-based deformable registration preserved accuracy of air trapping quantification and was similarly predictive of spirometry-based Global Initiative for Chronic Obstructive Lung Disease stage when compared with an iterative reference method.

Introduction

Diseases affecting the small airways—such as chronic obstructive pulmonary disease (COPD) (1), bronchiolitis obliterans related to stem cell transplant or chronic lung allograft dysfunction (2), and cystic fibrosis (3)—can manifest as pulmonary air trapping, which can go undetected at routine inspiratory chest CT. For each of these diseases, chronic inflammation and obstruction of the small airways limit the rate and volume of gas expulsion during expiratory phase, which is typically diagnosed at pulmonary function testing by measuring forced expiratory volume in 1 second (FEV₁) and FEV₁/forced vital capacity (4). Although air trapping may sometimes be observed as mosaic attenuation at expiratory phase CT (5), evidence has shown that diffuse air trapping can be difficult to detect visually (6). In contrast, quantitative measurements with a dedicated inspiratory and expiratory lung CT protocol can facilitate air trapping assessment, which has been shown to prognosticate both disease progression and mortality (1,7,8).

Several methods for quantifying air trapping have been proposed. Early methods approximated air trapping by measuring low attenuation areas (LAAs) on expiratory phase CT images (9), although these measurements can be confounded by areas of emphysema. More recent methods quantify air trapping by registering inspiratory and expiratory phase images using lung deformable registration, thus enabling regional discrimination of areas where gas exchange is impaired by air trapping from areas that are emphysematous (10–14). These iterative deformable registration algorithms incorporate diffeomorphic constraints to enforce transformation invertibility (ie, limit voxel folding) and improve registration accuracy, but they require minutes to hours to perform, thereby increasing computational cost and limiting feasibility for use in routine clinical care.

Recently, deep convolutional neural network (CNN) algorithms have shown promise to perform deformable registration in a variety of organs and modalities (15–21), each with the potential to reduce computational time while preserving accuracy. We therefore sought to develop a CNN-based algorithm to perform deformable lung registration while incorporating several mathematical constraints to ensure applicability for lobar air trapping quantification: (a) lobar segmentations to preserve anatomic boundaries, (b) displacement field regularization to encourage physically realistic transformations, and (c) the Jacobian determinant to limit nonanatomic voxel folding. To assess the effectiveness of the proposed algorithm, we compared it with a standard iterative deformable registration algorithm for (a) anatomic overlap of lobar segmentations, (b) percentage of folding voxels, (c) colocalization of lung landmarks, (d) measurements of air trapping from inspiratory and expiratory CT, and (e) computational runtime.

Materials and Methods

Patient Dataset

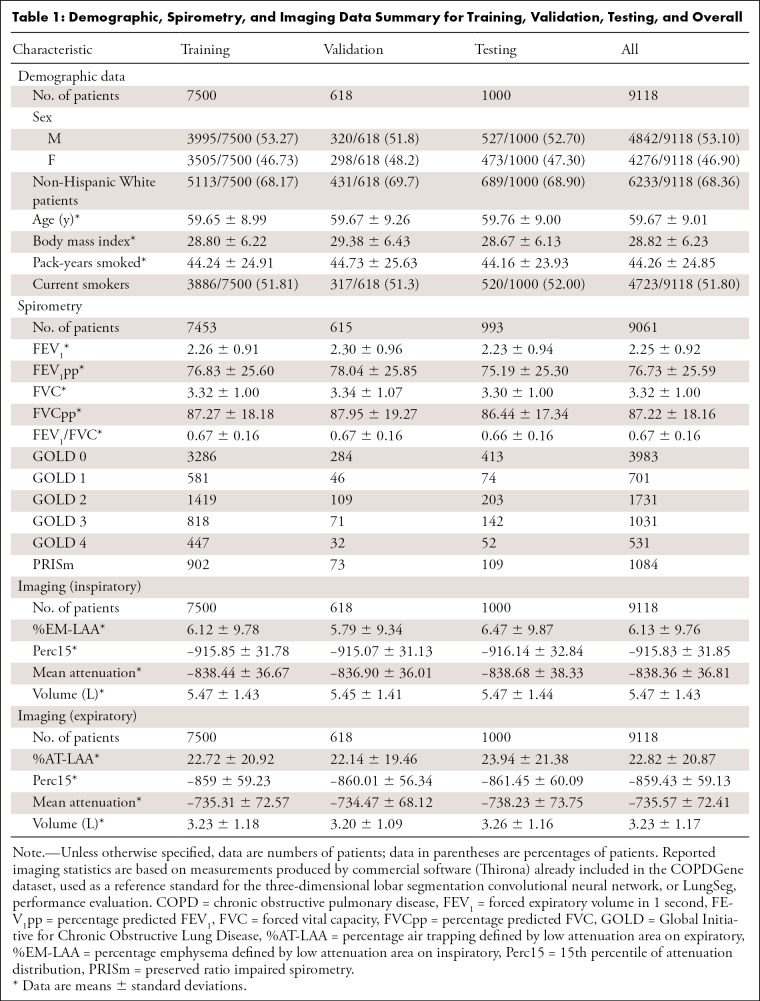
This retrospective Health Insurance Portability and Accountability Act–compliant study was approved by the institutional review boards of the participating institutions, with waived requirement for written informed consent. We included non-contrast CT and spirometric data for 9649 patients; the data were collected between 2007 and 2012 and obtained as part of the COPDGene Study (22). The COPDGene project has resulted in more than 400 publications from other research groups. The analysis presented in this article, which proposes a CNN-based deformable registration algorithm for air trapping quantification, has not been previously performed on the COPDGene dataset. Exclusion criteria were missing inspiratory or expiratory CT (n = 531), resulting in 9118 patients who were included in this study. Demographic data are provided in Table 1.

Table 1:

Demographic, Spirometry, and Imaging Data Summary for Training, Validation, Testing, and Overall

Inspiratory (200 mAs) and expiratory (50 mAs) CT series of the entire thorax were acquired without contrast material with use of multidetector General Electric, Philips, or Siemens scanners, each with at least 16 detector channels. Images were reconstructed using a standard soft-tissue kernel and used submillimeter section thickness (0.625–0.9 mm) and intervals (0.45–0.625 mm), with smooth and edge-enhancing algorithms. Additional details on the COPDGene imaging protocols and parameters are described by Regan et al (22).

The COPDGene dataset also included lung CT measurements computed using commercial software (Thirona, http://www.thirona.eu): mean attenuation (Hounsfield units), lung volume (liters), 15th percentile of attenuation distribution (Hounsfield units), and percentage emphysema defined by LAA on inspiratory (%EM-LAA) (% voxels less than or equal to −950 HU) or percentage air trapping defined by LAA on expiratory (%AT-LAA) (% voxels less than or equal to −856 HU) from inspiratory and expiratory acquisitions for the lungs and each lung lobe (1). To assess localization error of the proposed lung deformable registration, we obtained 10 inspiratory and expiratory CT series pairs publicly available through the Deformable Image Registration (DIR) Laboratory database (24,25). Each series pair contains 300 landmark annotations uniformly distributed across the entirety of both lungs as a reference standard. Thorough detail on the DIR Laboratory landmark selection is included in Castillo and colleagues (24,25).

Spirometric measurements included FEV₁, percent predicted FEV₁, and forced vital capacity following administration of 180 μg of albuterol. Spirometric measurements were used to classify patients according to the Global Initiative for Chronic Obstructive Lung Disease (GOLD) staging system for COPD severity (23).

Demographic, imaging, and spirometric data were de-identified by COPDGene before data transfer, using study ID as the only identifier.

Study Design

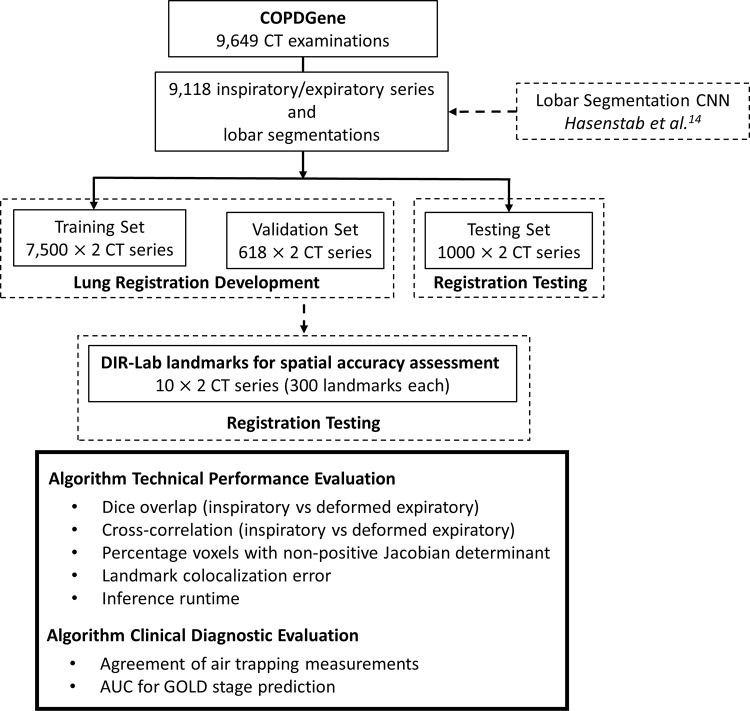
The study design is shown in Figure 1. A previously developed three-dimensional (3D) lobar segmentation CNN (LungSeg) was first applied to the 9118 inspiratory and expiratory series pairs from the COPDGene Study. We then trained our proposed algorithm for performing deformable registration of lung CT (LungReg) to perform expiratory-to-inspiratory registration using the CT images and corresponding lobar segmentations. LungReg was then evaluated across several technical and clinical diagnostic metrics.

Figure 1:

Study design. A previously developed three-dimensional lobar segmentation convolutional neural network (CNN) (LungSeg) was applied to 9118 inspiratory and expiratory series pairs from the COPDGene Study, creating segmentations of the trachea and each lung lobe. We then trained our proposed lung deformable registration algorithm (LungReg) to perform expiratory-to-inspiratory registration using the CT images and corresponding lobar segmentations. LungReg was then evaluated across several technical and clinical diagnostic metrics. AUC = area under the receiver operating characteristic curve, COPD = chronic obstructive pulmonary disease, DIR-Lab = Deformable Image Registration Laboratory, GOLD = Global Initiative for Chronic Obstructive Lung Disease.

Automated Lung CT Measurements

To automate lung CT measurements, we combined LungSeg and LungReg, together referred to as LungQuant (Fig E1 [supplement]). Inspiratory and expiratory series are first propagated through LungSeg for lung lobe segmentation. Expiratory series are then deformably registered to inspiratory series with use of LungReg, after which lobar segmentations are used to extract various lung measurements (Table E2, Table E3, Fig E3 [supplement]), including air trapping, from the inspiratory, expiratory, and deformed expiratory images. Code and model parameters for both LungSeg and LungReg are available online at https://github.com/jtabalon/LungQuant.

LungSeg CNN

Briefly, LungSeg is a previously developed U-Net–inspired CNN designed to segment the lungs, lung lobes, and trachea with use of a single volumetric lung CT scan as input (14). It enables quantification of lung CT measurements, including air trapping, across the lungs and lung lobes. Technical details on LungSeg development and testing are included in Appendix E1 (supplement).

LungReg CNN

Image preprocessing.—Inspiratory and expiratory series and segmentations were standardized feet-first supine and resized to 192 × 192 × 192 resolution with use of cubic spline interpolation. CT voxel attenuations were scaled by a factor of 1/3000. Expiratory whole-lung masks were then affine-registered (translation, rotation, scaling, no shearing) to inspiratory whole-lung masks for initial lung alignment with use of mutual information as an image similarity metric within the Advanced Normalization Tools in Python package (version 0.2.2; Python Software Foundation; https://github.com/ANTsX/ANTsPy). Affine parameters were subsequently applied to the expiratory series.

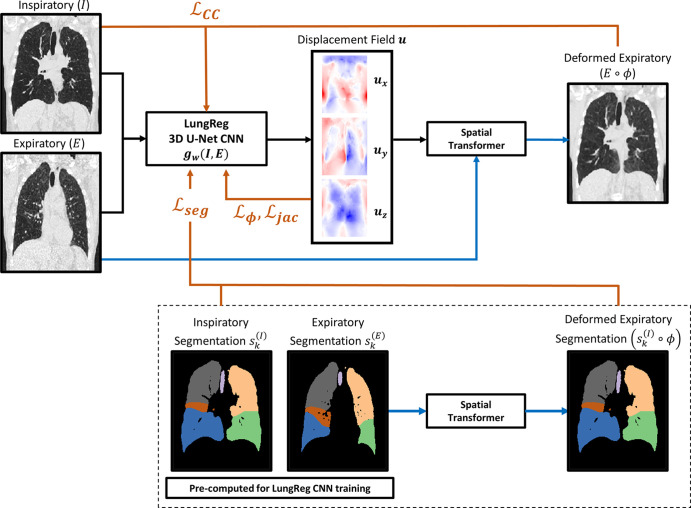
LungReg framework.—The proposed LungReg algorithm (Fig 2) is based on the VoxelMorph deformable registration framework, initially validated for brain registration (15). Inspiratory and affine-registered expiratory images are first propagated through a 3D U-Net CNN (Fig 3), using the input-level fusion mode to predict a spatial transformation function parameterized by a displacement field. The spatial transformation is then applied to the affine-registered expiratory image, via a spatial transformer layer (26), to deformably register the affine-registered expiratory image to the inspiratory image. The U-Net is trained to predict a displacement field that maximizes colocalization of anatomic structures between the inspiratory and deformed expiratory images resulting from the output level. Technical details on LungReg and the U-Net CNN are included in Appendix E2 (supplement).

Figure 2:

Flow diagram of loss functions incorporated into the training of the lung deformable image registration algorithm (LungReg). Inspiratory (I) and affine-registered expiratory (E) images are propagated through a three-dimensional (3D) U-Net convolutional neural network (CNN), g_w(I,E), to predict a displacement field (u). The spatial transformation is then applied to affine-registered expiratory images using a spatial transformer to deformably register expiratory images to inspiratory images. Four loss function components point to the U-Net because they are used to optimize U-Net weights: cross-correlation for image similarity (ℒ_CC), displacement regularization for smooth deformations (ℒ_φ), Dice overlap score for alignment of anatomic structures (ℒ_seg), and percentage of voxels with nonpositive Jacobian determinants (ℒ_jac) to encourage transformation invertibility. Note the segmentations are only used during LungReg training and are not required during inference time. Black lines = forward propagation, blue lines = spatial transformations, orange lines = loss functions, ϕ = spatial transformation function.

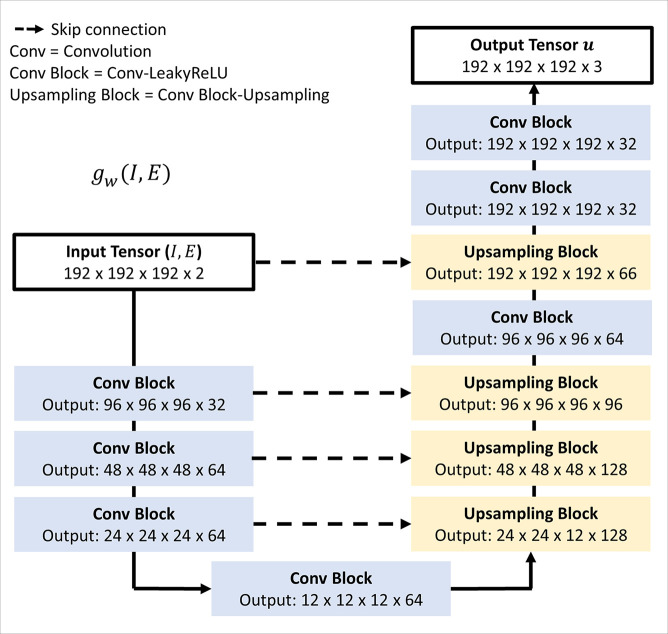
Figure 3:

Three-dimensional (3D) U-Net convolutional neural network, g_w(I,E), used to predict the displacement field defining the deformation. Input comprises a 192 × 192 × 192 × 2 array representing inspiratory (I) and affine-registered expiratory (E) images concatenated along the channel axis. Output is a 192 × 192 × 192 × 3 displacement field. The encoder consists of sequences of 3D convolutions with stride 2 and kernel size 3, each followed by a Leaky rectified linear unit (LeakyReLU) layer with parameter of 0.2. The decoder alternates between convolutions, Leaky rectified linear unit layers, and 3D upsampling.

Loss functions.—We use gradient descent to optimize U-Net weights by minimizing a loss function comprising four components: cross-correlation loss (ℒ_CC), displacement field loss (ℒ_ϕ), Dice loss (ℒ_seg), and Jacobian loss (ℒ_jac).

ℒ_CC encourages local similarity between inspiratory and affine-registered expiratory images while being robust to shifts in attenuation distribution attributed to higher density areas of the lungs typically observed in expiratory phase acquisitions. Smaller ℒ_CC values imply higher cross-correlations between images, which is indicative of stronger image similarity.

We encourage physically realistic transformations by regularizing the smoothness of the displacement field with use of a constraint on the magnitude of spatial gradients within the displacement field.

During LungReg training, we encourage overlap of the trachea and five lung lobes corresponding to the inspiratory and deformed expiratory segmentations by using a Dice loss function. ℒ_seg is calculated as the average Dice value across the six structural segmentations.

We impose an additional displacement field penalty by regularizing its Jacobian determinants to encourage deformations that result in fewer regions of noninvertibility (ie, foldings). ℒ_jac imposes a stronger loss penalty on deformation fields with a large number of nonpositive Jacobian determinants.

The LungReg loss function is a linear combination of the four losses,

L_Reg = ℒ_CC + αℒ_ϕ + βℒ_seg + γℒ_jac,

where α, β, and γ greater than 0 are parameters that control the effect of the respective loss component on the LungReg loss function. Technical details on each loss component are included in Appendix E2 (supplement).

CNN training.—Series pairs and segmentations were randomly partitioned to 7500, 618, and 1000 for training, validation, and testing, respectively. LungReg was then trained using the Adam stochastic optimizer with an initial learning rate of 0.0001 and a batch size of 1 for 20 epochs (150 000 steps) with default random uniform weight initialization. Owing to long training times (approximately 48 hours), we optimized α: α = {0, 0.01, 0.1, 0.5, 1, 2}; β = 0; γ = 0, then β: α = 1; β = {0, 0.01, 0.1, 0.5, 1,2}; γ = 0, then γ: α = 1; β = 0.1; γ = {0, 10⁻⁶, 2 × 10⁻⁶, 10^-3, 10^-1, 1}. We denote the final model with optimal regularization parameters, α = 1; β = 0.1; γ = 2 × 10⁻⁶ as LungReg_α,β,γ. Note that training of LungReg is completely unsupervised when β equals 0 and does not require a ground truth. LungReg when β does not equal 0 is a semisupervised algorithm that requires the ground truth lobar segmentations. Ground truth lobar segmentations are not required during test time, however. The CNN was trained in Python (version 3.6; Python Software Foundation; https://www.python.org) using the TensorFlow graphics processing unit (GPU) (version 2.2.0; https://www.tensorflow.org) deep learning library on a Quadro RTX 8000 graphics card (NVIDIA).

CNN testing.—LungReg_α,β,γ was compared with affine registration as a naive benchmark, an iterative symmetric diffeomorphic registration (SyN) deformable registration algorithm (14,27), and versions of LungReg with alternative loss functions excluding ℒ_seg and ℒ_jac (LungReg_α) or ℒ_jac (LungReg_α,β). With use of the testing set, algorithms were compared using Dice overlap between inspiratory and registered expiratory segmentations, cross-correlation between inspiratory and registered expiratory series, and percentage voxels with nonpositive Jacobian determinant. Spatial accuracy for each algorithm was also assessed using landmark colocalization error (LCE) measured by 3D Euclidean distance in millimeters between inspiratory and deformed expiratory landmarks for the 10 DIR Laboratory reference cases.

Runtime analysis.—Central processing unit (CPU)–based runtimes for affine, SyN, and LungReg inference on the testing set were recorded in seconds. GPU-based runtimes for LungReg inference were also recorded.

Air Trapping Measurements and GOLD Stage Prediction

We computed percentage air trapping–attenuation difference map (%AT-ADM), defined as the percentage of nonemphysematous voxels with attenuation differences less than or equal to 100 HU between the deformed expiratory and inspiratory series (14). Agreement between %AT-ADM measurements computed using LungReg or SyN was assessed. We also compared the ability of LungReg and SyN to predict the spirometrically defined GOLD stages by using %EM-LAA and %AT-ADM as predictors.

Statistical Analysis

Statistical analysis was performed by K.A.H., a biostatistician with 11 years of experience using RStudio (version 3.6.1). Agreement was assessed using the intraclass correlation coefficient. Dice overlap scores, cross-correlations, and percentage nonpositive Jacobian determinants were compared across algorithms by using paired t tests. LCE for each algorithm was compared using a linear mixed effects model to account for correlations between intrapatient observations, with landmarks nested within patients as random effects and a four-level categorical variable representing SyN and each LungReg algorithm as a fixed effect. Bonferroni correction was used to control for familywise error rate. 95% CIs were analytically calculated as appropriate. Statistical significance was assessed using a 5% type I error threshold; any use of the word significance refers to statistical significance. Runtimes were reported descriptively. GOLD stage prediction was performed using logistic regressions and assessed using receiver operating characteristic curve analysis; area under the receiver operating characteristic curve was calculated and compared using bootstrapping.

Results

LungReg Performance

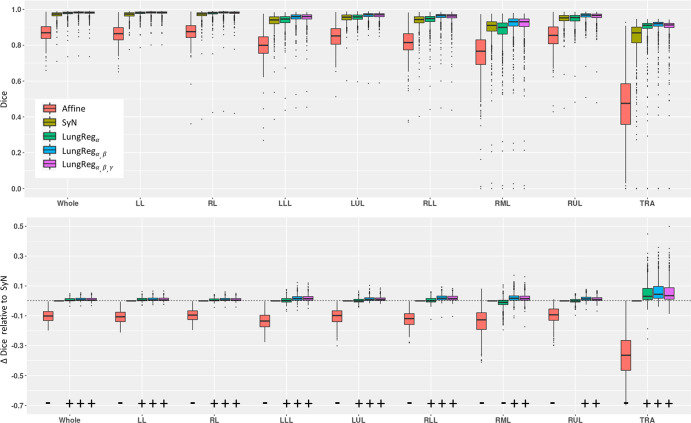
Dice scores and cross-correlations for each algorithm and corresponding paired differences with SyN are shown in Figures 4 and E4 (supplement), respectively. As expected, affine registration consistently produced significantly lower Dice scores and cross-correlations (P < .001) across all algorithms and structures. LungReg algorithms significantly outperformed SyN for all structures, except for the right middle and right upper lobes, where LungReg_α without the use of segmentations during training (and hence without any emphasis on lobar boundaries) produced significantly lower Dice values for the RML (P < .001) and was not significant for the RUL (P = .718). LungReg_α,β and LungReg_α,β,γ with training segmentations showed a significant increase in Dice overlap (P < .001). LungReg cross-correlation was significantly greater than affine and SyN (P < .001), but differences with SyN were unsubstantial in magnitude for the individual lung structures.

Figure 4:

Dice scores across algorithms and anatomic structures (top row) and paired differences with symmetric diffeomorphic registration (iterative) (SyN) (bottom row). α,β,γ correspond to the algorithm for performing deformable registration of lung CT (LungReg) with the cross-correlation loss, segmentation loss, and Jacobian loss, respectively. Significance and direction of paired differences are indicated by (+) and (−). Affine registration shows significantly lower Dice values across all algorithms and structures (P < .001). LungReg algorithms show a significantly larger Dice value than SyN for all structures, except the right middle lobe (RML) and right upper lobe (RUL), where LungReg_α without the use of segmentations during training produced significantly lower Dice values for the RML (P < .001)and was not significantly different for the RUL (P = .718). LungReg_α,β and LungReg_α,β,γ with training segmentations showed a significant increase in Dice overlap score (P < .001). LL = left lung, LLL = left lower lobe, LUL = left upper lobe, RL = right lung, RLL = right lower lobe, TRA = trachea, Whole = both lungs.

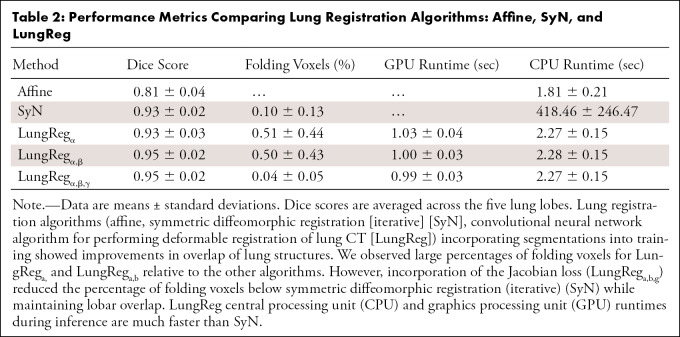
Percentage voxels with nonpositive Jacobian determinants for each algorithm are shown in Table 2. LungReg algorithms without the ℒ_jac showed five times the percentage of nonpositive Jacobian determinants than SyN. However, LungReg_α,β,γ with the ℒ_jac had a significantly lower percentage of these voxels (P < .001) than all other algorithms, including SyN, and with less variability.

Table 2:

Performance Metrics Comparing Lung Registration Algorithms: Affine, SyN, and LungReg

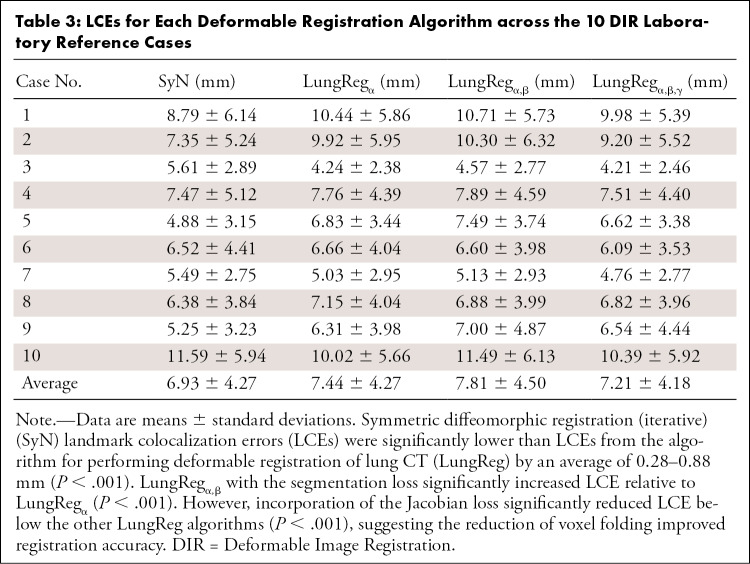
Average LCE for each algorithm (Table 3) was 7.21–7.81 mm for LungReg and 6.93 mm for SyN. SyN had the lowest LCE across all algorithms (P < .001), but LungReg_α,β,γ with the ℒ_jac had the lowest LCE of the CNN-based algorithms (P < .001).

Table 3:

LCEs for Each Deformable Registration Algorithm across the 10 DIR Laboratory Reference Cases

Runtime Analysis

On CPU, affine runtime (Table 2) was significantly faster than the deformable registration algorithms (P < .001). LungReg runtimes were magnitudes faster (418 times) than SyN (P < .001), with considerably less runtime variability. LungReg implementation on GPU reduced runtime by half, requiring only an average of approximately 1 second for inference.

Case Example

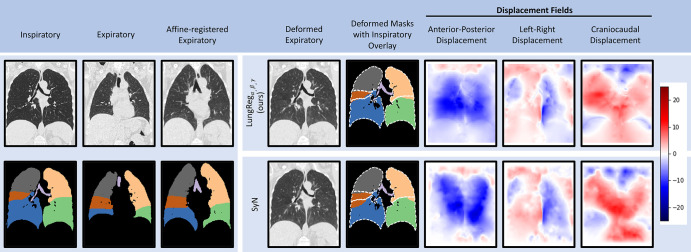
A case example applying LungReg_α,β,γ versus SyN to a test set participant (61-year-old White woman) is shown in Figure 5. Incorporation of masks into LungReg_α,β,γ training improves overlap of lung structures, especially for the right middle lobe (Dice overlap score, 0.93 [LungReg] vs 0.87 [SyN]). Visual assessment of displacement fields suggests similar anatomic transformations between algorithms, but with greater emphasis on the lung boundaries.

Figure 5:

Case example comparing deformed images, segmentations, and displacement fields for the algorithm for performing deformable registration of lung CT (LungReg_α,β,γ) and symmetric diffeomorphic registration (iterative) (SyN). Dashed white lines are overlaid inspiratory segmentations. Positive displacements (red) are posterior-to-anterior, left-to-right, and inferior-to-superior. Deformed expiratory images appear similar across LungReg_α,β,γ and SyN. However, overlap of lung structures improves, especially for the right middle lobe. Displacement fields suggest similar anatomic transformations between algorithms, but with greater emphasis on the lung boundaries, as evidenced by the lung outline presence visible in each LungReg_α,β,γ field.

Air Trapping Measurements and GOLD Stage Prediction

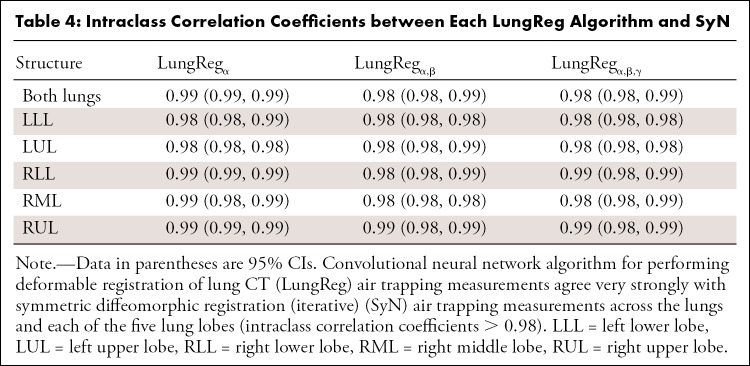
Intraclass correlation coefficients (Table 4) indicate strong agreement (range, 0.98–0.99) between LungReg and SyN air trapping measurements for each lung structure. Air trapping measurements appear robust to the inclusion of the segmentation and ℒ_jac functions. For GOLD stage prediction (Fig 6), LungReg areas under the receiver operating characteristic curves were not significantly different from SyN areas under the receiver operating characteristic curves (P = .31–.95) for predicting GOLD stages, which suggests that LungReg can replace SyN to enable fast air trapping quantification.

Table 4:

Intraclass Correlation Coefficients between Each LungReg Algorithm and SyN

Figure 6:

Receiver operating characteristic curves and area under the receiver operating characteristic curves (AUCs) for each lung deformable registration algorithm for predicting Global Initiative for Chronic Obstructive Lung Disease (GOLD) stages with use of percentage emphysema low attenuation area, or %EM-LAA, and percentage air trapping–attenuation difference map, or %AT-ADM, as predictors. Algorithms showed near-identical performance for each respective GOLD stage. Areas under the receiver operating characteristic curves for the algorithm for performing deformable registration of lung CT (LungReg) were not significantly different from those for symmetric diffeomorphic registration (iterative) (SyN), which suggests that LungReg air trapping measurements could supplant SyN air trapping measurements.

Discussion

In this study, we illustrate the capability of CNNs to perform deformable registration across the inspiratory and expiratory phases of the respiratory cycle, comprehensively evaluating the specific CNN's performance across multiple technical end points and assessing its ultimate application to quantification of lobar air trapping. We observed that a hybrid loss function incorporating lobar segmentation overlap and the Jacobian determinant each improved algorithm performance. This approach achieved its primary goal, reducing inference runtime from as much as approximately 15 minutes to approximately 2.25 seconds on CPU and to approximately 1 second on GPU, without loss of accuracy. The final model, LungReg_α,β,γ, achieved greater overlap of lung structures and comparable spatial accuracy to the iterative SyN algorithm while generating displacement fields with fewer regions of nonanatomic noninvertibility (folding voxels). Further, when we applied LungReg_α,β,γ to CT scans from phase 1 of the COPDGene Study, we observed similar ability to predict spirometric GOLD stage, which requires voxel-wise registration of inspiratory and expiratory phase images.

The accuracy of our proposed algorithm is partially attributed to the incorporation of the lobar segmentation loss in the hybrid loss function. The addition of a segmentation loss encourages lobar overlap during training, thereby improving colocalization of lung structures at the lobar boundaries. As a result, we observed improved lobar overlap, particularly for the right middle lobe. This is particularly important for computing regional lung characteristics, such as air trapping, at the lobar level. Prior studies have also highlighted the advantages of segmentation-constrained learning to perform inspiratory and expiratory deformable registration (28–30). Eppenhof and colleagues (28,29) used whole-lung segmentations to focus CNN training on voxels within the lungs, but this approach did not ensure the overlap of substructures such as the lung lobes. In a manner similar to that of our study, Hering et al (30) incorporated lobar segmentations during training but observed a smaller Dice overlap of 92% (compared with 95% Dice overlap in our study), possibly owing to their smaller training sample size of 500 images. Rather than use segmentation-constrained learning, Hu et al (31) used landmark-constrained learning to reduce LCE but also observed a smaller Dice overlap of 93%, possibly due to the placement of landmarks, which were not located near the lobar boundaries.

Because the lung lobes span large territories, deformations within the lobes can be relatively unconstrained and subject to areas of voxel folding (ie, areas of physically unrealistic and noninvertible transformations measured by the percentage of nonpositive Jacobian determinants) (15). To enforce transformation invertibility (ie, to reduce voxel folding), some CNN deformable registration algorithms explicitly restrict transformations to be diffeomorphic (21,31,32). In contrast, we applied an alternative strategy, incorporating the Jacobian determinant as an additional loss component, which improved LCE while maintaining lobar overlap and reduced folding voxels to 0.04%, which outperformed the SyN algorithm. Overall, we found LungReg performance, measured according to Dice overlap (0.95), voxel folding (0.04%), LCE (7.21 mm), and runtime (approximately 1 second), to be comparable to that of other methods described in the literature, which reported Dice overlap of 92%–93% (30,31), voxel folding of 0.02%–2.1% (30,33), LCE of 1.39–7.98 mm (33), and runtime of 0.2–2 seconds (31,33). In our study, we expanded on these prior works, recognizing the need to address multiple end points for deformable registration and confirming the utility of CNN-based deformable registration to quantify air trapping and stratify patients from the COPDGene Study.

Our study had several potential limitations. Due to long training times, we optimized LungReg hyperparameters successively, and we did not thoroughly explore alternative CNN architectures for segmentation and registration. Future studies should focus on efficient joint hyperparameter optimization and additional architectures to further improve performance in the context of lung measurements. In addition, segmentation overlap following deformable registration was calculated using lobar segmentations inferred by a previously developed lung segmentation CNN rather than manually hand-drawn 3D segmentations. Manual 3D segmentation of 1000 series pairs would not be feasible, and we felt that the trade-off of the high volume of test data outweighed the potential benefits of a ground truth defined by manual segmentation. We also note that the test data included data solely from the COPDGene Study, which used a standardized imaging protocol and may not reflect the variability of scans collected using clinical imaging acquisition protocols. However, this multi-institutional study comprised 21 participating institutions and, in our opinion, adequately spans the interinstitutional variability of inspiratory-expiratory CT scans. It is important to note, however, that this study sample primarily includes outpatient examinations of patients who do not have pneumonia or other acute pathologic processes that may potentially complicate lung segmentation or registration algorithms. Future work may be required to ensure quality of segmentation and registration in other populations and disease processes.

In conclusion, we showed that our CNN-based deformable lung registration algorithm accurately quantifies air trapping measurements in a broad sample of patients with a wide range of pulmonary air trapping, reduces inference runtime, improves lobar overlap, and reduces voxel folding. Fast, fully automated CNN-based lung deformable registration algorithms can facilitate translation of these measurements into clinical practice, potentially improving the diagnosis and severity assessment of small airway diseases.