The Temporal Correlation Between Positive Testing and Death in Italy: From the First Phase to the Later Evolution of the COVID-19 Pandemic

Abstract

Background and aim:

After the global spread of the coronavirus disease 2019 (COVID-19), research has concentrated its efforts on several aspects of the epidemiological burden of pandemic. In this frame, the presented study follows a previous analysis of the temporal link between cases and deaths during the first epidemic wave (Phase 1) in Italy (March-June 2020).

Methods:

We here analyze the COVID-19 epidemic in the time span from March 2020 to June 2021.

Results:

The elaboration of the curves of cases and deaths allows identifying the temporal shift between the positive testing and the fatal event, which corresponds to one week from W2 to W33, two weeks from W34 to W41, and three weeks from W42 to W67. Based on this finding, we calculate the Weekly Lethality Rate (WLR). The WLR was grossly overestimated (~13.5%) in Phase 1, while a mean value of 2.6% was observed in most of Phase 2 (starting from October 2020), with a drop to 1.4% in the last investigated weeks.

Conclusions:

Overall, these findings offer an interesting insight into the magnitude and time evolution of the lethality burden attributable to COVID-19 during the entire pandemic period in Italy. In particular, the analysis highlighted the impact of the effectiveness of public health and social measures, of changes in disease management, and of preventive strategies over time. (www.actabiomedica.it)

Appendix Supplementary files

Introduction

The Coronavirus Disease 2019 (COVID-19) pandemic that started in China in the last months of 2019 is causing a global health emergency, the solution of which seems yet far to be achieved despite the enormous efforts made to mitigate its spread, and the development of therapeutic and effective preventive strategies (1-3). Currently, the official number of cases (i.e., infected subjects) is approaching 200 million with nearly four million deaths (4,5). The pandemic has non-uniformly affected almost all continents and countries (4), often with a fast and intricate evolution resulting from the combination of many factors, namely (a) the use of personal protective equipment, (b) restrictions to the people mobility applied by public authorities that were periodically released in a difficult attempt to prevent or limit the infections without destroying local economies, (c) the seasonality of viral respiratory diseases, (d) the progressive appearance of SARS-CoV-2 variants endowed with increased infection rates, and (e) the recent implementation of vaccination campaigns (2,3,6,7).

In this scenario, the gathering of information on the burden of the disease is of utmost importance for better understanding the origin and evolution of the pandemic spreading, as well as the effectiveness of public health interventions (3). By analyzing the evolution of the pandemic outbreak in Italy, the center of the first main outbreak among Western countries, we have recently examined the temporal correlation between the positive COVID-19 testing and deaths in the first phase, i.e., the period March-June 2020 (8,9). In particular, we found, on average, a one-week delay between the positive test and the fatal event. Despite the straightforwardness of the approach and the heterogeneity of the available data, we exploited this finding to propose a lethality measure denoted as Weekly Lethality Rate (WLR), which is based on the ratio between the number of deaths occurring in a certain week and the number of positive tests detected in the previous weeks (8).

In order to further investigate the lethality impact of the infection in Italy, we have extended this analysis to the entire pandemic, by monitoring the temporal link between positive testing and death from the summer 2020 to June 2021. As for the initial phase, we quantified the temporal correlation between these events, and found a progressively increasing time gap. On this basis, we conceived an approach to generalize the WLR. The implications of these findings on the evolution of the Italian outbreak will be discussed, considering the impact and effectiveness of political interventions, changes in disease management, and preventive strategies.

Materials and Methods

Study Design and Data Source

We performed a longitudinal retrospective analysis on the time-trend of the lethality due to COVID-19 in Italy through the data from the freely accessible national integrated surveillance system (10). More specifically, we gathered the daily number of diagnostic tests, confirmed cases, and deceased related to SARS-CoV-2 (Table S1). We traced data over 67 weeks (denoted as W₁, W₂, . . ., W₆₇) covering the period from March 2^nd, 2020 to June 13^th, 2021 (Table S2).

Table S1.

Daily cases, deaths, and tests in the time interval March 2^nd, 2020 - June 13^th, 2021 collected from the Reports of the Italian National Institute of Health (ISS)

Date	Daily cases	Daily deaths	Daily tests
02-Mar	335	11	2218
03-Mar	466	27	2511
04-Mar	587	28	3981
05-Mar	769	41	2525
06-Mar	778	49	3997
07-Mar	1247	36	5703
08-Mar	1492	133	7875
09-Mar	1797	97	3889
10-Mar	1577	168	6935
11-Mar	1713	196	12393
12-Mar	2651	189	12857
13-Mar	2547	250	11477
14-Mar	3497	175	11682
15-Mar	3590	368	15729
16-Mar	3385	349	13063
17-Mar	3374	345	10695
18-Mar	4207	475	16884
19-Mar	5322	427	17236
20-Mar	5986	627	24109
21-Mar	6557	793	26336
22-Mar	5560	651	25180
23-Mar	4790	601	17066
24-Mar	5249	743	21496
25-Mar	5210	683	27481
26-Mar	6153	712	36615
27-Mar	5909	919	33019
28-Mar	5974	889	35447
29-Mar	5217	756	24504
30-Mar	4050	812	23329
31-Mar	4053	837	29609
01-Apr	4782	727	34455
02-Apr	4668	760	39809
03-Apr	4585	766	38617
04-Apr	4805	681	37375
05-Apr	4316	525	34237
06-Apr	3599	636	30271
07-Apr	3039	604	33713
08-Apr	3836	542	51680
09-Apr	4204	610	46244
10-Apr	3951	570	53495
11-Apr	4694	619	56609
12-Apr	4092	431	46720
13-Apr	3153	566	36717
14-Apr	2972	602	26779
15-Apr	2667	578	43715
16-Apr	3786	525	60999
17-Apr	3493	575	65705
18-Apr	3491	482	61725
19-Apr	3047	433	50708
20-Apr	2256	454	41483
21-Apr	2729	570	52126
22-Apr	3370	401	63101
23-Apr	2646	464	66658
24-Apr	3021	420	62447
25-Apr	2357	415	65387
26-Apr	2324	260	49916
27-Apr	1739	333	32003
28-Apr	2019	382	57272
29-Apr	2086	323	63827
30-Apr	1872	285	68456
01-May	1965	269	74208
02-May	1900	474	55412
03-May	1389	174	44935
04-May	1221	195	37631
05-May	1075	236	55263
06-May	1444	369	64263
07-May	1401	274	70359
08-May	1327	243	63775
09-May	1083	194	69171
10-May	802	165	51678
11-May	744	179	40740
12-May	1402	172	67003
13-May	888	195	61973
14-May	992	262	71876
15-May	789	242	68176
16-May	875	153	69179
17-May	675	145	60101
18-May	451	99	36406
19-May	813	162	63158
20-May	665	161	67195
21-May	642	156	71679
22-May	652	130	75380
23-May	669	119	72410
24-May	531	50	55824
25-May	300	92	35241
26-May	397	78	57674
27-May	584	117	67324
28-May	593	70	75893
29-May	516	87	72135
30-May	416	111	69342
31-May	333	75	54118
01-Jun	200	60	31394
02-Jun	319	55	52159
03-Jun	322	71	37299
04-Jun	177	88	49953
05-Jun	519	85	65028
06-Jun	270	72	72485
07-Jun	197	53	49478
08-Jun	280	65	27112
09-Jun	283	79	55003
10-Jun	202	71	62699
11-Jun	380	53	62472
12-Jun	163	56	70620
13-Jun	347	78	49750
14-Jun	337	44	56527
15-Jun	301	26	28107
16-Jun	210	34	46882
17-Jun	329	43	77701
18-Jun	332	66	58154
19-Jun	251	47	57541
20-Jun	264	49	54722
21-Jun	224	24	40545
22-Jun	221	23	28972
23-Jun	113	18	40485
24-Jun	190	30	53266
25-Jun	296	34	56061
26-Jun	255	30	52768
27-Jun	175	8	61351
28-Jun	174	22	37346
29-Jun	126	6	27218
30-Jun	142	23	48273
01-Jul	182	21	55366
02-Jul	201	30	53243
03-Jul	223	15	50096
04-Jul	235	21	52011
05-Jul	192	7	37462
06-Jul	208	8	22166
07-Jul	137	30	43219
08-Jul	193	15	50443
09-Jul	214	12	52552
10-Jul	276	12	47953
11-Jul	188	7	45931
12-Jul	234	9	38259
13-Jul	169	13	23933
14-Jul	114	17	41867
15-Jul	162	13	48449
16-Jul	230	20	50432
17-Jul	231	11	50767
18-Jul	249	14	48265
19-Jul	218	3	35525
20-Jul	190	13	24253
21-Jul	128	15	43110
22-Jul	280	9	49318
23-Jul	306	10	60311
24-Jul	252	5	53334
25-Jul	273	5	51671
26-Jul	252	5	40526
27-Jul	170	5	25551
28-Jul	181	11	48170
29-Jul	289	6	56018
30-Jul	382	3	61858
31-Jul	379	9	60944
01-Aug	295	5	60383
02-Aug	238	8	43269
03-Aug	159	12	24036
04-Aug	190	5	43788
05-Aug	384	10	56451
06-Aug	401	6	58673
07-Aug	552	3	59196
08-Aug	347	13	53298
09-Aug	463	2	37637
10-Aug	259	4	26432
11-Aug	412	6	40642
12-Aug	476	10	52658
13-Aug	522	6	51188
14-Aug	574	3	46723
15-Aug	627	4	53123
16-Aug	479	4	36807
17-Aug	320	4	30666
18-Aug	401	5	53976
19-Aug	642	7	71095
20-Aug	840	6	77442
21-Aug	947	9	71996
22-Aug	1071	3	77674
23-Aug	1209	7	67371
24-Aug	952	4	45914
25-Aug	876	4	72341
26-Aug	1365	13	93529
27-Aug	1409	5	94024
28-Aug	1462	9	97065
29-Aug	1444	1	99108
30-Aug	1365	4	81723
31-Aug	999	6	58518
01-Sep	984	8	81050
02-Sep	1332	6	102959
03-Sep	1402	10	92790
04-Sep	1738	11	113085
05-Sep	1700	16	107658
06-Sep	1303	7	76856
07-Sep	1107	12	52553
08-Sep	1366	10	92403
09-Sep	1434	14	95990
10-Sep	1597	10	94186
11-Sep	1616	10	98880
12-Sep	1499	6	92706
13-Sep	1458	7	72143
14-Sep	1008	14	45309
15-Sep	1229	9	80517
16-Sep	1450	12	100607
17-Sep	1585	13	101773
18-Sep	1906	10	99839
19-Sep	1638	24	103223
20-Sep	1587	15	83428
21-Sep	1349	17	55862
22-Sep	1392	14	87303
23-Sep	1640	20	103696
24-Sep	1786	23	108019
25-Sep	1912	20	107269
26-Sep	1869	17	104387
27-Sep	1766	17	87714
28-Sep	1493	16	51109
29-Sep	1647	24	90185
30-Sep	1851	19	105236
01-Oct	2548	24	118236
02-Oct	2498	23	120301
03-Oct	2844	27	118932
04-Oct	2578	18	92714
05-Oct	2257	16	60241
06-Oct	2676	28	99742
07-Oct	3678	31	125314
08-Oct	4458	22	128098
09-Oct	5372	28	129471
10-Oct	5724	29	133084
11-Oct	5456	26	104658
12-Oct	4616	39	85442
13-Oct	5901	41	112544
14-Oct	7331	43	152196
15-Oct	8803	83	162932
16-Oct	10010	55	150377
17-Oct	10925	47	165837
18-Oct	11704	69	146541
19-Oct	9335	73	98862
20-Oct	10874	89	144737
21-Oct	15198	127	177848
22-Oct	16079	136	170392
23-Oct	19139	91	182032
24-Oct	19644	151	177669
25-Oct	21268	128	161880
26-Oct	17007	141	124686
27-Oct	21991	221	174398
28-Oct	24989	205	198952
29-Oct	26826	217	201452
30-Oct	31082	199	215085
31-Oct	31756	297	215886
01-Nov	29907	208	183457
02-Nov	22250	233	135731
03-Nov	28242	353	182287
04-Nov	30547	352	211831
05-Nov	34498	428	219884
06-Nov	37807	446	234245
07-Nov	39809	425	231673
08-Nov	32614	331	191144
09-Nov	25263	356	147725
10-Nov	35098	580	217758
11-Nov	32960	623	225640
12-Nov	37978	636	234672
13-Nov	40896	550	254908
14-Nov	37253	544	227695
15-Nov	33977	546	195275
16-Nov	27354	504	152663
17-Nov	32188	731	208458
18-Nov	34283	753	234834
19-Nov	36173	653	250186
20-Nov	37239	699	238077
21-Nov	34767	692	237225
22-Nov	28334	562	188747
23-Nov	22925	630	148945
24-Nov	23231	853	188659
25-Nov	25851	722	230007
26-Nov	28993	822	232711
27-Nov	28344	827	222803
28-Nov	26321	686	225940
29-Nov	20647	541	130524
30-Nov	16374	672	130524
01-Dec	19350	785	182100
02-Dec	20703	684	207143
03-Dec	23236	993	220047
04-Dec	24099	814	212741
05-Dec	21052	662	194984
06-Dec	18846	564	163550
07-Dec	13612	528	111217
08-Dec	14733	634	149232
09-Dec	12652	499	118475
10-Dec	16887	887	171586
11-Dec	18550	761	190416
12-Dec	19738	649	196439
13-Dec	17818	484	152697
14-Dec	11965	491	103584
15-Dec	14714	846	164431
16-Dec	17431	680	199489
17-Dec	18136	683	185320
18-Dec	17989	674	179800
19-Dec	16306	553	176185
20-Dec	15104	352	137420
21-Dec	10860	415	87889
22-Dec	13294	628	157705
23-Dec	14521	553	183864
24-Dec	18040	505	193777
25-Dec	19037	459	152334
26-Dec	10429	261	81564
27-Dec	8909	305	59879
28-Dec	8583	445	68681
29-Dec	11212	659	128740
30-Dec	16202	575	169045
31-Dec	23476	555	186004
01-Jan	22205	462	157524
02-Jan	11831	364	67174
03-Jan	14243	347	102974
04-Jan	10797	348	77993
05-Jan	15373	649	135106
06-Jan	20331	548	121275
07-Jan	18016	414	140267
08-Jan	17531	620	172119
09-Jan	19976	483	139758
10-Jan	18625	361	139758
11-Jan	12532	448	91656
12-Jan	14241	616	141641
13-Jan	15771	507	175429
14-Jan	17244	522	160585
15-Jan	16146	477	273506
16-Jan	16309	475	261404
17-Jan	12545	377	211078
18-Jan	8824	377	158674
19-Jan	10494	603	254070
20-Jan	13548	524	279762
21-Jan	14078	521	267567
22-Jan	13633	472	264728
23-Jan	13330	488	286331
24-Jan	11627	299	216211
25-Jan	8552	420	126931
26-Jan	10580	541	256287
27-Jan	15192	467	293770
28-Jan	14361	492	275579
29-Jan	13572	477	268750
30-Jan	12712	421	298010
31-Jan	11252	237	213364
01-Feb	7916	329	142419
02-Feb	9653	499	244429
03-Feb	13186	476	279307
04-Feb	13654	421	270142
05-Feb	14215	377	270507
06-Feb	13441	385	282407
07-Feb	11640	270	206789
08-Feb	7952	307	144270
09-Feb	10621	422	274263
10-Feb	12947	336	310994
11-Feb	15131	391	292533
12-Feb	13899	316	287619
13-Feb	13524	311	290534
14-Feb	11061	221	205642
15-Feb	7333	258	179278
16-Feb	10378	336	274019
17-Feb	12067	369	294411
18-Feb	13753	347	288458
19-Feb	15462	348	297128
20-Feb	14929	251	306078
21-Feb	13439	232	250986
22-Feb	9615	274	170672
23-Feb	13292	356	303850
24-Feb	16409	318	340247
25-Feb	19875	308	353704
26-Feb	20485	253	325404
27-Feb	18901	280	323047
28-Feb	17447	192	257024
01-Mar	13094	246	170633
02-Mar	17039	343	335983
03-Mar	20864	347	358884
04-Mar	22839	339	339635
05-Mar	24028	297	378463
06-Mar	23600	307	355024
07-Mar	20745	207	271336
08-Mar	13878	318	184684
09-Mar	19615	376	345972
10-Mar	22385	332	361040
11-Mar	25639	373	372217
12-Mar	26793	380	369636
13-Mar	26051	317	372944
14-Mar	21300	264	273966
15-Mar	15247	354	179015
16-Mar	20377	502	369375
17-Mar	23025	431	369084
18-Mar	24907	423	353737
19-Mar	25816	386	364822
20-Mar	23718	401	354480
21-Mar	20149	300	277086
22-Mar	13820	386	169196
23-Mar	18744	551	335189
24-Mar	21239	460	363767
25-Mar	23798	460	349472
26-Mar	23982	457	354982
27-Mar	23839	380	357154
28-Mar	19611	297	272630
29-Mar	12954	417	156692
30-Mar	16000	529	301451
31-Mar	22439	467	351221
01-Apr	23634	501	356085
02-Apr	21918	481	331154
03-Apr	21253	376	359214
04-Apr	18025	326	250933
05-Apr	10676	296	102795
06-Apr	7745	421	112962
07-Apr	13696	627	339939
08-Apr	17207	487	362162
09-Apr	18922	718	349003
10-Apr	17558	344	334862
11-Apr	15737	331	253100
12-Apr	9781	358	190635
13-Apr	13439	476	304990
14-Apr	16157	469	334766
15-Apr	16954	380	319633
16-Apr	15937	429	327704
17-Apr	15364	310	331734
18-Apr	12693	251	230116
19-Apr	8859	317	146728
20-Apr	12066	392	294045
21-Apr	13658	365	350034
22-Apr	16229	361	364804
23-Apr	14758	344	315700
24-Apr	13816	324	320780
25-Apr	13154	218	239482
26-Apr	8438	303	145819
27-Apr	10401	374	302734
28-Apr	13379	345	336336
29-Apr	14319	289	330075
30-Apr	13445	264	338771
01-May	12962	226	378202
02-May	9146	144	156872
03-May	5945	256	121829
04-May	9110	305	315506
05-May	10576	267	327169
06-May	11802	258	324640
07-May	10552	207	328612
08-May	10173	224	338436
09-May	8289	139	226006
10-May	5077	198	130000
11-May	6942	251	286428
12-May	7849	262	306744
13-May	8080	201	287026
14-May	7560	182	298186
15-May	6654	136	294686
16-May	5752	93	202573
17-May	3452	140	118924
18-May	4446	201	262864
19-May	5501	149	287256
20-May	5738	164	251037
21-May	5215	133	269744
22-May	4715	125	286603
23-May	3994	72	179391
24-May	2486	110	107481
25-May	3222	166	252646
26-May	3933	121	260962
27-May	4146	171	243967
28-May	3738	126	249911
29-May	3350	83	247330
30-May	2947	44	164495
31-May	1820	82	86977
01-Jun	2482	93	221818
02-Jun	2892	62	226272
03-Jun	1967	59	97633
04-Jun	2555	73	220939
05-Jun	2436	57	238632
06-Jun	2272	51	149958
07-Jun	1271	65	84567
08-Jun	1895	102	220917
09-Jun	2198	77	218738
10-Jun	2070	88	188120
11-Jun	1900	69	217610
12-Jun	1723	52	212966
13-Jun	1390	26	134136

Table S2.

Week definition with starting and ending date

Week	Starting Date	Ending Date
W1	02/03/2020	08/03/2020
W2	09/03/2020	15/03/2020
W3	16/03/2020	22/03/2020
W4	23/03/2020	29/03/2020
W5	30/03/2020	05/04/2020
W6	06/04/2020	12/04/2020
W7	13/04/2020	19/04/2020
W8	20/04/2020	26/04/2020
W9	27/04/2020	03/05/2020
W10	04/05/2020	10/05/2020
W11	11/05/2020	17/05/2020
W12	18/05/2020	24/05/2020
W13	25/05/2020	31/05/2020
W14	01/06/2020	07/06/2020
W15	08/06/2020	14/06/2020
W16	15/06/2020	21/06/2020
W17	22/06/2020	28/06/2020
W18	29/06/2020	05/07/2020
W19	06/07/2020	12/07/2020
W20	13/07/2020	19/07/2020
W21	20/07/2020	26/07/2020
W22	27/07/2020	02/08/2020
W23	03/08/2020	09/08/2020
W24	10/08/2020	16/08/2020
W25	17/08/2020	23/08/2020
W26	24/08/2020	30/08/2020
W27	31/08/2020	06/09/2020
W28	07/09/2020	13/09/2020
W29	14/09/2020	20/09/2020
W30	21/09/2020	27/09/2020
W31	28/09/2020	04/10/2020
W32	05/10/2020	11/10/2020
W33	12/10/2020	18/10/2020
W34	19/10/2020	25/10/2020
W35	26/10/2020	01/11/2020
W36	02/11/2020	08/11/2020
W37	09/11/2020	15/11/2020
W38	16/11/2020	22/11/2020
W39	23/11/2020	29/11/2020
W40	30/11/2020	06/12/2020
W41	07/12/2020	13/12/2020
W42	14/12/2020	20/12/2020
W43	21/12/2020	27/12/2020
W44	28/12/2020	03/01/2021
W45	04/01/2021	10/01/2021
W46	11/01/2021	17/01/2021
W47	18/01/2021	24/01/2021
W48	25/01/2021	31/01/2021
W49	01/02/2021	07/02/2021
W50	08/02/2021	14/02/2021
W51	15/02/2021	21/02/2021
W52	22/02/2021	28/02/2021
W53	01/03/2021	07/03/2021
W54	08/03/2021	14/03/2021
W55	15/03/2021	21/03/2021
W56	22/03/2021	28/03/2021
W57	29/03/2021	04/04/2021
W58	05/04/2021	11/04/2021
W59	12/04/2021	18/04/2021
W60	19/04/2021	25/04/2021
W61	26/04/2021	02/05/2021
W62	03/05/2021	09/05/2021
W63	10/05/2021	16/05/2021
W64	17/05/2021	23/05/2021
W65	24/05/2021	30/05/2021
W66	31/05/2021	06/06/2021
W67	07/06/2021	13/06/2021

Statistical Analysis

Numbers of cases, deaths, and tests were grouped in a week-based manner (Table S3). The average daily values (also denoted as weekly-averaged values) of cases and deaths were obtained by dividing the total weekly number by seven.

Table S3.

Cases and deaths per week of Phase 1 (blue, W₁-W₁₇) and Phase 2 (green, W₃₂-W₆₇). Average daily values were obtained dividing the total weekly number of cases/deaths by seven

Week	Average number of cases	Average number of deaths
W1	811	46
W2	2482	206
W3	4913	524
W4	5500	758
W5	4466	730
W6	3916	573
W7	3230	537
W8	2672	426
W9	1853	320
W10	1193	239
W11	909	193
W12	632	125
W13	448	90
W14	286	69
W15	285	64
W16	273	41
W17	203	24
W18	186	18
W19	207	13
W20	196	13
W21	240	9
W22	276	7
W23	357	7
W24	478	5
W25	776	6
W26	1268	6
W27	1351	9
W28	1440	10
W29	1486	14
W30	1673	18
W31	2208	22
W32	4232	26
W33	8470	54
W34	15934	114
W35	26223	213
W36	32252	367
W37	34775	548
W38	32905	656
W39	25187	726
W40	20523	739
W41	16284	635
W42	15949	611
W43	13584	447
W44	15393	487
W45	17236	489
W46	14970	489
W47	12219	469
W48	12317	436
W49	11958	394
W50	12162	329
W51	12480	306
W52	16575	283
W53	20316	298
W54	22237	337
W55	21891	400
W56	20719	427
W57	19460	442
W58	14506	461
W59	14332	382
W60	13220	332
W61	11727	278
W62	9492	237
W63	6845	189
W64	4723	141
W65	3403	117
W66	2346	68
W67	1778	68

Following our previous study of the time evolution of COVID-19 lethality during the first wave (8,9), our analysis included:

1. Identification of the different phases of the epidemic. On the basis of the inspection of the cases and deaths curves, we conventionally set the end of the first phase on June 28^th, 2020, latest day of week 17 (W₁₇); hence, the first phase (also referred to as Phase 1) lasted 17 weeks (119 days). Similarly, the beginning of the second phase (Phase 2) was set on October 5^th, 2020, first day of W₃₂; thus, the second phase has lasted 36 weeks so far (252 days).

2. Dissection of the data and analytical modeling of the detected cases/deaths: we first described the lockdown-driven fall of Phase 1 and the initial rise of Phase 2 with a decreasing exponential and a sigmoidal function, respectively. Exponential and sigmoidal functions with calibrated parameters were then used for the falls and rises of all other curves.

3. The temporal shift of the cases/deaths curves was obtained by examining the derived functions. In addition, we performed a sensitivity analysis relying on the sum of squared residuals (SSR) in order to evaluate the quality of the fitting between the aforementioned curves upon specific shifts.

4. Depending on the detected shift at different phases/subphases of the pandemic, the WLR values were calculated by dividing the average daily number of deaths of a given week (W_i) by the average daily number of cases of one week (W_i-1), two weeks (W_i-2), or three weeks (W_i-3) before. In detail, the WLR values were computed applying a 1-week, 2-week, and 3-week shift between positive test and death in the time intervals W₁-W₃₃, W₃₄-W₄₁, and W₄₂-W₆₇, respectively.

In order to detect the temporal link between positive testing to the virus and death (as done for Phase 1 (8)), we partitioned Phase 2 into three distinct subphases, referred to as 2.1, 2.2, and 2.3, defined on the basis of the peaks detected in the cases/deaths curves on Nov 13^th/Dec 3^rd, 2020, Jan 6^th/8^th, 2021, and Mar 12^th/Apr 9^th, 2021 (Figures 1 and S1), respectively.

Figure 1.

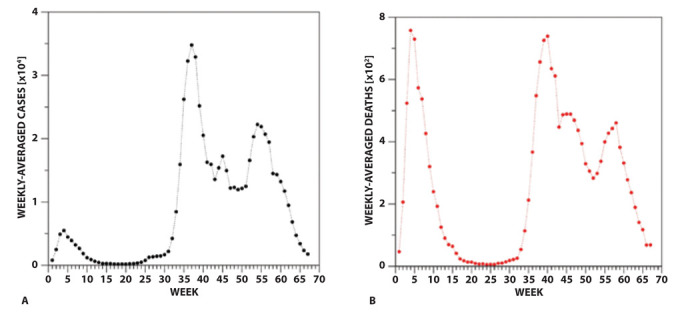
Evolution of the weekly-averaged (A) cases (positive tests) and (B) deaths. Weeks have been numbered according to Table S2.

Figure S1.

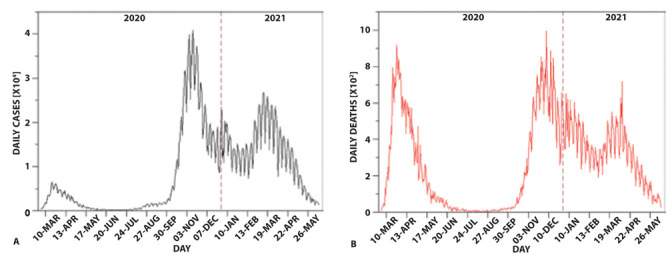
Daily evolutions of (A) cases (positive tests) and (B) deaths in the time interval March 2^nd, 2020 - June 13^th, 2021.

In our post-hoc sensitivity analysis, the application of the temporal 1-week shift scheme – successfully applied to analyze Phase 1 (8) (Figure 2A) – produced a very poor fitting between the cases and deaths curves of Phase 2 (Figure 2B). Better fittings were obtained by applying shifts of two or three weeks to the curve of the cases (Figure 2C and 2D). A closer inspection of the fitting clearly indicates that a unique week shift scheme cannot account for the complexity of Phase 2.

Figure 2.

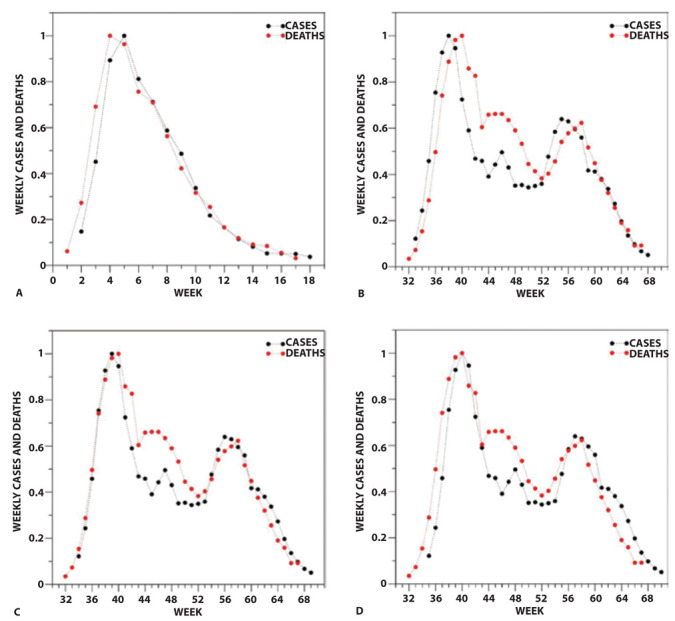
Comparison of the evolution of the weekly cases (black) and deaths (red) upon normalization of the curves in (A) Phase 1 (W₁-W₁₇) and (B-D) Phase 2 (W₃₂-W₆₇) of the pandemic. The normalization was performed by dividing the actual values by the maximum of each ensemble. The curve of cases is 1-week (A, B), 2-week (C), 3-week (D) shifted ahead.

The analytical modeling of the weekly-averaged cases/deaths in Phase 2 was performed as follows. As a first step:

• - the lockdown-driven fall of the deaths of Phase 1 was favorably described with a decreasing exponential (Figure S3) 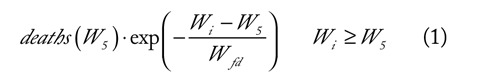the time constant W_fd of which was calibrated to 3.8 weeks to obtain the best agreement between (1) and the real data.

• - the initial deaths rise of Subphase 2.1 was described with the sigmoidal function (Figure S3) 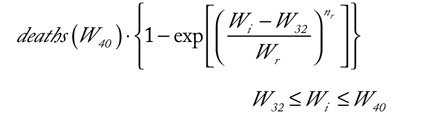where the time constant W_r and power factor n_r were adjusted to 4.1 weeks and 2.5, respectively (Figure S3); deaths(W₄₀) represents the peak value of this subphase.

  Subsequently, exponential and sigmoidal functions with the same values for W_fd, W_r, and n_r were adopted also to model the deaths falls of Subphases 2.1, 2.2, 2.3, as well as the rises of Subphases 2.2 and 2.3, respectively (Figure 3A). As an example, the fall of Subphase 2.1 was described with 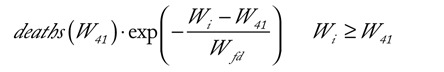and the rise of Subphase 2.2 with 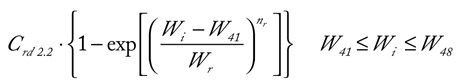C_rd2.2 being a fitting parameter tuned to ensure the best matching between the overall model and real data (Figure 3B).

  A similar strategy was used to model the evolution of the weekly-averaged cases. First, it was noted that the rise of Subphase 2.1 was accurately described by the same sigmoidal function (and same parameters) exploited for the deaths (Figure 4A), i.e., 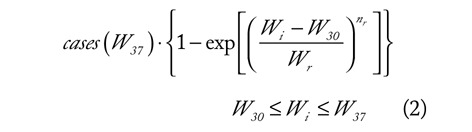cases(W₃₇) being the peak reached during this subphase. Equation (2) was also used to model the rises of cases of Subphases 2.2 and 2.3 (Figure 4A); as an example, 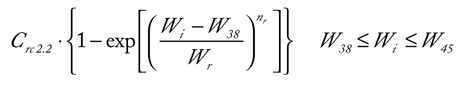was employed for Subphase 2.2, C_rc2.2 being a fitting parameter.

  A reasonably faster time constant W_fc=3.2 weeks was adopted in the decreasing exponentials used to describe the falls of cases in Subphases 2.1, 2.2, and 2.3 (Figure 4A); as far as Subphase 2.1 is concerned, the exponential function is

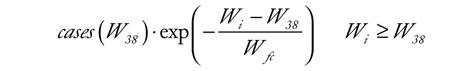
Figure S3.

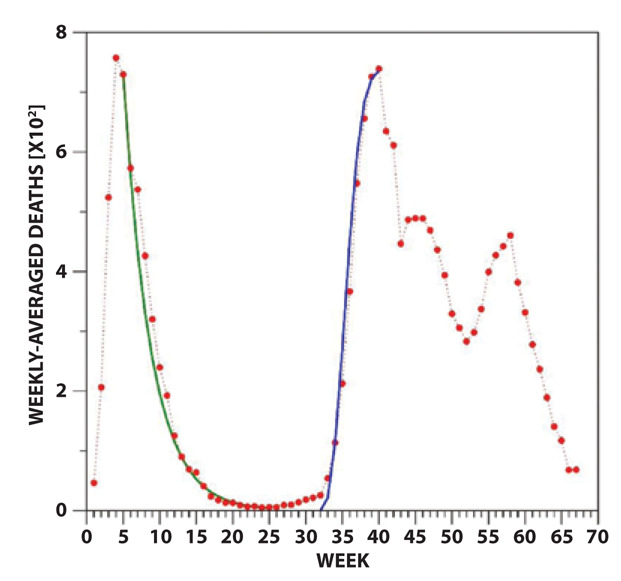
Modeling of the lockdown-driven fall of Phase 1 and the rise of Subphase 2.1 of the curve of deaths with a decreasing exponential (time constant 3.8) and a sigmoidal (exponent 2.5 and time constant 4.1) function, respectively.

Figure 3.

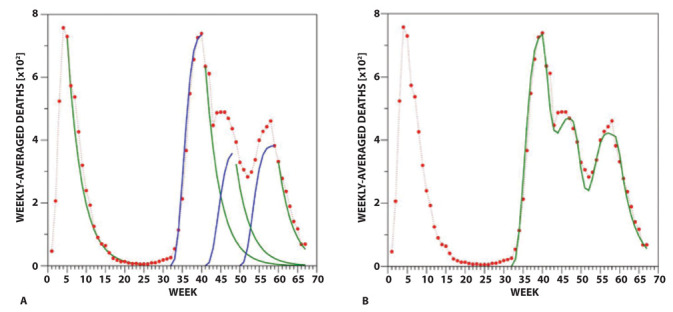
(A) Modeling of the three subphases of the curve of deaths of Phase 2 with mathematical functions. For the rises, sigmoidal functions making use of exponent 2.5 and time constant 4.1 were exploited. The time constant 3.8 calibrated for the fall of deaths occurring in Phase 1 was also employed for the falls of the three subphases of Phase 2. (B) Model (sum of the 3 modeled subphases) of Phase 2 superimposed to the real data.

Figure 4.

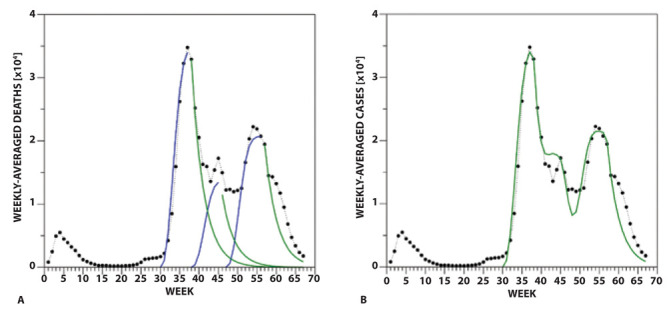
(A) Modeling of the three subphases of Phase 2 of the curve of cases with mathematical functions. For the rises, sigmoidal functions making use of exponent 2.5 and time constant 4.1 were exploited. The time constant 3.2 was employed for the falls of the three Phase 2 subphases. (B) Model (sum of the 3 modeled subphases) superimposed to the real data.

The deconvolution of the deaths/cases curves also provides a measure of the temporal shift between the positive testing and the fatal event. A comparison of the equations used to fit the experimental data indicates that the rise of the deaths in Subphase 2.1 is shifted two weeks ahead with respect to the corresponding testing: weeks W₃₂ and W₃₀ are indeed used to identify the rise onsets of deaths and cases, respectively. On the other hand, for the subsequent subphases the equations suggest a 3-week shift; as far as Subphase 2.2 is concerned, weeks W₃₈ and W₄₁ are adopted for cases and deaths. These results are in line with those obtained through a comparative analysis performed by shifting the normalized curve of daily cases with respect to the deaths counterpart and calculating the SSR between them; this approach was also exploited to examine Phase 1 in (8).

Based on the variable shifts between the curves of deaths/cases detected throughout the pandemic, we adapted the definition of the WLR previously introduced (8) by alternatively considering a 1-week, a 2-week, or a 3-week shift. A regression analysis was performed on the WLR values in the weeks W₅₀-W₆₇ to quantify its decrease. 95% confidence intervals (95% CI) were computed according to a Poisson approximation. The significance level (0.05) of the decrease was assessed by calculating the p-value. Data were analyzed with MATLAB R2014b and R statistical software v. 4.0.0 (11,12).

The study did not involve participants and information were gathered from freely accessible public databases, and data were analyzed in aggregated form and without any identifier. Therefore, no ethical approval was required for this research. The analyses adhere to the Guidelines for Accurate and Transparent Health Estimates Reporting (GATHER) (13).

Results

Comparative analysis of the evolution of cases and deaths

The inspection of the daily deaths/cases curves (Figures 1 and S1) clearly indicates that the country suffered from two main outbreaks (here denoted as Phase 1 and Phase 2). The first started at the end of February 2020 and ended in the summer of the same year. Moreover, starting from the fall 2020 a second remarkable increase of both cases and deaths was experienced. Although this second phase is progressively regressing, it is still ongoing (June 2021). Notably, the maxima of the deaths curve are pretty similar in the two phases while the maximum of the cases is significantly higher in the second phase compared to the first one.

As previously explained, the application of the temporal 1-week shift scheme that was successfully exploited to analyze Phase 1 (8) (Figure 2A) produced a very poor fitting of the curves of Phase 2 (Figure 2B). Better fittings are obtained by using shifts of two or three weeks to the curve of the cases (Figure 2C and 2D). A closer inspection of the fitting clearly indicates that a unique shift scheme cannot account for the complexity of Phase 2. This observation is not surprising considering the remarkable time span of Phase 2 (~9 months). A similar conclusion is reached when the SSR between the normalized daily cases/deaths is calculated upon the systematic shifts of the curve of the cases of Phase 2. As shown in Figure S2, the SSR values present a marked weekly periodicity due to the daily dependence of testing and death registrations. Interestingly, two nearly identical global minima corresponding to shifts of either 13 or 20 days are evident. In this scenario, considering the complexity of Phase 2, we deconvolute the global cases/deaths curves by identifying the underlying curves corresponding to the three subphases (2.1, 2.2., and 2.3) (Figure 3A and Figure 4A). This was done by noticing that the ascending parts of the curves can be described by sigmoidal increases whereas the descending regions are characterized by exponential decreases (see Methods for details). In this framework, the main parameter for the exponential function was derived from the fitting of deaths of the descendent region of Phase 1.

Figure S2.

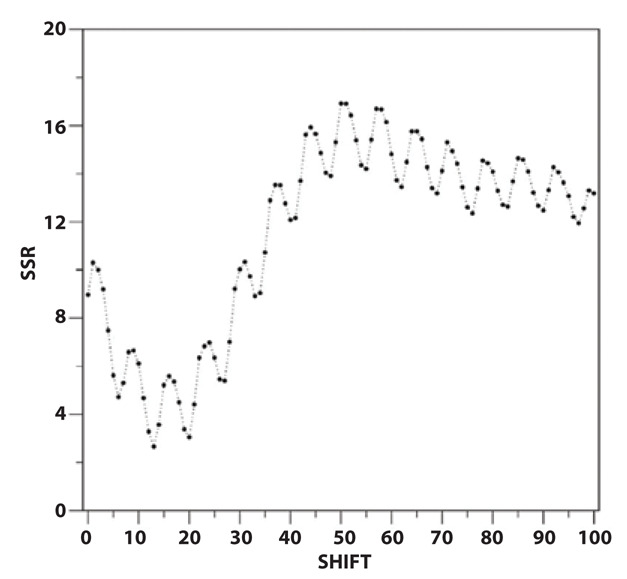
Sum of squared residuals (SSR) as a function of day shift of the curves in Phase 2 (W₃₂-W₆₇). The normalized curve of the daily cases is shifted ahead with respect to the normalized curve of the daily deaths.

The superposition of the deconvoluted curves (Figure 3B and Figure 4B) shows a remarkable agreement with the real cases/deaths. The only significant discrepancies are observed in the time interval W₄₂-W₄₅ that corresponds to mid-December – mid-January when, due to the holiday season, the recording of cases and deaths was occasionally postponed. Such a deconvolution also provides a measure of the temporal shift between the positive testing and the fatal event. An inspection of the equations used to fit the experimental data indicates that the rise of the deaths in Subphase 2.1 is shifted by two weeks from the corresponding positive testing; in the fitting curve, the parameter W₃₂ or W₃₀ is indeed present for deaths and cases, respectively. On the other hand, for the subsequent weeks the equations suggest a 3-week shift since the parameter in the equations is either W₄₁ (deaths) or W₃₈ (cases). These observations are confirmed by the indications provided by the SSR analysis described above.

Weekly Lethality Rate

Based on the variable shifts between the curves of deaths/cases detected throughout Phase 2, we adapted the definition of the WLR previously introduced (8) by alternatively considering a single week (from W₂ to W₃₃) shift, a 2-week shift (from W₃₄ to W₄₁), or a 3-week (from W₄₂ to W₆₇) shift. As shown in Figure 5 and Table S4, we observed significant changes of this parameter in the different stages of the pandemic. In particular, the value of WLR was grossly overestimated (~13.5%) in Phase 1 (8). This is likely due to the severe underestimation of the cases at that time. A WLR value of about 2.6% was observed in most of Phase 2. Interestingly, a slow but significant reduction of this parameter has taken place in the last weeks (W₅₀-W₆₇; February 8^th – June 13^th, 2021). In particular, at W₆₇ the WLR assumes a value (1.4%) that is almost halved when compared to the nearly constant one detected in the period W₃₄-W₄₉.

Figure 5.

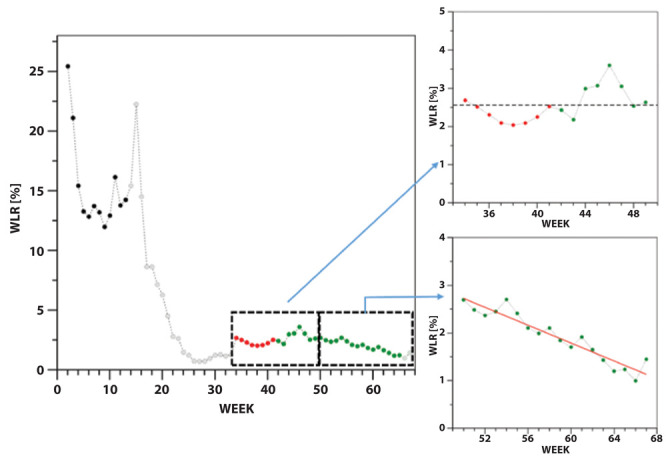
Weekly lethality rate (WLR) evolution in the overall pandemic. The WLR values were calculated applying a 1-week (black and grey), 2-week (red), and 3-week (green) shift between positive test and death in the time intervals W₂-W₃₃, W₃₄-W₄₁, and W₄₂-W₆₇, respectively. Values computed for the weeks (W₁₄-W₃₃, W₆₆-W₆₇) with less than 70 weekly-averaged deaths are in light grey. The average WLR value (2.56%) detected in the time interval W₃₄-W₄₉ is shown as a dashed line. The linear regression analysis of the WLR values in the weeks W₅₀-W₆₇ provides a correlation coefficient R=-0.95 (p-value<10^-5). The regression line (y = 7.4091 - 0.093675 x) is shown in red.

Table S4.

Weekly lethality rate (WLR) values with 95% confidence intervals (95%CI). The WLR values were calculated applying a 1-week, 2-week, and 3-week shift between positive test and death in the time intervals W₁-W₃₃, W₃₄-W₄₁, and W₄₂-W₆₇, respectively. WLR values were calculated by dividing the average daily number of deaths of a given week (W_i) by the average daily number of cases of one week (W_i-1), two weeks (W_i-2), or three weeks (W_i-3) before

Week	WLR 1-week shift		Week	WLR 2-week shift		Week	WLR 3-week shift
		95% CI			95% CI			95% CI
W2	25.43	(24.1 – 26.8)	W34	2.68	(2.5 – 2.9)	W42	2.43	(2.4 – 2.5)
W3	21.10	(20.4 – 21.8)	W35	2.51	(2.4 – 2.6)	W43	2.18	(2.1 – 2.3)
W4	15.42	(15.0 – 15.8)	W36	2.30	(2.2 – 2.4)	W44	2.99	(2.9 – 3.1)
W5	13.27	(12.9 – 13.6)	W37	2.09	(2.0 – 2.2)	W45	3.07	(3.0 – 3.2)
W6	12.83	(12.4 – 13.2)	W38	2.03	(2.0 – 2.1)	W46	3.60	(3.5 – 3.7)
W7	13.72	(13.3 – 14.1)	W39	2.09	(2.0 – 2.1)	W47	3.05	(2.9 – 3.2)
W8	13.20	(12.7 – 13.7)	W40	2.25	(2.2 – 2.3)	W48	2.53	(2.4 – 2.6)
W9	11.98	(11.5 – 12.5)	W41	2.52	(2.4 – 2.6)	W49	2.63	(2.5 – 2.7)
W10	12.92	(12.3 – 13.6)				W50	2.69	(2.6 – 2.8)
W11	16.14	(15.3 – 17.0)				W51	2.48	(2.4 – 2.6)
W12	13.78	(12.9 – 14.7)				W52	2.37	(2.3 – 2.5)
W13	14.24	(13.2 – 15.4)				W53	2.45	(2.3 – 2.6)
W14	15.42	(14.1 – 16.9)				W54	2.70	(2.6 – 2.8)
W15	22.25	(20.2 – 24.4)				W55	2.41	(2.3 – 2.5)
W16	14.51	(12.9 – 16.3)				W56	2.10	(2.0 – 2.2)
W17	8.63	(7.4 – 10.1)				W57	1.99	(1.9 – 2.1)
W18	8.64	(7.2 – 10.3)				W58	2.10	(2.0 – 2.2)
W19	7.15	(5.8 – 8.8)				W59	1.84	(1.8 – 1.9)
W20	6.28	(5.1 – 7.7)				W60	1.70	(1.6 – 1.8)
W21	4.52	(3.5 – 5.8)				W61	1.92	(1.8 – 2.0)
W22	2.80	(2.1 – 3.7)				W62	1.65	(1.6 – 1.7)
W23	2.64	(2.0 – 3.5)				W63	1.43	(1.4 – 1.5)
W24	1.48	(1.0 – 2.0)				W64	1.20	(1.1 – 1.3)
W25	1.22	(0.9 – 1.7)				W65	1.24	(1.2 – 1.3)
W26	0.74	(0.5 – 1.0)				W66	1.00	(0.9 – 1.1)
W27	0.72	(0.6 – 0.9)				W67	1.45	(1.3 – 1.6)
W28	0.73	(0.6 – 0.9)
W29	0.96	(0.8 – 1.2)
W30	1.23	(1.0 – 1.5)
W31	1.29	(1.1 – 1.5)
W32	1.16	(1.0 – 1.3)
W33	1.27	(1.1 – 1.4)

Discussion

One of the most striking and worrying features of the COVID-19 pandemic is its unpredictable evolution: with the exception of an extremely limited number of nations that have been able to control the infections, the vast majority of the countries have suffered from phases characterized by a high COVID-19 burden that was alternated with time periods in which the pandemic was essentially under control. This articulated evolution has also been experienced in Italy, the center of the first main outbreak across Western countries. In the initial stage of the pandemic (February – June 2020), quite strong measures were taken by the governmental authorities to severely limit the mobility of people and therefore the diffusion of the infection (2,8). Despite the gross underestimation of cases in the early months of the outbreak (due to the emergency phase and a low capacity of case detecting), the enforcement of severe lockdown restrictions contributed to the clear-cut shape of the curves, with an ascending curve followed by a monotonic descending one (Figure 1). The analogous trends displayed by the curves reporting cases and deaths prompted us to search for a temporal link between them. A remarkable good fitting between these two profiles was obtained when the curve of the cases was shifted by one week (8). The well-defined quantification of this temporal link provided us the opportunity to define a time-dependent WLR that was nearly constant in the first months of the pandemic. The inspection of the WLR profile indicates that, after assuming rather large values (~13.5%) in Phase 1 due to the underestimation of cases, it decreased to very low values (below 1%) during the summer of 2020 (Figure 5). Although the marked reduction in the number of cases/deaths observed in this period makes the calculated WLR less reliable, its drop may be ascribed to different factors including the lockdown measures, the seasonality of viral respiratory diseases, and an increased virus circulation amongst young people who are less susceptible to severe and fatal COVID-19 outcomes (14,15). Therefore, after the initial outbreak and the summer months, when the infections were essentially under control, from fall 2020 Italy suffered a second phase (Phase 2) of the pandemic that is still ongoing. Differently from the first, Phase 2 has been characterized by an intricate evolution with multiple rises and decreases of the infections. On the basis of the peaks that we observed in the curves of both cases and deaths, we were able to identify and model three distinct subphases. As a whole, the shape of the Phase 2 curve mirrored the differences in virus circulation and type of restrictive public health measures compared to Phase 1. From an epidemiological standpoint, in the first half of 2020, the major spread of SARS-CoV-2 was limited to northern regions of the country, which registered the biggest COVID-19 outbreak in terms of both cases and death toll (16); from September 2020, the virus has been circulating across the entire country (14). Again, in order to reduce the social and economic consequences of protracted lockdown restrictions, governmental authorities adopted less-stringent limiting measures, the impact of which was reflected in the curves. A system of region-based risk levels was implemented, which allowed the easing of measures according to a set of indicators (for instance, number of cases and deaths, number of intensive care unit [ICU] admissions, percentage of occupied ICU beds, etc.), with different extents of SARS-CoV-2 circulation across regions and weeks (14).

Interestingly, despite the heterogeneity of the data that are separately collected in the twenty-one regions/territories of the country and the complexity of Phase 2, we could quantify the temporal link between cases and deaths. Notably, the shift between the positive testing and the fatal event is longer than that observed in Phase 1 (one week) and is progressively increasing during Phase 2 (two or three weeks). This difference can be ascribed to the improved timeliness of the testing, which was only reserved to people displaying symptoms in Phase 1 and, possibly, to some improvement in the therapeutic interventions that delayed the death in Phase 2. Moreover, the identification of this temporal link gave us the opportunity to evaluate the lethality attributable to COVID-19 in Italy during the whole epidemic period, from March 2020 to June 2021, using complete epidemiological data of SARS-CoV-2 spread in the country.

A significant increase of the WLR took place in October 2020, concurrently with a new increase of the virus spread and its following circulation in susceptible populations, like elder individuals or people in fragile states (14,15). From the beginning of Phase 2 to the beginning of February 2021 the WLR assumed a rather constant value (~2.6%) (Figure 5). Starting from mid-February 2021 (W₅₁), the WLR is significantly decreasing. It is important to note in this time interval the WLR practically halved from 2.6 to 1.3%, the value detected at the beginning of June 2021. Notably, this period also coincides with the progressive increase of the vaccination coverage in Italy, primarily in at-risk and susceptible subjects, with a consequent positive impact on COVID-19 burden and lethality reduction (7). Further research is needed to better investigate the impact of vaccines and vaccination campaign on SARS-CoV-2 diffusion and lethality.

Some limitations of our study should be acknowledged. First, as for our previous analysis of lethality during the first epidemic wave (8), the research included information measured through surveillance systems where data were provided in aggregated form and without any case stratification; thus, it was not possible to evaluate uncertainty sources and adjust results for potential independent predictors of death, but this research was intended as a straightforward strategy to assess the time-trend of the proportion of cases who died from the disease. Second, the WLR uses the number of subjects that tested positive as population (denominator), thus being influenced by the number of tests performed on a certain time-point. However, the combination of data on a weekly-aggregated manner greatly reduced possible differences across different week-days. Lastly, even if the 1- to 2-week and 2- to 3-week shifts were based on static denominators, the WLR calculated a ratio representing relative rates of deaths which reflect analytical expressions of lethality proxy over time.

In conclusion, our study provides interesting insights into the evolution of the COVID-19 pandemic in Italy by highlighting some distinctive features, in terms of trend complexity of the lethality rate in the different phases of the pandemic. Our approach also documented the impact of the public health measures on SARS-CoV-2 spread and associated lethality, also highlighting the possible positive effect of vaccination efforts, but more studies assessing this hypothesis should be implemented in the near future. The application of the proposed approach could help examine data from other contexts, allowing comparison with the lethality associated with SARS-CoV-2 in other countries.

Funding:

This research was funded by Regione Campania project “RicErCa e sviluppO VERsus COVID19 in Campania RECOVER-COVID19” (POR FESR CAMPANIA 2014-2020 - Asse III Obiettivo Specifico 1.3 - Azione 1.3.1).

Conflicts of Interest:

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.