Mathematical modeling and stability analysis of the COVID-19 with quarantine and isolation

Abstract

The present paper focuses on the modeling of the COVID-19 infection with the use of hospitalization, isolation and quarantine. Initially, we construct the model by spliting the entire population into different groups. We then rigorously analyze the model by presenting the necessary basic mathematical features including the feasible region and positivity of the problem solution. Further, we evaluate the model possible equilibria. The theoretical expression of the most important mathematical quantity of major public health interest called the basic reproduction number is presented. We are taking into account to study the disease free equilibrium by studying its local and global asymptotical analysis. We considering the cases of the COVID-19 infection of Pakistan population and find the parameters using the estimation with the help of nonlinear least square and have ${\mathcal{R}}_0\approx 1.95$. Further, to determine the influence of the model parameters on disease dynamics we perform the sensitivity analysis. Simulations of the model are presented using estimated parameters and the impact of various non-pharmaceutical interventions on disease dynamics is shown with the help of graphical results. The graphical interpretation justify that the effective utilization of keeping the social-distancing, making the quarantine of people (or contact-tracing policy) and to make hospitalization of confirmed infected people that dramatically reduces the number of infected individuals (enhancing the quarantine or contact-tracing by 50% from its baseline reduces 84% in the predicted number of confirmed infected cases). Moreover, it is observed that without quarantine and hospitalization the scenario of the disease in Pakistan is very worse and the infected cases are raising rapidly. Therefore, the present study suggests that still, a proper and effective application of these non-pharmaceutical interventions are necessary to curtail or minimize the COVID-19 infection in Pakistan.

Introduction

The novel coronavirus pandemic also known as COVID-19 is still posing a stressful time for the human around the globe. This infection was first emerged in December of 2019, in Wuhan, a city in Central China [1], [2]. The COVID-19 infection has now spread to more than 210 countries. The countries or regions on the globe not yet infected with this infection is still at risk of this novel pandemic. According to the recent WHO measurements, more than 214 million COVID-19 cases are confirmed and over 4.4 million people are died globally due to this infection  [2], [3], [4]. Although, there is no specific treatment for COVID-19 and the vaccines are in experimental stage, still more than 2.17 million of the whole infected population are recovered so far. Mostly, the severe cases and deaths due to this novel infection are reported in people with older age. Additionally, the people with co-morbidities and any chronic respiratory disease that suppress or compromise the immune system are at high risk from this infection [5]. This main transmission pattern known so far is through direct social contacts of one human to an infectious person [6]. A person can also catch the virus via direct contact with contaminated surfaces or objects and during the inhalation of droplets discharge from the nose while spitting, coughing or sneezing from both either symptomatic or asymptomatically infective humans [6]. The time to show symptoms takes 5–6 days from initial infection, however, the period of incubation usually ranges from 2–14 days  [2], [7], [8]. Over 80% COVID-19 victims show no clinical or negligible symptoms of the disease, however, the common symptoms founds in infected people are dry cough, severe fever, aches and pains, headache and excessive fatigue, short breathing etc [9].

Pakistan is one of the highly affected countries in Asia from this novel infection. In Karachi, Pakistan, the first case has been identified in the end of February 2020. After then, by 18 March the infection spread into the whole country. The curative tested positive cases so far across the country are 1.11 million with total mortality are 24,573. Although the incidence rate in Pakistan is not significant as in first wave of the infection but still the disease is not completely eradicated and the country is facing fourth wave of this novel infection. The number of infected cases was raising day by day as a result the on 1 April, the Pakistani government decided a strict lock-down nationwide and later due to worse scenario of infected cases, it was extended twice until 9 May. There were reported many cases of infection and deaths that make Pakistan to be listed in most inflected countries with high number of infectivities [10], [11]. According to the recent statistics recorded on 21 May 2020, the total confirmed COVID-19 infected cases are more than 50,000 with 15,201 recoveries and 1,067 deaths national-wide [12], [13]. A recent cases reported from COVID-19 infection right now on December 2021, were 1,294,031 with the number of deaths 28,912. There are many recovered cases after the person is being isolated, hospitalized etc are 1,255,204.

Although, there is some vaccines available in the market for the use in humans against the COVID-19 infection. But it is not yet known how this vaccines can be fully capable to eradicate the infection. Therefore, the implementation of non-pharmaceutical strategies, such as social-distancing and other interventions for minimizing the community interactions, such as community lock-downs, using face-masks, quarantine of people or having interaction with infected individuals, isolation and hospitalization of tested positive cases, etc are still needed to mitigate the pandemic incidence [14]. The proper and timely implementation of these control interventions reduces the newly infected cases very significantly everywhere around the world including Pakistan. According to a report submitted to the Supreme Court of Pakistan by April 25, the number of infected cases is feared to reach 50,000, however, the number by then remained under 13,000, less than half of what was expected.

Mathematical models were considered effective while dealing with the problems in science and engineering, see some related work [15], [16], [17], [18]. In these works, the authors focused to consider, the coronavirus infection using different perspective as well as the use of the fractional operators. The mathematical modeling of the problems in science and engineering with fractional operators are also considering attentions from researchers around the world, see [19], [20], [21], [22], [23], [24]. In the suggested aforementioned papers, the authors used the mathematical modeling approach to study, the disease and physical problems arises science and engineering fields. In the last couple of years, the main focus of the researchers is to study the complex dynamical patterns and to set effective controlling measures in order put down this infection. Mathematical modeling is one of the effective tools in this regard and has historically been utilized to explore deeper insight into the dynamics of emerging and re-emerging transmittable diseases. The rigorous mathematical analysis, coupled with the application to real data in order to parameterize the models can be consequently used to make predictions about the disease transmission. In the recent few months after the emergence of the pandemic, many mathematical models can be found in literature to explore the dynamics of this infection in different regions around the globe. In [25], the authors studied the impact of exposed or latency period on the incidence of COVID-19 by formulating two mathematical model and shown a reasonable fit to the cases reported in China. Rigorous analysis of coronavirus pandemic in the selected countries namely is carried out in [26]. A fractional study of COVID-19 by utilizing the non-singular operator coupled with real data of China is presented [27]. They have used the fractional operator because this operator provides a better understanding of the disease dynamics. The impact of non-pharmaceutical interventions like quarantine of exposed people and isolation/hospitalization of confirmed individuals for China is rigorously analyzed in [28]. They have shown that the trend of the epidemics mainly depends on quarantined and suspected cases. A similar analysis demonstrating the impact of the use of face mask in the American population is conducted in detail in [29]. A new mathematical model with optimal control and cost-effective analysis describing the negative aspects of quarantine on diabetics individual is conducted in [30]. The impact of environmental role on the COVID-19 transmission is studied in  [31].

Some recent study related to the modeling of infectious diseases and their dynamical analysis are considered in  [19], [21], [32], [33], [34]. For example, the analysis of COVID-19 with quarantine and isolation study is suggested in [32], while the authors used the real data from Pakistan, and constructed an optimal control model for COVID-19 infection and give possible recommendations about the eliminations of infection [33]. A vaccination study of Hepatitis B model and its analysis is considered in [21]. A SARS-COV-2 study and its dynamical study with real cases is explored in [19]. Modeling and optimal control dynamics of the recent cases in Pakistan is given in [34]. The COVID-19 model in non-integer differential equation is formulated in [20]. A study in [35] focuses about the face masks effects in the disease dynamics of COVID-19. COVID-19 with effects of lockdown and their transmission dynamics is explored in [36]. Some work about the COVID-19 dynamics in different perspective can be seen in [37], [38], [39], [40].

The present study focuses on the construction of a compartmental model to analyze the dynamics of COVID-19 infection in Pakistan. We will consider the reported cases in the country and will use the analysis of least square curve fit to estimate the dynamics of infection in Pakistan. The present study demonstrates a realistic assessment of the burden of the pandemic in the selected region. Further, we also analyze the impact of quarantine, isolation/hospitalization and social-distancing on the control of disease in Pakistan. The detail organization of this work is as: The model formulation based on the COVID-19 transmission is shown in Section “Mathematical model”. Some basic features of the proposed model is explored in See “Model theoretical analysis”. The procedure of the parameters estimation from the real statistical cases is carried out in Section “Data fitting and estimation procedure”. The sensitivity indices with graphical interpretation is demonstrated in See “Sensitivity analysis”. The simulation results showing the role of various model important parameters on disease dynamics and possible control are shown in Section “Simulation results and discussion”. The paper is concluded with a brief concluding remarks summarized given “Conclusion”.

Mathematical model

This section briefly explain the formulation of the COVID-19 model using a classical integer-order derivative. To develop the model total human population at the time $t$, represented by $N\left(t\right)$, is classified into seven mutually-exclusive sub-compartments containing the suspectable $S\left(t\right)$, exposed $E\left(t\right)$, infectious processes symptoms (symptomatic) $I\left(t\right)$, infectious showing no or mild symptoms of coronavirus (asymptotically) $A\left(t\right)$, individuals who are in quarantine $Q\left(t\right)$, hospitalized $H\left(t\right)$ and the recovered or the removed people is symbolized by $R\left(t\right)$. The recruitment rate of the healthy people is given by the symbol $\Lambda$ while $\mu$ shows the natural mortality rate in each class of the epidemiological model. The suspectable humans catch virus after having contacts with symptomatically or asymptomatically infective people at the rate $\frac{\beta (I+\psi A)S}{N}$, where $\beta$ shows the transmission coefficient or the effective contact rate causing infection while the term $\psi \in [0,1]$, measures the disease transmissibility of asymptomatic individuals. The exposed individuals develop the infection and move to infectious stage at the rate $\omega$. A fraction (denoted by $\theta$) shows symptoms and join the symptomatic class while the remaining having no symptoms enter to the compartment $A\left(t\right)$. The exposed individuals contacted with infected people are quarantine at the rate ${\delta }_1$ which are further hospitalized at the rate ${\delta }_2$ if they develop the infection. The symptomatic infected individuals are hospitalized at the rate $\gamma$. The symptomatic and asymptomatic infected people are recovered and they join directly the recovery class at the rate ${\tau }_1$ and ${\tau }_2$ respectively. The recovery class is further increased by the recovery of quarantined and hospitalized individuals at the rates ${\varphi }_1$ and ${\varphi }_2$ respectively. The disease-induced death rate due to COVID-19 in the $I\left(t\right)$ and $H\left(t\right)$ is respectively shown by ${\xi }_1$ and ${\xi }_2$. Thus we summarized the COVID-19 transmission with the help of following system:

$$\begin{array}{c}\frac{dS}{dt}=\Lambda -\frac{\beta (I+\psi A)}{N}S-\mu S,\hfill \\ \hfill \\ \frac{dE}{dt}=\frac{\beta (I+\psi A)}{N}S-(\omega +{\delta }_1+\mu )E,\hfill \\ \hfill \\ \frac{dI}{dt}=\theta \omega E-({\tau }_1+\mu +{\xi }_1+\gamma )I,\hfill \\ \hfill \\ \frac{dA}{dt}=(1-\theta )\omega E-({\tau }_2+\mu )A,\hfill \\ \hfill \\ \frac{dQ}{dt}={\delta }_{1}E-(\mu +{\varphi }_1+{\delta }_2)Q,\hfill \\ \hfill \\ \frac{dH}{dt}=\gamma I+{\delta }_{2}Q-(\mu +{\varphi }_2+{\xi }_2)H,\hfill \\ \hfill \\ \frac{dR}{dt}={\tau }_{1}I+{\tau }_{2}A+{\varphi }_{1}Q+{\varphi }_{2}H-\mu R.\hfill \end{array}$$ (1)

The corresponding initial conditions are

$$\begin{array}{c}S\left(t_0\right)=S_0\ge 0,E\left(t_0\right)=E_0\ge 0,I\left(t_0\right)=I_0\ge 0,A\left(t_0\right)=A_0\ge 0,\hfill \\ Q\left(t_0\right)=Q_0\ge 0,H\left(t_0\right)=H_0\ge 0,R\left(t_0\right)=R_0\ge 0.\hfill \end{array}$$ (2)

In order to simplifies system (1), let we denote

$$\lambda \left(t\right)=\frac{\beta (I+\psi A)}{N},$$

and

$$k_1=(\omega +{\delta }_1+\mu ),k_2=({\tau }_1+\mu +{\xi }_1+\gamma ),k_3=({\tau }_2+\mu )$$

$$k_4=(\mu +{\varphi }_1+{\delta }_2),k_5=(\mu +{\varphi }_2+{\xi }_2).$$

Utilizing above setting, model (1) can be written as

$$\begin{array}{c}\frac{dS}{dt}=\Lambda -\lambda S-\mu S,\hfill \\ \hfill \\ \frac{dE}{dt}=\lambda S-k_{1}E,\hfill \\ \hfill \\ \frac{dI}{dt}=\theta \omega E-k_{2}I,\hfill \\ \hfill \\ \frac{dA}{dt}=(1-\theta )\omega E-k_{3}A,\hfill \\ \hfill \\ \frac{dQ}{dt}={\delta }_{1}E-k_{4}Q,\hfill \\ \hfill \\ \frac{dH}{dt}=\gamma I+{\delta }_{2}Q-k_{5}H,\hfill \\ \hfill \\ \frac{dR}{dt}={\tau }_{1}I+{\tau }_{2}A+{\varphi }_{1}Q+{\varphi }_{2}H-\mu R.\hfill \end{array}$$ (3)

Model theoretical analysis

We shall study in the given section, the mathematical for the model considered in (3). We will investigate, the boundedness and the positivity of the model, determining the equilibrium points, the computation of the basic reproduction number, study the stability analysis of the equilibrium point (disease free). Keeping in view the importance of the basic reproduction number, the stability analysis will be discussed. So, first, we present the following Lemma, to show the boundedness and positivity of the model (3).

Positivity of the model and its boundedness

The following result is given to show the positivity and boundedness of the model (3).

Lemma 1

With the non-negative initial data, say $\zeta \left(0\right)$ and $\zeta \left(0\right)=(S,E,I,A,Q,H,R)$ representing the state variables, then, each of the solutions curve of the model (3) will be non-negative $\forall$ for $t>0$ . Additionally,

$$\underset{t\to \infty }{lim}supN\left(t\right)\le \Lambda /\mu .$$

Proof

Let $t_1=sup\{t>0:\zeta \left(t\right)>0\in [0,t]\}$, and then use the first equation of coronavirus (3), we have

$$\frac{dS}{dt}=\Lambda -(\lambda +\mu )S.$$ (4)

The Eq. (4) can be describes as

$$\frac{d}{dt}\left\{S\left(t\right)exp\left(\mu t+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma \right)\right\}=\Lambda exp\left(\mu p+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma \right).$$

So,

$$S\left(t_1\right)exp\left(\mu t_1+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma \right)-S\left(0\right)={\int }_0^{t_1}\Lambda \times exp\left(\mu p+{\int }_0^p\lambda \left(\tilde{\varsigma }\right)d\tilde{\varsigma }\right)dp.$$ (5)

Finally, we obtain the following solution for (5),

$$S\left(t\right)=S\left(0\right)exp\left\{-\left(\mu t_1+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma \right)\right\}+exp\left\{-\left(\mu t_1+{\int }_0^{t_1}\lambda \left(\varsigma \right)d\varsigma \right)\right\}\times {\int }_0^{t_1}\Lambda exp\left(\mu p+{\int }_0^p\lambda \left(\tilde{\varsigma }\right)d\tilde{\varsigma }\right)dp>0.$$

Similarly, for the rest of the equations of the model considered above (3), we can show that the state variables are non-negative. So, we are able to say that the solution of the model given by (3) is non-negative for every time $t>0$.

For the rest of the part of the proof in the considered Lemma 1, we have $0<\zeta \left(0\right)\le N\left(t\right)$, and summing the equations involve in the system (3), we arrive at the following expression,

$$\frac{dN\left(t\right)}{dt}=\Lambda -\mu N\left(t\right)-{\xi }_{1}I\left(t\right)-{\xi }_{2}H\left(t\right)\le \Lambda -\mu N\left(t\right).$$

Hence,

$$\underset{t\to \infty }{lim}sup\left\{N\left(t\right)\right\}\le \Lambda /\mu .\square$$

Invariant region

We provide the following biological feasible region that will be considered to study the dynamics of the system (3), given by

$$\Xi \subset {\mathbb{R}}_{+}^7,$$

where

$$\Xi =\left\{(S,E,A,I,Q,H,R)\in {\mathbb{R}}_{+}^7:N\left(t\right)\le \Lambda /\mu \right\}.$$

Lemma 2

Letting the region be $\Xi \subset {\mathbb{R}}_{+}^7$ , is positively invariant for the model given in (3) , with non-negative initial conditions in ${\mathbb{R}}_{+}^7$ .

Proof

It can be observed from Lemma 1,

$$\frac{dN\left(t\right)}{dt}\le \Lambda -\mu N\left(t\right).$$ (6)

We can see that

$$\frac{dN\left(t\right)}{dt}\le 0,ifN\left(0\right)\ge \frac{\Lambda }{\mu }.$$

Some calculations enable us to arrive at the following expression of (6),

$$N\left(t\right)\le N\left(0\right)e^{-\mu t}+\frac{\Lambda }{\mu }\left(1-e^{-\mu t}\right).$$

Particularly, $N\left(t\right)\le \Lambda /\mu$, and thus, the region $\Xi$ is positively invariant. Moreover, all solutions trajectories will be attracted in ${\mathbb{R}}_{+}^7$. □

Equilibria and its analysis

The COVID-19 model (3) has a $DFE$, denoted by ${\mathcal{D}}_0$ which can be given by the following expressions,

$${\mathcal{D}}_0=(S^0,0,0,0,0,0,0)=\left(\Lambda /\mu ,0,0,0,0,0,0\right).$$

Further, to calculate ${\mathcal{R}}_0$, which gives the information, when the number of average infected cases of COVID-19 introduced into a population of purely susceptible and generate further secondary infected cases of COVID-19 in the population. This important threshold quantity that can measure the level of infection in a population about its spread and control based on its value. If its value below one then the infection may not be spread and can easily controlled while exceeding the value than one, there may epidemic and the disease can spread in the community. In order to analyze of our model with the real cases, we need to compute the expression for the basic reproduction number, using the concept of next generation approach given [41]. Here, we obtain the required matrices for the computation of ${\mathcal{R}}_0$ for the system (3) given by:

$$\mathcal{F}=\left(\begin{array}{c}\hfill \frac{\beta (I+\psi A)S}{N}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\mathcal{V}=\left(\begin{array}{c}\hfill k_1\hfill \\ \hfill k_{2}I-\theta \omega E\hfill \\ \hfill k_{3}A-(1-\theta )\omega A\hfill \\ \hfill k_{4}Q-{\delta }_{1}E\hfill \\ \hfill k_{4}H-\gamma I-{\delta }_{2}Q\hfill \end{array}\right).$$

Further, using [41], we compute the following results:

$$F=\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill \beta \hfill & \hfill \beta \psi \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),$$

$$V=\left(\begin{array}{ccccc}\hfill k_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\theta \omega \hfill & \hfill k_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -(1-\theta )\omega \hfill & \hfill 0\hfill & \hfill k_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\delta }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill k_4\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\gamma \hfill & \hfill 0\hfill & \hfill -{\delta }_2\hfill & \hfill k_5\hfill \end{array}\right).$$

Hence, utilizing the concept ${\mathcal{R}}_0=\rho \left(F{V}^{-1}\right)$, the expression for this biologically crucial quantity is obtained as

$${\mathcal{R}}_0=\underset{{\mathcal{R}}_1}{\underbrace{\frac{\beta \omega (1-\theta )\psi }{k_1{k}_3}}}+\underset{{\mathcal{R}}_2}{\underbrace{\frac{\beta \omega \theta }{k_1{k}_2}}}.$$

It should be noted that ${\mathcal{R}}_0={\mathcal{R}}_1+{\mathcal{R}}_2$.

Endemic equilibrium (EE) of the model

The possible EE of the epidemic model (3) is represent by ${\mathcal{D}}_{\ast \ast }$ which is sown in the following result

$$\left\{\begin{array}{c}{S}^{\ast \ast }=\frac{\Lambda }{{\lambda }^{\ast \ast }+\mu },\hfill \\ \hfill \\ E^{\ast \ast }=\frac{{\lambda }^{\ast \ast }{S}^{\ast \ast }}{k_1},\hfill \\ \hfill \\ I^{\ast \ast }=\frac{\theta \omega }{k_1}{E}^{\ast \ast },\hfill \\ \hfill \\ A^{\ast \ast }=\frac{(1-\theta )\omega }{k_2}{E}^{\ast \ast },\hfill \\ \hfill \\ Q^{\ast \ast }=\frac{{\delta }_2}{k_4}{E}^{\ast \ast },\hfill \\ \hfill \\ H^{\ast \ast }=\frac{\gamma I^{\ast \ast }+\delta Q^{\ast \ast }}{k_5},\hfill \\ \hfill \\ R^{\ast \ast }=\frac{{\tau }_1{T}^{\ast \ast }+{\tau }_2{I}^{\ast \ast }+{\varphi }_1{Q}^{\ast \ast }+{\varphi }_2{H}^{\ast \ast }}{\mu },\hfill \end{array}\right)$$

and

$${\lambda }^{\ast \ast }=\frac{\beta (I^{\ast \ast }+\psi A^{\ast \ast })}{S^{\ast \ast }+E^{\ast \ast }+I^{\ast \ast }+A^{\ast \ast }+Q^{\ast \ast }+H^{\ast \ast }+R^{\ast \ast }},$$

stratifies the following polynomial

$$P\left({\lambda }^{\ast \ast }\right)=m_1{\left({\lambda }^{\ast \ast }\right)}^2+m_2{\lambda }^{\ast \ast }.$$ (7)

The coefficient in (7) are as follow:

$$m_1=\Lambda (k_3(k_4(\gamma \theta \omega (\mu +{\varphi }_2)+\delta k_2(\mu +{\varphi }_1))+\delta {\delta }_2{k}_2(\mu +{\varphi }_2)+k_4^2(\theta \omega (\mu +{\tau }_1)+k_2\mu ))+k_2{k}_4^2(1-\theta )\omega (\mu +{\tau }_2)),$$

$$m_2=k_1{k}_2{k}_3{k}_4^2\Lambda \mu (1-{\mathcal{R}}_0).$$ (8)

Clearly, $m_1>0$ and $m_2\ge 0$ if ${\mathcal{R}}_0<1$, and ${\lambda }^{\ast \ast }=-\frac{m_2}{m_1}\le 0$. Thus, no endemic equilibrium will exists if ${\mathcal{R}}_0<1$.

Stability of DFE

Theorem 1

The $DFE$ , ${\mathcal{D}}_0$ of the model (3) is $\mathcal{LAS}$ if ${\mathcal{R}}_0<1$ and unstable otherwise.

Proof

The following Jacobian matrix $J_{{\mathcal{D}}_0}$ is found about the DFE ${\mathcal{D}}_0$

$$J_{{\mathcal{P}}_0}=\left(\begin{array}{ccccccc}\hfill -\mu \hfill & \hfill 0\hfill & \hfill -\beta \hfill & \hfill -\beta \psi \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -k_1\hfill & \hfill \beta \hfill & \hfill \beta \psi \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \theta \omega \hfill & \hfill -k_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill (1-\theta )\omega \hfill & \hfill 0\hfill & \hfill -k_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\delta }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -k_4\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \gamma \hfill & \hfill 0\hfill & \hfill {\delta }_2\hfill & \hfill -k_5\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\tau }_1\hfill & \hfill {\tau }_2\hfill & \hfill {\varphi }_1\hfill & \hfill {\varphi }_2\hfill & \hfill -\mu \hfill \end{array}\right).$$

It follows from the Jacobian matrix $J_{{\mathcal{D}}_0}$, that the eigenvalues $-\mu$, $-\mu$, $-k_3$, $-k_4$ containing negative real parts. The rest of (three) eigenvalues are the roots of the following equations given below:

$${\lambda }^3+C_1{\lambda }^2+C_2\lambda +C_3=0,$$ (9)

where the coefficients are:

$$C_1=k_1+k_2+k_3,$$

$$C_2=k_2{k}_3+k_1{k}_3(1-{\mathcal{R}}_1)+k_1{k}_2(1-{\mathcal{R}}_2),$$

$$C_3=k_1{k}_2{k}_3(1-{\mathcal{R}}_0).$$

Clearly, $C_j$ for $j=1,2$ can be positive if ${\mathcal{R}}_1<1$ and ${\mathcal{R}}_2<1$. Similarly $C_3$ can be positive if ${\mathcal{R}}_0<1$. Further, it is easy to show that $C_1{C}_2>C_3$. Thus, it follows from the Routh–Hurwitz criteria that the system (3) at the $DFE$ is $\mathcal{LAS}$. □

The global asymptotical stability of $DFE$, ${\mathcal{D}}_0$ of the epidemic model (3) is investigated in the below theorem.

Theorem 2

The point ${\mathcal{D}}_0$ of (3) is globally asymptotically stable ( $\mathcal{GAS}$ ) if ${\mathcal{R}}_0\le 1$ , otherwise unstable.

Proof

Consider the Lyapunov function of the form:

$$\mathcal{K}\left(t\right)={\mathcal{C}}_{1}E+{\mathcal{C}}_{2}I+{\mathcal{C}}_{3}A,$$

where ${\mathcal{C}}_1,{\mathcal{C}}_2,{\mathcal{C}}_3$, are positive constants and to be chosen later. The derivative of Lyapunov $\mathcal{K}\left(t\right)$ is given by:

$$\frac{d\mathcal{K}\left(t\right)}{dt}={\mathcal{C}}_1\left\{\frac{\beta S(I+\psi A)}{N}-k_{1}E\right\}+{\mathcal{C}}_2\{\theta \omega E-k_{2}I\}+{\mathcal{C}}_3\{(1-\theta )\omega E-k_{3}A\}\le {\mathcal{C}}_1\left\{\beta (I+\psi A)-k_{1}E\right\}+{\mathcal{C}}_2\{\theta \omega E-k_{2}I\}+{\mathcal{C}}_3\{(1-\theta )\omega E-k_{3}A\},S/N\le 1.=\{{\mathcal{C}}_1\beta -{\mathcal{C}}_2{k}_2\}I+\{{\mathcal{C}}_1\beta \psi -{\mathcal{C}}_3{k}_3\}A+\{{\mathcal{C}}_2\theta \omega +(1-\theta )\omega {\mathcal{C}}_3-{\mathcal{C}}_1{k}_1\}E=\{{\mathcal{C}}_1\beta -{\mathcal{C}}_2{k}_2\}I+\{{\mathcal{C}}_1\beta \psi -{\mathcal{C}}_3{k}_3\}A+{\mathcal{C}}_1{k}_1\left\{\frac{{\mathcal{C}}_2\theta \omega +(1-\theta )\omega {\mathcal{C}}_3}{{\mathcal{C}}_1{k}_1}-1\right\}E.$$

Now choosing

$${\mathcal{C}}_1=k_2,{\mathcal{C}}_2=\beta ,{\mathcal{C}}_3=\frac{\beta \psi k_2}{k_3}.$$

Using the above values, and have some computations, we arrive at,

$$\frac{d\mathcal{K}\left(t\right)}{dt}\le k_1{k}_2\left({\mathcal{R}}_0-1\right)E.$$ (10)

Here, we can observe that ${\mathcal{R}}_0\le 1$ then $\frac{d\mathcal{K}\left(t\right)}{dt}\le 0$. The largest compact invariant set in $\Xi$ is therefore the singleton set ${\mathcal{D}}_0$. So, we can follow from the LaSalle’s invariant principle [42], the equilibrium ${\mathcal{D}}_0$ is $\mathcal{GAS}$ in $\Xi$. □

Data fitting and estimation procedure

In order to conduct the present study in a realistic way, we estimate the model parameters from the reported disease incidence data in Pakistan. It provides an accurate prediction about the infection dynamics. This section presents the model fitting and in a result we obtain the estimated values of the parameters. For this purpose we utilized the well-known least square approach and consider the actual COVID-19 incidence data for a specific period of time found in Pakistan and is taken from [12], [13]. In order to conduct parametrization procedure of the model under consideration is performed via two approaches. The estimation procedure of recruitment, natural death and disease-induced mortality rates are performed as:

• (i).Natural mortality rate $\mu$: The average life expectancy in Pakistan is approximately 67.7 years [43], so as a result, we obtain $\mu =1/(67.7\ast 365)$ per day.
• (i)i.The recruitment rate $\Lambda$: For the demographic parameter, $\Lambda$, the birth rate is calculated from the total population of Pakistan and found as $\Lambda =8939$/day.
• (iii).Coronavirus induced death rate ${\xi }_1$: The mortality induced by infection in Pakistan was reported as 2.2% [13], thus the we have estimated value for this parameter as ${\xi }_1=0.022$.

The parameters other than the above estimated one are fitted from statistical data via least square technique application of which can be found in [44], [45]. The respective objective function involved in the process of estimation is described in the following equation:

$$\hat{\Theta }=argmin\sum _{l=1}^m{(I_{t_l}-{\overline{I}}_{t_l})}^2,$$

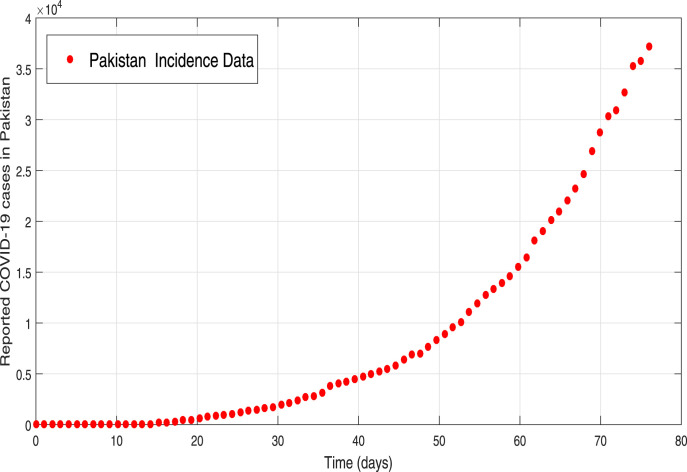
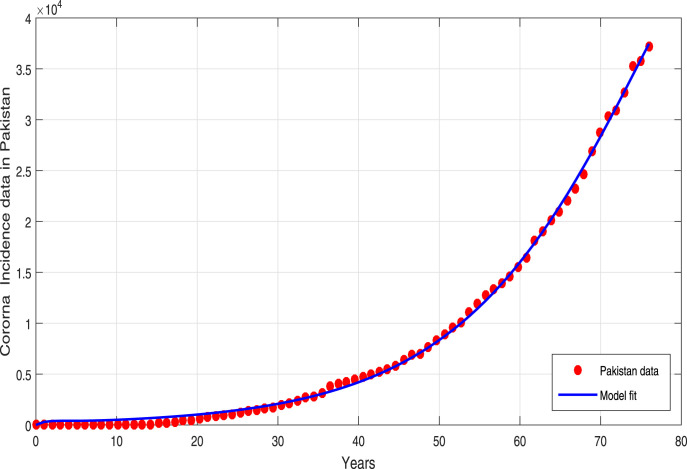
where, ${\overline{I}}_{t_l}$ shows the observed total COVID-19 confirm case and $I_{t_l}$ encounter the model predicted infected case at time $t_l$, while $m$ accounts the considered data points. The graph of total observed cases in Pakistan are depicted in Fig. 1 while the best model simulated infected curve is shown in plot 2. One can observe that our predicted curve provides a good match to the real data plot. The resulting model parameters values both estimated and fitted are shown in Table 1. The internal condition are taken as $S\left(0\right)=220870336$, $E\left(0\right)=10000$, $I\left(0\right)=4$, $A\left(0\right)=500$, $Q\left(t\right)=H\left(t\right)=R\left(0\right)=0$. The estimated value of basic reproductive number obtained with the help of estimated parameters is ${\mathcal{R}}_0\approx 1.95$.

Fig. 1.

Reported cumulative COVID-19 individuals in Pakistan for a selected period.

Fig. 2.

Model simulated curve (solid) versus statical data curve (dotted).

Table 1.

Values of parameters with biological detail.

Parameter	Description	Value (per day)	Source
$\Lambda$	Recruitment rate	$\mu \times N\left(0\right)$	Estimated
${\xi }_1$	Disease induced mortality rate	0.022	[13]
$\psi$	The infectiousness of asymptomatic people	0.5120	Fitted
$\omega$	Incubation period	0.2471	Fitted
$\theta$	Faction of individuals show symptoms	0.1620	Fitted
$\gamma$	Rate of hospitalization of $I$ class	0.3764	Fitted
${\xi }_2$	Death rate due to infection in $H$ compartment	0.0084	Fitted
${\varphi }_1$	Recovery/removal rate in $Q$	0.4018	Fitted
${\varphi }_2$	Recovery/removal in $H$	0.4346	Fitted
${\tau }_1$	Recovery rate of $I$	0.2766	Fitted
${\tau }_2$	Recovery rate of $A$	0.0760	Fitted
${\delta }_1$	Quarantined rate of $E$ people	0.1315	Fitted
$\beta$	Effective contact causes disease transmission	0.6262	Fitted
${\delta }_2$	Quarantined rate of hospitalized population	0.0017	Fitted

Sensitivity analysis

The study of sensitivity of model parameters is one of the important aspect of current work. It provides the relevant sensitivity indices of each parameter under consideration showing its role of on disease dynamics. This section presents the sensitivity analysis of various parameters versus threshold quantity ${\mathcal{R}}_0$. The sensitivity results demonstrate the impact of the various model parameters to the disease dynamics and its transmission. This analysis is also helpful to point out those parameters have a high influence on ${\mathcal{R}}_0$. In order to do the sensitivity analysis, the normalized forward sensitivity index of a variable with respect to a given parameter is obtained. The sensitivity index of ${\mathcal{R}}_0$ with respect to the parameter say $\varpi$ is defined through the following formula.

Definition 1

Let ${\mathcal{R}}_0$ is differentiable w.r.t the parameter $\varpi$, then the normalized sensitivity index of ${\mathcal{R}}_0$ relative $\varpi$ is defined as follows:

$${{\rm Y}}_{\varpi }^{{\mathcal{R}}_0}=\frac{\varpi }{{\mathcal{R}}_0}\frac{\partial {\mathcal{R}}_0}{\partial \varpi }.$$ (11)

The obtained sensitivity indices of various model parameters calculated via above expression given in (11) are given in Table 2. From the Table 2, it can be seen that parameters $\beta$, $\psi$ and $\omega$ have a positive indices showing that ${\mathcal{R}}_0$ increases with the parameter. The rest of parameters have negative sensitivity indices which demonstrate that ${\mathcal{R}}_0$ decreases with increase in these parameters. More precisely, an increase (or decrease) of 10% in the value of $\beta$, $\psi$ and $\omega$ will increase (or decrease) the basic reproductive number by 10%, 9.5% and 3.7% respectively. In contrast, an increase of 10% in the values of ${\tau }_2$, ${\delta }_1$ and $\gamma$ will decrease the basic reproduction number by 7.9%, 3.4% and 2.5% respectively.

Table 2.

Sensitivity indices of ${\mathcal{R}}_0$ corresponding to the parameters of COVID-19 model (3).

Parameter	Sensitivity
$\beta$	＋1
$\mu$	−0.193589
${\xi }_1$	−0.00150974
$\psi$	0.952665
$\omega$	0.37184
$\theta$	−0.136832
$\gamma$	−0.258302
${\tau }_1$	−0.0189815
${\tau }_2$	−0.797639
${\delta }_1$	−0.33429

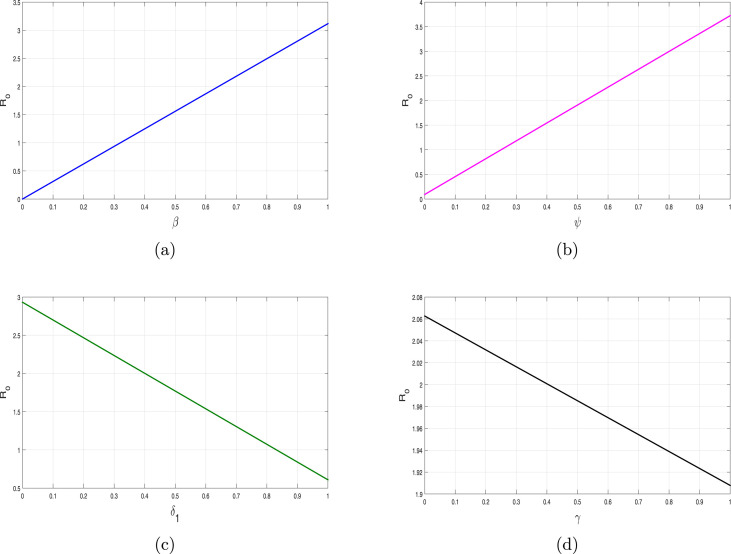
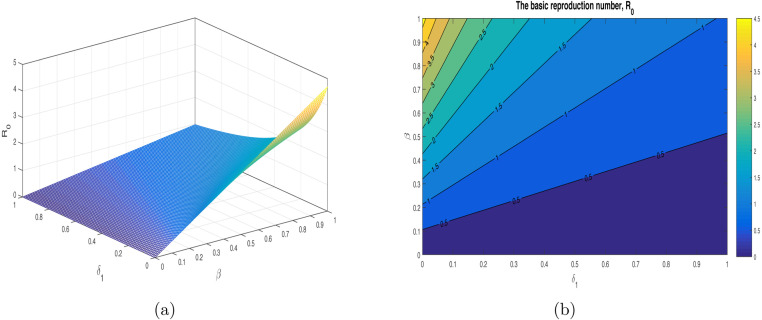
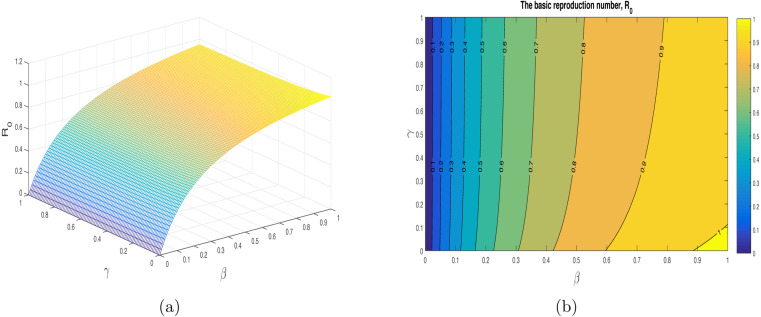
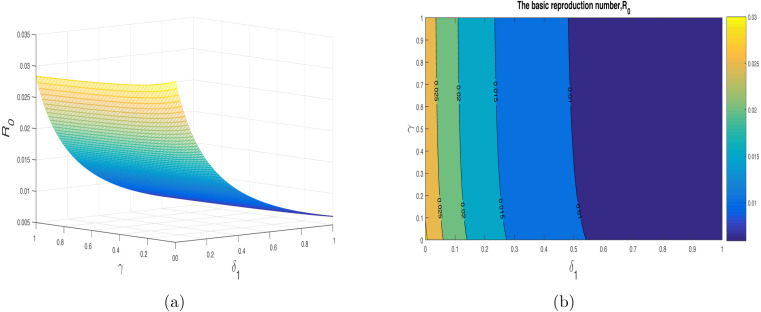
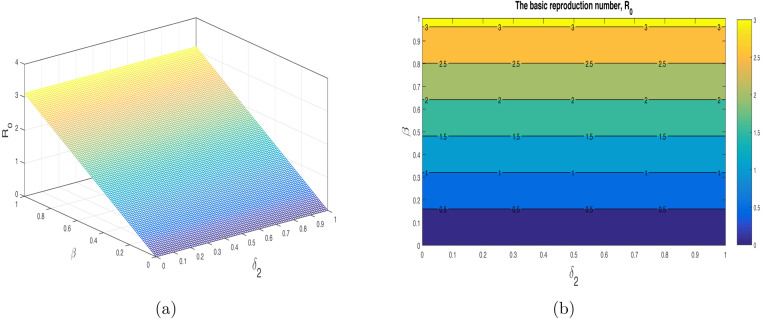
We have shown the impact of few important parameters on ${\mathcal{R}}_0$ graphically in Fig. 3. The combine influence of $\beta$ (disease transmission rate) and ${\delta }_1$ (quarantine rate) is shown in Fig. 4. The corresponding contour plot is depicted in Fig. 4(b). The impact of $\beta$ (disease transmission rate) and $\gamma$ (hospitalization rate) is depicted in Fig. 5 with the contour plot is shown in 5(b). It can be seen that ${\mathcal{R}}_0$ is increasing with the increase of $\beta$ while it is decreased with increase in $\gamma$. The combine effect of ${\delta }_1$ (quarantine rate) and $\gamma$ (hospitalization rate) with the contour plot is shown in Fig. 6(a) and (b) respectively. It is worth mentioning that ${\mathcal{R}}_0$ remain very low with the increasing both quarantine and hospitalization rates. In other words the COVID-19 infection can be totally eradicated with the implantation of both quarantine and hospitalization interventions. The behavior of ${\mathcal{R}}_0$ versus other model parameters with contour plots are depicted in Fig. 7, Fig. 8.

Fig. 3.

The influence of (a) $\beta$ versus ${\mathcal{R}}_0$, (b) $\psi$ versus ${\mathcal{R}}_0$, (c)${\delta }_1$ versus ${\mathcal{R}}_0$ and (d) $\gamma$ versus ${\mathcal{R}}_0$.

Fig. 4.

The impact of the parameters $\beta$ (disease transmission coefficient), and ${\delta }_1$ (quarantined rate) on ${\mathcal{R}}_0$ using the contour plot.

Fig. 5.

Impact of $\beta$ (disease transmission coefficient) and $\gamma$ (hospitalization rate) on ${\mathcal{R}}_0$ with contour plot.

Fig. 6.

Influence of the combine $\gamma$ (hospitalization rate) and ${\delta }_1$ (quarantined rate) on ${\mathcal{R}}_0$ with contour plot.

Fig. 7.

Impact of $\beta$ (disease transmission coefficient) and ${\delta }_2$ (hospitalization rate of quarantined people) on ${\mathcal{R}}_0$ with contour plot.

Fig. 8.

Impact of $\psi$ (reduction in infectiousness due to ($A\left(t\right)$)) and ${\delta }_1$ (quarantined rate) on ${\mathcal{R}}_0$ with contour plot.

Simulation results and discussion

This section includes the numerical simulation of the proposed epidemic model describing the transmission dynamics of the novel COVID-19 (3) using the estimated parameters values shown in

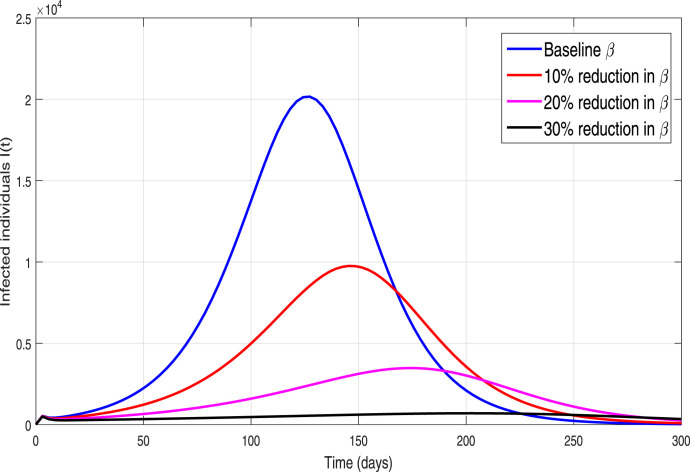
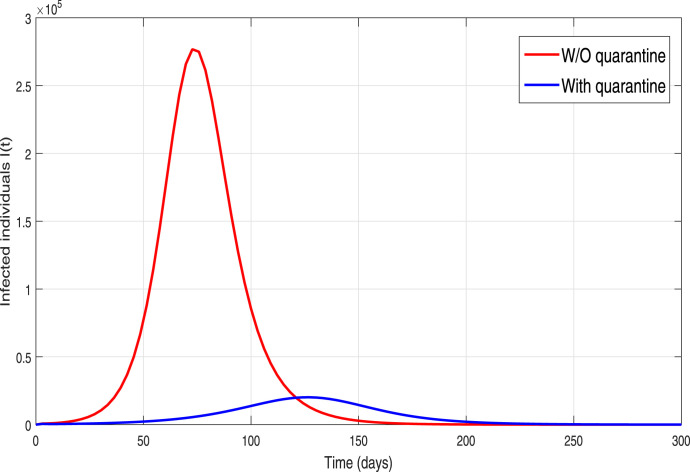
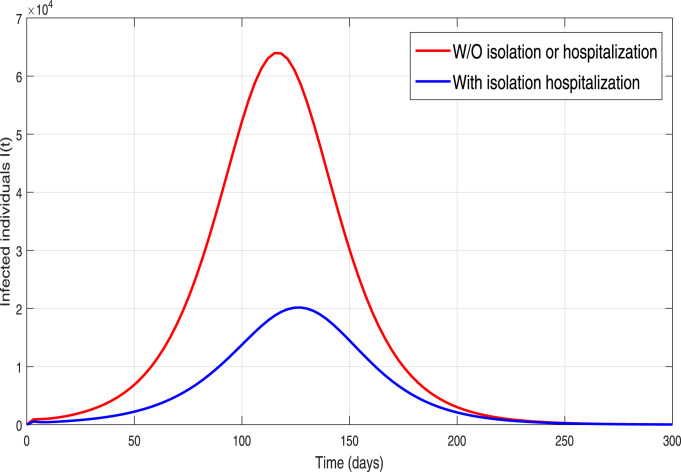
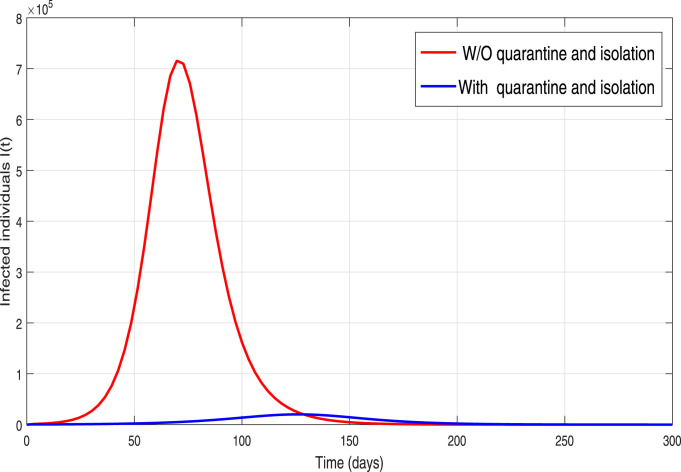
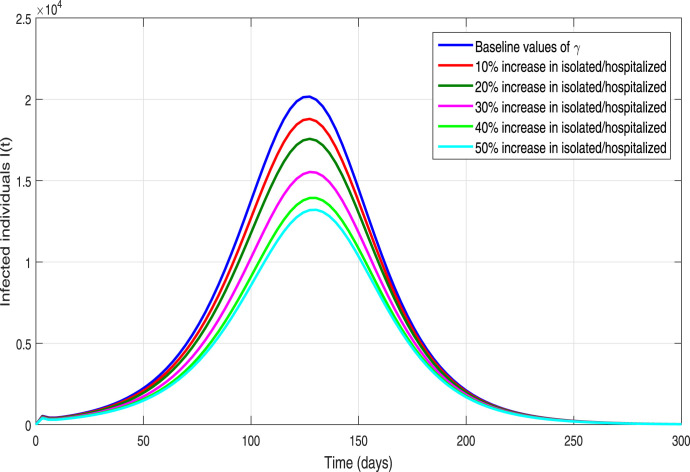
Table 1. These results are demonstrated in order to explore the dynamical influence of possible control interventions on the incidence of infection in Pakistan. To solve the model, we used the well-known and efficient numerical methods, Runge–Kutta (RK4) and achieved the required results. The simulation results are plotted for 300 days. In the given graphical results, we considered different non-pharmaceutical strategies with their baseline values (unless otherwise stated in captions). We mainly focused and analyzed the impact of effective contacts or social distancing ($\beta$), the quarantined rate of people exposed, and are contacted with COVID-19 people and at last, the isolation or quarantine on the infected cases. Firstly, we simulate the model (3) in order to explore the role of effective contact or social-distancing parameter $\beta$ by reduction in its estimated baseline value. The resulting graphical interpretation is plotted in Fig. 9 demonstrating a projected 21,000 new infected COVID-19 individuals at the pandemic peak. Further Fig. 9 demonstrates that with the improvement of social-distancing above the baseline effectiveness levels a significant reduction of COVID-19 occurs. Particularly, for the situation that the social-distancing decreases the contact rate parameter denoted by $\beta$ with 10% to its estimated value, the cumulative expected infected reported cases at pandemic peak decline below to 10,000. Moreover, with the scenario of social-distancing strategy with a high rate gives effective results that decrease a 40% the $\beta$), the peak of confirmed reported infected cases dramatically reduce to less than 1,000. Thus our study suggests that a strict and effective social-distancing guarantee the elimination of COVID-19 in Pakistan in late December 2020. The dynamics of the new COVID-19 confirmed case with and without quarantine rate or contact-tracing is monitored in Fig. 10. It is worth noticing that quarantine rate or contact-tracing the situation is very worse and the infected cases raised surprisedly very high (approximately 26,0000). But the implementation of quarantine rate only at baseline level dramatically reduces the peak number of new COVID-19 cases. We further monitored the dynamics of infected cases with and without hospitalization in Fig. 11. It is observed that without hospitalization peak number of new COVID-19 cases raised to 65,000 and with hospitalization it reduces to 20 000. This analysis suggests that hospitalization is not as much important as the quarantine or contact-tracing of people being exposed and contacted by COVID-19 infected people. Furthermore, we have also analyzed the combined impact of quarantine and hospitalization on the infected cases as shown in Fig. 12. The implementation of both quarantine and hospitalization is very effective and reduced the number of reported infected cases significantly.

Fig. 9.

Simulation of new infected cases for different scenario, for $\beta$. A graphical measurement of the effectiveness of the social-distancing.

Fig. 10.

Simulation of the epidemic model (3) with and without the effect of quarantine.

Fig. 11.

Simulation of the COVID-19 model (3) with and without hospitalization/isolation.

Fig. 12.

Behavior of the COVID-19 infected individuals in the model (3) with and without quarantine and hospitalization/isolation.

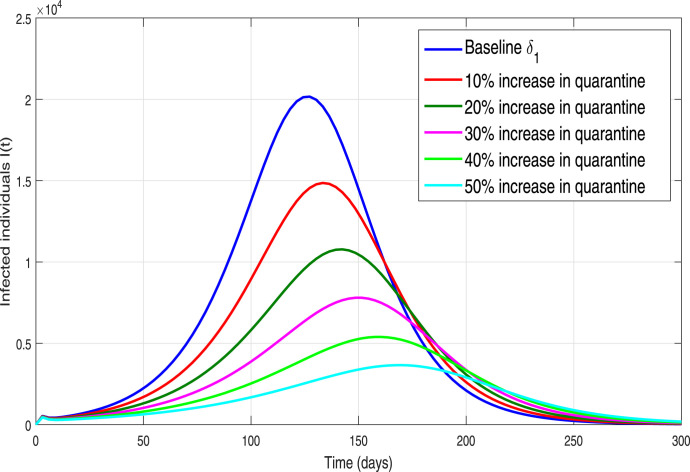
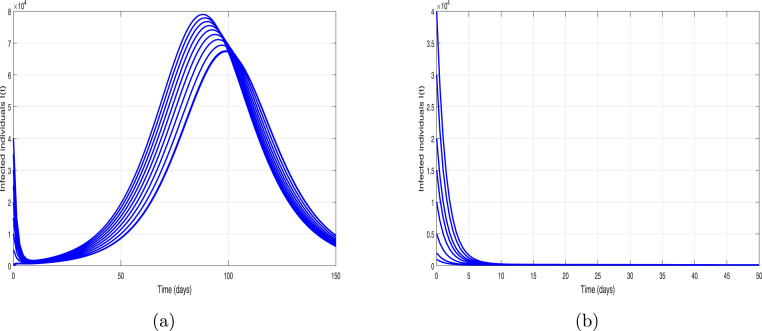
We further analyzed the impact of contact-tracing or quarantined rate parameter ${\delta }_1$ on the incidence and control of the ongoing novel pandemic. We simulate the epidemic model (3) utilizing the fixed parameters values shown in Table 1 and by making variation in ${\delta }_1$ with different percentages. The resulting behavior is depicted in Fig. 13, showing the worst-case scenario of 21,000 infected cases on the pandemic peak. Furthermore, it is shown that if the implementation of the contact-tracing parameter is enhanced with 10% to its baseline values, in a result it flattened the pandemic peak of newly reported cases by 25%. While enhancing the quarantine or contact-tracing by 50% reduces the infected cased to approximately 3000, representing 84% reduction in the predicted number of confirmed infected cases. Similarly, we further simulate the COVID-19 model in order to carry out the impact of the hospitalization rate parameter of symptomatic infected individuals (denoted by $\gamma$) by increasing its value with different percentages to its baseline value. The resulting behaviors is shown in Fig. 14. It is also be seen the size of the peak of the number of new COVID-19 cases reduces with the increase of hospitalization rate but not comparatively much effective as the contact-tracing or quarantined intervention. Finally, the behavior of infected individuals with different initial conditions is shown in Fig. 15. It is observed that for ${\mathcal{R}}_0>1$ all the curves converge to endemic state (see 15(a)) and for ${\mathcal{R}}_0>1$ all the solution curves converge to disease-free state (see 15(b)).

Fig. 13.

Simulation results describing the impact of variation in quarantine rate $(i.e.,{\delta }_1)$ on the cumulative cases.

Fig. 14.

Simulation results describing the impact of variation in isolation/hospitalization rate $(i.e.,\gamma )$ to the cumulative cases.

Fig. 15.

Simulation of the model (3) (a) when ${\mathcal{R}}_0>1$ and (b) when ${\mathcal{R}}_0<1$ with different initial conditions.

Conclusion

This work analyzed the dynamics and possible control of novel coronavirus pandemic in Pakistan utilizing mathematical modeling approach. Initially, we explored some of the basic necessary mathematical properties of the proposed model. The model equilibria and the most crucial mathematical quantity of major public health interest known the basic reproduction number is obtained. The stability results of model equilibria are shown both theoretically and graphically. Then using the least square curve fitting statistical technique, the model is fitted to the COVID-19 confirm cases reported from 1 March 2020 to 15 May 2020, in Pakistan. It is shown that the model predicted infection curve is an excellent agreement to the real infected cases. Based on the fitted parameters the numerical value of the basic reproduction is obtained as ${\mathcal{R}}_0\approx 1.95$. Further, we carried out the sensitivity analysis to determine the impact of model parameters on the disease dynamics and control. Also, the influence of the model important parameters on ${\mathcal{R}}_0$ is depicted graphically. Furthermore, detailed simulation results showing the role of effective contacts or social distancing ($\beta$), the quarantined rate of people exposed and are contacted with COVID-19 people (${\delta }_1$) and finally, the effect of hospitalization or isolation on the COVID-19 infected cases ($\gamma$) is depicted. It is worth mentioning that with these control interventions the situation is very worse and the infected cases raised surprisedly very high. We studied the effect of various quarantine rates in order to determine how this variation influences the epidemic trend. When the quarantine rate was increased by 10% to its baseline value it reduces the newly predicted infected cases by 25%. When the quarantine rates are enhanced by 50% the predicted peak value of newly confirmed cases would reach approximately 3000, representing a significant reduction i.e., 84% in the infected cases. In the case of hospitalization, it is observed that although the peak number of newly infected cases decreases with the increase of hospitalization rate but not comparatively much effective as contact-tracing or quarantined intervention.

In summary, our study suggests that in Pakistan, the prevention and control measures have made significant efforts in controlling COVID-19 infection, still it is needed to carefully follows the recommendations of the World Health Organization (WHO) such as the social distancing, quarantine of infected cases, hospitalization of the infected people with high infectivity, stay at home during the cases are increasing, avoid gathering, etc. Also it is necessary to maintain the quarantine level at a relatively high level to curtail the infection completely. Moreover, professional and qualified medical care staff should supervise centralized quarantine at certain quarantine sites in order to better monitor the infected individuals and prevent further transmission of infection. We hope that the present model for the understanding of COVID-19 infection will be useful in decision making process and to get back the population into its normal position. This model is useful and can be used for the other countries infected data of COVID-19, can estimate their basic reproduction inline with the WHO and can make the analysis of the model in order to have the decrease in the infected cases. We will extend this work in near future to optimal control and vaccination study to observe the impact of vaccination on the population and its controlling.

CRediT authorship contribution statement

Yu Gu: Resources, Software, Validation, Writing – review & editing. Saif Ullah: Funding acquisition, Resources, Software, Validation, Writing – review & editing. Muhammad Altaf Khan: Funding acquisition, Resources, Software, Validation, Writing – original draft, Validation, Formal analysis, Writing – review & editing. Mohammad Y. Alshahrani: Validation, Writing – review & editing, Visualization. Mohammad Abohassan: Validation, Writing – review & editing, Visualization. Muhammad Bilal Riaz: Validation, Writing – review & editing, Visualization.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.