SUMMARY
Connectomes generated from electron microscopy images of neural tissue unveil the complex morphology of every neuron and the locations of every synapse interconnecting them. These wiring diagrams may also enable inference of synaptic and neuronal biophysics, such as the functional weights of synaptic connections, but this requires integration with physiological data to properly parameterize. Working with a stereotyped olfactory network in the Drosophila brain, we make direct comparisons of the anatomy and physiology of diverse neurons and synapses with subcellular and subthreshold resolution. We find that synapse density and location jointly predict the amplitude of the somatic postsynaptic potential evoked by a single presynaptic spike. Biophysical models fit to data predict that electrical compartmentalization allows axon and dendrite arbors to balance independent and interacting computations. These findings begin to fill the gap between connectivity maps and activity maps, which should enable new hypotheses about how network structure constrains network function.
eToc blurb
Liu et al. compare the anatomy and physiology of diverse synaptic connections in the central brain of Drosophila, finding that synapse density and location predict unitary postsynaptic potential amplitude. Modeling reveals that a neuron’s basic architecture of arbors and cables constrains the computations it performs.
INTRODUCTION
The brain coordinates perception and action using networks of diverse neurons with heterogenous synaptic connections1. Understanding how these networks operate requires a synthesis of structural and functional information2–5. Theoretical network models can unify diverse sources of information into a common framework, but to make the most informed computational predictions, modeled neurons and synapses should correspond to real neurons and synapses and should obey known biophysical principles6–8. With densely reconstructed connectivity maps from electron microscopy (EM) images, real network anatomy can now constrain the structure of large network models, improving biological accuracy9–13. However, other sources of biophysical diversity, such as variations in synaptic connection weights (i.e., the physiological strength between synaptic partners) or subcellular electrical compartmentalization are not fully constrained by connectivity maps. Instead, these are often treated as free parameters to be optimized or assumed to be homogeneous. These unconstrained variables make connectivity maps difficult to link directly to activity maps, because different biophysical parameters can produce divergent network function14.
It has been proposed that a small number of anatomical features measurable from a complete connectome might be sufficient to predict true synaptic connection weights and to determine when axons or dendrites need to be explicitly modeled7. Examining this requires a direct comparison of physiology and anatomy across a diverse set of neurons and synapses. Compellingly, postsynaptic density size linearly relates to unitary excitatory postsynaptic potential (uEPSP) amplitude for a single type of neocortical synapse in mouse15, but scaling this to more diverse populations is limited, in part, by the current lack of a full wiring diagram of the mouse brain. However, a recent connectome details the diversity of neural morphologies and synaptic connections throughout half of the central brain of the adult fruit fly, Drosophila melanogaster (the “hemibrain”)16.
Here, we ask how anatomical patterns of connectivity and neuron morphology predict physiological connection strengths and subcellular electrical compartmentalization in the Drosophila brain. We focus on the lateral horn, an anatomically diverse olfactory network (analogous to mammalian cortical amygdala)17–21. In this network, second-order projection neurons (PNs) connect to third-order lateral horn neurons (LHNs)22. Because connectivity and morphology are stereotyped23,24, we can study the anatomy and physiology of the same neurons and connections in different flies. We thus used the hemibrain connectome along with a recent dataset of electrical recordings of identified PN-LHN uEPSPs25 to make comparisons between anatomy and physiology at the elemental level of single neurons and single synaptic connections.
We report three main findings. First, physiological connection weight (i.e., uEPSP amplitude) increases linearly with synapse density (the number of synapses per unit area of postsynaptic membrane) across a diverse sample of connection types. Second, connection weight (measured at the soma) decreases with distance, but primarily from the “inter-arbor cable” that connects the axon and dendrite arbors. In contrast, specific synaptic location within each arbor has little impact. Subcellular electrical compartmentalization can thus be predicted by a neuron’s anatomical arrangement of arbors and cables. Third, biophysical models constrained by anatomical and physiological data predict that LHNs are shaped to maximize input gains in each arbor, while still allowing for passive interactions between arbors. This highlights a potential functional role for the inter-arbor cable in regulating subcellular computation. Together, these findings reveal important links between connectivity maps and activity maps, which should enable construction of more biologically naturalistic network models.
RESULTS
PN-LHN connections and LHN sizes reflect anatomical diversity of the whole brain
Within the lateral horn, PN axons carrying information from each of ~50 olfactory antennal lobe glomeruli converge and diverge onto hundreds of morphologically distinct LHN types (one example pair in Figure 1A), providing an anatomical foundation for diverse transformations of the incoming PN odor code17–21,23–26. In Drosophila, connections between neurons typically consist of multiple synaptic contacts, with each contact of fairly similar physical size (we use “synapse” to refer to individual contact sites, and “connection” to refer to all the synapses between two neurons)16,27. We focus on uniglomerular cholinergic (excitatory) PNs (subsequently referred to simply as “PNs”), which were the PN types studied physiologically25.
Figure 1. Matching diverse LHNs between light and electron microscopy datasets.
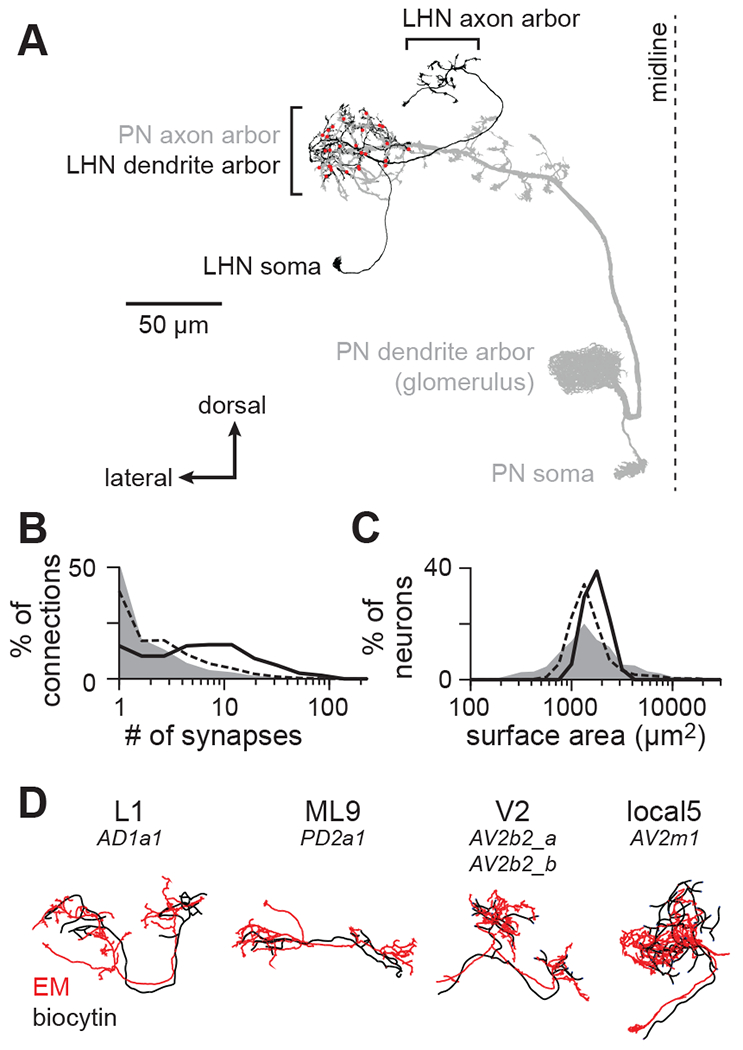
(A) Morphology of a single PN-LHN connection. The PN’s axon arbor targets the lateral horn, where it forms multiple synapses (red points) onto an LHN’s dendrite arbor.
(B) Distribution of the number of synapses per connection for a representative sample of connections across the hemibrain (random sample of 214,245 connections, gray), for all 17,506 PN-LHN connections (dashed line), and for the 135 PN-LHN connections matched to physiology data (solid line)
(C) Distribution of the total membrane surface area for a representative sample of neurons across the hemibrain (random sample of 1000 neurons, gray), for all 1496 LHNs (dashed line), and for the 54 LHNs matched to physiology data (black line).
(D) Example matching morphologies. Black: biocytin fill (physiology dataset). Red: EM morphology (anatomy dataset). LHN names follow a prior study25 with corresponding hemibrain names provided below24. Note that matching morphologies do not always align with hemibrain cell type boundaries. Some types (e.g., V2) correspond to multiple hemibrain types; others do not correspond to all bodyIds of a given hemibrain type.
The hemibrain connectome annotates 100 PNs and 1496 LHNs24, with 17,506 connections between them (most of the 149,600 PN-LHN pairs are not connected). The distribution of synapse counts per connection spans more than two orders of magnitude (Figure 1B). The distribution of LHN surface areas spans about one order of magnitude (Figure 1C). Distributions of both PN-LHN synapse counts and LHN surface areas are similar to (but somewhat narrower than) distributions for connections and neurons throughout the brain (Figure 1B,C).
Cellular morphology identifies PNs and LHNs between datasets
To study anatomy and physiology of the same neurons, we used the hemibrain connectome in conjunction with previous current clamp recordings of LHNs during stimulation of PNs25. Taking advantage of the stereotyped anatomy of the antennal lobe and lateral horn23,24, we identified the same PN and LHN types across these two datasets. PN types were matched by the glomerulus innervated by their dendrites, which uniquely and unambiguously identifies them28,29. Glomeruli vary in the number of PNs innervating them, but we only considered glomeruli with one PN, which allowed us to resolve single uEPSPs in LHN recordings (STAR Methods). LHN types were matched by quantitatively comparing biocytin fills with neuron morphologies in the hemibrain30 (STAR Methods; Figure 1D, S1; Table S1). In total, we matched 12 PNs and 13 LHN types between datasets.
The anatomical properties of this subset were representative of the entire lateral horn, but modestly biased towards larger connections and surface areas. Comparing connections from this subset of PN-LHN pairs to those from all pairs in the lateral horn shows that our sample has modestly higher synapse counts (Figure 1B) and the surface areas of these LHNs are slightly larger than surface areas of all LHNs (Figure 1C). In addition, PN-LHN connections of the same type have similar synapse counts (Figure S2A) and LHNs of the same type have similar surface areas (Figure S2B), although there is some diversity present.
Unitary PN-LHN synaptic potentials are physiologically diverse
We analyzed LHN membrane voltages measured in response to two-photon optogenetic activation of single PNs (Figure 2A)25. Activation of individual PNs produces distinct uEPSP waveforms in the LHN (each corresponding to one PN spike; Figure 2B). We extracted each uEPSP for each PN-LHN connection within a recording (STAR Methods; Figure 2C). Overall, uEPSPs were measurable and reliably detected over multiple LHN recordings for 29 unique PN-LHN pairs. No synaptic responses were evident in 106 pairs, so we considered these to have uEPSP amplitudes of 0 mV. The remaining pairs had inconsistent or unquantifiable synaptic responses and were omitted (STAR Methods), yielding a population of 135 unique PN-LHN pairs matched to anatomy and with reliable estimates of physiology.
Figure 2. PN-LHN connections have diverse physiological weights.
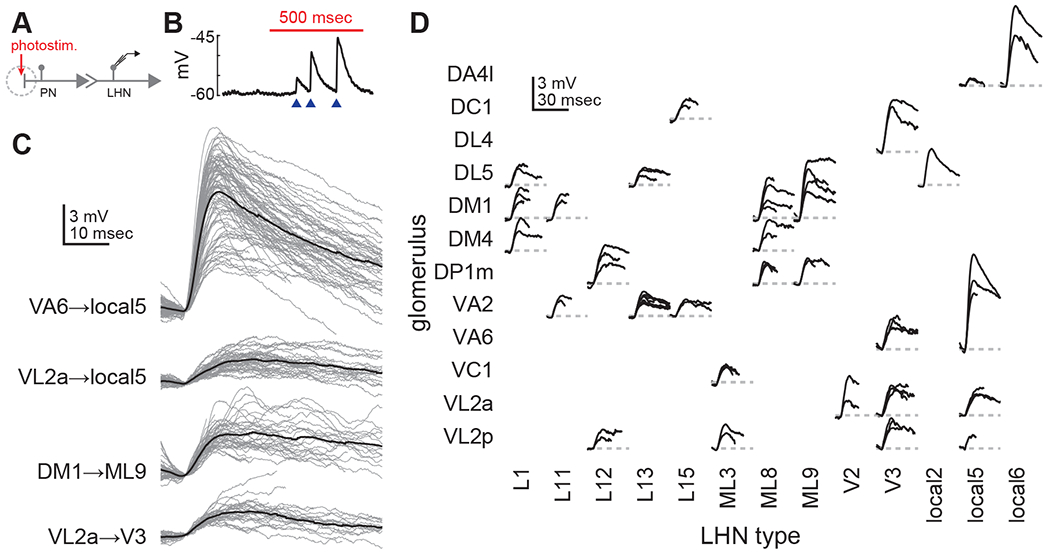
(A) Schematic of experimental configuration. PN dendrites are photostimulated during patch-clamp recording from single LHNs.
(B) Example trace recorded from an LHN during PN stimulation (red bar). Blue arrowheads denote single uEPSPs corresponding to single PN spikes. The increasing uEPSP sizes likely reflect modest short-term facilitation of this connection.
(C) Overlaid traces (gray) of all individual uEPSPs (aligned by start time) detected from individual recordings of four different PN-LHN connections. Each black trace is the mean of all uEPSPs from one recording of one connection type.
(D) Mean uEPSP traces for all identified connections. Multiple recordings (from different flies) of the same connection type are overlaid. Variability between mean uEPSP amplitudes for different connection types is greater than for repeated recordings within the same types (ANOVA, F = 8.8, p = 3.3 × 10−13). All LHN type correspondences with hemibrain type names and bodyIds are provided in Table S2.
Mean uEPSP amplitudes spanned a ~10-fold range (0.4mV to 6.6mV), with distinct and characteristic values for different connection types, but with some variability (Figure 2B–D). The variability of individual uEPSP waveforms within a single recording (e.g., Figure 2C) was consistent across connections (CV 0.35±0.09). This consistency suggests that properties of short-term plasticity or stochastic transmitter release are similar across connections. Occasional variability of mean uEPSP waveforms for the same PN-LHN connection type across recordings may reflect fly-to-fly variability in synapse counts, or differences in long-term plasticity or neuromodulatory state. Despite this variability, clear differences in waveforms between PN-LHN connection types were still observable (Figure 2D). We averaged mean uEPSPs across recordings for each PN-LHN connection type to compare to anatomical data from the same connections.
Anatomical diversity linearly predicts physiological diversity of synaptic connections
Next, we compared the anatomical and physiological strengths of PN-LHN connections. In the quiescent (ex vivo) condition of our recordings, LHNs likely operate in a passive regime, where synaptic potentials are known to reflect the product of synaptic conductance, driving force, and membrane resistance31. Because our measured uEPSPs are relatively small compared to the synaptic reversal potential (estimated to be ~45 mV above rest; STAR Methods), driving force is approximately constant. Therefore, synapse density (synapse count normalized by LHN surface area) should predict uEPSP amplitude, because surface area is inversely proportional to membrane resistance (assuming spatial uniformity of membrane conductances), consistent with recent PN models27. Accordingly, synapse density predicted average uEPSP amplitude well (Figure 3A, solid line; r2 = 0.77, p = 1.0 × 10−43). Importantly, this correlation persisted even without the largest connections or the pairs with both 0 synapses and 0 mV uEPSP amplitudes. Moreover, it agreed with data for connections in the antennal lobe and mushroom body (Figure S3). Thus, anatomical features can predict average physiological weights for diverse connection types.
Figure 3. Anatomical diversity predicts physiological diversity of PN-LHN connections.
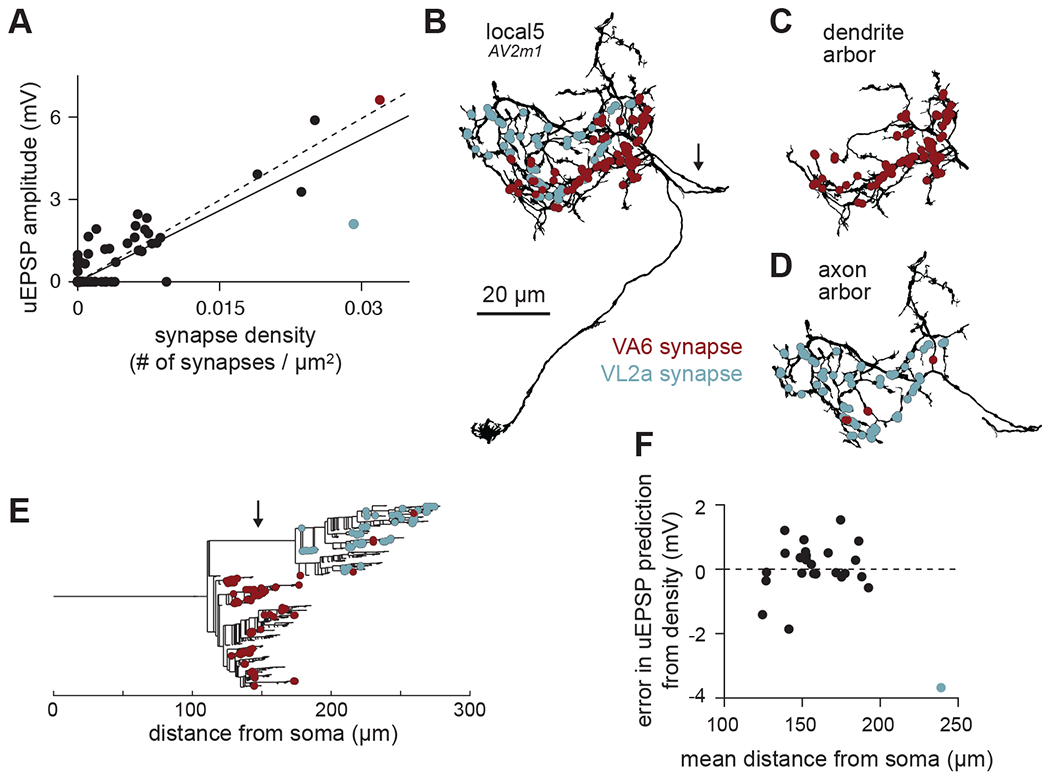
(A) Scatter plot of uEPSP amplitude vs. synapse density for all connections in our sample. Each point is the average value for all samples per connection type. Red and blue points correspond to the VA6 and VL2a connections onto local5. Note that many points are overlaid at the origin, corresponding to connections with no synapses detected in the hemibrain and no uEPSPs detected in physiology. Solid line is linear fit including the axo-axonic VL2a-local5 connection; dashed line excludes this connection.
(B) Morphology of a local5 neuron (hemibrain type AV2m1), with all VA6 and VL2a synapse locations labeled. Arrow identifies the inter-arbor cable, which follows a meandering path to connect the two intermingled arbors.
(C) As in (B) but showing just the dendrite arbor. Almost all the VA6 synapses are formed onto this part of the neuron.
(D) As in (B) but showing just the axon arbor. All of the VL2a synapses are formed onto this part of the neuron.
(E) Dendrogram showing the branching structure of the same local5 neuron as in (D)-(F). Almost all of the synapses onto the axon arbor are more distant from the soma than the synapses onto the dendrite arbor, which is due primarily to the inter-arbor cable (identified by arrow).
(F) Residual error in uEPSP amplitude from synapse density prediction, showing no linear correlation with mean distance of synapses from the soma. uEPSP amplitudes of dendritic inputs are thus not strongly dependent on distance. Each point is the average across all samples per connection type.
Interestingly, one outlier stood out in this analysis: the connection from the VL2a PN onto local5 LHNs. This uEPSP was smaller than predicted by its high synapse density (blue point in Figure 3A). Interestingly, local5 LHNs also received a connection from the VA6 PN, which had a similarly high synapse density, but a large uEPSP amplitude (red point in Figure 3A). The VL2a-local5 uEPSP also had relatively slow kinetics (Figure 2C): the time to the peak of the VL2a uEPSP was longer (11.9 ± 1.7 msec) than for the corresponding VA6 uEPSP (7.1 ± 0.2 msec). However, the uEPSPs between VL2a and a different LHN (“V2”) exhibited a short time to peak (7.9 ± 0.3 msec), indicating that slow kinetics cannot be due to slower synaptic release from the VL2a PN.
The small amplitude and slow kinetics in the VL2a-local5 connection suggests unusually strong cable filtering, which attenuates and delays synaptic potentials32. We thus asked whether the VL2a PN targets local5 more distally than the VA6 PN. The neurites of local5, like those of most local LHNs, organize into two polarized arbors: one biased towards input synapses (dendrite) and one biased towards output synapses (axon)23,24. The arbors of local5 extensively intermingle (Figure 3B), but when viewed separately, a segregated pattern emerges. VA6 synapses almost exclusively target the dendrite arbor (Figure 3C), while VL2a synapses exclusively target the axon arbor (which is more distant from the soma; Figure 3D,E). Thus, the longer distance to the soma for the VL2a connection predicts greater cable filtering and reduced somatic uEPSP amplitude, when compared to the VA6 connection.
Given this role of synaptic distance, we reasoned that it might also impact uEPSP amplitudes for other PN-LHN connections. Surprisingly, after regressing out the effect of synapse density from uEPSP predictions, the residual variability showed no obvious relation to mean synapse distance, other than for the VL2a-local5 connection (Figure 3F). Because all other connections in our dataset target LHN dendrites, this points to some aspect of arbor identity (axon vs. dendrite), instead of distance alone, as an essential determinant of postsynaptic filtering. In light of this, we recomputed the prediction of average uEPSP amplitude from synapse density using only the dendritic connections. This yielded a stronger correlation (r2 = 0.84; Figure 3A, dashed line). Collectively, these results show that synapse density and location both matter for determining somatic uEPSP amplitudes, but that the role of location is not a simple linear function of distance.
Passive compartmental models accurately predict diverse uEPSP amplitudes
To better understand how synapse location and LHN morphology impact uEPSP amplitudes, we turned to biophysical modeling. First, we built single-compartment models for every LHN in our sample by jointly optimizing membrane resistance and capacitance per unit area, and conductance per synapse to fit uEPSP amplitudes (STAR Methods; synaptic conductance waveform shape was adapted from a prior model33 and not explicitly optimized here). These parameters were constrained to be uniform across LHNs, with whole-cell properties varying solely due to variability in neuron size. As expected, these models forced a compromise between underpredicting dendritic and overpredicting axonal uEPSPs (RMS error = 0.95mV; Figure 4A,B). This illustrates the insufficiency of single compartment models for neurons with multiple arbors.
Figure 4. Multi-compartment models accurately predict uEPSP amplitudes better than single compartment models.
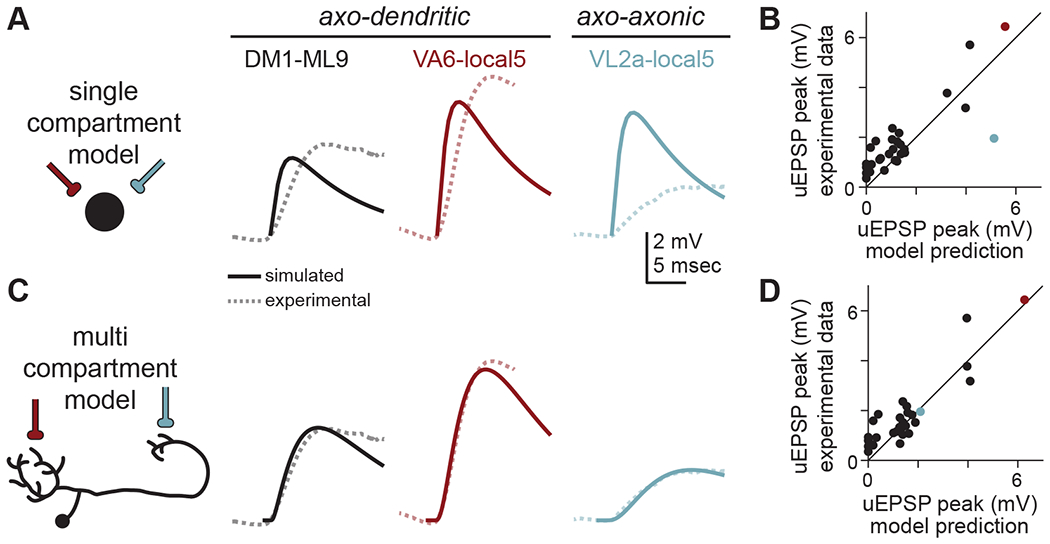
(A) A single compartment (point) model (schematized at left) fit to all PN-LHN uEPSPs in our sample (dashed lines) produces somatic uEPSP waveforms (solid lines) that underpredict true uEPSP amplitudes for axo-dendritic connections and overpredicts the axo-axonic connection.
(B) Peak somatic uEPSP amplitudes for all connections in our sample (with detectable uEPSPs) compared to predictions from the single compartment models. Note the blue point (corresponding to the VL2a-local5 connection) is well below the unity line, while most other points (including small amplitude connections) are above the line. Each point is the average across all samples per connection type.
(C) As in (A) but for multi-compartment models. The optimized model fits axo-dendritic connections as well as the axo-axonic connection.
(D) As in (B) but for the multi-compartment model.
See also Table S2.
We then fit multi-compartment models (with morphology and synapse locations explicitly constrained by hemibrain data) by additionally optimizing axial resistance (STAR Methods). Again, all parameters were uniform across different LHNs, so models only vary due to morphology and synapse location (the synaptic conductance waveform was identical to that in the single-compartment model). These models predicted the amplitude of uEPSPs across our dataset with better accuracy (RMS error = 0.68mV; Figure 4C,D). This indicates that differences in uEPSP amplitude for connections onto different arbors can be parsimoniously explained by differences in passive filtering arising from neuronal morphology, requiring neither active conductances nor cell-type or subcellular specificity of passive properties.
Models predict that arbors democratize synaptic efficacies, while inter-arbor cables stratify them
We next used multi-compartment models to understand the complex relation between anatomical synapse locations and physiological synapse amplitude, focusing exclusively on local LHNs because they receive PN input onto both dendrite and axon arbors. Using the parameter values determined by the model fits in Figure 4D, we built models for 49 local LHNs, including local5 (STAR Methods). These models allowed us to “stimulate” single synapses and “record” from any neuronal location. Accordingly, we decomposed uEPSPs into the constituent potentials evoked by individual synapses, called miniature EPSPs (mEPSPs), measured either at the synaptic location or the spike initiation zone (SIZ; located near the base of the dendritic arbor33; Figure 5A). We refer to the amplitude of the mEPSP at the SIZ as “synaptic efficacy,” and note that voltage at the soma largely tracks voltage at the SIZ, but with additional passive filtering.
Figure 5. Arbors democratize and cables stratify synaptic efficacy.
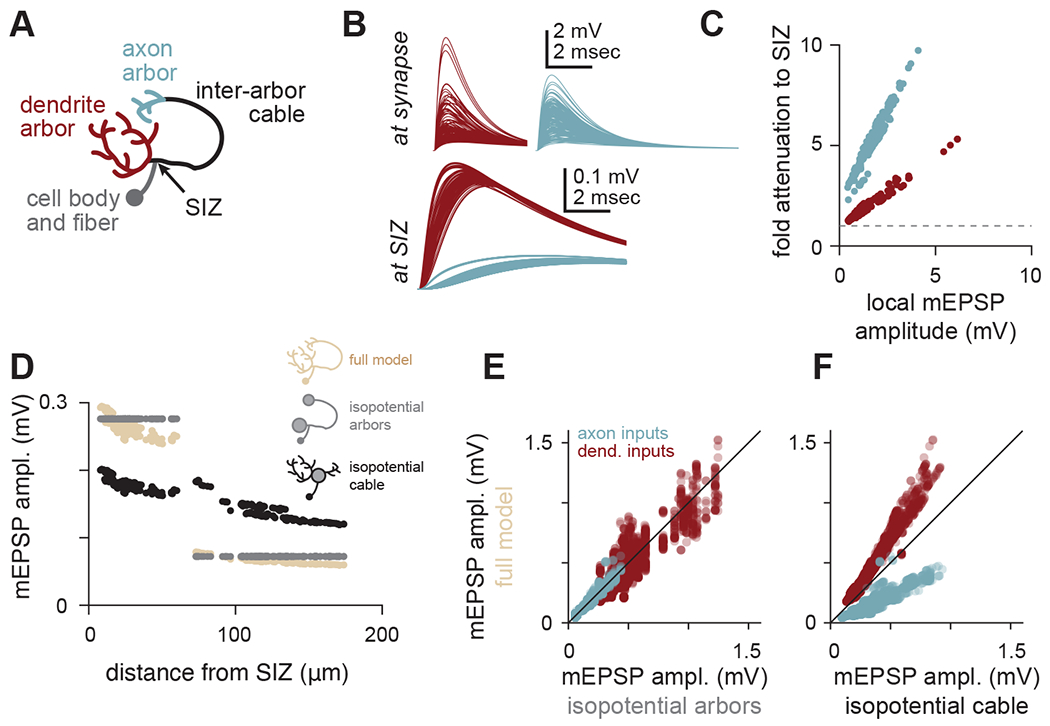
(A) Schematic of arbors, cables, and spike initiation zone (SIZ) in local LHNs.
(B) Top: traces of simulated mEPSPs measured at each synapse (red, dendritic; blue, axonal) onto a local5 LHN (same example as Figure 3). Local mEPSPs are large with similar amounts of variability between arbors. Bottom: traces of simulated mEPSPs measured at the SIZ (note different voltage scale). Differences in mEPSPs are apparent between arbors.
(C) Local mEPSP amplitudes relate linearly to their voltage attenuation en route to the SIZ. Within each arbor, synapses with larger local depolarizations also face proportionally larger attenuation. This proportionality is different for each arbor. Red points are dendritic mEPSPs, blue points are axonal mEPSPs.
(D) mEPSP amplitudes for all ePN synapses onto the same local5 LHN (hemibrain type AV2m1), as a function of distance from the SIZ (tan). The inter-arbor cable introduces a discontinuity in this relationship: while the most proximal axonal synapses are nearly the same distance from the SIZ as the most distal dendritic synapses (~60 μm), they evoke strikingly smaller mEPSP amplitudes. Grey points are the same measurements, but for a model with isopotential arbors. Black points are for a model with an isopotential inter-arbor cable.
(E) mEPSP amplitudes simulated with the full model vs. the isopotential arbor model for all synapses across all local LHNs in our sample. The isopotential arbor model was a good predictor of the mEPSPs in the full model (r2 = 0.87).
(F) mEPSP amplitudes simulated with the full model vs. the isopotential cable model for all synapses across all local LHNs in our sample. The isopotential cable model introduces systematic biases in mEPSP amplitudes, making it a less good predictor of mEPSPs in the full model (r2 = 0.47).
We first measured mEPSPs at synaptic sites in our models, to ask whether local morphological differences yield systematic electrical differences between axon and dendrite arbors. In the local5 LHN model, mEPSPs at synaptic sites were diverse, with no major differences between arbors (Figure 5B). Because the conductance is the same for all synapses in our model, all diversity in mEPSPs must come from variations in local input resistance. Therefore, local electrical properties at each synapse are variable, but axons and dendrites have similar amounts of variation.
We then measured the same mEPSPs at the SIZ of the local5 LHN. There we saw the opposite pattern: mEPSPs were similar for synapses on the same arbor, but different for synapses on different arbors (Figure 5B). This suggests subcellular processing by LHNs democratizes synaptic efficacies within arbors, but stratifies efficacies (i.e., introduces characteristic differences) between arbors.
To better understand the within-arbor democracy, we compared local mEPSP amplitudes with the fold attenuation to the SIZ (local amplitude divided by amplitude at the SIZ; Figure 5C). This revealed strong linear correlations for synapses within each arbor, but different slopes and intercepts for different arbors. Therefore, synapses within an arbor generate widely different local depolarizations, but these differences are mostly normalized by compensatory voltage attenuation en route to the SIZ (tan points in Figure 5D). Synaptic efficacies from the “perfect” democracy implemented by a model with isopotential arbors were minimally different from the full model (gray points in Figure 5D), which was consistent for synapses across all local LHNs we studied (Figure 5E, STAR Methods).
In contrast to the democracy of the arbors, the inter-arbor cable stratifies synaptic efficacies. This is evident from the fact that the isopotential arbor model retains the differences between arbors (Figure 5D,E). Notably, in a model with an isopotential cable, synaptic efficacies took on intermediate values, varying smoothly with distance; Figure 5D,F). Therefore, the long and thin inter-arbor cable introduces compartmentalization between arbors. Parallel effects occur for mEPSP latency (Figure S4). Stratifying synaptic efficacies between arbors but not within arbors results from cable theory34. Voltage decays exponentially along the inter-arbor cable, mimicking an infinite cable because each arbor acts like a current sink. In contrast, voltage decays minimally within arbors, because the sealed ends of neurites direct nearly all synaptic current towards the arbor root.
PN connections onto local LHNs mostly target individual arbors
The most straightforward way for subcellular compartmentalization of LHNs to participate in transforming the incoming PN odor code is if individual PNs from different glomeruli target different arbors. We have shown already that VA6 and VL2a PNs target different arbors of local5 LHNs, but it is not clear whether this patterning occurs frequently. Strikingly, we found that 72% of connections onto local LHNs (of 5 synapses or larger) targeted one arbor nearly exclusively (≥90% of synapses targeting one arbor), much more than expected from random targeting (Figure S5A,B). However, systematic targeting of PN synapses to sub-arbor structures appeared less pronounced (Figure S5C–F). Thus, connections from PNs closely track the compartmentalization of LHNs, largely isolating their synapses to either the dendrite or axon arbor, but with less organization within each arbor.
Models predict that inter-arbor cables establish independent, robust, and maximal local input gain
While the SIZ is of clear importance, individual arbors may also perform local functions. For instance, direct excitation of axons may modulate spike-evoked neurotransmitter release or drive graded release without spikes35. However, this requires some degree of electrotonic independence between arbors, which appears at odds with our observation of inter-arbor voltage propagation. How do LHNs strike a balance between independence and interaction between arbors?
We first used our compartmental models to investigate each arbor’s local input gain. For the same synaptic conductance, an arbor with higher input gain will exhibit a larger local depolarization. We thus approximated input gain by the mean mEPSP amplitude across all synapses in an arbor (measured at each arbor’s primary branch point). Input gain was larger in axon arbors than in dendrite arbors (Figure 6A). This corresponded to differences in arbor surface areas (Figure 6B). Accordingly, local arbor membrane resistance almost completely predicted the variability in local input gain for both axon and dendrite inputs (r2 = 0.87; Figure 6C). Thus, each arbor operates with its own input gain, largely determined by its surface area.
Figure 6. Inter-arbor cable lengths balance independence of and interaction between arbors.
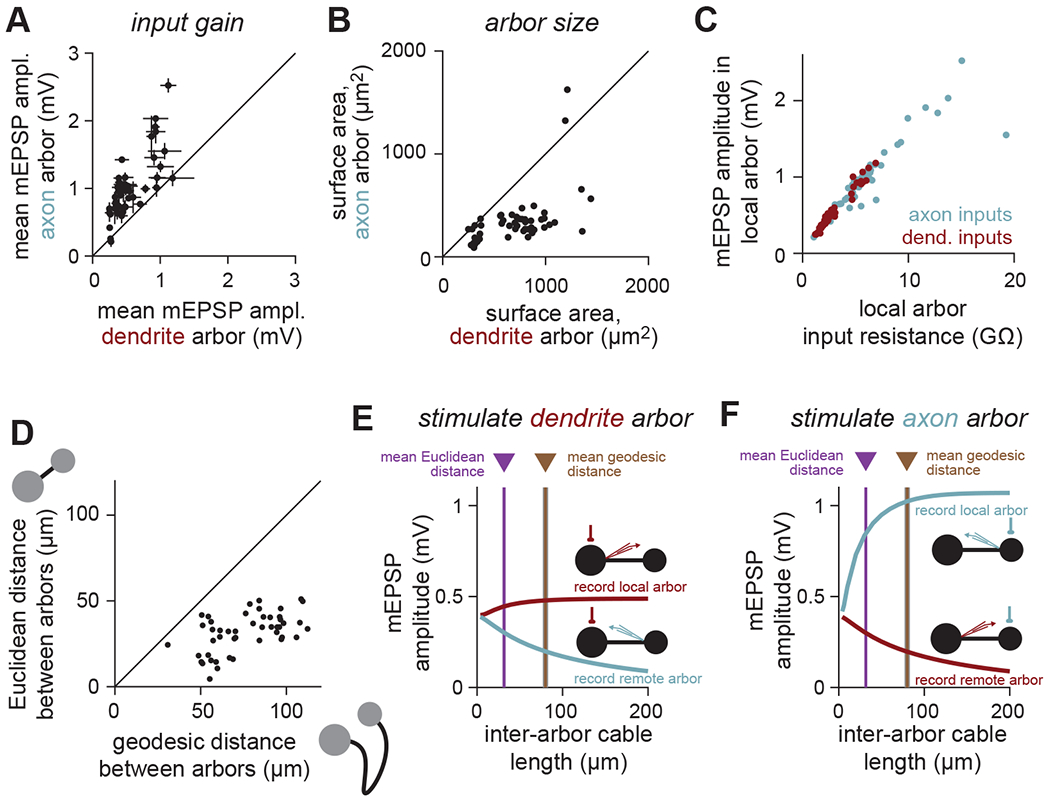
(A) The local arbor input gain (measured as mean mEPSP amplitude at the first branch point of each arbor across all synapses on that arbor) is larger in axons than dendrites (i.e., the same size synaptic conductance depolarizes the axon more than the dendrite). Each point denotes one local LHN (error bars denote S.D.).
(B) The surface area of axon arbors is smaller than dendrite arbors. Each point denotes one local LHN.
(C) Input gain (mean local mEPSP amplitude) can be predicted by the local arbor input resistance, for both axon and dendrite inputs. Consequently, each arbor is minimally affected by distant current sinks, such as the other arbor. The shared slope comes from the shared specific membrane resistance.
(D) Geodesic distance (path length) of local LHN inter-arbor cables is longer than the Euclidean distance (straight line path) between arbors. Each point denotes one local LHN.
(E,F) Input gain (local arbor mEPSP amplitude) in the barbell (simplified isopotential arbor) model of an average local LHN depends strongly on the length of the inter-arbor cable. The true (geodesic) length of the cable balances maximizing local input gain while minimizing signal loss between arbors.
Membrane resistances, however, can fluctuate dramatically due to synaptic activity or intrinsic plasticity36,37. We therefore wondered whether local arbor input gain is robust to changes in remote membrane resistance. We simulated an average local LHN with a simplified “barbell” model: a single compartment for each arbor and a multi-compartment cable connecting them (STAR Methods). We then systematically varied the membrane resistance of the remote arbor while measuring local mEPSP amplitude. Strikingly, local input gain was insensitive to variations in remote arbor membrane resistance (Figure S6).
We next looked more closely at inter-arbor cables. In local LHNs these meander along paths that deviate from the shortest (Euclidean) path between arbors (2.8±1.7 times longer; Figure 6D; arrow in Figure 3B). Cable length may thus be tuned to perform computational functions – such as maintaining independent input gains while allowing inter-arbor interactions – rather than simply connecting axons to dendrites.
To test this, we manipulated the inter-arbor cable length in the average barbell model. Longer cables increased local arbor input gain (top curves in Figure 6E,F) by impairing the other arbor’s ability to siphon off current. However, input gain saturated once the cable was long enough to resemble a semi-infinite cable38 (from the perspective of the local arbor). Interestingly, the geodesic (true) mean cable length yielded mEPSPs close to the point of saturation (dendrite, 97.3±2.0%; axon, 94.7±4.6%), such that further lengthening would have vanishing effects on local input gain. Lengthening the inter-arbor cable also decreased mEPSP amplitudes measured from the remote arbor. However, these continued to decrease after the local mEPSPs saturated (bottom curves in Figure 6E,F).
Collectively, these analyses suggest that the independence of each arbor is established by an inter-arbor cable that is long enough to maximize local input gains. However, the cable is also short enough to permit passive exchange of information, allowing axonal input to contribute to depolarizing the SIZ. Thus, the inter-arbor cable balances independence and interaction between arbors, potentially expanding the computational repertoire of single neurons.
Predicted functions of compartmentalized neurons
How might independent input gains in each arbor affect how a neuron transforms inputs into outputs? While our model did not allow for direct simulation of active properties, we used prior measurements of spike threshold and general properties of transmitter release to predict how input to each arbor controls output. Revisiting the barbell model of the average local LHN, we made functional predictions for three configurations of activation: input only to the dendrite arbor, input only to the axon arbor, and input to both arbors together.
First, when inputs arrive only onto the dendrite arbor, the LHN operates in a “feedforward spiking drive” mode. With a spike threshold 15mV above rest at the SIZ19,26, strong dendritic input (0.03 synapses/μm2) can rapidly evoke spikes, while a weaker input (0.0075 synapses/μm2) does not (Figure 7A). Varying synapse density and input spike rate shows that only the strongest connections evoke spikes on their own; weaker connections would require coincident activity of multiple inputs (Figure 7B). Passive propagation to the axon arbor strongly attenuates these signals (Figure 7C,D)33.
Figure 7. Predicted functions of compartmentalized neurons.
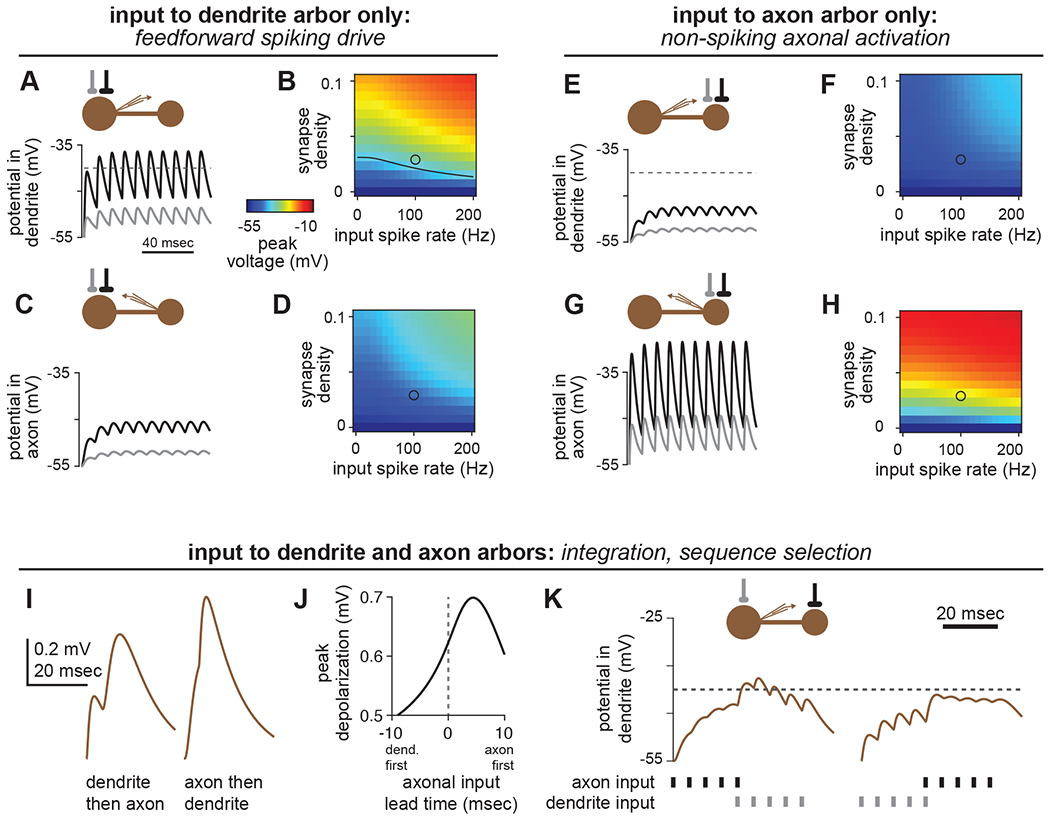
(A,B) Input to the dendrite arbor alone can readily drive spikes in local LHNs. (A) In the average local LHN, a strong connection (0.03 synapses/μm2, black trace) driven at 100Hz evokes EPSPs that depolarize the SIZ above spike threshold (−40mV). A weaker connection (0.0075 synapses/μm2, gray trace) does not reach spike threshold. (B) Peak voltages (encoded by color) obtained for dendritic stimulation for a range of synapse densities and input spike rates. Black line in the plot corresponds to the spike threshold of −40mV. The black and gray circles correspond to the black and gray traces in (A), respectively.
(C,D) As in (A-B), but with recording in the axon arbor.
(E-H) Input to the axon arbor alone cannot drive spikes, but substantially depolarizes the axon. Panels are as in (A-D), but with stimulation to the axon arbor.
(I-K) Temporal delays along the inter-arbor cable create selective responses to different input sequences. (I,J) A spike impinging on the axon before a spike impinging on the dendrite yields a larger peak depolarization at the SIZ than the opposite sequence. (K) Spike packets can depolarize the SIZ of an LHN past spike threshold in one sequence, but not the other. In each panel, the connection onto the axon is stronger than the connection onto the dendrite, to compensate for attenuation.
Second, when inputs arrive only onto the axon arbor, the LHN operates in a “nonspiking axonal activation” mode. Even the strongest physiologically plausible inputs (simultaneous activation of all PN inputs to an LHN axon) with high spike rates are insufficient to depolarize the SIZ to spike threshold (Figure 7E,F). However, these inputs strongly depolarize the axon directly (Figure 7G,H), potentially causing graded (spike-independent) transmitter release, which starts at voltages of ~10-15mV above rest in invertebrates35,39–41.
Third, when inputs arrive on both the dendrite and axon, the LHN operates in one of several modes. In the simplest case, these inputs may simply integrate. In another case, direct depolarization of the axon might alter the amount of neurotransmitter released by action potentials, reminiscent of effects in cortical neurons42,43. Finally, the delay introduced by propagation along the inter-arbor cable (Figure S4) may enable sequence-selective responses. With spike generation occurring near the dendrite arbor, synaptic input sequences that activate the axon before the dendrite cause larger depolarizations of the SIZ than the opposite sequences (Figure 7I–K). Together, these simulations provide a framework for generating explicit hypotheses about how neuronal morphology shapes subcellular computation within the context of network-level function.
DISCUSSION
Predicting synaptic function from connectomic data
Our results show that much of the diversity in mean physiological connection weights between PNs and LHNs can be explained by anatomical properties measurable in EM images. The number of synapses and LHN surface area successfully predict somatic uEPSP amplitudes for dendritic connections, but severely underpredict amplitudes for axonal connections. However, a more complex model incorporating neural morphology and synapse locations accurately predicted the physiology of connections onto both arbors, highlighting the insufficiency of neural point models (which ignore morphology). It is perhaps surprising that such a strong correspondence occurs with purely passive models, given the plethora of voltage-gated ion channels expressed in neurons44. However, the quiescent network state (ex vivo preparation) and the minimal stimulation (single spike resolution in single neurons) are both favorable conditions for remaining in a passive regime.
We found it striking that the relationship between dendritic synapse density and uEPSP amplitude was largely linear, and that connections in the antennal lobe and mushroom body were consistent with this relationship. This suggests a conservation of fundamental biophysics across neurons and synapses. Notably, the capacitance of neural membrane and the resistance of intracellular medium are fairly consistent in different neurons and species45. Although membrane resistance is more variable due to differences in ion channel expression and activation, the quiescent network state likely quenches many of these differences. The size and shape of the synaptic conductance waveform is likely fairly uniform across cholinergic synapses in the Drosophila brain16,27, but does vary in a use-dependent manner46,47. Synapses using different transmitters and receptors will encounter different driving forces and will likely have different conductance waveforms. We thus anticipate that our predictions of cellular and synaptic function from PN-LHN connections will apply to other cholinergic connections in the fly brain (although some features will remain idiosyncratic).
Our results also highlight the importance of comparing structure and function with single neuron and single spike resolution. While we found that connectomic data accurately predicted uEPSPs evoked by single spikes in single neurons, a recent study (using the same data sources) reported lower predictive power for compound EPSP amplitudes evoked by multiple spikes in multiple neurons24. Future efforts to link connectivity and physiology may thus face challenges if sufficient physiological resolution is not obtained, but our results suggest that biophysical models could fill the gap in certain instances. For example, spatial and temporal integration across neural populations can be explicitly modeled to match commonly used experimental measures, such as voltage imaging from neuropil containing multiple cells or cell types.
Arbors and cables in cellular computation
Our results show that individual arbors passively integrate synaptic input democratically. This occurs because large local variations in mEPSP amplitude are mostly offset by compensatory variations in voltage attenuation. The electrotonic structure of central Drosophila neuron arbors may thus be similar to the dendrites of cerebellar Purkinje cells, which orchestrate a similar dendritic democracy with passive mechanisms in a heavily branched arbor48. This configuration has been attributed to the lack of a central trunk neurite (Figure S7)49. Drosophila neurons may therefore rely on branching structure to achieve uniform synaptic efficacy without special spatial patterning of ion channel expression or synaptic conductances50. In addition, because most PN-LHN connections target a single arbor with multiple spatially distributed synapses, much of the residual variability due to synapse location will average out for larger connections. This supports the idea that single arbors may be fundamental “units” of computation in Drosophila neurons.
Inter-arbor cables strike a balance between interaction and independence between arbors. Interaction enables neurons to compare inputs arriving on different arbors. This is especially relevant because each arbor receives its own complement of synaptic inputs. Inter-arbor cables in local LHNs are also longer than necessary to connect the arbors, enabling discrimination of temporal sequences on behaviorally relevant scales of ~10 msec51,52. In contrast, independence between arbors can enable some functions to remain arbor-specific. For instance, arbor-specific structural plasticity53 or active conductances (e.g., voltage-gated potassium channels54,55) could implement different transformations within each arbor prior to comparison via the inter-arbor cable. This could enable more complex computations such as multiplication56.
The abstraction of intricate morphologies into arbors and cables should prove useful for studying other neurons. In flies, a wide range of configurations exist, including neurons with one arbor and no cable (some local neurons24,57), neurons with one arbor and one cable (Kenyon cells without axonal branching), three arbors with interposed cables (optic lobe neurons58,59), and 2-dimensional arrays of dozens of arbors (amacrine neurons60). An intriguing possibility is that the arbor and cable configuration largely determines the passive biophysics of these neurons, providing a simple framework for predicting the function of diverse neurons.
From connectivity maps to activity maps
The pairing of network connectivity maps with knowledge of neuronal and synaptic physiology provides a foundation to formulate hypotheses about activity maps, because assumptions about the function of each component can be calibrated7. We take important steps in this direction by showing how synapse densities predict uEPSP amplitudes and how morphology predicts subcellular computation. Moreover, we demonstrate that the simplified barbell model balances biological accuracy with computational tractability. Incorporating these results into simulations of large neural networks should yield more precise hypotheses about the function of previously unexplored brain circuits.
An important goal for the future will be to incorporate additional sources of knowledge to constrain other properties, such as synaptic plasticity, active conductances, and neuromodulation. For example, short-term plasticity can correlate with the number of presynaptic vesicles or the location of a synapse along the dendrite61,62. Active properties of neurons are less likely to be predictable from ultrastructure but could be predicted from proteomics and transcriptomics63,64. Neuromodulation can reconfigure network function65, for example by altering synaptic strengths, but it is not clear if such changes are visible in EM images47,66. High resolution mapping of biochemical processes would thus be a valuable companion to a connectome67.
Connectivity maps of increasingly large brain volumes bring new opportunities for understanding network organization, but predicting function from structure remains famously difficult68. While we have focused here on the function of individual components (i.e., neurons and synapses), a central challenge will be identifying how the operation of entire networks depends on those components. Although physiological properties of synapses and neurons are most easily characterized in quiescent network states (e.g., ex vivo), many network operations occur in highly active states (e.g., in vivo)36. The combination of connectivity maps with validated models of synaptic and neuronal function should help to bridge this gap, by generating testable predictions of how the anatomy and physiology of neurons and synapses constrain activity maps during behavior.
STAR★Methods
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, James M. Jeanne (james.jeanne@yale.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
Analyzed physiology and morphology data are included as Supplemental Data S1–S4. Other data analyzed by this paper are publicly accessible, as listed in the key resources table.
All NEURON model files, interfacing Python scripts, and MATLAB model files have been deposited in Zenodo. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Hemibrain connectome, v1.1 | Scheffer et al.16 | Neuprint.janelia.org |
| Matched and corrected LHN morphologies | This paper and Scheffer et al.16 | Data S1 |
| Analyzed physiology data | This paper and Jeanne et al.25 | Data S2 |
| mEPSP simulation data | This paper | Data S3 |
| Subcellular anatomical details of LHLNs | This paper and Scheffer et al.16 | Data S4 |
| Software and algorithms | ||
| MATLAB R2020a | Mathworks | http://mathworks.com |
| Python 3.7.0 | Python Software Foundation | http://python.org |
| R Studio 1.2.5033 | RStudio, Inc. | http://www.rstudio.org |
| Natverse | Bates et al.69 | http://natverse.org |
| NEURON 7.7.2 | Hines and Carnevale70 | http://neuron.yale.edu/neuron |
| Code to identify LHNs between biocytin fills and hemibrain skeletons | This paper | 10.5281/zenodo.5711439 |
| NEURON model files | This paper | 10.5281/zenodo.5716323 |
| Barbell model files | This paper | 10.5281/zenodo.5716321 |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Electrophysiology recordings from adult Drosophila melanogaster were analyzed from previously published data. The associated publication reports all relevant details of experimental procedures and key resources25.
METHOD DETAILS
Data sources and inclusion
Whole-cell patch-clamp recordings (one recording per fly) from brain explant (ex vivo) preparations were analyzed from a previously published study of physiological connectivity in the lateral horn25. These data also included skeletons of each recorded neuron traced from confocal images of biocytin fills. Detailed anatomy data were obtained from the publicly accessible database of traced neurons in the “hemibrain” EM connectome (version 1.1)16.
To ensure reliable estimates, we only included LHN types in our analysis if at least two neurons of that type were recorded as a part of the physiology dataset25. In addition, connections were excluded when they were not detected reliably (we required a connection to be detected at least two times across all recordings of that LHN type in Jeanne et al.25) or when distinct uEPSPs could not be identified. In two cases (DL5-local2 and VL2p-local5), uEPSPs could only be identified in one of two recordings but a connection was clearly visible (without distinct uEPSPs) in the other recording, so we included these connections using solely the uEPSPs from one recording. We also excluded from all subsequent analysis those recordings of PN-LHN connections with fewer than three uEPSP waveform samples. Of the 156 unique PN-LHN type connections, 21 were excluded for the reasons listed here, yielding 135 connections with reliable and quantifiable physiological responses.
The bilateral LHN type CML2 was omitted from analysis because its contralateral processes exited the hemibrain EM volume, so full morphology information was not available. LHN type ML4 was omitted because this neuron sometimes exhibited spontaneous (independent of photostimulation) synaptic activity, making it impossible to assign specific EPSPs to specific PNs. In total, the 13 included LHN types consisted of 54 individual LHN hemibrain body IDs. The bodyIds of all matched PNs and LHNs are provided in table S1.
In the process of analyzing the electrophysiology traces, we made several minor adjustments from the connections reported in Jeanne et al.25. The VA7l-local6 connection reported in that study was found to be misidentified and was corrected to be from glomerulus VA7m here. Connections from DP1m to ML8 and ML9 and from VA2 to L11 did not meet the time-averaged depolarization threshold requirement for detection in Jeanne et al.25, but each nonetheless exhibited several clear uEPSP waveforms, so we included them. Within the set of 13 LHN types, we never observed reliable and measurable connectivity from five single-PN glomeruli (VC2, VM4, DM3, VA4, and VA7l), so the PNs innervating these glomeruli were excluded from all analyses.
For modeling of the expanded population of local LHNs (figure 5E,F, 6, and 7), we selected neurons for analysis by the following procedure. First, we considered only local LHNs because they receive inputs from PNs on both axon and dendrite arbors. To identify local LHNs, we searched the hemibrain database for neurons with 80% or more of their synaptic inputs within the lateral horn neuropil and with 80% or more of their synaptic outputs within the lateral horn neuropil. We then visually inspected each of these 215 bodyIds to identify neurons with minimally intertwined axon and dendrite arbors (we took this step because the intertwining often led to improper automated splitting and merging of neurites which required manual correction; see section “manual correction of neuron morphologies” below). This yielded 41 bodyIds. Any minor merge or split errors were corrected manually. These 41 LHNs were added to 8 of the 10 local LHNs that we had already matched to our physiology data (we omitted the two local2 LHN bodyIds from this analysis, since they only have one arbor), yielding a total of 49 local LHNs which served as the basis for all analyses in figures 5–7.
A complete accounting of the hemibrain bodyIds and physiology data included in each figure panel is provided in Table S2.
Matching morphologies between light microscopy and electron microscopy data
PNs were matched between the physiology and anatomy datasets based on the glomerulus innervated, an unambiguous identifier of uniglomerular cholinergic PN type. We focused here on only PNs of glomeruli with a singular uniglomerular cholinergic PN (see “Detection and quantification of PN-LHN uEPSPs” for details). In total, 12 different PNs elicited measurable uEPSPs in LHNs.
LHN types were matched between the physiology and anatomy datasets solely based on morphology by comparing biocytin fills recovered from patch-clamp recordings with traced skeletons from the hemibrain connectome. We first applied bridging transformations69 to bring the biocytin fills and hemibrain neuron skeletons into the same coordinate space (JRC2018F). When necessary, we mirrored biocytin fills across the midline so that all neurons appeared on the right side of the template brain (where all hemibrain LHNs reside). Due to left-right symmetry23, all biocytin-filled neurons included in this analysis are expected to exist on both sides of the brain. We identified all 1496 neurons in the hemibrain volume that enter the lateral horn neuropil and quantitatively compared their morphologies to the biocytin fills using NBLAST30.
LHN cell types were defined as previously determined25. Morphological matches to EM neurons were thus made without regard to cell typing that has been performed in the hemibrain connectome. This is important because hemibrain cell types were defined by both morphology and connectivity24. Nonetheless, many of the matching EM neurons for each cell type closely followed hemibrain cell-type boundaries (Supplemental Table S1), although the correspondence was not always one-to-one.
Owing to the inherently lower resolution of confocal microscopy relative to electron microscopy, we employed two strategies to improve comparisons of traced neurons between imaging modalities. First, we emphasized long range neurites over dendritic arbors by employing the “useAlpha” parameter of the NBLAST function. Second, we pruned the shortest processes in the EM neurons (all processes shorter than 5 μm in length).
NBLAST scores for all pairwise comparisons were computed as the mean of “forward” and “reverse” scores and were normalized to enable better comparison across diverse morphologies30. We then selected the best matching EM neurons (top 2% based on scores) for expert visual inspection (blinded to connectivity). We were able to readily rule-in or rule-out each of these top-scoring EM neurons as a match to the biocytin fills by directly examining similarities and differences of morphology in the common coordinate template space. Particular emphasis was placed on the course and contour of primary arbors of axonal and dendritic trees as well as the inter-arbor cable, since these were consistently present in both the light and electron microscopy volumes. This approach was necessary given the differences between light and electron microscopy noted above. The corresponding EM neuron bodyIds and NBLAST scores for each cell type in the physiology dataset are provided in Table S2. Two-dimensional projections of morphologies are provided in Figure S1 and skeletons of all biocytin fills and hemibrain neurons in the same brainspace are provided in Supplemental Data S1.
In total, 54 LHNs from the connectome could be matched to 13 LHN types defined morphologically from their biocytin fills (each LHN type consisted of multiple neurons; Table S1; mean ± s.d. NBLAST score = 0.453±0.066), corresponding to a mean NBLAST rank = 8.07 of 1496). We were thus able to identify 156 distinct PN-LHN type pairs in both the connectome and the physiology dataset.
Although all matches ranked among the highest NBLAST scores, some scores were still relatively low, compared to other studies30. This likely results from two minor artifacts in our biocytin morphologies: the occasional loss of the primary neurite (and cell body) when retracting the patch pipette at the end of a recording session and distortions arising from registering each individual brain to a common template25. In all cases, expert visual inspection easily compensated for these artifacts. In addition, restricting the analysis in Figure 3A to only those connections from LHN types with mean NBLAST scores greater than 0.45 did not appreciably change the magnitude or significance of the correlation. Therefore, the main conclusions do not rely on the LHN types with the lowest confidence matches between light and electron microscopy.
Manual correction of neuron morphologies
All LHN morphologies were exported directly from the hemibrain dataset via the neuprint_read_neurons function (with “heal” set to “true”) of the Natverse toolbox69. This produced anatomical models where each neurite was defined by many short cylindrical segments, with diameters matched to the EM data. A handful of LHNs (mostly local neurons) had heavily intertwined neurites, and the automated morphological extraction often merged or separated neurites incorrectly (as judged by visual comparison to the raw EM images using Neuroglancer). To compensate for this, we visually inspected all LHN morphologies using NeuTube70, and manually corrected all merge and separation errors by direct comparison to the raw EM data. Datafiles (.swc format) of all LHN morphologies included in this study (incorporating all manual corrections) are provided as Supplemental Data S1.
QUANTIFICATION AND STATISTICAL ANALYSIS
Detection and quantification of PN-LHN uEPSPs
Unitary excitatory postsynaptic potentials (uEPSPs) were measured from recordings of LHNs during independent photostimulation of each of 39 PN types25. Stimulated PNs analyzed here were exclusively of the anterodorsal or lateral lineage and each innervate a single glomerulus. Each glomerulus is innervated by a stereotyped set of 1-8 uniglomerular cholinergic PNs16,71 and most or all PNs from each glomerulus target the same LHNs24–26. Here, we studied only the PNs of glomeruli with just one uniglomerular cholinergic PN (i.e., PN types consisting of just one neuron each). This is because photostimulation of glomeruli with multiple PNs drove regularly-spaced spikes in each PN, but at slightly different times and rates, evoking a complex compound EPSP in the LHN25. This made reliable detection of individual distinct uEPSPs possible only for glomeruli with one PN. In these cases, regularly spaced uEPSPs were clearly discernable.
All uEPSPs were manually identified from the recorded LHN traces. The identity of the presynaptic PN was determined by the identity of the stimulated glomerulus in each trace. Each experiment included multiple stimulation sites in each glomerulus and all the trials corresponding to a given glomerulus were grouped together. Each uEPSP was identified by its characteristic asymmetric waveform (fast rise and slow decay) and its start time was manually annotated by two expert (unblinded) scorers. To minimize user-specific annotation errors, only those uEPSPs annotated by both scorers with less than 3 msec difference in start times were included (the start time was taken to be the minimum of the two times, when there was a difference).
For each recorded connection, all uEPSP waveforms were averaged to generate each trace in Figure 2D. If a connection was identified in a particular recording in Jeanne et al.25, but we could not reliably detect uEPSPs, that connection was excluded from computing the average, which is why a few PN-LHN pairs (DL5-local2, VL2p-local5, and DA4l-local5) have only a single trace in Figure 2D. If a connection was not identified in a particular recording in Jeanne et al.25, the uEPSP amplitude was considered to be zero and included in the average. To enable comparisons with anatomical measures, we averaged the peak uEPSP amplitude for all samples of the same PN and LHN types. To ensure good estimates, we only considered those connections which were detected in at least two flies (with the two exceptions noted above).
The comparison of uEPSP amplitude and synapse density (Figures 3A and S3) reveal several points that lie on the horizontal and vertical axes. These points are likely due to methodological constraints in measuring uEPSPs, rather than an indication of silent synapses or indirect connections. The points on the horizontal axes likely occur because of baseline recording noise, which prevented us from reliably identifying uEPSPs of amplitude less than ~0.2mV. This can make the uEPSPs of very small connections completely undetectable (yielding an estimate of 0mV). In other cases, it can introduce a modest positive bias to the mean uEPSP amplitudes (if the only detectable uEPSPs are larger than the true average). This likely accounts for why many of the small connections have slightly larger recorded uEPSPs than predicted as well as why others had uEPSPs of 0mV (i.e., points on the horizontal axis in Figure 3A and S3). The points on the vertical axis likely occur due to animal-to-animal variability of connection strengths, or from rare off-target photostimulation of PNs25. These points were infrequent (4/135; 2.9%) and likely not due to indirect connectivity, since PN photostimulation usually did not drive LHN spikes, and potential polysynaptic excitatory pathways that could explain these particular points (e.g., PN-PN axo-axonal connectivity) do not exist in the hemibrain. In addition, many data points (73/135; 54%) had both a uEPSP amplitude of zero and a synapse density of zero (i.e., at the origin in Figure 3A). These are to be expected in a relatively sparsely connected network, and further suggest that the effects of indirect pathways are unlikely to impact our results.
Mean uEPSP amplitudes and corresponding synapse densities are provided in Table S3.
Anatomical analysis of neurons and synaptic connections
Synapse counts for each connection were extracted from the hemibrain EM database using the Natverse package69. Surface areas of each neuron were computed for each neuron assuming a cylindrical approximation for each segment using the Trees Toolbox72. Surface areas computed from a triangular mesh representation of each neuron yielded similar values but were modestly larger (7.9% on average). Because NEURON simulates neurons using a cylindrical representation, we used the cylindrical approximation for all surface area calculations, to maintain consistency. Synapse density was computed as the ratio of synapse count to surface area.
Analysis of axon and dendrite targeting was conducted by splitting each neuron’s synaptic inputs by arbor identity. The random distribution in Figure S5B was obtained by redistributing each connection’s synapses onto axon and dendrite arbors following the distribution of all ePN synapses onto that neuron. Shuffling in Figure S5C–F was conducted by randomly permuting the synapse labels (i.e. the identity of each presynaptic partner neuron) either within each arbor or throughout the entire neuron. This was repeated 1000 times to obtain 95% confidence intervals.
A modest minority (~24%) of the LHN morphologies had artefactual “pinch points” along their inter-arbor cables (short segments where the neurite diameter narrows considerably). These accounted for, at most, 2.7% of the length of any inter-arbor cable, and had only a tiny impact on electrical excitation spread (mEPSP amplitudes were essentially unchanged after eliminating pinch points). We therefore did not correct for these artefacts in our analysis.
Single- and multi-compartment models of LHNs
Single compartment models were constructed using Python. The surface area for each model neuron was set to the total surface area of the corresponding hemibrain neuron, based on a cylindrical approximation for each segment. Multi-compartment models of LHNs were constructed in the NEURON simulation environment73. For these models, corrected neuron morphologies were imported into NEURON, where they were divided into short isopotential compartments using the maximal available spatial resolution from the morphological SWC file, consistent with the d-lambda rule74. Synapse locations were determined from annotations in the hemibrain dataset and mapped to the corresponding compartment in the model using a k-nearest neighbors algorithm.
For both types of models, specific biophysical properties were jointly optimized to minimize the error in peak uEPSP amplitude across all connections (the peak amplitude was the most reliable metric for model fitting because the full waveform of each uEPSP was sometimes obscured by subsequent uEPSPs, due to stimulation of multiple PN spikes). The free parameters for the single compartment neuron model were specific membrane resistance and capacitance. The multi-compartment neuron model also included the axial resistance as a free parameter. A leave-one-out bootstrap procedure was implemented to validate that our parameter values were robust to variations in the set of training connections. The best fit values for specific membrane resistance (17.2 kΩ cm2), specific membrane capacitance (0.6 μF/cm2), and specific axial resistivity (350 Ω cm), were in very close agreement with experimentally constrained values for PNs and visual amacrine cells27,33,60. As in those studies, these biophysical parameters were assumed to be uniform within and between neurons. However, whole-cell properties vary between modeled neurons due to their different sizes. The PN to LHN synaptic conductance waveform shape was modeled as a sum of two exponentials (the time constant of rise was 0.2 msec and the time constant of decay was 1.1 msec), matching a previous model of the ORN-PN synapse27. We did not attempt to optimize the waveform shape, which may explain the modest overestimate of predicted EPSP timecourses in Figure 4C. The peak amplitude of the synaptic conductance waveform was an additional free parameter (optimized jointly with the passive biophysical properties). The best fit value was 0.055 nS, similar to a previous fit27. The resting membrane potential was set to −55mV and the cholinergic synaptic reversal potential was set to −10 mV75. Importantly, using identical parameter values to those in prior models of Drosophila neurons yielded qualitatively similar findings about subcellular compartmentalization, supporting the robustness of our models27,33,60.
Voltage measurements from specific compartments of the model were obtained by placing a virtual pipette in the appropriate location and recording in current clamp mode. Individual mEPSPs were evoked by opening a synaptic conductance (with the waveform determined above) at the location of each individual synapse. mEPSPs were recorded either locally (in the same compartment as the synapse) or at the SIZ (defined here as the first branch point of the dendrite arbor). uEPSPs were evoked by simultaneously opening conductances at all synapses corresponding to the presynaptic PN. Input and transfer impedance measurements (such as of transfer impedance in Figure S7) were made using the Impedance class in NEURON.
Subregions of each LHN (axon arbor, dendrite arbor, inter-arbor cable, and cell body fiber) were segmented manually using neuTube. For each arbor, the start node was identified manually, and all daughter nodes were considered part of the arbor. In some LHNs, 1-3 additional branches that were not downstream of the start node were manually identified as part of the arbor. The axon arbor was distinguished from the dendrite arbor by the longer cable connection from the cell body fiber junction, a defining characteristic of arbor identify in LHNs23. To verify the distinction between axon and dendrite, the ratio of input to output synapses was computed to locate the flow centrality of each neuron76. In all cases, the identities of axon and dendrite via flow centrality agreed with our manual annotations. The inter-arbor cable was defined as the neurite spanning between the start nodes of each arbor, excluding any additional arbor branches (as defined above), and the cell body and cell body fiber. One neuron type, Local2, did not have an obvious inter-arbor cable, and had no obvious polarity of input vs. output synapse locations. We therefore determined that this neuron type only has one arbor, and no inter-arbor cable.
Perturbations to the compartmental models (Figure 5D–F) were carried out by adjusting the axial resistivity of specific compartments to make certain parts of the neuron isopotential. Because NEURON does not allow an axial resistivity of 0, it was set to a very small positive value (0.001 Ω cm). Simulations of neurons with isopotential subregions were carried out using Crank-Nicholson integration with fixed timestep (0.06 msec).
Barbell model simulation
The barbell model is a simplified isopotential arbor model and was implemented in MATLAB. All sub-arbor shape information was abstracted away, retaining only the size of each arbor, and the length and mean diameter of the inter-arbor cable. The inter-arbor cable was simulated as a series of 1 μm long compartments with diameter matching the true mean diameter, and each arbor was simulated as a single compartment. The surface area of the cell body and cell body fiber was added to the dendrite arbor, since these structures are nearby. The SIZ was therefore isopotential with the dendrite compartment. The total surface area was nearly identical to the full model (with the only differences coming from the fixed-diameter approximation for the inter-arbor cable). In addition, all core biophysical parameters (Rm, Ri, Cm, and Gsyn) were unchanged from the best fit values obtained for the full models. Numerical integration was performed using the backward Euler method74 with a fixed timestep of 0.01ms. The range of simulated PN spike rates used in Figure 7 (0-200Hz) approximated the known dynamic range of these neurons77. The abstraction of the barbell model was also useful because it could be used to simulate an “average” LHN (Figures 6E,F, and all of Figure 7). To do this, a single LHN was modeled with axon arbor size, dendrite arbor size, and inter-arbor cable size all equal to their average values across the population of LHNs under consideration.
Statistics
Central tendencies are reported as means, and dispersions are reported as standard deviations, except for figure S5, where dispersions are reported as 95% confidence intervals.
Supplementary Material
Table S2: Identity of each LHN included in each figure panel. Related to Figures 1–7.
Lists which hemibrain neurons and which patch-clamp physiology data are included in each figure panel of the manuscript. Panel letters given in uppercase indicate that anatomy or physiology data are used directly. Panel letters given in lowercase indicate that a computational model of that bodyId is used. Panel letters given in parentheses indicate that the anatomy of that bodyID is used to generate a single average barbell model. This also includes the full list of bodyIds for the expanded set of local LHNs.
Data S1: Skeletons of biocytin fills (light microscopy) and hemibrain neurons (electron microscopy). Related to Figure 1. The folder “LM-EM matching” provides all neuron skeletons matched in this study via NBLAST (biocytin and hemibrain), organized by their Jeanne et al.25 cell type name. These skeletons are in the JRC2018F brainspace. The folder “corrected morphologies” includes all hemibrain LHN morphologies used in this study, including the expanded set of local LHNs. Morphologies that have been manually corrected (STAR Methods) are labeled as such. These morphologies are all in the “JRCFIB2018F” brainspace, with units of voxels (8nm).
Data S2: Mean EPSP waveform data for each recording of each connection. Related to Figure 2.
Data S3: Simulated mEPSP amplitudes for each uPN synapse. Related to Figure 5.
Highlights.
Comparison of anatomy and physiology of synaptic connections in Drosophila
Unitary postsynaptic potentials are well-predicted by synapse density and location
Synaptic efficacy is similar for locations within an arbor, but not between arbors
Cables allow arbors to operate with both independent and interacting computations
ACKNOWLEDGEMENTS
We thank Stephen Plaza for help with the hemibrain dataset and Greg Jefferis for assistance with neuroanatomical analysis. We thank Michael Higley, Damon Clark, Mehmet Fişek, and members of the Jeanne Lab for helpful discussions and for comments on the manuscript. Electrophysiology data were obtained by J.M.J in the lab of Rachel Wilson. This work was supported by NIH grants R01 DC018570 and R01 NS116584, the Richard and Susan Smith Family Award for Excellence in Biomedical Research, the Klingenstein-Simons Fellowship Award in Neuroscience, and an innovative research award from the Kavli Institute for Neuroscience at Yale University to J.M.J. T.X.L. was supported by the Yale College Dean’s Research Fellowship and the Rosenfeld Science Scholars Program. P.A.D was supported by NIH medical scientist training grant T32GM136651. K.M.L. was supported by a James Hudson Brown – Alexander Brown Coxe Postdoctoral Fellowship in the Medical Sciences at Yale University School of Medicine and NIH fellowship F32 DC019521.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- 1.Reid RC (2012). From functional architecture to functional connectomics. Neuron 75, 209–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bargmann CI (2012). Beyond the connectome: how neuromodulators shape neural circuits. Bioessays 34, 458–465. [DOI] [PubMed] [Google Scholar]
- 3.Lee WC, and Reid RC (2011). Specificity and randomness: structure-function relationships in neural circuits. Curr Opin Neurobiol 21, 801–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Briggman KL, and Bock DD (2012). Volume electron microscopy for neuronal circuit reconstruction. Curr Opin Neurobiol 22, 154–161. [DOI] [PubMed] [Google Scholar]
- 5.Denk W, Briggman KL, and Helmstaedter M (2012). Structural neurobiology: missing link to a mechanistic understanding of neural computation. Nat Rev Neurosci 13, 351–358. [DOI] [PubMed] [Google Scholar]
- 6.Friedrich RW, and Wanner AA (2021). Dense Circuit Reconstruction to Understand Neuronal Computation: Focus on Zebrafish. Annu Rev Neurosci 44, 275–293. [DOI] [PubMed] [Google Scholar]
- 7.Litwin-Kumar A, and Turaga SC (2019). Constraining computational models using electron microscopy wiring diagrams. Curr Opin Neurobiol 58, 94–100. [DOI] [PubMed] [Google Scholar]
- 8.Marder E (1998). From biophysics to models of network function. Annu Rev Neurosci 21, 25–45. [DOI] [PubMed] [Google Scholar]
- 9.Eschbach C, Fushiki A, Winding M, Schneider-Mizell CM, Shao M, Arruda R, Eichler K, Valdes-Aleman J, Ohyama T, Thum AS, et al. (2020). Recurrent architecture for adaptive regulation of learning in the insect brain. Nat. Neurosci 23, 544–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wanner AA, and Friedrich RW (2020). Whitening of odor representations by the wiring diagram of the olfactory bulb. Nat. Neurosci 23, 433–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Vishwanathan A, Ramirez AD, Wu J, Sood A, Yang R, Kemnitz N, Ih D, Turner N, Lee K, Tartavull I, et al. (2021). Predicting modular functions and neural coding of behavior from a synaptic wiring diagram. bioRxiv. 10.1101/2020.10.28.359620. [DOI] [Google Scholar]
- 12.Tschopp FD, Reiser MB, and Turaga SC (2018). A Connectome Based Hexagonal Lattice Convolutional Network Model of the Drosophila Visual System. arXiv. arXiv:1806.04793v2. [Google Scholar]
- 13.Zarin AA, Mark B, Cardona A, Litwin-Kumar A, and Doe CQ (2019). A multilayer circuit architecture for the generation of distinct locomotor behaviors in Drosophila. Elife 8, e51781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bargmann CI, and Marder E (2013). From the connectome to brain function. Nat Methods 10, 483–490. [DOI] [PubMed] [Google Scholar]
- 15.Holler S, Kostinger G, Martin KAC, Schuhknecht GFP, and Stratford KJ (2021). Structure and function of a neocortical synapse. Nature 591, 111–116. [DOI] [PubMed] [Google Scholar]
- 16.Scheffer LK, Xu CS, Januszewski M, Lu Z, Takemura SY, Hayworth KJ, Huang GB, Shinomiya K, Maitlin-Shepard J, Berg S, et al. (2020). A connectome and analysis of the adult Drosophila central brain. Elife 9, e57443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Frechter S, Bates AS, Tootoonian S, Dolan MJ, Manton J, Jamasb AR, Kohl J, Bock D, and Jefferis G (2019). Functional and anatomical specificity in a higher olfactory centre. Elife 8, e44590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kohl J, Ostrovsky AD, Frechter S, and Jefferis GS (2013). A bidirectional circuit switch reroutes pheromone signals in male and female brains. Cell 155, 1610–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fişek M, and Wilson RI (2014). Stereotyped connectivity and computations in higher-order olfactory neurons. Nat. Neurosci 17, 280–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dolan MJ, Frechter S, Bates AS, Dan C, Huoviala P, Roberts RJ, Schlegel P, Dhawan S, Tabano R, Dionne H, et al. (2019). Neurogenetic dissection of the Drosophila lateral horn reveals major outputs, diverse behavioural functions, and interactions with the mushroom body. Elife 8, e43079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ruta V, Datta SR, Vasconcelos ML, Freeland J, Looger LL, and Axel R (2010). A dimorphic pheromone circuit in Drosophila from sensory input to descending output. Nature 468, 686–690. [DOI] [PubMed] [Google Scholar]
- 22.Amin H, and Lin AC (2019). Neuronal mechanisms underlying innate and learned olfactory processing in Drosophila. Curr Opin Insect Sci 36, 9–17. [DOI] [PubMed] [Google Scholar]
- 23.Bates AS, Schlegel P, Roberts RJV, Drummond N, Tamimi IFM, Turnbull R, Zhao X, Marin EC, Popovici PD, Dhawan S, et al. (2020). Complete connectomic reconstruction of olfactory projection neurons in the fly brain. Curr. Biol 30, 3183–3199.e3186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schlegel P, Bates AS, Sturner T, Jagannathan SR, Drummond N, Hsu J, Serratosa Capdevila L, Javier A, Marin EC, Barth-Maron A, et al. (2021). Information flow, cell types and stereotypy in a full olfactory connectome. Elife 10, e66018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jeanne JM, Fisek M, and Wilson RI (2018). The organization of projections from olfactory glomeruli onto higher-order neurons. Neuron 98, 1198–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jeanne JM, and Wilson RI (2015). Convergence, divergence, and reconvergence in a feedforward network improves neural speed and accuracy. Neuron 88, 1014–1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tobin WF, Wilson RI, and Lee WA (2017). Wiring variations that enable and constrain neural computation in a sensory microcircuit. Elife 6, e24838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marin EC, Jefferis GS, Komiyama T, Zhu H, and Luo L (2002). Representation of the glomerular olfactory map in the Drosophila brain. Cell 109, 243–255. [DOI] [PubMed] [Google Scholar]
- 29.Wong AM, Wang JW, and Axel R (2002). Spatial representation of the glomerular map in the Drosophila protocerebrum. Cell 109, 229–241. [DOI] [PubMed] [Google Scholar]
- 30.Costa M, Manton JD, Ostrovsky AD, Prohaska S, and Jefferis GS (2016). NBLAST: Rapid, Sensitive Comparison of Neuronal Structure and Construction of Neuron Family Databases. Neuron 91, 293–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Johnston D, and Wu SM-S (1995). Foundations of cellular neurophysiology (MIT Press; ). [Google Scholar]
- 32.Rall W (1967). Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input. J. Neurophysiol 30, 1138–1168. [DOI] [PubMed] [Google Scholar]
- 33.Gouwens NW, and Wilson RI (2009). Signal propagation in Drosophila central neurons. J. Neurosci 29, 6239–6249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rall W (1962). Theory of physiological properties of dendrites. Ann. N.Y. Acad. Sci 96, 1071–1092. [DOI] [PubMed] [Google Scholar]
- 35.Graubard K, Raper JA, and Hartline DK (1980). Graded synaptic transmission between spiking neurons. Proc. Natl. Acad. Sci. USA 77, 3733–3735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Destexhe A, Rudolph M, and Pare D (2003). The high-conductance state of neocortical neurons in vivo. Nat Rev Neurosci 4, 739–751. [DOI] [PubMed] [Google Scholar]
- 37.Zhang W, and Linden DJ (2003). The other side of the engram: experience-driven changes in neuronal intrinsic excitability. Nat Rev Neurosci 4, 885–900. [DOI] [PubMed] [Google Scholar]
- 38.Rall W (1959). Branching dendritic trees and motoneuron membrane resistivity. Exp Neurol 1, 491–527. [DOI] [PubMed] [Google Scholar]
- 39.Burrows M, and Siegler MV (1978). Graded synaptic transmission between local interneurones and motor neurones in the metathoracic ganglion of the locust. J. Physiol 285, 231–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Graubard K (1978). Synaptic transmission without action potentials: input-output properties of a nonspiking presynaptic neuron. J. Neurophysiol 41, 1014–1025. [DOI] [PubMed] [Google Scholar]
- 41.Angstadt JD, and Calabrese RL (1991). Calcium currents and graded synaptic transmission between heart interneurons of the leech. J. Neurosci 11, 746–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shu Y, Hasenstaub A, Duque A, Yu Y, and McCormick DA (2006). Modulation of intracortical synaptic potentials by presynaptic somatic membrane potential. Nature 441, 761–765. [DOI] [PubMed] [Google Scholar]
- 43.Alle H, and Geiger JR (2006). Combined analog and action potential coding in hippocampal mossy fibers. Science 311, 1290–1293. [DOI] [PubMed] [Google Scholar]
- 44.Littleton JT, and Ganetzky B (2000). Ion channels and synaptic organization: analysis of the Drosophila genome. Neuron 26, 35–43. [DOI] [PubMed] [Google Scholar]
- 45.Borst A, and Haag J (1996). The intrinsic electrophysiological characteristics of fly lobula plate tangential cells: I. Passive membrane properties. J Comput Neurosci 3, 313–336. [DOI] [PubMed] [Google Scholar]
- 46.Kazama H, and Wilson RI (2008). Homeostatic matching and nonlinear amplification at genetically-identified central synapses. Neuron 58, 401–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hige T, Aso Y, Modi MN, Rubin GM, and Turner GC (2015). Heterosynaptic plasticity underlies aversive olfactory learning in Drosophila. Neuron 88, 985–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Roth A, and Hausser M (2001). Compartmental models of rat cerebellar Purkinje cells based on simultaneous somatic and dendritic patch-clamp recordings. J. Physiol 535, 445–472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jaffe DB, and Carnevale NT (1999). Passive normalization of synaptic integration influenced by dendritic architecture. J. Neurophysiol 82, 3268–3285. [DOI] [PubMed] [Google Scholar]
- 50.Cuntz H, Forstner F, Haag J, and Borst A (2008). The morphological identity of insect dendrites. PLoS Comput Biol 4, e1000251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Egea-Weiss A, Renner A, Kleineidam CJ, and Szyszka P (2018). High Precision of Spike Timing across Olfactory Receptor Neurons Allows Rapid Odor Coding in Drosophila. iScience 4, 76–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sehdev A, Mohammed YG, Triphan T, and Szyszka P (2019). Olfactory Object Recognition Based on Fine-Scale Stimulus Timing in Drosophila. iScience 13, 113–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liu Q, Tabuchi M, Liu S, Kodama L, Horiuchi W, Daniels J, Chiu L, Baldoni D, and Wu MN (2017). Branch-specific plasticity of a bifunctional dopamine circuit encodes protein hunger. Science 356, 534–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Diao F, Chaufty J, Waro G, and Tsunoda S (2010). SIDL interacts with the dendritic targeting motif of Shal (K(v)4) K+ channels in Drosophila. Mol Cell Neurosci 45, 75–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Rogero O, Hammerle B, and Tejedor FJ (1997). Diverse expression and distribution of Shaker potassium channels during the development of the Drosophila nervous system. J. Neurosci 17, 5108–5118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gabbiani F, Krapp HG, Koch C, and Laurent G (2002). Multiplicative computation in a visual neuron sensitive to looming. Nature 420, 320–324. [DOI] [PubMed] [Google Scholar]
- 57.Chou YH, Spletter ML, Yaksi E, Leong JC, Wilson RI, and Luo L (2010). Diversity and wiring variability of olfactory local interneurons in the Drosophila antennal lobe. Nat. Neurosci 13, 439–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fischbach KF, and Dittrich APM (1989). The optic lobe of Drosophila melanogaster. I. A Golgi analysis of wild-type structure. Cell Tissue Res. 258, 441–475. [Google Scholar]
- 59.Yang HH, St-Pierre F, Sun X, Ding X, Lin MZ, and Clandinin TR (2016). Subcellular Imaging of Voltage and Calcium Signals Reveals Neural Processing In Vivo. Cell 166, 245–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Meier M, and Borst A (2019). Extreme Compartmentalization in a Drosophila Amacrine Cell. Curr. Biol 29, 1545–1550 e1542. [DOI] [PubMed] [Google Scholar]
- 61.Xu-Friedman MA, and Regehr WG (2004). Structural contributions to short-term synaptic plasticity. Physiol Rev 84, 69–85. [DOI] [PubMed] [Google Scholar]
- 62.Abrahamsson T, Cathala L, Matsui K, Shigemoto R, and Digregorio DA (2012). Thin dendrites of cerebellar interneurons confer sublinear synaptic integration and a gradient of short-term plasticity. Neuron 73, 1159–1172. [DOI] [PubMed] [Google Scholar]
- 63.Davie K, Janssens J, Koldere D, De Waegeneer M, Pech U, Kreft L, Aibar S, Makhzami S, Christiaens V, Bravo Gonzalez-Blas C, et al. (2018). A Single-Cell Transcriptome Atlas of the Aging Drosophila Brain. Cell 174, 982–998 e920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Croset V, Treiber CD, and Waddell S (2018). Cellular diversity in the Drosophila midbrain revealed by single-cell transcriptomics. Elife 7, e34550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Harris-Warrick RM, and Marder E (1991). Modulation of neural networks for behavior. Annu Rev Neurosci 14, 39–57. [DOI] [PubMed] [Google Scholar]
- 66.Cohn R, Morantte I, and Ruta V (2015). Coordinated and compartmentalized neuromodulation shapes sensory processing in Drosophila. Cell 163, 1742–1755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Aso Y, and Rubin GM (2020). Toward nanoscale localization of memory engrams in Drosophila. J Neurogenet 34, 151–155. [DOI] [PubMed] [Google Scholar]
- 68.Marder E (2015). Understanding brains: details, intuition, and big data. PLoS Biol 13, e1002147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bates AS, Manton JD, Jagannathan SR, Costa M, Schlegel P, Rohlfing T, and Jefferis GS (2020). The natverse, a versatile toolbox for combining and analysing neuroanatomical data. Elife 9, e53350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Feng L, Zhao T, and Kim J (2015). neuTube 1.0: A New Design for Efficient Neuron Reconstruction Software Based on the SWC Format. eNeuro 2, (1) ENEURO.0049-0014.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zheng Z, Lauritzen JS, Perlman E, Robinson CG, Nichols M, Milkie D, Torrens O, Price J, Fisher CB, Sharifi N, et al. (2018). A Complete Electron Microscopy Volume of the Brain of Adult Drosophila melanogaster. Cell 174, 730–743 e722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Cuntz H, Forstner F, Borst A, and Hausser M (2010). One rule to grow them all: a general theory of neuronal branching and its practical application. PLoS Comput Biol 6, e1000877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Hines ML, and Carnevale NT (1997). The NEURON simulation environment. Neural Comput. 9, 1179–1209. [DOI] [PubMed] [Google Scholar]
- 74.Carnevale NT, and Hines ML (2006). The NEURON Book (Cambridge University Press; ). [Google Scholar]
- 75.McCarthy EV, Wu Y, Decarvalho T, Brandt C, Cao G, and Nitabach MN (2011). Synchronized bilateral synaptic inputs to Drosophila melanogaster neuropeptidergic rest/arousal neurons. J. Neurosci 31, 8181–8193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Schneider-Mizell CM, Gerhard S, Longair M, Kazimiers T, Li F, Zwart MF, Champion A, Midgley FM, Fetter RD, Saalfeld S, and Cardona A (2016). Quantitative neuroanatomy for connectomics in Drosophila. Elife 5, e12059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Bhandawat V, Olsen SR, Schlief ML, Gouwens NW, and Wilson RI (2007). Sensory processing in the Drosophila antennal lobe increases the reliability and separability of ensemble odor representations. Nat. Neurosci 10, 1474–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S2: Identity of each LHN included in each figure panel. Related to Figures 1–7.
Lists which hemibrain neurons and which patch-clamp physiology data are included in each figure panel of the manuscript. Panel letters given in uppercase indicate that anatomy or physiology data are used directly. Panel letters given in lowercase indicate that a computational model of that bodyId is used. Panel letters given in parentheses indicate that the anatomy of that bodyID is used to generate a single average barbell model. This also includes the full list of bodyIds for the expanded set of local LHNs.
Data S1: Skeletons of biocytin fills (light microscopy) and hemibrain neurons (electron microscopy). Related to Figure 1. The folder “LM-EM matching” provides all neuron skeletons matched in this study via NBLAST (biocytin and hemibrain), organized by their Jeanne et al.25 cell type name. These skeletons are in the JRC2018F brainspace. The folder “corrected morphologies” includes all hemibrain LHN morphologies used in this study, including the expanded set of local LHNs. Morphologies that have been manually corrected (STAR Methods) are labeled as such. These morphologies are all in the “JRCFIB2018F” brainspace, with units of voxels (8nm).
Data S2: Mean EPSP waveform data for each recording of each connection. Related to Figure 2.
Data S3: Simulated mEPSP amplitudes for each uPN synapse. Related to Figure 5.
Data Availability Statement
Analyzed physiology and morphology data are included as Supplemental Data S1–S4. Other data analyzed by this paper are publicly accessible, as listed in the key resources table.
All NEURON model files, interfacing Python scripts, and MATLAB model files have been deposited in Zenodo. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited data | ||
| Hemibrain connectome, v1.1 | Scheffer et al.16 | Neuprint.janelia.org |
| Matched and corrected LHN morphologies | This paper and Scheffer et al.16 | Data S1 |
| Analyzed physiology data | This paper and Jeanne et al.25 | Data S2 |
| mEPSP simulation data | This paper | Data S3 |
| Subcellular anatomical details of LHLNs | This paper and Scheffer et al.16 | Data S4 |
| Software and algorithms | ||
| MATLAB R2020a | Mathworks | http://mathworks.com |
| Python 3.7.0 | Python Software Foundation | http://python.org |
| R Studio 1.2.5033 | RStudio, Inc. | http://www.rstudio.org |
| Natverse | Bates et al.69 | http://natverse.org |
| NEURON 7.7.2 | Hines and Carnevale70 | http://neuron.yale.edu/neuron |
| Code to identify LHNs between biocytin fills and hemibrain skeletons | This paper | 10.5281/zenodo.5711439 |
| NEURON model files | This paper | 10.5281/zenodo.5716323 |
| Barbell model files | This paper | 10.5281/zenodo.5716321 |


