Serotonin neurons modulate learning rate through uncertainty

SUMMARY

Regulating how fast to learn is critical for flexible behavior. Learning about the consequences of actions should be slow in stable environments, but accelerate when that environment changes. Recognizing stability and detecting change are difficult in environments with noisy relationships between actions and outcomes. Under these conditions, theories propose that uncertainty can be used to modulate learning rates (“meta-learning”). We show that mice behaving in a dynamic foraging task exhibit choice behavior that varied as a function of two forms of uncertainty estimated from a meta-learning model. The activity of dorsal raphe serotonin neurons tracked both types of uncertainty in the foraging task as well as in a dynamic Pavlovian task. Reversible inhibition of serotonin neurons in the foraging task reproduced changes in learning predicted by a simulated lesion of meta-learning in the model. We thus provide a quantitative link between serotonin neuron activity, learning, and decision making.

In brief

Learning about actions and their outcomes is not a static process and should be adapted to complement the environment. Grossman et al. show evidence of variable learning rates in mice that can be characterized by uncertainty-driven meta-learning and demonstrate a role for serotonin neuron activity in tracking uncertainty to modulate learning.

INTRODUCTION

Models from control theory and reinforcement learning (RL) propose that behavioral policies are learned through interactions between the nervous system and the environment.^1,2 In some models in this framework, an animal learns from discrepancies between expected and received outcomes of actions (reward prediction errors [RPEs]). The rate at which learning occurs is usually treated as a constant, but optimal learning rates vary when the environment changes.^3–6 Consequently, animals should vary how rapidly they learn in order to behave adaptively and maximize reward. Normatively, learning rates should vary as a function of uncertainty.^7–9 When some amount of uncertainty is expected (also referred to as outcome variance or risk), learning rates should decrease.^10–14 Slower learning helps maximize reward when relationships between actions and outcomes are probabilistic but stable. This modulation prevents animals from abandoning an optimal choice due to short-term fluctuations in outcomes. However, it is also important to detect changes in the underlying statistics of an environment. Here, deviations from expected uncertainty (“unexpected uncertainty”) should increase learning rates.^{8,12,13,15–18} Tuning decision making in this way is known as “meta-learning’“ and there is evidence that humans and other animals use this strategy.^{9,12,13,19–23} How does the nervous system control how rapidly to learn from recent experience?

Several theories propose that neuromodulatory systems enable meta-learning.^5,8,24 One such system comprises a small number of serotonin-releasing neurons (on the order of 10⁴ in mice)²⁵ with extensive axonal projections. This small group of cells affects large numbers of neurons in distributed regions^26–29 that are responsible for learning and decision making. The activity of these neurons changes on behaviorally relevant timescales—both fast (hundreds of milliseconds) and slow (tens of seconds).^30–33 Serotonin receptor activation can induce short-term changes in excitability^34,35 as well as long-lasting synaptic plasticity.³⁶

Prior research demonstrates that serotonin neurons modulate flexible behavior in changing environments.^33,37–42 Serotonin axon lesions^37,38 or reversible inactivation of dorsal raphe serotonin neurons³³ impaired behavioral adaptation to changes in action- or stimulus-outcome mappings. Importantly, in these experiments animals were still capable of adapting their behavior, but did so more slowly. Conversely, brief excitations of serotonin neurons in a probabilistic choice task enhanced learning rates after long intervals between outcomes.⁴² These studies show that serotonin neurons modulate how quickly an animal adapts to a change in correlational relationships in the environment. Thus, serotonin neurons may guide learning using the statistics of recent outcomes. However, a mechanistic understanding of the relationship between serotonin neuron activity and meta-learning has not been established.

We designed a dynamic foraging task for mice and recorded action potentials from dorsal raphe serotonin neurons. We developed a generative model of behavior by modifying an RL model to include meta-learning. Adding meta-learning to the model captured unique features of observed behavior that a model of behavior with a static learning rate could not explain. We found that the activity of approximately half of serotonin neurons correlated with the “expected uncertainty” variable from the model on long timescales (tens of seconds to minutes) and “unexpected uncertainty” at the time of outcome. Simulated removal of meta-learning from the model predicted specific changes in learning that were reproduced by chemogenetic inhibition of dorsal raphe serotonin neurons. Thus, we demonstrate a quantitative link between serotonin neuron activity and uncertainty about decision outcomes used to modulate learning rates.

RESULTS

Mice display meta-learning during dynamic decision making

We trained thirsty, head-restrained mice (20 female, 28 male) on a dynamic foraging task in which they made choices between two alternative sources of water.⁴³ Sessions consisted of about 300 trials (Figures S1A–S1C; 278 ± 103) with forced inter-trial intervals (1 – 31 s, exponentially distributed). Each trial began with an odor “go” cue that informed the animal that it could make a choice, but otherwise gave no information (Figures 1A and 1B). During a response window (1.5 s), the mouse could make a decision by licking either the left or the right spout. As a consequence of its choice, water was delivered probabilistically from the chosen spout. The reward probabilities (P(R)ϵ {0.1,0.5,0.9} or P(R)ϵ {0.1, 0.4, 0.7}) assigned to each spout changed independently and randomly (not signaled to the animal), in blocks of 20–35 trials.

Figure 1. Mice forage dynamically for rewards.

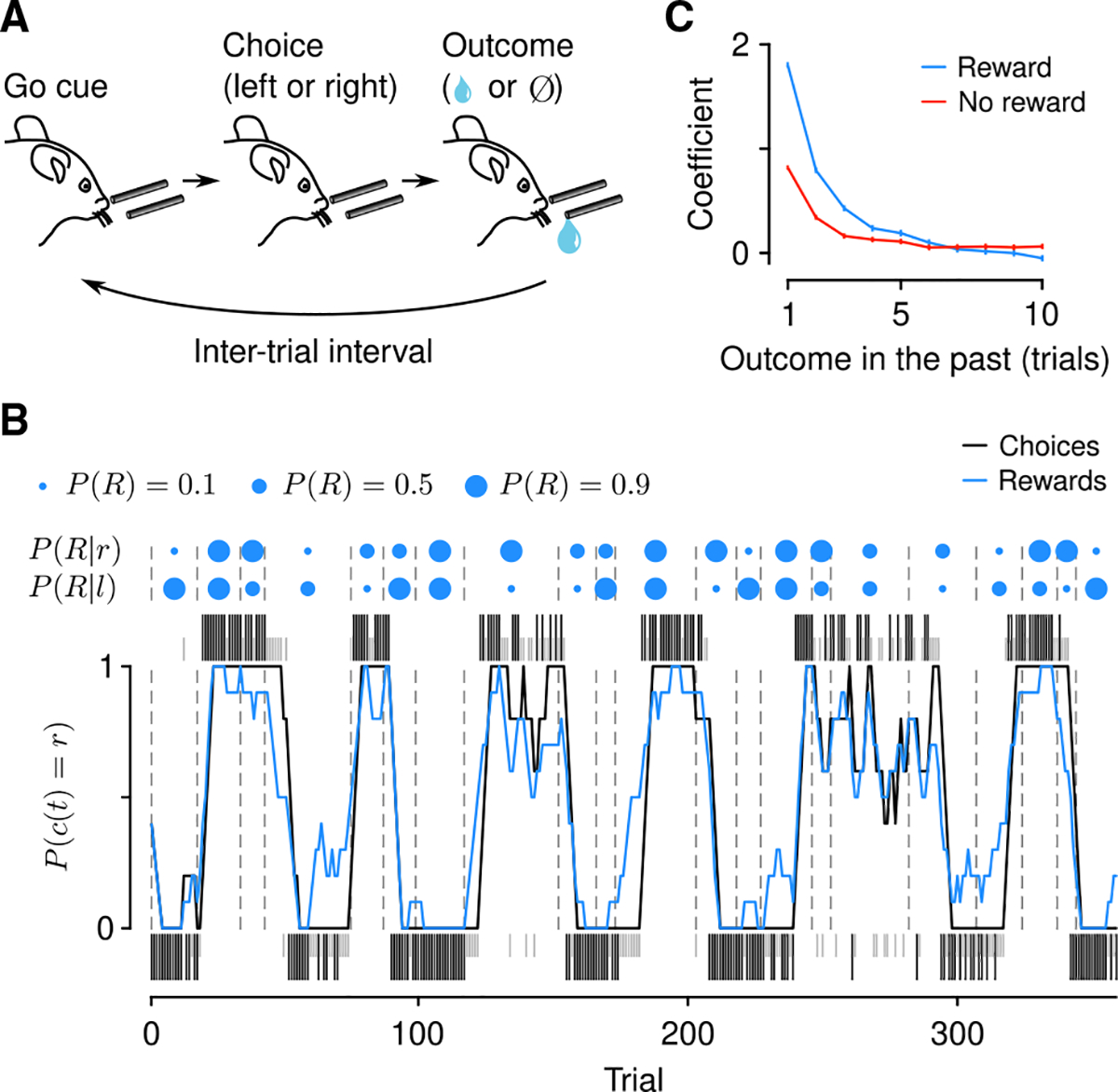
(A) Dynamic foraging task in which mice chose freely between a leftward and rightward lick, followed by a reward with a probability that varied over time.

(B) Example mouse behavior from a single session in the task. Black (rewarded) and gray (unrewarded) ticks correspond to left (below) and right (above) choices. Black curve: mouse choices (smoothed over 5 trials, boxcar filter). Blue curve: Rewards (smoothed over 5 trials, boxcar filter). Blue dots indicate left/right reward probabilities, and dashed lines indicate a change in reward probability (P(R)) for at least one spout.

(C) Logistic regression coefficients for choice as a function of outcome history. Error bars: 95% CI. See also Figure S1.

Mice mostly chose the higher- or equal-probability spout (Figure S1D; correct rate, 0.66 ± 0.038) and harvested rewards (reward rate, 0.55 ± 0.027 rewards trial⁻¹) over many sessions (16.1 ± 10.7 sessions mouse⁻¹). Mouse performance was better than a random agent, but worse than an optimized one (Figure S1D). We first fit statistical models to quantify the effect of outcome history on choice. These logistic regressions revealed that mice used experience of recent outcomes to drive behavior (Figure 1C; time constants, 1.35 ± 0.24 trials for rewards, 1.03 ± 0.14 trials for no rewards, 95% confidence interval [CI]). Similarly, we quantified the effect of outcomes on the latency to make a choice following the go cue. Consistent with previous findings,⁴³ this model demonstrated a large effect of recent rewards on speeding up response times (Figure S1E; time constant, 1.88 ±0.18 trials, 95% CI).

These statistical findings indicate that mice continually learned from recent experience. To understand the nature of this learning, we constructed a generative model from a family of RL models called Q-learning.^1,2 This class of models creates a behavioral policy by maintaining an estimate of the value of each action (the expected reward from making that action). Using these values to make choices, the model then learns from those choices by using the RPE to update the action values, thereby forming a new policy (Figure 2A). How much to learn from RPEs is determined by the learning rate parameters. While these parameters are typically fit as constants across behavior, they need not be; they could vary according to statistics of the environment (meta-learning).^{9,12,13,19,21–23}

Figure 2. Mice learn at variable rates as a function of outcome history.

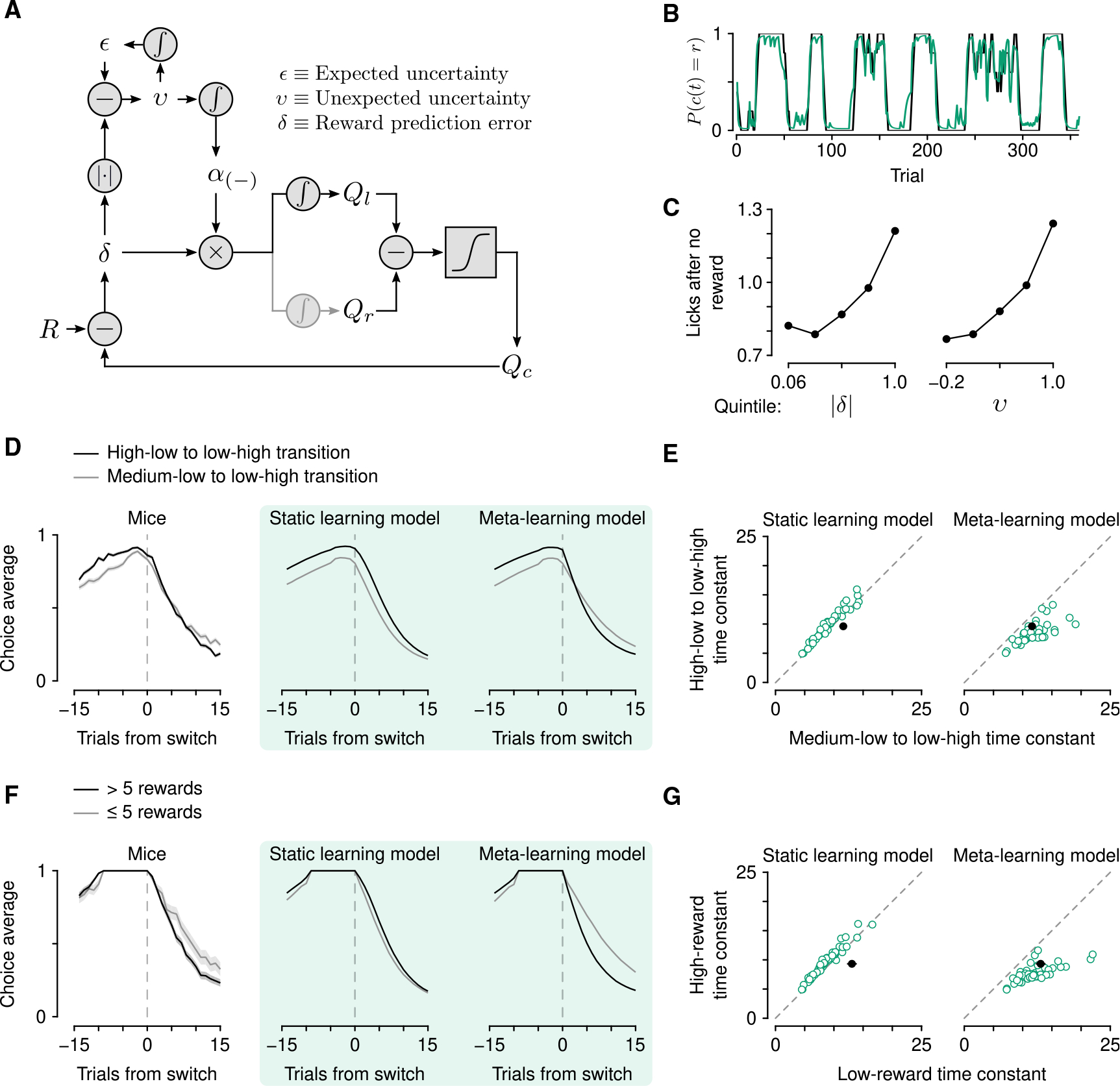
(A) Schematic of the meta-learning model algorithm. Relative value (Q_r − Q_l) is used to make choices through a softmax decision function. The predicted value of a choice(Qc) is compared with reward (R) to generate a reward prediction error (δ). Expected uncertainty (ε) is a recent, weighted history of |δ|. ε is compared with |δ| on a given trial to generate unexpected uncertainty (v). On no-reward trials, v is then integrated to determine how rapidly to learn from δ, thereby updating Qc.

(B) Estimated choice probability of actual behavior (black, same as Figure 1B) and choice probability estimated with the meta-learning model (green) smoothed over 5 trials (boxcar filter).

(C) Spout licks following no reward as a function of |δ| from the static learning model (left, regression coefficient = 0.45, p < 10⁻²⁰) or v from the meta-learning model (right, regression coefficient = 0.56, p < 10⁻²⁰).

(D) Left: Actual mouse behavior at transitions in which reward probabilities changed simultaneously(n = 384 high-low to low-high transitions, n = 347 medium-low to low-high transitions). Lines are mean choice probability relative to the spout that initially had the higher probability. Shading is Bernoulli SEM. Middle: Simulated behavior at transitions using static learning model parameters fit to actual behavior. Right: Simulated behavior at transitions using meta-learning model parameters fit to actual behavior.

(E) Time constants from exponential curves fit to simulated choice probabilities (like those shown in B) for each mouse (n = 48, green circles) compared with the actual mouse behavior (black circle). Left: Static-learning model (probability that mouse data come from simulated data distribution, p < 10⁻⁴). Right: Meta-learning model (p = 0.51).

(F) Left: Actual mouse behavior using transitions from (D) in which the animal exclusively chose the previously high or previously medium spout for 10 trials prior to the transition. Transitions were sorted into low (n = 98) and high (n = 288) reward history experienced during those 10 trials. Middle: Simulated behavior from the static learning model. Right: Simulated behavior from the meta-learning model.

(G) Time constants from exponential fits to actual (black circles) and simulated (green circles) behavior for the static (p < 10⁻¹³) and meta-learning (p = 0.38) models. See also Figures S2 and S3.

We first fit a model to mouse behavior in which learning rates were constant. The model included separate parameters for learning from positive and negative RPEs because learning from rewards and no rewards was demonstrably asymmetric (Figure 1C), consistent with previous reports.^44–46 This model fit overall behavior well,^43,47 but was unable to capture a specific feature of behavior around transitions in reward probabilities (Figures 2D and 2F). In rare instances, both reward probabilities were reassigned within 5 trials of each other. When the probability assignments flipped from high and low to low and high (for example, from 0.9 on the left and 0.1 on the right to 0.1 on the left and 0.9 on the right), mice rapidly shifted their choices to the new higher-probability alternative. However, when reward probabilities transitioned from medium and low to low and high (for example, from 0.5 on the left and 0.1 on the right to 0.1 on the left and 0.9 on the right), mice took longer to adapt to the change (Figures 2D and 2E; effect of trial from transition F_1,28 = 176, p < 10⁻¹² and trial from transition × transition type interaction F_1,28 = 5.23, p = 0.030, linear mixed-effects model). This difference in choice adaptation was even more apparent when choice histories prior to the transition were identical and behavior was sorted by experienced reward history (Figures 2F and 2G; effect of trial from transition F_1,28 = 307, p < 10⁻¹⁵ and trial from transition × transition type interaction F_1,28 = 4.69, p = 0.039, linear mixed-effects model), demonstrating that the difference in outcome history—and not simply choice history—is responsible for this effect on choice adaptation.

Animal choice switches are often more abrupt than they appear on average (Figures 1B and S1B). We fit a simple step-function model to individual transitions in order to estimate transition points and the choice probabilities before and after that point. Aligned to the estimated transition point, choice probabilities before and after differed depending on the assigned reward probability condition (Figure S2B).

Based on outcome history, the transition from high-to-low reward probability is more obvious than the transition from medium to low. This observation is consistent with learning rates varying as a function of how much outcomes deviate from a learned amount of variability (expected uncertainty). Thus, we designed a model (Figure 2A) that learns an estimate of the expected uncertainty of the behavioral policy by calculating a moving, weighted average of unsigned RPEs.⁹ Increases in expected uncertainty cause slower learning. This computation helps maximize reward when outcomes are probabilistic but stable.^7,11,14 The model then calculates the difference between expected uncertainty and unsigned RPEs (unexpected uncertainty) and integrates these differences over trials to determine how quickly the brain learns from those outcomes.^15,16,18,48 Intuitively, large RPEs that differ from recent history carry more information because they may signal a change in the environment and should therefore enhance learning.

When we modeled mouse behavior with meta-learning in this way, the model explained behavior better than the static learning model (Figures 2B and S2D). Simulations using fitted parameters also reproduced the transition behavior (Figures 2D–2G). It was only necessary to modulate learning from negative RPEs to capture the behavior of mice around these transitions, perhaps due to the asymmetric effect of rewards and no rewards on behavior (Figure 1C). Interestingly, not all forms of meta-learning were capable of mimicking mouse behavior. We were unable to reproduce the observed behavior using a model previously proposed to modulate learning rates and explain serotonin neuron function (Figure S3).^24,49 A Pearce-Hall model,⁵⁰ which modulates learning as a function of RPE magnitude in a different way, was also unsuccessful, as was a model without expected value estimates (Figure S3).

To capture this transition behavior, our meta-learning model leveraged a higher learning rate following high-low to low-high transitions than following medium-low to low-high transitions. Prior to the transitions, expected uncertainty was lower when the animal was sampling the high-probability spout as opposed to the medium-probability spout (Figure S2C; t₆₂₆ = 17.5, p < 10⁻⁵⁵, two-sample t test). When the reward probabilities changed, the deviation from expected uncertainty was greater when high changed to low (t₆₂₆ = −13.0, p < 10⁻³³, two-sample t test), resulting in faster learning rates (t₆₂₆ = − 13.7, p < 10⁻³⁶, two-sample t test). We also looked at the dynamics of the latent variables within blocks to see whether they evolved on timescales relevant to behavior and task structure. While block lengths were prescribed to be 20–35 trials long, the block length experienced by the animal was often shorter (8.65 ± 2.83) due to the probabilities changing independently at each spout and the animals switching choices (which begins a new experienced block). We found that when entering a new block (from the animals’ perspective), expected uncertainty became lower in the high block relative to the medium block within approximately 5 trials (4.80 ± 1.34). The number of trials the model took to distinguish between reward probabilities in this way was less than the average experienced block lengths (Figures S2F and S2G; t₄₈ = 8.18, p < 10⁻⁹, paired t test). Thus, the updating rate of expected uncertainty allows for the calculation of expected uncertainty and detection of probability changes on timescales relevant to the task and behavior.

We also found evidence of meta-learning in the intra-trial lick behavior. Following no reward, mice consistently licked the chosen spout several times. We found that the number of licks was better explained by unexpected uncertainty from the meta-learning model than by RPE magnitude from the static learning model (Figure 2C). In other words, mice licked more when the no-reward outcome was most unexpected.

Serotonin neuron firing rates correlate with expected uncertainty

To quantify the link between serotonin neurons and meta-learning, we recorded action potentials from dorsal raphe serotonin neurons in mice performing the foraging task (66 neurons from 4 mice). To identify serotonin neurons, we expressed the light-gated ion channel channelrhodopsin-2 under the control of the serotonin transporter promoter in Slc6a4-Cre (also known as Sert-Cre) mice (Figures 3A and S4A). We delivered light stimuli to the dorsal raphe to “tag” serotonin neurons at the end of each recording (Figures 3B, S4B, and S4C). Most serotonin neurons demonstrated brief increases in firing rates during the go cue relative to the inter-trial interval preceding it (Figures 3C, 3D, and 3F). This was also the case across the population (t₆₅ = 6.61, p < 10⁻⁸; Figure 3D). The activity of most serotonin neurons distinguished rewards from no rewards during the outcome period and many neurons maintained this representation during the inter-trial interval (Figures 3E and 3G). Across the population, there was no significant tendency for neurons to increase or decrease responses to rewards relative to lack of rewards (t₆₅ = − 1.48, p = 0.14; Figure 3E).

Figure 3. Serotonin neuron firing rates respond to observable variables.

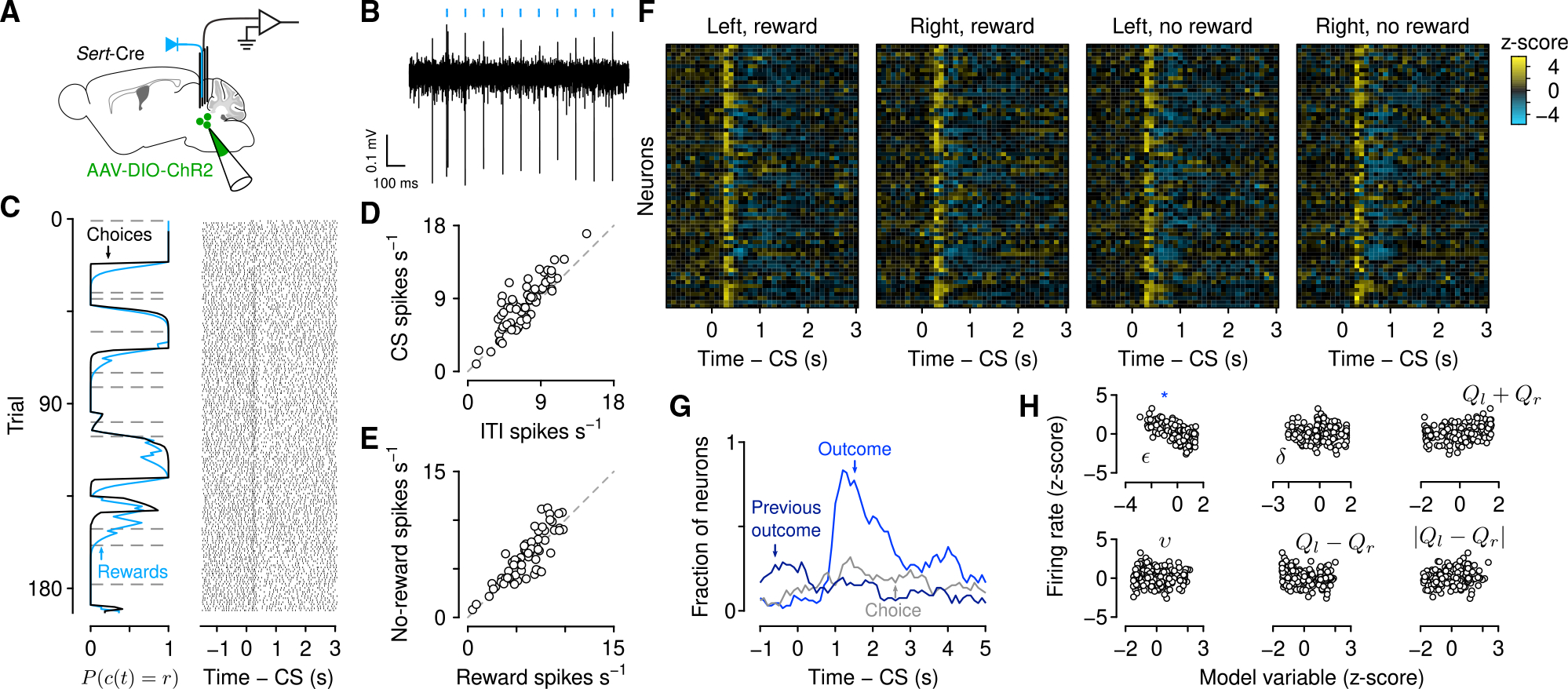
(A) Schematic of electrophysiological recording of identified serotonin neurons.

(B) Example “tagging” of a serotonin neuron, using channelrhodopsin-2 stimulation.

(C) Left: Choice and outcome probabilities for an example session, as in Figure 1B. Right: Action potential raster plots for an example neuron from that session aligned to the go cue (conditioned stimulus [CS]). Each row is a single trial aligned to the go cue.

(D) Mean firing rates during go cue and inter-trial interval for individual neurons (48 of 66 with significant increases and 14 of 66 with significant decreases, paired t tests).

(E) Mean firing rates during the outcome period (1 s after second lick) for individual neurons (13 of 66 with significantly higher responses to rewards and 30 of 66 with significantly higher responses to no rewards, two-sample t tests).

(F) Heatmap of Z-scored firing rates for all serotonin neurons, aligned to go cue, for each of the choice-outcome contingencies.

(G) Rate of significant coefficients from linear regressions of firing rates (500 ms bins) on observable variables at each time point (100 ms steps) before, during, and after the trial.

(H) The Z-scored inter-trial interval firing rates from the example neuron in (C) plotted as functions of model variables. There was a significant negative correlation with ε (blue asterisk), but not with other variables.

Outcomes are essential to the computation of cognitive variables. First focusing on the apparent long-term dynamics, we calculated firing rates during the inter-trial intervals and compared the activity to the behavioral model variables (Figure 3H). We found a significant relationship between firing rate and expected uncertainty in 50% (33 of 66) of serotonin neurons (Figures 4A–4D; regression of inter-trial interval firing rates on expected uncertainty). We observed both positive (12 of 33) and negative correlations (21 of 33), the latter of which could be described as a relationship with certainty, predictability, or reliability. When we regressed out slow, monotonic changes in firing rates and expected uncertainty over the course of the session, this relationship held (Figure S4D). By contrast, we did not find such prevalent relationships in a multivariate regression of firing rates on other latent model variables, such as relative value or RPE (Figures 3H and S4E).

Figure 4. Serotonin neuron firing rates correlate with expected uncertainty on slow and fast timescales.

(A) Action potential raster plots for an example neuron with a significant correlation with expected uncertainty during the go cue aligned to cue onset (left) and outcome (second lick, right) and ordered by increasing ε.

(B) Activity of the example neuron in (A) averaged within terciles (increasing values of ε represented by darker hues) of ε and aligned to the go cue (CS, gray rectangle) and outcome.

(C) The t-statistics across all neurons from a linear regression, modeling firing rates during the inter-trial interval as a function of ε(t). Blue bars indicate neurons with significant regression coefficients.

(D) Population Z-scored firing rates plotted as a function of ε(t). Inset shows population split by positive and negative correlations. Main plot combines these neurons by “sign-flipping” positively correlated firing rates (also used in E and F). Pie chart shows ratio of significant neurons (blue).

(E) Within-trial dynamics of expected uncertainty (ε(t), ε(t + 1), top row) aligned to go cue (CS, left column) and outcome (right column) across all significant neurons. Scale bar, 0.5 Z score. Gray curve: Response time (RT) distribution (cut off at 1 s).

(F) The Z-scored firing rates of serotonin neurons split by e(f) tercile. Scale bar, 0.5 Z score.

(G) Example dynamics of ε(t) estimated from behavior and neuronal firing rates.

(H) Log-log plot of the expected uncertainty update rate (ψ) from the firing rate model for each neuron and from the behavioral model derived from simultaneous choice behavior. See also Figure S4.

Remarkably, firing rates were stable within inter-trial intervals. Dividing expected uncertainty into terciles, we found that serotonin neuron firing rates were relatively constant as time elapsed within inter-trial intervals (Figure 4F; regression coefficient = 9.3 ×10⁻⁷ from a linear model of tercile difference on time in inter-trial interval). Because expected uncertainty evolved somewhat slowly as a function of RPE magnitude and the activity of neurons on this timescale (tens of seconds) fluctuated slowly as well, the two may be similarly autocorrelated.⁵¹ To control for spurious correlations due to comparison of two autocorrelated variables, we first compared the actual neural data with simulated expected uncertainty terms (Figure S4F). We found stronger statistical relationships across the population with the actual expected uncertainty than with simulated values. Additionally, we simulated neural activity with quantitatively matched autocorrelation functions to the real neurons and compared this activity with the actual expected uncertainty values. Again, we found stronger statistical relationships in the real data as opposed to the simulated data (Figures S4G–S4I).

To further examine the robustness of this relationship, we fit the meta-learning model to the inter-trial interval firing rates of neurons that had a significant correlation with expected uncertainty. The meta-learning algorithm was essentially the same as before, but we fit firing rates as a function of expected uncertainty as opposed to fitting choices as a function of relative action values. We found that the updating rate for expected uncertainty from the firing rate model covaried with the same parameter from the choice model across sessions (Figures 4G and 4H; R² = 0.228, p = 0.003, linear regression). Additionally, how well the model fit to the firing rates was predicted by how well correlated the firing rates were to the expected uncertainty variable from the behavioral model (Figure S4J). This result suggests that the neural and behavior data, independently, predict similar expected uncertainty dynamics.

Serotonin neuron firing rates correlate with unexpected uncertainty at outcomes

How does the presence or absence of reward update the slowly varying firing rates of serotonin neurons? According to the model, expected uncertainty changes as a function of unexpected uncertainty. In particular, the model thus predicts a firing rate change at the time of outcome that could be used to update expected uncertainty.

To test this, we calculated firing rates of serotonin neurons within trials, while mice made choices and received outcomes. We found that firing rate changes on fast timescales (hundreds of milliseconds) correlated with expected uncertainty (ε(t)) throughout the period when mice received go cues and made choices (26 of 66; Figure 4E). These correlations persisted during the outcome (reward or no reward), as ε(t) updated to its next value (ε(t +1)). By contrast, firing rates correlated with unexpected uncertainty (v(t)) primarily during the outcome (17 of 66; Figures 5A–5D). These correlations were mostly positive (15 of 17). Thus, brief firing rate changes in serotonin neurons could be integrated to produce more slowly varying changes. In this computation, firing rates may be interpreted as encoding two forms of uncertainty, one slowly varying (ε), one more transient (v). While some individual neurons had significant correlations for both forms of uncertainty (2 neurons, CS-ε and outcome-v; 3 neurons, inter-trial-interval-ε and outcome-v; and 4 neurons with significant correlations with those variables during all 3 epochs), most only correlated with one (5 of 66 neurons CS-ε 11 inter-trial-interval-ε, and 8 outcome-v), suggesting that the computation is performed across the population (Figure 5E).

Figure 5. Serotonin neuron firing rates correlate with unexpected uncertainty on fast timescales.

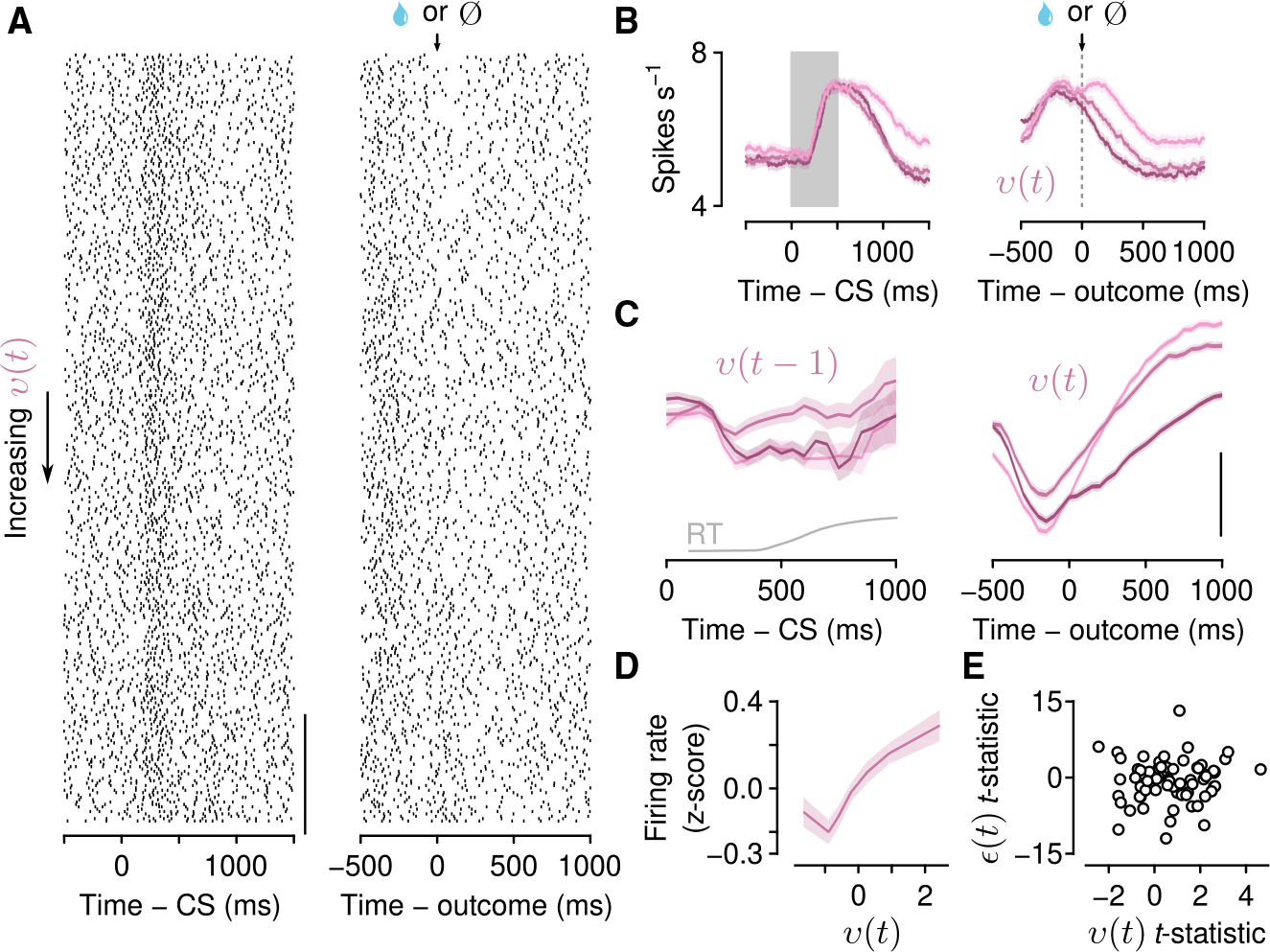
(A) Action potential raster plots for an example neuron with a significant correlation with unexpected uncertainty during the outcome aligned to cue onset (left) and outcome (second lick, right) and ordered by increasing v.

(B) Activity of the example neuron in (A) averaged within terciles (increasing values of v represented by lighter hues) of v and aligned to the go cue (gray rectangle, left, v(t − 1)) and outcome (dashed lined, right, v(t)).

(C) Within-trial dynamics of unexpected uncertainty (v(t − 1), v(t)) aligned to go cue (CS, left column) and outcome (right column) for all significant neurons (pooled by “sign-flipping” negatively correlated firing rates, also used in D). Scale bar, 0.5 Z score. Gray curve: RT distribution (cut off at 1 s).

(D) Population Z-scored firing rates plotted as a function of v(t).

(E) The t-statistics from linear regressions of outcome firing rates on v(t) and CS firing rates on ε(t) for all identified serotonin neurons.

Serotonin neuron firing rates correlate with uncertainty in a Pavlovian task

Based on the results from the first experiment, we made two predictions. First, we hypothesized that correlations between serotonin neuron activity and uncertainty generalize to other behavioral tasks. To test this prediction, we trained 9 mice on a Pavlovian version of the task in which an odor cue predicted probabilistic reward after a 1 s delay (Figure 6A). The probability of reward changed in blocks within each session (Figure 6B). This task required no choice to be made. Rather, mice simply licked toward a single water-delivery spout in anticipation of a possible reward.

Figure 6. Serotonin neuron firing rates correlate with expected and unexpected uncertainty in a dynamic Pavlovian task.

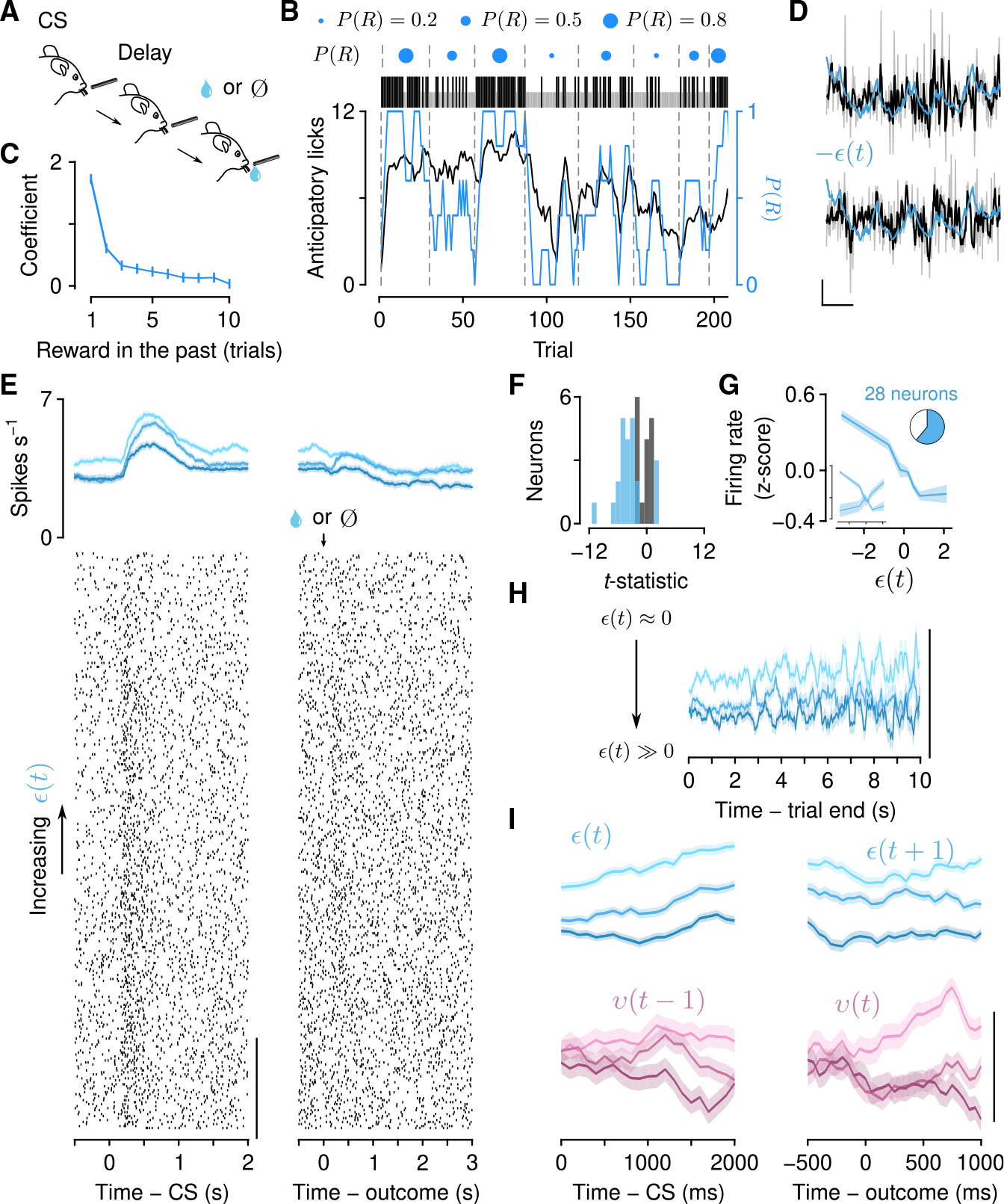
(A) Schematic of Pavlovian task in which the probability of reward (P(R)) varied over trials.

(B) Example behavior showing anticipatory licking, in the delay before outcome, as P(R) varied. Black ticks: Rewarded trials. Gray ticks: Unrewarded trials.

(C) Linear regression coefficients of licking rate on reward history.

(D) Two example neurons showing negative correlations between inter-trial interval firing rates and expected uncertainty (−ε is plotted) when the monotonic trends are regressed out. Scale bars, 1 Z score, 50 trials.

(E) Example serotonin neuron showing a negative correlation between CS firing rates and expected uncertainty (ε(t)). Top: Firing rates averaged within terciles (represented by hue) of E and aligned to the CS (left, ε(t)) and outcome (right, ε(t +1)). Bottom: Action potential raster plots aligned to cue onset (left) and outcome (second lick, right) and ordered by increasing E.

(F) The t-statistics from linear regression, modeling inter-trial interval firing rate as a function of ε(t) as in Figure 3F.

(G) Population “tuning curves,” as in Figure 3G.

(H) Stable firing rates within inter-trial intervals, as in Figure 3I. Scale bar, 0.5 Z score.

(I) Within-trial, Z-scored firing rates as a function of uncertainty as in Figures 4E and 5C. Scale bar, 0.5 Z score. See also Figure S5.

The number of anticipatory licks during the delay between cue and outcome (presence or absence of reward) reflected recent reward history (Figure 6C). To estimate uncertainty in this task, we modified the meta-learning model to generate anticipatory licks as a function of the expected value of the cue (Figure S5A). While the model was capable of explaining behavior and accurately estimating reward probabilities (Figure S5B), interestingly, we found no clear behavioral evidence of variable learning rates (Figures S5C–S5E). However, recordings of dorsal raphe serotonin neurons from mice behaving in this task revealed that the activity of these neurons correlated with expected uncertainty at similar rates to those recorded in the dynamic foraging task (Figures 6D–6G and S5F–S5H; 61%, 25 of 41 neurons from 5 mice) and were mostly negatively correlated (20 of 25). Similar to observations in the foraging task, neurons in the Pavlovian task showed stable firing rates within inter-trial intervals (Figure 6H; regression coefficient = −3.1 ×10⁻⁶ from a linear model of tercile difference on time in inter-trial interval). Serotonin neuron firing rates also correlated with expected uncertainty throughout its update interval (27 of 41 during cue and delay, 25 of 41 after outcome; Figures 6E and 6I) and with unexpected uncertainty at the time of the outcome (11 of 41; Figure 6I). Thus, the nervous system may maintain running estimates of two forms of uncertainty that generalize across behavioral tasks.

Serotonin neuron inhibition disrupts meta-learning

In our second prediction from the dynamic foraging experiment, we asked whether inactivating serotonin neurons rendered mice unable to adjust learning rates. The meta-learning model makes specific predictions about the role of uncertainty in learning. To test the predictions of the model under the hypothesis that serotonin neurons encode uncertainty, we expressed an inhibitory designer receptor exclusively activated by designer drugs (DREADD) conjugated to a fluorophore (hM4Di-mCherry) in dorsal raphe serotonin neurons (Figures 7A and S6A). Sert-Cre mice received injections of a Cre-dependent virus containing the receptor (AAV5-hSyn-DIO-hM4D(Gi)-mCherry, n = 6 mice) into the dorsal raphe. Control Sert-Cre mice were injected with the same virus containing only the fluorophore (n = 6 mice). On consecutive days, mice received an injection of vehicle (0.5% DMSO in 0.9% saline), the DREADD ligand agonist 21 (3 mg kg⁻¹ in vehicle),^52–54 or no injection. Because simultaneous changes of reward probabilities were rare, we modified the task to include them with slightly higher frequency.

Figure 7. Serotonin neuron inhibition disrupts meta-learning.

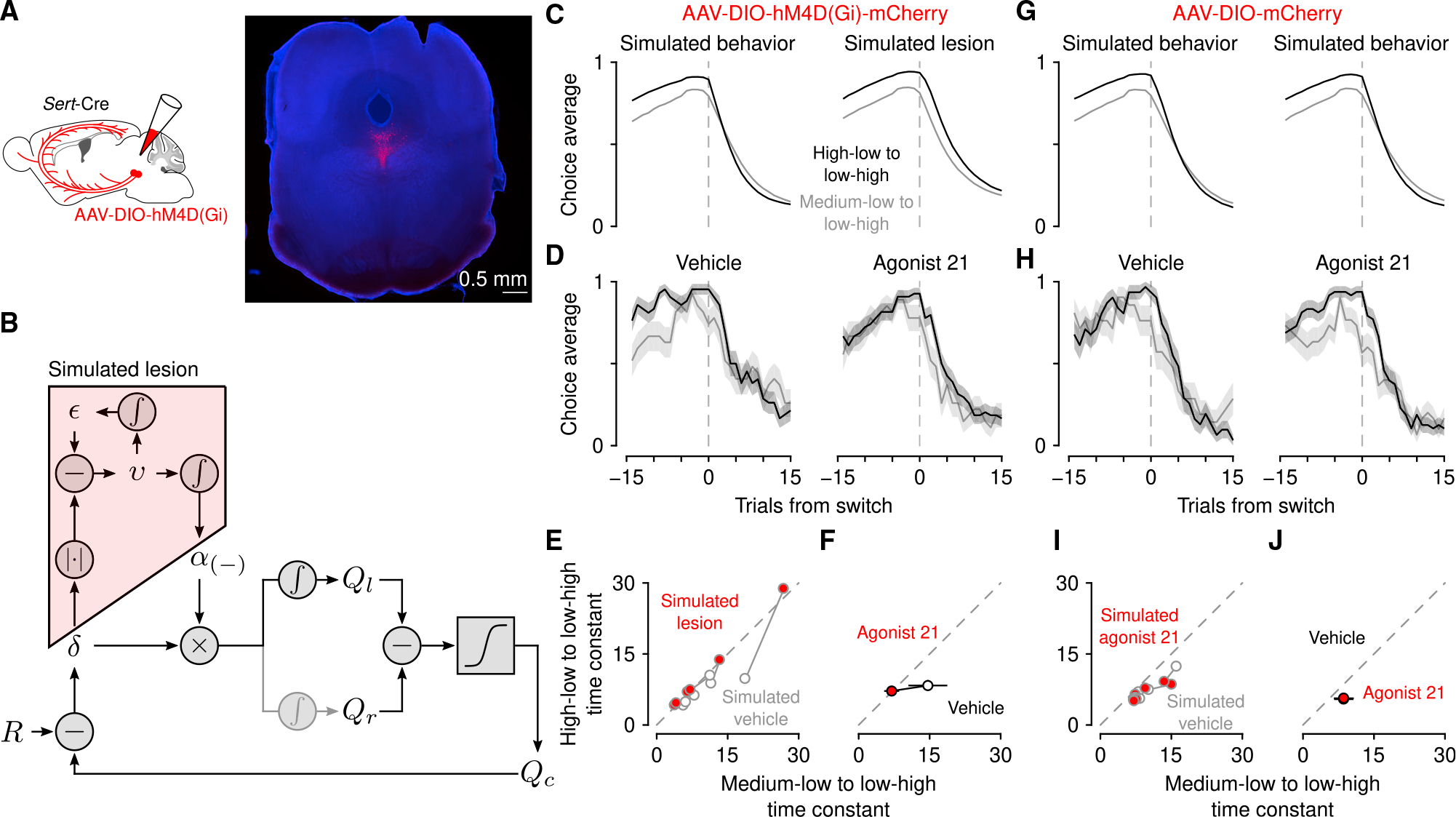
(A) Schematic of experiment to reversibly inactivate serotonin neurons and representative expression of hM4Di-mCherry in dorsal raphe serotonin neurons.

(B) Schematic of simulated lesion in which models were fit to mouse behavior from vehicle sessions and then meta-learning variables (i.e., ε and v) were set to zero.

(C) Simulated behavior with meta-learning intact, fit to vehicle behavior (left) and simulated lesion (right).

(D) Mouse behavior with vehicle injections (control experiment) and drug (agonist 21). Lines are mean choice probability and shading is Bernoulli SEM.

(E) Exponential time constants for transitions from simulated behavior and simulated lesions.

(F) Time constants from mice (with 95% CI). (G) Simulated behavior from mice expressing mCherry in serotonin neurons with vehicle (left) and agonist 21 (right) injections.

(H) Mouse behavior with vehicle injections and drug (agonist 21).

(I) Simulation time constants from fluorophore-control mice.

(J) Time constants from fluorophore-control mice (with 95% CI).

See also Figure S6.

To quantify the change in behavior predicted by the model, we first fit the model to mouse behavior on vehicle injection days and used those parameters to simulate behavior. We then simulated a lesion by fixing expected and unexpected uncertainty to 0 (essentially fixing the negative RPE learning rate to its median value) and simulated behavior again (Figure 7B). The simulated lesion diminished the differences in transition speed between the pre-transition reward conditions (Figures 7C and 7E), identical to a static learning model.

On days with agonist 21 injections, mice expressing hM4Di in serotonin neurons demonstrated changes in learning at transitions (Figures 7D and 7F; effects of trial from transition F_1,58 = 87.9, p < 10⁻¹², trial × transition type interaction F_1,58 = 13.7, p = 0.003, transition type F_1,58 = 9.15, p = 0.004, and drug condition F_1,58 = 21.2, p < 10⁻⁴, linear mixed effects model) matching the predictions of the simulated lesion model (Figures 7C and 7E; effects of trial from transition F_1,58 = 226, p < 10⁻²⁰, trial × transition interaction F_1,58 = 5.16, p = 0.027, and transition type × drug condition interaction F_1,58 = 9.9, p = 0.003). Mice expressing a fluorophore alone in serotonin neurons showed no effect of agonist 21 (Figures 7H and 7J; effects of trial from transition F_1,58 = 81.2, p < 10⁻¹¹, transition type F_1,58 = 17.4, p < 10⁻³, and trial × transition type interaction F_1,58 = 23.8, p < 10⁻⁵), consistent with simulations from the meta-learning model fit separately to vehicle and agonist 21 behavior (Figures 7G and 7I; effects of trial from transition F_1,58 = 255, p < 10⁻²² and trial × transition interaction F_1,58 = 4.14, p = 0.046). Serotonin neuron inhibition did not slow response times (Figure S6B), change how outcomes drove response times (Figure S6C), nor cause mice to lick during inter-trial intervals. Thus, the observed effects of reversible inhibition are consistent with a role for serotonin neurons signaling uncertainty to modulate learning rates.

DISCUSSION

To behave flexibly in dynamic environments, learning rates should vary according to the statistics of those environments.^5,7,8,19,55 Our model captures differences in learning by estimating expected uncertainty: a moving average of unsigned prediction errors that tracks variability in the outcomes of actions. This quantity is used to modulate learning rate by determining how unexpected an outcome is relative to that expected uncertainty. When outcomes are probabilistic but stable, expected uncertainty also slows learning. The model captured observed changes in learning rates that could not be reproduced with an RL model that uses static learning rates. The activity of the majority of identified serotonin neurons correlated with the expected uncertainty variable from the model when fit to dynamic foraging behavior. This relationship held in a different behavioral context, with similar fractions of serotonin neurons tracking expected uncertainty in a dynamic Pavlovian task. During dynamic foraging, chemogenetic inhibition of serotonin neurons caused changes in choice behavior that were consistent with the changes in learning predicted by removing meta-learning from the model.

While serotonin neuron firing rates change on multiple time-scales,³¹ the observed changes that correlated with expected uncertainty occurred over relatively long periods of time. How rapidly RPE magnitudes are integrated tracks variability in outcomes on a timescale relevant to experienced block lengths. Consequently, deviations from expected uncertainty reliably indicate changes in reward probabilities. In addition to the computational relevance of activity on this timescale, serotonin neuron firing rate changes may be optimized for the nervous system to implement these computational goals. Slow changes in serotonin neuron activity could enable gating or gain control mechanisms,^56,57 bidirectional modulation of relevant inputs and outputs,^58–60 or other previously observed circuit mechanisms that modulate how new information is incorporated⁶¹ to drive flexible behavior.

We also observed changes in serotonin neuron activity on shorter timescales that correlated with both expected and unexpected uncertainty. The timing of these brief signals may be important to update the slower dynamics correlated with expected uncertainty, as predicted from the model (i.e., ε essentially integrates v). Alternatively, serotonin neurons could “multiplex” across timescales, whereby brief changes in firing rates may have different downstream functions than slower changes.

Several conceptualizations of expected uncertainty have been proposed with different consequences for learning and exploratory behavior.⁹ For example, there can be uncertainty about a specific correlational relationship between events in the environment or between a specific action and the environment. There is evidence that the activity of norepinephrine and acetylcholine neurons may be related to these types of uncertainty.^8,62,63 It should be noted that both norepinephrine neurons in the locus coeruleus⁶⁴ and acetylcholine neurons in the basal forebrain⁶⁵ receive functional input from dorsal raphe serotonin neurons. Dorsal raphe serotonin neurons also receive input from locus coeruleus.⁶⁶

Here, we studied a more general form of expected uncertainty that tracks variability in outcomes regardless of the specific action taken. This type of uncertainty may apply to learned rules or separately, states in a model-based framework.⁶⁷ It may also be conceptually related to the level of commitment to a belief, which can scale learning in models that learn by minimizing surprise.^15,16,18 In these ways, our model may approximate inference or change detection in certain behavioral contexts.^12,13 Our notion of expected uncertainty is also related to reward variance, risk, or outcome uncertainty,^{10,11,67–69} but with respect to an entire behavioral policy as opposed to a specific action. It will be important for future studies to determine whether the present observations generalize. For example, serotonin’s known effects on neurons in sensory areas^57,70–72 may play a role in sensory prediction learning.

Unexpected uncertainty has also been previously defined in numerous ways. In our model, the negative RPE learning rate is a function of recent deviations from expected uncertainty and thus may be most related to a subjective estimate of environmental volatility. This interpretation is consistent with learning rates increasing as a function of increasing volatility.¹⁹ An estimate of volatility may also reflect the surprise that results from the violation of a belief.^15,16,18 Our observation that brief changes in serotonin neuron firing rates at the time of outcome correlated with unexpected uncertainty is also consistent with previous work showing that serotonin neuron activity correlated with “surprise” when cue-outcome relationships were violated.³³

Our model proposes one learning system with variable learning rates, but these results may also be consistent with models that combine contributions of different learning systems.^73–75 From this perspective, the uncertainty representations we observed may be related to the uncertainty or reliability of one of those learning systems, consistent with their generalization across actions. Unreliability of a slower learning system around transitions may enhance contributions from a faster learning system, for example. A somewhat related alternative is that serotonin neurons provide this signal to refine more complex and flexible learning systems implemented in recurrent neural networks.⁷⁶

We did not find any evidence in the dynamic Pavlovian behavior that distinguished meta-learning from static learning. It may be that differences in these models are not observable in this behavior. Also, the dynamic foraging task engages regions of the brain that are not necessary for the dynamic Pavlovian task.⁴³ Consequently, uncertainty may be incorporated in other ways to drive behavior. Alternatively, the brain may keep track of statistics of the environment that are not always used in behavior.

In the meta-learning RL model as we have formulated it, only the negative RPE learning rate is subject to meta-learning. This is an empirical finding and one that may be a consequence of the structure of the task. For example, the reward statistics might result in a saturation of learning from rewards such that its modulation is unnecessary. Asymmetries in the task structure (the absence of trials in which P(R) = 0.1 for both spouts) and mouse preference (mice regularly exploited the P(R) = 0.5 spout) also result in rewards carrying more information about which spout is likely “good enough” (P(R) = 0.9 or P(R) = 0.5). Another possibility, not mutually exclusive with the first, is that learning about rewards and lack thereof could be asymmetric.^44,77–80 This asymmetry could result from ambiguity in the non-occurrence of the expected outcome, differences in the magnitude of values of each outcome, or separate learning mechanisms entirely. Similarly, because outcomes are binary in our tasks, learning from negative and positive RPEs could be asymmetric. Alternatively, as described above, this parameterization might just better approximate a more complex cognitive process (e.g., inference) in this specific behavioral context.

Our findings and conceptual framework, including the effect on learning from worse-than-expected outcomes, are consistent with previous observations and manipulations of serotonin neuron activity. In a Pavlovian reversal task, changes in cue-outcome mappings elicited responses from populations of serotonin neurons that decayed as mice adapted their behavior to the new mapping.³³ Chemogenetic inhibition of serotonin neurons in this task impaired behavioral adaptation to a cue that predicted reward prior to the reversal, but not after. The manipulation did not affect behavior changes in response to the opposite reversal. In reversal tasks in which action-outcome contingencies were switched, lesions or pharmacological manipulations of serotonin neurons also resulted in impairments of adaptive behavior at the time of reversal.^37–41 Specifically, lesioned animals continued to make the previously rewarded action. These findings are consistent with a role for serotonin neuron activity in tracking expected uncertainty and driving learning from worse-than-expected outcomes. More recent work in mice demonstrated that serotonin neuron activation increased the learning rate after longer intervals between outcomes but that learning after shorter intervals was already effectively saturated (i.e., win-stay, lose-shift).⁴² An intriguing possibility is that serotonin neurons mediate the contributions of different learning systems, like faster, working-memory-based learning, and slower, plasticity-dependent learning or model-based and model-free learning.^{42,73–75,81–84}

Previous recordings from dorsal raphe neurons generally and identified serotonin neurons demonstrated a relationship between their activity and the expected value of cues or contexts on different timescales.^{31–33,85–87} These findings suggest that serotonin neuron activity may track state value. It is possible that this information could be used to drive learning in a similar way as uncertainty, but not in the manner proposed by the opponency or global reward state models that we tested. To explain foraging behavior, there would need to be some change detection component to the state value computation in order to drive learning adaptively. Similarly, the signal we observed may be related to state uncertainty.⁶⁷

Our results may also be consistent with those from human studies in which the serotonin system is manipulated. Tryptophan depletion results in low blood contents of serotonin and leads to impaired learning about the aversive consequences of actions or stimuli,^88,89 enhances perseverative decision making,^90,91 and alters the relative contributions of model-free and model-based contributions to decision making,⁸² among other effects. Selective serotonin reuptake inhibitors have also been shown to disrupt learning in probabilistic reversal learning tasks.^92,93

A number of studies have also examined the role of serotonin neuron activity in patience and persistence for rewards.^86,94–96 These studies demonstrated that activating serotonin neurons increased waiting times for or active seeking of reward. In all cases, animals can be thought of as learning from lack of rewards at each point in time. Under the proposed meta-learning framework, manipulating uncertainty could slow this learning, resulting in prolonging waiting times or enhancing persistence.

What are the postsynaptic consequences of slow changes in serotonin release? Target regions involved in learning and decision making, like the prefrontal cortex, ventral tegmental area, and striatum, express a diverse range of serotonin receptors capable of converting a global signal into local changes in circuit dynamics. The activity in these regions also correlates with latent decision variables that update with each experience,^{22,43,97,98,99} providing a potential substrate through which serotonin could modulate learning. For example, the gain of RPE signals produced by dopamine neurons in the ventral tegmental area is modulated by the variance of reward value.^100,101

What is the presynaptic origin of uncertainty computation in serotonin neurons? Synaptic inputs from the prefrontal cortex¹⁰² may provide information about decision variables used in this task.⁴³ Local circuit mechanisms in the dorsal raphe^102,103 and long-lasting conductances in serotonin neurons^104–108 likely contribute to the persistence of these representations.

Learning is dynamic. Flexible decision making requires using recent experience to adjust learning rates adaptively. The observed foraging behavior demonstrates that learning is not a static process, but a dynamic one. The meta-learning RL model provides a potential mechanism by which recent experience modulates learning adaptively, and reveals a quantitative link between serotonin neuron activity and flexible behavior.

STAR⋆METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for reagents should be directed to the Lead Contact, Jeremiah Y. Cohen (jeremiah.cohen@jhmi.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

Data have been deposited on Dryad (https://doi.org/10.5061/dryad.cz8w9gj4s).

EXPERIMENTAL MODELS AND SUBJECT DETAILS

Animals and surgery

We used 67 male and female mice, backcrossed with C57BL/6J and heterozygous for Cre recombinase under the control of the serotonin transporter gene (Slc6a4^tm1(cre)Xz, The Jackson Laboratory, 0145540).¹⁰⁹ Four male mice were used for electrophysiological recordings in the dynamic foraging task, 5 mice were used for electrophysiological recordings in the dynamic Pavlovian task (1 female, 4 male), 44 mice (20 female, 24 male) were used for additional behavior in the dynamic foraging task, 4 male mice were used for additional behavior in the dynamic Pavlovian task, and 12 mice (3 female, 9 male) were used for the chemogenetic experiments. Surgery was performed on mice between the ages of 4–8 weeks, under isoflurane anesthesia (1.0%–1.5% in O₂) and in aseptic conditions. During all surgeries, custom-made titanium headplates were surgically attached to the skull using dental adhesive (C&B-Metabond, Parkell). After the surgeries, analgesia (ketoprofen, 5 mg kg⁻¹ and buprenorphine, 0.05–0.1 mg kg⁻¹) was administered to minimize pain and aid recovery.

For electrophysiological experiments, we implanted a custom microdrive targeting dorsal raphe using a 16° posterior angle, entering through a craniotomy at 5.55 mm posterior to bregma and aligned to the midline.

For all experiments, mice were given at least one week to recover prior to water restriction. During water restriction, mice had free access to food and were monitored daily in order to maintain 80% of their baseline body weight. All mice were housed in reverse light cycle (12h dark/12h light, dark from 08:00–20:00) and all experiments were conducted during the dark cycle between 10:00 and 18:00. All surgical and experimental procedures were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and approved by the Johns Hopkins University Animal Care and Use Committee.

METHOD DETAILS

Behavioral task

Before training on the tasks, water-restricted mice were habituated to head fixation for 1–3 d with free access to water from the provided spouts (two 21 ga stainless steel tubes separated by 4 mm) placed in front of the 38.1 mm acrylic tube in which the mice rested. The spouts were mounted on a micromanipulator (DT12XYZ, Thorlabs) with a custom digital rotary encoder system to reliably determine the position of the lick spouts in XYZ space with 5–10 μm resolution.⁴³ Each spout was attached to a solenoid (ROB-11015, Sparkfun) to enable retraction (see Behavioral tasks: dynamic foraging). The odors used for the cues (p-cymene and (−)-carvone) were dissolved in mineral oil at 1:10 dilution (30 μl) and absorbed in filter paper housed in syringe adapters (Whatman, 2.7 μm pore size). The adapters were connected to a custom-made olfactometer¹¹⁰ that diluted odorized air with filtered air by 1:10 to produce a 1.0 L min⁻¹ flow rate. The same flow rate was maintained outside of the cue period so that flow rate was constant throughout the task.

Licks were detected by charging a capacitor (MPR121QR2, Freescale) or using a custom circuit (Janelia Research Campus 2019–053). Task events were controlled and recorded using custom code (Arduino) written for a microcontroller (ATmega16U2 or ATmega328). Water rewards were 2–4 μl, adjusted for each mouse to maximize the number of trials completed per session and to keep sessions around 60 minutes. Solenoids (LHDA1233115H, The Lee Co) were calibrated to release the desired volume of water and were mounted on the outside of the dark, sound-attenuated chamber used for behavior tasks. White noise (2–60 kHz, Sweetwater Lynx L22 sound card, Rotel RB-930AX two-channel power amplifier, and Pettersson L60 Ultrasound Speaker), was played inside the chamber to block any ambient noise.

Behavioral tasks: dynamic foraging

During the 1–3 days of habituation, mice were trained to lick both spouts to receive water. Water delivery was contingent upon a lick to the correct spout at any time. Reward probabilities were chosen from the set {0,1} and reversed every 20 trials.

In the second stage of training (5–12 d), the trial structure with odor presentation was introduced. Each trial began with the 0.5 s delivery of either an odor “go cue” (P = 0.95) or an odor “no-go cue” (P = 0.05). Following the go cue, mice could lick either the left or the right spout. If a lick was made during a 1.5 s response window, reward was delivered probabilistically from the chosen spout. The unchosen spout was retracted at the time of the tongue contacting the other spout so that mice would not try to sample both spouts within a trial. The unchosen spout was replaced 2.5 s after cue onset. Following a no-go cue, any lick responses were neither rewarded nor punished. Reward probabilities during this stage were chosen from the set {0,1} and reversed every 20–35 trials. During this period of training only, water was occasionally manually delivered to encourage learning of the response window and appropriate switching behavior. Reward probabilities were then changed to {0.1,0.9} for 1–2 days of training prior to introducing the final stage of the task. Rewards were never “baited,” as in previous versions of the task.^43,111–113 We did not penalize switching with a “change-over delay.” If a directional lick bias was observed in one session, the lick spouts were moved horizontally 50–300 μm prior to the following session such that the spout in the biased direction was further away.

After the 1.5 s response window, inter-trial intervals were generated as draws from an exponential distribution with a rate parameter of 0.3 and a maximum of 30 s. This distribution results in a flat hazard rate for inter-trial intervals such that the probability of the next trial did not increase over the duration of the inter-trial interval.¹¹⁴ Inter-trial intervals (the times between consecutive go cue onsets) were 7.45 s on average (range 2.5–32.5 s). As in previous studies, mice made a leftward or rightward choice in greater than 99% of trials.⁴³ Mice completed 280 ± 66.6 trials per session (range, 79–655 trials).

In the final stage of the task, the reward probabilities assigned to each lick spout were drawn pseudorandomly from the set {0.1,0.5,0.9} in all the mice from the behavior experiments (n = 46), all the mice from the DREADDs experiments (n = 10), and half of the mice from the electrophysiology experiments (n = 2). The other half of mice from the electrophysiology experiments (n = 2) were run on a version of the task with probabilities drawn from the set {0.1,0.4,0.7}. The probabilities were assigned to each spout individually with block lengths drawn from a uniform distribution of 20–35 trials. To stagger the blocks of probability assignment for each spout, the block length for one spout in the first block of each session was drawn from a uniform distribution of 6–21 trials. For each spout, probability assignments could not be repeated across consecutive blocks. To maintain task engagement, reward probabilities of 0.1 could not be simultaneously assigned to both spouts. If one spout was assigned a reward probability greater than or equal to the reward probability of the other spout for 3 consecutive blocks, the probability of that spout was set to 0.1 to encourage switching behavior and limit the creation of a direction bias. If a mouse perseverated on a spout with reward probability of 0.1 for 4 consecutive trials, 4 trials were added to the length of both blocks. This procedure was implemented to keep mice from choosing one spout until the reward probability became high again.

To minimize spontaneous licking, we enforced a 1 s no-lick window prior to odor delivery. Licks within this window were punished with a new, randomly-generated inter-trial interval followed by a 2.5 s no-lick window. Implementing this window significantly reduced spontaneous licking throughout the entirety of behavioral experiments.

Behavioral tasks: dynamic Pavlovian

On each trial either an odor “CS + “ (P = 0.95) or an odor “CS − “ (P = 0.05) was delivered for 1 s followed by a delay of 1 s. CS + predicted probabilistic reward delivery, whereas CS− predicted nothing. Mice were allowed 3 s to consume the water, after which any remaining reward was removed by a vacuum. Each trial was followed by an inter-trial interval, drawn from the same distribution as in the dynamic foraging task. The time between trials (CS on to CS on) was 9.34 s on average (range 6–36 s).

The reward probability assigned to CS + was drawn pseudorandomly from the set {0.2,0.5,0.8} or, in separate sessions, alternated between the probabilities in the set {0.2,0.8}. The probability changed every 20–70 trials (uniform distribution). The CS + probability of the first block of every session was 0.8.

Electrophysiology

We recorded extracellular signals from neurons at 32 or 30 kHz using a Digital Lynx 4SX (Neuralynx, Inc.) or Intan Technologies RHD2000 system (with RHD2132 headstage), respectively. The recording systems were connected to 8–16 implanted tetrodes (32–64 channels, nichrome wire, PX000004, Sandvik) fed through 39 ga polyimide guide tubes that could be advanced with the turn of a screw on a custom, 3D-printed microdrive. The impedances of each wire in the tetrodes were reduced to 200–300 kΩ by gold plating. The tetrodes were wrapped around a 200 μm optic fiber used for optogenetic identification. After each recording session, the tetrode-optic-fiber bundle was driven down 75 μm. The median signal was subtracted from raw recording traces across channels and bandpass-filtered between 0.3–6 kHz using custom MATLAB software. To detect peaks, the bandpass-filtered signal, x, was thresholded at 4 σ_n where ${\sigma }_n=\mathrm{median}\left(\frac{|x|}{0.6745}\right)$¹¹⁵ Detected peaks were sorted into individual unit clusters offline (Spikesort 3D, Neuralynx Inc.) using waveform energy, peak waveform amplitude, minimum waveform trough, and waveform principal component analysis. We used two metrics of isolation quality as inclusion criteria: L-ratio (< 0.05)¹¹⁶ and fraction of interspike interval violations (< 0.1% interspike intervals < 2 ms).

Individual neurons were determined to be optogenetically-identified if they responded to brief pulses (10 ms) of laser stimulation (473 nm wavelength) with short latency, small latency variability, and high probability of response across trains of stimulation (10 trains of 10 pulses delivered at 10 Hz). We used an unsupervised k-means clustering algorithm to cluster all neurons based on these features. The elbow method and Calinkski-Harabasz criterion were used to determine that the optimal number of clusters was 4. Members of the cluster (66 neurons) with the highest mean probability of response, shortest mean latency, and smallest mean latency standard deviation were considered as identified. The responses of individual neurons were manually inspected to ensure light re- sponsivity. In addition to the presence of identified serotonin neurons, targeting of dorsal raphe was confirmed by performing electrolytic lesions of the tissue (20 s of 20 μA direct current across two wires of the same tetrode) and examining the tissue after perfusion.

Viral injections

To express channelrhodopsin-2 (ChR2), hM4Di, or mCherry in dorsal raphe serotonin neurons, we pressure-injected 810 nL of rAAV5-EF1a-DIO-hChR2(H134R)-EYFP (3×10¹³ GC ml⁻¹), pAAV5-hSyn-DIO-hM4D(Gi)-mCherry (1.2×10¹³ GC ml⁻¹), or pAAV5-hSyn-DIO-mCherry (1.0×10¹³ GC ml⁻¹) into the dorsal raphe of Sert-Cre mice at a rate of 1 nL s⁻¹ (MMO-220A, Narishige). pAAV-hSyn-DIO-hM4D(Gi)-mCherry and pAAV-hSyn-DIO-mCherry were gifts from Bryan Roth (Addgene viral preps 44362-AAV5 and 50459-AAV5). We made three injections of 270 nL at the following coordinates: {4.63,4.57,4.50} mm posterior of bregma, {0.00,0.00,0.00} mm lateral from the midline, and {2.80,3.00,3.25} mm ventral to the brain surface. The pipette was inserted through a craniotomy at −5.55 mm posterior to bregma and aligned to midline, using a 16° posterior angle. Before the first injection, the pipette was left at the most ventral coordinate for 10 minutes. After each injection, the pipette was withdrawn 50 μm and left in place for 5 min. The craniotomy after a hM4Di or mCherry injection was covered with silicone elastomer (Kwik-Cast, WPI) and dental cement. For electrophysiology experiments with rAAV5-EF1a-DIO-hChR2(H134R)-EYFP injections, the microdrive was implanted through the same craniotomy.

Inactivation of serotonin neurons

Six mice were injected with pAAV-hSyn-DIO-hM4D(Gi)-mCherry and 6 mice were injected with pAAV-hSyn-DIO-mCherry as a control. One of the hM4D mice failed to perform the task and so was excluded. After training mice, we injected either 3.0 mg kg⁻¹ agonist 21 (Tocris) dissolved in 0.5% DMSO/saline or an equivalent volume of vehicle (0.5% DMSO/saline alone) I.P. on alternating days (5 sessions per injection type per mouse).

Histology

After experiments were completed, mice were euthanized with an overdose of isoflurane, exsanguinated with saline, and perfused with 4% paraformaldehyde. The brains were cut in 100-μm-thick coronal sections and mounted on glass slides. We validated expression of rAAV5-EF1a-DIO-hChR2(H134R)-EYFP, pAAV-hSyn-DIO-hM4D(Gi)-mCherry, or pAAV-hSyn-DIO-mCherry with epifluorescence images of dorsal raphe (Zeiss Axio Zoom.V16) with immunostaining against tryptophan hydroxylase-2 (goat α-TPH2, Abcam 121020, at 1:400) as a marker of serotonin neurons and donkey α-goat conjugated to Cy5 (Abcam 6566) as a secondary antibody. In electrophysiological experiments, we confirmed targeting of the optic-fiber-tetrode bundle to the dorsal raphe by location of the electrolytic lesion.

QUANTIFICATION AND STATISTICAL ANALYSIS

Data analysis

All analyses were performed with MATLAB (Mathworks) and R. All data are presented as mean ± SD unless reported otherwise. All statistical tests were two-sided. In Figures 2E and 2G, the probability that the time constants from the actual behavior belonged to the distribution of simulated behavior time constants was calculated by finding the Mahalanobis distance of the former from the latter, calculating the cumulative density function of the chi-square distribution at that distance, and subtracting it from 1. For all analyses, no-go (dynamic foraging) and CS− (dynamic Pavlovian) cues were ignored and treated as part of the inter-trial interval.

Data analysis: descriptive models of behavior

We fit logistic regression models to predict choice as a function of outcome history for each mouse using the model

$$\log \left(\frac{P\left(c_r(t)\right)}{1-P\left(c_r(t)\right)}\right)=\sum _{i=1}^{10}{\beta }_i^R\left(R_r(t-i)-R_l(t-i)\right)+\sum _{i=1}^{10}{\beta }_i^N\left(N_r(t-i)-N_l(t-i)\right)+{\beta }_0,$$

where c_r(t) = 1 fora right choice and 0 for a left choice, R = 1 fora rewarded choice and 0 for an unrewarded choice, and N = 1 for an unrewarded choice and 0 for a rewarded choice. To predict response times (RT), we first z-scored the lick latencies by spout, to correct for differences due to relative spout placement and bias. Then, for each animal we fit the model

$$\text{RT}(\text{t})=\sum _{i=1}^{10}{\beta }_i^R\left(R_r(t-i)+R_l(t-i)\right)+{\beta }_0,$$

including a variable for trial number. We fit exponentials with the equation $a{e}^{-{\beta }_{1.10}^R/\tau }$ to the regression coefficients, averaged across animals, from the choice and response time models.

Data analysis: generative model of behavior with static learning

We applied a generative RL model of behavior in the foraging task with static learning rates.⁴³ This RL model estimates action values (Q_l(t) and Q_r(t)) on each trial to generate choices. Choices are described by a random variable, c(t), corresponding to left or right choice, c(t)ϵ {l,r}. The value of a choice is updated as a function of the RPE, and the rate at which this learning occurs is controlled by the learning rate parameter α. Because we observed asymmetric learning from rewards and no rewards (Figure 1C), consistent with previous reports,^43,47 we included separate learning rates for the different outcomes. For example, if the left spout was chosen, then

$$Q_l(t+1)=\{\begin{array}{ll}{Q}_l(t)+{\alpha }_{(+)}\delta (t),\hfill & \text{if}\delta (t)>0\hfill \\ Q_l(t)+{\alpha }_{(-)}\delta (t),\hfill & \text{if}\delta (t)<0\hfill \end{array}$$

$$Q_r(t+1)=\zeta Q_r(t),$$

where δ(t) = R(t) − Q_l(t) and ζ represents the forgetting rate parameter. The forgetting rate captures the increasing uncertainty about the value of the unchosen spout.

The Q-values are used to generate choice probabilities through a softmax decision function:

$$P(c(t)=r)=\frac{1}{1+e^{-\beta \left(Q_r(t)-Q_l(t)+bias\right)}},$$

$$P(c(t)=l)=1-P(c(t)=r),$$

where β, the “inverse temperature” parameter, controls the steepness of the sigmoidal function. In other words, β controls the stochasticity of choice.

Data analysis: generative model of behavior with meta-learning

We observed mouse behavior that the static learning model failed to capture and that suggested that learning rate was not constant overtime. Thus, we added a component to the model that modulates RPE magnitude and α₍₋₎ (“meta-learning”). Because learning should be slow in stable but variable environments, expected uncertainty scaled RPEs, such that learning is decreased when expected uncertainty is high. If the left spout was chosen, the values of actions were updated according to

$$Q_l(t+1)=\{\begin{array}{cc}{Q}_l(t)+{\alpha }_{(+)}\delta (t)(1-ϵ(t)),& \text{if}\delta (t)>0\\ Q_l(t)+{\alpha }_{(-)}(t)\delta (t)(1-ϵ(t)),& \text{if}\delta (t)<0\end{array}$$

$$Q_r(t+1)=\zeta Q_r(t),$$

where ε is an evolving estimate of expected uncertainty calculated from the history of unsigned RPEs:

$$v(t)=|\delta (t)|-ϵ(t),$$

$$ϵ(t+1)=ϵ(t)+{\alpha }_{v}v(t).$$

The rate of RPE magnitude integration is controlled by α_v. Deviations from the expected uncertainty are captured by unexpected uncertainty, v, and may indicate that a change has occurred in the environment. Changes in the environment should drive learning to adapt behavior to new contingencies so α₍₋₎ varies as a function of how surprising recent outcomes are:

$${\alpha }_{(-)}(t)=\{\begin{array}{ll}{\alpha }_{(-)}(t-1)\text{if}\delta (t)>0\hfill & \hfill \\ \psi \left(v(t)+{\alpha }_{{(-)}_0}\right)+(1-\psi )\left({\alpha }_{(-)}(t-1)\right)\hfill & \text{if}\delta (t)<0\hfill \end{array}$$

where α₍₋₎₀ is the baseline learning rate from no reward and c controls how quickly unexpected uncertainty is integrated to update α₍₋₎. As it is formulated, α₍₋₎ increases after surprising no-reward outcomes. This learning rate was not allowed to be less than 0, such that

$${\alpha }_{(-)}(t)=0,\text{if}{\alpha }_{(-)}(t)<0$$

To generate choice probabilities, the Q-values were fed into the same softmax decision function as the static-learning model.

We also examined two other meta-learning models from the Q-learning family of RL models. The first is an updated form of the opponency model²⁴ referred to as the global reward state model.⁴⁹ In this model, a global reward history variable influences learning from rewards and no rewards asymmetrically, as those outcomes carry different amounts of information depending on the richness of the environment. In this model, the value of a chosen action, for example Q_l, is updated according to

$$Q_l(t+1)=Q_l(t)+\alpha \delta (t),$$

$$Q_r(t+1)=\zeta Q_r(t),$$

while the unchosen action value, Q_r is forgotten with rate ζ. The prediction error, δ, is calculated by

$$\delta (t)=R(t)-Q_l(t)+\omega \overline{R}(t).$$

where R is the outcome, $\overline{R}$ is a global reward history term and ω is a weighting parameter that can be positive or negative. $\overline{R}$ is updated on each trial:

$$\overline{R}(t+1)=\overline{R}(t)+{\alpha }_{\overline{R}}(\overline{R}(t)-R(t)).$$

Here, ${\alpha }_{\overline{R}}$ is the learning rate for the global reward term. The learned action values are converted into choice probabilities using the same softmax decision function described above.

The second model we tested is an adapted Pearce-Hall model⁵⁰ in which the learning rate is a function of RPE magnitude. If the left action is chosen, Q_l is updated by the learning rule

$$Q_l(t+1)=\{\begin{array}{ll}{Q}_l(t)+{\kappa }_{(+)}\alpha (t)\delta (t),\hfill & \text{if}\delta (t)>0\hfill \\ Q_l(t)+{\kappa }_{(-)}\alpha (t)\delta (t),\hfill & \text{if}\delta (t)<0\hfill \end{array}$$

$$Q_r(t+1)=\zeta Q_r(t),$$

where κ₍₊₎ and κ₍₋₎ are the salience parameters for rewards and no rewards, respectively. Having separate salience parameters is a modification of the original model that we made to improve fit and mirror the asymmetry in our own meta-learning model and the global reward state model. The learning rate α is updated as a function of RPE:

$$\alpha (t+1)=\alpha (t)+\eta (\alpha (t)-|\delta (t)|).$$

Here, η controls the rate at which the learning rate is updated. In this way, the model enhances learning rates when the recent average of RPE magnitudes is large. This approach contrasts with our meta-learning model which diminishes the learning rate as a result of large recent RPE magnitudes if they are consistent.

Data analysis: firing rate model

We developed a version of our meta-learning model to fit inter-trial firing rates to see if neural activity and choice behavior reported similar dynamics of expected uncertainty. The learning components of the models were identical, but the firing rate model fit z-scored firing rates as a function of expected uncertainty:

$$\mu (t)=slope\cdot \epsilon +intercept,$$

$$FR(t)~\mathcal{N}(\mu (t),\sigma ),$$

where slope and intercept scale expected uncertainty into the mean predicted firing rate, μ. Real, z-scored firing rates, FR, are modeled as a draw from a Gaussian distribution with mean μ and some fixed amount of noise, σ.

Data analysis: model fitting

We fit and assessed models using MATLAB (Mathworks) and the probabilistic programming language, Stan (https://mc-stan.org/) with the MATLAB interface, MatlabStan (https://mc-stan.org/users/interfaces/matlab-stan) and the GPU optimization option (Nvidia GeForce RTX 2080 Ti). Stan was used to construct hierarchical models with mouse-level hyperparameters to govern session-level parameters. This hierarchical construction uses partial pooling to mitigate overfitting to noise in individual sessions (often seen in the point estimates for session-level parameters that result from other methods of estimation) without ignoring meaningful session-to-session variability. For each session, each parameter in the model (for example, α_v for the meta-learning model) was modeled as a draw from a mouse-level distribution with mean μ and variance σ. Models were fit using noninformative (uniform distribution) priors for session-level parameters ([0,1] for all parameters except β which was [0,10]) and weakly informative priors for mouse-level hyperparameters. These mouse-level hyperparameters were chosen to achieve model convergence under the assumption that individual mice behave similarly across days. The parameters were sampled in an unconstrained space and transformed into bounded values by a standard normal inverse cumulative density function. The parameters for updating expected uncertainty, α_v, and for updating the negative RPE learning rate, ψ, were ordered such that ψ > α_v. The ordering operated under the assumption that learning rate should be integrated more quickly than expected uncertainty in order to detect change. The ordering also helped models to converge more quickly. Stan uses full Bayesian statistical inference to generate posterior distributions of parameter estimates using Hamiltonian Markov chain Monte Carlo sampling.¹¹⁷ The default no-U-turn sampler was used. The Metropolis acceptance rate was set to 0.9–0.95 to force smaller step sizes and improve sampler efficiency. The models were fit with 10,000 iterations and 5,000 warmup draws run on each of 7 chains in parallel. Default configuration settings were used otherwise.

Data analysis: extracting model parameters and variables, behavior simulation

For extracting model variables (like expected uncertainty), we took at least 1,000 draws from the Hamiltonian Markov Chain Monte Carlo samples of session-level parameters, ran the model agent through the task with the actual choices and outcomes, and averaged each model variable across runs. For comparisons of individual parameters across behavioral and neural models, we estimated maximum a posteriori parameter values by approximating the mode of the distribution: binning the values in 50 bins and taking the median value of the most populated bin. For simulations of behavior, we took at least 1,000 draws from the Hamiltonian Markov Chain Monte Carlo samples of mouse-level parameters and simulated behavior and outcomes in a number of random sessions per sample. For the transition analysis, that number was proportional to the number of rare transitions that each animal contributed to the actual data. For other analyses that number was fixed.

Data analysis: model comparison

We used two-fold cross-validation in order to compare the predictive accuracy of the behavioral models. For each mouse and model, behavior sessions were split into two groups and the model was fit separately to each group. Parameter samples from each fit were used to calculate log pointwise predictive densities for the corresponding, held out data. The log pointwise predictive densities for both fits were summed and normalized by number of trials.

Data analysis: linear regression models of neural activity

For comparisons of firing rates to the behavioral-model-generated uncertainty terms we regressed z-scored firing rates on z-scored uncertainty using the MATLAB function “fitlm.” For some neurons and sessions, firing rates and model variables demonstrated monotonic changes across the session. To control for the effect of these dynamics in comparisons of inter-trial interval firing rates to model variables, we regressed out the monotonic effects for each term separately, then regressed the firing rate residuals on the expected uncertainty residuals. Here, we found similar rates of correlation across the population of neurons. We also looked for relationships between the neural activity and other model variables that evolved as a function of action and outcome history. For the analysis of the dynamic foraging task data, we added total value (Q_r + Q_l) relative value (Q_r − Q_l), value confidence (|Q_r − Q_l|), RPE, and reward history as regressors in the same model (Figure S4E). Value confidence captures how much better the better option is on each trial. Reward history is an arbitrarily smoothed history of all rewards, generated by convolving rewards with a recency-weighted kernel. The kernel was derived from an exponential fit to the coefficients from the regression of choices on outcomes. For the dynamic Pavlovian task data, we added RPE and reward history as regressors (Figure S5G).

Data analysis: linear mixed effect models

To analyze the changes in transition behavior we constructed a linear mixed effects model that predicted choice averages after transition points as a function of trial since transition, transition type, and the interaction between the two. The model is described by the following Wilkinson notation:

$$choiceaverages~trialfromtransition\ast transitiontype\text{.}$$

For assessing the affect of chemogenetic manipulation, we added drug condition (vehicle or agonist 21) as a fixed effect as well as the interaction between transition type and drug condition:

$$choiceaverages~trialfromtransition\ast transitiontype+transitiontype\ast drugcondition.$$

In the case of simulated data, these fixed effects were grouped by mouse, treated as a random effect that affects both slope and intercept, given by:

$$\begin{array}{l}choiceaverages~trialfromtransition\ast transitiontype+transitiontype\ast drugcondition+(trialfromtransition\\ \ast transitiontype\mid mouse)+\left(transitiontype\ast drugcondition\mid mouse\right)\end{array}$$

In all models, we z-scored all choice probabilities to center the data.

Data analysis: autocorrelation controls

To control for potential statistical confounds in correlating two variables with similar autocorrelation functions—in particular, firing rates of serotonin neurons and dynamics of expected uncertainty—we simulated each variable and compared it to the real data. We simulated 1,000 expected uncertainty variables by using maximum a posteriori parameter estimates to simulate a random sequence of choices and outcomes of the same length as the real session. For each simulation we extracted model variables using the sampling and averaging method described above. Linear regressions of real firing rates on each simulated variable were performed. If the t-statistics from the regression of real firing rate on real model variable fell beyond the 95% boundary of the distribution of t-statistics from the comparisons with simulated variables, then the relationship was deemed significant. We view this control analysis as an estimate of a lower bound on the true rate of correlated variables; for example, in a recent paper, only approximately one-third of true correlations were recoverable with this simulation.⁵¹

Conversely, we simulated neural data with autocorrelation functions matched to those of the actual neuron. For each neuron, we computed the autocorrelation function for lags of 10 trials and calculated the sum. The autocorrelation function sum was mapped onto the scale of a half-Gaussian smoothing kernel (width of 10 trials) using a log transformation. Neurons were then simulated as a random walk such that the firing rate at a given trial was the sum of the previous 10 trials weighted by the smoothing kernel plus some normally distributed noise $(\mathcal{N}(0,1))$. We found that the autocorrelation functions and the distributions of simulated firing rates were similar to those of the real neurons. For each real neuron, we performed 1,000 simulations and compared them to the real expected uncertainty in the same way as described above.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Goat anti-TPH2	Abcam	Cat#121020
Donkey anti-goat conjugated to Cy5	Abcam	Cat#6566
Bacterial and Virus Strains
rAAV5-EF1a-DIO-hChR2(H134R)-EYFP	Addgene	Cat#20298-AAV5
pAAV5-hSyn-DIO-hM4D(Gi)-mCherry	Addgene	Cat#44362-AAV5
pAAV5-hSyn-DIO-mCherry	Addgene	Cat#50459-AAV5
Chemicals, Peptides, and Recombinant Proteins
DREADD agonist 21 (Compound 21) dihydrochloride	Hello Bio Inc	Cat#HB6124
Experimental Models: Organisms/Strains
Slc6a4tm1(cre)Xz	The Jackson Laboratory	014554
Deposited data	Dryad	https://doi.org/10.5061/dryad.cz8w9gj4s

Highlights.

• Mice demonstrate variable behavioral flexibility during decision making

• Flexible behavior can be characterized as meta-learning guided by uncertainty

• Serotonin neuron activity correlates with expected and unexpected uncertainty

• Reversible inhibition of serotonin neuron activity impairs meta-learning