Abstract
Automatic classification of brain tumor plays a vital role to speed up the treatment procedure, plan and boost the survival rate of patients. Nowadays, Magnetic Resonance Imaging (MRI) is employed for determining brain tumor. However, manual identification of brain tumor is purely based on the sensitivity and experience of medical professionals. Thus, more research works towards brain tumor classification have been implemented for minimizing the human factor. Different imaging approaches are employed for detecting brain tumors. Though, MRI is mainly employed owing to the better quality of images due to the non ionizing radiation of images. One of the major categories of machine learning is called deep learning, which shows an outstanding performance, mainly on solving the segmentation and classification issues. The aim of this paper to introduce a new brain tumor classification model based on the intelligent segmentation and classification approaches. The main phases of the proposed model are (a) Data collection, (b) Pre-processing, (c) Tumor segmentation, and (d) Tumor Classification. Initially, the datasets related to the brain tumor are gathered from several benchmark sources and subjected to the pre-processing step. Here, it is performed by the median filtering and contrast enhancement techniques. The first contribution of this paper is the development of an enhanced segmentation approach termed as Adaptive Fuzzy Deformable Fusion (AFDF)-based Segmentation, which merges the two concepts of Fuzzy C-Means Clustering (FCM) and snake deformable approach. Here, the significant parameters of the AFDF are optimized by the improved Deer Hunting Optimization Algorithm (DHOA) termed Adaptive Coefficient Vector-based DHOA (ACV-DHOA). The classification of images is performed by the Optimized Convolutional Neural Network with Ensemble Classification (OCNN-EC) after segmenting the tumor. In the proposed deep learning classification, the number of convolutional layers and hidden neurons of CNN is optimized by the ACV-DHOA, and the fully connected layer is replaced by the ensemble classifier with Deep Neural Network (DNN), autoencoder, and Support Vector Machine (SVM). The classifier which is getting high rank is considered as the optimal one. The experimentation results are performed on the standard database that shows the high classification accuracy of the developed model by evaluating with other conventional methods.
Keywords: Automatic classification of brain tumor, Magnetic resonance imaging, Adaptive fuzzy deformable fusion segmentation, Adaptive coefficient vector-based deer hunting optimization algorithm, Optimized convolutional neural network with ensemble classification
Introduction
Brain is the central part of managing the activities in the human body, which is answerable for executing the entire actions through a huge number of neurons with many connections. When any abnormal growth of cells in the brain is occurred, it is named as brain tumor that affects the functionality of the human nerve system [15]. Many types of brain tumors are found at recent years that can be benign or malignant. Thus, the segmentation and classification of the tumor is the emerging research field, which distinguishes the non-tumorous and tumorous cells to diagnosis the tumor level [16]. The analysis of brain tumor classes are usually based on the computer-assisted diagnosis and medical experience of doctors, which increases the accuracy of detection. The early detection of tumor stage is depended on the medical professional’s experience and knowledge that intends to recover survival rate and reduces the mortality rate [9]. An automated brain tumor classification model is an efficient tool to support the general practitioners in offering a successful treatment [10]. Different research works have been implemented several automated models to identify and classify the brain tumors with MRI modalities. The early detection of tumors is necessary for avoiding uncontrollable stage. MRI [11, 12] is a useful approach that provides the data concerning with the human soft tissue framework.
The texture or pattern recognition with classification from widely variable images requires more human effort and time while processing the huge amount of data [18, 19]. The brain tumor is the third common cancer around world, which is occurred between young people and teenagers. The brain tumor segmentation plays a major role with processing of medical images [23, 24]. The techniques for the segmentation of brain tumors are classified into automatic approaches or interactive approaches, and semi-automatic approaches. Moreover, the unsupervised classification approaches are introduced for segmenting the tumors because of the efficiency of those approaches without any additional training dataset. The unsupervised techniques are used for extracting the rules-based on classification from the image data [22].
If the brain tumor is detected earlier, the tumor can be reduced before spreading to another area of your body. Automated segmentation and classification of medical images is an important task in diagnosis, prediction of brain tumors stage and growth, and treatment of brain tumors. The early identification of brain tumors is now feasible owing to the progressions in the machine learning algorithms [47] and computation intelligence methods. The tumor classification from MRI is a challenging task due to the availability of diverse imaging modalities. The tumor classification from MRI is performed by proposing diverse methods such as SVM [20], FCM [21], Expectation Maximization (EM) algorithm [13], knowledge-based techniques and Artificial Neural Network (ANN) [14] that is accepted approaches for segmentation process that depends on regions to extract the significant data by different clinical image modalities. The past knowledge is necessary as the lack of training data is observed to generate a reasonable output [17], which adopts many classification approaches to propose an automatic systems for developing the brain tumor detection model based on multiple MRI modality [25].
The major contribution of the developed brain tumor segmentation and classification model is given here.
Adaptive Fuzzy Deformable Fusion (AFDF)-based tumor segmentation is developed, which merges the concepts of Fuzzy C-Means Clustering (FCM) and snake deformable approach. Here, the AFDF is optimized by the improved Deer Hunting Optimization Algorithm (DHOA) termed Adaptive Coefficient Vector-based DHOA (ACV-DHOA) that could enhances the accuracy of tumor segmentation.
The Optimized Convolutional Neural Network with Ensemble Classification (OCNN-EC) performs the classification of the images using the tuor segmented images. A new adaptive-optimization algorithm termed ACV-DHOA is proposed for developing a new segmentation and classification approach by optimizing the cluster centroid of FCM and the weight parameters of snake deformation model and also the convolution layers and the count of hidden neurons of CNN in order to attain the best segmentation and classification outcome.
Literature survey
In 2020, Kaplan et al. [1] have developed two diverse feature extraction methods like αLBP and nLBP (Local Binary Patterns) to classify the brain tumor categories like Pituitary, Meningioma and Glioma brain tumors. The correlation for each pixel around the neighbours was used for forming the nLBP, which has a parameter to specify the distance among successive neighbors. Here, it has attained diverse patterns for diverse parameter values. These values of each pixel were computed based on the αLBP operator by adopting the angle values. The design and training procedure are very difficult. This system is useful for the radiologists to make decisions. The classification method was offered through different methods like ANN, K-Nearest Neighbor (K-NN), Random Forest (RF), Linear Discriminant Analysis (LDA), and A1DE with the features attained from the images in the data set using classical LBP, αLBP and nLBP techniques.
In 2019, Gumaei et al. [2] have employed “a Regularized Extreme Learning Machine (RELM)” with hybrid feature extraction technique to develop an exact classification model of brain tumor. Initially, the features from the brain images were extracted through hybrid feature extraction technique. Secondly, the covariance matrix was calculated from the attained features for attaining a useful set of features based on principle component analysis. The classification was performed by considering the RELM. The proposed model was evaluated and compared with different experimentations by applying on public dataset of brain images. The training speed is very high and the complexity is very low. The over fitting issue occurs in this method. The numerical results have confirmed the efficiency of the designed model regarding accuracy than traditional approaches.
In 2019, Sultan et al. [3] have implemented a deep learning-based classification system by using CNN, which was applied on two publicly available datasets. It has classified the tumors into pituitary, glioma, and meningioma tumor whereas the second one has classified the grades of glioma into three grades. The developed network framework has attained considerable performance in terms of overall accuracy. By tuning the system, training for small dataset is possible. More time requires for this method. Therefore, the developed model can be applied for the multi-classification of brain tumors.
In 2020, Huang et al. [4] have suggested a brain tumor classification model by CNN based on complex networks (CNNBCN) by modifying the activation function through MRI modalities. The developed model has not manually constructed and optimized by using randomly created graph techniques. These graphs were mapped through a network generator to attain a computable neural network. The proposed modified CNNBCN model has attained high accuracy rate for brain tumor classification when compared with different existing approaches. Moreover, the modified CNNBCN model for brain tumor classification has attained less rate of test loss than MobileNet, DenseNet and ResNet systems. This method is useful for generating the reference for designing the network structures. It needs large number of features for generating large number of images. The considered modified CNNBCN model has attained reasonable results for the classification along with the neural network model.
In 2020, Afshar et al. [5] have implemented a Bayesian CapsNet structure termed BayesCap for providing the mean predictions, which was measured by considering the entropy measure to show the prediction uncertainty. The experimentation results have shown that the accuracy of the developed system has been improved through eradicating the uncertain prediction. This method has the capability for handling small datasets to manage the uncertainty. The noise affects the parameters in this method. The experimentation results have confirmed the efficiency of the developed model to improve the network interpretability by using a suitable approach.
In 2020, Kumar et al. [6] have proposed an optimized deep learning strategy called “Dolphin Echolocation-based Sine Cosine Algorithm (Dolphin-SCA)” for efficient classification decisions and improving accuracy. The developed model has used the “fuzzy deformable fusion model with Dolphin-SCA” for efficient segmentation process. Then, the features were extracted using statistical features like skewness, mean, and variance and power Local Directional Pattern (LDP). The attained features were forwarded to the Deep CNN to perform the classification through considering the training algorithm as Dolphin-SCA. The over fitting problem occurs in this method. This method increases the accuracy of the optimization process. The extensive results were offered on “BRATS database and Q7 SimBRATS”, which has shown the high accuracy rate and better performance than traditional approaches.
In 2020, Raja et al. [7] have designed a hybrid deep autoencoder (DAE)-based brain tumor classification model using Bayesian Fuzzy Clustering (BFC)-based segmentation. Firstly, the gathered images from the BRATS 2015 database were given to the pre-processing phase, which was done by non-local mean filter to denoise the images. Then, the segmentation process was performed using BFC method. The segmented images were subjected to the feature extraction procedure, where the robust features were attained by wavelet packet tsallis entropy approach, Scattering Transform (ST) and information theoretic metrics. Moreover, the tumor parts in the brain were classified using hybrid DAE-based Jaya optimization algorithm (JOA) through a softmax regression method. It is very difficult for classifying the auto-encoder. This method is useful for learning the features. The developed model was implemented in a MATLAB platform, and the experimental analysis was conducted that has shown the high classification accuracy than other existing approaches.
In 2020, Amin et al. [8] have developed a fusion procedure for combining the textural and structural information based on the MRI sequences like T2, T1, Flair, and T1C to detect the brain tumor. The fusion process was performed using Daubechies wavelet kernel and Discrete Wavelet Transform (DWT) that has offered more significant information regarding tumor region by comparing with individual MRI single sequence. Then, the noise was removed by applying a partial differential diffusion filter. This model has gathered information from five datasets like “BRATS 2012, BRATS 2013, BRATS 2015, BRATS 2013 Leader board and BRATS 2018” and the experimental analysis was carried out. This method is very slower when compared to others. It can easily detect the important features without any human intervention. From the simulation results, the fused images have offered superior outcomes than individual sequences.
Thus, the above mentioned challenges are helpful for developing a new method. Even though there are several methods for brain tumor classification, still there are some disadvantages with the existing methodologies. The methodologies for brain tumor classification revolve around the benefits of the deep learning and machine learning algorithms, yet they suffer from other limitations in factors like cost, training time, and dataset size. The hardware requirement is also quite large; such constraints urge us with the need for new model implementation for classifying the brain tumor effectively. The proposed ACV-DHOA-AFDF is very easy to implement. The convergence rate and the performance are very high. The communication is very flexible. Because of these advantages, this method overcomes the existing methods.
Materials and methods
Proposed model and description
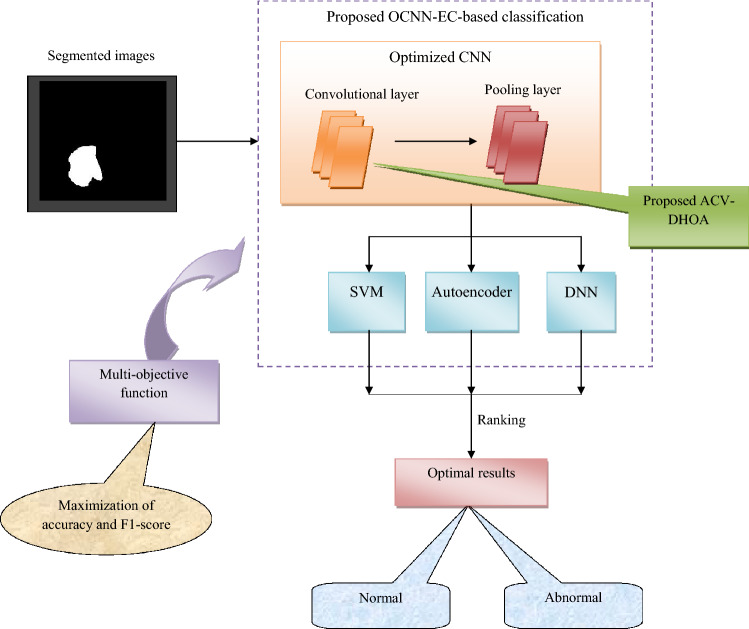
The proposed brain tumor segmentation and classification model is represented in Fig. 1.
Fig. 1.
Proposed brain tumor segmentation and classification model
The proposed model adopts intelligent approaches for efficient segmentation and classification of brain tumor from MRI images. This model consists of different stages like “(a) Data collection, (b) Pre-processing, (c) Tumor segmentation, and (d) Classification”. The MR images are collected from the publically available dataset called kaggle. The gathered images are given to the pre-processing step for removing the artifacts and identifying the significant regions, which is carried out using median filtering and contrast enhancement approaches. Therefore, the noise removed images and contrast enhanced images are given to the tumor segmentation process. The developed model includes two significant contribution in both segmentation and classification stages. The tumor segmentation is improved by fusing the FCM and snake deformation model through newly proposed ACV-DHOA technique. The efficient segmentation process is performed by adopting the multi-objective function concerned with minimization of entropy and variance, which is performed by optimizing the centroid of FCM and the parameters like and of snake deformation model through proposed ACV-DHOA. The segmented images are classified by implementing a new OCNN-EC-based technique to classify images into abnormal and normal. The classification technique is enhanced by adopting the OCNN-EC by integrating SVM, auto encoder, and Deep Neural Network (DNN). Here, the multi-objective function concerned with maximization of accuracy and F1-score is solved using the optimization of convolution layers and number of hidden neurons through ACV-DHOA approach. Therefore, this improved segmentation and classification processes increases the accuracy of the designed brain tumor classification model.
Dataset description
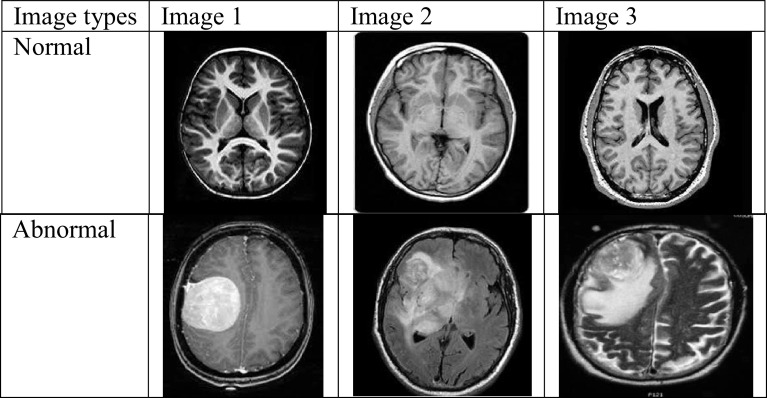
The developed model gathers data from kaggle dataset [44]. Only one dataset is used for test and verification. The total images are 253. This dataset is publically available and includes 253 images with abnormal images 155 and normal images 98. The images used in this dataset are 2D slice. The total number of images in the dataset is considered as and is a set of input images, where . The sample images from the dataset are given in Fig. 2.
Fig. 2.
Sample images
taken from the dataset with normal and abnormal images
Pre-processing of MRI images
The collected input images are given to the pre-processing stage of proposed model, which is done by using median filtering and contrast enhancement approaches. The pre-processing step is essential for improving the image data by enhancing the significant image features. It reduces the distortions and eliminates the noise and also unnecessary falsification. The approaches are explained here.
Median filtering [27] [45] It includes superior noise reduction effects to improve the performance, reduce the unnecessary noise, enhances the edges and preserves the sharp features in the input images. Median filtering is a non linear filter that performs through the substitution of noisy and neighbourhood pixels of images. Further, it is sorted through the image gray levels for improving the performance of noise reduction. The input images are processed by median filter as given in Eq. (1).
| 1 |
In Eq. (1), the 2D-mask is denoted as , the pre-processed images using median filtering is termed as that is further given to contrast enhancement approach.
Contrast enhancement [28] [46] It is performed by applying the histogram equalization approach to adjust image intensities for enhancing the contrast. It processes the spatial domain in the images by computing the histogram of image for increasing the global contrast of the images. It is processed by considering the grayscale input image as as formulated in Eq. (2).
| 2 |
In the abovementioned equation, is the total number of gray levels in the image, indicates the probability distribution function, the total number of pixels in the image is denoted as , and the total number of pixels with the same intensity level is termed as . Therefore, the pre-processed images are represented as , which are given to the tumor segmentation stage.
Proposed AFDF-based tumor segmentation
The proposed brain tumor diagnosis model develops a new AFDF segmentation approach using FCM and snake deformation model for efficient tumor segmentation. The pre-processed images are given to the FCM and the clustering results are further given to the snake deformation model for increasing the segmentation accuracy. But, the segmentation of MRI is a more tedious task regarding the varied size of images and large number of datasets. Here, the improved AFDF segmentation is implemented based on the developed ACV-DHOA technique. It is proposed by optimizing the centroid of FCM and the parameters like and of snake deformation model for satisfying the multi-objective function concerned with minimization of variance and entropy.
FCM [29] This approach is selected for attaining the enhanced segmentation results for overlapped dataset. It also has faster convergence rate, superior accuracy and reduces the time complexity. However, this approach suffers from long computational time in terms of cluster processing, Apriori selection of number of clusters and also affects performance while using huge number of prototypes and high dimensional datasets. Therefore, this approach is improved by optimizing the centroid of FCM through ACV-DHOA technique. Initially, it creates the fuzzy matrix through the determining the Euclidean distance to perform the clustering, which is formulated in Eq. (3).
| 3 |
In Eq. (30), the total number of pixels in is termed as , the pixel position is denoted as , the membership function matrix is represented as , the fuzziness variable is considered as and the Euclidean distance is expressed as , indicates the degree of fuzziness that should be greater than 1, and the distance among the cluster and cluster centre is equated in Eq. (4).
| 4 |
Here, the pixel is termed as and the cluster centers are denoted as and the clustering process is initiated by considering the cluster center as expressed in Eq. (5).
| 5 |
While performing the clustering process, the fuzzy matrix is varied using the cluster centers as shown in Eq. (6).
| 6 |
This process is performed until this method finds the suitable cluster centroid by ACV-DHOA, where is the membership function matrix, in which the degree of fuzziness is termed as and Mahalanobis distance is considered as and finally, the segmented images using FCM approach is indicated as , which is further given to the snake deformation model.
Snake deformation model [30] It is one of the famous segmentation approaches, which is developed using the energy constraints for separating the region of interest in images. This approach is employed in different applications like stereo tracking and motion tracking. This snake deformable approach has different features such as high segmentation accuracy and accurate segmentation of tumors in images. However, this model include some problems like sensitive to local minimum cases, representation of single objects, lack of determining the contour of every object and dependency in accuracy based on their convergence rate. Therefore, an existing snake deformable approach is modified here by optimizing the weight parameters through ACV-DHOA approach to get optimal segmented outcomes. The parametric curve of the snake deformable model is modeled in Eq. (7).
| 7 |
In the abovementioned equation, the parametric domain is termed as , where and the coordinate functions are represented as and . In general, these curves are attained based on the B-splines functions, which helps for depicting a smoothing and continuous parameterized contour. A spline function is specified in the B-spline form by considering the weighted sum of basis functions and thus B-splines is given as . A control point should be described and the curve is a weighted vector sum of such control points as given in Eq. (8).
| 8 |
Here, the curve parameter is denoted as , polynomial basis function is termed as and denotes a point in the image. The first B-spline basis function is formulated in Eq. (9).
| 9 |
When the active contours are considered as closed lines, then the function can be modified through arithmetic modular as equated in Eq. (10).
| 10 |
Moreover, an energy function is used for associating each active contour approach as measured in Eq. (11).
| 11 |
Here, terms and denotes the external energy and internal energy at contour, respectively. The internal energy is employed for preventing the discontinuity in the contour and for controlling the rate of stretch as formulated in Eq. (12) that is associated with contour elasticity.
| 12 |
The weighting parameters are indicated as and , which is used for controlling the tension and rigidity of snakes, respectively. Similarly, the external energy is formulated in Eq. (13).
| 13 |
Therefore, the weighting parameters like and are optimized using the developed ACV-DHOA technique for proposing a new segmentation model. Finally, the FCM is fused with snake deformable model for efficient segmentation, and, the segmented images using snake deformable approach is termed as , which is subjected to the classification process, which is represented in Fig. 3.
Fig. 3.
Proposed AFDF-based brain tumor segmentation model
The proposed brain tumor segmentation model considers major objective as the minimization of entropy and variance for attaining the efficient segmentation performance as given in Eq. (14).
| 14 |
Here, terms and denotes the entropy and variance, respectively. The variance is considered as “the average of the squared differences from the mean”, which is formulated in Eq. (15).
| 15 |
In Eq. (15), term is the mean of pixels; the total number of pixels in images is denoted as and represents the value of pixel. The average information or entropy of an image can be “determined approximately from the histogram of the image” as shown in Eq. (16).
| 16 |
Here, denotes the normalized histogram counts or the probability function. The efficient segmentation process is developed by optimizing the cluster centroid of FCM and the parameters like and of snake deformation model, which is termed as AFDF model. The optimization of segmentation is formulated in Fig. 4.
Fig. 4.

Solution encoding of the AFDF segmentation process using ACV-DHOA approach
Here, the range of cluster centroid in FCM is considered from 0 to 255, where and specifies the total number of clusters. Similarly, the weight parameters like and are in the bounding limit of [1, 10]. The proposed AFDF-based segmentation model is executed by considering the number of iterations as 50.
Proposed OCNN-EC-based tumor classification
The proposed brain tumor classification model proposes a new classification technique termed OCNN-EC through a new ACV-DHOA algorithm. It is developed by optimizing the convolution layers and number of hidden neurons through ACV-DHOA approach. Here, the multi-objective function concerned with maximization of accuracy and F1-score is considered for attaining the better classification results. The proposed OCNN-EC classification technique is performed by giving the segmented images using AFDF technique to the OCNN. The features extracted from the OCNN are further given to ensemble classification method, connected with SVM, auto encoder, and DNN. The developed OCNN-EC-based technique aims to classify the images into normal and abnormal based on the ranking procedure, in which the optimal results attained by the classifier are decided based on the high rank.
OCNN-EC [31] The classification of the tumor is an emerging field for differentiating the non-tumorous cells and the tumorous cells to diagnose the level of tumor. Numerous approaches were proposed in recent studies for the classification of brain tumor, however it suffers from inefficient decision making and lack of accuracy and thus improved classification approach is required. In literature, CNN is eminent for classification of tumor cells. DNN has several features like automatic detection of significant features, computationally efficient approach, attains high accuracy, faster implementation and efficient prediction of images. However, CNN poses diverse challenges like attains less accuracy owing to the shallow depth network and takes more computational power while processing the large number of datasets. Therefore, there is a new improvement offered in the proposed brain tumor classification model by developing the novel OCNN-EC, where O-CNN is used for feature learning and EC with SVM, autoencoder and DNN is used for classification. The considered CNN model has convolutional layer and pooling layer, where the convolutional layer is required to deal with controlling of lifting and heavy computation and also extracts different features from the segmented images. Moreover, the pooling layer are used for subsampling the feature maps to minimize the computation of network and parameters by decreasing the spatial size of representation, which also handles functions at independent manner and overfitting problems on every input slice. The segmented images are given as the input of OCNN and the result attained through the conventional layers is formulated in Eq. (17).
| 17 |
In Eq. (16), the feature maps created from every conventional filter through scanning the input image is denoted as , and , the bias of convolution layer is specified as , denotes the weights of conventional layer, indicates the output generated from the conventional layers centered as and the convolutional operator to generate the local patterns from conventional layers is termed as .The activation function is employed in the convolutional layer for removing the negative values and to simplify the computation. The output created from the conventional layer is considered as the activation function of layer as expressed in Eq. (18).
| 18 |
The pooling layers are employed to perform fixed operation. Finally, the features attained from the pooling layer are given to the ensemble approach, which is performed by adopting SVM, autoencoder and DNN methods.
SVM [32] It is a supervised learning method based on binary classification that attains more accurate results when compared with existing classifiers. The classification is performed by SVM classifier to attain two classes through the construction of hyper-plane in the high dimensional feature space. Further, the SVM classifier processes the features of pooling layer to classify into normal and abnormal classes based on kernel functions.
Autoencoder [33] It extracts and selects the features at manual process through fixing the number of hidden neurons, which use the low dimensional output produced through NN for representing the high dimensional input. This approach learns the useful representations of input data by adding the sparsity restrictions.
DNN [34] It extracts the robust features by learning the structure of input data through their convolutional layers. It consists of six layers with several weight constraints. DNN derives the high level functions from the input data by transforming the data into a more abstract and creative component. This network employs the softmax function for the output layer and sigmoid function for hidden layers.
EC-based tumor classification The EC is performed based on the ranking approach by using SVM, autoencoder and DNN methods. The features from the pooling layers are given to three classifiers and the highest ranking results are considered as optimal classification outcomes as normal and abnormal classes. The proposed OCNN-EC-based tumor classification using ACV-DHOA technique is represented in Fig. 5.
Fig. 5.
Proposed OCNN-EC-based Tumor Classification
The proposed model considers the major objective as the maximization of accuracy and F1-score for efficient tumor classification, which is performed with ACV-DHOA technique as given in Eq. (19).
| 19 |
A new OCNN-EC-based tumor classification is developed by optimizing the convolution layers and number of hidden neurons of CNN through ACV-DHOA approach. Here, terms and represent the accuracy and F1-score for classification. Accuracy is a “ratio of the observation of exactly predicted to the whole observations” as formulated in Eq. (20).
| 20 |
F1-score is the “harmonic mean between precision and recall. It is used as a statistical measure to rate the performance” as shown in Eq. (21).
| 21 |
Here,,,, indicates “the true positives, true negatives, false positives, and false negatives”, respectively. The solution encoding of the proposed OCNN-EC-based tumor classification by ACV-DHOA technique is represented in Fig. 6.
Fig. 6.

Solution encoding of the proposed OCNN-EC-based tumor classification by ACV-DHOA approach
The convolution layers and number of hidden neurons of CNN are optimized with the designed ACV-DHOA approach, in which is ranging from 1 to 5 and the count of hidden neurons is in the bounding limit of [5, 255]. The proposed OCNN-EC-based tumor classification is executed by considering the number of iterations as 25.
ACV-DHOA for tumor segmentation and classification
This proposed tumor segmentation and classification model proposes a new algorithm called ACV-DHOA for developing an improved segmentation by AFDF technique and an enhanced tumor classification through OCNN-EC method. The developed ACV-DHOA algorithm is used for optimizing the cluster centroid of FCM and the weight parameters like and of snake deformation model and also the convolution layers and the number of hidden neurons of CNN.
The developed ACV-DHOA method is implemented by formulating a new weight function by fitness function for modifying the coefficient vector. This algorithm is completely based on the fitness function, and thus it is called as adaptive algorithm. The DHOA [26] algorithm is developed by considering the hunting nature of the humans towards the deer, which uses the mobility of hunters towards attaining the best location with solutions named as “leader and successor”. The positions of deer are updated until find the deer. Initially, this procedure encloses the deer by following some constraints like deer position and wind angle. The DHOA is efficient due to the efficient teamwork among hunters for finding the deer, in which the attacking procedure is performed through position of leader and successor for finding the optimal location of prey. Moreover, the deer has different special characters as given in [26], which are studied for efficient hunting process. Thus, these algorithms are generally employed in different real world applications for solving the classification problems. DHOA is formulated by initializing the population as given in Eq. (22).
| 22 |
Here, term indicates the number of hunters in the population. Secondly, the parameters such as deer position and wind angle are initialized as given Eq. (23) and Eq. (24), respectively.
| 23 |
| 24 |
In the abovementioned equation, wind angle is computed because of the encircling area is considered as circle. Here, the wind angle is given as , the recent iteration is denoted as , the deer’s position angle is denoted as and specifies the random number, which is ranging from [0, 1]. Further, the positions are propagated based on different constraints. At initial stage, the position of the optimal search area is unidentified and thus, the solutions are assumed, which is near to the optimal space based on the fitness function and it is considered as best solution. Two solutions are considered here as leader position and successor position, which are represented as and that is also known as the first best position and successor position of the hunter, respectively.
(i) Leader’s position propagation Initially, the best positions are determined, and then the best position is obtained for every individual in the population. The enclosing action for deer is formulated in Eq. (25).
| 25 |
In Eq. (24), term indicates the position of the next iteration, is the random number of wind speed, which is ranging from 0 to 2, indicates the position of current iteration and coefficient vectors are represented as and that are modeled in Eq. (26) and Eq. (27), respectively.
| 26 |
| 27 |
Here, term is a parameter in the bounding limit of [−1, 1] the maximum iteration is denoted as , and represents the random number ranging among -1 and 1. In the developed DHOA algorithm, the coefficient vector is modified based on the weight as given in Eq. (28). The weight function is formulated based on the fitness function as given in Eq. (28).
| 28 |
In Eq. (28), the best fitness solution is denoted as , current fitness is represented as and mean fitness is termed as and thus the weight function is completely based on the fitness values.
(ii)Position angle propagation The position angle is considered in the search space for updating the position, which is required for computing the hunter position for avoiding the unknown position of prey. The visualization angle of the deer or prey is determined for making the hunting process as efficient one that is given in Eq. (29).
| 29 |
A new parameter is computed with the variation among the wind angle and visual angle of the deer to update position angle as shown in Eq. (30).
| 30 |
The position angle for next iteration is updated by Eq. (31).
| 31 |
The position is updated by position angle as given in Eq. (32).
| 32 |
In Eq. (32), the best position is represented as .
(iii) Successor’s position propagation In the exploration process, the enclosing behavior is introduced by altering the vector . When , the random search is performed. Consequently, the position is updated with the position of the successor with the first best solution attained, which permits a global search as given in Eq. (33).
| 33 |
Here, the successor position of the search agent in the recent population is represented as . The pseudo code of the proposed algorithm is given in Algorithm 1.
In the proposed ACV-DHOA algorithm, the population is initialized and the position of the search agents is updated based on the attained best solution at each iteration. Determine the new coefficient vector based on the weight function with fitness functions. The best solution is selected when and the positions are updated, then the search agents are selected randomly when . The adaptive optimization algorithms are proposed by modifying the any functions or parameters that leads to performance enhancement [35]. The self-improvement in optimization algorithms reports efficient use of adaptive optimization operators and their significance [36]. The position is updated till the best position is reached at each iteration.
Results and discussions
Experimental setup
The proposed brain tumor segmentation and classification model was executed in MATLAB version R2020a by considering the number of population as 10. The OS used in this method is Windows 10 64 bit OS. The storage of RAM is 8 GB. The preprocessing is executed by Median filtering and contrast enhancement. This developed model was compared over the existing models concerned with different measures like “accuracy, sensitivity, specificity, precision, Negative Predictive Value (NPV), F1Score and Mathews correlation coefficient (MCC), False positive rate (FPR), False negative rate (FNR), and False Discovery Rate (FDR)”. The proposed AFDF-based segmentation model using the ACV-DHOA was evaluated by diverse segmentation approaches like region growing [37], Level set segmentation [38], FCM [29] and snake deformation model [30]. The developed ACV-DHOA technique with OCNN-EC model was compared with different heuristic-based techniques such as PSO [39], GWO [40], WOA [41] and DHOA [26] and different classifiers such as DT [42], SVM [32], NN [43], DNN [34], CNN [31], and AUTOENCODER [33].
Performance measures
Diverse performance metrics are employed for the analysis of the developed brain tumor segmentation and classification system. , , , indicates “the true positives, true negatives, false positives, and false negatives”, respectively.
(a) MCC “correlation coefficient computed by four values”.
| 34 |
(b) NPV “probability that subjects with a negative screening test truly don't have the disease”.
| 35 |
(c) Specificity “the number of true negatives, which are determined precisely”.
| 36 |
(d) FDR “the number of false positives in all of the rejected hypotheses”.
| 37 |
(e) Precision It is “the ratio of positive observations that are predicted exactly to the total number of observations that are positively predicted”.
| 38 |
(f) Sensitivity “the number of true positives, which are recognized exactly”.
| 39 |
(g) FNR “the proportion of positives which yield negative test outcomes with the test”.
| 40 |
(h) FPR “the ratio of count of false positive predictions to the entire count of negative predictions”.
| 41 |
Segmented Results
The sample segmented image results of the suggested brain tumor segmentation model using AFDF with different approaches are represented in Fig. 7.
Fig. 7.
Sample segmented image results of the proposed brain tumor segmentation model using optimized AFDF model
Segmentation analysis
The proposed ACV-DHOA-AFDF-based segmentation approach was compared with different segmentation techniques as given in Table 1. The accuracy of the suggested ACV-DHOA-AFDF is 0.43, 1.3, 1, 1.06, and 0.32% superior to region growing, level set segmentation, FCM, snake deformation model, and AFDF, respectively. Thus, the developed ACV-DHOA-based AFDF segmentation model increased the performance than conventional methods.
Table 1.
Performance analysis for the proposed segmentation model with diverse segmentation approaches
| Measures | Region growing [37] | Level set segmentation [38] | FCM [29] | Snake deformation model [30] | AFDF | ACV-DHOA-AFDF |
|---|---|---|---|---|---|---|
| “Accuracy” | 0.95809 | 0.94945 | 0.95163 | 0.95208 | 0.95912 | 0.96222 |
| “Sensitivity” | 0.97649 | 0.96962 | 0.96936 | 0.97055 | 0.97812 | 0.98481 |
| “Specificity” | 0.51212 | 0.47188 | 0.50434 | 0.51474 | 0.51145 | 0.53243 |
| “Precision” | 0.9798 | 0.97751 | 0.98014 | 0.97931 | 0.99253 | 0.99627 |
| “FPR” | 0.48788 | 0.52812 | 0.49566 | 0.48526 | 0.48189 | 0.47757 |
| “FNR” | 0.023508 | 0.030379 | 0.030645 | 0.029448 | 0.028621 | 0.025191 |
| “NPV” | 0.51212 | 0.47188 | 0.50434 | 0.51474 | 0.55265 | 0.58243 |
| “FDR” | 0.020203 | 0.02249 | 0.019858 | 0.020686 | 0.019827 | 0.013734 |
| “F1-Score” | 0.97814 | 0.97355 | 0.97472 | 0.97491 | 0.97951 | 0.9805 |
| “MCC” | 0.47058 | 0.40618 | 0.42139 | 0.44284 | 0.47384 | 0.48288 |
Performance analysis of the proposed brain tumor classification in terms of heuristic-based approaches
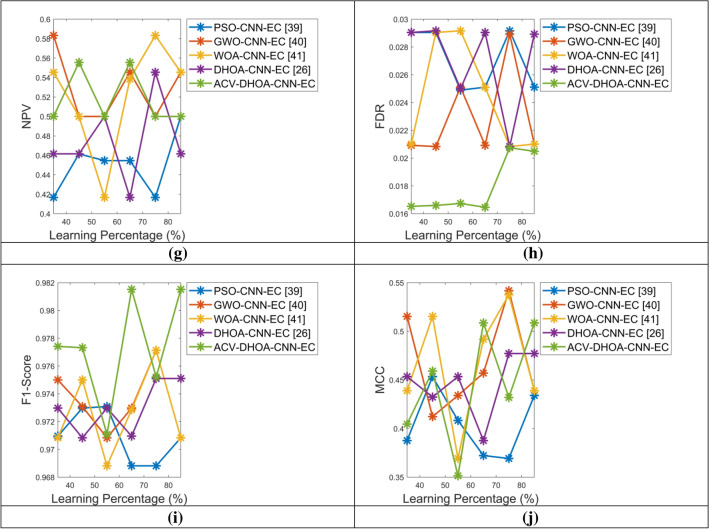
The performance of the proposed ACV-DHOA-CNN-EC based classification is compared with different meta-heuristic-based techniques as given in Fig. 8. At 85%, the accuracy of the developed ACV-DHOA-CNN-EC is 1, 1.9, 1.04 and 2.4% advanced than PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, and DHOA-CNN-EC, respectively. For 45%, the F1-score of the designed ACV-DHOA-CNN-EC is 0.9% progressed than PSO-CNN-EC, GWO-CNN-EC, respectively and 0.69% progressed than WOA-CNN-EC and DHOA-CNN-EC, respectively. While taking the 55%, the FDR of the ACV-DHOA-CNN-EC is 43.7, 43.7, 34.8 and 22.3% better than PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC and DHOA-CNN-EC, respectively. The FNR of the ACV-DHOA-CNN-EC is 33, 53, 51.7 and 95% superior to PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC and DHOA-CNN-EC, respectively for learning percentage as 45. At 85%, the FPR of the designed ACV-DHOA-CNN-EC is 11.6%, superior to PSO-CNN-EC, GWO-CNN-EC, and WOA-CNN-EC, respectively and 19.6% superior to DHOA-CNN-EC. For 85%, the MCC of the designed ACV-DHOA-CNN-EC is 8.5, 4, and 37.8% increased than PSO-CNN-EC, GWO-CNN-EC, and DHOA-CNN-EC, respectively. While taking the learning percentage as 85, the NPV of the suggested ACV-DHOA-CNN-EC is 11.6% progressed than PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, respectively and 22.6% progressed than DHOA-CNN-EC. For 55%, the precision of the considered ACV-DHOA-CNN-EC is 1.23, 1.25, 0.5 and 0.86% better than PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, and DHOA-CNN-EC, respectively. For 45%, the sensitivity of the implemented ACV-DHOA-CNN-EC is 0.9, 0.92, 0.89 and 0.89% enhanced than PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, and DHOA-CNN-EC, respectively. At 85%, the specificity of the designed ACV-DHOA-CNN-EC is 16% improved than PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, respectively and 27.7% improved than DHOA-CNN-EC. Hence, the performance of the developed brain tumor classification with ACV-DHOA-CNN-EC outperforms the traditional meta-heuristic-based approaches.
Fig. 8.
Performance analysis of the brain tumor diagnosis model with developed and traditional meta-heuristic-based algorithms concerned with “a Accuracy, b Sensitivity, c Specificity, d Precision, e FPR, f FNR, g NPV, h FDR, i F1-score and j MCC”
Performance analysis of the developed brain tumor classification model with different classifiers
The performance of the developed ACV-DHOA-CNN-EC based classification is compared with different classifiers by varying learning percentages as given in Fig. 9. The ACV-DHOA-AFDF is very easy to implement. The convergence rate and the performance are very high. The communication is very flexible. Because of these advantages, this method performs better than the other existing methods. The disadvantage of the existing methods is: DT is unstable and it is inaccurate often. SVM needs large training time for large dataset. NN requires more data than the other methods. The code of the DNN is very obsolete. At 85%, the accuracy of the developed ACV-DHOA-CNN-EC is 3.1%, 2%, 4.3%, 1.04%, 1.04% and 1.5% better than DT, SVM, NN, DNN, CNN, and autoencoder, respectively. At 85%, the sensitivity of the proposed ACV-DHOA-CNN-EC is 5.3%, 4.2%, 3%, 2%, 2.6% and 3.7% increased than DT, SVM, NN, DNN, CNN, and autoencoder, respectively. At 85%, the specificity of the designed ACV-DHOA-CNN-EC is 22%, 37.5%, 30.9%, 17%, 10% and 7.8% superior to DT, SVM, NN, DNN, CNN, and autoencoder, respectively. While taking the 85%, the precision of the suggested ACV-DHOA-CNN-EC is 1%, superior to DT and autoencoder, respectively and 2%, superior to SVM, NN, DNN, CNN, respectively. For 85%, the precision of the suggested ACV-DHOA-CNN-EC is 1%, superior to DT and autoencoder, respectively and 2%, superior to SVM, NN, DNN, CNN, respectively. At 85%, the FPR of the designed ACV-DHOA-CNN-EC is 18%, 22.4%, 22.4%, 19.6%, 10% and 11.7% improved than DT, SVM, NN, DNN, CNN, and autoencoder, respectively. At 85%, the FPR of the designed ACV-DHOA-CNN-EC is 18%, 22.4%, 22.4%, 19.6%, 10% and 11.7% improved than DT, SVM, NN, DNN, CNN, and autoencoder, respectively. For 85%, the FNR of the implemented ACV-DHOA-CNN-EC is 40.8%, 16%, 27.5%, 5%, 16.3% and 93.8% maximized than DT, SVM, NN, DNN, CNN, and autoencoder, respectively. At 85%, the NPV of the proposed ACV-DHOA-CNN-EC is 24%, 40%, 33%, 21.7%, 12% and 7.69% progressed than DT, SVM, NN, DNN, CNN, and autoencoder, respectively. The FDR of the designed ACV-DHOA-CNN-EC is 12.5%, 16%, 12.5%, 16%, 16% and 4.5% advanced than DT, SVM, NN, DNN, CNN, and autoencoder, respectively at 85%. The F1-score of the suggested ACV-DHOA-CNN-EC is 23.7%, 20.7%, 16.4%, 15%, 13.7% and 4.2% increased than DT, SVM, NN, DNN, CNN, and autoencoder, respectively at 85%. The MCC of the suggested ACV-DHOA-CNN-EC is 37.8%, 21.4%, 27.5%, 6.25%, 2% and 21.4% better than DT, SVM, NN, DNN, CNN, and autoencoder, respectively at 85%. Hence, the proposed brain tumor classification model attains superior performance than traditional approaches.
Fig. 9.
Performance analysis of the brain tumor diagnosis model with developed and classifiers concerned with “a Accuracy, b Sensitivity, c Specificity, d Precision, e FPR, f FNR, g NPV, h FDR, i F1-score and j MCC”
Comparison of ACV-DHOA-CNN-EC over existing models
The comparison of ACV-DHOA-CNN-EC over existing models is shown in the Fig. 10. At learning percentage 45, the accuracy of the proposed ACV-DHOA-CNN-EC performs 3.15%, 3.16%, 2.11%, and 3.16% better than RELM, CNNBCN, CapNet, and DAE-JOA. At learning percentage 55, the MCC of the proposed ACV-DHOA-CNN-EC performs 9.75% better than RELM, 8.57% better than CNNBCN, 11.76% better than CapNet, 16.17% better than DAE-JOA. Thus, the overall performance of the proposed ACV-DHOA-CNN-EC is better than the existing methods.
Fig. 10.
Comparison of ACV-DHOA-CNN-EC over existing models a accuracy, b sensitivity, c specificity, d precision, e FPR, f FNR, g NPV, h FDR, i F1-score and j MCC
Overall performance analysis
The overall performance of the brain tumor diagnosis model is given in Tables 2 and 3 by comparing with different optimization-based algorithms and classifiers, respectively. The accuracy of the designed ACV-DHOA-CNN-EC is 1.6%, 2%, 0.8%, 1.6%, 2.5%, 1.24%, 1.6% 2%, 2.5% and 2.5% better than PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, DT, SVM, NN, DNN, CNN and autoencoder, respectively. Similarly, the F1-score of the implemented ACV-DHOA-CNN-EC is 0.89%, 1.1%, 0.44%, 0.878%, 1.3%, 0.66%, 0.86%, 1%, 1.3% and 1.3% superior to PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, DT, SVM, NN, DNN, CNN and autoencoder, respectively. The overall performance analysis of the proposed ACV-DHOA-CNN-EC over the classifier is shown in the Table 4. The specificity of the RELM, CNNBCN, CapNet, DAE-JOA, and the proposed ACV-DHOA-CNN-EC are 0.53846, 0.53846, 0.5, 0.53333, and 0.5. Likewise, the overall performance of the developed system is enhanced than conventional measures for all measures. Thus, the overall performance of the proposed brain tumor classification is superior to existing methods.
Table 2.
Overall Performance analysis for the proposed brain tumour diagnosis model over diverse meta heuristic-based approaches
| Measures | PSO-CNN-EC [35] | GWO-CNN-EC [36] | WOA-CNN-EC [26] | DHOA-CNN-EC [27] | ACV-DHOA-CNN-EC |
|---|---|---|---|---|---|
| “Accuracy” | 0.94862 | 0.94466 | 0.95652 | 0.94862 | 0.96443 |
| “Sensitivity” | 0.9749 | 0.97083 | 0.97917 | 0.96694 | 0.98354 |
| “Specificity” | 0.5 | 0.46154 | 0.53846 | 0.54545 | 0.5 |
| “Precision” | 0.97083 | 0.97083 | 0.9751 | 0.97908 | 0.97951 |
| “FPR” | 0.5 | 0.53846 | 0.46154 | 0.45455 | 0.5 |
| “FNR” | 0.025105 | 0.029167 | 0.020833 | 0.033058 | 0.016461 |
| “NPV” | 0.5 | 0.46154 | 0.53846 | 0.54545 | 0.5 |
| “FDR” | 0.029167 | 0.029167 | 0.024896 | 0.020921 | 0.020492 |
| “F1-Score” | 0.97286 | 0.97083 | 0.97713 | 0.97297 | 0.98152 |
| “MCC” | 0.49179 | 0.43237 | 0.53765 | 0.45703 | 0.50865 |
Table 3.
Overall Performance analysis for the proposed brain tumour diagnosis model over diverse classifies
| Measures | DT [37] | SVM [38] | NN [39] | DNN [34] | CNN [31] | Autoencoder [33] | ACV-DHOA-CNN-EC |
|---|---|---|---|---|---|---|---|
| “Accuracy” | 0.94071 | 0.95257 | 0.94862 | 0.94466 | 0.94071 | 0.94071 | 0.96443 |
| “Sensitivity” | 0.96281 | 0.97908 | 0.96708 | 0.97095 | 0.95885 | 0.9668 | 0.98354 |
| “Specificity” | 0.45455 | 0.5 | 0.5 | 0.41667 | 0.5 | 0.41667 | 0.5 |
| “Precision” | 0.9749 | 0.97095 | 0.97917 | 0.97095 | 0.97899 | 0.97083 | 0.97951 |
| “FPR” | 0.54545 | 0.5 | 0.5 | 0.58333 | 0.5 | 0.58333 | 0.5 |
| “FNR” | 0.03719 | 0.020921 | 0.032922 | 0.029046 | 0.041152 | 0.033195 | 0.016461 |
| “NPV” | 0.45455 | 0.5 | 0.5 | 0.41667 | 0.5 | 0.41667 | 0.5 |
| “FDR” | 0.025105 | 0.029046 | 0.020833 | 0.029046 | 0.021008 | 0.029167 | 0.020492 |
| “F1-Score” | 0.96881 | 0.975 | 0.97308 | 0.97095 | 0.96881 | 0.96881 | 0.98152 |
| “MCC” | 0.37226 | 0.51531 | 0.41221 | 0.38762 | 0.37856 | 0.36919 | 0.50865 |
Table 4.
Overall performance analysis of the proposed ACV-DHOA-CNN-EC over classifier
| Methods | RELM [2] | CNNBCN [4] | CapNet [5] | DAE-JOA [7] | Proposed ACV-DHOA-CNN-EC |
|---|---|---|---|---|---|
| Accuracy | 0.92885 | 0.90909 | 0.90514 | 0.92885 | 0.95257 |
| Sensitivity | 0.95 | 0.92917 | 0.92531 | 0.95378 | 0.97119 |
| Specificity | 0.53846 | 0.53846 | 0.5 | 0.53333 | 0.5 |
| Precision | 0.97436 | 0.9738 | 0.9738 | 0.97009 | 0.97925 |
| FPR | 0.46154 | 0.46154 | 0.5 | 0.46667 | 0.5 |
| FNR | 0.05 | 0.070833 | 0.074689 | 0.046218 | 0.028807 |
| NPV | 0.53846 | 0.53846 | 0.5 | 0.53333 | 0.5 |
| FDR | 0.025641 | 0.026201 | 0.026201 | 0.029915 | 0.020747 |
| F1-Score | 0.96203 | 0.95096 | 0.94894 | 0.96186 | 0.97521 |
| MCC | 0.40919 | 0.35233 | 0.30852 | 0.4365 | 0.43192 |
Conclusion
This paper has developed a new automated brain tumor classification model by proposing a new segmentation and classification model. The proposed model has adopted a new algorithm called ACV-DHOA for improving the performance and efficiency of the segmentation and classification processes. The pre-processing of the collected images was done by median filtering and contrast enhancement approaches, which were subjected to the segmentation process. It was performed by using new AFDF model through ACV-DHOA along with multi-objective function. Finally, the brain tumor diagnosis was performed by OCNN-EC method with feature learning and ensemble classification stratergy. Moreover, from the analysis, the accuracy of the proposed ACV-DHOA-CNN-EC was 1.6%, 2%, 0.8%, 1.6%, 2.5%, 1.24%, 1.6% 2%, 2.5% and 2.5% superior to PSO-CNN-EC, GWO-CNN-EC, WOA-CNN-EC, DT, SVM, NN, DNN, CNN and autoencoder, respectively. Hence, the proposed brain tumor segmentation and classification has established better performance than traditional methods.
Declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical Statement
This paper does not contain any studies with human participants or animals performed by any of the authors.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Kaplan K, Kaya Y, Kuncan M, MetinErtunç H. Brain tumor classification using modified local binary patterns (LBP) feature extraction methods. Med Hypotheses. 2020;139:109696. doi: 10.1016/j.mehy.2020.109696. [DOI] [PubMed] [Google Scholar]
- 2.Gumaei A, Hassan MM, Hassan MR, Alelaiwi A, Fortino G. A hybrid feature extraction method with regularized extreme learning machine for brain tumor classification. IEEE Access. 2019;7:36266–36273. doi: 10.1109/ACCESS.2019.2904145. [DOI] [Google Scholar]
- 3.Sultan HH, Salem NM, Al-Atabany W. Multi-classification of brain tumor images using deep neural network. IEEE Access. 2019;7:69215–69225. doi: 10.1109/ACCESS.2019.2919122. [DOI] [Google Scholar]
- 4.Huang Z, et al. Convolutional neural network based on complex networks for brain tumor image classification with a modified activation function. IEEE Access. 2020;8:89281–89290. doi: 10.1109/ACCESS.2020.2993618. [DOI] [Google Scholar]
- 5.Afshar P, Mohammadi A, Plataniotis KN. BayesCap: a Bayesian approach to brain tumor classification using capsule networks. IEEE Signal Process Lett. 2020;27:2024–2028. doi: 10.1109/LSP.2020.3034858. [DOI] [Google Scholar]
- 6.Kumar S, Mankame DP. Optimization driven deep convolution neural network for brain tumor classification. Biocybern Biomed Eng. 2020;40(3):1190. doi: 10.1016/j.bbe.2020.05.009. [DOI] [Google Scholar]
- 7.Siva Raja PM, Rani AV. Brain tumor classification using a hybrid deep autoencoder with Bayesian fuzzy clustering-based segmentation approach. Biocybern Biomed Eng. 2020;40(1):440–453. doi: 10.1016/j.bbe.2020.01.006. [DOI] [Google Scholar]
- 8.Amin J, Sharif M, Gul N, Yasmin M. Shafqat Ali Shad, “Brain tumor classification based on DWT fusion of MRI sequences using convolutional neural network”. Pattern Recogn Lett. 2020;129:115–122. doi: 10.1016/j.patrec.2019.11.016. [DOI] [Google Scholar]
- 9.Dandıl E., Çakıroğlu M., Ekşi Z. Computer-Aided Diagnosis of Malign and Benign Brain Tumors on MR Images. In: Bogdanova A., Gjorgjevikj D. (eds) ICT Innovations 2015. Advances in Intelligent Systems and Computing, vol 311;pp. 157–166.
- 10.Pereira S, Pinto A, Alves V, Silva CA. Brain tumor segmentation using convolutional neural networks in MRI images. IEEE T Med Imag. 2016;35:1240–1251. doi: 10.1109/TMI.2016.2538465. [DOI] [PubMed] [Google Scholar]
- 11.Tiwari A, Srivastava S, Pant M. Brain tumor segmentation and classification from magnetic resonance images: review of selected methods from 2014 to 2019, Pattern Recogn Lett, 2019. Volume 131;Pages 244–260.
- 12.Mohan G, Subashini MM. MRI based medical image analysis: Survey on brain tumor grade classification. Biomed Signal Process Control. 2018;39:139–161. doi: 10.1016/j.bspc.2017.07.007. [DOI] [Google Scholar]
- 13.Hinton G, Sabour S, and Frosst N, “Matrix capsules with EM routing,” Learn representations, 2018; pp. 1–15.
- 14.El Abbadi NK, Kadhim NE. Brain cancer classification based on features and artificial neural network. Int J Adv Res Comput Commun Eng. 2017;8(1):123–134. doi: 10.17148/IJARCCE.2017.6125. [DOI] [Google Scholar]
- 15.Paul JS et al., Deep learning for brain tumor classification Soc Photo-Opt Instrum Eng 2017; 10137.
- 16.Mohsen H, et al. Classification using deep learning neural networks forbrain tumors. Future Comput Inform J. 2018;3(1):68–71. doi: 10.1016/j.fcij.2017.12.001. [DOI] [Google Scholar]
- 17.Wang H, Yeung D. A survey on Bayesian deep learning. ACM Comput. Surv. 2020;53:1–37. [Google Scholar]
- 18.Wong SC, Gatt A, Stamatescu V, and McDonnell MD, ``Understanding data augmentation for classification: When to warp?'' 2016, arXiv:1609.08764.
- 19.Nasrabadi NM. Pattern recognition and machine learning. J. Electron. Imag. 2007;16(4):049901. doi: 10.1117/1.2819119. [DOI] [Google Scholar]
- 20.Machhale K, Nandpuru HB, Kapur V, and Kosta L, ”MRI brain cancer classication using hybrid classier (SVM-KNN)”' Ind. Instrum. Control (ICIC), pp. 6065, 2015.
- 21.Aparajeeta J, Nanda PK, Das N. Modified possibilistic fuzzy C-means algorithms for segmentation of magnetic resonance image. Appl Soft Comput. 2016;41:104–19. doi: 10.1016/j.asoc.2015.12.003. [DOI] [Google Scholar]
- 22.Rao CR, Kumar MNVSS, Rao GSB. “A novel segmentation algorithm for feature extraction of brain MRI tumor. Information and decision sciences”. Springer, vol 701. Springer; pp. 455–63, 2018.
- 23.Malathi M, Sinthia P. MRI brain tumour segmentation using hybrid clustering and classification by back propagation algorithm. Asian Pacific J Cancer Prev. 2018;19(11):3263. doi: 10.31557/APJCP.2018.19.11.3257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhao X, Wu Y, Song G, Li Z, Zhang Y, Fan Y. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation. Med Image Anal. 2018;43:98–111. doi: 10.1016/j.media.2017.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Anaraki AK, Ayati M, Kazemi F. Magnetic resonance imaging based brain tumor grades classication and grading via convolutional neural networks and genetic algorithms. Biocybernetics Biomed. Eng. 2019;39(1):6374. [Google Scholar]
- 26.Brammya G, Praveena S, Ninu Preetha NS, Ramya R, Rajakumar BR, and Binu D, Deer hunting optimization algorithm: a new nature-inspired meta-heuristic paradigm, 24 May 2019
- 27.Zhu Y, Huang C. An improved median filtering algorithm for image noise reduction. Physics Procedia. 2012;25:609–616. doi: 10.1016/j.phpro.2012.03.133. [DOI] [Google Scholar]
- 28.Patel O, Maravi YPS, Sharma S. A comparative study of histogram equalization based image enhancement techniques for brightness preservation and contrast enhancement. Signal Image Process. 2013;4(5):11–25. [Google Scholar]
- 29.Abdenour M, Karim M. Improved fuzzy C-means based Particle Swarm Optimization (PSO) initialization and outlier rejection with level set methods for MR brain image segmentation. Computer Methods Programs Biomed. 2015;122(2):266–281. doi: 10.1016/j.cmpb.2015.08.001. [DOI] [PubMed] [Google Scholar]
- 30.Setola R, Montoni LM and Zobel BB Chapter 27 - Motion Artifacts Compensation in DCE-MRI Framework Using Active Contour Model Emerging Trends in Computer Science and Applied Computing, pp. 391–409, 2016.
- 31.Tu F, Yin S, Ouyang P, Tang S, Liu L, Wei S. Deep convolutional neural network architecture with reconfigurable computation patterns. IEEE Trans Very Large Scale Integr Syst. 2017;25(8):2220–2233. doi: 10.1109/TVLSI.2017.2688340. [DOI] [Google Scholar]
- 32.Wang Z, Dreyer F, Pulvermüller F, Ntemou E, Vajkoczy P, Fekonja LS, Picht T. Support vector machine based aphasia classification of transcranial magnetic stimulation language mapping in brain tumor patients. NeuroImage Clinic. 2021;29:102536. doi: 10.1016/j.nicl.2020.102536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jia W, Yang M, Wang S-H Three-category classification of magnetic resonance hearing loss images based on deep autoencoder J Med Syst. 2017; 41(10) ; first page165 . [DOI] [PubMed]
- 34.Ghassemi N, Shoeibi A, Rouhani M. Deep neural network with generative adversarial networks pre-training for brain tumor classification based on MR images. Biomed Signal Process Control. 2020;57:101678. doi: 10.1016/j.bspc.2019.101678. [DOI] [Google Scholar]
- 35.Rajakumar BR and Aloysius G, “A new adaptive mutation technique for genetic algorithm”, IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), pp. 1–7, 2012.
- 36.Swamy SM, Rajakumar BR and Valarmathi IR “Design of hybrid wind and photovoltaic power system using opposition-based genetic algorithm with cauchy mutation”, IET Chennai Fourth International Conference on Sustainable Energy and Intelligent Systems, 2013.
- 37.Soltani-Nabipour J, Khorshidi A, Noorian B. Lung tumor segmentation using improved region growing algorithm. Nucl Eng Technol. 2020;52(10):2313–2319. doi: 10.1016/j.net.2020.03.011. [DOI] [Google Scholar]
- 38.Seo J, Im C, Kwak S, Lee C, Jung H. An improved particle swarm optimization algorithm mimicking territorial dispute between groups for multimodal function optimization problems. IEEE Trans Magn. 2008;44(6):1046–1049. doi: 10.1109/TMAG.2007.914855. [DOI] [Google Scholar]
- 39.Mesadi F, Cetin M, Tasdizen T. Disjunctive normal parametric level set with application to image segmentation. IEEE Trans Image Process. 2017;26(6):2618–2631. doi: 10.1109/TIP.2017.2682980. [DOI] [PubMed] [Google Scholar]
- 40.Emary E, Zawbaa HM, Grosan C. Experienced gray wolf optimization through reinforcement learning and neural networks. IEEE Transactions Neural Netw Learn Syst. 2018;29(3):681–694. doi: 10.1109/TNNLS.2016.2634548. [DOI] [PubMed] [Google Scholar]
- 41.Hassouneh Y, Turabieh H, Thaher T, Tumar I, Chantar H, Too J. Boosted whale optimization algorithm with natural selection operators for software fault prediction. IEEE Access. 2021;9:14239–14258. doi: 10.1109/ACCESS.2021.3052149. [DOI] [Google Scholar]
- 42.Lelis VM, Guzmán E, Belmonte M. Non-invasive meningitis diagnosis using decision trees. IEEE Access. 2020;8:18394–18407. doi: 10.1109/ACCESS.2020.2966397. [DOI] [Google Scholar]
- 43.Bhaskar N, Suchetha M, Philip NY. Time series classification-based correlational neural network with bidirectional LSTM for automated detection of kidney disease. IEEE Sensors J. 2021;21(4):4811–4818. doi: 10.1109/JSEN.2020.3028738. [DOI] [Google Scholar]
- 44.“https://www.kaggle.com/navoneel/brain-mri-images-for-brain-tumor-detection/downloads/brain-mri-images-for-brain-tumor-detection.zip/1, Access date: 2021–03–19”
- 45.https://in.mathworks.com/help/images/ref/medfilt2.html.
- 46.https://in.mathworks.com/help/images/contrast-enhancement-techniques.html.
- 47.Shende, D.K., Sonavane, S.S. CrowWhale-ETR: CrowWhale optimization algorithm for energy and trust aware multicast routing in WSN for IoT applications, 2020; Wireless Netw 26,pp 4011–4029.