Abstract
To perform activities of daily living (ADL), people with lower limb amputation depend on the prosthetic socket for stability and proprioceptive feedback. Poorly fitting sockets can cause discomfort, pain, limb tissue injuries, limited device usage, and potential rejection. Semi-passively controlled adjustable socket technologies exist, but these depend upon the user’s perception to determine safe interfacial pressure levels. This paper presents a framework for automatic control of an adjustable transtibial prosthetic socket that enables active adaptation of residuum-socket interfacial loading through localized actuators, based on soft tissue injury risk estimation. Using finite element analysis, local interfacial pressure vs. compressive tissue strain relationships were estimated for three discrete anatomical actuator locations, for tissue injury risk assessment within a control structure. Generalized Predictive Control of multiple actuators was implemented to maintain interfacial pressure within estimated safe and functional limits. Controller simulation predicted satisfactory dynamic performance in several scenarios. Actuation rates of 0.06–1.51 kPa/s with 0.67% maximum overshoot, and 0.75–1.58 kPa/s were estimated for continuous walking, and for a demonstrative loading sequence of ADL, respectively. The developed platform could be useful for extending recent efforts in adjustable lower limb prosthetic socket design, particularly for individuals with residuum sensory impairment.
Keywords: Adjustable prosthetic socket, Finite element analysis, Generalized predictive control, Interface pressure control, Transtibial
Introduction
The socket is the fundamental interface between a person with an amputation (PWA) and her/his prosthetic, and hence the first element of the device that determines their perception of comfort. It is responsible for direct transfer of the ground reaction force (GRF) to the musculoskeletal system during activities of daily living (ADL). The contact pressure and shear stresses at the interface between the prosthetic socket and the residuum skin, plus the strain of the underlying soft tissues greatly determine comfort and tissue injury risk. Poorly fitting sockets can cause discomfort and pain, and potentially limit prosthetic usage due to vascular occlusion, skin breakdown and tissue injuries such as degenerative stump ulcers, which in severe cases could lead to re-amputation or life threatening conditions [1]. The most serious complications are associated with Deep Tissue Injury (DTI), which initiates in the internal tissues close to bony prominences and develops towards the residual limb surface [2].
Generally, prosthetic sockets are bespokely fitted by specialized clinicians, and require iterative replacement to accommodate changes in residual limb volume and shape [3]. Standard transtibial socket designs present unmet challenges affecting wearer comfort. Some individuals experience pistoning [4], longitudinal movement between the prosthetic socket and the residual limb during cyclic loading. Others report sensitivity to residuum volume and shape changes, with up to 8.5% volumetric fluctuation per hour during a typical day [5, 6]. A solution may be socket designs that allow user-operated [7] or automated socket fit adjustment [8–13] or have spatially variable socket wall impedance [14], for reduction of interfacial pressure gradients that cause discomfort, and accommodation of diurnal and long-term residuum changes.
The Infinite Socket™ (LIM Innovations, CA, USA), Socket-less Socket™ (MartinBionics, OK, USA), and RevoFit™ (Click Medical, CO, USA) are manually adjustable commercially available devices. Socket size adjustments are made to flexible socket frame struts using straps, laces and clamps, or to moveable cabled panels introduced to a conventional socket. They offer benefits of easy within-day comfort-based adjustments by the user. The socket biomechanical functional outcomes and the impact of adjustments on sub-dermal tissues are, however, unknown. Also, the literature reports powered user-controlled [7], and automatically adjustable interventions aiming at reducing interfacial stresses [8, 10, 13] or compensating for limb volume fluctuations [9], or both [11, 12]. The adjustments are made using movable socket panels and motorized cables [7], or actuatable intra-socket bladders and interface pressure sensors [8–13]. These socket designs might be described as passive and semi-passive, aiming to maintain singular pre-determined user comfort and fit levels, as opposed to adjusting throughout dynamic, cyclic loading. Furthermore, they do not consider the internal tissue strain arising from the interfacial loading, which is the established predictor of DTI [15, 16]. The safety of these designs may be further improved by active control based on interfacial sensor measurements and tissue injury indicators [17], to address the cumulative effect of longer-duration loads, and to avoid the risk of users over-tightening the socket and inadvertently generating strains in the residuum tissues beyond safe levels, especially where vascular pathologies may diminish sensation.
Interface pressure is practically measurable but it does not necessarily generate high deviatoric tissue strain [18] associated with DTI risk [2]. Therefore, the purpose of this study is to describe a framework for developing an adaptive socket system that incorporates an actuatable residuum/socket interface to actively modulate interfacial pressure within estimated safe tissue strain levels. Finite element analysis (FEA) was used to predict the relationships between internal strain and socket-limb interfacial pressure at specific anatomical regions of the residual limb, at several instants during the gait cycle. These relationships were used as training data for tissue injury risk assessment to determine control targets for socket interface actuation over sustained loading. Generalized Predictive Control (GPC) was simulated and optimized to minimize cumulative residuum tissue injury risk.
Methods
Finite element analysis
A previously reported FE model [19, 20] was adapted for this study (Fig. 1), to evaluate the relationships between predicted internal tissue strain and interfacial pressure at three anatomical regions of interest (ROI), to provide training data for actuator control based on minimizing tissue damage risk. Briefly, the model was developed from MRI scans of a person with unilateral transtibial amputation wearing a gel liner, segmented and meshed in Scan-IP software (Scan-IP N-2018.03, Synopsys Inc., USA) to represent liner, bones (tibia, fibula, patella and femur), soft tissue (combining muscles, skin and subcutaneous fat), patella tendon and quadriceps tendon, and intra-articular structures. A socket model was generated by replicating the liner external surface up to the participant’s normal socket brim-line, and applying a non-uniform 0 to 2% cross-sectional area scaling factor about the residual tibia’s axis, to represent a simplified Total Surface Bearing (TSB) [21design. A socket model was generated by replicating the liner external surface up to the participant’s normal socket brim-line, and applying a non-uniform 0 to 2% cross-sectional area scaling factor about the residual tibia’s axis, to represent a simplified Total Surface Bearing (TSB) [21] design. The liner-skin interface was bonded and contact with 0.5 coefficient of friction was simulated between the liner and socket. Quasi-static 2D sagittal plane loading was applied to the model with a proximal force (Fz), an anterior force (Fx) and a sagittal plane moment (My, extension positive) (Fig. 1), for approximation of typical prosthetic use during the stance phase of gait [22]. The load values were extracted from studies of dynamic load-cell data for unilateral transtibial prosthesis users walking at self-selected speed [23, 24]. The applied quasi-static loads represented the heel strike, foot flat, mid stance, heel off and toe off stages of gait (Appendix). The loads were applied across a circular region of nodes at the base of the socket whilst for boundary conditions the model was constrained at the proximal cut surface of the femur and the quadriceps tendon. The model permitted limited passive knee flexibility under load, and the socket-tip forces were applied in the tibial frame of reference, to account for knee flexion across the simulations.
Fig. 1.
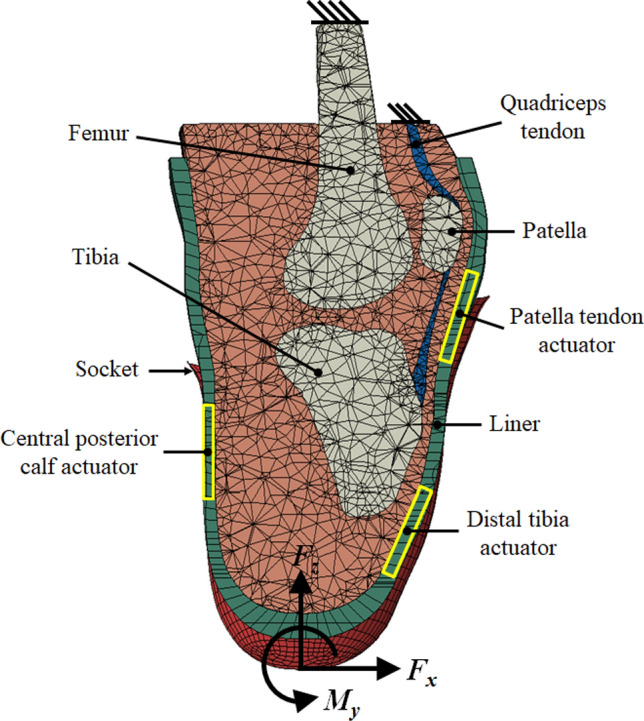
A sagittal section of the FE model illustrating geometry, loading configuration and boundary conditions, plus the regions of interest for actuation: the patella tendon (PT), central posterior calf (PC) and distal tibia (DT)
Concerning the actuator models, three locations were chosen (Fig. 1). First, the load tolerant patellar tendon region (PT) was selected as it is prioritised for load transfer, but may still be overloaded. Second, the vulnerable distal tibia region (DT) was selected as it may benefit from protection over sustained prosthesis use. Finally, a load-tolerant fleshy region in the posterior calf (PC) was selected as it may be exploited for maintaining suspension during the swing phase of gait [25]. Estimates of pressure at the residuum surface and internal strain within the soft tissue ROIs were extracted from the model. 95th percentile values were used to avoid any single-node concentrations that may occur as artefacts of loading. The minimum principal strain, ε3, and maximum shear strain, γmax, were inspected. The predicted interfacial pressure-compressive strain relationships were used to build surrogate models for tissue injury risk evaluation for actuator control.
Interface actuation model
Suitable techniques for functional interface actuation within an active socket system should have measurable, easily interpretable and controllable mechanical and/or electrical parameters. Typical liquid bladder socket inserts are thin expandable liquid cells applied in the inner socket wall to replace residuum volume losses, and provide pressure relief at the residuum-socket interface [5, 12, 13]. They are reported to be a better option for residuum volume loss accommodation compared to air bladders due to the lower compressibility of liquids [26]. In this study, such socket inserts were simulated as connected to a controllable ideal pressure source, capable of delivering and maintaining the desired pressure level. This actuation method was modelled in the Simulink environment (MATLAB R2016a, MathWorks®, USA) as a hydro-mechanical transducer system. It was estimated as an ideal transducer with incompressible fluid, and Pascal’s law was applied assuming small fluid displacements. The pressure applied on the residuum surface at any instant is directly measurable using an interface sensor, and considered to be equal to the pressure in the fluid insert. Liquid socket bladders typically contain water as the primary medium [5]. The relevant variables used to model this actuator were derived from the properties of water, taken at 35 °C, close to the average residuum skin temperature (34.1 °C) after 30 min of treadmill walking with a prosthesis [27] (Table 1).
Table 1.
Representative interface actuator property modelling values for water at 35 °C
| Property | Value |
|---|---|
| Density, ρ (kg m−3) | 993.7 |
| Kinematic viscosity, ν (m2 s−1) | 7.45 × 10–7 |
| Bulk/Volume modulus, K @ atmospheric pressure (Pa) | 2.24 × 109 |
| Thermal conductivity, k @ 1 bar (W/m.K) | 621.6 × 10–3 |
GPC implementation for interface actuation
A suitable control scheme for the adaptive socket system described in this study requires particular characteristics in order to meet operational requirements: accommodation of multiple variables, sensors and actuators, capability for real-time, bounded control, capability to estimate unobservable states, and capacity for disturbance rejection for elements external to the system, such as gait information and prosthetic alignment effects. Generalized predictive control is a model-based control method [28], which is widely adopted in industry due to its capability to handle multivariable, high model order and unstable open loop systems, dead time, and maintaining good stability margins [29, 30]. This control approach computes current control inputs based on anticipated future input demands and predicted model behaviour over a finite horizon, ny, into the future. The predicted output is derived from a plant model (1) and is dependent on the current measured variable and input. Matrix methods are used to recursively derive the equations for n-steps ahead prediction. At each sampling instant, a new control output prediction, (2) is computed based on anticipated future control targets, and the control input is adjusted accordingly. The level of model fidelity directly affects the allowable number of reliable control moves, nu, at each step for dynamic performance optimization during transients [30].
| 1 |
| 2 |
where A(z) = a(z)Δ(z) and Δ(z) = 1 − z−1, k is the current sample step, Δu is the vector of control input increments, and H, P, Q are the prediction matrices.
Control inputs are determined by minimizing a cost function, J, (3) (4) such that control action (5) and closed-loop performance minimize overall interfacial pressure magnitudes and tissue injury risk. This minimization tends towards stability for a given horizon and allows for optimization to achieve a balance between adequate system sensitivity and the aggressiveness of control action. Optimization also involves application of a weighting constant, λ, that expresses the relative significance of control inputs compared to the tracking errors [31]. Only the first element, E1, in the future control increments vector (the optimum input trajectory) is applied at each sampling instant.
| 3 |
where r is the vector of control targets, the safe target pressures at the residuum interface for each actuator location, generated from a tissue injury risk evaluation protocol described below. e denotes the vector of tracking errors.
| 4 |
| 5 |
The input waveforms applied for simulating the adaptive socket system in Simulink® were determined from interfacial pressures arising from corresponding prosthesis loading regimes, estimated using FEA. Pairs of interface pressure and corresponding tissue strain values were extracted from the FE model, and used to create surrogate models for quick reference by the controller. The surrogate models employed either linear regression or Simulink ‘lookup table’ blocks, and were positioned either side of a ‘dynamic saturation’ block model that incorporated the sigmoid strain–time threshold curve published by Gefen et al. [16]. The first surrogate took the simulated interface pressure measurement and predicted the corresponding tissue strain. The dynamic saturation block then provided the permitted safe strain level based on the loading history and forecast at this location, and used the ‘donned’ scenario as the lower bound for pressure and strain. Finally, the second surrogate then took the target safe strain level and identified the safe upper bound, ‘target’ pressure, which was used to define the actuator response. The lookup tables contained the pressure and strain values arranged in increasing order, and were evaluated top-down using cubic spline interpolation, so that they would predict worst-case strain and provide conservative pressure targets. As an initial step, an input signal of 600 kPa, about twice the maximum interfacial pressure value predicted for standard gait (Fig. 2a), was applied to generate estimates of local interfacial pressure–time safety thresholds for all ROI. The endurance limits for early and delayed onset tissue damage due to large compressive strains are defined as within 0–63 ± 37 min and 176–285 ± 55 min, respectively [16].
Fig. 2.
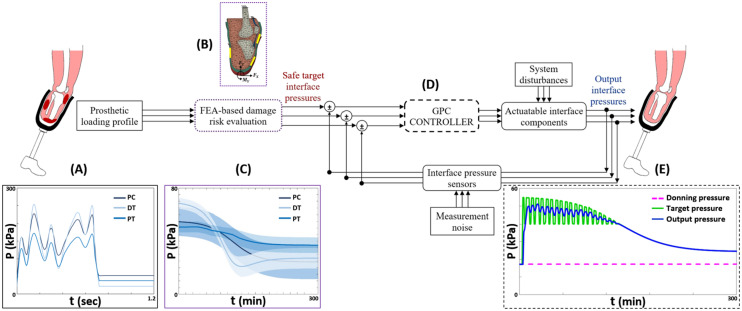
An illustration of the adaptive prosthetic socket system concept. a Input gait loading signal, representative of pressure sensing at the residuum/socket interface for one gait cycle,. b Sagittal section of a 3D FEA model illustrating loading configuration, boundary conditions and actuator locations. c Estimated pressure–time injury risk thresholds, for 0–300 min, corresponding to the sigmoid strain–time curve [16]. b and c represent the tissue injury risk evaluation protocol utilizing biomechanical FEA output predictions of localized interfacial pressure-strain relationships to determine control targets for interface actuation. d GPC system for maintaining safe tissue strain levels by adaptive actuation of intra-socket liquid bladders. e Exemplar control output at the posterior calf location. P—interfacial pressure, t—time
The actuator plant model was converted into a CARIMA (Controlled Auto Regressive and Integrated Moving Average) model transfer function of the form outlined in (1) [28, 30]. The controller was initiated at the pressure expected upon socket donning at the selected ROI, and the output sampling time was 15 s. Optimization was carried out to meet design goals of fast rise time and no overshoot, by examining the influence of the control weighting constant, λ, for satisfactory performance without over-aggressive actuation. Desirable control action was defined as that which minimizes overall pressure magnitudes, actuation rates and pressure changes in order to minimize tissue strain injury risk, reduce the overall power consumption of the system, and in case large, fast actuations may cause wearer discomfort. Suitable values of the control horizon nu, the feedforward horizon na, and the output prediction horizon ny were determined by experiment through preliminary work by control performance evaluation. na allows for identification of key future control target changes not covered within the control horizon. In designing for target tracking and control optimization with GPC, an increase in λ demands an increase in nu that in turn may require an increase in na and/or ny. Large values of ny and na resulted in increased output deviation from the target, whereas large values of nu resulted in finer control moves per step and faster actuation. It was expected that values of ny, nu and na should vary across the ROI, due to distinct interfacial pressure-strain relationships, and between different locomotive modes.
The feasibility and performance of the GPC formulation for the proposed interface actuator model was firstly assessed for a standard gait input waveform (Fig. 2a) corresponding to the forces and moments across the socket-tibia-knee joint construct [32]. The durations of stance and swing phases during one gait cycle were determined as 0.72 and 0.48 s, respectively, as reported for persons with unilateral transtibial amputation [33]. The input sampling rate was 50 Hz, to preserve up to 99% of gait signal power (~ 15 Hz) [34]. The output prediction horizon ny was chosen as between 30 and 100 min, i.e. 120–400 sample steps (ss), corresponding to the short loading exposure period after which there is notable decrease in muscle tissue compressive strain endurance [16]. Preliminary work indicated variation of λ in increment steps of one order of magnitude from 10–2 to 102 across all ROI for optimization. Also, close resemblance was noted in the estimated GPC safe target pressure profiles at the PC and PT actuator locations, with cyclic loading in timeframes under 2 h. nu values of 10, 20, and 10 sample steps (i.e. 2.5, 5, and 2.5 min) were selected for the PT, PC and DT actuator locations, respectively, whereas the na values were 20, 30, and 100 sample steps (i.e. 5, 7.5 and 25 min).
A second assessment was carried out to examine the efficacy and performance of GPC for a demonstrative loading sequence of some typical ADL that might be performed by active prosthesis users. These included donning the prosthesis, 30 min sitting, 15 min standing, 45 min walking, and finally sitting again for 30 min. For the FEA to determine inputs for this loading scenario, the user was considered to be a person with unilateral transtibial amputation weighing approximately 90 kg [23]. The output prediction horizon ny was selected between 15–30 min. Preliminary analysis dictated variation of λ from minimum 0.1 to maximum 10 across all ROI for optimization. nu values of 20, 20, and 15 sample steps (i.e. 5, 5, and 3.75 min) were selected for the PT, PC and DT actuator locations, respectively, whereas the na values were 30, 25, and 50 sample steps (i.e. 7.5, 6.25, and 12.5 min).
Results
Finite element analysis
For the three loading cases, the local interfacial pressure estimated at actuator locations ranged from 25.5–155.1 kPa, 54.9–112.1 kPa and 42.3–116.1 kPa, for the DT, PC and PT locations, respectively. Compressive strain in the soft tissues ranged between 40.7–81.2%, 56.3–85.3% and 47.4–72.2%, while the shear strain was between 6.1–15.1%, 7.7–17.1% and 4.6–9%, for the DT, PC and PT locations, respectively. Variations in the pressure and strain estimates were consistent across the loading cases throughout the gait cycle. Figure 3 shows the predicted distributions of compressive strain on a sagittal plane section view through the tibia, and interfacial pressure for the five gait instances, for one loading case. During heel strike to mid stance, areas of high compressive strain were the lateral femoral epicondyle, fibula head, tibial tuberosity and anterior distal tibia. For heel off and toe off, the strain was concentrated at the patella tendon, the patella and the distal tibia. Areas of high interfacial pressure were the tibial tuberosity, anterior distal tibia, proximal posterior calf close to the popliteal fossa and the fibula head during heel strike to mid stance, and the patella, patella tendon, central posterior calf and fibula head during heel off and toe off.
Fig. 3.

Top: Sagittal plane section views through the tibia showing the internal residuum compressive strain and, Bottom: the full field residuum interface pressure estimates during five key stages of stance for one loading case [22]
Regression analysis of predicted interfacial pressure-compressive strain relationships, showed a linear relationship (R2 = 0.9) at the PC location, but more complex relationships at the DT and PT locations (Fig. 4), which were described with cubic splines. Moreover, at the DT location, predicted compressive and shear strains were highest around the load-acceptance and push-off gait stages, whereas at the PC and PT locations the strains increased from heel strike to toe off.
Fig. 4.

Interface pressure vs. residuum tissue strain relationships at the posterior calf, distal tibia and patella tendon locations, showing combined results for all the three loading cases applied to a reference, unactuated socket model. HS—Heel Strike, FF—Foot Flat, MS—Mid Stance, HO—Heel Off, TO—Toe Off. The dashed lines indicate the region for safe interface pressure actuation control, up to the 57% tissue damage strain threshold [16], and the shaded area indicates the high damage risk region
GPC performance evaluation
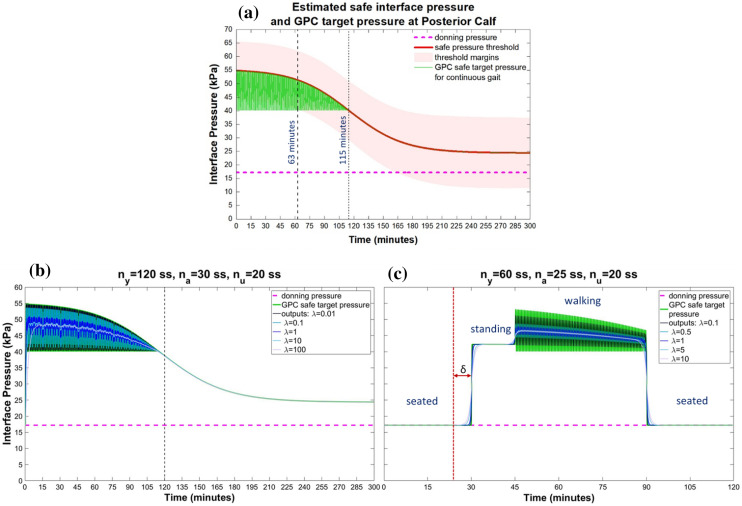
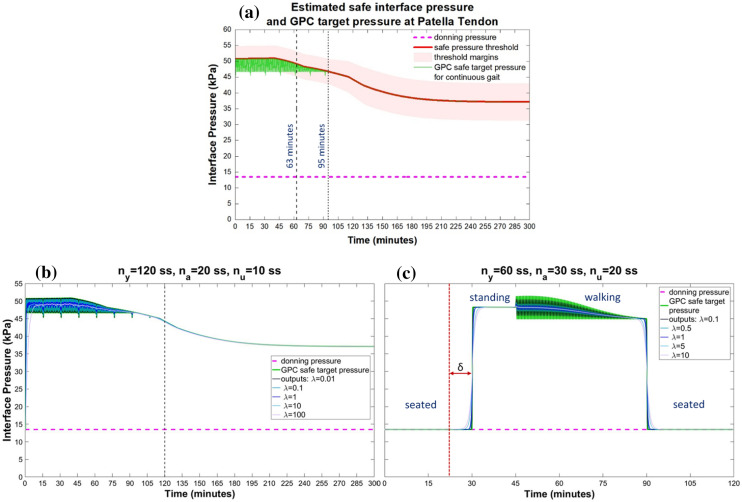
At the tissue injury risk estimation stage the interface pressure-strain surrogate models were applied, and the GPC acted to limit the interface pressure within the DTI threshold at all locations. Estimated pressure safety limits were obtained from the Gefen sigmoid strain–time curve [16]. For early onset tissue damage, exemplar thresholds at t = 0 min were 54.8 kPa, 50.8 kPa and 68.4 kPa at the PC, PT and DT regions, respectively. For delayed onset tissue damage, exemplar thresholds at t = 176 min were 27.6 kPa, 38.6 kPa and 24.5 kPa at the PC, DT and PT regions, respectively (Figs. 5a, 6a, 7a).
Fig. 5.
Top: a Estimated interface pressure safety threshold, and GPC safe target pressure plots for a standard continuous ambulation waveform at the posterior calf location. Bottom: GPC performance for a liquid bladder actuator for different values of the control weighting constant, λ, for b a standard continuous ambulation waveform, and (c) a demonstrative loading sequence of typical ADL, δ = 6.25 min and denotes the minimum delay, na, that may be required between loading input measurements and controlled actuation in practical application. ss—sample steps
Fig. 6.
Top: a Estimated interface pressure safety threshold, and GPC safe target pressure plots for a standard continuous ambulation waveform at the patella tendon location. Bottom: GPC performance for a liquid bladder actuator for different values of the control weighting constant, λ, for b a standard continuous ambulation waveform, and c a demonstrative loading sequence of typical ADL, δ = 7.5 min and denotes the minimum delay, na, that may be required between loading input measurements and controlled actuation in practical application. ss—sample steps
Fig. 7.
Top: a Estimated interface pressure safety threshold, and GPC safe target pressure plots for a standard continuous ambulation waveform at the distal tibia location. Bottom: GPC performance for a liquid bladder actuator for different values of the control weighting constant, λ, for b a standard continuous ambulation waveform, and c a demonstrative loading sequence of typical ADL, δ = 12.5 min and denotes the minimum delay, na, that may be required between loading input measurements and controlled actuation in practical application. ss—sample steps
The gait input pressure signals produced cyclic estimated output pressure signals up to the pressure–time safety thresholds for the first approximately 115 and 95 min for the PC and PT locations, respectively (Figs. 5a, 6a), and tracked the thresholds after this time. For the DT location, the estimated output pressure signal followed the pressure–time safety threshold for the entire 300 min period (Fig. 7a). GPC output profiles and actuation control performance measures for a standard continuous gait waveform at the three ROI are presented in Figs. 5b, 6b, 7b, and Table 2. Larger values of λ resulted in smaller, slower actuations, and increased control output deviation from the target. For timeframes below 2 h, control acted to maintain interfacial pressures below the safety threshold at all ROIs. After this time, safe target tracking was maintained at the PC and PT locations, but overshoots of 0.67–4.15% were predicted at the DT location.
Table 2.
Summary of simulated GPC output performance for a liquid bladder actuator by residuum location for a standard continuous gait waveform, and a demonstrative loading sequence of typical ADL
| Actuator location | Peak Actuation Pressure Magnitude (kPa) | Peak Actuation Rate (kPa/s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Continuous Gait | λ | 0.01 | 0.1 | 1 | 10 | 100 | 0.01 | 0.1 | 1 | 10 | 100 |
| PC | 14.29 | 12.16 | 5.12 | 0.95 | 0.40 | 0.95 | 0.81 | 0.34* | 0.06* | 0.03 | |
| PT | 5.42 | 4.28 | 1.68 | 0.38 | 0.33 | 0.36* | 0.29* | 0.11* | 0.03 | 0.02 | |
| Rise time (seconds) | |||||||||||
| DT | 43.4 | 44.5 | 65.6 | 134.7 | 300.0 | 4.01 | 3.71 | 1.51* | 0.51* | 0.20 | |
| Peak Actuation Pressure Magnitude (kPa) | Peak Actuation Rate (kPa/s) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ADL Loading Sequence | λ | 0.1 | 0.5 | 1 | 5 | 10 | 0.1 | 0.5 | 1 | 5 | 10 |
| PC | 21.19 | 14.48 | 11.21 | 5.57 | 4.02 | 1.41* | 0.97* | 0.75* | 0.37 | 0.27 | |
| PT | 29.39 | 20.08 | 15.55 | 7.59 | 5.43 | 1.96 | 1.34* | 1.04* | 0.51 | 0.36 | |
| DT | 34.76 | 23.74 | 18.38 | 8.95 | 6.39 | 2.32 | 1.58* | 1.23* | 0.60 | 0.43 | |
| Actuator location | Maximum Error (%) | Maximum Overshoot (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Continuous Gait | λ | 0.01 | 0.1 | 1 | 10 | 100 | 0.01 | 0.1 | 1 | 10 | 100 |
| PC | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| PT | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| DT | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.67 | 4.15 | |
| ADL Loading Sequence | λ | 0.1 | 0.5 | 1 | 5 | 10 | 0.1 | 0.5 | 1 | 5 | 10 |
| PC | 11 | 31 | 40 | 58 | 63 | 0 | 0 | 0 | 0 | 0 | |
| PT | 20 | 54 | 71 | 101 | 109 | 0 | 0 | 0 | 0 | 0 | |
| DT | 33 | 91 | 119 | 170 | 184 | 0 | 0 | 0 | 0 | 0 | |
* indicates results within preferred actuation rate range
For the simulations of GPC for a loading sequence of typical ADL, peak actuation magnitudes and rates were predicted where the largest changes in target pressure occurred, during transitions from sitting to standing and walking to sitting actions for the PC and PT locations, and during transitions from standing to walking and walking to sitting actions for the DT location (Figs. 5c, 6c, 7c).
Discussion
This study presents development of a framework for an adaptive transtibial prosthetic socket that enables active interface actuation to modulate tissue strain within estimated safe levels. Local interfacial pressure and compressive strain estimates throughout the gait cycle were observed to be comparable to related studies [22]: the distal anterior and proximal posterior parts of the residual limb were predicted to be loaded around heel strike and unloaded around toe off, as a result of socket flexion and extension moments. The opposite loading trend was predicted at the proximal anterior and distal posterior locations (Fig. 3). Peak soft tissue compressive strains were estimated as 81.2%, 85.3% and 72.2% at the DT, PC and PT regions, respectively, consistent with maxima reported in similar FEA studies [35]. Furthermore, peak shear strain of 15.1% was predicted at the distal tibia, comparable to other published predictions [36]. These results provide some corroboration to the model predictions, though there will be considerable inter-person variability in these measures, as well as recognized variation in FEA predictions across studies attributed to differences in model structures and levels of sophistication, material properties, loading regimes, and the methods applied for evaluating model outputs [37].
Numerous previous studies have quantified prosthesis-limb normal interfacial pressures and shear stresses in efforts to optimize lower limb prosthetic socket design for user comfort and the quality of socket fit. An important finding of the current study is that relatively low interfacial pressures, 27–55 kPa, can result in large local internal compressive strains, above 50% (Fig. 4) indicating theoretical DTI risk for weight-bearing periods longer than 1 h [16]. This observation is particularly important for prosthetic socket fitting for users with peripheral neurological deficiency due to vascular disease, who may lack adequate sensorial alert to onset of tissue damage. Other studies have also shown that interfacial pressures alone are misleading for determining susceptibility to DTI, owing to inter-person variability and distinct geometry of bones and soft tissue layers, and tissue properties [38], and high interfacial pressures may not necessarily correspond to high internal tissue strain. Portnoy et al. [18] reported 65 kPa pressure against 73% compressive strain for one participant, and 92 kPa against < 35% strain for another. A different study investigating impact of long-term wheelchair use reported peak pressure of 18 ± 3 kPa under the gluteus ischial tuberosity against peak strain of 74 ± 7% in the gluteus muscle [39].
In the present study, GPC control was simulated with a cost function optimization to minimize residuum tissue injury risk with a liquid bladder actuator. For the three actuator locations considered, interface actuation maintained pressure within the estimated safety thresholds, and above the nominal levels predicted upon socket donning alone, which was used as prediction of ensuring prosthesis suspension during swing (Figs. 5, 6, 7). According to related studies evaluating user outcomes for the elevated vacuum socket suspension system, over 72% of users reported preferred variations in vacuum of 3.4–6.8 kPa (≈1–2 inHg) during ambulation [40]. Consequently, in the current study, estimates of preferred actuation performance for continuous walking were indicated as up to 0.34, 0.36 and 1.51 kPa/s for the PC, PT and DT locations, respectively, with a maximum overshoot of 0.67% at DT, and similarly, 1.41, 1.34 and 1.58 kPa/s with no overshoot, for the loading sequence of typical ADL (Table II). Additionally, during continuous walking, cyclic control action observed at the PC (Fig. 5b) and PT locations (Fig. 6b) for timeframes under 2 h may be beneficial for enhancing blood flow to the residuum tissues [41].
This study provides local interfacial pressure–time safety threshold estimates for the three actuator locations, generated based on an existing strain injury threshold [16]. Though external validity of these interfacial pressure thresholds is limited owing to different input data and conditions between the two studies, they offer some novel representative approximations for assessing injury risk of residuum tissues as a result of in-socket loading. Some comparable studies on semi-passive self-adjusting sockets involving actuatable magneto-rheological fluid socket inserts [12], an air-cuff liner [10], and intra-socket fluid bladders [13] reported improved performance compared to conventional sockets [42] with regards to measured peak interfacial pressure: 70, 57 and 72 kPa versus 170, 83 and 79 kPa, at the patella tendon, central posterior calf and distal residuum regions, respectively. The results of the current study indicate that although existing self-adjusting sockets may show reduced pressures compared to standard sockets, additional measures may be necessary to sufficiently eliminate the risk of DTI in residuum tissues under long-term loading (Figs. 5a, 6a, 7a).
For the sequence of typical ADL, the GPC formulation based on future targets was predicted to enable smooth transitions between actions, avoiding large instantaneous pressure changes. Control outputs were below estimated pressure thresholds and errors did not represent poor control action, but rather could be applied as criteria for selecting control parameters for different modes of socket control for the different activities. For real implementation, explicit programming of a minimum delay equivalent to na between current interfacial pressure measurements and controlled actuation would be essential to enable timely detection of imminent control target changes based on user movements (Figs. 5c, 6c, 7c).
This study indicates that GPC could be applied to give satisfactory interface actuation performance and minimize tissue damage risk for an adaptive prosthetic socket with multiple in-socket actuators, in several scenarios. Control parameters can be selected which would be predicted to meet operational requirements and avoid deviations into high tissue damage risk, for an exemplar liquid bladder actuator model.
Limitations
The present FEA study involved quasi-static loading at several gait stages, an analysis simplification justified by the slow walking cases of interest. Also, only a limited set of prosthetic loading cases were applied, taken from published literature. Further studies involving full dynamic analysis, additional prosthetic loading scenarios and characterization of effects of different walking speeds could generate more robust surrogate models for DTI risk evaluation, and ideally the load cases would match the individual from whom the modelling geometry was obtained. Moreover, the study only considered three discrete anatomical regions of the transtibial residuum for in-socket actuation. Additional actuator locations and combinations should be evaluated to assess possible requirement of a more complex control structure [43]. The present study does not repeat general analysis of limb-socket interface pressure distribution, reported in [19], but it should be noted that the proposed control framework should be applied as a means to improve the robustness of an initially well-fitting socket. Sensor arrays could be explored to evaluate pressure distribution on the surface during actuation. Furthermore, the FE analysis in the present study was based on a single model. In a proposed practical application of this study, conducting person-specific, image-based FEA for each candidate patient would be prohibitively expensive. Instead, such a control framework might be tuned using simpler models [44] based on linear ultrasound measurements [45] of soft tissue coverage thickness over bone at key residuum regions, ultrasound elastography [46] or indenter measurements of skeletal tissue compliance [47], and population-driven techniques assessing effects of different residuum morphologies and geometries on biomechanical measurements [20]. Extrapolation of the predictions obtained in the current study is further limited by several model simplifications and assumptions. More advanced models might be compared, considering the effects of different tissue continuum material models, multi-layered models with distinct tissue layers or discrete muscle bodies, residuum interface boundary conditions considering the influence of temperature and humidity, and personalised tissue structures and mechanical properties. This is of particular importance because the tissue injury prediction process considers strain [19], and such studies would be useful for defining more detailed pressure-strain data capturing individual variability in tissue biomechanical response to loading. The strain–time tissue damage threshold curve applied in this study relates DTI and normal pressure [16]; studies exploring the contribution of shear stress could provide a more complete assessment of contact stress effects throughout the gait cycle. In the present study, the donned case illustrated that the magnitudes of pressure and shear stresses were very low and comfortably under the tissue damage threshold, and did not tackle modelling the swing phase, with the additional simulation complexity of slightly distal directed (‘tensile’) inertial loading.
The current study is a theoretical analysis of GPC feasibility, and practical implementation may be different. GPC applies unbiased predictions in the steady state, and to improve accuracy for a physical implementation low-pass filters may be required to adequately handle additional impact of prosthetic alignment and other biomechanical gait effects, and measurement noise. This may enhance disturbance rejection by reducing input signal sensitivity to high frequency noise, and improving output prediction accuracy by eliminating bias due to past random changes [30]. Also, the control optimization parameters and constraints applied here may differ for a practical implementation due to system losses and gait effects. The study demonstrates that interface actuation performance measures can be manipulated within the GPC formulation to achieve various control objectives, and trade-offs between them. In a pathway to clinical translation, studies considering end-user feedback are required to assist in prioritizing actuation performance metrics based on comfort levels, and to perform multi-objective optimization to identify minimal values for actuation rates and pressure changes. Design validation entailing prototyping with embedded actuators, including electroactive polymers (EAPs) for example, and interface sensors is required to robustly test the described socket concept. Development studies could be extended to further evaluate GPC performance measures for variation of actuator sites, multi-modal capacity for transitioning between different locomotion modes, or within multi-level control strategies with gait recognition [48].
Conclusion
This study presents a framework for controlling a self-adjusting transtibial prosthetic socket based on minimizing an estimated residuum soft tissue injury risk. The study establishes the use of FEA to generate socket adjustment control training data for DTI risk assessment. It further demonstrates the feasibility of the GPC formulation for adaptive interface actuation control minimizing tissue injury risk in several scenarios, and the influence of a cost function optimization on actuation performance of intra-socket actuators. The presented platform could be useful for extending recent efforts in adjustable lower limb prosthetic sockets.
Appendix
See Table 3.
Table 3.
The quasi-static loads applied to the FE model representing the heel-strike, foot flat, mid stance, heel off and toe-off stages of gait identified from corresponding prosthesis loading regimes in the literature
| Reference | Load | Heel Strike (HS) | Foot Flat (FF) | Mid Stance (MS) | Heel Off (HO) | Toe Off (TO) |
|---|---|---|---|---|---|---|
| Koehler 2014 [23] | % stance | 15 | 24 | 41 | 64 | 80 |
| Fx (N) | 89.1 | 83.5 | 54.9 | − 28.4 | − 93.8 | |
| My (Nm) | 6.4 | 3.4 | − 3.8 | − 36.5 | − 58.3 | |
| Fz (N) | 716.8 | 792.9 | 791.9 | 795.7 | 924.8 | |
| Neumann 2013, S2[24] | % stance | 15 | 20 | 27 | 54 | 69 |
| Fx (N) | 39.3 | 1.5 | − 0.5 | − 3.1 | − 91.3 | |
| My (Nm) | 18.2 | 15.4 | − 0.1 | − 52.3 | − 87.5 | |
| Fz (N) | 785.1 | 892.3 | 942.9 | 830.8 | 1029.2 | |
| Neumann 2013, S3 [24] | % stance | 20 | 23 | 26 | 55 | 66 |
| Fx (N) | 3.1 | − 1.5 | − 40.6 | − 6.2 | − 107.5 | |
| My (Nm) | 15.2 | 12.3 | − 0.1 | − 47.7 | − 57.0 | |
| Fz (N) | 590.2 | 676.9 | 726.5 | 661.5 | 772.6 |
Funding
This work was supported by: FMM: the Commonwealth Scholarship Commission UK under Ref. No. CA-16–28. JWS: the University of Southampton’s EPSRC Doctoral Training Program under Ref. No. EP/M508147/1. ASD: the Royal Academy of Engineering UK under Ref. No. RF/130.
Data availability
Supporting data are openly available from the University of Southampton repository at: 10.5258/SOTON/D2032.
Declaration
Conflict of interest
None of the authors has any conflict of interest to declare.
Ethical approval
Ethics permission obtained through the University of Southampton secondary data ethics approval, references ERGO#29927 and ERGO#41476.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
F. M. Mbithi, Email: f.mbithi@soton.ac.uk
A. J. Chipperfield, Email: a.j.chipperfield@soton.ac.uk
J. W. Steer, Email: joshua.steer@soton.ac.uk
A. S. Dickinson, Email: alex.dickinson@soton.ac.uk
References
- 1.Dudek NL, Marks MB, Marshall SC, Chardon JP. Dermatologic conditions associated with use of a lower-extremity prosthesis. Arch Phys Med Rehabil. 2005;86(4):659–663. doi: 10.1016/j.apmr.2004.09.003. [DOI] [PubMed] [Google Scholar]
- 2.Oomens CWJ, Loerakker S, Bader DL. The importance of internal strain as opposed to interface pressure in the prevention of pressure related deep tissue injury. J Tissue Viability. 2010;19(2):35–42. doi: 10.1016/j.jtv.2009.11.002. [DOI] [PubMed] [Google Scholar]
- 3.Sanders JE, Youngblood RT, Hafner BJ, Ciol MA, Allyn KJ, Gardner D, et al. Residual limb fluid volume change and volume accommodation: Relationships to activity and self-report outcomes in people with trans-tibial amputation. Prosthet Orthot Int. 2018;42(4):415–427. doi: 10.1177/0309364617752983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yiǧiter K, Şener G, Bayar K. Comparison of the effects of patellar tendon bearing and total surface bearing sockets on prosthetic fitting and rehabilitation. Prosthet Orthot Int. 2002;26(3):206–212. doi: 10.1080/03093640208726649. [DOI] [PubMed] [Google Scholar]
- 5.Sanders JE, Redd CB, Cagle JC, Hafner BJ, Gardner D, Allyn KJ, et al. Preliminary evaluation of a novel bladder-liner for facilitating residual limb fluid volume recovery without doffing. J Rehabil Res Dev. 2016;53(6):1107–1120. doi: 10.1682/JRRD.2014.12.0316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sanders JE, Allyn KJ, Harrison DS, Myers TR, Ciol MA, Tsai EC. Preliminary investigation of residual-limb fluid volume changes within one day. J Rehabil Res Dev. 2012;49(10):1467–1478. doi: 10.1682/JRRD.2011.12.0236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sanders JE, Garbini JL, McLean JB, Hinrichs P, Predmore TJ, Brzostowski JT, et al. A motor-driven adjustable prosthetic socket operated using a mobile phone app: a technical note. Med Eng Phys. 2019;68:94–100. doi: 10.1016/j.medengphy.2019.04.003. [DOI] [PubMed] [Google Scholar]
- 8.Carrigan W, Nothnagle C, Savant P, Gao F, Wijesundara MBJ. Pneumatic actuator inserts for interface pressure mapping and fit improvement in lower extremity prosthetics. Conference Proceedings of IEEE RAS and EMBS ICBRB. 2016; 574–579. 10.1109/BIOROB.2016.7523687.
- 9.Mercier M, Shirley C, Stafford S, Hitzke S, Byju A, Kevorkian C, et al. Fluidic Flexible Matrix Composites for Volume Management in Prosthetic Sockets. Conference Proceedings of ASME Smart Materials, Adaptive Structures and Intelligent Systems. 2014; 46155:V002T06A015. doi:10.1115/SMASIS2014-7706.
- 10.Pirouzi G, Abu Osman NA, Oshkour AA, Ali S, Gholizadeh H, Wan Abas WAB. Development of an air pneumatic suspension system for transtibial prostheses. Sensors (Basel) 2014;14(9):16754–16765. doi: 10.3390/s140916754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Phillips VL. Socket insert having a bladder system. US; WO 2004/071337 A2, 2004.
- 12.Ogawa A, Obinata G, Hase K, Dutta A, Nakagawa M. Design of lower limb prosthesis with contact pressure adjustment by MR fluid. Conference Proceedings of IEEE EMBS. 2008; 330–333. doi:10.1109/IEMBS.2008.4649157. [DOI] [PubMed]
- 13.Greenwald RM, Dean RC, Board WJ. Volume management: smart variable geometry socket (SVGS) technology for lower-limb prostheses. J Prosthetics Orthot. 2003;15(3):107–112. doi: 10.1097/00008526-200307000-00011. [DOI] [Google Scholar]
- 14.Sengeh DM, Herr H. A variable-impedance prosthetic socket for a transtibial amputee designed from magnetic resonance imaging data. JPO. 2013;25(3):129–137. doi: 10.1097/JPO.0b013e31829be19c. [DOI] [Google Scholar]
- 15.Oomens CWJ, Bader DL, Loerakker S, Baaijens F. Pressure induced deep tissue injury explained. Ann Biomed Eng. 2015;43(2):297–305. doi: 10.1007/s10439-014-1202-6. [DOI] [PubMed] [Google Scholar]
- 16.Gefen A, van Nierop B, Bader DL, Oomens CW. Strain-time cell-death threshold for skeletal muscle in a tissue-engineered model system for deep tissue injury. J Biomech. 2008;41(9):2003–2012. doi: 10.1016/j.jbiomech.2008.03.039. [DOI] [PubMed] [Google Scholar]
- 17.Gupta S, Loh KJ, Pedtke A. Sensing and actuation technologies for smart socket prostheses. Biomed Eng Lett. 2020;10:103–118. doi: 10.1007/s13534-019-00137-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Portnoy S, Siev-Ner I, Shabshin N, Kristal A, Yizhar Z, Gefen A. Patient-specific analyses of deep tissue loads post transtibial amputation in residual limbs of multiple prosthetic users. J Biomech. 2009;42(16):2686–2693. doi: 10.1016/j.jbiomech.2009.08.019. [DOI] [PubMed] [Google Scholar]
- 19.Steer JW, Worsley PR, Browne M, Dickinson A. Key considerations for finite element modelling of the residuum–prosthetic socket interface. Prosthet Orthot Int. 2021;45(2):138–146. doi: 10.1177/0309364620967781. [DOI] [PubMed] [Google Scholar]
- 20.Steer JW, Worsley PR, Browne M, Dickinson AS. Predictive prosthetic socket design: part 1—population-based evaluation of transtibial prosthetic sockets by FEA-driven surrogate modelling. Biomech Model Mechanobiol. 2020;19(4):1331–1346. doi: 10.1007/s10237-019-01195-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Staats TB, Lundt J. The UCLA total surface bearing suction below-knee prosthesis. Clin Prosthetics Orthot. 1987;11(3):118–130. [Google Scholar]
- 22.Kobayashi T, Orendurff MS, Zhang M, Boone DA. Socket reaction moments in transtibial prostheses during walking at clinically perceived optimal alignment. Prosthet Orthot Int. 2016;40(4):503–508. doi: 10.1177/0309364615588345. [DOI] [PubMed] [Google Scholar]
- 23.Koehler SR, Dhaher YY, Hansen AH. Cross-validation of a portable, six-degree-of-freedom load cell for use in lower-limb prosthetics research. J Biomech. 2014;47(6):1542–1547. doi: 10.1016/j.jbiomech.2014.01.048. [DOI] [PubMed] [Google Scholar]
- 24.Neumann ES, Brink J, Yalamanchili K, Lee JS. Regression estimates of pressure on transtibial residual limbs using load cell measurements of the forces and moments occurring at the base of the socket. J Prosthetics Orthot. 2013;25(1):1–12. doi: 10.1097/JPO.0b013e31827b360c. [DOI] [Google Scholar]
- 25.Zhang M, Lee WCC. Quantifying the regional load-bearing ability of trans-tibial stumps. Prosthet Orthot Int. 2006;30(1):25–34. doi: 10.1080/03093640500468074. [DOI] [PubMed] [Google Scholar]
- 26.Sanders JE, Jacobsen AK, Fergason JR. Effects of fluid insert volume changes on socket pressures and shear stresses. Prosthet Orthot Int. 2006;30(3):257–269. doi: 10.1080/03093640600810266. [DOI] [PubMed] [Google Scholar]
- 27.Klute GK, Huff E, Ledoux WR. Does activity affect residual limb skin temperatures? Clin Orthop Relat Res. 2014;472(10):3062–3067. doi: 10.1007/s11999-014-3741-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Clarke DW, Mohtadi C, Tuffs PS. Generalized predictive control—Parts I and II. Automatica. 1987;23(2):137–160. doi: 10.1016/0005-1098(87)90087-2. [DOI] [Google Scholar]
- 29.Faudzi AM, Mustafa ND, Osman K, Azman MA, Suzumori K. GPC controller design for an intelligent pneumatic actuator. Procedia Eng. 2012;41:657–663. doi: 10.1016/j.proeng.2012.07.226. [DOI] [Google Scholar]
- 30.Rossiter JA. Model-based predictive control: a practical approach. Boca Raton, FL, USA: CRC Press; 2004. [Google Scholar]
- 31.Elshafei AL, Elnaggar A, Dumont G. Stability and convergence analysis of an adaptive GPC based on state space modeling. Conference Proceeings of IEEE Decision and Control. 1996; 3498–3503. doi:10.1109/CDC.1996.573711.
- 32.BS ISO 14243–1:2009. Implants for surgery—Wear of total knee-joint prostheses. Part 1: Loading and displacement parameters for wear-testing machines with load control and corresponding environmental conditions for test. 2009.
- 33.Kobayashi T, Orendurff MS, Arabian AK, Rosenbaum-Chou TG, Boone DA. Effect of prosthetic alignment changes on socket reaction moment impulse during walking in transtibial amputees. J Biomech. 2014;47(6):1315–1323. doi: 10.1016/j.jbiomech.2014.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Angeloni C, Riley PO, Krebs DE. Frequency content of whole body gait kinematic data. IEEE Trans Rehabil Eng. 1994;2(1):40–46. doi: 10.1109/86.296343. [DOI] [Google Scholar]
- 35.Portnoy S, Yizhar Z, Shabshin N, Itzchak Y, Kristal A, Dotan-Marom Y, et al. Internal mechanical conditions in the soft tissues of a residual limb of a trans-tibial amputee. J Biomech. 2008;41(9):1897–1909. doi: 10.1016/j.jbiomech.2008.03.035. [DOI] [PubMed] [Google Scholar]
- 36.Moerman KM, Solav D, Sengeh D, Herr H. Automated and data-driven computational design of patient-specific biomechanical interfaces. engrXiv Prepr. 2016. doi:10.31224/osf.io/g8h9n.
- 37.Loerakker S, Bader DL, Baaijens FPT, Oomens CWJ. Which factors influence the ability of a computational model to predict the in vivo deformation behaviour of skeletal muscle? Comput Methods Biomech Biomed Engin. 2013;16(3):338–345. doi: 10.1080/10255842.2011.621423. [DOI] [PubMed] [Google Scholar]
- 38.Ceelen KK, Stekelenburg A, Loerakker S, Strijkers GJ, Bader DL, Nicolay K, et al. Compression-induced damage and internal tissue strains are related. J Biomech. 2008;41(16):3399–3404. doi: 10.1016/j.jbiomech.2008.09.016. [DOI] [PubMed] [Google Scholar]
- 39.Linder-Ganz E, Shabshin N, Itzchak Y, Gefen A. Assessment of mechanical conditions in sub-dermal tissues during sitting: A combined experimental-MRI and finite element approach. J Biomech. 2007;40(7):1443–1454. doi: 10.1016/j.jbiomech.2006.06.020. [DOI] [PubMed] [Google Scholar]
- 40.Gerschutz MJ, Denune JA, Colvin JM, Schober G, Haynes ML, Nixon D. Technical notes on elevated vacuum suspension: amputee patient outcomes evaluating patient verbal opinion and pressure data. Ohio Willow Wood®. Mt. Sterling, OH, USA; 2011.
- 41.Bramley JL, Worsley PR, Bostan LE, Bader DL, Dickinson AS. Establishing a measurement array to assess tissue tolerance during loading representative of prosthetic use. Med Eng Phys. 2020;78:39–47. doi: 10.1016/j.medengphy.2020.01.011. [DOI] [PubMed] [Google Scholar]
- 42.Ali S, Abu Osman NA, Mortaza N, Eshraghi A, Gholizadeh H, Bin Wan Abas WAB. Clinical investigation of the interface pressure in the trans-tibial socket with Dermo and Seal-In X5 liner during walking and their effect on patient satisfaction. Clin Biomech. 2012;27(9):943–948. doi:10.1016/j.clinbiomech.2012.06.004. [DOI] [PubMed]
- 43.Mbithi FM, Chipperfield AJ, Steer JW, Dickinson AS. Predictive control for an active prosthetic socket informed by FEA-based tissue damage risk estimation. Conference Proceedings of IEEE EMBS. 2019; 2073–2076. doi:10.1109/EMBC.2019.8857155. [DOI] [PubMed]
- 44.Portnoy S, Yarnitzky G, Yizhar Z, Kristal A, Oppenheim U, Siev-Ner I, et al. Real-time patient-specific finite element analysis of internal stresses in the soft tissues of a residual limb: a new tool for prosthetic fitting. Ann Biomed Eng. 2006;35(1):120–135. doi: 10.1007/s10439-006-9208-3. [DOI] [PubMed] [Google Scholar]
- 45.Wang XQ, Mill J, Kravchuk O, Kimble RM. Ultrasound assessed thickness of burn scars in association with laser Doppler imaging determined depth of burns in paediatric patients. Burns. 2010;36(8):1254–1262. doi: 10.1016/j.burns.2010.05.018. [DOI] [PubMed] [Google Scholar]
- 46.Frauziols F, Molimard J, Navarro L, Badel P, Viallon M, Testa R, et al. Prediction of the biomechanical effects of compression therapy by finite element modeling and ultrasound elastography. IEEE Trans Biomed Eng. 2015;62(4):1011–1019. doi: 10.1109/TBME.2014.2378553. [DOI] [PubMed] [Google Scholar]
- 47.Petron A, Duval JF, Herr H. Multi-indenter device for in vivo biomechanical tissue measurement. IEEE Trans Neural Syst Rehabil Eng. 2017;25(5):426–435. doi: 10.1109/TNSRE.2016.2572168. [DOI] [PubMed] [Google Scholar]
- 48.Wolf EJ, Cruz TH, Emondi AA, Langhals NB, Naufel S, Peng GCY, et al. Advanced technologies for intuitive control and sensation of prosthetics. Biomed Eng Lett. 2020;10:119–128. doi: 10.1007/s13534-019-00127-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Supporting data are openly available from the University of Southampton repository at: 10.5258/SOTON/D2032.