Abstract
Advancement of implanted left ventricular assist device (LVAD) technology includes modern sensing and control methods to enable online diagnostics and monitoring of patients using on-board sensors. These methods often rely on a cardiovascular system (CVS) model, the parameters of which must be identified for the specific patient. Some of these, such as the systemic vascular resistance (SVR), can be estimated online while others must be identified separately. This paper describes a three-staged approach for designing a parameter identification algorithm (PIA) for this problem. The approach is demonstrated using a two-element Windkessel model of the systemic circulation (SC) with a time-varying elastance for the left ventricle (LV). A parameter identifiability stage is followed by identification using an unscented Kalman filter (UKF), which uses measurements of LV pressure (Plv), aortic pressure (Pao), aortic flow (Qa), and known input measurement of LVAD flowrate (Qvad). Both simulation and experimental data from animal experiments were used to evaluate the presented methods. By bounding the initial guess for left ventricular volume, the identified CVS model is able to reproduce signals of Plv, Pao, and Qa within a normalized root mean squared error (nRMSE) of 5.1%, 19%, and 11%, respectively, during simulations. Experimentally, the identified model is able to estimate SVR with an accuracy of 3.4% compared with values from invasive measurements. Diagnostics and physiological control algorithms on-board modern LVADs could use CVS models other than those shown here, and the presented approach is easily adaptable to them. The methods also demonstrate how to test the robustness and accuracy of the identification algorithm.
1 Introduction
According to the American Heart Association's 2020 report [1], an estimated 6.2 million American adults suffered from heart failure (HF). The report also projects the prevalence of HF to increase by 46% from 2012 to 2030. The best treatment for end-stage HF is heart transplantation, but donor hearts are limited, so mechanical circulatory devices called left ventricular assist devices (LVADs) are commonly used to support patients waiting for a donor heart (Bridge-to-Transplant) [2]. LVADs are implantable pumps that comprise an inflow cannula to intake blood from a failing left ventricle (LV), pumping through an outflow cannula to deliver blood to the aorta. This device helps ensure there is sufficient blood delivered to other organs. In some cases, LVADs can provide sufficient support until a patient's heart can recover (Bridge-to-Recovery). Alternatively, LVADs are a necessary life-saving solution for heart failure patients who are ineligible for transplantation (Destination Therapy).
As the technology of LVADs has improved and matured, opportunities for more reliable and therapeutic operation are made possible using smart sensing [3–6] and high-level control algorithms [7,8]. These advances often rely on a suitably chosen mathematical model of the cardiovascular system (CVS). Notably, it is common to approximate the systemic circulation (SC) in the CVS using Windkessel models [9,10] with the left ventricle modeled by a time-varying elastance [11]. Models of the significant hemodynamic effects are often represented using lumped-parameter hydraulic elements, often conveyed using analog electrical circuits. Key model element parameters include, for example, aortic compliance and systemic vascular resistance (SVR). Higher order models of the CVS, such as the one used in Gohean et al. [12], are of interest when a wider range of dynamics need to be studied. However, for physiological estimation and control algorithms, model complexity must be balanced with computational efficiency [13]. In recent works, even a simple two-element Windkessel model has been successfully used for physiological estimation and control [14]. Further, a natural consequence of using the aforementioned models for the design of such algorithms is the need to identify suitable model parameters for a given model using the measurements available. A higher order model could mean identification of a large number of parameters under the same measurement constraints. Not only are the values of these parameters patient-specific, but they may also vary over time [15].
Determining these parameters for a given patient can be classified as a parameter identification problem [16], either prior to or alongside the initialization and implantation of an LVAD. Real-time parameter identification of the CVS remains a challenge. One reason is that measurements needed to perform the identification procedure often require invasive sensors, which are undesirable and impractical for long-term implantation, and there has been a lack of reliable sensorless techniques [7,8,17]. On the other hand, considerable efforts have been made toward offline approaches where taking relevant measurements invasively may be acceptable. For example, these measurements could be collected during the surgical implantation procedure for the LVAD. In such a scenario, it is desirable for the offline parameter identification algorithm (PIA) to rely on a minimal set of measurements.This paper presents a three-staged approach for designing a PIA for offline identification of a CVS model. In the first stage, we study parameter identifiability to determine a subset of parameters that can be identified using available measurements. This stage can highlight the set of unidentifiable parameters using the measurements available, thereby motivating the need to secure more measurements, or to approximate their values based on acceptable ranges for the patient type. Using the insights from the first stage, the PIA is designed in the second stage where we use available measurements and inputs to estimate the identifiable parameters of the CVS using an unscented Kalman filter (UKF) based on the CVS model. Finally, the third stage comprises methods to test the performance and robustness of the algorithm. The remainder of the paper provides a demonstration of how this approach can be applied to a specific model in order to design an offline identification procedure. In particular, we demonstrate the identification of a two-element Windkessel model with available measurements of Pao, Plv, and Qa. The LVAD flowrate, Qvad, is required as an input to the CVS model and is assumed to be measured as well.
2 Background
For the purposes of modeling, the CVS can be divided into three major segments, namely, the LV, SC, and a lumped representation of the right heart and pulmonary circulation (PC). Researchers have sufficiently demonstrated the ability to identify systemic circulation parameters using measurements of aortic pressure (Pao) and aortic flow signals (Qa). Among the various methods reported in literature, we might highlight Kalman Filter-based approaches in Yu et al. [4] and the references therein, and least squares approaches compared in Avanzolini et al. [18] and the references therein. In most of these works, the PC is represented either by a constant pressure source or by a single fluid compliance. A time-varying elastance (inverse of compliance) approach to model the LV pressure (Plv) was initially proposed by Suga and Sagawa [11] and has been widely adopted. According to this approach, Plv can be calculated using the volume of blood (Vlv) inside a chamber that exhibits a time-varying elastance value. Several mathematical functions have been formulated to model this time-varying elastance, and each function has a different set of parameters. Unlike the SC, there is little consensus in the choice of this mathematical expression and the identification procedure for its parameters. Previous research has been done on use of linear regression and nonlinear least squares methods for estimating the elastance curve parameters using measurements of Plv and LV volume (Vlv) [19,20]. The use of least squares curve fitting to estimate a portion of the Plv is demonstrated in Refs. [21] and [22]. The earliest work in use of nonlinear model-based estimators to identify parameters of the time-varying elastance model for Plv generation was reported in Ref. [23] and, more recently, nonlinear optimization has been used to identify the LV function parameters using arterial pressure and cardiac output (CO) measurement in Ref. [24]. Most of these works use a specific CVS model and set of measurements, both of which could differ depending on the application of the end user. In the absence of an identifiability stage, i.e., a technique for determining whether parameters can be identified using available measurements, the applicability of these methods for a specific application is not assured.
In this paper, we address this issue by developing a systematic approach that includes an identifiability stage that can be applied to a broad range of system models and measurement sets. We investigate the use of the UKF [25] to identify a simplified model of the CVS, which can be used in sensing and control applications. The key benefits of using the UKF can be summarized as follows:
Unlike nonlinear optimization methods, there is no need to preprocess the measurement signals to remove noise.
The UKF can handle model nonlinearities in certain cases better than other Bayesian estimators such as the higher-order extended Kalman filter (EKF).
Unlike the EKF, no linear approximations (e.g., Jacobians or Hessians) of the model equations need to be calculated, thereby making the UKF more computationally efficient.
In particular, we were interested in identifying the parameters of the LV model used in Ref. [12] and in a previous work by our group on estimation of SVR [6].
3 Materials and Methods
3.1 System Model.
The choice of a CVS model affects the ability to reproduce representative physiological signals of pressures and flows. Complex models can replicate both low and high frequency dynamics found in such signals. However, when designing model-based algorithms for physiological parameter estimation and control, these models exert additional computational burden. This is undesirable for LVAD applications where the intent is to deploy these algorithms on-board microcontrollers. As discussed in Sec. 1, we can divide the CVS model into three sections of LV, SC, and PC. The CVS model used in this paper is shown in Fig. 1, conveyed using an analog electrical circuit. The LVAD is thus represented as a current source with flowrate, Qvad. Each section of this model is briefly discussed below.
Fig. 1.
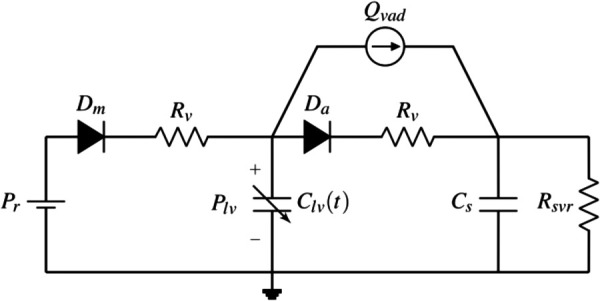
Electric analog circuit of two element model
Left ventricle model: There is wide consensus on the use of a time-varying elastance model for the LV. The choice of the mathematical expressions used for the elastance functions and Plv are key differentiators among different approaches. In this paper, we adopt a model presented in Ref. [12] that uses Eq. (1) to generate Plv,
| (1) |
Here, en represents normalized elastance, which is a function of the normalized time (tn, normalized with cardiac cycle time tc) and is parameterized with respect to the ventricular contraction time (tvc); i.e., . The variable is the difference between Vlv and the unstressed blood volume in the LV (V0), . The term Emax is the maximum elastance that occurs at peak ventricular contraction, while A and B are parameters that characterize the passive elastance exponent when the ventricle is at rest.
Systemic circulation model: For the SC, we use the two-element Windkessel representation as shown in Ref. [10] that has a single systemic capacitive element with compliance, Cs, and a fluid resistive element for SVR, Rsvr. Although this simplified representation does not capture high frequency characteristics accurately, it has demonstrated satisfactory performance for physiological estimation and control purposes [14]. In Sec. 5, we discuss the use of such a model to estimate SVR within 3.4% of its actual value.
Pulmonary circulation: The PC side of CVS is approximated as a pressure source (Pr) [4,5]. This simplifies the model by removing the dynamics of the right side of the heart and the pulmonary circulation by setting the systemic venous pressure and left atrial pressure to a constant value in the model.
Valve flows: In the CVS, the aortic valve (AV) connects the LV to the SC and the mitral valve (MV) connects the PC to the LV. Each unidirectional valve is represented by a diode with a series resistor in the circuit diagram, and a square root law is used to model the flowrate dependence on pressure drop ( ) [12]. The same resistance parameter, Rv, is used for each series resistor in this study.
All the parameters of the model presented above, referred to as CVS model hereafter, are summarized in Table 1.
Table 1.
List of parameters of the CVS model
| Parameter | Description | Units |
|---|---|---|
| Pr | Constant pulmonary circulation pressure | mmHg |
| Rv | AV and MV resistance | mmHg s/mL |
| A | Passive LV elastance | mmHg |
| B | Passive LV elastance | 1/mL |
| E max | Maximum LV elastance | mmHg/mL |
| R svr | Systemic vascular resistance | mmHg s/mL |
| Cs | Systemic compliance | mL/mmHg |
| t vc | Ventricular contraction time | s |
The main objective of this paper is to use the three-staged approach outlined earlier to design a method for identifying each of these parameters. The dynamic equations of the CVS model are summarized in state space form as follows:
| (2) |
where . The vector-valued function depends on the switching index s, which can either be 1 (representing ejection), 2 (representing filling), or 3 (representing isovolumetric contraction/expansion). For each of these modes, the definition of is given by Eqs. (4)–(6). Consequently, the dynamical system can be classified as a switched system, where the switching between different modes is based upon the state of the flow through the aortic valve, Qa, and flow through the mitral valve, Qm. Both valves cannot permit flow through them simultaneously, and this is ensured in the dynamical model by allowing only one valve to be open at a time. It is permissible for both valves to be closed simultaneously during isovolumetric contraction or expansion of LV. In this study, we assumed that the measurement of Qa is available while Qm is estimated by the UKF. Both of these are used to determine the mode according to Eq. (3).
| (3) |
| (4) |
| (5) |
| (6) |
3.2 Parameter Identifiability.
The CVS model presented above has eight parameters that need to be identified, as summarized in Table 1. We assume that the available measurements are Plv, Pao, and Qa, each of which can be expressed as a function of CVS model states, parameters and inputs appearing in Eq. (2). The input to the CVS model, Qvad, is also assumed to be known. Further, the measurement of the central venous pressure (Pcvp) is available, but omitted during the parameter identifiability study since it is approximated in our model using a constant pressure source (Pr). As will be shown, this measurement can be used to calculate the value of Rsvr.
In this section, we demonstrate the use of parameter identifiability in the first stage of our approach, to highlight a subset of CVS model parameters that can be identified using available measurements. When such a study is done early during the design of the identification algorithm, it helps identify parameters that will need approximation, and may justify the need for additional measurements. For the CVS model represented by equation set (2), we investigate if the available measurements can be used to identify most, if not all, of the parameters. A parameter is identifiable if the outputs of the model are sensitive to changes in the value of that parameter [26]. We use the approach proposed by Yao et al. [27] where the CVS model is simulated with nominal parameter values within the physiologically expected range. Available measurements are used to construct a sensitivity matrix to highlight the most identifiable parameter. A residual is calculated iteratively for the remaining parameters which ranks them based on their identifiability. An advantage of this approach over nonlinear observability is the ability to highlight unidentifiable parameters, i.e., parameters with a low residual, which can then be approximated or estimated indirectly.
The CVS model shown here comprises three modes as outlined in Sec. 3. Consequently, parameter identifiability is analyzed for each of them, namely, ejection, filling, and isovolumic contraction/expansion. Table 2 summarizes parameters in descending order of identifiability for each mode and includes their residual values. Based on parameter identifiability, the following decisions are made:
Table 2.
Descending order of parameter identifiability (residual is calculated for parameters following the most identifiable one)
| Ejection | Filling | Isovolumic | |||
|---|---|---|---|---|---|
| Parameter | Residual | Parameter | Residual | Parameter | Residual |
| B | — | E max | — | E max | — |
| E max | 39.21 | B | 136.45 | B | 207.54 |
| Pr | 6.89 | Rv | 20.10 | Rv | 96.58 |
| A | 0.38 | A | 9.74 | A | 9.41 |
| Cs | 0.5 | Cs | 3.35 | ||
| R svr | 2.05 | ||||
| Pr | 0.41 | ||||
During systole (combination of Isovolumic contraction and Ejection), B and Emax are identified.
During diastole (combination of Isovolumic expansion and Filling), the values of B and Emax estimated from systole are used, and A is identified.
Both Pr and Rv are ranked lower during Ejection and Filling. During Filling, although Rv is ranked above A, we failed to reliably identify this parameter in simulation tests. Consequently, we choose to not identify Pr and Rv using Eq. (2).
It is not possible to identify Cs when using the complete CVS model (Eq. (2)) with available measurements.
The identifiability study reveals that four of the eight parameters, namely, Pr, Rsvr, Cs, and tvc cannot be identified using Eq. (2) with the available measurements. The identification of these parameters must be done using a different model, or indirectly; the process for which is addressed shortly. The value of tvc and Pr can be approximated using the Plv measurement heuristically as follows:
The heart rate (HR) can be determined by identifying the peaks in the Plv measurement waveform. The estimation of HR becomes easier if an electrocardiogram trace is available. An equation that relates HR to tvc, such as the one presented in Ref. [12] or Ref. [28] can then be used to approximate its value. If these values do not result in satisfactory identification of other parameters, then the Plv waveform can be graphically analyzed to approximate tvc. During simulation experiments, we were able to approximate tvc using the equation from Ref. [12]. However, we had to graphically approximate tvc during experimental tests. In both cases, identification of other parameters was satisfactory.
The value of Pr can be approximated as the left ventricle pressure at the onset of ventricular contraction, and this value can be tuned heuristically as needed. This approach worked well for us in both simulation and experimental tests.
The value of Rsvr can be approximated using the standard relation, , where Pmap is the mean arterial pressure, Pcvp is the mean central venous pressure, and CO is the cardiac output. The value of Pcvp is usually small ( mmHg) compared to Pmap, and can be approximated if Pcvp is not available for measurement.
To identify Cs, we can use the SC portion of the CVS model, hereby termed as SC model. The state dynamics comprise a system with a single differential equation,
| (7) |
Parameter identifiability confirms that measurements of Pao and Qa can be used with this equation to identify Cs. Additionally, Rv is also revealed to be identifiable using this model, and we thus omit it from the list of parameters to identify using the previous model (2). This is consistent with the findings of previous works on the identification of SC as discussed in Ref. [4]. Section 3.3 outlines the second stage of our approach, where an algorithm is designed to sequentially estimate identifiable parameters and approximate the others.
3.3 Parameter Identification Algorithm.
This section describes the algorithm used to identify or approximate all of the eight parameters of the CVS model. The algorithm comprises four steps that are briefly described as follows. A block diagram of the algorithm is shown in Fig. 2 as well.
Fig. 2.
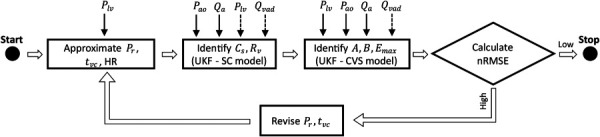
Algorithm used for parameter identification of CVS model. Solid lines on top of the boxes represent signals provided as measurements and dashed lines represent signals provided as inputs. The high and low limits for nRMSE can be manually set.
Step 1: Using the Plv waveform, approximate the value of Pr and tvc as described in Sec. 3.2.
Step 2: Using the values of Pr and tvc from step 1, perform identification of Cs and Rv using a UKF based on the SC model (7) with measurements of Pao and Qa.
Step 3: Values identified or approximated from steps 1 and 2 are used to perform identification of A, B, and Emax using a UKF based on the CVS model (Eq. (2)) with measurements of Plv, Pao, and Qa. As discussed in Sec. 3.2, within each cardiac cycle B and Emax are first identified during systole, and A is identified during diastole. The mode of the system is determined using equation (3). To avoid erroneous switching, we pass the Qa signal through a lowpass filter with a cutoff frequency of 30 Hz.
Step 4: The identified CVS model is simulated using matlab R2019b (The MathWorks, Inc., Natick, Massachusetts), and the normalized root mean squared error (nRMSE) is calculated between simulated and measured signals of Plv, Pao, and Qa. If the nRMSE is satisfactory, the identified model can be used as a basis for other physiological algorithms. If the nRMSEs are not satisfactory, steps 1–4 are repeated with adjusted values of Pr and tvc in step 1. Our study deemed nRMSEs as satisfactory when the identified model could estimate SVR with accuracy 10%.
Unscented Kalman filter for model based identification: The identification of parameter sets {Cs, Pr} and { } is performed recursively using a UKF that is based on the system models from Eqs. (2) and (7), respectively. The system states for both cases are augmented with the unknown parameters to form an augmented state vector. Zero dynamics are assumed for the parameter states, as they are assumed to remain constant over the period of observation. A compact form of the UKF equations is provided in Table 3. The scaling parameters of the UKF were set as . A detailed discussion of the UKF can be found in Ref. [25].
Table 3.
UKF Equations based on a discretized system and measurement model
3.4 Description of Tests.
As a description of the third and final stage of our approach, this section summarizes how results from simulations and from animal experiments were used to evaluate the performance and robustness of the PIA. In both simulations and experiments, it is assumed that measurements of Plv, Pao, Qa, and Qvad are available.
Simulations: Simulations were conducted using a CVS with 12 dynamic states [12], providing a richer dynamic dataset to be analyzed with the simplified models used for estimation. The 12 state model was numerically solved with Euler integration using a step size of 1 μs, and Gaussian white noise was added to the relevant signals. This model is referred to as the computational model hereafter.
Data from animal experiments: Our study makes use of data collected during acute animal experiments conducted by Windmill Cardiovascular Systems, Inc. (Austin, TX) in an animal laboratory at UTHealth-Houston. An anesthetized calf was implanted with a pulsatile TORVADTM (Windmill Cardiovascular Systems, Inc., Austin, Texas) system, an LVAD under development. The TORVADTM was operated in synchronous mode, delivering a mean flowrate of 1.9 L/min. LVAD pump blood flow was measured with an ultrasonic flow probe attached to the pump inflow cannula (ME11PXL Transonic Systems Inc, Ithaca, NY). The pressure and flow sensors used in the acute experiments follow methods as in Ref. [29]. The internal carotid and jugular veins were exposed, and central venous pressure was measured via the left internal jugular vein. Left atrial pressure (Pla) was measured with a fluid-filled pressure transducer (Becton Dickinson DTX Plus transducer, ref 682018, Becton Dickinson Infusion Therapy Systems, Sandy, UT) via a catheter placed in the left atrial appendage. Left ventricular pressure (Plv) was measured with a Millar catheter (model SPR-524 3.5F Mikro-tip Millar Instruments, Inc., Houston, TX) placed near the LV apex through a 4F sheath. Aortic pressure (Pao) was measured with a Millar catheter placed in the ascending aorta. Aortic blood flow (Qa) was measured with a 20 mm perivascular ultrasonic flow probe at the base of the aorta (MA20PAX, Transonic Systems Inc, Ithaca, NY).
Data testing: Three tests were conducted using the data generated from simulations and collected during the animal experiment.
Test I: To evaluate the performance of the parameter identification algorithm, it was applied to three data sets. The first two data sets were generated by simulating the 12-state computational model with its parameters set to mimic a healthy patient and one with critical heart failure. Parameter values chosen to represent each patient state were taken from Ref. [12]. The third data set was taken from the acute animal experiment database. For each run of the algorithm, the estimated parameters were plotted against time to observe convergence, and the nRMSE of the identified CVS model was compared to the measured data.
Test II: The true values of , and Rv were sampled from a uniform distribution with a range of ±20% of the base values taken from Ref. [12], and used to generate noisy data by simulating the computational model. A total of 100 data sets representative of a healthy patient, and 100 representative of one with critical heart failure were generated. Since the approximation of Pr and tvc requires visual inspection of the Plv waveform, the values of these two parameters were fixed for the healthy and heart failure cases. In order to maintain the same value of tvc, HR was not varied. For all healthy cases, the value of was set to 150 mL and for all heart failure cases, it was set to 250 mL. For each data set, the parameter identification algorithm was applied and the mean and standard deviation in the errors of estimated parameters was calculated. Additionally, the correlation between true and estimated parameter values was calculated.
Test III: The parameter identification algorithm presented in this paper requires an initial guess of . The value of this initial guess was varied to evaluate convergence and nRMSE of the identified CVS model during simulations of healthy and heart failure patient.
4 Results
Test I: For each of the three data sets, the parameter identification algorithm was applied to first approximate the value of Pr and tvc, and then to recursively estimate the values of {Cs, Rv} and { }. A plot of the recursive parameter estimates versus time is shown for the heart failure and animal experiment data sets in Figs. 3 and 4, respectively. The figures also compare the signals generated from the identified CVS model to the measured signals. Table 4 summarizes identified parameters and nRMSEs for each dataset.
Fig. 3.
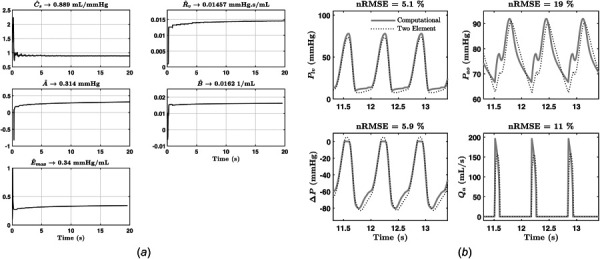
Results from heart failure patient simulation: (a) estimated parameters versus time and (b) nRMSE of signals generated from identified model versus simulation
Fig. 4.
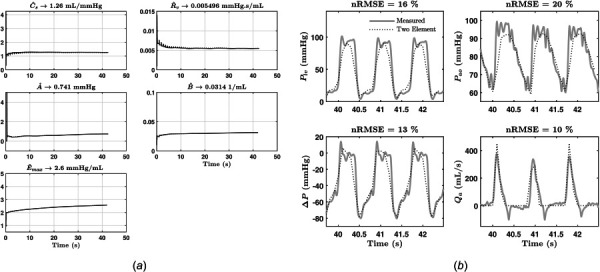
Results from animal experiment: (a) estimated parameters versus time and (b) nRMSE of signals generated from identified model versus measured during animal experiment
Table 4.
Summary of results from test I
| Healthy | Heart failure | Experiment | |||
|---|---|---|---|---|---|
| Actual | Estimate | Actual | Estimate | Estimate | |
| A (mmHg) | 0.03 | 0.0252 | 0.18 | 0.314 | 0.741 |
| B (1/mL) | 0.05 | 0.0492 | 0.016 | 0.016 | 0.0314 |
| Emax (mmHg/mL) | 3.25 | 3.2 | 0.3 | 0.34 | 2.6 |
| Cs (mL/mmHg) | 1.25 | 1.31 | 0.65 | 0.889 | 1.26 |
| Rv (mmHg s/mL) | 0.0025 | 0.00479 | 0.0025 | 0.015 | 0.0055 |
| Rsvr (mmHg s/mL) | 0.975 | 0.9748 | 1.075 | 1.0752 | 0.7684 |
| Pr (mmHg) | — | 3 | — | 13.8 | 18 |
| tvc (s) | — | 0.41 | — | 0.39 | 0.6 |
| nRMSE Plv | 1.77% | 5.1% | 16.45% | ||
| nRMSE Pao | 15.28% | 19% | 20.4% | ||
| nRMSE Qa | 6.76% | 11% | 10.48% | ||
Test II: The errors in identifying each of , and Rv were collected for all 200 runs, and the mean values ( ) and standard deviations (σe) were calculated. Additionally, the linear correlation between actual parameters (R2) and identified parameters was calculated. The parameters Pr and tvc were excluded from this analysis because for each case (healthy and heart failure), a fixed value was assigned to them as described in Sec. 3.4. Table 5 summarizes all resulting statistics.
Table 5.
Summary of results from test II
| A (mmHg) | 0.1402 | 0.197 | 0.39 |
| B (1/mL) | 0.0026 | 0.006 | 0.87 |
| Emax (mmHg/mL) | 0.0488 | 0.085 | 0.99 |
| Cs (mmHg/mL) | 0.1578 | 0.087 | 0.98 |
| Rv (mmHg/mL) | 0.0074 | 0.005 | 0.003 |
Test III: The initial guess for was varied between 130 to 155 mL for the healthy case and 202 to 247 mL for the heart failure case to give a total of 50 test runs of the parameter identification algorithm. For each test run, the identified CVS model was simulated and its outputs, namely, Plv, Pao, and Qa, were compared to the corresponding signals generated from the computational model. The nRMSE of these outputs from each test run was analyzed to calculate the mean and standard deviation. These statistics are summarized in Table 6.
Table 6.
Summary of results from test III
| Signal | Mean nRMSE (%) | Standard deviation of nRMSE (%) |
|---|---|---|
| P lv | 4.67 | 1.06 |
| P ao | 20.72 | 3 |
| Qa | 9.32 | 1.37 |
5 Discussion
The objective of Test I was to study the performance of the PIA in terms of convergence time and identification accuracy. As shown in Fig. 2, the first step of the identification procedure involves visually inspecting the Plv waveform to determine an approximate value of Pr and tvc. After completing the identification of , and Emax, the PIA is terminated if nRMSEs are satisfactory. In order to determine what can be considered satisfactory for the nRMSEs, we used the identified parameters for the animal experiment data for the CVS model, and performed SVR estimation based on this model as shown in Ref. [6]. We were able to achieve an estimation accuracy of %. The satisfactory accuracy of SVR estimation indicates the sufficiency of the nRMSE values shown for the animal experiment dataset. Similar, if not lower, values of nRMSE were achieved for the healthy and heart failure data sets, and all data sets showed convergence within 20 s.
Test II was used to study the robustness of PIA. Over the 200 test cases, there was good correlation between identified and true values for the parameters Emax and Cs. Parameters A and B are weakly correlated to the true values, and Rv was not correlated to its true value. All 200 runs resulted in stable convergence of the parameters. These results indicate that Rv is the least sensitive of the identified parameters, but is identified in a stable manner nevertheless and the overall identified CVS model satisfactorily replicates the measured signals and can be used for accurate SVR estimation. A possible reason for the poor correlation of Rv is the absence of an inertial element in the CVS model used for this paper. In the more complex computational model, inductors represent inertial effects in the systemic circulation and in the absence of these model elements, it may fall upon Rv to try and compensate for those effects, thereby departing from the true value.
The PIA presented in this paper relies upon an initial guess for . In the absence of a measurement of Vlv, the identified CVS model is nonunique. This fact was discussed in Ref. [23], and was confirmed through Test III. When the initial guess for was varied, the identified values for A and B changed such that the final nRMSE of the identified CVS model was similar for all runs with a maximum standard deviation in nRMSE observed at 5.5% for Qa. Parameters A and B directly affect Plv generated from the CVS model, and these two parameters appear to compensate for different values of .
The primary motivation of this work was to outline a three-staged approach for designing a PIA and to demonstrate this for a specific model. Of the three stages, the first stage of parameter identifiability can help plan for data collection before, during and after the LVAD implantation procedure. Section 3.2 demonstrates the utility of this stage in highlighting unidentifiable parameters that needed approximation, and in clinical scenarios, this insight could guide the inclusion or exclusion of measurements from the LVAD recipient in advance.
6 Conclusions
As the technology for LVADs improves and their reliability increases, researchers are investigating the use of on-board physiological control and estimation algorithms. For model-based algorithms, identification of these models becomes a necessary step before LVAD implantation. These models often trade fidelity for low computational burden and thus are lower order. The identification procedure must serve to initialize this model so that the end goal of physiological estimation/control is met with satisfactory accuracy. This paper presents a systematic three-staged approach to solving the parameter identification problem that can be applied to a variety of scenarios.
Depending on the available measurements, the parameter identifiability step can help isolate those parameters of the chosen model basis, which need to be approximated.
Once identifiable parameters have been selected, we demonstrate the use of the UKF for parameter identification. Due to its ability to handle nonlinear dynamics without using Jacobians and Hessians, the UKF can be adapted to different models and measurements with satisfactory performance.
Finally, the paper demonstrates how to test the performance and robustness of the PIA. In particular, the nRMSE tests could ensure that the identified CVS model is able to reproduce the measurement signals so that final physiological control/estimation accuracy is satisfactory.
In the future, we plan to compare the performance of the UKF with a second-order EKF. In this paper, we visually study the Plv waveform to fix values of Pr and tvc. A possible extension of the work could investigate ways of automating this procedure, possibly leading to improved identification accuracy.
Acknowledgment
Research reported in this publication was supported by the National Heart, Lung, and Blood Institute (NHLBI) of the National Institutes of Health (NIH) under Award No. R44HL142432 (Funder ID: 10.13039/100000002). The experiments at UTHealth-Houston were conducted with and directed by collaborator Dr. Richard W. Smalling, Cardiology Division, UTHealth-Houston.
References
- [1]. Virani, S. S. , Alonso, A. , Benjamin, E. J. , Bittencourt, M. S. , Callaway, C. W. , Carson, A. P. , Chamberlain, A. M. , et al., 2020, “ Heart Disease and Stroke Statistics—2020 Update: A Report From the American Heart Association,” Circulation, 141(9), pp. E139–E596. 10.1161/CIR.0000000000000757 [DOI] [PubMed] [Google Scholar]
- [2]. Prinzing, A. , Herold, U. , Berkefeld, A. , Krane, M. , Lange, R. , and Voss, B. , 2016, “ Left Ventricular Assist Devices—Current State and Perspectives,” J. Thorac. Dis., 8(8), pp. E660–E666. 10.21037/jtd.2016.07.13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3]. Ruchti, T. L. , Brown, R. H. , Jeutter, D. C. , and Feng, X. , 1993, “ Identification Algorithm for Systemic Arterial Parameters With Application to Total Artificial Heart Control,” Ann. Biomed. Eng., 21(3), pp. 221–236. 10.1007/BF02368178 [DOI] [PubMed] [Google Scholar]
- [4]. Yu, Y. C. , Boston, R. , Simaan, M. A. , and Antaki, J. F. , 2001, “ Minimally Invasive Estimation of Systemic Vascular Parameters,” Ann. Biomed. Eng., 29(7), pp. 595–606. 10.1114/1.1380420 [DOI] [PubMed] [Google Scholar]
- [5]. Wu, Y. , Allaire, P. E. , Tao, G. , and Olsen, D. , 2007, “ Modeling, Estimation, and Control of Human Circulatory System With a Left Ventricular Assist Device,” IEEE Trans. Control Syst. Technol., 15(4), pp. 754–767. 10.1109/TCST.2006.890288 [DOI] [Google Scholar]
- [6]. Rapp, E. S. , Pawar, S. R. , Gohean, J. R. , Larson, E. R. , Smalling, R. W. , and Longoria, R. G. , 2019, “ Estimation of Systemic Vascular Resistance Using Built-In Sensing From an Implanted Left Ventricular Assist Device,” ASME J. Eng. Sci. Med. Diagn. Ther., 2(4), p. 041008. 10.1115/1.4045204 [DOI] [Google Scholar]
- [7]. AlOmari, A.-H. H. , Savkin, A. V. , Stevens, M. , Mason, D. G. , Timms, D. L. , Salamonsen, R. F. , and Lovell, N. H. , 2013, “ Developments in Control Systems for Rotary Left Ventricular Assist Devices for Heart Failure Patients: A Review,” Physiol. Meas., 34(1), pp. R1–R27. 10.1088/0967-3334/34/1/R1 [DOI] [PubMed] [Google Scholar]
- [8]. Pauls, J. P. , Stevens, M. C. , Bartnikowski, N. , Fraser, J. F. , Gregory, S. D. , and Tansley, G. , 2016, “ Evaluation of Physiological Control Systems for Rotary Left Ventricular Assist Devices: An In-Vitro Study,” Ann. Biomed. Eng., 44(8), pp. 2377–2387. 10.1007/s10439-016-1552-3 [DOI] [PubMed] [Google Scholar]
- [9]. Noordergraaf, A. , 1978, Circulatory System Dynamics, Academic Press, New York. [Google Scholar]
- [10]. Westerhof, N. , Lankhaar, J. W. , and Westerhof, B. E. , 2009, “ The Arterial Windkessel,” Med. Biol. Eng. Comput., 47(2), pp. 131–141. 10.1007/s11517-008-0359-2 [DOI] [PubMed] [Google Scholar]
- [11]. Suga, H. , and Sagawa, K. , 1974, “ Instantaneous Pressure-Volume Relationships and Their Ratio in the Excised, Supported Canine Left Ventricle,” Circ. Res., 35(1), pp. 117–126. 10.1161/01.RES.35.1.117 [DOI] [PubMed] [Google Scholar]
- [12]. Gohean, J. R. , George, M. J. , Pate, T. D. , Kurusz, M. , Longoria, R. G. , and Smalling, R. W. , 2013, “ Verification of a Computational Cardiovascular System Model Comparing the Hemodynamics of a Continuous Flow to a Synchronous Valveless Pulsatile Flow Left Ventricular Assist Device,” ASAIO J., 59(2), pp. 107–116. 10.1097/MAT.0b013e31827db6d4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Avanzolini, G. , Barbini, P. , Cappello, A. , and Massai, M. R. , 1989, “ Sensitivity Analysis of the Systemic Circulation With a View to Computer Simulation and Parameter Estimation,” J. Biomed. Eng., 11(1), pp. 43–47. 10.1016/0141-5425(89)90164-7 [DOI] [PubMed] [Google Scholar]
- [14]. Parlikar, T. A. , Heldt, T. , Ranade, G. V. , and Verghese, G. C. , 2007, “ Model-Based Estimation of Cardiac Output and Total Peripheral Resistance,” 2007 Computers in Cardiology, Durnham, NC, Sept. 30–Oct. 3, pp. 379–382. 10.1109/CIC.2007.4745501 [DOI] [Google Scholar]
- [15]. Vandenberghe, S. , Segers, P. , Steendijk, P. , Meyns, B. , Dion, R. A. , Antaki, J. F. , and Verdonck, P. , 2006, “ Modeling Ventricular Function During Cardiac Assist: Does Time-Varying Elastance Work?,” ASAIO J., 52(1), pp. 4–8. 10.1097/01.mat.0000196525.56523.b8 [DOI] [PubMed] [Google Scholar]
- [16]. Lennart, L. , 1999, System Identification: Theory for the User, PTR Prentice Hall, Upper Saddle River, NJ, pp. 1–14. [Google Scholar]
- [17]. Boston, J. R. , Antaki, J. F. , and Simaan, M. A. , 2003, “ Hierarchical Control of Heart-Assist Devices,” IEEE Rob. Autom. Mag., 10(1), pp. 54–64. 10.1109/MRA.2003.1191711 [DOI] [Google Scholar]
- [18]. Avanzolini, G. , Barbini, P. , and Cappello, A. , 1992, “ Comparison of Algorithms for Tracking Short-Term Changes in Arterial Circulation Parameters,” IEEE Trans. Biomed. Eng., 39(8), pp. 861–867. 10.1109/10.148394 [DOI] [PubMed] [Google Scholar]
- [19]. Shishido, T. , Hayashi, K. , Shigemi, K. , Sato, T. , Sugimachi, M. , and Sunagawa, K. , 2000, “ Single-Beat Estimation of End-Systolic Elastance Using Bilinearly Approximated Time-Varying Elastance Curve,” Circulation, 102(16), pp. 1983–1989. 10.1161/01.CIR.102.16.1983 [DOI] [PubMed] [Google Scholar]
- [20]. Clark, J. W. , Ling, R. Y. , Srinivasan, R. , Cole, J. S. , and Pruett, R. C. , 1980, “ A Two-Stage Identification Scheme for the Determination of the Parameters of a Model of Left Heart and Systemic Circulation,” IEEE Trans. Biomed. Eng., 27(1), pp. 20–29. 10.1109/TBME.1980.326687 [DOI] [PubMed] [Google Scholar]
- [21]. Chang, K.-C. , and Kuo, T.-S. , 1997, “ Single-Beat Estimation of the Ventricular Pumping Mechanics in Terms of the Systolic Elastance and Resistance,” J. Theor. Biol., 189(1), pp. 89–95. 10.1006/jtbi.1997.0498 [DOI] [PubMed] [Google Scholar]
- [22]. Sunagawa, K. , Yamada, A. , Senda, Y. , Kikuchi, Y. , Nakamura, M. , Shibahara, T. , and Nose, Y. , 1980, “ Estimation of the Hydromotive Source Pressure From Ejecting Beats of the Left Ventricle,” IEEE Trans. Biomed. Eng., 27(6), pp. 299–305. 10.1109/TBME.1980.326737 [DOI] [PubMed] [Google Scholar]
- [23]. Deswysen, B. A. , 1977, “ Parameter Estimation of a Simple Model of the Left Ventricle and of the Systemic Vascular Bed, With Particular Attention to the Physical Meaning of the Left Ventricular Parameters,” IEEE Trans. Biomed. Eng., 24(1), pp. 29–38. 10.1109/TBME.1977.326205 [DOI] [PubMed] [Google Scholar]
- [24]. Guarini, M. , Urzua, J. , Cipriano, A. , and Gonzalez, W. , 1998, “ Estimation of Cardiac Function From Computer Analysis of the Arterial Pressure Waveform,” IEEE Trans. Biomed. Eng., 45(12), pp. 1420–1428. 10.1109/10.730436 [DOI] [PubMed] [Google Scholar]
- [25]. Wan, E. A. , and Van Der Merwe, R. , 2000, “ The Unscented Kalman Filter for Nonlinear Estimation,” Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, Oct. 4, pp. ; 153–158. 10.1109/ASSPCC.2000.882463 [DOI] [Google Scholar]
- [26]. Grewal, M. , and Glover, K. , 1976, “ Identifiability of Linear and Nonlinear Dynamical Systems,” IEEE Trans. Autom. Control, 21(6), pp. 833–837. 10.1109/TAC.1976.1101375 [DOI] [Google Scholar]
- [27]. Yao, K. Z. , Shaw, B. M. , Kou, B. , McAuley, K. B. , and Bacon, D. W. , 2003, “ Modeling Ethylene/Butene Copolymerization With Multi-Site Catalysts: Parameter Estimability and Experimental Design,” Polym. React. Eng., 11(3), pp. 563–588. 10.1081/PRE-120024426 [DOI] [Google Scholar]
- [28]. Yu, Y. C. , 1998, “ Minimally Invasive Estimation of Cardiovascular Parameters,” Ph.D. thesis, University of Pittsburgh, Pittsburgh, PA. [Google Scholar]
- [29]. Letsou, G. V. , Pate, T. D. , Gohean, J. R. , Kurusz, M. , Longoria, R. G. , Kaiser, L. , and Smalling, R. W. , 2010, “ Improved Left Ventricular Unloading and Circulatory Support With Synchronized Pulsatile Left Ventricular Assistance Compared With Continuous-Flow Left Ventricular Assistance in an Acute Porcine Left Ventricular Failure Model,” J. Thorac. Cardiovasc. Surg., 140(5), pp. 1181–1188. 10.1016/j.jtcvs.2010.03.043 [DOI] [PubMed] [Google Scholar]


