Kingdom-Wide Analysis of Fungal Protein-Coding and tRNA Genes Reveals Conserved Patterns of Adaptive Evolution

Abstract

Protein-coding genes evolved codon usage bias due to the combined but uneven effects of adaptive and nonadaptive influences. Studies in model fungi agree on codon usage bias as an adaptation for fine-tuning gene expression levels; however, such knowledge is lacking for most other fungi. Our comparative genomics analysis of over 450 species supports codon usage and transfer RNAs (tRNAs) as coadapted for translation speed and this is most likely a realization of convergent evolution. Rather than drift, phylogenetic reconstruction inferred adaptive radiation as the best explanation for the variation of interspecific codon usage bias. Although the phylogenetic signals for individual codon and tRNAs frequencies are lower than expected by genetic drift, we found remarkable conservation of highly expressed genes being codon optimized for translation by the most abundant tRNAs, especially by inosine-modified tRNAs. As an application, we present a sequence-to-expression neural network that uses codons to reliably predict highly expressed transcripts. The kingdom Fungi, with over a million species, includes many key players in various ecosystems and good targets for biotechnology. Collectively, our results have implications for better understanding the evolutionary success of fungi, as well as informing the biosynthetic manipulation of fungal genes.

Introduction

The billion-year-old kingdom Fungi, comprising at least 1.5 million species, is deeply intertwined with the diversification and maintenance of terrestrial ecosystems (Berbee et al. 2017). Paleobotanical studies owe the successful colonization of land by primitive plants—resulting in the greening of the Earth that facilitated the evolution of more complex animal forms—to their mutualistic symbioses with soil fungi (Field et al. 2015). Indeed, 90% of extant plant species still rely on mycorrhizal fungi for nutrient uptake and resistance to pathogens and abiotic stressors (Chen et al. 2018). Many fungi are also pathogens of plants, fungi, and animals, and pose an emerging medical threat to humans (Janbon et al. 2019). The diversity of fungal bioproducts is leveraged in biotechnology to manufacture commercial enzymes, medicines, and even biofuel (Seppälä et al. 2017). Therefore, a comprehensive understanding of the evolution of fungal genomes and traits is valuable to several applications.

Codon usage analysis is an established framework for studying the evolution of protein-coding genes. Although the genetic code assigns 61 mRNA codons to 20 amino acids, most organisms have evolved an unequal representation of synonymous codons, or codon usage bias. The widely accepted mutation-selection-drift theory posits that codon usage bias is generated by evolutionary forces that imprinted nonadaptive (neutral) and adaptive mutations at the silent sites within coding sequences (Grantham 1980; Bulmer 1991). But far from being silent, functional studies in model fungal systems such as Neurospora crassa and Saccharomycescerevisiae (baker’s yeast) demonstrates how the influence of synonymous mutations percolates through all layers of gene expression, from mRNA transcription (Zhao et al. 2021), steady-state mRNA levels (Sharp and Li 1987), mRNA stability (Presnyak et al. 2015), elongation rate of protein synthesis (Tuller et al. 2010), and cotranslational protein folding (Pechmann and Frydman 2013).

Because transfer RNAs (tRNAs) universally translate codons to amino acids during protein synthesis, codon usage variation within genomes may reflect selection for balancing codon demand with tRNA supply in order to fine-tune mRNA translation (Hershberg and Petrov 2008). Ideally, for each of the 61 sense codons, there should be 61 distinct tRNA anticodon types. However, species usually lack the full complement of tRNA types because tRNAs often engage in wobble decoding (Marck and Grosjean 2002). Moreover, the genomic dosage of different tRNAs takes on a dynamic range, from single copy to even hundreds of identical or near-identical copies within the same genome. This imbalance in the supply decoding tRNAs among synonymous codons establishes the selective pressure that underlies adaptive codon usage bias in several species, including S.cerevisiae (Ikemura 1982). Indeed, a hallmark of adaptive codon usage bias is the preference of highly abundant mRNAs for translationally optimal codons that are decoded by abundant tRNAs (Sharp et al. 2010; Novoa et al. 2012). Therefore, disentangling the signals of neutral and adaptive forces on codon usage offers insight into the evolutionary processes that contribute to the fitness and biodiversity of species (Novoa et al. 2019). However, outside of model species, codon usage patterns across the fungal phylogeny remain largely uncharacterized.

Comparative studies aim to disentangle the trait variation due to shared ancestry versus adaptation. Because of common descent, phenotypic traits from closely related species are likely to violate the identically and independently distributed requirement of standard regression tests which risks an increase in type I errors. Phylogenetic comparative methods (PCMs) are regression algorithms that were developed to account for phylogenetic signal in comparative trait data (Felsenstein 1985). Phylogenetic signal is the tendency of closely related species to exhibit greater similarities in traits than other species when sampled randomly from the same phylogenetic tree. The strength and direction of the phylogenetic signal are used to infer whether trait variation exhibits signs of evolution due to genetic drift, stabilizing selection, divergent, or convergent evolution (Pagel 1999; Blomberg et al. 2003). PCMs have been applied to interrogate macroevolutionary questions, such as the evolution of fungal modes of nutrition (James 2006), evolution of physiological and behavioral traits in primates (Kamilar and Cooper 2013), plant-pollinator coevolution (Smith 2010), and trait evolution by adaptive radiation in reptiles and avians (Pincheira-Donoso et al. 2015; McEntee et al. 2018). However, the application of PCMs is rather limited in cross-species codon usage studies (Sharp et al. 2010; LaBella et al. 2019). Recent large-scale sequencing projects have advanced our understanding of fungal phylogeny (Grigoriev et al. 2014; Ahrendt et al. 2018), thereby broadening the scope for comparative studies.

Here, we aimed to detail the evolutionary and functional underpinnings of codon usage variation in Kingdom Fungi by analyzing coding sequences and tRNA data from over 450 representative species that are distributed across 18 taxonomic classes and six major phyla (Spatafora et al. 2017). Principal component analysis (PCA) of codon usage frequencies effectively separated the species into respective subkingdoms, with the rare codons AUA^Ile and GGG^Gly driving the codon-specific variation. Using phylogenetic reconstruction methods, we inferred the evolutionary processes, including adaptive mechanisms that explain change in codon usage and tRNA patterns over time. We also performed genome-level analyses to examine the relationship between codon usage, tRNA supply, and gene expression levels. Phylogenetic signals of codon frequencies and genomic tRNA abundance were weaker than expected by genetic drift and phylogenetic relatedness. Yet, most genomes converged toward translation bias, wherein the most abundant mRNAs are enriched with codons for major tRNAs, in contrast to the low abundant mRNAs having greater codon bias for minor tRNAs. Finally, given the prevalence of adaptive codon usage, we present a neural network, Codon2Vec, that directly takes the coding sequences as input to reliably predict expression (median accuracy of 83.8% ±0.05). Altogether, our results support that natural selection for the efficiency of mRNA translation is a conserved influence among fungi.

Results

Adaptative Radiation Best Explains the Macroevolution of Codon Usage Bias

We obtained predicted protein-coding and tRNA genes from 459 species sampled from six out of the eight recognized fungal phyla (Materials and Methods). Namely, 57 species belonging to the four early-diverging phyla of Chytridiomycota, Blastidiomycota, Zoopagomycota, Mucoromycota, and 402 species from the two dikarya phyla Basidiomycota and Ascomycota. Dikarya is the more species-rich subkingdom comprising 98% of all fungi—but 90% of our data set—and is characterized by a more complex sexual lifecycle (Stajich et al. 2009).

Codon Usage Bias Is Evolutionarily Correlated with the Usage of GC-Ending Codons

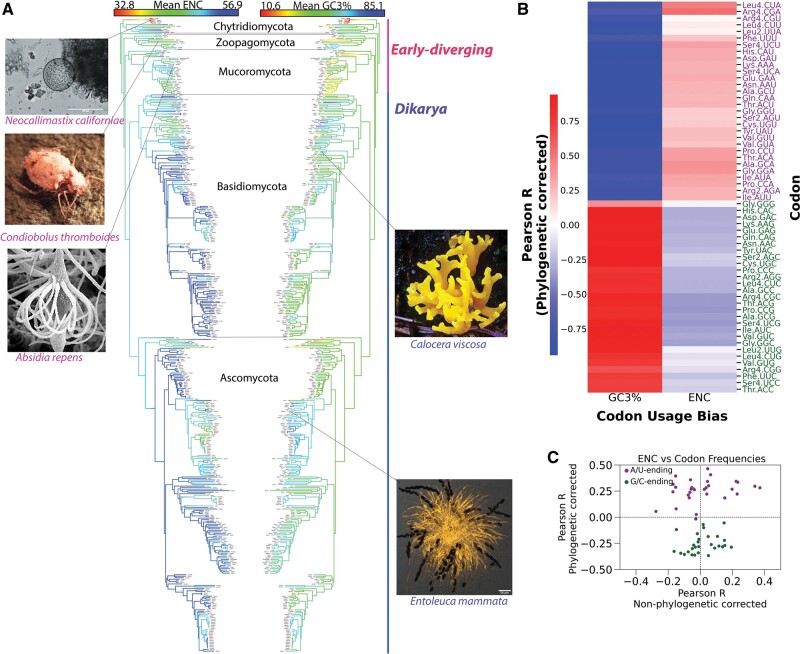
We measured the degree of codon usage bias by computing the effective number of codons, ENC, for each species (Wright 1990). ENC ranges from 20 to 61, where 20 represents extreme bias of using only one codon per amino acid, whereas 61 represents uniform synonymous codon usage, that is, no bias. The mean ENC values ranged from 32.8 (high bias) to 56.9 (weak bias). To visualize the macroevolutionary pattern of codon usage bias, we applied continuous maximum-likelihood ancestral state reconstruction (Revell 2013) that projected the species ENC values onto a pruned phylogenetic tree. The ancestral reconstruction shows that the more biased genomes accumulate in the early diverging lineages (fig. 1A) with the most codon-biased genomes occurring in Neocallimastigomycota, the earliest diverging class of free-living fungi (Berbee et al. 2017). Also, there is more fluctuation in codon bias along the upper branches that slows down upon the divergence of Agaricomycotina, the largest class (∼70%) in Basidiomycota. Similarly, species in Ascomycota exhibit less variation in their codon bias. Variation in the GC content at the third codon position (GC3%) is closely linked to codon usage bias because all degenerate amino acids allow for silent G or C substitutions. The mean GC3% ranges from 10.6% to 85.1%, with a median of 57%. Overall, early-diverging fungi exhibit, on average, lower GC3% but more variability among individual values (fig. 1A).

Fig. 1.

Inferring the tempo and mode of the evolution of codon usage bias and GC3% in fungi. (A) Ancestral reconstruction of the codon usage bias, measured by the mean effective number of codons (ENC), and GC3% projected onto a pruned fungal phylogenetic tree (number of tips = 417 species). Color gradient represents the trait values for species at the tips and estimated trait values for internal nodes. Species with higher codon usage bias-lower ENC— and low GC3% primarily accumulate in the early diverging lineages. Size of tree obscures tip labels but greater details are available in supplementary data, Supplementary Material online. Sample species photo credits: https://mycocosm.jgi.doe.gov/mycocosm/. (B) Cluster heatmap showing phylogenetic corrected Pearson’s R correlation between normalized codon usage, GC3 content (GC3%), and ENC. G/C-ending codons are all positively correlated with GC3% and codon usage bias, whereas as A/U-ending codons are all negatively correlated with GC3% and codon usage bias. (C) Scatterplot showing Pearson’s R correlation coefficients between individual codon frequencies and codon usage bias (ENC) with and without correcting for phylogenetic signal.

Next, we assessed the evolutionary relationship between codon usage bias and GC3% using phylogenetic independent contrast (PIC). PIC regression corrects for phylogenetic nonindependence by using the contrasts between nodes instead of the trait values directly (Garland et al. 1992). For the entire tree, the PIC model ENC∼GC3 yielded a negative coefficient of −14.1 (adjusted R² = 11.8%, P value = 3.79e⁻¹³). Because PIC is calculated without an intercept term, the R² coefficient is the square of the Pearson’s R correlation coefficient. Therefore, codon usage bias and GC3% are moderately correlated (Pearson’s R = 34.4%). Although it may be reasonable to assume the evolutionary GC3 bias is driven by the usage of G/C-ending codons, it was found that the usage of certain G/C-ending codons was negatively correlated with GC3 bias in some plants and prokaryotes (Palidwor et al. 2010). To evaluate the relationship between codon usage and GC3 bias, we computed the phylogenetic-corrected Pearson’s correlation between individual codon frequencies (normalized for amino acid usage), GC3%, and ENC, separately. The usage of all G/C-ending codons are positively correlated with GC3%, whereas all A/U-ending codons are anticorrelated with GC3% (fig. 1B). All G/C-ending codons negatively correlated with ENC, which means that the increase in usage of G/C-ending codons correlates with an increase in codon bias. Conversely, the usage of all A/U ending negatively correlates with codon bias. Interestingly, we obtained different correlation values between codon bias and the normalized codon frequencies with and without phylogenetic correction. Without the correction, some A/U codons positively correlate with codon bias, and some G/C-ending codons negatively correlate with codon bias (fig. 1C). This discrepancy suggests that codon frequencies also have phylogenetic signal.

Because the relationship between codon bias and GC3% seems inverted for the early-diverging and dikaryic lineages (fig. 1), we split the tree into the separate subkingdoms and re-evaluated the phylogenetic correlation between codon usage bias and GC3%. Codon bias and GC3% are evolutionarily anticorrelated in the early-diverging subtree (coefficient = 21.1, R² = 32.6%, P value = 9.02e⁻⁰⁶, number of tips = 51 species). In contrast, dikarya species are positively GC3% biased (coefficient = −30.1, R² =50.2%, P value < 2.16e⁻¹⁶; number of tips = 364).

Fitting Macroevolutionary Models to Codon Usage Bias

Phenotypic variation among extant species is a confluence of shared ancestry and responses to neutral and adaptive processes. Interspecies codon usage bias is widely ascribed to neutral drift (Grantham et al. 1980). To determine the pattern of evolution that best explains codon usage bias, we fitted four different likelihood models of macroevolution to the ENC and GC3 values: 1) Brownian motion (BM) (drift/random walk), 2) Ornstein–Uhlenbeck (fluctuating directional selection), 3) early burst (exponential decrease in trait variation over time), and 4) delta (rate-shifted BM) (Pennell et al. 2014). Notably, Brownian motion is the null hypothesis of genetic drift that models interspecies trait data as a random walk (Felsenstein 1985). Based on the goodness-of-fit Akaike information criterion (AIC) scores, the early-burst model, which simulates adaptive radiation, best explained the phylogenetic variation of both codon bias and GC3% (supplementary table 2, Supplementary Material online). Macroevolution by adaptive radiation is characterized by higher rates of trait evolution early in a clade’s history followed by an exponential decline through time (Simpson 1953).

Codon-Level Macroevolutionary Analysis Reveals Codon Frequencies as Mostly Deviate from Genetic Drift

Because variation in the frequencies of synonymous codons underlies codon usage bias, we examined the macroevolutionary trends of the individual codons. First, we quantified genome-wide relative synonymous codon usage (RSCU) of the 59 degenerate codons (Sharp et al. 1986). RSCU = 1 means codons are used according to neutral or uniform expectation. Importantly, RSCU normalizes codon frequencies within their amino acid class, which minimizes amino acid composition effects. To characterize which codons fungi generally prefer for making proteins, we quantified the most (highest RSCU) and least (lowest RSCU) preferred codons. Overall, C-ending codons consistently had the highest transcriptomic representation across the amino acid types (supplementary fig. S1A and C, Supplementary Material online).

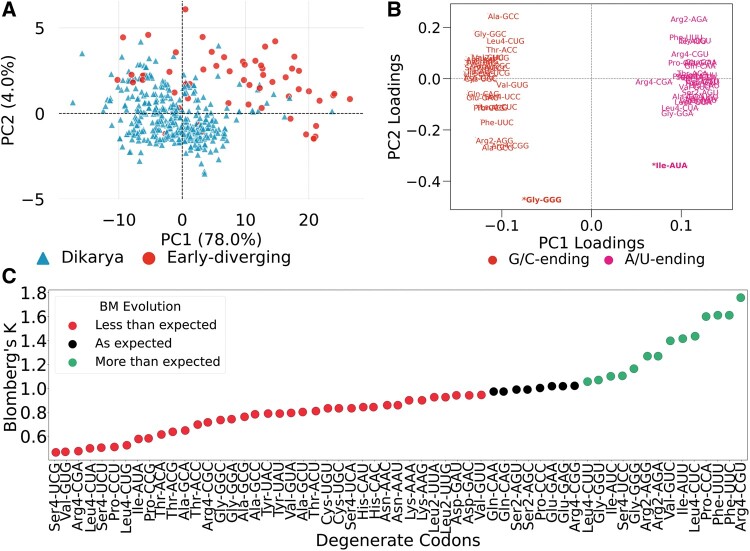
To summarize variation of interspecies codon usage, we performed multivariate analysis using PCA on the 59 RSCU × 459 species matrix. The first two principal components explained 82% of the interspecies variation (fig. 2A). PC1 (78% explained variance) separated species according to differences in GC content at the third codon position (GC3%), wherein loadings of G/C- and A/U-ending codons are equally but inversely correlated to PC1 (fig. 2B). This finding aligns with previous work that establishes variation in G + C content as the major determinant of interspecies differences in codon usage bias (Chen et al. 2004; Novoa et al. 2019). The second principal component, PC2, 4.0% explained variance is driven by differences in individual codon frequencies, with the strongest signal due to the rare codons GGG^Gly and AUA^Ile (fig. 2B andsupplementary fig. S1B, Supplementary Material online). Notably, PCA separated the species into their subkingdoms (fig. 2A).

Fig. 2.

Phylogenetic analysis of genome-wide codon usage frequencies. (A) PCA on RSCU matrix separates species into the dikarya and early-diverging sub-kingdoms, primarily along the axis of the second principal component (PC2). Each dot is a species whose color and shape represent the sub-kingdom. (B) Loadings plot showing the correlation between codons and the first two principal components. Codons are colored based on the G/C or A/U composition at the third base. A/U- and G/U-ending codons equally but inversely contribute to the PC1 scores. On the other hand, PC2 scores are differently influenced by codons, with the most influential being the rare codons, GGG^Gly and AUA^Ile (see also supplementary fig. S1D, Supplementary Material online). (C) Stripplot showing the variation in the phylogenetic signal of the usage of degenerate codons. A total of 51/59 codons reported Blomberg’s K not equal to 1 suggesting they evolved at a rate less than or greater than expected by genetic drift as modeled by Brownian motion. All P values are statistically significant (<0.05).

The subkingdom clustering by the PCA led us to measure the extent to which phylogenetic effect (i.e., phylogenetic relatedness) underlies the choice of codon representation of the genome. To this end, we computed the Blomberg’s K statistic (Materials and Methods) of the normalized codon frequencies. Blomberg’s K measures the strength and direction of trait evolution relative to that expected under the BM model that considers the phylogenetic distance as the only predictor of trait similarity among species (Blomberg et al. 2003). All codons reported statistically significant phylogenetic signals (P values < 0.05). However, the strength and direction of evolution, even among synonymous codons, varied (fig. 2C). A total of 37/59 codons exhibited low phylogenetic signal (K < 1), suggesting variation due to convergent evolution (Revell et al. 2008; Kamilar and Cooper 2013). Eight out of the 59 codons followed the expected Brownian process (K = 1) of genetic drift. A total of 14 out of the 59 codons exhibited high phylogenetic signal (K > 1) indicative of either stabilizing selection or low rates of evolution (Blomberg et al. 2003). We also fitted different models of macroevolution to the individual codon frequencies. Like genomic codon usage bias, adaptive radiation was the best fitting model for all the 59 degenerate codons (supplementary data, Supplementary Material online). Taken together, these findings highlight that individual codons follow different modes of evolution. Importantly, the frequencies of 51 out of 59 codons are not fully explained by phylogenetic relatedness that is expected under genetic drift.

Identification of Phylogenetically Rare tRNAs and Strong Evolutionary Preference for Inosine34-Modified tRNAs

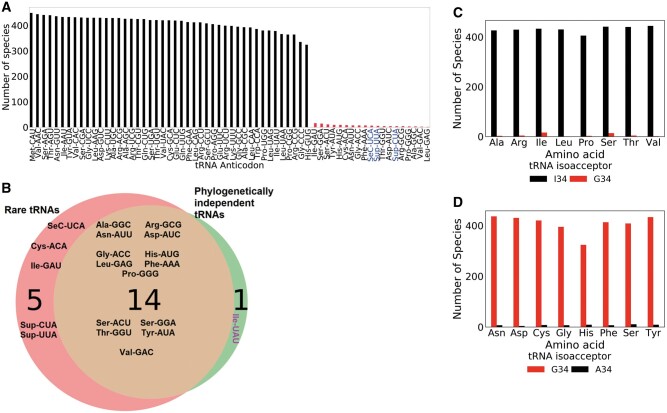
Considering that the frequencies of most codons deviated from genetic drift, the next logical step was to analyze the tRNA gene sets because codon usage is widely believed to coevolve with tRNA supply in several species (Sharp et al. 2010). Both the number of distinct tRNA anticodon types and total tRNA genes (tRNAome) vary widely across the 459 genomes under study. The median number of distinct anticodon types is 44, ranging from a maximum of 58 in Ascobolus immersus and a minimum of 18 in Sporobolomyces linderae (supplementary fig. S2A, Supplementary Material online). Like all previously studied genomes, no species in our data set possessed the full theoretical complement of 61 tRNA anticodon families (Marck and Grosjean 2002). Interestingly, we identified 11 species possessing less than 30 anticodons, which is the theoretical minimum for decoding the standard genetic code (Marck and Grosjean 2002). The median tRNAome is 144 genes, with a minimum of 24 and a maximum of 4,547. Caecomyces churrovis, Ascobolus immersus, and Melampsora allii populina possessed unusually large tRNAomes of 4547, 3481, and 2216 genes, respectively (supplementary fig. S2B, Supplementary Material online).

Next, we measured the phylogenetic signal of the copy number for tRNAs that are cognate to the 59 degenerate sense codons. Like most codons, tRNAs also exhibited phylogenetic signal that is lower than expected by drift, with K ranging from 0.02 to 0.70. These weak phylogenetic signals are consistent with tRNA gene dosage as evolutionarily labile (Velandia-Huerto et al. 2016). A total of 44 out of 59 sense tRNAs yielded statistically significant phylogenetic signal (P < 0.05). The lack of phylogenetic signal (P > 0.05) in the remaining 15 tRNAs implies that they either evolved completely independent of phylogeny or are mostly absent in the fungal genomes because entire tRNA families are known to be extinct in certain clades (Rak et al. 2018). To this end, we identified 19 tRNA anticodon types that rarely occur among the fungal genomes, three of which are nonsense suppressors (tRNA^Sup [UUA], tRNA^Sup [CUA], tRNA^SeC [UCA]) (fig. 3A). In total, 14 out of the 16 rare sense tRNAs overlapped with the 15 tRNAs that lacked phylogenetic signal (fig. 3B). Only tRNA^Ile (UAU) is prevalent yet lacking a phylogenetic signal. In other words, close relatives are no similar in their genomic copies of tRNA^Ile (UAU) than if they were randomly placed on the tree. This finding may be explained by highly accelerated birth–death evolution or anticodon shifts of tRNA^Ile (UAU) along the phylogeny (Velandia-Huerto et al. 2016).

Fig. 3.

Analysis of tRNA gene composition across the phylogeny. (A) Presence of each tRNA anticodon type across the 459 fungal genomes based on tRNAscanSE2.0 predictions. Low-quality tRNA and pseudogenes with a covariance score below 50.0 are not included. Rare tRNAs are highlighted in red. (B) Overlap between tRNAs rarely present in fungal genomes and tRNAs with nonsignificant phylogenetic signal (P value > 0.05 for Blomberg’s K). tRNA^Ile (UAU) is the only phylogenetically nonsignificant tRNA that is not rare. This suggests that this tRNA gene’s evolution is decoupled from phylogeny. (C, D) Evolutionary bias for the inosine-34 modification. For amino acids decoded by both ANN and GNN tRNAs, when the first anticodon position is a target of A-to-I editing, the INN tRNAs are more prevalent while the GNN isoacceptor is rare. (D) However, if the ANN tRNA is not a target of A-to-I editing, then the GNN isoacceptor is more prevalent and the ANN is rare.

Detection of Selenocysteine-tRNAs in Dikarya Genomes

Here, we would like to report the detection of selenocysteine tRNA (SeC-tRNA). At the time of this finding, tRNAs corresponding to the 21st amino acid selenocysteine were considered absent in all fungi (Lobanov et al. 2007) until Mariotti et al. (2019) uncovered the presence of tRNA^SeC (UCA) in nine early-diverging fungi. However, all three of our Sec-tRNA positive fungi—Rhodocollybia butyracea, Sugiyamaella americana, and Lollipopaia minuta—are dikarya from Basidiomycota and Ascomycota phyla (Supplementary table S3, Supplementary Material online`). We identified the presence of tRNA^SeC (UCA) in these three genomes based on overlapping results from at least one of the general-purpose tRNA gene finders, tRNAscanSE2.0 (Chan and Lowe 2016) or aragorn1.2.38 (Laslett and Canback 2004), and the specialized tRNA^SeC gene finder Secmarker (Santesmasses et al. 2017). As a negative control, we repeated the analysis on the well-studied fungal genomes of S.cerevisiae and N.crassa. Even with the unrealistically relaxed parameters, tRNA^SeC (UCA) was not detected in either genome.

Next, we examined the prevalence of inosine-modified tRNAs. Adenosine-to-inosine (6-deaminated adenosine) conversion is the most common post-transcriptional editing in eukaryotic RNAs (Nishikura 2016). In eukaryotes, A34-to-I34 conversion is restricted among the eight tRNA types: tRNA^Thr(AGU), tRNA^Ile(AAU), tRNA^Pro(AGG), tRNA^Arg(ACG), tRNA^Leu(AAG), tRNA^Ala (AGC), tRNA^Val(AAC), and tRNA^Ser(AGA). Inosine-34 tRNAs (INN) decode both NNC and NNU codons in eukaryotes (Rafels-Ybern et al. 2018). Although both INN and GNN tRNAs decode C-ending codons, the I: C anticodon–codon bond is known to be less stable than G:C bond (Hoernes et al; 2018). Yet, we found that for the amino acids that are recognized by isoacceptor pairs of GNN and a putatively inosinylated ANN, the GNN iso-acceptor is mostly absent within the genomes (fig. 3C). For example, tRNA^Leu (GAG) is the rarest tRNA being predicted in only 1/459 species (fig. 3A), yet its Watson–Crick cognate codon CUC is the commonly most preferred for encoding leucine (347/459 species; supplementary fig. 2A, Supplementary Material online). Likewise, the usage of AUC codon is frequently the most preferred for isoleucine, yet its cognate tRNA^Ile (GAU) is rarely present (16/459 species). According to wobble rules, both Leu-CUC and Ile-AUC codons are decoded by inosine-modified tRNA^Leu (AAG) and tRNA^Ile (AAU), respectively. In contrast, when the ANN tRNA is not a target of inosinylation, the GNN iso-acceptor is far more prevalent (fig. 3D). As previously mentioned, genomes in our data set are mostly biased for NNC codons (supplementary fig. S2A, Supplementary Material online) so this finding suggests that inosine-modified tRNAs are positively selected for in fungi. To summarize, phylogenetic comparative analyses revealed that the interspecies variation of codon usage bias and individual codon frequencies do not support genetic drift as the dominant mode of evolution.

Signatures of Neutral and Adaptive Evolution on Intragenomic Codon Usage Bias

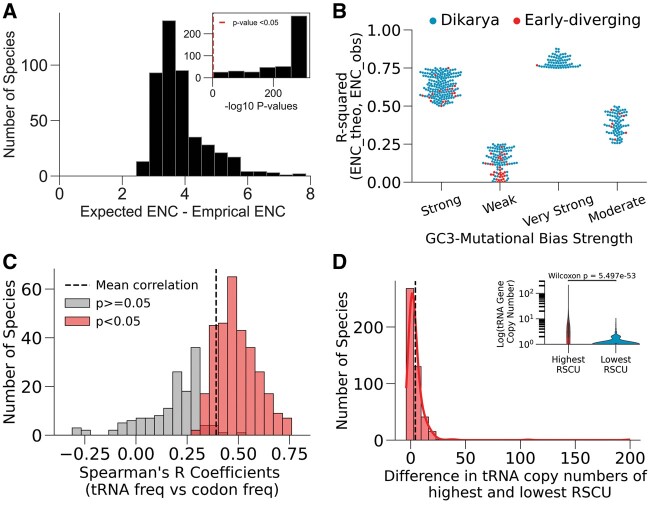
Having analyzed codon usage patterns at the macroevolutionary scale, we next sought to disentangle the signatures of adaptive and neutral evolution on within-genome codon usage bias. At the organismal level, codon usage bias is a composite of drift, neutral, and adaptive mutational bias (dos Reis and Wernisch 2009). To determine whether codon usage bias is driven solely by GC-compositional mutational bias in each species, we compared the empirical ENC of all coding sequences to their theoretical ENC that is expected under the neutral-mutational model. The neutral-mutational model is the null hypothesis that selection pressure does not act on the synonymous third codon position sites; rather codon bias is only a function of GC3% (Wright 1990). The ENC of 458 out of 459 species deviated significantly from neutral expectation (paired Wilcoxon signed-rank test P values < 0.05; fig. 4A). Next, we assessed each species’ fit to neutral expectation by computing the R² between empirical and theoretical ENC (LaBella et al. 2019) of all coding sequences within each genome (fig. 4B). The R² values ranged from 0.0001 to 0.88. A total of 70 genomes, mostly dikarya, reported an R² value of at least 0.75 (“Very Strong”), which indicates that their codon usage is largely influenced by neutral mutational bias. Notably, early-diverging species make up 12% of the data set, but 28% of the genomes with “Weak” neutral mutational bias.

Fig. 4.

Signatures of mutational bias and natural selection on within-genome codon usage bias. (A) Deviation of genomic ENC values from Wright’s neutral mutational model. The outer histogram shows the distribution of the mean difference between the empirical ENC and theoretical ENC of coding sequences that is expected by GC3-compositional bias measured in each of the 459 species. Inset displays the Wilcoxon signed-rank P values (log base 10) that measures the significance of deviation. A total of 458/459 species reported significant P values (right of red dashed line). Both y-axes represent the number of species. (B) Variation in the influence of neutral pressures on species’ codon usage . Swarmplot of species’ R² values (n points = 459 species) that measures the fit between empirical (“ENC_obs”) and theoretical (“ENC_theo”) codon usage bias expected solely due to GC3-compositional bias, grouped by “Very Strong” (R² ≥ 0.75), “Strong” (0.75 > R² ≥ 0.5), “Moderate” (0.5 > R² ≥ 0.25), and “Weak” (R² < 0.25). (C) Codon frequency correlates with tRNA copy number. Histogram shows the distribution of Spearman ρ correlation coefficient between RSCU and cognate tRNA gene copy number. A total of 312/459 species reported statistically significant P values (P < 0.05). The black line is the mean correlation coefficient of all species. (D) Histogram showing differences in the tRNA copy numbers for the codons with highest and lowest representation (RSCU) in the genome over all the 459 species Inset: Distribution of the log base 10 copy numbers of tRNAs (y-axis) for the codons with highest (red) and least (blue) genome-wide RSCU. The most frequently used codons are decoded by tRNAs with higher copy numbers, whereas the least frequent codons are decoded low copy-number tRNAs.

Fungal genome-wide Codon Usage and tRNA Copy Number Are Positively Correlated

Another signature of natural selection is the correlation between codon frequencies and the supply of cognate tRNAs (Sharp et al. 2010). To explore this, we computed the Spearman’s rank coefficient between genome-wide relative codon frequencies (RSCU) and tRNA gene copy number. Codon frequency and tRNA copy number were significantly correlated in 312 of the 459 species (P values < 0.05), all of which yielded positive correlations (mean Spearman’s ρ = 0.49; fig. 4C). Those species with nonsignificant correlation generally possessed single-copy tRNA gene sets. Additionally, the most overrepresented codons—that is, highest RSCU—are cognates of tRNAs with a higher copy number (mean tRNA gene copy number of 5.2) compared with the most underrepresented codons (mean tRNA gene copy number of 1.4, one-sided paired Wilcoxon signed ranked test P value = 5.50e⁻⁵³; fig. 4D).

In summary, we showed that variation in the genome-level codon usage bias is influenced by both neutral (GC3 composition) and adaptive mutational bias (cognate tRNAs).

Differential Adaptation to the tRNA Abundance Underlies Expression-Linked Codon Usage Bias

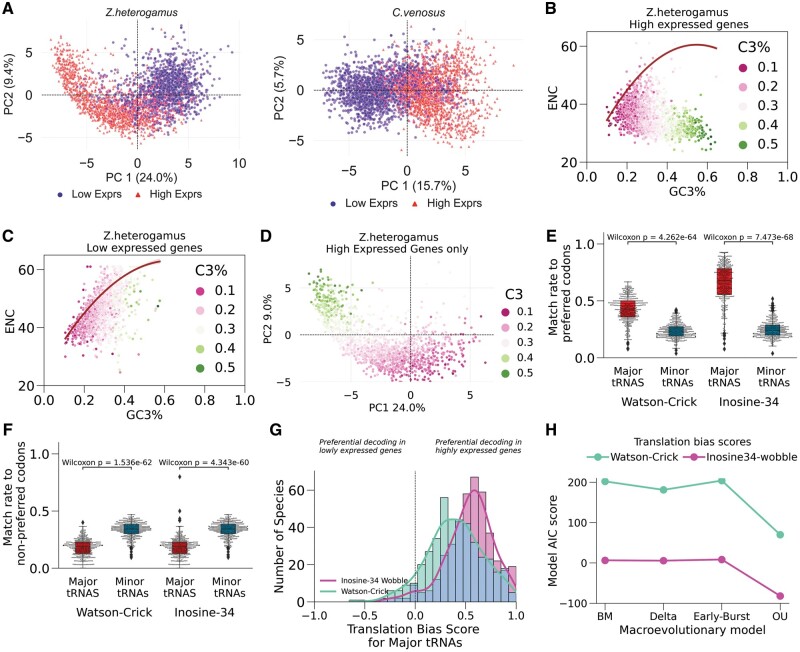
Here, we explored the functional implications of adaptive codon usage bias by analyzing the contribution of gene expression to codon preferences. Because we have RNAseq data for most species in our data set (420/459) we could empirically investigate expression-linked codon usage bias. To this end, we selected the top 10% (“high”) and bottom 10% (“low”) of expressed coding sequences as the working data set for each species since directional selection tends to act at the extremes. We observed that for most species, PCA of the 59-dimensional matrix of codon frequencies (RSCU) separated the genes according to expression level (fig. 5A). The trend suggests that gene expression level is also driver of codon usage patterns.

Fig. 5.

Expression-linked codon usage bias correlates with tRNA supply. (A) High and low expressed genes exhibit different codon usage patterns. Examples of PCA applied to the codon usage 59-dimensional RSCU matrix of the top (“high”) and bottom (“low”) 10% expressed genes. Each dot is a gene. The right panel is the more common cluster pattern. The left panel depicts a Guttman (“arch”) effect in the high expressed genes of Z. heterogamus. (B–D) ENC-GC3 plot of Z. heterogamus genes elucidates source of PCA arch effect. The solid red line in scatterplots B and C represents the expected curve when codon usage bias is only affected by neutral mutation pressure. (B) ENC of high expressed genes deviate strongly from neutral expectation while becoming more C3-biased whereas (C) low expressed genes better fit expected neutrality. (D) Arch effect captured the variation in C3% due to neutral and selection pressures. (E and F) Highly expressed genes are generally biased for translationally optimal codons. (E) Boxplot of the fraction of preferred codons (significantly enriched in the top 10% of expressed genes) that are decoded by major (most abundant) and minor (least abundant) tRNA isoacceptors, with and without the inclusion of inosine-34 modification across the species (n = 420 species) . (F) Boxplot of the fraction of nonpreferred codons (significantly enriched in the bottom 10% expressed genes) recognized by major and minor tRNAs, with and without the inclusion of inosine-34 modification. (G) Distribution of the translation bias scores across 420 species. Translation bias score is the difference between the fraction of prefererred and nonpreferred codons decoded by major tRNAs normalized by their sum. The positively skewed distribution indicates that the highest expressed transcripts are generally codon biased for rapid translation. (H) Akaike-Information-Criterion (AIC) goodness-of-fit test to evaluate various maximum-likelihood macroevolutionary models fitted to translation bias score (n species tips = 384). “BM”, Brownian motion; “OU”, Orhnstein–Uhlenbeck. The OU model of fluctuation directional selection yielded the lowest AIC, and therefore the best fit model.

Not an Artifact: PCA Arch of High Expressed Genes Caused by Strong Deviation from Neutral Compositional Bias

Intriguingly, the pattern of only the high expressed genes clustering as an arch in Z. heterogamus also appeared in 26 other species (fig. 5A, left panel; supplementary data, Supplementary Material online). Guttman or arch effect in dimensionality reduction techniques, such as PCA or correspondence analysis, is observed when the first two transformed axes are curvilinear because the structure of the data is dominated by a single latent variable that gradually shifts from one extreme to the another, that is, the data points lie on a gradient (Diaconis et al. 2008; Nguyen and Holmes 2019). Given that codon usage is influenced by both directional neutral and selection pressures, we hypothesized that the latent gradient underlying the high expressed genes represents the shift in influence of neutral to selection pressures. To explore this in Z. heterogamus, we generated an ENC-GC3 neutrality plot in which the standard curve represents the expected relationship between ENC and GC3% when codon usage is solely explained by neutral compositional bias (Wright 1990). The neutrality plot confirmed our hypothesis as the genes are more C3 biased with increasing distance from the neutral curve (fig. 5B). However, the codon usage of low expressed gene set did not exhibit such marked deviation from neutral expectation (fig. 5C). Indeed, the latent gradient responsible for the arch is defined by diametric usage of C-ending (fig. 5D) and A-ending (supplementary S3A–C, Supplementary Material online) codons. We identified a similar pattern for 18 of the remaining 26 “arch” species in which their high expressed genes also lie on a C3% gradient when projected onto the first two principal components (supplementary fig. S3G, Supplementary Material online), and deviating from the expected neutral compositional bias (supplementary fig. S3H, Supplementary Material online). This led us to revisit the compositional bias analysis performed in the previous section, where we found that 23 out of these 27 species, including Z.heterogamus, fell in the “Weak” category (fig. 4B and supplementary fig. S3D, Supplementary Material online). Additionally, 23/27 of them are AU3 biased (mean GC3 < 50%), and 21 of them are early-diverging fungi (supplementary fig. S3D, Supplementary Material online). Together, these results suggest that selection is particularly stronger in the highly expressed genes of these species.

High Expressed Genes Preferentially Use Codons Decoded by Major tRNAs but Avoid Codons Decoded by Minor tRNAs

We then asked if the divergent codon preference between the high and low expressed genes is related to adaptation to translation efficiency (Duret 2000). To this end, we measured the fraction of preferred and nonpreferred codons that are decoded by major and minor tRNAs per species. Preferred codons are significantly enriched (higher RSCU) in the high expression gene set, whereas nonpreferred codons are enriched (higher RSCU) in the low expression set (Benjamini–Hochberg adjusted P values < 0.05) (Yannai et al. 2018). We observed that C-ending codons are mostly preferred by high expressed genes compared with A-ending codons in low expressed genes (supplementary fig. S3E, Supplementary Material online). Major and minor tRNAs have the highest and lowest copy numbers, respectively, within an amino acid class. Overall, highly expressed genes preferentially use codons that are decoded by major tRNAs, which is indicative of selection for rapidly translated codons (fig. 5E). On average, 43% of preferred codons are recognized by major tRNAs compared with 24% by minor tRNAs (fig. 5E; paired Wilcoxon signed-rank test P value = 4.26e⁻⁶⁴). Conversely, nonpreferred codons better matched minor tRNAs (mean fraction = 34%) than major tRNAs (fig. 5F; mean fraction = 18%; Wilcoxon P value = 1.53 e⁻⁶²).

Because we identified the widespread preference of inosine-modified tRNAs, we extended our analysis to account for inosine-34 wobble decoding. This resulted in a marked increase in the mean fraction of preferred decoded by major tRNAs from 43% to 65% (Wilcoxon P value = 7.47e⁻⁶⁸), but the mean fraction of preferred codons matching minor tRNAs remained the same. For example, the match rate in Z.heterogamus rose from 56% to 81%. In 84% of the species, at least 50% of their preferred codons are cognates of major tRNAs when inosine-34 decoding is considered (fig. 5E). However, the inclusion of I34 modification did not substantially alter the fraction of nonpreferred codons decoded by minor tRNAs or major tRNAs (18%; Wilcoxon P value = 4.34e⁻⁶⁰) (fig. 5F). Therefore, the codon bias in high expressed genes can be partially explained by selective usage of inosine-34 decoded codons. These results align with experiments in mammalian and bacterial systems that demonstrated improved agreement between codon usage and tRNA abundance when I34 modification is accounted for and that transcripts with codon compositions that matched I34 tRNAs were more efficiently translated (Novoa et al. 2012).

Prevalence of Codon Optimization for Translation in High Expressed Genes Shows Signs of Convergent Evolution

To quantify the association between expression-linked codon bias and adaptation to the tRNA supply in a genome, we derived the translation bias score (Materials and Methods). Formally, translation bias score is the difference between the fractions of preferred codons and nonpreferred codons for major tRNAs normalized by their sum. A translation bias score of +1 indicates that the codon bias of highly expressed genes confers them exclusive access to the most abundant tRNAs in the cellular pool compared with the lowest expressed genes; whereas a translation bias score of 0 means that there is no competition for major tRNAs between the high and lowest expressed gene sets. Among the 420 species analyzed, the mean translation bias score is +0.39 when restricted to Watson–Crick pairing, and a mean of +0.53 when I34 wobble is considered (fig. 5G). That is, on average, 53% more of the major tRNAs are decoding high expressed genes than the low expressed genes, which we interpret as selection for translation speed. However, there are a few species that possess negative translation bias score meaning their low expressed genes are more codon biased for major tRNAs.

We wondered if the positive skewness of the translation bias score was mainly a consequence of phylogenetic relatedness is, because species richness is unevenly distributed along our fungal tree. To measure the strength of phylogenetic effect of the TBS values, we computed Blomberg’s K statistic which yielded K = 0.12 for Watson–Crick pairing and K = 0.18 for inosine-34 wobble decoding (both P values = 0.01). These low K values indicate that distantly related species have more similar TBSs than expected by phylogenetic distance, a pattern often attributed to convergent evolution (Revell et al. 2008). As a complementary approach, testing of different macroevolutionary models supports the Ornstein–Uhlenbeck process of fluctuating directional selection as the best fit for translation bias (fig. 5H). Additionally, the ancestral state reconstruction shows that similarly high translation bias is distributed across multiple and distant lineages (supplementary fig. S3F, Supplementary Material online). Therefore, both phylogenetic methods agree on adaptive codon usage—at least in the context of gene expression—as a realization of convergent evolution. Altogether, the concordance between tRNA supply and expression-linked codon preferences supports natural selection on fungal protein-coding genes for translation accuracy and speed.

Codon2Vec Neural Network for Predicting the Expression of Coding Sequences

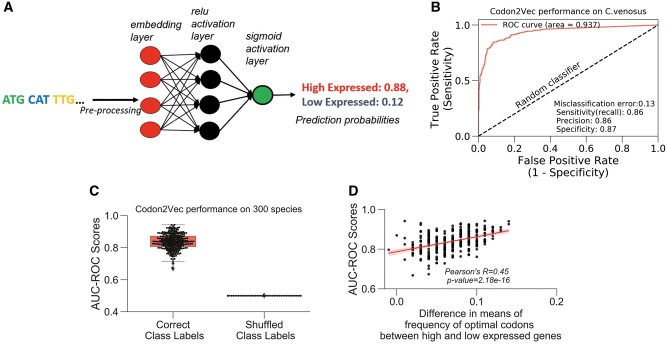
Building predictive models for gene expression remains a pertinent challenge in genomics. Inspired by distributed representation models for natural language processing (Zhong et al. 2016), we implemented a three-layer neural network—Codon2Vec—that predicts expression class (“high” or “low”) directly from input coding sequences (fig. 6A; Materials and Methods). A neural network is a supervised algorithm that can model complex nonlinear patterns that underlie the data. The first layer of Codon2Vec performs featurization of input sequences by mapping each codon type to a real-valued vector or “embeddings” in Euclidean space. The codon embeddings are adjusted during model training to minimize the error between the predicted and ground truth labels.

Fig. 6.

Neural network uses codons as features to predict gene expression. (A) Schema of Codon2Vec. Codon2vec is a fully connected multilayer neural network that uses an embedding layer to transform codons in the input coding sequences to a real-valued vector. The final output of the model is a vector of probabilities for each gene expression class (i.e., “high” or “low”). Detailed description in Materials and Methods. (B) Codon2Vec’s performance on a single species. Model performance is evaluated on the hold-out test sets based on the AUC-ROC. An AUC score of 0.5 (dashed line) represents random predictions. (C) Model generalizability: Codon2Vec achieves high predictive performance on 300 different species. However, shuffling of ground truth labels independent of input sequences ablated Codon2Vec’s ability to learn meaningful associations. (D) Codon2Vec’s prediction accuracy (AUC-ROC) positively and significantly correlates with differential usage of optimal codons between high and low expressed genes. The frequency of optimal codons (FOP) is another standard metric for codon usage bias (Ikemura 1982; Materials and Methods).

To achieve a balanced data set, we trained Codon2Vec on the coding sequences from the top and bottom 10% expression. The training data were split into 70:20:10 for training: validation: test sets. Model selection was determined based on the training and validation sets. Final predictive performance was reported on the hold-out test set using the following metrics: misclassification error, area-under-the-receiver-operator-characteristic curve (AUC-ROC), sensitivity, and specificity (Materials and Methods). An AUC-ROC of 0.5 indicates that a model failed at learning and instead makes random predictions. When applied separately to 300 different species, Codon2Vec achieved a high median AUC-ROC score of 83.8% (fig. 6C). Randomizing the association between the input and class labels ablated Codon2Vec’s discriminative power and drove the AUC-ROC to 0.5 or random predictions (fig. 6C and supplementary fig. S4D, Supplementary Material online).

We hypothesized that the model’s decision boundary is the differential codon bias that exists between the sequences in the high expression and low expression classes. To this end, we computed the difference between the mean ENC of the expression classes (DOM-ENC) and measured the Spearman’s rank correlation between the species-specific AUC-ROC scores and the DOM-ENCs, but there was no significant correlation (R = 0.1, P value = 0.074). Because codons are the features, we repeated the procedure using the frequency of optimal codon (Ikemura 1982) (DOM-FOP). This resulted in a significant and positive correlation (Spearman’s rank coefficient R = 0.45, P value = 1.05e⁻¹⁶) (fig. 6D). We interpret this as the model performing better on genomes that have a wider margin of optimal codon content between the high and low expressed genes. As a sanity check to see if the length of coding sequences was a confounding variable, we found no significant correlation (R = 0.1, P value = 0.0755). Remarkably, Codon2Vec learned the intrinsic differences in optimal codon content between high and low expressed genes even though we did not explicitly provide this sequence property.

Discussion

Much of our understanding of codon usage bias is based on collating findings from single-species studies. To better detail the evolutionary mechanisms that have shaped codon usage patterns through time in Kingdom Fungi, we employed a phylogenetic comparative approach to analyze hundreds of representative species that span the six major phyla. We showed how neglecting phylogenetic effect can lead to different conclusions about the influence of individual codons on the degree of codon bias (fig. 1C). Our macroevolutionary analyses support, contrary to the widely held neutral-drift hypothesis, adaptive mechanisms as the driver of interspecies codon usage patterns in fungi. Fitting of different likelihood models of trait evolution to our 452-taxa phylogenetic tree showed that variation in codon usage bias and GC3% best fit the pattern generated by adaptive radiation. Additionally, the phylogenetic effect of most codon frequencies was found to be stronger or weaker than expected by random drift, a sign that is usually interpreted as stabilizing selection or convergent evolution, respectively (Revell et al. 2008; Losos 2011a). Adaptive codon usage was also evident at the genome-level analyses. Gene expression level and codon usage were broadly correlated as PCA on RSCU values separated out the highest and lowest expressed genes. In some fungi, primarily early-diverging, the deviation of high expressed genes from neutral compositional bias was strong enough to dominate the signal captured by both principal components resulting in a Guttman effect. Because differential codon bias could arise by a neutral mechanism such as GC-biased gene conversion (Marais 2003), we demonstrated how this prevalent trend of expression-linked codon bias is associated with differences in the adaptation to tRNA copy number abudance, a proxy for translation efficiency. Broadly, the high expressed genes preferentially used codons matching the most abundant tRNAs; whereas the low expressed genes were more biased for codons read by the least abundant tRNAs. Moreover, the widespread trend of codon optimization of high expressed genes for translation efficiency, which we quantified using our translation bias scores, suggests convergent evolution as the phylogenetic effect was significantly weaker than expected by Brownian motion trait evolution. Altogether, these findings are consistent with the influence of natural selection on codon usage to promote translation efficiency. Our results on the prevalence of adaptive codon usage bias in fungi are consistent with the recent subphylum wide codon usage analysis of Sacchoromycotina budding yeasts (LaBella et al.2019).

Macroevolutionary Analyses of Codon Usage Reveal the Influence of Adaptive Mechanisms

Although claims about codon usage are usually based on single-species analyses, we believed that inferences about the mode and tempo of the macroevolution of codon usage bias would further elucidate its adaptive nature . Principally, we found that the tempo of codon usage bias, and the evolutionarily correlated GC3%, in our 452-taxa tree best follow the pattern of adaptive radiation. Other fungal phylogenomic studies, primarily in mushroom-forming (Agaricomycetes) lineages, have also reported evidence of adaptative radiation for certain morphological traits (Nagy et al. 2012; Gaya et al. 2015; Varga et al. 2019). Various hypotheses exist for the intrinsic and ecological drivers of fungal radiations, including the evolution of complex fruiting bodies (Varga et al. 2019), transition to mutualism (Sánchez-Garcí and Matheny 2017), and defense mechanisms (Nagy et al. 2012; Gaya et al. 2015). Previous studies have linked codon usage bias to ecological specialization (Botzman and Margalit 2011; Roller et al. 2013). Badet et al. (2017) uncovered that generalist parasitic fungi are more codon biased than nonparasitic fungi. Our finding raises the question of what are the ecological opportunities that underlie the macroevolution of codon usage bias. Visual inspection of our ancestral reconstruction shows that the decreased in the variability of codon usage bias coincides with the divergence within Basidiomycota. Basidiomycota (club fungi) comprises about one-third of all fungi (Stajich et al. 2009). Saprophytic Agaricomycotina accounts for two-thirds of basidiomycetic fungi, whereas Puccinomycotina and Ustilaginomycotina are mostly plant parasites (Mao and Wang 2019). Relatedly, ancestral reconstruction of fungal nutritional modes showed that parasitism is nonrandomly distributed along the tree and more prevalent in earlier-diverged lineages (James et al. 2006). Taken together, the evolution of codon usage bias in fungi may be connected to lifestyle adaptation. We believe that a deeper study of the macroevolutionary relationship between codon preferences and the various ecological specialization in fungi is needed.

Selection for Translation Efficiency May Explain Convergent Codon Usage in Fungi

Macroevolutionary analyses revealed that variation in synonymous codons is mostly convergent. The normalized frequencies of 37/59 codons yielded significantly low Blomberg’s K values, indicating distantly related lineages are more similar in their codon choices than expected by phylogenetic relatedness, that is, a sign of convergence (Kamilar and Cooper 2013). Causes of convergent evolution are generally attributed to either shared constraints (molecular/genetic/physiological/ecological, etc.) that limit or bias the production of phenotypic variation, or, to a lesser extent, random chance (Losos 2011a). Here, we reason that the macroevolutionary convergence of codon usage frequencies reflects the shared constraints imposed by neutral—for example, GC-compositional bias—and adaptive pressures, for example, selection for balancing codon representation with tRNA supply (figs. 4B and C and 5E). Moreover, the maximum likelihood best fits the translation bias scores to the Ornstein–Uhlenbeck process of optima-directed trait evolution (Butler and King 2004), lends further evidence that adaptative mechanisms have influenced codon usage patterns over time. That is, the convergence of matching codon usage with tRNA supply, especially in highly expressed genes, suggests that efficient protein synthesis is one of the selective optima that has constrained the evolution of fungal protein-coding genes. This assertion is consistent with genome-engineering experiments that first demonstrated how codon optimization in highly expressed genes exerts global effects on cellular fitness by promoting rapid turnover of free ribosomes enabling translation initiation on other transcripts (Frumkin et al. 2018).

Selection for translation efficiency is expected to favor those codons with better anticodon–codon pairing kinetics (Higgs and Ran 2008). Possibly, the weaker I: C anticodon–codon bond (Hoernes et al. 2018) promotes faster dissociation of the discharged tRNA from the ribosomal E-site, leading to less ribosome pausing and more available free ribosomes. This model may explain the conserved preference for inosine-modified tRNAs (INN) over GNN isoacceptors (fig. 3C), especially the general bias for tRNA^INN-decoded codons—primarily C-ending—observed in high expressed genes (fig. 5E). In light of this, a component of the general GC3 bias among fungi is likely a C3 bias due to selection for decoding by inosine-modified tRNAs.

Here, we highlight the limitations of our study and potential areas for improvement. We assumed that tRNA concentration scale with tRNA copy number which is the general case in unicellular organisms, for example, chromatin profiling in S.cerevisiae revealed all tRNA genes as transcriptionally active (Harismendy et al. 2003). Like all statistical models, inference from PCM is constrained by assumptions and uncertainty. The main assumptions of PCMs are: 1) the phylogenetic tree is accurate, 2) all the extant taxa are represented, and 3) there is measurement error in the trait data. Our 452-taxa tree does not preclude biased inference due to uneven taxon sampling because we used a limited number of representative species per clade. Although we used the best available molecular tree, given the vastness of the kingdom Fungi and ongoing sequencing campaigns, we foresee updates in the fungal phylogeny (Ahrendt et al. 2018). Lastly, various evolutionary processes may give rise to the same phylogenetic pattern and current macroevolutionary models may be limited in their capability to capture more complex patterns of trait evolution (Losos 2011b).

In a minority of species, the low expressed genes were more codon biased for the major tRNAs (fig. 5G). This rather counterintuitive finding joins two previous works that challenge the default view that selection is reserved for codon usage of highly expressed genes (Zhou et al. 2009; Yannai et al. 2018). Codon usage in low expressed CDS may be influenced by selection for mRNA structure, mRNA stability to support sufficient protein production, or cotranslational protein folding of structural sites that are sensitive to translation speed or accuracy (Zouridis and Hatzimanikatis 2008; Zhou et al. 2009). Other than translation efficiency, the covariation between CUB and gene expression levels may reflect selection for mRNA stability as certain codons mitigate ribosomal stalling, as observed in S.cerevisiae (Presnyak et al. 2015), or linked to transcriptional efficiency as seen in N. crassa (Zhou et al. 2016, 2021).

We also identified fungi possessing less than the theoretical minimum of 30 tRNA anticodons required for standard mRNA translation (Marck and Grosjean 2002). Interestingly, 7 out of these 11 species are mutualistic symbionts—Sporobolomyces linderae, Cenococcum geophilum, Meliniomyces bicolor, Neocallimastix californiae—or pathogens/parasites—Teratosphaeria nubilosa, Mixia osmundae, Elsinoe ampelina. Perhaps their reduced tRNA gene set reflect lifestyle adaptations such as selection for rapid DNA replication, or importing necessary tRNA molecules from the host—a rare mechanism for eukaryotes that was first observed in plasmodium parasites (Bour et al. 2016). This mechanism may specifically explain how Mixia osmundae maintains survival as a biotrophic intracellular parasite in plants (Toome et al. 2014). Also, these minimalist fungi may also employ promiscuous super-wobbling decoding, as observed in plastomes of vascular plants (Rogalski et al. 2008). Therefore, these minimalist symbionts would make ideal candidates for studying nonstandard translation of the genetic code and the coevolution of decoding strategies within a eukaryotic host–symbiont pair.

Codon2Vec: Addition of a Sequence-to-Expression Model to the Functional Codon Usage Toolkit

We believe the value of Codon2Vec is two-fold. Because the model is trained on whole coding sequences, it learns a more biologically meaningful representation of the codon usage patterns. Codon order, such as codon-pair bias, has been shown to also contribute to protein yield of highly expressed genes (Cannarozzi et al. 2010; Gamble et al. 2016). But standard codon-based approaches are limited in capturing effects due to codon frequency. Because the model algorithm represents codons as vectors (“embeddings”) in Euclidean space, in principle, contextually related codons are projected close together embedding space (Mikolov et al. 2013). Second, unlike standard approaches, Codon2Vec is not restricted to a pre-defined reference set of genes. Moreover, Codon2Vec bypasses the need for artisanal feature engineering because it extracts information directly from the coding sequences and expression data, and the function that maps codons to real-valued vectors is also learned during training. Although neural networks are regarded as decision “black boxes,” we showed that the model is at least learning to classify coding sequences based on differences in codon optimality. However, neural networks can learn complex functions there may be other sequence/codon usage properties that it may have learned. Embedding neural networks have also been used for other biological applications, such as predicting chemical physicochemical properties from protein sequences (Yang et al. 2018). Once trained on the host’s gene expression data, Codon2Vec can then serve as an oracle to guide the codon optimization of exogenous genes. A nice follow up would be to experimentally validate Codon2Vec’s predictions in optimizing heterologous gene expression system.

In conclusion, by combining genomics and macroevolutionary analyses, we characterized the significance of and prevalence of adaptive processes in shaping fungal protein-coding genes. In the age of “big genomics data,” it would be interesting to see if similar macroevolutionary modes and mechanisms explain interspecific codon usage variation in other clades.

Materials and Methods

Genomic Data Acquisition

Genomic and gene expression data of all 459 fungi were downloaded from the US DOE Joint Genome Institute’s MycoCosm database (https://mycocosm.jgi.doe.gov; last accessed December 2021; Grigoriev et al. 2014). Only coding sequences (CDS) longer than 150 bp with annotated start and stop codons were retained for downstream analysis.

RNA sequencing

Most transcriptomes were sequenced using Illumina from RNA samples collected across multiple conditions and pooled together. From these samples, libraries were prepared using tube- or plate-based RNA sample processing protocols. Plate-based RNA sample preparation was performed on the PerkinElmer Sciclone NGS robotic liquid handling system using Illumina’s TruSeq Stranded mRNA HT Sample Prep Kit utilizing poly-A selection of mRNA following the manufacturer’s guide starting with 1 μg total RNA per sample and 8–10 PCR cycles were used for library amplification. For the tube-based method, stranded cDNA libraries were generated using the Illumina Truseq Stranded mRNA Library Prep Kit, for which mRNA was purified from 1 μg (200 ng for low input RNA) of total RNA using magnetic beads containing poly-T oligos, fragmented, and reverse transcribed using random hexamers and SSII (Invitrogen) followed by second-strand synthesis. The fragmented cDNA was treated with end pair, A-tailing, adapter ligation, and eight cycles (ten cycles for low input RNA) of PCR. The prepared libraries were quantified using the Next-generation Sequencing Library qPCR Kit (KAPA Biosystems) and run on a Roche LightCycler 480 real-time PCR instrument. Sequencing of the flow cells was performed on the Illumina HiSeq or NovaSeq, following a 2 × 150 indexed run recipe. Additional details may be available from the corresponding genome publications listed on MycoCosm (https://mycocosm.jgi.doe.gov/fungi/fungi.info.html; last accessed December 2021).

tRNA gene prediction

tRNA genes were predicted with tRNA-scanSE2.0 (Chan and Lowe 2016) with eukaryotic-specific parameters. For quality control, only high-confidence tRNA genes with a covariance score of at least 50 were retained for analyses. tRNA gene copy number was used as the proxy for tRNA abundance.

Seleno-Cysteine tRNA Identification

High-confidence tRNA genes are assigned a tRNA-scanSE score of 50 and over. After applying the cut-off covariance score of 50, six genomes still retained high-scoring Sec-tRNA genes. To independently validate these tRNAscanSE predictions, these genomes were reanalyzed with another highly accurate but more conservative general-purpose tRNA gene finder aragorn1.2.38 (Laslett and Canback 2004) using eukaryotic-specific parameters and a SeC-tRNA-specific gene finder Secmarker (2015 Guigo). The final SeC-positive species were taken as an overlap of any of these general gene finders with the specialized Secmarker program.

Codon Usage Metrics

The ENC, which measures the degree of synonymous codon bias of gene or genome, was computed from coding sequences using CodonW 1.4.4 (Wright 1990; Peden 1999).

The theoretical ENC is the expected value estimated solely based on GC3% due to neutral mutational bias. The theoretical ENC of a gene g that is only influenced by GC3-compositional bias was computed according to Wright (1990) using custom python3 code.

$${\text{ENC}}_{\text{theo}}=2+{\text{GC}3}_{\mathrm{g}}+\left(29/{(\text{GC}3}_{\mathrm{g}}{}^2+{\left(1-{\text{GC}3}_{\mathrm{g}}\right)}^2)\right)$$

G + C composition at 3rd codon position (GC3 content)

GC3%was computed using CodonW 1.4.4 (Peden 1999).

RSCU is the ratio of observed usage to the expected uniform usage within its amino acid class. RSCU is invariant to sequence length or amino acid composition. The RSCU of the 59 degenerate codons was computed using custom python3 scripts according to Sharp et al. (1986). Six-fold amino acids (Leucine, Serine, and Arginine) were split into 2- and 4-fold codon groups.

Preferred and nonpreferred codons were selected in each species based on the top and bottom 10% of expressed coding sequences. A codon is considered preferred if its RSCU value was significantly higher in the highly expressed CDS set (Mann–Whitney U test, Benjamini–Hochberg adjusted P value <0.05). Conversely, a nonpreferred codon reported a significantly higher RSCU in the low expressed CDS set. With this definition, more than one synonymous codon of an amino acid may be preferred or nonpreferred.

Frequency of optimal codons (Fop)

Fop was computed according to Ikemura (1982) using custom python3 scripts based on optimal codons derived from a reference set of top 30 highly expressed ribosomal genes.

Translation bias score We introduce our translation bias score to measure the extent to which the codon usage of an organism’s gene expression reflects adaptation for the cellular tRNA supply based on the equation:

$$\left(\left(\text{fraction of preferred codons decoded by major tRNAs}\right)–\left(\text{fraction of nonpreferred codons decoded by major tRNAs}\right)\right)/\left(\text{sum of the fractions}\right)$$

Major tRNAs are the most abundant tRNA isoacceptor within an amino acid class, either based on gene copy number or tRNA concentration. In this article, we used gene copy number as a proxy for cellular tRNA concentrations.

Comparative Phylogenetic Calculations

We downloaded the fungal phylogenetic tree from MycoCosm (https://mycocosm.jgi.doe.gov; last accessed February 2020). The phylogenetic tree was then pruned using Dendropy package (v4.40) in python3.7. Taxonomic ranks were obtained from National Center for Biotechnology Information (NCBI).

PICs model the trait covariation according to the formula Y = β X + ε, where Y and X are traits and β is the evolutionary correlation coefficient that quantifies the degree of coevolution between traits X and Y. PIC was computed with the picante package (Kembel et al. 2010) in R v3.6.0 (R Core Team 2019).

Maximum-likelihood continuous ancestral trait reconstruction was performed using contMap (model=Brownian motion) function from the package phytools (Revell 2012). Blomberg’s K statistic were computed using the phylosig() function in phytools library (Revell 2012) implementation in R which P values are calculated based on 100 permutations.

Fitting and evaluation of maximum-likelihood macroevolutionary models for continuous character evolution were performed using the geiger library (v2.0.6.3; Pennell et al. 2014) in R.

Correlation, Hypothesis, and Multivariate Analyses

All correlation and significance tests were performed using the scipy (v1.3.1) and statsmodels(0.10.1) libraries in python3.7. PCA was performed using the scikit learn (v0.21.3; Pedregosa et al. 2011) in python3.7.

Supervised Neural Network Codon2Vec

Codon2Vec is an ANN that learns the species-specific dependency between the codon composition (features) of a coding sequence (CDS) and expression level. A neural network is a class of machine learning algorithms that uses layers of interconnected computation nodes to learn complex patterns that underlie the data. We implemented and trained Codon2Vec using the keras (v2.2.4) (Chollet 2015) with tensorflow v1.8 backend, and scikit-learn libraries in Python3.7.

Available as a command-line tool for download at this github repository https://github.com/rhondene/Codon2Vec.

Data Set Collection and Preprocessing

We selected CDS from the top and bottom 10% of expression distribution relative to the mean expression. Each CDS was represented as a vector of codons in sequence. Then each unique codon is assigned a unique integer (tokenization) such that each CDS becomes recoded as a vector of integers. Finally, the lengths of the CDS were set to a fixed size of 2,000, either by trimming longer sequences or padding with zeroes. The input and output data were shuffled and partitioned into 70% training set, 20% validation set, and 10% test set. The training set is used to learn the model weights, whereas the validation set is used to fine-tune the model’s generalizability by evaluating whether the model is over- or under-fitting on data it was not trained on. The final evaluation is performed on the test set.

Model Training

Codon2Vec is a feedforward ANN with three fully connected computation layers—embedding layer, rectified linear unit (ReLu) activation layer, and sigmoid output layer. We also incorporated “drop-out” regularization to reduce overfitting. Each layer is described in more detail in the subsequent paragraphs.

Learning Optimized Model Weights

A node is the fundamental computation unit of an ANN. In a fully connected ANN, all nodes of a layer receive the weighted output of each node from the previous layer. The weights (W) represent the relative importance of a node to the model performance. During the forward pass of training, the input (X) undergoes a series of matrix multiplications and nonlinear transformations (Φ) as it flows sequentially between nodes in each layer until the predicted output is generated in the final layer.

$$\text{Generating}\mathrm{ }\text{prediction}:\mathrm{ }\widehat{\mathit{Y}}\mathrm{ }=\mathrm{ }\Phi \left(\mathit{W}\mathrm{T}\mathrm{ }\mathit{X}\right),\mathrm{ }\mathrm{where}\mathrm{ }\mathit{X}\mathrm{ }\mathrm{and}\mathrm{ }\mathit{W}\mathrm{ }\mathrm{are}\mathrm{ }\mathrm{matrices}.$$

Model weights (W) were randomly initialized based on the Glorot uniform distribution. We chose the binary cross-entropy loss as the optimization objective that computes the error between the predicted output ($\widehat{\mathit{Y}}$) and ground truth (Y).

$$\text{Loss}(\mathit{Y},\widehat{\mathit{Y}})=-(\mathit{Y}*\hspace{0.17em}\text{log}(\widehat{\mathit{Y}})+\left(1-\mathit{Y}\right)*\hspace{0.17em}\text{log}(1-\widehat{\mathit{Y}}))$$

where ($\widehat{\mathit{Y}})\in \{\mathrm{0,1}\}$ and Y is binary encoded as 0 or 1.

In the backward pass of training, the contribution of the current set of weights (W) to the model error is computed by taking the partial derivative of the loss function with respect to each layer’s weights (W). The weights are then updated by their gradients in the direction that minimizes the loss function. Weights were tuned via backpropagation using the Adam optimization, a variant of stochastic gradient descent based on adaptive learning.

Model Architecture

The first layer serves as feature extraction by learning the weights that map each of the 64 unique codon features to a meaningful dense real-valued four-dimensional vector (embeddings) in Euclidean space. The number 4 is a hyperparameter. The advantages of embedding representation are: 1) the features that maximize model performance are learned directly from the CDS, 2) the numerical transformation of codons makes modeling amenable to neural networks, and 3) it is more computationally efficient than the alternative one-hot representation as each codon would have been assigned a 1 × 64 dimensional sparse vector of mostly zeroes compared with Codon2Vec’s 1 × 4 dimensional dense vector.

The second layer applies the ReLu activation function to the weighted sum of outputs from the embedding layer. The ReLu function is a widely preferred nonlinear transformation for the inner (hidden) layers of neural networks because it speeds up convergence, and is robust to vanishing gradients.

$$\text{ReLu}\left(x\right)=\text{max}\left(0,x\right)$$

Finally, the output layer applies the sigmoid function that maps the continuous values to a real value between 0 and 1, such that the final output is a two-dimensional vector of the prediction probabilities for each expression class.

Model Evaluation

We evaluated Codon2Vec’s predictive performance using misclassification error, sensitivity, specificity, and precision on the test set. Let TP, TN, FP, FN denote true positives, true negatives, false positives, and false negatives, respectively:

$$\begin{array}{c}\text{Misclassification error}=1-\left(\text{TP}+\text{TN}\right)/\left(\text{TP}+\text{TN}+\text{FP}+\text{FN}\right)\\ \text{Sensitivity}=\text{TP}/\left(\text{TP}+\text{FN}\right)\\ \text{Specificity}=\text{TN}/\left(\text{TN}+\text{FP}\right)\\ \text{Precision}=\text{TP}/\left(\text{TP}+\text{FP}\right)\end{array}$$

Furthermore, we plotted the receiver-operating characteristic curves and calculated the area under the ROC curve (AUC-ROC).

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.