Abstract
A number of developmental theories have been proposed that make differential predictions about the links between age and temporal discounting, or the devaluation of future rewards. Most empirical studies examining adult age differences in temporal discounting have relied on economic intertemporal choice tasks, which pit choosing a smaller, sooner monetary reward against choosing a larger, later one. Although initial studies using these tasks suggested older adults discount less than younger adults, follow-up studies provided heterogeneous, and thus inconclusive, results. Using an open science approach, we test the replicability of adult age differences in temporal discounting by conducting a preregistered systematic literature search and meta-analysis of adult age differences in intertemporal choice tasks. Across 37 cross-sectional studies (Total N = 104,737), a planned meta-analysis found no sizeable relation between age and temporal discounting (r = −0.068, 95% CI [−0.170, 0.035]). We also found little evidence of publication bias or p-hacking. Exploratory analyses of moderators found no effect of research design (e.g., extreme-group vs. continuous age), incentives (hypothetical vs. real rewards), duration of delay (e.g., days, weeks, months, or years), or quantification of discounting behavior (e.g., proportion of immediate choices vs. parameters from computational modeling). Additional analyses of 12 participant-level data sets found little support for a nonlinear relation between age and temporal discounting across adulthood. Overall, the results suggest that younger, middle-aged, and older adults show similar preferences for smaller, sooner over larger, later rewards. We provide recommendations for future empirical work on temporal discounting across the adult life span.
Keywords: aging, time preference, meta-analysis, life span development
“Patience is just another word for getting old”
from Fireworks, lyrics by Maracin Oez, Sebastian Maschat, and Erland Oeye of The Whitest Boy Alive
“At my age, nothing should be postponed”
Alexander von Humboldt, at 60 years of age (Wulf, 2015)
Many everyday decisions involve tradeoffs between immediate satisfaction and long-term well-being. Should one spend a monetary bonus now or save it for a later occasion, by investing the money in a retirement fund? When faced with such tradeoffs, people show a tendency to discount future rewards (i.e., diminish the value of future relative to immediate or sooner rewards)—a phenomenon known as temporal or time discounting (Frederick et al., 2002). There is debate about whether temporal discounting changes systematically throughout adulthood as a function of socioemotional or neurobiological age-related changes (cf. Eppinger et al., 2012; Samanez-Larkin et al., 2011). Although some lay and scientific theories favor the idea that patience increases with age (e.g., Duckworth & Steinberg, 2015), others share Alexander von Humboldt’s idea that old age can accept no delays in gratification (e.g., Carstensen, 2006). In this paper, we test these views by offering a preregistered systematic review and meta-analysis of potential age-related differences in temporal discounting. We first provide an overview of theoretical perspectives and associated mechanisms that could produce age differences in temporal discounting. Second, we briefly review extant empirical findings, and, third, give an overview of and offer a rationale for the present quantitative review.
Theoretical Perspectives on Age Differences in Temporal Discounting
There are a number of theoretical frameworks or models that suggest that temporal discounting may change across adulthood (cf. Read & Read, 2004). In what follows, we describe some of these theories and their hypothesized age effect on temporal discounting. Table 1 offers an overview of the different theories discussed.
Table 1.
Overview of Potential Mechanisms Linking Age and Temporal Discounting
| Mechanism(s) | Age effect |
|---|---|
| Limited time horizon: Reduction in the perceived probability of future reward due to a limited time horizon (Carstensen, 2006) | ↑ discounting with age |
| Limited time horizon + Delay: Limited time horizon in older adults (Carstensen, 2006) only operates for long(er) delays (e.g., months/years vs. days/weeks; Richter & Mata, 2018) | ↑ discounting with age for longer delays |
| Affective forecasting: Improvement in affective forecasting with age (Scheibe et al., 2011) increases salience of future needs (cf. Löckenhoff et al., 2011) | ↓ discounting with age |
| Time perception: Perceived speeding up of time with age (Block et al., 1998) reduces salience of time delay (cf. Löckenhoff, 2011) | ↓ discounting with age |
| Impulsivity: Reductions in impulsive behavior from adolescence to adulthood due to reductions in reward sensitivity and increased cognitive control (e.g., Duckworth & Steinberg, 2015) | ↓ discounting with age, particularly between young adulthood and middle-age |
| Impulsivity + Limited time horizon: Reductions in impulsivity from adolescence to adulthood (Duckworth & Steinberg, 2015) + limited time horizon in old age (Carstensen, 2006; Trostel & Taylor, 2001) | U-shaped function of age |
| Impulsivity + Declines in executive function: Reductions in impulsivity from adolescence to adulthood (Duckworth & Steinberg, 2015) + age-related declines in executive function (Verhaeghen & Cerella, 2002) leading to increased impulsivity | U-shaped function of age |
| Mortality: increased likelihood of mortality and the associated cost of waiting leads to more discounting in older and younger adults, respectively (Sozou & Seymour, 2003), although this may vary based on life history (Griskevicius et al., 2011). | U-shaped function of age |
| Confound of cognitive ability: Age-related reductions in cognitive ability leads to differences in temporal discounting due to choice-inconsistency (Olschewski et al., 2018) | Varies by task demands |
Some adult developmental theories suggest that because their future time is more limited than younger adults, older adults are more present-oriented (Carstensen, 2006; Lang & Carstensen, 2002). It follows that because of their limited time horizons, older adults may view the future as more uncertain. This uncertainty may lead older adults to discount future rewards more than younger adults (Trostel & Taylor, 2001), particularly over larger time delays (Richter & Mata, 2018). However, there are several other theoretical reasons why one would predict the opposite relationship between age and temporal discounting. For instance, the subjective perception that time passes faster as we age (Block et al., 1998; Löckenhoff, 2011) could lead older adults to view a potential delay as shorter in duration. This subjectively shorter delay may make the delayed reward seem subjectively closer to older adults, and thus lead them to discount less. Likewise, studies have suggested that older adults may be better than younger adults at predicting their future emotions (i.e., affective forecasting; Scheibe et al., 2011). This enhanced ability to imagine and predict future states in older adults may make the future seem subjectively closer to them, and thus lead them to discount less (Löckenhoff, 2011). Further, early adult development of stronger volitional processes with age, including better executive function and metacognitive strategies (Duckworth & Steinberg, 2015), could decrease the influence of impulsigenic processes such as reward sensitivity and sensation seeking. If this process continues across adulthood it could lead to less discounting in older individuals. Consistent with this idea, there is some evidence that overall self-control in everyday life is higher at older compared to younger ages (Burr et al., 2020). Thus, prominent developmental theories make opposite predictions about the direction of age-related change in temporal discounting.
In contrast to the linear patterns above, other theories posit more complex trajectories. For instance, because risk taking is increased for younger adults and mortality is increased for older adults, it is possible that younger and older individuals will die before a delayed reward is realized. Because of this potential delay cost, these age groups display more discounting than middle-aged persons, creating a U-shaped function with age (Sozou & Seymour, 2003). Similarly-shaped functions are predicted by combining theories. For instance, combining declining impulsivity with limited time horizons predicts a U-shaped curve—increasing volitional control in early adulthood decreases discounting in middle-aged adults, where limited time horizons then change goals to be more present-oriented, leading to increased discounting in older adults. Likewise, combining declining impulsivity with age-related declines in executive function can create a U-shaped function. Whereas increasing volitional control in early adulthood leads to decreases in discounting, declining executive function in older adulthood (Verhaeghen & Cerella, 2002) could lead to increases in discounting. Further, declining executive function in adulthood could also lead to choice-inconsistency, depending on how demanding the choice task is (Olschewski et al., 2018). As summarized in Table 1, there is great diversity in theoretical predictions about the development of temporal discounting across the adult life span.
Empirical Findings on Temporal Discounting Across Adulthood and Aging
The empirical literature on aging and temporal discounting is decidedly mixed. Although initial studies of temporal discounting and aging suggested that people become more patient with age and discount less (Green et al., 1994), follow-up studies suggested that socioeconomic status was a stronger predictor of temporal discounting than age (Green et al., 1996). More recent behavioral studies are equally inconsistent, with studies reporting increased discounting with age (e.g., Read & Read, 2004), no discounting with age (e.g., Rieger & Mata, 2015), and decreased discounting with age (e.g., Löckenhoff et al., 2011). Similarly, neuroimaging studies have shown mixed results, with smaller, initial studies showing age differences in functional neural activity during temporal discounting (Eppinger et al., 2012; Samanez-Larkin et al., 2011) but larger, subsequent studies showing no age differences in functional neural activity during temporal discounting across adulthood (Seaman et al., 2018). These contradictory results make it difficult to summarize or draw conclusions about the impact of aging on temporal discounting. We aim to address this current state of affairs by systematically gathering and summarizing the existing research in a meta-analysis.
Overview and Rationale for the Present Meta-analysis
Because of the theoretical and empirical heterogeneity introduced above, we decided to investigate adult age-related differences in temporal discounting. The goal of our study was to systematically gather and summarize the existing research in a meta-analysis that was preregistered on the Open Science Framework (OSF) at https://osf.io/e4anc and ResearchGate at https://www.researchgate.net/project/Age-differences-in-temporal-discounting. Fully embracing an open science approach, we have also provided study-level data and code for all analyses on OSF (https://osf.io/ch9eg). Based on our intuitive reading of the literature and our own work, we predicted a nonsignificant or very small negative effect of age on time discounting (i.e., older adults discount less than younger adults). It should be noted, however, that because the authors had some prior knowledge of some of the studies included in this meta-analysis, this prediction is not an ideal a priori hypothesis (Nosek et al., 2018).
Our analysis followed four main steps. First, we conducted a systematic literature search following PRISMA guidelines (Liberati et al., 2009). Consequently, we identified potentially relevant studies for the meta-analysis, defining relevant studies as original research articles that compared either temporal discounting in younger and older adults or correlations between age and temporal discounting in an adult sample. We also solicited unpublished results via decision-making listservs, online preregistrations, and follow-up emails to authors presenting unpublished results at decision-making conferences.
Second, we used meta-analytic methods to summarize the relation between age and temporal discounting as well as to test the role of potential moderators in determining the link between age and temporal discounting. We selected a number of potential moderators: The first potential moderator was research design; specifically, we classified studies as to whether age was treated as a continuous variable or a grouping variable. Prior studies have shown that extreme-group designs can bias estimates (Preacher et al., 2005). The second potential moderator identified was whether the incentives used were real or hypothetical. Although there are strong correlations between real and hypothetical incentives (e.g., Seaman et al., 2018), the use of real rewards (vs. hypothetical rewards) has been shown to reduce discounting (e.g., Coller & Williams, 1999). The third potential moderator identified was the duration of delay (e.g., days, weeks, months, or years). Prior work has shown that the duration of delay can impact discounting (e.g., Richter and Mata, 2018). The final potential moderator identified was the quantification of discounting behavior (e.g., parameter estimation of discount rate or proportion of delayed options chosen). Again, although prior studies have found a strong correlation between parameter estimates and proportional measures (e.g., Seaman et al., 2018), parameter estimation may be more sensitive to small effects than proportional measures. Each of these potential moderators was tested in a separate analysis.
Third, it has been argued that the field of aging may be affected by research practices that lead to bias in published results due to incentives associated with identifying significant age differences. Thus, it is important to quantify possible bias in the aging literature (Isaacowitz & Lind, 2019). We looked for evidence of publication bias and p-hacking in the studies included in our analysis. Publication bias, or the file drawer problem, refers to the tendency to publish studies showing a significant effect whereas studies that show a null effect go unpublished. We examine the included studies for publication bias using funnel plots, which visualize the effect sizes versus study precision, and Egger’s test, which tests for asymmetry in the distribution. Asymmetry suggests that there may be a publication bias in the literature. P-hacking refers to situations where the researcher selectively reports only data or analyses that show a significant effect. We examine the included studies for p-hacking using p-curve analysis, which plots the p-value versus the percentage of studies in the sample. A left-skewed p-curve suggests that researchers may be p-hacking in order to get to p = 0.05.
Fourth, and finally, we explored curvilinear relationships between age and temporal discounting for those raw data sets that were publicly available or we received from our requests to authors. As noted in Table 1, some theories have suggested that temporal discounting differs in a nonlinear fashion across the adult life span. Thus, we were interested in assessing whether current data sets reveal any significant convex (or concave) effects of age on temporal discounting.
Methods
Literature Search
We conducted a systematic review of the literature on January 2, 2019 to identify original empirical articles that estimated adult age differences in temporal discounting. Our procedure is illustrated in a flow diagram based on the PRISMA guidelines (Figure 1) and a detailed description follows:
Figure 1. Systematic Review Diagram.
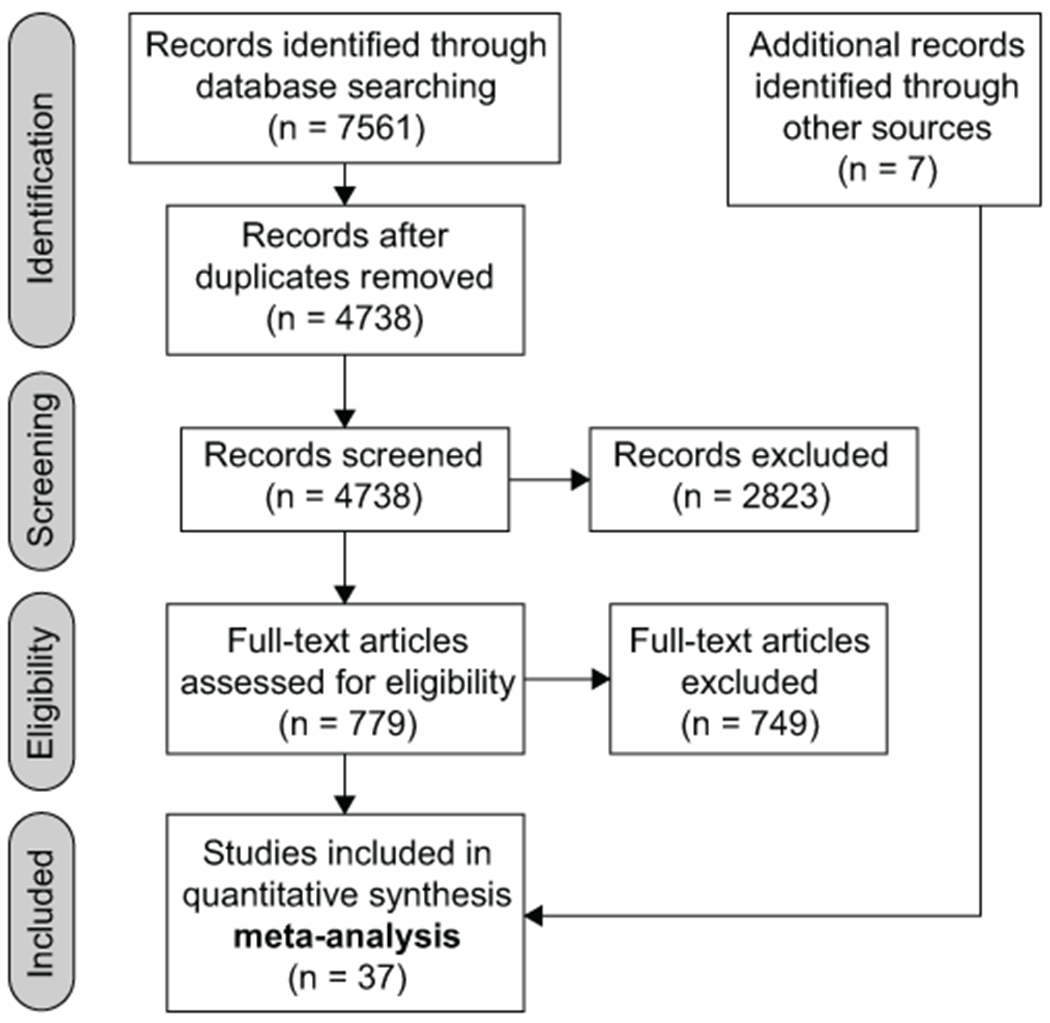
Prisma flow chart detailing the database searches, the number of abstracts screened and the full texts retrieved. Seven additional raw data sets were acquired outside of this systematic review.
We used the digital databases PsycINFO, PubMED and Web of Science (WoS) core collection database for our literature search with a combination of keywords related to time preferences (e.g., delay of gratification, delay discounting, temporal discounting, intertemporal choice, delay aversion). The keywords also included the names of frequently used questionnaires or tasks to measure temporal discounting. These instruments had to be noted in the general literature reviews of temporal discounting. We also included terms concerning age differences or aging (e.g., aging, older adults, elderly, age differences).
In addition, we performed a literature search in PsycINFO, PubMED and WoS for articles citing the original paper reporting any of the discounting measures mentioned in the general literature review described above (The Kirby questionnaire; Kirby et al., 1999; Kirby & Maraković, 1996; Delay Discounting Task, Coller & Williams, 1999; and Delay of Gratification Task, Mischel et al., 1989).
Papers cited in the reviews on aging and decision making were either individually searched in PubMED or cross referenced (Brown & Ridderinkhof, 2009; Hsu et al., 2008; Lim & Yu, 2015; Löckenhoff, 2011; Mather, 2006; Peters et al., 2007; Spreng, 2016).
After completing an initial literature review, we checked the references of the articles that met our inclusion criteria.
In December 2017 we emailed two listservs for unpublished results or data (Society for Judgment and Decision Making; European Association for Decision Making);
In April 2017 we uploaded our preregistration onto the Open Science Framework (https://osf.io/e4anc) and ResearchGate (https://www.researchgate.net/project/Age-differences-in-temporal-discounting), advertising our efforts and asking for any additional references, results, or data.
Most of our procedures were outlined in our preregistration (see below for a list and rationale for deviations from the preregistered protocol). Details of the search can be found on our OSF repository at https://osf.io/ch9eg/. The keyword search (Point 1 above) resulted in the following numbers of hits: PubMED (167), PsycInfo (152), and WoS (714). The article citation search (Point 2 above) resulted in the following number of hits: PubMED (801), PsycInfo (598) and WoS (2603). An additional 2,526 articles were added from references included in reviews on aging and decision making (Point 3 above) and from references of included articles (Point 4 above). All papers retrieved were collected in a Zotero group and then uploaded into the online software, Covidence (Covidence Systematic Review Software, 2020). In the literature-review process, we used Covidence for the abstract and full-text screening, and also for extracting the relevant data for our analysis. All articles were first screened by abstract and studies were excluded if they clearly did not meet the inclusion criteria listed below. If the information was ambiguous, the study was included for full-text screening. For example, if the age range was not explicitly stated in the abstract (e.g., undergraduates) the study was included for the full-text screen. At all stages there were two individuals performing the screening (Z. F. & S. A.). In the event of a conflict a third independent individual (K. S.) resolved the issue by going through the disagreed-upon studies.
Inclusion Criteria
Studies or measures were included if they reported:
results based on a behavioral measure of temporal discounting involving real or hypothetical rewards, or results based on a self-report questionnaire of temporal discounting behavior,
a temporal discounting outcome (e.g., proportion of choices, k parameter, area under the curve, indifference points) concerning at least one comparison between a group of younger (approx. 18–35 years) and older (approx. 65–85 years) individuals, reporting the outcome for each age group (mean, standard deviation) in numerical or graphical format, a test statistic that can be used to compute an effect size corresponding to age-related differences, or this information is attainable from the authors, or
a correlation between age and at least one measure of temporal discounting in an adult sample (i.e., majority of respondents are older than 18 years of age) and a minimum age range of 25 years, or this information is attainable from the authors.
Exclusion Criteria
We limited our analyses to those studies that focus on the effect of age on temporal discounting. Studies or measures were excluded if:
the sample was a subsample of another included study,
the sample primarily consisted of people with cognitive impairment (e.g., Parkinson’s disease, Alzheimer’s disease, or mild cognitive impairment) or other disorders that are known to influence cognition (e.g., depression, attention deficit hyperactivity disorder, addictive disorders),
the measure examined probability or effort discounting or combined temporal discounting with probability or effort discounting,
a non-monetary reward was used (e.g., juice), or
the study was not included in a peer-reviewed publication (e.g., thesis or book chapter).
Title and abstract screening resulted in 779 references that were then subjected to full-text screening. This resulted in a total of 30 studies for inclusion in our analyses. Reasons for exclusions, along with numbers of studies excluded for those reasons, can be seen in Supplementary Materials Table 1. In addition to the systematic literature search, direct contact with researchers (Points 5 and 6) resulted in four unpublished data sets and three additional published data sets. Collectively, a total of 37 independent studies were included.
Changes to Initial Preregistration
Our procedures were outlined in the preregistration; however, we made a number of changes to our protocol as we began the systematic review, with the goal of ensuring comprehensiveness of our search or clarifying exclusion criteria. We list these here: First, the Web of Science database search and an expanded list of keyword search terms were added (see Supplementary Materials for full list of search terms) to the search criteria to further increase the comprehensiveness of our review. Second, we expanded the exclusion criteria to explicitly exclude addiction disorders such as drug or alcohol addiction and pathological gambling. Third, we explicitly excluded studies using nonmonetary rewards. Fourth, we excluded book chapters and dissertations, with the reasoning that they are not peer reviewed, could not be comprehensively assessed, and could be published in another form. Fifth, we excluded studies that we could not access through the University of Basel or Duke University libraries and were not freely available online. Sixth, we excluded loss discounting conditions, as discounting for losses is not commonly investigated and it shows different response pattern than discounting for gains (e.g. Estle et al., 2006).
Acquisition of Raw Data Sets
We emailed listservs—Judgment and Decision Making Society (www.sjdm.com) and the European Association for Decision Making (eadm.eu)—to identify unpublished data sets that met our inclusion criteria (N = 2; O’Hora et al., 2016; Sisso, Itay, n.d.). Here we opted to include unreviewed material because (1) we would review the data and supporting material when it was shared with us and (2) we would be completing the data analyses ourselves. The first author also reached out to inquire about unpublished data sets that were presented at the 2017 Association for Consumer Research conference and the 2018 Society for Neuroscience conference (N = 3; Hampton et al., 2018; Lempert et al., 2018; Li et al., 2020). After a preliminary literature review in Fall 2017, a research assistant contacted the first and last authors of all papers to request raw data (N = 5; (Chao et al., 2009; Halfmann et al., 2013; Kirby et al., 2002; Löckenhoff et al., 2011; Tschernegg et al., 2015). One raw data set was downloaded from OSF (N = 1; Lee 2018). The first author also contributed her own data set (N = 1; Seaman et al., 2016). Through these efforts, we gained access to the 12 raw data sets used in the nonlinear analyses described below.
Analyses
We analyzed all temporal discounting outcomes (e.g., proportion of delay options, k values, area under the curve, indifference points) that were used in more than one study. To estimate the effect of age on temporal discounting, we used the metafor (Viechtbauer, 2010) and esc (Lüdecke, 2019) packages in R. For each study we calculated the Fisher’s z transformation of either:
the standardized mean difference (d) in discounting between two age groups using group means and standard deviations or standard errors, F values from ANOVAs or t values from t-tests comparing two age groups (Table 2), or
the correlation (r) between age and discounting (Table 3).
Table 2.
Extreme Group Studies Included in Meta-analysis
| Study | Incentive | Delay | Measure | Younger | Older | z | Var z | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||||||
| N | Age |
N | Age |
||||||||||
| Mean | Range | SD | Mean | Range | SD | ||||||||
| Bauer 2010 | hypothetical | years | proportion | 291 | 24.02 | 20-29 | -- | 241 | 39.91 | 30-74 | -- | 0.06 | 0.00 |
| Buono 2015 | hypothetical | years | parameter | 20 | 22.50 | 18-27 | -- | 18 | 50.00 | 45-55 | -- | 0.35 | 0.03 |
| Eppinger 2012 | real | weeks | proportion | 15 | 20.90 | 18-28 | 3 | 15 | 69.70 | 65-80 | 4.4 | −0.85 | 0.04 |
| Eppinger 2018 | real | weeks | proportion | 25 | 24.80 | -- | 2.5 | 25 | 71.20 | -- | 5.6 | −0.31 | 0.02 |
| Garza 2016 | hypothetical | years | parameter | 139 | 57.00 | 50-64 | -- | 9 | 70.50 | 65-76 | -- | −0.03 | 0.01 |
| Green 1994 | hypothetical | years | parameter | 12 | 20.30 | -- | -- | 12 | 67.90 | -- | -- | −0.91 | 0.05 |
| Halfmann 2016 | hypothetical | days | parameter | 77 | 21.00 | -- | -- | 36 | 77.00 | -- | -- | −0.10 | 0.01 |
| Jimura 2011 | hypothetical | years | parameter | 20 | 20.00 | -- | -- | 20 | 71.00 | 60-84 | 7.5 | 0.34 | 0.03 |
| Li 2013 | hypothetical | months | parameter | 173 | 24.76 | 18-29 | 2.91 | 163 | 66.39 | 60-82 | 4.93 | −0.08 | 0.00 |
| Liu 2016 | hypothetical | days | parameter | 745 | 43.27 | 31-60 | 6.74 | 192 | 68.63 | >61 | 5.46 | 0.07 | 0.00 |
| Roalf 2012 | real | days | parameter | 29 | 30.14 | 21-45 | 5.53 | 25 | 71.30 | 65-85 | 4.36 | 0.14 | 0.02 |
| Samanez-Larkin 2011 | real | weeks | proportion | 12 | 22.00 | 19-26 | -- | 13 | 73.40 | 63-85 | -- | 0.04 | 0.05 |
| Sparrow 2018 Study 1 | real | days | proportion | 32 | 25.28 | 18-35 | 5.22 | 30 | 70.57 | 65-85 | 4.88 | −0.51 | 0.02 |
| Sparrow 2018 Study 2 | real | days | proportion | 31 | 20.84 | 18-30 | 2.67 | 23 | 71.35 | 65-97 | 6.96 | −0.04 | 0.02 |
| Sparrow 2019 | real | days | proportion | 36 | 21.00 | 18-30 | 3.44 | 36 | 70.11 | 65-85 | 4.91 | 0,03 | |
| Whelan 2009 | hypothetical | years | parameter | 16 | 46.00 | -- | 3.4 | 10 | 73.00 | -- | 4.12 | 0.10 | 0.04 |
Table 3.
Continuous Age Studies Included in Meta-analysis
| Study | Incentive | Delay | Measure | Age |
N | z | Var z | |
|---|---|---|---|---|---|---|---|---|
| Mean | SD | |||||||
| Bickel 2014 | hypothetical | days | parameter | 31.64 | 11.25 | 1163 | −0.05 | 0.00 |
| Boyle 2012 | hypothetical | months | parameter | 83.1 | 6.7 | 388 | −0.04 | 0.00 |
| Chao 2009 | hypothetical | days | parameter | 46.52 | 15.09 | 175 | 0.08 | 0.01 |
| Göllner 2018 | hypothetical | days | parameter | 46.48 | -- | 96 | 0.13 | 0.01 |
| Halfmann 2013 | hypothetical | weeks | parameter | 68.19 | 19.74 | 48 | 0.05 | 0.02 |
| Hampton 2018 | hypothetical | years | parameter | 41 | -- | 2564 | −0.04 | 0.00 |
| Johnson 2015 | hypothetical | hours | parameter | 35.57 | -- | 197 | −0.23 | 0.01 |
| Kirby 2002 | real | days | parameter | 27.4* | -- | 154 | 0.31 | 0.01 |
| Lee 2018 | hypothetical | days | parameter | 26.79 | 9.1 | 11157 | −0.07 | 0.00 |
| Lempert 2018 | hypothetical | days | parameter | 72.07 | 6.83 | 74 | −0.07 | 0.01 |
| Li 2020 Study 2 | hypothetical | days | parameter | 45.52 | 16.28 | 619 | 0.06 | 0.00 |
| Löckenhoff 2011 | real | days | parameter | 52 | 20.5 | 98 | −0.34 | 0.01 |
| Mahalingam 2018 Sample 3 | hypothetical/real | year | parameter | 36.16 | 12.11 | 189 | −0.02 | 0.01 |
| Mahalingam 2018 Sample 4 | hypothetical | year | parameter | 38.01 | 13.42 | 208 | 0.10 | 0.00 |
| Mahalingam 2018 Sample 5 | hypothetical | year | parameter | 27.81 | 18.71 | 151 | 0.01 | 0.01 |
| Mahalingam 2018 Sample 6 | hypothetical | year | parameter | 35.79 | 11.5 | 420 | 0.03 | 0.00 |
| O’Hora 2016 | hypothetical | years | parameter | 30.93 | 12.1 | 840 | −0.01 | 0.00 |
| Reimers 2009 | hypothetical | months | proportion | -- | -- | 42863 | −0.05 | 0.00 |
| Sanchez-Roige 2018 | hypothetical | days | parameter | 53.79 | 16.08 | 23664 | 0.00 | 0.00 |
| Seaman 2018 | real | weeks | parameter | 49.71 | 17.92 | 89 | 0.12 | 0.01 |
| Sheffer 2016 | hypothetical | days | parameter | 34 | 11 | 1122 | 0.05 | 0.00 |
| Sisso 2020 | hypothetical | weeks | proportion | 49.34 | 14.64 | 2630 | −0.01 | 0.00 |
| Stoeckel 2013 | real | days | parameter | 33.4 | 9.8 | 19 | −0.67 | 0.06 |
| Tschernegg 2015 | hypothetical | months | proportion | 25.22 | -- | 70 | −0.10 | 0.01 |
| Wolfe 2017 | hypothetical | years | proportion | 36.92 | 11.7 | 13198 | 0.04 | 0.00 |
Data Cleaning and Missing Information
There were several studies that reported multiple measurements of discounting for each individual, either under different conditions or in separate sessions (N = 7; Eppinger et al., 2018; Hampton et al., 2018; Johnson et al., 2015; Li et al., 2013; Liu et al., 2016; Mahalingam et al., 2018; Whelan & McHugh, 2009). In these instances, we calculated the average effect size across all conditions/sessions. Similarly, there were a number of studies that reported multiple age groups (N = 2; Garza et al., 2016; Liu et al., 2016). In these instances, we averaged the effect sizes across age group comparisons, reasoning that if there is a linear effect of age, the true effect would be best captured by the average of these estimates. For studies that did not report all of the necessary information for calculating effect size in the main text or the tables, we either calculated the necessary information from raw data (N = 2; Halfmann et al., 2013; Whelan & McHugh, 2009) or extracted information from graphs using Web Plot Digitizier (Rohatgi, 2019); N = 3, Eppinger et al., 2018; Sparrow et al., 2019; Sparrow & Spaniol, 2018).
Due to the various ways discounting behavior was quantified, some measures of discounting were coded such that higher values reflected more discounting whereas others were coded such that higher values reflected less discounting (e.g., discount rate or factor). To account for these differences in direction, the effect sizes in studies using discounting measures where higher values reflected less discounting (N = 8; Green et al., 1994; Hampton et al., 2018; Li et al., 2013; Löckenhoff et al., 2011; Sparrow et al., 2019; Sparrow & Spaniol, 2018; Wolfe & Patel, 2017) were reverse coded. Thus, in our analysis positive effect sizes reflect more discounting with age whereas negative effect sizes reflect less discounting with age.
Meta-Analytic Procedures
Given the wide variation in methodology and in the reported outcome measures, the measures of effect size (Fisher’s z) were entered into a random-effects model as it assumes between-study variance unlike the fixed-effects model and allows for greater generalization (Field & Gillett, 2010). The random-effects model was estimated using the meta package in R (Balduzzi et al., 2019) using the Hartung-Knapp-Sidik-Jonkman (HKSJ) method for estimating between-study variance (IntHout et al., 2014). We report effect sizes along with 95% prediction intervals (IntHout et al., 2016). We also ran a post hoc Bayesian meta-analysis using the brms package in R (Bürkner, 2017, 2018) upon a request from an anonymous reviewer. To explore the amount of heterogeneity in the meta-analytic data set, we calculate and report Cochran’s Q and I2. as well as performing outlier and influence analyses using the dmetar package in R (Harrer et al., 2019).
Next, we ran meta-regressions to examine the potential moderator variables. The potential moderators explored were: (a) research design, (b) incentive type, (c) magnitude of delay, and (d) quantification. Research design was coded as “age continuous” if age was treated as a continuous variable or “extreme group” if age groups were used. Incentive type was coded as either “real” if participants were compensated based on their performance or “hypothetical” if they were not. Magnitude of delay was coded based as “hours”, “days”, “weeks”, “months” or “years”. If more than one label applied, the longest time delay was used for the moderator analysis. Quantification was coded as “parameter” if an estimated model parameter was reported or “proportion” if the proportion of delayed options chosen was reported. Each potential moderator was first entered into a separate mixed-effects model. Then, significant moderators were all entered into a single mixed-effects model to test for potential confounding among moderators.
We explored possible sources of bias in the meta-analysis using the dmetar package in R (Harrer et al., 2019). First, we examined funnel plots, or plots of effect sizes by their standard error. These plots were assessed for symmetry both visually and statistically using the Egger test (Egger et al., 1997). This test uses regression to determine whether the effect size decreases with increasing sample size and asymmetry in the funnel plot is significant. Next, we used “p-curve” analyses (Simonsohn et al., 2014) to examine the distribution of p-values. This analysis tests whether there were more p-values near the alpha level (e.g., 0.05) than would be expected by chance (Nuzzo, 2014).
Analyses of Raw Data Sets
We were able to identify and analyze 12 data sets for which the majority of participants was over 18 years of age, the range of ages spanned at least 25 years, and the temporal discounting outcome was on an ordinal or continuous scale (i.e., we did not consider studies that consisted of a single binary outcome per participant because these would be difficult to compare). For those studies that included both gains and losses we considered only the gains conditions (Halfmann et al., 2013; Loeckenhoff et al., 2011). We recoded the outcome measure of some studies so that across studies higher values of the temporal discounting measure reflect more discounting. We also recoded age as decades. For each data set we fit and compared regression models (Gaussian family) that estimated either (a) a linear effect of age or (b) both a linear and quadratic effect of age on temporal discounting. We also conducted an additional analysis that relaxes the assumption of a specific functional-form, the two-lines test, an algorithm developed to provide higher power to detect U-shaped relations (Simonsohn, 2018). In this manner, we aimed to obtain an assessment of the proportion of studies that revealed significant nonlinear effects of age on temporal discounting using these different methods.
Results
Meta-analysis
A random-effects meta-analysis suggested that there are no significant adult age differences in temporal discounting (r = −0.068, 95% CI [−0.170, 0.035], Fisher’s z = −1.30, p = 0.193). Figure 2 presents a forest plot with the correlation and respective 95% confidence intervals (CI) for each study included in the meta-analysis, as well as the sample size (N) and the weight given to each study in both the fixed- and random-effects analysis. The strongest effect was found for the earliest study of aging and temporal discounting: Green et al. (1994). However, all subsequent studies found smaller effects, no effects, or effects in the opposite direction. There was also evidence of a small study effect (Sterne et al., 2000)—strong effects in either direction came from small studies (N < 200) whereas studies with very large sample sizes (N > 10,000) tended to show small or no effects of age on discounting behavior.
Figure 2. Forest Plot for all Studies.
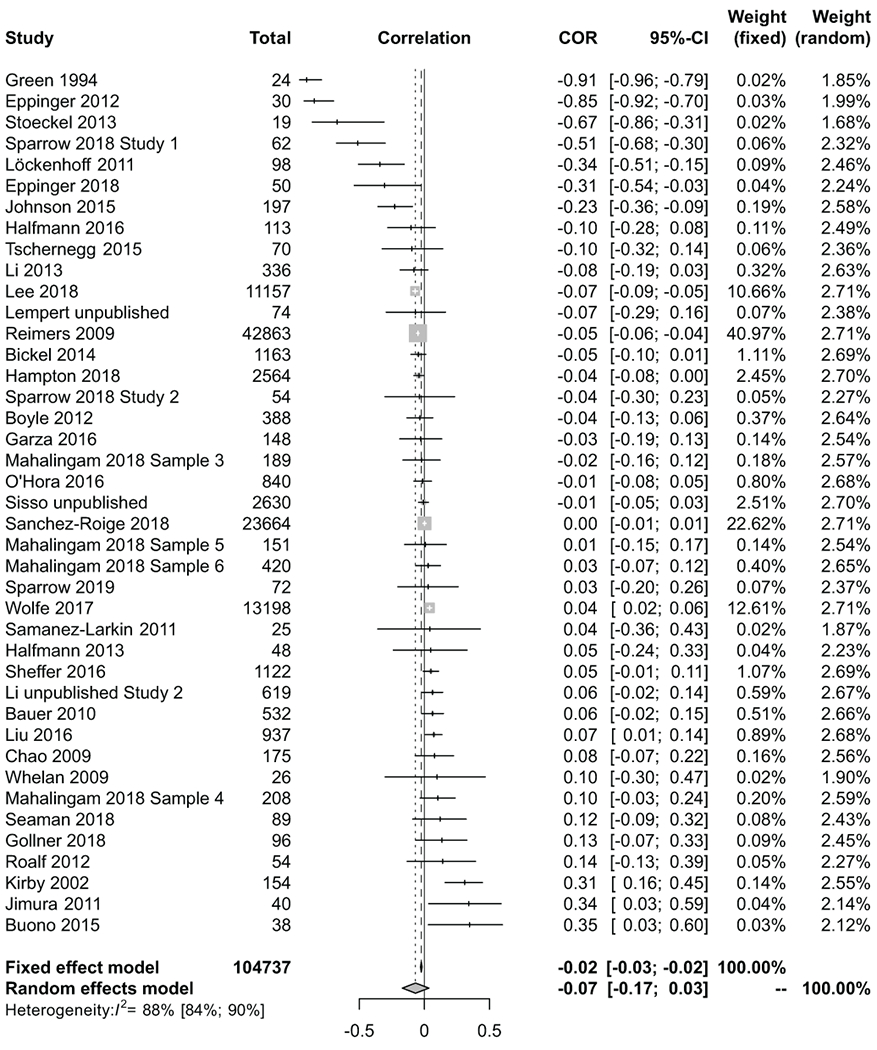
The position of the squares on the x-axis indicates the effect size for each study; the bars indicate the 95% confidence interval for the effect size and the squares represent the inverse of the standard error. Positive effect sizes reflect more discounting with age whereas negative effect sizes reflect less discounting with age.
There was substantial heterogeneity in our set of studies, Cochran’s Q(40) = 327.79, p < .001 and I2 = 87.8%, 95% CI [84.4%; 90.5%], so we conducted an outlier analysis. This analysis identified eight outliers in the random-effects model, four of which had large negative effects (Eppinger et al., 2012; Green et al., 1994; Sparrow & Spaniol, 2018 Study 1; Stoeckel et al., 2013) and one of which had a large positive effect (Kirby et al., 2002). Even excluding these outliers, there was still significant heterogeneity in the analysis (Q(32) = 196,81, p; < 001; I2 = 82.2%, 95% CI [76.2%; 86.7%]) and still no significant relationship between age and temporal discounting (r = −0.004, 95% CI [−0.046; 0.038], z = −0.18, p = 0.855).
We also conducted a post hoc Bayesian meta-analysis upon a request from an anonymous reviewer (see Supplemental Materials for more details). Consistent with our frequentist analysis, the model produced a very small estimate of the pooled effect size, μ = −0.05, 95% CI [−0.13, 0.03] whose credible interval contains zero, and an estimate of study heterogeneity, τ = 0.27, 95% CI [0.22, 0.34], Using the posterior distribution (Figure S1), we found little support for the effect of age on discounting being greater than zero (9% probability z > 0), strong evidence to support the hypothesis that the effect of age on discounting was less than zero (91% probability z < 0), and little support for the hypothesis that this was a medium or strong effect (13.1% probability that z < −0.1). Collectively, these results suggest that age has no sizeable effect on discounting, with zero being included in the credible interval for both the frequentist and Bayesian meta-analyses. However, the latter analysis provides support for the hypothesis that age may have a negative, albeit very small, effect on discounting.
The position of the squares on the x-axis indicates the effect size for each study; the bars indicate the 95% confidence interval for the effect size and the squares represent the inverse of the standard error. Positive effect sizes reflect more discounting with age whereas negative effect sizes reflect less discounting with age.
A funnel plot, Egger’s test, and a p-curve analysis were conducted to examine publication bias. Although the funnel plot shows some asymmetry in the data (Figure 3), the Egger’s test was not significant (t = −0.17, p = 0.865). We also conducted a full p-curve analysis that included the 15 studies (36.59% of sample) with significant effect sizes (p < .05) and a half p-curve analysis that included the 10 studies (24.39% of the sample) with p < .025. For both analyses, the right-skew analysis was significant (full: z = −10.281, p < .001; half: z = −13.125, p < .001), indicating that the significant results likely did not arise from p-hacking. Also, for both analyses the flatness test was not significant (full: z = 7.873, p > 0.999; half: z = 11.719, p > 0.999) and power was adequate (power = 99%, 95%CI [96%–99%]), suggesting that the power of the studies included is sufficient to detect an effect. Collectively, these analyses provide no support for the idea that the meta-analytic results are the product of publication bias or p-hacking.
Figure 3. Funnel plot.
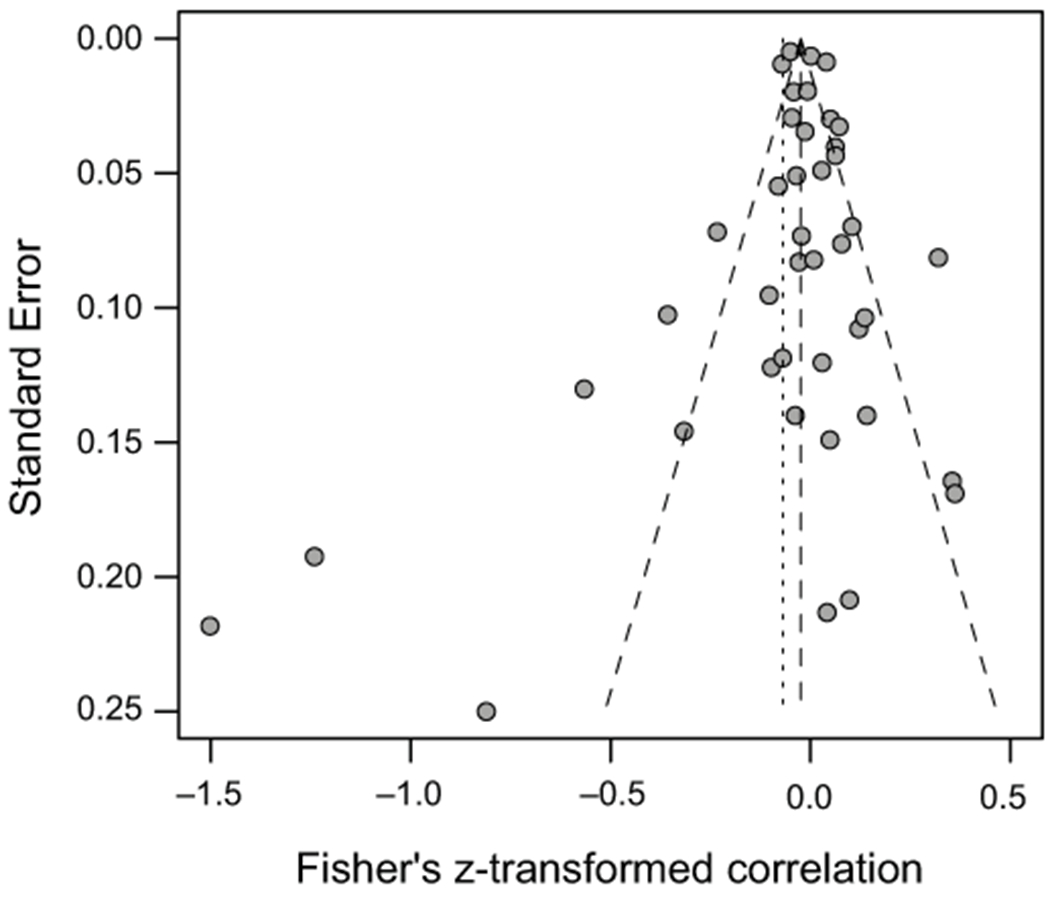
Diagram showing the effect size of each study on the x-axis and the standard error of each study on the y-axis (with larger studies plotted towards the top of the y-axis).
We explored several possible moderators to determine whether methodological differences could account for some of the heterogeneity in effect sizes. We tested four meta-regression models, each with a different moderator. The potential moderators explored were: (a) research design, (b) incentive type, (c) magnitude of delay, and (d) quantification. There was no significant difference in effects based on research design (only 0.93% of heterogeneity accounted for, χ2(1) = 1.30, p = 0.255), incentive type (3.11% of heterogeneity accounted for, χ2(1) = 2.12, p = 0.145), magnitude of delay (0.00% of heterogeneity accounted for, χ2(4) = 134, p = 0.854) or method of quantification (1.22% of heterogeneity accounted for, χ2(1) = 1.428, p = 0.232). Because none of these moderators were significant, we did not explore any models with multiple moderators.
Analyses of Raw Data Sets
Table 4 shows the results for each of the raw data sets that were independently analyzed. Across the 12 data sets, only one study showed a significantly better fit for the quadratic relative to a simple linear effect of age (Tschemegg et al., 2015), showing relatively stable discount rates until approximately 30 years, and a decrease from 30 years onwards. The two-lines test (Simonsohn, 2018) showed a significant effect for another study (Li et al., 2020), denoting an increase in temporal discounting until approximately aged 55 years and a decrease from 55 years onwards, but neither the increase nor decrease was significant according to the two-line test. All in all, these results provide little support for a systematic nonlinear relation between age and temporal discounting in these samples.
Table 4.
Results of the Analyses of Raw Data Sets
| Study | N | Model 1: Age | Model 2: Age + Age2 | Difference | U | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Int | Age | R 2 | F | p | Int | Age | Age2 | R 2 | F | p | F | p | |||
| Chao et al. (2009) | 175 | −0.24 | 0.05 | 0.01 | 1.05 | 0.31 | −0.47 | 0.16 | −0.01 | 0.01 | 0.61 | 0.55 | 0.17 | 0.68 | ns |
| Halfmann et al (2013) | 48 | −0.17 | 0.02 | <0.01 | 0.11 | 0.74 | −2.09 | 0.76 | −0.06 | 0.04 | 1.00 | 0.38 | 1.88 | 0.18 | ns |
| Hampton et al. (2018) | 946 | −0.13 | 0.04 | <0.01 | 1.10 | 0.29 | 0.68 | −0.38 | 0.05 | <0.01 | 1.77 | 0.17 | 2.44 | 0.12 | ns |
| Kirby et al. (2002) | 516 | −0.42 | 0.13 | 0.04 | 22.67 | 0.00 | −0.48 | 0.17 | <0.01 | 0.04 | 11.36 | 0.00 | 0.09 | 0.77 | ns |
| Lee et al. (2018) | 11157 | 0.21 | −0.08 | 0.01 | 53.95 | 0.00 | 0.28 | −0.13 | 0.01 | 0.01 | 27.33 | 0.00 | 0.71 | 0.40 | ns |
| Lempert et al. (2018) | 75 | −0.73 | 0.10 | <0.01 | 0.35 | 0.56 | 2.90 | −0.88 | 0.07 | 0.01 | 0.23 | 0.80 | 0.11 | 0.74 | ns |
| Li et al. (2020) | 619 | −0.17 | 0.04 | <0.01 | 2.39 | 0.12 | 0.38 | −0.24 | 0.03 | 0.01 | 2.84 | 0.06 | 3.28 | 0.07 | sig |
| Loeckenhoff et al. (2011) | 98 | −0.06 | 0.01 | <0.01 | 0.05 | 0.82 | −0.42 | 0.17 | −0.01 | <0.01 | 0.18 | 0.84 | 0.30 | 0.59 | ns |
| O’Hora et al (2016) | 840 | 0.03 | −0.01 | <0.01 | 0.15 | 0.70 | −0.11 | 0.07 | −0.01 | <0.01 | 0.24 | 0.79 | 0.32 | 0.57 | ns |
| Seaman et al. (2016) | 92 | 0.10 | −0.02 | <0.01 | 0.13 | 0.72 | 0.33 | −0.13 | 0.01 | <0.01 | 0.10 | 0.90 | 0.08 | 0.78 | ns |
| Sisso et al. (2017) | 2630 | 0.02 | −0.01 | <0.01 | 0.14 | 0.71 | 0.15 | −0.06 | 0.01 | <0.01 | 0.33 | 0.72 | 0.52 | 0.47 | ns |
| Tschernegget al. (2015) | 70 | 1.61 | −0.64 | 0.12 | 9.56 | 0.00 | −4.21 | 3.48 | −0.69 | 0.21 | 9.11 | 0.00 | 7.71 | 0.01 | ns |
Note. Int = Intercept; U = Two-line test (Simonshon, 2018), ns = non-significant, sig = significant
Discussion
Given the large heterogeneity in theoretical predictions and empirical findings in the literature concerning the link between age and temporal discounting, we conducted a preregistered systematic literature search and meta-analysis of adult age differences in intertemporal choice tasks. Contrary to the rich psychological literature on the possible links between aging and temporal discounting, our results suggest overall no sizeable effect of adult age on intertemporal choice and a lack of moderation by a number of possible factors. Both frequentist and Bayesian analyses estimated a very small, negative effect of age on discounting, with zero (no effect of age) being included in both the confidence and credible intervals. Both the frequentist and Bayesian estimates of effect size are well below the recommended minimum effect size that represents a practically significant effect for the social sciences generally (Ferguson, 2016), and gerontology specifically (Brydges, 2019).This means an effect of this size would not be useful for individual difference or group analyses; only at the population level could an effect this small be of practical use (Rutledge et al., 2016).
In what follows, we discuss the strengths and limitations of our work and associated implications for additional work on temporal discounting across adulthood.
Strengths and Limitations
Our approach to describing potential age differences in temporal discounting has a number of strengths, including the use of a systematic literature review, preregistration, open materials and code, coordination across judges from different labs and using appropriate software to ensure reliability and independence (e.g., Covidence), and statistical checks for publication biases (e.g., p-curve).
Our work also has a number of limitations. First and foremost, one should note that the use of meta-analysis does not guarantee an appropriate estimate of a true effect because it is by its very nature constrained by the extant available literature. Notably, some seminal studies (e.g., Read & Read, 2004) did not provide enough information to estimate the effect size and thus could not be included in this meta-analysis. Ideally, future studies will share data to avoid this problem, but at a minimum, studies should include bivariate correlations between effects of interest or group means with some measure of variance to facilitate inclusion in future meta-analyses. In addition to missing studies, comparisons of meta-analytic estimates and preregistered multiple-laboratory replication projects show inflated effects estimated from the former relative to the latter, suggesting that meta-analysis cannot fully eliminate underlying publication and reporting biases (Kvarven et al., 2020).
Second, there are specific limitations in the execution of our work, including small deviations from our initial preregistration and the lack of a systematic assessment of study quality (e.g., assessment of bias in sample selection or attrition in the primary studies included in the meta-analysis). Our main deviations from our preregistered protocol followed from our goal to increase the comprehensiveness of our search. In turn, we did not engage in a detailed assessment of bias in the primary studies because such aspects are overall poorly detailed in the primary literature. Naturally, ensuring a more detailed protocol and assessment of bias would be desirable in future systematic reviews of the aging literature.
Third, we were unable to consider an important mediator: socioeconomic status. Over half of the studies included in this meta-analysis (N=20) did not report any measure of socioeconomic status or income, and for those that did report income, inconstancy in reporting made it difficult to include as a moderator. As first noted by Green and colleagues (1996), socioeconomic status is a strong predictor of discounting behavior such that those with lower incomes tend to show greater discounting than those with higher levels of income. Further, recent work has suggested that discounting increases with age for those with lower income, but remains constant with age for those with higher incomes (Burro et al., 2020). It is important to note that it can be difficult to disentangle socioeconomic status from age because typical markers of socioeconomic status reliably shift over the lifespan. For instance, income will increase as individuals begin work in early adulthood, increase more as individuals gain status and work experience, and then decrease when individuals leave the workforce with retirement. Likewise, wealth generally increases across working life and then begins to decrease after retirement. Thus, including multiple measures of socioeconomic status—including income, wealth, and subjective estimates of status—may be necessary to separate out the contributions of socioeconomic status and age to temporal discounting.
Fourth, our work is limited by our focus on a single operationalization of temporal discounting, the intertemporal choice task. Choice in intertemporal choice tasks is multidetermined and may fail to isolate a single psychological mechanism responsible for age differences in temporal discounting because it involves expectations of changing utility, beliefs about the probability of obtaining the future reward, and some cognitive demands (Frederick et al., 2002; Olschewski et al., 2018). One should also note that intertemporal choice tasks are often treated as capturing impulsivity but do not show strong convergent validity with other measures of impulsivity, perhaps reflecting a unique set of demands (e.g., Duckworth & Kern, 2011; Sharma et al., 2014). Future work could consider alternatives to intertemporal choice tasks to capture age differences in temporal preferences. For example, time preferences can be studied using foraging-like problems including patch-leaving (Stephens & Krebs, 1986) or temporal sequencing tasks (Löckenhoff et al., 2019). Past aging research using foraging tasks suggests that older adults are more patient relative to younger adults, in the sense of staying longer in patches with dwindling resources (Mata et al., 2009, 2013), but it is unclear whether such differences are accounted for by age differences in the representations of the distribution of resources and/or perception or valuation of time intervals. Past research using temporal sequencing has yielded mixed findings that also suggest a lack of consistent age differences in temporal preferences (Löckenhoff et al., 2012, 2019, 2020; Löckenhoff & Samanez-Larkin, 2019; Strough et al., 2019).
Lastly, our review is limited by a focus on monetary gains. Some theories (Carstensen et al., 2000) and empirical findings (Seaman et al., 2016) suggest that monetary and social rewards are differentially salient to older adults, which could have implications for age differences in temporal discounting for these different types of rewards. Similar arguments could be made for other types of rewards, including differences between primary (e.g., juice) and secondary (i.e., money) rewards (Jimura et al., 2011), or the role of gains versus losses (Halfmann et al., 2013; Löckenhoff et al., 2011; Sparrow et al., 2019; Sparrow & Spaniol, 2018). Of course, meta-analyses cannot ensure sufficient power to assess the role of these and other theoretically relevant factors that have not been thoroughly examined across several primary studies.
All in all, one possible avenue for future work could involve preregistered projects that systematically assess the link between age and temporal discounting using multiple tasks and outcomes, and assessing potential moderators.
An alternative path forward, given the meta-analytic evidence for a lack of adult age differences in temporal discounting, would be the evaluation of what accounts for individual differences in intertemporal choice within age groups, in particular within older populations. Future work should consider the possibility that changes in discounting with age may be a predictor of mild cognitive impairment or other cognitive decline (Lempert et al., 2018). In many situations, prioritizing the present may be wise for older adults but in other situations it could be maladaptive. For example, many adults are making shortsighted financial decisions at retirement by underestimating both their own longevity and their growing financial needs in very old age. Early retirement and early withdrawal of Social Security benefits in the U.S. and other retirement income suggests that discounting the future may have long-term financial and physical health consequences. Many interventions have focused on reducing time discounting in young adulthood (Rung & Madden, 2018) but fewer have focused on the flexibility of discounting in older age (Sasse et al., 2017). Identifying individual factors that account for discounting in older age specifically (e.g., Lempert et al., 2020) may provide insight into the development of interventions for optimizing future-oriented choice later in life.
Conclusion
Some have asked whether aging research has systematically produced a literature that overestimates age-related effects (Isaacowitz & Lind, 2019). Our results suggest that despite the proliferation of theory and empirical work on the relation between adult age and temporal discounting, the current picture is that there is overall no sizeable association between age and temporal discounting across adulthood. This pattern of results might be seen as an example of the “winner’s curse” in the scientific literature (Young et al., 2008), in which seminal studies tend to provide exaggerated estimates of the effects of interest. The first study of aging and temporal discounting (Green et al., 1994) found the strongest effect of age on temporal discounting and has been highly influential on the development of this literature, having been cited the most frequently of all studies reported here (1317 times, according to Google Scholar on May 1, 2020), almost four times more than the next most-frequently cited study (Reimers et al., 2009; 362 citations as of May 1, 2021). Despite a follow-up study showing that the age effects reported in the 1994 paper were likely due to socioeconomic status (Green et al., 1996; 565 citations as of May 1, 2021), the notion that temporal discounting systematically decreases with age may still be prevalent in the literature, given that the seminal article has been cited many times more often than any other study in this literature. We hope that the results of our systematic review can help introduce a healthy dose of skepticism and critical examination of both theory and measurement not only on the topic of age differences in temporal discounting, but also of aging research more generally.
Supplementary Material
Figure 4. P-curve analysis.
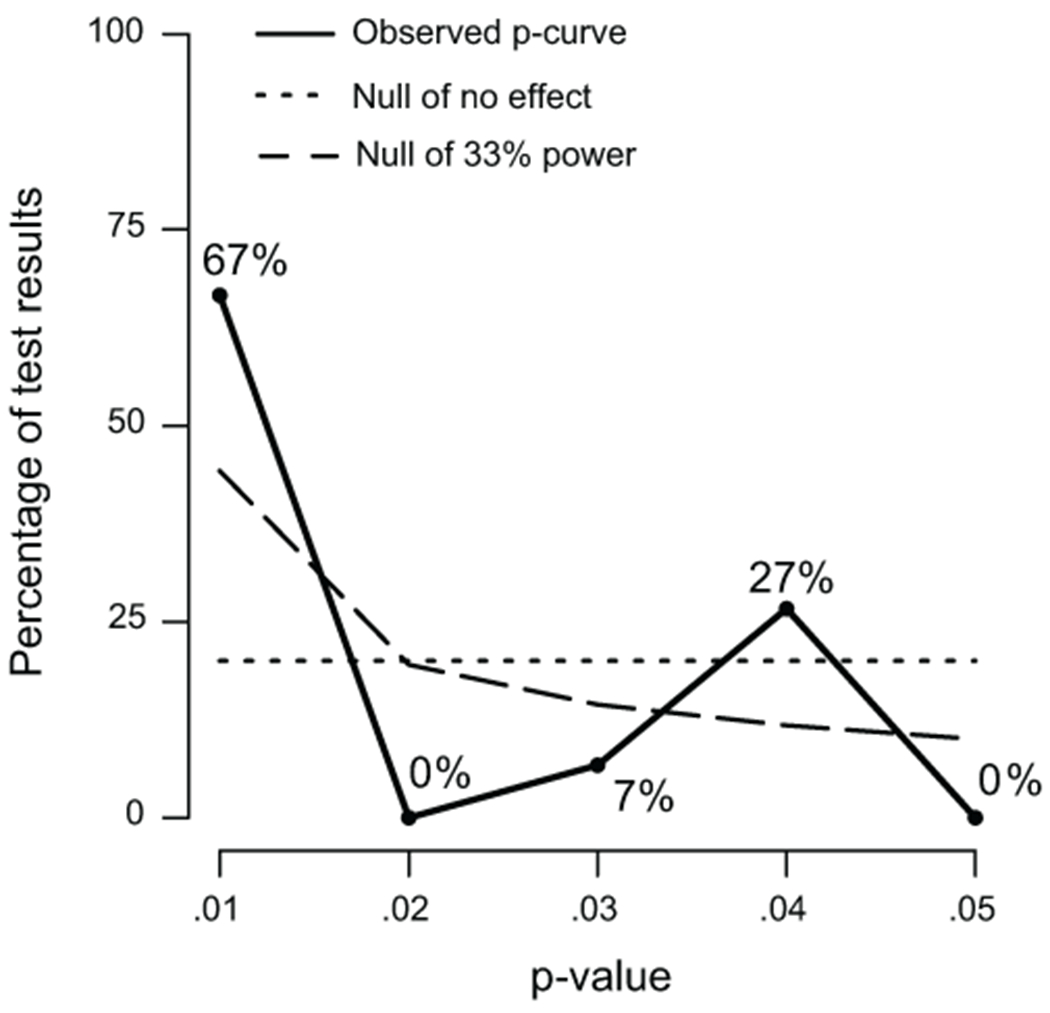
Plot showing the p-value of each study on the x-axis and the percentage of study results at that level on the y-axis. The solid blue line denotes the observed p-curve, which has an estimated power of 99%. There is no evidence of a right-skewness (green dashed line) or flatness (red dotted line) in the included data.
Acknowledgements:
This study was supported by grants from the National Institutes of Health (R00-AG042596, PI: Samanez-Larkin, Gregory; T32-AG000029, PI: Cohen, Harvey; R01-AG044838, PI: Zald, David). Thank you to Galen McAllister for contacting authors for raw data on behalf of the research team and Laura Wiles for providing editing services.
Footnotes
This study was preregistered Open Science Framework (https://osf.io/e4anc)> and ResearchGate (https://www.researchgate.net/project/Age-differences-in-temporal-discounting), in April 2017. An early version of this project was presented at the 2018 Society for Neuroscience conference and earlier versions of this manuscript were posted on the PsyArXiv preprint server (https://psyarxiv.com/7ysxa/) in June and July 2020.
Data: Preregistration, synthesized data, and code used in the manuscript can be viewed at and downloaded from https://osf.io/ch9eg/.
Contributor Information
Kendra L. Seaman, Department of Psychology, University of Texas at Dallas, Center for Vital Longevity, University of Texas at Dallas.
Sade J. Abiodun, Center for Cognitive Neuroscience, Duke University.
Zöe Fenn, Department of Psychology, University of Basel.
Gregory R. Samanez-Larkin, Department of Psychology and Neuroscience, Duke University, Center for Cognitive Neuroscience, Duke University.
Rui Mata, Department of Psychology, University of Basel, Max Planck Institute for Human Development.
References
- Balduzzi S, Rücker G, & Schwarzer G (2019). How to perform a meta-analysis with R: A practical tutorial. Evidence-Based Mental Health, 22(4), 153–160. 10.1136/ebmental-2019-300117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Block RA, Zakay D, & Hancock PA (1998). Human aging and duration judgments: A meta-analytic review. Psychology and Aging, 13(4), 584–596. 10.1037/0882-7974.13.4.584 [DOI] [PubMed] [Google Scholar]
- Brown SBRE, & Ridderinkhof KR (2009). Aging and the neuroeconomics of decision making: A review. Cognitive, Affective, & Behavioral Neuroscience, 9, 365–379. 10.3758/CABN.9.4.365 [DOI] [PubMed] [Google Scholar]
- Brydges CR (2019). Effect Size Guidelines, Sample Size Calculations, and Statistical Power in Gerontology. Innovation in Aging, 3(4), igz036. 10.1093/geroni/igz036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buono FD, Whiting SW, & Sprong ME (2015). Comparison of temporal discounting among obese college students and obese adults. Behavior Analysis: Research and Practice, 15(2), 139. 10.1037/bar0000015 [DOI] [Google Scholar]
- Bürkner P-C (2017). brms: An R Package for Bayesian Multilevel Models Using Stan. Journal of Statistical Software, 80(1), 1–28. 10.18637/jss.v080.i01 [DOI] [Google Scholar]
- Bürkner P-C (2018). Advanced Bayesian Multilevel Modeling with the R Package brms. The R Journal, 10(1), 395–411. [Google Scholar]
- Burr DA, Castrellon JJ, Zald DH, & Samanez-Larkin GR (2020). Emotion dynamics across adulthood in everyday life: Older adults are more emotionally stable and better at regulating desires. Emotion. 10.1037/emo0000734 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burro G, McDonald R, Read D, & Taj U (2020). Patience Decreases With Age for the Poor but Not for the Rich: An International Comparison (SSRN Scholarly Paper ID 3649102). Social Science Research Network. 10.2139/ssrn.3649102 [DOI] [Google Scholar]
- Carstensen LL (2006). The Influence of a Sense of Time on Human Development. Science, 312(5782), 1913–1915. 10.1126/science.1127488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carstensen LL, Pasupathi M, Mayr U, & Nesselroade JR (2000). Emotional experience in everyday life across the adult life span. Journal of Personality and Social Psychology, 79(4), 644–655. 10.1037/0022-3514.79.4.644 [DOI] [PubMed] [Google Scholar]
- Chao L-W, Szrek H, Pereira NS, & Pauly MV (2009). Time preference and its relationship with age, health, and survival probability. Judgment and Decision Making, 4(1), 1–19. [PMC free article] [PubMed] [Google Scholar]
- Coller M, & Williams MB (1999). Eliciting Individual Discount Rates. Experimental Economics, 2(2), 107–127. 10.1023/A:1009986005690 [DOI] [Google Scholar]
- Covidence systematic review software,. (2020). Veritas Health Innovation. www.covidence.org
- Cross CP, Copping LT, & Campbell A (2011). Sex differences in impulsivity: A meta-analysis. Psychological Bulletin, 137(1), 97–130. 10.1037/a0021591 [DOI] [PubMed] [Google Scholar]
- Duckworth AL, & Kern ML (2011). A meta-analysis of the convergent validity of self-control measures. Journal of Research in Personality, 45(3), 259–268. 10.1016/j.jrp.2011.02.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duckworth AL, & Steinberg L (2015). Unpacking Self-Control. Child Development Perspectives, 9(1), 32–37. 10.1111/cdep.12107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egger M, Smith GD, Schneider M, & Minder C (1997). Bias in meta-analysis detected by a simple, graphical test. BMJ, 315(7109), 629–634. 10.1136/bmj.315.7109.629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eppinger B, Heekeren HR, & Li S-C (2018). Age Differences in the Neural Mechanisms of Intertemporal Choice Under Subjective Decision Conflict. Cerebral Cortex, 28(11), 3764–3774. 10.1093/cercor/bhx239 [DOI] [PubMed] [Google Scholar]
- Eppinger B, Nystrom LE, & Cohen JD (2012). Reduced Sensitivity to Immediate Reward during Decision-Making in Older than Younger Adults. PLOS ONE, 7(5), e36953. 10.1371/journal.pone.0036953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estle SJ, Green L, Myerson J, & Holt DD (2006). Differential effects of amount on temporal and probability discounting of gains and losses. Memory & Cognition, 34(4), 914–928. 10.3758/BF03193437 [DOI] [PubMed] [Google Scholar]
- Ferguson CJ (2016). An effect size primer: A guide for clinicians and researchers (p. 310). American Psychological Association. 10.1037/14805-020 [DOI] [Google Scholar]
- Field AP, & Gillett R (2010). How to do a meta-analysis. British Journal of Mathematical and Statistical Psychology, 63(3), 665–694. 10.1348/000711010X502733 [DOI] [PubMed] [Google Scholar]
- Frederick S, Loewenstein G, & O’Donoghue T (2002). Time Discounting and Time Preference: A Critical Review. Journal of Economic Literature, 40(2), 351–401. 10.1257/002205102320161311 [DOI] [Google Scholar]
- Garza KB, Ding M, Owensby JK, & Zizza CA (2016). Impulsivity and Fast-Food Consumption: A Cross-Sectional Study among Working Adults. Journal of the Academy of Nutrition and Dietetics, 116(1), 61–68. 10.1016/j.jand.2015.05.003 [DOI] [PubMed] [Google Scholar]
- Green L, Fry AF, & Myerson J (1994). Discounting of Delayed Rewards: A Life-Span Comparison. Psychological Science, 5(1), 33–36. 10.1111/j.1467-9280.1994.tb00610.x [DOI] [Google Scholar]
- Green L, Myerson J, Lichtman D, Rosen S, & Fry A (1996). Temporal discounting in choice between delayed rewards: The role of age and income. Psychology and Aging, 11(1), 79–84. 10.1037/0882-7974.11.1.79 [DOI] [PubMed] [Google Scholar]
- Griskevicius V, Tybur JM, Delton AW, & Robertson TE (2011). The influence of mortality and socioeconomic status on risk and delayed rewards: A life history theory approach. Journal of Personality and Social Psychology, 100(6), 1015–1026. 10.1037/a0022403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halfmann K, Hedgcock W, & Denburg NL (2013). Age-related differences in discounting future gains and losses. Journal of Neuroscience, Psychology, and Economics, 6(1), 42–54. 10.1037/npe0000003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampton WH, Asadi N, & Olson IR (2018). Good Things for Those Who Wait: Predictive Modeling Highlights Importance of Delay Discounting for Income Attainment. Frontiers in Psychology, 9. 10.3389/fpsyg.2018.01545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrer M, Cuijpers P, Furukawa T, & Ebert D (2019). dmetar: Companion R Package For The Guide ‘Doing Meta-Analysis in R (0.0.9000) [Computer software]. http://dmetar.protectlab.org
- Hsu M, Lin HT, & McNamara PE (2008). Neuroeconomics of decision-making in the aging brain: The example of long-term care. Advances in Health Economics and Health Services Research, 20, 203–225. 10.1016/S0731-2199(08)20009-9 [DOI] [PubMed] [Google Scholar]
- IntHout J, Ioannidis JPA, Rovers MM, & Goeman JJ (2016). Plea for routinely presenting prediction intervals in meta-analysis. BMJ Open, 6(7), e010247. 10.1136/bmjopen-2015-010247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- IntHout J, Ioannidis JP, & Borm GF (2014). The Hartung-Knapp-Sidik-Jonkman method for random effects meta-analysis is straightforward and considerably outperforms the standard DerSimonian-Laird method. BMC Medical Research Methodology, 14(1), 25. 10.1186/1471-2288-14-25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaacowitz DM, & Lind M (2019). Open Science is for Aging Research, Too. Innovation in Aging, 3(4), igz028. 10.1093/geroni/igz028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimura K, Myerson J, Hilgard J, Keighley J, Braver TS, & Green L (2011). Domain independence and stability in young and older adults’ discounting of delayed rewards. Behavioural Processes, 87(3), 253–259. 10.1016/j.beproc.2011.04.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson PS, Herrmann ES, & Johnson MW (2015). Opportunity costs of reward delays and the discounting of hypothetical money and cigarettes. Journal of the Experimental Analysis of Behavior, 703(1), 87–107. 10.1002/jeab.110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirby KN, Godoy R, Reyes-García V, Byron E, Apaza L, Leonard W, Pérez E, Vadez V, & Wilkie D (2002). Correlates of delay-discount rates: Evidence from Tsimane’ Amerindians of the Bolivian rain forest. Journal of Economic Psychology, 23(3), 291–316. 10.1016/S0167-4870(02)00078-8 [DOI] [Google Scholar]
- Kirby KN, & Maraković NN (1996). Delay-discounting probabilistic rewards: Rates decrease as amounts increase. Psychonomic Bulletin & Review, 3(1), 100–104. 10.3758/BF03210748 [DOI] [PubMed] [Google Scholar]
- Kirby KN, Petry NM, & Bickel WK (1999). Heroin Addicts Have Higher Discount Rates for DelayedRewards Than Non-Drug-Using Controls. Journal of Experimental Psychology. General, 128(1), 10. [DOI] [PubMed] [Google Scholar]
- Kvarven A, Strømland E, & Johannesson M (2020). Comparing meta-analyses and preregistered multiple-laboratory replication projects. Nature Human Behaviour, 4(4), 423–434. 10.1038/s41562-019-0787-z [DOI] [PubMed] [Google Scholar]
- Lang FR, & Carstensen L (2002). Time counts: Future time perspective, goals, and social relationships. Psychology and Aging, 17(1), 125–139. 10.1037/0882-7974.17.1.125 [DOI] [PubMed] [Google Scholar]
- Lempert KM, MacNear KA, Wolk DA, & Kable JW (2020). Links between autobiographical memory richness and temporal discounting in older adults. Scientific Reports, 10(1), 6431. 10.1038/s41598-020-63373-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lempert KM, Wolk DA, & Kable J (2018). Declarative memory, but not executive function, is associated with temporal discounting in older adults. 10.31234/osf.io/vb743 [DOI]
- Li Y, Baldassi M, Johnson EJ, & Weber EU (2013). Complementary cognitive capabilities, economic decision making, and aging. Psychology and Aging, 28(3), 595–613. 10.1037/a0034172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Zaval Lisa, & Johnson Eric J. (2020). Hedonic wisdom: Older consumers show less future anhedonia [Working Paper]. [Google Scholar]
- Liberati A, Altman DG, Tetzlaff J, Mulrow C, Gøtzsche PC, Ioannidis JPA, Clarke M, Devereaux PJ, Kleijnen J, & Moher D (2009). The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: Explanation and elaboration. Journal of Clinical Epidemiology, 62(10), e1–e34. 10.1016/j.jclinepi.2009.06.006 [DOI] [PubMed] [Google Scholar]
- Lim KTK, & Yu R (2015). Aging and wisdom: Age-related changes in economic and social decision making. Frontiers in Aging Neuroscience, 7(JUN), 1–11. 10.3389/fnagi.2015.00120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L, Chen X, Cui J, Wang J, Zhang Y, Neumann DL, Shum DHK, Wang Y, & Chan RCK (2016). Age differences in delay discounting in Chinese adults. Personality and Individual Differences, 90, 205–209. 10.1016/j.paid.2015.11.006 [DOI] [Google Scholar]
- Löckenhoff CE (2011). Age, time, and decision making: From processing speed to global time horizons. Annals of the New York Academy of Sciences, 1235, 44–56. 10.1111/j.1749-6632.2011.06209.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Löckenhoff CE, O’Donoghue T, & Dunning D (2011). Age differences in temporal discounting: The role of dispositional affect and anticipated emotions. Psychology and Aging, 26(2), 274–284. 10.1037/a0023280 [DOI] [PubMed] [Google Scholar]
- Löckenhoff CE, Reed AE, & Maresca SN (2012). Who saves the best for last? Age differences in preferences for affective sequences. Psychology and Aging, 27(4), 840–848. 10.1037/a0028747 [DOI] [PubMed] [Google Scholar]
- Löckenhoff CE, Rutt JL, Samanez-Larkin GR, Gallagher C, O’Donoghue T, & Reyna VF (2020). Age Effects in Sequence-Construction for a Continuous Cognitive Task: Similar Sequence-Trends but Fewer Switch-Points. The Journals of Gerontology: Series B, 75(4), 762–771. 10.1093/geronb/gby090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Löckenhoff CE, Rutt JL, Samanez-Larkin GR, O’Donoghue T, & Reyna VF (2019). Preferences for Temporal Sequences of Real Outcomes Differ Across Domains but do not Vary by Age. The Journals of Gerontology: Series B, 74(3), 430–439. 10.1093/geronb/gbx094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Löckenhoff CE, & Samanez-Larkin GR (2019). Age Differences in Intertemporal Choice: The Role of Task Type, Outcome Characteristics, and Covariates. The Journals of Gerontology: Series B, gbz097. 10.1093/geronb/gbz097 [DOI] [PMC free article] [PubMed]
- Lüdecke. (2019). esc: Effect Size Computation for Meta Analysis (0.5.0) [Computer software]. [Google Scholar]
- Mahalingam V, Palkovics M, Kosinski M, Cek I, & Stillwell D (2018). A Computer Adaptive Measure of Delay Discounting. Assessment, 25(8), 1036–1055. 10.1177/1073191116680448 [DOI] [PubMed] [Google Scholar]
- Mata R, Wilke A, & Czienskowski U (2009). Cognitive Aging and Adaptive Foraging Behavior. The Journals of Gerontology Series B: Psychological Sciences and Social Sciences, 64B(4), 474–481. 10.1093/geronb/gbp035 [DOI] [PubMed] [Google Scholar]
- Mata R, Wilke A, & Czienskowski U (2013). Foraging across the life span: Is there a reduction in exploration with aging? Frontiers in Neuroscience, 7. 10.3389/fnins.2013.00053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mather M (2006). A Review of Decision-Making Processes: Weighing the Risks and Benefits of Aging. In When I’m 64. 10.1017/CBO9781107415324.004 [DOI] [Google Scholar]
- Mischel W, Shoda Y, & Rodriguez MI (1989). Delay of gratification in children. Science, 244(4907), 933–938. 10.1126/science.2658056 [DOI] [PubMed] [Google Scholar]
- Nosek BA, Ebersole CR, DeHaven AC, & Mellor DT (2018). The preregistration revolution. Proceedings of the National Academy of Sciences, 115(11), 2600–2606. 10.1073/pnas.1708274114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuzzo R (2014). Scientific method: Statistical errors. Nature News, 506(1487), 150. 10.1038/506150a [DOI] [PubMed] [Google Scholar]
- O’Hora D, Carey R, Kervick A, Crowley D, & Dabrowski M (2016). Decisions in Motion: Decision Dynamics during Intertemporal Choice reflect Subjective Evaluation of Delayed Rewards. Scientific Reports, 6(1), 20740. 10.1038/srep20740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olschewski S, Rieskamp J, & Scheibehenne B (2018). Taxing cognitive capacities reduces choice consistency rather than preference: A model-based test. Journal of Experimental Psychology: General, 147(4), 462. 10.1037/xge0000403 [DOI] [PubMed] [Google Scholar]
- Pauli-Pott U, & Becker K (2015). Time windows matter in ADHD-related developing neuropsychological basic deficits: A comprehensive review and meta-regression analysis. Neuroscience & Biobehavioral Reviews, 55, 165–172. 10.1016/j.neubiorev.2015.04.011 [DOI] [PubMed] [Google Scholar]
- Peters E, Hess TTM, Västfjäll D, & Auman C (2007). Adult Age Differences in Dual Information Processes: Implications for the Role of Affective and Deliberative Processes in Older Adults’ Decision Making. Perspectives on Psychological Science, 2(1), 1–23. 10.1111/j.1745-6916.2007.00025.x [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Rucker DD, MacCallum RC, & Nicewander WA (2005). Use of the Extreme Groups Approach: A Critical Reexamination and New Recommendations. Psychological Methods, 10(2), 178–192. 10.1037/1082-989X.10.2.178 [DOI] [PubMed] [Google Scholar]
- Read D, & Read NL (2004). Time discounting over the lifespan. Organizational Behavior and Human Decision Processes, 94(1), 22–32. 10.1016/j.obhdp.2004.01.002 [DOI] [Google Scholar]
- Reimers S, Maylor EA, Stewart N, & Chater N (2009). Associations between a one-shot delay discounting measure and age, income, education and real-world impulsive behavior. Personality and Individual Differences, 47(8), 973–978. 10.1016/j.paid.2009.07.026 [DOI] [Google Scholar]
- Richter D, & Mata R (2018). Age differences in intertemporal choice: U-shaped associations in a probability sample of German households. Psychology and Aging, 33(5), 782–788. 10.1037/pag0000266 [DOI] [PubMed] [Google Scholar]
- Rieger M, & Mata R (2015). On the Generality of Age Differences in Social and Nonsocial Decision Making. The Journals of Gerontology: Series B, 70(2), 200–212. 10.1093/geronb/gbt088 [DOI] [PubMed] [Google Scholar]
- Rohatgi A (2019). WebPlotDigitizer: HTML5 based online tool to extract numerical data from plot images (4.2) [Computer software]. https://automeris.io/WebPlotDigitizer/
- Rung JM, & Madden GJ (2018). Experimental reductions of delay discounting and impulsive choice: A systematic review and meta-analysis. Journal of Experimental Psychology: General, 147(9), 1349–1381. 10.1037/xge0000462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutledge RB, Smittenaar P, Zeidman P, Brown HR, Adams RA, Lindenberger U, Dayan P, & Dolan RJ (2016). Risk Taking for Potential Reward Decreases across the Lifespan. Current Biology, 26(12), 1634–1639. 10.1016/j.cub.2016.05.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samanez-Larkin GR, Mata R, Radu PT, Ballard IC, Carstensen LL, & McClure SM (2011). Age Differences in Striatal Delay Sensitivity during Intertemporal Choice in Healthy Adults. Frontiers in Neuroscience, 5. 10.3389/fnins.2011.00126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasse LK, Peters J, & Brassen S (2017). Cognitive Control Modulates Effects of Episodic Simulation on Delay Discounting in Aging. Frontiers in Aging Neuroscience, 9. 10.3389/fnagi.2017.00058 [DOI] [PMC free article] [PubMed]
- Scheibe S, Mata R, & Carstensen LL (2011). Age differences in affective forecasting and experienced emotion surrounding the 2008 US presidential election. Cognition and Emotion, 25(6), 1029–1044. 10.1080/02699931.2010.545543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seaman KL, Brooks N, Karrer TM, Castrellon JJ, Perkins SF, Dang LC, Hsu M, Zald DH, & Samanez-Larkin GR (2018). Subjective value representations during effort, probability and time discounting across adulthood. Social Cognitive and Affective Neuroscience, 13(5), 449–459. 10.1093/scan/nsy021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seaman KL, Gorlick MA, Vekaria KM, Hsu M, Zald DH, & Samanez-Larkin GR (2016). Adult age differences in decision making across domains: Increased discounting of social and health-related rewards. Psychology and Aging, 31(7), 737–746. 10.1037/pag0000131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma L, Markon KE, & Clark LA (2014). Toward a theory of distinct types of “impulsive” behaviors: A meta-analysis of self-report and behavioral measures. Psychological Bulletin, 140(2), 374–408. 10.1037/a0034418 [DOI] [PubMed] [Google Scholar]
- Simonsohn U (2018). Two Lines: A Valid Alternative to the Invalid Testing of U-Shaped Relationships With Quadratic Regressions. Advances in Methods and Practices in Psychological Science, 1(4), 538–555. 10.1177/2515245918805755 [DOI] [Google Scholar]
- Simonsohn U, Nelson LD, & Simmons JP (2014). p-Curve and Effect Size: Correcting for Publication Bias Using Only Significant Results. Perspectives on Psychological Science, 9(6), 666–681. 10.1177/1745691614553988 [DOI] [PubMed] [Google Scholar]
- Sisso Itay & Shayo M (n.d.). When in Rome—The Effect of Financial Market Exposure on Maximizing Tendencies. [Google Scholar]
- Sozou PD, & Seymour RM (2003). Augmented discounting: Interaction between ageing and time-preference behaviour. Proceedings of the Royal Society of London. Series B: Biological Sciences, 270(1519), 1047–1053. 10.1098/rspb.2003.2344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sparrow EP, Armstrong BA, Fiocco AJ, & Spaniol J (2019). Acute stress and altruism in younger and older adults. Psychoneuroendocrinology, 100, 10–17. 10.1016/j.psyneuen.2018.09.025 [DOI] [PubMed] [Google Scholar]
- Sparrow EP, & Spaniol J (2018). Aging and altruism in intertemporal choice. Psychology and Aging, 33(2), 315–324. 10.1037/pag0000223 [DOI] [PubMed] [Google Scholar]
- Spreng RN (2016). Cognitive, social, and neural determinants of diminished decision-making and financial exploitation risk in aging and dementia: A review and new model. 28, 320–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens DW, & Krebs JR (1986). Foraging Theory. Princeton University Press. [Google Scholar]
- Sterne JAC, Gavaghan D, & Egger M (2000). Publication and related bias in meta-analysis: Power of statistical tests and prevalence in the literature. Journal of Clinical Epidemiology, 53(11), 1119–1129. 10.1016/S0895-4356(00)00242-0 [DOI] [PubMed] [Google Scholar]
- Stoeckel LE, Murdaugh DL, Cox JE, Cook EW, & Weller RE (2013). Greater impulsivity is associated with decreased brain activation in obese women during a delay discounting task. Brain Imaging and Behavior, 7(2), 116–128. 10.1007/s11682-012-9201-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strough J, Bruine de Bruin W, & Parker AM (2019). Taking the Biggest First: Age Differences in Preferences for Monetary and Hedonic Sequences. The Journals of Gerontology: Series B, 74(6), 964–974. 10.1093/geronb/gbx160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trostel PA, & Taylor GA (2001). A Theory of Time Preference. Economic Inquiry, 39(3), 379–395. 10.1093/ei/39.3.379 [DOI] [Google Scholar]
- Tschernegg M, Pletzer B, Schwartenbeck P, Ludersdorfer P, Hoffmann U, & Kronbichler M (2015). Impulsivity relates to striatal gray matter volumes in humans: Evidence from a delay discounting paradigm. Frontiers in Human Neuroscience, 9. 10.3389/fnhum.2015.00384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verhaeghen P, & Cerella J (2002). Aging, executive control, and attention: A review of meta-analyses. Neuroscience & Biobehavioral Reviews, 26(7), 849–857. 10.1016/S0149-7634(02)00071-4 [DOI] [PubMed] [Google Scholar]
- Viechtbauer W (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. 10.18637/jss.v036.i03 [DOI] [Google Scholar]
- Whelan R, & McHugh LA (2009). Temporal Discounting of Hypothetical Monetary Rewards by Adolescents, Adults, and Older Adults. The Psychological Record, 59(2), 247–258. 10.1007/BF03395661 [DOI] [Google Scholar]
- Wolfe MT, & Patel PC (2017). Instant gratification: Temporal discounting and self-employment. Small Business Economics, 48(4), 861–882. 10.1007/s11187-016-9823-9 [DOI] [Google Scholar]
- Wulf A (2015). The Invention of Nature. Alfred A. Knopf. [Google Scholar]
- Young NS, Ioannidis JPA, & Al-Ubaydli O (2008). Why Current Publication Practices May Distort Science. PLOS Medicine, 5(10), e201. 10.1371/journal.pmed.0050201 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


