Skip to main content
PMC home page
Science Advances logoLink to Science Advances
. 2022 Feb 9;8(6):eabk0832. doi: 10.1126/sciadv.abk0832

Characterization of photoinduced normal state through charge density wave in superconducting YBa2Cu3O6.67

Hoyoung Jang 1,2,†, Sanghoon Song 3,†, Takumi Kihara 4, Yijin Liu 5, Sang-Jun Lee 5, Sang-Youn Park 1, Minseok Kim 1, Hyeong-Do Kim 1, Giacomo Coslovich 3, Suguru Nakata 6, Yuya Kubota 7,8, Ichiro Inoue 7, Kenji Tamasaku 7, Makina Yabashi 7,8, Heemin Lee 9, Changyong Song 2,9, Hiroyuki Nojiri 4, Bernhard Keimer 6, Chi-Chang Kao 10, Jun-Sik Lee 5,*
PMCID: PMC8827649  PMID: 35138893

Abstract

The normal state of high-Tc cuprates has been considered one of the essential topics in high-temperature superconductivity research. However, compared to the high magnetic field study of it, understanding a photoinduced normal state remains elusive. Here, we explore a photoinduced normal state of YBa2Cu3O6.67 through a charge density wave (CDW) with time-resolved resonant soft x-ray scattering, as well as a high magnetic field x-ray scattering. In the nonequilibrium state where people predict a quenched superconducting state based on the previous optical spectroscopies, we experimentally observed a similar analogy to the competition between superconductivity and CDW shown in the equilibrium state. We further observe that the broken pairing states in the superconducting CuO2 plane via the optical pump lead to nucleation of three-dimensional CDW precursor correlation. Ultimately, these findings provide a critical clue that the characteristics of the photoinduced normal state show a solid resemblance to those under magnetic fields in equilibrium conditions.

A transient normal state triggered by the laser-driven quench of the superconducting state in YBCO is revealed by the CDW study.

INTRODUCTION

High-Tc cuprate is one of the most studied systems in strongly correlated materials since the first discovery of high-temperature superconductivity (HTSC) was reported in 1986 (1). Despite this high level of focus, a fundamental mechanism of HTSC is unclear because of many conundrums (2–4). Even with the tremendous research efforts in this field, realizing room temperature SC under the ambient pressure remains a huge challenge. Meanwhile, it has been considered that understanding the normal states of high-Tc cuprates and their corresponding features, e.g., pseudogap (5, 6) and charge density wave (CDW) (7–20), could shed light on a direction to approach room temperature SC. In this regard, an in-depth study on the ground state of the normal state is of profound significance to HTSC research.

An experimental study on the ground state problem is generally accompanied by the cooling of samples because they should be at the lowest possible energy state. In the HTSC case, due to the emergence of SC below Tc; however, it is difficult to resolve the normal state at low temperature. Typically, this difficulty is overcome by quenching the superconducting state at low temperature by an external magnetic field (21–30). For example, x-ray scattering studies on YBa2Cu3O6+δ cuprates under high magnetic fields revealed that the three-dimensional (3D) CDW correlation is the ideal ordering state in the normal state (24–30). Meanwhile, quenching the SC through the optical pump is considered another approach and has been demonstrated in many cuprates (31–39). However, a study on corresponding a normal state triggered by the laser-driven quench of the superconducting state is still in the early stage, although a photoinduced CDW state was recently reported on YBa2Cu3O6+δ (40). In addition, findings through the pump-probe approach and corresponding implications represent fundamental physics of the nonequilibrium state, while the magnetic field study secures the equilibrium state. In this manner, despite that these two approaches’ successful implementations in many high-Tc cuprates, it is still premature to reach a common ground on the normal state studied through those two approaches. Hence, it is timely to establish a scientific connection between the equilibrium state and the nonequilibrium state in HTSC.

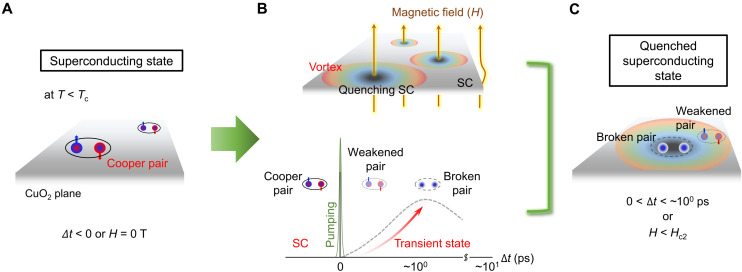
Here, we explore a photoinduced normal state of ortho-VIII YBa2Cu3O6.67 (YBCO) by using a time-resolved resonant soft x-ray scattering (tr-RSXS) study and also carry out a pulsed high magnetic field x-ray scattering experiment (see Materials and Methods). For this purpose, we focus on investigating CDW phenomena of YBCO, while the superconducting state is quenched by the optical pump. This is because we are motivated by the fact that the CDW correlation is a normal state phenomenon (3, 4) and has ubiquitously been established in high-Tc cuprates (7–20). In particular, there exist extensive previous studies, even with magnetic fields, on the CDW phenomena in YBa2Cu3O6+δ cuprates (12–14, 24–30, 40). Thus, it allows us to compare this study to the CDW phenomena measured with the magnetic field, leading to an in-depth insight into the connection between the equilibrium and nonequilibrium states in the high-Tc cuprates. Moreover, there is no systematic experimental study regarding intertwined phenomena between the photoinduced CDW and the quenched SC state. In this study, we directly observe that both intensity and correlation length of the CDW order in YBCO are enhanced, while the optical pump suppresses the superconducting state, indicating that the competition between CDW and SC shows a strong resemblance to that under those magnetic fields (13, 24–30). It is also worthwhile to note that we basically assume a quench of the SC state through the previous optical demonstrations (31–39). We further observe an emergence of a 3D CDW precursor correlation (27) under the photoinduced normal state of YBCO. From these findings, we bring up a point that CDW phenomena in the equilibrium state are characteristically identical to those in the nonequilibrium state. In addition, we suggest that the broken Cooper pairing physics could be discussed in the context of the nucleation of the vortex state through the external magnetic field. Inversely, it allows us to extend our scientific consideration even under the equilibrium state into the fact that the nonequilibrium approach could generate a transient superconducting state nearly up to room temperature (41–44).

RESULTS

CDW of ortho-VIII YBCO under the equilibrium state

One of the profound discoveries in high-Tc cuprates is the universal existence of a static CDW (or charge order) in CuO2 planes (7–20). In the underdoped YBa2Cu3O6+δ cuprates, a CDW typically appears in the pseudogap phase (12–14, 24–30). In other words, the onset temperature of CDW (Tcdw) exists in the normal state. Many researchers believe that its ground state is critical to understand the superconducting behavior in YBa2Cu3O6+δ (3, 28).

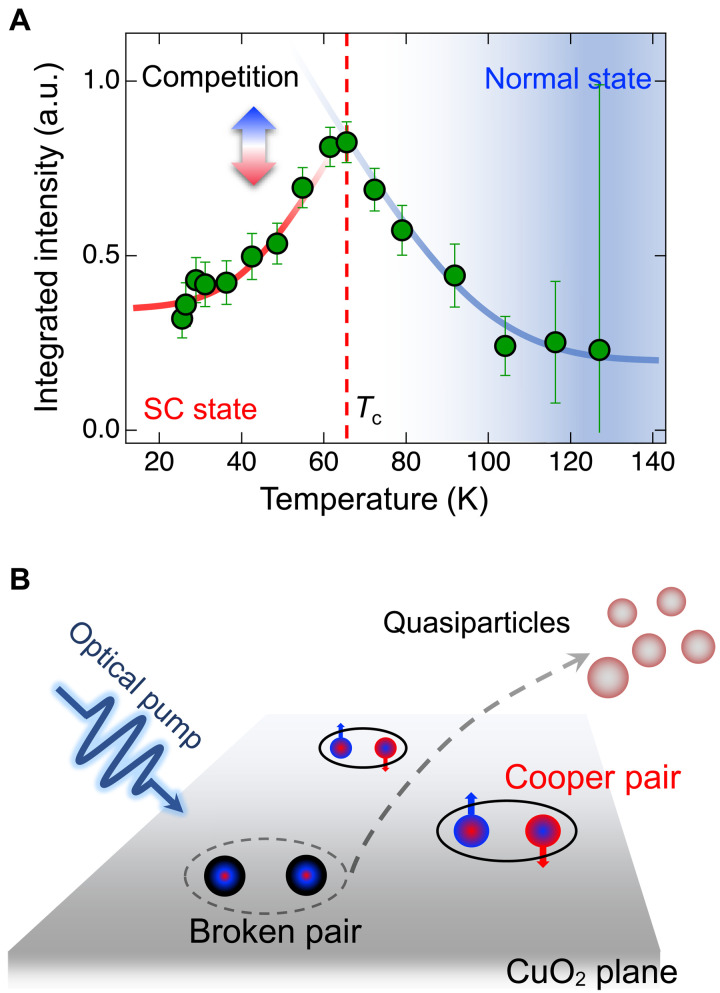
Figure 1A shows a temperature dependence of static CDW of the YBCO crystal, which was measured by RSXS measurement (see Materials and Methods). We observed CDW peaks at Q = (0, qcdw, ~1.45), where qcdw is around −0.32 reciprocal lattice unit (r.l.u.) in the CuO2 plane (fig. S1). The CDW appears below ~150 K, which is consistent with previous studies (24–27). As expected, the CDW, which is developed from the normal state, is suppressed, while the superconducting state emerges below Tc = 65.5 K. This suppression demonstrates the existence of competition between CDW and SC in YBCO, as shown in other YBa2Cu3O6+δ cuprates (12–14, 24–30). At the same time, it reveals that a study of CDW’s ground state at low temperature (i.e., the normal state) is challenging because of the coexistence of SC and its competition with the CDW. Hence, to investigate a low-temperature state of CDW, the SC needs to be quenched. As a magnetic field causes a vortex state (i.e., quenched SC state), an optical pump can also break Cooper pairs in superconducting CuO2 planes (31–40) when the pumping conditions are appropriately tuned (see Fig. 1B).

Fig. 1. Normal and superconducting states in the CuO2 plane of the YBCO.

Fig. 1.

Open in a new tab

(A) Temperature dependence of a static CDW order. It shows the integrated intensity of CDW peak at Q = (0, qcdw, ~1.45) as a function of temperature, where qcdw is around −0.32 r.l.u. The CDW emerges below ~150 K. Below Tc = 65.5 K (dashed line), the CDW peak becomes suppressed with the development of the SC. Solid lines are guides to the eye. a.u., arbitrary units. (B) A schematic sketch for the optical pump effect in a superconducting CuO2 plane. The solid and dashed ellipses are a superconducting Cooper pair state and its broken state, respectively. The broken pairs transform to quasiparticles due to an optical pump.

CDW of YBCO under the nonequilibrium state

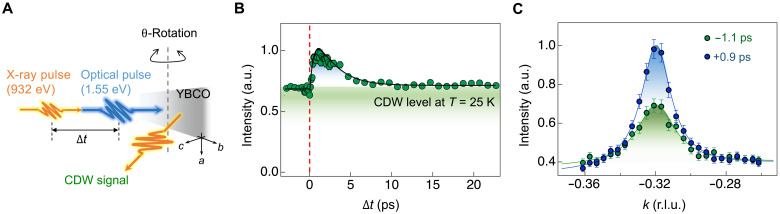
Figure 2A shows an experimental configuration of tr-RSXS, aiming to explore CDW phenomena of YBCO at low temperatures. We used a 1.55-eV (800 nm) optical laser with a fluence of 15 μJ/cm2 (see Materials and Methods), aimed to minimize thermal heating (see the Supplementary Materials). Figure 2B shows the temporal behavior of the CDW order at T = 25 K, which was measured at Q = (0, −0.32, 1.45). Before the pump—i.e., time delay (∆t) < 0, it shows a persistent CDW signal suppressed by the competition with SC. After the pump, we observed an enhancement of the CDW for 0 < ∆t < ~7 ps, which is consistent with the previous work (40). For the 0 < ∆t < 0.5 ps range, the CDW suppression is associated by a photoexcited charge carrier, while SC is suppressed (see fig. S6) (35). Also, the maximum enhancement of the CDW occurs at ∆t ≈ +0.9 ps. Figure 2C shows the CDW peak profiles at ∆t < 0 and ∆t = +0.9 ps. The photoinduced CDW peak at ∆t = +0.9 ps becomes stronger and sharper than that at the negative time delay (∆t = −1.1 ps). This implies that the CDW volume fraction in CuO2 planes at the pumped moment is recovered from that suppressed by the SC.

Fig. 2. tr-RSXS on YBCO.

Fig. 2.

Open in a new tab

(A) Schematic experimental configuration for YBCO sample. The orange- and blue-colored pulses denote x-ray (932 eV, Cu L3 edge) and optical laser (1.55 eV), respectively. θ Scans were performed to find a CDW peak at Q = (0, qcdw, l). (B) CDW intensity at Q = (0, qcdw, ~1.45) as a function of ∆t, measured at T = 25 K (below Tc). For ∆t < 0, the CDW height indicates the suppressed, but nonzero, CDW due to the competition with SC. For 0 < ∆t < ~7 ps, the CDW height is enhanced by the optical pump. The solid line presents a fit to exponential functions. The dashed line indicates ∆t = 0. (C) CDW peak profiles at ∆t = −1.1 ps (i.e., before pumping) and ∆t = +0.9 ps (i.e., maximum pumping effect on CDW). Solid lines are Lorentzian fits to the data with a linear background. Green- and blue-colored shades are guides to the eye to denote unpumped (i.e., static) and photoinduced CDW, respectively.

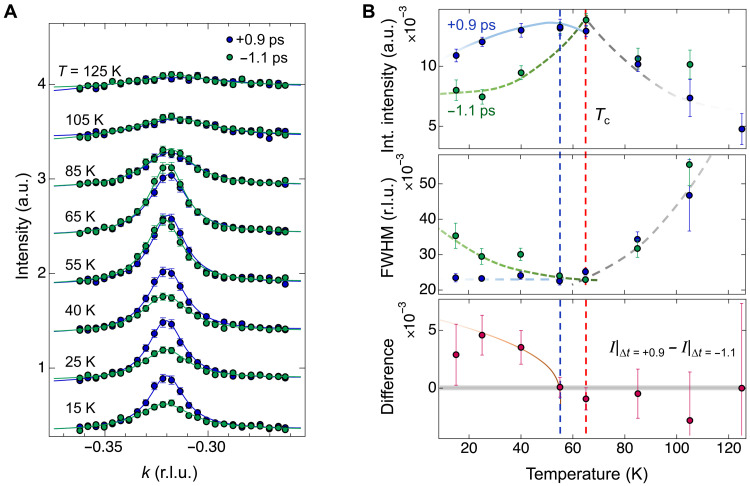
To scrutinize the photoinduced phenomena, we explored the temperature dependence of CDW scanned at Q = (0, k, ~1.45). Figure 3A shows the CDW peak profiles measured at both ∆t = −1.1 and +0.9 ps with different sample temperatures. Note that full delay scans are shown in fig. S2. Below Tc, the photoinduced behavior becomes more pronounced. This indicates that the CDW enhancement behavior is associated with the quenched SC state. For more quantitative analysis, we fitted both peak profiles and plotted a summary [CDW area (i.e., integrated intensity), peak width, and area difference] in Fig. 3B. The enhanced CDW area clearly shows a contrast below Tc. The correlation length, ξ = 2/FWHM (where FWHM is the full width at half maximum of the Lorentzian profile) of the photoinduced CDW peak at T = 15 K is estimated to be ~88 Å, which is about a 60% increase compared to the case at ∆t = −1.1 ps. Under the scattering perspective, this deduces that the domain size of CDW becomes larger (i.e., its volume fraction), while SC’s volume fraction could be suppressed by the pump. These findings show a strong resemblance to CDW phenomena under external magnetic fields (24–30). Moreover, the optically pumped CDW area is maximized at T ~ 55 K. This indicates that the Tc under the optically pumped condition is shifted lower because the superconducting state needs more energy to form under this pumped condition, which is consistent with typical behavior of a superconductor under a magnetic field (22, 45–46). However, the photoinduced CDW peak measured at 65 K (~Tc) is slightly weaker (~17.7%) than the CDW peak measured at ∆t = −1.1 ps. It means that optical pumping causes melting of not only SC in the CuO2 planes but also some portion of the CDW regardless of the existence of SC, like the case of pure CDW material (35). Nevertheless, it is possible to observe the photoinduced CDW behavior in YBCO because the temporal dynamics of CDW are slightly faster (about 100 fs) than that of SC (see fig. S4). Hence, the photoinduced CDW features observed at ∆t = +0.9 ps could be attributed to a combined response from both the melted portion by optical pumping and recovered portion by photoinduced suppression of SC.

Fig. 3. Temperature dependence of photoinduced CDW.

Fig. 3.

Open in a new tab

(A) CDW peak profiles at (0, k, ~1.45) measured at ∆t = +0.9 ps (blue) and −1.1 ps (green) with varying sample temperature. Solid lines are Lorentzian fits to the data with a linear background. (B) Fitted results of temperature dependence at ∆t = +0.9 ps (blue) and −1.1 ps (green) for integrated intensity (top) and peak width (FWHM; middle). Bottom panel shows a difference of integrated intensities between ∆t = +0.9 ps and −1.1 ps. Red and blue vertical dashed lines, respectively, represent Tc before (∆t < 0) and after (∆t = +0.9 ps) optical pumping. Solid and dashed lines are guides to the eye. The error bars represent 1 SD of the fit parameters.

Three-dimensional CDW correlation in the photoinduced normal state of YBCO

Considering the temperature dependence on the photoinduced CDW behavior in YBCO, it is reasonable to find a crossover in CDW phenomena between the optical pump approach and the magnetic field (H) approach as a next step. This triggered us to explore a signature of the long-ranged 3D CDW under the normal state that occurs when an H field stronger than 50% of Hc2 is applied (27–29). In this sense, we performed L dependence measurement of the CDW under the transient state, aiming to explore whether the optical pump also induces a 3D CDW behavior in YBCO.

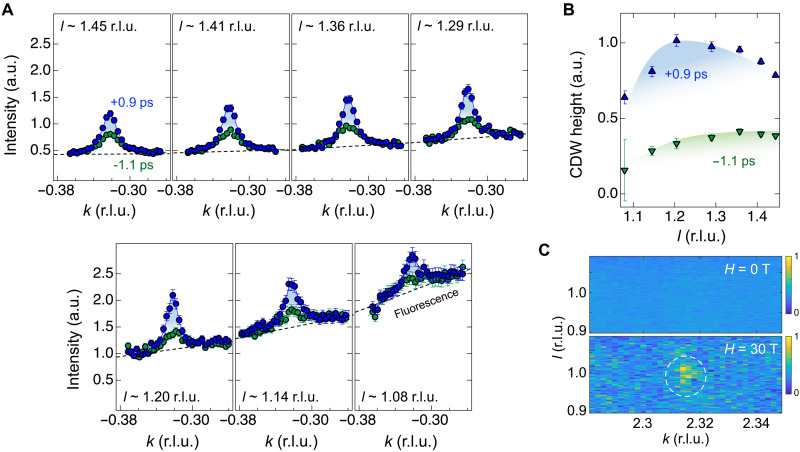
Figure 4A shows CDW peak profiles at both ∆t = −1.1 and +0.9 ps with different detector (2θ) angles (i.e., L dependence) at T = 25 K. Note that details of this detector angle-dependent measurement are shown in the Supplementary Materials. At ∆t = −1.1 ps, the CDW peak gets weaker when the l value moves toward 1 r.l.u. (see summarized CDW peak heights in Fig. 4B), which reproduces the typical quasi-2D CDW behavior in YBa2Cu3O6+δ cuprates that the CDW intensity is maximized around a half-integer (l ~ 1.5 r.l.u.) (12–14, 24–30). For ∆t = +0.9 ps, we observed a different photoinduced behavior with varying 2θ (also see fig. S3). The photoinduced CDW behavior gets pronounced as the l value decreases from ~1.45 to ~1.08 r.l.u. Nevertheless, no clear feature of a long-ranged 3D order was observed that would have been clearly visible in this YBCO under the high magnetic field (see Fig. 4C). However, as shown in Fig. 4B summary, we found an interesting tendency that the photoinduced CDW order is maximized at l ~ 1.2 r.l.u., which is close to an integer l value. This L dependence of the photoinduced CDW indicates a 3D CDW precursor correlation observed in high magnetic field measurements (27). It would also be worthwhile to note that the photoinduced state is still a mixture between the transient state and the reduced SC portion because of not reaching a full 3D CDW order.

Fig. 4. L dependence of photoinduced CDW.

Fig. 4.

Open in a new tab

(A) The CDW peak profiles of YBCO measured at ∆t = +0.9 and −1.1 ps with varying detector positions (i.e., L dependence) and T = 25 K. The dashed lines indicate a fluorescence background slope at each geometrical (detector) position. As detector 2θ decreases (i.e., l decreases), the fluorescence background is more pronounced because of geometrical effects such as elongation of the beam footprint. Solid lines are Lorentzian fits to the data with a linear fluorescence background. (B) Fitted CDW heights with the different l position (i.e., 2θ) at ∆t = +0.9 ps (up-triangles) and −1.1 ps (down-triangles). Blue- and green-colored shades are guides to the eye. The error bars represent 1 SD of the fit parameters. (C) Observed 3D CDW of YBCO via a pulsed magnet experiment (see Materials and Methods). The field-induced CDW appears (4 shots average) around (0, 2 + qcdw, 1), compared to the zero field (80 shots average).

According to the magnetic field experiments on YBa2Cu3O6+δ cuprates (12–14, 24–30), the development of the 3D CDW precursor suggests that the SC quenching effect via our optical pump condition is equivalent to that of the external magnetic field effect of between H = 10 and 14 T. Note that this field estimation is the simplest scaling analysis based on the assumption that the primary mechanism of CDW formation is electronic (see fig. S8). Although the lattice is always strongly coupled to an electron and somewhat affects the dynamics when an optical pump induces a thermal effect, the photoinduced CDW order’s L dependence (Fig. 4B and fig. S3), which cannot be explained by the lattice change, supports that the thermal heating is not dominant in this case. In this regard, the Tc shift shown in Fig. 3 is also interpreted to correspond to the equilibrium state under the estimated magnetic field (24, 25). Furthermore, considering some portion of the CDW in the CuO2 planes melted by the optical pump, the practical CDW portion in the optical pump is smaller than that in the magnetic field approach. Thus, it allows us to reconcile why the observed photoinduced effect corresponds to the relatively weak H field.

DISCUSSION

Using the tr-RSXS study on the CDW behavior in YBCO, we explore the intertwined phenomena between the CDW and SC in the normal state induced by the optical pump. We reveal that the CDW characteristic behaviors in the nonequilibrium state show close similarity with those under the magnetic field. These findings could provide a clue that the transient state characteristics show a solid analogy to the normal state under equilibrium conditions demonstrated by the magnetic field.

Beyond this, we further discuss the implications of our finding. The fact that CDW and/or spin density wave orders in high-Tc cuprates are enhanced by the external magnetic field (24, 26–28, 47–49) indicates that the vortex state is related to the quenched SC by H field. Such a circumstance is depicted as cartoons in Fig. 5 (A and B, top). As the external magnetic field is increased, the number of vortices corresponding increases, leading to an increase in the fraction of the quenched SC volume (i.e., increase in the normal state fraction) in the CuO2 plane (49). In the same manner, we depict that the Cooper-paired SC states (Fig. 5A) are transformed into the broken/weakened Cooper pairs through a proper optical pump (Fig. 5B, bottom) (33–40). For a short while, it leads to a transient state that becomes dominant over the reduced SC portion in the CuO2 plane. After all, the two approaches through the optical pump and the external magnetic field drive the quenched SC state, and their corresponding CDW responses are characteristically identical to the normal state. In this sense, we infer that an essential physics in the nonequilibrium state would be in a crossover with the equilibrium physics. This inference suggests that expanding the vortex liquid state by increasing the magnetic field could be alternatively interpreted by physics of the broken Cooper pairing in the CuO2 plane (see Fig. 5C). Ultimately, it implies that demonstrating the quenched SC state with either approach could be delivering the equivalent physics in HTSC. Inversely, with the equilibrium state, it is considerable that optical pump approaches are possible to drive room temperature transient SC (41–44). Moreover, understanding such a discussion presents a rich opportunity for detailed experimental investigations (e.g., CDW study through synchronizing three pulses between x-ray, an optical pump, and magnetic field) and theoretical interpretations in the future.

Fig. 5. Connection between equilibrium and nonequilibrium states.

Fig. 5.

Open in a new tab

(A) Schematic cartoon of YBCO’s superconducting state below Tc. The presence of Cooper pairs denotes SC. (B) Two independent ways to quench SC of YBCO, transforming into the normal state. Top and bottom are an external magnetic field approach (representing the equilibrium state) and optical pumping approach (representing the nonequilibrium state), respectively. The magnetic field approach causes the nucleation of the vortex state; the optical pumping denotes three kinds of pairing states (schematic inset: initial Cooper pair, weakened pair, and broken pair) within negative to a picosecond time frame, while SC state is transformed to a transient normal state. (C) A characterization of transient state in YBCO. The quenched SC states by either the vortex or the increased distribution of the broken (or weakened) pairs are equivalent.

MATERIALS AND METHODS

Sample preparation

Single crystals of YBa2Cu3O6.67 (Tc = 65.5 K) were grown using a flux method (50), and the oxygen content was adjusted by annealing under well-defined oxygen partial pressure. The sample was mechanically detwinned by heating under uniaxial stress (50 to 60 MPa was applied at 400°C). The dimensions of the single crystal were 2.10 mm by 1.05 mm by 0.38 mm along the crystallographic a, b, and c axes, respectively (lattice parameters: a ~ 3.82 Å, b ~ 3.88 Å, and c ~ 11.725 Å). The single crystal was thoroughly characterized by measuring the static CDW signal at the Stanford Synchrotron Radiation Lightsource (SSRL) beamline 13-3 using Cu L3-edge RSXS measurements (fig. S1).

tr-RSXS measurement

All tr-RSXS experiments were carried out at the SSS-RSXS endstation of PAL-XFEL (51). The sample was mounted on a six-axis open-circle cryostat manipulator and a base temperature of ~15 K using liquid helium. The sample surface was perpendicular to the crystalline c axis, and the horizontal scattering plan was parallel to the bc plane. X-ray pulses with an ~80-fs pulse duration and a 60-Hz repetition rate were used for the soft x-ray probe. The x-ray was linearly and horizontally polarized (π polarization), and the photon energy was tuned around the Cu L3 edge (932 eV). A 1.55-eV (800 nm) optical laser pump with an ~50-fs pulse duration and p polarization was provided by a Ti:sapphire laser (see Fig. 2A and fig. S7). It is commonly appreciated that the laser pulses at 800 nm are able to strongly perturb SC in cuprates (33–35, 39, 40, 52–55). The optical laser was nearly parallel to the incident x-ray beam as the angle difference is less than 1°. A pump fluence of 15 μJ/cm2 was mainly used (see fig. S5). The time delay between pump and probe pulses was controlled by a mechanical delay stage. The spot size of the x-ray at the sample position was 100 (H) × 200 (V) μm2 in FWHM, and the spot diameter of optical laser was ~500 μm in FWHM. The x-ray scattering signal was collected by an avalanche photodiode, which was enclosed in an aluminum cage, and the front was covered by a 300-nm-thick aluminum filter to ensure light tightness. All signals were recorded by high-speed digitizers and analyzed on a shot-to-shot basis.

X-ray scattering measurement with a high magnetic field

The high-field pulsed-magnet experiments were performed at the BL2-EH3 hutch of the SACLA (56). The YBCO sample was attached on a sapphire rod. The rod was mounted on a closed-cycle cryocooler with a capability of a sample base temperature ~10 K. X-ray pulses with a 7-fs pulse duration and a 30-Hz repetition rate were used. The x-ray was linearly and horizontally polarized (π polarization), and the photon energy was tuned to 8.8 keV, just below the Cu K edge to reduce the fluorescence background (26). X-ray pulse arrived at the top of ~1-ms duration pulsed magnetic field with ~30 T. To obtain zero-field background, 10 shots of x-ray–only scattering signal were obtained before and after the shot with a magnetic pulse. As shown in Fig. 4C, therefore, the noise levels between H = 0 T (80 shots accumulated) and 30 T (4 shots) appear differently (see fig. S9). A half-megapixel multi-port charge-coupled device was used to capture the 2D scattering profile.

Acknowledgments

We thank D. Zhu for insightful discussions.

Funding: The RSXS experiments were carried out at the SSRL (beamline 13-3), SLAC National Accelerator Laboratory, supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515. The tr-RSXS experiments were performed at the SSS-RSXS endstation (proposal number: 2020-1st-SSS-016) of the PAL-XFEL funded by the Korea government (MSIT). Self-flux growth was performed at Scientific Facility Crystal Growth in the Max Planck Institute for Solid State Research, Stuttgart, Germany with the support of the technical staff. The pulsed-magnet experiments were performed at the BL2-EH3 hutch of the SACLA with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (proposal nos. 2017B8059, 2019B8001, and 2020A8012) of the SACLA funded by KAKENHI 19H00647. H.J. acknowledges the support by the National Research Foundation grant funded by the Korea government (MSIT) (grant no. 2019R1F1A1060295).

Author contributions: H.J., S.-Y.P., M.K., H.-D.K., H.L., C.S., and J.-S.L. carried out tr-RSXS experiment and analyzed the data. H.J., S.S., Y.L., T.K., Y.K., I.I., K.T., M.Y., H.N., and J.-S.L. carried out the pulsed magnet experiment and analyzed the data. S.-J.L. and J.-S.L. carried out the RSXS experiment and analyzed the data. S.N. and B.K. synthesized the crystal. H.J., S.S., S.-J.L., G.C., C.-C.K., and J.-S.L. wrote the manuscript with input from all authors. J.-S.L. coordinated the project.

Competing interests: The authors declare that they have no competing interests.

Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S9

Click here for additional data file. (1.5MB, pdf)

REFERENCES AND NOTES

  • 1.Bednorz J. G., Müller K. A., Possible highTc superconductivity in the Ba−La−Cu−O system. Z. Physik B 64, 189–193 (1986). [Google Scholar]
  • 2.Fradkin E., Kivelson S. A., Ineluctable complexity. Nat. Phys. 8, 864–866 (2012). [Google Scholar]
  • 3.Fradkin E., Kivelson S. A., Tranquada J. M., Colloquium: Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015). [Google Scholar]
  • 4.Keimer B., Kivelson S. A., Norman M. R., Uchida S., Zaanen J., From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015). [DOI] [PubMed] [Google Scholar]
  • 5.Varma C. M., Littlewood P. B., Schmitt-Rink S., Abrahams E., Ruckenstein A. E., Phenomenology of the normal state of Cu-O high-temperature superconductors. Phys. Rev. Lett. 63, 1996–1999 (1989). [DOI] [PubMed] [Google Scholar]
  • 6.Timusk T., Statt B., The pseudogap in high-temperature superconductors: An experimental survey. Rep. Prog. Phys. 62, 61–122 (1999). [Google Scholar]
  • 7.Tranquada J. M., Sternlieb B. J., Axe J. D., Nakamura Y., Uchida S., Evidence for stripe correlations of spins and holes in copper oxide superconductors. Nature 375, 561–563 (1995). [Google Scholar]
  • 8.Kivelson S. A., Fradkin E., Emery V. J., Electronic liquid-crystal phases of a doped Mott insulator. Nature 393, 550–553 (1998). [Google Scholar]
  • 9.Kivelson S. A., Bindloss I. P., Fradkin E., Oganesyan V., Tranquada J. M., Kapitulnik A., Howald C., How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 75, 1201–1241 (2003). [Google Scholar]
  • 10.Hoffman J. E., Hudson E. W., Lang K. M., Madhavan V., Eisaki H., Uchida S., Davis J. C., A four unit cell periodic pattern of quasi-particle states surrounding vortex cores in Bi2Sr2CaCu2O8+δ. Science 295, 466–469 (2002). [DOI] [PubMed] [Google Scholar]
  • 11.Abbamonte P., Rusydi A., Smadici S., Gu G. D., Sawatzky G. A., Feng D. L., Spatially modulated ‘Mottness’ in La2-xBaxCuO4. Nat. Phys. 1, 155–158 (2005). [Google Scholar]
  • 12.Ghiringhelli G., Tacon M. L., Minola M., Blanco-Canosa S., Mazzoli C., Brookes N. B., Luca G. M. D., Frano A., Hawthorn D. G., He F., Loew T., Sala M. M., Peets D. C., Salluzzo M., Schierle E., Sutarto R., Sawatzky G. A., Weschke E., Keimer B., Braicovich L., Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x. Science 337, 821–825 (2012). [DOI] [PubMed] [Google Scholar]
  • 13.Blanco-Canosa S., Frano A., Schierle E., Porras J., Loew T., Minola M., Bluschke M., Weschke E., Keimer B., Le Tacon M., Resonant x-ray scattering study of charge-density wave correlations in YBa2Cu3O6+x. Phys. Rev. B 90, 054513 (2014). [DOI] [PubMed] [Google Scholar]
  • 14.Wu T., Mayaffre H., Krämer S., Horvatić M., Berthier C., Hardy W. N., Liang R., Bonn D. A., Julien M.-H., Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy. Nature 477, 191–194 (2011). [DOI] [PubMed] [Google Scholar]
  • 15.Comin R., Frano A., Yee M. M., Yoshida Y., Eisaki H., Schierle E., Weschke E., Sutarto R., He F., Soumyanarayanan A., He Y., Tacon M. L., Elfimov I. S., Hoffman J. E., Sawatzky G. A., Keimer B., Damascelli A., Charge order driven by fermi-arc instability in Bi2Sr2−xLaxCuO6+δ. Science 343, 390–392 (2014). [DOI] [PubMed] [Google Scholar]
  • 16.Tabis W., Li Y., Tacon M. L., Braicovich L., Kreyssig A., Minola M., Dellea G., Weschke E., Veit M. J., Ramazanoglu M., Goldman A. I., Schmitt T., Ghiringhelli G., Barišić N., Chan M. K., Dorow C. J., Yu G., Zhao X., Keimer B., Greven M., Charge order and its connection with Fermi-liquid charge transport in a pristine high-Tc cuprate. Nat. Commun. 5, 5875 (2014). [DOI] [PubMed] [Google Scholar]
  • 17.da Silva Neto E. H., Comin R., He F., Sutarto R., Jiang Y., Greene R. L., Sawatzky G. A., Damascelli A., Charge ordering in the electron-doped superconductor Nd2–xCexCuO4. Science 347, 282–285 (2015). [DOI] [PubMed] [Google Scholar]
  • 18.Jang H., Asano S., Fujita M., Hashimoto M., Lu D. H., Burns C. A., Kao C.-C., Lee J.-S., Superconductivity-insensitive order at q∼1/4 in electron-doped cuprates. Phys. Rev. X 7, 041066 (2017). [Google Scholar]
  • 19.Miao H., Lorenzana J., Seibold G., Peng Y. Y., Amorese A., Yakhou-Harris F., Kummer K., Brookes N. B., Konik R. M., Thampy V., Gu G. D., Ghiringhelli G., Braicovich L., Dean M. P. M., High-temperature charge density wave correlations in La1.875Ba0.125CuO4 without spin–charge locking. Proc. Natl. Acad. Sci. U.S.A. 114, 12430–12435 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Wen J.-J., Huang H., Lee S.-J., Jang H., Knight J., Lee Y. S., Fujita M., Suzuki K. M., Asano S., Kivelson S. A., Kao C.-C., Lee J.-S., Observation of two types of charge-density-wave orders in superconducting La2-xSrxCuO4. Nat. Commun. 10, 3269 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Miura N., Nakagawa H., Sekitani T., Naito M., Sato H., Enomoto Y., High-magnetic-field study of high-Tc cuprates. Physica B 319, 310–320 (2002). [Google Scholar]
  • 22.Grissonnanche G., Cyr-Choinière O., Laliberté F., René de Cotret S., Juneau-Fecteau A., Dufour-Beauséjour S., Delage M.-È., LeBoeuf D., Chang J., Ramshaw B. J., Bonn D. A., Hardy W. N., Liang R., Adachi S., Hussey N. E., Vignolle B., Proust C., Sutherland M., Krämer S., Park J.-H., Graf D., Doiron-Leyraud N., Taillefer L., Direct measurement of the upper critical field in cuprate superconductors. Nat. Commun. 5, 3280 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Kemper J. B., Vafek O., Betts J. B., Balakirev F. F., Hardy W. N., Liang R., Bonn D. A., Boebinger G. S., Thermodynamic signature of a magnetic-field-driven phase transition within the superconducting state of an underdoped cuprate. Nat. Phys. 12, 47–51 (2016). [Google Scholar]
  • 24.Chang J., Blackburn E., Holmes A. T., Christensen N. B., Larsen J., Mesot J., Liang R., Bonn D. A., Hardy W. N., Watenphul A., Zimmermann M. v., Forgan E. M., Hayden S. M., Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67. Nat. Phys. 8, 871–876 (2012). [Google Scholar]
  • 25.Blanco-Canosa S., Frano A., Loew T., Lu Y., Porras J., Ghiringhelli G., Minola M., Mazzoli C., Braicovich L., Schierle E., Weschke E., Le Tacon M., Keimer B., Momentum-dependent charge correlations in YBa2Cu3O6+ δ superconductors probed by resonant x-ray scattering: Evidence for three competing phases. Phys. Rev. Lett. 110, 187001 (2013). [DOI] [PubMed] [Google Scholar]
  • 26.Gerber S., Jang H., Nojiri H., Matsuzawa S., Yasumura H., Bonn D. A., Liang R., Hardy W. N., Islam Z., Mehta A., Song S., Sikorski M., Stefanescu D., Feng Y., Kivelson S. A., Devereaux T. P., Shen Z.-X., Kao C.-C., Lee W.-S., Zhu D., Lee J.-S., Three-dimensional charge density wave order in YBa2Cu3O6.67 at high magnetic fields. Science 350, 949–952 (2015). [DOI] [PubMed] [Google Scholar]
  • 27.Chang J., Blackburn E., Ivashko O., Holmes A. T., Christensen N. B., Hücker M., Liang R., Bonn D. A., Hardy W. N., Rütt U., Zimmermann M. v., Forgan E. M., Hayden S. M., Magnetic field controlled charge density wave coupling in underdoped YBa2Cu3O6+x. Nat. Commun. 7, 11494 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Jang H., Lee W.-S., Nojiri H., Matsuzawa S., Yasumura H., Nie L., Maharaj A. V., Gerber S., Liu Y.-J., Mehta A., Bonn D. A., Liang R., Hardy W. N., Burns C. A., Islam Z., Song S., Hastings J., Devereaux T. P., Shen Z.-X., Kivelson S. A., Kao C.-C., Zhu D., Lee J.-S., Ideal charge-density-wave order in the high-field state of superconducting YBCO. Proc. Natl. Acad. Sci. U.S.A. 113, 14645–14650 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Jang H., Lee W.-S., Song S., Nojiri H., Matsuzawa S., Yasumura H., Huang H., Liu Y.-J., Porras J., Minola M., Keimer B., Hastings J., Zhu D., Devereaux T. P., Shen Z.-X., Kao C.-C., Lee J.-S., Coincident onset of charge-density-wave order at a quantum critical point in underdoped YBa2Cu3Ox. Phys. Rev. B 97, 224513 (2018). [Google Scholar]
  • 30.Choi J., Ivashko O., Blackburn E., Liang R., Bonn D. A., Hardy W. N., Holmes A. T., Christensen N. B., Hücker M., Gerber S., Gutowski O., Rütt U., Zimmermann M. v., Forgan E. M., Hayden S. M., Chang J., Spatially inhomogeneous competition between superconductivity and the charge density wave in YBa2Cu3O6.67. Nat. Commun. 11, 990 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Giannetti C., Capone M., Fausti D., Fabrizio M., Parmigiani F., Mihailovic D., Ultrafast optical spectroscopy of strongly correlated materials and high-temperature superconductors: A non-equilibrium approach. Adv. Phys. 65, 58–238 (2016). [Google Scholar]
  • 32.Demsar J., Non-equilibrium phenomena in superconductors probed by femtosecond time-domain spectroscopy. J. Low Temp. Phys. 201, 676–709 (2020). [Google Scholar]
  • 33.Kaindl R. A., Woerner M., Elsaesser T., Smith D. C., Ryan J. F., Farnan G. A., McCurry M. P., Walmsley D. G., Ultrafast mid-infrared response of YBa2Cu3O7-δ. Science 287, 470–473 (2000). [DOI] [PubMed] [Google Scholar]
  • 34.Kusar P., Kabanov V. V., Demsar J., Mertelj T., Sugai S., Mihailovic D., Controlled vaporization of the superconducting condensate in cuprate superconductors by femtosecond photoexcitation. Phys. Rev. Lett. 101, 227001 (2008). [DOI] [PubMed] [Google Scholar]
  • 35.Stojchevska L., Kusar P., Mertelj T., Kabanov V. V., Toda Y., Yao X., Mihailovic D., Mechanisms of nonthermal destruction of the superconducting state and melting of the charge-density-wave state by femtosecond laser pulses. Phys. Rev. B 84, 180507 (2011). [Google Scholar]
  • 36.Hinton J. P., Koralek J. D., Lu Y. M., Vishwanath A., Orenstein J., Bonn D. A., Hardy W. N., Liang R., New collective mode in YBa2Cu3O6+x observed by time-domain reflectometry. Phys. Rev. B 88, 060508 (2013). [Google Scholar]
  • 37.Coslovich G., Giannetti C., Cilento F., Dal Conte S., Ferrini G., Galinetto P., Greven M., Eisaki H., Raichle M., Liang R., Damascelli A., Parmigiani F., Evidence for a photoinduced nonthermal superconducting-to-normal-state phase transition in overdoped Bi2Sr2Ca0.92Y0.08Cu2O8+δ. Phys. Rev. B 83, 064519 (2011). [Google Scholar]
  • 38.Coslovich G., Giannetti C., Cilento F., Dal Conte S., Abebaw T., Bossini D., Ferrini G., Eisaki H., Greven M., Damascelli A., Parmigiani F., Competition between the pseudogap and superconducting states of Bi2Sr2Ca0.92Y0.08Cu2O8+δ single crystals revealed by ultrafast broadband optical reflectivity. Phys. Rev. Lett. 110, 107003 (2013). [DOI] [PubMed] [Google Scholar]
  • 39.Boschini F., da Silva Neto E. H., Razzoli E., Zonno M., Peli S., Day R. P., Michiardi M., Schneider M., Zwartsenberg B., Nigge P., Zhong R. D., Schneeloch J., Gu G. D., Zhdanovich S., Mills A. K., Levy G., Jones D. J., Giannetti C., Damascelli A., Collapse of superconductivity in cuprates via ultrafast quenching of phase coherence. Nat. Mater. 17, 416–420 (2018). [DOI] [PubMed] [Google Scholar]
  • 40.S. Wandel, F. Boschini, E. H. da S. Neto, L. Shen, M. X. Na, S. Zohar, Y. Wang, G. B. Welch, M. H. Seaberg, J. D. Koralek, G. L. Dakovski, W. Hettel, M.-F. Lin, S. P. Moeller, W. F. Schlotter, A. H. Reid, M. P. Minitti, T. Boyle, F. He, R. Sutarto, R. Liang, D. Bonn, W. Hardy, R. A. Kaindl, D. G. Hawthorn, J.-S. Lee, A. F. Kemper, A. Damascelli, C. Giannetti, J. J. Turner, G. Coslovich, Light-enhanced charge density wave coherence in a high-temperature superconductor. Preprint at https://arxiv.org/abs/2003.04224 (2020).
  • 41.Hu W., Kaiser S., Nicoletti D., Hunt C. R., Gierz I., Hoffmann M. C., Le Tacon M., Loew T., Keimer B., Cavalleri A., Optically enhanced coherent transport in YBa2Cu3O6.5 by ultrafast redistribution of interlayer coupling. Nat. Mater. 13, 705–711 (2014). [DOI] [PubMed] [Google Scholar]
  • 42.Kaiser S., Hunt C. R., Nicoletti D., Hu W., Gierz I., Liu H. Y., Le Tacon M., Loew T., Haug D., Keimer B., Cavalleri A., Optically induced coherent transport far above Tc in underdoped YBa2Cu3O6+δ. Phys. Rev. B 89, 184516 (2014). [Google Scholar]
  • 43.Mankowsky R., Subedi A., Först M., Mariager S. O., Chollet M., Lemke H. T., Robinson J. S., Glownia J. M., Minitti M. P., Frano A., Fechner M., Spaldin N. A., Loew T., Keimer B., Georges A., Cavalleri A., Nonlinear lattice dynamics as a basis for enhanced superconductivity in YBa2Cu3O6.5. Nature 516, 71–73 (2014). [DOI] [PubMed] [Google Scholar]
  • 44.Liu B., Först M., Fechner M., Nicoletti D., Porras J., Loew T., Keimer B., Cavalleri A., Pump frequency resonances for light-induced incipient superconductivity in YBa2Cu3O6.5. Phys. Rev. X 10, 011053 (2020). [Google Scholar]
  • 45.Ramshaw B. J., Day J., Vignolle B., LeBoeuf D., Dosanjh P., Proust C., Taillefer L., Liang R., Hardy W. N., Bonn D. A., Vortex lattice melting and Hc2 in underdoped YBa2Cu3Oy. Phys. Rev. B 86, 174501 (2012). [Google Scholar]
  • 46.Marcenat C., Demuer A., Beauvois K., Michon B., Grockowiak A., Liang R., Hardy W., Bonn D. A., Klein T., Calorimetric determination of the magnetic phase diagram of underdoped ortho II YBa2Cu3O6.54 single crystals. Nat. Commun. 6, 7927 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Lake B., Lefmann K., Christensen N. B., Aeppli G., McMorrow D. F., Ronnow H. M., Vorderwisch P., Smeibidl P., Mangkorntong N., Sasagawa T., Nohara M., Takagi H., Three-dimensionality of field-induced magnetism in a high-temperature superconductor. Nat. Mater. 4, 658–662 (2005). [DOI] [PubMed] [Google Scholar]
  • 48.Yu Y., Kivelson S. A., Fragile superconductivity in the presence of weakly disordered charge density waves. Phys. Rev. B 99, 144513 (2019). [Google Scholar]
  • 49.Shi Z., Baity P. G., Sasagawa T., Popović D., Vortex phase diagram and the normal state of cuprates with charge and spin orders. Sci. Adv. 6, eaay8946 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Hinkov V., Pailhès S., Bourges P., Sidis Y., Ivanov A., Kulakov A., Lin C. T., Chen D. P., Bernhard C., Keimer B., Two-dimensional geometry of spin excitations in the high-transition-temperature superconductor YBa2Cu3O6+x. Nature 430, 650–654 (2004). [DOI] [PubMed] [Google Scholar]
  • 51.Jang H., Kim H.-D., Kim M., Park S. H., Kwon S., Lee J. Y., Park S.-Y., Park G., Kim S., Hyun H., Hwang S., Lee C.-S., Lim C.-Y., Gang W., Kim M., Heo S., Kim J., Jung G., Kim S., Park J., Kim J., Shin H., Park J., Koo T.-Y., Shin H.-J., Heo H., Kim C., Min C.-K., Han J.-H., Kang H.-S., Lee H.-S., Kim K. S., Eom I., Rah S., Time-resolved resonant elastic soft x-ray scattering at Pohang Accelerator Laboratory x-ray free electron laser. Rev. Sci. Instrum. 91, 083904 (2020). [DOI] [PubMed] [Google Scholar]
  • 52.Perfetti L., Loukakos P. A., Lisowski M., Bovensiepen U., Eisaki H., Wolf M., Ultrafast electron relaxation in superconducting Bi2Sr2CaCu2O8+δ by time-resolved photoelectron spectroscopy. Phys. Rev. Lett. 99, 197001 (2007). [DOI] [PubMed] [Google Scholar]
  • 53.Demsar J., Podobnik B., Kabanov V. V., Wolf T., Mihailovic D., Superconducting Gap ∆c, the pseudogap ∆p, and pair fluctuations above Tc in OVerdoped Y1-xCaxBa2Cu3O7-δ from femtosecond time-domain spectroscopy. Phys. Rev. Lett. 82, 4918–4921 (1999). [Google Scholar]
  • 54.Averitt R. D., Rodriguez G., Lobad A. I., Siders J. L. W., Trugman S. A., Taylor A. J., Nonequilibrium superconductivity and quasiparticle dynamics in YBa2Cu3O7-δ. Phys. Rev. B 63, 140502 (2001). [Google Scholar]
  • 55.Mitrano M., Lee S., Husain A. A., Delacretaz L., Zhu M., de la Peña Munoz G., Sun S. X.-L., Joe Y. I., Reid A. H., Wandel S. F., Coslovich G., Schlotter W., van Driel T., Schneeloch J., Gu G. D., Hartnoll S., Goldenfeld N., Abbamonte P., Ultrafast time-resolved x-ray scattering reveals diffusive charge order dynamics in La2–xBaxCuO4. Sci. Adv. 5, eaax3346 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Ishikawa T., Aoyagi H., Asaka T., Asano Y., Azumi N., Bizen T., Ego H., Fukami K., Fukui T., Furukawa Y., Goto S., Hanaki H., Hara T., Hasegawa T., Hatsui T., Higashiya A., Hirono T., Hosoda N., Ishii M., Inagaki T., Inubushi Y., Itoga T., Joti Y., Kago M., Kameshima T., Kimura H., Kirihara Y., Kiyomichi A., Kobayashi T., Kondo C., Kudo T., Maesaka H., Maréchal X. M., Masuda T., Matsubara S., Matsumoto T., Matsushita T., Matsui S., Nagasono M., Nariyama N., Ohashi H., Ohata T., Ohshima T., Ono S., Otake Y., Saji C., Sakurai T., Sato T., Sawada K., Seike T., Shirasawa K., Sugimoto T., Suzuki S., Takahashi S., Takebe H., Takeshita K., Tamasaku K., Tanaka H., Tanaka R., Tanaka T., Togashi T., Togawa K., Tokuhisa A., Tomizawa H., Tono K., Wu S., Yabashi M., Yamaga M., Yamashita A., Yanagida K., Zhang C., Shintake T., Kitamura H., Kumagai N., A compact x-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 6, 540–544 (2012). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Text

Figs. S1 to S9

Click here for additional data file. (1.5MB, pdf)

Articles from Science Advances are provided here courtesy of American Association for the Advancement of Science

RESOURCES