Gigantic floating leaves occupy a large surface area at an economical material cost

Abstract

The giant Amazonian waterlily (genus Victoria) produces the largest floating leaves in the plant kingdom. The leaves’ notable vasculature has inspired artists, engineers, and architects for centuries. Despite the aesthetic appeal and scale of this botanical enigma, little is known about the mechanics of these extraordinary leaves. For example, how do these leaves achieve gigantic proportions? We show that the geometric form of the leaf is structurally more efficient than those of other smaller species of waterlily. In particular, the spatially varying thickness and regular branching of the primary veins ensures the structural integrity necessary for extensive coverage of the water surface, enabling optimal light capture despite a relatively low leaf biomass. Leaf gigantism in waterlilies may have been driven by selection pressures favoring a large surface area at an economical material cost, for outcompeting other plants in fast-drying ephemeral pools.

Giant Amazonian waterlilies occupy a large surface area for light capture, despite a low biomass relative to other waterlilies.

INTRODUCTION

The leaves of giant Amazonian waterlilies (genus Victoria, family Nymphaeaceae) are among the most astounding feats of natural engineering (Fig. 1A). They are the largest floating leaves of any plant, growing up to 3 m in diameter, and form vast networks on the surface of their native Amazon River Basin. The leaves are also an important example of biomimetics (the design of systems and materials through biomimicry) in architecture (1). The form of the vascular system inspired Joseph Paxton’s design of the support structure for the large glass panes that made up the Victorian Crystal Palace in London—an 18-acre glass and iron construction, designed in 1851 and destroyed by fire 85 years later (2, 3). Despite their archetypal beauty, more than two centuries since their discovery, unexpectedly, little is known about the structural properties of these floating leaves. In recent years, however, important progress has been made in understanding the geometry and deformation of floating sheets (4–12). Here, we draw on these developments to elucidate the mechanical functionality inherent in the geometric form of the leaves of the giant Amazonian waterlily.

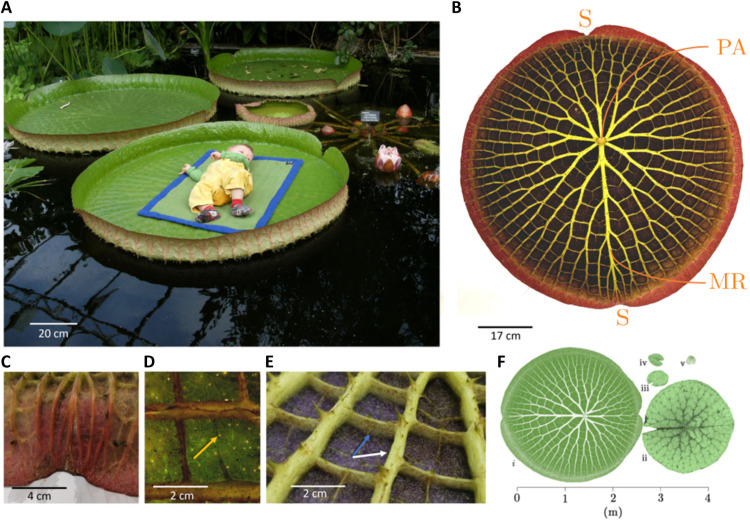
Fig. 1. Giant Amazonian waterlily (V. cruziana).

(A) Giant floating leaves can support the weight of a small child. (B) Underside of the leaf showing the vascular network and the petiolar attachment (PA), midrib (MR), and sinuses (S) in the upturned margin. (C and D) Sinuses and stomatodes (yellow arrow) function as part of a rainwater drainage system. (E) The complex vascular network is composed of a radiating series of thick girders (white arrow) and thinner, orthoradial connective anastomoses (blue arrow). (F) Relative size of waterlily leaves: (i), Victoria, (ii) Euryale, (iii) Nymphaea, (iv) Nuphar, and (v) Barclaya. In the five genera that make up the family Nymphaeaceae, gigantism is restricted to the sister genera Victora and Euryale.

Circular peltate leaves, characterized by a petiole attached centrally to the under surface of the lamina, are widespread (13). This leaf form is suggested to be adaptive where no leaf overlap occurs, which is common among plants that live on the water surface where the effective area for photosynthesis is equal to the habitat area (14). Giant Amazonian waterlilies produce circular peltate leaves, like most waterlilies, but the adaptive significance of their extreme size—which is unique to the genus Victoria and, to a lesser extent, their sister genus Euryale (Fig. 1F)—is not understood. Natural selection generally favors leaf forms that maximize the ratio of net photosynthesis to water loss by transpiration, and size is limited by strength (15, 16). Although an aquatic life history negates the risk of water loss and physically supports large leaf laminae (through buoyancy), giant circular leaves do not occur in other waterlilies or in aquatics elsewhere in the plant kingdom.

Strength is not the only constraint on leaf size: The benefit from the light energy absorbed by a leaf is balanced by the cost (in energetic terms) required to construct and maintain it (17). Plants with floating leaves tend to have a much smaller biomass than terrestrial herbaceous plants due to a high leaf turnover—old leaves, covered by newly formed ones, become submerged and lose their function as a photosynthetic apparatus (18). This suggests that the unique form of the Amazonian waterlily may have evolved as a natural engineering solution to selection pressures that favored both a low leaf biomass while maintaining a large surface area available for photosynthesis.

From above, giant Amazonian waterlily leaves resemble floating disks with upturned margins. However, the underside of the leaf is decorated by a fractal-like network of branching veins that—from an engineering perspective—provide structural support to the leaf lamina. Girder-like veins radiate from the petiolar (leaf stalk) attachment and are dissected by smaller veins (anastomoses) at right angles (Fig. 1B). The lamina is relatively thin for such a large leaf (ca. 1 mm), provides extensive coverage and surface area for photosynthesis, and contains small cylindrical pores (stomatodes; Fig. 1D) that, together with the sinuses, function as a rainwater drainage system. The undersurface of the leaf is also covered in numerous robust spines (Fig. 1E) that protect the lamina from herbivory. At the leaf’s edge, the upturned margin contains two diametrically opposite sinuses in the median plane (Fig. 1, B and C). The morphology of these distinctive features at the leaf edge have been attributed to mechanics; analogously, a thin elastic plate that grows subject to a nonuniform strain field (19) can develop an out-of-plane fold at its edge (owing to accumulated radial stress) that closely resembles the upturned rim of the leaf.

Here, we focus on the how vascular architecture differentiates the leaves of giant Amazonian waterlilies from the smaller leaves of other species. First, we measure the mechanical response of waterlily leaves to applied loads and compare our results to the ideal case of a floating elastic sheet of uniform thickness. Informed by differences in leaf structure associated with different species of waterlily, we then perform numerical simulations of model floating leaves with various geometries. Last, we describe the evolutionary history of Victoria cruziana before demonstrating that the vasculature architecture of the world’s largest floating leaves could also inspire structurally efficient, freestanding platforms.

RESULTS

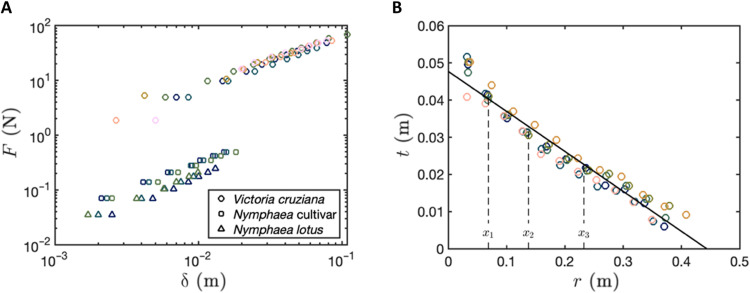
When subject to an applied force, leaves deform downward and displace water, which generates a restoring buoyancy force. In all cases, the measured displacement was found to be proportional to the applied load F (Fig. 2A). The constant of proportionality is an effective stiffness that combines both the leaves resistance to bending and the buoyancy effect of the underlying liquid, i.e., F = Kδ with stiffnesses K_Victoria = 690.8 ± 17.3 N m⁻¹, K_{N. cultivar} = 30.7 ± 1.0 N m⁻¹ and K_{N. lotus} = 18.5 ± 0.7 N m⁻¹. Our results confirm that Victoria are orders of magnitude stiffer than Nymphaea, which almost resemble flat disks. This is expected, because the thickness of the prominent vasculature of the Victoria is much greater than that of Nymphaea. We note, however, that although the thickness profile of the Victoria vasculature varies with distance from the petiole (Fig. 2B), the ratio of maximum vasculature thickness to lamina thickness is max(h_vein)/h_lamina ∼ 50 for Victoria yet only ∼2.7 for Nymphaea. This implies that the leaves of smaller species of waterlily more closely resemble flat disks, while the leaves of Victoria have a highly pronounced vasculature architecture. This raises the possibility that the form of Victoria distributes material in a structurally efficient manner that enables the gigantic proportions of the leaf.

Fig. 2. Mechanical stiffness of giant waterlily leaves.

(A) Force, F, measured as a function of indentation distance, δ, for different species of waterlily: V. cruziana (circles), Nymphaea cultivar “Black Princess” (squares), and N. lotus (triangles). Tests performed on different leaves are represented by different color markers. Inset: Scaling the force by the measured stiffness collapses the data onto one curve. (B) Vasculature thickness of V. cruziana, as a function of radial distance from the petiole attachment (markers) and a line of best fit. Dashed lines represent the mean radial position at which branching occurs; x_i indicates the position at which the ith bifurcation.

To explore this hypothesis, we compare our empirical findings for Victoria leaves to model leaves of the same size (i.e., equal volume and radial extent) with various thickness profiles. First, we consider the analogous case of a floating elastic sheet of uniform thickness before examining the role of the nonuniform vasculature architecture via computer simulations of model leaves (Fig. 3, A to C).

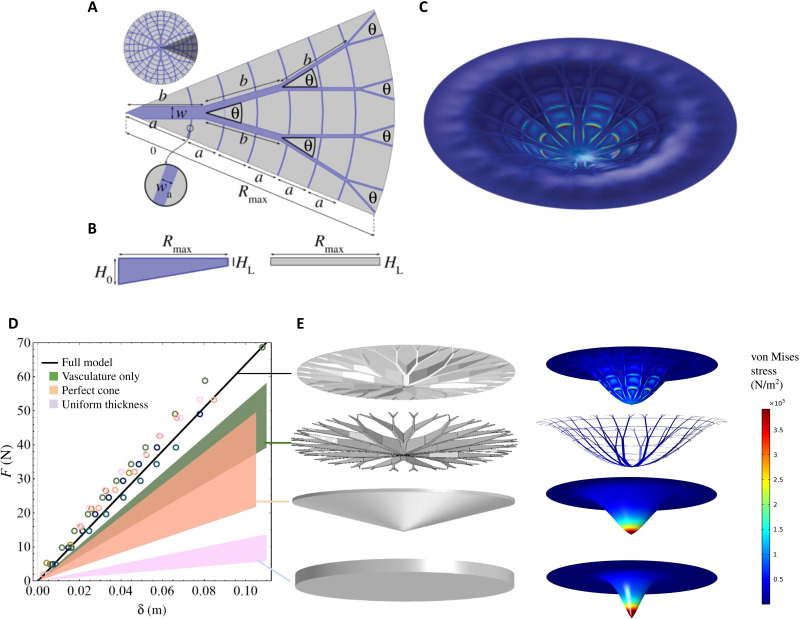
Fig. 3. Modeling the vasculature architecture.

(A) Schematic view of one-eighth of the waterlily model constructed with branching length b = 12 cm and branching angle θ = 16^∘. The width of the first generation of branches w = 20 mm; following generations have w/2, w/4, and w/8. The first anastomose (orthoradial branch) is located a distance a₀ = 10 cm from the center; subsequent anastomoses are separated by a distance a = 5 cm, and their widths are w_a = 1.5 mm. (B) Side view of vasculature (blue) and lamina (gray). The vascular thickness decreases from H₀ = 5 cm at the center to H_L = 1.5 mm at the leaf edge, and the lamina is a uniform sheet of thickness H_L. (C) Finite element simulations of the structure shown in (A), indented by 10 cm, incorporating the leaf vasculature, different Young’s moduli for lamina and vasculature and the buoyancy of the underlying liquid. (D) Comparing experimental force-indentation relations for V. cruziana (circles) and computed force-displacement curves for a circular disk of uniform thickness (pink region); a disk with linearly decreasing thickness (orange region), the vasculature only (green region), and the full waterlily model (the black line), comprising vasculature and lamina. All four structures have the same volume, equal to that of the leaves of V. cruziana on which the experiments were performed, and force-displacement curves are bounded by the range of measured Young’s moduli (i.e., E = 0.6 to 2.7 MPa), except the full waterlily model that explicitly uses E_vein = 0.6 MPa and E_lamina = 2.7 MPa. (E) Thickness profiles used in simulations for the four scenarios from (D) (gray surfaces) and resulting indentation profiles (colors); colors correspond to surface von Mises stress (color bar). The indentation axis is scaled by a factor of 2 for visual clarity.

For a floating elastic sheet of uniform thickness, a combination of indentation-induced bending stresses in the sheet and the restoring buoyancy force results in a linear relation between force and displacement, F = K_diskδ for δ < t_disk (7), where the stiffness coefficient K_disk = 8(Bρg)^1/2, ρ is the density of water, g is the gravitational constant, and the bending stiffness of the sheet $B=E{t}_{\text{disk}}^3/[12(1-{\mathrm{\nu }}^2)]$ depends on the material properties (E is the Young’s modulus and ν is the Poisson’s ratio) and the thickness, t_disk, of the sheet [the pre-tension in the leaf—induced by the surface tension of the water acting at the leaf boundary—is negligible, i.e., insufficient to stretch the leaf; this corresponds to the case of low mechanical bendability τ = γ_lv/(ρgB)^1/2 ≪ 1, where γ_lv is the surface tension at the air-water interface (7)]. The volume and radius of V. cruziana leaves in the collection were found to be V ≈ 2500 cm³ and R = 41 cm, respectively; a circular disk of equal volume would therefore have thickness t_disk = V/(πR²) = 0.47 cm. This gives a stiffness coefficient $K_{\text{disk}}=8{(B\mathrm{\rho }g)}^{\frac{1}{2}}=66.6 \text{to} 141.4$ N m⁻¹ (see the pink shaded region in Fig. 3, D and E), depending on whether we use the Young’s modulus of the leaf vasculature, E_vein = 0.6 MPa, or leaf lamina, E_lamina = 2.7 MPa (see Materials and Methods). Thus, the measured stiffness coefficient of V. cruziana K_Victoria is significantly larger than that of a floating disk of uniform thickness, $\frac{K_{\mathit{\text{Victoria}}}}{K_{\text{disk}}}\approx 5 \text{to} 10$ (equivalently, a circular disk with comparable bending stiffness to that of the measured leaves requires a volume in the range V_disk = πR²t_disk ≈ 7200 to 11,900 cm³, which is approximately three to five times more than the measured volume of a waterlily leaf with a girder-like structure). To understand better why an Amazonian waterlily leaf is stiffer than (i) the leaves of other species of waterlily and (ii) a thin disk of equal volume, diameter, and elastic modulus, we now turn our attention to the nonuniform vasculature network that decorates the underside of the leaf.

Vascular architecture

Leaf venation in floating waterlily leaves is characterized by a distinctive pattern of numerous lateral primaries or secondaries radiating from the petiolar attachment. A venation pattern that is strongly actinodromous (circular) and weakly brochidodromous (loop forming) is unique to Victoria and its sister genus Euryale (20), which produce leaves ca. 10× larger than their relatives (Fig. 1F). As in all leaves, the system of veins also functions as a transport network for water and nutrients. Transport networks are often hierarchical in form (21); here, the loops formed by circular anastomoses maintain connectivity across the entire lamina by enabling fluid to bypass any site of injury (22, 23), providing resilience to localized venation damage or impedance of flow transport through the leaf (24). Requirements for connectivity may be similar in terrestrial and floating leaves; however, the support of underlying water (a liquid substrate) is known to affect the leaf morphogenesis of aquatic, floating plants specifically (25). The unusual pattern of radial veins and circular anastomoses may be an adaptation balanced between optimal transport and network connectivity across a giant lamina, on the one hand, and conferring strength to support a giant leaf lamina on the water surface, on the other.

The venation system of V. cruziana comprises eight main veins that extend radially from the petiole. All veins undergo regular branching events—the two veins that make up the central midrib trifurcate while the others bifurcate—resulting in a hierarchical, fractal-like network (Fig. 1B).

The vertical thickness of the main, radial veins decreases linearly with radial distance from the petiole attachment (Fig. 2B) [the width of the branches (ca. 1 cm) also decreases with radial distance but much less significantly]. At larger radial distances, structural rigidity is therefore provided by a greater number of thinner branches. The arc length separating radial veins, λ = rθ, where r is radial distance from the petiole position and θ the angle between primary veins, was measured and found to be approximately constant, λ = 3.93 ± 0.54 cm, at all radial positions (fig. S1), which implies that all the anastomoses are comparable in length.

Neither the main veins nor the secondary anastomoses are rigid (26), rather they are flexible enough to accommodate applied loads [i.e., from flooding or wading birds and animals such as the “lily trotter” (Jacana jacana)] through elastic deformation. As such, the vascular network underlying the leaf lamina provides a resistance to deformation that is analogous to the structural support (anchoring) provided by the dichotomously branching rootlets of giant, fossilized lycophyte trees (27), which, in life, resisted movement when the aerial parts of the tree were subject to lateral forces. The vascular network present in the giant Amazonian waterlily leaves is reminiscent of nonfloating biological venation networks, such as those found in tree leaves, which have recently been shown to be well modeled by discrete networks of bending beams that are optimized for maximal rigidity against gravitational stresses (28).

The complex form and nonuniform thickness of the vascular network mean the elastic bending stiffness of the leaf cannot be determined from material and geometrical properties alone. However, from our measurements of the spring stiffness of V. cruziana, we can determine an effective bending stiffness, B_eff = K²/(64ρg) = 0.76 Pa m³. We use this to estimate the length scale for which bending stresses in the waterlily leaf are comparable to gravitational stresses, known as the elastogravity bending length $L_{\text{eff}}^b\sim {(B_{\text{eff}}/(\mathrm{\rho }g))}^{1/4}=9.38$ cm (7), and note that it is comparable to the average radial distance between branching points, ${\overline{x}}_b=<x_{i+1}-x_i>=8.5\pm 0.2$ cm (Fig. 2B).

Modeling

To test the stiffening effect of the vasculature of V. cruziana, we simulated the mechanical response of floating disks, of equal volume and radial extent, with nonuniform thickness profiles using COMSOL. We examined the case of an axisymmetric disk with a thickness that decreases linearly from center to edge (see orange region in Fig. 3, D and E). A linear thickness profile increases the mechanical stiffness of a floating disk (relative to a disk of uniform thickness) but underestimates the measured stiffness of giant Amazonian waterlily leaves. A more realistic model of a V. cruziana leaf was developed (Fig. 3, A to C; further details in the Supplementary Materials and figs. S2 to S4) by combining a thin disk-like lamina of uniform thickness with a vasculature architecture of spatially varying thickness governed by the following design rules: (i) the thickness decreased linearly from leaf center to rim; (ii) the length between consecutive bifurcation points and the angle between bifurcating veins were both fixed; (iii) the width of veins was varied between branching generations [according to Leonardo’s rule (29); see also section 3 of Supplementary Materials] to ensure that the sum of the cross-sectional area was conserved across branching events; and (iv) secondary, orthoradial veins of fixed width and thickness, separated by a constant radial distance, connected primary veins. The good agreement shown in Fig. 3D (black line) between our empirical measurements of the mechanical response of giant Amazonian waterlily leaves and the results of our simulations of model floating leaves confirms that the enhanced stiffness of V. cruziana, relative to the disk-like form observed in smaller leaves of other genera of waterlily, arises from the nonuniform vasculature network on the underside of the leaf.

We conclude that the form taken by the vasculature architecture distributes material in a structurally efficient manner—providing greater rigidity for a given volume of plant matter.

In other words, the branched vasculature serves the biological function of providing greater surface area for photosynthesis with less biomass (for a given structural integrity). As for tree branches (29), the fractal-like nature of the venation system could also act to homogenize stress throughout the leaf and thus inhibit localized, catastrophic failure. However, the branched vasculature alone does not account for the measured bending stiffness of water lily leaves (see the green shaded region in Fig. 3D); a discrete network of veins underestimates the measured response. Instead, contributions to the load-bearing response of Amazonian waterlily leaves come from both the bending stiffness of the nonuniform vasculature network and a restoring buoyancy pressure that arises from the displacement of water by the deforming leaf lamina.

Evolution

We now consider the evolutionary history of the Amazonian waterlily to infer why it produces gigantic leaves. Angiosperms (flowering plants) represent the last major group of land plants to appear in the fossil record in the Early Cretaceous and diversified to ecological prominence in most terrestrial ecosystems by the Late Cretaceous (30). The waterlily lineage (Nymphaeales) diverges near the base of the flowering plant family tree (31) and has ecophysiological traits linked to aquatic, often sunny habitats, such as the absence of vascular cambium and floating leaves with high photosynthetic rates (32). Herbaceousness is believed to have evolved as an innovation during the shift to an aquatic life history in the Nymphaeales (33).

The South American genus Victoria forms a monophyletic clade with the Asian genus Euryale, which produces similar, somewhat smaller, and more elliptical leaves. This clade shows a unique combination of traits including gigantism (leaves ≳1 m across), a palinactinodromous (radiating) primary venation, and brochidodromous (loop-forming) secondary venation. This indicates that these features are ancestral (20) and presumably conferred a selective advantage in the common ancestor of Victoria and Euryale preceding the opening of the Atlantic Ocean 125 to 130 million years ago. Annual herbaceousness evolved in the common ancestor of these genera and, convergently, in the Hydatellaceae (33). The Hydatellaceae is a family of grass-like annuals that are morphologically dissimilar to other genera in the Nymphaeales. Most species are ephemeral aquatics that flower in temporary (vernal) pools—Amazonian waterlilies, in particular, inhabit temporarily flooded habitats where they survive for fewer than 6 months (34). This supports the suggestion that adaptation to drying pools may have triggered the evolution of rapid growth and accelerated reproduction in the Nymphaeales (35).

Fast-growing plants are known to have a greater capacity to acquire nutrients and produce a higher leaf surface area and lower root mass than those with a slower relative growth rate (36), which is consistent with the anatomy of the giant Amazonian waterlily. Giant, fast-growing leaves could therefore have evolved as an adaptation to outcompeting other seasonal plants, maximizing photosynthetic assimilation potential, in ephemeral aquatic habitats.

Load-bearing structures

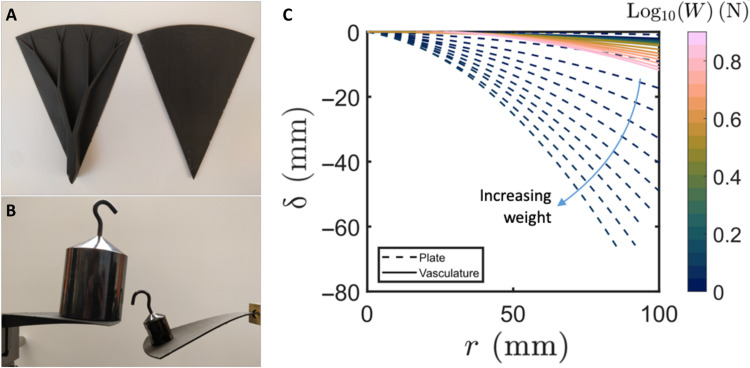
Last, we discuss how simple design rules, such as those used to model the vasculature of V. cruziana, could be used in the development of load-bearing platforms with structurally efficient shapes for use in architecture and civil engineering. We tested the resistance to deformation of freestanding structures with thickness profiles that mimicked the vasculature of Victoria by hanging weights from the tips of plastic platforms. Synthetic structures, with either a vasculature-like variation in thickness (based on the design used in our model) or a uniform thickness, were three-dimensionally printed in plastic (Formlabs) from an equal amount of material (Fig. 4A). The vascularized structures deflected far less than the structures with uniform thickness, even when subjected to significantly greater loads (Fig. 4B). By fixing the platforms in place at one end and hanging weights from the other end, we were able to systematically test the resistance to deformation of these structures. Deflection profiles, measured relative to the initially flat undeformed position, were extracted from images using processing techniques developed in MATLAB. The results (Fig. 4C and figs. S5 and S6) demonstrate that the enhanced stiffness is not localized to a small region around the thickest part of the vasculature, rather it is transmitted through the branched network to the tip of the structure.

Fig. 4. Biomimetric load-bearing structures.

(A) Leaf-like structures, with a thickness profile that mimicked that of Victoria (left) and with a uniform thickness (right), were three-dimensionally printed from an equal amount of plastic. (B) The vascularized structure (left) and plate-like structure (right) supporting 500 and 50 g weights, respectively. (C) Deflection profiles of the vascularized (solid curves) and uniform (dashed lines) platforms measured for increasing weight, W, of applied load (color bar).

DISCUSSION

Recently, Ronellenfitsch (28) elegantly described how the form of biological, branching networks (such as tree branches and leaf venation) evolved through natural selection to take on optimized forms that resist deformation under gravity. Here, we examine a natural floating platform that is instead supported by the buoyancy of an underlying liquid. When subjected to an applied load, both elastic bending and buoyancy of the underlying liquid substrate resist deformation. Our in situ experiments and computer simulations suggest that the superstructure of the Amazonian waterlily leaf—comprising a thin lamina supported by a branching network of strong, yet flexible, underlying girders—is an economy of matter that could have evolved in response to the cost-benefit associated with leaf size (i.e., benefit accrued by photosynthesis balanced by the costs of construction and maintenance). Specifically, the structural efficiency of the form taken by the leaf vasculature distinguishes gigantic waterlilies from their smaller relatives, which have leaves with a more disk-like form. The simple design rules we used to accurately model the load-bearing properties of V. cruziana may unlock cost-effective engineering solutions for the design of floating platforms for renewable energy production, such as offshore wind turbines (37) and facilities for the conversion of CO₂ extracted from seawater into synthetic fuel (38) or the development of offshore societies [“seasteads” (39)]. Looking beyond floating platforms, we propose that the translation of complex biological forms into simple architectural rules can inspire the design and development of shape-efficient structures for load-bearing applications.

MATERIALS AND METHODS

To test the mechanical strength of floating waterlily leaves, we performed in situ indentation tests on the leaves of a giant V. cruziana and on the smaller leaves of the related genus Nymphaea—a typical waterlily (Nymphaea cultivar “Black Princess”) and Nymphaea lotus—by applying a localized load, F, to the floating leaf and measuring the resultant displacement, δ, relative to the initially flat configuration (see the Supplementary Materials for further details). We tested six giant leaves and three from each of the two Nymphaea taxa. The petiolar attachment was chosen as point of load application for experiments because the vasculature network emanates from this point, and as such, we were able to avoid perforating the thin lamina during testing. The volume of Victoria leaves was also measured by submerging the leaves in a water-filled tank of known dimensions and measuring the corresponding rise in water level (i.e., via Archimedes principle), while the vein thickness and angular distance between main veins were measured from images using image processing techniques developed in MATLAB (see the Supplementary Materials for further details). Other geometrical measurements (i.e., the leaf radius, the width of the main veins, and the thickness of the lamina) were performed with either a rule or digital calipers. The Young’s modulus of both the vasculature, E_vein, and the lamina, E_lamina, of Victoria leaves were measured using an Instron structural testing system and found to be E_vein = 0.6 MPa and E_lamina = 2.7 MPa, respectively. These measurements provided a range of elastic moduli that we input into numerical simulations and permit comparison between waterlily leaves with a disk-like shape and homogeneous composition and floating structures with more complex geometries.

Supplementary Materials

This PDF file includes:

Supplementary details on experimental testing of waterlily leaves

Supplementary details on modeling

Discussion of Leonardo’s rule for vascular branching

Supplementary details on load-bearing structures

Figs. S1 to S6

Other Supplementary Material for this manuscript includes the following:

Data S1