Spin-lattice relaxation in liquid entrapped in a nanocavity

Abstract

We consider the spin lattice relaxation in bulk liquid and liquid entrapped in a nanocavity. The kinetic equation which describes the spin lattice relaxation is obtained by using the theory of the nonequilibrium state operator. A solution of the kinetic equation gives the quadrature expression for the relaxation time, T₁. The calculated relaxation time agrees well with the experimental data.

The spin-lattice relaxation time is calculated for nanocavities with a characteristic size much less than 700 nm, with the assumption that the spin-lattice relaxation mechanism is determined by nanocavity fluctuations. The resulting expression shows an explicit dependence of the relaxation time T₁ on the volume, density of nuclear spins, and parameters of the cavity (shape and orientation relatively to the applied field). To compare with the experiment on the detection of the anisotropy of the relaxation time, we average the expression that describes the relaxation time over the orientation of the nanocavities relative to the applied magnetic field. The good agreement with the experimental data for fibril tissues was achieved by adjustment of few fitting parameters - the standard deviation, averaged fiber direction, and weight factors - which characterize the ordering of fibrils.

1. Introduction

Spin dynamics provides the ideal arena to deal with various types of multiparticle interactions [1,2]. One can obtain a system of linear equations for quantities that could be measured in experiments and governed by the influence of the spin-spin and spin-lattice interactions. This is a very general description, but allows one to obtain clear physical conclusions.

Understanding the spin-spin and spin-lattice relaxations requires solving the Liouville-von Neumann equation for a spin system and considering all interactions of the spins with each other and their surroundings. In general, this is a very difficult task as the spin-spin and spin-lattice interactions can be time-dependent. One of the powerful ways to analytically approximate the time evolution of spin systems is to average the Hamiltonian over time, which results in the systems to be described by time-independent Hamiltonians [3,4]. The average method has been successfully applied to explain the results of the high-resolution NMR experiments with solids [3,4]. The explanation of the observed line narrowing in solid state NMR experiments was the major success of the average-Hamiltonian theory [5,6].

Recently an approach based on the averaging of the spin Hamiltonian with account of the restricted Brownian motion of molecules in liquid was used to explain the anisotropy of the transverse relaxation time of liquids entrapped in nanocavities [7–15]. It has been shown that the Hamiltonian which describes the average dipole-dipole (DD) interactions can be characterized by a single average coupling constant. The approach that averages the Hamiltonian can be applied only to liquids enclosed in cavities with a characteristic size much less than 700 nm [7–15]. This simplification of a spatial part of the Hamiltonian has led to some analytically solvable models with very non-trivial spin dynamics and secured the analytical expressions for the transverse relaxation time and spin-lattice relaxation time under spin-locking [7–15]. This approach well describes the angle anisotropy obtained in the experiments with collagen fibril tissues, such as tendons, cartilages, nerves [7–15], fibrils of which are about 280–300 nm in length and several nm in diameter [16].

In this paper we develop two approaches to determine the spin-lattice relaxation time T₁: (i) using the obtained by us kinetic equations by applying the method of nonequilibrium state operator [17,18] (without averaging the Hamiltonian); (ii) based on using the space averaged spin Hamiltonian.

We consider the DD interactions in the presence of spatial diffusion in a restricted space. Interaction of a molecule with a cavity wall leads to the disturbance of the spin flip-flop transitions. Therefore, we must compare the time which characterizes the flip–flop transitions t_NMR and the moving time scale required by the water molecules for achieving the wall, t_dif [7–15]. With a reliable small parameter t_dif/ t_NMR ≪ 1 allows to average the DD Hamiltonian over the cavity volume and to obtain the nonzero contribution into the DD Hamiltonian even for the cavity volume which is much larger than a molecule size. The condition, t_dif/ t_NMR- ≪ 1, allows us to estimate the upper limit of the characteristic size of the nanocavity, l ~ 700 nm [15].

The outline of this paper is as follows: in the second sections, we obtain a kinetic equation which can describe the evolution of the local Zeeman energy, analyze the relaxation process, and calculate the spin-lattice relaxation time T₁ for bulk liquid. In the next section, using the space averaged DD Hamiltonian we obtain the expression for the spin-lattice relaxation time in the case when the characteristic size of the cavity is much less than 700 nm. In the following section the relaxation time was estimated for fibril tissues and compared with experimental data. In the last section, our results are discussed and summarized.

2. Kinetic equation for bulk liquid

The main issue in nonequilibrium statistical mechanics is to derive a kinetic equation, starting from the Liouville equation. We consider a system that consists of N nuclear spins, I = 1/2, enclosed in a large cavity and located in an external field ${\overrightarrow{H}}_0$ directed along the z- axis. The dynamics of the system can be described by a solution of the equation for the state operator ρ(t)

$$i\hslash \frac{d\rho (t)}{dt}=[H(t),\rho (t)]$$ (1)

where ℏ is Planck’s constant. The Hamiltonian H of the spin system written in units of frequency can be presented as [1]:

$$H=H_Z+H_{dd}+H_L$$ (2)

where H_Z is the Zeeman Hamiltonian,

$$H_Z={\omega }_0\sum _{\mu =1}^N{I}_{z\mu }$$ (3)

${\omega }_0=\gamma \left|{\overrightarrow{H}}_0\right|$ is the Larmor frequency of the nuclei, γ is the gyromagnetic ratio of nuclei, and I_zμ is the projection of the spin operator ${\overrightarrow{I}}_{\mu }$ of the μ-th nuclear spin (μ=1, 2, …, N) onto the z- axis. The dipolar Hamiltonian can be presented as [1]:

$$H_{dd}={\gamma }^2\hslash \sum _{\mu >\eta }^N\frac{1}{r_{\mu \eta }^3}\left({\overrightarrow{I}}_{\mu }{\overrightarrow{I}}_{\eta }-3\frac{\left({\overrightarrow{I}}_{\mu }{\overrightarrow{r}}_{\mu \eta }\right)\left({\overrightarrow{I}}_{\eta }{\overrightarrow{r}}_{\mu \eta }\right)}{r_{\mu \eta }^2}\right),$$ (4)

where $r_{\mu \eta }=\left|{\overrightarrow{r}}_{\mu \eta }\right|,{\overrightarrow{r}}_{\mu \eta }$ is the vector connecting the μ-th and the η-th nuclei (μ, η=1, 2, …, N). The Hamiltonian H_L describes the lattice.

The dipolar Hamiltonian can be divided on the secular $H_d^{(s)}$ and non-secular $H_d^{(ns)}$ parts [1] as

$$H_{dd}=H_d^{(s)}+H_d^{(ns)},$$ (5)

where

$$\begin{gathered} H_d^{(s)}={\gamma }^2\hslash \sum _{\mu >\eta }^N{H}_{\mu \eta }^{(s)} \\ ={\gamma }^2\hslash \sum _{\mu >\eta }^N\frac{1}{r_{\mu \eta }^3}\left(1-3{\text{cos}}^2{\theta }_{\mu \eta }\right)\left[I_{z\mu }{I}_{z\eta }-\frac{1}{4}\left(I_{+\mu }{I}_{-\eta }+I_{-\mu }{I}_{+\eta }\right)\right] \end{gathered}$$ (6)

and

$$\begin{gathered} H_d^{(ns)}={\gamma }^2\hslash \sum _{\mu >\eta }^N{H}_{\mu \eta }^{(ns)} \\ =-\frac{3}{4}{\gamma }^2\hslash \sum _{\mu >\eta }^N\frac{1}{r_{\mu \eta }^3}\{\text{sin}2{\theta }_{\mu \eta }[e^{-i{\varphi }_{\mu \eta }}\left(I_{z\mu }{I}_{+\eta }+I_{+\mu }{I}_{z\eta }\right) \\ +e^{i{\varphi }_{\mu \eta }}\left(I_{z\mu }{I}_{-\eta }+I_{-\mu }{I}_{z\eta }\right)] \\ +{\text{sin}}^2{\theta }_{\mu \eta }\left[e^{-2i{\varphi }_{\mu \eta }}{I}_{+\mu }{I}_{+\eta }+e^{2i{\varphi }_{\mu \eta }}{I}_{-\mu }{I}_{-\eta }\right]\}. \end{gathered}$$ (7)

Here r_μη, θ_μη, ϕ_μη are the spherical coordinates of the vector ${\overrightarrow{r}}_{\mu \eta }$; I_±μ = I_xμ ± iI_yμ; I_xμ and I_yμ are the projections of the spin operator of the μ-th nuclear spin onto the x- and y-axes, respectively.

By introducing a nuclear spin density operator [17,18]:

$$\overrightarrow{I}(\overrightarrow{r})=\sum _{\mu =1}^N\delta \left(\overrightarrow{r}-{\overrightarrow{r}}_{\mu }\right){\overrightarrow{I}}_{\mu },$$ (8)

where $\overrightarrow{r}$ is the radius-vector and ${\overrightarrow{r}}_{\mu }$ is the radius-vector of the μ-th nuclear spin.

Using Eq. (8), the density of the nuclear Zeeman Hamiltonian and the nuclear dipolar Hamiltonian can be written down in the forms

$$H_Z(\overrightarrow{r})={\omega }_0\sum _{\mu =1}^N\delta \left(\overrightarrow{r}-{\overrightarrow{r}}_{\mu }\right)I_{z\mu }$$ (9)

and

$$H_d^{(k)}(\overrightarrow{r})={\int }_{V}d\overrightarrow{r}\prime \sum _{\mu >\eta }^N\delta \left(\overrightarrow{r}-{\overrightarrow{r}}_{\mu }\right)\delta \left(\overrightarrow{r}\prime -{\overrightarrow{r}}_{\eta }\right)H_{\mu \eta }^{(k)},$$ (10)

where the index k = s, ns and the symbol $d\overrightarrow{r}\prime$ is used to represent integration over the sample volume V.

Taking all operators (8)–(10) in the Heisenberg representation and using the commutation rules between the components of the spin density operator (8), we can obtain the following equations in the form of the localized law of conservation of the Zeeman spin energy density [17,18]:

$$\frac{\partial H_Z(\overrightarrow{r},t)}{\partial t}=K_d^{(ns)}(\overrightarrow{r},t),$$ (11)

Note, that spin diffusion does not play a role in relaxation of the liquid and we assume that the heat capacity of the lattice is much larger than nuclear spin heat capacity. That is experimentally realizable. In Eq. (11) the left side represents the Zeeman energy variation in time. The right side of Eq. (11) $K_d^{(ns)}(\overrightarrow{r},t)$ describes the change of the Zeeman energy density due to the interaction with the lattice (the spin-lattice relaxation). With account (8) this operator can be written as:

$$\begin{gathered} K_d^{(ns)}(\overrightarrow{r},t)=-\frac{3{\gamma }^2\hslash {\omega }_0}{2}{\int }_V\frac{d\overrightarrow{r}\prime }{{\left|\overrightarrow{r}\prime -\overrightarrow{r}\right|}^3} \\ \times \{\text{sin}2\theta (\overrightarrow{r}\prime ,\overrightarrow{r}(t))[e^{i\varphi \left(\overrightarrow{r}\prime ,{\overrightarrow{r}}_{(t)}\right)}{I}_z(\overrightarrow{r},t)I_{-}\left(\overrightarrow{r}\prime ,t\right) \\ -e^{-i\varphi \left(\overrightarrow{r}\prime ,\overrightarrow{r}(t)\right)}{I}_z(\overrightarrow{r},t)I_{+}\left(\overrightarrow{r}\prime ,t\right)]+{\text{sin}}^2\theta \left(\overrightarrow{r}\prime ,\overrightarrow{r}(t)\right) \\ \times [e^{2i\varphi \left(\overrightarrow{r}\prime ,{\overrightarrow{r}}_{(t)}\right)}{I}_{-}(\overrightarrow{r},t)I_{-}\left(\overrightarrow{r}\prime ,t\right) \\ -e^{-2i\varphi }\left(\overrightarrow{r}\prime ,{\overrightarrow{r}}_{(t)}\right)I_{+}(\overrightarrow{r},t)I_{+}\left(\overrightarrow{r}\prime ,t\right)]\}. \end{gathered}$$ (12)

To obtain the kinetic equation describing the evolution of the local Zeeman energy $H_Z(\overrightarrow{r})$, we will use the method of the nonequilibrium state operator [17,18] and the density matrix. In the framework of this method the nonequilibrium state operator can be written as

$$\begin{gathered} \rho =Z^{-1}\text{exp}\{-{\beta }_L{H}_L-{\int }_{V}d\overrightarrow{r}{\beta }_Z(\overrightarrow{r},t)H_Z(\overrightarrow{r},t) \\ +{\int }_{-\infty }^{0}d{t}^{\prime }{e}^{\epsilon t^{\prime }}\left({\beta }_L\frac{\partial H_L\left(t^{\prime }\right)}{\partial t^{\prime }}+{\int }_{V}d\overrightarrow{r}{\beta }_Z\left(\overrightarrow{r},t^{\prime }+t\right)\frac{\partial H_Z\left(\overrightarrow{r},t^{\prime }\right)}{\partial t^{\prime }}\right)\}, \end{gathered}$$ (13)

where Z = Trexp{…} is the partition function and the transition to the limit ε → +0 should be made after the calculation of the integral, β_L is the inverse lattice temperature and ${\beta }_Z(\overrightarrow{r},t)$ is the local inverse spin temperature of the nuclear Zeeman reservoir. In Eq. (13) all operators are taken in the Heisenberg representation.

At the linear approximation with respect to the DD interactions we can rewrite the density matrix (13) in the following form [17,18]:

$$\rho =\left\{1-{\int }_0^{1}d\lambda \left[B(t+i\lambda )-{\langle B(t+i\lambda )\rangle }_{eq}\right]\right\}{\rho }_{eq}$$ (14)

where the thermodynamic average 〈…〉_eq corresponds to an average with the quasi-equilibrium operator ρ_eq = e^−A/Tr(e^−A).

$$A(t)={\beta }_L{H}_L+{\int }_{V}d\overrightarrow{r}{\beta }_Z(\overrightarrow{r},t)H_Z(\overrightarrow{r},t),$$ (15)

$$B(t+i\lambda )={\int }_{-\infty }^{0}d{t}^{\prime }{e}^{\epsilon t^{\prime }}\times {\int }_{V}d\overrightarrow{r}\left\{\left[{\beta }_Z\left(\overrightarrow{r},t+t^{\prime }\right)-{\beta }_L\right]e^{-\lambda \mathbf{\text{A}}\left(t^{\prime }\right)}{K}_d^{(ns)}\left(\overrightarrow{r},t^{\prime }\right)e^{\lambda \mathbf{\text{A}}\left(t^{\prime }\right)}\right\}.$$ (16)

By using Eqs. (11) and (14)–(16) we obtain the kinetic equation

$$\frac{\partial {\beta }_Z(\overrightarrow{r},t)}{\partial t}=-\frac{1}{T_1(\overrightarrow{r})}\left[{\beta }_Z(\overrightarrow{r},t)-{\beta }_L\right]$$ (17)

with the boundary conditions

$${\frac{\partial }{\partial \overrightarrow{r}}{\beta }_Z(\overrightarrow{r},t)|}_{r=\zeta }=0,{\frac{\partial }{\partial \overrightarrow{r}}{\beta }_Z(\overrightarrow{r},t)|}_{\Sigma }=0$$ (18)

and

$${\beta }_Z(\overrightarrow{r},t\to \infty )={\beta }_L,$$ (19)

where ς is the diameter of the molecule, Σ is the boundary of the considered volume.

The right side of Eq. (17) gives a rate of change of ${\beta }_Z(\overrightarrow{r},t)$ due to thermal exchange between the spin system and lattice. The exchange is characterized by the relaxation rate $T_1^{-1}(\overrightarrow{r})$ which is given by the following expression obtained by averaging of Eq. (12) using Eq. (14):

$$\frac{1}{T_1(\overrightarrow{r})}=\frac{3}{8}{\left({\gamma }^2\hslash \right)}^2[{\int }_{-\infty }^{0}dt{e}^{\epsilon t}{e}^{-\frac{\left|t\right|}{{\tau }_c}}{\int }_{V}d\overrightarrow{r}\prime \frac{1}{|\overrightarrow{r}-\overrightarrow{r}\prime {|}^6}({\text{sin}}^2\left(2\theta \left(\overrightarrow{r},\overrightarrow{r}\prime \right)\right)\text{cos}\left({\omega }_{0}t\right)+4{\text{sin}}^4\left(\theta \left(\overrightarrow{r},\overrightarrow{r}\prime \right)\right)\text{cos}\left(2{\omega }_{0}t\right))].$$ (20)

Here we assume that in the high-temperature approximation the molecules tumble isotropically, then it is usually assumed that the correlation function decays exponentially with respect to time, $~e^{-\frac{\left|t\right|}{{\tau }_c}}$ [1,19]. The correlation time τ_c of the molecules motion characters the properties of liquid.

The integration over time of Eq. (20) gives

$$\frac{1}{T_1(\overrightarrow{r})}=\frac{3}{8}{\left({\gamma }^2\hslash \right)}^2[{\int }_{V}d\overrightarrow{r}\prime \frac{1}{|\overrightarrow{r}-\overrightarrow{r}\prime {|}^6}({\text{sin}}^2\left(2\theta \left(\overrightarrow{r},\overrightarrow{r}\prime \right)\right)\frac{{\tau }_c}{1+{\omega }_0^2{\tau }_c^2}+4{\text{sin}}^4\left(\theta \left(\overrightarrow{r},\overrightarrow{r}\prime \right)\right)\frac{{\tau }_c}{1+4{\omega }_0^2{\tau }_c^2})].$$ (21)

To describe the relaxation, we can use Eq. (17). In this case the normalized relaxation function, $R(t)=\frac{{\beta }_Z(t)-{\beta }_Z(\infty )}{{\beta }_Z(0)-{\beta }_Z(\infty )}$ takes the form [20–23]

$$R(t)={\left(\frac{1}{V}{\int }_v^{V}d\overrightarrow{r}{e}^{-\frac{t}{T_1(\overrightarrow{r})}}\right)}^N.$$ (22)

In the limit of N → ∞ we have

$$R(t)=e^{-c{\int }_v^{V}d\overrightarrow{r}\left(1-e^{-\frac{t}{T_1(\overrightarrow{r})}}\right)},$$ (23)

where v is the volume of a molecule, C is the spin density.

After a direct integration in the exponent over r in the range from ς to L(ϑ, φ), we have

$$R(t)=\text{exp}\{-C{\int }_0^{2\pi }d\phi {\int }_0^{\pi }\text{sin}\vartheta d\vartheta [\frac{1}{3}(\left(1-e^{-\frac{A(\vartheta )}{L^6(\vartheta ,\phi )}t)}\right)L^3(\vartheta ,\phi )-\left(1-e^{-\frac{A(\vartheta )}{{\varsigma }^6}t}\right){\varsigma }^3)-\frac{1}{3}\sqrt{\pi A(\vartheta )t}\left(erf\left(\frac{\sqrt{A(\vartheta )t}}{L^3(\vartheta ,\phi )}\right)-erf\left(\frac{\sqrt{A(\vartheta )t}}{{\varsigma }^3}\right)\right)]\},$$ (24)

where ϑ, φ are the angle coordinates of the radius-vector $\overrightarrow{r}$ and the z-axis is directed along the applied magnetic field; L(ϑ, φ) gives the boundary of the considered volume;

$$A(\vartheta )=\frac{3}{8}{\left({\gamma }^2\hslash \right)}^2\left({\text{sin}}^{2}2\vartheta \frac{{\tau }_c}{1+{\omega }_0^2{\tau }_c^2}+{\text{sin}}^4\vartheta \frac{4{\tau }_c}{1+4{\omega }_0^2{\tau }_c^2}\right).$$ (25)

At $\frac{\sqrt{A(\vartheta )t}}{{\varsigma }^3}\ll 1$ the normalized relaxation function takes the following form

$$R(t)=\text{exp}\left\{-\frac{t}{T_1}\right\},$$ (26)

with the relaxation rate accounting that L ≫ ς:

$$\frac{1}{T_1}=\frac{4\pi }{15}\frac{C{\tau }_c}{{\varsigma }^3}{\left({\gamma }^2\hslash \right)}^2\left(\frac{1}{1+{\omega }_0^2{\tau }_c^2}+\frac{4}{1+4{\omega }_0^2{\tau }_c^2}\right).$$ (27)

One can see from Eq. (27) that $\frac{1}{T_1}$ is proportional to the density of spins and depends on τ_c in accordance with the well-known expression for $\frac{1}{T_1}$ in bulk liquid [1]. For correlation times τ_c much shorter than the inverse Larmor frequency of the spins, ω₀τ_c ≪ 1 it is following that the inverse relaxation times is proportional to τ_c. Estimation with $C=66\frac{\mathit{\text{spin}}}{n{m}^3}$, ω₀ = 63.862 MHz at the applied magnetic field 1.5 T, and τ_c ≃ 3.6 × 10⁻¹¹ s, gives T₁ ≃ 3.675 s which coincides with the experimental data [1]. Using Eq. (27), the dependences of T₁ on the correlation time τ_c is presented in Fig. 1. Estimation shows that $\frac{\sqrt{A(\vartheta )t}}{{\varsigma }^3}\ll 1$ is valid till t about 200 s, that is much larger than time when the relaxation can be observed in experiment.

Fig. 1.

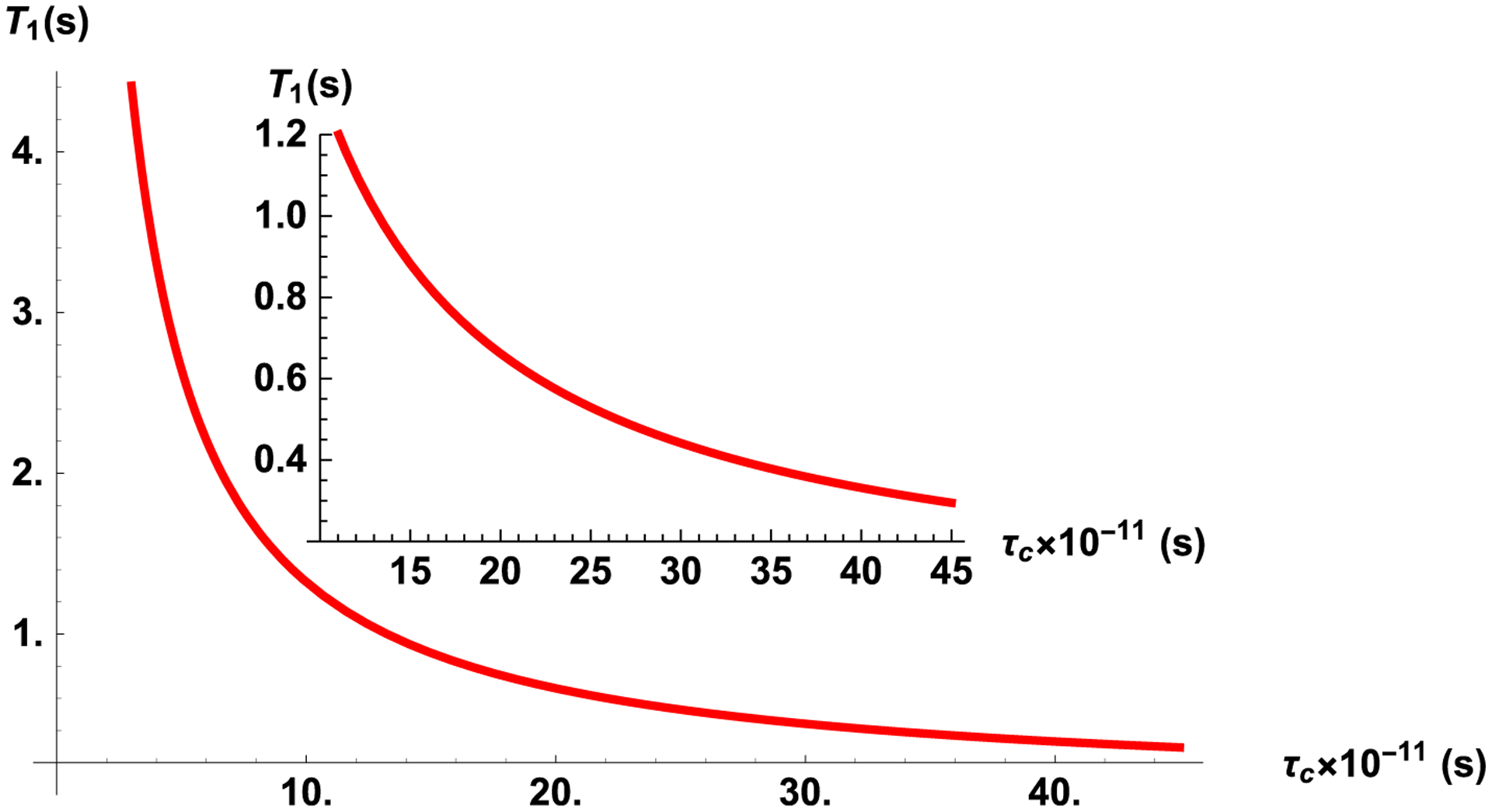
The dependence of T₁ on the correlation time τ_c at the spin-lattice relaxation process, calculated by using Eq. (27). The insert shows zoom at a relatively large correlation time.

Experiments with nanostructured samples [16] have shown that in liquid entrapped in a nanocavity, the relaxation time T₁ is shorter than in bulk, and lies in the range from 0.25 s to 0.9 s. What is more, the relaxation time T₁ depends on the sample structure and its orientation relative to the applied magnetic field.

To explain the peculiarities of spin-lattice relaxation in liquids entrapped in a nanocavity, the same relaxation mechanisms can be considered and Eq. (27) for estimation of the spin-lattice relaxation time is proposed to be applied with only single difference in the correlation time τ_c [16]. Following [16] the correlation time is estimated by analyzing the experimental data: at the applied magnetic field of 1.5 T (ω₀ = 63.862 MHz) and for experimentally measured T₁ ≃ 0.368 s estimation gives τ_c ≃ 0.36 × 10⁻¹¹s (dependence of T₁ on low τ_c is presented in the insert on Fig. 1).

The experiments showed that the relaxation time T₁ depends on the volume and form of nanocavities as well as their orientation. However, Eq. (27) for the spin-lattice relaxation time, obtained using the non-averaged Hamiltonian, do not explicitly contain the dependence on these parameters.

To obtain the dependence of the relaxation time on cavity parameters, the next section let us consider the approach based on averaging of the Hamiltonian, which is valid for nanocavities with a characteristic size much less than 700 nm.

3. Space averaged spin Hamiltonian and spin-lattice relaxation time

In a nanocavity, in contrast to the bulk, space diffusion of molecules of gas or liquid is restricted; but the molecules can still move randomly throughout the whole cavity with the time t_dif. We will consider the case in which this time is shorter than the NMR time scale t_NMR, t_dif ≪ t_NMR and the Hamiltonian is not averaged to zero unlike bulk liquid. The characteristic size of a water-filled nanocavity, at which the averaged Hamiltonian is not zero must be much smaller than 700 nm [7–15].

According to the ergodic hypothesis, the averaging of the space parameters of the Hamiltonian (4) over time can be replaced by the averaging over the statistical ensemble in space [24]. The detailed description of the averaging has been given elsewhere [25,26]. Therefore, the spin evolution in a nanocavity can be described by an averaged DD interaction Hamiltonian. The time-averaged of the secular part (6), $H_d^{(s)}$ can be presented in the following form for an axis-symmetrical nanocavity [25,26]:

$$\stackrel{-(s)}{H_d}=\frac{{\gamma }^2\hslash F}{4V}\left(1-3{\text{cos}}^2\Theta \right)\left(3I_z^2-{\overrightarrow{I}}^2\right)$$ (28)

where ${\overrightarrow{I}}^2=I_x^2+I_y^2+I_z^2$ is the square of the total nuclear spin operator, $I_v{=}_{\mu =1}^N{I}_{v\mu }$ are the operators of the projections of the total spin operator onto the ν-axes (ν = x, y, z), F is the form-factor associated with the ellipsoidal nanocavity [25]:

$$F=\pi \left\{\begin{array}{l}\frac{2}{3}+2\left(\frac{1}{{\epsilon }^2}-1\right)\left(1-\frac{1}{\epsilon }\text{arctanh}\epsilon \right),a⩽b\hfill \\ \frac{2}{3}-2\left(\frac{1}{|\epsilon {|}^2}+1\right)\left(1-\frac{1}{\left|\epsilon \right|}\text{arctan}\left|\epsilon \right|\right),a⩾b\hfill \end{array}\right\}$$ (29)

and ${\epsilon }^2=1-\frac{a^2}{b^2}$, $-\frac{4\pi }{3}<F<\frac{2\pi }{3}$, Θ is the angle between the main axis a of the nanocavity, b = c, and the external magnetic field, ${\overrightarrow{H}}_0$.

The form factor for a cylindrical cavity with diameter d and length ℓ is [14]:

$$F=2\pi \frac{1}{\sqrt{{(2d/\ell )}^2+1}}$$ (30)

The non-secular part of the DD interaction Hamiltonian (7), $H_d^{(ns)}$ after averaging takes the form

$${\overline{H}}_d^{(ns)}={\gamma }^2\hslash \sum _{q=-2,q\ne 0}^2{G}^{(q)}{S}^{(q)},$$ (31)

where G^(q) are the average dipolar coupling constants

$$\begin{array}{l}{G}^{(1)}=\left(-\frac{3}{8V}\right)F\text{sin}(2\Theta )e^{-i\psi },\\ G^{(2)}=\left(-\frac{3}{8V}\right)F{\text{sin}}^2(\Theta )e^{-2i\psi },\\ G^{(-q)}=G^{(q)*}\end{array}$$ (32)

S^(q) are operators acting only on the spin variables

$$\begin{array}{l}{S}^{(1)}=I_z{I}_{+}+I_{+}{I}_z\\ S^{(2)}=I_{+}{I}_{+}\\ S^{(-q)}=S^{(q)+}.\end{array}$$ (33)

where $I_{\pm }=\sum _{\mu =1}^N{I}_{\pm \mu }$ are the total raising and lowering operators, ψ is the azimuthal angle of the main axis of the nanocavity.

The averaged non-secular part ${\overline{H}}_d^{(ns)}$ of the Hamiltonian containes four effective constatnts for each pair of spins. Similary to the effective constant of the secular part these constants depend on the volume, form, and orientation of the nanocavity.

Random fluctuations of walls of a nanocavity [27] we will simulate by fluctuations of the constants G^(q). We assume that time dependence of G^(q)(t) are determined by random functions of the cavity volume V, form factor F, and orientation Θ. Due to the characteristic time of molecular motion is much less than the spin flip-flop times, t_dif ≪ t_NMR in a nanocavity [25,26], the effective constants are the same for all the spin pairs even in fluctuating nanocavity. To apply the interaction representation the averaged non-secular part of the Hamiltonian is rewritten as:

$${\overline{H}}_d^{(ns)}(t)={\gamma }^2\hslash \sum _{q=-2,q\ne 0}^2{G}^{(q)}(t)S^{(q)}(t),$$ (34)

where the definitions are introduced

$$S^{(q)}(t)=e^{i{H}_{Z}t}{S}^{(q)}{e}^{-i{H}_{Z}t}=S^{(q)}{e}^{-iq{\omega }_{0}t}.$$ (35)

We assume that the nanocavity fluctuations are an isotropic and introduce the correlation functions

$$\langle G^{(q)}(t)G^{\left(q^{\prime }\right)*}(t+\tau )\rangle ={\delta }_{q{q}^{\prime }}\langle G^{(q)}(0)G^{\left(q^{\prime }\right)*}(0)\rangle g^{(q)}(\tau ),$$ (36)

where g^(q)(τ) = g^(−q)(τ) are the reduced correlation function (q = ±1, ±2) and

$$\begin{array}{l}\langle G^{(1)}(0)G^{(-1)}(0)\rangle =\langle G^{(-1)}(0)G^{(1)}(0)\rangle ={\left(\frac{3F}{8V}\text{sin}2\Theta \right)}^2\\ \langle G^{(2)}(0)G^{(-2)}(0)\rangle =\langle G^{(-2)}(0)G^{(2)}(0)\rangle ={\left(\frac{3F}{8V}{\text{sin}}^2\Theta \right)}^2\end{array}$$ (37)

By using Eqs. (34)–(37) and the usual procedure (see e.g. [1]) we obtain the spin-lattice relaxation rate

$$T_1^{-1}=3{\left(\frac{3}{8}\right)}^3\frac{C}{V}{\left(F{\gamma }^2\hslash \right)}^2\left[J^{(1)}\left({\omega }_0\right){\text{sin}}^{2}2\Theta +J^{(2)}\left(2{\omega }_0\right){\text{sin}}^4\Theta \right],$$ (38)

where J⁽¹⁾(ω₀) and J⁽²⁾(2ω₀) are the spectral densities g⁽¹⁾(τ) and g⁽²⁾(τ), respectively [1]

$$\begin{array}{l}{J}^{(1)}\left({\omega }_0\right)={\int }_{-\infty }^{\infty }{g}^{(1)}(\tau )e^{-i{\omega }_0\tau }d\tau ,\hfill \\ J^{(2)}\left(2{\omega }_0\right)={\int }_{-\infty }^{\infty }{g}^{(2)}(\tau )e^{-2i{\omega }_0\tau }d\tau .\hfill \end{array}$$ (39)

Usually the correlation function is approximated by an exponential function [1]. However, using the exponential reduced correlation function we cannot obtain from Eq. (38) the relaxation time corresponding to experimental data [28,29]. We assume that the reduced correlation functions g⁽¹⁾(τ) and g⁽²⁾(τ) are the same and represented by

$$g^{(q)}(\tau )=\frac{\left|\tau \right|}{{\tau }_{cc}}{e}^{-\frac{\left|\tau \right|}{{\tau }_{cc}}},q=1,2,$$ (40)

where τ_cc is the correlation time of random fluctuation of a nanocavity. The spin-lattice relaxation rate then becomes

$$T_1^{-1}=3{\left(\frac{3}{8}\right)}^3\times \frac{C}{V}{\left(F{\gamma }^2\hslash \right)}^2{\tau }_{cc}\left[\frac{\left({\omega }_0^2{\tau }_{cc}^2-1\right)}{\left({\omega }_0^2{\tau }_{cc}^2+1\right)}{\text{sin}}^{2}2\Theta +\frac{\left(4{\omega }_0^2{\tau }_{cc}^2-1\right)}{\left(4{\omega }_0^2{\tau }_{cc}^2+1\right)}{\text{sin}}^4\Theta \right].$$ (41)

Eq. (41) gives the dependence of the spin-lattice relaxation rate on an external magnetic field ω₀, the correlation time τ_cc, volume V, density of nuclear spins C, shape F and nanocavity orientation relative to a magnetic field, Θ. Estimation of the correlation time, τ_cc at field strength 2.0 T (ω₀ = 85. 147 MHz) according to Eq. (41) with $C=66\frac{\mathit{\text{spin}}}{n{m}^3}$, F = 2π (for a long cylindrical cavity ℓ ≫ d), V ≃ 2500 nm³ and the experimental data T₁ ≃ 0.54 s [28,29] gives τ_cc ≃ 1.5 × 10⁻⁵s.

Fig. 2 shows the dependences of T₁ on the correlation time τ_cc for the external field of 2 T (ω₀ = 85. 147 MHz) in an elongated cylindrical nanocavity with form factor F = 2π at angle Θ = 55°. We note that according to our estimation in a nanocavity the correlation time is six orders of magnitude longer than in bulk liquid and the spin-lattice relaxation time becomes dependent on the orientation of the cavity relative to the magnetic field, angle Θ (Fig. 3).

Fig. 2.

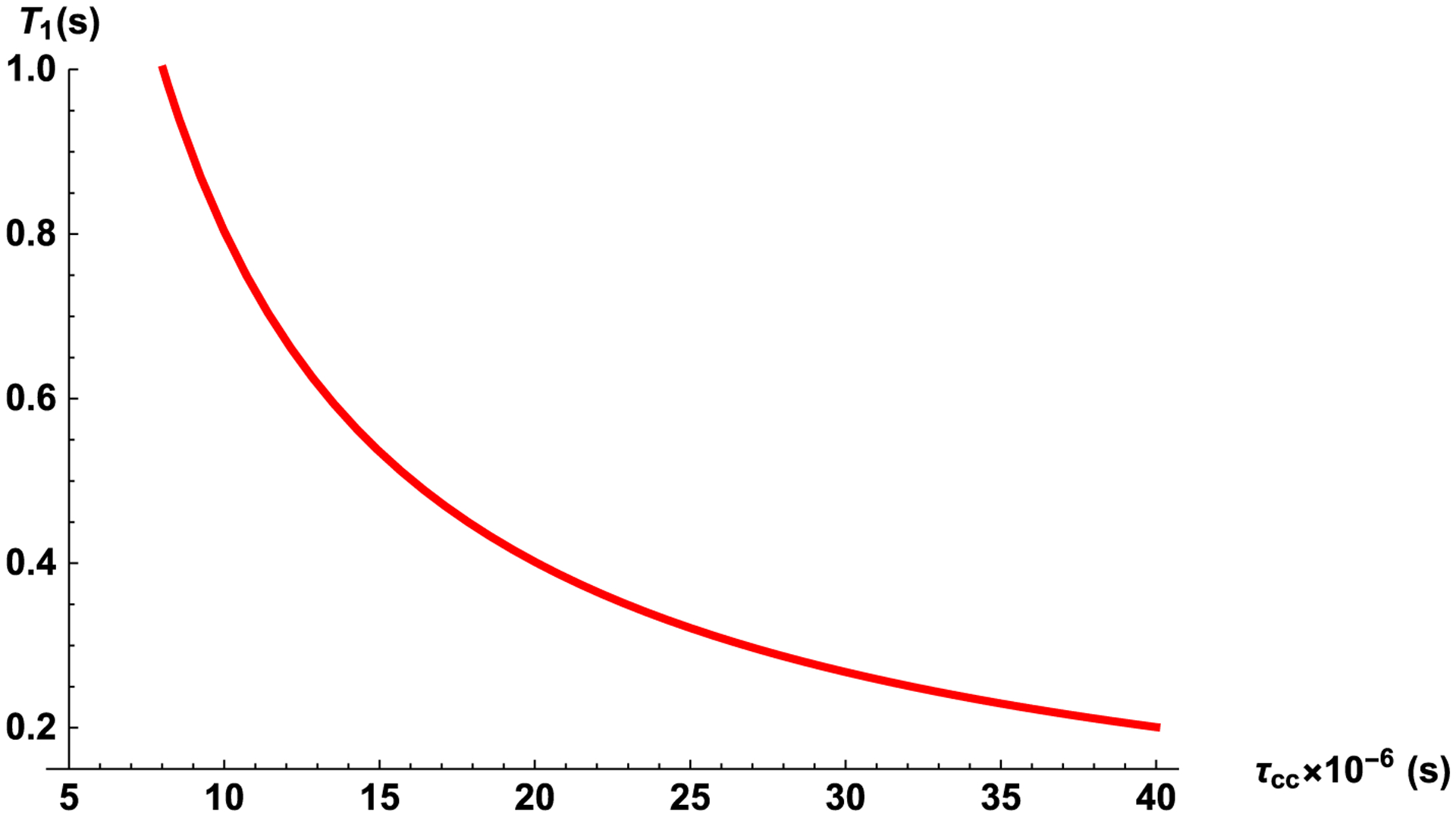
The dependence of T₁ on the correlation time τ_cc in the magnetic field of 2 T (ω₀ = 85.147 MHz) in an elongated cylindrical nanocavity with volume V = 2500 nm³, form factor F = 2π at angle Θ = 55°.

Fig. 3.

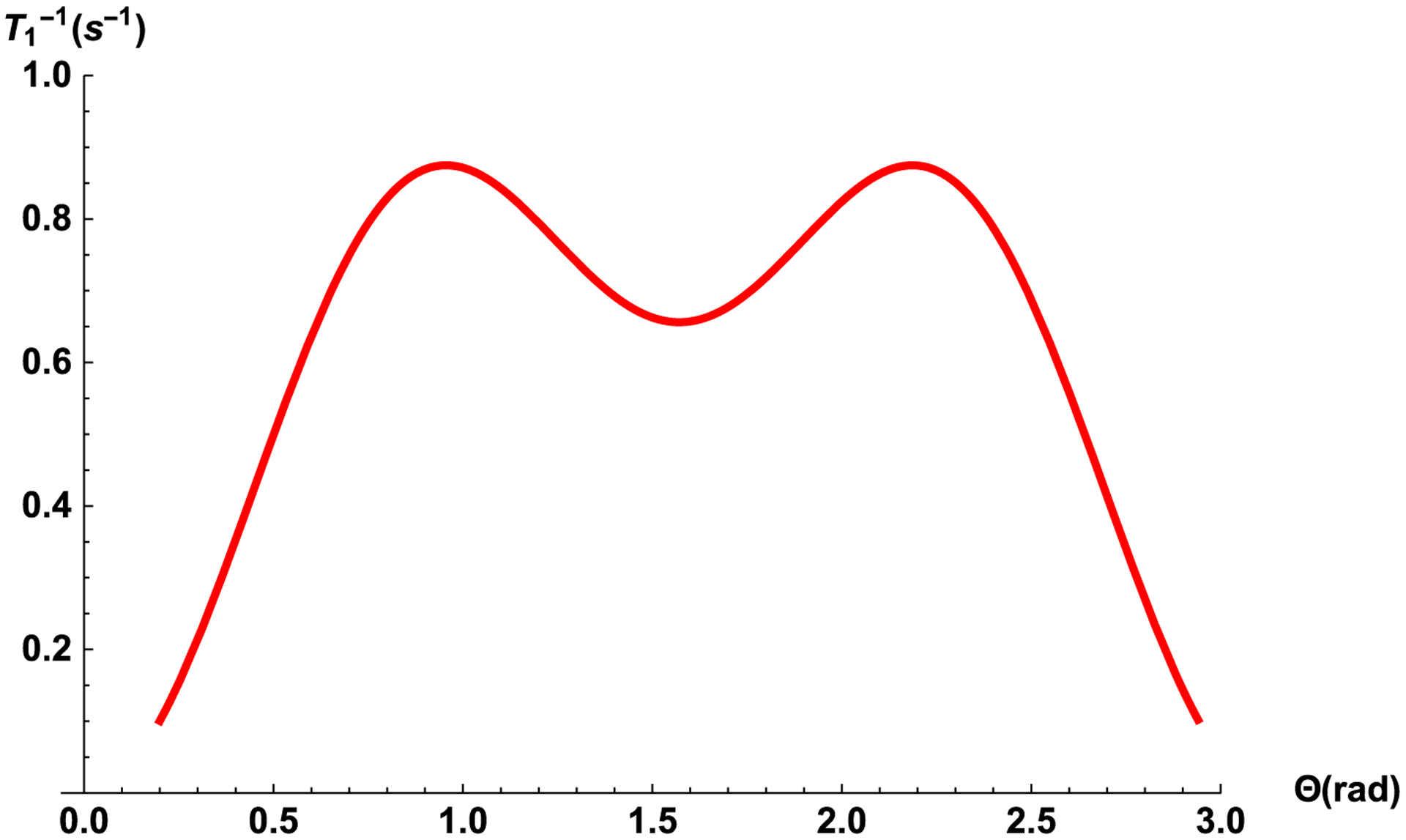
The relaxation rate $T_1^{-1}$ in liquid entrapped in a nanocavity as the function of the nanocavity orientation in the magnetic field of 2 T according Eq. (41). Nanocavities are simulated as elongated cylinders with form factor F = 2π, V = 2500 nm³ and τ_cc = 10⁻⁵ s.

4. Spin-lattice relaxation for fibril tissues

Usually, experiments on measuring the spin-lattice relaxation time T₁ for water inside nanocavities are performed with samples containing a set of nanocavities differing in orientation, shape, and volume. In experiment the observed anisotropy of the time T₁ depends on the degree of ordering of the nanocavities.

To explain the difference of the relaxation rate T₁ given by (41) and experimentally observed angular dependence of the rate in the bovine tendon (Fig. 2 in [28]) and the Achilles tendon (Fig. 1 in [29]), we apply the approach developed in [15]: we consider a fibril tissue as a set of imperfectly orientated nanocavities containing water. (There is a natural distribution of the fibril volumes and their directions). Here we analyze the angular dependence of this rate using the normalized form

$$R_1=\frac{\underset{\Theta }{\text{max}}\left(T_1(\Theta )\right)}{T_1(\Theta )}.$$ (42)

Assuming that the angular distributions of all nanocavity types are the same, we obtain

$$\langle R_1\rangle =\langle \frac{\underset{\Theta }{\text{max}}\left(T_1(\Theta )\right)}{T_1(\Theta )}\rangle$$ (43)

In NMR experiments, the angle θ₀ between the sample Z₀-axis and the magnetic field is determined and the relaxation time as a function of this angle is studied. In the general case, the angle does not coincide with a “preferred direction”, an averaged orientation, of the collagen fibrils. Let us determine the deviation of the main axis of each collagen fibril from the Z₀-direction by the polar angle α and azimuthal angle χ. Suggesting the Gaussian distribution of nanocavities directions over the both angles, the polar α and the azimuthal χ angles with the bivariate normal distribution function

$$\langle R_1\rangle =\frac{1}{2\pi {\sigma }_{\alpha }{\sigma }_{\chi }\Gamma }{\int }_0^{2\pi }d\chi {\int }_0^{\pi }d\alpha \text{sin}\alpha e^{-\frac{{\left(\alpha -{\alpha }_0\right)}^2}{2{\sigma }_{\alpha }}-\frac{{\left(\chi -{\chi }_0\right)}^2}{2{\sigma }_{\chi }}}{R}_1\left({\theta }_0,\alpha ,\chi \right),$$ (44)

where σ_α and σ_χ are the standard deviations, α₀ and χ₀ are the means of the distributions and give distinction of the “preferred direction” of the fibrils from the sample axis,

$$\Gamma =\frac{1}{2\pi {\sigma }_{\alpha }{\sigma }_{\chi }}\underset{{\theta }_0}{\text{max}}{\int }_0^{2\pi }d\chi {\int }_0^{\pi }d\alpha \text{sin}\alpha e^{-\frac{{\left(\alpha -{\alpha }_0\right)}^2}{2{\sigma }_{\alpha }}-\frac{{\left(\chi -{\chi }_0\right)}^2}{2{\sigma }_{\chi }}}{R}_1\left({\theta }_0,\alpha ,\chi \right).$$ (45)

The angular dependences of the normalized relaxation rate 〈R₁〉 are given by Eq. (44) in which there are unknown parameters: standard deviations (σ_α and σ_χ) and distribution means (α₀ and χ₀). These parameters can be considered as parameters which characterize the fibril structure of a tissue. To take into account the real forms of the fibers and their distinction of the orientation, the fibril structure of the tendon was represented as a superposition of two types of nanocavity distributions (termed Sp and Rd) with different preferred orientations of the fibrils [15].

The good agreement of the experiment [28] and the theoretical results was achieved (Fig. 4) when the difference between the preferred fibril orientations is about 90°. The normalized inverse relaxation time for the relaxation as a function of the angle between the sample axis and the magnetic field can be presented as

$$\langle R_1\left({\theta }_0\right)\rangle ={\xi }_{sp}{\langle R_1\rangle }_{sp}+{\xi }_{rd}{\langle R_1\rangle }_{rd}$$ (46)

where ξ_sp and ξ_rd are the weight factors of the distributions with ξ_sp + ξ_rd = 1.

Fig. 4.

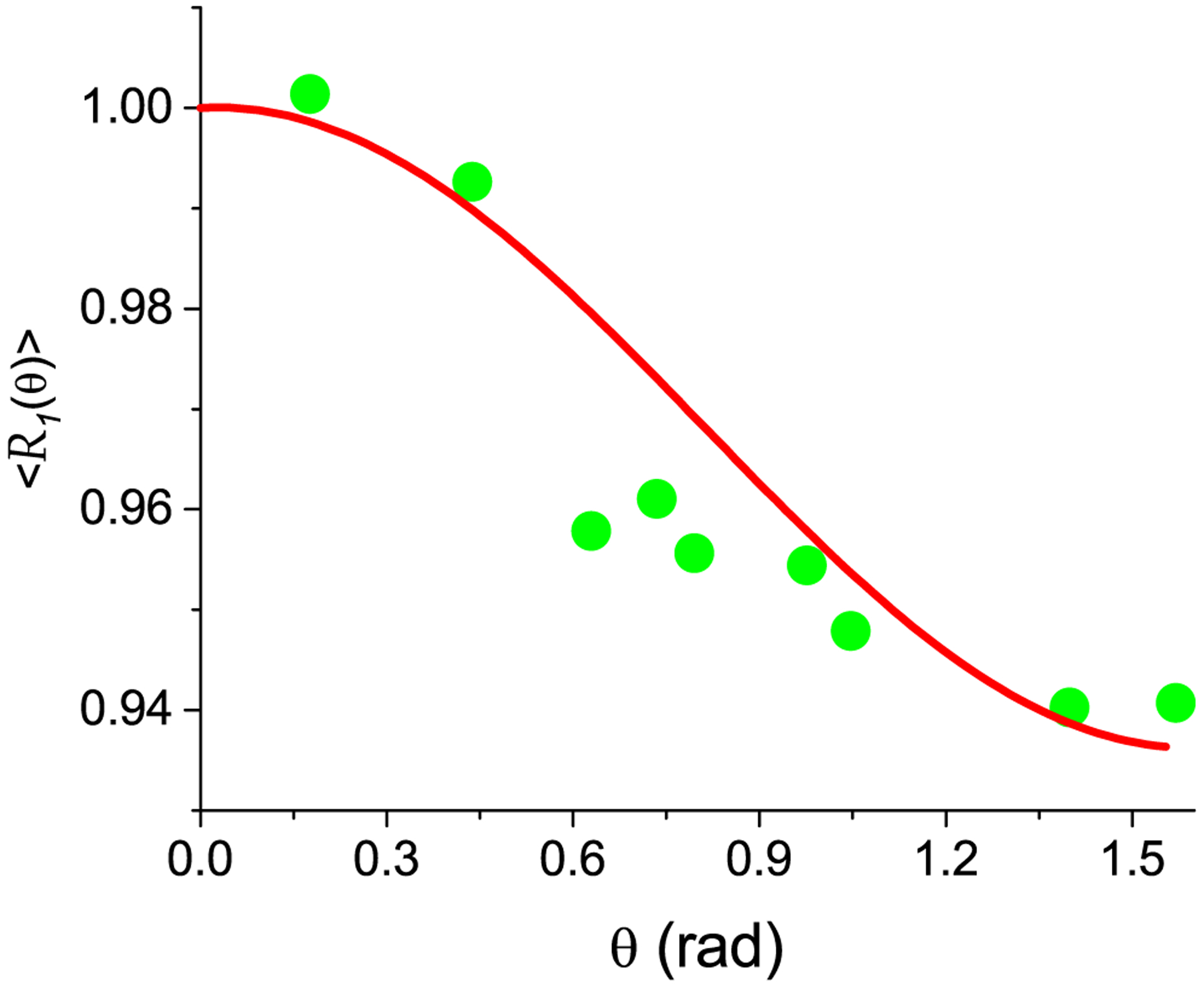
The normalized relaxation rate 〈R₁(θ₀)〉of the bovine flexor tendon as a function of the specimen orientation in the magnetic field of 2 T. Nanocavities are simulated as elongated cylinders with form factor F = 2π and V = 2500 nm³. Green circles are experimental data [28], red solid curve is theoretical calculation according to Eq. (46).

To determine the fitting parameters, 〈R₁(θ₀)〉 was calculated by using the mean relative error method with variation of the parameters in wide ranges and then the best parameter set was found from the condition that an averaged relative error

$$\Psi =\frac{1}{6}\sum \frac{\left|\langle R_1\left({\theta }_0\right)\rangle -{\langle R_1\left({\theta }_0\right)\rangle }_{\text{exp}}\right|}{{\langle R_1\left({\theta }_0\right)\rangle }_{\text{exp}}}$$ (47)

is minimal. Here 〈R₁(θ₀)〉_exp is the measured relaxation rate at angle θ₀ and summation through all experimental data for an analyzed sample. Fig. 4 shows the results for the bovine flexor tendon in a magnetic field of 2 T [28], where the maximum of 〈R₁(θ₀)〉 at θ₀ = 0 and the best matching of the calculations according to Eq. (46) with the relative error Ψ = 0.007 was achieved at ${\alpha }_{0sp}=\frac{\pi }{2}$, α_0rd = 0, ξ_sp = 0.1, ξ_rd = 0.9, σ_αsp = 0.45, σ_αrd = 0.47, and σ_χsp = σ_χsp = 1.8. Fig. 5 shows the results for the Achilles tendon in a magnetic field of 7 T [29], where the maximum of 〈R₁(θ₀)〉 at θ₀ = 0 and the best matching of the calculations according to Eq. (46) with the relative error Ψ = 0.009 was achieved at ${\alpha }_{0sp}=\frac{\pi }{2}$, α_0rd = 0, ξ_sp = 0.1, ξ_rd = 0.9, σ_αsp = 0.8, σ_αrd = .9, and σ_χsp = σ_χsp = 1.96.

Fig. 5.

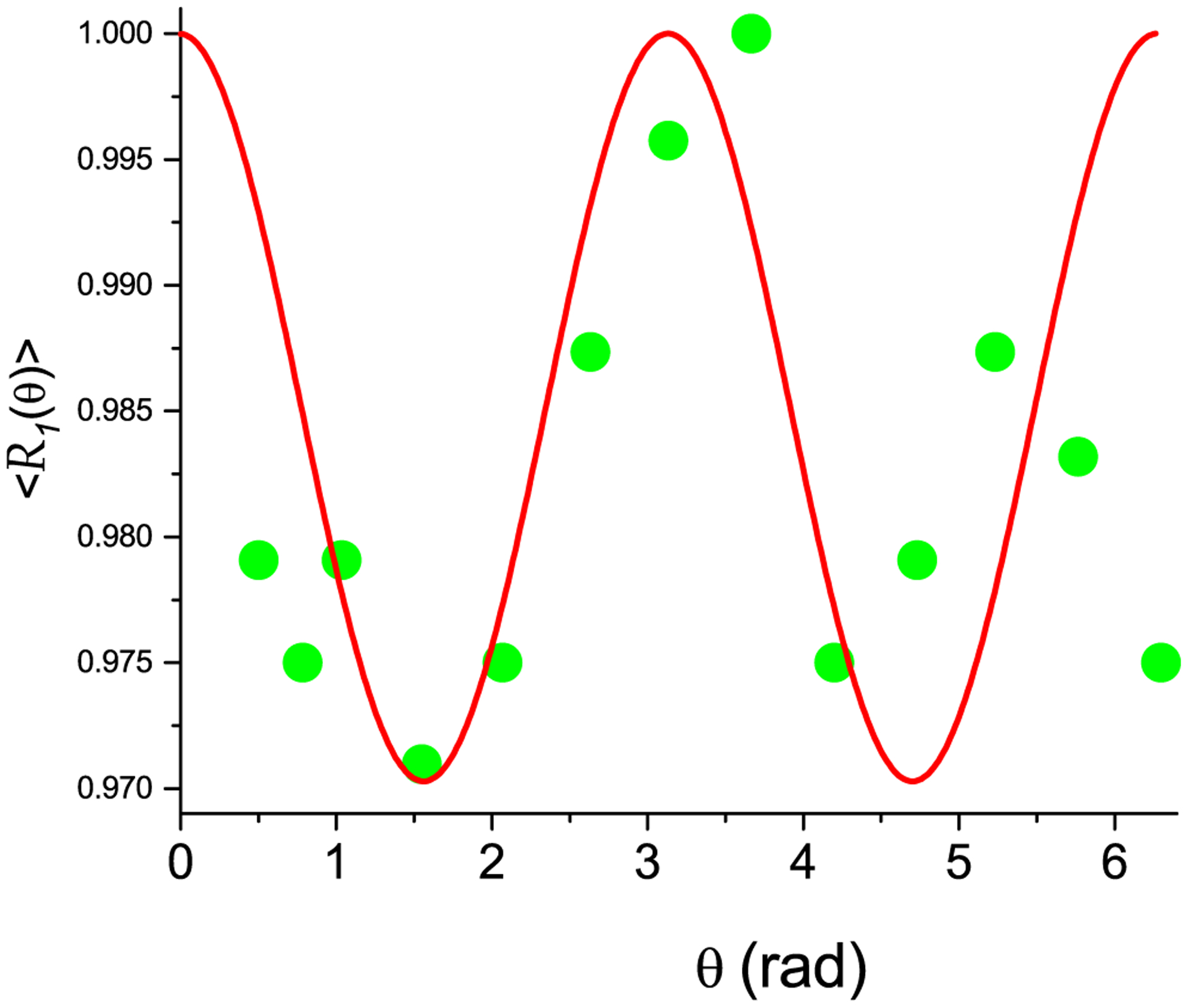
The normalized relaxation rate 〈R₁(θ₀)〉 of the Achilles tendon as a function of the specimen orientation in magnetic field of 7 T. Nanocavities are simulated as elongated cylinders with form factor F = 2π and V = 2500 nm³. Green circles are experimental data [29], red solid curve is theoretical calculation according to Eq. (46).

5. Discussion and conclusions

Using the method of nonequilibrium state operator [17,18], we have obtained the kinetic equation which takes into account the spin-lattice relaxation processes in bulk liquid. We were able to solve the kinetic equation and to obtain an expression in quadratures for the spin-lattice relaxation time T₁. The estimation of the relaxation time T₁ coincides with experimental data [1] at the correlation time τ_c ≃ 10⁻¹¹ s. It is shown that this relaxation time T₁ is independent of the orientation and applied magnetic field as well as of volume and form of nanocavities and this approach cannot explain the observed experimental results for samples containing nanocavities filled by liquid.

For nanocavities with the characteristic size much less than 700 nm, we have developed an alternative method for investigation of spin-lattice relaxation and determination of the spin-lattice relaxation time. First, the Hamiltonian is averaged over random molecular motions taking into account restriction of their motion, and then using the obtained averaged Hamiltonian the spin-lattice relaxation time is calculated. When determining the time, we assumed that the spin-lattice relaxation mechanism is effected by nanocavity fluctuations with the correlation function $\frac{|\tau |}{{\tau }_{cc}}{e}^{-\frac{|\tau |}{{\tau }_{cc}}}$ (see Eq. (40)). The obtained expression shows an explicit dependence of the relaxation time T₁ on volume V, density of nuclear spins C, and parameters of the nanocavity: shape (form factor F) and orientation relatively to the applied magnetic field, angle Θ (Fig. 3).

We also note that for both the bulk liquid and for the liquid entrapped in a nanocavity the relaxation time T₁ does not depend practically on the magnetic field. However, the reasons for this result are different: in the bulk liquid the correlation time is very short and ω₀τ_c ≪ 1 in Eq. (27). In the case of a nanocavity, on the contrary, this factor is large, ω₀τ_cc ≫ 1, (Eq. (41)).

In the case of nanocavities, for comparison with the experiment on detection of the anisotropy of the relaxation time T₁ for fibril tissues, these tissues were represented as a set of nanocavities containing water. We averaged the normalized relaxation rate over orientation of the nanocavities relative to the magnetic field. The good agreement with the experimental data was obtained by adjustment of few fitting parameters - the standard deviation, averaged fiber direction, and weight factors - which all have physical meanings which characterize the ordering of fibrils. Thus, the value of the fitting parameters obtained at matching of theoretic results to experimental data can be used in future investigations for characterizing the fine fibril structure of biological samples, in particular, the differentiation of fibril structures between healthy and lesioned samples.