Deep neural network models of sound localization reveal how perception is adapted to real-world environments

Abstract

Mammals localize sounds using information from their two ears. Localization in real-world conditions is challenging, as echoes provide erroneous information, and noises mask parts of target sounds. To better understand real-world localization we equipped a deep neural network with human ears and trained it to localize sounds in a virtual environment. The resulting model localized accurately in realistic conditions with noise and reverberation. In simulated experiments, the model exhibited many features of human spatial hearing: sensitivity to monaural spectral cues and interaural time and level differences, integration across frequency, biases for sound onsets, and limits on localization of concurrent sources. But when trained in unnatural environments without either reverberation, noise, or natural sounds, these performance characteristics deviated from those of humans. The results show how biological hearing is adapted to the challenges of real-world environments and illustrate how artificial neural networks can reveal the real-world constraints that shape perception.

Introduction

Why do we see or hear the way we do? Perception is believed to be adapted to the world – shaped over evolution and development to help us survive in our ecological niche. Yet adaptedness is often difficult to test. Many phenomena are not obviously a consequence of adaptation to the environment, and perceptual traits are often proposed to reflect implementation constraints rather than the consequences of performing a task well. Well-known phenomena attributed to implementation constraints include aftereffects^1,2, masking^3,4, poor visual motion and form perception for equiluminant color stimuli⁵, and limits on the information that can be extracted from high-frequency sound^6–8.

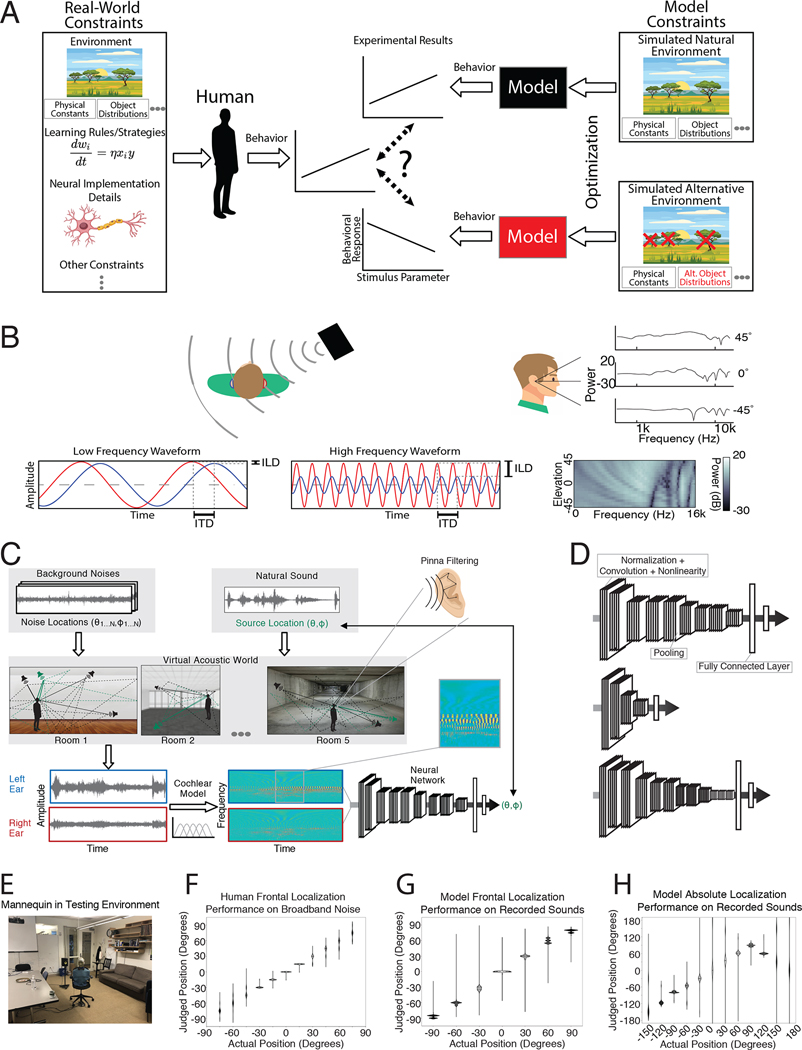
Evolution and development can be viewed as an optimization process that produces a system that functions well in its environment. The consequences of such optimization for perceptual systems have traditionally been revealed by ideal observer models – systems that perform a task optimally under environmental constraints^9,10, and whose behavioral characteristics can be compared to actual behavior. Ideal observers are typically derived analytically, but as a result are often limited to simple psychophysical tasks^11–16. Despite recent advances, such models remain intractable for many real-world behaviors. Rigorously evaluating adaptedness has thus remained out of reach for many domains. Here we extend ideas from ideal observer theory to investigate the environmental constraints under which human behavior emerges, using contemporary machine learning to optimize models for behaviorally relevant tasks in simulated environments. Human behaviors that emerge from machine learning under a set of naturalistic environmental constraints, but not under alternative constraints, are plausibly a consequence of optimization for those natural constraints (i.e., adapted to the natural environment) (Fig. 1A).

Figure 1.

Overview of approach. A. Illustration of method. A variety of constraints (left) shape human behavior. Models optimized under particular environmental constraints (right) illustrate the effect of these constraints on behavior. Environment simulators can instantiate naturalistic environments as well as alternative environments in which particular properties of the world are altered, to examine the constraints that shape human behavior. B. Cues to sound location available to humans: interaural time and level differences (left and center) and spectral differences (right). Time and level differences are shown for low and high frequency sinusoids (left and center, respectively). The level difference is small for the low frequency, and the time difference is ambiguous for the high frequency. C. Training procedure. Natural sounds (green) were rendered at a location in a room, with noises (natural sound textures, black) placed at other locations. Rendering included direction-specific filtering by the head/torso/pinnae, using head-related transfer functions from the KEMAR mannequin. Neural networks were trained to classify the location of the natural sound source (azimuth and elevation) into one of a set of location bins (spaced 5 degrees in azimuth and 10 degrees in elevation). D. Example neural network architectures from the architecture search. Architectures consisted of sequences of “blocks” (a normalization layer, followed by a convolution layer, followed by a nonlinearity layer) and pooling layers, culminating in fully connected layers followed by a classifier that provided the network’s output. Architectures varied in the total number of layers, the kernel dimensions for each convolutional layer, the number of blocks that preceded each pooling layer, and the number of fully connected layers preceding the classifier. Labels indicate an example block, pooling layer, and fully connected layer. The model’s behavior was taken as the average of the results for the 10 best architectures (assessed by performance on a held-out validation set of training examples). E. Recording setup for real-world test set. Mannequin was seated on a chair and rotated relative to the speaker to achieve different azimuthal positions. Sound was recorded from microphones in the mannequin ears. F. Free-field localization of human listeners, replotted from a previous publication¹⁵⁴. Participants heard a sound played from one of 11 speakers in the front horizontal plane and pointed to the location. Graph plots kernel density estimate of participant responses for each actual location. G. Localization judgments of the trained model for the real-world test set. Graph plots kernel density estimates of response distribution. For ease of comparison with F, in which all locations were in front of the listener, positions were front-back folded. H. Localization judgments of the model without front-back folding. Model errors are predominantly at front-back reflections of the correct location.

Sound localization is one domain of perception where the relationship of behavior to environmental constraints has not been straightforward to evaluate. The basic outlines of spatial hearing have been understood for decades^17–20. Time and level differences in the sound that enters the two ears provide cues to a sound’s location, and location-specific filtering by the ears, head, and torso provide monaural cues that help resolve ambiguities in binaural cues (Fig. 1B). However, in real-world conditions, background noise masks or corrupts cues from sources to be localized, and reflections provide erroneous cues to direction²¹. Classical models based on these cues thus cannot replicate real-world localization behavior^22–24. Instead, modeling efforts have focused on accounting for observed neuronal tuning in early stages of the auditory system rather than behavior^25–31, or have modeled behavior in simplified experimental conditions using particular cues^{24,30,32–36}. Engineering systems must solve localization in real-world conditions, but typically adopt approaches that diverge from biology, using more than two microphones and/or not leveraging cues from ear/head filtering^37–44. As a result we lack quantitative models of how biological organisms localize sounds in realistic conditions. In the absence of such models, the science of sound localization has largely relied on intuitions about optimality. Those intuitions were invaluable in stimulating research, but on their own are insufficient for quantitative predictions.

Here we exploit the power of contemporary artificial neural networks to develop a model optimized to localize sounds in realistic conditions. Unlike much other contemporary work using neural networks to investigate perceptual systems^45–50, our primary interest is not in potential correspondence between internal representations of the network and the brain. Instead, we aim to use the neural network as a way to find an optimized solution to a difficult real-world task that is not easily specified analytically, for the purpose of comparing its behavioral characteristics to those of humans. Our approach is thus analogous to the classic ideal observer approach, but harnesses modern machine learning in place of an ideal observer for a problem where one is not analytically tractable.

To obtain sufficient labeled data with which to train the model, and to enable the manipulation of training conditions, we used a virtual acoustic world⁵¹. The virtual world simulated sounds at different locations with realistic patterns of surface reflections and background noise that could be eliminated to yield unnatural training environments. To give the model access to the same cues available to biological organisms, we trained it on a high-fidelity cochlear representation of sound, leveraging recent technical advances⁵² to train the large models that are required for such high-dimensional input. Unlike previous generations of neural network models^{24,37,40,42,44}, which were reliant on hand-specified sound features, we learn all subsequent stages of a sound localization system to obtain good performance in real-world conditions.

When tested on stimuli from classic laboratory experiments, the resulting model replicated a large and diverse array of human behavioral characteristics. We then trained models in unnatural conditions to simulate evolution and development in alternative worlds. These alternative models deviated notably from human-like hearing. The results suggest that the characteristics of human hearing are indeed adapted to the constraints of real-world localization, and that the rich panoply of sound localization phenemona can be explained as consequences of this adaptation. The approach we employ is broadly applicable to other sensory modalities, providing a way to test the adaptedness of aspects of human perception to the environment and to understand the conditions in which human-like perception arises.

Results

Model construction

We began by building a system that could localize sounds using the information available to human listeners. The system thus had outer ears (pinnae), and a simulated head and torso, along with a simulated cochlea. The outer ears and head/torso were simulated using head-related impulse responses recorded from a standard physical model of the human⁵³. The cochlea was simulated with a bank of bandpass filters modeled on the frequency selectivity of the human ear^54,55, whose output was rectified and low-pass filtered to simulate the presumed upper limit of phase locking in the auditory nerve⁵⁶. The inclusion of a fixed cochear front-end (in lieu of trainable filters) reflected the assumption that the cochlea evolved to serve many different auditory tasks rather than being primarily driven by sound localization. As such, the cochlea seemed a plausible biological constraint on localization.

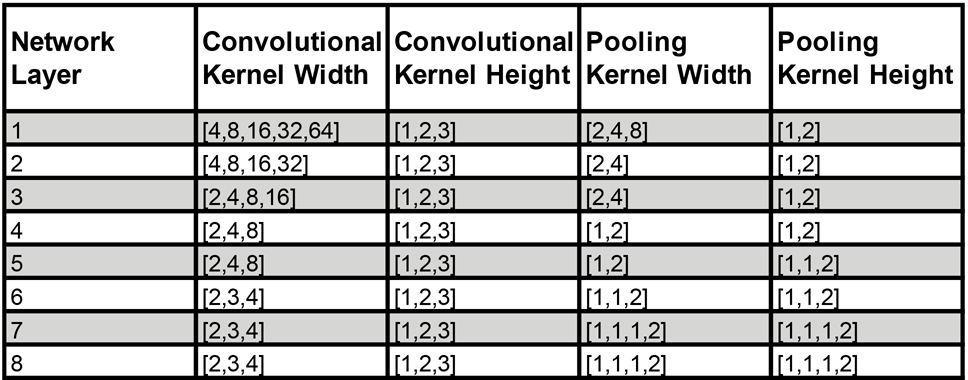
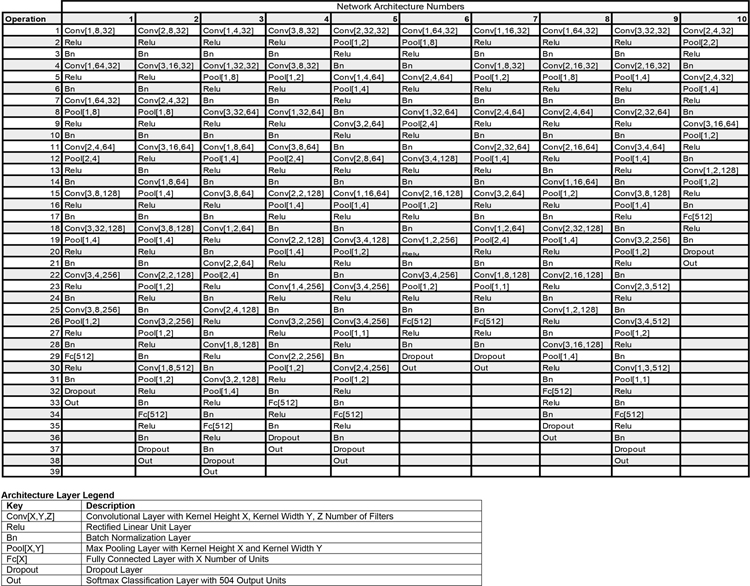
The output of the two cochlea formed the input to a standard convolutional neural network (Fig. 1C). This network instantiated a cascade of simple operations – filtering, pooling, and normalization – culminating in a softmax output layer with 504 units corresponding to different spatial locations (spaced 5° in azimuth and 10° in elevation). The parameters of the model were tuned to maximize localization performance on the training data. The optimization procedure had two phases: an architecture search in which we searched over architectural parameters to find a network architecture that performed well (Fig. 1D), and a training phase in which the filter weights of the selected architectures were trained to asymptotic performance levels using gradient descent.

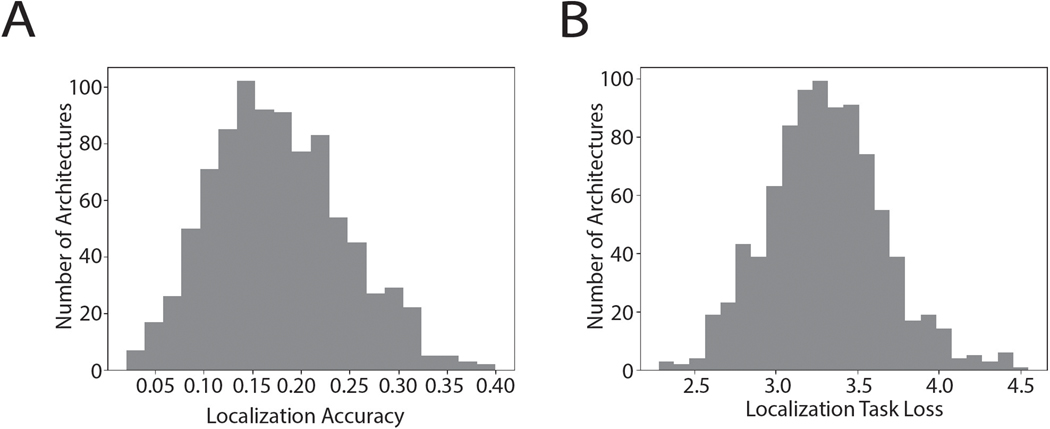
The architecture search consisted of training each of a large set of possible architectures for 15000 training steps with 16 1s stimulus examples per step (240k total examples; see Extended Data Fig. 1 for distribution of localization performance across architectures, and Extended Data Fig. 2 for the distributions from which architectures were chosen). We then chose the 10 networks that perfomed best on a validation set of data not used during training (Extended Data Fig. 3). The parameters of these 10 networks were then reinitialized and each trained for 100k training steps (1.6M examples). Given evidence that internal representations can vary somewhat across different networks trained on the same task⁵⁷, we present results aggregated across the top 10 best-performing architectures, treated akin to different participants in an experiment⁵⁸. Most results graphs present the average results for these 10 networks, which we collectively refer to as “the model”.

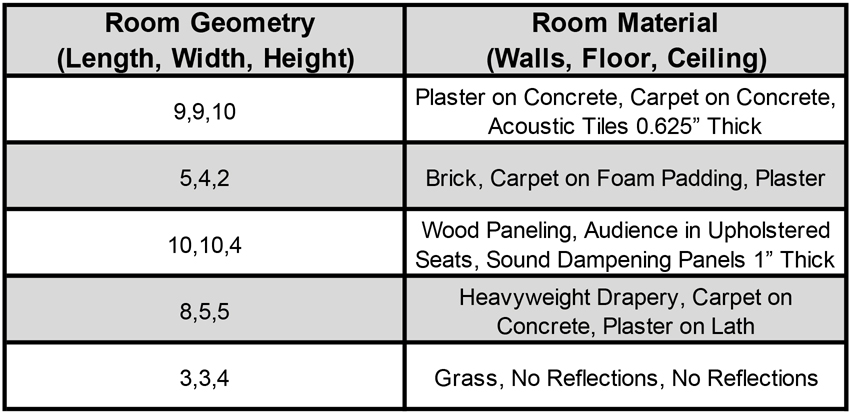
The training data was based on a set of ~500,000 stereo audio signals with associated 3D locations relative to the head (on average 988 examples for each of the 504 location bins; see Methods). These signals were generated from 385 natural sound source recordings (Extended Data Fig. 4) rendered at a spatial location in a simulated room. The room simulator used a modified source-image method^51,59 to simulate the reflections off the walls of the room. Each reflection was then filtered by the (binaural) head-related impulse response for the direction of the reflection⁵³. Five different rooms were used, varying in their dimensions and in the material of the walls (Extended Data Fig. 5). To mimick the common presence of noise in real-world environments, each training signal also contained spatialized noise. Background noise was synthesized from the statistics of a natural sound texture⁶⁰, and was rendered at between 3 and 8 randomly chosen locations using the same room simulator, in order to produce noise that was diffuse but non-uniform, intended to replicate common real-world sources of noise. At each training step the rendered natural sound sources were randomly paired with rendered background noises. The neural networks were trained to map the binaural audio to the location of the sound source (specified by its azimuth and elevation relative to the model’s “head”).

Model evaluation in real-world conditions

The trained networks were first evaluated on a held-out set of 70 sound sources rendered using the same pipeline used to generate the training data (yielding a total of ~47,000 stereo audio signals). The best-performing networks produced accurate localization for this validation set (the mean error was 5.3 degrees in elevation and 4.4 degrees in azimuth, front-back folded, i.e. reflected about the coronal plane, to discount front-back confusions).

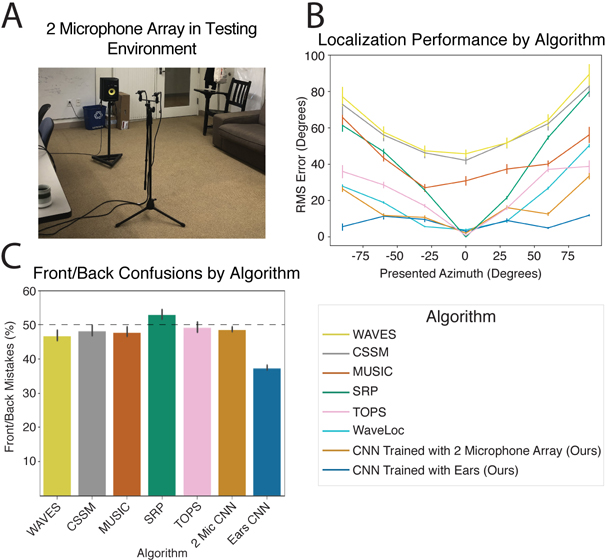
To assess whether the model would generalize to real-world stimuli outside the training distribution, we made binaural recordings in an actual conference room using a mannequin with in-ear microphones (Fig. 1E. Humans localize relatively well in such free-field conditions (Fig. 1F). The trained networks also localized real-world recordings relatively well (Fig. 1G), on par with human free-field localization, with errors limited to the front-back confusions that are common to humans when they cannot move their heads (Fig. 1H)^61,62.

For comparison, we also assessed the performance of a standard set of two-microphone localization algorithms from the engineering literature^63–68. In addition, we trained the same set of neural networks to localize sounds from a two-microphone array that lacked the filtering provided to biological organisms by the ears/head/torso but that included the simulated cochlea (Extended Data Fig. 6A). Our networks that had been trained with biological pinnae/head/torso outperformed the set of standard two-microphone algorithms from the engineering community, as well as the neural networks trained with stereo microphone input without a head and ears (Extended Data Fig. 6B&C). This latter result confirms that the head and ears provide valuable cues for localization. Overall, performance on the real-world test set demonstrates that training a neural network in a virtual world produces a model that can accurately localize sounds in realistic conditions.

Model behavioral characteristics

To assess whether the trained model replicated the characteristics of human sound localization, we simulated a large set of behavioral experiments from the literature, intended to span many of the best-known and largest effects in spatial hearing. We replicated the conditions of the original experiments as closely as possible (e.g. when humans were tested in anechoic conditions, we rendered experimental stimuli in an anechoic environment). We emphasize that the networks were not fit to human data in any way. Despite this, the networks reproduced the characteristics of human spatial hearing across this broad set of experiments.

Sensitivity to interaural time and level differences

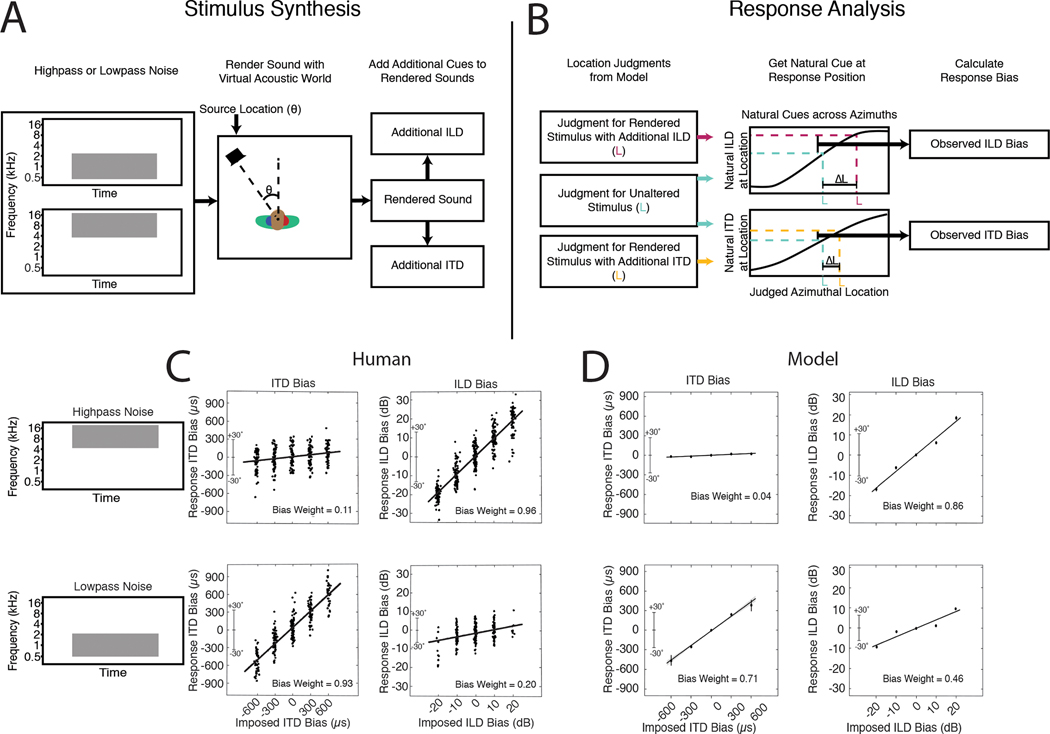
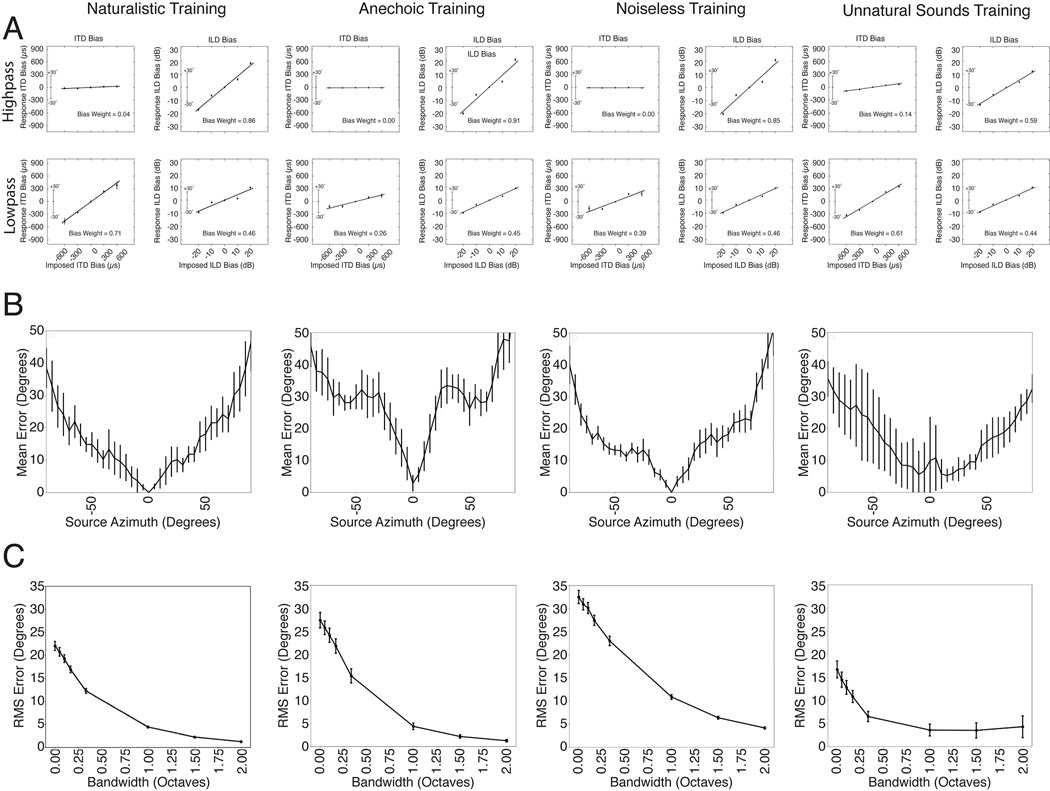
We began by assessing whether the networks learned to use the binaural cues known to be important for biological sound localization. We probed the effect of interaural time and level differences (ITDs and ILDs, respectively) on localization behavior using a paradigm in which additional time and level differences are added to high- and low-frequency sounds rendered in virtual acoustic space⁶⁹ (Fig. 2A). This paradigm has the advantage of using realistically externalized sounds and an absolute localization judgment (rather than the left/right lateralization judgments of simpler stimuli that are common to many other experiments^70–73).

Figure 2.

Sensitivity to interaural time and level differences. A. Schematic of stimulus generation. Noise bursts filtered into high or low frequency bands were rendered at a particular azimuthal position, after which an additional ITD or ILD was added to the stereo audio signal. B. Schematic of response analysis. Responses were analyzed to determine the amount by which the perceived location (L) was altered (ΔL) by the additional ITD/ILD, expressed as the amount by which the ITD/ILD would have changed if the actual sound’s location changed by ΔL. C. Effect of additional ITD and ILD on human localization. Y axis plots amount by which the perceived location was altered, expressed in ITD/ILD as described above. Each dot plots a localization judgment from one trial. Data reproduced from a previous publication⁶⁹. D. Effect of additional ITD and ILD on model localization. Same conventions as B. Error bars plot SEM, bootstrapped across the 10 networks.

In the original experiment⁶⁹, the change to perceived location imparted by the additional ITD or ILD was expressed as the amount by which the ITD or ILD would change in natural conditions if the actual location were changed by the perceived amount (Fig. 2B). This yields a curve whose slope indicates the efficacy of the manipulated cue (ITD or ILD). We reproduced the stimuli from the original study, rendered them in our virtual acoustic world, added ITDs and ILDs as in the original study, and analyzed the model’s localization judgments in the same way.

For human listeners, ITD and ILD have opposite efficacies at high and low frequencies (Fig. 2C), as predicted by classical “duplex” theory¹⁷. An ITD bias imposed on low-frequency sounds shifts the perceived location of the sound substantially (bottom left), whereas an ITD imposed on high-frequency sound does not (top left). The opposite effect occurs for ILDs (right panels), although there is a weak effect of ILDs on low-frequency sound. This latter effect is inconsistent with the classical duplex story but consistent with more modern measurements indicating small but reliable ILDs at low frequencies⁷⁴ that are used by the human auditory system^75–77.

As shown in Fig. 2D, the model qualitatively replicated the effects seen in humans. Added ITDs and ILDs had the largest effect at low and high frequencies, respectively, but ILDs had a modest effect at low frequencies as well. This produced an interaction between the type of cue (ITD/ILD) and frequency range (difference of differences between slopes significantly greater than 0; p<.001, evaluated by bootstrapping across the 10 networks). However, the effect of ILD at low frequencies was also significant (slope significantly greater than 0; p<.001, via bootstrap). Thus, a model optimized for accurate localization both exhibits the dissociation classically associated with duplex theory, but also its refinements in the modern era.

Azimuthal localization of broadband sounds

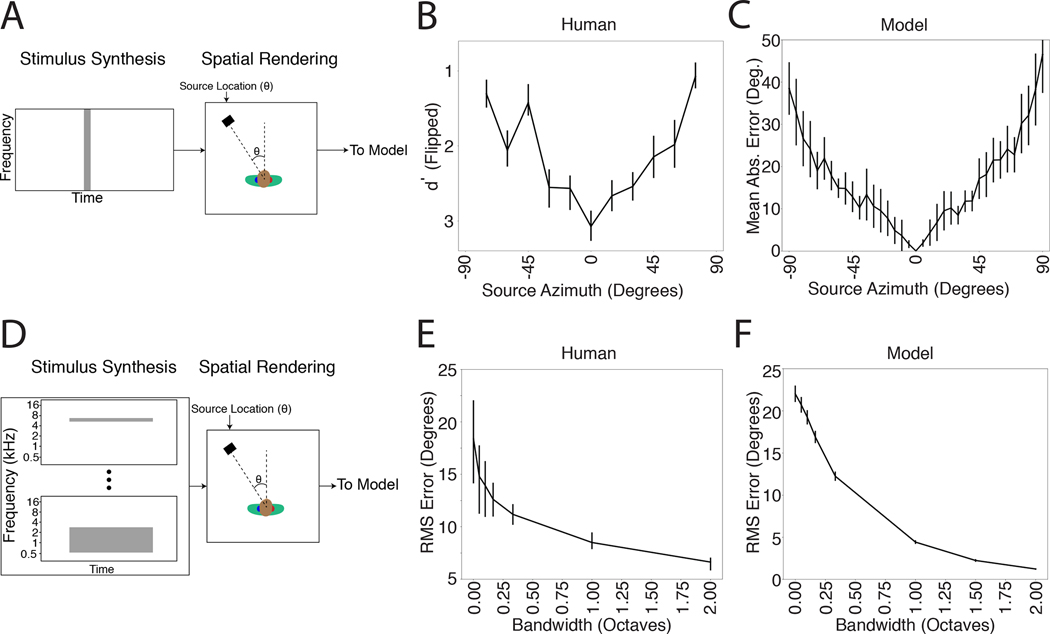
We next measured localization accuracy of broadband noise rendered at different azimuthal locations (Fig. 3A). In humans, localization is most accurate near the midline (Fig. 3B), and becomes progressively less accurate as sound sources move to the left or right of the listener^78–80. One explanation is that the first derivatives of ITD and ILD with respect to azimuthal location decrease as the source moves away from the midline²¹, providing less information about location²⁸. The model qualitatively reproduced this result (Fig. 3C).

Figure 3.

Azimuthal localization is most accurate at the midline and improves with stimulus bandwidth. A. Schematic of stimuli from experiment measuring localization accuracy at different azimuthal positions. B. Localization accuracy of human listeners for broadband noise at different azimuthal positions. Data were scanned from a previous publication⁸⁰, which measured discriminability of noise bursts separated by 15 degrees (quantified as d’). Error bars plot SEM. C. Localization accuracy of our model for broadband noise at different azimuthal positions. Graph plots mean absolute localization error of the same noise bursts used in the human experiment in B. Error bars plot SEM across the 10 networks. D. Schematic of stimuli from experiment measuring effect of bandwidth on localization accuracy. Noise bursts varying in bandwidth were presented at particular azimuthal locations; participants indicated the azimuthal position with a keypress. E. Effect of bandwidth on human localization of noise bursts. Error bars plot SD. Data are replotted from a previous publication⁸². F. Effect of bandwidth on model localization of noise bursts. Networks were constrained to report only the azimuth of the stimulus. Error bars plot SEM across the 10 networks.

Integration across frequency

Because biological hearing begins with a decomposition of sound into frequency channels, binaural cues are thought to be initially extracted within these channels^20,25. However, organisms are believed to integrate information across frequency to achieve more accurate localization than could be mediated by any single frequency channel. One signature of this integration is improvement in localization accuracy as the bandwidth of a broadband noise source is increased (Fig. 3D&E)^81,82. We replicated one such experiment on the networks and they exhibited a similar effect, with accuracy increasing with noise bandwidth (Fig. 3F).

Use of ear-specific cues to elevation

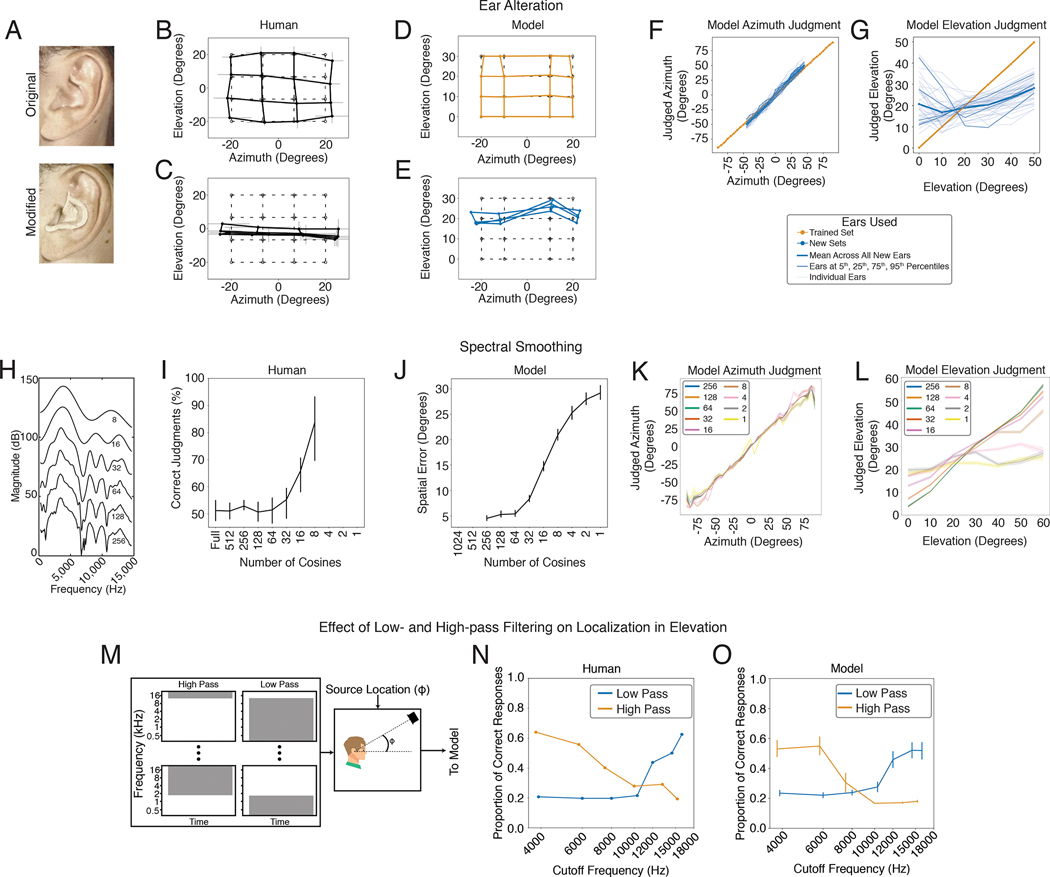
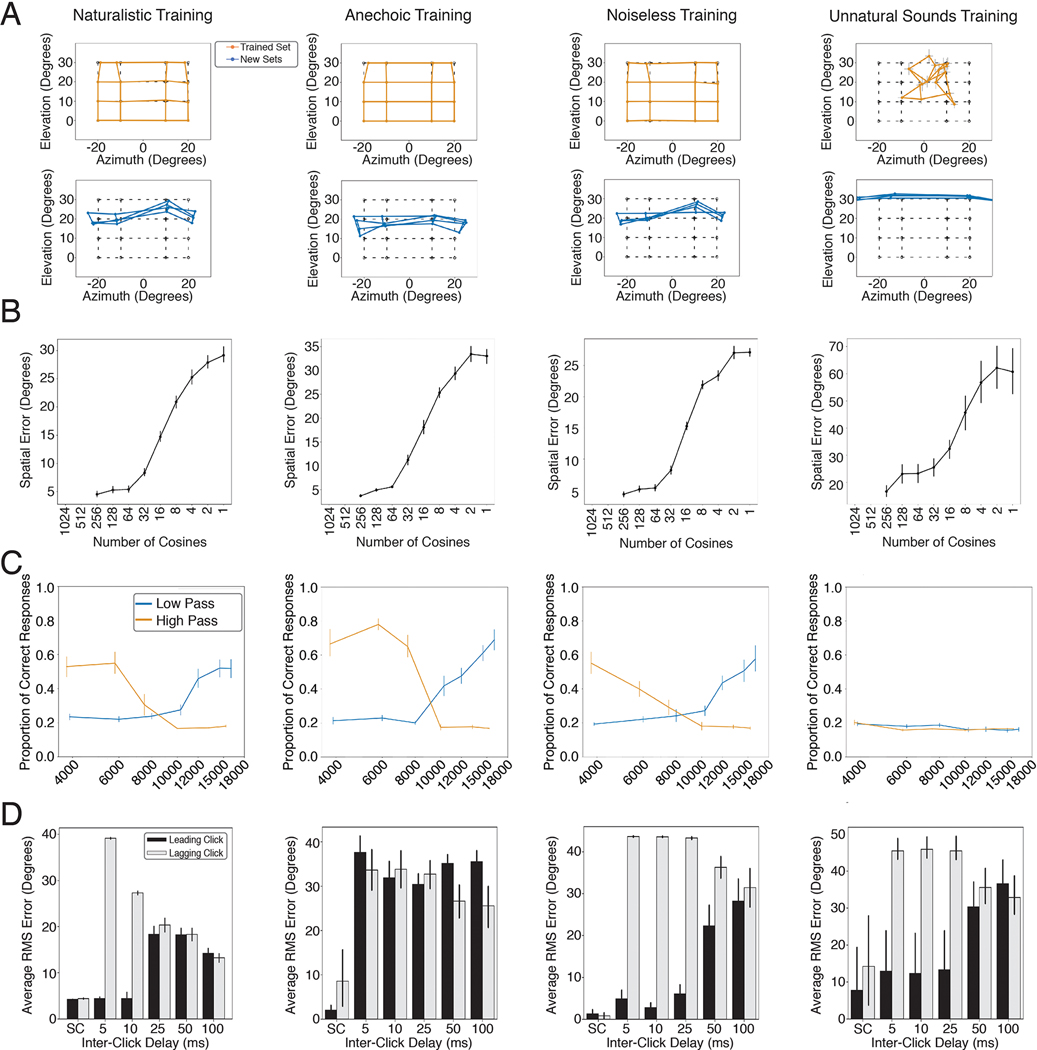
In addition to the binaural cues that provide information about azimuth, organisms are known to make use of the direction-specific filtering imposed on sound by the ears, head and torso^18,83. Each individual’s ears have resonances that “color” a sound differently depending on where it comes from in space. Individuals are believed to learn the specific cues provided by their ears. In particular, if forced to listen with altered ears, either via molds inserted into the ears⁸⁴ or via recordings made in a different person’s ears⁸⁵, localization in elevation degrades even though azimuthal localization is largely unaffected (Fig. 4A–C).

Figure 4.

Dependence of elevation perception on ear-specific transfer functions. A. Photographs of ear alteration in humans (reproduced from a previous publication⁸⁴). B. Sound localization by human listeners with unmodified ears. Graph plots mean and SEM of perceived locations for 4 participants, superimposed on grid of true locations (dashed lines). Data scanned from original publication⁸⁴. C. Effect of ear alteration on human localization. Same conventions as B. D. Sound localization in azimuth and elevation by the model, using the ears (head-related impulse responses) from training, with broadband noise sound sources. Graph plots mean locations estimated by the 10 networks. Tested locations differed from those in the human experiment to conform to the location bins used for network training. E. Effect of ear alteration on model sound localization. Ear alteration was simulated by substituting an alternative set of head-related impulse responses into the sound rendered following training. Graph plots average results across all 45 sets of alternative ears (averaged across the 10 networks). F. Effect of individual sets of alternative ears on localization in azimuth. Graph shows results for a larger set of locations than in D and E to illustrate the generality of the effect. G. Effect of individual sets of alternative ears on localization in elevation. Bolded lines show ears at 5^th_, 25^th_, 75^th_, and 95^th percentiles when the 45 sets of ears were ranked by accuracy. H. Smoothing of head-related transfer functions, produced by varying the number of coefficients in a discrete cosine transform. Reproduced from original publication⁸⁶. I. Effect of spectral smoothing on human perception. Participants heard two sounds, one played from a speaker in front of them, and one played through open-backed earphones, and judged which was which. The earphone-presented sound was rendered using HRTFs smoothed by various degrees. In practice participants performed the task by noting changes in sound location. Data scanned from original publication⁸⁶. Error bars plot SEM. Conditions with 4, 2, and 1 cosine coefficients were omitted from the experiment, but are included on the x-axis to facilitate comparison with the model results in J. J. Effect of spectral smoothing on model sound localization accuracy (measured in both azimuth and elevation). Conditions with 512 and 1024 cosine components were not realizable given the length of the impulse responses we used. K. Effect of spectral smoothing on model accuracy in azimuth. L. Effect of spectral smoothing on model accuracy in elevation. M. Stimuli from experiment in N and O. Noise bursts varying in low- or high-pass cutoff were presented at particular elevations. N. Effect of low-pass and high-pass cutoff on accuracy in humans. Data scanned from original publication⁹⁰; error bars were not provided in the original publication. O. Effect of low-pass and high-pass cutoff on model accuracy. Networks were constrained to report only elevation. Here and in J, K, and L, error bars plot SEM across the 10 networks.

To test whether the trained networks similarly learned to use ear-specific elevation cues, we measured localization accuracy in two conditions: one where sounds were rendered using the head-related impulse response set used for training the networks, and another where the impulse responses were different (having been recorded in a different person’s ears). Because we have unlimited ability to run experiments on the networks, in the latter condition we evaluated localization with 45 different sets of impulse responses, each recorded from a different human. As expected, localization of sounds rendered with the ears used for training was good in both azimuth and elevation (Fig. 4D). But when tested with different ears, localization in elevation generally collapsed (Fig. 4E), much like what happens to human listeners when molds are inserted in their ears (Fig. 4C), even though azimuthal localization was nearly indistinguishable from that with the trained ears. Results for individual sets of alternative ears revealed that elevation performance transferred better across some ears than others (Fig. 4F&G), consistent with anecdotal evidence that sounds rendered with HRTFs other than one’s own can sometimes be convincingly localized in three dimensions.

Limited spectral resolution of elevation cues

Elevation perception is believed to rely on the peaks and troughs introduced to a sound’s spectrum by the ears/head/torso^18,21,83 (Fig. 1B, right). In humans, however, perception is dependent on relatively coarse spectral features – the transfer function can be smoothed substantially before human listeners notice abnormalities⁸⁶ (Fig. 4 H&I), for reasons that are unclear. In the original demonstration of this phenomenon, human listeners discriminated sounds with and without smoothing, a judgment that was in practice made by noticing changes in the apparent location of the sound. To test whether the trained networks exhibited a similar effect, we presented sounds to the networks with similarly smoothed transfer functions and measured the extent to which the localization accuracy was affected. The effect of spectral smoothing on the networks’ accuracy was similar to the measured sensitivity of human listeners (Fig. 4J). The effect of the smoothing was most prominent for localization in elevation, as expected, but there was also some effect on localization in azimuth for the more extreme degrees of smoothing (Fig. 4K&L), consistent with evidence that spectral cues affect azimuthal space encoding⁸⁷.

Dependence on high-frequency spectral cues to elevation

The cues used by humans for localization in elevation are primarily in the upper part of the spectrum^88,89. To assess whether the trained networks exhibited a similar dependence, we replicated an experiment measuring the effect of high-pass and low-pass filtering on the localization of noise bursts⁹⁰ (Fig. 4M). Model performance varied with the frequency content of the noise in much the same way as human performance (Fig. 4N&O).

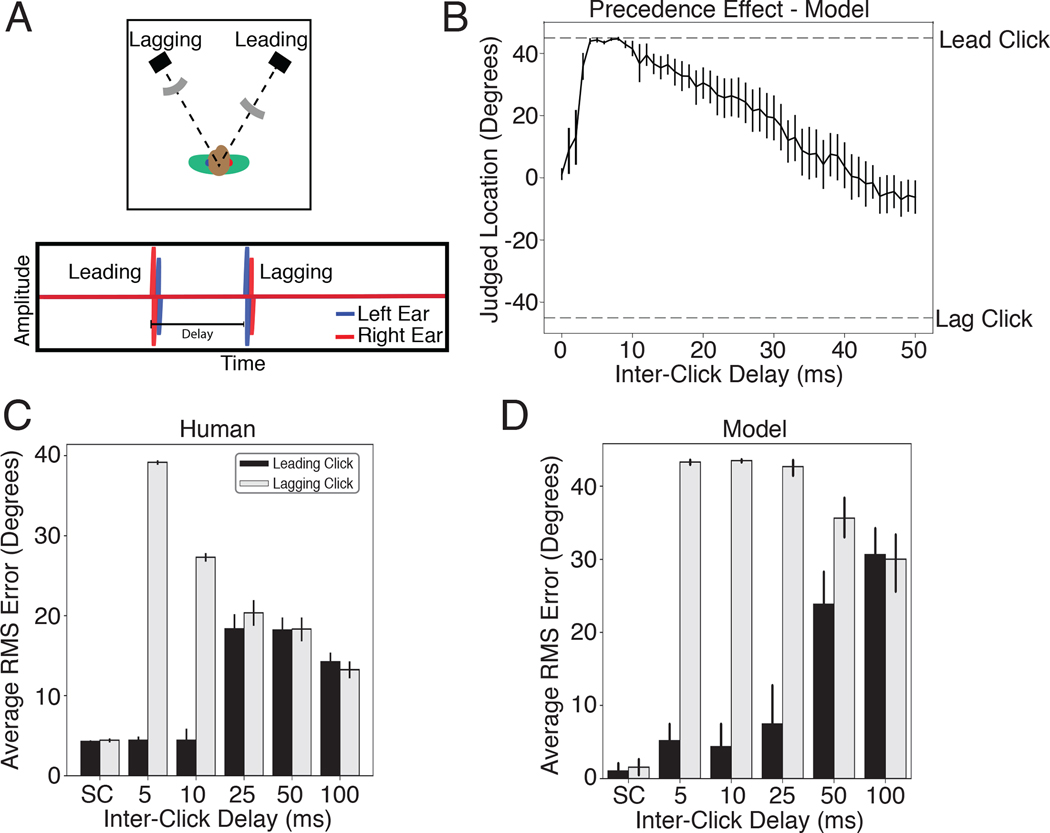
The precedence effect

Another hallmark of biological sound localization is that judgments are biased towards information provided by sound onsets^21,91. The classic example of this bias is known as the “precedence effect”^92–94. If two clicks are played from speakers at different locations with a short delay (Fig. 5A), listeners perceive a single sound whose location is determined by the click that comes first. The effect is often hypothesized to be an adaptation to the common presence of reflections off of environmental surfaces (Fig. 1C) – reflections arrive from an erroneous direction but traverse longer paths and arrive later, such that basing location estimates on the earliest arriving sound might avoid errors²¹. To test whether our model would exhibit a similar effect, we simulated the classic precedence experiment, rendering two clicks at different locations. When clicks were presented simultaneously, the model reported the sound to be centered between the two click locations, but when a small inter-click delay was introduced, the reported location switched to that of the leading click (Fig. 5B). This effect broke down as the delay was increased, as in humans, though with the difference that the model cannot report hearing two sounds, and so instead reported a single location intermediate between those of the two clicks.

Figure 5.

The precedence effect. A. Diagram of stimulus. Two clicks are played from two different locations relative to the listener. The time interval between the clicks is manipulated and the listener is asked to localize the sound(s) that they hear. When the delay is short but non-zero, listeners perceive a single click at the location of the first click. At longer delays listeners hear two distinct sounds. B. Localization judgments of the model for two clicks at +45 and −45 degrees. The model exhibits a bias for the leading click when the delay is short but non-zero. At longer delays the model judgments (which are constrained to report the location of a single sound, unlike humans), converge to the average of the two click locations. Error bars plots SEM across the 10 networks. C. Error in localization of the leading and lagging clicks by humans as a function of delay. SC denotes a single click at the leading or lagging location. Error bars plot SD. Data scanned from original publication⁹⁵. D. Error in localization of the leading and lagging clicks by the model as a function of delay. Error bars plots SEM across the 10 networks.

To compare the model results to human data, we simulated an experiment in which participants reported the location of both the leading and lagging click as the inter-click delay was varied⁹⁵. At short but non-zero delays, humans accurately localize the leading but not the lagging click (Fig. 5C; because a single sound is heard at the location of the leading click). At longer delays the lagging click is more accurately localized, and listeners start to mislocalize the leading click, presumably because they confuse which click is first⁹⁵. The model qualitatively replicated both effects, in particular the large asymmetry in localization accuracy for the leading and lagging sound at short delays (Fig. 5D).

Multi-source localization

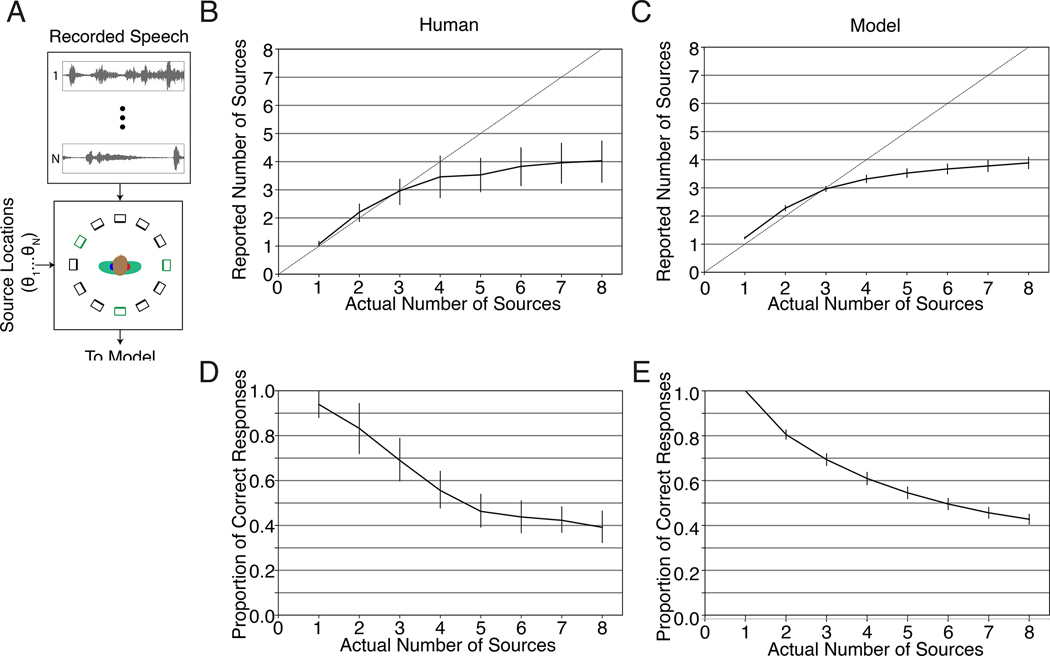
Humans are able to localize multiple concurrent sources, but only to a point^96–98. The reasons for the limits on multi-source localization are unclear⁹⁷. These limitations could reflect human-specific cognitive constraints. For instance, reporting a localized source might require attending to it, which could be limited by central factors not specific to localization. Alternatively, localization could be fundamentally limited by corruption of spatial cues by concurrent sources or other ambiguities intrinsic to the localization problem. To assess whether the model would exhibit limitations like those observed in humans, we replicated an experiment⁹⁸ in which humans judged both the number and location of a set of speech signals played from a subset of an array of speakers (Fig. 6A). To enable the model to report multiple sources we fine-tuned the final fully-connected layer to indicate the probability of a source at each of the location bins, and set a probability criterion above which we considered the model to report a sound at the corresponding location (see Methods). The weights in all earlier layers were “frozen” during this fine-tuning, such that all other stages of the model were identical to those used in all other experiments. We then tested the model on the experimental stimuli.

Figure 6.

Multi-source localization. A. Diagram of experiment. On each trial, between 1 and 8 speech signals (each spoken by a different talker) was played from a subset of the speakers in a 12-speaker circular array. The lower panel depicts an example trial in which three speech signals were presented, with the corresponding speakers in green. Participants reported the number of sources and their locations. B. Average number of sources reported by human listeners, plotted as a function of the actual number of sources. Error bars plot standard deviation across participants. Here and in D, graph is reproduced from original paper⁹⁸ with permission of the authors. C. Same as B, but for the model. Error bars plot standard deviation across the 10 networks D. Localization accuracy (measured as the proportion of sources correctly localized to the actual speaker from which they were presented), plotted as a function of the number of sources. Error bars plot standard deviation across participants. E. Same as D, but for the model. Error bars plot standard deviation across the 10 networks.

Humans accurately report the number of sources up to three, after which they undershoot, only reporting about four sources in total regardless of the actual number (Fig. 6B). The model reproduced this effect, also being limited to approximately four sources (Fig. 6C). Human localization accuracy also systematically drops with the number of sources (Fig. 6D); the model again quantitatively reproduced this effect (Fig. 6E). The model-human similarity suggests that these limits on sound localization are intrinsic to the constraints of the localization problem, rather than reflecting human-specific central factors.

Effect of optimization for unnatural environments

Despite having no previous exposure to the stimuli used in the experiments, and despite not being fit to match human data in any way, the model qualitatively replicated a wide range of classic behavioral effects found in humans. These results raise the possibility that the characteristics of biological sound localization may be understood as a consequence of optimization for real-world localization. However, given these results alone, the role of the natural environment in determining these characteristics is left unclear.

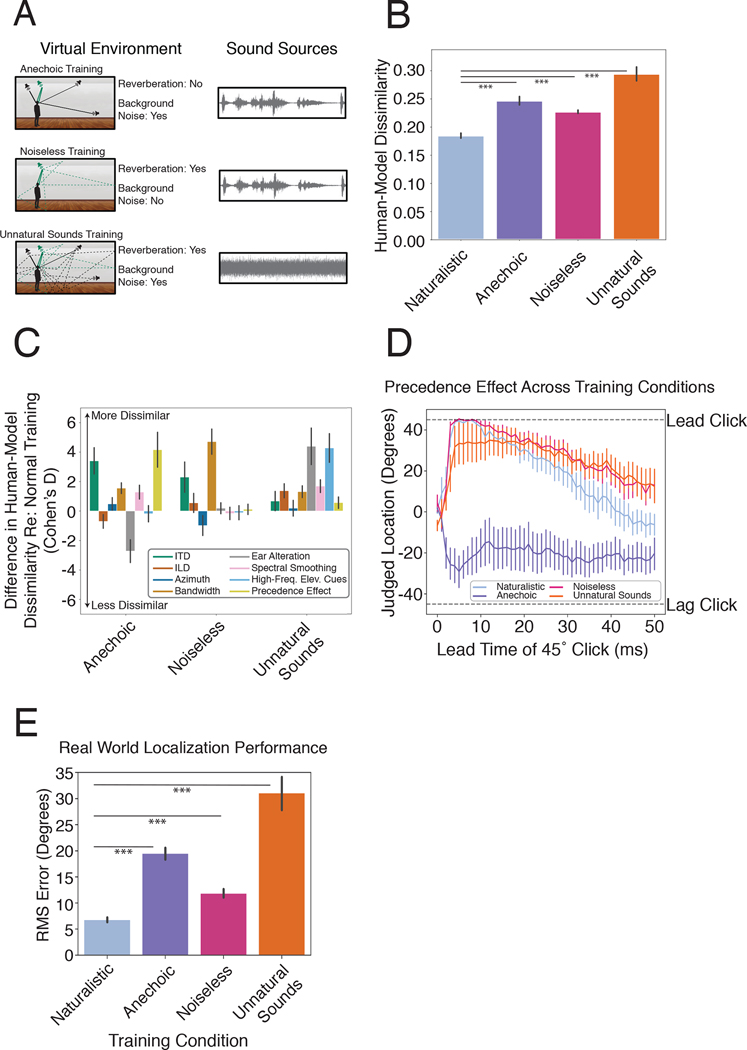
To assess the extent to which the properties of biological hearing are adapted to the constraints of localization in natural environments, we took advantage of the ability to optimize models in virtual worlds altered in various ways, intended to simulate the optimization that would occur over evolution and/or development in alternative environments (Fig. 1A). We altered the training environment in one of three ways (Fig. 7A): 1) by eliminating reflections (simulating surfaces that absorb all sound that reaches them, unlike real-world surfaces), 2) by eliminating background noise, and 3) by replacing natural sound sources with artificial sounds (narrowband noise bursts). In each case we trained the networks to asymptotic performance, then froze their weights and ran them on the full suite of psychophysical experiments described above. The psychophysical experiments were identical for all training conditions; the only difference was the strategy learned by the model during training, as might be reflected in the experimental results. We then quantified the dissimilarity between the model psychophysical results and those of humans as the mean squared error between the model and human results, averaged across experiments (normalized to have uniform axis limits; see Methods).

Figure 7.

Effect of unnatural training conditions. A. Schematic depiction of altered training conditions, eliminating echoes or background noise, or using unnatural sounds. B. Overall human-model dissimilarity for natural and unnatural training conditions. Error bars plot SEM, bootstrapped across networks. Asterisks denote statistically significant differences between conditions (p<.001, two-tailed), evaluated by comparing the human-model dissimilarity for each unnatural training condition to a bootstrapped null distribution of the dissimilarity for the natural training condition. C. Effect of unnatural training conditions on human-model dissimilarity for individual experiments, expressed as the effect size of the difference in dissimilarity between the natural and each unnatural training condition (Cohen’s d, computed between human-model dissimilarity for networks in normal and modified training conditions). Positive numbers denote a worse resemblance to human data compared to the model trained in normal conditions. Error bars plot SEM, bootstrapped across the 10 networks D. The precedence effect in networks trained in alternative environments. E. Real-world localization accuracy of networks for each training condition. Error bars plot SEM, bootstrapped across the 10 networks. Asterisks denote statistically significant differences between conditions (p<.001, two-tailed), evaluated by comparing the mean localization error for each unnatural training condition to a bootstrapped null distribution of the localization error for the natural training condition.

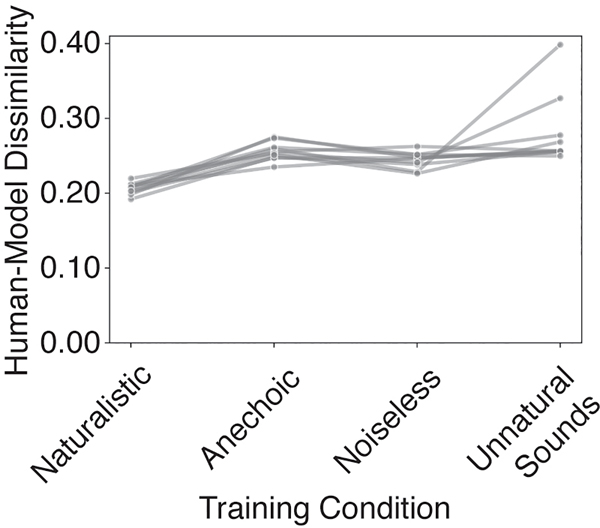
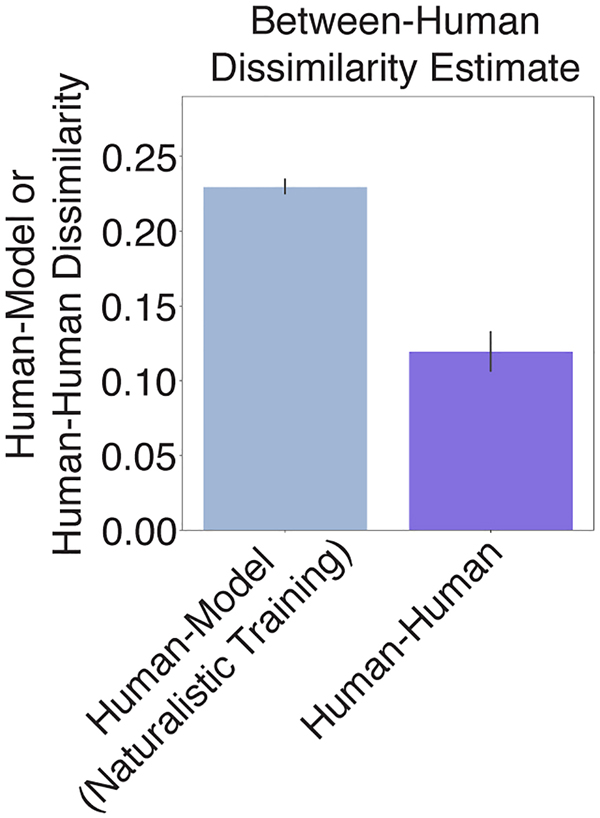
Fig. 7B shows the average dissimilarity between the human and model results on the suite of psychophysical experiments, computed separatedly for each model training condition. The dissimilarity was lowest for the model trained in natural conditions, and significantly higher for each of the alternative conditions (p<.001 in each case, obtained by comparing the dissimilarity of the alternative conditions to a null distribution obtained via bootstrap across the 10 networks trained in the naturalistic condition; results were fairly consistent across networks, Extended Data Fig. 7). The effect size of the difference in dissimilarity between the naturalistic training condition results and each of the other training conditions was large in each case (d=3.06, Anechoic; d=3.05, Noiseless; d=3.01, Unnatural Sounds). This result provides additional evidence that the properties of spatial hearing are consequences of adaptation to the natural environment – human-like spatial hearing emerged from task optimization only for naturalistic training conditions.

To get insight into how the environment influences perception, we examined the human-model dissimilarity for each experiment individually (Fig. 7C). Because the absolute dissimilarity is not meaningful (in that it is limited by the reliability of the human results, which is not perfect; see Extended Data Fig. 8), we assessed the differences in human-model dissimilarity between the natural training condition and each unnatural training condition. These differences were most pronounced for a subset of experiments in each case.

The anechoic training condition produced most abnormal results for the precedence effect, but also produced substantially different results for ITD cue strength. The effect size for the difference in human-model dissimilarity between anechoic and natural training conditions was significantly greater in both these experiments (precedence effect: d=4.16; ITD cue strength: d=3.41) than in the other experiments (p<0.001, by comparing the effect sizes of one experiment to the distribution of the effect size for another experiment obtained via bootstrap across networks). The noiseless training condition produced most abnormal results for the effect of bandwidth (d=4.71; significantly greater than that for other experiments, p<0.001, via bootstrap across networks). We confirmed that this result was not somehow specific to the absence of internal neural noise in our cochlear model, by training an additional model in which noise was added to each frequency channel (see Methods). We found that the results of training in noiseless environments remained very similar. The training condition with unnatural sounds produced most abnormal results for the experiment measuring elevation perception (d=4.4 for the ear alteration experiment; d=4.28 for the high-frequency elevation cue experiment; p<0.001 in both cases, via bootstrap across networks), presumably because without the pressure to localize broadband sounds, the model did not acquire sensitivity to spectral cues to elevation. These results indicate that different worlds would lead to different perceptual systems with distinct localization strategies.

The most interpretable example of environment-driven localization strategies is the precedence effect. This effect is often proposed to render localization robust to reflections, but others have argued that its primary function might instead be to eliminate interaural phase ambiguities, independent of reflections⁹⁹. This effect is shown in Fig. 7D for models trained in each of the four virtual environments. Anechoic training completely eliminated the effect, even though it was largely unaffected by the other two unnatural training conditions. This result substantiates the hypothesis that the precedence effect is an adaptation to reflections in real-world listening conditions. See Extended Data Figs. 9 and 10 for full psychophysical results for models trained in alternative conditions.

In addition to diverging from the perceptual strategies found in human listeners, the models trained in unnatural conditions performed more poorly at real-world localization. When we ran models trained in alternative conditions on our real-world test set of recordings from mannequin ears in a conference room, localization accuracy was substantially worse in all cases (Fig. 7E; p<.0.001 in all cases). This finding is consistent with the common knowledge in engineering that training systems in noisy and otherwise realistic conditions aids performance^37,42,44,100. Coupled with the abnormal psychophysical results of these alternatively trained models, this result indicates that the classic perceptual characteristics of spatial hearing reflect strategies that are important for real-world localization, in that systems that deviate from these characteristics localize poorly.

Model predictions of sound localizability

One advantage of a model that can mediate actual localization behavior is that one can run large numbers of experiments on the model, searching for “interesting” predictions that might then be tested in human listeners. Here we used the model to estimate the accuracy with which different natural sounds would be localized in realistic conditions. We chose to examine musical instrument sounds as these are both diverse and available as clean recordings in large numbers. We took a large set of instrument sounds¹⁰¹ and rendered them at a large set of randomly selected locations. We then measured the average localization error for each instrument.

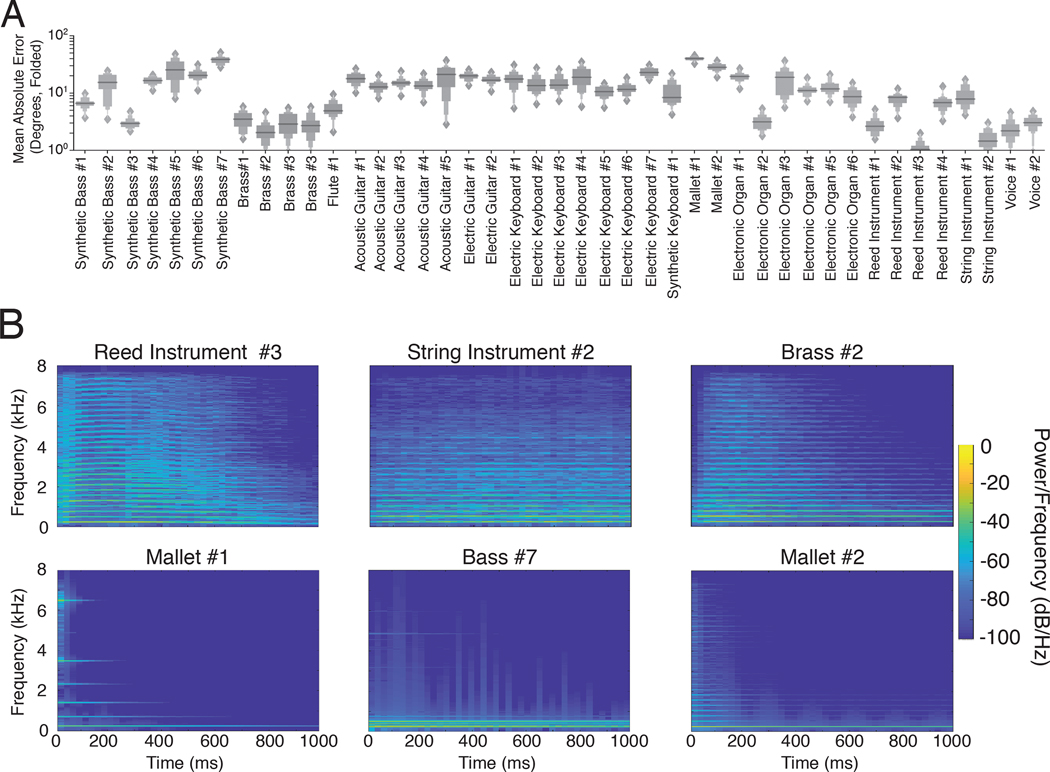
As shown in Fig. 8A, there was reliable variation in the accuracy with which instrument sounds were localized by the model. The median error was as low as 1.06 degrees for Reed Instrument #3 and as high as 40.02 degrees for Mallet #1 (folded to discount front-back confusions; without front-back folding the overall error was larger, but the ordinal relations among instruments was similar). The human voice was also among the most acurately localized sounds in the set we examined, with a mean error of 2.39 degrees (front-back folded).

Figure 8.

Model localization accuracy for musical instrument sounds. A. Mean model localization error for each of 43 musical instruments. Each of a set of instrument notes was rendered at randomly selection locations. Graph shows letter-value plots¹⁵⁷ of the mean localization error across notes, measured after actual and judged positions were front-back folded. Letter-value plots are boxplots with additional quantiles. The widest box depicts the middle two quartiles (1/4) of the data distribution, as in a box plot, the second widest box depicts the next two octiles (1/8), the third widest box depicts the next two hexadeciles (1/16), etc., up to the upper and lower 1/64 quantiles. Horizontal line plots median value and diamonds denote outliers. B. Spectrograms of example note (middle C) for the three most and least accurately localized instruments (top and bottom, respectively).

Fig. 8B displays spectrograms for example notes for the three best- and worst-localized instruments. The best-localized instruments are spectrally dense, and thus presumably take advantage of cross-frequency integration (which improve localization accuracy in both humans and the model; Fig. 3E&F). This result is consistent with the common idea that narrowband sounds are less well localized, but the model provides a quantitative metric of localizability that we would not otherwise have.

To assess whether the results could be predicted by simple measures of spectral sparsity, we measured the spectral flatness¹⁰² of each instrument sound (the ratio of the geometric mean of the power spectrum to the arithmetic mean of the power spectrum). The average spectral flatness of an instrument was significantly correlated with the model’s localization accuracy (r_s = .77, p<.001), but this correlation was well below the split-half reliability of the model’s accuracy for an instrument (r_s = .99). This difference suggests that there are sound features above and beyond spectral density that determine a sound’s localizability, and illustrates the value of an optimized system to make perceptual predictions.

We had intentions of running a free-field localization experiment in humans to test these predictions, but had to halt experiments due to COVID-19. We have hopes of running the experiment in the future. However, we note that informal observation by the authors listening in free-field conditions suggest that the sounds that are poorly localized by the model are also difficult for humans to localize.

Discussion

We trained artificial neural networks to localize sounds from binaural audio rendered in a virtual world and heard through simulated ears. When the virtual world mimicked natural auditory environments, with surface reflections, background noise, and natural sound sources, the trained networks replicated many attributes of spatial hearing found in biological organisms. These included the frequency-dependent use of interaural time and level differences, the integration of spatial information across frequency, the use of ear-specific high-frequency spectral cues to elevation and robustness to spectral smoothing of these cues, localization dominance of sound onsets, and limitations on the ability to localize multiple concurrent sources. The model successfully localized sounds in an actual real-world environment better than alternative algorithms that lacked ears. The model also made predictions about the accuracy with which different types of real-world sounds could be localized. But when the training conditions were altered to deviate from the natural environment by eliminating surface reflections, background noise, or natural sound source structure, the behavioral characteristics of the model deviated notably from human-like behavior. The results suggest that most of the key properties of mammalian spatial hearing can be understood as consequences of optimization for the task of localizing sounds in natural environments. Our approach extends classical ideal observer analysis to new domains, where provably optimal analytic solutions are difficult to attain but where supervised machine learning can nonetheless provide optimized solutions in different conditions.

The general method involves two nested levels of computational experiments: optimization of a model under particular conditions, followed by a suite of psychophysical experiments to characterize the resulting behavioral phenotype. This approach provides an additional tool with which to examine the constraints that yield biological solutions^103,104, and thus to understand evolution¹⁰⁵. It also provides a way to link experimental results with function. In some cases these links had been hypothesized but not definitively established. For example, the precedence effect was often proposed to be an adaptation to reverberation^21,92, though other functional explanations were also put forth⁹⁹. Our results suggest it is indeed an adaptation to reverberation (Fig. 7D). We similarly provide evidence that sensitivity to spectral cues to elevation emerges only with the demands of localizing somewhat broadband sounds¹⁰⁶. In other cases the model provided explanations for behavioral characteristics that previously had none. One such example is the relatively coarse spectral resolution of elevation perception (Fig. 4H–J), which evidently reflects the absence of reliable information at finer resolutions. Another is the number of sources that can be concurrently localized (Fig. 6B–C), and the dependence of localization accuracy on the number of sources (Fig. 6D–E). Without an optimized model there would be no way to ascertain whether these effects reflect intrinsic limitations of localization cues in auditory scenes or some other human-specific cognitive limit.

Prior models of sound localization required cues to be hand-coded and provided to the model by the experimenter^22–24,36. In some cases previous models were able to derive optimal encoding strategies for such cues²⁸, which could be usefully compared to neural data¹⁰⁷. In other cases models were able to make predictions of behavior in simplified conditions using idealized cues³⁶. However, the idealized cues that such models work with are not well-defined for arbitrary real-world stimuli¹⁰⁸, preventing the modeling of general localization behavior. In addition, ear-specific spectral cues to elevation (Fig. 1B, right) are not readily hand-coded, and as a result have remained largely absent from previous models. It has thus not previously been possible to derive optimal behavioral characteristics for real-world behavior.

Our results highlight the power of contemporary machine learning coupled with virtual training environments to achieve realistic behavioral competence in computational models. Supervised learning has traditionally been limited by the need for large amounts of labeled data, typically acquired via painstaking human annotation. Virtual environments allow the scientist to generate the data, with the labels coming for free (as the parameters used to generate the data), and have the potential to greatly expand the settings in which supervised learning can be used to develop models of the brain¹⁰⁹. Virtual environments also allow tests of optimality that would be impossible in biological systems, because they enable environmental conditions to be controlled, and permit optimization on rapid timescales.

Our approach is complementary to the long tradition of mechanistic modeling of sound localization. In contrast with mechanistic modeling, we do not produce specific hypotheses about underlying neural circuitry. However, the model gave rise to rich predictions of real-world behavior, and normative explanations of a large suite of perceptual phenomena. It should be possible to merge these two approaches, both by training model classes that are more faithful to biology (e.g. spiking neural networks)^110,111, and by building in additional known biological structures to the neural network (e.g. replicating brainstem circuitry)^112,113.

One limitation of our approach is that optimization of biological systems occurs in two distinct stages of evolution and development, which are not obviously mirrored in our model optimization procedure. The procedure we used had separate stages of architectural selection and weight training, but these do not cleanly map onto evolution and development in biological systems. This limitation is shared by classical ideal observers, but limits the ability to predict effects that might be specific to one stage or the other, for instance involving plasticity¹¹⁴.

Our model also shares many limitations common to current deep neural network models of the brain¹¹⁵. The learning procedure is unlikely to have much in common with biological learning, both in the extent and nature of supervision (which involves millions of explicitly labeled examples) and in the learning algorithm, which is often argued to lack biological plausibility¹¹⁰. The model class is also not fully consistent with biology, and so does not yield detailed predictions of neural circuitry. The analogies with the brain thus seem most promising at the level of behavior and representations. Our results add to growing evidence that task-optimized models can produce human-like behavior for signals that are close to the manifold of natural sounds or images^50,116,117. However, artificial neural networks also often exhibit substantial representational differences with humans, particularly for unnatural signals derived in various ways from a network^118–122, and our model may exhibit similar divergences.

We chose to train models on a fixed representation of the ear. This choice was motivated by the assumption that the evolution of the ear was influenced by many different auditory tasks, such that it may not have been strongly influenced by the particular demands of sound localization, instead primarily serving as a constraint on biological solutions to the sound localization problem¹¹⁷. However, the ear itself undoutedly reflects properties of the natural environment¹²³. It could thus be fruitful to “evolve” ears along with the rest of the auditory system, particularly in a framework with multiple tasks⁵⁰. Our cochlear model also does not replicate the fine details of cochlear physiology^124–126 due to practical constraints of limited memory resources. These differences could in principle influence the results, although the similarity of the model results to those of humans suggests that the details of peripheral physiology beyond those that we modeled do not figure critically in the behavioral traits we examined.

The virtual world we used to train our models also no doubt differs in many ways from real-world acoustic environments. The rendering assumed point sources in space, which is inaccurate for many natural sound sources. The distribution of source locations was uniform relative to the listener, and both the listener and the sound sources were static, all of which are often not true of real-world conditions. And although the simulated reverberation replicated many aspects of real-world reverberation, it probably did not perfectly replicate the statistical properties of natural environmental impulse responses¹²⁷, or their distribution across environments. Our results suggest that the virtual world approximates the actual world in many of the respects that matter for spatial hearing, but the discrepancies with the real world could make a difference for some behaviors.

We also emphasize that despite presenting our approach as an alternative to ideal observer analysis^9,10, the resulting model almost surely differs in some respects from a fully ideal observer. The solutions reached by our approach are not provably optimal like classic ideal observers, and the model class and optimization methods could impose biases on the solutions. It is also likely that the architecture search was not extensive enough to find the best architectures for the task. Those caveats aside, the similarity to human behavior, along with the strong dependence on the training conditions, provides some confidence that the optimization procedure is succeeding to a degree that is scientifically useful.

Our focus in this paper has been to study behavior, as there is a rich set of auditory localization behaviors for which normative explanations have traditionally been unavailable. However, it remains possible that the model we trained could be usefully compared to neural data. There is a large literature detailing binaural circuitry in the brainstem¹²⁸ that could be compared to the internal responses of the model. The model could also be used to probe for functional organization in the auditory cortex, for instance by predicting brain responses using features from different model stages^45–50, potentially helping to reveal hierarchical stages of localization circuitry.

A model that can predict human behavior should also have useful applications. Our model showed some transfer of localization for specific sets of ears (Fig. 4G), and could be used to make predictions about the extent to which sound rendering in virtual acoustic spaces (which may need to use a generic set of head-related transfer functions) should work for a particular listener. It can also predict which of a set of sound sources will be most compellingly localized, or worst localized (Fig. 8). Such predictions could be valuable in enabling better virtual reality, or in synthesizing signals that humans cannot pinpoint in space.

One natural extension of our model would be to incorporate moving sound sources and head movements. We modeled sound localization in static conditions because the vast majority of experimental data has been collected in this setting. But in real-world conditions sound sources often move relative to the listener, and listeners move their head^129,130, often to better disambiguate front from back⁶² and more accurately localize. Our approach could be straightforwardly expanded to moving sound sources in the virtual training environment, and a model that can learn to move its head⁴², potentially yielding explanations of auditory motion perception^131–133. The ability to train models that can localize in realistic conditions also underscores the need for additional measurements of human localization behavior – front-back confusions, localization of natural sounds in actual rooms, localization with head movements etc. – with which to further evaluate models.

Another natural next step is to instantiate both recognition and localization in the same model, potentially yielding insight into the segregation of these functions in the brain¹³⁴, and to the role of spatial cues in the ‘cocktail party problem’^135–141. More generally, the approach we take here – using deep learning to derive optimized solutions to perceptual or cognitive problems in different operating conditions – is broadly applicable to understanding the forces that shape complex, real-world, human behavior.

Methods

Training Data Generation

Virtual acoustic simulator - Image/Source method

We used a room simulator⁵¹ to render Binaural Room Impulse Responses (BRIRs). This simulator used the image-source method, which approaches an exact solution to the wave equation if the walls are assumed to be rigid⁵⁹, as well as an extension to that method that allowed for more accurate calculation of the arrival time of a wave¹⁴². This enabled the simulator to correctly render the relative timing between the signals received by the two simulated ears, including reflections (enabling both the direct sound and all reflections to be rendered with the correct spatial cues). Our specific implementation was identical to that used in the original paper⁵¹, except for some custom optimization to take advantage of vectorized operations and parallel computation.

The room simulator operated in three separate stages. First, the simulator calculated the positions of reflections of the source impulse forward in time for 0.5s. For each of these positions, the simulator placed an image symmetrically reflected about the wall of last contact. Second, the simulator accounted for the absorption spectra of the reflecting walls for each image location and filtered a broadband impulse sequentially using the absorption spectrum of the simulated wall material. Third, the simulator found the direction of arrival for each image and convolved the filtered impulse with the head-related impulse response in the recorded set whose position was closest to the computed direction. This resulted in a left and right channel signal pair for each path from the source to the listener. Lastly, each of these signal pairs was summed together, factoring in both the delay from the time of arrival and the level attenuation based on the total distance traveled by each reflection. The original authors of the simulator previously assessed this method’s validity and found that simulated BRIRs were good physical approximations to recorded BRIRs provided that sources were rendered more than one meter from the listener⁵¹.

We used this room simulator to render BRIRs at each of a set of listener locations in 5 different rooms varying in size and material (listed in Extended Data Fig. 5) for each of the source location bins in the output layer of the networks: all pairings of 7 elevations (between 0° and 60°, spaced 10°), and 72 azimuths (spaced 5° in a circle around the listener), at a distance of 1.4 meters. This yielded 504 source positions per listener location and room. Listener locations were chosen subject to three constraints. First, the listener location had to be at least 1.4 meters from the nearest wall (because sounds were rendered 1.4 meters from the listener). Second, the listener locations were located on a grid whose axes ran parallel to the walls of the room, with locations spaced 1 meter apart in each dimension. Third, the grid was centered in the room. These constraints yielded 4 listener locations for the smallest room and 81 listener locations for the largest room. This resulted in 71,064 pairs of BRIRs, each corresponding to a possible source-listener-room spatial configuration. Each BRIR took approximately 4 minutes to generate when parallelized across 16 cores. We parallelized¹⁴³ the generation of the full set of BRIRs across approximately 1000 cores on the MIT OpenMind Cluster, which allowed us to generate the full set of BRIRs in approximately 4 days.

Virtual acoustic simulator - HRIRs

The simulator relied on empirically derived Head Related Impulse Responses (HRIRs) to incorporate the effect of pinna filtering, head shadowing, and time delays without solving wave equations for the ears/head/torso. Specifically, the simulator used a set of HRIRs recorded with KEMAR – a mannequin designed to replicate the acoustic effects of head and torso filtering on auditory signals. These recordings consisted of 710 positions ranging from −40° to +90° elevation at 1.4 meters⁵³. A subset of these positions corresponded to the location bins into which the network classified source locations.

Virtual acoustic simulator - Two-microphone array

For comparison with the networks trained with simulated ears, we also trained the same neural network architectures to localize sounds using audio recorded from a two-microphone array (Extended Data Fig. 6). To train these networks, we simulated audio received from a two-microphone array by replacing each pair of HRIRs in the room simulator with a pair of fractional delay filters (i.e, that delayed the signal by a fraction of a sample). These filters consisted of 127 taps and were constructed via a sinc function windowed with a Blackman window, offset in time by the desired delay. Each pair of delay filters also incorporated signal attenuation from a distance according to the inverse square law, with the goal of replicating the acoustics of a two-microphone array. After substituting these filters for the HRIRs used in our main training procedure, we simulated a set of BRIRs as described above.

Natural sound sources

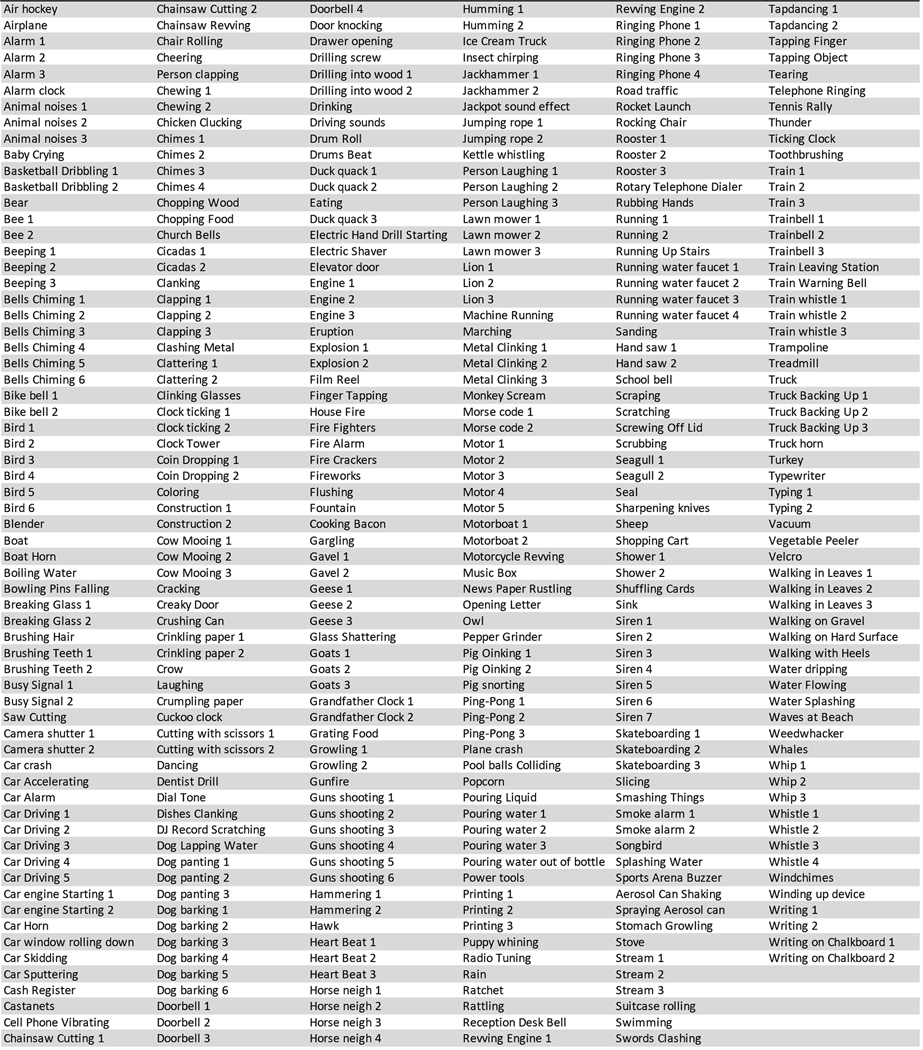
We collected a set of 455 natural sounds, each cut to two seconds in length. 300 of these sounds were drawn from a set used in previous work in the lab¹⁴⁴. Another 155 sounds were drawn from the BBC Sounds Effects Database, selected by the first author to be easily identifiable. The sounds included human and animal vocalizations, human actions (chopping, chewing, clapping, etc.), machine sounds (cars, trains vacuums, etc.), and nature sounds (thunder, insects, running water). The full list of sounds is given in Extended Data Fig. 4. All sounds were sampled at 44.1 kHz. Of this set, 385 sounds were used for training and another 70 sounds were withheld for model validation and testing. To augment the dataset, each of these was bandpass filtered with a two-octave-wide second-order Butterworth filter with center frequencies spaced in one-octave steps starting from 100 Hz. This yielded 2,492 (2,110 training, 382 testing) sound sources in total.

Background noise sources

Background noise sources were synthesized using a previously described texture generation method that produced texture excerpts rated as highly realistic⁵⁵. The specific implementation of the synthesis algorithm was that used in⁶⁰, with a sampling rate of 44.1 kHz. We used 50 different source textures obtained from in-lab collections¹⁴⁵. Textures were selected that synthesized successfully, both subjectively (sounding perceptually similar to the original texture) and objectively (the ratio between mean squared statistic values for the original texture and the mean squared error between the statistics of the synthesized and original texture was greater than 40dB SNR). We then rendered 1,000 5-second exemplars for each texture, cut to 2 seconds in length, for a total of 50,000 unique waveforms (1000 exemplars x 50 textures). Background noises were created by spatially rendering between 3 and 8 exemplars of the same texture at randomly chosen locations using the virtual acoustic simulator described above. We made this choice on grounds of ecological validity, based on the intuition that noise sources are typically not completely spatially uniform⁹⁶ despite being more diffuse than sounds made by single organisms or objects. By adding noises rendered at different locations we obtained background noise that was not as precisely localized as the target sound sources, which seemed a reasonable approximation of common real-world conditions.

Generating training exemplars

To reduce the storage footprint of the training data, we separately rendered the sound sources to be localized, and the background noise, and then randomly combined them to generate training exemplars. For each source, room, and listener location we randomly rendered each of the 504 positions with a probability $p=\frac{0.025\cdot \#oflistenerlocationsinsmallestroom}{\#oflistenerlocationsinroombeingrendered}$. We used a base probability of 2.5% to limit the overall size of the training set and normalized by the number of listener locations in the room being used to render the current stimulus so that each room was represented equally in the dataset. This yielded 545,566 spatialized natural sound source stimuli in total (497,935 training, 47,631 testing). This resulted in 988 examples per training location, on average.

For each training example, the audio from one spatialized natural sound source and one spatialized background texture scene was combined (with a signal-to-noise ratio sampled uniformly from 5 to 30 dB SNR) to create a single auditory scene that was used as a training example for the neural network. The resulting waveform was then normalized to have an rms amplitude of 0.1. Each training example was passed through the cochlear model before being fed to the neural network.

Stimulus preprocessing: Cochlear model

Training examples were pre-processed with a cochlear model to simulate the human auditory periphery. The output of the cochlear model is a time-frequency representation intended to represent the instantaneous mean firing rates in the auditory nerve. The cochlear model was chosen to approximate the time and frequency information in the human cochlea subject to practical constraints on the memory footprint of the model and the dataset. Cochleagrams were generated using a filter bank like that in previous work from our lab⁵⁵. However, the cochleagrams we used provided fine timing information to the neural network by passing rectified subbands of the signal instead of the envelopes of the subbands. This came at the cost of substantially increasing the dimensionality of the input relative to an envelope-based cochleagram. The dimensionality was nonetheless considerably lower than what would have resulted from a spiking model of the auditory nerve, which would have been prohibitive given our hardware.

The waveforms for the left and right channels were first upsampled to 48 kHz, then separately passed through a bank of 36 bandpass filters. These filters were regularly spaced on an equivalent rectangular bandwidth (ERB)_N scale⁵⁴ with bandwidths matched to those expected in a healthy human ear. Filter center frequencies ranged from 45 Hz to 16,975 Hz. Filters were zero-phase, with transfer functions in the frequency domain shaped as the positive portion of a cosine function. These filters perfectly tiled the frequency axis such that the summed squared response of all filters was flat and allowed for reconstruction of the signal in the covered frequency range. Filtering was performed by multiplication in the frequency domain, yielding a set of subbands. The subbands were then transformed with a power function (0.3 exponent) to simulate the outer hair cells’ nonlinear compression. The results were then half-wave rectified to simulate auditory nerve firing rates and were lowpass filtered with a cutoff frequency of 4 kHz to simulate the upper limit of phase-locking in the auditory nerve⁵⁶, using a Kaiser-windowed sinc function with 4097 taps. The results of the lowpass filtering were then downsampled to 8 kHz to reduce the dimensionality of the neural network input (without information loss because the Nyquist limit matched the lowpass filter cutoff frequency). Because the lowpass filtering and downsampling were applied to rectified filter outputs, the representation retained information at all audible frequencies, just with limits on fidelity that were approximately matched to those believed to be present in the ear. We note also that the input was not divided into “frames” as are common in audio engineering applications, as these do not have an obvious analogue in biological auditory systems. All operations were performed in Python but made heavy use of the NumPy and SciPy library optimization to decrease processing time. Code to generate cochleagrams in this way is available on the McDermott lab webpage (http://mcdermottlab.mit.edu).

To minimize artificial onset cues at the beginning and end of the cochleagram that would not be available to a human listener in everyday listening conditions, we removed the first and last .35 seconds of the computed cochleagram and then randomly excerpted a 1-second segment from the remaining 1.3 seconds. The neural network thus received 1s of input from the cochlear model, as a 36×8000×2 tensor (36 frequency channels × 8000 samples at 8kHz × 2 ears).

For reasons of storage and implementation efficiency, the cochlear model stage was in practice implemented as follows, taking advantage of the linearity of the filter bank. First, the audio from each spatialized natural sound source and each spatialized background texture scene was run through the cochlear filter bank. Second, we excerpted a 1-second segment from the resulting subbands as described in the previous pararaph. Third, the two sets of subbands were stored in separate data structures. Fourth, during training, the subbands for a spatialized natural sound source and a spatialized background scene were loaded, scaled to achieve the desired SNR (sampled uniformly from 5 to 30 dB), summed, and scaled to correspond to a waveform with rms amplitude of 0.1. The resulting subbands were then half-wave rectified, raised to the power of 0.3 to simulate cochlear compression, and downsampled to 8 kHz to simulate the upper limit of auditory nerve phase locking. This “cochleagram” was the input to the neural networks.

Environment Modification for Unnatural Training Conditions

In each unnatural training condition, one aspect of the training environment was modified.

Anechoic environment

All echoes and reflections in this environment were removed. This was accomplished by setting the room material parameters for the walls, floor, and ceiling to completely absorb all frequencies. This can be conceptualized as simulating a perfect anechoic chamber.

Noiseless environment

In this environment, the background noise was removed by setting the SNR of the scene to 85dB. No other changes were made.

Unnatural sound sources

In this environment, we replaced the natural sound sources with unnatural sounds consisting of repeating bandlimited noise bursts. For each 2 second sound source, we first generated a 200 ms 0.5 octave-wide noise burst with a 2 ms half-Hanning window at the onset and offset. We then repeated that noise burst separated by 200 ms of silence for the duration of the signal. The noise bursts in a given source signal always had the same center frequency. The center frequencies (the geometric mean of the upper and lower cutoffs) across the set of sounds were uniformly distributed on a log scale between 60 Hz and 16.8 kHz.

Neural Network Models

The 36×8000×2 cochleagram representation (representing 1s of binaural audio) was passed to a convolutional neural network (CNN), which instantiated a feedforward, hierarchically organized set of linear and nonlinear operations. The components of the CNNs were standard; they were chosen because they have been shown to be effective in a wide range of sensory classification tasks. In our CNNs, there were four different kinds of layers, each performing a distinct operation: (1) convolution with a set of filters, (2) a point-wise nonlinearity, (3) batch normalization, and (4) pooling. The first three types of layers always occurred in a fixed order (batch normalization, convolution, and a point-wise nonlinearity). We refer to a sequence of these three layers in this order as a “block”. Each block was followed by either another block or a pooling layer. Each network ended with either one or two fully connected layers feeding into the final classification layer. Below we define the operations of each type of layer.

Convolutional layer

A convolutional layer consists of a bank of K linear filters, each convolved with the input to produce K separate filter responses. Convolution performs the same operation at each point in the input, which in our case was the cochleagram. Convolution in time is natural for models of sensory systems as the input is a temporal sequence whose statistics are translation invariant. Convolution in frequency is less obviously natural, as translation invariance does not hold in frequency. However, approximate translation invariance holds locally in the frequency domain for many types of sound signals, and convolution in frequency is often present, implicitly or explicitly, in auditory models^146,147. Moreover, imposing convolution greatly reduces the number of parameters to be learned, and we have found that neural network models train more readily when convolution in frequency is used, suggesting that it is a useful form of model regularization.

The input to a convolutional layer is a three-dimensional array with shape (n_in,m_in,d_in) where n_in and m_in are the spectral and temporal dimensions of the input, respectively, and d_in is the number of filters. In the case of the first convolutional layer, n_in = 36 and m_in = 16,000, corresponding to the temporal and spectral dimensions of the cochleagram, and d_in = 2, corresponding to the left and right audio channels.

A convolution layer is defined by five parameters:

1. n_k: The height of the convolutional kernels (i.e., their extent in the frequency dimension)

2. m_k: The width of the convolutional kernels (i.e., their extent in the time dimension)

3. K: The number of different kernels

4. W: The kernel weights for each of the K kernels; this is an array of dimensions (n_k, m_k, d_in, K).

5. B: The bias vector, of length K

For any input array X of shape (n_in,m_in,d_in), the output of this convolutional layer is an array Y of shape (n_in,m_in - m_k +1,K) (due to the boundary handling choices described below):

$$Y[i,j,k]=B[k]+\sum _{n=-n_k/2,m=-m_k/2,d=0}^{n_k/2,m_k/2,d_{in}}W[n,m,d,k]\odot X[i+n,j+n,d]$$

where i ranges from (1, …, n_in), j ranges (1, …, m_in), ⊙ represents pointwise array multiplication.

Boundary handling via valid padding in time

There are several common choices for boundary handling during convolution operations. In order to have the output of a convolution be the same dimensionality as the input, the input signal is typically padded with zeros. This approach - often termed ‘same’ convolution – has the downside of creating an artificial onset in the data that would not be present in continuous audio in the natural world, and that might influence the behavior of the model. To avoid this possibility, we used ‘valid’ convolution in the time dimension. This type of convolution only applies the filter at positions where every element of the kernel overlaps with the actual input. This eliminates artificial onsets at the start/end of the signal but means that the output of the convolution will be slightly smaller than its input, as the filters cannot be centered over the first and last positions in the input without having part of the filter not overlap with the input data. We used ‘same’ convolution in the frequency dimension because the frequency dimension has lower and upper limits in the cochlea, such that boundary effects are less obviously inconsistent with biology. In addition, the frequency dimension was much smaller than the time dimension, such that it seemed advantageous to preserve channels at each convolution stage.

Pointwise nonlinearity

If a neural network consists of only convolution layers, it can be mathematically reduced to a single matrix operation. A nonlinearity is needed for the neural network to learn more complex functions. We used rectified linear units (a common choice in current deep neural networks) that operate pointwise on every element in the input map according to a piecewise linear function:

$$f(x)=\{\begin{array}{cc}x& x>0\\ 0& else\end{array}$$

Normalization layer

The normalization layer applied batch normalization¹⁴⁸ in a pointwise manner to the input map. Specifically, for a batch B of training examples, consisting of examples {X₁, …, X_M}, with shape (n_in,m_in,d_in), each example is normalized by the mean and variance of the batch:

$${\mu }_B[n,m,d]=\frac{1}{M}\sum _{i=0}^M{X}_i[n,m,d]{\sigma }_B^2[n,m,d]=\frac{1}{M}\sum _{i=0}^M{\left(X_i[n,m,d]-{\mu }_B[n,m,d]\right)}^2$$

$${\widehat{X}}_i[n,m,d]=\frac{X_i[n,m,d]-{\mu }_B[n,m,d]}{\sqrt[2]{{\sigma }_B^2[n,m,d]+ϵ}}$$

Where ${\widehat{X}}_i$ is the normalized three-dimensional matrix of the same shape as the input matrix and ϵ = 0.001 to prevent division by zero.

Throughout training, the batch normalization layer maintains a cumulative mean and variance across all training examples, μ_Total and ${\sigma }_{Total}^2$. At test time ${\widehat{X}}_i$ is calculated using μ_Total and ${\sigma }_{Total}^2$ in place of μ_B and ${\sigma }_B^2$.

Pooling layer

A pooling layer allows downstream layers to aggregate information across longer periods of time and wider bands of frequency. It downsamples its input by aggregating values across nearby time and frequency bins. We used max pooling, which is defined via 4 parameters:

1. p_h, the height of the pooling kernel

2. p_w, the width of the pooling kernel

3. s_h, the stride in the vertical dimension

4. s_w, the stride in the horizontal dimension

A pooling layer takes array X of shape (n_in,m_in,d_in) and returns array Y with shape (n_in/s_w,m_in/s_h,d_in) according to:

$$Y(i,j,k)=max\left(N_{p_w{p}_h}\left(X,i\cdot s_w,j\cdot s_h,k\right)\right)$$

where $N_{p_w{p}_h}(X,i,j,k)$ is a windowing function that takes a (p_w, p_h) excerpt of X of centered at (i,j) from filter k. The maximum is over all elements in the resulting excerpt.

Fully connected layer

A fully connected layer, also often called a dense layer, does not use the weight sharing found in convolutional layers, in which the same filter is applied to all positions within the input. Instead, each (input unit, output unit) pair has its own learned weight parameter and each output unit has its own bias parameter. Given input X with shape (n_in,m_in,d_in), it produces output Y with shape (n_out). It does so in two steps:

1. Flattens the input dimensions creating an input X_flat of shape (n_in · m_in · d_in)

2. Multiplies X_flat by weight and bias matrices of shape (n_out, n_in · m_in · d_in) and (n_out) respectively. This is implemented as:

$$Y\left(n_i\right)=B\left(n_i\right)+\sum _{l=1}^{n_{in}\cdot m_{in}\cdot d_{in}}W\left(n_i,l\right)X_{flat}(l);n_i\in \left\{1\dots n_{out}\right\}$$

where B(n_out) is the bias vector, W(n_out, l) is the weight matrix, and l ranges from 1 to (n_in · m_in · d_in) and indexes all positions in the flattened input matrix.

Softmax classifier

The final layer of every network was a classification layer, which consists of a fully connected layer where n_out is the number of class labels (in our case 504). The output of that fully connected layer was then passed through a normalized exponential (softmax) function. Together this was implemented as:

$$y(i)=\frac{exp\left({\sum }_{j=0}^{n_T}{w}_{ij}{x}_j\right)}{{\sum }_{k=0}^{n_{out}}exp\left({\sum }_{j=0}^{n_T}{w}_{kj}{x}_j\right)}$$

The vector y sums to 1 and all entries are greater than zero. This is often interpreted as a vector of label probabilities conditioned on the input.

Dropout during training

For each new batch of training data, dropout was applied to all fully connected layers of a network. Dropout consisted of randomly choosing 50% of the weights in the layer and temporarily setting them to zero, thus effectively not allowing the network access to the information at those positions. The other 50% of the weights were scaled up such that the expected value of the sum over all inputs was unchanged. This was implemented as:

$$dropout\left(W_{i,j}\right)=\{\begin{array}{cc}{W}_{i,j}\cdot \frac{1}{(1-.5)}& j\notin WeightstoDrop\\ 0& j\in WeightstoDrop\end{array}$$

Dropout is common in neural network training and can be viewed as a form of model averaging where exponentially many models using different subsets of the input vector are being trained simultaneously ¹⁴⁹. During evaluation, dropout was turned off (and no weight scaling was performed) so that all weights were used.

Neural Network Optimization

Architecture search - Overview

When neural networks are applied to a new problem it is common to use architectures that have previously produced good results on similar problems. However, most standard CNN architectures that operate on two-dimensional inputs have been designed for visual tasks and make assumptions based on the visual world. For example, most architectures assume that the units in the x and y dimension are equivalent, such that square filter kernels are a reasonable choice. However, in our problem the two input dimensions are not comparable (frequency vs time). Additionally, our input dimensionality is several orders of magnitude larger than standard visual stimuli (70k vs 1.1M), even though some relevant features occur on the scale of a few samples. For example, an ITD of 400 μs (a typical value) corresponds to only a 6 sample offset between channels. Given that our problem was distinct from many previous applications of standard neural network architectures, we performed an architecture search to find architectures that were well-suited to our task. First, we defined a space of architectures described by a small number of hyperparameters. Next, we defined discrete probability distributions for each hyperparameter. Lastly, we independently sampled from these hyperparameter distributions to generate architectures. We then trained each architecture for a brief period and selected the architectures that performed best on our task for further training.

Architecture search – Distribution over hyperparameters

To search over architectures we defined a space of possible architectures that were encoded via a set of hyperparameters. The space had the following constraints:

• There could be between 3 and 8 pooling layers for any given network.

• A pooling layer was preceded by between 1 and 3 blocks. Each block consisted of a batch norm, followed by a convolution, followed by a rectified linear unit.

• The number of channels (filters) in the network was always 32 in the first convolutional layer and could either double or remain the same in each successive convolutional layer.

• The penultimate stage of each network consisted of 1 or 2 fully connected layers containing 512 units each. Each of these was followed by a dropout layer.

• The final stage of each network was always a Softmax Classifier with 504 output units, corresponding to the 504 locations the network could report.

We picked the pooling and convolutional kernel parameters at each layer by uniformly sampling from the lists of values in Extended Data Fig. 2. We chose these distributions to skew toward smaller values at deeper layers, approximately in line with the downsampling that resulted from pooling operations. Multiple copies of the same number increased the probability of that value being chosen for the kernel size. Note that differences between the time and frequency dimensions of cochlear responses motivate the use of filters that are not square.

Filter weight training

Throughout training, the parameters in each convolutional kernel and all weights from fully connected layers were iteratively adjusted to improve task accuracy via Mini-Batch Stochastic Gradient Descent (SGD)¹⁵⁰. Training was performed with 1.6 million sounds (100,000 training steps each with a batch of 16 training examples) generated by looping over the 500,000 foreground sounds and combining each with a randomly selected background sound. Networks were assessed via a held-out set of 50,000 test stimuli created by looping over the 48,000 sound sources in the validation set in the same manner. We used a batch size of 16 and a Softmax Cross-Entropy loss function. The trainable weights in the convolutional layers and fully connected layers were updated using the gradient of the loss function, computed using backpropagation.

Gradient checkpointing

The dimensionality of our input is sufficiently large (due to the high sampling rates needed to preserve the fine timing information in the simulated auditory periphery) as to preclude training neural networks using standard methodology. For example, consider training a network consisting of four pooling layers (2 × 1 kernel), each preceded by one block. If there are 32 convolutional filters in the first layer, and double the number of filters in each successive layer, this network would require approximately 80GB of memory at peak usage, which exceeded the maximum memory of GPUs that were standard at the time of model training (available GPUs varied between 12GB and 32GB). We addressed this problem using a previously proposed solution called gradient checkpointing⁵².

In the standard backpropagation algorithm, we must retain the output from each layer of a network in memory because it is needed to calculate gradients for each updatable parameter. The gradient checkpointing algorithm we used trades speed for lower memory usage by not retaining each layer’s output during the forward pass, instead recomputing it a second time during the backward pass when gradients are computed. In the most extreme version, this would result in laboriously recomputing each layer starting with the original network input. Instead, the algorithm creates sparse, evenly spaced checkpoints throughout the network that save the output of selected layers. This strategy allows re-computation during backpropagation to start from one of these checkpoints, saving compute time. In practice, it also provides users with a parameter that allows them to select a speed/memory tradeoff that will maximize speed subject to a network fitting onto the available GPU. We created checkpoints at every pooling layer and found it kept our memory utilization below the 16GB limit of the hardware we used for all networks in the architecture search.

Network architecture selection and training

We performed our architecture search on the Department of Energy’s Summit Supercomputer at Oak Ridge National Laboratory. First, we randomly drew 1,500 architectures from our hyperparameter distribution. Next, we trained each architecture (i.e., optimized the weights of the convolutional and fully connected layers) using Mini-Batch Stochastic Gradient Descent for 15,000 steps, each with a batch size of 16, for a total of 240,000 unique training examples, randomly drawn from the training set described above. We then evaluated the performance of each architecture on left-out data. This length of this training period was determined by the job limits on Summit; however, it was long enough to see significant reductions in the loss function for many networks. We considered the procedure adequate for architecture selection given that performance early in training is a good predictor of training performance late in training¹⁵¹. In total, this architecture search took 2.05 GPU years and 45.2 CPU years.

We selected the ten best-performing architectures. They varied significantly, ranging from 4 to 6 pooling layers. We then retrained these 10 architectures until a point where performance on the withheld validation set began to decrease, evaluating every 25,000 iterations. This occurred at 100,000 iterations for the naturalistic, anechoic, and noiseless training conditions and at 150,000 iterations for the unnatural sounds training condition. Model architectures and the trained weights for each model are available online in the associated codebase: www.github.com/afrancl/BinauralLocalizationCNN.

Real-World Evaluation

We tested the model in real-world conditions to verify generalization from the virtual training environment. We created a series of spatial recordings in an actual conference room (part of our lab space, with dimensions distinct from the rooms in our virtual training environment) and then presented those to the trained networks. We also made recordings of the same source sounds and environment with a two-microphone array to test the importance of naturally induced binaural cues (from the ears/head/torso).

Sound sources

We used 100 sound sources in total. 50 sound sources were from our validation set of withheld environmental sounds, and the remaining 50 sound sources were taken from the GRID dataset of spoken sentences¹⁵². For the examples from the GRID dataset, we used 5 sentences from each of 10 speakers (5 male and 5 female). The model performed similarly for stimuli from the GRID dataset as for our validation set stimuli. All source signals were normalized to the same peak amplitude before the recordings were made.

Recording setup

We made the set of real-world evaluation recordings using a KEMAR head and torso simulator mannequin built by Knowles Electronics to replicate the shape and absorbency of a human head, upper body, and pinna. The KEMAR mannequin contains a microphone in each ear, recording audio similar to that which a human would hear in natural conditions. The audio from these microphones was then passed through Etymotic Research preamplifiers designed for the KEMAR mannequin before being passed to the Zoom 8 USB to Audio Converter. Finally, it was passed to Audacity where the left and right channels were simultaneously recorded at 48kHz.

We made recordings of all 100 sounds at every azimuth (relative to the KEMAR mannequin) from 0° to 360° in 30° increments. This led to 1,200 recordings in total. All source sounds were played 1.5 meters from the vertical axis of the mannequin using a KRK ROKIT 7 speaker positioned at approximately 0° elevation. The audio was played using Audacity and converted to an analogue signal using a Zoom 8 USB to Audio Converter.

Recordings were made in our main lab space in building 46 on the MIT campus, which is roughly 7×6×3 meters. The room is filled with furniture, shelves and has multiple windows and doors (Fig. 1E). This setup was substantially different from any of the simulated rooms in the virtual training environment, in which all rooms were convex, empty, and had smooth walls. During the recordings, there was low-level background noise from the HVAC system, the refrigerator, and lab members talking in surrounding offices. For all recordings, the mannequin was seated in an office chair, with the head approximately 1 meter from the ground.

Two-microphone array baseline

We made a second set of recordings using the same sound sources, room, and recording equipment as above, but with the KEMAR mannequin replaced with a 2-microphone array consisting of two Beyerdynamic MM-1 Omnidirectional Microphones separated by 15cm (the same distance separating the two microphones in the mannequin ears). The microphone array was also elevated approximately 1 meter from the floor using a microphone stand (Extended Data Fig. 6A).

Baseline algorithms

We evaluated our trained neural networks against a variety of baseline algorithms. These comprised: Steered-Response Power Phase Transform (SRP)⁶⁵, Multiple Signal Classification (MUSIC)⁶⁴, Coherent Signal-Subspace Method (CSSM)⁶³, Weighted Average of Signal Subspaces (WAVES)⁶⁶, Test of Orthogonality of Projected Subspaces (TOPS)⁶⁷, and the WavLoc Neural Network⁶⁸. With the exception of the WavLoc model, in each case we used the previously validated and published algorithm implementations in Pyroomacoustics¹⁵³. For the WavLoc model, we used a reference GitHub implementation and confirmed that we could reproduce the results of the original paper⁶⁸ before testing with our KEMAR mannequin recordings. We also created a baseline model trained using a simulation of the two-microphone array described in the previous section within the virtual training environment (the same 10 neural network architectures used for our primary model were trained to localize sounds using audio recorded from simulated a two-microphone array).

The results shown in Extended Data Fig. 6B&C for the baselines (aside from our two-microphone array baseline neural network model) all plot localization of the KEMAR mannequin recordings. We found empirically that the baseline methods performed better for the KEMAR recordings than for the two-microphone array recordings, presumably because the mannequin head increases the effective distance between the microphones. The baseline algorithms require prior knowledge of the inter-microphone distance. In order to make the baselines as strong as possible relative to our method, we searched over all distances less than 50cm and found that an assumed distance of 26cm yielded the best performance. We then evaluated the baselines at that assumed distance. This optimal assumed distance is greater than the actual inter-microphone distance of 15cm, consistent with the idea that the mannequin head increases the effective distance between microphones.

Comparison with human listeners

To provide an example of free-field human sound localization, Fig. 1F plots the results of an experiment by Yost and colleagues¹⁵⁴. In that experiment, humans were presented with noise bursts (lowpass filtered white noise with a cutoff of 6 kHz, 200ms in duration, with 20ms cosine onset and offset ramps) played from one of 11 speakers in an anechoic chamber. The speakers were spaced every 15 degrees, with the array centered on the midline. Speakers were visible to participants. Participants indicated the speaker from which the sound was played by entering a number corresponding to the speaker. Results are shown for 45 participants (34 female), ages 21–49. Because the human experiment was restricted to speakers in front of the participants, for ease of comparison Fig. 1G plots model results after front-back folding of actual and judged positions (Fig. 1H shows model results without front-back folding). Fig. 1F–1H display kernel density estimates of the response distributions, generated using the seaborn statistical data visualization library.

Psychophysical Evaluation of Model

Overview

We simulated a suite of classic psychoacoustic experiments on the 10 trained neural networks, using the same stimuli for each network. We then calculated the mean response across networks for each experimental condition and calculated error bars by bootstrapping across the 10 networks. This approach can be interpreted as marginalizing out uncertainty over architectures in a situation in which there is no single obviously optimal architecture (and where the space of architectures is so large that it is probably not possible to find the optimum even if it exists). Moreover, recent work suggests that internal representations across different networks trained on the same task can vary considerably⁵⁷, so this approach aided in mitigating the individual idiosyncrasies of any given network. The approach could also be viewed as treating every network as an individual experimental participant, calculating means and error bars as one would in a standard human psychophysics experiment.

In each experiment, stimuli were run through our cochlear model and passed to each of the networks, whose localization responses were recorded for each stimulus. Stimuli were generated as 2s sound signals, normalized to have an rms amplitude of 0.1. The output of the cochlear model was then cropped to 1s (by excerpting the middle 1s), which provided the input to the networks.

Front-back folding

For experiments in which human participants judged locations within the frontal hemifield, we front-back folded the model responses to enable a fair comparison. This consisted of treating each model response in the rear hemifield as though it was a response in the corresponding front hemifield. For example, the 10° and 170° azimuthal positions were considered equivalent.

Sensitivity to interaural time and level differences – Stimuli

We reproduced the experimental stimuli from⁶⁹, in which ITDs and ILDs were added to 3D spatially rendered sounds. In the original experiment, participants stood in a dark anechoic room and were played spatially rendered stimuli with modified ITDs or ILDs via a set of headphones. After each stimulus presentation, participants oriented their head towards the perceived location of the stimulus and pressed a button. The experiment included 13 participants (5 male) ranging in age from 18–35 years old.

Stimulus generation for the model experiment was identical to that in the original experiments apart from using our acoustic simulator to render the sounds. First, we generated highpass and lowpass noise bursts with passbands of 4–16 kHz and 0.5–2 kHz, respectively (44.1 kHz sampling rate). Each noise burst was 100 ms long with a 1 ms squared-cosine ramp at the beginning and end of the stimulus. We randomly jittered the starting time of the noise burst by padding the signal to 2,000 ms in total length, constrained such that the entire noise burst was contained in the middle second of the 2s audio signal (the noise onset was uniformly distributed subject to this constraint). These signals were then rendered at 0° elevation, with azimuth varied from 0°−355° (in 5° steps) for a total of 72 locations. All signals were rendered using our virtual acoustic simulator in an anechoic environment without any background noise.

Next, we created versions of each signal with an added ITD or ILD bias. ITD biases were ±300 μs and ±600 μs and ILD biases were ±10 dB and ±20 dB (Fig. 2A). As in the original publication⁶⁹, we prevented presentation of stimuli outside the physiological range by restricting the 400μs/10dB biases to signals rendered less than 40° away from the midline and restricting the 600μs/20dB biases to signals rendered less than 20° away from the midline. In total there were 4 stimulus sets (2 passbands x 2 types of bias) of 266 stimuli (72 locations with no bias, 52 locations at ± medium bias, 45 locations ± large bias). We replicated the above process 20 times with different exemplars of bandpass noise, increasing each stimulus set size to 5,320 (20 exemplars of 266 stimuli).

Sensitivity to interaural time and level differences – Analysis

We measured the perceptual bias induced by the added ITD or ILD bias in the same manner as the published analysis of human listeners⁶⁹.

We first calculated the naturally-occurring ITD and ILD for each sound source position (varying in azimuth, at 0° elevation) from the HRTFs used to train our networks. For ITDs, we ran the HRTFs for a source position through our cochlear model and found the ITD by cross-correlating the cochlear channels whose center frequency was closest to 600, 700, and 800 Hz and taking the median ITD from the three channels. For ILDs, we computed power spectral density estimates via Welch’s method (29 samples per window, 50% overlap, Hamming windowed) for each of the two HRTFs for a source position and integrated across frequencies in the stimulus passband. We expressed the ILD as the ratio between the energy in the left and right channel in decibels, with positive values corresponding to more power in the right ear. This set of natural ILDs and ITDs allowed us to map the judged position onto a corresponding ITD/ILD.

For each stimulus with added ITD, we used the response mapping described above to calculate the ITD of the judged source position. Next, we calculated the ITD for the judged position of the unaltered stimulus using the same response mapping. The perceptual effect of the added ITD was calculated as the difference between these two ITD values, quantifying (in microseconds) how much the added stimulus bias changed the response of the model. The results graphs plot the added stimulus bias on the x-axis and the resulting response bias on the y-axis. The slope of the best-fitting regression line (the ‘Bias Weight’ shown in the subplots of Fig. 2 C&D) provides a unitless measure of the extent to which the added bias affects the judged position. We repeated an analogous process for ILD bias using the natural ILD response mapping, yielding the bias in decibels. The graphs in Fig. 2D plot the mean response across the 10 networks with standard error of the mean (SEM) computed via bootstrap over networks.

Azimuthal localization of broadband sounds – Stimuli

We reproduced the stimulus generation from⁸⁰. In the original experiment, participants were played 6 broadband white noise bursts, with 3 bursts (15 ms in duration, 5ms cosine ramps, repeated at 10 Hz) played from a reference speaker followed by 3 noise bursts played from one of two target speakers, located 15° to the left or right of the reference speaker. Participants reported whether the latter 3 noise bursts were played to the left or the right of the reference speaker, and performance was expressed as d’. The experiment included 16 participants between the ages of 18 and 35 years old.

We measured network localization performance using the same stimuli as in the original paper, but for simplicity rendered the stimulus at a single location and measured performance with an absolute, instead of relative, localization task. The stimuli presented to the networks consisted of 3 pulses of broadband white noise. Each noise pulse was 15 ms in duration and the delay between pulses was 100 ms. A 5 ms cosine ramp was applied to the beginning and end of each pulse. We generated 100 exemplars of this stimulus using different samples of white noise (44.1 kHz sampling rate). The stimuli were zero-padded to 2,000 ms in length, with the temporal offset of the three-burst sequence randomly sampled from a uniform distribution such that all three noise bursts were fully contained in the middle second of audio. We then rendered all 100 stimuli at 0° elevation and azimuthal positions ranging from 0° to 355° in 5° steps. All stimuli were rendered in an anechoic environment without any background noise using our virtual acoustic simulator. This led to 7,200 stimuli in total (100 exemplars at each of 72 locations).

Azimuthal localization of broadband sounds – Analysis

Because human participants in the analogous experiment judged relative position in the frontal hemifield, prior to calculating the model’s accuracy we eliminated front-back confusions by mirroring model responses of each stimulus across the coronal plane. We then calculated the difference in degrees between the rendered azimuthal position and the position judged by the model. We calculated the mean error for each rendered azimuth for each network. The graph in Fig. 3C plots the mean error across networks. Error bars are SEM, bootstrapped over networks.

Integration across frequency – Stimuli

We reproduced stimuli from⁸². In the original experiment, human participants were played a single noise burst, varying in bandwidth and center frequency, from one of 8 speakers spaced 15° in azimuth. Participants judged which speaker the noise burst was played from. The experimenters then calculated the localization error in degrees for each bandwidth and center frequency condition. The experiment included 33 participants (26 female) between the ages of 18 and 36 years old.

The stimuli varied in bandwidth (pure tones, and noise bursts with bandwidths of ½0, 1/10, 1/6, 1/3, 1, and 2 octaves wide; all with 44.1 kHz sampling rate). All sounds were 200 ms long with a 20 ms squared-cosine ramp at the beginning and end of the sound. All pure tones had random phase. All other sounds were bandpass-filtered white noise with the geometric mean of the passband cutoffs set to 250, 2,000, or 4,000 Hz (as in the original paper⁸²).

For the model experiment, the stimuli were zero-padded to 2000ms in length, with the temporal offset of the noise burst randomly sampled from a uniform distribution such that the noise burst was fully contained in the middle second of audio. We generated 30 exemplars of each bandwidth/frequency pair using different exemplars of white noise (or of random phase for the pure tone stimuli). Next, we rendered all stimuli at 0° elevation and azimuthal positions ranging from 0° to 355° in 5° steps. All stimuli were rendered in an anechoic environment without any background noise using our virtual acoustic simulator. This led to 45,360 stimuli in total (30 exemplars x 72 positions x 3 center frequencies x 7 bandwidths).

Integration across frequency – Analysis

Because human participants in the original experiment judged position in the frontal hemifield, prior to calculating the model’s accuracy we again eliminated front-back confusions by mirroring model responses of each stimulus across the coronal plane. We then calculated the difference in degrees between the rendered azimuthal position and the azimuthal position judged by the model. For each network, we calculated the root-mean-squared error for each bandwidth. The graph in Fig. 3F plots the mean of this quantity across networks. Error bars are SEM, bootstrapped over networks.

Use of ear-specific cues to elevation – Stimuli

We simulated a change of ears for our networks, analogous to the ear mold manipulation in⁸⁴). In the original experiment⁸⁴, participants sat in a dark anechoic room and were played broadband white noise bursts from a speaker on a robotic arm that moved ±30° in azimuth and elevation. Participants reported the location of each noise burst by saccading to the perceived location. After collecting a baseline set of measurements, participants were fitted with plastic ear molds (Fig. 4A), which modified the location-dependent filtering of their pinnae, and performed the same localization task a second time. The experimenters plotted the mean judged location for each actual location before and after fitting subjects with the plastic ear molds (Fig. 4B&C). The experiment included 4 participants between the ages of 22 and 44 years old.

For the model experiment, instead of ear molds we substituted HRTFs from the CIPIC dataset¹⁵⁵. The CIPIC dataset contains 45 sets of HRTFs, each of which is sampled at azimuths from −80 to +80 in 25 steps of varying size, and elevations from 0 to 360 in 50 steps of varying size. For the sound sources to be localized, we generated 500 ms broadband (0.2–20 kHz) noise bursts sampled at 44.1 kHz (as in⁸⁴). We then zero-padded these sounds to 2,000 ms, with the temporal offset of the noise burst randomly sampled from a uniform distribution such that it was fully contained in the middle second of audio. We generated 20 such exemplars using different samples of white noise. We then rendered each stimulus at ±20 and ±10° azimuths and 0°, 10°, 20°, and 30° elevation for all 45 sets of HRTFs as well as the standard set of HRTFs (i.e., the one used for training the model). This led to a total of 14,720 stimuli (46 HRTFs x 4 azimuths x 4 elevations). The rendered locations were slightly different from those used in⁸⁴ as we were constrained by the locations that were measured for the CIPIC dataset.

Use of ear-specific cues to elevation – Analysis

The results graphs for this experiment (Fig. 4B–E) plot the judged source position for each of a set of rendered source positions, either for humans (Fig. 4B&C) or the model (Fig. 4D&E). For the model results, we first calculated the mean judged position for each network for all stimuli rendered at each source position. The graphs plot the mean of this quantity across networks. Error bars are the SEM, bootstrapped over networks. In Fig. 4D we plot model responses for stimuli rendered using the HRTFs used during network training. In Fig. 4E we plot the average model responses for stimuli rendered with 45 sets of HRTFs from the CIPIC database (none of which were used during network training). In Figs. 4F&G we plot the results separately for each alternative set of HRTFs, averaged across elevation or azimuth. The thickest bolded line denotes the mean performance across all HRTFs, and thinner bolded lines denote HRTFs at the 5^th, 25^th, 75^th, and 95^th percentiles order by error. Each line plots the mean over the 10 networks.

Limited spectral resolution of elevation cues – Stimuli

We ran a modified version of the spectral smoothing experiment in⁸⁶ on our model using the training HRTFs. The original experiment⁸⁶ measured the effect of spectral detail on human sound localization. The experimenters first measured HRTFs for 4 participants. Participants then sat in an anechoic chamber and were played broadband white noise bursts presented in one of two ways. The noise burst was either played directly from a speaker in the room or virtually rendered at the position of the speaker using the participant’s HRTF and played from a set of open-backed earphones worn by the participant. The experimenters manipulated the spectral detail of the HRTFs as described below. On each trial, two noise bursts (one for each of the two presentation methods) were played in random order and participants judged which of the two noise bursts were played via earphones. In practice, this judgment was performed by noticing changes in the apparent sound position that occurred when the HRTFs were sufficiently degraded. The results of the experiment were expressed as the accuracy in discriminating between the two modes of presentation as a function of the amount of spectral detail removed (Fig. 4I). The experiment included 4 participants.

The HRTF is obtained from the Fourier transform of the head-related impulse response (HRIR), and thus can be expressed as:

$$H[k]=\sum _{n=0}^{N-1}{x}_n\cdot e^{-\frac{i2\pi nk}{N}}$$

where x is the head-related impulse response, N is the number of samples in the HRTF, and k = [0,N-1]. To smooth the HRTF, we first compute the log-magnitude of H[k]. This log-magnitude HRTF can be decomposed into frequency components via the discrete cosine transform:

$$\log |H[k]|=\sum _{n=0}^{M}C(n)cos(2\pi nk/N)$$

where C(n) is the nth cosine coefficient of log|H[k]| and M = N/2.

As in the original experiment⁸⁶, we smoothed the HRTF by reconstructing it with M < N/2. In the most extreme case where M=0, the magnitude spectrum was perfectly flat at the average value of the HRTF. Increasing M increases the number of cosines used for reconstruction, leading to more spectral detail (Fig. 4H). After smoothing, we calculated the minimum phase filter from the smoothed magnitude spectrum, adding a frequency-independent time delay consistent with the original HRIR. Our HRIRs consisted of 512 time points, corresponding to a maximum of 256 points in its cosine series.

We repeated this smoothing process for each left and right HRTF at each spatial position. We then generated 20 exemplars of broadband white noise (0.2–20kHz, 2000 ms length) with a 10 ms cosine ramp at the beginning and end of the signal. Each exemplar was rendered at 0° elevation and azimuthal positions ranging from 0° to 355° in 5° steps using each smoothed set of HRTFs. This yielded 12,960 stimuli (9 smoothed sets of HRTFS × 20 exemplars × 72 locations).

Limited spectral resolution of elevation cues – Analysis

For the model, the effect of the smoothing was measured as the average absolute difference in degrees between the judged position and the rendered position for each stimulus. Fig. 4J plots the mean error across networks for each smoothed set of HRTFs. Error bars are SEM, bootstrapped over networks. Figs. 4K&L plot the mean judged azimuth (left) and elevation (right) vs. the actual rendered azimuth and elevation, plotted separately for each smoothing level. Each line is the mean response pooled across networks. Error bars are shown as bands around the line and show SEM, bootstrapped over networks.

Dependence on high-frequency spectral cues to elevation – Stimuli

In the original experiment⁹⁰, human participants were played high-pass and low-pass noise bursts. The high-pass cutoff frequencies took on one of six values: 3.8, 5.8, 7.5, 10.0, 13.2, and 15.3kHz; low-pass cutoff frequencies took on one of seven values: 3.9, 6.0, 8.0, 10.3, 12.0,14.5, and 16.0 kHz (imposed with an analogue Cauer-Chebychev filter). The sampling rate was 44.1 kHz. Each noise burst was 1000 ms in duration, with a 5 ms squared-cosine ramp at the beginning and end. Each stimulus was presented from one of 9 speakers spaced along the midline at 30° increments in elevation from −30° to 210°, with 0° being frontal horizontal. Participants judged which speaker the noise burst was played from, indicating their judgment with a keypress. The results graph (Fig. 4N) plots the proportion correct for each condition (error bars were not plotted in the original publication, and the raw data were no longer available). The experiment included 10 participants.

Stimuli for the model experiment were similar to those from the human experiment apart from being presented from a subset of elevations used in the human experiment due to the constraints of the HRTF set in the model. We generated 50 exemplars of each cutoff frequency used in the human experiment, each with a different exemplar of white noise. Filtering was performed in the frequency domain by setting Fourier coefficients beyond the cutoff to zero. We then rendered all 650 noise bursts at one of 6 locations along the midline: 0°, 30°, 60°, 120°, 150°, and 180°, with 0° being frontal horizontal. This led to 3,900 stimuli in total (650 noise bursts at each of 6 locations). All stimuli were rendered in an anechoic environment without any background noise using our virtual acoustic simulator.

Dependence on high-frequency spectral cues to elevation – Analysis

We determined the model’s response in the experiment to be the elevation in the stimulus set that was closest to the elevation of the softmax class bin with the maximum activation. Fig. 4O plots the proportion of correct responses for each high-pass and low-pass cutoff frequency, averaged across the 10 networks. Error bars are SEM, bootstrapped over networks.

Precedence effect – Stimuli

For the basic demo of the precedence effect (Fig. 5B) we generated a click consisting of a single sample at +1 surrounded by zeros. We then rendered that click at ±45 azimuth and 0° elevation in an anechoic room without background noise using our virtual acoustic simulator. We added these two rendered signals together, temporally offsetting the −45° click behind the 45° click by an amount ranging from 1 to 50 ms. We then zero-padded the signal to 2000 ms, sampled at 44.1 kHz, and randomly varied the temporal offset of the click sequence, constrained such that all nonzero samples occurred in the middle second of the stimulus. For each delay value, we created 100 exemplars with different start times.

To quantitatively compare the precedence effect in our model with that in human participants, we reproduced the stimuli from⁹⁵. In the original experiment, participants were played two broadband pink noise bursts from two different locations. The leading noise burst came from one of 6 locations (±20°, ±40°, or ±60°) and the lagging noise burst came from 0°. The lagging noise burst was delayed relative to the leading noise burst by 5, 10, 25, 50, or 100 ms. For each pair of noise bursts, participants reported whether they perceived one or two sounds and the judged location for each perceived sound. The experimenters then calculated the mean localization error separately for the leading and lagging click for each time delay (Fig. 5C). The experiment included 10 participants (all female) between the ages of 19 and 26 years old.

For both the human and model experiments, stimuli were 25 ms pink noise bursts, sampled at 44.1kHz, with a 2 ms cosine ramp at the beginning and end of the burst. For the model experiment, we generated two stimuli for each pair of noise burst positions, one where the 0° noise burst was the lead click and another where it was the lag click. For each delay value, location and burst order, we created 100 exemplars with different start times. This was achieved by zero-padding the signal to 2000 ms and randomly varying the temporal offset, constrained such that all nonzero samples occurred in the middle second of the stimulus.

Precedence effect – Analysis

Because human experiments on the precedence effect typically query participants about positions in the frontal hemifield, we corrected for front-back confusions in the analysis of both the precedence effect demo and the Litovsky and Godar experiment by mirroring model responses of each stimulus across the coronal plane. Fig. 5B plots the mean judged position at each inter-click delay, averaged across the means of the 10 individual networks. Error bars are SEM, bootstrapped over networks.

To generate Fig. 5D (plotting the results of the model version of the Litovsky and Godar experiment) we calculated errors for each stimulus between the model’s judged position and the positions of the leading and lagging clicks. We calculated the average lead click error and average lag click error for each network at each delay. Fig. 5D plots the mean across the mean error for each network. Error bars are SEM, bootstrapped over networks.

Multi-source localization – Stimuli

We reproduced stimuli from the original experiment⁹⁸, in which human participants were played between 1 and 8 concurrent speech stimuli. Each stimulus was played from a different location (out of 12 possible, evenly spaced in azimuth). Participants judged the number of stimuli as well as the locations at which stimuli were presented in each trial. The experimenters then plotted the mean number of sources perceived versus the actual number of sources presented (Fig. 6B) and localization accuracy (proportion correct) versus the number of sources presented (Fig. 6D). The experiment included 8 normal-hearing participants.

Stimuli were 10 seconds in duration and consisted of a concatenation of 10 1-second recordings of a person saying the name of a country (randomly drawn without replacement from a list of 24 countries). Each stimulus used recordings from a single talker (out of 12 possible talkers; 6 female). Each stimulus was presented from one of 12 speakers at 0° elevation, spaced 30° apart in azimuth (Fig. 6A). On each trial, between 1 and 8 stimuli were simultaneously presented, each spoken by a different talker and presented from a different speaker.

The model experiment used the same 1-second recordings used in the original experiment (kindly provided by Bill Yost), but presented a single 1-second recording (of a speaker saying a single country name, rather than the sequence of 10 such recordings used in the human experiment) at each location, to accommodate the 1-second input length of the model. For each number of sources (1 to 8) we computed each possible spatial source configuration and rendered 20 scenes for each configuration, randomly sampling talkers and country names for each trial (without replacement). All stimuli were rendered in an anechoic environment without any background noise using the virtual acoustic simulator. This led to 75,920 stimuli in total (20 exemplars in each of 3796 spatial configurations).

Multi-source localization – Output layer fine-tuning

To enable the model to perform the multi-source localization experiment, we altered the softmax output layer, which was designed to report one source at a time. We replaced the softmax function with independent sigmoid functions for each output unit. This allowed the model to independently report the probability of a source at each location. To allow our model to use this new output representation, we retrained this new final model stage. We froze all weights in each network except for those in the final fully-connected layer, which we then trained using gradient descent for 10,000 steps (“fine-tuning”). The fine-tuning used a dataset consisting of auditory scenes generated and rendered in the same manner as the original training data (as described in Training Data Generation above), with two exceptions. First, each scene contained between 1 to 8 natural sounds, each rendered at a different location. Second, the scenes did not contain background noise. This process was repeated for each network to allow the model to utilize its features on the multi-source localization task.

To measure accuracy after fine-tuning, we created a multi-source validation set using the natural sounds from the main model validation set. We measured the area under the curve (AUC) for the receiver operator characteristic (ROC) curve over the entire multi-source validation set. The average AUC across fine-tuned networks after fine-tuning was 0.73.

Multi-source localization – Analysis

The output layer of the multi-source model contained a unit for each location, like the main single-source localization model, but differed in that the unit activation represented the judged probability that a source was present at that location. To enable the model to perform the multi-source experiment, we implemented a decision rule whereby the model would determine a source to be present at a location if the probability for that location exceeded a criterion. We set this criterion such that the model would correctly estimate the number of sources when a single source was present. We found empirically that the absolute activations resulting from the sigmoid output units varied considerably across sounds, presumably because the networks were trained with a softmax output layer that normalizes the output activations (which was no longer present in the multi-source decision layer). We thus adopted a criterion that was a proportion of the maximum probability across all output units, and found that this yielded results that were stable across stimuli. Using all the experiment stimuli containing one source, we successively lowered the criterion from 1, each time running through the full set of scenes and estimating confidence intervals on the average predicted number of sources, until the 95% confidence interval for the predicted number of sources (after front-back folding) included 1. This yielded a decision criterion of .09 times the maximum probability across all output unit activations for the stimulus.

To perform a trial in the experiment, we first selected the model’s location bins whose probability exceeded the criterion of .09 times the maximum proability across all output unit activations for the stimulus. We then mapped these locations to the 12 possible speaker locations in the experiment (for each output location bin, we selected the speaker location closest in azimuth). The number of sources was calculated as the number of these 12 speaker locations to which a localized source was mapped (Fig. 6C). The proportion correct was calculated as the hit rate – the fraction of the 12 speaker locations at which the model correctly judged there to be a source (Fig. 6E).

Evaluation of Models Trained in Unnatural Conditions

Once trained, each alternative model was run on each of the psychophysical experiments. The exception was the multi-source localization experiment, which was omitted because it was not clear how to incorporate the background noise training manipulation into the fine-tuning of the model output layer. The psychophysical experiments were identical for all training conditions.

Analysis of Results of Unnatural Training Conditions

Human-model dissimilarity

We assessed the effect of training condition on model behavior by quantifying the extent of the dissimilarity between the model psychophysical results and the human results. For each results graph, we measured human-model dissimilarity as the root-mean-squared error between corresponding y-axis values in the human and model experiments. In order to compare results between experiments, before measuring this error, we min-max normalized the y-axis to range from 0 to 1. For experiments with the same y-axis for human and model results, we normalized the model and human data together (i.e., taking the min and max values from the pooled results). For experiments where the y-axes were different for human and model results (because the tasks were different, as in Figs. 3B&C and 4I&J), we normalized the data individually for human and model results.

The one exception was the Ear Alteration experiment (Fig. 4A–G), in which the result of primary interest was the change in judged location relative to the rendered location, and for which the locations were different in the human and model experiments (due to constraints of the HRTF sets that we used). To measure the human-model dissimilarity for this experiment, we calculated the error between the judged and rendered location for each point on the graph, for humans and the model. We then calculated human-model dissimilarity between these error values, treating the two grids of locations as equivalent. This approach would fail to capture some patterns of errors but was sufficient to capture the main effects of preserved azimuthal localization along with the collapse of elevation localization.

This procedure yielded a dissimilarity measure that varied between 0 and 1 for each experiment, where 0 represents a perfect fit to the human results. For Fig. 7B, we then calculated the mean of this dissimilarity measure over the seven experiments. To generate error bars, we bootstrapped across the 10 networks and recalculated all results graphs and the corresponding mean normalized error for each bootstrap sample. Error bars in Fig. 7B plot the SEM of this distribution. Additionally, we plotted the mean normalized error individually for each of the 10 networks (Extended Data Fig. 7).

Between-human dissimilarity

The dissimilarity that would result between different samples of human participants puts a lower bound on model-human dissimilarity, and would thus be useful to compare to the dissimilarity plotted in Fig. 7B. This between-human dissimilarity could be estimated using data from the original individual human participants. Unfortunately, the individual participant data was unavailable for nearly all of the experiments that we modeled, many of which were conducted several decades ago. Instead, we used the error bars in the published results figures to simulate different samples of human participants given the variability observed in the original experiments. Error bars were provided for only some of the original experiments (the exceptions being the experiments in Figs. 2 and 4N), so we were only able to estimate the between-human dissimilarity for this subset. We then compared the estimated between-human dissimilarity to the model-human dissimilarity for the same subset of experiments (Extended Data Fig. 8).

We assumed that human data for each experimental condition were independently normally distributed with a mean and variance given by the mean and error bars for that condition. Depending on the experiment, the error bars in the original graphs plotted the standard deviation, the standard error of the mean (SEM), or the 95% confidence interval of the data. In each case we estimated the variance from the mean of the upper and lower error bar (for SD: the square of the error bar; for SEM:$variance={(\sqrt{N}\times SEM)}^2$; for 95% CI:$variance={(\sqrt{N}\times (errorbarwidth)/1.96)}^2$, where N is the number of participants). To obtain behavioral data for one simulated human participant, we sampled from the Gaussian distribution for each condition. We sampled data for the number of participants run in the original experiment, and obtained mean results for this set of simulated participants. We then calculated the root-mean-squared error (described in previous section) between the simulated human data and actual human data (normalized as described in the previous section for the human-model dissimilarity). We repeated this process 10,000 times for each experiment, yielding a distribution of dissimilarities for each experiment. We then calculated the mean dissimilarity across experiments and samples. Extended Data Fig. 8 plots this estimated between-human dissimilarity (with confidence intervals obtained from the distribution of between-human dissimilarity) alongside the human-model dissimilarity for the same subset of experiments.

Models with internal noise

To test for the possibility that the noiseless training environments might have had effects that were specific to the lack of internal noise in the cochlear model used as input to our networks, we trained an alternative model with internal noise added to the output of the cochlear stage. This alternative model was identical to the main model used throughout the paper except that independent Gaussian noise was added to each frequency channel prior to the rectification stage of the cochlear model. The noise was sampled from a standard normal distribution and then scaled so that its power was on average 60.6 dB below the average power in the subbands of the input signal (intended to produce noise at 9.4 dB SPL assuming sources at 70 dB SPL¹⁵⁶). In practice we pre-generated 50,000 noise arrays, sampled one at random on each trial, and added it to the output of the cochlear filters at the desired SNR.

Cohen’s d

To assess how training conditions impacted individual psychophysical effects, we measured the effect size of the difference between human-model dissimilarity in the naturalistic and alternative training conditions for each psychophysical effect. Specifically, we measured Cohen’s d for each experiment:

$$d=\frac{{\mu }_{modified}-{\mu }_{normal}}{s}$$

$$S=\sqrt{\frac{{\sigma }_{modified}^2+{\sigma }_{normal}^2}{2}}$$

where μ and σ are the mean and variance of the human-model dissimilarity across our 10 networks for the normal or modified training condition. We calculated error bars on Cohen’s d by bootstrapping across the 10 networks, computing the effect size for each bootstrap sample. Fig. 7C plots the mean and SEM of this distribution.

Instrument Note Localization

Instrument note localization – Stimuli

To assess the ability of the model to predict localization behavior for natural sounds, we rendered a set of instruments playing notes at different spatial positions. Instruments were sourced from the Nsynth Dataset¹⁰¹, which contains a large number of musical notes from a wide variety of instruments. We used the validation set component of the dataset, which contained 12,678 notes sampled from 53 instruments. For each note, room in our virtual environment, and listener location within each room, we randomly rendered each of the 72 possible azimuthal positions (0° elevation, 0°−355° azimuth in 5° steps) with a probability $p=\frac{0.025\cdot \#oflocationsinsmallestroom}{\#oflocationsincurrentroom}$. We used a base probability of 2.5% to limit the overall size of the test set and normalized by the number of locations in the current room so that each room was represented equally in the test set. This yielded a total of 456,580 stimuli.

Instrument note localization – Analysis

We anticipated performing a human instrument note localization experiment in an environment with speakers in the frontal hemifield, so we corrected for front-back confusions by mirroring model responses of each stimulus across the coronal plane. Different instruments in the dataset contained different subsets of pitches. To ensure that differences in localization accuracy would not be driven solely by the instrument’s pitch range, we limited analysis to instruments for which the dataset contained all notes in the octave around middle C (MIDI note 55 through 66) and performed all analysis on notes in that range. This yielded 43 instruments and 1860 unique notes. We calculated the mean localization error for each network judgment by calculating the absolute difference, in degrees, between the judged and rendered location. We then averaged the error across networks and calculated the mean error for each of the 1860 remaining notes from the original dataset. We plotted the distributions of the mean error over notes for each instrument (8A) using letter-value plots¹⁵⁷.

To characterize the density of the spectrum we computed its spectral flatness. We first estimated the power spectrum x(n) using Welch’s method (window size of 2000 samples, 50% overlap). The spectral flatness was computed for each note of each instrument as:

$$\text{Spectral}\text{Flatness}=\frac{\sqrt[N]{{\prod }_{n=0}^{N-1}x(n)}}{\frac{1}{N}{\sum }_{n=0}^{N-1}x(n)}$$

We averaged the spectral flatness across all notes of an instrument and then computed the Spearman correlation of this measure with the network’s mean accuracy for that instrument.

Statistics

Real-world localization

For plots comparing real-world localization across models (Extended Data Fig. 6B&C), error bars are SEM, bootstrapped over stimuli (because there was only one version of the baseline models).

Psychophysical experiments

For plots assessing duplex theory (Fig. 2D), azimuth sensitivity (Fig. 3C), bandwidth sensitivity (Fig. 3F), ear alteration (Fig. 4D&E), spectral smoothing (Fig. 4J), sensitivity to low-pass and high-pass filtering (Fig. 4O), the precedence effect (Fig. 5B&D) and multi-source localization (Fig. 6 C&E) error bars are SEM, bootstrapped across networks. In some cases the graph of human results used SD rather than SEM for error bars because that is what was used in the original paper, the results of which were scanned from the original figure. We opted to use SEM error bars for all model results for the sake of consistency.

To assess the significance of the interaction between the stimulus frequency range and the magnitude of the ITD/ILD bias weights (Fig. 2D), we calculated the difference of differences in bias weights across the 4 stimulus/cue-type conditions:

$$\text{Difference}\text{of}\text{Differences}=(B_{ILD}^{Highpass}-B_{ILD}^{Lowpass})-(B_{ITD}^{Highpass}-B_{ITD}^{Lowpass})$$

where B denotes the bias weight for each condition). We calculated the difference of differences bootstrapped across models with 10,000 samples, and compared it to 0. As this difference of differences exceeded 0 for all 10,000 bootstrap samples, we fit a Gaussian distribution to the histogram of values for the 10,000 bootstrap samples and calculated the p-value (two-tailed) for a value of 0 or smaller from the fitted Gaussian.

We assessed the significance of the lowpass ILD bias weight (Fig. 2D) by bootstrapping across networks, again fitting a Gaussian distribution to the histogram of bias weights from each bootstrap sample and calculating the p-value (two-tailed) for a value of 0 or smaller from the fitted Gaussian.

Statistical significance of unnatural training conditions

We assessed the statistical significance of the effect of individual unnatural training conditions (Fig. 7B) by comparing the human-model dissimilarity for each unnatural training condition to a null distribution of the dissimilarity for the natural training condition. The null distribution was obtained by bootstrapping the human-model dissimilarity described above across networks. We fit a Gaussian distribution to the histogram of the dissimilarity for each bootstrap sample and calculated the p-value (two-tailed) of obtaining the value of the dissimilarity measure (or smaller) obtained for each unnatural training condition under the fitted Gaussian. The effect size of the difference in dissimilarity between training conditions was quantified as Cohen’s d (calculated as described above for individual experiments, but with the dissimilarity aggregated across experiments, as is plotted in Fig. 7B).

We also assessed the statistical significance of the effect size of the change to individual experiment results (relative to other experiments) when training in alternative conditions (Fig. 7C). We first measured Cohen’s d as described above for 10,000 bootstrap samples of the 10 networks, leading to a distribution over Cohen’s d for each experiment and each training condition. For each experiment of interest, we assessed the probability under its bootstrap distribution that a value at or below the mean Cohen’s d of each other experiment could have occurred. The histogram of bootstrap samples was non-Gaussian so we calculated this probability by counting the number of values at or below the mean for each condition and reported the proportion of such values as the p-value (two-tailed).

We assessed the statistical significance of the effect of training condition on real-world localization performance (Fig. 7E) by bootstrapping the RMS localization error across networks. We fit a Gaussian distribution to the histogram of RMS error for the normal training condition. The reported p value (two-tailed) is the probability that a value could have been drawn from that Gaussian at or above the mean RMS error for each alternative training condition.

Data Availability

Data used to train and analyze the main model in this paper, as well as the weights of the trained networks in the model, are available at: www.github.com/afrancl/BinauralLocalizationCNN

Training data for the unnatural training conditions are not posted publicly as their overall size is prohibitive, but will be shared upon request to the corresponding authors.

Code Availability

Code used to train and analyze the model in this paper is available at: www.github.com/afrancl/BinauralLocalizationCNN

Extended Data

Extended Data Figure 1.

A. Histogram of validation set accuracies (proportion correct) for neural network architectures after 15k steps of training during architecture search. Here and in B, histograms include the 897 architectures that remained (out of the initial set of 1500) at this point in the architecture search. B. Histogram of validation set losses for neural network architectures after 15k steps of training during architecture search.

Extended Data Figure 2.

Discrete prior distributions used for architecture search. Pooling and convolutional kernel parameters at each layer were uniformly sampled from the lists of values.

Extended Data Figure 3.

Summary of the 10 network architectures. These architectures performed best in the architecture search and were used as “the model” in all experiments in this paper.

Extended Data Figure 4.

Natural sounds used in training. The set of sources contained multiple exemplars of some of the sound classes, denoted with the numeral at the end of the source name.

Extended Data Figure 5.

Room configurations used in virtual training environment.

Extended Data Figure 6.

Comparison of our model to alternative two-microphone localization systems. A. Photo of two-microphone array. Microphone spacing was the same as that in the KEMAR mannequin (shown in Fig. 1E) used to record our real-world test set, but the recordings lacked the acoustic effects of the pinnae, head, and torso. B. Localization accuracy of standard two-microphone localization algorithms, our neural network localization model trained with ear/head/torso filtering effects (same data as plotted in Fig. 1G and 1H), and neural networks trained instead with simulated input from the two-microphone array. Localization judgments are front-back folded. Error bars here and in C plot SEM, obtained by bootstrapping across stimuli. C. Front-back confusions by each of the algorithms from B. Chance level is 50%. Our main model (i.e., the one trained with ears) is the only model whose front-back confusions are substantially below chance levels, confirming the utility of head-related transfer function cues for partially resolving front-back ambiguity.

Extended Data Figure 7.

Human-model dissimilarity for natural and unnatural training conditions for each of the 10 individual neural networks.

Extended Data Figure 8.

Human-model dissimilarity and human-human dissimilarity (root-mean-square error; RMSE) calculated over the subset of experiments for which across-participant variability could be estimated (typically from error bars in the original results graphs).

Extended Data Figure 9.

Model psychophysical results across training conditions for first three psychophysical experiments. A. Model sensitivity to interaural time and level differences (Figure 2D). B. Model accuracy for broadband noise at different azimuthal positions (Figure 3C). C. Effect of bandwidth on model localization of noise bursts (Figure 3F). All plotting conventions are the same as in the corresponding figures in the main text.

Extended Data Figure 10.

Model psychophysical results across training conditions for fourth through seventh psychophysical experiments. A. Sound localization by the model in azimuth and elevation before and after ear alteration (Figure 4 D&E). B. Effect of spectral smoothing on model localization accuracy (Figure 4J). C. Effect of low-pass and high-pass cutoff on model localization accuracy for elevation (Figure 4O). D. Model error in localization of the leading and lagging clicks in the precedence effect experiment, as a function of delay (Figure 5D). All plotting conventions are the same as in the corresponding figures in the main text.