Abstract
This unit is the first in a series of four units covering the analysis of nucleic acid structure by molecular modeling. This unit provides an overview of computer simulation of nucleic acids. Topics include the static structure model, computational graphics and energy models, generation of an initial model, and characterization of the overall three-dimensional structure.
Subject Group: Nucleic Acid Chemistry, Nucleic Acid Structure and Folding, Structural Analysis of Biomolecules, Experimental Determination of Structure, Folding and Conformational Change
Molecular modeling, loosely defined, relates to the use of models to investigate the three-dimensional structure, dynamics, energetics, and properties of a molecule or set of molecules. At the heart of this is specification of a molecular model, which provides a molecular structure at an appropriate level of granularity, usually in terms of three-dimensional atomic coordinates. Molecular modeling can be approached on many levels, ranging from energy minimization (finding the set of coordinates that minimizes the energy) with a complete ab-initio quantum-mechanical treatment of the energetics, to sampling “reasonable” conformations with a simplified energy representation or potential, to physically manipulatable models where no implicit energy representation is included. These methods serve not only as tools to aid in the interpretation of experimental data, but to directly complement such data by providing a relationship between the macroscopic behaviors observed experimentally and the microscopic properties represented in the model or simulation.
As discussed in other units, various molecular modeling tools can serve as conformational search engines for sampling conformational space subject to the restraints inferred from nuclear magnetic resonance (NMR; see UNIT 7.2) and crystallography (see UNIT 7.1 and UNIT 7.6) experiments. This is a critical step in the refinement of three-dimensional atomic structure. Inclusion of some representation of the energy, such as through the use of a specially parameterized empirical force field, can aid in this endeavor by limiting sampling to more realistic (in terms of energy) conformations.
As mentioned above, molecular mechanics methods (described in greater detail in UNIT 7.8) can be used not only as a tool in structure refinement, but can directly complement experimental data. For instance, molecular dynamics simulations can be used to aid in the interpretation of NMR order parameters, or to estimate anisotropic rotational diffusion. In addition, computer simulation techniques have the potential to give structural and dynamic insight into the atomic interactions occurring on a time scale (< msec) typically not observable due to averaging in crystallography and NMR experiments. Ultimately, as methods are proven reliable, they can then be applied in cases where experimentation is limited, difficult, or unfeasible, such as studying highly flexible systems, investigating proposed chemical modifications that have yet to be synthesized, or to represent extremes of pressure, temperature, and concentration. As will become apparent, the methods are steadily improving to the point that reliable predictions are emerging.
A critical point that needs to be made at the outset is that these methods cannot be treated as a “black box” or hands-off procedure; there is no standard protocol that can be applied to every system. Modeling is really more of an art. As each situation has differing requirements and needs, various choices need to be made as to what level of treatment to apply and what model to use. These choices rely on a critical understanding of the limitations in the methods. Therefore, the purpose of this discussion is to open up this black box a bit to allow some understanding of the options and choices a modeler makes, highlighting the tradeoffs that must be made in accuracy, system size, and time. The discussion here and in UNITS 7.8 to 7.10 is not meant to provide a complete review of nucleic acid modeling or to substitute for the more complete treatment discussed in the primary literature. Instead, these units are intended to provide a framework that describes molecular modeling of nucleic acids, points out common issues and limitations, and points the reader to other useful information sources.
Implicit in this discussion is a realization that a molecular model is more than a simple representation of the covalent connectivity or static structure. The model may also include some representation of the energetics of the system and perhaps the dynamics over a particular time scale. With current state of the art computer capabilities, where hundreds or even many thousands of CPUs and GPUs are available in modern High Performance Computing facilities, the field of molecular modeling and simulations is now beginning to study simulations of nucleic acid structure and dynamics on the microsecond timescales and rapidly approaching the millisecond range. The explosion in computer power lets us finely tune our protocols to expose unrealized errors within the methods and representations, and to ultimately overcome and fix limitations in the protocols. Still, it is critical to understand the applicability, reliability, and limitations of these methods. In other words, the choice of the model depends on the question being asked.
The remainder of the discussion in this unit introduces the simplest levels of molecular modeling applied to nucleic acids. These include generation, evaluation, and characterization of the initial molecular model. At this simplest level, a nucleic acid model is limited to a static representation of the structure in the gas phase. Evaluation of this given model’s utility is therefore based on the chemical intuition of the modeler, where manipulations to the model are limited to rotation about single bonds. To move beyond this level, supplement units in this series will delve more deeply into the myriad of issues involved in the computer simulation of nucleic acids. These include describing the common energy representations for nucleic acids that may be applied (UNIT 7.8), and discussion of how to properly represent the electrostatic interactions and solvation effects (UNIT 7.9). Additionally, various methods to find more representative structures are introduced, with a focus on molecular dynamics simulation methodologies. Finally, a description of practical issues in nucleic acid simulations will be provided (UNIT 7.10), such as what force fields are appropriate to apply, how simulations of nucleic acid are set up with explicit solvent and counter ions, and how crude relative free energy differences can be estimated from molecular dynamics simulations. In these discussions, the focus will be on the middle ground in terms of size, time scale, and accuracy—that is, the simulation of small nucleic acids (typically less than ~250 base pairs), with explicit representation of the environment (if feasible or necessary), empirical pairwise potential functions, and time scales ranging from the analysis of individual snapshots to microsecond-length simulations. For those readers more interested in learning about the simulation of larger nucleic acid systems (~1,000 to 15,000 base pairs), a variety of reviews can be consulted (Bishop, 2005; Olson, 1996; Sanbonmatsu, Blanchard, & Whitford, 2013; Schlick, 1995; Vologodskii & Cozzarelli, 2003).
MOLECULAR MODELING
The practice of molecular modeling basically involves the generation of an initial molecular model, evaluation of the model’s utility, and perhaps manipulation of the molecular model (followed by further evaluation; see Figure 7.5.1).
Figure 7.5.1.
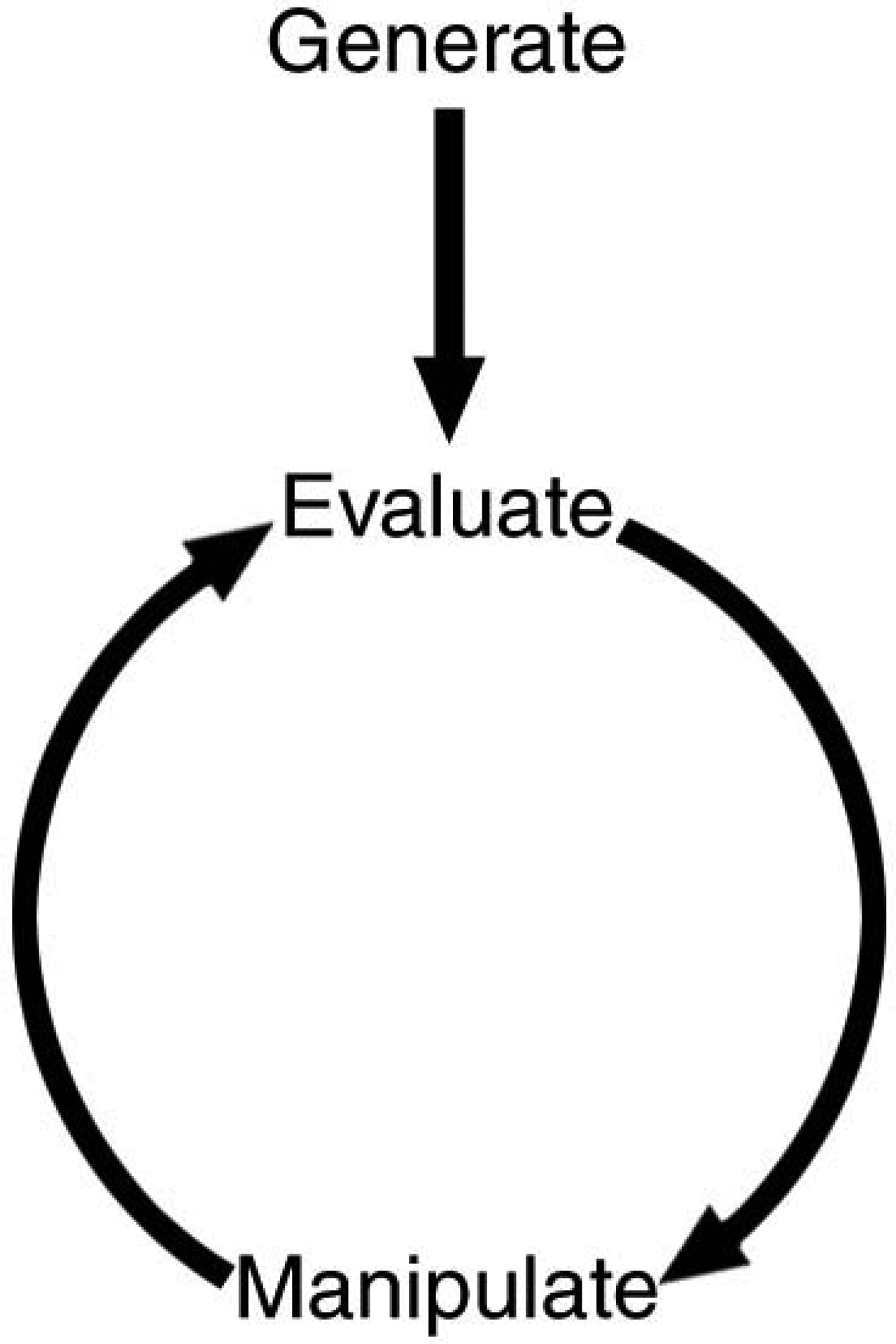
Schematic representation of molecular modeling analysis.
Prior to generating an initial molecular model, it is necessary to choose its representation or level of detail. For nucleic acids, the structural representation can be approached on many levels, ranging from the sub-atomic level (including electrons) to coarser levels, such as those that model structure using a single point per base pair. The realism of the model directly depends on this choice of representation and further depends on what properties one is trying to represent. As shown in Table 7.5.1, modeling can be considered a tradeoff between the accuracy, the size and granularity of the system, and the time scale to be represented. If the model only concerns a single conformation or small set of conformations of a molecule of < 500 atoms, a very accurate energy model and a description that includes all the atoms and electrons can be used (such as ab-initio quantum mechanics with a fairly large basis set and even correlation). However, to investigate the supercoiling of a small DNA plasmid over a microsecond time scale, the system can no longer be represented at the atomic level, and a much simpler description of the energetics and a coarser representation of the structure must be imposed. However, this may be sufficient to represent the properties of interest. Between a full quantum mechanical treatment appropriate for small molecules and the coarse-grained single point per base pair model appropriate for large systems, molecular dynamics methods with an empirical potential may give reliable results as long as no “chemistry” is involved (such as bond forming, bond breaking, or electron transfer) and highly polarizable metal ions are treated at a very approximate level. These methods can give reliable insight into the sequence-specific structure and dynamics of a small nucleic acid duplex in solution.
Table 7.5.1.
Tradeoffs in Molecular Modeling
| Accuracy (increasing) | Time scale Limit (decreasing) | System size (decreasing) | Granularity (finer grain) |
|---|---|---|---|
| Effective potential | Microseconds | Supercoiled DNA, plasmid | One point per base pair, elastic rod |
| Molecular mechanics (implicit solvent) | Nanoseconds to milliseconds | <1000 base pairs | All atom, implicit solvent |
| Molecular mechanics (explicit solvent) | Nanoseconds to milliseconds | <250 base pairs | All atom, explicit solvent |
| Quantum mechanics | Individual snapshots | ~500 atoms, few waters/ions | All atom plus electrons, implicit solvent |
The Static Structure Model
At the simplest level, and where the representation of the model does not include any reality beyond the covalent connectivity, molecular modeling can be performed by building and manipulating by hand “physical” models. Physical models can be purchased or built and used to represent different levels of granularity.
To represent nucleic acid structure the models should be able to depict the atoms and bonds and, therefore, the covalent connectivity of a molecule.
There are a few common types of models in use that can be classified as either space-filling or bond-oriented “physical” models. The most common space-filling models are of the Corey-Pauling-Koltun (CPK) variety, named after the researchers that developed them. These space-filling models represent the various atoms as cut-out spheres of a size proportional to the van der Waals radius, which are colored and shaped according to atom type and can be connected together (based upon the hybridization state and possible connectivity of the atom). The most common bond-filling models are polyhedral models. These provide a series of pieces that are in various polyhedral shapes with holes for pegs, which represent the bonds. The shape, color, and number of holes represent the various atom types (and hybridization state), and connecting pegs represent the bonds.
Although these models are useful for teaching and for building models of small molecules, they are not appropriate for building macromolecular models, such as of a DNA duplex. To build a larger molecule, special-purpose and more durable physical models can be purchased. These provide larger building units (such as DNA bases) in addition to smaller atom/half-bond units, which can be connected together. The scale of these models is usually in the 1 cm to 1 inch per Å range. Some models that have been used successfully are the Maruzen models, such as the HGS Biochemistry Molecular Model or the Molymods models (see Internet Resources). Coarser folded-chain models, such as protein models that represent a connection/bond for each α-carbon, are also in use.
Physically manipulatable bond-oriented models—although tedious to build and often fragile—are very useful for gaining insight into atomic structure. In addition, the models can be manipulated (which can lead to problems with larger model structures, as they tend to deform). Although the models have rigid bonds and angles, they typically allow free rotation about single bonds. This can provide insight into the correlated conformational changes that occur upon change in a given coordinate. One example is the change in sugar pucker conformation from C2ʹ-endo to C3ʹ-endo, which lowers the rise between base pairs and shifts the conformation not only of the atoms in the ribose ring but also of the nucleic acid backbone. In fact, modeling B-DNA with physically manipulatable models led to the formulation of Calladine’s rules (Calladine, 1982), rules which suggest means to overcome strong steric hindrances between adjacent purines in opposite strands as the base pair propeller twist increases to improve stacking.
Computational Graphics and Energy Models
A problem with physically manipulatable models is that there is no reliable means to include a description of the energy. With these models, energy can only be represented rather crudely, such as by inhibiting free rotation because of the connectivity or by the addition of physical restraints to prevent rotation about double bonds. This allows a minimal interpretation of the intramolecular or internal energetics of the system (related to the connectivity of the molecule).
In addition to intramolecular interactions, a realistic depiction of the energy requires representation of the intermolecular interactions (e.g., van der Waals or steric repulsion and dispersion attraction interactions, hydrogen bonding, and electrostatic interactions). Although the solid-sphere models can represent steric repulsion, they cannot be used to accurately describe the total energy; however, a realistic treatment of the energetics can readily be calculated by computer. Coupled with molecular graphics (digital display of molecular models), computational energy models open the door for much more realistic and reliable molecular modeling. Prior to the advent of molecular graphics, physical models were routinely used as aids for crystallographic refinement.
Molecular visualization programs are now abundant (see INTERNET RESOURCES at the end of this unit) and allow very nice and realistic display of molecular structure. The generality of the programs removes some of the tedium and cost of building physical models. However, since the computer graphics display is two-dimensional, the ease of seeing the three-dimensional model is lost and needs to be recovered by coloring, shading, or rotating the model to project the third dimension. Alternatively, stereo-view displays can be used which allow three-dimensional viewing with special glasses (either through shuttering, as with the Crystal Eyes display, with polarization filters, or with coloring and shading). In addition to more general usage, adding a description of the conformational energy to the molecular model is easier on the computer than with a physically manipulatable model.
Including a visualization of the energy along with the molecular graphics can provide greater insight and help aid in the evaluation of the model. Examples include coloring regions of a molecule based on favorable electrostatic potential or highlighting atoms that show significant steric overlap. The manipulations possible at the simplest level mirror those of physical models and include a variety of coordinate manipulations, such as rotating about bonds or chemically modifying the structure. However, rather than manipulating the model by hand as with physically manipulatable models, hooks need to be provided in the molecular graphics software to allow selection and rotation of various parts of the molecule.
Given a reliable initial model structure, molecular modeling with simple coordinate manipulations may be sufficient for many applications, such as suggesting that it is not feasible to fit a particular drug into the minor groove of a double-helical nucleic acid without seriously distorting the duplex, or showing that a certain chemical modification to the phosphodiester backbone is incompatible with the model structure. Simple modeling and molecular graphics were used as a guide in the initial design of peptide nucleic acid (PNA), an isosteric and stable backbone modification to DNA proposed for use as an antisense therapeutic agent (Nielsen, Egholm, Berg, & Buchardt, 1991).
Manipulation of molecular graphics or physical models, when coupled with an appropriate chemical/structural intuition, can give useful information. Examples include understanding steric effects, such as the interaction of drugs with the grooves or base pairs of nucleic acid duplexes or correlated changes in structure due to rotation about particular bonds. However, a major issue with this type of modeling is evaluation of the molecular models. Evaluation and interpretation of the meaning of the molecular model depends on the quality of the initial model, the reliability of the energy representation (if any), and the choice of coordinate manipulations to the model that might be made. Without a reliable guide into the conformational energetics and coordinate manipulations necessary to “improve” the model, evaluation of the model depends solely on the chemical intuition of the modeler. This intuition is necessary to rule out unfeasible or unrealistic models or to suggest manipulations to the model that may improve the property of interest.
Because there is no easy way to judge the quality of these models within this simple modeling framework, the conclusions made are often tenuous in the absence of experimental verification. For example, the initial model may not have been at all representative of what is seen experimentally or structural manipulations may lead to a model structure that is energetically unreasonable. Although the situation, in principle, improves with more advanced treatments because the energy is included and unreasonable coordinate manipulations are avoided, there are still many limitations in the methods. This is compounded by the sheer complexity of rugged energy landscapes for biomolecular structures, which makes evaluation of the reliability of a model structure difficult. In this sense, it should not be immediately assumed that “better” results are seen with more advanced treatments only because more reliable methods are used. There is still an essential need to compare the model with experimental data and to critically evaluate and assess the model.
To aid the modeler with simple molecular modeling, perhaps the ultimate molecular modeling environment might involve viewing a molecular graphics depiction of the model as it updates in real time according to the underlying energy potential, while the model is manipulated according to the whims of the modeler. A legacy example of this type of program is Sculpt (Surles et al., 1994), which allowed real-time minimization of the structure as it was manipulated. Broadly envisioned, further enhancement to this type of environment could come from visual and aural feedback from the system, such as a bang sound and flash of red light, to discourage manipulations by the modeler that move atoms into sterically forbidden regions. More involved haptic feedback mechanisms are also possible, such as increasing the difficulty of performing a given manipulation in proportion to the energetic penalty. Ultimately, when the first version of this unit was written in the late 1990’s, we expected that molecular modeling environments of this type would become more widely available and that they would incorporate visual, aural, and tactile feedback mechanisms, coupled with stereoscopic three-dimensional display in a virtual reality “cave” (Cruz-Neira, Sandin, DeFranti, Kenyon, & Hart, 1992), to guide the modeler as the model is manipulated. Although software and environments to perform this type of real-time modeling started to become available in the mid- to late 1990’s, over the past decade, contrary to our expectations, these molecular modeling environments have remained one-off experiments and their usage has effectively languished except as educational tools. A very nice example is adaptation of the Wii remote and console for MD simulation by researchers at the Pittsburgh Supercomputing Center (WiiMD of Shawn Brown, 2008).
Perhaps lack of development of these methods has come from the inherent complexity of the calculations that limits the treatment to fairly approximate and inaccurate representations of the energetics. Moreover, even with the development of the idealized and ultimate molecular modeling facility, such environments do not give a complete understanding of the molecular structure. The energy (enthalpy) alone is insufficient to describe the relative stability of various models, and care needs to be levied in judging the reliability of models based on differences in energy. In addition to describing the energy of the system, it is also necessary to include entropic effects. When entropic effects are included, free energy values may be obtained, providing the connection with reality and experimental measurement. With free energy, the modeler has a handle on the relative population of each state or can equivalently understand the various thermally accessible conformations of the molecule in its native environment.
To add entropic effects, some means of sampling the space of accessible conformations (according to the relative probability of observing a given conformation or equivalently according to the Boltzmann distribution) is needed. To do this, molecular dynamics (MD) or Monte Carlo (MC) simulation (discussed in more detail in UNIT 7.8) can be done with the given energy representation. This, however, tremendously increases the cost and complexity of modeling. Moreover, the question of whether the sampled conformational space is “representative” depends on the reliability of the energy description, the amount of conformational sampling, and the reliability of the initial model. However, it should be emphasized that more costly and detailed treatments do not always lead to “better” insight and are not always necessary to address the question at hand.
Generating the Initial Model
The first step in any modeling endeavor is creation of the initial molecular model, where “model” refers to a particular set of three-dimensional coordinates that define the structure of interest. In this discussion, which concerns nucleic acid structure on an atomic level (as opposed to the more coarse-grained bead models appropriate for modeling larger nucleic acid structures), this model is the set of three-dimensional atomic coordinates. Generally, a model of the coordinates is built by hand de novo or selected from another source (such as a database of experimentally derived structures). As will become apparent later in this overview, the quality of the modeling in large part relates to the quality of the initial model or the ability to find or sample the “correct” structure given the initial model. In this regard, studying an unknown RNA structure is likely to be unfeasible at present, since it is unrealistic to imagine correctly folding up the RNA structure in dynamics simulations (due to barriers to conformational transition that cannot be overcome during the time scale of the simulations, and to inaccuracies in the energetic representation). Although there has been tremendous progress in predicting RNA secondary structure, predicting the overall tertiary structure (i.e., three-dimensional atomic coordinates) is still a major unsolved challenge. In spite of this, there have been a few attempts (Hershkovitz, Sapiro, Tannenbaum, & Williams, 2006; Schneider, Morávek, & Berman, 2004), there is a long list of programs available for studying RNA folding (an example is available from Das, Karanicolas, & Baker, 2010), and more detailed reviews are available (Laing and Schlick, 2011; Seetin and Mathews, 2012; Sim et al., 2012). Therefore, it is best to base the modeling on experimentally derived structures. Since DNA tends to adopt regular duplex structures, one can often use the canonical structures as an initial guess. The canonical models were derived from X-ray fiber diffraction studies of large DNA fibers and give an average idealized (denoted canonical) geometry and structure representative of DNA under specific conditions (such as A-DNA under low humidity and B-DNA under physiological conditions; Arnott and Hukins, 1972). Crystallography provides another source of high-resolution structures, such as the left-handed Z-DNA duplex (Arnott, Chandrasekaran, Birdsall, Leslie, & Ratliff, 1980). The common canonical forms of DNA (A-DNA, B-DNA and Z-DNA) are shown in Figure 7.5.2 as stereo views. High-resolution DNA and RNA structures are also now common from NMR spectroscopy (see UNIT 7.2). A good and updated resource for general information on the structure of DNA is available in the text “Computational Studies of RNA and DNA” (Sponer & Lankas, 2006).
Figure 7.5.2.
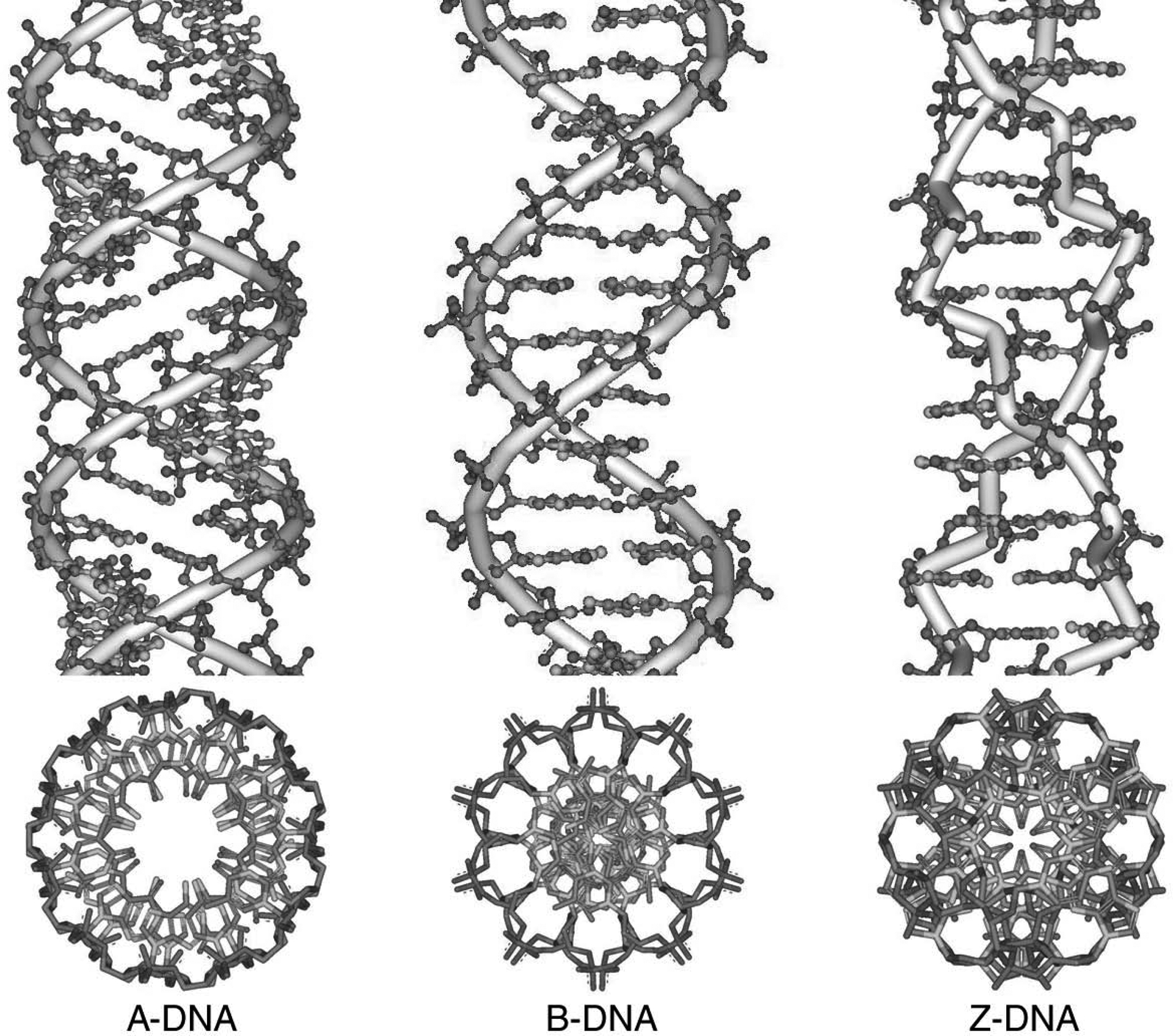
Canonical structures of DNA built with the Nucleic Acid Builder program available in AmberTools 12 (Macke T. J. & Case, 1997)
Many of the experimentally derived nucleic acid structures are freely available through either the Protein Data Bank (PDB; see Internet Resources; Abola et al., 1987) or the Nucleic Acid Database (NDB; see Internet Resources; Berman et al., 1992), both of which contain the coordinates for a variety of nucleic acid structures and protein-nucleic acid complexes derived from crystallography or NMR experiments. If an experimental structure is not available, it may still be possible to generate a reasonable model structure. A tool (or more accurately, a language for molecular manipulation) that can help develop such an initial model is Nucleic Acid Builder (NAB) which was developed by Tom Macke and Dave Case and is distributed within the AmberTools suite of programs (Macke T. J. & Case, 1997). The NAB molecular manipulation language allows a specification of rigid body translations, specification of restraints, distance geometry methods, and various other tools to aid in the generation of arbitrary structures. This has been used to generate model structures of synthetic Holliday junctions, protein-DNA complexes, RNA pseudoknots, supercoiled DNA, and other structures (Macke T. J. & Case, 1997). If the model shares properties with other known structures, such as common secondary structure elements or sequence, it may be possible to model by homology to the known structures or, alternatively, to build up the structure from a library of smaller pieces of known structure. This approach has been used to model RNA tertiary structure (Major et al., 1991) and the structure of DNA single strands (Erie, Breslauer, & Olson, 1993).
Recent surveys of crystal structures in the Cambridge Structure Database (which contains a variety of high-resolution structures of mononucleosides and mononucleotides; Allen et al., 1979) and the NDB (Berman et al., 1992) provide a set of parameters that can serve as the beginnings of a dictionary for standard nucleic acid geometry. These surveys investigate the geometry of the bases (Clowney et al., 1996), the sugar and phosphate backbone (Gelbin et al., 1996; Schneider, Neidle, & Berman, 1997) and the specific hydration of nucleic acids and interaction with metal ions (Schneider & Kabeláč, 1998; Schneider et al., 1993). High-level theoretical techniques can also give useful information. Ab initio quantum-mechanical simulations with a reasonable basis set (6–31G* or better) and some inclusion of electronic correlation can accurately represent geometry and polarization effects, and therefore properly represent nucleic acid interaction with various ions, metals, or nucleic acid bases. Monte Carlo and molecular dynamics simulation can also be used to obtain specific insight into ion association and hydration.
Completing the Initial Model
Often the experimentally determined structures obtained from the PDB or NBD lack explicit hydrogen atoms. Additionally, the nomenclature used is invariably different from that of the given modeling program, and the user has to impose various contortions to coerce the file into the expected naming and numbering conventions. Therefore it is fairly common to have to modify a PDB file to conform to the particular program’s pedantic conventions and, additionally, to add hydrogen atoms to the structure. Almost all of the modeling programs are equipped with some facility for adding missing atoms, particularly hydrogens. For more advanced treatments, solvent and counter ions can also be added (discussed in UNIT 7.9).
It is always a good idea to check the initial structure carefully to determine if the conformation and nomenclature is as expected and whether the hydrogens are added with the correct stereochemistry and in appropriate protonation states. It would be very disappointing to discover, after spending weeks running molecular dynamics simulations of solvated DNA, that one of the H1ʹ atoms on a particular residue was inadvertently added with the wrong stereochemistry, leading to an α-glycosyl linkage rather than the expected β linkage. It is likewise critical to check the stereochemistry of the structure after manipulations to the molecular model are made, as structure can be distorted or the stereochemistry altered under some conditions, such as when using distance geometry methods, when performing stringent minimization with large restraints, or also during high-temperature MD annealing or replica-exchange simulation. Although not all modeling programs adhere to IUPAC naming conventions (see Internet resources), these conventions are a good reference to check the naming, orientation, and placement of the various atoms. Additionally, there are a variety of tools for characterizing the nucleic acid structure, which are discussed in the next section. However, these methods do not necessarily check stereochemistry, depend on the use of correct hydrogen naming conventions, or enforce IUPAC naming conventions.
Although the PDB format is a common and well-defined standard for three-dimensional atomic coordinates, not all programs understand or interpret the standard PDB format, and they instead rely on some subtle variant or expect another coordinate format entirely. To aid in converting between the large set of formats available for many of the various modeling tools, the program Babel is very useful (see Internet Resources) and the authors routinely update their software to accept more than 110 different file formats (O’Boyle et al., 2011). Not only can this program perform direct conversions among various coordinate formats, it can assign connectivity, bond orders, and hybridization when this information is not present.
Characterizing Nucleic Acid Structure
In order to characterize the quality of an initial molecular model or to later evaluate the conformational changes that occur as the model is manipulated (for example, during MD simulation), it is useful to characterize the overall three-dimensional structure. In proteins, one is typically only concerned with the ϕ and ψ backbone angles and perhaps some of the side-chain χ angles; the overall structure is characterized by the particular secondary structure elements and folding class. In contrast, with nucleic acids, there are many angles of interest. These range from the backbone angles α, β, γ, ε, and ζ, to the puckering conformation of the furanose ring, to the χ angle representing the orientation of the sugar to the base (Neidle, 2008). To characterize the conformation of the sugar moiety (the furanose ring), the Altona and Sundaralingam concept of pseudorotation is generally used (Altona & Sundaralingam, 1972). This defines the sugar pucker amplitude (representing how far the ring is from planar) and the pseudorotation phase angle (representing the correlated values of the individual torsions making up the ring). Various values of the pseudorotation phase angle, more commonly referred to as the sugar pucker, represent different puckerings out of the plane (on the same side as the C5ʹ atom, endo, or to the opposite side, exo). Methods for calculating these values are straightforward and are typically included in most modeling packages.
In addition to characterizing the overall backbone structure, sugar pucker, and χ angle of a single polynucleotide strand, it is also desirable to characterize the commonly occurring duplex structures that result from complementary base pairing between strands. Helicoidal analysis is typically applied to characterize global properties of the duplex (such as the helical repeat or overall helical twist), properties between adjacent base pairs (such as the rise), or properties of individual bases (such as the propeller twist). These properties represent the extent of rotation or translation of the bases or base pairs with respect to a common reference frame, typically the helical axis.
The nomenclature and definitions were standardized at an EMBO workshop on DNA curvature and bending (Dickerson, 1989). See Figure 7.5.3 for a graphical description of these values. Despite the standard nomenclature and definitions, the precise details of the mathematics were not standardized. Therefore, among the variety of programs commonly used to analyze helicoidal structure, each differed in the details regarding the exact definition of the helical axis, reference frame, and pivot points. The most developed and consistent mathematical treatment of the helicoidal parameters is likely either that of Babcock and Olson or that of Elhassan and Calladine, which is fully reversible (Elhassan & Calladine, 1995). The former has symmetrical definitions on a uniform scale for the various rotations and defines pivot points or axes that minimize mathematically induced artifactual correlations between the various rotational and translational parameters. A further distinction relates to the definition of the helical axis; reference to a local helical axis typically relates to the axis between adjacent base pairs, whereas global helicoidal parameters are in reference to some best-fit global and smoothed helical axis over the whole helical structure. Although these methods give qualitatively comparable results, care should be taken in quantitative comparison of helicoidal values calculated from different programs due to the sensitivity of the method to definition of the reference frame and helical axis. This is discussed in more detail in published work by Lu and Olson (Lu & Olson, 1999).
Figure 7.5.3.
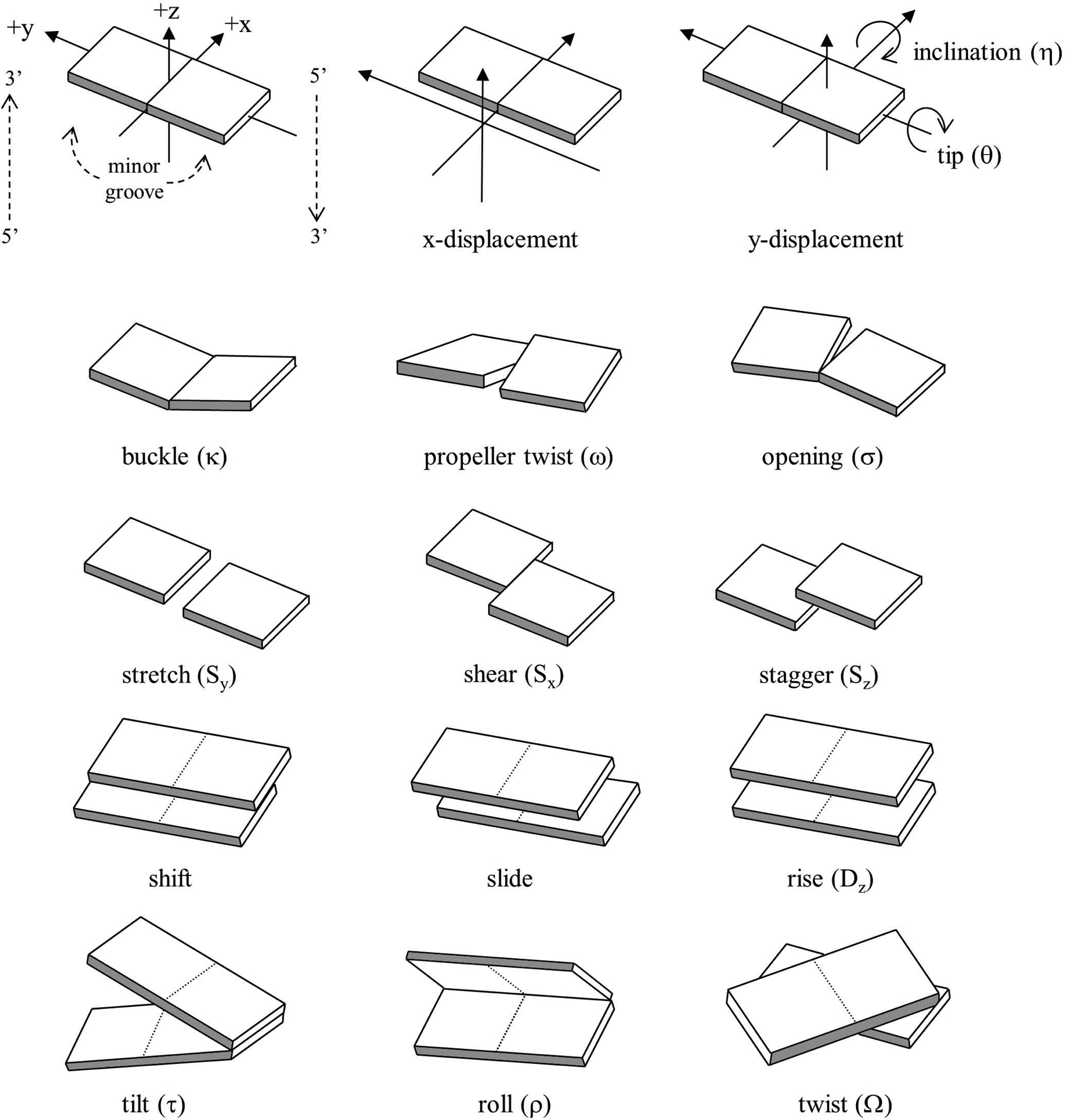
Pictorial definition of the helicoidal parameters
Although a number of programs for calculating helicoidal parameters are available, the most commonly used programs include Curves+ (Lavery, Moakher, Maddocks, Petkeviciute, & Zakrzewska, 2009), which uses a global helical axis by default, and 3DNA (Lu, 2003), which uses a local helical axis definition. Although the methods referencing a global helical axis typically display more regular values (and less individual variation), the global axis may not be sufficiently determined for small duplexes (such as those with less than a full helical repeat) or for distorted duplexes (such as an RNA duplex with a bulge), giving rise to misleading helicoidal parameters. The global helical axis may therefore not always be appropriate. Moreover, given that the overall structure is determined by local interactions between adjacently stacked base pairs, local helicoidal parameters may be more representative. When comparing helicoidal values calculated during modeling to those in the literature, care should be taken to ensure that consistent reference frames (local versus global) and definitions of the values are applied. In addition to standard helicoidal analysis, groove structure is also commonly investigated, such as the relative width and depth of the minor or major groove (see, for example, (Stofer & Lavery, 1994).
Helicoidal analysis and calculation of the various backbone angles can also be applied to the individual coordinate snapshots (for like conformations) or a representative coordinate-averaged structure generated during modeling, such as from a molecular dynamics or Monte Carlo simulation. Although it is often the case that average backbone angles calculated as the average of individual values for each coordinate snapshot are close to the values determined from the average structure, this is not typically true for helicoidal parameters, which are very sensitive to the conformation (T. E. Cheatham & Kollman, 1997). Modelers should keep in mind that the average structure obtained, such as that seen in crystallography or NMR experiments, hides the detailed dynamics. Moreover, straight coordinate-averaged conformations (after best-fits to a common reference frame) are not equivalent to torsion-averaged structures. Therefore, care should be taken in various coordinate comparisons. The common means to compare structures is through the use of best-fit root-mean-squared deviations (RMSd) between the coordinates or torsion angles. This indicator is very useful for determining the degree of similarity between two structures (when the RMSd values are small), but does less well at representing dissimilarity, since small differences in structure can lead to large root-mean-squared differences.
SUMMARY
This unit has introduced molecular modeling of nucleic acids on the simplest level. The modeling process can be described in three stages:
Generation: Create an initial model either by hand building it based on the molecular connectivity or by obtaining the coordinates from a depository of experimentally derived structures. In the absence of a complete experimental structure, base the structure on known (canonical) structure and/or use tools (e.g., Nucleic Acid Builder) to complete the model.
Evaluation: Is the structure valid? Judge this based on chemical/structural intuition and comparison with experimentally derived structures. The structure can be described in terms of the backbone angles, sugar pucker, glycosidic χ torsion, and helicoidal parameters. Additionally, it is important to check the stereochemistry and hydrogen placement.
Manipulation: Coordinate manipulations can be made by simple rotation around chemical bonds. Some representation of the energy should be included (if possible) to avoid bad steric overlap and unrealistic rotations.
Other units delve more deeply into methods for evaluating and manipulating the models and representations of nucleic acids that go beyond the single static gas-phase structure model. This includes a discussion of how to properly represent the long-range electrostatic interactions and how to include some representation of the effect of the environment (solvent and ionic strength effects; see UNIT 7.9). With a more realistic representation of the energy (UNIT 7.8), the energy can be used as a guide to suggest coordinate manipulations. Evaluation of the model depends on the reliability of the energy and how the system is represented, coupled with the chemical intuition of the modeler and comparison to experimental data.
ACKNOWLEDGEMENT
This is an update to the original protocols article by Thomas E. Cheatham III, Bernard R. Brooks, Peter A. Kollman (Current Protocols in Nucleic Acid Chemistry, UNIT 7.5, 2001). We would like to thank members of the lab for critical readings, specifically Sean Cornillie, Hamed Hayatshahi, Niel Henriksen, and Daniel Roe, and acknowledge funding from the NIH R01 GM-081411 and R01 GM-098102 along with extensive computational support from the NSF XSEDE MCA01S027 and the University of Utah Center for High Performance Computing.
INTERNET RESOURCES
Simulation codes
The home page for the AMBER suite of programs for molecular mechanics and dynamics. See also the subpage: http://ambermd.org/tutorials/basic/tutorial1/ for a tutorial that describes in detail setting up, equilibrating, and running molecular dynamics simulations using AMBER on a small DNA duplex in solution.
The GROMOS molecular mechanics/dynamics software home page.
http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software
The home page for the GRASP continuum electrostatics and molecular graphics display code developed by Anthony Nicholls.
The CHARMM molecular mechanics/dynamics software home page at the National Institutes of Health.
http://nmr.cit.nih.gov/xplor-nih/
The home page for X-Plor-NIH.
http://www.ks.uiuc.edu/Research/namd
The home page for the NAMD molecular mechanics/dynamics simulation package developed by Klaus Schulten’s group at the University of Illinois.
http://dasher.wustl.edu/tinker
The home page for the TINKER molecular mechanics/dynamics software. Includes an extensive list of WWW links to other MM/MD resources.
Molecular graphics programs
http://www.cgl.ucsf.edu/chimera/index.html
The UCSF Chimera “extensible molecular modeling system” and molecular graphics program.
The PyMOL molecular graphics program.
http://www.ks.uiuc.edu/Research/vmd
The Visual Molecular Dynamics molecular graphics program.
Model building and analysis tools, nucleic acid nomenclature
The home page for the AMBER and where the NAB (nucleic acid building programming language and) suite of programs can be downloaded.http://x3dna.org/
The 3DNA program for calculating helicoidal parameters in a consistent manner using a local helical axis definition.
http://gbio-pbil.ibcp.fr/Curves_plus/Curves+.html
The Curves+ program for analyzing the structure of nucleic acids.
The home page of the Molecular Structure Information Interchange Hub or the program babel developed in Professor Dan Dolata’s group by Pat Walters and Matt Stahl. This program is very useful for interconverting a variety of different molecular modeling program file formats.
http://www.chem.qmul.ac.uk/iupac
A repository of many of the IUPAC naming conventions. This site has a very nice Web page describing in detail the notation and naming conventions that apply to nucleic acids.
The site for the company that makes the Maruzen physical molecular models (HGS). For protein and nucleic acids, of particular interest is the Maruzen Biochemistry Molecular Models.
Another company with good quality model kits.
Coordinate repositories and information resources
The Protein Data Bank server at the Research Collaboratory for Structural Bioinformatics (Rutgers, SDSC, NIST).
The Nucleic Acid Database server maintained by Helen Berman and others at Rutgers University.
The computational chemistry list archives. This contains information about a number of modeling programs, conference listings, and job postings.
Footnotes
Publisher's Disclaimer: This PDF receipt will only be used as the basis for generating PubMed Central (PMC) documents. PMC documents will be made available for review after conversion (approx. 2–3 weeks time). Any corrections that need to be made will be done at that time. No materials will be released to PMC without the approval of an author. Only the PMC documents will appear on PubMed Central -- this PDF Receipt will not appear on PubMed Central.
LITERATURE CITED
- Abola EE, Bernstein FC, Bryant SH, Koetzle TF, & Weng J (1987). Protein Data Bank. In Allen FH, Bergerhoff G, & Sievers R (Eds.), Crystallographic Databases—Information Content, Software Systems, Scientific Applications (pp. 107–132). Bonn/Cambridge/Chester. [Google Scholar]
- Allen FH, Bellard S, Brice MD, Cartright BA, Doubleday A, Higgs H, Hummelink T, et al. (1979). The Cambridge Crystallographic Data Centre: Computer-based search, retrieval, analysis and display of information. Acta Crystallographica, B35. [Google Scholar]
- Altona C, & Sundaralingam M (1972). Conformational analysis of the sugar ring in nucleosides and nucleotides. New description using the concept of pseudorotation. Journal of the American Chemical Society, 94(23), 8205–8212. doi: 10.1021/ja00778a043 [DOI] [PubMed] [Google Scholar]
- Arnott S, Chandrasekaran R, Birdsall DL, Leslie AGW, & Ratliff RL (1980). Left-handed DNA helices. Nature, 283(5749), 743–745. doi: 10.1038/283743a0 [DOI] [PubMed] [Google Scholar]
- Arnott S, & Hukins DWL (1972). Optimised parameters for A-DNA and B-DNA. Biochemical and Biophysical Research Communications, 47(6), 1504–1509. doi: 10.1016/0006-291X(72)90243-4 [DOI] [PubMed] [Google Scholar]
- Berman HM, Olson WK, Beveridge DL, Westbrook J, Gelbin A, Demeny T, Hsieh SH, et al. (1992). The Nucleic Acid Database—A comprehensive relational database of 3-dimensional structures of nucleic acids. Biophysical Journal, 63, 751–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop TC (2005). Molecular dynamics simulations of a nucleosome and free DNA. Journal of Biomolecular Structure & Dynamics, 22(6), 673–86. doi: 10.1080/07391102.2005.10507034 [DOI] [PubMed] [Google Scholar]
- Brown S (2008). PSC’s “WiiMD” Wins Best Demonstration at TG ‘08. Retrieved March 25, 2013, from http://www.psc.edu/index.php/newscenter/2008/201-pscs-qwiimdq-wins-best-demonstration-at-tg-08
- Calladine CR (1982). Mechanics of sequence-dependent stacking of bases in B-DNA. J. Mol. Biol 161, 343–352. [DOI] [PubMed] [Google Scholar]
- Clowney L, Jain SC, Srinivasan AR, Westbrook J, Olson WK, & Berman HM (1996). Geometric Parameters in Nucleic Acids: Nitrogenous Bases. Journal of the American Chemical Society, 118(3), 509–518. doi: 10.1021/ja952883d [DOI] [Google Scholar]
- Cruz-Neira C, Sandin DJ, DeFranti TA, Kenyon RV, & Hart JC (1992). The CAVE: audio visual experience automatic virtual environment. Communications of the ACM, 35, 65–72. Retrieved from http://cacm.acm.org/magazines/1992/6/9342-the-cave-audio-visual-experience-automatic-virtual-environment/abstract [Google Scholar]
- Das R, Karanicolas J, & Baker D (2010). Atomic accuracy in predicting and designing noncanonical RNA structure. Nature Methods, 7(4), 291–4. doi: 10.1038/nmeth.1433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickerson RE (1989). Definitions and nomenclature of nucleic acid structure components. Nucleic Acids Research, 17(5), 1797–1803. doi: 10.1093/nar/17.5.1797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elhassan MA, & Calladine CR (1995). The assessment of the geometry of dinucleotide steps in double-helical DNA; a new local calculation scheme. Journal of Molecular Biology, 251(5), 648–64. doi: 10.1006/jmbi.1995.0462 [DOI] [PubMed] [Google Scholar]
- Erie DA, Breslauer KJ, & Olson WK (1993). A Monte Carlo method for generating structures of short single-stranded DNA sequences. Biopolymers, 33(1), 75–105. doi: 10.1002/bip.360330109 [DOI] [PubMed] [Google Scholar]
- Gelbin A, Schneider B, Clowney L, Hsieh SH, Olson WK, & Berman HM (1996). Geometric Parameters in Nucleic Acids: Sugar and Phosphate Constituents. Journal of the American Chemical Society, 118(3), 519–529. doi: 10.1021/ja9528846 [DOI] [Google Scholar]
- Hershkovitz E, Sapiro G, Tannenbaum A, & Williams LD (2006). Statistical analysis of RNA backbone. IEEE/ACM transactions on computational biology and bioinformatics / IEEE, ACM, 3(1), 33–46. doi: 10.1109/TCBB.2006.13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laing C and Schlick T (2011). Computational approaches to RNA structure prediction, analysis, and design. Curr. Opin. Struct. Biol 21, 306–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavery R, Moakher M, Maddocks JH, Petkeviciute D, & Zakrzewska K (2009). Conformational analysis of nucleic acids revisited: Curves+. Nucleic Acids Research, 37(17), 5917–29. doi: 10.1093/nar/gkp608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X-J (2003). 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Research, 31(17), 5108–5121. doi: 10.1093/nar/gkg680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X-J, & Olson WK (1999). Resolving the discrepancies among nucleic acid conformational analyses. Journal of Molecular Biology, 285(4), 1563–75. doi: 10.1006/jmbi.1998.2390 [DOI] [PubMed] [Google Scholar]
- Macke TJ, & Case DA (1997). Molecular Modeling of Nucleic Acids. (Leontis NB & SantaLucia J, Eds.) (Vol. 682, pp. 379–393). Washington, DC: American Chemical Society. doi: 10.1021/bk-1998-0682 [DOI] [Google Scholar]
- Major F, Turcotte M, Gautheret D, Lapalme G, Fillion E, & Cedergren R (1991). The combination of symbolic and numerical computation for three-dimensional modeling of RNA. Science, 253(5025), 1255–1260. doi: 10.1126/science.1716375 [DOI] [PubMed] [Google Scholar]
- Neidle S (2008). Principles of Nucleic Acid Structure. Angewandte Chemie (Vol. 98, pp. 762–762). University of London, UK: Elsevier B.V. doi: 10.1002/ange.19860980837 [DOI] [Google Scholar]
- Nielsen P, Egholm M, Berg R, & Buchardt O (1991). Sequence-selective recognition of DNA by strand displacement with a thymine-substituted polyamide. Science, 254(5037), 1497–1500. doi: 10.1126/science.1962210 [DOI] [PubMed] [Google Scholar]
- O’Boyle NM, Banck M, James CA, Morley C, Vandermeersch T, & Hutchison GR (2011). Open Babel: An open chemical toolbox. Journal of Cheminformatics, 3(1), 33. doi: 10.1186/1758-2946-3-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson WK (1996). Simulating DNA at low resolution. Current Opinion in Structural Biology, 6(2), 242–256. doi: 10.1016/S0959-440X(96)80082-0 [DOI] [PubMed] [Google Scholar]
- Sanbonmatsu KY, Blanchard SC, & Whitford SP (2013). Molecular Dynamics Simulations of the Ribosome. Biophysics for the Life Sciences, 1, 51–68. [Google Scholar]
- Schlick T (1995). Modeling superhelical DNA: recent analytical and dynamic approaches. Current Opinion in Structural Biology, 5(2), 245–262. doi: 10.1016/0959-440X(95)80083-2 [DOI] [PubMed] [Google Scholar]
- Schneider B, Cohen DM, Schleifer L, Srinivasan AR, Olson WK, & Berman HM (1993). A systematic method for studying the spatial distribution of water molecules around nucleic acid bases. Biophysical Journal, 65(6), 2291–303. doi: 10.1016/S0006-3495(93)81306-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider B, & Kabeláč M (1998). Stereochemistry of Binding of Metal Cations and Water to a Phosphate Group. Journal of the American Chemical Society, 120(1), 161–165. doi: 10.1021/ja972237+ [DOI] [Google Scholar]
- Schneider B, Morávek Z, & Berman HM (2004). RNA conformational classes. Nucleic Acids Research, 32(5), 1666–77. doi: 10.1093/nar/gkh333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider B, Neidle S, & Berman HM (1997). Conformations of the sugar-phosphate backbone in helical DNA crystal structures. Biopolymers, 42(1), 113–124. doi: [DOI] [PubMed] [Google Scholar]
- Seetin MG and Mathews DH (2012). RNA structure prediction: an overview of methods. Methods Mol. Biol 905, 99–122. [DOI] [PubMed] [Google Scholar]
- Sim AY, Minary P and Levitt M (2012). Modeling nucleic acids. Curr. Opin. Struct. Biol 22, 273–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sponer J, & Lankas F (Eds.). (2006). Computational studies of RNA and DNA (1st ed.). Springer Netherlands. Retrieved from http://www.springer.com/chemistry/theoretical+and+computational+chemistry/book/978-1-4020-4794-7 [Google Scholar]
- Stofer E, & Lavery R (1994). Measuring the geometry of DNA grooves. Biopolymers, 34(3), 337–46. doi: 10.1002/bip.360340305 [DOI] [PubMed] [Google Scholar]
- Cheatham TE, I., Brooks BR, & Kollman PA (2001). Molecular Modeling of Nucleic Acid Structure - Current Protocols. Current Protocols in Nucleic Acid Chemistry. Retrieved from http://www.currentprotocols.com/WileyCDA/CPUnit/refId-nc0705.html [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheatham TE, I., & Kollman PA (1997). Molecular Dynamics Simulations Highlight the Structural Differences among DNA:DNA, RNA:RNA, and DNA:RNA Hybrid Duplexes. Journal of the American Chemical Society, 119(21), 4805–4825. doi: 10.1021/ja963641w [DOI] [Google Scholar]
- Vologodskii AV, & Cozzarelli NR (2003). Conformational and Thermodynamic Properties of Supercoiled DNA. Annual Review of Biophysics and Biomolecular Structure. Retrieved from http://www.annualreviews.org/doi/abs/10.1146/annurev.bb.23.060194.003141 [DOI] [PubMed] [Google Scholar]


