Recent progress in minimizing the warpage and shrinkage deformations by the optimization of process parameters in plastic injection molding: a review

Abstract

The quality control of plastic products is an essential aspect of the plastic injection molding (PIM) process. However, the warpage and shrinkage deformations continue to exist because the PIM process is easily interfered with by several related or independent process parameters. Thus, great efforts have been devoted to optimizing process parameters to minimize the warpage and shrinkage deformations of products during the last decades. In this review, we begin by introducing the manufacturing process in PIM and the cause of warpage and shrinkage deformations, followed by the mechanism about how process parameters, like mold temperature, melt temperature, injection rate, injection pressure, holding pressure, holding and cooling duration, affect those defects. Then, we summarize the recent progress of the design of experiments and four advanced methods (artificial neural networks, genetic algorithm, response surface methodology, and Kriging model) on optimizing process parameters to minimize the warpage and shrinkage deformations. In the end, future perspectives of quality control in injection molding machines are discussed.

Introduction

Plastic injection molding (PIM) is one of the most widely used manufacturing techniques for producing plastic products with various shapes and complex geometries. A large quantity of medical protective equipment, such as medical goggles [1], protective clothing [2, 3], and disinfection medicine barrels, is produced to protect people from viruses by this technology during the period of COVID-19. However, the manufacture of these injection products mainly relies on traditional manual operations and trial-and-error methods [4–6], which has disadvantages in the part quality [7] and influences the efficiency and energy consumption [8, 9] of a company. Therefore, many scientists are devoted to finding a more scientific method in the PIM process.

Recently, much attention has been focused on the minimization of the warpage and shrinkage deformations, which represents the most common problem scientists have encountered in the PIM process. It runs through every link in the selection of materials [10, 11], the design of plastic parts and molds [12–14], the settings and optimization of process parameters [15]. The warpage and shrinkage minimization relies on a more balanced physical mechanical polymer property, a more even contraction and cooling condition, and a better edge angle effect in the runner and the wall of the mold. Through the comprehensive modification of the product’s shape or 3D model, the optimal design of the injection molding machine’s pouring system, cooling system, ejection mechanism, and the adjustment of process parameters, the quality of the injection products can be guaranteed and the extra cost can be saved.

During the PIM process, designs of the product and injection machine are usually determined in the initial stage of product manufacture, which cannot be easily changed. However, the warpage and shrinkage deformations will be more sensitive to the change in process parameters, so it will be more feasible and reasonable to systematically optimize process parameters for plastic products. Process parameters consist of the mold and melt temperature, the injection rate, the injection pressure, the holding pressure, etc. By the real-time detection of process parameters in the PIM production [16], we can further diagnose and guide the PIM process to reduce the warpage and shrinkage deformations of the product.

Traditionally, setting process parameters is mainly based on the experience of a skilled plastic engineer, which cannot ensure the optimum value of process parameters. For the analytical approach, a series of advanced optimal design methods have been proposed for deriving proper process parameters of PIM [17]. The optimization approach has the advantages to improve the injection machine’s production efficiency, reliability, and consistency [18] and can reduce the overall cost and reliance on existing experience, which positively promotes the development and improvement of the injection molding field.

In this paper, the recent advance relating to the study of the optimization design in PIM is summarized and reviewed. It focuses on the mechanism of the warpage and shrinkage deformations, the introduction of process parameters, and the optimization design methods in PIM so that readers can obtain useful information and an overview of the optimization design appearing in the injection machine. This paper is outlined as follows. Section 1 provides a general background of PIM. Then, Section 2 gives a specific description of the warpage and shrinkage deformations. And Section 3 discusses the effects of process parameters in the PIM process. At last, we synthesize the recent research about the optimization approaches of process parameters for the warpage and shrinkage deformations of plastic parts in PIM in Section 4.

Warpage and shrinkage deformations in plastic injection molding

Plastic injection molding process

As an extremely complex process, PIM can be divided into the following five stages: filling, packing, holding, cooling, and ejecting (Fig. 1a). During the whole process, the polymer undergoes complex dynamic changes in temperature and pressure [19] in an injection machine (Fig. 1b). The polymer is first transported and heated in the injection unit. Later, the molten polymer is injected into the mold cavity with a constant volumetric rate and the holding process is performed to prevent the influence of the reduction in specific volume. After cooling and ejecting, a reliable molded part is obtained if everything runs normally.

Fig. 1.

(a) Injection molding flow chart (b) A simplified model of an injection modeling machine

Warpage and shrinkage deformations

Warpage [20–22] and shrinkage [23–25] deformations are two major challenges in the PIM process. They are inevitable in many cases, especially for productions with complex geometries [26, 27], thin-walled parts [28–30], micro-parts [31, 32], certain materials [33, 34], etc. They cause the loss of economic and waste of materials in industries and are extremely unfriendly to industrial manufacturing, which needs to be resolved urgently. The specific performance of the acceptable product and parts with severe warpage and severe volumetric shrinkage is shown in Fig. 2.

Fig. 2.

(a) Acceptable product (b) Product with severe warpage (c) Product with severe volumetric shrinkage [86]

Warpage is a kind of defect of the injected part that usually presents a bend-like shape deviation from the designed geometry along a certain direction [35]. Once the internal stress appears during the molding process in a plastic part, the deformation occurs. When the shape of an injection-molded article deviates from the shape of the mold cavity, it is called the warpage deformation, which is one of the main defects of the plastic part (Fig. 2b). This frequently encountered defect has adverse impacts on the appearance, assembly and performance of the product.

Shrinkage is used to evaluate the part volume decline when the polymer cools from melt condition to room temperature (Fig. 2c). Volumetric shrinkage reflects the difference between the actual volume and the volume after ejecting from the mold cavity of a product. The final volume can be calculated by the density and the mass of the product. Jansen [24] has classified the shrinkage into three types: (a) in mold shrinkage, which occurs at the mold and is extremely rare, (b) mold shrinkage, which is a type of shrinkage that shows after the mold is opened, (c) post-shrinkage, which happens during the storage of the material.

The cause of warpage and shrinkage deformations

The cause of the warpage and shrinkage deformations can be classified into four categories: (a) Molecular flow orientation: the orientation of the polymer molecule has effect on unbalanced physical mechanical properties in the plastic part internally, resulting in a poorer strength in the vertical direction than that in the parallel direction of the molecular chain [36]. It is possible that the plastic part will warp or crack when this difference reaches a critical value; (b) Uneven contraction: the temperature difference in different regions of the plastic part makes contributions to various shrinkage ratios. Because of the different shrinkage ratio along the thickness direction of the article, it leads to the warpage deformation [37]; (c) Uneven cooling: when pre-cooled polymer molecules are already solidified with small shrinkage, some molecules have not yet cooled. After ejecting from the mold, molecules continue cooling and will warp on the side where the cooling rate is relatively slow without the holding effect of the cavity [36]; (d) Edge effect: this effect needs to consider both the cooling effect and the molecular orientation together [38].

More specifically, the selection of materials [10, 11], the structure of plastic parts [12, 14], the structure of the machine [13], and the determination of process parameters [15] can affect the warpage and shrinkage of products. In general, the deformation of semi-crystalline materials is greater than that of crystalline and amorphous materials because of the different densities of each product part [10]. As for the different shapes and structures of plastic parts, it can lead to the different orientations of the internal molecular, resulting in the different directions of internal stress. Some parts of the stress can cancel each other out, and thus it can resist the deformation [12]. Meanwhile, the influence of the gating system on the deformation of the plastic part is mainly reflected in the length of the runner in an injection machine [14]. A longer length will produce greater internal stress and more serious deformation. Also, problems in the design of the cooling system can cause uneven cooling of all parts of the mold [36]. If the design of the demolding mechanism is inappropriate, the ejection starts when the temperature of the plastic part is still high. If the injection pressure and the injection speed are too slow, or the pressure holding time and the injection cycle are too short under over-filling conditions during the debugging operation of the PIM process, the melt will not be plasticized uniformly, eventually causing the plastic parts to warp and shrink [39].

The role of process parameters in influencing warpage and shrinkage deformations

Main strategies to reduce warpage and shrinkage deformations in production are shown as follows: (a) Modify the shape or 3D model of the product [40]. If the product structure is unreasonable, we can modify the product shape. If the product cannot be modified, the 3D model of the product should be adjusted by reverse deformation. (b) Optimize the design of pouring system, cooling system, ejection mechanism, etc. in the injection molding machine [41, 42], which is also an effective approach to avoid warpage. (c) Adjust process parameters [43], such as the mold temperature, holding pressure, cooling time and so on, according to the actual production situation.

Among those methods, the designs of products and injection machines are usually determined in the initial stage of product manufacture, which cannot be easily changed. However, the warpage and shrinkage deformations are more sensitive to change in process parameters, so it is more feasible and reasonable to systematically optimize the process parameters for some products with micro-scale geometry, a high ratio of length to diameter, and high local precision [16]. It is an important issue to predict and optimize the warpage and shrinkage deformations before manufacturing in PIM. The role of process parameters playing in PIM will be introduced in the following section.

Process parameters

It is a preferable solution to develop systematic and scientific methods to determine a set of process parameters for ensuring a reliable product quality control in the practical application [44, 45]. The process of PIM contains dozens of process parameters like mold and melt temperature, injection rate, injection pressure, holding pressure, holding and cooling duration [46]. Process parameters can affect the quality of the product to a large extent, especially for the problem of warpage and shrinkage deformations. However, the effects of these parameters are coupled to each other and rely heavily on the long-term experience of skilled operators [47], which makes it difficult to set a proper process parameters combination.

The way to obtain process parameters

The measurement of process parameters relies on sensor technology. By introducing pressure sensors, displacement sensors or/and temperature sensors [45] for detecting the polymer melt behavior, injection molding conditions become a visible problem that can be analyzed scientifically [16, 48]. Recently, in-cavity sensors have been applied to gain the machine’s working data of each shot online, and the sensing information has been monitored to control the part quality. Depending on the installation location in injection molding, sensors can be divided into three categories: in-cavity sensors [49], nozzle sensors [50, 51], and tie bar sensors [52] (Fig. 3).

Fig. 3.

Tie bar sensors used in injection molding [54]

For example, Lin et al. [49] designed an apparatus named as pressure sensor bushing module in the mold to evaluate the melt viscosity during the injection process, which overcame difficulties while mounting or dismounting the pressure sensor and allowed us to perform pressure measurements in PIM process more conveniently. Wang et al. [53] presented a novel online pressure–volume–temperature testing equipment to predict the service performance and service life of polymers (ABS, PS, LDPE, PA6, and PP) and optimized process parameters. Chen et al. [54] and Huang et al. [52] utilized strain sensors mounted on tie bars to reveal the dynamics of the mutative clamping force during injection molding. Based on the tie-bar elongation with various clamping force settings, they also developed a novel searching algorithm to identify the proper clamping force value to set, which could feasibly improve the injection molding quality.

The effect of process parameters

The arrangement of process parameters directly affects the deformation of the products. The warpage and shrinkage happen because of inappropriate settings of these parameters, which may change the resistance of the polymer and increase the difficulty of filling [55]. Figure 4a-d displays the optimization of process parameters of large thin-walled parts in whole stages of PIM and the effect of process parameters in minimizing the warpage is shown in Fig. 4d. In this regard, corresponding parameters should be adjusted separately according to the specific situation. The specific effect of the parameters is presented as follows.

Fig. 4.

(a) Warpage in injection molding (b) Warpage versus temperature difference (c) Warpage versus wall thickness (d) Influence of processing parameters on total warpage ((A) mold temperature, (B) melt temperature, (C) packing pressure, (D) packing time and (E) cooling time) [72]

Mold temperature

The mold temperature affects the production efficiency and quality of the product. Adjusting and maintaining an appropriate mold temperature can effectively enhance the mechanical property, increase the dimensional accuracy, improve the surface quality, and reduce the warpage and shrinkage deformations of the products. In addition, it can shorten the cooling time and improve the production efficiency.

Melt temperature

As the melt temperature increases, the viscosity of polymer melt decreases. Additionally, it can prolong the solidified time, which is conducive to the molecular orientation. However, if the melt temperature is too high, it is easy to overheat and degrade the material, and the part will shrink greatly after cooling to room temperature. In short, the melt temperature needs to be set in a suitable interval to melt the plastic uniformly.

Injection rate

By increasing the injection rate, the tendency of the product to generate deformation decreases. On the one hand, the material has a faster flow rate, resulting in a more intense shearing and a greater molecular orientation effect. But on the other hand, the filling time is greatly shortened under the same injection pressure, which makes the product denser and less likely to warp and shrink.

Injection pressure

Excessive injection pressure can promote the difference in molecular orientation and formation of the residual stress, causing the occurrence of warpage.

Holding pressure

The holding pressure can compensate the deformation of the product during the cooling process and can ensure the product’s dimensional stability. If the pressure difference between the gate and the end of the injection unit is too large, the product deforms. The pressure in the mold cavity usually decreases from the end of the filling, causing a greater volume shrinkage of the polymer melt away from the gate than that around gate [22].

Holding time

Extending the pressure holding time is beneficial to reduce the backflow of the melt to the gate, enhance the feeding effect, and make the product denser. However, if the holding time is extended after the gate is frozen, it will only extend the cycle of the PIM process, and will not have a feed effect.

Cooling time

The melt in the cavity does not reach the ejection temperature if the cooling time is too short, and large deformation will occur after ejection. By contrast, if the cooling time is too long, the injection process will be inefficient.

How to ensure the coordination of process parameters and the quality of the product is indeed a problem that plagues so many people. It is difficult to ensure the consistency of the product’s quality in injection molding process. Even if the system pressure for pushing the screw forward is accurate, an injection molding process performed under same machine condition settings will produce a varying cavity pressure curve and result in an inconsistent part quality [45]. Many researchers have worked tirelessly and many methods have been conducted for the purpose of obtaining consistent quality molded parts (Table 1). The recent progress to optimize process parameters for solving the problem of warpage and shrinkage deformations will be explained in the next section.

Table 1.

The related research about process parameters optimization

Author(s)	Year	Approach(es)	Objective function(s)	Process parameters
Chang and Faison [70]	2001	Taguchi method	Shrinkage	Holding pressure, holding time, mold temperature, injection pressure, melt temperature, back pressure, and cooling time.
Wen et al. [72]	2014	Taguchi method	Warpage	Melt temperature, cooling time, packing pressure, packing time, and mold temperature.
Barghash et al. [79]	2014	Taguchi method and multistage experimental design	Shrinkage and warpage	Cooling channel diameter, gate diameter, melt temperature, pressure holding time, filling time, and cooling inlet temperature.
Azaman et al. [74]	2015	Taguchi method	Residual stresses, shrinkage and warpage	Packing pressure, packing time, mold temperature, and cooling time.
Xu et al. [60]	2015	BPNN and PSO	Warpage	Melt temperature, mold temperature, injection pressure, injection time, holding pressure, holding time, and cooling time.
Zhao et al. [62]	2015	NSGA-II, IEGO and Kriging model	Warpage, volumetric shrinkage and sink marks	Injection time, melt temperature, packing time, packing pressure, cooling temperature, and cooling time.
Zhang et al. [61]	2016	LHD, EBFNN, and MOPSO	Warpage and clamping force	Valve gate open timing, molding temperature, melt temperature, injection time, packing pressure, packing time, and cooling time.
Li et al. [57, 119]	2017	Orthogonal experiment design, BP / GA	Warpage	Fiber content, fiber aspect ratio, melting temperature, injection pressure, holding pressure, and filling time.
Heidari et al. [85]	2017	CCD, RSM	Warpage and shrinkage	Coolant temperature, mold temperature, melt temperature, packing time, injection time, and packing pressure.
Lin et al. [75]	2017	Taguchi method	Residual stress	Melt temperature, filling time, packing time, and mold temperature.
Kitayama et al. [87, 88]	2017	RBF	Cycle time and warpage	Melt temperature, injection time, packing pressure, packing time, cooling time, and cooling temperature.
Singh et al. [82]	2018	Orthogonal array design and Taguchi method	Cycle time and warpage	Injection pressure, melt temperature, packing time, and packing pressure.
Li et al. [112]	2018	Taguchi method, RSM and NSGA-II	Product warpage, volumetric shrinkage and residual stress	Mold temperature, melt temperature, flow rate, and packing pressure.
Mukras et al. [86]	2019	Kriging model	Warpage and volumetric shrinkage	Mold temperature, melt temperature, packing pressure, packing time, cooling time, injection speed, and injection pressure.
Usman et al. [78]	2020	Taguchi method	Surface roughness and shrinkage	Injection temperature, injection pressure, injection speed, and mold temperature.
Song et al. [30]	2020	BPNN, GA, RSM and support vector machines	Warpage and volume shrinkage	Mold temperature, melt temperature, injection time, holding time, cooling time, and holding pressure.
Byon et al. [98]	2020	GA and DOE	Warpage	Gate position, gate size, packing time, and melt temperature.
Rosli et al. [108]	2020	RSM	Volumetric shrinkage and warpage	Melt temperature, mold temperature, injection pressure and cavity layout.
Fuat [106]	2020	RSM and Grey Wolf Optimization	Warpage, volumetric shrinkage and cycle time	Fiber ratio, mold temperature, melt temperature, injection pressure, and injection time.
Lockner et al. [96]	2021	ANN	Part quality	Injection flow rate, holding pressure time, holding pressure, cooling time, melt temperature and cavity wall temperature.
Zhou et al. [113]	2021	Kriging model and RSM	Product quality, productivity and cost	Melt temperature, mold temperature, injection time, packing pressure, packing time, and cooling time.
Li et al. [114]	2021	Kriging model	Warpage	Packing time, packing pressure, melt temperature, injection time, mold temperature, cooling time.

Optimization methods

The warpage and shrinkage deformations are inevitably caused by parameters manipulation. It is a challenging but meaningful process for scientists and manufacturers to achieve better quality control in injection molding. Previously, the determination of process parameters greatly relied on the experience of operators, this is, the so-called trial and error methods. Trial and error methods are traditional approaches that highly depend on the operator’s “know-how” and intuitive sense acquired from long-term practice [56]. Rather than through an analytical and theoretical computation, setting process parameters by operators is really a skilled job. Nowadays, there are many efficient approaches such as the design of experiments and some intelligent algorithms, which can greatly reduce the reliance on experience and are less time-consuming [57–62]. The following section will highlight the latest use of those methods for the optimization of process parameters to minimize the warpage and shrinkage deformations of the plastic part.

Design of experiments

To design a satisfactory quality of the molded part, the experiment conducts one process parameter at a time for an ad hoc experimental design approach [56]. Experiments and responses are performed to investigate characteristics and evaluate whether it has been reached to objectives, relatively. The purpose of DOE is to determine the allocation and ways of experiments to approach objectives. The common DOE process is illustrated in Fig. 5.

Fig. 5.

General DOE process [56]

Compared to other trial and error methods, this method is relatively easy to apply and occupies less computation cost. It has been earned a large quantity of application in the field of biology, medicine, machinery, material, etc. Some researches that use this technique in PIM are presented following.

Taguchi method

The Taguchi design method is a well-proven statistical-based technique for the optimization of complex problems in many fields, including manufacturing, engineering, biotechnology, marketing and advertising [63–65]. It offers technology for improving the manufactured good through a systematic process of statistical analysis and experimental trials [66]. Importantly, the Taguchi method provides the maximum amount of information from a minimum number of experimental runs and is hence extremely useful in optimizing complex processes with many interrelated variables, for which traditional trial-and-error approaches are inefficient, time-consuming and expensive [67]. In general, signal-to-noise (S/N) and analysis of variance (ANOVA) approaches are commonly needed to assess the quality of the outcome acquired from each experimental run in implementing the Taguchi method [68]. The S/N ratio reflects both the average and the variation of the quality characteristic while the analysis-of-variance (ANOVA) contains the effect of all other sources not controlled or measured during the experiment [69]. In this way, we can determine the final optimal process parameters.

To comprehensively explore the influence of process conditions on the shrinkage of three plastics: high-density polyethylene (HDPE), general-purpose polystyrene (GPS) and acrylonitrile-butadiene-styrene (ABS), the Taguchi method was utilized to systematically verify and validate the optimal conditions at the beginning of the 21st century [70]. The prediction value of GPS showed good consistency with the experiment. With the discovery of the dramatically continuous warpage of a large thin-walled workpiece during the free-cooling stage after ejection [71], Wen et al. [72] investigated the combined effect of processing parameters on warpage in injection and free-cooling stages of a type of motorcycle seat support made of polypropylene (PP) with the combination of the Taguchi method and finite element modeling (FEM) analysis. In the same way, an approach of manufacturing a hard mold with micro-features for micro-plastic injection molding was proposed, which significantly reduced a new optical element development cycle time [73]. In order to raise the persuasiveness and confidence, multiple criteria including practicality, efficacy, ease of construction, and adequate accuracy were considered collectively to favor the Taguchi method. Azaman et al. [74] studied the effect of injection-molding parameters during the post-filling stage (packing pressure, packing time, mold temperature, and cooling time) with the assistance of numerical simulations, the Taguchi method, S/N ratio, and ANOVA. The study showed the reduction of trial molding times and the improvement of part quality and could serve as a reference in the further investigation of molding defects of thin-walled parts fabricated using lignocellulosic polymer composite. Additionally, a Taguchi method of $L_9$ integrated with computer-aided engineering (CAE) simulations were generated to find variability of procedure parameters of the injection molding considering the birefringence effect, and eventually, minimize the residual stress within the molded Fresnel lens and hence reduce its birefringence [75]. The present study integrated the Taguchi design method with Moldex3D simulations [76] to determine optimal injection molding processing conditions in a more efficient and versatile manner, which gave rise to a better aesthetic appearance of the final sintered product and an enhanced mechanical strength [67, 77]. Meanwhile, multi-response optimization of PIM process parameters of polystyrene and polypropylene to minimize surface roughness and shrinkage using an integrated approach of S/N ratio and composite desirability function was put forward by Usman et al. [78]. Wang et al. [39] conducted the orthogonal experiment to analyze the influence of injection process parameters on the evaluation index and employed the Taguchi method to obtain an signal-to-noise ratio. The final minimum warpage was acquired as 6.405 mm, significantly reduced compared with other tests.

Orthogonal array design

Orthogonal array design is another type of method. It is a fractional factorial design that allows experimenters to study main effects and desired interaction effects in a minimum number of trials or experimental runs. Generally, $2^{k-p}$ is presented in the design, where k is the number of factors and ${(1/2)}^p$ represents the fraction of the full factorial $2^k$. Take $2^{5-2}$ as an example, it is a 1/4th fraction of a 25 full factorial experiment, which means it is enough to study five factors at two levels in just eight experimental trials rather than 32 trials [56].

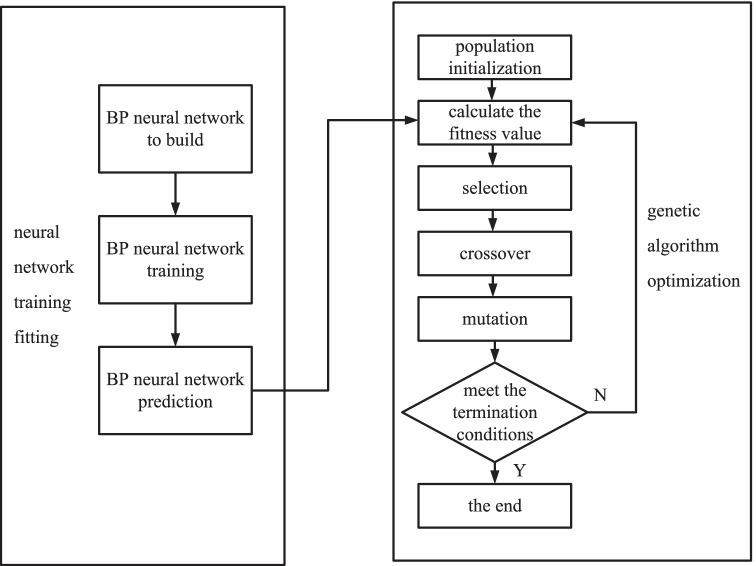
The relatively research of the orthogonal array design is also significant. The multistage experimentation [79], with Taguchi’s experimentation stage for classifying important factors and a full-factorial design of experiments stage that analyzed both main and interaction effects, was conducted to assist the modeling shrinkage and warpage up to an error value of 0.23 and 0.07mm, respectively. $L_9$ [75], $L_{18}$ [80], $L_{25}$ [81], $L_{27}$ [82] orthogonal arrays were generated for multi-response optimization of PIM process parameters to reduce the cycle time and warpage. Huang and Lin [80, 83] offered an innovative searching method to achieve robust injection molding quality based on a regression model. By minimizing the volumetric shrinkage as a goal of the light-guided plate (LGP), the experimental results demonstrated that this searching method was practical indeed. At the same time, with the help of orthogonal experiment design, the Taguchi method [72, 74, 84], BPNN/GA [57] was interfaced with this predictive model to improve the warpage significantly by optimizing design parameters, and the results showed that those combination approaches were effective methods for the warpage optimization of PIM process. The outline of the combined (BPNN) / GA optimization algorithm is explained in Fig. 6.

Fig. 6.

Flowchart of BPNN / GA [57]

There are many other DOE methods such as Central composite design (CCD) [85, 86], Box–Behnken design (BBD) [87, 88], and Latin hypercube design (LHD) [61]. These methods are less common in the optimization of PIM process parameters. Thus, we will not give a detailed introduction to the limitation of this article.

Advanced models

In terms of industrial manufacturing processes, the PIM process is particularly qualified for data-driven optimization because of its high non-linear process behavior and complex relationship between machine, process, and quality parameters [89]. The PIM process is multivariable and involves large time delays, time variations, nonlinearity. An accurate description of the process behavior based on physical modeling is not possible, e.g., due to the viscoelastic thermoplastic material characteristics. Thus, a mathematical approximation algorithm seems to be the most appropriate method to establish the relationship mentioned above. Common mathematical approximation algorithms include artificial neural networks (ANN), genetic algorithm (GA), response surface methodology (RSM), and Kriging model.

Artificial neural network

Artificial neural network (ANN) is a widespread method which emulates the neural reasoning behavior of biological neural systems. The system is consisted by three layers: the input, the hidden and the output layer. But in the most situation, more than one hidden layer is employed to fit a more reliable model. After methodically examining a series of input values and their associated outputs (supervised learning method), we can get a required trained neural network system. A trained ANN system can transform nonlinear mathematical modeling into a simplified black-box structure that is able of generalizing the set of previously learned instances [90].

Owning to the excellent performance, it is extremely popular to apply the ANN algorithm to control the quality of products in the injection molding and the results always show how remarkable this model is. Usually, the mold temperature, melt temperature, holding time, cooling time, injection rate, holding pressure and injection pressure are taken in account as input parameters, while the maximum shear stress served as an evaluation parameter in the component, as this is the main origin for warpage. The detailed configuration of ANN is shown in Fig. 7.

Fig. 7.

Configuration of the ANN model [60]

Shi et al. [91] mainly focused on process operating parameters, such as mold temperature, melt temperature, injection time and injection pressure and used ANN as a surrogate model to develop an offline optimization approach, which greatly reduced the expensive computation required during the period of underdeveloped computing ability. Later, the forward and reverse mapping of artificial neural networks were put forward by Manjunath et al. [92] to predict dimensional shrinkage and an appropriate set of process parameters respectively with an error level of less than ten percent. Alejandro et al. [93] constructed a predictive model for warpage based on artificial neural networks and finite element analysis software Moldflow. A combined artificial neural network and particle swarm optimization (PSO) algorithm method to describe the process-induced warpage and the mechanical behavior of product correctly [60]. The parameter of valve gate open timing [61] was added in the optimization, promoting a structural optimization on the oil cooler cover cooling and a cooling channel improvement. Compared with other regression algorithms, Nagorny et al. [94] concluded that ANN always had better predictions scores. Chen et al. [95] integrated an ANN-based expert system to injection molding process to detect some unavoidable shrinkage and uncontrollable process condition variations, and the result showed that a high prediction accuracy of 98.34$\%$ with the coefficient of determination $R^2$ of 91.37$\%$ was achieved. Recently, induced network-based transfer learning has been used to reduce the necessary amount of PIM process data for the training of an artificial neural network to conduct a data-driven machine parameter optimization for PIM processes by Lockner and Hopmann [96].

Genetic algorithm

Genetic algorithm (GA) is a category of evolutionary algorithms. Without the prior information on PIM, we can obtain the optimum parameters settings with the aid of GA. Selection, crossover, and mutation operators are used in the process of function optimization to enhance the global optimization ability and improve the precision of convergence in GA. Similar to natural evolution, solution candidates and the set of selection are called individuals and population respectively. In the selection process, either stochastic or completely deterministic, unqualified individuals are abandoned while excellent individuals are reproduced. The so-called fitness is applied to assess the quality of an individual with respect to the optimization task. New solutions within the search space by the variation of existing ones are produced by crossover and mutation. Recent studies tend to connect this approach with other methods to optimize process parameters in the injection molding machine.

Zhao et al. [62] developed a two-stage framework consisting of the improved efficient global optimization (IEGO) algorithm to improve optimization iterations in the first stage and the non-dominated sorting-based genetic algorithm II (NSGA-II) algorithm to find a much better spread of design solution and better convergence near the true Pareto optimal front in the second stage. By considering process and fiber parameters on the effect of part quality, Li et al. [97] systematically studied the warpage defect and proposed a combined Taguchi, response surface methodology, and non-dominated sorting genetic algorithm II (NSGA-II) approach. SVM-BP-GA [30], a model combined with support vector machine (SVM), backpropagation (BP) neural network, and GA, was an effective method for injection molding to reduce warpage and volume shrinkage of thin-walled parts. The gate position and the gate size were introduced with GA to minimize both the stress and deformation in medical suction device components by Byon et al. [98]. There were also other methods like control volume finite element method (CVFEM) [99], Gaussian process (GP) [100], response surface methodology (RSM) [101], CAE [102], Moldflow [103], ANN [91, 104, 105], DOE [104, 105] to combine with GA, which helped effectively to reduce the warpage and shrinkage of injection parts.

Response surface methodology

As a set of statistical and applied mathematical technology, response surface methodology (RSM) plays a role to establish empirical models between objective characteristics and design variables. It usually generates polynomial formulas as response surface (RS) models to express the relationship of input and output. RSM can save the expensive analysis cost that happened in finite element calculation and reduce the associated numerical noise as well. The mathematical relationship used in the RSM is a complete second-order polynomial model, as expressed in Eq. (1).

$$\begin{array}{c}\hfill Y={\beta }_0+\sum _{\mathrm{i}=1}^4{\beta }_i{x}_i+\sum _{i=1}^4{\beta }_{\mathit{ii}}{x}_{\mathit{ii}}^2+\sum _{i<j=1}^4{\beta }_{\mathit{ij}}{x}_i{x}_j\end{array}$$ 1

where ${\beta }_o$, ${\beta }_i$, ${\beta }_{\mathit{ii}}$ and ${\beta }_{\mathit{ij}}$ are constant value, linear effect, second effect and reciprocal effects of the regression coefficient, respectively. $x_i$ and $x_j$ are independent coded variables [106].

Heidari et al. [85] used RSM, based on the central composite design (CCD), to explore the effect of process factors on the PLA-based bone screws. Coolant temperature, mold temperature, melt temperature, packing time, injection time, and packing pressure were investigated to minimize the shrinkage and warpage of three polylactic acid (PLA) materials. At the same time, the design of experiment (DOE) - response surface methodology (RSM) with central composite design (CCD) having three factors namely mold temperature, melt temperature and injection rate was designed to optimize tensile properties of injection molded $\alpha$-nucleated polypropylene to decrease the amount of warpage [107]. Rosli et al. [108] found that the “H” branching cavity layout could get small differences error value between solution and simulation, nearly 0.31% for volumetric shrinkage and 0.126% for warpage by using RSM. Among the scientific research based on RSM in optimization of injection parameters, we could also find the usage of the grey wolf optimization [106], the Taguchi Method [109], and the non-dominated sorting genetic algorithm II (NSGA II) [58]. However, unlike the genetic algorithm as a global optimization way, sometimes, RSM was trapped in the local extremum. Thus, most authors utilized other methods to enhance the model or to compare the conclusion with each other. Gradient-based optimization techniques were always applied to be in conjunction with RSM in many pieces of research the most of the time [110].

Kriging model

Geologist Krige first proposes the Kriging model, which is based on structural analysis and variation function theory and can unbiasedly optimize the design of regionalized variables [111]. The Kriging model was used in the estimation of the reserve distribution of mineral deposits in the early years and gradually applied in the optimized design. An approximation relationship between input (process parameters) and output (molding quality), thus preventing the time-consuming finite element reanalysis in the complicated, non-linear, implicit and multimodal engineering progress. The input variable and the response value of the Kriging model are decided by Eq. (2):

$$\begin{array}{c}\hfill y(x)=f(x)+\mu (x)\end{array}$$ 2

where f(x) is a fixed item of the known polynomial function x, $\mu (x)$ is an approximate random function reflecting the local difference. Under the condition of a few samples, a certain fitting accuracy can be guaranteed by the application of the Kriging model. Through the effect of the correlation function, the optimization design can be defined as a local estimation problem, which has been well applied to the reducing of the warpage.

Wang et al. [59] performed the optimization of warpage by employing dynamic filling and packing process parameters for the first time. The Kriging model was utilized to approximately characterize the unclear relationship between the objective (maximum warpage) and process parameters. By using the expected improvement (EI) and the finite element method (FEM) to balance local and global search and simulate the micro-injection molding process of polymer stent respectively, an adaptive optimization method based on the kriging surrogate model was proposed to reduce the residual stress and warpage of stent during its injection molding [112], as shown in Fig. 8. Zhou et al. [113] proposed a differential sensitivity fusion method for product quality and productivity improvement. Some classical methods, like the Kriging model, were conducted to compare the performance and prediction accuracy of the method. Li et al. [114] established the Kriging model to map the nonlinear function relationship between the warpage and some valuable factors in order to reduce the warpage of transparent parts.

Fig. 8.

Complete process of the optimization algorithm based on the Kriging model [112]

In addition, particle swarm optimization (PSO) [60, 61, 73, 104, 115–119], model-free optimization (MFO) [120, 121], support vector machines (SVM) [122], simulated annealing, and hill-climbing are all advanced and effective ways to conduct the optimization design of process parameters. These models can be used to construct a mathematical approximation to replace expensive finite element analyses. They have similar effects in optimization and will not be specifically listed here.

Conclusions

As presented in the above sections, great achievements have been made in the minimization of the warpage and shrinkage deformations using optimal design approaches in the past decades. Also, the selection of materials, the design of plastic parts and molds, and the settings and optimization of process parameters can significantly reduce the generation of warpage and shrinkage deformations in injection molding. More importantly, the advanced approaches have great potential in optimizing process parameters for their sensitivity in the product’s warpage and shrinkage deformations.

However, there remain many challenges in the quality control of injection molding, such as (1) develop a perfect polymer plasticization model, which is difficult owing to the simplification of the complex plasticization process. (2) precisely and/or programmably control the mold clamping and injection process and (3) combine micro-electro-mechanical system (MEMS), the advanced sensing technology, and the autonomous learning driven by big data. We believe that with continuous improvements and breakthroughs in injection molding, more and more high-quality polymer products will be manufactured and applied in many engineering fields like the aerospace industry, biomedical application and environmental protection.

Author contributions

Nan-yang Zhao contributed to writing—original draft, methodology, and conceptualization. Jiao-yuan Lian performed writing—review and editing. Peng-fei Wang performed writing—review and editing. Zhong-bin Xu performed supervision and project administration.

Funding information

This work was supported by National Natural Science Foundation of China (No. 52073247) and by Institute of Robotics at Zhejiang University under (Grant K12105).

It declares that codes are not available for this research.

Declarations

Consent to publish

All the authors consent to publish the research. There are no potential copy-right/plagiarism issues involved in this research.

Consent to participate

All the authors consent to participate in this research and contribute to the research.

Ethical approval

The authors claim that there are no ethical issues involved in this research.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Competing interests

The authors declared that they have no conflicts of interest within the last 3 years of beginning the work.