Morphological principles of neuronal mitochondria

Abstract

In the highly dynamic metabolic landscape of a neuron, mitochondrial membrane architectures can provide critical insight into the unique energy balance of the cell. Current theoretical calculations of functional outputs like adenosine triphosphate and heat often represent mitochondria as idealized geometries, and therefore, can miscalculate the metabolic fluxes. To analyze mitochondrial morphology in neurons of mouse cerebellum neuropil, 3D tracings of complete synaptic and axonal mitochondria were constructed using a database of serial transmission electron microscopy (TEM) tomography images and converted to watertight meshes with minimal distortion of the original microscopy volumes with a granularity of 1.64 nanometer isotropic voxels. The resulting in-silico representations were subsequently quantified by differential geometry methods in terms of the mean and Gaussian curvatures, surface areas, volumes, and membrane motifs, all of which can alter the metabolic output of the organelle. Finally, we identify structural motifs present across this population of mitochondria, which may contribute to future modeling studies of mitochondrial physiology and metabolism in neurons.

1 |. INTRODUCTION

Significant amounts of energy are required in the brain to maintain the flow of information (Harris et al., 2012). Neurons, as the main active cell type participating in these information flows, are highly polarized cells with extended axons, and exhibit fast electrochemical signals based on ion redistribution, which imposes an energetic burden on them (Misgeld & Schwarz, 2017). The energy requirements of a synapse, where information is transmitted from one neuron to another, have been estimated for the different subprocesses at multiple millions of adenosine triphosphate (ATP) molecules per second (Attwell & Laughlin, 2001; Harris et al., 2012). Presynaptic mitochondria are known to be strategically located to respond to the local energy demand of synaptic transmission and have specialized features on the molecular and morphological levels (Devine & Kittler, 2018; Perkins et al., 2010). Furthermore, mitochondrial dysfunction and synaptic homeostasis are believed to contribute to neurodegeneration (Devine & Kittler, 2018; Mnatsakanyan & Jonas, 2020). The connection between neuronal metabolic dysfunction and mitochondrial ultrastructure has been documented for diseases, such as Leigh syndrome, where models correlate insufficient ATP production with compromised morphology (Siegmund et al., 2018). Therefore, understanding the interplay between the molecular and morphological organization of mitochondria may contribute new insights into brain energy homeostasis, synaptic function, and mechanisms of neurodegeneration.

Mitochondrial architecture consists of two compositionally and functionally distinct membranes: the outer membrane (OM) and the inner membrane (IM), shown in Figure 1a. The IM is composed of two contiguous structures: the inner boundary membrane (IBM) and the cristae membrane (CM). The IBM is the outer surface which remains in close opposition to the OM (Figure 1b), while the CM forms the internal network of compartments connected to the IBM via narrow tubular structures known as cristae junctions (CJs) (Frey & Mannella, 2000; Perkins et al., 1997). This compartmentalized structure provides a highly specialized and adaptable framework for the conversion of metabolic substrates to ATP. The matrix, a volume encapsulated by the IBM and CM, consists of the molecular components needed for the tricarboxylic acid cycle. The CM itself is the site of the electron transport chain (ETC). Further localization of ETC complexes within the CM is facilitated by variations in membrane curvature which have been shown to correlate with protein placement and function (Cogliati et al., 2013). The morphology of cristae compartments is often described as either lamellar (sheet-like) or tubular, with a single neuronal mitochondrion commonly exhibiting both types (Perkins et al., 2001). While a tubular region will have relatively uniform curvature, a lamellar region consists of two nearly flat sheets connected by regions of intense curvature. In addition to promoting a non-uniform distribution of proteins, the highly variable surface created by these structures can optimize the internal surface area and is thought to control the reaction rates of ETC enzymes as well as the formation of supercomplexes (Cogliati et al., 2013).

FIGURE 1.

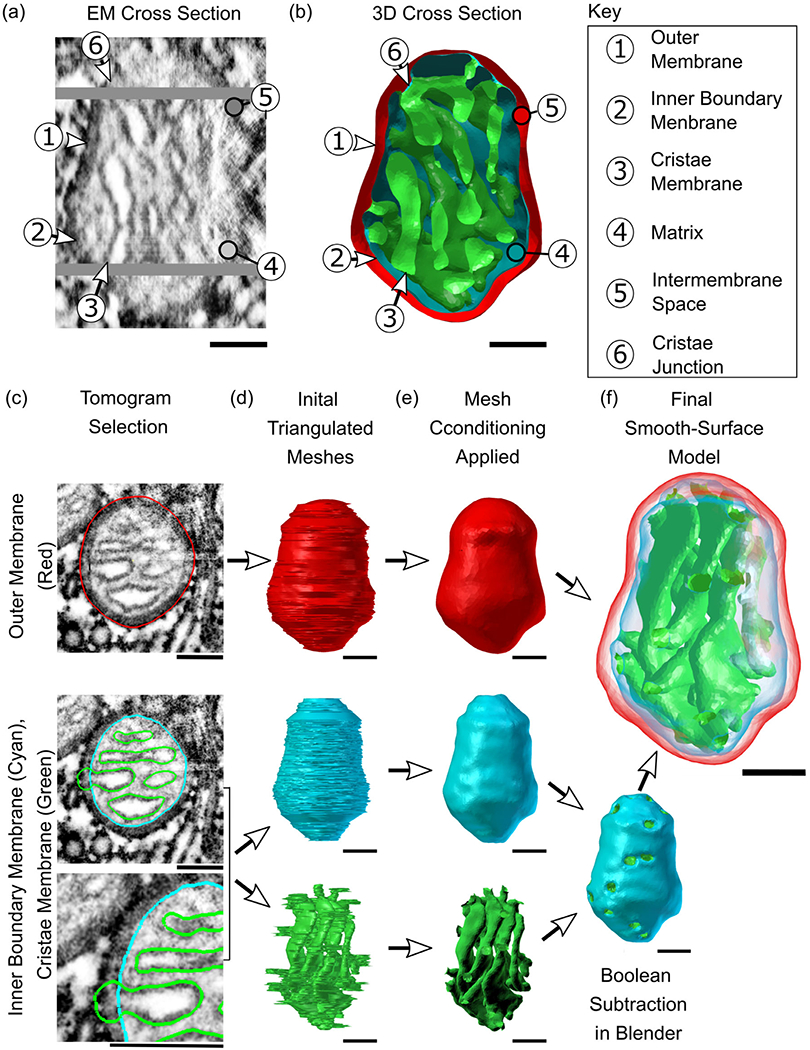
From high-resolution 2D representations of mitochondria to high-quality 3D reconstructions. (a and b) Serial electron tomographic images of mouse cerebellum neuropil at an isotropic voxel size of 1.64 nm are used to reconstruct the two lipid bilayer membranes of a mitochondrion, exemplified here with reconstruction #12. One specific EM cross section is shown here, highlighting the physical section in the tomogram and its associated 3D cross section reconstruction. The spatial organization of these membranes generates a number of compartments and submembrane regions specified here. (c)The hand-traced contours used in the reconstructions are shown overlayed on a cutout from the respective tomographic image. These three overlays show traces of the three membrane structures; the outer membrane (OM, in red), inner boundary membrane (IBM, in cyan), and cristae membrane (CM, in green). Although the inner membrane (IM) is a single structure comprised of the IBM and CM, these two components are treated as separate objects and are combined later. (d)The 3D reconstructions of the membranes are created using the program Contour Tiler (Edwards et al., 2014). Jaggedness in the model’s surface was found to be due to noise resulting from human tracing error. (e) The noise is smoothed out using GAMer 2 mesh conditioning operations (Lee, Laughlin, Moody, et al., 2020) to create the smooth-surface models shown here. The IBM and CM have been joined into one object via Boolean subtraction. (f) Meshes are made transparent and shown together. All scale bars: 100 nm.

Within the dense network of tunnels formed by the CM, both low-energy and high-energy structures exist simultaneously. The protein localization and operation, which depend on this complex framework, make morphometric analysis essential for understanding and modeling mitochondrial function (Garcia et al., 2019). Recent advances in electron microscopic tomography (Phan et al., 2016) and reconstruction methods allow for the creation of three-dimensional models of mitochondria with nanometer-level detail (Perkins et al., 2003; Perkins et al., 2001; Perkins et al., 2010; Siegmund et al., 2018). In this work, we systematically and quantitatively reconstruct and analyze the ultrastructural and geometric features of a population of presynaptic mitochondria from mouse cerebellum. Each mitochondrion is reconstructed in its entirety, allowing for the study of mitochondria as functional units. We use our analysis methods to identify the key geometric features of these mitochondria, such as surface area-to-volume relationships and surface curvatures, which are essential markers of metabolic activity. These analyses have been used to identify the structural motifs that define mitochondrial structure, elucidating the physical framework on which presynaptic energy production occurs. To our knowledge, this is the first quantitative morphological analysis of multiple near-complete mitochondria from presynaptic neurons, which includes their surface curvatures and functional motifs. This lays the foundation for defining structure-function relationships in these critical organelles.

2 |. MATERIALS AND METHODS

Two serial tomographic data sets from the molecular layer of the cerebellum of two mice yielded eight presynaptic and four axonal mitochondria. The surrounding synapses and unmyelinated axons are from parallel fibers (presynaptic) and Purkinje neurons (postsynaptic). These organelles were fully contained in the samples with a tomographically reconstructed isotropic voxel size of 1.64 nm. With physical serial sections of 300 nm each, a single mitochondrion spans 1–3 physical sections. At the area between these sections, missing material of approximately 15–20 nm and distortion caused by the slicing process was corrected for using state-of-the-art image alignment (Wetzel et al., 2016) and gap interpolation techniques described later in this section. This allowed for the complete reconstruction of 12 mitochondria, with high enough image quality to generate complete reconstructions of all membranes for nine of them.

High-image resolution enables the contours of the OM, IBM, and CM of a mitochondrion to be observed and manually traced on each virtual section (Figure 1c) using reconstruction software. The process of creating a three-dimensional surface mesh from the traced contours and smoothing out surface noise using mesh conditioning algorithms resulted in reconstructed surfaces with only 3.5 nm total error in surface placement (Figure 1b–f).

2.1 |. Specimen preparation

A mouse (C57BL/6NHsd, male, 1-month old) was anesthetized with ketamine/xylazine and fixed by transcardial perfusion. The vasculature was briefly flushed with oxygenated Ringer’s solution, followed by 2.5% glutaraldehyde, 2% formaldehyde, 2 mM CaCl₂ in 0.15 M sodium cacodylate buffer for 10 min. The fixative solution was initially at 37°C and was cooled on ice during perfusion. The brain was removed from the cranium and placed in the same fixative solution for 1 h at 4°C. The cerebellar vermis was cut into 100 μm-thick sagittal slices on a vibrating microtome in ice-cold 0.15 M cacodylate buffer containing 2 mM CaCl₂ and briefly stored in same buffer prior to high-pressure frozen (HPF). A 1.2 mm tissue punch was used to take tissue from vibratome slices. Punches were placed into 100 μm-deep membrane carriers and tissue was surrounded with 20% bovine serum albumin (Sigma) in cacodylate buffer to prevent air pockets. The carrier was then frozen with a Leica EM PACT2. Freeze substitution was performed in a Leica AFS2 using extra dry acetone (Acros) as follows: 0.1% tannic acid at −90°C for 24 h, washed 3–20 min in acetone, 2% OsO₄/0.1% uranyl acetate at −90°C for 48 h, warmed for 15 h to −60°C, held at −60°C for 10 h, and warmed to 0°C over 16 h. The specimen was in infiltrated with a series of Durcupan ACM: acetone solutions at room temperature and then embedded in 100% Durcupan at 60°C for 48 h.

2.2 |. Electron tomography

A diamond knife was used to collect ribbons of 300 nm-thick serial sections on 50 nm-thick Luxel slot grids. Sections were glow discharged and coated by dipping grid briefly in 10 nm colloidal gold solution (Ted Pella). Serial tomographic reconstructions were generated of parallel fiber-Purkinje cell synapses using an FEI Titan 300 kV transmission electron microscopy (TEM) equipped with a 4k x 4k CCD camera (Gatan Ultrascan). For each region of interest (ROI), tilt series were collected with 0°, 45°, 90°, and 135° degrees of in-plane specimen rotation. Each of these tilt series were collected from −60° to 60° with 1° tilt increments. Images were collected with a pixel size of 0.4 nm, then binned by 4 prior to tomographic reconstruction with TxBR (Phan et al., 2016). Since the ROIs spanned multiple serial sections, serial tomographic reconstructions were created.

2.3 |. Alignment of serial tomographic volumes

The two serial tomographic data sets consist of four and seven physical serial sections. Within a serial data set, the tomographic reconstruction of each 300 nm-thick physical section results in a separate volume for its respective section of neuropil. We used image registration software, SWiFT-IR (Wetzel et al., 2016), to precisely align the physical section volumes with one another. To accomplish this, alignment was performed between the last virtual section of a given physical section and the first virtual section of the next physical section. No alignment was performed between the virtual sections within a physical section as the tomographic reconstruction produces virtual sections that are already aligned. It is important to note that the physical sections sustained a certain unknown amount of inelastic deformation due to the cutting forces of the diamond knife during sectioning. Because of this deformation, we used SWiFT-IR to bring the sections into the best alignment possible using only 2D affine transformation implemented as X translation, Y translation, rotation, X scale, Y scale, and X skew. To further constrain the alignment transformation, we noted that the determinant of the 2D affine transformation matrix can be interpreted as the scaling of the area of a unit square. After an initial alignment step, we analyzed the determinant of the affine transform between each pair of physical sections and identified the physical section which required the least overall deformation of the area. We then defined this section as the alignment reference for the serial data set by fixing the transform for this section to the identity transform and adjusting the remaining transforms in the data set accordingly. This yielded the final aligned volume for each serial tomographic data set, spanning all its physical sections.

2.4 |. Interpolation of gaps between serial sections

Both data sets are composed of a number of physical serial sections of neuropil. While spacing between reconstructed virtual sections is 1.64 nm, the spacing between the physical sections is somewhat larger. When the physical sections are joined with the same 1.64 nm spacing, an obvious discontinuity in the shapes of the mitochondria and other subcellular structures is visible at the interface between one physical section and the next. This is especially apparent in the XZ or YZ projections of the volumes that allow the full image stacks to be viewed from the side (Figure 2a). As the alignment of the physical sections by SWiFT-IR was excellent, we surmised that the discontinuity was due to a gap (i.e., missing virtual sections) in the Z spacing. In order to estimate the proper Z spacing, the XYZ mode of IMOD was used to compile six evenly spaced cross sections from each data set in the XZ and YZ planes. This allowed the degree of discontinuity to be assessed visually at six locations for each physical gap. The space seen at the junction between images was increased until the membranes could be connected by a smooth, continuous curve rather than a jagged line (Figure 2b). The amount of Z spacing added to achieve continuity is an average for each of the six views. The average gap sizes for Data set 1 and Data set 2 are (15.6 ± 0.8) nm and (18.6 ± 1.6) nm, respectively. Gaps of these sizes are equivalent to approximately 10 and 11 missing virtual tomographic sections at a thickness of 1.64 nm. Ten blank virtual sections were inserted at each gap and additional contours were drawn on these sections in order to create complete reconstructions. This manual interpolation of contours was assisted by IMOD’s spherical and linear interpolation tools (Kremer et al., 1996).

FIGURE 2.

Alignment and gap insertion. (a) A side view of all sections in the Data set 1 image stack compiled perpendicular to the tomographic sections with spacing of 1.64 nm between tomographs. The stack is shown before and after alignment with SWiFT-IR and the addition of appropriate spacing to account for gaps between physical sections. Spacing of 16.4 nm is added at each gap. In green is a single membrane feature traced on each image for comparison. The black box indicates the mitochondrion shown in Figure 1. (b) A closeup to this organelle with a section of outer membrane traced in red to demonstrate improved continuity across sections after alignment and gap insertion.

2.5 |. Manual tracing of mitochondria

The tomographic volumes were visualized in a 3DEM software, Reconstruct (Fiala, 2005) or IMOD (Kremer et al., 1996), and the membrane-bounded mitochondrial structures were identified. The contours of the outer leaflet of the OM, and the inner leaflet of the IBM and CM were manually traced as separate objects. Although the IBM and CM form one contiguous structure in mitochondria, they were traced as two separate objects (Figure 1c) and later combined (Figure 1f). This procedure averts the meshing challenges posed by a single set of contours with deep invaginations. At CJs, the IBM object was traced as passing over the junction. The separate CM object at the CJ was then traced to follow the curvature at the mouth of the junction before smoothly intersecting and protruding beyond the tracing of the IBM. These protrusions acted as markers of the junctions to distinguish them from artifact and preserve the shape during the mesh smoothing process performed at later stages. Contours were traced on the most clearly visible membrane leaflet for each object (the cytosol side of the OM and the matrix side of the IBM and cristae). Three mitochondria were traced multiple times to estimate the error due to manual tracing. We estimate the tracing error to be approximately one half the membrane thickness, 3.5 nm.

2.6 |. Mesh generation

The CellBlender (Bartol et al., 2015) modeling plug-in for Blender was used for 3D mesh generation and analysis. The program Contour Tiler (Edwards et al., 2014), which is integrated with the NeuropilTools module of CellBlender, was employed to create triangulated surface meshes from the traced contours. The resulting surface meshes retain the exact shape and dimensions of each contour down to the subnanometer level. This curvature triangulation was performed separately for the three membrane objects in each mitochondrion. A Blender “Boolean Difference Modifier” was subsequently applied to subtract the CM object from the IBM object (Figure 1e and f). This created the cavities in the IBM due to the CJs and CM. In the operation, the protrusions disappeared and the CJ curvature was preserved. Although no alterations have been made to the traces at this stage, the intrinsic human tracing errors make the mesh jagged and uneven. To improve the meshes, we used the Smooth and Normal Smooth mesh improvement tools in GAMer 2 (Lee, Laughlin, Angliviel de La Beaumelle, et al., 2020). The noise of the improved surface mesh is greatly reduced, and when overlayed on the original, the denoised mesh is seen to pass between the peaks and valleys of the noise of the original boundary traces, thus reducing the tracing error. Finally, to verify if any compression artifact had occurred in the 3DEM data set, we traced and reconstructed synaptic vesicles. Analysis of vesicle shape revealed 23.9% shrinkage in the Z direction of the image stacks. We scaled the reconstructed meshes by a factor of 1.27 in the Z direction to obtain spherical vesicles of 40 nm diameter. This Z-scaling factor was then applied to the mitochondria meshes.

2.7 |. Mesh analysis

All mesh analysis and characterization were performed in Blender using Blender add-ons. Surface area, volume and genus were measured with Cellblender mesh analysis, and linear distances were computed with MeasureIT. Skeletons of the OM and IM were generated with the mesh skeletonization tool of the CGal library (Tagliasacchi et al., 2012), interfaced in Blender through the Python API (this generated code is also provided). For this purpose, meshes needed to be converted to OFF format with a Blender OFF Add-on. The skeletons were further used to calculate the radius of the organelle at positions along its length, projecting points from the skeleton to the mesh and calculating the radial distance to it. Several points are used to measure the radius at each location in the skeleton, all with a distance smaller than 0.01 μm to the perpendicular plane set at the location. With a similar approach, we calculated the length of the organelles.

We estimated the diameter of the CJs from the measurements of the area of the IBM with and without CJs (i.e., before and after the performed Boolean operation). The average surface area taken up by CJs is: CJ area = (SA IBM closed – SA IBM )/# CJs. We further assume the CJ area is circular, and from this area, we calculated the radius: CJ area = π r².

Curvature analysis was carried out with GAMer 2 (Lee, Laughlin, Angliviel de La Beaumelle, et al., 2020; Lee, Laughlin, Moody, et al., 2020) through its Blender interface, using the MDSB algorithm (Meyer et al., 2003) for curvature calculation. For all curvature analyses, the smooth curvature after one iteration was considered. This smoothing is the average curvature of a vertex and its neighbors.

Idealized shapes were generated with Netgen (Schoberl, 1997). All statistical analysis and plots were generated using Python 3.8, with the libraries NumPy (Harris et al., 2020), SciPy (Virtanen et al., 2020), Matplotlib (Hunter, 2007), and Scikit-learn (Pedregosa et al., 2011). The K-means clustering algorithm implemented in Scikit-learn was used to cluster geometric features of the organelles. Given a sets of points (two-dimensional in our case), this algorithm partitions the points into k sets (k = 2 in our case) minimizing the sum of squares (i.e., the variance). Statistical significance was assessed using a nonparametric method, the two-sample Kolmogorov–Smirnov (KS) test implemented in SciPy.

3 |. RESULTS

To analyze the architecture of neuronal mitochondria from mouse cerebellum neuropil, 3D reconstructions of eight presynaptic and four axonal mitochondria were generated using serial TEM tomography images. Each mitochondrion reconstruction has been assigned a reference number and its placement in the neuropil has been evaluated (Figure 3 and Table 1). Nine of these mitochondria were captured at high enough image quality to fully reconstruct the CM, allowing for complete models of all membranes. From manual membrane traces, we created high-quality meshes at a scale of 1.64 nm isotropic voxel size. New procedures and tools, including the mesh processing software GAMer 2 (Lee, Laughlin, Angliviel de La Beaumelle, et al., 2020; Lee, Laughlin, Moody, et al., 2020), state-of-the-art image alignment (Wetzel et al., 2016) and gap interpolation techniques, were implemented to minimize distortion from the original microscopy images (see Methods for further details). The fine detail of the resulting smooth meshes (Figure 3) is thus well-preserved for point-by-point calculation of curvature, a comprehensive method for quantifying geometric features of a surface (Kreyszig, 1968; Struik, 1961). As can be appreciated in Figure 3, this level of detail makes it possible to perform such analysis on features as small as CJs, which are approximately 25 nm wide (Perkins et al., 1997; Siegmund et al., 2018). Each of the three membrane components were characterized using these procedures, beginning with the OM.

FIGURE 3.

High-quality 3D reconstructions of axonal and presynaptic mitochondria from mouse cerebellum neuropil. Twelve outer membrane reconstructions were generated (in red). For nine of them, the inner membrane was also reconstructed and is shown here as two separate objects for visual purposes: the inner boundary membrane (in cyan) and the cristae membrane (in green). Each mitochondrion is assigned a reconstruction number for reference. All reconstructions are displayed in the same orientation relative to their placement in the neuropil. In the cristae view, additional surface area has been included from the inner membrane view in order to better showcase the cristae junctions.

TABLE 1.

Characterization of sampled mitochondria

Mito #	Location	Distance to the PM (nm)	Anchor to PM (nm)	Distance to the AZ (nm)	Prot	Distance to the ER (nm)	Ves
1	Presynaptic	9	97	194	N	6	Y
2	Presynaptic	8	64	90	N	7	Y
3	Presynaptic	8	54	119	N	7	Y
4	Axonal	7	133	N/A	N	5	N
5	Axonal	4	53	N/A	Y	8	N
6	Axonal	X	X	N/A	Y	X	N
7	Presynaptic	X	X	X	N	X	Y
8	Presynaptic	10	13	X	N	14	Y
9	Presynaptic	9	23	490	Y	5	Y
10	Presynaptic	10	90	300	N	4	Y
11	Axonal	6	105	N/A	Y	X	Y
12	Presynaptic	10	155	213	N	4	Y

Note: Measurements of mitochondrion placement relative to other organelles are presented for each reconstruction number. Location in either a synaptic bouton (labeled presynatic) or another part of the axon (axonal) is determined by the presence of a synapse and vesicles, as well as an enlarged cell diameter. Along with measurements of proximity to nearby components within the axon (PM, plasma membrane; AZ, active zone; and ER, endoplasmic reticulum), the presence of a mitochondrial outer membrane protrusion (Prot) is labeled with a Y (yes) or N (no). The presence of vesicles (Ves) is specified with the same convention. An X signifies areas where the data were too obscured to evaluate. Since the size of the data sets only enabled the evaluation of features in close proximity, distances to the nearest active zone are not provided for mitochondria outside the synaptic bouton. Distance measurements reflect the smallest distance from the mitochondrial OM to the given feature. The width of the PM tether is the maximum width of contact between the mitochondrial OM and the PM on a single tomograph. All measurements are given in nanometers. We estimate the uncertainty of these measurements at 7 nm based on tests of line placement precision during membrane tracing (see Methods).

3.1 |. Geometric features of the OM reveal a diversity of mitochondrial shapes

Due to their large variability (Figure 3), we began by analyzing the geometric features of the OM of 12 mitochondria. For each mitochondrion, we calculated the volume, surface area, radii along the length, and total length of the OM (refer to the repository with additional material). The volume enclosed by the OM spans a wide range across the reconstructed mitochondria (Figure 4a), varying almost by an order of magnitude; the smallest measured volume was (0.0062 μm³), while the largest was (0.0459 μm³). The surface area of the OM scales with the volume following a power law (Figure 4a, S = αV^γ) with coefficient of γ0.71 and α 1.93 (with R² of 0.98 and p-value of 2x10⁻⁸).

FIGURE 4.

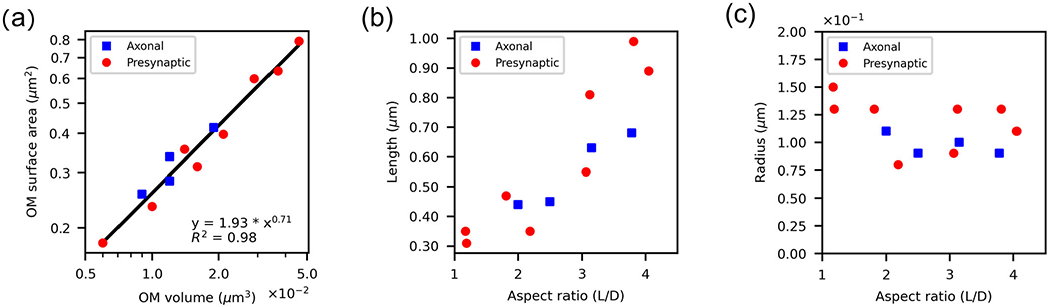
Wide-ranging variation of reconstructed mitochondrial volumes, and their correlation with spatial location. (a) OM membrane surface area correlates with the volume enclosed by the OM. Axonal mitochondria are shown in blue and presynaptic mitochondria in red. (b) The length of the organelles increases with the aspect ratio. (c) The mean radius of the organelles presents some variability for larger aspect ratio.

The shape of the OM also varies within our data set, from globular to significantly elongated. To quantify this observation, we calculated the aspect ratio of each OM shape. We defined the aspect ratio as the length of the reconstructed mesh divided by its width, such that elongated shapes are expected to have a higher aspect ratio and globular shapes are expected to have aspect ratio values close to one (Figure 4b). The width used to compute the aspect ratio is the average of values along the length of a mitochondrion, using a generated skeleton of the mesh (Methods). We contrasted the OM aspect ratio with the radius (Figure 4c) and found some variability on the organelles’ radius for longer organelles, with an average value of (0.11 ± 0.02) μm.

We grouped the mitochondrial reconstructions into two categories based on two geometric properties: the aspect ratio and the average principal curvature (refer to the next section for further details). The populations were identified using the K-means clustering algorithm. For each group, we calculated means and variances of five key geometric features: volume, surface area, radius, length, and aspect ratio, see Table 2. The globular group has smaller aspect ratio (mean value 1.9) than the elongated one (mean value 3.4), with statistically different aspect ratio values (p-value < .026). As expected, the globular group is also shorter in length than the elongated one (although this difference is not significant). Some of the elongated organelles are also thinner, and for this reason, the volume, albeit larger, is not significantly different than in the globular population (Table 2).

TABLE 2.

Morphological properties of the outer membrane

Property	Globular (N = 6)	Elongated (N = 6)	p-value
Aspect ratio	1.9 ± 0.7	3.4 ± 0.6	.026*
Length (μm)	0.5 ± 0.2	0.7 ± 0.2	.143
Width (μm)	0.24 ± 0.04	0.20 ± 0.03	.474
Volume (μm3)	0.02 ± 0.01	0.02 ± 0.01	1
Surface area (μm2)	0.3 ± 0.2	0.5 ± 0.2	.474
Average first principal curvature (k1) (μm−1)	−0.4 ± 0.5	2 ± 1	.002**
Average second principal curvature (k2) (μm−1)	−13 ± 3	−16 ± 3	.47

^*p < .05

^**p < .01.

Note: Specific measurements were performed for each reconstruction. Averages and standard deviations over two distinct populations of mitochondria are presented. Two clusters were determined based on the aspect ratio and average of the first principal curvature of the OM (see Methods for details).

3.2 |. OM curvature

To fully characterize the structure of mitochondria, we employed tools from differential geometry (Kreyszig, 1968; Struik, 1961). We hypothesize that membrane curvature is correlated with metabolic capacity, and therefore quantified the curvatures of the surface reconstructions of the mitochondrial membranes.

For a given membrane, the principal curvatures characterize the major geometric properties and allow for the analyses of different structural motifs. The first principal curvature (k₁) represents the maximum curvature at a given point on a surface and the second principal curvature (k₂) corresponds to the minimum curvature (Kreyszig, 1968; Struik, 1961). We use the principal components and their independent combinations; the mean curvature, given by H = (k₁ + k₂) / 2, and the Gaussian curvature, by K = k₁ x k₂, to perform curvature analysis of the reconstructed membranes. The analysis was carried out with GAMer 2 (Lee, Laughlin, Angliviel de La Beaumelle, et al., 2020; Lee, Laughlin, Moody, et al., 2020), using the Meyer, Desbrun, Schroder, and Barr (MDSB) algorithm (Meyer et al., 2003) for curvature calculations. Positive curvatures occur when the outward facing normal and the curvature have the same directions, that is, at concave regions.

To quantitatively understand what the curvature distributions of the OM mean, we compared them to the curvature distributions of idealized geometries. We consider spherical and capsule-like shapes (consisting of a cylinder with hemispherical ends), resembling approximations of globular and elongated geometries, respectively. Both principal curvatures of a sphere of radius R are equal to 1/R, and negative with the sign convention considered (Figure 5a and b). For the capsule-like shape, the principal curvature has contributions from the sphere (1/R) and zero from the cylinder (Figure 5a and b), while the second principal curvature receives contributions 1/R from all the vertices.

FIGURE 5.

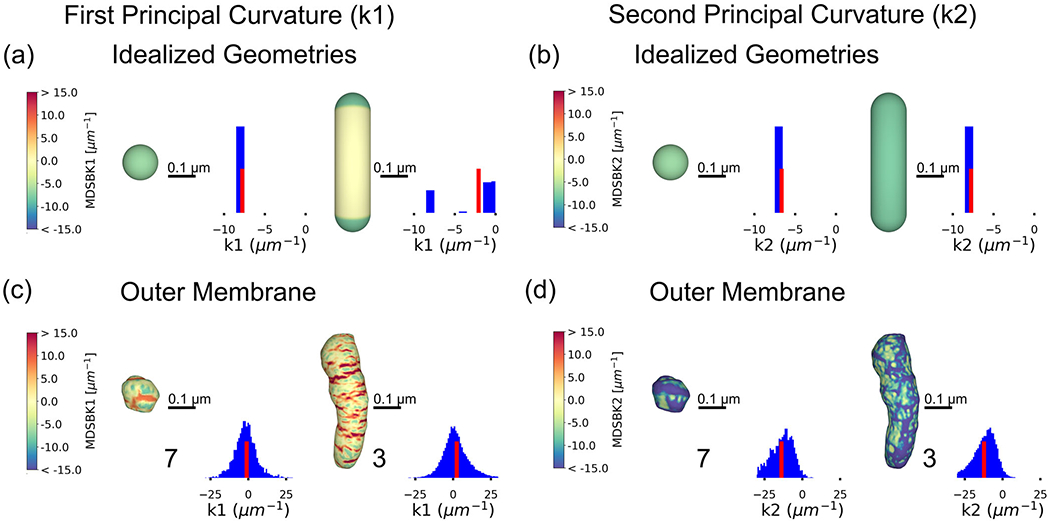
Curvature analysis of idealized geometries and the outer membrane. Heat maps of the first principal curvature k₁, representing the maximum curvature at each vertex in the mesh for (a) a spherical shape and a capsule-like shape (composed of a cylinder and two hemispheres), and their respective curvature distributions. The sphere has a radius of 0.13 μm, thus, its curvature is approximately −7.7 μm⁻¹. A histogram of the curvature values is represented beside the shapes, with a red bar representing the average curvature of the distribution. The radius of the cylinder is 0.13 μm and its length is 0.98 μm. Therefore, the first curvature is approximately −7.7 μm⁻¹ at vertices belonging to the semispheres and zero at the cylinder. (b) For the same shapes, heat maps of the second principal curvature k₂, corresponding to the minimum curvature at each vertex in the mesh. For a sphere, the second curvature is equal to the first, 1/R, −7.7 μm⁻¹ in this example. For the capsule-like shape, the contribution of all vertices is similar and equal to 1/R, −7.7 μm⁻¹. (c) Heat maps of the first principal curvatures for two reconstructed outer membranes, representatives of the globular and elongated populations, respectively. The curvature values mapped are between the 5th and 95th percentiles. The distribution of k₁ values is positive and negative, showing different membrane concavities; positive values correspond with concave regions and negative ones with convex regions. A histogram of the curvature values is represented beside the shapes, with a red bar representing the average curvature of the distribution. (d) Heat map of the second principal curvature for the same outer membrane reconstructions. Values represented are between the 5th and 95th percentiles. The distribution of k₂ values is mostly negative. All curvatures were calculated with the MDSB algorithm implemented in GAMer 2. Color bars represent values of the curvatures in units of μm⁻¹. Scale bar 0.1 μm.

For the idealized geometries considered here, the average first principal curvature is smaller for the sphere and larger for the capsule-like shape, whereas the second principal curvature is equal for both geometries (the average of the distributions is represented with a red bar in Figure 5). The average first principal curvature in the capsule-like shape is greater than the sphere due to the contributions of the flat cylindrical regions (where k₁ = 0) to the average. Using the insight provided by the average principal curvatures, we can thus differentiate between globular and elongated geometries.

In Figure 5c and d, we show two representative reconstructions of the OM, with their respective first and second curvature distributions mapped to the membrane. The first curvature takes on positive and negative values, representing areas of different concavity. The vertices with negative curvature primarily occur at the ends of the shape, at convex regions, while the positive ones are distributed at the central part. Similarly to the idealized geometries, the average first principal curvature is smaller for the globular shape (Figure 5c and d). In contrast, the average second principal curvatures are similar between groups.

We clustered the reconstructions based on the values of the aspect ratio and the average first principal curvature using the K-means algorithm (Figure 6a). The globular population has an average k₁ and aspect ratio significantly smaller than the elongated population (p-value < .002 and < .026, respectively), while the average k₂ is not significantly different between both groups, as expected from the analysis with the idealized shapes (Table 2 and Figure 6b). The globular set is mostly composed of presynaptic mitochondria, with five organelles out of six located at boutons. On the other hand, the elongated group is composed of a mixture of axonal (N = 3) and presynaptic mitochondria (N = 3).

FIGURE 6.

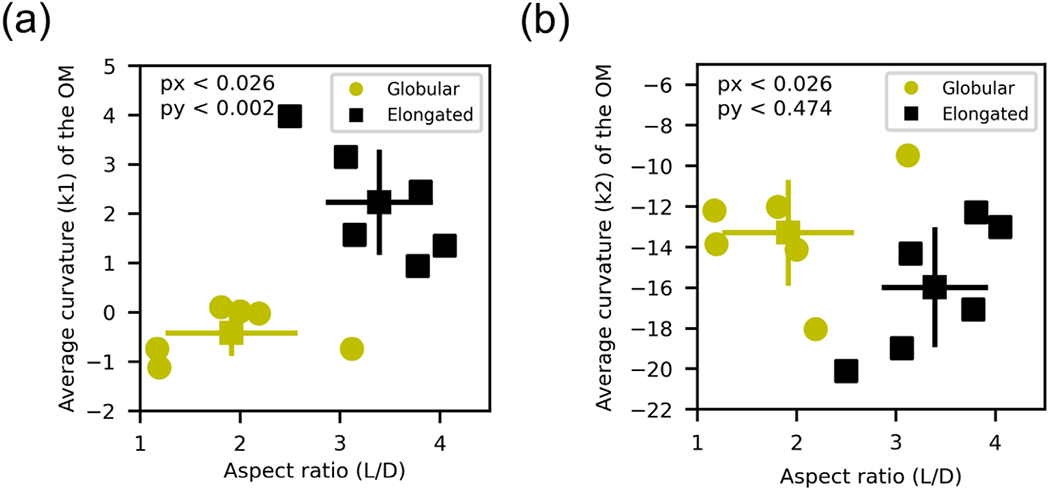
Two populations of organelles are identified using the principal curvature k₁ and the aspect ratio as key features. (a) Average principal curvature (k₁) of the outer membrane and aspect ratio of the shape. Organelles are separated into two clusters employing the K-means clustering algorithm. The globular population (yellow circles) has a smaller aspect ratio and average first principal curvature, while the elongated one (black squares) has greater aspect ratio and average first curvature. The mean values and standard deviations are represented for each population. Both populations are statistically significantly different in regards to both variables (with p-values < .05 in both axes). (b) Average second principal curvature and aspect ratio for both identified populations. The second principal curvature is similar for both populations (p-value < .5) as expected comparing with the idealized shapes (refer to main text for further details)

Interestingly, a small set of the organelles (N = 4) present protrusions in the OM. This feature has been previously reported in neuronal mitochondria (Yao et al., 2020). In all cases within this sample, an area of positive and high curvature at the neck of a protrusion is followed by an area of high-negative curvature. These organelles have an average radius of (0.09 ± 0.01) μm, which is significantly smaller than for the rest of the group (0.12 ± 0.02) μm, (p-value < .02). While the average length of these two groups is similar, the volume is smaller for ones with protrusions: (0.011±0.005) μm³ compared to (0.02 ± 0.01) μm³, although this difference is not significant (p-value < .5). These measurements not only give us quantitative insights into the geometric features of the OM, but, as we will discuss later, can also inform the design of geometries in spatial simulations.

3.3 |. Geometric features of the IM

We next analyzed the geometric features of the inner mitochondrial membrane. The ultrastructure of neuronal mitochondria is composed of a complex network of lamellar and tubular cristae (Figure 7a and b), which generates a number of sub-compartments known as the intracristal space (ICS), intermembrane space (IMS), and the matrix (Figure 1a). The ICS is encapsulated by the CM, opening into the inter membrane space (between the IBM and OM) via CJs. Figure 7a and b shows five reconstructions of the CM along with three of their skeletons. We first measured global features of the IM and its sub-compartments as the surface areas and volumes, and then quantified the number of CJs on the membrane for each of the nine reconstructed mitochondria. Based on these measurements, we determined various ratios of surface areas and volumes of the mitochondria ultrastructure to facilitate comparison with the literature (Table 3). We assessed features of the membrane, such as its continuity, and analyzed the motif composition using tools from differential geometry.

FIGURE 7.

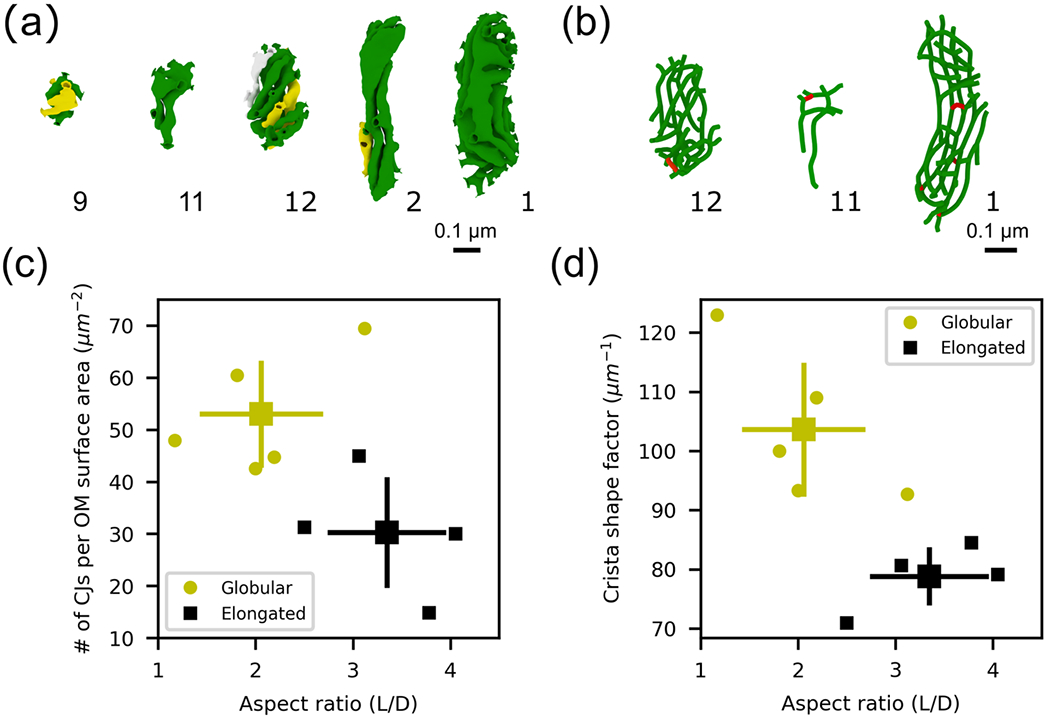
Morphological characterization of the internal structure for nine mitochondrial inner membrane reconstructions. The cristae membranes form a complex network of tubular and laminar structures. (a) Five cristae membrane reconstructions from the indicated mitochondria. A different color is used for each separate, non-interconnected cristae section. (b) Three skeletons of the cristae membrane from the indicated mitochondria (see Methods). Red indicates connected segments between compartments. (c) The density of cristae junctions, defined as the # of CJs per OM surface area, is greater for globular organelles (yellow circles, p-value < .143). (d) The cristae surface area-to-volume ratio, also known as the crista shape factor, is also larger for globular organelles (p-value < .016). The mean values and standard deviation bars of each cluster are represented.

TABLE 3.

Morphological properties of the inner membrane for both populations identified with the aspect ratio and mean curvature of the outer membrane (Table 2)

Property	Globular (N = 5)	Elongated (N = 4)	p-value
# of CJs per OM surface area (μm−2)	53 ± 10	30 ± 11	.143
Crista shape factor (μm−1)	104 ± 11	79 ± 5	.016*
CM density (μm−1)	23 ± 3	17 ± 3	.079
Matrix volume/OM volume	0.44 ± 0.06	0.36 ± 0.04	.286
IMS volume/OM volume	0.29 ± 0.03	0.39 ± 0.04	.016*
Intracristal volume/OM volume	0.23 ± 0.05	0.22 ± 0.04	.873
IBM surface area/OM surface area	0.76 ± 0.06	0.72 ± 0.05	.429
CM surface area/OM surface area	1.1 ± 0.2	0.7 ± 0.3	.286
CJs radius (nm)	12 ± 3	13 ± 1	.746
# of CJs	21 ± 13	12 ± 5	.746

^*p < .05.

Note: Averages and standard deviations over each population are presented.

Variability of CJ density and the CM surface area-to-volume ratio, also called crista shape factor in the literature (Perkins et al., 2020), were compared against aspect ratio (Figure 7c and d). We found that both quantities are larger for globular organelles, that is, organelles with smaller aspect ratios (Figure 7c and d). The larger density of CJs for globular organelles can be explained by the smaller OM surface area of globular organelles and the larger number of CJs found in globular organelles (Table 3). These geometric features have been previously associated with the energy capacity of a given organelle. In particular, the density of CJs, the crista shape factor, and the crista density (CM surface area divided by the OM volume) were reported to be larger in outer hair cells mitochondria from young mice in comparison to older animals (Perkins et al., 2020). Moreover, larger crista shape factor and crista density were also reported to be larger in presynaptic mitochondria from fast-spiking interneurons in comparison to regular-spiking interneurons (Cserep et al., 2018).

Given the high quality of the reconstructed meshes, we also quantified the surface areas and volumes of the different organelle’s sub-compartments. We calculated the total volume taken up by each of the three compartments: the ICS , the IMS, and the matrix, relative to the OM volume. Averaged quantities are presented in Table 3, for the globular and elongated populations previously identified. Our measurements are consistent with previous work reporting a cristae to OM surface area ratio of ≈1 for presynaptic cerebellar mitochondria (Perkins et al., 2010).

Multiple tubular cristae near the CJs are seen connecting to form larger, lamellar compartments in the center of the IM, consistent with other neuronal mitochondria reconstructions (Perkins et al., 2001). We determined different aspects of these cristae networks by analyzing their continuity. All cristae in the mitochondria reconstructed here are connected to the IBM through CJs, meaning that there are no self-contained compartments of ICS. Therefore, we classiffied the CM which forms these compartments as contiguous with the IBM. We further explored the interconnectivity within the CM (disregarding for now the IBM). In one third (three) of the nine IM reconstructions, the entire ICS forms a single, fully connected compartment, and so does the CM. In another third, there are two disconnected ICS, and in the remaining three reconstructions, there are three disconnected ICS in each mesh. The latter two can be described as different cases where the CM is discontiguous with itself. In Figure 7a, we labeled the cristae with the same color when the CM is contiguous (as in reconstruction # 11 and # 1 in Figure 7a), and we used a different color to signal when the membrane is discontinuous. The continuity of the cristae was based on our analysis of the reconstructed meshes using tools in Blender (refer to Methods section). However, to further identify the connections between different cristae, we generated skeletons of the CM (Figure 7b), and highlighted in red the tubular structures connecting different cristae compartments. This level of connectivity between membranes and the compartments they form could have significant implications for molecular diffusion, as we discuss in the next section.

In five out of the nine CM reconstructions, we also observed that lamellar cristae sheets form corkscrew-like twists, which were always right-handed. Two examples are reconstructions # 12 and # 2 in Figure 7a. These structures are similar to the distributions of CJs that were recently shown in yeast and cultured mammalian cell lines (Stoldt et al., 2019). Additionally, the spatial distribution of CJs is irregular, seeming to concentrate at the ends of the elongated mitochondria, as already reported in the literature (Perkins et al., 2001). Cristae structures with a helicoidal twist appear to have a higher CJ density on the top and bottom of the twist compared to the center.

Another important geometric property of an orientable surface is its genus; defined as the number of holes it has. As an example, a sphere has a genus of zero, while a torus has a genus of one. We evaluated this property for all the reconstructed IMs, and found a large variability, with values ranging from 4 to 47 (refer to Methods section for details). The largest value is found in the reconstruction with the most CJs and a fully interconnected IM (reconstruction # 1 in Figure 7a), while the smallest value is found in the organelle with the least CJs (reconstruction # 5, Figure 3). CJ number and IM genus are therefore highly correlated (R² = 0.98). Interestingly, the organelles with outer membrane protrusions (N = 3) have an average genus of five, whereas those without protrusions have an average genus of 22 (p-value < .02).

3.4 |. IM curvature

To dissect the structural components of the complex network of cristae, we performed curvature analysis of the inner mitochondrial membrane. Given the intricate architecture of the IM, in addition to quantifying the curvature, we also developed tools to quantify geometric motifs on the membrane.

To begin, we calculated the first principal curvature at each vertex of the IM and color-coded its values in a heat map representation (Figure 8a) for values between the 5th and 95th percentiles. For visualization purposes, only the CM is shown; however, the entire IM is analyzed to preserve the curvature at each vertex. The distribution of the first curvature is primarily positive, with the highest values found at CJs, at the connection site between cristae, branch sites of cristae, at the edge of lamellar cristae, and along the length of tubular cristae. Similarly, we generated a heat map of the second principal curvature of the IM, representing the minimum curvature at each vertex (Figure 8b), for values between the 5th and 95th percentiles. The values of k₂ are mainly negative, and particularly high at CJs, connections between cristae, and at the branch sites of cristae, complementing in some regions the high and positive k₁ curvature. Remarkably, there are also small areas of positive curvature at the ridge of cristae, additionally quantified as geometric motifs.

FIGURE 8.

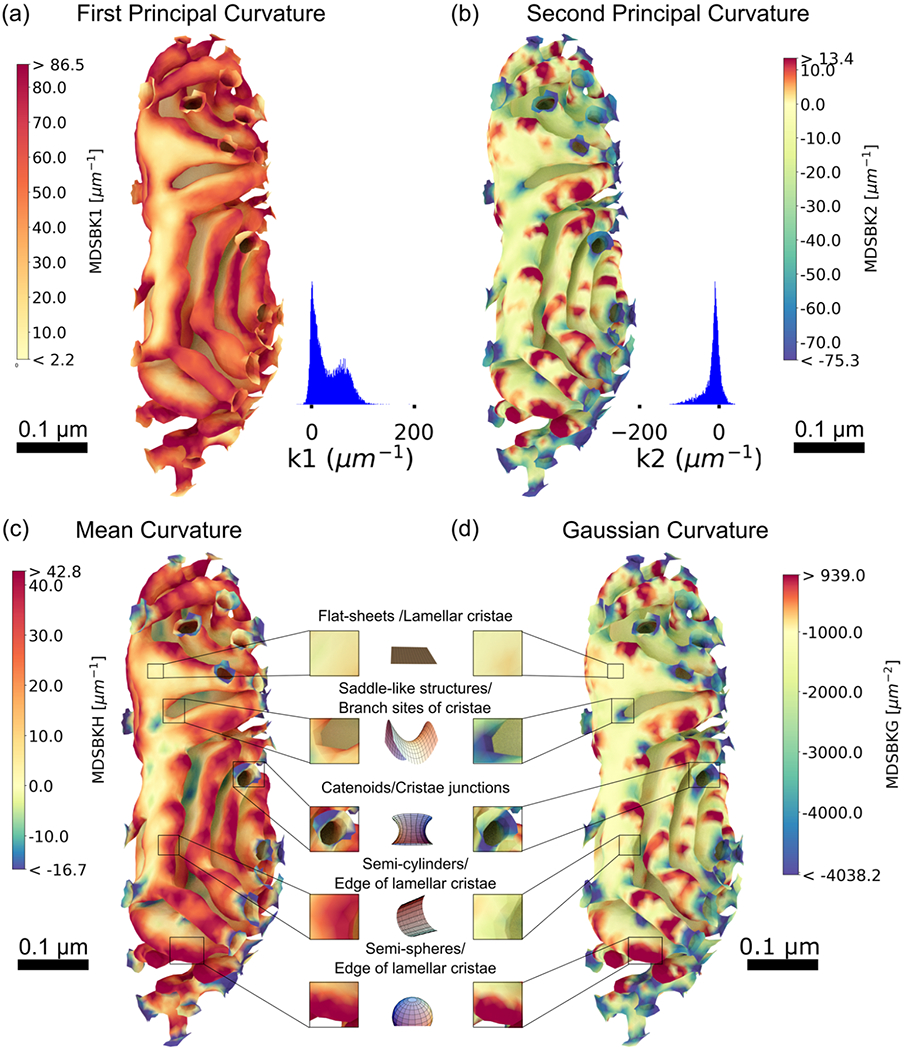
Curvature analysis of the inner membrane of reconstruction # 1. (a) Curvature heat map of the first principal curvature k₁, representing the maximum curvature at each vertex in the mesh (only the cristae membrane is represented), for values between the 5th and 95th percentiles, and their respective distribution values. The distribution of k₁ is mostly positive, with the highest values found at cristae junctions, the connection site between cristae, branch sites of cristae, at the edge of lamellar cristae, and along the length in tubular cristae. (b) Curvature heat map of the second principal curvature k₂, corresponding to the minimum curvature at each vertex in the mesh, for values between the 5th and 95th percentiles. The distribution of k₂ is mostly negative, and particularly high at cristae junctions, connections between cristae, and at the branch sites of cristae, complementing the high-positive curvature k₁ as expected for minimal surfaces. (c) Heat map of the mean curvature, corresponding to the average value of the first k₁ and second curvature k₂, for values between the 5th and 95th percentiles. (d) Heat map of the Gaussian curvature, corresponding to the product of first and second curvatures, for values between the 5th and 95th percentiles. Four characteristic structural motifs emerged in the cristae membrane: flat-sheets are in lamellar cristae with mean and Gaussian curvatures approximately zero; saddle-like structures with zero mean and nonzero Gaussian curvature are at cristae junctions and branch sites of cristae; at the edge of lamellar cristae, we found two characteristic shapes: semi-spherical like shapes with nonzero mean and Gaussian curvature and semi-cylindrical shapes with nonzero mean and zero Gaussian curvature. Curvatures were calculated with the MDSB algorithm implemented in GAMer 2. Color bars represent values of the curvatures in units of μm⁻² for the Gaussian curvature and μm⁻¹ for all the rest. Scale bars 0.1 μm. Structural motif representations were generated with different notebooks from MathWorld (Weisstein, 2008, 2013, 2014a, 2014b, 2015).

3.5 |. Structural motifs in the inner mitochondrial membrane

To further assess the presence of structural motifs on the CM, we calculated the mean curvature (H) and the Gaussian curvature (K) at each vertex of the IM reconstructions (Figure 8c and d), corresponding to the mean and product of the principal curvatures, respectively. Across all the CMs analyzed, we found four characteristic shapes in the CM, corresponding to different combinations of the mean (H) and Gaussian curvature (K) (Kreyszig, 1968; Struik, 1961), flat-sheets for which both curvatures vanish (H = 0 and K = 0), saddle-like structures (H = 0 and K ≠ 0), semispherical shapes (H > 0 and K ≠ 0), and semicylindrical shapes (H ≠ 0 and K = 0).

Flat-sheets are present in lamellar cristae, with mean and Gaussian curvature of approximately zero. For all quantitative analyses, we consider zero mean curvatures smaller in absolute value than 10 μm⁻¹, and Gaussian curvatures smaller in absolute value than 300 μm⁻²). Surprisingly, we found a multitude of saddle-like structures with zero mean and nonzero Gaussian curvature at CJs, branch sites of cristae, and in some areas of the lamella (Figure 8c and d). In particular, the structures found at CJs are reminiscent of catenoids (with H = 0 and K < 0). These types of neck-like structures form connections between regions of different curvatures, as previously discussed (Chabanon & Rangamani, 2018). Flat-sheets and saddle-like structures are made entirely of saddle points where two opposite curvatures generate a mean curvature of zero. The presence of these structures is reminiscent of minimal surfaces in differential geometry and has been noted in the endoplasmic reticulum (ER) reconstructions as well (Marshall, 2013; Terasaki et al., 2013).

At the edges of lamellar and tubular cristae, we found two characteristic shapes: half-spherical shapes and half-cylindrical shapes. The spherical regions have high mean and Gaussian curvature values (Figure 8c and d). The Gaussian curvature, defined as the product of the two principal curvatures, is therefore positive when the principal curvatures have the same sign, as found in these regions. In contrast, the Gaussian curvature vanishes in cylindrical shapes, as found in some regions of lamellar and tubular cristae (Figure 8c and d).

Thus, using our curvature quantification, we have classified four structural motifs: flat-sheets, saddle-like structures, semi-cylindrical edges of lamellar cristae, and hemispherical edges of lamellar cristae (representations of these reconstructions for two reconstructions are shown in Figure 9). We quantified the presence of the aforementioned four structural motifs in all the reconstructions by computing the fraction of the CM with mean and Gaussian curvatures similar to their respective idealized values, to the total CM surface area (Table 4). Remarkably, the percentage of flat-sheets and spherical shapes is not significantly different between the globular and elongated populations (Table 4). However, the presence of saddle-like structures consists of approximately 2.3% of the CM for the globular population and 3.7% for the elongated population (p-value < .079). The presence of semi-cylindrical shapes is also different between the two populations, with larger portions of the membrane occupied by this structural motif in elongated mitochondria at 6%, with4% for the globular group (p-value < .016, Table 4).

FIGURE 9.

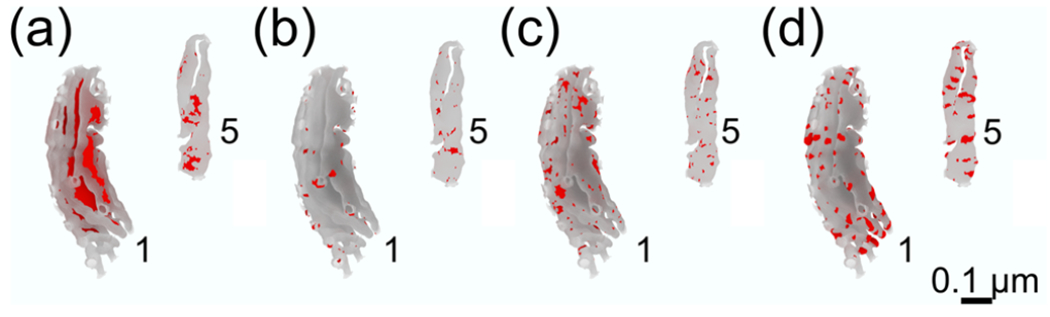
Structural motifs representation for two representative reconstructions from both groups, # 1 from the globular set and # 5 from the elongated one, in (a) flat-sheets, (b) saddle-like structures, (c) semi-cylindrical shapes, and (d) semi-spherical shapes. We quantify the presence of structural motifs for both populations, globular and elongated, averages and standard deviations over each population are shown in Table 4

TABLE 4.

Quantification of the presence of four structural motifs for both globular and elongated mitochondria populations (see Table 2)

Property	Globular (N = 5)	Elongated (N = 4)	p-value
% flat-sheets	12 ± 10	11 ± 4	.746
% saddle-like structures	2.3 ± 0.5	3.7 ± 0.7	.079
% semi-cylindrical shapes	4 ± 1	6 ± 1	.016*
% semi-spherical shapes	13 ± 5	13 ± 2	.746

^*p < .05.

Note: Averages and standard deviations over each population are shown for the % cristae membrane surface area occupied by each motif.

Furthermore, we quantified the surface area of CM formed by vertices with intense curvature. To clearly visualize these regions, we generated heat maps of the first principal curvature color coding only the curvature values larger than 80 μm⁻¹ for the globular and elongated populations (Figure 10a and b, respectively). Additionally, we analyzed the fraction of the CM surface area formed by intense curvature regions to the OM surface area (Figure 10c). Globular organelles have on average a larger fraction of the CM with high curvature values relative to the OM surface area (11 ± 5), whereas in elongated mitochondria, the ratio is (5 ± 2). Since ATP synthases accumulate at regions of most intense curvature, we consider this area as a proxy of the energetic capabilities of a given mitochondrion. Therefore, our results suggest that globular organelles show features of high energy capacity.

FIGURE 10.

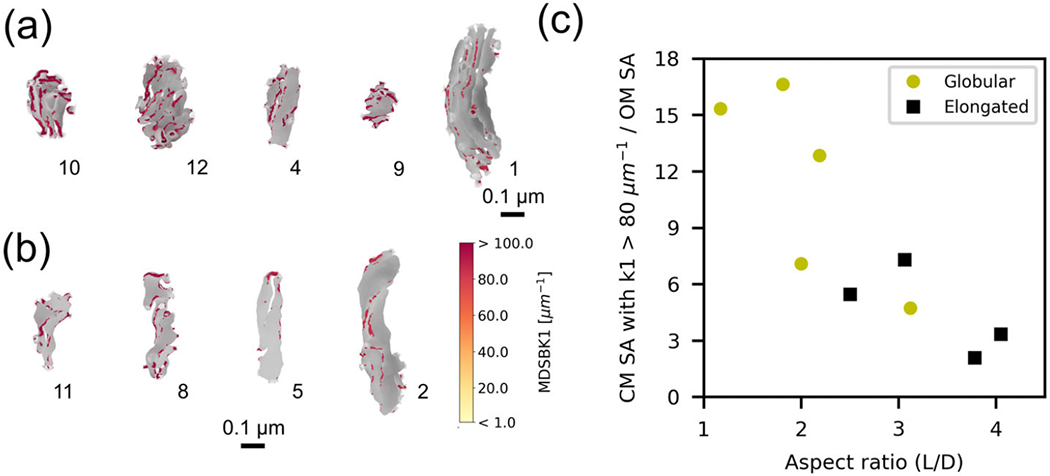
High curvature regions of the inner mitochondrial membrane. (a and b) Only vertices of the cristae membrane with the first principal curvature k₁ greater than 80 μm⁻¹ are shown in color according to the color bar. Remaining vertices are in gray. (a) Globular mitochondria population and (b) elongated mitochondria population. (c) Surface area formed by vertices of the cristae membrane with first principal curvature k₁ greater than 80 μm⁻¹ divided by the OM surface area, as a function of the OM aspect ratio for the globular (yellow circles) and the elongated (black squares) populations. Average values for both populations are 11 ± 5 for the globular group and 5 ± 2 for the elongated one, p-value < .286

4 |. CONCLUSIONS

Brain activity is accompanied by a large energy demand, and therefore, relies on efficient energy metabolism. In particular, neurons and their synaptic connections are energetic “hot spots” and predominantly rely on mitochondrial ATP production. For this purpose, presynaptic mitochondria seem to exhibit a specialized morphology, but their functional consequence is still not fully understood. Here, we used electron tomography to investigate structural properties of these specialized organelles. Electron tomography has proven to be a powerful tool for obtaining high-resolution images of in-situ organelles (Frey et al., 2006) and particularly useful to resolve the presynaptic structure (Perkins et al., 2015). The final resolution of electron tomograms depends on several factors, including sample preparation, section thickness, and electron microscope voltage. In this work, samples were HPF followed by freeze-substitution with fixatives (Sosinsky et al., 2008), producing a large volume of a well-preserved tissue that is subsequently sectioned with minimal material loss. This combination of factors generates serial tomograms with an isotropic voxel size of 1.64 nm that are employed to segment and reconstruct mitochondria from axons and presynaptic terminals. High-quality whole organelle reconstructions produced with the developed workflow, that includes new mesh processing software GAMer 2 (Lee, Laughlin, Angliviel de La Beaumelle, et al., 2020; Lee, Laughlin, Moody, et al., 2020) and new alignment methods (Wetzel et al., 2016), not only allow for nuanced geometric characterization of the internal architecture, as presented in this work, but also provide in-silico representations for spatial computational modeling (Garcia et al., 2019). These types of reconstructions and quantifications are hard to conduct on a routine basis because of the technical challenges involved. Here, we have overcome these challenges with newly developed methods. Such interdisciplinary effort lays the foundation for future studies that can map internal mitochondrial physiology, energy production, and metabolism in neurons.

Our analysis reveals that the 12 mitochondria we analyzed can be categorized as elongated or globular. Profound architectural differences between globular and elongated mitochondria are not only reflected in the external structure but also in the internal architecture (Figure 7). We found that globular organelles have on average higher density of CJs, cristae surface area-to-volume ratio, and cristae density (Table 3), and notably, the fraction of the area formed by vertices with extreme curvature is larger in these organelles (Figure 10c). Since dimeric complexes of ATP synthases accumulate in regions with high curvature of the CM and form ribbon structures which enforce that curvature (Paumard et al., 2002; Strauss et al., 2008), the increment in high curvature regions in our globular reconstructions suggests that globular organelles show features of high-energy capacity. Moreover, measurements of the number of CJs per OM surface area, cristae density, and cristae shape factor were previously reported to be larger in organelles located at high-energy demanding locations, namely outer hair cells of young mice (Perkins et al., 2020) and high-spiking interneurons (Cserep et al., 2018), in accordance with our results.

Other features reported here have also been measured previously for axonal and presynaptic mitochondria, including the lengths, widths, CJ diameters (Mannella, 2000; Perkins et al., 1997; Siegmund et al., 2018), density of CJs (Perkins et al., 2001; Perkins et al., 2010) and are in reasonable agreement with the values reported in the literature. In addition to the features listed above, we also calculated the principal curvatures for the membrane surfaces and found important structural motifs. Such calculations have implications in our understanding of disease states. For example, near total loss of ATP synthase dimerization due to a neurodegenerative mutation caused profound disturbances of mitochondrial crista ultrastructure in fibroblast cultures derived from a Leigh syndrome patient (Siegmund et al., 2018). One of the key architectural features different than in control cells is an increment in the angle of curvature at the tips of the cristae. This feature relates to our curvature measurement of the IM. Another feature of the patient mitochondria is reduced crista surface area-to-volume ratio (Siegmund et al., 2018). Further investigation using the methods developed here would allow for a deeper understanding of potentially impaired mechanisms.

The ultrastructure of neuronal mitochondria forms a complex geometric structure. We evaluated features of this membrane which were inaccessible before, such as its continuity. We used skeletons of the reconstructions to automatically measure structural features and also to identify the connections between different cristae. Contiguous compartments can share resources, molecules, and proteins. They can potentially reach all adjacent spaces diffiusing through the connected volumes or membranes. These possibilities and their functional consequences can be further explored with computational modeling by quantifying the diffiusion capacity within the membranes and in the confined 3D space.

New tools to estimate the curvature at each vertex in the reconstructions (implemented in GAMer 2) allowed us to quantify features of the membranes that would remain as qualitative observations otherwise. We used the curvature to objectively separate the organelles into two distinct sets, to identify protrusions in the membrane, and to quantify the presence of structural motifs in the CM. Beside the large variability found in the CMs, the percentage of flat-sheets and spherical motifs is on average the same in both populations. However, this is not the case for saddle-like structures and semicylinders.

The structural motifs identified in our analysis of membrane surfaces suggest that the geometry of mitochondrial membranes may be understood from mechanical reasoning. The shape of a cellular membrane can be thought to be a minimum energy state for the bending energy of the lipid bilayer (Helfrich, 1973). Several mechanisms can generate positive or negative curvature in membranes (McMahon & Gallop, 2005), including changes in the lipid composition, cytoskeletal proteins, scaffolding by external membrane proteins, and influence of integral membrane proteins. Semi-cylindrical and semi-spherical shapes, as found in mitochondria, would require high membrane asymmetry of lipid composition to be maintained (Zimmerberg & Kozlov, 2006). It is highly likely that the crowded mitochondrial milieu, combination of peripheral and integral membrane proteins coupled with external forces, play a role in generating these membrane shapes.

One curious feature about our observations is the large fraction of flat-sheets and saddle-like structures, which are minimal surfaces, so-called because they minimize a surface energy associated with curvature. It is at its lowest at saddle points, where two opposing curves of equal intensity form a saddle-like shape (Alimohamadi & Rangamani, 2018; Chabanon & Rangamani, 2018).

The classic illustration of minimal surfaces shows a soap film stretched along a wire frame. These soap films, much like cellular membranes, are lipid structures, which will take whatever shape that will minimize the surface energy. This propensity for membranes to form minimal surfaces has been demonstrated using the catenoid shape of neck-like structures, which form during fission and fusion as well as in endo and exocytosis (Chabanon & Rangamani, 2018). As seen with the wire frame required to create a minimal surface from a soap film, membranes require structural elements around which these low-energy shapes can develop. A number of proteins have been identified as key regulators of cristae organization and remodeling, among them OPA1, MICOS complex, and ATP synthase have been recognized as the main regulators (Giacomello et al., 2020). And in particular, OPA1 and MICO complexes have been shown to regulate CJs (Kondadi et al., 2020; Stephan et al., 2020). These protein complexes can potentially act as the scaffolds or integral proteins applying the forces required to bend the membrane.

To summarize, we have quantified multiple morphological features of presynaptic mitochondria using end-to-end reconstructions. Analyses of these mitochondria have revealed common principles of organization across the sampled population, suggesting that there exist design criteria for healthy mitochondria.

Recently, a series of studies on synaptic geometry and structural plasticity have been conducted by us and others (Bartol et al., 2015; Bell et al., 2019; Cugno et al., 2019; Mahajan & Nadkarni, 2019). Parallel studies have focused on the role of the ER and mitochondria in regulating the spine calcium and how internal organelles can alter the calcium and ATP dynamics (Garcia et al., 2019; Leung et al., 2021; Singh et al., 2021). We anticipate that the mitochondrial geometry features we describe here will now serve as a platform for future high-dimensional simulations of mitochondrial dynamics and quantitative mapping of the mitochondrial structure-neuronal energy landscape.

DATA AVAILABILITY STATEMENT

All the serial tomographic data sets, 3D reconstructions, and software generated during the current study are available in the repository: https://github.com/RangamaniLabUCSD/Morphological_principles_of_neuronal_mitochondria