Abstract
The series of advanced nanocomposites consisting of Gd2O3 nanoparticles (NPs) embedded into periodic porous SiO2 matrix have been investigated with respect to their structural and magnetocaloric properties. By means of small angle neutron scattering and transmission electron microscopy, regular nanopores organized in the cubic or hexagonal superlattice have been documented. The pores are occupied by the NPs of progressive concentration within the nanocomposite series. All of the examined systems have exhibited extraordinarily high values of magnetic entropy change (up to 70 J kg−1 K−1) at low temperatures with the absence of thermal hysteresis, indicating their perspective utilization in cryogenic refrigeration. Profound analysis of magnetic entropy change data via scaling laws has been applied to the nanocomposite materials for the very first time. With the aid of scaling analysis, conclusions on magnetic properties and phase transition type have been made, even for the conditions unavailable in the laboratory.
Subject terms: Energy science and technology, Nanoscience and technology, Physics
Introduction
The demand for eco-friendly technologies we are facing in recent years is the impetus for the development of advanced energy-efficient systems and devices. It is evident, in particular, in the scope of refrigeration, what is documented by an increasing number of related scientific publications1–3. It is expected that conventional technology based on gas expansion will be soon replaced by a fundamentally different principle exploiting magnetocaloric effect (MCE). MCE is related to magneto-thermodynamic phenomenon, i.e. a temperature change induced in a material by the variation of applied magnetic field. Even though the effect has been investigated over the century4, only the current progress in material science and nanotechnologies in particular facilitates its operative application up to room temperature5,6. Besides improved energy efficiency, low manufacturing costs, and negligible environmental impact, there is a number of scientific criteria that perspective magnetic refrigerant material has to meet. This is where nanoscale materials may manifest their unique benefits. The main advantage of nanoparticles over the bulk materials stems from wider options for tuning the characteristics of the refrigerant material. While the change of working temperature, refrigeration capacity or phase transition character in bulk materials can be induced almost exclusively by chemical composition, in the case of NPs, size, shape, capping layer or dilution of nanoparticle system affect those qualities. Moreover, it is assumed that nanomagnets could exhibit enhanced magnetic entropy change (ΔSM) because of high magnetic-moment density in a single magnetic particle. This is in fact observed in nanoparticles with large magnetic moments of individual atoms which may easily and coherently change their alignment even upon the application of a low magnetic field. Several compounds, particularly those based on rare earth (RE) elements, are therefore currently under investigation as promising candidates for significant MCE promotion. It is well known that RE3+ ions exhibit enhanced magnetic performance due to their specific electron configuration. If the electrons occupying partially unfilled 4f. shell are well localized, magnetic moments of RE could be quite large7,8. Usually, RE intermetallic compounds undergo magnetic transitions at low temperatures. However, their extensive scrutinization in recent years shows an ample variability in tuning their properties towards further applications. It has been found that TmZn manifests giant MCE even at lower applied field changes and its transition temperature and magnetic entropy change can be regulated by preassure7. The family of ternary RE ompounds manifest excellent MCE performance in wide temperature range depending on the specific composition and crystallic structure7,8. The composite systems exhibiting table-like MCE can be designed and prepared by their appropriate mixture. By this manner a composite covering wide working temperature range from 40 to 100 K has been proposed based on quaternary RE compounds containing La and Pr9. However, its drawbacks related to the thermal and magnetic hysteresis have yet to be overcome. Interestingly, even amorphous ribbons may exhibit large MCE, where − ΔSM up to 18 J Kg−1 K−1 (at field change 5 T) has been reported for RE60Co20Ni20 (RE = Ho, Er) recently10. Among the most perspective RE-based candidates for MCE applications, gadolinium compounds are thoroughly investigated in particular11–15. We contribute to the scope with our study of gadolinium oxide nanocomposite series (see Scheme 1). The analysis of magnetic entropy change data by means of scaling laws allows for the determination of phase transition mechanism, which is in the case of nanoscale systems at low temperatures often very elusive. Although the employed scaling analysis has been established for bulk materials, we demonstrate its first valid application to the nanocomposite systems. The results presented in this work are set into the context of our profound experimental and theoretical analysis that we have carried out to the systems of this kind in recent years16–22. Altogether they provide a comprehensive insight into the nature and performance of advanced nanocomposites that we have prepared and examined.
Scheme 1.
Illustration of the SiO2/Gd2O3 nanocomposite preparation and structure organization. Hollow silica matrices with regular pores organized into hexagonal (upper panel) and cubic (lower panel) superlattices were modified by the introduction of Gd2O3 nanoparticles (right-hand schemes).
Results
Structure and morphology
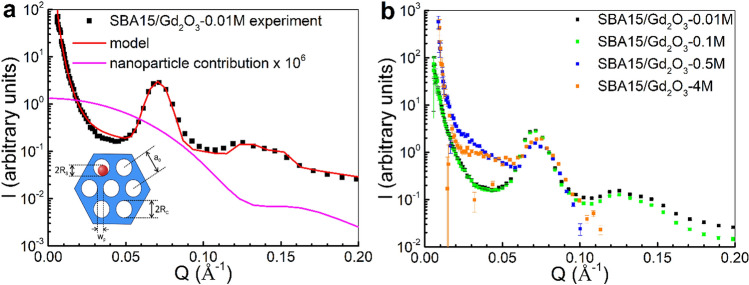
In order to examine the influence of nanoparticle abundance on nanocomposite properties, four SBA15/Gd2O3 systems with increasing concentration of Gd2O3 NPs (gadolinium precursor concentrations 0.01 M, 0.1 M, 0.5 M and 4 M) have been prepared and denoted as SBA15/Gd2O3-0.01 M, SBA15/Gd2O3-0.1 M, SBA15/Gd2O3-0.5 M and SBA15/Gd2O3-4 M. The structure of SBA15/Gd2O3 nanocomposite series has been investigated by means of small angle neutron scattering (SANS). Neutrons with their excellent penetration ability are recognized as an appropriate tool for the examination of structures hidden in the bulk material. Unlike the X-rays, neutrons are dominantly scattered by the nuclei and their interaction with electron shell of the atoms in the compound is negligible. The amplitude of neutron scattering varies independently of the element’s position in the periodic table and differs for isotopes of the same element. Due to this, neutron scattering offers a specific sensitivity to certain elements.
Figure 1a shows SANS data obtained for the SBA15/Gd2O3-0.01 M composite. The system is characteristic of very low nanoparticle concentration what has been evidenced by a number of experimental methods (HRTEM, HE-XRD, nitrogen adsorption/desorption volumetry, magnetic measurements) previously16,18. The matrix pores are therefore deemed sparsely occupied by the Gd2O3 NPs and the scattering signal from the composite is supposed to closely resemble that of the hollow SBA15 matrix. In order to address the structure of the system, we have applied the model that we have developed for similar series of nanocomposites, where Fe2O3 instead of Gd2O3 NPs were introduced into the SBA15 matrix17. Briefly, total SANS intensity of the composite is assumed as a superposition of signals corresponding to the two subsystem contributions – scattering from the blank matrix and the system of Gd2O3 NPs. Employing the model, we have analyzed the SANS data of SBA15/Gd2O3-0.01 M (Fig. 1a) composite with the following results. As expected, the contribution of nanoparticle subsystem to the total scattering has been found about six orders of magnitude lower than the signal corresponding to the model of hollow silica matrix. Hence, features characteristic of the amorphous SBA15 matrix with regular cylindrical pores arranged in hexagonal symmetry (the schematics in the inset of the Fig. 1a) can be unequivocally recognized. It is the major peak at momentum transfer value Q ~ 0.07 Å−1, followed by the two less clearly resolved minor peaks at Q ~ 0.13 Å−1 and Q ~ 0.15 Å−1. These peaks attribute to the system of cylinders (pores) with average radius Rc ~ 4 nm (σc = 0.5) that are arranged in the regular lattice with parameter a0 ~ 9.8 nm (σa = 0.0006).
Figure 1.
(a) The best model fit (red line) to the SANS experimental data (black squares) corresponding to the SBA15/Gd2O3-0.01 M composite. The magenta line represents a million-fold rescaled (facilitating the comparison) contribution of the polydisperse spheres (nanoparticles) to the total SANS intensity. Inset at the bottom left shows the schematics of nanocomposite with depicted structural parameters. (b) SANS data corresponding to the series of nanocomposites with increasing Gd2O3 nanoparticle concentrations (0.01, 0.1, 0.5 and 4 M) in the pores of SBA15 matrix.
Figure 1b presents SANS data of our complete series of the examined SBA15 nanocomposites. One can notice the similarities between the I(Q) patterns corresponding to the two systems with a low concentration of gadolinium oxide NPs (i.e., 0.01 M and 0.1 M). Apparently, only a modest difference in the SANS data between the 0.01 M and 0.1 M systems suggests a low degree of Gd2O3 nanoparticles incorporation into the pores. To proceed further, let’s consider the changes in the I(Q) pattern of 0.5 M and 4 M systems with respect to those of low particle concentration. The first significant feature is the increase in the scattered neutron intensity in the range of 0.01 Å−1 < Q < 0.06 Å−1. This can be explained by the progressive occupation of the pores by the NPs. The elevated population of the Gd2O3 particles is reflected in the increase of its scattering contribution (see the magenta curve in Fig. 1a) to the total SANS signal. Since the pores are partially filled with NPs, the matrix pattern is becoming less resolved and the major peak at Q ~ 0.07 Å−1 smeared.
The presence of Gd2O3 nanoparticles within the matrix pores is evidenced by the transmission electron microscope (TEM) images in Fig. 2. The periodic structure with hexagonal symmetry (upper panel) and cubic symmetry (lower panel) is documented by the high resolution transmission electron microscopy (HRTEM) in STEM mode. The unit cell parameter of the hexagonal structure in SBA15/Gd2O3-4 M matrix has been estimated from the HRTEM micrographs to a0 ~ 12 nm, while a0 ~ 15 has been attributed to the cubic system SBA16/Gd2O3-4 M. Hexagonal and cubic pore diameters have been determined to be dSBA15 ~ 7 nm and dSBA16 ~ 10 nm, respectively, in good agreement with references22,23.
Figure 2.
HRTEM micrographs depicting the SiO2/Gd2O3 nanocomposite structure organization for the systems with hexagonal (a–c) (upper panel) and cubic (d–f) (lower panel) symmetry. (a, b) represent blanck hexagonal matrix and c represents Gd2O3 nanoparticles in SBA15 matrix. (d, e) represent blank cubic matrix and (f) Gd2O3 nanoparticles in SBA16 matrix.
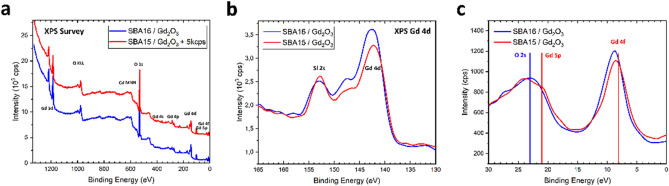
The survey X-ray photoelectron spectroscopy (XPS) spectrum is shown in Fig. 3a. The results of the XPS survey confirm the chemical composition of studied SBA15/Gd2O3 and SBA16/Gd2O3 samples without additional chemical contamination. This verifies the existence of Si, Gd, and O atoms only in studied samples. The core-level spectra from XPS, Fig. 3b, clearly exhibit essentially broader Gd 4d peaks in core-level spectra. The valence band (VB) area up to 30 eV was recorded for the samples and compared with that of the Gd-Ox XPS external standard (see Fig. 3c). The range of binding energies (BE) from 18 to 24 eV usually belongs to the O 2 s electronic core-like states for the case of simple oxides, vertical blue line. The band at 22.51 eV is from the partial contribution from Gd 5p due to band overlap. The manifestation of the strongly asymmetric shoulder at 8.5 eV (see Fig. 3c, red line) allows us to assume that this is also from the Gd 4f electronic states. XPS analysis confirms the presence of Gd2O3 nanoparticles without any further contamination.
Figure 3.
(a) Survey XPS spectrum of the SBA16/Gd2O3 (cubic) and SBA15/Gd2O3 (hexagonal) nanocomposites, (b) XPS core-level spectra from Gd2O3 (cubic) and Gd2O3 (hexagonal), (c) XPS valence bands (VB) mapping of Gd2O3 (cubic) and Gd2O3 (hexagonal).
Magnetic entropy study and scaling analysis
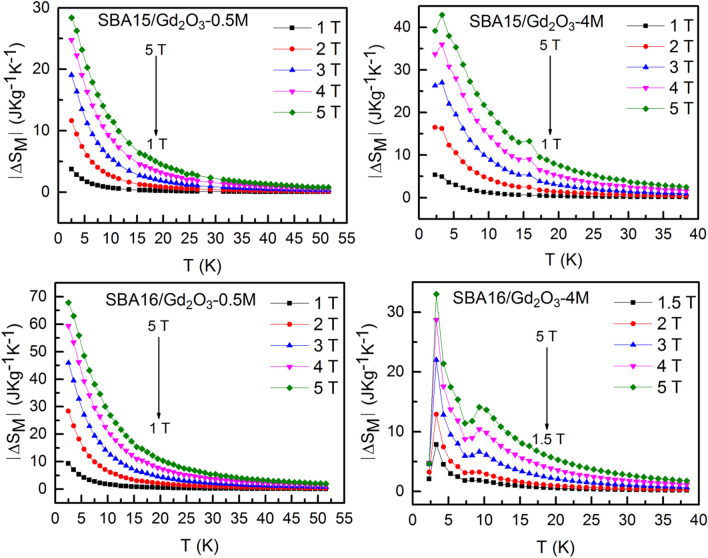
The magnetocaloric effect has been evaluated in the series of nanocomposites with higher nanoparticle concentration, i.e. 0.5 M and 4 M, in both SBA15 and SBA16 matrix types. Figure 4 shows the temperature dependence of magnetic entropy change − ΔSM calculated for the examined systems according to Eq. (1) (Methods section) for the field change from 0 to 5 T. All of the systems exhibit typical paramagnetic behavior with abrupt − ΔSM(T) increase when approaching low temperatures. The only exception is SBA16/Gd2O3-4 M composite, where two peaks of − ΔSM(T) dependences at T ~ 3 K and T ~ 9 K have been recognized.
Figure 4.
Magnetic entropy change of the examined nanocomposites calculated from experimental M(H,T) data for the applied field change up to 5 T.
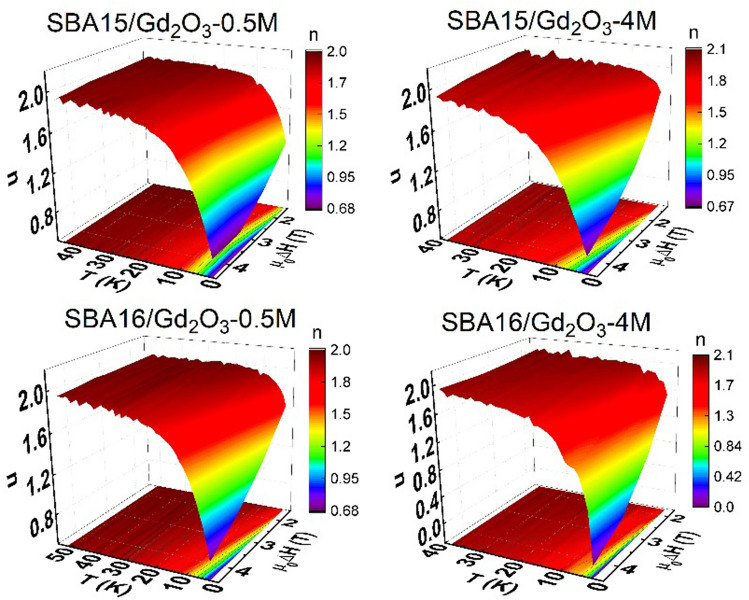
Apparently, there is a lack of data at low temperature region for the clear − ΔSM(T) peak recognition. Consequently, the direct application of scaling analysis was not possible and the universal curve had to be constructed alternatively. For this purpose, the exponent n characterizing applied field dependence of ΔSM ∝ Hn has been calculated according to the Eq. (2) and the data are displayed in Fig. 5.
Figure 5.
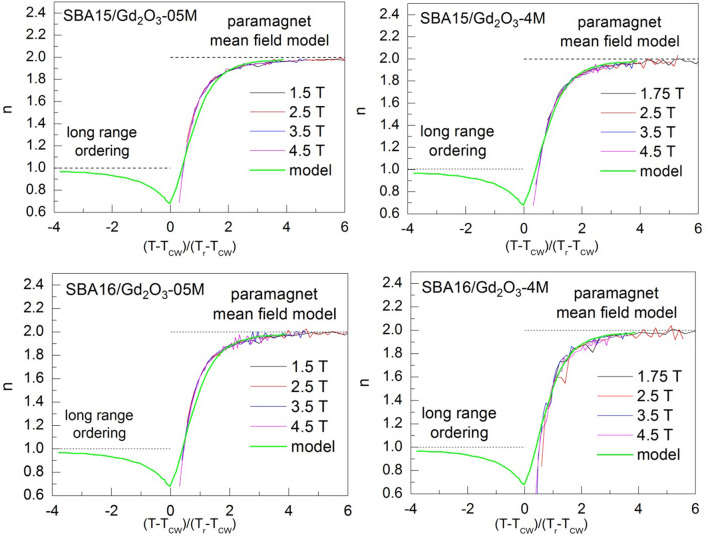
Temperature dependence of n index in the studied nanocomposite systems.
The common feature of all the examined systems is a steep increase of n at low temperatures (up to T ~ 9 K) while in the higher temperature region it converges to the value n = 2 regardless of applied field magnitude. One can also recognize that data are noisy when approaching higher temperatures (T > 25 K). This is a consequence of low field dependence of ΔSM in the region (significant thermal fluctuations) that is the source of inaccuracy when calculating logarithm and differentiating according to the Eq. (2). In the case of the second order phase transition (SOPT), n(T,H) curves should collapse onto universal curve after rescaling temperature axis (Section Methods). Due to the absence of a peak in the both −ΔSM(T) (except of SBA16/Gd2O3-4M) and its corresponding minimum in n(T) data (all the systems), we have determined the TCW = − 2 K from the Curie–Weiss law fit to the magnetic susceptibility data (Supplementary Figure 1). Further, Tr has been selected for each branch of n(T) as temperature corresponding to n = 1.62 for the composites SBA15/Gd2O3-0.5 M, SBA16/Gd2O3-0.5 M and n = 1.55 for SBA15/Gd2O3-4 M and SBA16/Gd2O3-4 M (Supplementary Figure 2). The values have been set arbitrarily, although with the requirement of the proximity to the expected phase transition. The collapse of the data along with its comparison to the SOPT model of mean field theory24 can be seen in the Fig. 6.
Figure 6.
Universal curves constructed for n(T) data and their comparison to the SOPT according to the mean field model.
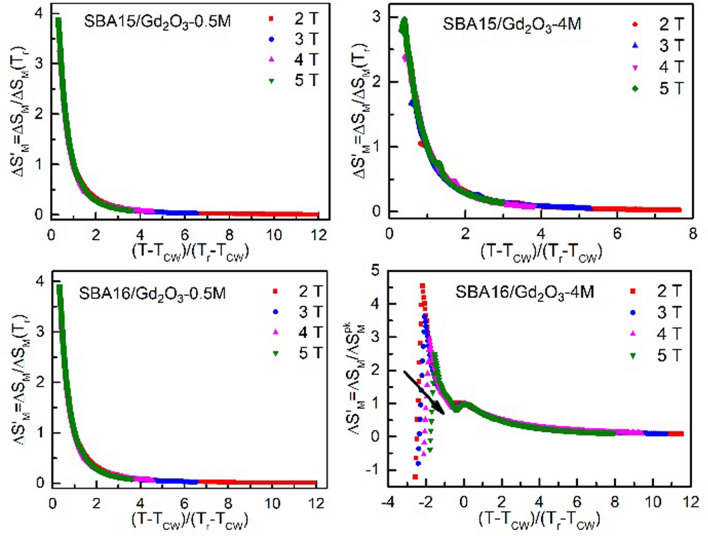
Employing rescaled temperature axis, the collapse of ΔS′M = ΔSM/ΔSM(Tr) has been obtained for the systems SBA15/Gd2O3-0.5 M, SBA16/Gd2O3-0.5 M and SBA15/Gd2O3-4 M, Fig. 7 (section Discussion). Due to the presence of minor peak (T ~ 9 K) in the − ΔSM (T) data, the collapse has not been achieved in the case of SBA15/Gd2O3-4 M. Therefore, an alternative (standard) method has been applied24. We assigned TCW to the peak value − ΔSpkM at T ~ 9 K. Magnetic entropy change values have been rescaled according to ΔS′M = ΔSM/ΔSpkM while temperature axis with respect to Tr that corresponds to the ΔSM(Tr) = 0.7ΔSpkM. The rescaled data are shown in Fig. 7. Apparently, the universal curve has been obtained on the right side of the minor peak, whereas in the lower temperature region the scaling failed.
Figure 7.
Collapse of magnetic entropy change onto the universal curve utilizing parameters derived from n(T,H) analysis of SBA15/Gd2O3-0.5 M, SBA16/Gd2O3-0.5 M and SBA15/Gd2O3-4 M. Scaling of the SBA16/Gd2O3-4 M has been performed directly employing the parameters obtained from − ΔSM(T) peak at T ~ 9 K.
Discussion
Detailed analysis of the Gd2O3 particles’ abundance in the matrix by means of SANS is hampered by the fundamental drawback that is inherent to the gadolinium nuclei. Gd is recognized as the element with by far the highest thermal neutron capture cross section among all stable isotopes25. Evidence on enhanced neutron absorption of the systems with higher Gd2O3 nanoparticle abundance (4 M vs. 0.5 M) is documented clearly in the Q-range over 0.1 Å−1, Fig. 1. Despite of pronounced absorption effect, the fingerprints corresponding to the structural features of SBA15 matrix have been resolved (peaks at Q ~ 0.07, 0.13 and 0.15 Å−1), while its gradual smearing with increasing nanoparticle concentration suggests the progressive occupation of the pores by Gd2O3 NPs. As it has been evidenced in the case of nanocomposite series containing Fe2O3 NPs22, matrix symmetry significantly affects magnetic performance of the system. For the equivalent nanoparticle concentration, stronger inter-particle interactions (hallmarks of superspin glass) have been documented in the systems with cubic matrix, while weak dipolar interactions have been found in the hexagonal matrix. This behavior has been ascribed to the larger distances among the NPs in the latter series. In the case of Gd2O3 NPs, the effect is not observed. In fact, SiO2/Gd2O3 nanocomposites do not exhibit superparamagnetic, but pure paramagnetic properties. It is evidenced by the ZFC–FC magnetization data16, Supplementary Figure S1, where the absence of thermal hysteresis (irreversibility of the curves) along with the absence of ZFC peak have been manifested. Hence, we can conclude that magnetic properties of SiO2/Gd2O3 are determined by the magnetic moments of single atoms and not by the collective behavior of nanoparticle superspins like in nanocomposite series SiO2/Fe2O322. The presence of inter-particle interactions may suppress magnetocaloric performance of the system. Since mutualy interacting moments are less susceptible to follow applied magnetic field change, the magnitude of magnetic entropy change may decrease accordingly. The absence of inter-particle interactions and thermal hysteresis therefor can be assumed as significant factors leading to enhanced MCE observed in our SiO2/Gd2O3 nanocomposites and suggests them for possible magnetic refrigeration applications.
The support of successful filling process of porous matrix system with NPs is provided also by the magnetization vs temperature data16. With the increasing concentration of Gd2O3 NPs in nanocomposites with hexagonal symmetry, the magnetization measured at corresponding temperatures is gradually enhanced. On the other hand, the magnetization curves recorded in nanocomposites with cubic symmetry show that presumably there is a critical precursor concentration limit for the nanoparticle nucleation within the pores. This would explain unexpected higher magnetization values bellow this critical limit and lower magnetization values beyond the limit. This suggests a scenario that in the case of cubic nanocomposites, certain fraction of Gd2O3 is evicted out from internal surface pores during the matrix modification by the precursor of high concentration (apparently above 0.5 M).
The analysis of magnetic susceptibility vs temperature data revealed typical paramagnetic behavior of all the examined systems at higher temperatures (Supplementary Figure 1). Although steep increase of − ΔSM is expected for the paramagnetic salts when approaching low temperatures, the values obtained at ~ 2 K for the field change 5 T in our nanocomposites (above ~ 30 J Kg−1 K−1) are remarkably high, Fig. 4. Among the family of gadolinium oxides, the candidates that would approach that level of − ΔSM under comparable conditions (T ~ 2 K, µ0ΔH = 5 T ) are extremaly scarce. Recently, a series of works devoted to RE bulk compounds with orthorhombic double perovskite type structure have been published. Regarding magnetocaloric properties, the most perspective of them appear those containing gadolinium atoms Gd2ZnMnO626, Gd2FeAlO627 and Sr2GdNbO628 with the largest − ΔSM ~ 26 J Kg−1 K−1 determined for the latter compound. From nanoscaled structures, it is worth to mention Eu doped Gd2O3 nanorods29 that exhibit enhancened MCE when compared with the pure Gd2O3 nanotubes30. Here, the promotion of magnetic entropy change up to 20 J Kg−1 K−1 has been ascribed to the surface spin disorder. Apparently, at present none of these systems exceeds the qualities of our nanocomposites. Neither in magnetic entropy change magnitudes, nor in the potential working temperature range. In particular, magnitude ~ 70 J Kg−1 K−1 observed in the composite SBA16/Gd2O3-0.5 M belongs to the group of the highest |ΔSM| ever reported31. Undoubtedly, the present phenomenon deserves profound scrutiny in order to determine its nature. For this purpose we employed scaling analysis proposed by Franco et al.24 (Section Methods) that is based on the collapse of the − ΔSM (T,ΔH) data onto single universal curve. The application of magnetic entropy scaling laws may deliver information on the type of the phase transition, the presence of interactions or multiple phases in examined system. However, direct utilization of the method is hampered by the absence of a peak in the − ΔSM(T,ΔH) data corresponding to our nanocomposites (except of SBA16/Gd2O3-4 M). An alternative method for the universal curve construction therefor has been employed. The exponent n(T,H) derived from magnetic entropy change vs temperature data also collapse onto single master curve. The universal curve characteristic of the SOPT calculated in terms of the mean field theory model is shown in the Fig. 6 (green line) along with rescaled n(T,H) data of our nanocomposites. Very good agreement of rescaled data with the SOPT model for the three systems SBA15/Gd2O3-0.5 M, SBA16/Gd2O3-0.5 M and SBA15/Gd2O3-4 M has been achieved, while in the case of SBA16/Gd2O3-4 M the collapse is not sufficiently plausible. Nevertheless, the exponent characterizing field dependence of magnetic entropy change ΔSM ∝ Hn approaches the value of n = 2 at higher temperatures, what is common for the all examined nanocomposites. In this temperature region, we assume paramagnetic behavior of the systems following Curie–Weiss law M = CH/(T − TCW), where C is Curie–Weiss constant. Application of the Eq. (1) to the Curie–Weiss law yields ΔSM ~ H2 what in fact we observe. Recent works show that n(T,H) dependence can be utilized as a reliable quantitative criterion for determining the order of magnetic phase transitions. It has been theoreticaly justified and experimentaly evidenced in the series of compound families32 that overshooting of n = 2 value is one of the hallmarks unequivocally corresponding to the first order magneto-structural phase transitiuon (FOPT). Employing the criterion, FOPT has been recognized in RE6Co2Ga compounds when RE = Ho, Dy, wherease only SOPT has been observed in the case of introducing Gd33. Accurate determination of the phase transition nature is important both from fundamental and application point of view. Thermal hysteresis accompanying FOPT affects the cyclicality of the compound performance. Further very valuable benefit of scaling analysis is its ability to extrapolate the data to conditions not available in the laboratory. In the case of the systems SBA15/Gd2O3-0.5 M, SBA16/Gd2O3-0.5 M and SBA15/Gd2O3-4 M, it allows us for concluding on magnetic phase transition character that apparently occurs at negative temperature TCW ~ − 2 K. According to the mean field model of SOPT24, n has a minimum at T = TCW and its value is n = 2/3. The comparison of our collapsed data with the model in the vicinity of critical temperature shows a rather good agreement. Therefor one can conclude on correct determination of TCW ~ − 2 K and the long range magnetic ordering below the TCW for the three systems although experimental confirmation is by nature impossible. On the other hand, the collapse of SBA16/Gd2O3-4 M data is apparently not conclusive, Fig. 6. The scaling was unsuccessful due to the presence of two − ΔSM(T) peaks. Their superimposition hinders determination of the correct Tr value. For the n(T) data corresponding to lower or higher field change Tr is attributed to different T ~ 3 K or T ~ 9 K maximum (Supplementary Figure 2). Taking into account that the peak occurrence in − ΔSM(T) and corresponding minimum in n(T) data is a signature of relaxation process24, one should treat each of the maxima separately with respective scaling parameters TCW, Tr and − ΔSpkM. Based on the analogy to the rest of our nanocomposites from the series, we can ascribe low temperature maximum (T ~ 3 K) to the SOPT. Indeed, we concluded on the SOPT in our earlier work devoted to the SBA16/Gd2O3-4 M system19. Hence, elucidation of the nature of the second − ΔSM(T) peak (T ~ 9 K) that emerges only in the SBA16/Gd2O3-4 M system from the series is yet to be done. Characteristic feature of the second peak is its onset at Δµ0H ~ 1.5 T and progressive promotion with higher applied field change. Likewise behavior is observed also for the respective minimum in the n(T,H) data (Supplementary Figure 2). This is in contradiction with the mean field theory24 where n(T) minimum is field independent attaining constant value n = 2/3 at the critical temperature TCW. However, according to Franco et al.24, this peculiar behavior may be indicative of multiple magnetic phase presence in the system. Therefore, − ΔSM(T,ΔH) data of SBA16/Gd2O3-4 M have been rescaled with respect to the second peak using corresponding parameters obtained directly from − ΔSM, Fig. 7.
The universal curve has been constructed for the data on the right side of the second peak, whereas in the lower temperature region scaling failed. The data exhibit typical signature of the minor magnetic phase presence in the system described by Franco et al.34, Fig. 7, where the arrow indicates the evolution of the curves with increasing magnetic field. The evidence of multiple magnetic phase coexistence is manifested also by the wasp-waist hysteresis loop at 2 K observed only for SBA16/Gd2O3-4 M from the nanocomposite series16. Despite of a peak absence, master curves have been obtained even in the magnetic entropy change data of SBA15/Gd2O3-0.5 M, SBA16/Gd2O3-0.5 M and SBA15/Gd2O3-4 M, Fig. 7. It was facilitated by the rescaled temperature axis that we adopted from the n(T) scaling analysis, Fig. 6. No signatures of multiple magnetic phase presence in the three systems have been recognized. Although the evidence on the physical nature of the − ΔSM(T) peak at T ~ 9 K in the SBA16/Gd2O3-4 M has been gathered, an unambiguous determination of its origin is difficult. Based on the enhanced neutron absorption apparent from SANS data (Fig. 1b) along with analogy to similar nanocomposite16,35 containing iron oxide NPs instead of Gd2O3, larger nanoparticles’ formation on the surface of the SBA16/Gd2O3-4 M nanocomposite is presumable. One can hypothesize on the coexistence of magnetic phases corresponding to the larger nanoparticles with higher crystallinity and small particles in the matrix pores with significant lattice disorder. In fact, crystalline Gd2O3 phase has been experimentally evidenced by X-ray diffraction only in the case of SBA16/Gd2O3-4 M system from the series16. However, due to the complexity of the examined nanocomposite systems, any conclusion on the phase composition without extra supporting data would be speculative.
Conclusions
Based on the analysis of experimental data provided by SANS, HRTEM, XPS and magnetometry along with the context of results obtained for the likewise systems earlier, the following conclusions regarding the examined nanoporous SiO2/Gd2O3 nanocomposite series have been made. During matrix modification, progressive occupancy of the pores by the nanoparticles with increasing gadolinium precursor concentration was confirmed. In the case of the matrix with cubic symmetry (SBA16), a scenario of critical precursor concentration above 0.5 M was evidenced. All of the systems exhibited extraordinarily large values of magnetic entropy change at low temperatures that were nanoparticle concentration and matrix type dependent. Application of scaling analysis that was modified and applied to the nanocomposite systems for the first time revealed the nature of the enhanced magnetocaloric effect observed in the investigated series. With the aid of scaling laws, signatures of the second order phase transition from paramagnetic to long range ordered (antiferromagnetic) phase were determined, although the conditions were unavailable in the laboratory. The combination of unique magnetocaloric performance (SOPT, high − ΔSM(T), absence of thermal and magnetic hysteresis) along with nanoscale dimensions that facilitate a low cost production of the presented nanocomposites favor our SBA15/Gd2O3 and SBA16/Gd2O3 systems for cryogenic magnetocaloric applications.
Methods
SANS technique
Small angle neutron scattering (SANS) measurements were carried out at the IBR-2 pulsed reactor in Frank Laboratory of Neutron Physics, Joint Institute for Nuclear Research in Dubna (Russia). The wavelength distribution of the incident thermal neutron beam resembles a modified Maxwell distribution ranging from ~ 0.2 to 6 Å with a spectral distribution maximum at ~ 1.8 Å. A small-angle time-of-flight spectrometer YuMO was used, allowing to cover the scattering vector Q range 0.006–0.6 Å−1 (Q = (4π/λ)sinθ, where λ is the neutron wavelength and 2θ is the scattering angle)36. Samples in powder form were loaded in aluminum cells and exposed to neutrons for approximately one hour at room temperature. The scattering from an empty cell was measured and subtracted from the sample scattering. The averaged scattering patterns were corrected for detector efficiency absorption, solvent scattering, and instrumental background. Raw data treatment was performed by the SAS software37.
XPS technique
The X-ray photoelectron spectroscopy (XPS) spectra were measured at the constant pass energy of 50 eV. The energy scale of the spectrometer was calibrated by setting the measured Au 4f 7/2 and Cu 2p 3/2 binding energies to 84.00 ± 0.05 eV and 932.66 ± 0.05 eV, respectively, in reference to Fermi energy EF. The energy drift due to charging effects was calibrated, taking the XPS C1s (284.6 eV) core level spectrum of hydrocarbons as it was suggested for dielectric materials.
Magnetic measurements
Magnetic measurements were performed by SQUID based magnetometer MPMS 5XL (Quantum Design). Powder samples of the nanocomposite systems were encapsulated in a gelatine capsule and fixed in the plastic straw. The signal contribution of the empty gel cap and the straw was subtracted from the total signal and the data were corrected for the diamagnetic contribution using Pascal’s constants. Isothermal magnetization data were obtained as follows. The sample was cooled in the absence of applied magnetic field down to initial temperature. Then the magnetization vs increasing applied field M(H) was recorded up to 5 T. Further, the temperature was elevated, fixed to higher value (up to 50 K) and another branch of M(H) was taken. Magnetic susceptibility was calculated from magnetization vs temperature (1.8–300 K) data obtained in zero field cooling (ZFC) regime under applied static field 100 Oe during progressive sample heating.
Magnetocaloric properties
Magnetocaloric properties of the systems have been evaluated from the series of magnetization data. The collected M(H,T) data have been processed assuming the Maxwell relation38 μ0(∂M/∂T)H = (∂S/∂H)T that yields the expression for magnetic entropy change ΔSM at applied field change from H1 to H2
| 1 |
where μ0 is the free-space magnetic permeability. In practice, the partial derivative was replaced by finite differences and the experimental data were integrated numerically19. ΔSM(T,ΔH) data have been employed for further analysis where the local values of the exponent n characterizing the field dependence of ΔSM ∝ Hn has been calculated as39
| 2 |
Again, the partial derivative was replaced by finite differences during data procession. The collapse of n(T,H) dependences onto universal curve has been performed by rescaling temperature axis to relative temperature39 θ = (T − TCW)/(Tr − TCW), where TCW is Curie–Weiss temperature and the reference temperature Tr corresponds to the certain value of n(T) selected arbitrarily24. Once the rescaled temperature axis is constructed, the normalization of the ΔSM curves can be done using24 ΔS′M = ΔSM/ΔSM(Tr).
Supplementary Information
Acknowledgements
This work was supported by the Slovak Research and Development Agency under the contracts Nos. APVV-18-0197, APVV-20-0512, by the VEGA Nos. 1/0829/21, 1/0865/21, 1/0743/19 and by support from the Team TRIANGEL at the Faculty of Science, P. J. Šafárik University in Košice. The authors acknowledge the access to the IBR-2 facility through the FLNP-JINR user program and the support through the JINR topical themes 04-4-1121-2015/2020 and 04-4-1133-2018/2020.
Author contributions
A.Z., P.H. and A.B. performed magnetic measurements and their evaluation. O.S. performed XPS experiments. A.K. and A.Z. conducted SANS experiments, O.I. processed the raw data that were subsequently evaluated by P.H. and N.K. P.H. and A.Z. wrote the manuscript. V.G. performed TEM measurements. V.Z. and A.Z. conceived and designed the study. All the authors reviewed and approved the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-022-06132-8.
References
- 1.Alahmer A, Al-Amayreh M, Mostafa AO, Al-Dabbas M, Rezk H. Magnetic refrigeration design technologies: State of the art and general perspectives. Energies. 2021;14:4662. doi: 10.3390/en14154662. [DOI] [Google Scholar]
- 2.Zhang H, et al. Review on the materials and devices for magnetic refrigeration in the temperature range of nitrogen and hydrogen liquefaction. Phys. B Condens. Matter. 2019;558:65–73. doi: 10.1016/j.physb.2019.01.035. [DOI] [Google Scholar]
- 3.Franco V, Blázquez JS, Ingale B, Conde A. The magnetocaloric effect and magnetic refrigeration near room temperature: Materials and models. Annu. Rev. Mater. Res. 2012;42:305–342. doi: 10.1146/annurev-matsci-062910-100356. [DOI] [Google Scholar]
- 4.Smith A. Who discovered the magnetocaloric effect? Eur. Phys. J. H. 2013;38:507–517. doi: 10.1140/epjh/e2013-40001-9. [DOI] [Google Scholar]
- 5.Aprea C, Greco A, Maiorino A, Masselli C. Magnetic refrigeration: An eco-friendly technology for the refrigeration at room temperature. J. Phys. Conf. Ser. 2015;655:1–13. doi: 10.1088/1742-6596/655/1/012026. [DOI] [Google Scholar]
- 6.Tishin AM, Spichkin YI, Zverev VI, Egolf PW. A review and new perspectives for the magnetocaloric effect: New materials and local heating and cooling inside the human body. Int. J. Refrig. 2016;68:177–186. doi: 10.1016/j.ijrefrig.2016.04.020. [DOI] [Google Scholar]
- 7.Li L, Yan M. Recent progresses in exploring the rare earth based intermetallic compounds for cryogenic magnetic refrigeration. J. Alloys Compd. 2020;823:153810. doi: 10.1016/j.jallcom.2020.153810. [DOI] [Google Scholar]
- 8.Zhang Y. Review of the structural, magnetic and magnetocaloric properties in ternary rare earth RE2T2X type intermetallic compounds. J. Alloys Compd. 2019;787:1173–1186. doi: 10.1016/j.jallcom.2019.02.175. [DOI] [Google Scholar]
- 9.Ma Z, Dong X, Zhang Z, Li L. Achievement of promising cryogenic magnetocaloric performances in La1-xPrxFe12B6 compounds. J. Mater. Sci. Technol. 2021;92:138–142. doi: 10.1016/j.jmst.2021.02.055. [DOI] [Google Scholar]
- 10.Wang Y, Guo D, Wu B, Geng S, Zhang Y. Magnetocaloric effect and refrigeration performance in RE60Co20Ni20 (RE = Ho and Er) amorphous ribbons. J. Magn. Magn. Mater. 2020;498:166179. doi: 10.1016/j.jmmm.2019.166179. [DOI] [Google Scholar]
- 11.Yang Z, et al. Large magnetocaloric effect in gadolinium borotungstate Gd3BWO9. J. Mater. Chem. C. 2020;8:11866–11873. doi: 10.1039/D0TC02449J. [DOI] [Google Scholar]
- 12.Nguyen Ba D, et al. Magnetocaloric effect in flexible, free-standing gadolinium thick films for energy conversion applications. Phys. Rev. Appl. 2021;15:64045. doi: 10.1103/PhysRevApplied.15.064045. [DOI] [Google Scholar]
- 13.Essajai R, et al. Revisiting the magnetic and magnetocaloric properties of bulk gadolinium: A combined DFT and Monte Carlo simulations. Phys. Scr. 2020;96:15808. doi: 10.1088/1402-4896/abc984. [DOI] [Google Scholar]
- 14.Ke Y-J, Zhang X-Q, Wang J-F, Cheng Z-H. Giant magnetic entropy change in gadolinium orthoferrite near liquid hydrogen temperature. J. Alloys Compd. 2018;739:897–900. doi: 10.1016/j.jallcom.2017.12.358. [DOI] [Google Scholar]
- 15.Zeleňák V, et al. Large and tunable magnetocaloric effect in gadolinium-organic framework: Tuning by solvent exchange. Sci. Rep. 2019;9:1–9. doi: 10.1038/s41598-019-51590-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zeleňák V, et al. Fe 2 O 3 and Gd 2 O 3 nanoparticles loaded in mesoporous silica: Insights into influence of NPs concentration and silica dimensionality. RSC Adv. 2019;9:3679–3687. doi: 10.1039/C8RA05576A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zeleňáková A, et al. Size and distribution of the iron oxide nanoparticles in SBA-15 nanoporous silica via SANS study. Sci. Rep. 2019;9:1–9. doi: 10.1038/s41598-019-52417-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zeleňáková A, et al. Controlling of magnetocaloric effect in Gd2O3@SiO2nanocomposites by substrate dimensionality and particles’ concentration. AIP Adv. 2018;8:048105. doi: 10.1063/1.4993974. [DOI] [Google Scholar]
- 19.Zeleňáková A, Hrubovčák P, Kapusta O, Zeleňák V, Franco V. Large magnetocaloric effect in fine Gd2O3 nanoparticles embedded in porous silica matrix. Appl. Phys. Lett. 2016;109:122412. doi: 10.1063/1.4963267. [DOI] [Google Scholar]
- 20.Berkutova A, Zeleňáková A, Hrubovčák P, Kapusta O. Low-temperature heat capasity measurements in Gd-based nanocomposites. Acta Phys. Pol. A. 2020;137:911–913. doi: 10.12693/APhysPolA.137.911. [DOI] [Google Scholar]
- 21.Hrubovčák P, Kučerka N, Zeleňáková A, Zeleňák V. Particle size determination in SBA15 nanocomposite using model based analysis of SANS and magnetization experimental data. Acta Phys. Pol. A. 2020;137:730–732. doi: 10.12693/APhysPolA.137.730. [DOI] [Google Scholar]
- 22.Zeleňáková A, Zeleňák V, Bednarčík J, Hrubovčák P, Kováč J. Magnetic nanocomposites of periodic mesoporous silica: The influence of the silica substrate dimensionality on the inter-particle magnetic interactions. J. Alloys Compd. 2014;582:483–490. doi: 10.1016/j.jallcom.2013.07.188. [DOI] [Google Scholar]
- 23.Zeleňák V, Zeleňáková A, Kováč J. Insight into surface heterogenity of SBA-15 silica: Oxygen related defects and magnetic properties. Colloids Surf. A Physicochem. Eng. Asp. 2010;357:97–104. doi: 10.1016/j.colsurfa.2010.01.001. [DOI] [Google Scholar]
- 24.Franco V, Conde A. Scaling laws for the magnetocaloric effect in second order phase transitions: From physics to applications for the characterization of materials. Int. J. Refrig. 2010;33:465–473. doi: 10.1016/j.ijrefrig.2009.12.019. [DOI] [Google Scholar]
- 25.Rivera, A. C. et al. Detection of thermal neutrons using gadolinium-oxide-based nanocrystals. In Proceedings SPIE vol. 8018 (2011).
- 26.Li L, et al. Magnetic properties and excellent cryogenic magnetocaloric performances in B-site ordered RE2ZnMnO6 (RE = Gd, Dy and Ho) perovskites. Acta Mater. 2020;194:354–365. doi: 10.1016/j.actamat.2020.05.036. [DOI] [Google Scholar]
- 27.Wu B, Zhang Y, Guo D, Wang J, Ren Z. Structure, magnetic properties and cryogenic magneto-caloric effect (MCE) in RE2FeAlO6 (RE = Gd, Dy, Ho) oxides. Ceram. Int. 2021;47:6290–6297. doi: 10.1016/j.ceramint.2020.10.207. [DOI] [Google Scholar]
- 28.Xu P, Ma Z, Wang P, Wang H, Li L. Excellent cryogenic magnetocaloric performances in ferromagnetic Sr2GdNbO6 double perovskite compound. Mater. Today Phys. 2021;20:100470. doi: 10.1016/j.mtphys.2021.100470. [DOI] [Google Scholar]
- 29.Hazarika S, Behera PS, Mohanta D, Nirmala R. Magnetocaloric effect of Gd2O3 nanorods with 5% Eu-substitution. Appl. Surf. Sci. 2019;491:779–783. doi: 10.1016/j.apsusc.2019.05.266. [DOI] [Google Scholar]
- 30.Paul R, et al. Magnetocaloric effect at cryogenic temperature in gadolinium oxide nanotubes. J. Magn. Magn. Mater. 2016;417:182–188. doi: 10.1016/j.jmmm.2016.05.057. [DOI] [Google Scholar]
- 31.Pecharsky VK, Gschneidner KA. Tunable magnetic regenerator alloys with a giant magnetocaloric effect for magnetic refrigeration from ∼20 to ∼290 K. Appl. Phys. Lett. 1997;70:3299–3301. doi: 10.1063/1.119206. [DOI] [Google Scholar]
- 32.Law JY, et al. A quantitative criterion for determining the order of magnetic phase transitions using the magnetocaloric effect. Nat. Commun. 2018;9:1–9. doi: 10.1038/s41467-018-05111-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Guo D, et al. First- and second-order phase transitions in RE6Co2Ga (RE = Ho, Dy or Gd) cryogenic magnetocaloric materials. Sci. China Mater. 2021;64:2846–2857. doi: 10.1007/s40843-021-1711-5. [DOI] [Google Scholar]
- 34.Franco V, Caballero-Flores R, Conde A, Dong QY, Zhang HW. The influence of a minority magnetic phase on the field dependence of the magnetocaloric effect. J. Magn. Magn. Mater. 2009;321:1115–1120. doi: 10.1016/j.jmmm.2008.10.034. [DOI] [Google Scholar]
- 35.Zeleňáková A, et al. Size and distribution of the iron oxide nanoparticles in SBA-15 nanoporous silica via SANS study. Sci. Rep. 2019 doi: 10.1038/s41598-019-52417-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kuklin AI, et al. Small-angle neutron scattering at the pulsed reactor IBR-2: Current status and prospects. Crystallogr. Rep. 2021;66:231–241. doi: 10.1134/S1063774521020085. [DOI] [Google Scholar]
- 37.Soloviev AG, et al. SAS program for two-detector system: Seamless curve from both detectors. J. Phys. Conf. Ser. 2017;848:012020. doi: 10.1088/1742-6596/848/1/012020. [DOI] [Google Scholar]
- 38.Franco V, et al. Magnetocaloric effect: From materials research to refrigeration devices. Prog. Mater. Sci. 2018;93:112–232. doi: 10.1016/j.pmatsci.2017.10.005. [DOI] [Google Scholar]
- 39.Franco V, Conde A, Romero-Enrique JM, Blázquez JS. A universal curve for the magnetocaloric effect: An analysis based on scaling relations. J. Phys. Condens. Matter. 2008;20:285207. doi: 10.1088/0953-8984/20/28/285207. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.