Abstract
The ability to generalize across specific experiences is vital for the recognition of new patterns, especially in speech perception considering acoustic–phonetic pattern variability. Indeed, behavioral research has demonstrated that listeners are able via a process of generalized learning to leverage their experiences of past words said by difficult-to-understand talker to improve their understanding for new words said by that talker. Here, we examine differences in neural responses to generalized versus rote learning in auditory cortical processing by training listeners to understand a novel synthetic talker. Using a pretest–posttest design with EEG, participants were trained using either (1) a large inventory of words where no words were repeated across the experiment (generalized learning) or (2) a small inventory of words where words were repeated (rote learning). Analysis of long-latency auditory evoked potentials at pretest and posttest revealed that rote and generalized learning both produced rapid changes in auditory processing, yet the nature of these changes differed. Generalized learning was marked by an amplitude reduction in the N1–P2 complex and by the presence of a late negativity wave in the auditory evoked potential following training; rote learning was marked only by temporally later scalp topography differences. The early N1–P2 change, found only for generalized learning, is consistent with an active processing account of speech perception, which proposes that the ability to rapidly adjust to the specific vocal characteristics of a new talker (for which rote learning is rare) relies on attentional mechanisms to selectively modify early auditory processing sensitivity.
INTRODUCTION
A fundamental problem faced by all theories of speech perception is to explain how listeners understand speech despite extensive variability and noise in acoustic patterns across talkers and contexts. One explanation is that listeners overcome acoustic–linguistic variability by remapping the relationship of acoustic cues to linguistic categories by generalizing across their recent experiences (Weatherholtz & Jaeger, 2016; Heald & Nusbaum, 2014). Under this view, listeners leverage their past experiences with a talker to presumably form an abstract representation of the talker’s acoustic–phonetic (vocal) space that ultimately can be used by the listener to better modify attention toward the most diagnostic acoustic cues for that talker. This form of learning has the benefit of improving recognition for even previously unheard words said by the same talker. However, many studies investigating the neural correlates of generalized learning in such settings have focused on generalization acquired after long-term rote training (Tremblay, Ross, Inoue, McClannahan, & Collet, 2014; Ross & Tremblay, 2009), where listeners are trained and tested on a small set of repeating words. Although rote training may be one way to rapidly learn the meaning associated with a small set of acoustic patterns (Fenn, Margoliash, & Nusbaum, 2013), it is not the most effective way of producing generalization (Fenn et al., 2013; Greenspan, Nusbaum, & Pisoni, 1988). Instead, broad exposure to a variety of patterns promotes rapid learning of general perceptual categories, particularly for speech (generalized training; Heald & Nusbaum, 2014).
The ability for listeners to generalize beyond their perceptual experiences to novel acoustic patterns has been shown to depend on the type of experience or training a learner is given. When participants are trained on a difficult-to-understand computer-generated (synthetic) talker, a listener’s ability to generalize beyond the words in the training set has been shown to depend on whether they were given all novel words during training (generalized training) or if they were given a small set of words that repeated (rote training; Greenspan et al., 1988). Participants who are given all novel words during training demonstrate significantly better generalization compared with participants who were trained on a small set of words that repeated. The notion that equal amounts of rote and generalized training yield different performance outcomes suggests that they may be mediated by different processes. The work of Fenn et al. (2013) supported this idea by showing that memory consolidation during sleep selectively benefited generalized learning, but not rote learning. However, this conjecture of different neural processes underlying online rote and generalized learning has not been directly tested.
The evidence that type of training (rote vs. generalized) can determine the degree to which learning will transfer beyond previous experiences raises questions as to what cognitive and neural mechanisms allow for such transfer of learning or generalization. Although the neural underpinnings of rapid generalized learning have, to our knowledge, not been empirically examined, rapid generalized learning has been described cognitively as being dependent on the mechanism of selective attention. From a cognitive view, rapid generalized learning improves perception by orienting attention toward the most phonetically relevant acoustic cues and away from irrelevant ones for a given circumstance (Francis & Nusbaum, 2002; Goldstone, 1998; Nosofsky, 1986). In the context of speech perception, the process of generalized learning has been utilized to understand how listeners come to learn a difficult-to-understand talker given more listening experience. The emphasis on selective attention in the context of learning a difficult-to-understand talker, as opposed to one that emphasizes, say, learning new perceptual categories, stems from the idea that adult listeners already possess a complete phonological category system (Liberman, 1970; Chomsky & Halle, 1968). As such, a listener adjusting to the circumstance of trying to understand a difficult-to-understand talker—provided they are speaking the same language—has been discussed as a process of narrowing attention toward the most diagnostic acoustic–phonetic cues for the given talker and away from uninformative ones. Indeed, the work of Francis and Nusbaum (2009) has shown that generalized learning modifies the way available attentional and working memory capacity is used, which has led many to draw on resource allocation models of perception (e.g., Lavie, 1995) to explain how training leads to such improvements (e.g., Heald & Nusbaum, 2014). According to these cognitive accounts, the initial poor intelligibility manifests because listeners do not know which acoustic cues to focus their attention on to derive meaning appropriately, and as such, ongoing recognition is associated with higher attentional and working memory costs. Following rapid generalized learning, however, this selective attention account suggests that listening will be much less effortful for new words spoken by the same talker, as listeners are able to shift attention to the subset of acoustic features that are most diagnostic of the phonemes produced by the talker (Francis, Baldwin, & Nusbaum, 2000). For this reason, training on synthetic speech offers a promising way to investigate how selective attention works in the context of perceptual learning.
Although synthetic speech learning has been used as a model to understand how listeners adapt to difficult-to-understand speech (e.g., foreign accented, deaf, dysarthric, or time compressed), it has been argued that the processes underlying synthetic speech learning may be reflective of learning mechanisms that are critical in speech processing in general (see Heald & Nusbaum, 2014). Specifically, generalized learning mechanisms have been used to understand how listeners overcome the huge amount of acoustic variability in their listening environment. Even when speech is putatively easy to understand, listeners encounter many circumstances when the underlying acoustic-to-phonetic mapping changes—such as a shift in talker, speaking rate, or social register (cf. Miller, 1987; Liberman, Cooper, Shankweiler, & Studdert-Kennedy, 1967; Ladefoged & Broadbent, 1957). In these cases, behavioral work shows that a momentary increase in load on attentional and working memory resources occurs (e.g., Magnuson & Nusbaum, 2007), potentially indicative of a learning process in which listeners must determine which acoustic cues are most diagnostic in that setting. For this reason, neural changes found to underlie synthetic speech learning may indeed be pertinent to speech perception in general. Indeed, the application of generalized learning mechanisms likely extends beyond speech perception, as this approach to speech perception (where the acoustic–phonetic mappings are dynamically modified by experience) is consistent with general category learning models, where the need to remap is tied to changes in how cues relate to category membership (e.g., Goldstone, 1994).
Neuroimaging studies have shown that instruction to selectively attend to phonetic content modulates activity in anterior parts of the auditory cortex, whereas instruction to selectively attend to a spatial location modulates posterior activity (Woods et al., 2009; Ahveninen et al., 2006; Petkov et al., 2004). This dissociation—likely related to the “what” and “where” processing streams proposed by Rauschecker and Tian (2000)—is mirrored in electrophysiological studies demonstrating that the combined activity of these two sources (anterior and posterior) contributes to the morphology of the N1, a negative peak around 100 msec in the auditory evoked potential (McEvoy, Levänen, & Loveless, 1997). The electrophysiological measures indicate that activity in anterior parts of the auditory cortex has a longer latency than activity arising from the posterior source, which has been argued to reflect why the process of identifying an object takes longer than recognizing its spatial origin (Picton, 2011). As such, although N1 as a whole has been argued as a marker of attention, the more posterior, earlier-latency N1 source appears to support the gating of awareness to novel sounds, and the more anterior, later-latency N1 source supports a subsequent attentional focus to acoustic features comprising the auditory object (Gutschalk, Micheyl, Oxenham, von Kriegstein, & Warren, 2008; Jääskeläinen et al., 2004; Tiitinen, May, Reinikainen, & Näätänen, 1994). This differentiation between early and late N1 sources relates to earlier the work of McCallum and Curry (1979), who argued that the N1 wave should be differentiated into separate waves. Specifically, McCallum and Curry (1979) proposed that the N1 wave should be approached as three separate waves, an N1a wave (with a frontotemporal maximal peak at ∼70 msec), an N1b wave (with a vertex maximal peak at ∼100 msec), and an N1c wave (with a temporal maximal peak at ∼140 msec). Adopting this framework, Picton (2011) has speculated that the N1c wave can be recognized as arising from this anterior, longer-latency N1 source. Given that selective attention is thought to exclusively alter how attention is aligned to featural information in phoneme recognition for generalized learning, we hypothesize that the rapid generalized learning of a synthetic talker may exclusively alter the longer-latency N1 activity (see Figure 1A).
Figure 1. .
Schematic of hypothesized time of changes to the ERP signal as a consequence of generalized learning compared with rote learning. (A) We hypothesize that an overall decrease in potentiation for the longer-latency N1 source or N1c will be observed in the generalized learning condition, but not in the rote learning condition, if the longer-latency N1 source or N1c is sensitive to the demands of attention toward features comprising an auditory object. (B) We hypothesize that an overall decrease in P2 potentiation will be observed in the generalized learning condition, but for not the rote learning condition, if P2 is sensitive to the number of active featural relationships searing current recognition. (C) We hypothesize that an overall decrease in late negativity should be found in the generalized learning condition, but not in the rote learning condition, if late negativity is reflective of a prediction error correction process that supports perception.
Although neural studies on selective attention offer some context to our current question, research on the neural correlates of auditory perceptual learning can also offer additional insight. However, it is important to note that generalized perceptual learning of synthetic speech marks a departure from other paradigms used to study the neural underpinnings of perceptual learning. First, extant neural studies investigating perceptual learning have almost exclusively focused on rote (not generalized) perceptual learning, in which participants are repeatedly trained and tested on the same, small set of stimuli. Second, in extant perceptual learning paradigms, participants have been required to either learn (1) to differentially label sounds that are functionally equivalent in their native language (Tremblay et al., 2014; Ross & Tremblay, 2009) or (2) to separately label two concurrently presented vowels (with the same spatial origin; Alain & Snyder, 2008; Alain, Snyder, He, & Reinke, 2007; Reinke, He, Wang, & Alain, 2003). Neither of these paradigms examines learning that occurs at the phonological system level, which is critical for understanding a difficult-to-understand talker. Rather, these paradigms emphasize the learning of tokens—either labeling nonnative tokens (new phonological categories) or distributing attention over known tokens in novel ways in the case of labeling two stimuli at once. For this reason, past paradigms that have been used to understand perceptual learning may only offer partial clues into what neural mechanisms support rapid generalized perceptual learning.
Perceptual learning paradigms where participants are given experience with a novel phonetic contrast not in their native language have documented that learning is marked by an overall decrease in N1 amplitude (maximal at vertex ∼100 msec; Alain, Campeanu, & Tremblay, 2010; Ross & Tremblay, 2009). Work in this paradigm, however, has argued that this N1 change in this context may be a consequence of habituation and not learning, as the stimulus set only consists of two sounds played repeatedly, often as participants passively listen (Tremblay et al., 2014). However, in more active tasks, in which participants are asked to rapidly learn to segregate concurrently presented vowels, learning has been demonstrated to lead to a positive shift in the ERP wave ∼130 msec from stimulus onset in temporal electrodes (Alain & Snyder, 2008; Alain et al., 2007). As previously mentioned, Picton (2011) has argued that this temporal positive going shift can be taken as a modulation in the longer-latency N1 source that supports a subsequent attentional focus to acoustic features comprising the auditory object (Gutschalk, Micheyl, & Oxenham, 2008; Jääskeläinen et al., 2004; Tiitinen et al., 1994). As such, this finding suggests that a similar positive change (i.e., smaller negative amplitude) in the longer-latency N1 may be observed following the rapid generalized learning for a difficult-to-understand synthetic talker (see Figure 1A).
In contrast to rapid generalized learning, rote learning of speech tokens may be more similar to paired-associate learning. Successful paired-associate learning entails the formation of associations between stimuli and associated responses rather than the systematic relationships among the speech tokens as a phonological system for a single talker. If rapid rote learning of specific utterances from a difficult-to-understand synthetic talker is characterized by the encoding and retrieval of episodic memories, then such learning will not be marked by a change in sensory processing because there is no need to develop a systematic relationship between the talker’s phonetic idiosyncrasies and the native phonological system. Instead, listeners may simply memorize the limited set of acoustic patterns and their associated meanings. From this perspective, rapid rote learning should not modify attention to acoustic–phonetic properties and therefore should not influence longer-latency N1 activity (see Figure 1A).
Multiday rote perceptual learning experiments have also reported an increase in the auditory evoked P2 response after 2 or 3 days of training (Bosnyak, Eaton, & Roberts, 2004). The change in the auditory evoked P2 response, which occurs around 200 msec poststimulus (Ross et al., 2013; Näätänen & Winkler, 1999) is thought to reflect a relatively slow learning process, perhaps relating to the consolidation of a featural representation for the nonnative phonetic contrast that participants are learning in long-term memory (Tremblay et al., 2014; Ross & Tremblay, 2009). In the context of learning to understand a difficult-to-understand synthetic talker via generalized learning, it is unclear if a change in the auditory evoked P2 response would be observed. If the change in the auditory evoked P2 response marks the consolidation of a newly learned featural representation in long-term memory, then P2 changes should not be observed following generalized learning of a difficult-to-understand talker. However, given that the evoked P2 response has been shown to increase after new perceptual categories have been formed (Tremblay et al., 2014; Tremblay, Shahin, Picton, & Ross, 2009), another interpretation is that the auditory evoked P2 response may simply be sensitive to the number of active featural representations serving current recognition. Such an interpretation is consistent with research showing that the P2 response is sensitive to spectral complexity but only for experts who presumably rely on more featural representations as spectral complexity increases (Shahin, Roberts, Pantev, Trainor, & Ross, 2005) If the auditory evoked P2 response is sensitive to the number of active feature representations that underlie perceptual recognition, then rapid generalized learning of a difficult-to-understand talker may indeed yield immediate effects on the auditory evoked P2 response. Specifically, if rapid generalized learning leads to a reduction in the ambiguity of how acoustic patterns match to linguistic categories by reducing the number of active feature representations required for ongoing perception, we should see an immediate reduction in the auditory evoked P2 response following training (see Figure 1B). In contrast to generalized learning, it is unlikely that any change would be observed for rote learning of a difficult-to-understand talker because rote learning of a difficult-to-understand talker may rely more on the encoding and retrieval of episodic memories. Consequently, rote learning of a difficult-to-understand talker should not alter the number of active featural representations nor, by this logic, should it elicit a change in the auditory P2 (see Figure 1B).
Although previous research examining cortical and subcortical evoked activity associated with perceptual learning has largely focused on changes in the auditory N1 and P2 waves (sometimes referred to collectively as the N1–P2 complex), a decrease in late negativity in the auditory evoked potential starting 600 msec poststimulus onset has also been found to be coincident with improved perception following training (Tremblay et al., 2014). Given that negative deflections in event-related potentials are often affiliated with processes related to error correction (e.g., N400, late difference negativity, and error-related negativity), changes in the late negativity wave posttraining may represent a change in an error monitoring mechanism that supports learning. This is consistent with perceptual learning models that specify that the reorganization or formation of perceptual categories (which are implicit in nature) should be dependent on a trial-by-trial prediction error correction process (Ashby & O'Brien, 2005; Ashby, Alfonso-Reese, Turken, & Waldron, 1998). Under this view, changes in late negativity in the auditory evoked potential posttraining should only be found when training leads to changes in the reorganization or formation of implicit categories (such as those that presumably guide perception). As this view suggests that learning should lead to an improvement in trial-by-trial prediction error monitoring, as attention becomes appropriately organized, we hypothesize that the late negativity wave should lessen as a consequence of generalized learning, but not rote learning (see Figure 1C).
The goal of this study is to examine how neural responses produced by generalized learning or rote learning of synthetic speech differ. Specifically, we assess whether generalized and rote learning are marked by different changes in neural activity during early sensory auditory processing (i.e., during the first 250 msec) or only during later processing. To test this, we used a pretest–training–posttest design while performing EEG. We trained participants using either (1) a large inventory of words in which no words were repeated across the experiment (generalized learning) or (2) a small inventory of words where words were repeated (rote learning; see Figure 2). Although participants in the rote learning condition can adopt a simple memorization strategy, participants in the generalized learning condition cannot use such a strategy as no words were repeated across the experiment. Using 128 electrodes and nonparametric significance testing using a permutation test procedure, we compared auditory evoked potentials from stimuli at pretest to those at posttest for each learning condition. If resource allocation models of perception are correct (Heald & Nusbaum, 2014), we should find that only generalized learning leads to changes in N1–P2 window posttraining. Such a finding would suggest that generalized learning improves perception by constraining how listeners selectively attend to and process acoustic information. Additionally, to the degree that an error correction process is needed to guide the reorganization of attention (as suggested by perceptual learning models, see Ashby & O’Brien, 2005; Ashby et al., 1998), we should observe decreases in the late negativity wave as listeners become more successful in selectively attending to and processing the difficult-to-understand speech.
Figure 2. .
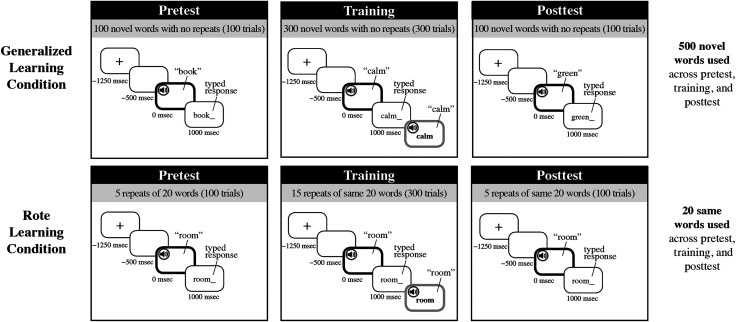
Schematic for trial structure for the generalized learning condition and rote learning condition at pretest, training, and posttest. Trial time is relativized against initial word onset (black bolded screen). All trials start with a fixation cross (1250 msec before initial word onset), followed by a blank screen (500 msec before initial word onset). At 1000 msec after initial word onset, participants are asked to type the word that they heard. In training, this identification procedure was followed by visual written feedback in tandem with an additional auditory presentation of the initial word (gray bolded screen). Participants in the rote condition were given an additional test of 100 novel words (not shown) to behaviorally assess their generalization performance (EEG during this additional test was not recorded).
METHODS
Participants
Twenty-nine individuals participated in the generalized learning portion of the experiment (M = 21.4 years, SD = 3.94 years, age range: 18–38, 13 women, 2 left-handed), and 33 participants participated in the rote learning portion of the experiment (M = 20.3 years, SD = 2.19 years, age range: 18–26, 17 women, 5 left-handed). These two groups of participants did not statistically differ in terms of age, t(60) = 1.38, p = .17; gender (Fisher’s exact test, p = .62); or handedness (Fisher’s exact test, p = .43). All participants were recruited from the University of Chicago and surrounding community. Participants were paid or granted course credit for their participation. All participants identified as native English speakers, with no reported history of either a hearing or speech disorder. Upon completion of the task, all participants reported no prior experience with the stimuli heard in the experiment. Additionally, informed consent was obtained from all participants, and the research protocol was approved by the University of Chicago institutional review board.
Stimuli
Stimuli consisted of 500 monosyllabic words produced using the text-to-speech synthesizer Rsynth (Ing-Simmons, 1994). These words were taken from or modeled after a phonetically balanced inventory of words that approximate the distribution of phonemes in American English (Egan, 1948; see Open Science Framework for a complete list of the words used, https://osf.io/kwcsv/?view_only=ee2b903d3c2c467aa6b954b19c7a2afa). Rsynth uses a formant synthesizer (Klatt, 1980), together with relatively primitive orthography-to-speech rules, and it has a reduced and degraded acoustic–phonetic cue set with low acoustic cue covariation compared with natural speech. For these reasons, the intelligibility for Rsynth is quite low. However, listeners show rapid improvement even after a 1-hr training session, even when no words were repeated across the experiment, increasing their understanding on average by 15 words (15% improvement) compared with their performance at pretest (Fenn et al., 2013; Fenn, Nusbaum, & Margoliash, 2003; Schwab, Nusbaum, & Pisoni, 1985). This is similar to the work of Nygaard and Pisoni (1998), which has demonstrated that listeners learning the speech of a particular (nonsynthetic) talker show significant improvements in speech recognition even for words not previous trained on. Similarly, research with accented talkers shows that learning the accent improves recognition for untrained words (Bradlow & Bent, 2008).
For the generalized learning condition, two test lists containing 100 words each (Test 1, average word duration of 354 msec, SD = 75 msec, and Test 2, average word duration of 331 msec, SD = 83 msec) and a training list containing 300 word (average word duration of 348 msec, SD = 80 msec) were constructed from the synthesized set of 500 words. For the rote learning condition, 20 words were picked from the generalized training list of 300 words to serve as the test (both pretest and posttest) and training words. The same 20 words were used for each participant in this condition (average word duration of 348 msec, SD = 82 msec). The two tests (Test 1 and Test 2) for generalized learning were piloted to be performance balanced in terms of difficulty. Although no words were repeated across test and training in the generalized learning condition, there was repetition of words in the rote learning condition such that the 20 selected words were repeated 5 times each during testing (100 items per test) and 15 times each during training (300 training items).
To ensure that the 20 selected rote words approximated the properties of the full 500 words from the generalized learning condition, we made a random selection of 20 words from the generalized list (500 possible words) and calculated the number of unique phonemic items in this set, repeating this process 10,000 times to generate a distribution against which we could evaluate our observed number of unique phonemes in the actual rote set. The actual rote set possessed 24 unique elements, which fell within the 95% confidence interval (CI) of the constructed distribution (21–28 unique phonemes). In addition to this, we also calculated the percent overlap between the top 24 phonemes that occurred the most in the generalized word list (500 possible words) and the 24 unique phonemes identified in the actual rote word list. We observed that there was an 85% overlap between these two lists. To evaluate this statistic, we again created a distribution of this statistic by making a random selection of 20 words from the generalized list (500 possible words) and calculating the percent overlap between this set and the top 24 phonemes found in the generalized word list, repeating this process 10,000 times. Our observed percent overlap fell within the 95% CI of the constructed distribution (70–95%). These analyses suggest that the 20 selected rote words well approximated the properties of the generalized word list, given their set size.
Procedure
Behavioral work has clearly demonstrated that performance changes due to perceptual learning are long-lasting (for a review, see Goldstone, 1998). Specifically, research by Schwab et al. (1985) has demonstrated that improvements in understanding from rapid generalized training of a difficult-to-understand synthetic voice lasts for 6 months. To avoid obvious carryover effects, participants were either assigned to engage in generalized learning or rote learning. For both groups, informed consent was obtained before beginning the experiment. All participants were initially tested (pretest), trained (training), and retested (posttest) on their identification performance for monosyllabic synthetic speech stimuli (see Figure 2 for a schematic of trial and condition structure).
In both groups, stimuli were presented binaurally using MATLAB 2015 with Psychtoolbox 3 over insert earphones (3M E-A-RTONE GOLD) at 65–70 dB SPL In the generalized learning condition, the test lists used at pretest and posttest were counterbalanced across participants to ensure that any change in performance from pretest to posttest would reflect learning. As the testing material for the rote learning condition was the same at pretest (5 repetitions for each word–100 test trials), training (15 repetitions for each word–300 training trials), and posttest (5 repetitions for each word–100 test trials), there was no need to counterbalance the tests for the rote learning condition. For both rote and generalized learning, test trials consisted of participants hearing a synthetic speech token and, after a short delay, being asked to type back what they heard. For training, this identification procedure was followed by visual written feedback in tandem with an additional auditory presentation of the synthetic speech token. In the generalized learning condition, no words were ever repeated across the experiment (i.e., participants heard 100 unique words during the pretest, 300 unique words during training, and 100 unique words during the posttest).
At the conclusion of the experiment, participants in the rote condition were given a generalized learning test of 100 novel words (identical to Test 1 in the generalized learning condition). This was done to replicate previous research that showed that rote learning training leads to poorer generalization to untrained words compared with training on all novel words when learning a difficult-to-understand talker (Fenn et al., 2013; Greenspan et al., 1988). Important to our present hypotheses, these previous studies show that rote learning training for 20 repeat words of a difficult-to-understand talker does allow for some generalization to untrained words, but that this generalization is significantly weaker than the generalization found for those who are trained on all novel words (Fenn et al., 2013; Greenspan et al., 1988). For this reason, we expect generalization performance for rote individuals to be better than the generalized learning conditions’ pretest performance but worse than their posttest performance. EEG signals were recorded continuously during pretest, training, and posttest. After the experiment concluded, participants’ heads were photographed using a geodesic dome with 11 mounted infrared cameras to precisely determine the location of all 128 electrodes (Russell, Jeffrey Eriksen, Poolman, Luu, & Tucker, 2005).
Data Acquisition
Neurophysiological responses were obtained using an Electrical Geodesics, Inc. (EGI) GES 300 Amp system (output resistance of 200 MΩ, with a recording ranging from 0.01 to 1000 Hz). The high-density EEG (128 electrodes) was recorded at 250 samples/sec in reference to vertex using unshielded HCGSN 130 nets. Before both pretest and posttest periods, impedances were minimized by reseating or, if necessary, by rewetting electrode sponges using a transfer pipette and saline (to 50 kΩ or less). Resulting amplified EEG signals were recorded using EGI Net Station software (v. 4.5.7) on a computer running Mac OSX (10.6) operating system. No filtering was applied to the EEG signal at acquisition. Trial types were tagged in Netstation using the Netstation Toolbox in Psychtoolbox. Timing of tags was corrected during preprocessing as a mean tagging latency of 15 msec (SD = 2.4 msec) was found between the stimulus presentation computer running Mac OSX and Net Station via EGI’s audio timing test kit.
EEG Preprocessing
EEG recordings were preprocessed in Brain Electrical Source Analysis (BESA) software (BESA Research 7.0). Electrode coordinates from individuals’ net placement photos were used to assign individual sensor locations for each participant. Recordings were filtered with 0.3–50 Hz band pass and 60 Hz notch filters to remove electrical noise. Voltage was rereferenced to the average of all electrodes. Based on the trial tags, epochs of interest around the times of stimuli presentation were selected as 200 msec before to 800 msec after the onset of the stimulus. Epochs were then examined for artifacts including eye blinks and movements. Beyond visual inspection, voltage threshold detection was also used (voltage thresholds for eye movements were 150 μV for horizontal movements picked up in the EOG electrodes and 250 μV for vertical movements). Artifacts were removed from the epochs of interest using ocular source components using BESA (BESA Research 7.0; Picton et al., 2000; Berg & Scherg, 1994). In some cases, artifacts due to large movements or to sweat could not be removed by independent component analysis. In these cases, the contaminated trials were not included in further analysis. Individual channels that were problematic for a majority of trials (amplitude of >150 μV indicating excessive noise, <0.01 μV indicating low signal, or changes of >75 μV from one sample to the next) were replaced by interpolation using surrounding channels. Because electrode impedances were only checked before pretest and posttest periods, we declined to analyze EEG data from the training block to ensure we only present the highest quality data.
The data collected from three participants in the generalized learning condition (two men, one woman; all right handed) and three participants in the rote learning condition (two men, one woman; all right handed) were removed from further analysis because of excessive artifact contamination (removal of more than 30 trials in either pretest or posttest). In the generalized learning condition, the remaining 26 participants had an average of 90 trials remaining for the pretest (SD = 8.69, range: 74–100), and an average of 88 trials remaining for the posttest (SD = 7.22, range: 75–99). In the rote learning condition, the remaining 30 participants had an average of 89 trials remaining for the pretest (SD = 8.10, range: 71–100) and an average of 91 trials remaining for the posttest (SD = 8.43, range: 70–100). For each participant, averaged waveforms for the conditions of interest (e.g., pretest and posttest) were created, as were corresponding files for topographic analysis in RAGU (RAndomization Graphical User interface; Koenig, Kottlow, Stein, & Melie-García, 2011). The 100-msec prestimulus period was used to baseline correct the ERP averages by subtracting the average during the prestimulus period from each time point in the waveform. To compute topographic maps, participant-specific 3-D electrode locations were used. The averaged ERP data, participant-specific electrode location files, specific words used in each condition, and behavioral data have been made available on Open Science Framework (https://osf.io/kwcsv/?view_only=ee2b903d3c2c467aa6b954b19c7a2afa).
Statistical Analyses
Global Analyses
To conduct global analyses over the course of the entire epoch using every electrode, we used RAGU, an open-source MATLAB-based program that performs nonparametric significance testing by generating 5000 simulations in which data from the conditions of interest have been randomly shuffled to bootstrap a control data set (see www.thomaskoenig.ch/index.php/software/ragu/download). This set of simulations functions as a null distribution, against which the observed data can be compared, usually using a measure of effect size such as global field power (GFP; or the standard deviation across electrodes at a given time point) or global map dissimilarity (a measure that captures scalp topography differences between conditions at a given time point). This avoids biases associated with a priori assumptions about which time windows and electrodes should be included in the analysis (Koenig et al., 2011; Murray, Brunet, & Michel, 2008). We used RAGU to perform a GFP analysis and a topographic ANOVA (TANOVA) that compared strength of scalp field potential and scalp topography, respectively, between pretest and posttest.
RAGU calculates GFP at every time point in the epoch of interest as follows:
where n is the number of electrodes, μi is the voltage of electrode i, and μ is the mean voltage across all electrodes (Koenig, Gianotti, & Lorena, 2009). Thus, GFP is a measure of standard deviation across electrodes. Conceptually, this means that if there is a strong response over part of the scalp, then the GFP will be greater due to more variance across locations, whereas weak responses will yield low GFPs. GFP also has the benefit of being entirely reference independent. Once the observed GFP is calculated, the data are shuffled between conditions and GFP is recalculated. This reshuffling procedure is carried out 5000 times at each time point to obtain the null distribution of GFP for a given time point. At each time point, a p value is calculated that represents the proportion of randomized GFPs that exceed the observed GFP.
Although GFP is a good measurement of differences in the strength of potentials across the scalp, potentially important topographical information is lost by calculating standard deviation across all electrodes. RAGU’s TANOVA measures differences in topographical distributions of voltage between pairs of conditions or time points. The measure of effect size used is generalized dissimilarity s across the experimental conditions:
where c is the number of conditions, n is the number of electrodes, υij is the mean voltage of condition i at electrode j across participants, and υj is the mean voltage at electrode j across all participants, with conditions averaged together (Koenig & Melie-García, 2010). Because this measure accounts for differences between condition-wise maps at individual electrodes, it preserves topographical information, unlike GFP: The farther apart the voltage at electrode j in condition A versus B, the larger the squared difference added to s and therefore the larger the difference in voltage patterns on the scalp.
Once RAGU has calculated the generalized dissimilarity (s) from the data, it shuffles the data between conditions and recalculates s 5000 times to generate a null distribution of generalized dissimilarities. These are the effect sizes that would be expected in the absence of a true difference between the conditions. A p value is calculated at each time point by comparing this null distribution to the observed data as with GFP. The TANOVA was used to identify periods of interest as time windows where there appeared to be significant map differences between pretest and posttest (p < .05). Before the TANOVA analysis, we normalized data by dividing all voltage values of a given map by its time-specific GFP. This was done so that significant differences found between the conditions in the TANOVA analysis could be attributed solely to underlying differences in source contributions in the brain.
For both GFP and TANOVA analyses, we also report whether the window passed a duration threshold test. This was done by collecting the duration of continuous windows found to be significant in the bootstrapped data. The distribution of these durations represents the distribution of duration under the null hypothesis that the data are interchangeable between conditions, as they were obtained from the shuffled data (in which the data are interchanged between conditions randomly). For each test, we set the threshold for the duration as the 95th percentile of spurious window durations that appear across the 5000 random permutations. Windows in the observed data that pass this threshold testing are clearly noted; however, we decided to report all windows, especially those before 300 msec, given the transient nature of the N1 and P2 auditory evoked potentials (Picton, 2011) of interest to us here.
Beyond the RAGU analysis, we used BESA Statistics 2.0 to ascertain which electrodes were responsible for the observed topographic changes. To do this, we averaged each electrode’s voltage over the windows identified in the TANOVA analysis and performed paired-samples t tests between pretest and posttest. This analysis used a spatiotemporal permutation-based correction to adjust for multiple comparisons. For these analyses, we used a cluster alpha level of .05 for cluster building, 5000 permutations, and a channel distance of 4 cm that resulted in an average of 6.58 neighbors per channel for the generalized learning condition and an average of 7.09 neighbors per channel for the rote learning condition. The small difference in neighbors in the cluster analysis between the two conditions is due to small variation in head size between the two conditions, as a geodesic dome with 11 mounted infrared cameras was used to precisely determine the location of all 128 electrodes for each participant.
Source Level Analysis
To investigate the intracranial sources underlying the topographic window changes identified by the TANOVA analysis in RAGU, we used the local auto regressive average (LAURA) model in BESA Research 7.0. LAURA is a distributed source localization method that does not make a priori assumption with respect to the number of discrete sources. Similar to other distributed volume inverse imaging methods, LAURA seeks to find a solution where the distribution of the current over all source points is minimized while optimally trying to explain the observed topography. LAURA, however, uses a spatial weighting function to account for the fact that source strength should decrease by the inverse of the cubic distance between a putative source and recording electrodes on the scalp. The result of this technique is a spatiotemporal projection of current density in a neuroanatomical space similar to a functional map in fMRI. LAURA modeling was applied to the full ERP epoch (−200 to 800 msec) for each participant. Using a cluster-based permutation test in BESA Statistics 2.0, we computed average distributed source images across the time windows identified by the TANOVA analysis in RAGU. These average distributed source images were then contrasted between pretest and posttest for each learning condition using a cluster-based permutation test (contrast: posttest–pretest). This analysis allowed us to identify anatomical locations in the brain volume responsible for the topographical differences identified by the TANOVA analysis. For this analysis, cluster values were ascertained by the sum of all t values within a given cluster. The significance of observed clusters is determined by generating and comparing clusters from 5000 permutations of the data between stimulus conditions. Statistically, the results reported from this analysis are highly conservative as BESA corrects for multiple comparisons across all voxels and time points to control the familywise error rate. Because of the conservative nature of this analysis and that the windows we are investigating have been previously identified through the TANOVA analysis in RAGU, all identified clusters from this analysis are reported including null results.
RESULTS
Behavioral Results
Generalized Learning Behavioral Results
Word recognition performance (i.e., the number of words transcribed correctly) at posttest was subtracted from word recognition performance at pretest to obtain a participant-specific learning score. Pretest performance averaged 29 words correct out of 100 (SD = 8.19, range: 15–45). After training, recognition performance on the posttest significantly increased to an average of 42 words correct out of 100 (SD = 13.27, range: 20–71; paired-samples t test: t(25) = 7.11, p < .00001, Cohen’s d = 1.402). This means that individuals significantly recognized more words at posttest than they did at pretest, despite no words repeating across the tests (or training) in the generalized learning condition. To verify that the tests were indeed performance balanced, we compared pretest, posttest, or learning performance between the two test orders in the generalized learning condition. We found no evidence for any difference in performance (pretest: Welch’s two-sample independent-sample t test: t(24.0) = −0.93, p = .36, Cohen’s d = 0.37; posttest: Welch’s two-sample independent-sample t test: t(23.7) = −1.30, p = .22, Cohen’s d = 0.51; learning: Welch’s two-sample independent-sample t test: t(23.5) = −1.00, p = .32, Cohen’s d = 0.39).
Rote Learning Behavioral Results
Similar to generalized learning, word recognition performance at posttest was subtracted from word recognition performance at pretest to obtain a participant-specific learning score. Pretest performance averaged 16 words correct out of 100 (SD = 7.83, range: 4–30).1 After training, recognition performance on the posttest significantly increased to an average of 95 words correct out of 100 (SD = 8.6, range: 68–100; paired-samples t test: t(29) = 41.48, p < .00001, Cohen’s d = 7.571). This indicates that training significantly helped individuals to appropriately recognize the words shown at pretest by the posttest in the rote learning condition.
Performance on the additional generalized learning test (all novel words) for those in the rote learning condition shows that participants, on average, correctly identified 36 words correctly out of 100 (SD = 8.7, range: 13–47 words). Although this performance was better than the performance demonstrated by individuals in the generalized learning condition at pretest (independent, equal variance unassumed two-sample [Welch’s] t test: t(53.55) = 2.77, p = .008, Cohen’s d = 0.74), it was also significantly worse than performance by those in the generalized learning condition at posttest (independent, equal variance unassumed two-sample [Welch’s] t test: t(41.90) = −2.18, p = .035, Cohen’s d = 0.60). This finding replicates previous work showing that although rote training (repeat experience on a small subset of words) can yield some generalized learning, such generalized learning is significantly weaker than generalized learning that results from training on a set of all novel words.
Electrophysiology Results
Generalized Learning Electrophysiology Results
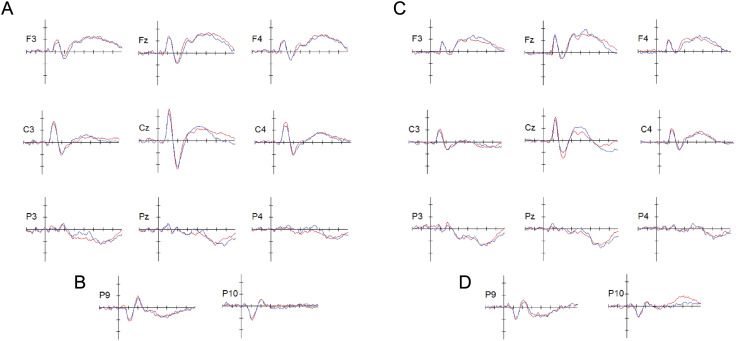
Figure 3A shows the grand-averaged ERPs (across all participants in the generalized learning condition) elicited during both pretest and posttest. For both pretest and posttest, N1 and P2 had maximal voltages at central sites (e.g., C3, Cz, C4). At pretest, N1 peaked at 112 msec at Cz, whereas P2 peaked at 200 msec at Cz. At posttest, N1 peaked at 108 msec at Cz, whereas P2 peaked at 200 msec at Cz. Consistent with prior research, inverted polarity for the N1 and P2 waves was found over sites P9 (left temporal) and P10 (right temporal; see Figure 3B) below the Sylvian fissure, thereby suggesting that the neural generators for both N1 and P2 are in or near primary auditory cortex (Yvert, Fischer, Bertrand, & Pernier, 2005; Liégeois-Chauvel, Musolino, Badier, Marquis, & Chauvel, 1994; Andrews, Knight, & Kirby, 1990; Scherg, Vajsar, & Picton, 1989).
Figure 3. .
Grand-averaged ERPs for generalized learning (A) and rote learning (C) for the nine centralized locations using a virtual montage of the 10–20 system available in BESA Research 7.0 (F3, Fz, F4, C3, Cz, C4, P3, Pz, P4). Grand-average ERPs for P9 and P10 electrodes for generalized learning (B) and rote learning (D) demonstrate the inversion of the N1–P2 complex that is typical of auditory evoked potentials. The ERPs associated with pretest trials are shown in red, and the ERPs associated with posttest trials are shown in blue. Horizontal tick marks span 100 msec, and vertical tick marks represent 1 μV; negative is plotting up. Word onset was used to register and align the EEG traces for averaging, and thus, 0 msec in these plots represents word onset time. Average duration of words in the generalized learning condition was ∼340 msec, whereas the average duration of words in the rote learning condition was ∼350 msec.
Rote Learning Electrophysiology Results
Figure 3C shows the grand-averaged ERPs (obtained by averaging across all participants in the rote learning condition) elicited during pretest and posttest. At both pretest and posttest, N1 and P2 had maximal voltages at central sites (e.g., C3, Cz, C4), with the highest peak at Cz. At pretest, N1 peaked at 112 msec at Cz, whereas P2 peaked at 200 msec at Cz. At posttest, N1 peaked at 108 msec at Cz, whereas P2 peaked at 200 msec at Cz. Similar to the generalized learning condition, inverted polarity for the N1 and P2 waves was found over sites P9 (left temporal) and P10 (right temporal) below the Sylvian fissure in the rote learning condition (see Figure 1D), indicating that the neural generators for both N1 and P2 in this condition are also in or near primary auditory cortex (Yvert et al., 2005; Liégeois-Chauvel et al., 1994; Andrews et al., 1990; Scherg et al., 1989).
Analysis of Overall Amplitude Difference for Generalized Learning
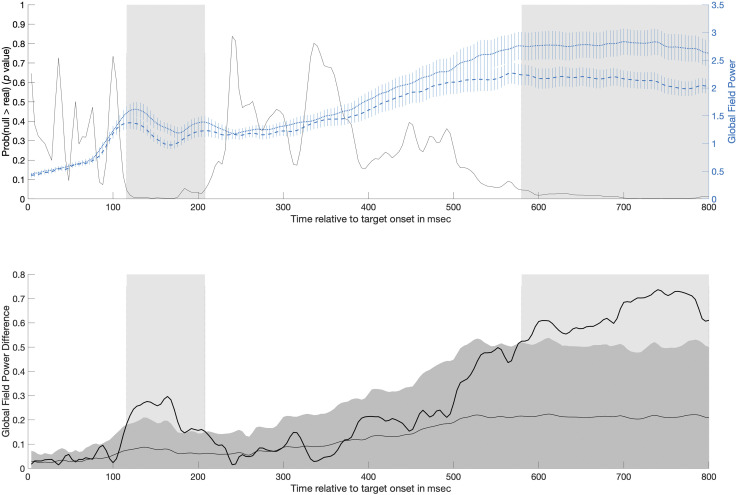
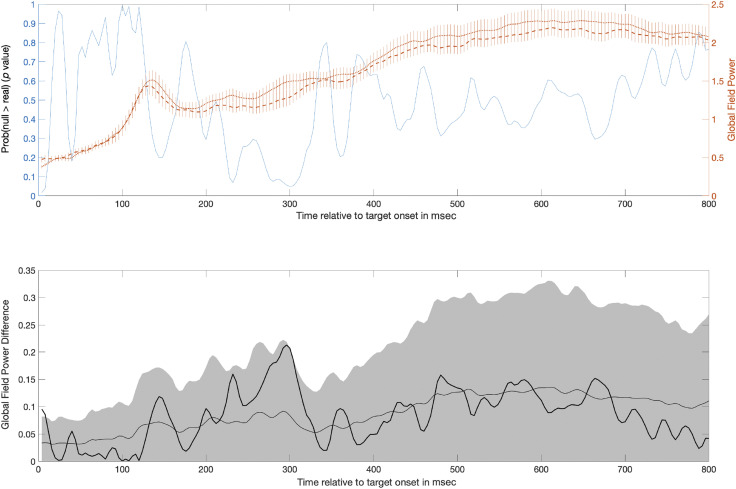
Based on the analysis with RAGU, we identified two windows in the time series of auditory evoked potential in which the observed GFP difference exceeded the top bound of the null distribution’s 95% CI. Both of these windows had sufficient length and passed window thresholding.2 In the first window from 116 to 208 msec, GFP was shown to be lower at posttest (mean = 1.16 μV, SD = 0.14) compared with pretest (mean = 1.39 μV, SD = 0.14; see Figure 4, top plot). The mean GFP difference in the observed data in this time window was 0.22 μV (posttest–pretest). The mean GFP difference under the null was 0.073 μV, 95% CI [0.03, 0.14]. During this time window, the RAGU GFP procedure showed that, on average, there was .02 probability that the effect size of GFP under the null was larger than the observed difference in GFP (minimum and maximum p values of where the observed data fall in the null distribution for GFP difference in this interval are .002 and .05, respectively; see Figure 4, bottom plot).
Figure 4. .
The top plot shows mean GFP (right y-axis) over time for both pretest (short dashed line) and posttest (long dashed line; error bars show ±1 SE) in the generalized learning condition overlaid on the probability over time that the GFP difference under the null was larger than the observed difference in GFP (black line; left y-axis). Significant time periods identified by the GFP analysis are shaded gray: one occurring from 116 to 208 msec and another occurring from 580 to 800 msec. The bottom plot shows the difference in GFP between pretest and posttest (dark black line). For context, the mean (light gray line) and 95% CI (dark gray area) for the GFP difference expected due to random chance (estimated from randomizing the data 5000 times) has been plotted. Significant time periods are again shaded gray, although note that these periods are identified by the observed difference in GFP exceeding the upper bound of the 95% CI of the shuffled data.
In the second window from 580 to 800 msec, GFP was shown to be lower at posttest (M = 2.14 μV, SD = 0.08) compared with pretest (M = 2.77 μV, SD = 0.05; see Figure 4, top). The mean GFP difference in the observed data in this time window was 0.64 μV (posttest–pretest). The mean GFP difference under the null was 0.21 μV, 95% CI [0.05, 0.49]. During this time window, the RAGU GFP procedure showed that, on average, there was .01 probability that the effect size of GFP under the null was larger than the observed difference in GFP (minimum and maximum p values of where the observed data falls in the null distribution for GFP difference in this interval are .0014 and .05, respectively; see Figure 4, bottom).
Analysis of Overall Amplitude Difference for Rote Learning
Using the same analysis on the rote learning data yielded no significant GFP differences. The top panel of Figure 5 plots the observed GFP values over time at pretest and posttest for rote learning, along with the probability of obtaining a GFP difference by chance more extreme than the observed GFP difference. The only time that the observed data came close to falling in the extreme tail (p < .05) of the null distribution is around 300 msec. The bottom panel of Figure 5 shows where the observed GFP difference fell relative to the null distribution (mean and 95% CI are shown).
Figure 5. .
The top plot shows mean GFP (right y-axis) over time for both pretest (short dashed line) and posttest (long dashed line) in the rote learning condition (error bars show ±1 SE) overlaid on the probability over time that the GFP difference under the null was larger than the observed difference in GFP (black line; left y-axis). No significant time windows were observed. The bottom plot shows the difference in GFP between pretest and posttest. For context, the mean (light gray line) and 95% CI (dark gray area) for the GFP difference expected due to random chance (estimated from randomizing the data 5000 times) has been plotted.
Analysis of Overall Topographic Difference for Generalized Learning
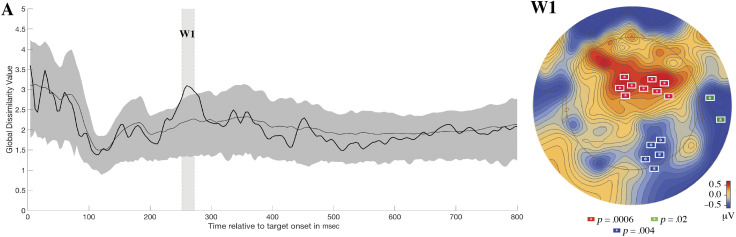
We used RAGU to generate the generalized dissimilarity between pretest and posttest that may be obtained due to chance by shuffling the data 5000 times. This distribution for the generalized dissimilarity statistic under the null was then compared with the observed generalized dissimilarity statistic. For generalized learning, only one window (250–272 msec) for topographic change was identified (see Figure 6A).3 Although this interval did not pass the window threshold test in RAGU, its appearance at the end of the N1–P2 time window (previous to 300 msec) fits our prediction that generalized perceptual learning modifies sensory evoked responses. The average observed generalized dissimilarity statistic between pretest and posttest in this time window was 2.99, whereas the average generalized dissimilarity statistic between pretest and posttest under the null was 2.22, with 95% CI [1.76, 2.77]. During this time window, the RAGU TANOVA procedure showed that, on average, there was .011 probability that the generalized dissimilarity statistic between pretest and posttest under the null was larger than the observed difference in the generalized dissimilarity statistic (minimum and maximum p values of where the observed data fall in the null distribution for the generalized dissimilarity statistic in this interval are .01 and .04, respectively; see Figure 6A).
Figure 6. .
Plot A shows how the generalized dissimilarity statistic between pretest and posttest topographies varies overtime in the generalized learning condition (black line). For context, the mean (light gray line) and 95% CI (medium gray area) for the generalized dissimilarity statistic expected due to random chance (estimated from randomizing the data 5000 times) has been plotted. Plot W1 shows the results of the spatiotemporal permutation-based analysis that was performed on the W1 window found in RAGU. This plot shows the average topographic difference between pretest and posttest (contrast: posttest–pretest) and indicates where the three significant electrode clusters (p < .05) are topographically located.
A spatiotemporal permutation-based analysis performed in BESA Statistics 2.0 on average surface electrode activity during this time window identified three significant electrode clusters driving the topographic change between pretest and posttest (see Figure 6, W1). The first significant cluster (p = .0006) was found between frontal and central electrodes left of the midline and comprised the following EGI electrodes (an approximate of 10–10 equivalent is included if available; Luu & Ferree, 2000): 6 (Fcz), 7, 12, 13 (FC1), 110, 111 (FC4), 112 (FC2), 117(FC6), and 118. The second significant cluster (p = .0038) was found over the left preauricular region and comprised the following EGI electrodes: 114 (T10) and 113. The third significant cluster (p = .0154) was found between parietal and occipital electrode left of the midline and comprised the following EGI electrodes (an approximate of 10–10 equivalent is included if available): 83 (O2), 84, 89, 90 (PO8), and 91.
Analysis of Overall Topographic Difference for Rote Learning
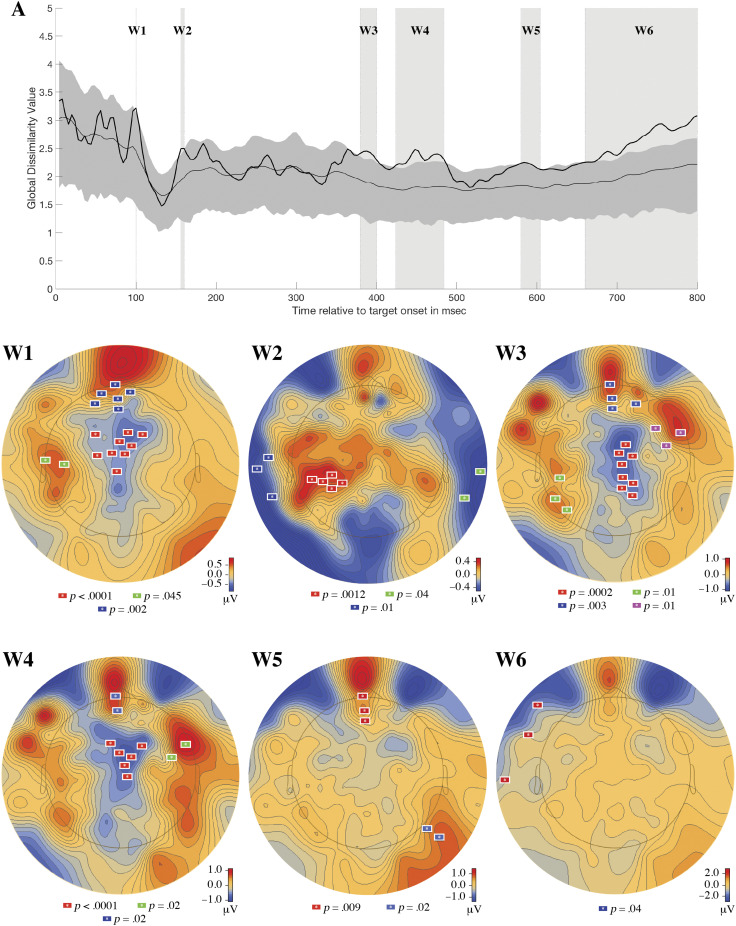
To determine if a change in the scalp distribution of brain electrical activity occurred because of rote learning, we used RAGU to calculate the observed generalized dissimilarity statistic between pretest and posttest, along with this statistic for 5000 shuffles of the data, to calculate a null distribution. This analysis identified six windows (see Figure 7A: W1, W2, W3, W4, W5, and W6) where the observed generalized dissimilarity statistic exceeded the top bound of the null distribution’s 95% CI. However, only two of these windows (W4: 424–484 msec and W6: 660–800 msec) passed the window threshold test in RAGU. Table 1 reports (1) the observed generalized dissimilarity statistic between pretest and posttest, (2) the mean, and (3) 95% CI for the generalized dissimilarity statistic between pretest and posttest under the null, as well as (4) the probability of the observed data given the shuffled data for each of these identified time windows.
Figure 7. .
Plot A shows the time-varying generalized dissimilarity between pretest and posttest topographies for rote learning (black line). For context, the mean (light gray line) and 95% CI (medium gray area) for the generalized dissimilarity expected due to random chance (estimated from randomizing the data 5000 times) has been plotted. Six windows were identified where the observed data exceeded the upper bound of the 95% CI of the shuffled data. Plots W1, W2, W3, W4, W5, and W6 show the results of the spatiotemporal permutation-based analysis that was performed on each window. All electrode clusters shown, uniquely colored on each plot, are significant at a p < .05 level.
Table 1. .
Significant Time Windows Showing Topographic Change from Pretest to Posttest Identified by the TANOVA RAGU Analysis in the Rote Learning Condition
| Window | Time | Observed GD | Mean GD from the Permutation Distribution | 95% CI for GD from the Permutation Distribution | Probability of the Observed GD Statistic (or Greater) under the Permutation Distribution |
|---|---|---|---|---|---|
| W1 | 100 msec | 3.22 | 2.46 | [1.92, 3.14] | .04 |
| W2 | 156–160 msec | 2.5 | 1.96 | [1.58, 2.43] | .04 |
| W3 | 380–400 msec | 2.4 | 1.89 | [1.55, 2.3] | .02 |
| W4 | 424–484 msec | 2.33 | 1.8 | [1.48, 2.19] | .03 |
| W5 | 580–604 msec | 2.2 | 1.81 | [1.51, 2.17] | .04 |
| W6 | 660–800 msec | 2.66 | 2.05 | [1.72, 2.4] | .01 |
For each window, the observed generalized dissimilarity (GD) between pretest and posttest is reported along with the mean and the 95% CI from the permutation distribution. The final column (Probability of the Observed GD statistic (or Greater) under the Permutation Distribution) reports the percentage of the 5000 shuffled versions of the data that obtained a GD statistic between pretest and posttest more extreme than actually observed. Data in bold indicate windows that pass the duration threshold in RAGU.
To identify significant electrode clusters driving the topographic differences during these periods, a spatiotemporal permutation-based analysis was performed in BESA Statistics 2.0 for each of these time windows. An examination of the first of these periods to pass the window threshold test (W4) revealed three significant clusters of electrodes that showed significantly different activity from pretest to posttest (see Figure 7, W4). The first significant cluster (p < .0001) was centered between the Cz and Fz electrodes and comprised the following EGI electrodes (an approximate of 10–10 equivalent is included if available; Luu & Ferree, 2000): 5, 6 (Fcz), 7, 20, 30, 55 (CpZ), 106, 112 (FC2), and 118. The second significant cluster (p = .0214) in W4 was located over the Fpz region and included the following EGI electrodes (an approximate of 10–10 equivalent is included if available): 14 (Fpz), 15 (Fcz), 16 (Afz), 17, 21, and 22 (Fp1). The final significant cluster (p = .022) in W4 was found over the frontal–temporal region and comprised the following EGI electrodes (an approximate of 10–10 equivalent is included if available): 39 and 40. The analysis of the second time period to pass the window threshold test (W6) revealed one significant cluster of electrodes (p = .04) that centered near FT9 and F9 electrodes. This cluster consisted of EGI electrodes (an approximate of 10–10 equivalent is included if available): 48, 128, and 127 (see Figure 7, W6).
Analysis of Source Difference for Generalized Learning
To estimate the source activations that lead to the map difference in the generalized learning condition that spanned from 252 to 272 msec, average distributed source images obtained from LAURA modeling were contrasted between pretest and posttest using a cluster-based permutation test in BESA Statistics 2.0 (contrast: posttest–pretest). For each identified source cluster, the closest cortical region was determined using the MATLAB toolbox version of the Brede Database (Nielsen, 2003). For generalized learning, four clusters were identified as decreasing in activity following training: a cluster near superior temporal gyrus (31.5, −30.9, 9.7, p = .231), a cluster in left superior parietal (−17.5, −79.9, 37.7, p = .335), a cluster in left anterior cingulate gyrus (−17.5, 11.1, 23.7, p = .39), and a cluster in right anterior cingulate gyrus (10.5, 25.1, 9.7, p = .559. Although these four clusters do not pass the significance threshold of p < .05, these identified regions directly align with areas that would be expected given our hypothesis that generalized learning of a difficult-to-understand talker helps to alleviate attention by reorganizing attention to the most diagnostic phonological features for the talker.
Analysis of Source Difference for Rote Learning
Similar to Generalized Learning, we estimated the source activations that led to the six identified map differences (W1, W2, W3, W4, W5, and W6) in the rote learning condition by contrasting pretest and posttest average distributed source images obtained from LAURA modeling using a cluster-based permutation test in BESA Statistics 2.0 (contrast: posttest–pretest). For each identified source cluster, the closest cortical region in Talairach coordinate space was determined using the MATLAB toolbox version of the Brede Database (Nielsen, 2003). Table 2 reports the results of the cluster-based permutation analysis for each of the six windows identified through the RAGU TANOVA analysis. It is important to note that the areas implicated by this analysis in the rote learning condition are to some extent consistent with episodic learning models (Spaniol et al., 2009).
Table 2. .
Results of the Cluster-based Permutation Analysis on the Average Distributed Source Images Obtained from LAURA Modeling Comparing Pretest and Posttest for Each of the Six Windows Identified through the RAGU TANOVA Analysis for the Rote Learning Condition
| Window | Time | Sources | Lobar Anatomy | Cluster Significance | Pretest Activity | Posttest Activity |
|---|---|---|---|---|---|---|
| W1 | 100 msec | −17.5, −51.9, −25.3 | Left cerebellum | .01 | 0.137 | 0.1026 |
| 31.5, 60.1, 23.7 | Right middle frontal gyrus | .02 | 0.173 | 0.1302 | ||
| 59.5, −51.9, −18.3 | Right inferior temporal gyrus | .07 | 0.1237 | 0.9824 | ||
| −31.5, 4.1, 16.7 | Left inferior frontal gyrus | .11 | 0.1821 | 0.1469 | ||
| W2 | 145–160 msec | 24.5, −23.9, 16.7 | Right superior temporal gyrus | <.0001 | 0.1855 | 0.1406 |
| 10.5, −79.9, 44.7 | Right medial parietal/precuneus | .44 | 0.0327 | 0.0263 | ||
| W3 | 380–400 msec | 10.5, −30.9, 9.7 | Right posterior cingulate | .18 | 0.2578 | 0.185 |
| 10.5, 32.1, 16.7 | Right anterior cingulate | .31 | 0.5819 | 0.4024 | ||
| 52.5, 18.1, 9.7 | Right inferior frontal gyrus | .48 | 0.1492 | 0.1135 | ||
| W4 | 424–484 msec | 24.4, −23.9, 16.7 | Right superior temporal gyrus | .14 | 0.2937 | 0.2148 |
| −31.5, −9.9, 9.7 | Left temporal insula | .38 | 0.3886 | 0.3078 | ||
| W5 | 580–604 msec | −31.5, −23.9, 9.7 | Left Heschl’s gyrus | .07 | 0.4862 | 0.3298 |
| −17.5, −72.9, 30.7 | Left medial parietal/precuneus | .2 | 0.212 | 0.1597 | ||
| W6 | 660–800 msec | −31.5, −2.9, 23.7 | Left inferior frontal gyrus | .23 | 0.4096 | 0.3171 |
| −3.5, −79.9, −4.3 | Lingual gyrus | .29 | 0.1262 | 0.1626 | ||
| −24.4, −65.9, 30.7 | Left precuneus | .31 | 0.2423 | 0.1797 | ||
For each identified cluster, the x, y, z location of peak activation is reported in Talairach coordinate space. Data in bold indicate windows that pass the duration threshold in RAGU TANOVA analysis.
DISCUSSION
One model of generalization and abstraction in memory is that individual experiences are encoded as rote representations and that generalization emerges from the aggregate response of long-term memory given a novel test item. The test item elicits responses from prior experiences that are stored, and the emergent response to the novel item is a generalization over those individual traces (McClelland & Rumelhart, 1985). If this were the case, there should be substantial similarities in rote learning and generalized learning with the primary difference being the strength of representation in rote learning (more instances of encoding the same trace). However, prior research has argued there are different mechanisms underlying rote and generalized perceptual learning of synthetic speech (Fenn et al., 2013) by showing different patterns of consolidation for each type of learning during sleep. The present patterns of neural responses support this latter view. In this study, generalized learning was marked by an amplitude reduction in the latter portion of the N1 wave into the peak of the P2 wave from 116 to 208 msec not seen in rote learning. These generalization training effects were followed by (1) a source configuration change from 250 to 272 msec that was estimated to arise from a decrease in activity in the right superior temporal gyrus, the left superior parietal, and the anterior cingulate gyrus bilaterally and (2) late negativity in the auditory evoked potential 580–800 msec poststimulus onset. Unlike generalized learning, rote learning was only marked by a series of source configuration changes mostly occurring 380 msec after stimulus onset. The demonstration of changes in the N1–P2 complex for generalized learning, but not for rote learning, supports the theoretical view that the transfer of learning beyond talker-specific experiences is garnered through an attentional reorganization process that adaptively modifies early auditory processing to cope with systematic acoustic variability. This is consistent with the work of Francis et al. (2000) that has demonstrated that generalized learning reduces attention to uninformative acoustic cues and increases it to informative ones. An alternative to this account is that the observed reduction in the N1–P2 complex is reflective of an automatization of sensory processing (Shiffrin & Schneider, 1977). Generalized learning on this kind of synthetic speech has been shown to reduce working memory demands, consistent with increased automatization and reduced cognitive load (Francis & Nusbaum, 2009). However, one might expect that if automatization were the explanation of the N1–P2 change observed in generalized learning, the same change should have been observed for rote learning, given that overtraining with a small set of stimuli is much more consistent with the conditions for automatization.
As previously discussed, the auditory evoked N1 potential has been argued to be composed of at least two physically and arguably functionally distinct sources (Picton, 2011; Jääskeläinen et al., 2004; McEvoy et al., 1997), with the temporally earlier N1 source supporting mechanisms by which novel, unattended sounds are brought into awareness and the temporally later N1 source supporting additional attentional focus to features comprising the auditory object (Jääskeläinen et al., 2004). Our GFP analysis in the generalized learning condition revealed a significant change in the later part of the N1 time period, from 116 to 208 msec, starting approximately at the height of the N1 peak and lasting through to the P2 component. The absence of change in the temporally earlier N1 source and presence of the change during the temporally later N1 source is additionally consistent with the view that generalized learning of synthetic speech is related to a substantial reduction in the demands of attention toward features comprising an auditory object (Gutschalk, Micheyl, & Oxenham, 2008; Jääskeläinen et al., 2004; Tiitinen et al., 1994). The absence of a similar decrease in N1 following rote training supports the idea that rote learning in this setting does not substantially alter early attentional processes and as such may be much more similar to memory encoding of episodic traces. Consequently, it also offers an explanation as to why transfer of learning is found to a much greater extent following generalized training compared with rote training in the context of learning a difficult-to-understand talker.
Changes found in the P2 component of the auditory evoked potential in the generalized learning condition differ from those found in previous studies examining perceptual learning (Ross & Tremblay, 2009; Tremblay et al., 2014). Although previous studies demonstrate postsleep increases in the P2 component following training, generalized learning here coincided with an immediate reduction in P2 amplitude (see the Analysis of Overall Amplitude Difference for Generalized Learning section). Given the reliance on sleep to consolidate rapidly acquired learning into long-term representations (Nusbaum, Uddin, Van Hedger, & Heald, 2018), previous studies have argued that the sleep-dependent P2 change marks the consolidation of a feature-based representation in long-term memory (Tremblay et al., 2014; Ross & Tremblay, 2009). Here, we highlight an implication of this interpretation: If the P2 component is sensitive to the formation of an additional featural representation in long-term memory, it indicates that the auditory evoked P2 response may be sensitive to the number of active featural representations serving current recognition. Under this view, the change in P2 following generalized training suggests that generalized training decreases the number of active featural representations required for ongoing perception. Beyond the observed change in GFP following generalized training during the first half of the P2 response due to generalized training, the TANOVA analysis indicated a change in topography in the latter half of the P2 component between 250 and 272 msec (see the Analysis of Overall Topographic Difference for Generalized Learning section). Although this window did not pass the duration threshold for RAGU, its appearance during the N1–P2 complex arguably elevates its relevance, and as such, we interpret its appearance. The distributed source modeling with LAURA estimates that this window of topographic change was driven by a decrease in activity in the right superior temporal gyrus, the left superior parietal, and the anterior cingulate gyrus bilaterally. Although the physics of volume conduction, as well as individual differences in neuroanatomy, can limit the specificity with which we can draw inferences about particular neural sources, we consider it noteworthy that the results of the distributed source estimation using LAURA aligns closely with the a priori dipole model derived from past fMRI work (Uddin, Reis, Heald, Van Hedger, & Nusbaum, 2020; Wong, Nusbaum, & Small, 2004). Indeed, both superior parietal cortex as well as the anterior cingulate have been argued to be responsible for attentional resource allocation for ongoing processing (Myers & Theodore, 2017; Piai, Roelofs, Acheson, & Takashima, 2013; Wong et al., 2004). Furthermore, the superior temporal gyrus has been associated with processing that is sensitive to talker-specific phonology (Myers & Theodore, 2017; Wong et al., 2004). These regions therefore appear to comprise a network capable of reorganizing attentional resources to acoustic cues, which are most diagnostic for a to-be-learned, difficult-to-understand talker. Although the alignment of our distributed source modeling with LAURA to these past studies should not be taken as confirmatory, it can be said that our data are consistent with an existing theoretical model in which a network of middle/superior temporal and superior parietal regions is leveraged when normalizing across idiosyncratic differences between talkers to facilitate the perception of speech categories. Taken collectively, the observed source changes during the P2 window in the current study adds to mounting evidence that the transfer of learning beyond utterance-specific experiences is accomplished by modifying attention toward features that are most informative. Again, the lack of similar changes in the P2 component following rote training supports the idea that rote learning (at least in the context of understanding a difficult-to-understand talker) does not substantially alter early attentional processes and as such may be best thought of as a process that involves the simple formation of memory representations or associations between phonetic patterns and their meanings.
Results from distributed source modeling with LAURA at the windows of topographic changes found in the rote learning condition appear to support this view, with many of the identified areas (see Table 2) implicated in episodic learning models (Spaniol et al., 2009). As such, our source analysis work supports the view that the performance differences found between rote and generalized learning arise from the engagement of two distinct learning strategies. In rote learning, brain regions focused on the memory encoding and retrieving of specific learned patterns were engaged, whereas in generalized learning, brain regions involved in the reorganizing of attention during early sensory processing were active. According to the reverse hierarchy theory (RHT; Ahissar, Nahum, Nelken, & Hochstein, 2009), these differences in neural changes offer explanation for (1) why rote recognition performance reaches ceiling or near ceiling for the small, trained set of words and (2) why this group shows significantly weaker generalized learning compared with those in the generalized learning condition at posttest. According to RHT, the level that learning occurs at is determined by the minimum-level representation needed to observe and uncover systematic pattern variability. As stimulus variability increases, higher, more abstract representations are needed to understand the relationships among the stimuli, as there will be little experience with specific stimulus patterns to guide learning. According to a predictive coding framework of the brain, given that rote and generalized learning fundamentally alter different types of representations, these forms of learning should lead learners to make fundamentally different kinds of predictions to guide perception. In rote learning, representations tied to specific stimulus patterns are likely strengthened with training, which in turn fosters strong, stimulus-level predictions for the trained words to guide perception. Learning at this level of representation, however, does little for predicting the meaning of untrained, novel words. In generalized learning, more abstract representations, perhaps tied to modeling the talker’s acoustic–phonetic space, are needed to drive learning. Learning at this level would yield more abstract predictions that support better predictions for novel words by helping to orient attention to acoustic cues that are most diagnostic of the speech sound categories for the given talker. This trickling down of learning to lower processing levels is consistent with RHT, which largely casts perceptual learning as a top–down process that is organized by higher-level representations.
Beyond changes in the N1–P2 complex, we observed a decrease in the late negativity of the auditory evoked potential starting 580 msec poststimulus onset following generalized learning, but not following rote learning. This mirrors results by Tremblay et al. (2014), who found late negativity in the auditory evoked potential starting 600 msec poststimulus onset following training. As previously mentioned, this decrease in this late negative potential may be reflective of an improvement in trial-by-trial, prediction error monitoring that helps to drive the reorganization of attention (Ashby & O’Brien, 2005; Ashby et al., 1998). According to a predictive coding framework of the brain, a reduction in prediction error monitoring in the context of generalized learning would suggest that trial-by-trial predictions have improved as a consequence of attentional realignment to more diagnostic cues. As previously mentioned, this improvement in the prediction of novel words is entirely predicted according to RHT, which asserts that, in generalized learning, higher-level representations, perhaps reflective of the to-be-learned talker’s acoustic–phonetic space, should develop to suppor better predictions for novel words. Our observation that a decrease in the late negativity was only found in the generalized learning condition suggests that different forms of learning selectively engages and impacts prediction error monitoring. This is consistent with an active–cognitive view of speech recognition in general, which has argued that the cognitive resources recruited during perception (such as selective attention, working memory, and learning) are dynamically determined by an interplay between the ambiguity of the speech signal and context (here training type) in which it occurs (Heald & Nusbaum, 2014).
Conclusion
Previous research has suggested that generalized and rote learning may be mediated by different neural mechanisms (Fenn et al., 2013). This study tested this directly by comparing how patterns of neural responses during speech recognition change following rote and generalized learning. The present results demonstrate substantial differences in neural responses for these two types of learning. On the one hand, rote and generalized learning might have been supported by the same neural process of encoding (McClelland & Rumelhart, 1985). Under this view, generalization and abstraction is an emergent property of experience, captured by the aggregate response of long-term memory traces that are utilized to process novel stimuli. Although this view corresponds to an entire class of memory models, the present data reject this view, showing that generalized learning entails early sensory changes in processing that may be attributed to changes in attention that are not seen in rote learning. This difference argues against a passive, bottom–up fixed speech processing system that simply records auditory traces that are then later brought in aggregate to afford generalization. Rather, the data support the view that speech perception is mediated by active neural processing, in which listeners are able to leverage their recent experience to selectively attend to and process the most meaningful acoustic cues for a given situation. Given that the capacity for generalized learning can be used to understand how listeners are able to adaptively respond to and overcome the lack of invariance problem in the speech signal, the present work makes clear the need for further work to demonstrate whether or not the neural markers found in the current study—in the context of learning to understand a difficult talker—are also present in more naturalistic circumstances when the underlying acoustic-to-phonetic mapping has been disrupted systematically (such as a shift in talker, speaking rate, or social register).
Acknowledgments
The authors thank Sophia Uddin for her helpful comments on an earlier draft, as well as Nina Bartram, Edward Wagner, and Brendan Colson for their assistance with data collection.
Reprint requests should be sent to Shannon L. M. Heald, Department of Psychology, The University of Chicago, Chicago, IL 60637, or via e-mail: smbowdre@uchicago.edu.
Author Contributions
Shannon L. M. Heald: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Project administration; Software; Supervision; Visualization; Writing—Original draft; Writing—Review & editing. Stephen C. Van Hedger: Writing—Review & editing. John Veillette: Data curation; Writing—Review & editing. Katherine Reis: Data curation; Writing—Review & editing. Joel S. Snyder: Supervision; Writing—Review & editing. Howard C. Nusbaum: Conceptualization; Funding acquisition; Methodology; Resources; Supervision; Writing—Review & editing.
Funding Information
This work was supported in part by the Multidisciplinary University Research Initiatives (MURI) Program of the Office of Naval Research (https://dx.doi.org/10.13039/100000006), grant number: DOD/ONR N00014–13-1-0205 and NSF NCS (https://dx.doi.org/10.13039/100000169), grant number: 1835181.
Diversity in Citation Practices
Retrospective analysis of the citations in every article published in this journal from 2010 to 2021 reveals a persistent pattern of gender imbalance: Although the proportions of authorship teams (categorized by estimated gender identification of first author/last author) publishing in the Journal of Cognitive Neuroscience (JoCN) during this period were M(an)/M = .407, W(oman)/M = .32, M/W = .115, and W/W = .159, the comparable proportions for the articles that these authorship teams cited were M/M = .549, W/M = .257, M/W = .109, and W/W = .085 (Postle and Fulvio, JoCN, 34:1, pp. 1–3). Consequently, JoCN encourages all authors to consider gender balance explicitly when selecting which articles to cite and gives them the opportunity to report their article’s gender citation balance.
Notes
Some readers may wonder why poorer performance was found at pretest in the rote learning condition (16 of 100 correct) compared to pretest in the generalized learning condition (29 of 100). One potential explanation for this could be the difference in phonetic diversity between the two lists given their word set size differences. Although the rote list was constructed to closely capture the phonetic diversity of the top occurring phonetic items in the generalized words list (see the Stimuli section), the rote list’s phonemic inventory is smaller than the generalized learning’s inventory simply because of the word set size differences between the lists. As such, the error rate for the rote word list may be higher than for the larger sample used in generalized learning. Moreover, we were less concerned about matching initial performance given that rote training is known to quickly move performance to ceiling with repeat practice.
An additional GFP analysis using “test order” as a between-subject covariate yielded near identical pre–post effects, suggesting that it is highly unlikely that the observed pre–post effects were driven by any one particular test order.
An additional TANOVA analysis using “test order” as a between-subject covariate yielded near identical pre–post effects, suggesting that it is highly unlikely that the observed pre–post effects were driven by any one particular test order.
REFERENCES
- Ahissar, M., Nahum, M., Nelken, I., & Hochstein, S. (2009). Reverse hierarchies and sensory learning. Philosophical Transactions of the Royal Society of London, Series B: Biological Sciences, 364, 285–299. 10.1098/rstb.2008.0253, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahveninen, J., Jääskeläinen, I. P., Raij, T., Bonmassar, G., Devore, S., Hämäläinen, M., et al. (2006). Task-modulated “what” and “where” pathways in human auditory cortex. Proceedings of the National Academy of Sciences, U.S.A., 103, 14608–14613. 10.1073/pnas.0510480103, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alain, C., Campeanu, S., & Tremblay, K. (2010). Changes in sensory evoked responses coincide with rapid improvement in speech identification performance. Journal of Cognitive Neuroscience, 22, 392–403. 10.1162/jocn.2009.21279, [DOI] [PubMed] [Google Scholar]
- Alain, C., & Snyder, J. S. (2008). Age-related differences in auditory evoked responses during rapid perceptual learning. Clinical Neurophysiology, 119, 356–366. 10.1016/j.clinph.2007.10.024, [DOI] [PubMed] [Google Scholar]
- Alain, C., Snyder, J. S., He, Y., & Reinke, K. S. (2007). Changes in auditory cortex parallel rapid perceptual learning. Cerebral Cortex, 17, 1074–1084. 10.1093/cercor/bhl018, [DOI] [PubMed] [Google Scholar]
- Andrews, R. J., Knight, R. T., & Kirby, R. P. (1990). Evoked potential mapping of auditory and somatosensory cortices in the miniature swine. Neuroscience Letters, 114, 27–31. 10.1016/0304-3940(90)90423-7, [DOI] [PubMed] [Google Scholar]
- Ashby, F. G., Alfonso-Reese, L. A., Turken, A. U., & Waldron, E. M. (1998). A neuropsychological theory of multiple systems in category learning. Psychological Review, 105, 442–481. 10.1037/0033-295X.105.3.442, [DOI] [PubMed] [Google Scholar]
- Ashby, F. G., & O’Brien, J. B. (2005). Category learning and multiple memory systems. Trends in Cognitive Sciences. 10.1016/j.tics.2004.12.003, [DOI] [PubMed] [Google Scholar]
- Berg, P., & Scherg, M. (1994). A multiple source approach to the correction of eye artifacts. Electroencephalography and Clinical Neurophysiology, 90, 229–241. 10.1016/0013-4694(94)90094-9, [DOI] [PubMed] [Google Scholar]
- Bosnyak, D. J., Eaton, R. A., & Roberts, L. E. (2004). Distributed auditory cortical representations are modified when non-musicians are trained at pitch discrimination with 40 Hz amplitude modulated tones. Cerebral Cortex, 14, 1088–1099. 10.1093/cercor/bhh068, [DOI] [PubMed] [Google Scholar]
- Bradlow, A. R., & Bent, T. (2008). Perceptual adaptation to non-native speech. Cognition, 106, 707–729. 10.1016/j.cognition.2007.04.005, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chomsky, N., & Halle, M. (1968). The sound pattern of English. Cambridge, MA: MIT Press. [Google Scholar]
- Egan, J. P. (1948). Articulation testing methods. Laryngoscope, 58, 955–991. 10.1288/00005537-194809000-00002, [DOI] [PubMed] [Google Scholar]
- Fenn, K. M., Margoliash, D., & Nusbaum, H. C. (2013). Sleep restores loss of generalized but not rote learning of synthetic speech. Cognition, 128, 280–286. 10.1016/j.cognition.2013.04.007, [DOI] [PubMed] [Google Scholar]
- Fenn, K. M., Nusbaum, H. C., & Margoliash, D. (2003). Consolidation during sleep of perceptual learning of spoken language. Nature, 425, 614–616. 10.1038/nature01951, [DOI] [PubMed] [Google Scholar]
- Francis, A. L., Baldwin, K., & Nusbaum, H. C. (2000). Effects of training on attention to acoustic cues. Perception & Psychophysics, 62, 1668–1680. 10.3758/BF03212164, [DOI] [PubMed] [Google Scholar]
- Francis, A. L., & Nusbaum, H. C. (2002). Selective attention and the acquisition of new phonetic categories. Journal of Experimental Psychology: Human Perception and Performance, 28, 349–366. 10.1037/0096-1523.28.2.349, [DOI] [PubMed] [Google Scholar]
- Francis, A. L., & Nusbaum, H. C. (2009). Effects of intelligibility on working memory demand for speech perception. Attention, Perception, & Psychophysics, 71, 1360–1374. 10.3758/APP.71.6.1360, [DOI] [PubMed] [Google Scholar]
- Goldstone, R. L. (1994). Influences of categorization on perceptual discrimination. Journal of Experimental Psychology: General, 123, 178–200. 10.1037/0096-3445.123.2.178 [DOI] [PubMed] [Google Scholar]
- Goldstone, R. L. (1998). Perceptual learning. Annual Review of Psychology, 49, 585–612. 10.1146/annurev.psych.49.1.585, [DOI] [PubMed] [Google Scholar]
- Greenspan, S. L., Nusbaum, H. C., & Pisoni, D. B. (1988). Perceptual learning of synthetic speech produced by rule. Journal of Experimental Psychology: Learning, Memory, and Cognition, 14, 421–433. 10.1037/0278-7393.14.3.421, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutschalk, A., Micheyl, C., & Oxenham, A. J. (2008). Neural correlates of auditory perceptual awareness under informational masking. PLoS Biology, 6, e138. 10.1371/journal.pbio.0060138, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutschalk, A., Micheyl, C., Oxenham, A. J., von Kriegstein, K., & Warren, J. (2008). Neural correlates of auditory perceptual awareness under informational masking. PLoS Biology, 6, e138. 10.1371/journal.pbio.0060138, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heald, S. L. M., & Nusbaum, H. C. (2014). Speech perception as an active cognitive process. Frontiers in Systems Neuroscience, 8, 35. 10.3389/fnsys.2014.00035, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ing-Simmons, N. (1994). RSYNTH: Complete speech synthesis system for UNIX [Computer software]. https://www.speech.cs.cmu.edu/comp.speech/Section5/Synth/rsynth.html.
- Jääskeläinen, I. P., Ahveninen, J., Bonmassar, G., Dale, A. M., Ilmoniemi, R. J., Levanen, S., et al. (2004). Human posterior auditory cortex gates novel sounds to consciousness. Proceedings of the National Academy of Sciences, U.S.A., 101, 6809–6814. 10.1073/pnas.0303760101, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klatt, D. H. (1980). Software for a cascade/parallel formant synthesizer. Journal of the Acoustical Society of America, 67, 971–995. 10.3758/BRM.42.3.863, [DOI] [PubMed] [Google Scholar]
- König, T., & Gianotti, L. (2009). Scalp field maps and their characterization. In Michel C., König T., Brandeis D., Gianotti L. & Wackermann J. (Eds.), Electrical Neuroimaging (pp. 25–48). Cambridge: Cambridge University Press. 10.1017/CBO9780511596889.003 [DOI] [Google Scholar]
- Koenig, T., Kottlow, M., Stein, M., & Melie-García, L. (2011). Ragu: A free tool for the analysis of EEG and MEG event-related scalp field data using global randomization statistics. Computational Intelligence and Neuroscience, 2011, 1–14. 10.1155/2011/938925, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig, T., & Melie-García, L. (2010). A method to determine the presence of averaged event-related fields using randomization tests. Brain Topography, 23, 233–242. 10.1007/s10548-010-0142-1 [DOI] [PubMed] [Google Scholar]
- Ladefoged, P., & Broadbent, D. E. (1957). Information conveyed by vowels. Journal of the Acoustical Society of America, 29, 98–104. 10.1121/1.1908694 [DOI] [PubMed] [Google Scholar]
- Lavie, N. (1995). Perceptual load as a necessary condition for selective attention. Journal of Experimental Psychology: Human Perception and Performance, 21, 451. 10.1037/0096-1523.21.3.451, [DOI] [PubMed] [Google Scholar]
- Liberman, A. M. (1970). The grammars of speech and language. Cognitive Psychology, 1, 301–323. 10.1016/0010-0285(70)90018-6 [DOI] [Google Scholar]
- Liberman, A. M., Cooper, F. S., Shankweiler, D. P., & Studdert-Kennedy, M. (1967). Perception of the speech code. Psychological Review, 74, 431–461. 10.1037/h0020279, [DOI] [PubMed] [Google Scholar]
- Liégeois-Chauvel, C., Musolino, A., Badier, J. M., Marquis, P., & Chauvel, P. (1994). Evoked potentials recorded from the auditory cortex in man: Evaluation and topography of the middle latency components. Electroencephalography and Clinical Neurophysiology/ Evoked Potentials, 92, 204–214. 10.1016/0168-5597(94)90064-7, [DOI] [PubMed] [Google Scholar]
- Luu, P., & Ferree, T. C. (2000). Determination of the geodesic sensor nets’ average electrode positions and their 10–10 international equivalents. Eugene, OR: Electronic Geodesics Inc.
- Magnuson, J. S., & Nusbaum, H. C. (2007). Acoustic differences, listener expectations, and the perceptual accommodation of talker variability. Journal of Experimental Psychology: Human Perception and Performance, 33, 391–409. 10.1037/0096-1523.33.2.391, [DOI] [PubMed] [Google Scholar]
- McCallum, W. C., & Curry, S. H. (1979). Hemisphere differences in event related potentials and CNV’s associated with monaural stimuli and lateralized motor responses. In D. Lehmann & E. Callaway (Eds.), Human evoked potentials (pp. 235–250). Springer. 10.1007/978-1-4684-3483-5_16 [DOI] [Google Scholar]
- McClelland, J. L., & Rumelhart, D. E. (1985). Distributed memory and the representation of general and specific information. Journal of Experimental Psychology: General, 114, 159–188. 10.1037/0096-3445.114.2.159, [DOI] [PubMed] [Google Scholar]
- McEvoy, L., Levänen, S., & Loveless, N. (1997). Temporal characteristics of auditory sensory memory: Neuromagnetic evidence. Psychophysiology, 34, 308–316. 10.1111/j.1469-8986.1997.tb02401.x, [DOI] [PubMed] [Google Scholar]
- Miller, S. M. (1987). Monitoring and blunting: Validation of a questionnaire to assess styles of information seeking under threat. Journal of Personality and Social Psychology, 52, 345. 10.1037/0022-3514.52.2.345, [DOI] [PubMed] [Google Scholar]
- Murray, M. M., Brunet, D., & Michel, C. M. (2008). Topographic ERP analyses: A step-by-step tutorial review. Brain Topography, 20, 249–264. 10.1007/s10548-008-0054-5, [DOI] [PubMed] [Google Scholar]
- Myers, E. B., & Theodore, R. M. (2017). Voice-sensitive brain networks encode talker-specific phonetic detail. Brain and Language, 165, 33–44. 10.1016/j.bandl.2016.11.001, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Näätänen, R., & Winkler, I. (1999). The concept of auditory stimulus representation in cognitive neuroscience. Psychological Bulletin, 125, 826–859. 10.1037/0033-2909.125.6.826, [DOI] [PubMed] [Google Scholar]
- Nielsen, F. Å. (2003). The Brede database: A small database for functional neuroimaging. Neuroimage, 19, 19–22. [Google Scholar]
- Nosofsky, R. M. (1986). Attention, similarity, and the identification-categorization relationship. Journal of Experimental Psychology: General, 115, 39–57. 10.1037/0096-3445.115.1.39, [DOI] [PubMed] [Google Scholar]
- Nusbaum, H. C., & Pisoni, D. B. (1985). Constraints on the perception of synthetic speech generated by rule. Behavior Research Methods, Instruments, & Computers, 17, 235–242. 10.3758/BF03214389, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum, H. C., Uddin, S., Van Hedger, S. C., & Heald, S. L. (2018). Consolidating skill learning through sleep. Current Opinion in Behavioral Sciences, 20. 10.1016/j.cobeha.2018.01.013 [DOI] [Google Scholar]
- Nygaard, L. C., & Pisoni, D. B. (1998). Talker-specific learning in speech perception. Perception & Psychophysics, 60, 355–376. 10.3758/BF03206860, [DOI] [PubMed] [Google Scholar]
- Petkov, C. I., Kang, X., Alho, K., Bertrand, O., Yund, E. W., & Woods, D. L. (2004). Attentional modulation of human auditory cortex. Nature Neuroscience, 7, 658–663. 10.1038/nn1256, [DOI] [PubMed] [Google Scholar]
- Piai, V., Roelofs, A., Acheson, D. J., & Takashima, A. (2013). Attention for speaking: Domain-general control from the anterior cingulate cortex in spoken word production. Frontiers in Human Neuroscience, 7, 832. 10.3389/fnhum.2013.00832, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picton, T. W. (2011). Human auditory evoked potentials. Ear and hearing (Vol. 33). San Diego: Plural Publishing. [Google Scholar]
- Picton, T. W., Van Roon, P., Armilio, M. L., Berg, P., Ille, N., & Scherg, M. (2000). The correction of ocular artifacts: A topographic perspective. Clinical Neurophysiology, 111, 53–65. 10.1016/S1388-2457(99)00227-8, [DOI] [PubMed] [Google Scholar]
- Rauschecker, J. P., & Tian, B. (2000). Mechanisms and streams for processing of “what” and “where” in auditory cortex. Proceedings of the National Academy of Sciences, U.S.A., 97, 11800–11806. 10.1073/pnas.97.22.11800, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinke, K. S., He, Y., Wang, C., & Alain, C. (2003). Perceptual learning modulates sensory evoked response during vowel segregation. Cognitive Brain Research, 17, 781–791. 10.1016/S0926-6410(03)00202-7, [DOI] [PubMed] [Google Scholar]
- Ross, B., Jamali, S., Tremblay, K. L., Abdi, H., Toga, A., Evans, A., et al. (2013). Plasticity in neuromagnetic cortical responses suggests enhanced auditory object representation. BMC Neuroscience, 14, 151. 10.1186/1471-2202-14-151, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross, B., & Tremblay, K. (2009). Stimulus experience modifies auditory neuromagnetic responses in young and older listeners. Hearing Research, 248, 48–59. 10.1016/j.heares.2008.11.012, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell, G. S., Jeffrey Eriksen, K., Poolman, P., Luu, P., & Tucker, D. M. (2005). Geodesic photogrammetry for localizing sensor positions in dense-array EEG. Clinical Neurophysiology, 116, 1130–1140. 10.1016/j.clinph.2004.12.022, [DOI] [PubMed] [Google Scholar]
- Scherg, M., Vajsar, J., & Picton, T. W. (1989). A source analysis of the late human auditory evoked potentials. Journal of Cognitive Neuroscience, 1, 336–355. 10.1162/jocn.1989.1.4.336, [DOI] [PubMed] [Google Scholar]
- Schwab, E. C., Nusbaum, H. C., & Pisoni, D. B. (1985). Some effects of training on the perception of synthetic speech. Human Factors, 27, 395–408. 10.1177/001872088502700404, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahin, A., Roberts, L. E., Pantev, C., Trainor, L. J., & Ross, B. (2005). Modulation of P2 auditory-evoked responses by the spectral complexity of musical sounds. NeuroReport, 16, 1781–1785. 10.1097/01.wnr.0000185017.29316.63, [DOI] [PubMed] [Google Scholar]
- Shiffrin, R. M., & Schneider, W. (1977). Controlled and automatic human information processing: II. Perceptual learning, automatic attending and a general theory. Psychological Review, 84, 127–190. 10.1037/0033-295X.84.2.127 [DOI] [Google Scholar]
- Spaniol, J., Davidson, P. S. R., Kim, A. S. N., Han, H., Moscovitch, M., & Grady, C. L. (2009, July). Event-related fMRI studies of episodic encoding and retrieval: Meta-analyses using activation likelihood estimation. Neuropsychologia, 47, 1765–1779. 10.1016/j.neuropsychologia.2009.02.028, [DOI] [PubMed] [Google Scholar]
- Tiitinen, H., May, P., Reinikainen, K., & Näätänen, R. (1994). Attentive novelty detection in humans is governed by pre-attentive sensory memory. Nature, 372, 90–92. 10.1038/372090a0, [DOI] [PubMed] [Google Scholar]
- Tremblay, K. L., Ross, B., Inoue, K., McClannahan, K., & Collet, G. (2014). Is the auditory evoked P2 response a biomarker of learning? Frontiers in Systems Neuroscience, 8, 28. 10.3389/fnsys.2014.00028, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay, K. L., Shahin, A. J., Picton, T., & Ross, B. (2009). Auditory training alters the physiological detection of stimulus-specific cues in humans. Clinical Neurophysiology, 120, 128–135. 10.1016/j.clinph.2008.10.005, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin, S., Reis, K. S., Heald, S. L., Van Hedger, S. C., & Nusbaum, H. C. (2020). Cortical mechanisms of talker normalization in fluent sentences. Brain and Language, 201, 104722. 10.1016/j.bandl.2019.104722, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weatherholtz, K., & Jaeger, T. F. (2016). Speech perception and generalization across speakers and accents. Oxford Research Encyclopedia of Linguistics. 10.1093/acrefore/9780199384655.013.95 [DOI] [Google Scholar]
- Wong, P. C. M., Nusbaum, H. C., & Small, S. L. (2004). Neural bases of talker normalization. Journal of Cognitive Neuroscience, 16, 1173–1184. 10.1162/0898929041920522, [DOI] [PubMed] [Google Scholar]
- Woods, D. L., Stecker, G. C., Rinne, T., Herron, T. J., Cate, A. D., Yund, E. W., et al. (2009). Functional maps of human auditory cortex: Effects of acoustic features and attention. PLoS One, 4. 10.1371/journal.pone.0005183, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yvert, B., Fischer, C., Bertrand, O., & Pernier, J. (2005). Localization of human supratemporal auditory areas from intracerebral auditory evoked potentials using distributed source models. Neuroimage, 28, 140–153. 10.1016/j.neuroimage.2005.05.056, [DOI] [PubMed] [Google Scholar]