Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jan 20;22(3):1183–1189. doi: 10.1021/acs.nanolett.1c04357

Dynamics of Two Distinct Exciton Populations in Methyl-Functionalized Germanane

Eugenio Cinquanta †,*, Samim Sardar ‡, Warren L B Huey §, Caterina Vozzi †, Joshua E Goldberger §, Cosimo D’Andrea ‡,∥,*, Christoph Gadermaier ‡,∥,*
PMCID: PMC8832397  PMID: 35050634

Abstract

graphic file with name nl1c04357_0004.jpg

Methyl-substituted germanane is an emerging material that has been proposed for novel applications in optoelectronics, photoelectrocatalysis, and biosensors. It is a two-dimensional semiconductor with a strong above-gap fluorescence associated with water intercalation. Here, we use time-resolved photoluminescence spectroscopy to understand the mechanism causing this fluorescence. We show that it originates from two distinct exciton populations. Both populations recombine exponentially, accompanied by the thermally activated transfer of exciton population from the shorter- to the longer-lived type. The two exciton populations involve different electronic levels and couple to different phonons. The longer-lived type of exciton migrates within the disordered energy landscape of localized recombination centers. These outcomes shed light on the fundamental optical and electronic properties of functionalized germanane, enabling the groundwork for future applications in optoelectronics, light harvesting, and sensing.

Keywords: 2D materials, germanane, excitons, time-resolved photoluminescence, intercalation, ultrafast spectroscopy

Two-dimensional (2D) materials are presently one of the most actively explored platforms for the development of nanoscaled (opto)electronic devices.1−3 Monoelemental 2D materials (Xenes) and their substituted counterparts (Xanes, e.g., GeH or GeCH3) are rapidly emerging alongside the much more well-studied transition metal dichalcogenide semiconductors because of high electron mobility, a wide range of band gaps, and the possible tuning of their morphology and physical properties.4−10 Germanane has been proposed recently as a novel active material for optoelectronics, photoelectrocatalysis, antibacterial coating, and biosensors, with the specific performances determined by the functional groups.11−16

The photoluminescence (PL) of multilayer GeCH3, conversely to its H-terminated counterpart, is tightly linked to the presence of water in the van der Waals gap.17 Water intercalation switches the PL spectrum reversibly between a bright red peak centered around 1.97 eV—significantly above the 1.62 eV bandgap—for the hydrated material, and a broad band-tail emission for the dry one. The PL excitation spectrum of the 1.97 eV emission starts at 2.1 eV and has its maximum at 3.5 eV, hence demonstrating that this emission arises from strong electronic transitions involving electronic levels above the conduction band minimum and/or below the valence band maximum. The strong above-gap PL and simultaneous suppression of the band-tail emission suggest that the involved above-gap levels have no allowed relaxation channel toward the band edges. A deeper insight into the electronic nature of the involved excited states, the interplay between them, and the associated time scales18−20 is vital for rationalizing Xanes’ optoelectronic and light-harvesting functionalities.

In this work, we exploit time-resolved photoluminescence (TRPL) to unveil the origin of the 1.97 eV above bandgap emission in GeCH3. From the analysis of the emission peak energy and intensity as a function of time and temperature, we assign the observed fluorescence to the interplay of two distinct exciton populations and discuss their electronic nature.

The polycrystalline powders of GeCH3 were synthesized following previously established procedures.17

For the TRPL measurements, we used a Ti:sapphire oscillator (Chameleon Ultra II Coherent) producing a train of 140 fs pulses with a repetition rate of 80 MHz at 800 nm. A β-barium borate (BBO) crystal was used to obtain the second harmonic at 400 nm. Spatial resolution was achieved through the incorporation of a homemade microscope in the setup.21 A long pass dichroic mirror at 530 nm was used to reflect the excitation beam (400 nm) that was then coupled to a 20× objective (Nikon) to focus onto the sample with a spot size of about 6 μm. The emission signals were collected in backscattering geometry using a 550 nm long-pass filter and analyzed by a spectrograph (Princeton Instruments Acton SP2300) coupled to a streak camera (Hamamatsu C5680, Japan) equipped with a synchro-scan voltage sweep module. In these measurements, the fluorescence intensity was obtained as a function of both wavelength and time with spectral and temporal resolutions of ∼1 nm (∼3 meV in our spectral range) and ∼20 ps (for 2 ns time window), respectively. Cryogenic measurements were performed using a cryostat (Oxford Instruments) cooled with liquid nitrogen under vacuum conditions (10–6 mbar). From the synthesized powder, we selected a bulk flake of a few hundred micrometer lateral size and glued it with two thin slices of carbon tape onto a fused silica substrate. The sample was then gently annealed at 150 °C under a vacuum for 15–18 h before measurement to remove most of the intercalated water and reach a water concentration that remains stable during the measurements at varying temperatures.

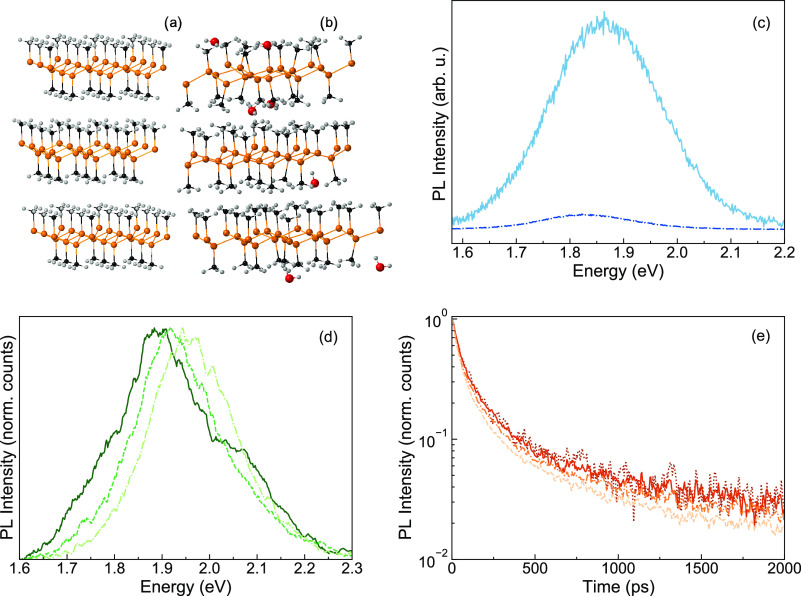
Panels a and b in Figure 1 show the ball-and-stick model of dry and water intercalated bulk GeCH3. For the investigation of the above bandgap emission, TRPL characterization was performed as described above. Figure 1c shows the time-integrated (0–2 ns) TRPL spectra for the dry (dash-dotted blue curve) and the hydrated (solid turquoise curve) sample. The fluorescence is largely quenched but still clearly detectable when the sample is placed in 1 × 10–6 mbar, confirming that the remaining H2O molecules are enough to induce the 1.9 eV emission.17

Figure 1.

Figure 1

Open in a new tab

Atomic structure of GeCH3 (a) without water intercalation and (b) with water intercalation. Ge atoms are orange, Carbon atoms are black, hydrogen atoms are white, and oxygen atoms are red. (c) Photoluminescence integrated over time for dry (under a vacuum, dash-dotted blue curve) and hydrated (in air, turquoise solid curve) GeCH3 acquired with a mean excitation power of 15 μW; (d) normalized TRPL spectra of the vacuum-treated “dry” sample at 77 K integrated into the 0 < t < 100 ps (dash-dotted curve), 200 ps < t < 300 ps (dashed curve) and 900 < t < 1000 ps (solid curve) temporal windows; (e) normalized spectrally integrated (1.65–2.25 eV) dynamics of the vacuum-treated “dry” sample at 77 K upon mean excitation powers of 3 μW (dots), 10 μW (solid curve), 30 μW (dash-dotted curve), and 100 μW (dashed curve).

The fluorescence of the vacuum-treated “dry” sample integrated into different temporal windows (0 < t < 100 ps, 200 ps < t < 300 ps and 900 < t < 1000 ps), shown in Figure 1d, changes shape and peak position with time t after excitation, indicating that the fluorescence originates from more than just one population of recombining e–h pairs. In this respect, previous TRPL measurements on GeCH3 flakes revealed the presence of two emitting species, therein assigned to midgap trap states and the band tail emission.22 The PL traces integrated over the spectral range 1.65–2.25 eV, as shown in Figure 1e, decay almost independently of the excitation fluence over 2 orders of magnitude. We deduce that the relevant relaxation processes are linear with the density of photogenerated population n, i.e., follow an exponential decay and do not involve any interaction between nongeminate photoexcited species. Indeed, if free charge carriers were photogenerated, we would expect a more noticeable change in the recombination dynamics with increasing fluence, due to the rate proportional to n2 of such dynamics.23 Therefore, our observation is consistent with the prediction of excitons with hundreds of meV binding energy as the primary photoexcited species in germanane,24,25 as observed in other 2D semiconductors.26−29

To gain further insight into the electronic nature and the recombination dynamics of the emitting states we explored the temperature dependence of TRPL from 77 to 323 K. Figures 2a and 2b show the spectrally integrated PL traces. Remarkably, the dynamics depend nonmonotonically on temperature. In the range from 77 K to approximately 200 K, the dynamics become gradually slower with increasing temperature, while at higher temperatures they quickly become faster again.

Figure 2.

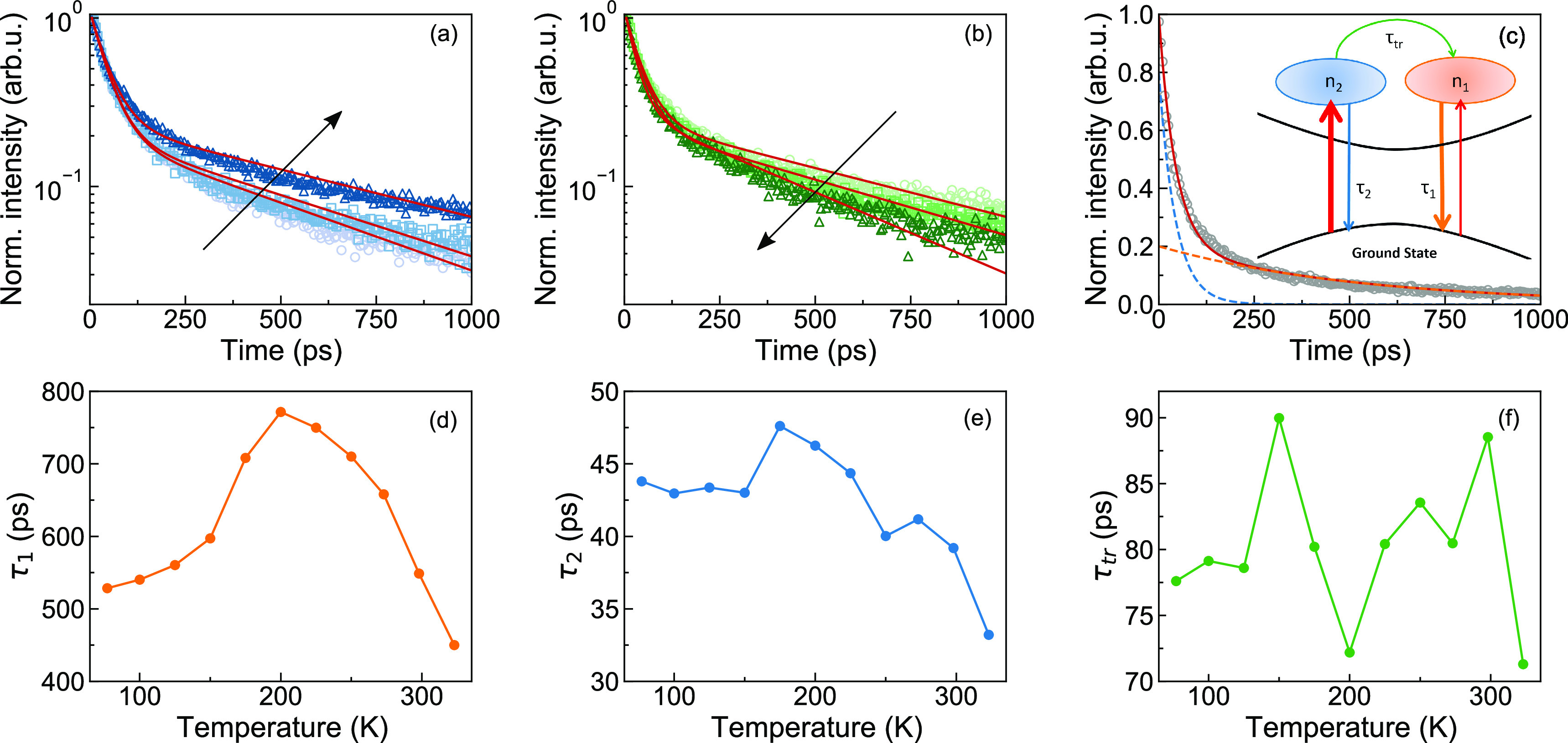
Figure 2

Open in a new tab

(a) Spectrally integrated dynamics acquired upon 10 μW excitation power at 77 K (circles), 150 K (squares), and 200 K (triangles) together with the fit to eq 1 (continuous red curve). (b) Spectrally integrated dynamics acquired upon 10 μW excitation power at 225 K (circles), 273 K (squares), and 323 K (triangles) together with the fit to eq 1 (continuous red curve). The black arrows indicate increasing temperature; (c) spectrally integrated dynamics acquired at 77 K (circles) upon 10 mW excitation power, fitted to eqs1 (continuous red curve), time-dependent populations of long- and short-lived excitons (orange and blue dashed lines, respectively); (d–f) time constants τ1, τ2, and τtr extracted from the fit to eq 1 as a function of temperature.

We propose a simple model for the temporal evolution of the fluorescence, sketched in the inset of Figure 2c and formulated in terms of rate equations (eq 1). We assume two distinct exciton populations n1 and n2, both localized at water-induced recombination centers (RCs). Each population is formed at a time scale shorter than our instrument response function and decays exponentially with its own time constant τ1 and τ2, which comprise both radiative and nonradiative recombination. Additionally, we assume transfer from n2 to n1 with a simple, Arrhenius-like thermal activation with a prefactor 1/τtr and activation energy Δε1:29

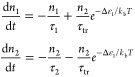graphic file with name nl1c04357_m001.jpg 1

The simple model fits the measured PL temporal evolution at different temperatures remarkably well (Figures 2a–c). For all temperatures, we obtained the best fit for initial populations of approximately 20% n1 and 80% n2. The exponential decay times are shown in Figure 2d, e, around 650 ps for τ1 and around 45 ps for τ2. These times vary by ±20% up to 300 K. Each of them comprises the radiative and nonradiative contributions τr and τnr. Hence, the small variations in τ1 and τ2, which both seem to peak around 200 K, may be due to small opposite trends of τr and τnr with temperature, resulting in weakly temperature-dependent PL quantum yields η1 = τnr1/(τnr1 + τr1) and η2 = τnr2/(τnr2 + τr2). τtr shown in Figure 2f is a prefactor to the Arrhenius term for the thermally activated transfer of excitons from population n2 to n1. The almost constant τtr around 80 ps confirms the assumed simple Arrhenius behavior with a fitted activation energy of Δε1 = 52 meV. A possible back transfer of population from n1 to n2 cannot be distinguished in our data due to the short lifetime of n2.

To deconvolve the spectral contribution of n1 and n2, we fitted the time-dependent fluorescence intensity I(E, t) at each wavelength as

graphic file with name nl1c04357_m002.jpg 2

where β1(T,E) = αη1(T)A1(E) and β2(T,E) = αη2(T)A2(E). Because all decay processes are exponential, the derivatives in eq 2 are proportional to the respective populations. Each recombining exciton emits a photon with a probability η1(T) and η2(T), respectively, corresponding to the temperature-dependent PL quantum yields of the two populations. Each emitted photon triggers a count on the detector with a probability α, which depends on the geometry of the sample and the measuring instrument and is assumed constant throughout all measurements. A1(E) and A2(E) are dimensionless functions whose integral over the whole spectral range is normalized to 1 and that reflects the shape of the PL spectra.

The fluorescence spectra of both populations η1(T)A1(E) and η2(T)A2(E), shown in Figure 3a–c are similar to single Gaussians with a width σ of around 100 meV. If we observed a simple relaxation or exciton migration within an energy distribution of recombination centers, this would always result in a red shift for increasing time t. In such a situation, our model would always yield A1(E) red-shifted relative to A2(E). However, A1(E), which is the spectrum of the longer-lived exciton species, is red-shifted relative to A2(E) at 100 and 323 K, whereas at 200 K it is blue-shifted. This confirms that we indeed observe two distinct populations of emitters with different temperature-dependent spectra.

Figure 3.

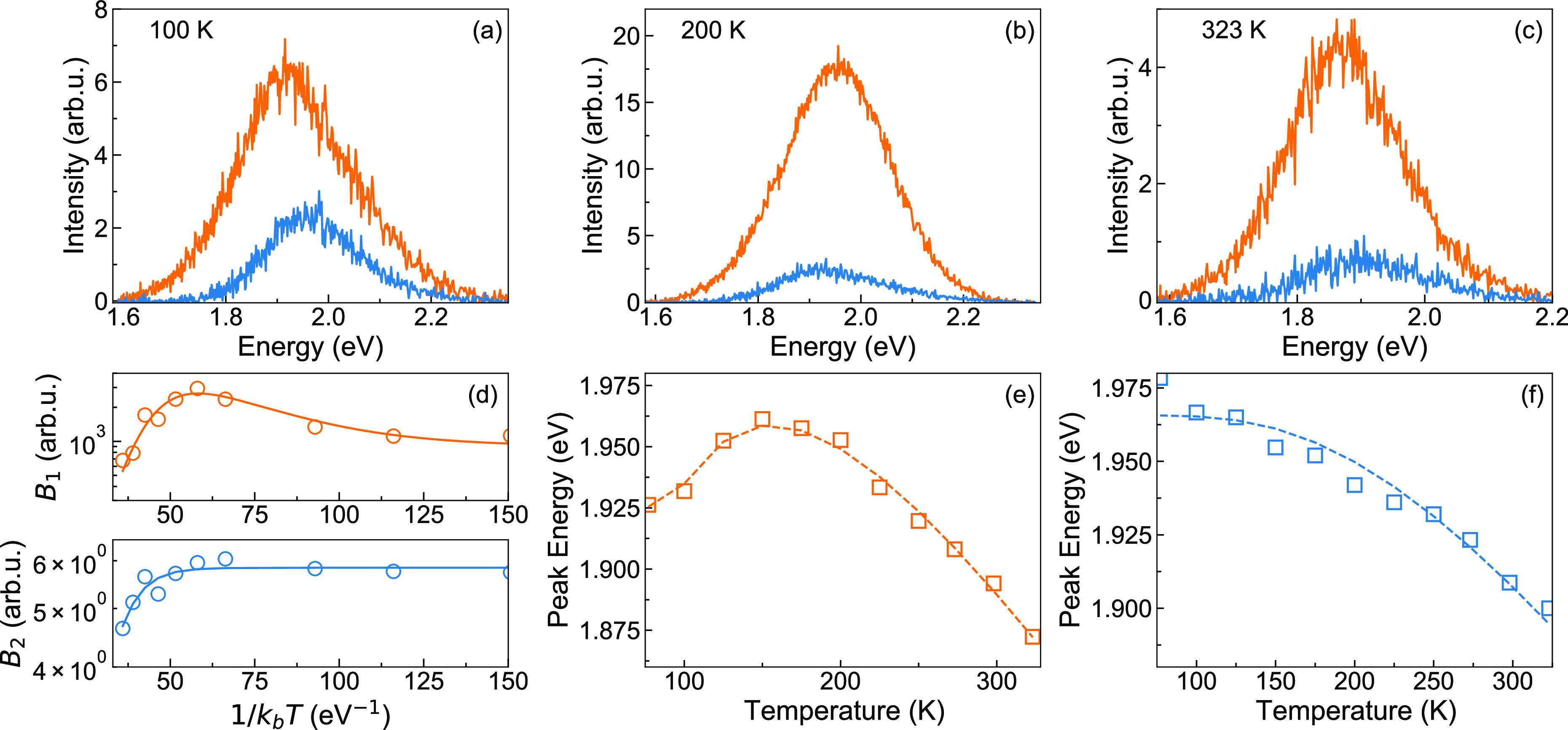
Figure 3

Open in a new tab

(a–c) Fluorescence spectra of long- (orange curve) and short-lived (blue curve) excitons at 100, 200, and 323 K, respectively. (d) Arrhenius plot of the integrated intensities B1 of long-lived centers (top panel, orange circles) together with the fit to eq 4 (solid orange curve) and B2 of short-lived centers (bottom panel, blue circles) together with the fit to eq 3 (solid blue curve). (e, f) Shift as a function of the temperature of long-lived centers (orange squares) together with the fit to eq 6 (dashed orange curve) and the short-lived centers (blue squares) together with the fit to eq 5 (dashed blue curve), respectively.

Given that the fluorescence spectra of the two populations as plotted in Figures 3c are proportional to the PL quantum yields, we plot B1(T) = ∫β1(T,E)dE and B2(T) = ∫β2(T,E)dE in Figure 3d to reveal additional nonradiative recombination channels. Remarkably, B2(T) suggests an Arrhenius-like thermally activated nonradiative channel:

graphic file with name nl1c04357_m003.jpg 3

where B2(0) is proportional to the quantum yield at 0 K, τnr2 is the Arrhenius prefactor of the additional thermally activated nonradiative channel, and Δεnr2 is the activation energy.

Fitting our results with eq 3, we obtain τnr2 ∼ 0.5 ps and Δεnr2 = 110 meV.

B1(T), on the other hand, starts to increase from 125 K, reaches its maximum value at 200 K, and then is quenched at higher temperatures. n1 is populated predominantly from n2 via thermal activation. Together with the introduction of an Arrhenius-type nonradiative term, this results in a more complex temperature-dependent quantum yield:

graphic file with name nl1c04357_m004.jpg 4

where B1(0) is proportional to the quantum yield at 0 K, Δε1 and Δεnr1 are the activation energies of the transfer from n2 to n1 and the nonradiative processes for n1, respectively, a1= τ1/τnr1, a2 = τ2/τtr, and c is the ratio between the initial populations n2 and n1.

This model is adapted from the one developed for a system including two emitter populations where (i) the carrier can recombine to the ground state from each of the populations; (ii) the species can migrate only from one population to the other and not vice versa.29 We note that this formalism has been developed for CW PL data. Because the CW PL intensity is proportional to the PL quantum yield, we can apply the same formalism to model our B1(T).

From the fit, we obtain Δε1 ∼ 45 meV, which is in good agreement with the value of 52 meV obtained from the fit of the spectrally integrated dynamics with eq 1. For the nonradiative processes, we extracted τnr1 ∼ 2 ps and an activation energy Δεnr1 ∼ 140 meV. The a2 ratio between τ2 and τtr extracted from the fit is ∼5, which is higher than the one obtained from the fit of the dynamics to eq 1 without this additional nonradiative process (a2 ∼ 2), whereas for c, we obtained n1 = 12% and n2 = 88%, in good agreement with the initial populations used to solve the rate equations (20%, 80%). The agreement between the fit parameters could be improved by iterating through eqs 1–4, but no added understanding would be gained. The activation energies of nonradiative processes of both n1 and n2 are ∼3 times that of the transfer from n2 to n1. It is plausible that this activation involves either excitation into different bands within the crowded band structure of GeCH3,17 from which nonradiative recombination occurs, or thermally activated exciton dissociation. In the latter case, the activation energy would be a measure of the exciton binding energy.

For further insight into the nature of the two exciton populations, we fit A1(E) and A2(E) with a Gaussian curve and plot the peak positions as a function of the temperature in Figure 3e, f. The A2(E) peak position follows the O’Donnell and Chen model,30 which is a refinement of the empirical Varshni equation31 and provides more insight into the electron–phonon coupling at the origin of the temperature-dependent bandgap:

graphic file with name nl1c04357_m005.jpg 5

where E0 is the PL peak at 0 K, S is the Huang–Rhys parameter, and ⟨Eph⟩ is the average energy of phonons coupling to the involved electronic levels. From the fit, we obtain E0 = 1.97 eV, S = 5.3, and ⟨Eph⟩ = 66 meV.

The temperature-dependent peak position of A1(E) exhibits first a blue shift from 77 to 150 K and a subsequent red shift from 175 to 323 K. Such “S shape” behavior has been previously reported for the high energy band of the GeCH3 PL emission,22 but it was not investigated in detail. The initial blue shift followed by a red shift of the emission peak energy has been observed in both CW and TRPL measurements for different semiconductor systems,29,32−39 including excitonic materials with a certain amount of disorder, such as organic–inorganic lead-halide perovskites,40,41 2D transition metal dichalcogenides,42−44 or phosphorene.45 It has been ascribed to thermal redistribution of excitons within an ensemble of width σ of localization centers with a mean activation energy ΔE. We obtain the temperature-dependent PL peak position:36

graphic file with name nl1c04357_m006.jpg 6
graphic file with name nl1c04357_m007.jpg 7

where the first two terms of eq 6 are the same as in eq 5. The third term accounts for exciton migration between RCs,35 with x(T) being the solution of eq 7. τ1 and τtr are temperature-dependent and are taken from panels d and f in Figure 2. From the fit reported in Figure 3e, we extracted E0 = 2.1 eV, S = 5.2, ⟨Eph⟩= 30 meV, ΔE = 37 meV, and, σ = 145 meV. Hence, we can conclude that the width of the distribution is similar to the width of the PL peaks and the activation energy for exciton migration is a fraction of this width.

Our results allow us to extract vital information about the nature of the two types of excitons at the origin of the observed fluorescence. The formalism of eqs 1 and 3–7 has been developed for arrays of two species of quantum wells (QWs),29,32−39 where both species of QWs show a certain distribution of exciton energy. Analogously, germanane provides a disordered energy landscape for exciton migration. The temperature-dependent A1(E) and A2(E) peak positions suggest that exciton migration is relevant only for the longer-lived exciton species.

Intriguingly, the temperature dependence of A1(E) and A2(E) as described in eqs 5–7 arises from coupling to phonons with mean energy ⟨Eph⟩ = 30 meV (240 cm–1) for A1(E) and ⟨Eph⟩ = 66 meV (530 cm–1) for A2(E), suggesting that the two excitons preferentially interact with different vibrational modes of the lattice. The presence of the 1.97 eV emission after annealing suggests that the residual water bears sufficient concentration to change the electronic structure locally and to provide a high density of recombination centers that enables exciton migration between them. Quantum chemical calculations17 have found a dense ensemble of electronic levels close to the valence and conduction band edges as a consequence of the small local structural distortions in each layer induced by the presence of H2O. We can thus assume two types of emitting excitons that have their electrons and/or holes in different levels from this ensemble. Our results prescribe the following requirements for the two emitting states: (i) both have an allowed transition to the ground state but not toward the band edges, (ii) one of them can transition to the other via thermal activation, and (iii) they couple with different lattice modes. Concerning the transition from n2 to n1, the energy difference between the A1(E) and A2(E) peaks in panels e and f in Figure 3 varies strongly with temperature. This variation is inconsistent with a simple Arrhenius-like thermally stimulated transfer with a fixed activation energy of 37 meV, as assumed in eq 1 and confirmed in Figure 3f. An alternative mechanism has recently been proposed for the interlayer exciton recombination in a heterostructure of two 2D monolayers.46 Low energy phonons periodically modulate the band structure between a direct and an indirect gap, leading to a recombination rate that has a temperature dependence very similar to an Arrhenius behavior with formal activation energy much higher than the energies of the phonons involved. We can assume a similar mechanism for the population transfer from n2 to n1 via a phonon-induced modulation of the band structure.

To summarize, we used TRPL spectroscopy at different temperatures to study the above bandgap fluorescence of GeCH3 samples. We find two distinct populations of emitting excitons localized at RCs within the intercalated water. Compared to 2D transition metal dichalcogenides, research on Xenes and Xanes is still in its infancy and the exciton binding energy, exciton transport mechanisms, trions, biexcitons, and higher many-body effects still need investigation, as well as fluorescence quantum yield and charge separation at interfaces as the groundwork for future applications in optoelectronics, light harvesting, and sensing.

Acknowledgments

E.C. and C.V. acknowledge financial support from MIUR PRIN aSTAR (Grant 2017RKWTMY), and from European Union’s Horizon 2020 research and innovation program through the MSCA-ITN SMART-X (GA 860553). Sample synthesis by W.L.B.H. and J.E.G. was supported by the Center for Emergent Materials, an NSF MRSEC, under award DMR-2011876. The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

E.C., J.E.G., C.D.A., and C.G. conceived the experiment. W.L.B.H. prepared the samples. S.S. performed the measurement. E.C., C.G., and S.S. analyzed the data. All the authors discussed the results and wrote the manuscript.

The authors declare no competing financial interest.

References

  1. Butler S. Z.; et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 2013, 7, 2898–2926. 10.1021/nn400280c. [DOI] [PubMed] [Google Scholar]
  2. Yan Y.; Xia B. Y.; Xu Z. C.; Wang X. Recent Development of Molybdenum Sulfides as Advanced Electrocatalysts for Hydrogen Evolution Reaction. ACS Catal. 2014, 4, 1693–1705. 10.1021/cs500070x. [DOI] [Google Scholar]
  3. Chhowalla M.; Jena D.; Zhang H. Two-dimensional semiconductors for transistors. Nat. Rev. Mater. 2016, 1, 16052. 10.1038/natrevmats.2016.52. [DOI] [Google Scholar]
  4. Molle A.; Goldberger J.; Houssa M.; Xu Y.; Zhang S.-C.; Akinwande D. Buckled two-dimensional Xene sheets. Nat. Mater. 2017, 16, 163–169. 10.1038/nmat4802. [DOI] [PubMed] [Google Scholar]
  5. Glavin N. R.; Rao R.; Varshney V.; Bianco E.; Apte A.; Roy A.; Ringe E.; Ajayan P. M. Emerging Applications of Elemental 2D Materials. Adv. Mater. 2020, 32, 1904302. 10.1002/adma.201904302. [DOI] [PubMed] [Google Scholar]
  6. Molle A.; Grazianetti C.; Tao L.; Taneja D.; Alam Md. H.; Akinwande D. Silicene, silicene derivatives, and their device applications. Chem. Soc. Rev. 2018, 47, 6370–6387. 10.1039/C8CS00338F. [DOI] [PubMed] [Google Scholar]
  7. Derivaz M.; Dentel D.; Stephan R.; Hanf M.-C.; Mehdaoui A.; Sonnet P.; Pirri C. Continuous Germanene Layer on Al(111). Nano Lett. 2015, 15 (4), 2510–2516. 10.1021/acs.nanolett.5b00085. [DOI] [PubMed] [Google Scholar]
  8. Grazianetti C.; Bonaventura E.; Martella C.; Molle A.; Lupi S. Optical Properties of Stanene-like Nanosheets on Al2O3(0001): Implications for Xene Photonics. ACS Appl. Nano Mater. 2021, 4 (3), 2351–2356. 10.1021/acsanm.0c03221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Jiang S.; Butler S.; Bianco E.; Restrepo O.; Windl W.; Goldberger J. E. Improving the stability and optoelectronic properties of germanane via one-step covalent methyl-termination. Nat. Commun. 2014, 5, 3389. 10.1038/ncomms4389. [DOI] [PubMed] [Google Scholar]
  10. Jiang S.; Arguilla M.; Cultrara N.; Goldberger J. Improved Topotactic Reactions for Maximizing Organic Coverage of Methyl Germanane. Chem. Mater. 2016, 28, 4735–4740. 10.1021/acs.chemmater.6b01757. [DOI] [Google Scholar]
  11. Jiang S.; Krymowski K.; Asel T.; Arguilla M. Q.; Cultrara N. D.; Yanchenko E.; Yang X.; Brillson L. J.; Windl W.; Goldberger J. E. Tailoring the Electronic Structure of Covalently Functionalized Germanane via the Interplay of Ligand Strain and Electronegativity. Chem. Mater. 2016, 28 (21), 8071–8077. 10.1021/acs.chemmater.6b04309. [DOI] [Google Scholar]
  12. Giousis T.; et al. Synthesis of 2D Germanane (GeH): a New, Fast, and Facile Approach. Ang. Chem. Int. Ed. 2021, 60, 360–365. 10.1002/anie.202010404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ng S.; Sturala J.; Vyskocil J.; Lazar P.; Martincova J.; Plutnar J.; Pumera M. Two-Dimensional Functionalized Germananes as Photoelectrocatalysts. ACS Nano 2021, 15 (7), 11681–11693. 10.1021/acsnano.1c02327. [DOI] [PubMed] [Google Scholar]
  14. Kouloumpis A.; Chatzikonstantinou A. V.; Chalmpes N.; Giousis T.; Potsi G.; Katapodis P.; Stamatis H.; Gournis D.; Rudolf P. Germanane Monolayer Films as Antibacterial Coatings. ACS Appl. Nano Mater. 2021, 4 (3), 2333–2338. 10.1021/acsanm.0c03149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Song Z.; Ang W. L.; Sturala J.; Mazanek V.; Marvan P.; Sofer Z.; Ambrosi A.; Ding C.; Luo X.; Bonanni A. Functionalized Germanene-Based Nanomaterials for the Detection of Single Nucleotide Polymorphism. ACS Appl. Nano Mater. 2021, 4 (5), 5164–5175. 10.1021/acsanm.1c00606. [DOI] [Google Scholar]
  16. Katayama Y.; Yamauchi R.; Yasutake Y.; Fukatsu S.; Ueno K. Ambipolar transistor action of germanane electric double layer transistor. Appl. Phys. Lett. 2019, 115, 122101. 10.1063/1.5094817. [DOI] [Google Scholar]
  17. Asel T. J.; Huey W. L. B.; Noesges B.; Molotokaite E.; Chien S.-C.; Wang Y.; Barnum A.; McPherson C.; Jiang S.; Shields S.; D’Andrea C.; Windl W.; Cinquanta E.; Brillson L. J.; Goldberger J. E. Influence of Surface Chemistry on Water Absorption in Functionalized Germanane. Chem. Mater. 2020, 32 (4), 1537–1544. 10.1021/acs.chemmater.9b04632. [DOI] [Google Scholar]
  18. Korn T.; Heydrich S.; Hirmer M.; Schmutzler J.; Schuller C. Low-temperature photocarrier dynamics in monolayer MoS2. Appl. Lett. 2011, 99, 102109. 10.1063/1.3636402. [DOI] [Google Scholar]
  19. Kozawa D.; Kumar R.; Carvalho A.; Kumar Amara K.; Zhao W.; Wang S.; Toh M.; Ribeiro R. M.; Castro Neto A. H.; Matsuda K.; Eda G. Photocarrier relaxation pathway in two-dimensional semiconducting transition metal dichalcogenides. Nature Commun. 2014, 5, 4543. 10.1038/ncomms5543. [DOI] [PubMed] [Google Scholar]
  20. Dal Conte S.; Trovatello C.; Gadermaier C.; Cerullo G. Ultrafast Photophysics of 2D Semiconductors and Related Heterostructures. Trends Chem. 2020, 2, 28–42. 10.1016/j.trechm.2019.07.007. [DOI] [Google Scholar]
  21. Bondelli G.; Sardar S.; Chiaravalli G.; Vurro V.; Paterno G. M.; Lanzani G.; D’Andrea C. Shedding Light on Thermally Induced Optocapacitance at the Organic Biointerface. J. Phys. Chem. B 2021, 125 (38), 10748–10758. 10.1021/acs.jpcb.1c06054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Livache C.; Ryan B. J.; Ramesh U.; Steinmetz V.; Gréboval C.; Chu A.; Brule T.; Ithurria S.; Prévot G.; Barisien T.; Ouerghi A.; Panthani M. G.; Lhuillier E. Optoelectronic properties of methylterminated germanane. Appl. Phys. Lett. 2019, 115, 052106. 10.1063/1.5111011. [DOI] [Google Scholar]
  23. Li Y.; Allegro I.; Kaiser M.; Malla A. J.; Richards B. S.; Lemmer U.; Paetzold U. W.; Howard I. A. Exciton versus free carrier emission: Implications for photoluminescence efficiency and amplified spontaneous emission thresholds in quasi-2D and 3D perovskites. Mater. Today 2021, 49, 35–57. 10.1016/j.mattod.2021.05.002. [DOI] [Google Scholar]
  24. Pulci O.; Gori P.; Marsili M.; Garbuio V.; Del Sole R.; Bechstedt F. Strong excitons in novel two-dimensional crystals: Silicane and germanane. Europhys. Lett. 2012, 98, 37004. 10.1209/0295-5075/98/37004. [DOI] [Google Scholar]
  25. Wei W.; Dai Y.; Huang B.; Jacob T. Many-body effects in silicene, silicane, germanene and germanane. Phys. Chem. Chem. Phys. 2013, 15, 8789–8794. 10.1039/c3cp51078f. [DOI] [PubMed] [Google Scholar]
  26. Chernikov A.; Berkelbach T. C.; Hill H. M.; Rigosi A.; Li Y. L.; Aslan O. B.; Reichman D. R.; Hybertsen M. S.; Heinz T. F. Exciton Binding Energy and Nonhydrogenic Rydberg Series in Monolayer WS2. Phys. Rev. Lett. 2014, 113, 076802. 10.1103/PhysRevLett.113.076802. [DOI] [PubMed] [Google Scholar]
  27. Ye Z. L.; Cao T.; O’Brien K.; Zhu H. Y.; Yin X. B.; Wang Y.; Louie S. G.; Zhang X. Probing excitonic dark states in single-layer tungsten disulphide. Nature 2014, 513, 214–218. 10.1038/nature13734. [DOI] [PubMed] [Google Scholar]
  28. Wang X.; Jones A. M.; Seyler K. L.; Tran V.; Jia Y.; Zhao H.; Wang H.; Yang L.; Xu X.; Xia F. Highly anisotropic and robust excitons in monolayer black phosphorus. Nat. Nanotechnol. 2015, 10, 517–521. 10.1038/nnano.2015.71. [DOI] [PubMed] [Google Scholar]
  29. Saint-Girons G.; Sagnes I. ″Photoluminescence quenching of a low-pressure metal-organic vapor-phase-epitaxy grown quantum dots array with bimodal inhomogeneous broadening″. J. Appl. Phys. 2002, 91, 10115–10118. 10.1063/1.1481968. [DOI] [Google Scholar]
  30. O’Donnell K. P.; Chen X. Temperature dependence of semiconductor band gaps. Appl. Phys. Lett. 1991, 58, 2924. 10.1063/1.104723. [DOI] [Google Scholar]
  31. Varshni Y. P. Temperature dependence of energy gap in semiconductor. Physica 1967, 34, 149. 10.1016/0031-8914(67)90062-6. [DOI] [Google Scholar]
  32. Kondow M.; Minagawa S.; Inoue Y.; Nishino T.; Hamakawa Y. Anomalous temperature dependence of the ordered Ga0.5In0.5P photoluminescence spectrum. Appl. Phys. Lett. 1989, 54, 1760. 10.1063/1.101283. [DOI] [Google Scholar]
  33. Cho Y.-H.; Gainer G. H.; Fischer A. J.; Song J. J.; Keller S.; Mishra U. K.; DenBaars S. P. S-shaped temperature-dependent emission shift and carrier dynamics in InGaN/GaN multiple quantum wells. Appl. Phys. Lett. 1998, 73, 1370. 10.1063/1.122164. [DOI] [Google Scholar]
  34. Bell A.; Srinivasan S.; Plumlee C.; Omiya H.; Ponce F. A.; Christen J.; Tanaka S.; Fujioka A.; Nakagawa Y. Exciton freeze-out and thermally activated relaxation at local potential fluctuations in thick AlxGa1-xN layers. J. Appl. Phys. 2004, 95, 4670. 10.1063/1.1689736. [DOI] [Google Scholar]
  35. Zeng H.; Li Z.; Cai W.; Liu P. Strong localization effect in temperature dependence of violet-blue emission from ZnO nanoshells. J. Appl. Phys. 2007, 102, 104307. 10.1063/1.2803712. [DOI] [Google Scholar]
  36. Wang Z.; Wang L.; Xing Y.; Yang D.; Yu J.; Hao Z.; Sun C.; Xiong B.; Han Y.; Wang J.; Li H.; Luo Y. Consistency on Two Kinds of Localized Centers Examined from Temperature-Dependent and Time-Resolved Photoluminescence in InGaN/GaN Multiple Quantum Wells. ACS Photonics 2017, 4, 2078–2084. 10.1021/acsphotonics.7b00516. [DOI] [Google Scholar]
  37. Chowdhury A. M.; Roul B.; Singh D. K.; Pant R.; Nanda K. K.; Krupanidhi S. B. Temperature Dependent S-Shaped Photoluminescence Behavior of InGaN Nanolayers: Optoelectronic Implications in Harsh Environment. ACS Appl. Nano Mater. 2020, 3, 8453–8460. 10.1021/acsanm.0c01930. [DOI] [Google Scholar]
  38. Li Q.; Xu S. J.; Cheng W. C.; Xie M. H.; Tong S. Y.; Che C. M.; Yang H. Thermal redistribution of localized excitons and its effect on the luminescence band in InGaN ternary alloys. Appl. Phys. Lett. 2001, 79, 1810. 10.1063/1.1403655. [DOI] [Google Scholar]
  39. Pecharroman-Gallego R.; Martin R. W.; Watson I. M. Investigation of the unusual temperature dependence of InGaN/GaN quantum well photoluminescence over a range of emission energies. J. Phys. D: Appl. Phys. 2004, 37, 2954–2961. 10.1088/0022-3727/37/21/003. [DOI] [Google Scholar]
  40. Baranowski M.; Urban J. M.; Zhang N.; Surrente A.; Maude D. K.; Andaji-Garmaroudi Z.; Stranks S. D.; Plochocka P. Static and Dynamic Disorder in Triple-Cation Hybrid Perovskites. J. Phys. Chem. C 2018, 122, 17473–17480. 10.1021/acs.jpcc.8b05222. [DOI] [Google Scholar]
  41. Shibata K.; Yan J.; Hazama Y.; Chen S.; Akiyama H. Exciton Localization and Enhancement of the Exciton – LO Phonon Interaction in a CsPbBr3Single Crystal. J. Phys. Chem. C 2020, 124, 18257–18263. 10.1021/acs.jpcc.0c06254. [DOI] [Google Scholar]
  42. Yan T.; Qiao X.; Liu X.; Tan P.; Zhang X. Photoluminescence properties and exciton dynamics in monolayer WSe2. Appl. Phys. Lett. 2014, 105, 101901. 10.1063/1.4895471. [DOI] [Google Scholar]
  43. Masenda H.; Schneider L. M.; Adel Aly M.; Machchhar S. J.; Usman A.; Meerholz K.; Gebhard F.; Baranovskii S. D.; Koch M. Energy Scaling of Compositional Disorder in Ternary Transition-Metal Dichalcogenide Monolayers. Adv. Electron. Mater. 2021, 7, 2100196. 10.1002/aelm.202100196. [DOI] [Google Scholar]
  44. Borys N. J.; Barnard E. S.; Gao S.; Yao K.; Bao W.; Buyanin A.; Zhang Y.; Tongay S.; Ko C.; Suh J.; et al. Anomalous Above-Gap Photoexcitations and Optical Signatures of Localized Charge Puddles in Monolayer Molybdenum Disulfide. ACS Nano 2017, 11, 2115–2123. 10.1021/acsnano.6b08278. [DOI] [PubMed] [Google Scholar]
  45. Pei J.; Gai X.; Yang J.; Wang X.; Yu Z.; Choi D.-Y.; Luther-Davies B.; Lu Y. Producing air-stable monolayers of phosphorene and their defect engineering. Nature Comm. 2016, 7, 10450. 10.1038/ncomms10450. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wang Z.; et al. Phonon-Mediated Interlayer Charge Separation and Recombination in a MoSe2/WSe2Heterostructure. Nano Lett. 2021, 21, 2165–2173. 10.1021/acs.nanolett.0c04955. [DOI] [PubMed] [Google Scholar]

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES